1 Introduction

The Sandia Fracture Challenge series are organized by Sandia National Laboratories to evaluate existing models in validation scenarios that approximate the conditions seen in practical applications. In the 2nd Challenge (SFC2), participants are asked to provide the prediction for load-deformation behavior and crack path of a specially designed sample. They shall select a suitable approach and calibrate model parameters with the given experimental results of tensile tests and V-notch tests under quasi-static and dynamic loading conditions. With a calibrated set of parameters at hand, they shall afterwards perform the blind prediction. Thus, individual participating teams are offered a blind prediction environment to evaluate the strengths and weaknesses of their methodologies. SFC2 was issued on 30th May 2014 and the due date of final prediction was 1st Nov. 2014. In total 14 teams supplied their predictions. The detailed comparison and discussion for the results from 14 teams are presented in the leading paper of SFC2 (Boyce et al. 2016). After blind prediction, we improved the parameter calibration scheme and modified boundary conditions applied in FE simulation for a better representation of the experimental facts.

For ductile materials, various types of damage mechanics models have been developed to predict the ductile fracture for decades. In general, the ductile damage models are divided into two groups, coupled and uncoupled models (Besson 2009). In the uncoupled models, the flow behavior is not influenced by the damage accumulation and normally a fracture strain criterion with a weighted function of the stress state is defined for the appearance of fracture. Many models have been formulated with different weighting functions with respect to the stress state (Bao and Wierzbicki 2004; Hancock and Brown 1983; Johnson and Cook 1985; McClintock 1968; Rice and Tracey 1969). The recent development in the last decade strongly focused on the Lode angle effect on the failure strain (Bai and Wierzbicki 2008, 2010; Barsoum and Faleskog 2007; Dunand et al. 2012; Gao et al. 2009; Lou et al. 2013; Luo et al. 2012; Mirone and Corallo 2010).

The coupled models, in contrast, incorporate the effect of the accumulated damage into the yield function. Two different approaches have been developed for the last decades, the micromechanically motivated Gurson-like models and the phenomenological continuum damage mechanics (CDM) model derived from a consistent thermodynamics framework. The Gurson-like models (Gurson 1977; Tvergaard 1981, 1982; Tvergaard and Needleman 1984) are derived based on the pioneering studies by McClintock (1968) and Rice and Tracey (1969) on the analytical derivation of the growth of cylindrical and spherical voids in a rigid plastic matrix. Further modifications (Gologanu et al. 1993, 1994, 1997; Kailasam and Castaneda 1998; Nahshon and Hutchinson 2008; Nielsen and Tvergaard 2009, 2010; Xue 2008) were introduced to account for the void shape change, void rotation effect and Lode angle effect. The continuum damage mechanics (CDM) based models (Kachanov 1999; Lemaitre 1985, 1992), do not explicitly interpret the underlying microstructural failure mechanisms as the damage variable, but treat damage evolution in a macroscopic and phenomenological way (Münstermann et al. 2012a). CDM based models have been continuously developed and used in the metal society for damage and fracture predictions (de Souza Neto 2002; Lubarda and Krajcinovic 1995; Teng 2008; Voyiadjis and Deliktas 2000; Voyiadjis and Park 1999). More advanced CDM models employ a tensorial damage variable instead of a scalar to account for damage anisotropy (Brunig et al. 2008; Chow and Jie 2009; Chow et al. 2003; Chow and Yang 2004; Chow et al. 2001; Niazi et al. 2012, 2013).

By taking the advantages of both uncoupled models (high accuracy and ease of formulation and material parameter calibration) and coupled models (integration of damage to material behavior), Lian et al. (2013) proposed a hybrid damage plasticity model that combines a phenomenological criterion for damage initiation related to the microstructure-level degradation of materials, and a CDM based damage evolution for progressive damage accumulation till final fracture. The damage initiation criterion relies on the Bai–Wierzbicki (BW) uncoupled damage model (Bai and Wierzbicki 2008), thus it is also referred to as the modified Bai–Wierzbicki (MBW) model (Lian et al. 2015). With this modelling approach, the multiscale characterization of both damage and fracture can be realized. As the damage initiation is related to the microstructure of materials, the damage initiation locus (DIL) and its stress-state dependency can be bridged from the mesoscale simulations accounting for the microstructural inhomogeneity (Lian et al. 2014). The significance of the model lies in the full exploitation of the material properties in the components manufacturing as the damage initiation gives an indication of the forming limit of materials.

Johnson–Cook model (1985) is widely and successfully applied for Ti–6Al–4V and various other metallic materials under high temperature and dynamic loading conditions. In Johnson–Cook model, the temperature and strain rate effects are described independently from each other and influence of strain on these effects is neglected. The model takes the advantage of simple parameter calibration procedures and is easy to be implemented in the numerical investigations. Zerilli and Armstrong (1987) investigated metallic materials with different crystal structures and proposed different equations for BCC and FCC materials. Their results show that the hardening behavior is barely influenced by the strain rate for BCC materials. While for FCC materials, the influence of strain rate on hardening should be accounted. El-Magd et al. (2006) later investigated the strain rate and temperature effects for Ti–6Al–4V and another two metallic materials. They addressed the hardening mechanisms under different strain rate ranges and described the flow curves for the materials over wide ranges of temperature and strain rate. On the basis of the investigation of El-Magd et al. (2006), Muenstermann et al. (2013) proposed an approach to describe and calibrate the correction factors for temperature and strain rate effects and Münstermann et al. (2012b) in machining process and dynamic mechanical testing.

In this study on the second Sandia Fracture Challenge (SFC2), the MBW model is used for the reaction force and fracture prediction under slow loading rate and the extended MBW model incorporating the effects of strain rate and temperature is applied to the prediction under fast loading rate. In the following sections, the formulation of the model is introduced in detail in Sect. 2. Section 3 briefly introduces the investigated material. The material parameter calibration of the model and the validation of the calibrated parameter set are described in detail in Sect. 4. With the calibrated material parameters, the fracture predictions of the challenge tests under both slow and fast loading rates are given in Sect. 5. In this work, the presented improved prediction is compared with the original contribution that was submitted to the SFC2 in Sect. 6. In Sect. 7, the main conclusions are drawn.

2 The MBW model

As a coupled model, the Young’s modulus in the MBW model is calculated as:

$$\begin{aligned} E^{*}=\left( {1-D} \right) \cdot E, \end{aligned}$$
(1)

where, E and \(E^{*}\) are the Young’s modulus without and with the coupled damage.

The yield potential of the model is given in Eq. 2. It is noted that the coupling effect of the damage into the yield function is only valid once the damage initiation criterion is fulfilled.

$$\begin{aligned} \varPhi= & {} \bar{\sigma } - \left( {1 - D} \right) \cdot \sigma _{{\mathrm{y}}} \left( {\bar{\varepsilon }^\mathrm{p} } \right) \cdot f_{{\text {s}}} \left( {\eta , \bar{\theta }} \right) \nonumber \\&\cdot f_{{\text {T}}} \left( T \right) \cdot f_\mathrm{e} \left( {\dot{\varepsilon }} \right) \le 0, \end{aligned}$$
(2)

In Eq. 2, D is the damage quantity representing the damage-induced softening, \( \sigma _{{\text {y}}} \left( {\bar{\varepsilon }^{{\text {p}}} } \right) \) stands for the flow curve under the reference condition, in the context, i.e. quasi-static tensile test at room temperature; \(f_\mathrm{s} \left( {\eta ,\bar{{\theta }}} \right) \), \(f_\mathrm{T} \left( T \right) \) and \(f_\mathrm{e} \left( {\dot{\varepsilon }} \right) \) are the correction functions of stress state, temperature and strain rate to the flow stress, respectively.

The isotropic yielding and hardening are employed based on the negligible difference between the flow responses from tensile tests along rolling and transverse direction for the investigated material according to experimental data from Sandia, as shown in Fig. 2 of the lead article (Boyce et al. 2016). However, a more general plasticity model (Bai and Wierzbicki 2008) to account for the stress state effect on yielding is employed, as defined in Eq. 3.

$$\begin{aligned} f_\mathrm{s} \left( {\eta ,\hbox {}\bar{{\theta }}} \right)= & {} \left[ {1-c_\mathrm{\eta } \cdot \left( {\eta -\eta _0 } \right) } \right] \nonumber \\&\cdot \left[ {c_\mathrm{\theta }^\mathrm{s} +\left( {c_\mathrm{\theta }^\mathrm{{ax}} -c_\mathrm{\theta }^\mathrm{s} } \right) \cdot \left( {\lambda -\frac{\lambda ^{m+1}}{m+1}} \right) } \right] . \end{aligned}$$
(3)

In Eq. 3, \(c_\mathrm{\eta } \) and \(\eta _0 \) are the material parameters to include the effect of stress triaxiality; \(c_\mathrm{\theta }^\mathrm{s} , c_\mathrm{\theta }^{\mathrm{ax}} , \lambda \) is a function of the Lode angle (see Eq. 8) and m is the material parameter to consider the effect of the Lode angle.

The stress state can be presented by stress triaxiality \(\eta \) representing hydrostatic pressure and Lode angle \(\theta \) that related to the third deviatoric stress invariant in the principal stress space as illustrated in Fig. 1. The stress triaxiality \(\eta \) and the normalized Lode angel \(\bar{{\theta }}\) are defined by Eqs. 4 and 5; the relation between Lode angle \(\theta \) and the normalized Lode angel \(\bar{{\theta }}\) is shown in Eq. 6:

$$\begin{aligned}&\eta =\frac{I_1 }{3\sqrt{3J_2 }}, \end{aligned}$$
(4)
$$\begin{aligned}&\bar{{\theta }}=1-\frac{2}{\pi }\cos ^{-1}\left( {\frac{3\sqrt{3}}{2}\frac{J_3 }{J_2^{3/2} }} \right) , \end{aligned}$$
(5)
$$\begin{aligned}&\bar{{\theta }} =1-\frac{3}{2}\pi \theta . \end{aligned}$$
(6)

In these equations, \(I_1 \) is the first invariant; \(J_2 \) and \(J_3 \) are the second and third invariants of deviatoric stress, respectively.

Fig. 1
figure 1

Schematic diagram of a stress state (Lian et al. 2013)

Full size image

More specifically, the parameters related to Lode angle \(c_\mathrm{\theta }^{\hbox {ax}} \) and \(\lambda \) are defined as:

$$\begin{aligned}&c_{\theta }^{\mathrm{ax}} =\left\{ {{\begin{array}{ll} {c_{\theta }^\mathrm{t} ,}&{} \quad {\bar{{\theta }}\ge 0} \\ {c_{\theta }^\mathrm{c} ,}&{}\quad {\bar{{\theta }}<0} \\ \end{array} }} \right. , \end{aligned}$$
(7)
$$\begin{aligned}&\lambda =\frac{\sqrt{3}}{2-\sqrt{3}}\left[ {\sec \left( {\frac{\bar{\theta } \pi }{6}} \right) -1} \right] . \end{aligned}$$
(8)

In Eqs. 3 and 7, \(c_\mathrm{\theta }^\mathrm{s}, c_\mathrm{\theta }^\mathrm{t} \) and \(c_\mathrm{\theta }^\mathrm{c} \) are the correction parameters corresponding to the stress states of shear, tension and compression, respectively.

The convexity of the yield locus coupled with \(f_\mathrm{s} \left( {\eta ,\bar{{\theta }}} \right) \) has been investigated by Lian et al. (2013).

In addition, the influences of strain rate and temperature on flow stress are also defined. A dimensionless factor, the ratio of the yield stress to the reference yield stress, is added to the yield potential function. Based on the functions given by Muenstermann et al. (2013), these factors are expressed as following:

$$\begin{aligned}&f_\mathrm{T} \left( T \right) =C_1^\mathrm{T} \cdot \hbox {exp}\left( {C_2^\mathrm{T} \cdot T} \right) +C_3^\mathrm{T} , \end{aligned}$$
(9)
$$\begin{aligned}&f_\mathrm{e} \left( {\dot{\varepsilon }} \right) = C_{1}^{{{{\dot{\varepsilon }}}}} \cdot {\text {ln}}\dot{\bar{\varepsilon }}^\mathrm{p} + C_{2}^{{{{\dot{\varepsilon }}}}} , \end{aligned}$$
(10)

in which, \(\dot{\bar{{\varepsilon }}}^{\mathrm{p}}\) is the plastic strain rate, and \(C_1^\mathrm{T} -C_3^\mathrm{T} \) and \(C_1^{\dot{\varepsilon }} -C_2^{{\dot{\varepsilon }}} \) are the model parameters that need to be calibrated from experimental results with varied testing temperatures and strain rates.

It is also noted that under the adiabatic condition, the temperature evolution is defined according to Eq. 11:

$$\begin{aligned} \dot{T} = \frac{{\delta \cdot \bar{\sigma } \cdot \dot{\bar{\varepsilon }}^{{\mathrm{p}}} }}{{\rho \cdot C_{{\mathrm{p}}} }}, \end{aligned}$$
(11)

where, \(\delta \) is the specific heat fraction, \(\rho \) is material density, and \(C_\mathrm{p} \) is specific heat capacity.

For damage modelling, a discontinuous damage evolution law is assumed. The initiation of damage is not associated with the beginning of plastic deformation but with a characteristic strain-based criterion depending on the stress state as represented in terms of stress triaxiality and normalized Lode angle. Afterwards, a simple linear evolution of the damage quantity is assumed with respect to the equivalent plastic strain, and the rate of damage evolution is governed by the energy dissipation after damage initiation.

As soon as the damage value reaches the critical value \(D_{\mathrm{crit}} \), the separation of the material occurs. The element deletion technique implemented in ABAQUS/Explicit is used to simulate the crack propagation. Equation 12 summarizes the complete damage evolution law:

$$\begin{aligned} D = \left\{ {\begin{array}{ll} {0,} &{}\quad {\bar{\varepsilon }^{\mathrm{{p}}} \le \bar{\varepsilon }_{\mathrm{{i}}}^{\mathrm{{p}}} } \\ {\int _{{\bar{\varepsilon }_{\mathrm{{i}}}^{\mathrm{{p}}} }}^{{\bar{\varepsilon }^{\mathrm{{p}}} }} \frac{{\sigma _{{{\text {y}}0}} }}{{G_{\mathrm{{f}}} }}{\text {d}}\bar{\varepsilon }^{\mathrm{{p}}} ,} &{}\quad {\bar{\varepsilon }_{\mathrm{{i}}}^{\mathrm{{p}}} < \bar{\varepsilon }^{\mathrm{{p}}} < \bar{\varepsilon }_{\mathrm{{f}}}^{\mathrm{{p}}} } \\ {D_{{{\text {crit}}}} ,} &{} \quad {\bar{\varepsilon }_{\mathrm{{f}}}^{\mathrm{{p}}} \le \bar{\varepsilon }^{\mathrm{{p}}} } \\ \end{array} } \right. \end{aligned}$$
(12)

where, \(G_\mathrm{f} \) is the energy dissipation parameter, \(\sigma _\mathrm{{y}0} \) is the yield stress at damage initiation considering the effects of temperature and strain rate, and \(\bar{{\varepsilon }}_\mathrm{f}^\mathrm{p} \) is the failure strain. The stress-state dependent damage initiation strain \(\bar{\varepsilon }_\mathrm{i}^\mathrm{p} \) is defined as:

$$\begin{aligned} \bar{\varepsilon }_{{\text {i}}}^{{\text {p}}} = \left[ {C_{1} e^{{ - C_{2} \eta }} - C_{3} e^{{ - C_{4} \eta }} } \right] \bar{\theta }^{2} + C_{3} e^{{ - C_{4} \eta }} , \end{aligned}$$
(13)

where, \(C_1 -C_4 \) are material parameters for DIL.

The critical damage value \(D_\mathrm{{crit}} \) is assumed to be a function of stress triaxiality and normalized Lode angle parameter as well. In the frame of SFC2, only the results of the tensile test and the V-notch test, which represent the loading condition of tension and shear respectively, are given. Thus, \(D_\mathrm{{crit}} \) dependence on the stress triaxiality is not taken into account due to the lack of experimental data.

The damage evolution by nature is not a linear process. Based on the damage evolution measurements for a copper 99.9 % material (Lemaitre 1984) and a dual-phase steel (Maire et al. 2008), it can be seen that the proposed concept consisting of a damage initiation and a linear evolution law gives a very good approximation of the damage process in reality for both materials. It is also assumed by several researchers that there exists a threshold value of the plastic strain, under which damage is not accumulated (Borvik et al. 2001; Bouchard et al. 2011). However, it is also proven by Lian et al. (2013) that the damage initiation strain is dependent on the stress states. Therefore, a general form of the damage initiation strain dependent on stress triaxiality and Lode angle parameter is used in the model. In addition to the significance to the material design application, the whole concept is also user-friendly for material parameter calibration, because the damage initiation strains can be experimentally measured and no iterative fitting is required. Besides the damage initiation parameters, there is also only one parameter required for the linear damage evolution law.

The model is implemented into a user material subroutine (VUMAT) for Abaqus/Explicit with the small strain formulation for stress updating procedure and all the simulation results presented in this investigation are conducted in this environment. The MBW model has been also implemented into a UMAT subroutine (Novokshanov et al. 2015).

3 Material

The material Ti–6Al–4V investigated in the SFC2 is one of the most widely used titanium alloys because of its excellent combination of strength and toughness together with extraordinary corrosion resistance. It contains 6 wt% Al and 4 wt% V and the microstructure matrix consists of \(\alpha \) phase, which has a hexagonal close-packed (HCP) crystal structure, and \(\beta \) phase, which has a body-centered cubic (BCC) crystal structure. The thermal conductivity of Ti–6Al–4V is around 6 W/(m K), which is relatively low compared to other metallic materials. The yield stress of the investigated material is around 980 MPa and the fracture elongation is 17 %. The plastic behavior of the material shows a tension–compression–shear asymmetry of yielding according to the set of experimental data provided by Sandia, which partially justifies the selection of a stress-state dependent plasticity model, but it needs to be further validated. The provided experimental data shows a negligible difference between the flow stress from tensile tests in rolling and transverse directions, but anisotropy may be not revealed by those material directions (Pack and Roth 2016).

4 Parameter calibration

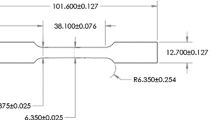
The proposed model involves a large number of material parameters for accurate description of material behavior. For a complete material parameter calibration procedure, several types of tests and specimens are required as described by Lian et al. (2013, 2015) and Buchkremer et al. (2014). Within the frame of the SFC2, experimental results from tensile tests and V-notch tests are provided for parameter calibration of the material model. The tensile tests and V-notch tests were loaded by a servo-hydraulic load frame under two loading rates: 0.0254 and 25.4 mm/s. With the loading direction along the rolling direction, five and three repetitions of the tensile tests are conducted for the slow and fast loading rate separately; for the V-notch tests under each loading rate two replicates are performed. With a measurement length of 38.1 mm for the tensile tests, the strain rates for the two loading rates are 0.00067 and \(0.67\, \hbox {s}^{-1}\), respectively. The geometries of the samples are shown in Fig. 2.

Fig. 2
figure 2

Sample geometries for parameter calibration a tensile specimen and b V-notch specimen (units in mm)

Full size image
Fig. 3
figure 3

a Flow curve for Ti–6Al–4V and its extrapolation, b force–displacement curves of tensile tests and the elastic–plastic simulation with the extrapolated flow curve

Full size image

Symmetric FE models of both tests are built for parameter calibration of the MBW model. A mesh size of 0.2 mm is applied in the strain localization area of the models in order to compromise the computational accuracy and computational resources. An 8-node linear brick element with reduced integration formulation (C3D8R) is applied in the simulations.

4.1 Plasticity properties

To achieve precise description of material behavior, the accurate calibration of plasticity properties is essential. The flow stress with strain hardening is derived from the force–displacement response of the quasi-static tensile test (loading rate 0.0254 mm/s) under room temperature. The Ludwik approach is employed for the extrapolation of the flow curve, as shown in following:

$$\begin{aligned} \sigma _{\mathrm{{y}}} \left( {\bar{\varepsilon }^\mathrm{{p}}} \right) = \sigma _{0} + K_{2} {{\bar{\varepsilon }}{}^\mathrm{p}}^{n_{2}}, \end{aligned}$$
(14)

where, \(\sigma _0, K_2\) and \(n_2 \) are constants.

Because the anisotropic properties are not considered in the presented damage mechanics model, only the tensile tests with samples taken along rolling direction are evaluated. In Fig. 3a, only the flow curve of Ti–6Al–4V (the blue dash line) derived from the tensile test RD5 under the loading rate of 0.0254 mm/s in the rolling direction is shown, since the flow curves derived from the replicates are identical to each other, and according to Eq. 14 the flow curve is extrapolated till large plastic strain (the red solid line). Figure 3b shows the elastic–plastic simulation results of the tensile test with the extrapolated flow curve.

Fig. 4
figure 4

a Experimental set-up of the V-notch test and b the boundary conditions in FE model

Full size image

The presented hybrid damage mechanics model considers the effect of states of stress on flow surface. By varying the notch radius on the notched sample different stress triaxialities can be achieved during the tensile test (Bai and Wierzbicki 2008). In this work, only flat samples shown in Fig. 2a were tested. Given no further information of tensile tests with notched samples, the influence of stress triaxiality on flow behavior is not taken into consideration. Thus, the material parameter \(c_{\eta } \) is set as zero. Since the flow stress from tensile tests is taken as the reference flow stress, \(c_{\theta }^\mathrm{t} \) is defined as one.

The shear-stress-state related material constant \(c_\mathrm{\theta }^\mathrm{s} \) is iteratively calibrated from the V-notch test with simulations by comparing the force–displacement curves in the plastic deformation range. Figure 4a shows the experimental set-up of the V-notch tests. In total 16 bolts were applied on the grips to minimize the rotation of the specimen during the tests. However, in FE simulation it is found that the slip between the V-notch sample and the grips cannot be overlooked. In order to perform a precise modelling of the V-notch test, the boundary conditions that define the displacement control in the V-notch test simulation are investigated. The displacement \(\hbox {d}_{1}\) and displacement \(\hbox {d}_{2}\) are defined to be parallel and perpendicular to the loading direction, respectively. The schematic sketch of the defined boundary condition is illustrated in Fig. 4b. The ratio of \(\hbox {d}_{1 }\) to \(\hbox {d}_{2}\) is adjusted to confirm the yield point from simulation to the experimental results. Figure 5 indicates that with \(\hbox {d}_{1}/\hbox {d}_{2 }= 2/1\) the simulated elastic behavior and the yielding point agree with that of the force–displacement curves from the V-notch test (VP6).

Fig. 5
figure 5

The comparison of force–displacement curves from simulations with different boundary conditions under the loading rate of 0.0254 mm/s

Full size image
Fig. 6
figure 6

Comparison of the local principal strains in V-notch specimen under the loading rate of 0.0254  mm/s

Full size image
Fig. 7
figure 7

Fractographies of the tensile tests along rolling direction with loading rate of a 0.0254  mm/s and b 25.4  mm/s

Full size image

In order to further validate the boundary condition used in V-notch simulation, the local strain response of the V-notch sample is also investigated. Stacked rosette strain gages with a gauge length of 3.18 mm were fixed to the center of the V-notch specimens, as shown in Fig. 6a, by which the principal strains \(\varepsilon _{1,2} \) can be obtained according to the derivation of Mohr’s strain circle:

$$\begin{aligned} \varepsilon _{1,2} =\frac{\varepsilon _x +\varepsilon _y }{2}\pm \frac{\sqrt{2}}{2}\sqrt{\left( {\varepsilon _x +\varepsilon _{45^{\circ }} } \right) ^{2}+\left( {\varepsilon _y +\varepsilon _{45^{\circ }} } \right) ^{2}}, \end{aligned}$$
(15)

where, \(\varepsilon _x , \varepsilon _y\) and \(\varepsilon _{45^{\circ }} \) are the strains along the S1, S3 and S2 directions (see Fig. 6a) respectively in this work.

Correspondingly, the maximum and minimum principal strains, \(\varepsilon _\mathrm{{max}} \) and \(\varepsilon _\mathrm{{min}} \), are extracted from the center element of the V-notch simulation. Figure 6b shows that with the boundary condition of \(\hbox {d}_{1}/\hbox {d}_{2 }= 2/1\) the simulated principal strain response over displacement confirms the strain gauge measurement.

With the previously determined boundary condition the Lode angle related material parameters that influence the plasticity are calibrated and summarized in Sect. 4.4.

4.2 Damage parameters

The fractographies of the specimens from tensile tests and V-notch tests demonstrate a typical ductile fracture, as illustrated in Figs. 7 and 8.

For the description of ductile damage, a coupled damage evolution law is applied in the MBW model as mentioned in Sect. 2. A stress-state dependent damage initiation strain \(\bar{\varepsilon }_\mathrm{i}^\mathrm{p} \), the energy dissipation parameter \(G_\mathrm{f} \) and the critical damage value \(D_\mathrm{{crit}} \) are required for the prediction of ductile fracture.

Fig. 8
figure 8

Fractographies of V-notch samples with loading rate a 0.0254 mm/s and b 25.4 mm/s

Full size image

4.2.1 Ductile DIL

The DIL is usually calibrated by tensile tests with the direct current potential drop (DCPD) method. With varied sample geometries, different stress states can be achieved during tensile tests (Lian et al. 2013). However, in the frame of SFC2 the required experimental data are not available. In the authors’ institute a database contains a collection of calibrated material parameters and the corresponding experimental results. According to the in-house experimental experience, the authors adjusted the DIL to achieve the best agreement to the force–displacement curves. Figure 9 illustrates the DIL of Ti–6Al–4V in the space of stress triaxiality and normalized Lode angle. The calibrated constants \(C_1 -C_4 \) for the mathematic expression of the DIL (Eq. 12) are summarized in Sect. 4.4.

Fig. 9
figure 9

Ductile DIL of Ti–6Al–4V

Full size image

4.2.2 Dissipation energy parameter and critical damage value

The energy dissipation parameter \(G_\mathrm{f} \) controls the degeneration of the material stiffness and needs to be calibrated as a material constant. From the existing experimental data, the failure strain is considered as stress-state dependent. Since no experimental data is provided to evaluate stress triaxiality effects, the critical damage value \(D_\mathrm{{crit}} \) that determines the separation of material is formulated as a function of normalized Lode angle parameter:

$$\begin{aligned} D_\mathrm{{crit}} =C_\mathrm{{cr}}^1 \cdot \bar{{\theta }}^{2}+C_\mathrm{{cr}}^2, \end{aligned}$$
(16)

where, \(C_\mathrm{{cr}}^1 \) and \(C_\mathrm{{cr}}^2\) are the material parameters for the fracture locus.

To determine those parameters, an iterative calibrating procedure is adopted. \(G_\mathrm{f}, C_\mathrm{{cr}}^1 \) and \(C_\mathrm{{cr}}^2 \) are varied until good agreement of the fracture points from simulations and experiments for both tensile and V-notch tests with the loading rate of 0.0254 mm/s, i.e. under the quasi-static condition, are achieved, as shown in Fig. 10.

Fig. 10
figure 10

Force–displacement curves under quasi-static condition from a tensile test and b V-notched test

Full size image

4.3 Temperature and strain rate parameters

The database of authors’ institute also provides the effects of temperature on the flow behavior of the titanium alloy Ti–6Al–4V, in which quasi-static tensile tests were conducted at varied temperatures from \(-60\) to \(160\,^{\circ }\hbox {C}\). The flow curves under different temperatures were derived and the flow stresses at the true strain of 0.04 were taken. Accordingly, the temperature dependent dimensionless factor on flow stress \(f\left( T \right) \) can be determined with the isothermal assumption (Eq. 9).

Fig. 11
figure 11

The influence of a temperature and b strain rate on flow stress and their fittings according to Eqs. 9 and 10

Full size image

In the SFC2, the experimental results for two loading rates are supplied. However, due to the geometries of V-notch sample and SFC2 sample that is introduced in the Sect. 5, the plastic deformation within the specimens during test is not uniform. For the simulations of the tests with the loading rate of 0.0254 mm/s, the tests can be seen as quasi-static. However, with the loading rate of 25.4 mm/s, the strain rate variation within the specimen due to the non-uniform distribution of plastic strain should not be neglected. Therefore, a consideration of the strain rate effect on flow curve is necessary.

For high strain rate tests, the isothermal assumption for quasi-static condition is not valid for Ti–6Al–4V due to its low thermal conductivity. Given the short testing time, the large plastic deformation during the high speed tensile test and the low thermal conductivity of the investigated material, the adiabatic condition is then assumed. With only tests under two loading rates provided in frame of SFC2, the adiabatic assumption for the tests under high loading rate is more realistic. Besides, by considering the heat transfer in FE simulation the required computational resources are dramatically increased. Thus, the adiabatic assumption is also a compromise in order to demonstrate the effect of temperature increase in dynamic loading without increasing too much computational cost. To determine strain rate influence on flow behavior, the flow curve determined from the tensile test \( \sigma _{\mathrm{{y}}}^{*} \left( {\bar{\varepsilon }^{\mathrm{{p}}} } \right) \) with the loading rate of 25.4 mm/s is firstly applied in simulations to identify the temperature increase \(\Delta T\) within the specimen at the equivalent plastic strain of 0.04 according to Eq. 11. The corresponding correction factor of temperature \(f_T \left( {T_0 +\Delta T} \right) \) can be then determined by Eq. 9. Consequently, the increase of the flow stress due to dynamic loading \(f_e \left( {\dot{\varepsilon }} \right) \) can be calculated by eliminating the effect of the temperature increase:

$$\begin{aligned} f_{e} \left( {\dot{\varepsilon } = 1{}s^{{ - 1}} } \right) = \frac{{\sigma _{\mathrm{{y}}}^{*} \left( {\bar{\varepsilon }^{\mathrm{{p}}} } \right) }}{{\sigma _{\mathrm{{y}}} \left( {\bar{\varepsilon }^{\mathrm{{p}}} } \right) }}/f_{T} \left( {T_{0} + \Delta T} \right) , \end{aligned}$$
(17)

in which, \(T_0 \) is the initial temperature of the specimen, i.e. the room temperature.

Table 1 Calibrated parameters of the hybrid damage mechanics model for Ti–6Al–4V
Full size table
Fig. 12
figure 12

Force–displacement curves under loading rate of 25.4 mm/s for a tensile test and b V-notched test

Full size image
Fig. 13
figure 13

Specimen geometry for blind failure prediction (in mm)

Full size image

Given the gauge section of the tensile specimen is 38.1 mm, we determined the relative strain rate of the tensile test under loading rate of 0.0254 mm/s is \(0.00067\,\hbox {s}^{-1}\) and that under loading rate of 25.4 mm/s is \(0.67\,\hbox {s}^{-1}\). With the \(f_e \left( {\dot{\varepsilon }} \right) \) values at strain rate of 0.00067 s\(^{-1}\), which is one, and at strain rate of 0.67 s\(^{-1}\), the strain rate related parameters \(C_1^{\dot{\varepsilon }} \) and \(C_2^{\dot{\varepsilon }} \) can be fitted according to Eq. 10. Figure 11 illustrates the dependences of the flow stress on temperature and strain rate.

The temperature and strain rate related parameters are collected in Sect. 4.4.

4.4 Validation of the parameter set with high speed tests

Table 1 summarizes the calibrated parameters used in the hybrid damage echanics model

The tensile and V-notch tests under the loading rate of 25.4 mm/s are employed for the validation of the calibrated parameters for MBW model, as illustrated in Fig. 12. The good agreement of reaction forces for the high speed tests validates the temperature and strain rate correction of plasticity. With the calibrated damage parameters from the quasi-static tests, the failure of samples under high loading rate is reproduced by simulations. Thus, the damage related parameters are assumed to be independent on strain rate.

5 Force and failure prediction for SFC2

5.1 FE model set-up

Figure 13 shows the specimen geometry applied in the SFC2 blind prediction. A set of clevis grips with a pin diameter of 17.93 mm were used to fix the specimen to the testing machine. To measure the change in displacement between the ‘knife edges’, namely COD1 as shown in Fig. 15, a COD gage was employed. During the test, the upper grip was fixed and the lower grip was loaded; meanwhile, a high speed camera was used for recording the crack path propagation. In total eleven and eight repetitions of the SFC2 tests are performed under the loading rate of 0.0254 and 25.4 mm/s respectively by two independent labs in Sandia.

Figure 14 shows a typical crack morphology captured by the camera during the SFC2 tests under quasi-static condition. The crack path under the loading rate of 25.4 mm/s was the same. The sequences of crack propagation for both loading rates were \(\hbox {B}\rightarrow \hbox {D}\rightarrow \hbox {E}\).

For the reaction force and failure prediction of SFC2, the numerical model is constructed based on the illustrated geometry. The dimension scatter resulted from the manufacturing process is neglected. A finer mesh with the mesh size of 0.2 mm is applied in the area, where the crack propagation may happen; whereas coarser mesh is applied on the rest of the model. The element length through the thickness of the sample is set as 0.2 mm as well. The same element type (C3D8R) as used in the simulations for parameter calibration is defined and the model finally consists of 284,250 elements. The pins are generated as steel with only elastic deformation and the contact interaction between the specimen and the pins are assumed to be frictionless. With respect to the actual experiment, the boundary condition is assigned accordingly. The upper pin is defined as fixing pin. The upper and lower surfaces of the upper pin are constrained in all degrees of freedom. Meanwhile, the lower pin is assigned to be the loading pin and a downward displacement is applied to the upper and the lower surfaces of the lower pin. The overview of the model before and after deformation is illustrated in Fig. 15. To reduce the calculation time a mass scaling factor of 1000 is applied in the simulations.

Fig. 14
figure 14

A typical crack morphology in SFC2 tests a before and b after unstable crack propagation

Full size image
Fig. 15
figure 15

FE model for blind prediction and the predicted crack path sequence

Full size image

5.2 Failure and crack path prediction

To compare the force-COD1 curves obtained from SFC2 tests, the crack opening distances COD1 (see Fig. 15) and the reaction forces from pins are extracted from the simulation results. As shown in Fig. 15, the predicted crack path propagations with the loading rate of 0.0254 and 25.4 mm/s agree with the observation of the experiments.

Figure 16 demonstrates the comparisons of the force-COD1 curves for both loading rates. The unstable crack growth of the simulated SFC2 test with the loading rate of 0.0254 mm/s happens at the COD1 of 3.03 mm, which conforms to the average experimental results (2.96 mm). Under the loading rate of 25.4 mm/s, the COD1 corresponding to the failure point of the SFC2 specimen predicted by FE simulation is 2.14 mm; while, the COD1 at unstable crack growth in experiments ranges from 2.27 to 2.52 mm.

Fig. 16
figure 16

Comparison of force–displacement curves for SFC2 tests a under quasi-static condition and b under loading rate of 25.4 mm/s

Full size image
Table 2 Comparison of reaction forces for SFC2
Full size table

The reaction forces from experiments and simulations are compared in Table 2. The differences between the simulated reaction forces and averaged experimental results under both loading rates are within 7.5 %. The computed maximum reaction force under loading rate of 0.0254 mm/s is 6.52 % higher; while, under the loading rate of 25.4 mm/s the calculated maximum reaction force is 2.79 % higher comparing with the experiments.

6 Comparisons with the SFC2 original contribution

The original submission at the end of the SFC2 showed a 12–15 % over-estimation of the simulated maximum reaction force. The original predicted crack paths indicated a competition between the damage evolutions under the stress states of tension and shear. The original predicted unstable crack growth occured later compared to the SFC2 experimental results.

Fig. 17
figure 17

Comparison of the predicted reaction force-COD1 curves for the SFC2 tests between the original contribution and the optimized prediction under the loading rate of a 0.0254 mm/s and b 25.4 mm/s

Full size image
Fig. 18
figure 18

Comparison of the predicted crack paths for SFC2 tests between a the original contribution and b the improved prediction

Full size image

To achieve an improved prediction, the damage related parameters, i.e. DIL, dissipation energy parameter and critical damage value, are more carefully calibrated according to the given tensile and V-notch tests under both loading rates. With the optimized parameters presented, as summarized in Table 1, the predictions for COD1 at unstable crack growth and crack path under both loading rates are significantly improved. With the optimized DIL, the damage initiation occurs firstly at the location B (under a shear loading condition), then at the location A (under a tension loading condition). The change of dissipation energy parameter from 20,000 to 2000 reinforces the local damage evolution at the position, where the damage initiation is triggered early. The amplified damage-induced softening strengthens the strain localization at B, which leads to a crack path confirm to the observation from actual experiments.

In addition, the FE model is modified for a more precise representation of the SFC2 tests. The pins in FE model are constructed as steel with only elastic behavior instead of rigid bodies used in the original contribution. The elastic deformation of the steel pins corrects the over-estimated simulated reaction force. Especially, the over-estimation of the maximum reaction force decreases from over 12 to 2–6 %.

Figures 17 and 18 show the comparisons between the original and the improved predictions. Table 3 indicates the differences of the reaction force between experiments and the predictions from the original contribution and the improved simulation.

Table 3 Differences of reaction forces between predictions and the experiments for SFC2
Full size table

7 Conclusions and discussion

As a coupled phenomenological damage mechanics model, the MBW model considers two essential aspects. First, the description of the hybrid plasticity ensures an accurate description of the stress-strain response during plastic deformation. Second, the stress-state dependent damage evolution law introduces the damage-induced softening, which further fosters the localization of strain and eventually leads to the final fracture of the material.

With the improved parameter calibration scheme, the MBW model proved to be capable of predicting the ductile fracture considering varied loading conditions by the following two achievements:

  1. 1.

    Given a more precise description of the SFC2 test in the FE model, the simulated reaction force–displacement curves of SFC2 tests show a good agreement with the experimental results for both loading rates.

  2. 2.

    The crack path and the fracture of SFC2 tests under both loading rates are successfully predicted by the simulations applying the stress-state dependent critical damage value implemented MBW model.

The consideration of anisotropy in the damage mechanics model could further improve the accuracy of the prediction. Additionally, the precision of crack path and failure prediction could benefit from a detailed investigation of the critical damage value under more stress states.