A homogenization based yield criterion for a porous Tresca material with ellipsoidal voids

Abstract

This paper presents a rate-independent analytical model for porous Tresca ($J_{3}$-dependent) materials containing general ellipsoidal voids. The model is based on the nonlinear variational homogenization method which uses a linear comparison material to estimate the response of the nonlinear porous solid and is denoted as “MVAR”. Specifically, the model is derived by an original approach starting from a novel porous single crystal model (Mbiakop et al. in Int J Solids Struct 64–65:100–119, 2015b, J Mech Phys Solids 84:436–467, 2015c) by considering the limiting case of infinite slip systems which leads readily to the corresponding Tresca criterion. The MVAR yield surface is then validated using FEM on different unit-cells and various parameters including several porosity levels, several stress triaxiality ratios, different Lode angle and general void shapes and orientations. The MVAR model is found to be in good agreement with the finite element results for all cases considered in this study. Both the MVAR and the FEM computations reveal a strong sensitivity upon the microstructure anisotropy (void shape and orientation), and a dependence of the effective behavior on the third invariant of the applied stress. To the best knowledge of the authors, this is the first model in the literature that is able to deal with porous Tresca material and general void shapes and orientations. Moreover, the MVAR is used in a predictive manner to investigate the complex response of porous Tresca cases with strong coupling between the $J_{3}$-dependent matrix behavior and the (morphological) anisotropy induced by the shape and orientation of the voids. The simplicity of the present analytical study opens the possibility to adapt the present model to experimental results for various materials.

1 Introduction

The modeling of ductile damage growth of composites has been the subject of numerous studies over the past 50 years. The large majority of available theories have been carried out in the context of two-phase material systems comprising an isotropic rate-(in)dependent von Mises matrix phase and a voided phase (pores of spherical, spheroidal or arbitrary ellipsoidal shapes). In general, these studies use either limit analysis (see for instance Tvergaard and Needleman 1984; Gologanu and Leblond 1993; Leblond et al. 1994; Monchiet et al. 2007) based on (Gurson 1977) pioneering work, or variational homogenization theories using the idea of a linear comparison composite (see for instance Ponte Castañeda 1991; DeBotton and Ponte Castañeda 1995; Danas and Ponte Castañeda 2009a).

Nevertheless, as discussed in Drucker (1949), for most isotropic metals the yield surface is between the Von Mises and the Tresca one. In addition, the yield Tresca criterion is the limiting case of infinite slip systems of the Schmid law describing slip at single crystal level and hence derives naturally from a physical-based model. Thus, an important question is the understanding of the overall mechanical response of porous solids with Tresca matrix, i.e. exhibiting a $J_2$ and a third invariant $J_3$ dependence, as well as a morphological anisotropy induced by the shape and orientation of the voids.

Nonetheless, there have been only very few models for porous plastic Tresca materials in the literature. These studies involve the study of rate-independent metals containing spherical voids under axisymmetric (Cazacu et al. 2014) or general loading conditions (Revil-Baudard and Cazacu 2014). While each one of these studies has its own significant contribution to the understanding of the effective response of porous plastic Tresca materials none of them is general enough in the sense of arbitrary void shapes and orientations.

The scope of the present work is to develop a three-dimensional model that is able to deal with Tresca matrix, arbitrary ellipsoidal void shapes and general loading conditions. The model is derived by an original approach starting from a novel porous single crystal model (Mbiakop et al. 2015b, c) and considering the limiting case on infinite slip systems.

More specifically, in Sect. 2, we present the original framework that leads to a fully analytical model, called the modified variational (MVAR) model (see Danas and Aravas 2012; Mbiakop et al. 2015b, c), in three-dimensions. Subsequently, in Sect. 3, we present in detail the finite element (FE) periodic unit-cells which will be used to assess the MVAR model as well as to visualize the underlying stress fields in the context of porous Tresca materials. Furthermore, in Sects. 4 and 5, we present comparison between the MVAR predictions, the FE computations and Cazacu et al. (2014) predictions for a wide range of porosities, arbitrary ellipsoidal void shapes and orientations, porosities and general loading conditions. Finally, we conclude with Sect. 6.

2 A MVAR porous Tresca model

Let us consider a representative volume element (RVE) of a porous plastic Tresca material occupying a domain $\varOmega$. The material is analyzed as a two-phase composite comprising the plastic Tresca matrix (subdomain $\varOmega ^{(1)}$) and the vacuous phase (subdomain $\varOmega ^{(2)}$). The hypothesis of separation of length scales is made and it implies that the size of the voids (microstructure) is much smaller than the size of the matrix and the variation of the loading conditions at the level of the matrix, thus allowing for the homogenization of such a material system.

2.1 Microstructure

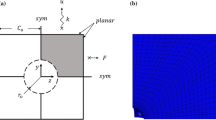
In the present study, following previous work of Willis (1977), we consider a “particulate” microstructure which is a generalization of the Eshelby (1957) dilute microstructure in the non-dilute regime. More specifically, we consider a “particulate” porous material (see Fig. 1) consisting of ellipsoidal voids aligned at a certain direction, whereas the distribution function, which is also taken to be ellipsoidal in shape, provides information about the distribution of the centers of the pores. For simplicity, one will also consider that the shape and orientation of the distribution function is identical to the shape and orientation of the voids themselves (see Danas and Ponte Castañeda 2009a). Nevertheless, this analysis can be readily extended to distribution of a different shape and orientation than the voids (Ponte Castañeda and Willis 1995; Kailasam and Ponte Castañeda 1998; Agoras and Ponte Castañeda 2013, 2014). Thus, as shown in Fig. 1, the internal variables characterizing the state of the microstructure are:

• The porosity or volume fraction of the voids $f = V_{2}/V$, where $V = V_{1} + V_{2}$ is the total volume, with $V_{1}$ and $V_{2}$ being the volume occupied by the matrix and the vacuous phase, respectively.

• The two aspect ratios of the lengths of the principal axes of the representative ellipsoidal void $2 a_{i}\,\left( i = 1,\,2,\,3\right)$, expressed as $w_{1} = a_{3}/a_{1}$, $w_{2} = a_{3}/a_{2}$ ($w_{3} = 1$).

• The orientation unit vectors of the representative ellipsoidal void $\mathbf{n }^{(i)}$, $\left( i = 1,\,2,\,3\right)$, defining an orthonormal basis set.

The above set of the microstructural variables can then be denoted by the set

$$\begin{aligned} s_{\alpha }=\left\{ f,\, w_{1},\, w_{2},\, \mathbf{n }^{(1)},\, \mathbf{n }^{(2)},\, \mathbf{n }^{(3)}\right\} \end{aligned}$$

(1)

To conclude, in the general case, where the aspect ratios and the orientation of the ellipsoidal voids are such that $w_{1} \ne w_{2} \ne 1$ and $\mathbf{n }^{(i)} \ne \mathbf{e }^{(i)}$, the overall porous material behavior becomes highly anisotropic. Therefore estimating its overall response is a difficult challenge.

Fig. 1

Representative volume element (b) constituted of representative ellipsoidal voids (c) embedded in a Tresca plastic matrix (a)

2.2 Constitutive behavior of the constituents

The matrix phase is an isotropic plastic material obeying the Tresca yield criterion. Thus, the onset of plastic deformation occurs when the maximum shear stress over all planes reaches a certain critical value, as described by the following relation

$$\begin{aligned} \max _{i,j}\left| \sigma _{i}-\sigma _{j}\right| =\sigma _{0}, \end{aligned}$$

(2)

where $\sigma _{i},\forall i=1,2,3$ and $\sigma _{0}$ denote respectively the Cauchy principal stresses and the uniaxial yield in tension.

It is useful to recall at this point that the Tresca yield criterion is a particular case of the Schmid yield criterion of a single crystal, when all the slip systems have the same critical resolved shear stress CRSS, and their number tends to infinite (see Mbiakop et al. 2015c for more details). This remark will be of major importance in the further developments.

2.3 Modified variational estimate for porous Tresca matrix

In the present work, we will make use of the general, nonlinear homogenization methods developed by Ponte Castañeda (1991, 2002), which are based on the construction of a linear comparison composite (LCC) with the same microstructure as the nonlinear composite. Using this suitably designed variational principle, it is shown in Mbiakop et al. (2015c) that a modified variational estimate of the effective viscoplastic stress potential of a general crystalline porous material can be defined such that

$$\begin{aligned} \widetilde{U}_{mvar}\left( \overline{\varvec{\sigma }}\right)= & {} (1-f)^{-n} \sum _{s=1}^{K} \frac{\dot{\gamma }_{0}^{(s)}\left( \tau _{0}^{(s)}\right) ^{-n}}{n+1}\nonumber \\&\times \left( \overline{\varvec{\sigma }}\cdot \widehat{\mathbf {S}}^{(s)}\cdot \overline{\varvec{\sigma }}\right) ^{(n+1)/2}, \end{aligned}$$

(3)

with

$$\begin{aligned}&\widehat{\mathbf {S}}^{(s)}\equiv \widehat{\mathbf {S}}^{mvar,(s)}=\widehat{\mathbf {S}}^{var,(s)}+\left( q_J^2-1\right) \mathbf {J}\cdot \widehat{\mathbf {S}}^{var,(s)}\cdot \mathbf {J}, \nonumber \\\end{aligned}$$

(4)

$$\begin{aligned}&\widehat{\mathbf {S}}^{var,(s)}=\varvec{\mu }^{(s)}\otimes \varvec{\mu }^{(s)}+\frac{f}{K} \widehat{\mathbf {S}}^{*}_{K}, \quad \forall s=1,K, \end{aligned}$$

(5)

where $n \ge 1$, K, $\dot{\gamma }_{0}^{(s)}$, $\tau _{0}^{(s)}$ and $\varvec{\mu }^{(s)}$ denote the creep exponent, the number of slip systems, the reference slip-rate, the reference flow stress (also denoted critical resolved shear stress CRSS) and the second-order Schmid tensor of the sth slip system, respectively. In addition, $\widehat{\mathbf {S}}^{*}_{K}$ is a microstructural tensor related to the Eshelby tensor $\mathbf {P}$ (Eshelby 1957). This tensor contains information on the void shape and orientation and is detailed in Mbiakop et al. (2015c) (in that reference the subscript K is not used). The factor $q_J$ has been originally introduced in Aravas and Ponte Castañeda (2004) and allows to recover the hydrostatic point corresponding to a composite spherical assemblages CSA (Hashin 1962; Gurson 1977; Leblond et al. 1994) voided microstructure and an isotropic (von Mises or Tresca) matrix. In the present case, it is set equal to

$$\begin{aligned} q_J=\sqrt{\frac{15}{4f}}\;\frac{1-f}{\ln (1/f)}. \end{aligned}$$

(6)

As we will see in the following, this allows to recover the (Gurson 1977) hydrostatic point in the case of spherical voids and pure hydrostatic loading.

One can then show after some lengthy algebra and numerical validation [see “Appendix” in Mbiakop et al. (2015c)] that in the limit of inifinte equiangular slip systems $K\rightarrow \infty$ the fourth order tensor $\widehat{\mathbf {S}}_{K}^{*}$ (see more details in “Appendix”) can be approximated in terms of the corresponding tensor for a von Mises matrix and takes the simple form

$$\begin{aligned} \widehat{\mathbf {S}}_{\infty }^{*}=\lim \limits _{K \rightarrow \infty } \frac{1}{K}\,\widehat{\mathbf {S}}^{*}_{K} \cong \frac{1}{5}\left( \widehat{\mathbf {Q}}^{-1}-\frac{1}{2}\,\mathbf {K}\right) . \end{aligned}$$

(7)

Here, $\mathbf {K}$ is the fourth-order deviatoric identity projection tensor and $\widehat{\mathbf {Q}}$ is a microstructural tensor directly associated to the Esheslby tensor for a porous material with a von Mises matrix. Detailed expressions for the evaluation of this tensor are given in “Appendix” of Cao et al. (2015) [see also “Appendix” in Aravas and Ponte Castañeda (2004)].

Moreover, as noted in the previous subsection, the Tresca yield criterion can be seen as a single crystal criterion consisting of infinite slip systems with equal CRSS $\tau _{0}^{(s)}\,{=}\,\tau _{0}$. First, we consider the rate-independent limit $n\longrightarrow \infty$ in Eq. (3), which leads to

$$\begin{aligned} \max _{s=1,K}&\left\{ \left( \frac{\overline{\tau }^{(s)}}{\tau _{0}}\right) ^{2} + \frac{f}{K\,\tau _{0}^2} \overline{\varvec{\sigma }} \cdot \left( \widehat{\mathbf {S}}_{K}^{*}-\mathbf {J}\cdot \widehat{\mathbf {S}}_{K}^{*}\mathbf {J}\right) \cdot \overline{\varvec{\sigma }} + \right. \nonumber \\&\left. \frac{f\,q_J^2}{K\,\tau _{0}^2} \overline{\varvec{\sigma }} \cdot \mathbf {J} \cdot \widehat{\mathbf {S}}_{K}^{*}\mathbf {J} \cdot \overline{\varvec{\sigma }}-\left( 1-f\right) ^{2} \right\} =0. \end{aligned}$$

(8)

Subsequently, we consider the limit of infinite slip systems, $K\rightarrow \infty$, by proper parametrization of the slip system orientations [see for instance “Appendix” in Mbiakop et al. (2015c)]. To achieve that, we first write down the identity

$$\begin{aligned} \lim \limits _{K \rightarrow \infty } \left( \max _{s=1,K} \left| \overline{\tau }^{(s)}\right| \right) = \frac{\max _{i,j}\left| \overline{\sigma }_{i}-\overline{\sigma }_{j}\right| }{2}, \end{aligned}$$

(9)

where $\overline{\sigma }_{i},\forall i=1,2,3$ denote the average principal stresses. Further, we set $\tau _0=\sigma _0/2$ with $\sigma _{0}$ being the yield stress in uniaxial tension in order to recover the original Tresca yield condition in the non-voided solid ($f=0$).

Then, by taking the limit $K\rightarrow \infty$ in (8) together with use of Eqs. (6), (7) and (9), we obtain the final porous Tresca yield condition

$$\begin{aligned}&\frac{\left( \max _{i,j}\left| \overline{\sigma }_{i}-\overline{\sigma }_{j}\right| \right) ^{2}}{\sigma _{0}^{2}} + \frac{4\,f}{\sigma _{0}^2} \overline{\varvec{\sigma }} \cdot \left( \widehat{\mathbf {S}}^{*}_{\infty }-\mathbf {J}\cdot \widehat{\mathbf {S}}^{*}_{\infty }\mathbf {J}\right) \cdot \overline{\varvec{\sigma }} + \nonumber \\&\quad \frac{15\,\left( 1-f\right) ^{2}}{\left( \sigma _{0}\,\ln {f}\right) ^{2}} \overline{\varvec{\sigma }} \cdot \mathbf {J} \cdot \widehat{\mathbf {S}}^{*}_{\infty }\mathbf {J} \cdot \overline{\varvec{\sigma }} - \left( 1-f\right) ^{2} = 0 \end{aligned}$$

(10)

In passing, we note that this model can be put in a pseudo-viscoplastic formulation following for instance the approach proposed by Han et al. (2013).

In the special case of spherical voids, it can be easily shown that

$$\begin{aligned} \left. \widehat{\mathbf {S}}^{*}_{\infty }\right| _{w_1=w_2=1} = \frac{1}{15}\mathbf {K} + \frac{1}{20}\mathbf {J}, \end{aligned}$$

(11)

and consequently the MVAR model becomes fully analytical, and takes the form

$$\begin{aligned}&\frac{\left( \max _{i,j}\left| \overline{\sigma }_{i}-\overline{\sigma }_{j}\right| \right) ^{2}}{\sigma _{0}^{2}} + \frac{8\,f}{45\,\sigma _{0}^2} \overline{\sigma }_{eq}^{2} \nonumber \\&\quad + \frac{9\,\left( 1-f\right) ^{2}}{\left( 2\,\sigma _{0}\,\ln {f}\right) ^{2}} \overline{\sigma }_{m}^{2} - \left( 1-f\right) ^{2} = 0. \end{aligned}$$

(12)

In the limit of purely hydrostatic loadings, the above expression recovers the Gurson hydrostatic point, i.e., $|\sigma _m|/\sigma _0=2 \ln (1/f)/3$.

In the general context of ellipsoidal voids, a numerical computation of the integrals involved in the evaluation of $\widehat{\mathbf {S}}^{*}_{\infty }$ is necessary, which can be easily performed following the procedure described in several studies (see Aravas and Ponte Castañeda 2004; Danas and Aravas 2012; Cao et al. 2015).

In the following, we present a numerical homogenization analysis which will serve to assess the accuracy of the proposed homogenization model.

3 Numerical homogenization

Numerical techniques such as the finite element method are able to solve for the local field in a porous material, provided that the exact location and distribution of the pores is known. However, in most cases of interest, the only available information is the void volume fraction (or porosity) and, possibly, the two-point probability distribution function of the voids (i.e., isotropic, orthotropic etc). In addition, for sufficient accuracy the element size that should be used in a finite element program must be much smaller than the size of the voids, which in turn is smaller than the size of the periodic unit-cell, especially when multiple pores are considered. This leads to very dense meshes and consequently time consuming computation. Therefore, it is very difficult to use the numerical results in a multi-scale analysis, especially when the unit-cell is rather complex.

Nevertheless, one could use the numerical periodic homogenization technique as a rigorous test-bed to assess the simpler analytical models as the one proposed in the previous section. More precisely, we can analyze the problem of a periodic porous material considering a unit-cell that contains a given distribution of voids. By the way, it is well known that a random porous material (e.g., the one in the analytical model presented in the previous section) and the periodic material exhibit similar effective behavior either in the case where the distribution of voids is complex enough (adequate for large porosity) or in the limiting case where the porosity is small enough. Moreover, in these cases, the periodic unit-cell estimates, and consequently the effective properties of the periodic composite, are independent of the prescribed periodic boundary conditions (Gilormini and Michel 1998). In this regard then, the comparison between the proposed model and the FE periodic unit-cell calculations are meaningful provided that complex periodic geometries are considered or porosity is small.

The following FE calculations have been carried out through the Mohr-Coulomb plasticity model of the commercial code (Abaqus 2009), where the friction angle of the material is taken equal to $\phi =0$ in order to reduce to the pressure-independent plastic Tresca model.

3.1 Unit-cell geometries

In order to validate the model, as explained before, FE periodic unit-cell calculations need to be carried out. Hence, several unit-cell geometries used in our computations, subjected to periodic boundary conditions, are presented in this subsection. The present FE calculations are carried out under a small strain assumption since the scope of the study is the estimation of the effective response of the porous material with a given microstructural realization but not the evolution of microstructure which is left for a subsequent work.

In the case of ellipsoidal voids, geometries with one void in the middle of the unit-cell can be used to estimate the effective behavior of the porous material, since small porosities ($f=1\,\%$) would be considered in the present study (see Fig. 3).

Fig. 2

Undeformed finite element unit-cell geometry in the case of a a single void axisymmetric spherical shell; b a single void axisymmetric cylindrical unit-cell, and c, d an isotropic distribution of 50 spherical voids;

Fig. 3

Undeformed unit-cell geometry with a single ellipsoidal void

Moreover, for spherical voids, one should consider more complex distribution of voids in order to address possible distribution effects. Indeed, let us consider for various porosities $f=0.01\,\%,\;0.1\,\%,\;1\,\%,\;2\,\%$, hydrostatic loading conditions applied on different geometries. First of all, an axisymmetric spherical shell consisting of quadrilateral 4-node elements CAX4 (see Fig. 2a), secondly an axisymmetric cylindrical unit-cell “one pore geometry” with axisymmetric elements CAX4 (see Fig. 2b) as the one used by Cazacu et al. (2014) and finally multipore geometries (here with 50 pores) to achieve isotropic distributions (Figs. 2c, d, 3).

In the context of this study, i.e. rate-independent Tresca matrix, the results obtained are compared in Fig. 4 with the theoretical hydrostatic limit of the effective behavior of composite spherical assemblages CSA (Hashin 1962; Gurson 1977; Leblond et al. 1994), expressed as $\overline{\sigma }_{m}=-2\,\sigma _{0}\,\ln (f)/3$. As it is shown, the axisymmetric spherical shell geometry (Fig. 2a) matches, as expected, to the exact average hydrostatic behavior in all the cases. However, the axisymmetric cylindrical unit-cell (Fig. 2b) tends to underestimate the overall response with a relative error of $\sim 3\,\%$ at small porosities ($f=0.01\,\%$) and reaching $\sim 10\,\%$ at moderate ones ($f=2\,\%$). Similar discrepancies were reported in Cazacu et al. (2014) where FE computation on an axisymmetric cylindrical unit-cell were also performed. Furthermore, the multipore geometries seems to deal well with the average hydrostatic behavior, since more sophisticated distribution of voids is chosen and thus tend to achieve isotropic distributions. These discrepancies are merely due to the fact that the cylindrical unit-cell in Fig. 2b is not isotropic. As the porosity becomes smaller ($f\le 0.01\,\%$) the void concentration becomes almost dilute and thus the distribution effects due to the unit-cell geometry less important. However, caution should always be made in this context to a rate-independent plasticity with a matrix phase described by a vertex-type yield criterion (Tresca matrix) since the material tends to localize strongly. Therefore, the interpretation of the FEM results should be interpreted with caution and maybe contrasted in the future with FFT results (see for instance Vincent et al. 2014).

Fig. 4

Representation of the average hydrostatic stress as a function of the porosity in a porous Tresca matrix, for several mesh geometries

Consequently, in the case of spherical voids, we should make use of monodisperse distributions (e.g. Fig. 2c) that are constructed by means of a random sequential adsorption algorithm (see Rintoul and Torquato 1997; Torquato 2002) which generates the coordinates of the pore centers. For monodisperse distributions, the radius of each void is

$$\begin{aligned} R_{m}=L\left( \frac{3\,f}{4\,\pi N}\right) ^{1/3}, \end{aligned}$$

(13)

with N being the number of pores in the unit-cell and f the porosity.

In addition, the sequential addition of voids is constrained so that the distance between a given void and the rest of the voids as well as the boundaries of the unit-cell takes a minimum value that guaranties adequate spatial discretization. In order to achieve this goal, we use the rules detailed in Segurado and Llorca (2002); Fritzen et al. 2012); Lopez-Pamies et al. 2013); Mbiakop et al. 2015c).

Furthermore, periodic boundary conditions have to be applied to these geometries since the validation of the model requires periodic FE unit-cell calculations.

3.2 Periodic boundary conditions and loading

The periodic boundary conditions are expressed in this case as (Michel et al. 1999; Miehe et al. 1999)

$$\begin{aligned} \mathbf{v }(\mathbf{x })=\overline{\varvec{D}}\cdot \mathbf{x }+\mathbf{v }^{*}(\mathbf{x }), \;\mathbf{v }^{*}\, \mathrm{periodic}, \end{aligned}$$

(14)

where the second-order tensor $\overline{\varvec{D}}$ denotes the symmetric part of the average velocity gradient, $\mathbf{x }$ denotes the spatial coordinates and $\mathbf{v }^{*}$ is a periodic field.

As shown in Mbiakop et al. (2015c), a simple algebraic analysis reveals that all periodic linear constraints between the nodes can be written in terms of the velocities of three corner nodes, i.e., $v_i(L_{1},0,0)$, $v_i(0,L_{2},0)$ and $v_i(0,0,L_{3})$. These, in turn, are given in terms of the average velocity gradient $\overline{\varvec{D}}$. This, further, implies that the only nodes that boundary conditions need to be applied are $(L_{1},0,0)$, $(0,L_{2},0)$ and $(0,0,L_{3})$ (together with the axes origin (0, 0, 0) which is fixed).

Moreover, in order to validate the model proposed in this study, it is convenient to apply $\overline{\varvec{D}}$ in such a way that the average stress triaxiality and Lode parameter in the unit-cell remain constant. In this regard then, one will use the methodology originally proposed by Barsoum and Faleskog (2007) and further discussed in Mbiakop et al. (2015c).

As a consequence of the above-defined load and the periodic boundary conditions, the average deformation in the unit-cell is entirely described by the displacements of the three corner nodes, e.g., $u_{1}(L_{1},0,0)=U_{1}(t)$, $u_{2}(0,L_{2},0)=U_{2}(t)$ and $u_{3}(0,0,L_{2})=U_{3}(t)$, denoted compactly as

$$\begin{aligned} \mathbf{U }= & {} \lbrace U_{1}(t),U_{2}(t),U_{3}(t)\rbrace , \nonumber \\ \dot{\mathbf{U }}= & {} \lbrace \dot{U}_{1}(t),\dot{U}_{2}(t),\dot{U}_{3}(t)\rbrace \equiv \lbrace v_{1}(t),v_{2}(t),v_{3}(t)\rbrace .\nonumber \\ \end{aligned}$$

(15)

The stress state in the unit-cell is then controlled via a time-dependent kinematic constraint (Michel et al. 1999) obtained by equilibrating the rate of work in the unit-cell with the rate of work done by the fictitious node on the unit-cell at time t. Next, in order to control the loading path in the stress space, we couple the average stress $\overline{\varvec{\sigma }}$ in the unit-cell with the generalized force vector associated with a fictitious node.

In addition, the principal components of the stress field can be expressed as a function of the average stress triaxiality $X_\varSigma$ and the average Lode angle $\overline{\theta }$, via

$$\begin{aligned}&\frac{3}{2\overline{\sigma }_{eq}}{\{\overline{\sigma }_{1},\overline{\sigma }_{2},\overline{\sigma }_{3}\}}=\left\{ \cos \overline{\theta }, -\cos \left( \overline{\theta }+\frac{\pi }{3}\right) ,\right. \nonumber \\&\quad \left. - \cos \left( \overline{\theta } -\frac{\pi }{3}\right) \right\} +\frac{3}{2}\,X_\varSigma \{1,1,1\}. \end{aligned}$$

(16)

where $\overline{\sigma }_{eq}$ denotes the equivalent Von Mises part of $\overline{\varvec{\sigma }}$.

Then, nonlinear kinematic constraints between the degrees of freedom corresponding to the sides of the unit-cell (i.e., $\mathbf{U }$) and the degrees of freedom of the fictitious node are applied in the finite element software ABAQUS (Abaqus 2009) by use of the multi-point constraint user subroutine (MPC) in order to control the loading path (stress triaxiality and Lode angle).

Furthermore, before proceeding with the results, it is useful to carry out a small numerical convergence study of the geometries. In order to achieve this goal, let us consider a porosity $f=1\,\%$, triaxial loading conditions $X_\varSigma =1,\,3$, $\overline{\theta }=0^{\circ }$ applied on several geometries, e.g. axisymmetric cylindrical unit-cell and, multipore unit-cells with $20, \,50, \, 100$ pores. As shown in Fig. 5 in almost all the cases, the axisymmetric cylindrical unit-cell (Fig. 2b) tends to underestimate the overall response provided by the multipore geometries. In addition, the convergence is reached with 50 pores for the range of stress triaxiality and Lode angle considered. Thus, since the numerical validation of the MVAR would be performed for the full range of stress triaxialities, all the simulations presented next would be carried out with the multipore geometry with 50 pores.

Fig. 5

Plots of the average hydrostatic stress as a function of the average hydrostatic strain for isotropic microstructures, i.e. spherical voids $w_{1} = w_{2} = 1$. Comparison between several geometries, precisely axisymmetric cylindrical unit-cell, multipore unit-cell with $20, \,50, \, 100$ pores, for a Lode angle $\overline{\theta }=0^{\circ }$, a porosity $f = 1\,\%$ and various triaxialities a $X_\varSigma =1$, b $X_\varSigma =3$

Fig. 6

Yield surfaces in the $\overline{\sigma }_{m}-\overline{\sigma }_{eq}$ plane for isotropic microstructures, i.e. spherical voids $w_{1} = w_{2} = 1$. Comparison between the FE multipore simulations and the modified variational MVAR for three Lode angles $\overline{\theta }=0^{\circ },\,30^{\circ },\,60^{\circ }$ and various porosities a $f = 0.1\,\%$, b $f = 1\,\%$, c $f = 2\,\%$, d $f = 4\,\%$. The blue color (line or points) corresponds to the Lode angle $\overline{\theta }=0^{\circ }$ while the red color corresponds to the Lode angle $\overline{\theta }=60^{\circ }$

4 Results-I: Assessment of the MVAR via FE simulations

This section presents results for the instantaneous effective behavior of the rate-independent porous Tresca material comprising voids with spherical and non-spherical shape, as predicted by the modified variational model (MVAR) proposed in this work. Next, the predictions of the yield surface obtained using the MVAR are compared with the FE simulations described in Sect. 3. The effect of the void shape on the resulting yield surface will ba particularly analyzed. Moreover, in the case of axisymmetric loadings, results will also be compared with predictions proposed by Cazacu et al. (2014) model.

4.1 Isotropic microstructures

The Fig. 6 displays yield surfaces for spherical voids (i.e., $w_{1} = w_{2} = 1$) as predicted by the FE simulations, the modified variational model (MVAR), the Cazacu et al. (2014) model, for four different porosities $f=\left( 0.1,\,1,\,2,\,4\right) \,\%$ and both axisymmetric (average Lode angle $\overline{\theta }=0^{\circ },\,60^{\circ }$) and non axisymmetric loadings conditions ($\overline{\theta }=30^{\circ }$). The agreement between the MVAR and the FE calculations is satisfactory for a large range of porosities and for full loading conditions (stress triaxiality, Lode angle). The largest difference between the MVAR and the FE is found for larger porosities ($f=4\,\%$). In the axisymmetric case ($\overline{\theta }=0^{\circ },\,60^{\circ }$), when the (Cazacu et al. 2014) model is also tested, we remark that the predictions coincide at deviatoric loadings, i.e. $\overline{\sigma }_{m} = 0$ but are different for most of the triaxiality considered. In addition, the MVAR gives a significantly softer prediction when $\overline{\sigma }_{m}$ increases. In the purely hydrostatic limit, i.e. $\overline{\sigma }_{eq} = 0$, the MVAR model attains the analytical spherical shell solution and coincides with the (Cazacu et al. 2014) model as expected.

Fig. 7

Yield surfaces in the $\overline{\sigma }_{m}-\overline{\sigma }_{eq}$ plane for isotropic microstructures, i.e. spherical voids $w_{1} = w_{2} = 1$, a porosity $f = 1\,\%$, Lode angle $\overline{\theta }=0^{\circ },\,30^{\circ }$. Comparison between the FE multipore simulations, the MVAR-Tresca porous model and the MVAR-Von Mises porous model

Fig. 8

Contours of the equivalent Von Mises stress in the case of spherical voids, a porosity $f = 1\,\%$, a triaxiality $X_\varSigma =3$ and a Lode angle $\overline{\theta }=0^{\circ }$ for a a Tresca matrix and b a Von Mises matrix

At this point, it is worth noting that for axisymmetric loadings, the (Cazacu et al. 2014) yield surface is not symmetric with respect to the $\overline{\sigma }_{m} = 0$ vertical axis. This implies that the plastic Tresca strain-rate corresponding to the normal of the yield surface for a purely deviatoric part exhibits a hydrostatic part, as already discussed in Danas et al. (2008a), Cazacu et al. (2014). This is attributed to the fact that the isotropic (Cazacu et al. 2014) yield surface exhibits a coupling between first and the third invariant, i.e., mean stress and Lode angle. Such coupling, also confirmed by the FE simulations, is not addressed in the more accurate MVAR model.

In the following, we attempt to reveal the differences between the predictions obtained by the MVAR in the context of a Mises ($J_2$-dependent) matrix and a Tresca matrix ($J_2,\,J_3$-dependent). Thus, Fig. 7 shows yield surfaces for spherical voids ($w_{1} = w_{2} = 1$) as predicted by the FE simulations, the MVAR-Tresca porous model and the MVAR-Von Mises porous model (Danas and Aravas 2012) for the porosity $f=1\,\%$ and both axisymmetric ($\overline{\theta }=0^{\circ }$) and non axisymmetric loadings conditions ($\overline{\theta }=30^{\circ }$).

Let us first consider the axisymmetric case, $\overline{\theta }=0^{\circ }$. The MVAR-Von Mises yield surface is as expected closer to the MVAR-Tresca yield surface as the MVAR-Von Mises model is not dependent up on the third invariant. Nonetheless, it is noted that the porous Von Mises material exhibits a $J_3$ dependence but only minor (see Danas et al. 2008b), and is not further discussed here.

In order to have a better understanding on the differences between porous Tresca and porous Von Mises yield surfaces, we present, next, contours of the equivalent Von Mises stress, for spherical voids, a porosity $f = 1\,\%$, a triaxiality $X_\varSigma =3$ and a Lode angle $\overline{\theta }=0^{\circ }$. Then, as observed in Fig. 8, the stress amplitude is in most of the unit-cell regions lower in the case of a Tresca matrix than in the Von Mises one. Thus, as previously discussed, the porous Tresca material is expected to be softer than a porous Von Mises material for the same microstructure considered, and in general lead to increase void growth at large triaxialities, in accord with recent results by Cazacu et al. (2014), Revil-Baudard and Cazacu (2014).

4.2 Anisotropic microstructures

Figure 9 shows FE simulations and MVAR yield surfaces for spherical voids ($w_{1} = w_{2} = 1$), prolate voids ($w_{1} = w_{2} = 3$), oblate voids ($w_{1} = w_{2} = 1/3$) and arbitrary ellipsoidal voids ($w_{1} = 3,\, w_{2} = 1/3$). The porosity is set equal to $f = 1\,\%$, whereas the loading is axisymmetric along the $x_1$-axis ($\overline{\theta }=0^{\circ }$). A good agrement between the numerical FE predictions and the MVAR is seen for the full range of stress triaxialities, except in the case of average purely deviatoric, where a relative difference in the order of 2–6 % is noticed. Furthermore, the main observation in this figure is that non-spherical void shapes have a dramatic influence on the yield surface of the porous material as predicted by both the MVAR model and FE simulations. First, the slopes of the yield surfaces depend strongly on the void shape. For instance, a porous material with ellipsoidal voids ($w_{1} = 3,\, w_{2} = 1/3$) is softer than that with oblate voids ($w_{1} = w_{2} = 1/3$) in the full range of stress triaxialities whereas they exhibit the same maximum average Von Mises stress (at $X_\varSigma =0$). Moreover, for the same value of porosity, non-spherical void shapes lead to a significantly more compliant response at high values of the mean stress, especially in the case of oblate and arbitrary ellipsoidal voids. Moreover, it is evident from this figure that arbitrary ellipsoidal shapes ($w_{1} = 3,\, w_{2} = 1/3$) lead to very different responses when compared with spheroidal shapes ($w_{1} = w_{2} = 3$ or $w_{1} = w_{2} = 1/3$).

Fig. 9

Yield surfaces in the $\overline{\sigma }_{m}-\overline{\sigma }_{eq}$ plane for isotropic (spherical voids $w_{1} = w_{2} = 1$) and anisotropic microstructures: prolate voids $w_{1} = w_{2} = 3$, oblate voids $w_{1} = w_{2} = 1/3$ and ellipsoidal voids $w_{1} = 3,\, w_{2} = 1/3$. Comparison between the FE simulations and the modified variational MVAR for $f = 1\,\%$ and Lode angle $\overline{\theta }=0^{\circ }$

Finally, one should mention at this point that a series of additional triaxial loading conditions and several void shapes have also been considered and the MVAR has been found to be in good agreement (similar to the one observed in the previous results) with the corresponding FE calculations. However, no such results are shown here for brevity.

5 Results - II: Coupling between the Tresca matrix behavior, void shape and orientation

Hereafter, we attempt to reveal the complex coupling between the Tresca yield criterion features and the (morphological) void anisotropy resulting from the ellipsoidal void shape and orientation.

5.1 Effect of void shape and orientation

In this section, we discuss in more detail the effect of microstructure anisotropy upon the effective response of the porous composite. Figure 10 displays several MVAR yield surfaces for a porous plastic Tresca material. The effect of porosity is investigated by setting $f=\left( 1\,\%,5\,\%,10\,\%\right)$ for different microstructures (a) $w_1=w_2=1$ and (b) $w_1=3$, $w_2=1/3$, $\mathbf{n }^{(1)}=\mathbf{e }^{(1)}$, $\mathbf{n }^{(2)}=\mathbf{e }^{(2)}$. In these figures, the yield surfaces exhibit as expected a gradual shrinking with increasing porosity for both spherical ($w_1=w_2=1$) and ellipsoidal ($w_1=w_2^{-1}=3$) voids. However, while for the case of spherical voids ($w_1=w_2=1$), in Fig. 10a, the curves are symmetric with respect to the $\overline{\sigma }_{eq}/\sigma _{0}$ axis, the curves for the ellipsoidal voids ($w_1=w_2^{-1}=3$), in Fig. 10b, become asymmetric as already discussed in the context of Fig. 9. As a consequence of this asymmetry, the MVAR estimates are found to be slightly stiffer in the negative pressure regime ($\overline{\sigma }_{m}/\sigma _{0} < 0$) than in the positive pressure regime ($\overline{\sigma }_{m}/\sigma _{0} > 0$).

Fig. 10

Yield surfaces for a porous plastic Tresca material. The effect of porosity is investigated by choosing $f=\left( 1\,\%,5\,\%,10\,\%\right)$ for different void shapes a $w_1=w_2=1$ and b $w_1=3$, $w_2=1/3$, $\mathbf{n }^{(1)}=\mathbf{e }^{(1)}$, $\mathbf{n }^{(2)}=\mathbf{e }^{(2)}$

Fig. 11

Yield surfaces for a porous plastic Tresca material with ellipsoidal voids. The porosity is set to $f=10\,\%$. The effect of (a) the void aspect ratios is investigated by choosing $w_1=w_2^{-1}=\left( 1/3,1,3\right)$ for an orientation $\mathbf{n }^{(1)}=\mathbf{e }^{(1)}$, $\mathbf{n }^{(2)}=\mathbf{e }^{(2)}$

The Fig. 11 shows yield surfaces in the $\overline{\sigma }_{m}/\sigma _{0}-\overline{\sigma }_{eq}/\sigma _{0}$ plane for a porous plastic Tresca material. The porosity is set to $f=10\,\%$. The effects of the void aspect ratios and orientation are investigated by choosing $w_1=w_2^{-1}=\left( 1/3,1,3\right)$ for an orientation $\mathbf{n }^{(1)}=\mathbf{e }^{(1)}$, $\mathbf{n }^{(2)}=\mathbf{e }^{(2)}$. For the two considered anisotropic microstructures , i.e. $w_1=w_2^{-1}=w=3$ and $w_1=w_2^{-1}=w=1/3$, the porous solids exhibit the same hydrostatic behavior. This can be explained by the fact that the second microstructure is derived from the first one through a $\pi /2$ rotation around the $x_{3}$ axis (see Fig. 11). Thus, since the hydrostatic loading is isotropic in character i.e. doesn’t exhibit any preferential direction, the overall hydrostatic response is expected to be the same in both cases. This feature was also discussed in earlier studies (Danas and Ponte Castañeda 2009b) and is a necessary requirement of any model that involves void shape effect. In addition, the MVAR estimates are found to be stiffer in the negative pressure regime ($\overline{\sigma }_{m}/\sigma _{0} < 0$) for $w_1=w_2^{-1}=w=3$ while the average behavior is softer in the negative pressure regime ($\overline{\sigma }_{m}/\sigma _{0} < 0$) for $w_1=w_2^{-1}=w=0.2$. Moreover, there is a strong sensitivity of the hydrostatic average behavior on the void aspect ratios, since $\overline{\sigma }_{m}/\sigma _{0}$ gets an increase of $50\,\%$ from the considered ellipsoidal microstructures ($w_1=w_2^{-1}=\left( 1/3,3\right)$) to the spherical one ($w_1=w_2=1$).

Fig. 12

Yield surfaces in the $\varPi$-plane (or octahedral plane) for a porous plastic Tresca material with a porosity $f = 1\,\%$, void shapes and orientations a $w_1=w_2=1$ and b $w_1=3$, $w_2=1/3$, $\mathbf{n }^{(1)}=\mathbf{e }^{(1)}$, $\mathbf{n }^{(2)}=\mathbf{e }^{(2)}$ at different level of pressure. The dashed line curves correspond to the negative pressure regime while the continuous one correspond to the positive pressure regime. The uniaxial yield in tension is set to $\sigma _0=1$

5.2 $\varPi$-plane cross sections

In this section, we investigate the effective response of the porous plastic Tresca material in the deviatoric plane, i.e. $\varPi$-plane.

Specifically, Fig. 12 displays yield surfaces in the $\varPi$-plane (or octahedral plane) corresponding to different fixed overall hydrostatic stresses $\overline{\sigma }_{m}=0,\,\overline{\sigma }_{m}=\pm 0.5\overline{\sigma }_{m}^{H},\,\overline{\sigma }_{m}=\pm 0.9\overline{\sigma }_{m}^{H}$, where $\overline{\sigma }_{m}^{H}$ denotes the hydrostatic point of the MVAR model for each of the given cases in Fig. 12a, b, respectively. Note that when the voids are spherical the hydrostatic MVAR point coincides with that of the CSA microstructure whereas in the case of ellipsoidal voids it is simply an estimate.

More specifically, in Fig. 12a, which corresponds to spherical voids ($w_1=w_2=1$), we observe a gradual shrinking of the curves with increasing $\overline{\sigma }_{m}$ as expected. At small values of $\overline{\sigma }_{m}=0$, the curve exhibits an almost discrete character. However, it is important to notice that as shown in the analytical expression of the model in relation (12), the MVAR yield surfaces are all “rounded”. Indeed, depending on the relative dominance of the terms ${\left( \max _{i,j}\left| \overline{\sigma }_{i}-\overline{\sigma }_{j}\right| \right) ^{2}}/{\sigma _{0}^{2}}$ and $\left( 8\,f\,\overline{\sigma }_{eq}^{2}\right) /\left( 45\,\sigma _{0}^2\right)$ in the Eq. (12), the surfaces are mainly “rounded” or exhibit “vertex - like” character. In the context of this study, since we focuss on small porosities (i.e. low f), the term $\left( 8\,f\,\overline{\sigma }_{eq}^{2}\right) /\left( 45\,\sigma _{0}^2\right)$ is smaller and thus, the “vertex-like” character is dominant. We stress however that the homogenized model (see Eq. 12) is strictly convex (even if the initial Tresca matrix is simply convex) as a result of the homogenization procedure. Furthermore, when one increases $\overline{\sigma }_{m}$, the porous Tresca preserves the original deviatoric symmetries of the Tresca matrix for all values of $\overline{\sigma }_{m}$. In particular, in this case the curve is fully symmetric with respect to the three axes $\overline{\sigma }^{\prime }_{1}$, $\overline{\sigma }^{\prime }_{2}$ and $\overline{\sigma }^{\prime }_{3}$ and exhibits the same symmetries as the ones of the original Tresca matrix. As we will see in the following this feature is not in agrement with FEM but only marginally.

In addition, Fig. 12b shows yield surfaces for ellipsoidal voids with aspect ratios $w_1=3$, $w_2=1/3$, aligned with the applied load, and the same level of hydrostatic stress. In this case, a gradual shrinking of the curves appears while increasing $\overline{\sigma }_{m}$, as expected. Again, as discussed previously, the curves exhibit a quasi discrete character even if rigourously there are no corners. Nevertheless, by contrast to the case of spherical voids microstructure, the yield surfaces exhibit full asymmetry for finite hydrostatic stresses $\overline{\sigma }_{m}=0$, but preserve the hexagonal symmetry ($\pi /3$ symmetry) for $\overline{\sigma }_{m}\ne 0$. The observed asymmetry is much more pronounced at higher values of $\overline{\sigma }_{m}$. Furthermore, it should be stressed that point symmetry of the curves with respect to the global origin and $\overline{\sigma }_{m}=0$ is still preserved if one compares the continuous ($\overline{\sigma }_{m}\ge 0$) with the dashed lines ($\overline{\sigma }_{m}\le 0$).

Fig. 13

Yield surfaces in the $\varPi$-plane (or octahedral plane) for a porous plastic Tresca material containing spherical voids with a porosity $f = 1\,\%$, at level of pressure a $\overline{\sigma }_m=0$ and b $\overline{\sigma }_m=\pm 0.5\,\overline{\sigma }^{H}_m$, where $\overline{\sigma }^{H}_m$ denotes the hydrostatic point for hydrostatic loading. Comparison between the FE multipore simulations and the MVAR-Tresca porous model when the uniaxial yield in tension is set to $\sigma _0=1$

Fig. 14

Representation of the normalized average equivalent Von Mises stress as a function of the average Lode angle in the $\varPi$-plane (or octahedral plane) for a porous plastic Tresca material containing spherical voids with a porosity $f = 1\,\%$, at level of pressure $\overline{\sigma }_m=0$ and $\overline{\sigma }_m=\pm 0.5\,\overline{\sigma }^{H}_m$, where $\overline{\sigma }^{H}_m$ denotes the hydrostatic point for hydrostatic loading. Comparison between the FE multipore simulations and the MVAR-Tresca porous model when the uniaxial yield in tension is set to $\sigma _0=1$. The dashed lines indicate the symmetry lines

Next, a numerical validation of the predictions of the MVAR model in the $\varPi$-plane is carried out for spherical voids with a porosity $f = 1\,\%$, at level of pressure $\overline{\sigma }_m=0$ (see Fig. 13a) and $\overline{\sigma }_m=\pm 0.5\,\overline{\sigma }^{H}_m$ (see Fig. 13b).

As shown in Fig. 13a, i.e. for isotropic microstructure and zero average hydrostratic stress, the agreement between the MVAR and the FE calculations is satisfactory for a large range of Lode angle and thus, the full $\varPi$-plane. Furthermore, for the intermediate pressure level cases $\overline{\sigma }_m=\pm 0.5\,\overline{\sigma }^{H}_m$ shown in Fig. 13b, the “rounded” character seems more pronounced in the FE results while the “vertex-like” character is dominant in the MVAR predictions. Moreover it is useful to precise that except in the limit of zero porosity, the “vertex-like” response does not correspond to perfectly flat sectors, as shown in Eq. (10) through the term $\left( 8\,f\,\overline{\sigma }_{eq}^{2}\right) /\left( 45\,\sigma _{0}^2\right)$. A similar qualitative result of a more rounded yield surface was already found in the (Revil-Baudard and Cazacu 2014) model. Nonetheless, a good quantitative agrement between the MVAR and the FE is still observed in such context. In addition, it is interesting to notice that as predicted by the MVAR, there is no significant difference between the positive and negative pressure regime, at least in the results shown here.

Furthermore, in order to assess the coupling between the invariants $\overline{\sigma }_{eq}$, $\overline{\sigma }_m=0$ and $\overline{\theta }$, the normalized average equivalent Von Mises stress is extracted from Fig. 13 and plotted in Fig. 14 as a function of the average Lode angle in the $\varPi$-plane (or octahedral plane) for a porous plastic Tresca material containing spherical voids with a porosity $f = 1\,\%$, at level of pressure $\overline{\sigma }_m=0$ and $\overline{\sigma }_m=\pm 0.5\,\overline{\sigma }^{H}_m$.

In the case of $\overline{\sigma }_m=0$, the average equivalent stress $\overline{\sigma }_{eq}$ exhibits a minimum and an axial symmetry for $\overline{\theta }=\pi /6$ whereas the maximum is reached for axisymmetric states, i.e $\overline{\theta }=0,\,\pi /3$. In contrast, when $\overline{\sigma }_m$ increases (for instance $\overline{\sigma }_m=\pm 0.5\,\overline{\sigma }^{H}_m$), the minimum is still observed for $\overline{\theta }=\pi /6$ but the $\pi /6$ symmetry is lost even marginally. Indeed, only the hexagonal symmetry ($\pi /3$ symmetry) is preserved for $\overline{\sigma }_{m}\ne 0$.

Such observations are in qualitative agrement with those made by Revil-Baudard and Cazacu (2014).

6 Conclusions

An analytical yield function in closed form for porous plastic Tresca materials has been proposed in this study. It is theoretically motivated using an original approach that consists in considering the limiting case of infinite slip systems in a variational homogenization porous single crystal model (Mbiakop et al. 2015b, c). The modified variational (MVAR) model presented in this study has been validated by comparison with full field FE calculations of single- and multi-void periodic unit-cells. The MVAR model has been found to be in good agreement with the FE results for a very wide range of parameters describing the porosity, the void shapes and orientations. The MVAR model has shown strong predictive capabilities while exhibiting critical qualitative features.

More precisely, the MVAR model has been able to predict the strong dependence of the effective response, and especially of the average hydrostatic stress upon the shape and orientation of the voids. Nonetheless, the MVAR model appears to retain the original symmetries of the pure Tresca matrix criterion when plotted to the $\varPi$-plane. This is in contrast with the full field FEM simulations which exhibit a transition from a $\pi /6$ symmetry at low triaxialities to a $\pi /3$ symmetry at high ones. Even if this symmetry breaking seems to be marginal in the yield surface the effects will be stronger at the normal and hence if void shape evolution is considered, since the normal to the octahedral plane controls the void shape evolution while the one to the meridional plane (precisely the hydrostatic strain rate) controls the void growth.

In addition, it is useful to note that the Tresca yield condition together with the von Mises yield condition are special cases of the (Hershey 1954) yield condition (see also Hosford 1972). In this regard, albeit not straightforward, it seems feasible that the existing class of the porous MVAR models for a von Mises matrix (Danas and Aravas 2012) and for a Tresca matrix, which is the scope of the present study, can be extended to include the case of a porous Hosford model (see for instance Cohen et al. 2009). Such a study is underway.

Finally, it is important to mention that several important issues, such as strain-hardening and microstructure evolution that were not studied in this paper will be considered in further studies. Moreover, it would also be interesting to study the effects of cyclic loading conditions upon microstructure evolution using similar ideas, as addressed numerically for instance in Mbiakop et al. (2015a) for a Von Mises material. Such developments are underway and will be presented in the future.

Appendix: Microstructural tensor in the limiting case of \(K \rightarrow \infty \) (isotropic Tresca matrix)

In the case of slip systems with identical CRSS $\tau _0$ and reference slip-rate $\dot{\gamma }_0$, the compliance tensor $\mathbf {S}_{K}$ of the linear comparison composite is given in Mbiakop et al. (2015b, c) by setting $\lambda ^{(s)}=\lambda$ and $\rho ^{(s)}=\rho$,

$$\begin{aligned} \mathbf {S}_{K}= & {} \frac{1}{2\lambda } \sum _{s=1}^{K} \mathbf {E}^{(s)} + \frac{1}{2\rho } \sum _{s=1}^{K} \mathbf {F}^{(s)} + \frac{1}{3\kappa }\mathbf {J}, \; \text {with} \nonumber \\ \mathbf {E}^{(s)}= & {} 2 \varvec{\mu }^{(s)} \otimes \varvec{\mu }^{(s)}, \, \mathbf {F}^{(s)}=\mathbf {K}-\mathbf {E}^{(s)}, \end{aligned}$$

(17)

$\forall s=1,K$, where $\lambda ,\,\rho ,\,\kappa$ serve to denote eigenvalues. While $\lambda$ is optimized in the context of the variational homogenization method, $\rho ,\,\kappa$ are set to infinity [see more details in Mbiakop et al. (2015c)].

In addition, the microstructural tensor can easily be computed in the case of an isotropic von Mises compliance matrix, whose compliance tensor of the corresponding linear comparison composite is $\mathbf {S}_{Mises} = (2 \mu _0)^{-1}\mathbf {K} + (3\kappa _0)^{-1}\mathbf {J}$), following for instance the numerical framework described in Aravas and Ponte Castañeda (2004) and Danas (2008).

Moreover, the numerical computation of the hydrostatic part of $\mathbf {S}^{*}/K$ in the infinite number of slip systems context (i.e. Tresca matrix) for spherical voids leads to a result (up to $2\,\%$) close to the microstructural tensor associated with the compliance tensor of a von Mises matrix. In addition, it was shown Benallal (2015) and we observe through FE simulations that a porous von Mises material and a porous Tresca material exhibit the same hydrostatic point. Hence, one can, as a first approximation, use the tensor $\mathbf {S}_{Mises}$ instead of $\mathbf {S}$ in the limiting case $K \rightarrow \infty$. Suitable values for $\mu _0$ and $\kappa _0$ must consequently be used. In order to achieve this goal, the deviatoric and hydrostatic projections of both tensors lead to

$$\begin{aligned} \mu _0=\frac{5}{\frac{K}{\lambda }+\frac{K}{\rho }}, \, \kappa _0=\kappa \end{aligned}$$

(18)

Thus, using the identity (18), one can readily show that in the limit $\rho \rightarrow \infty$, $\kappa \rightarrow \infty$ and $K \rightarrow \infty$, the microstructural tensor $\widehat{\mathbf {S}}^{*}_{K}$ leads to equation (7).