Evaluation of transformation region around crack tip in shape memory alloys

Abstract

When an edge cracked shape memory alloy (SMA) plate is loaded, phase transformation around the crack tip results in a non-homogeneous region composed of austenite and martensite phases that affects its fracture behavior. In this work, the size of the phase transformation region surrounding the tip of an edge crack in a thin SMA plate is calculated analytically using a transformation function that governs forward phase transformation, together with crack tip asymptotic stress equations. Stress intensity factors required in the asymptotic equations are obtained from a least squares fit of full displacement field, calculated using finite elements, to asymptotic near-tip opening displacement equation. The present work predicts the size and shape of the transformation region in closed form. For comparison purposes, the region is also calculated using ABAQUS with user defined material subroutines (UMAT) for plane strain and plane stress. Transformation regions calculated analytically and computationally are plotted with experimental, analytical and numerical results available in the literature; the results show a good agreement with the experimental results.

1 Introduction

Upon loading, edge cracked SMAs experience austenite to martensite phase transformation immediately around crack tip. In recent years, although works on the extent of martensitic and phase transformation regions around crack tip have been presented, accurate comparisons to experimental results are limited: Birman (1998) was the first to calculate the phase transformation region around a center crack in an SMA plate as a function of external loading using phase transformation equation of Tanaka and Sato (1986) together with crack tip asymptotic stress equations. Following a similar approach, Yi and Gao (2000) used the phase transformation function given by Sun and Hwang (1993a, b), which they called the yield condition of SMAs, to calculate the transformation region around the tip of an edge crack. Xiong and Liu (2007) extended the work of Birman (1998) by considering stress redistribution as a result of phase transformation, and calculated the extent of the transformation region analytically.

In addition to these analytical approaches the transformation region was also calculated numerically: Wang (2006) defined NiTi as an elastic-plastic material and used uniaxial tensile stress-strain data in ABAQUS to study phase transformation and to calculate plastically deformed region boundaries under mode I loading. Freed and Banks-Sills (2007) used the transformation surface equation proposed by Panoskaltsis et al. (2004), and crack tip asymptotic stress equations, to calculate the transformation region around the tip of an edge crack under mode I loading. Falvo et al. (2009) used both $\sigma _y = K_I / \sqrt{{2\pi r}}$ and $\sigma _y=K_{Ieff} /$ $\sqrt{2\pi ({r-r_y})}$ to predict the extent of phase transformation region (PTR) along the crack line in a NiTi based SMA under plane stress. They compared their prediction to the results they obtained using MARC and showed that improved results can be obtained when Irwin’s plasticity corrected formula is used. Very similar to their previous work (Falvo et al. 2009), Maletta and Furgiuele (2010) used bilinear stress-strain relation together with Irwin’s plasticity corrected equation to calculate the extent of martensitic region. They showed that their analytical calculations are in agreement with finite elements (FE) results. Baxevanis et al. (2012) implemented the constitutive model of Lagoudas et al. (1996) into ABAQUS to determine the size and the shape of the phase transformation region. They also estimated the size of the transformation region modifying Irwin’s formulation for mode II (Du and Hancock 1991), compared the two set of results and claimed that the formulation could be used to approximate the transformation zone.

In experimental studies, digital image correlation (DIC) and X-ray diffraction were used to obtain phase transformation region around the tip of a crack. Daly et al. (2007) used DIC on an edge cracked thin sheet of NiTi under mode I loading to measure strain field around the crack tip and determined the extent of the transformation along the crack. They obtained an empirical expression between the extent of transformation region and the applied load. Robertson et al. (2007) used X-ray diffraction to obtain local strain maps around the tip of an edge crack in a thin Nitinol specimen. They presented a detailed strain map that showed the transformed martensitic region; they concluded that although the size was different the transformation zone shape was consistent with the shape predicted by linear elastic fracture mechanics (LEFM). Gollerthan et al. (2008) conducted experiments on a compact tension (CT) specimen under mode I loading and observed the deformed region around the crack tip. They adopted the formulation proposed by Irwin, $r_p=\frac{1}{3\pi }\left( \frac{K_{max}}{\sigma _{ave}}\right) ^2$ where $K_{max}$ is critical stress intensity factor (SIF) at the onset of crack growth and $\sigma _{ave}$ is average plateau stress, to estimate the length of the phase transformation region ahead of crack. They claimed that phase transformation radius they calculated corresponded well to the visual post-mortem observations of the CT specimens. The radius from the crack tip to the affected zone (visually observable for polished superelastic NiTi surfaces) was about the same as the predicted radius (which is approximately 3mm). In a separate study, Gollerthan et al. (2009) obtained phase transformation zone around the crack tip of an edge cracked NiTi specimen using in-situ synchrotron measurements. They observed stress induced martensite (up to a martensite volume fraction, $\zeta$, of 0.4) around the tip with a small plastic region. However they did not compare their results to those of 2008. Recently, Young et al. (2013) measured strain field using synchrotron X-ray diffraction and determined phase transformation region around crack tip under mode I loading. They obtained a phase transformation region similar to the one presented by Gollerthan et al. (2009). They stated that, extent of the transformation zone calculated using equations presented by Gollerthan et al. (2008) was in agreement with the result of their experiments.

Table 1 Summary of studies in literature on PTR around crack tip in edge cracked SMAs under mode I loading. Works on other type of cracks are denoted

In literature, there are some studies that compare analytical calculations to experimental measurements: Lexcellent and Thiebaud (2008) used the LEFM based yield criterion of Lexcellent and Blanc (2004) together with asymptotic crack tip stress equations to determine the transformation region under mode I loading for both plane stress and plane strain. Their results showed a considerable difference with the experimental results of Robertson et al. (2007). Lexcellent et al. (2011) extended the study of Lexcellent and Thiebaud (2008) and determined the transformation region around the crack tip under mode II, mode III and mixed mode loading. Maletta and Young (2011) used the model of Maletta and Furgiuele (2010), that was limited to plane stress, to determine the length of the phase transformation region along the crack line under plane strain. The region they calculated for plane strain was smaller than that of plane stress. They compared their results to the experimental results of Gollerthan et al. (2009) and observed that experimentally calculated phase transformation length was between the length they calculated for plane stress and the one calculated for plane strain. Taillebot et al. (2012) predicted the size of the transformation region around the notched NiTi specimen using strain field obtained from DIC. Their experimental results showed that, the height of the transformation region is almost one third of the height they calculated using the formulation given by Lexcellent et al. (2011).

Works on the evaluation of transformation region around crack tip in SMAs are summarized in Table 1.

In this paper, the boundary of martensitic and phase transformation regions around a crack tip are calculated analytically using the transformation function proposed by Zaki and Moumni (2007) together with the asymptotic stress equations and also using FE. The analytical and computational results obtained are compared to experimental results presented by Robertson et al. (2007), Gollerthan et al. (2009) and Daly et al. (2007); analytical predictions of Freed and Banks-Sills (2007) and Maletta and Young (2011); and computational prediction of Baxevanis et al. (2012).

Fig. 1

a Edge cracked SMA CT specimen. b Uniaxial stress-strain behavior of super-elastic Nitinol

2 Problem statement and formulation

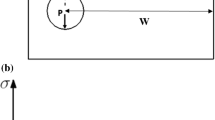
The geometry of the edge cracked thin SMA plate used in this study is shown in Fig. 1a. The plate is loaded in y-direction and a superelastic phase transformation occurs around the crack tip. Forward phase transformation is governed by the following transformation function, $F_{\zeta }$, proposed by Zaki and Moumni (2007):

$$\begin{aligned} {F}_{\zeta }= & {} \left\{ E^{\prime } \frac{\sigma _{e}^{2}}{3} +\frac{1}{2} \left( {\frac{1}{3} E^{\prime } + \nu ^{\prime }}\right) {\sigma _{ii}^2 }- C(T) \right\} \nonumber \\&+\, \sigma _{ij} {\varepsilon }_{ij}^{ori} -(\varGamma + b) \zeta - a (1 - \zeta ) \nonumber \\&-\,\left[ (\alpha - \beta ) \zeta + \frac{\beta }{2}\right] \left( \frac{2}{3}{\varepsilon }_{ij}^{ori} {\varepsilon }_{ij}^{ori} \right) . \end{aligned}$$

(1)

A summary of ZM model is given in the Appendix. When $F_{\zeta }=0$, transformation from austenite to martensite occurs. In Eq. (1) $\sigma _{e}$ is the von Mises stress, $\sigma _{e}=\sqrt{\frac{3}{2} \sigma ^{d}_{ij} \sigma ^{d}_{ij} }$, $\sigma _{ij}$ is the Cauchy stress tensor, $\sigma ^{d}_{ij}$ is the deviatoric part and $\sigma _{ii}$ is the trace of $\sigma _{ij}$. $E^{\prime }$ and $\nu ^{\prime }$ are given below:

$$\begin{aligned} E^{\prime }=\frac{(1+\nu )(E_A-E_M)}{E_AE_M},\quad \nu ^{\prime }=\frac{\nu (E_M-E_A)}{E_ME_A}, \nonumber \\ \end{aligned}$$

(2)

where $E_A$ and $E_M$ are the elastic moduli of austenite and martensite; $\nu$ is Poisson’s ratio of the material ($\nu _A=\nu _M=\nu$), $\zeta$ is volume fraction of martensite and a and b are defined as

$$\begin{aligned} a= & {} \frac{1}{2}\left[ \left( \frac{1}{E_M}\,{-}\,\frac{1}{E_A}\right) \frac{\sigma ^2_{MS}{-}\sigma ^2_{AF}}{2}\,{+}\, (\sigma _{MS}{-}\sigma _{AF})\varepsilon _0 \right] , \nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} b= & {} \frac{1}{2}\left[ \left( \frac{1}{E_M}\,{-}\,\frac{1}{E_A}\right) \frac{\sigma ^2_{MF}{-}\sigma ^2_{AS}}{2}\,{+}\, (\sigma _{MF}{-}\sigma _{AS})\varepsilon _0 \right] ,\nonumber \\ \end{aligned}$$

(4)

$\sigma _{MS}$, $\sigma _{MF}$, $\sigma _{AS}$ and $\sigma _{AF}$ are martensite start, martensite finish, austenite start and austenite finish stresses respectively; ${\varepsilon }_{{0}}$ is the equivalent transformation strain as shown in Fig. 1b. C(T) is phase change heat density. $\alpha$ controls the slope of the stress-strain curve corresponding to martensite orientation through relation $(\sigma _{rf}-\sigma _{rs})/({\varepsilon }_{{0}})$, where $\sigma _{rs}$ and $\sigma _{rf}$ are orientation start and finish stresses. $\beta$ controls the level of orientation of martensite variants and defined as $\sigma _{rf}/{\varepsilon }_{{0}}$. ${\varepsilon }_{ij}^{ori}$ is the strain as a result of orientation of martensite variants which can be defined as follows (Morin et al. 2011):

$$\begin{aligned} {\varepsilon }_{ij}^{ori}=\frac{3}{2}{\varepsilon }_{{o}}\frac{\sigma ^{d}_{ij}}{\sigma _{e}}. \end{aligned}$$

(5)

Stresses $\sigma _{ij}$ that are needed in the evaluation of the transformation function ${F}_{\zeta }$, are calculated using asymptotic stress equations given below (Williams 1957):

$$\begin{aligned}&\sigma _{xx} = \frac{{K_I }}{{\sqrt{2\pi r} }}\cos \frac{\theta }{2}\left[ {1 - \sin \frac{\theta }{2}\sin \frac{{3\theta }}{2}} \right] +\cdots \text {,} \end{aligned}$$

(6)

$$\begin{aligned}&\sigma _{yy}=\frac{{K_I }}{{\sqrt{2\pi r} }}\cos \frac{\theta }{2}\left[ {1 + \sin \frac{\theta }{2}\sin \frac{{3\theta }}{2}} \right] +\cdots \text {,} \end{aligned}$$

(7)

$$\begin{aligned}&\tau _{xy}=\frac{{K_I }}{{\sqrt{2\pi r} }}\cos \frac{\theta }{2}\sin \frac{\theta }{2}\cos \frac{{3\theta }}{2}+\cdots \end{aligned}$$

(8)

where $K_I$ is the mode I SIF.

3 Finite element analysis and evaluation of stress intensity factor

SIF that is needed in Eqs. (6), (7) and (8) are calculated using asymptotic near-tip opening displacement, $u_y$, and fitting to the equation the full displacement field obtained from finite elements (Oral et al. 2008);

$$\begin{aligned} { u }_{ y }\,=&\, \frac{ { K }_{ I } }{ 2\mu _{tip} } { \left( \frac{ r }{ 2\pi } \right) }^{ \frac{ 1 }{ 2 } }\sin \frac{ \theta }{ 2 } \left( \frac{ 3-\nu }{ 1+\nu } -\cos \theta \right) \nonumber \\&-\frac{ (T-stress) \nu }{ 2\mu _{tip} (1+\nu ) } r\sin \theta +\frac{ { K }_{ II } }{ 4\mu _{tip} } { \left( \frac{ r }{ 2\pi } \right) }^{ \frac{ 1 }{ 2 } } \nonumber \\&\times \, \left( \frac{ 5\nu -3 }{ 1{+}\nu } \cos \frac{ \theta }{ 2 } {-}\cos \frac{ 3\theta }{ 2 } \right) {+}{ A }_{ 1 }r\cos \theta +{ u }_{ 0y }, \end{aligned}$$

(9)

where T-stress is the stress component parallel to the crack plane, $A_1$ and $u_{oy}$ are rigid body rotation and displacement, $\nu$ is Poisson’s ratio, $\mu _{tip}$ is shear modulus of the crack tip. Using ABAQUS, the edge cracked problem shown in Fig. 1a is solved for $P=32$ N, $B=0.4$ mm (thickness), $W=10.8$ mm, $a=5.4$ mm, $h=6.4$ mm to compare to the results of Robertson et al. (2007). Assuming symmetry, only the upper half of the plate is modeled with eight-node biquadratic plane stress quadrilateral (CPS8R) elements. A more detailed example of implementation of ZM model in ABAQUS using UMAT to analyze the steady state crack growth can be found in Hazar et al. (2015). In the analysis, properties of Nitinol-SE508 from Nitinol Devices and Components Company (NDC) with austenite finish temperature ($A_f$) of $15^\circ$C are used; missing parameters are derived from experimental data provided by the study of Pelton et al. (2000).

All three values of $K_I$, $K_{II}$, and $T-stress$ with $A_1$ and $u_{0y}$, are obtained simultaneously through a least squares fit. $K_{II}$ is calculated to be $0.03~\mathrm{MPa}\sqrt{m}$ which is small compared to $K_I$=$7.3~\mathrm{MPa}\sqrt{m}$. If asymptotic equations with $K_I$ alone are used neglecting $K_{II}$; $K_I$ is obtained to be $7.35~\mathrm{MPa}\sqrt{m}$. Because $K_{II}$ is small in this study the rest of the calculations are carried out using $K_I$ only. Figure 2 shows displacement contour plots around the crack tip that are obtained by least squares fit of FE data to Eq. (9) and full field displacement contour plots obtained directly from FE.

Fig. 2

Contours of $u_y$. (Dashed lines with values in boxes are FE results, solid lines are from least squares fit of Eq. (9) to FE results

The stress intensity factor is also calculated using the following equation (Anderson 2004):

$$\begin{aligned} K = \frac{P}{B\sqrt{W}}f\left( \frac{a}{W}\right) , \end{aligned}$$

(10)

where $f(\frac{a}{W})$ is a geometric factor (ASTM 2013) with $P=32~N$ again. $K_I$ is obtained to be $K_{I}=7.5\,\mathrm{MPa}\sqrt{m}$. As expected $K_I$ calculated using Eq. (10), where phase transformation is not taken into account, is higher than the $K_I$ determined using FE. As a result in subsequent calculations $K_I=7.35$ $MPa\sqrt{m}$ is used in asymptotic equations to calculate stresses.

In Fig. 3 contours of $\sigma _{yy}$ obtained using Eq. (7) and contours obtained from ABAQUS are plotted together. Around crack tip, the difference in $\sigma _{yy}$ appears to be acceptable as shown in detail in Fig. 3b.

The same procedure is applied to calculate SIF under plane strain conditions to compare with the results of Gollerthan et al. (2009). In this case, the edge cracked problem shown in Fig. 1a is solved for $P=2860~N$, $B=8$ mm, $W=16$ mm and $a/W=0.55$ mm using eight-node plane strain (CPE8R) elements. In this case, $K_I$ calculated using Eq. (10) is close to $K_I$ determined using FE; $K_I$ is obtained to be $32.1~MPa\sqrt{m}$.

Fig. 3

a Contour plot of normalized opening stress, $\frac{\sigma _{yy}}{{\sigma _{0}}}$ ($\sigma _{0}$ being far field applied stress), calculated from the full field finite element solution (green lines) and from the asymptotic field (black lines). Red line represents martensite region $\zeta =1$ and the region between red and blue lines is the transformation region $0<\zeta <1$. In both cases crack tip is located at the origin and only half plate is shown. b close up view of the stress contours, $\frac{\sigma _{yy}}{{\sigma _{0}}}$, near the crack tip

4 Evaluation of transformation region under plane stress condition

Using asymptotic equations for $\sigma _{ij}$, $\sigma _{e}$ is obtained as follows:

$$\begin{aligned} \sigma _{e}=\frac{{K_I }}{{2 \sqrt{\pi r} } }\left[ 1 + \cos \theta + \frac{3 }{2}\sin ^2 \theta \right] ^{1/2}, \end{aligned}$$

(11)

similarly,

$$\begin{aligned}&\sigma _{ii}=\frac{{K_I }}{{2 \sqrt{\pi r} } }\left[ 1 + \cos \theta \right] ^{1/2}, \end{aligned}$$

(12)

$$\begin{aligned}&{\varepsilon }_{ij}^{ori}{\sigma _{ij}}={\varepsilon }_{{o}}\frac{{K_I }}{{2\sqrt{ \pi r} }} {\left[ 1 + \cos \theta + \frac{3 }{2}\sin ^2 \theta \right] }^{1/2}. \end{aligned}$$

(13)

If Eqs. (11), (12) and (13) are inserted into Eq. (1) and the result is equated to zero, the following equation will be obtained:

$$\begin{aligned}&E^{\prime } \frac{{K_I^2 }}{{12 \pi r_M} }\left[ 1 + \cos \theta + \frac{3 }{2}\sin ^2 \theta \right] \nonumber \\&\quad +\,\frac{1}{2} \left( {\frac{1}{3} E^{\prime } + \nu ^{\prime }}\right) {\frac{{K_I }^2}{{ 4 \pi r_M} } \left[ 1+\cos \theta \right] } \\&\quad -\,C(T)+ {\varepsilon }_{{o}}\frac{{K_I }}{{2\sqrt{ \pi r_M} }}\sqrt{\left[ 1 + \cos \theta + \frac{3 }{2}\sin ^2 \theta \right] } \nonumber \\&\quad -\,(\varGamma {+} b) \zeta -a(1-\zeta ){-} \left( (\alpha - \beta )\zeta {+} \frac{\beta }{2}\right) {\varepsilon }_{{o}}^2=0.\nonumber \end{aligned}$$

(14)

Equation (14) can then be solved for $r_M$, with martensite volume fraction, $\zeta = 1$, to obtain the extent of martensitic region around crack tip. Figure 4 shows martensitic transformation region obtained is in a good agreement with experimental measurements of Robertson et al. (2007).

Fig. 4

Martensitic region around crack tip

Using Eq. (14) and material properties of NiTi given by Daly et al. (2007) the phase transformation region, $r_{tr}$ (when $\zeta =0^+$), is calculated for four different loading conditions, $K_I=28 , 38, 47, 51~\mathrm{MPa} \sqrt{m}$, and plotted in Fig. 5. Figure 6 represents the comparison of extent of transformation region along the crack extension line calculated using Eq. (14) to the experimental results of Daly et al. (2007).

Fig. 5

Effect of SIF on transformation region. $W=13$ mm

Fig. 6

Effect of SIF on the extent of transformation region. $W=13$ mm, superelastic plateau stress $\sigma _{tr}=500$ MPa

5 Evaluation of transformation region under plane strain condition

Under plane strain condition Eqs. (11), (12) and (13) can be written as:

$$\begin{aligned}&{{\sigma }_{e}}=\frac{{{K}_{I}}}{2\sqrt{\pi r}}{{\left[ {{\left( 1-2\nu \right) }^{2}}(1+\cos \theta )+\frac{3}{2}{{\sin }^{2}}\theta \right] }^{\frac{1}{2}}} \end{aligned}$$

(15)

$$\begin{aligned}&\sigma _{ii}=\frac{{K_I }}{{ 2\sqrt{ \pi r} } } \left[ 1 + \cos \theta \right] ^{1/2}(1+\nu ) \end{aligned}$$

(16)

$$\begin{aligned}&{\varepsilon }_{ij}^{ori}{\sigma _{ij}}=\frac{{{K}_{I}}}{2\sqrt{\pi r}}{{\left[ {{\left( 1-2\nu \right) }^{2}}(1+\cos \theta )+\frac{3}{2}{{\sin }^{2}}\theta \right] }^{\frac{1}{2}}}\nonumber \\ \end{aligned}$$

(17)

If Eqs. (15), (16) and (17) are inserted into Eq. (1), and the result is equated to zero, the following equation will be obtained:

$$\begin{aligned}&E^{\prime } \frac{{K_I^2 }}{{12 \pi r_M} }\left[ (1 + \cos \theta )(1-2\nu )^2 + \frac{3 }{2}\sin ^2 \theta \right] \nonumber \\&\quad +\,\frac{1}{2} \left( {\frac{1}{3} E^{\prime } + \nu ^{\prime }}\right) {\frac{{K_I }^2}{{ 2 \pi r_M} } \left[ \cos \frac{\theta }{2} (1+\nu ) \right] ^2 }\nonumber \\&\quad -\,C(T)+ {\varepsilon }_{{o}}\frac{{K_I }}{{2\sqrt{ \pi r_M} }}\\&\quad \times \,\sqrt{\left[ (1 + \cos \theta )(1-2\nu )^2 + \frac{3 }{2}\sin ^2 \theta \right] }\nonumber \\&\quad -\,(\varGamma + b) \zeta -a(1-\zeta ){-} \left( (\alpha {-} \beta )\zeta {+} \frac{\beta }{2}\right) {\varepsilon }_{{o}}^2=0. \nonumber \end{aligned}$$

(18)

Figure 7 shows the comparison of phase transformation region ($\zeta =0^+$) calculated using Eq. (18) and also using FE to the measurements of Gollerthan et al. (2009) and analytical results of Maletta and Young (2011) under plane strain conditions. In the FE analysis, the CT specimen is modeled as given in Fig. 1, for $P=2860$ N using the material properties of NiTi SMA (SE508) given by Gollerthan et al. (2009). In the analytic calculation previously calculated SIF, $K_I=32.1$ $\,MPa\sqrt{m}$ is used. $\zeta$ contours calculated using Eq. (18) are also compared to measurements of Gollerthan et al. (2009) as shown in Fig. 8.

Fig. 7

Phase transformation region around crack tip. Dashed lines are plane strain and full lines (magenta, black, green) are plane stress results

Fig. 8

$\zeta$ contours around the crack tip. Blue lines are plane stress and red lines are plane strain results of the present study. Green lines represent the experimental results of Gollerthan et al. (2009)

Freed and Banks-Sills (2007) predicted the martensitic region ($\zeta =1$) using the following equation

$$\begin{aligned} {{r}_{M}}=\frac{1}{2\pi }{{\left[ \frac{{{K}_{I}}}{{{C}_{M}}(T-{{M}_{f}})} \right] }^{2}}{{\cos }^{2}}\frac{\theta }{2}\left[ {{\kappa }^{*}}+3\sin \frac{\theta }{2} \right] \text {,} \nonumber \\ \end{aligned}$$

(19)

and the PTR ($\zeta =0^+$), using

$$\begin{aligned} {{r}_{A}}=\frac{1}{2\pi }{{\left[ \frac{{{K}_{I}}}{{{C}_{M}}(T-{{M}_{s}})} \right] }^{2}}{{\cos }^{2}}\frac{\theta }{2}\left[ {{\kappa }^{*}}+3\sin \frac{\theta }{2} \right] \text {,} \nonumber \\ \end{aligned}$$

(20)

where $C_M$ is the slope of stress – martensite start temperature curve defined as; ${{\sigma }_{MS}}={{C}_{M}}(T-{{M}_{s}})$, ${M}_{s}$ and ${M}_{f}$ are martensite start and finish temperatures. ${{\kappa }^{*}}=1$ for plane stress and ${{\kappa }^{*}}=(1-2\nu )^2$ for plane strain.

Using the material properties given by Baxevanis et al. (2012) ($E_M=38$ GPa, $E_A=69$ GPa, $\sigma _{tr}=500$ MPa, $\epsilon _0=0.06$, ${M}_{f}=319$ K, ${M}_{s}=321$ K, $C_M=8.7$ MPa, $T=353$ K) the PTR and martensitic region calculated using Eqs. (19) and (20) are compared to the regions obtained using Eq. (18) and numerical results of Baxevanis et al. (2012) (see Fig. 9).

Fig. 9

Phase transformation region around crack tip. The length parameters are normalized by $R=\frac{{{K}_{I}}^{2}}{3\pi {{\sigma }_{MS}}}$ (Baxevanis et al. 2012)

6 Discussions and conclusions

In results presented in this work, the stress distribution around the crack tip does not match exactly the asymptotic stress distribution due to the existence of a phase transformation region surrounding the crack tip, but converges to an acceptable difference in the fully martensitic region (see Fig. 3). Hence FE calculations gave a better estimate of the extent of transformation region compared to analytical calculations as shown in Fig. 4, but still analytically calculated size and shape of the transformation region is in a good agreement with the experimental results of Robertson et al. (2007). In the only other comparison in literature, the yield criterion for Nitinol used by Lexcellent and Blanc (2004) predicts a transformation zone considerably larger than the experimental results of Robertson et al. (2007). In Fig. 4, dashed blue line represents the region of untransformed austenite grains that resisted transformation as a result of grain orientation (local texture); this region is surrounded by martensite. If that region is directly included to transformation region as well, results presented in this paper match even better the experimental results of Robertson et al. (2007).

As mentioned earlier, stress intensity factors have to be determined accurately for correct calculation of the phase transformation region using Eqs. (14) and (18). Daly et al. (2007) used Eq. (10) to calculate SIFs, which is used to estimate SIF for linear elastic materials. In their calculations, toughness increase due to phase transformation is not taken into consideration and predicted SIFs are expected to be higher. Using SIFs that are calculated by Daly et al. (2007) change in the size of the PTR is plotted in Fig. 5 to see the effect of the SIF on the transformation region. Then the extent of transformation region calculated is compared to the one given by Daly et al. (2007) and plotted in Fig. 6. Because Eq. (10) is used in SIF calculations, the extent of transformation region deviates from experimental measurements especially at higher stresses when the transformation region enlarges as seen in Fig. 6. For lower values of SIFs the results are in a better agreement with the experimental measurements.

In SMAs; equivalent stress dependency of phase transformation, existence of non-homogeneous phase transformation region and evolution of multi-axial transformation strains makes it difficult to predict PTR boundary when only uniaxial strains are considered. Daly et al. (2007) used the strain field measured from DIC and obtained the extent of transformation region at the point where, $\varepsilon _{22} \approx 1.5\,\%$ ($\varepsilon _{22}$ is the strain in loading direction). Whereas, experimental results of Young et al. (2013) showed that the largest micro-strains in the loading and transverse directions were not obtained at the point of highest martensite fraction. The phase transformation equation (Eq. 1) used in this work is a function of equivalent stress $\sigma _e$, orientation strain tensor ${\varepsilon }_{ij}^{ori}$ and also depends on transformation and orientation start and finish stresses ($\sigma _{MF}$, $\sigma _{MS}$, $\sigma _{AF}$, $\sigma _{AS}$, $\sigma _{rf}$, and $\sigma _{rs}$) through material parameters, and phase transformation region can be determined more accurately under multi-axial stress state.

In Fig. 7, the size and the shape of the calculated PTR are then compared to the experimental results (CT specimen) of Gollerthan et al. (2009) together with the results of Maletta and Young (2011) who compared their analytical calculations to the same experimental results. Results of the present study and those of Maletta and Young (2011) predicted a larger transformation zone for plane stress but a smaller one for plane strain compared to experimental results of Gollerthan et al. (2009). Maletta and Young (2011) stated that in the study of Gollerthan et al. (2009) the martensite fractions are measured as volumetric averages through the thickness of specimen. As a result, the experimental results of Gollerthan et al. (2009) are in between plane stress and plane strain results of Maletta and Young (2011) and the current study. The analytical calculations of Maletta and Young (2011) and the results of the current study are plotted in Fig. 7, where it is seen that the PTR found in this study is in better agreement with experimental results. Using Eqs. (14) and (18) $\zeta$ contours are plotted in Fig. 8 and the results are compared to $\zeta$ contours presented by Gollerthan et al. (2009) to show that phase transformation contours (for $\zeta =0.1$–0.3) that are plotted in Fig. 8 can be used to predict not only PTR boundary ($\zeta =0^+$) but also $\zeta$ contours ( $0<\zeta < 1$) around the crack tip.

In Fig. 9, phase transformation regions calculated by Baxevanis et al. (2012) and Freed and Banks-Sills (2007) are compared to the results of present study. The martensitic region ($\zeta =1$) around the crack tip calculated by Baxevanis et al. (2012) is smaller, and the region calculated by Freed and Banks-Sills (2007) is greater than the one calculated by present study. Although the PTR predictions of the presents study differ from the available analytical and numerical results, they are in good agreement with the experimental results. It is suggested that previous analytical and numerical studies should be compared to the results of experiments.

These comparisons with the experimental measurements show that, because Eqs. (14) and (18) are given in closed form, the size and the shape of the transformation region around the crack tip can be evaluated for a given load and material properties once the stress intensity factor is calculated properly. The proposed analytical solution can be used to calculate the energy dissipated around the crack tip as a result of phase transformation and to predict the effect of phase transformation on toughness.

Appendix

The Helmholtz free energy used in ZM model is formulated as follows:

$$\begin{aligned}&\varPsi \left( \varepsilon _{ij}^{A},\varepsilon _{ij}^{M},T,\zeta ,\varepsilon _{ij}^{ori}\right) =(1-\zeta )\left[ \frac{1}{2}\varepsilon _{ij}^{A} E_{ijkl}^{A}{\varepsilon }_{kl}^{A}\right] \nonumber \\&\qquad +\,\zeta \left[ \frac{1}{2}\left( {\varepsilon }_{ij}^{M} - {\varepsilon }_{ij}^{ori}\right) E_{ijkl}^{M}\left( {\varepsilon }_{kl}^{M} - {\varepsilon }_{kl}^{ori}\right) + C(T)\right] \\&\qquad +\,\varGamma \frac{\zeta ^{2}}{2} + \frac{\zeta }{2}\left[ \alpha \zeta + \beta (1 - \zeta )\right] \frac{2}{3} {\varepsilon }_{ij}^{ori} {\varepsilon }_{ij}^{ori}\text {.} \nonumber \end{aligned}$$

(21)

In the equation above ${\varepsilon }_{ij}^{M}$ and ${\varepsilon }_{ij}^{A}$ are local strain tensors of martensite and austenite phases. $\varGamma$ is defined as

$$\begin{aligned} \varGamma= & {} \frac{1}{2} \left[ \left( \frac{1}{E_M}-\frac{1}{E_A}\right) \frac{\sigma ^2_{MF}-\sigma ^2_{MS} + \sigma ^2_{AS}-\sigma ^2_{AF}}{2} \right. \nonumber \\&\left. +\, (\sigma _{MF}-\sigma _{MS}+\sigma _{AS}-\sigma _{AF} ) \varepsilon _0 - 2(\alpha -\beta ) \varepsilon ^2_0 \right] \nonumber \\ \end{aligned}$$

(22)

In the model, Reuss scheme is used to relate the total strain ${\varepsilon }_{ij}$ to the strains of austenite and martensite phases as given below:

$$\begin{aligned} {\varepsilon }_{ij}=(1 - \zeta ){\varepsilon }_{ij}^{A}+\zeta {\varepsilon }_{ij}^{M} \text {,} \end{aligned}$$

(23)

the internal state variable $\zeta$ should be bounded in the interval [0, 1], therefore:

$$\begin{aligned} \zeta \geqslant 0 \quad \text {and} \quad (1 - \zeta ) \geqslant 0 \text {,} \end{aligned}$$

(24)

and the equivalent orientation strain, $\varepsilon _{0}$ as shown in Fig. 1b, has the following maximum value:

$$\begin{aligned} {\varepsilon }_{0}-\sqrt{\frac{2}{3} {\varepsilon }_{ij}^{ori}{\varepsilon }_{ij}^{ori}} \geqslant 0 \text {.} \end{aligned}$$

(25)

Equations (23), (24) and (25) are used to build the following constraints potential ${\varPsi }_{c}$ (Moumni 1995):

$$\begin{aligned} \begin{aligned} {\varPsi }_{c}=&-\lambda _{ij} [{(1 - \zeta ) {\varepsilon }_{ij}^A+\zeta {\varepsilon }_{ij}^M-{\varepsilon }_{ij}}] \\&-\,\left( { {\varepsilon }_{0} -\sqrt{\frac{2}{3} {\varepsilon }_{ij}^{ori}{\varepsilon }_{ij}^{ori}}} \right) - \nu _{1} \zeta - \nu _{2} ({1 - z}) \text {,} \end{aligned} \end{aligned}$$

(26)

where the Lagrange multipliers $\lambda$, $\mu$, $\nu _{1}$, $\nu _{2}$ and $\mu$ obey the following conditions:

$$\begin{aligned} \begin{aligned}&\nu _{1} \geqslant 0 , \quad \nu _{1} \zeta = 0 ,\quad \nu _{2} \geqslant 0 , \quad \nu _{2} (1 - \zeta ) = 0\\&\text {and} \quad \mu \geqslant 0 , \mu \left( {\varepsilon }_{0} - \sqrt{\dfrac{2}{3} {\varepsilon }_{ori} {\varepsilon }_{ori} }\right) =0\text {.} \end{aligned} \end{aligned}$$

(27)

The sum of the Helmholtz energy density, Eq. (21), and the potential ${\varPsi }_{c}$, Eq. (26), gives the Lagrangian, which is then used to derive the state equations, and the following stress–strain relation is obtained:

$$\begin{aligned} \sigma _{ij} ={S_{ijkl}^{-1}}:\left( {{\varepsilon _{kl}}-\zeta {\varepsilon }_{kl}^{{ori}}}\right) \text {,} \end{aligned}$$

(28)

in which ${S_{ijkl}}$ is the compliance tensor defined as:

$$\begin{aligned} S_{ijkl} =(1 - \zeta ) S_{ijkl}^{A}+\zeta S_{ijkl}^{M}\text {,} \end{aligned}$$

(29)

where $S_{ijkl}^{A}$ and $S_{ijkl}^{M}$ are the compliance tensors of austenite and martensite phases respectively.

According to the theory of generalized standard materials with internal constraints represented by Halphen and Nguyen (1974), the thermodynamic forces that are related to the internal state variables $\zeta$ and ${\varepsilon }_{ij}^{{ori}}$ are sub-gradients of a pseudo-potential. The pseudo-potential of dissipation defined by Zaki and Moumni (2007) is given as follows:

$$\begin{aligned} \mathcal {D}(\dot{\zeta },\dot{\varepsilon }_{ij}^{{ori}}) =[{a (1 - \zeta )+ b \zeta }] |\dot{\zeta }| + \zeta ^{2} Y \sqrt{ \frac{2}{3} \dot{\varepsilon }_{ij}^{{ori}}\dot{\varepsilon }_{ij}^{{ori}} }\text {.} \end{aligned}$$

(30)

In the equation above Y is a positive material constant associated with $\sigma _{rs}$. The pseudo-potential of dissipation, $\mathcal {D}(\dot{\zeta },\dot{\varepsilon }_{ij}^{{ori}})$, allows the definition of transformation function, $F_{\zeta }$ given in Eq. (1).