ELECTRE II method based on the cosine similarity to evaluate the performance of financial logistics enterprises under double hierarchy hesitant fuzzy linguistic environment

Abstract

It is very common to use linguistic information to solve decision-making problems in real life, and the double hierarchy hesitant fuzzy linguistic term set (DHHFLTS) has been widely used because of its powerful ability of expressing complex linguistic information. There is no doubt that the comparison method of double hierarchy hesitant fuzzy linguistic elements (DHHFLEs) not only occupies an important theoretical and practical position, but also is the basis for further study of DHHFLTSs. However, the existing comparison methods of DHHFLEs still have some limitations. Therefore, this paper proposes a new DHHFLE comparison method, which is an improvement and perfection of the existing DHHFLE comparison methods. In addition, considering that the current research on distance and similarity measures of DHHFLEs is mostly based on the algebraic point of view, this paper proposes a cosine similarity measure of DHHFLEs, which fills the gap in the study of distance and similarity measures from the geometric point of view. Then, the cosine similarity-based DHHFL-ELECTRE II method is proposed to solve the multi-attribute decision-making (MADM) problem in the double hierarchy hesitant fuzzy linguistic environment. Finally, this method is used to solve a MADM problem in the performance evaluation of financial logistics enterprises. The results show that the proposed method has certain applicability and feasibility.

1 Introduction

As a medium of daily communication, natural language is the most commonly used way of communication and expression of views, and also the main carrier of expressing views on qualitative decision-making problems. Therefore, how to model linguistic information and make the right decision has extensive and profound practical significance. In order to evaluate the information contained in natural language, Zadeh (2012) proposed the concept of Computing with Words (CWW). On this basis, many scholars have made outstanding contributions (Morente-Molinera et al., 2015; Rodríguez et al., 2012; Wang & Hao, 2006). The double hierarchy linguistic term set (DHLTS) (Gou et al., 2017) is developed on the basis of the general linguistic term set (LTS). The first hierarchy LTS is described and supplemented by the second hierarchy LTS to enhance the ability of extracting linguistic information. The current research on DHLTS can be summarized as follows: Firstly, fundamental operational laws were put forward, and then, scholars proposed three methods to compare double hierarchy hesitant fuzzy linguistic elements (DHHFLEs) (Gou & Xu, 2021; Gou et al., 2017; Wang et al., 2020). On this basis, Gou et al. (2018) proposed several distance and similarity measures for DHHFLEs and DHHFLTSs. In terms of decision-making methods, scholars conducted in-depth research from three aspects: outranking-based decision-making method (Liu et al., 2019), aggregation function-based decision-making method (Gou et al., 2021) and mathematical programming model (Liu et al., 2018).

As mentioned above, the operational law of DHHFLEs is the cornerstone of the whole theory, and the comparison method of two DHHFLEs is more important. At present, there are three methods to compare DHHFLEs. Although these three methods can play their respective advantages to a certain extent, they still have some limitations. The comparison method based on expected and variance value is very simple and easy to understand, but this method can only determine the size order of DHHFLEs, and lacks a unified standard to reflect the specific size of DHHFLEs. Additionally, the comparison method based on possibility degree only considers the upper and lower bounds of DHHFLEs, which cannot adequately utilize all the primitive information. Finally, the logic of the comparison method based on hesitancy degree is not self-consistent. In addition, the existing research of the similarity measure of DHHFLEs is mainly from the algebraic point of view, and rarely from the perspective of geometry. Therefore, a function is introduced to transform the DHHFLEs into corresponding unit vectors in this paper, and then the cosine measure is used to measure the similarity between the DHHFLEs.

On the other hand, a lot of achievements have been made in the research of decision-making methods of DHHFLTS. There are many ways to establish an outranking relation, while the ELECTRE (ELimination Et Choix Traduisant la REalité in French) method is one of them, including ELECTRE I, II, III, IV and TRI (Roy, 1968; Roy & Bertier, 1971; Roy & Hugonnard, 1982). On this basis, scholars summarized the general rules and widely extended these methods to the fuzzy field (Liao et al., 2020; Nadya et al., 2018; Rashid et al., 2018; Wu & Chen, 2011). In this series of methods, ELECTRE II has irreplaceable advantages in understanding the theoretical basis of ELECTRE method and solving practical problems (Roy, 1996). In addition, and the double hierarchy hesitant fuzzy linguistic information itself is incomplete and uncertain, it is reasonable to utilize the outranking relation to deal with this kind of information.

Financial logistics is the product of the combination of logistics services and financial services, which can be divided into broad sense and narrow sense. In the narrow sense, financial logistics mainly refers to the innovative service of logistics and finance integration provided by third-party logistics enterprises in the process of implementing supply chain management; In a broad sense, financial logistics usually refers to the logistics services related to internal management activities and business links provided by third-party logistics enterprises for customers in specific industries, such as banks, insurance companies and other financial customers. The performance standards of financial logistics enterprises are complex and diverse, including both quantitative factors such as financial indicators and qualitative factors such as non-financial indicators. For many qualitative factors involved, it is generally difficult to score with accurate values, and only qualitative assessments such as "good" and "medium" can be given. How to model this kind of information is an urgent problem to be solved in performance appraisal. The DHLTS can more accurately convert natural language into mathematical variables that can be calculated and compared. Therefore, the decision-making method based on DHLTS has certain advantages from the extraction stage of the original information. In terms of decision-making methods, Technique for Order Preference bv Similarity to Ideal Solution (TOPSIS) is the most commonly used method in this field, but this method requires the data of each index, it is difficult to select the corresponding quantitative index, and it can be used only when there are more than two research objects. Therefore, better methods are needed to solve these problems.

The main innovations of this paper are as follows:

• (1) This paper proposes a new method to compare DHHFLEs, which combines the advantages of existing methods and makes up for the shortcomings.

• (2) This paper presents a method to measure the cosine similarity of DHHFLEs. Based on the comparison method proposed in this paper, the DHHFLEs can be transformed into the corresponding unit vector to obtain the cosine similarity.

• (3) Based on the cosine similarity proposed in this paper, a cosine similarity-based DHHFL-ELECTRE II method is proposed. In this method, by establishing the concordance set, the discordance set and the indifference set, the outranking relation among alternatives is established.

The rest of this paper is organized as follows: Sect. 2 reviews the basic knowledge of DHHFLTS, cosine similarity and ELECTRE method. Then, a new method to compare DHHFLEs and the corresponding cosine similarity measure are presented in Sect. 3. Afterwards, the cosine similarity-based DHHFL-ELECTRE II method is introduced in Sect. 4. Next, in Sect. 5, we use the method of this paper to evaluate the performance of financial logistics enterprises and compare the proposed method with other methods. Finally, the conclusion is given in Sect. 6.

2 Preliminaries

This section introduces the basic knowledge of DHHFLTS, cosine similarity and ELECTRE method.

2.1 Double hierarchy hesitant fuzzy linguistic term set

Definition 1

Gou et al. (2017). Let $S = \left\{ {s_{t} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau } \right\}$ be the first hierarchy linguistic term set (LTS) and $O = \left\{ {o_{k} |k = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\}$ be the second hierarchy LTS, they are fully independent. Then, a double hierarchy linguistic term set (DHLTS) $S_{O}$ is defined as:

$$ S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\} $$

(1)

we call $s_{{t < o_{k} > }}$ the double hierarchy linguistic term (DHLT), where $o_{k}$ represents the second hierarchy linguistic term of the first hierarchy linguistic term $s_{t}$.

Based on DHLTS, the definition of DHHFLTS is as follows:

Definition 2

Gou et al. (2017). Let $X$ be a fixed set and $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\}$ be a DHLTS. A double hierarchy hesitant fuzzy linguistic term set (DHHFLTS) $H_{{S_{O} }}$ on $X$, denoted by a mathematical form:

$$ H_{{S_{O} }} = \left\{ { < x_{i} ,h_{{S_{O} }} \left( {x_{i} } \right) > |x_{i} \in X} \right\} $$

(2)

$$ h_{{S_{O} }} \left( {x_{i} } \right) = \left\{ {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \left( {x_{i} } \right)|s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \left( {x_{i} } \right) \in S_{O} :l = 1,2, \ldots ,L;\phi_{l} = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;\varphi_{l} = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\} $$

(3)

we call $h_{{S_{O} }} \left( {x_{i} } \right)$ the double hierarchy hesitant fuzzy linguistic element (DHHFLE), which represents the possible membership degree of the linguistic variable $x_{i}$ to $S_{O}$, and $s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \left( {x_{i} } \right)$ in each $h_{{S_{O} }} \left( {x_{i} } \right)$ being the continuous terms in $S_{O}$, $L$ represents the number of DHLTs in $h_{{S_{O} }} \left( {x_{i} } \right)$.

Then, functions $f$ and $f^{ - 1}$ are proposed to realize the conversion between the subscript $\phi_{l} < \varphi_{l} >$ of the DHLT $s_{{\phi_{l} < o_{{\varphi_{l} }} > }}$ and the membership degree $\gamma_{l}$. Before using these functions, we first extend the DHLTS to its continuous form, where the value range of subscripts of $s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \left( {x_{i} } \right)$ is $\left\{ {\phi_{l} \in \left[ { - \tau ,\tau } \right];\varphi_{l} \in \left[ { - \varsigma ,\varsigma } \right]} \right\}$. Then, functions $f$ and $f^{ - 1}$ are defined as follows:

Definition 3

Gou et al. (2017). Let $\overline{S}_{O} = \{ s_{{\phi_{l} < o_{{\varphi_{l} }} > }} |\phi_{l} \in [ - \tau ,\tau ],\varphi_{l} \in [ - \varsigma ,\varsigma ]\}$ be a continuous DHLTS, the mutual conversion between the membership degree $\gamma_{l}$ and the subscript $\phi_{l} < \varphi_{l} >$ of the DHLT $s_{{\phi_{l} < o_{{\varphi_{l} }} > }}$ equivalent to $\gamma_{l}$ can be realized by the functions $f$ and $f^{ - 1}$:

$$ f:\left[ { - \tau ,\tau } \right] \times \left[ { - \varsigma ,\varsigma } \right] \to \left[ {0,1} \right],f\left( {\phi_{l} ,\varphi_{l} } \right) = \frac{1}{\tau } \times \frac{{\varphi_{l} + \varsigma }}{2\varsigma } + \frac{{\tau + \phi_{l} - 1}}{2\tau } = \frac{{\varphi_{l} + \left( {\tau + \phi_{l} } \right)\varsigma }}{2\tau \varsigma } = \gamma_{l} $$

(4)

$$ \begin{aligned} &f^{ - 1} :\left[ {0,1} \right] \to \left[ { - \tau ,\tau } \right] \times \left[ { - \varsigma ,\varsigma } \right], \\ f^{ - 1} (\gamma_{l} ) & = [2\tau \gamma_{l} - \tau ] < o_{{\varsigma (2\tau \gamma_{l} - \tau - [2\tau \gamma_{l} - \tau ])}} > = [2\tau \gamma_{l} - \tau ] + 1 < o_{{\varsigma ((2\tau \gamma_{l} - \tau - [2\tau \gamma_{l} - \tau ]) - 1)}} > \\ & = \left\{ \begin{gathered} s_{{\tau < o_{0} > }} , \, if \, \gamma_{l} { = 1} \hfill \\ s_{{\left[ {2\tau \gamma_{l} - \tau } \right] < o_{{\varsigma \left( {2\tau \gamma_{l} - \tau - \left[ {2\tau \gamma_{l} - \tau } \right]} \right)}} > }} , \, if \, 1 \le 2\tau \gamma_{l} - \tau \le \tau \hfill \\ s_{{0 < o_{{\varsigma \left( {2\tau \gamma_{l} - \tau } \right)}} > }} , \, if \, - 1 \le 2\tau \gamma_{l} - \tau \le 1 \hfill \\ s_{{\left[ {2\tau \gamma_{l} - \tau } \right] + 1 < o_{{\varsigma \left( {2\tau \gamma_{l} - \tau - \left[ {2\tau \gamma_{l} - \tau } \right] - 1} \right)}} > }} , \, if \, - \tau \le 2\tau \gamma_{l} - \tau \le - 1 \hfill \\ s_{{ - \tau < o_{0} > }} , \, if \, \gamma_{l} { = } - 1 \hfill \\ \end{gathered} \right. \end{aligned} $$

(5)

where $[ \cdot ]$ is rounding operation.

2.2 Cosine similarity

Cosine similarity is widely used in text similarity calculation. The more similar the words used between two texts, the more similar the content between two texts. Vector space model (VSM) is a common similarity calculation model in the field of natural language processing, we can calculate the word frequency vector according to the word frequency of the text, and imagine the word frequency vectors of two texts as two vectors in space, pointing in different directions from the coordinate origin. There must be an angle between two vectors. The smaller the included angle, the closer the calculated cosine value is to 1, that is, the more similar the two texts are. Vector space model assumes that the words in the text are independent of each other, so it can be expressed in the form of vector. This representation method not only simplifies the complex relationship between words in the text, but also makes the similarity of the text computable. Its principle is simple and easy to understand, and has been widely used in many fields. Salton and McGill (1983) extended cosine similarity to fuzzy domain for the first time. The cosine similarity of fuzzy sets is defined as follows:

Definition 4

Salton and McGill (1983). Let $X$ be a fixed set and $A_{1} = \left\{ {\mu_{{A_{1} }} \left( {x_{1} } \right),\mu_{{A_{1} }} \left( {x_{2} } \right), \ldots ,\mu_{{A_{1} }} \left( {x_{n} } \right)} \right\}$, $A_{2} =$ $\left\{ {\mu_{{A_{2} }} \left( {x_{1} } \right),\mu_{{A_{2} }} \left( {x_{2} } \right), \ldots ,\mu_{{A_{2} }} \left( {x_{n} } \right)} \right\}$ be two fuzzy sets, the cosine similarity between $A_{1}$ and $A_{2}$ is defined as:

$$ {\text{Cos}} \left( {A_{1} ,A_{2} } \right) = \frac{{\sum\nolimits_{i = 1}^{N} {\mu_{{A_{1} }} \left( {x_{i} } \right)} \mu_{{A_{2} }} \left( {x_{i} } \right)}}{{\sqrt {\sum\nolimits_{i = 1}^{N} {\mu_{{A_{1} }}^{2} \left( {x_{i} } \right)\sum\nolimits_{i = 1}^{N} {\mu_{{A_{2} }}^{2} \left( {x_{i} } \right)} } } }} $$

(6)

2.3 ELECTRE method

For the alternatives $a$ and $b$, the four preference situations based on the ELECTRE method are as follows (Figueira et al., 2010):

• (1) $I$ (Indifference) It means that there is clear evidence to show that the relation between $a$ and $b$ is equivalent.

• (2) $P$ (Strict Preference) It means that there is clear evidence to support that one alternative is strictly preferred to the other.

• (3) $Q$ (Weak Preference) It means that there is clear evidence to oppose that one alternative is strictly preferred to the other, but the evidence is not enough to infer strict preference for the other alternative or indifference between the two alternatives.

• (4) $R$ (Incomparability) It means that there is no clear evidence to prove that any of the aforesaid three relations are true.

Unlike other MADM methods, preferences in ELECTRE method are modeled by the comprehensive binary outranking relation $S$, whose meaning is “$at \, least \, as \, good{\text{ as}}$”; in general, $S = P \cup Q \cup I$. Consider two alternatives $\left( {a,b} \right) \in A \times A$. Modeling comprehensive preference information leads to the four situations:

• (1) $aSb$ and not $\left( {bSa} \right)$, i.e., $aPb$;

• (2) $bSa$ and not $\left( {aSb} \right)$, i.e., $bPa$;

• (3) $aSb$ and $\left( {bSa} \right)$, i.e., $aIb$;

• (4) not $\left( {aSb} \right)$ and not $\left( {bSa} \right)$, i.e., $aRb$.

In addition, all outranking based methods rely on the concepts of concordance and discordance. In a sense, these concepts reflect the reasons for and against an outranking situation.

Definition 5

Figueira et al. (2010). Concordance: to validate an outranking relation $aSb$, a sufficient majority of criteria in favor of this assertion must occur.

Definition 6

Figueira et al. (2010). Discordance: the assertion $aSb$ cannot be validated if a minority of criteria is strongly against this assertion.

3 Cosine similarity measure of DHHFLEs

In this section, we propose a new method to compare DHHFLEs. Afterwards, the cosine similarity measure of DHHFLEs based on this comparison method is introduced.

3.1 A new comparison method of DHHFLEs

The three existing methods to compare DHHFLEs are as follows:

• (1) The comparison method based on expected value and variance

Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\}$ be a DHLTS and $h_{{S_{O} }} = \left\{ {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} |s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \in S_{O} ;l = 1,2, \ldots ,L} \right\}$ be a DHHFLE with $L$ being the number of DHLTs in $h_{{S_{O} }}$. Then the expected value and variance of $h_{{S_{O} }}$ are as follows (Gou et al., 2017):

$$ E\left( {h_{{S_{O} }} } \right) = \frac{1}{L}\sum\limits_{i = 1}^{L} {f\left( {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} } \right)} $$

(7)

$$ v\left( {h_{{S_{O} }} } \right) = \frac{1}{L}\sum\limits_{i = 1}^{L} {\left( {f\left( {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} } \right) - E} \right)}^{2} $$

(8)

where $E\left( {h_{{S_{O} }} } \right)$ and $v\left( {h_{{S_{O} }} } \right)$ represent the expected value and variance of $h_{{S_{O} }}$ respectively.

• (2) The comparison method based on the envelopes of DHHFLEs

For a DHHFLE $h_{{S_{O} }}$, its envelope can be obtained by

$$ env\left( {h_{{S_{O} }} } \right) = \left[ {h_{{S_{O} }}^{ - } ,h_{{S_{O} }}^{ + } } \right] $$

(9)

The DHHFLE $h_{{S_{O} }}$ contains all the elements from the lower bound $h_{{S_{O} }}^{ - }$ to the upper bound $h_{{S_{O} }}^{ + }$.

Then, Gou and Xu (2019) proposed the possibility degree of DHHFLEs. Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\}$ be a DHLTS, $h_{{S_{{O_{1} }} }}$ and $h_{{S_{{O_{2} }} }}$ be two DHHFLEs, then

$$ p\left( {env\left( {h_{{S_{{O_{1} }} }} } \right) \ge env\left( {h_{{S_{{O_{2} }} }} } \right)} \right) = \min \left\{ {\max \left( {\frac{{f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)}}{{\left( {f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{1} }} }}^{ - } } \right)} \right) + \left( {f\left( {h_{{S_{{O_{2} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)} \right)}},0.5} \right),0} \right\} $$

(10)

can be called the possibility degree of that $h_{{S_{{O_{1} }} }}$ to $h_{{S_{{O_{2} }} }}$.

• (3) The comparison method based on hesitancy degree

Hesitancy degree is an important concept in the field of hesitant fuzziness (Li et al., 2015). Gou et al. (2018) defined the hesitancy degree of DHHFLEs. Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma } \right\}$ be a DHLTS, $h_{{S_{O} }}$ be a DHHFLE. Then we call

$$ u\left( {h_{{S_{O} }} } \right) = 1 - \frac{1}{L} $$

(11)

the hesitancy degree of $h_{{S_{O} }}$, where $L$ is the number of DHLTs included in $h_{{S_{O} }}$.

Then, Wang et al. (2020) developed a comparison method for DHHFLEs, denoted as Score-DHHeLiSF, and it is shown as follows:

$$ DHE\left( {h_{{S_{O} }} } \right) = \left( {1 - u\left( {h_{{S_{O} }} } \right)} \right) \times \left( {\frac{1}{L}\sum\limits_{l = 1}^{L} {f\left( {s_{{\phi_{l} < o_{{\varphi_{{_{l} }} }} > }} } \right)} } \right) \, $$

(12)

where $u\left( {h_{{S_{O} }} } \right)$ denotes the hesitancy degree of $h_{{S_{O} }}$.

However, the above three methods still have some defects. For example, the envelope of DHHFLEs only deals with the upper and lower bounds and ignores the other DHLTs. Therefore, some of the original information may be lost. The third method may get some comparison results that are not in accordance with common sense. For solving these problems, a new DHHFLEs comparison method is proposed.

Definition 7

Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1,}\right.$ $\left.{ \ldots ,\varsigma } \right\}$ be a DHLTS and $h_{{S_{O} }} = \left\{ {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} |s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \in S_{O} :l = 1,2,...,L} \right\}$ be a DHHFLE with $L$ being the number of DHLTs in $h_{{S_{O} }}$. Then the expected value of the envelope of $h_{{S_{O} }}$ is as follows:

$$ E^{ * } \left( {h_{{S_{O} }} } \right) = \frac{1}{L}\sum\limits_{l = 1}^{L} {f\left( {s_{{\phi_{l} < o_{{\varphi_{{_{l} }} }} > }} } \right)} - u\left( {h_{{S_{O} }} } \right)\left( {\frac{{f\left( {h_{{S_{O} }}^{ + } } \right) - f\left( {h_{{S_{O} }}^{ - } } \right)}}{2}} \right) $$

(13)

$$ L = \varphi_{ + } - \varphi_{ - } + \varsigma \left( {\phi_{ + } - \phi_{ - } } \right) + 1 $$

(14)

where $E^{ * } \left( {h_{{S_{O} }} } \right)$ represents the expected value of the envelope of $h_{{S_{O} }}$. $h_{{S_{O} }}^{ - }$ and $h_{{S_{O} }}^{ + }$ represent the upper and lower bounds of $h_{{S_{O} }}$ respectively. $\phi_{ + }$ and $\phi_{ - }$ denote the subscripts of the first hierarchy LT of $h_{{S_{O} }}^{ + }$ and $h_{{S_{O} }}^{ - }$ respectively. $\varphi_{ + }$ and $\varphi_{ - }$ denote the subscripts of the second hierarchy LT of $h_{{S_{O} }}^{ + }$ and $h_{{S_{O} }}^{ - }$ respectively.

Proposition 1

Let $h_{{S_{{O_{i} }} }} = \left\{ {s_{{\phi_{l}^{i} < o_{{\varphi_{l}^{i} }} > }} |s_{{\phi_{l}^{i} < o_{{\varphi_{l}^{i} }} > }} \in S_{O} ;l = 1,2, \ldots ,L_{i} } \right\}\left( {i = 1,2} \right)$ be two DHHFLEs with $L_{i}$ being the number of DHLTs in $h_{{S_{{O_{i} }} }}$, then the following properties hold:

• (1) If $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) < f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$;

• (2) If $\frac{1}{{L_{1} }}\sum\limits_{l = 1}^{{L_{1} }} {f\left( {s_{{\phi_{l}^{1} < o_{{\varphi_{l}^{1} }} > }} } \right)} = \frac{1}{{L_{2} }}\sum\limits_{l = 1}^{{L_{2} }} {f\left( {s_{{\phi_{l}^{2} < o_{{\varphi_{l}^{2} }} > }} } \right)}$ and $L_{1} > L_{2}$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$;

• (3) If $\frac{1}{{L_{1} }}\sum\limits_{l = 1}^{{L_{1} }} {f\left( {s_{{\phi_{l}^{1} < o_{{\varphi_{l}^{1} }} > }} } \right)} < \frac{1}{{L_{2} }}\sum\limits_{l = 1}^{{L_{2} }} {f\left( {s_{{\phi_{l}^{2} < o_{{\varphi_{l}^{2} }} > }} } \right)}$ and $L_{1} = L_{2}$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$;

• (4) If and only if $f\left( {h_{{S_{{O_{1} }} }}^{ - } } \right) = f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$ and $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) = f\left( {h_{{S_{{O_{2} }} }}^{ + } } \right)$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) = E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$.

Proof

• (1) Since $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) \le \frac{1}{{L_{1} }}\sum\limits_{l = 1}^{{L_{1} }} {f\left( {s_{{\phi_{l}^{1} < o_{{\varphi_{l}^{1} }} > }} } \right)} \le f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right)$, $f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right) \le E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$ and $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) < f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$.

• (2) If $L_{1} > L_{2}$, then $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{1} }} }}^{ - } } \right) > f\left( {h_{{S_{{O_{2} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$.

• (3) If $L_{1} = L_{2}$, then $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{1} }} }}^{ - } } \right) = f\left( {h_{{S_{{O_{2} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$, then $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$.

• (4) If $f\left( {h_{{S_{{O_{1} }} }}^{ - } } \right) = f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$ and $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) = f\left( {h_{{S_{{O_{2} }} }}^{ + } } \right)$, then $f\left( {h_{{S_{{O_{1} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{1} }} }}^{ - } } \right) = f\left( {h_{{S_{{O_{2} }} }}^{ + } } \right) - f\left( {h_{{S_{{O_{2} }} }}^{ - } } \right)$ and $L_{1} = L_{2}$. Therefore, $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) = E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$.□

Based on the comparison method proposed in this paper, DHHFLEs $h_{{S_{{O_{1} }} }}$ and $h_{{S_{{O_{2} }} }}$ can be compared through the following relationship:

• (1) If $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) > E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$, then $h_{{S_{{O_{1} }} }}$ is superior to $h_{{S_{{O_{2} }} }}$, denoted as $h_{{S_{{O_{1} }} }} \succ h_{{S_{{O_{2} }} }}$;

• (2) If $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) < E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$, then $h_{{S_{{O_{1} }} }}$ is inferior to $h_{{S_{{O_{2} }} }}$, denoted as $h_{{S_{{O_{1} }} }} \prec h_{{S_{{O_{2} }} }}$;

• (3) If $E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) = E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)$, then $h_{{S_{{O_{1} }} }}$ is indifferent to $h_{{S_{{O_{2} }} }}$, denoted as $h_{{S_{{O_{1} }} }} \sim h_{{S_{{O_{2} }} }}$.

Example 1

Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - 3, \ldots ,3;k = - 3, \ldots ,3} \right\}$ be a DHLTS, $h_{{S_{{O_{1} }} }} = \left\{ {s_{{ - 1 < o_{{ - {1}}} > }} } \right\}$, $h_{{S_{{O_{2} }} }} = \left\{ {s_{{{0} < o_{{0}} > }} ,s_{{{0} < o_{{1}} > }} } \right\}$ and $h_{{S_{{O_{3} }} }} = \left\{ {s_{{1 < o_{1} > }} ,s_{{1 < o_{2} > }} ,s_{{1 < o_{3} > }} } \right\}$ be three DHHFLEs. According to Eq. (13), we obtain $E^{*} \left( {h_{{S_{{O_{1} }} }} } \right) = 0.2778$, $E^{*} \left( {h_{{S_{{O_{2} }} }} } \right) = 0.5130$ and $E^{*} \left( {h_{{S_{{O_{3} }} }} } \right) = 0.7407$. Therefore, $h_{{S_{{O_{1} }} }} \prec h_{{S_{{O_{2} }} }} \prec h_{{S_{{O_{3} }} }}$.

The comparison method proposed in this paper improves the previous methods in the following aspects: firstly, this method ensures that the expected value of DHHFLE is greater than or equal to its lower bound, which ensures that the conclusions are in line with basic common sense. Secondly, the hesitancy degree is reflected in the process of comparison. Thirdly, the integrity of the original information is guaranteed, that is, each DHLT in a DHHFLE is taken into account. Finally, any DHHFLE in the same DHLTS can not only be sorted, but also be represented by an accurate value. Thus, by introducing the cosine similarity, the problems of existing comparison methods can be well solved.

3.2 Cosine similarity measure for DHHFLEs

Cosine similarity measures the similarity between vectors by calculating the cosine of the angle between vectors. The existing research on cosine similarity of fuzzy information mainly substitutes the membership degree, non-membership degree or the subscripts of LTs into cosine formula to measure the similarity between fuzzy information (Salton & McGill, 1983; Ye, 2011). However, this paper proposes two conversion functions based on the continuous DHLTS, which can transform DHLTs and DHHFLEs into unit vectors in the first quadrant of two-dimensional rectangular coordinate system.

Definition 8

Let $\overline{S}_{O} = \left\{ {s_{{t < o_{k} > }} |t \in \left[ { - \tau ,\tau } \right],k \in \left[ { - \varsigma ,\varsigma } \right]} \right\}$ be a continuous DHLTS, $h_{{S_{O} }} = \left\{ {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} |s_{{\phi_{l} < o_{{\varphi_{l} }} > }} \in \overline{S}_{O} ;l = 1,2, \ldots ,L} \right\}$ be a DHHFLE with $L$ being the number of DHLTs in $h_{{S_{O} }}$. Then we call.

$$ c:\left[ { - \tau ,\tau } \right] \times \left[ { - \varsigma ,\varsigma } \right] \to \left[ {0,90^{ \circ } } \right],c\left( {\phi_{l} ,\varphi_{l} } \right) = 90^{ \circ } \times \left( {1 - E^{ * } \left( {s_{{\phi_{l} < o_{{\varphi_{l} }} > }} } \right)} \right) $$

(15)

the angle of $S_{{\phi l < o_{{\phi l}} > }}$, denoted as $\theta _{{\phi l < o_{{\phi l}} > }}$ and the corresponding unit vector is denoted as $\overrightarrow {{s_{{\phi_{l} < o_{{\varphi_{l} }} > }} }} { = }\left( {\cos \left( {\theta_{{s_{{\phi_{l} < o\varphi_{l} > }} }} } \right),\sin \left( {\theta_{{s_{{\phi_{l} }} < o_{{\varphi_{l} }} > }} } \right)} \right)$.

Then we call

$$ C:\left[ { - \tau ,\tau } \right] \times \left[ { - \varsigma ,\varsigma } \right] \to \left[ {0,90^{ \circ } } \right],C\left( {h_{{S_{O} }} } \right) = 90^{ \circ } \times \left( {1 - E^{ * } \left( {h_{{S_{O} }} } \right)} \right) $$

(16)

the angle of $h_{{S_{O} }}$, denoted as $\theta_{{h_{{S_{O} }} }}$ and the corresponding unit vector is denoted as $\overrightarrow {{h_{{S_{O} }} }} { = }\left( {\cos \left( {\theta_{{h_{{S_{O} }} }} } \right),\sin \left( {\theta_{{h_{{S_{O} }} }} } \right)} \right)$.

The above functions make DHLTs or DHHFLEs one-to-one correspond to the unit vector with the angle range of $\left[ {0,90^{ \circ } } \right]$ between the positive half axis of the x-axis. For example, let $\overline{S}_{O} = \left\{ {s_{{t < o_{k} > }} |t \in \left[ { - 3,3} \right],k \in \left[ { - 3,3} \right]} \right\}$ be a continuous DHLTS. According to the function $c$, the angles of $s_{{ - 1 < o_{ - 1} > }}$, $s_{{0 < o_{0} > }}$ and $s_{{2 < o_{2} > }}$ are $65^{ \circ }$, $45^{ \circ }$ and $5^{ \circ }$ respectively, and the corresponding unit vectors are $\overrightarrow {{s_{{ - 1 < o_{ - 1} > }} }} { = }\left( {\cos 65^{ \circ } ,\sin 65^{ \circ } } \right)$, $\overrightarrow {{s_{{0 < o_{0} > }} }} { = }\left( {\cos 45^{ \circ } ,\sin 45^{ \circ } } \right)$ and $\overrightarrow {{s_{{2 < o_{2} > }} }} { = }\left( {\cos 5^{ \circ } ,\sin 5^{ \circ } } \right)$ respectively. The corresponding unit vectors are shown in Fig. 1.

Fig. 1

Calculation results based on the conversion functions

As can be seen from Fig. 1, the semantics of DHLTs is monotonic, and the cosine values from ${0}^{ \circ }$ to ${90}^{ \circ }$ are also monotonous, so we specify $\overrightarrow {{s_{{3 < o_{0} > }} }} = \left( {\cos 0^{ \circ } ,\sin 0^{ \circ } } \right)$ and $\overrightarrow {{s_{{ - 3 < o_{0} > }} }} = \left( {\cos 90^{ \circ } ,\sin 90^{ \circ } } \right)$. We can directly measure the similarity between two DHHFLEs by calculating the cosine of the angle between the corresponding vectors of two DHHFLEs. Therefore, the cosine similarity of DHHFLEs is as follows:

Definition 9

Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , - 1,0,1, }\right.$ $\left.{ \ldots ,\varsigma } \right\}$ be a DHLTS and $h_{{S_{{O_{i} }} }} = \left\{ {s_{{\phi_{l}^{i} < o_{{\varphi_{l}^{i} }} > }} |s_{{\phi_{l}^{i} < o_{{\varphi_{l}^{i} }} > }} \in S_{O} ;l = 1,2, \ldots ,L_{i} } \right\}$ $\left( {i = 1,2} \right)$ be two DHHFLEs with $L_{i}$ being the number of DHLTs in $h_{{S_{{O_{i} }} }}$, then we call.

$$ \rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = \cos \left( {90^{ \circ } \times \left| {E^{ * } \left( {h_{{S_{{O_{1} }} }} } \right) - E^{ * } \left( {h_{{S_{{O_{2} }} }} } \right)} \right|} \right) $$

(17)

the cosine similarity between $h_{{S_{{O_{1} }} }}$ and $h_{{S_{{O_{2} }} }}$.

Proposition 2

Let $h_{{S_{{O_{i} }} }} = \left\{ {s_{{\phi_{l}^{i} < o_{{\varphi_{l}^{i} }} > }} |s_{{\phi_{l}^{i} < o_{{\varphi_{l}^{i} }} > }} \in S_{O} ;l = 1,2, \ldots ,L_{i} } \right\}\left( {i = 1,2} \right)$ be two DHHFLEs with $L_{i}$ being the number of DHLTs in $h_{{S_{{O_{i} }} }}$, then the cosine similarity between $h_{{S_{{O_{1} }} }}$ and $h_{{S_{{O_{2} }} }}$ satisfies the following properties:

• (1) $0 \le \rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) \le 1$;

• (2) $\rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = \rho_{\cos } \left( {h_{{S_{{O_{2} }} }} ,h_{{S_{{O_{1} }} }} } \right)$;

• (3) $\rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = 1$, if and only if $h_{{S_{{O_{1} }} }} = h_{{S_{{O_{2} }} }}$.

In addition, the relationship between the cosine similarity measure proposed in this paper and its corresponding distance measure is as follows:

$$ d_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = 1 - \rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) $$

(18)

where $d_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right)$ denotes the distance measure between $h_{{S_{{O_{1} }} }}$ and $h_{{S_{{O_{2} }} }}$.

Example 2

Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - 3, \ldots ,3;k = - 3, \ldots ,3} \right\}$ be a DHLTS, $h_{{S_{{O_{1} }} }} = \left\{ {s_{{ - 1 < o_{{ - {1}}} > }} } \right\}$, $h_{{S_{{O_{2} }} }} = \left\{ {s_{{{0} < o_{{0}} > }} ,s_{{{0} < o_{{1}} > }} } \right\}$ and $h_{{S_{{O_{3} }} }} = \left\{ {s_{{1 < o_{1} > }} ,s_{{1 < o_{2} > }} ,s_{{1 < o_{3} > }} } \right\}$ be three DHHFLEs. According to Eq. (16), we obtain $C\left( {h_{{S_{{O_{1} }} }} } \right) = 65^{ \circ }$, $C\left( {h_{{S_{{O_{2} }} }} } \right) = 43.75^{ \circ }$ and $C\left( {h_{{S_{{O_{3} }} }} } \right) = 23.33^{ \circ }$, and their corresponding unit vectors are $\overrightarrow {{h_{{S_{{O_{1} }} }} }} { = }\left( {\cos 65^{ \circ } ,\sin 65^{ \circ } } \right)$, $\overrightarrow {{h_{{S_{{O_{2} }} }} }} { = }\left( {\cos 43.75^{ \circ } ,\sin 43.75^{ \circ } } \right)$ and $\overrightarrow {{h_{{S_{{O_{3} }} }} }} { = }\left( {\cos 23.33^{ \circ } ,\sin 23.33^{ \circ } } \right)$. According to Eq. (17), we obtain $\rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = 0.9320$, $\rho_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{3} }} }} } \right) = 0.7470$ and $\rho_{\cos } \left( {h_{{S_{{O_{2} }} }} ,h_{{S_{{O_{3} }} }} } \right) = 0.9372$. Then based on Eq. (18), we get $d_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = 0.068$, $d_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{3} }} }} } \right) = 0.253$ and $d_{\cos } \left( {h_{{S_{{O_{1} }} }} ,h_{{S_{{O_{2} }} }} } \right) = 0.0628$.

In addition, considering that different attributes are usually given different weights in the actual MADM problem, we give the weighted cosine similarity of DHHFLEs as follows:

Definition 10

Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;k = - \varsigma , \ldots , {-} 1,0,1, }\right.$ $\left.{\ldots ,\varsigma } \right\}$ be a DHLTS, $H_{{S_{{O_{1} }} }} = \left\{ {h_{{S_{{O_{11} }} }}^{\left( l \right)} ,h_{{S_{{O_{12} }} }}^{\left( l \right)} , \ldots ,h_{{S_{{O_{1n} }} }}^{\left( l \right)} } \right\}$ and $H_{{S_{{O_{2} }} }} = \left\{ {h_{{S_{{O_{21} }} }}^{\left( l \right)} ,h_{{S_{{O_{22} }} }}^{\left( l \right)} , \ldots ,h_{{S_{{O_{2n} }} }}^{\left( l \right)} } \right\}$ be two DHHFLTs, where $h_{{S_{Oij} }} = \left\{ {h_{{S_{Oij} }}^{\left( l \right)} |h_{{S_{Oij} }}^{\left( l \right)} \in S_{O} ;l = 1,2, \ldots ,L_{ij} } \right\}$ $\left( {i = 1,2;j = 1,2, \ldots ,n} \right)$ ($h_{{S_{{O_{ij} }} }}^{\left( l \right)}$ represents the $l - {\text{th}}$ DHLT in $h_{{S_{{O_{ij} }} }}$, $L_{ij}$ represents the number of DHLTs in $h_{{S_{{O_{ij} }} }}$). Let $w = \left( {w_{1} ,w_{2} , \ldots ,w_{j} , \ldots ,w_{n} } \right)^{T}$ be the weight vector, where $w_{j} \in [0,1]$ and $\sum\nolimits_{j = 1}^{n} {w_{j} = 1}$. Then we call.

$$ \rho_{\cos }^{w} \left( {H_{{S_{{O_{1} }} }} ,H_{{S_{{O_{2} }} }} } \right) = \cos \left( {90^{ \circ } \times \sum\nolimits_{j = 1}^{n} {w_{j} } \left| {E^{ * } \left( {h_{{S_{{O_{1j} }} }} } \right) - E^{ * } \left( {h_{{S_{{O_{2} j}} }} } \right)} \right|} \right) $$

(19)

the weighted cosine similarity between $H_{{S_{{O_{1} }} }}$ and $H_{{S_{{O_{2} }} }}$.

This method is the first one to study the measurement of DHHFLEs from a geometric point of view. In addition, this method does not need to add artificial information. The number of DHLTs in two DHHFLEs is usually different. Some existing distance and similarity measurement methods will add DHLTs to the short DHHFLE according to the decision maker’s risk preference until the number of DHLT in the two DHHFLEs is the same. However, adding artificial information can lead to inaccurate results. In the method proposed in this paper, function $C$ can integrate the information of all the DHLTs in DHHFLEs in advance, when the DHHFLEs are transformed into the corresponding vectors, the vectors are unique and accurate.

4 Cosine similarity-based DHHFL-ELECTRE II method

In this section, we introduce the cosine similarity-based DHHFL-ELECTRE II method. Let $S_{O} = \left\{ {s_{{t < o_{k} > }} \left| {t = - \tau , \ldots , - 1,0,1, \ldots ,\tau ;\;k = - \varsigma } \right., \ldots , - 1,0,} \right.\left. {1, \ldots ,\varsigma } \right\}$ be a DHLTS, $A = \left\{ {A_{1} ,A_{2} , \ldots ,A_{i} , \ldots ,A_{m} } \right\}$ be a set of alternatives, $C = \left\{ {C_{1} ,C_{2} , \ldots ,C_{j} , \ldots ,C_{n} } \right\}$ be a set of attributes, $w = \left( {w_{1} ,w_{2} ,...,w_{j} ,...,w_{n} } \right)^{T}$ be the weight vector of attributes, where $w_{j} \in [0,1]$, $\sum\nolimits_{j = 1}^{n} {w_{j} = 1}$. Then, the decision matrix based on the given DHLTS is as follows:

$$ H_{{S_{0} }} = \left[ {h_{{S_{{O_{ij} }} }} } \right]_{m \times n} = \left[ {\begin{array}{*{20}c} {h_{{S_{{O_{{{11}}} }} }} } & {h_{{S_{{O_{12} }} }} } & \cdots & {h_{{S_{{O_{{{\text{1n}}}} }} }} } \\ {h_{{S_{{O_{{{21}}} }} }} } & {h_{{S_{{O_{{{22}}} }} }} } & \cdots & {h_{{S_{{O_{2n} }} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {h_{{S_{{O_{m1} }} }} } & {h_{{S_{{O_{m2} }} }} } & \cdots & {h_{{S_{{O_{mn} }} }} } \\ \end{array} } \right] $$

where $h_{{S_{{O_{ij} }} }}$ represents the evaluation information of alternative $A_{i}$ on attribute $C_{j}$.

4.1 Determining the positive and negative ideal solutions

Based on the functions introduced in Sect. 3.2, the minimum and maximum DHHFLEs of each attribute are defined as follows:

$$ C^{ - } \left( {h_{{S_{{O_{j} }} }} } \right) = \mathop {\min }\limits_{i = 1,2, \ldots ,m} C\left( {h_{{S_{{O_{ij} }} }} } \right) $$

(20)

$$ C^{ + } \left( {h_{{S_{{O_{j} }} }} } \right) = \mathop {\max }\limits_{i = 1,2, \ldots ,m} C\left( {h_{{S_{{O_{ij} }} }} } \right) $$

(21)

Then the negative ideal solution $C^{ - } \left( {H_{{S_{O} }} } \right) = \left\{ {C^{ - } \left( {h_{{S_{{O_{1} }} }} } \right),C^{ - } \left( {h_{{S_{{O_{2} }} }} } \right), \ldots ,C^{ - } \left( {h_{{S_{{O_{n} }} }} } \right)} \right\}$ and the positive ideal solution $C^{ + } \left( {H_{{S_{O} }} } \right) = \left\{ {C^{ + } \left( {h_{{S_{{O_{1} }} }} } \right),} \right.$$\left. {C^{ + } \left( {h_{{S_{{O_{2} }} }} } \right), \ldots ,C^{ + } \left( {h_{{S_{{O_{n} }} }} } \right)} \right\}$ are obtained respectively.

4.2 Establishing the DHHFL-concordance, DHHFL-discordance and DHHFL-indifferent sets

Assuming that $A_{a}$ and $A_{b}$ are two alternatives, their evaluation values for the attribute $C_{j}$ can be expressed as $h_{{S_{{O_{aj} }} }}$ and $h_{{S_{{O_{bj} }} }}$ respectively. Then, the cosine similarity between $h_{{S_{{O_{aj} }} }}$ and the negative ideal solution and the positive ideal solution of the attribute $C_{j}$ can be expressed as $\rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right)$ and $\rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right)$ respectively. Similarly, the cosine similarity between $h_{{S_{{O_{bj} }} }}$ and the negative ideal solution and the positive ideal solution of the attribute $C_{j}$ can be expressed as $\rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right)$ and $\rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right)$ respectively.

For the assertion that $A_{a}$ is strictly preferred to $A_{b}$, the DHHFL-concordance set and the DHHFL-discordance set are defined as follows:

The DHHFL-concordance set, denoted as $J_{{C_{ab} }}$, is defined as follows:

$$ J_{{C_{ab} }} = \left\{ {j|\rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right) > \rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right){\kern 1pt} {\kern 1pt} and{\kern 1pt} {\kern 1pt} \rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right) < \rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right)} \right\} $$

(22)

The DHHFL-discordance set, denoted as $J_{{D_{ab} }}$, is defined as follows:

$$ J_{{D_{ab} }} = \left\{ {j|\rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right) < \rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right){\kern 1pt} {\kern 1pt} and{\kern 1pt} {\kern 1pt} \rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right) > \rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right)} \right\} $$

(23)

when the two alternatives have the same similarity with the positive ideal solution and the same similarity with the negative ideal solution, it can be assumed that there is no difference between two alternatives. Therefore, the DHHFL-indifferent set, denoted as $J_{{I_{ab} }}$, is defined as follows:

$$ J_{{I_{ab} }} = \left\{ {j|\rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right) = \rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ + } } \right){\kern 1pt} {\kern 1pt} and{\kern 1pt} {\kern 1pt} \rho_{\cos } \left( {h_{{S_{{O_{aj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right) = \rho_{\cos } \left( {h_{{S_{{O_{bj} }} }} ,h_{{S_{{O_{j} }} }}^{ - } } \right)} \right\} $$

(24)

4.3 Establishing the DHHFL-concordance and DHHFL-discordance matrices

The DHHFL-concordance index $c_{ab}$ represents the relative importance of $A_{a}$ to $A_{b}$ is defined as follows:

$$ c_{ab} = w_{C} \times \sum\nolimits_{{j \in J_{{C_{ab} }} }} {w_{{_{j} }} + } w_{I} \times \sum\nolimits_{{j \in J_{{I_{ab} }} }} {w_{{_{j} }} } $$

(25)

where $w_{j}$ represents the weight of attribute $C_{j}$, $w_{C}$ and $w_{I}$ represent the attitude weight of the DHHL-concordance set and the DHHFL-indifference set respectively.

Then, we call

$$ C = \left[ {\begin{array}{*{20}c} - & \ldots & {c_{1b} } & \ldots & {c_{{1\left( {m - 1} \right)}} } & {c_{1m} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {c_{a1} } & \ldots & {c_{ab} } & \ldots & {c_{{a\left( {m - 1} \right)}} } & {c_{am} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {c_{m1} } & \ldots & {c_{mb} } & \ldots & {c_{{m\left( {m - 1} \right)}} } & - \\ \end{array} } \right] $$

(26)

the DHHFL-concordance matrix.

The DHHFL-discordance index $d_{ab}$ represents the degree of opposition to “$A_{a}$ is strictly preferred to $A_{b}$” as follows:

$$ d_{ab} = \frac{{\min \left\{ {w_{D} \times \min \mathop {\rho_{\cos } }\limits_{{j \in J_{{D_{ab} }} }} \left( {w_{{_{j} }} h_{{S_{{O_{aj} }} }} ,w_{{_{j} }} h_{{S_{{O_{bj} }} }} } \right)} \right\}}}{{\mathop {\min }\limits_{j} \rho_{\cos } \left( {w_{{_{j} }} h_{{S_{{O_{aj} }} }} ,w_{{_{j} }} h_{{S_{{O_{bj} }} }} } \right)}} $$

(27)

where $w_{D}$ denotes the attitude weight of the DHHFL-discordance set. $\rho_{\cos } \left( {w_{{_{j} }} h_{{S_{{O_{aj} }} }} ,w_{{_{j} }} h_{{S_{{O_{bj} }} }} } \right)$ represents the weighted cosine similarity of the evaluation values of $A_{a}$ and $A_{b}$ on the attribute $C_{j}$.

Then, we call

$$ D = \left[ {\begin{array}{*{20}c} - & \ldots & {d_{1b} } & \ldots & {d_{{1\left( {m - 1} \right)}} } & {d_{1m} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {d_{a1} } & \ldots & {d_{ab} } & \ldots & {d_{{a\left( {m - 1} \right)}} } & {d_{am} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {d_{m1} } & \ldots & {d_{mb} } & \ldots & {d_{{m\left( {m - 1} \right)}} } & - \\ \end{array} } \right] $$

(28)

the DHHFL-discordance matrix.

4.4 Constructing the outranking relations

The DHHFL-concordance level reflects the average performance of all the DHHFL-concordance indexes. We call

$$ \overline{C}{ = }\sum\nolimits_{a = 1}^{m} {\sum\nolimits_{b = 1}^{m} {\frac{{c_{ab} }}{{m\left( {m - 1} \right)}}} } $$

(29)

the DHHFL-concordance level.

Furthermore, based on the DHHFL-concordance level $\overline{C}$ and the DHHFL-concordance matrix $C$, the DHHFL-concordance Boolean matrix $E$ is expressed as follows:

$$ E = \left[ {\begin{array}{*{20}c} - & \ldots & {e_{1b} } & \ldots & {e_{{1\left( {m - 1} \right)}} } & {e_{1m} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {e_{a1} } & \ldots & {e_{ab} } & \ldots & {e_{{a\left( {m - 1} \right)}} } & {e_{am} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {e_{m1} } & \ldots & {e_{mb} } & \ldots & {e_{{m\left( {m - 1} \right)}} } & - \\ \end{array} } \right] $$

(30)

where $e_{ab}$ is a binary variable, if $e_{ab} \ge \overline{C}$, then $e_{ab} = 1$, which means that from a consistency point of view, $A_{a}$ is preferred to $A_{b}$. If $e_{ab} < \overline{C}$, then $e_{ab} = 0$, which means that from a consistency point of view, there is no clear evidence to support the assertion that $A_{a}$ has priority over $A_{b}$.

Similarly, the DHHFL-discordance level reflects the average performance of the DHHFL-discordance indexes. We call

$$ \overline{D}{ = }\sum\nolimits_{a = 1}^{m} {\sum\nolimits_{b = 1}^{m} {\frac{{d_{ab} }}{{m\left( {m - 1} \right)}}} } $$

(31)

the DHHFL-discordance level.

Based on the DHHFL-discordance level $\overline{D}$ and the DHHFL-discordance matrix $D$, the DHHFL-discordance Boolean matrix $F$ is expressed as follows:

$$ F = \left[ {\begin{array}{*{20}c} - & \ldots & {f_{1b} } & \ldots & {f_{{1\left( {m - 1} \right)}} } & {f_{1m} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {f_{a1} } & \ldots & {f_{ab} } & \ldots & {f_{{a\left( {m - 1} \right)}} } & {f_{am} } \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ {f_{m1} } & \ldots & {f_{mb} } & \ldots & {f_{{m\left( {m - 1} \right)}} } & - \\ \end{array} } \right] $$

(32)

where $f_{ab}$ is a binary variable, if $f_{ab} \le \overline{D}$, then $f_{ab} = 1$, which means that from an inconsistency point of view, $A_{a}$ is preferred to $A_{b}$. If $f_{ab} > \overline{D}$, then $f_{ab} = 0$, which means that from an inconsistency point of view, there is no clear evidence to support the assertion that $A_{a}$ has priority over $A_{b}$.

4.5 Constructing the global matrix

For two alternatives $A_{a}$ and $A_{b}$, if $e_{ab} = 1$ and $f_{ab} = 1$, it means that from the perspective of consistency and inconsistency, there is obvious evidence that $A_{a}$ performs better than $A_{b}$. Consequently, the preference relation between $A_{a}$ and $A_{b}$ can be obtained by multiplying the concordance index $e_{ab}$ and the discordance index $f_{ab}$. Through the above process, we can get the preference relation between any two alternatives.

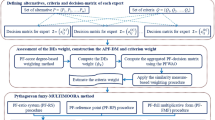
The step of the cosine similarity-based DHHFL-ELECTRE II method are as follows:

Step 1 Collect the evaluation information and express as the corresponding decision matrix.

Step 2 Determine the positive and negative ideal solutions for each attribute based on Eqs. (13 and 14).

Step 3 Calculate the cosine similarity between the evaluation value of all alternatives under each attribute and the corresponding negative and positive ideal solutions by Eq. (19).

Step 4 The DHHFL-concordance set is established based on Eq. (22), the DHHFL-discordance set is established based on Eq. (23) and the DHHFL-indifferent set is established based on Eq. (24).

Step 5 Calculate the DHHFL-concordance index through Eq. (25), and then form the corresponding DHHFL-concordance matrix $C$ through Eq. (26).

Step 6 Calculate the DHHFL-discordance index through Eq. (27), and then form the corresponding DHHFL-discordance matrix $D$ through Eq. (28).

Step 7 Calculate the DHHFL-concordance level through Eq. (29), and then form the DHHFL-concordance Boolean matrix through Eq. (30).

Step 8 Calculate the DHHFL-discordance level through Eq. (31), and then form the DHHFL-discordance Boolean matrix through Eq. (32).

Step 9 Construct the global matrix to obtain the final ranking results among all alternatives.

Step 10 Draw the ranking chart of all alternatives and select the best alternative.

The flow chart of the cosine similarity-based DHHFL-ELECTRE II method is shown in Fig. 2:

Fig. 2

Flow chart of the cosine similarity-based DHHFL-ELECTRE II method

5 Case study

In this section, we use the proposed method to solve a performance evaluation problem of financial logistics enterprises. Then, the existing decision-making methods are compared with the method proposed in this paper.

5.1 Case description

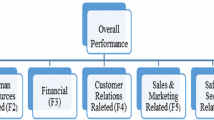
Financial logistics enterprises cover a variety of cross-business and independent businesses, with strong synergy. As an organic whole, the defects in any link of an enterprise may affect its market competitiveness. The performance evaluation of enterprises must give consideration to both target performance and comprehensive performance. Therefore, from the perspectives of customer, finance, learning and growth, the performance evaluation standard of financial logistics enterprises is established (Shen, 2009), as shown in Fig. 3.

Fig. 3

Performance evaluation system of financial logistics enterprises

The degree of customers’ recognition of an enterprise and its services is an important indicator to measure the business ability and development prospects of an enterprise. Due to the particularity of financial services, the requirement of customer recognition is much higher than that of general logistics industry. Customer recognition is mainly reflected in customer complaints $C_{1}$ and the customer satisfaction $C_{{2}}$.

The ultimate goal of enterprises is to make profits. like other industries, financial logistics industry needs to achieve the goal of maximizing shareholder value. Therefore, it is necessary to set up financial indicators to evaluate the performance of financial logistics enterprises from profitability $C_{{3}}$, sales $C_{{4}}$ and investment recovery $C_{{5}}$.

The sustainable development of enterprises is inseparable from team building. Therefore, improving employee satisfaction $C_{{6}}$ is also an indispensable part of the development of enterprise management.

There are four financial logistics enterprises, represented by $A = \left\{ {A_{1} ,A_{2} ,A_{{3}} ,A_{{4}} } \right\}$. These four enterprises are evaluated based on the above indicators. The indicators represented by $C = \left\{ {C_{1} ,C_{2} ,C_{{3}} ,C_{{4}} ,C_{{5}} ,C_{{6}} } \right\}$, and the weight vector of these indicators is $w = \left( {0.1,0.{2},0.{1},0.2{7},0.1{8},0.15} \right)^{T}$ (the determination of attribute weight is not the focus of this paper, which is directly given here). Let $S_{O} = \left\{ {s_{{t < o_{k} > }} |t = - 3, \ldots ,3;k = - 3, \ldots ,3} \right\}$ be a DHLTS, where

$$ \begin{aligned}S_{t} &= \left\{ {s_{ - 3} = extremely{\kern 1pt} {\kern 1pt} {\kern 1pt} poor,s_{ - 2} = very{\kern 1pt} {\kern 1pt} {\kern 1pt} poor,s_{ - 1} = poor,s_{0} = medium,}\right.\\ & \quad \left.{ s_{1} = good,s_{2} = very{\kern 1pt} {\kern 1pt} good,s_{3} = extremely{\kern 1pt} {\kern 1pt} {\kern 1pt} good} \right\} \end{aligned}$$

$$ O_{k} = \left\{ \begin{gathered} \{ o_{ - 3} = extremely,o_{ - 2} = very \, much,o_{ - 1} = much,o_{0} = just \, right, \hfill \\ o_{1} = a \, little,o_{2} = only \, a \, little, \, o_{3} = far \, from\} \, if \, s_{t} < s_{0} \hfill \\ \{ o_{ - 3} = far \, from,o_{ - 2} = only \, a \, little,o_{ - 1} = a \, little,o_{0} = just \, right, \hfill \\ o_{1} = much,o_{2} = very \, much, \, o_{3} = extremely\} \, if \, s_{t} \ge s_{0} \hfill \\ \end{gathered} \right. $$

5.2 Use the cosine similarity-based DHHFL-ELECTRE II method to solve the case

Step 1 Collect the evaluation information of the decision maker and express it as the corresponding decision matrix.

The decision matrix of decision makers is shown in Table 1:

Table 1 Decision matrix given by decision maker

Step 2 Determine the positive and negative ideal solutions of each attribute.

Based on Eqs. (13 and 14), we obtain

$$ \begin{aligned} C^{ + } \left( {h_{{S_{{O_{j} }} }} } \right) &= \left\{ {\left\{ {{\kern 1pt} s_{{1 < o_{1} > }} ,s_{{2 < o_{ - 1} > }} } \right\},\left\{ {s_{{2 < o_{2} > }} } \right\},\left\{ {s_{{2 < o_{2} > }} } \right\},\left\{ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s_{{2 < o_{1} > }} ,s_{{2 < o_{2} > }} } \right\},}\right. \\ & \quad \left.{\left\{ {s_{{2 < o_{0} > }} ,s_{{2 < o_{2} > }} } \right\},\left\{ {s_{{1 < o_{1} > }} ,s_{{2 < o_{1} > }} } \right\}} \right\} \end{aligned}$$

$$\begin{aligned} C^{ - } \left( {h_{{S_{{O_{j} }} }} } \right)& = \left\{ {\left\{ {s_{{ - 1 < o_{ - 3} > }} } \right\},\left\{ {s_{{{0} < o_{{ - {1}}} > }} } \right\},\left\{ {s_{{ - 2 < o_{{ - {1}}} > }} ,s_{{ - 1 < o_{ - 2} > }} } \right\},\left\{ {s_{{ - 2 < o_{ - 1} > }} ,s_{{ - 1 < o_{0} > }} } \right\},}\right. \\ & \quad \left.{\left\{ {s_{{ - {1} < o_{ - 2} > }} ,s_{{ - 1 < o_{1} > }} } \right\},\left\{ {s_{{ - {2} < o_{ - 1} > }} } \right\}} \right\} \end{aligned}$$

Therefore, the positive and negative ideal solutions of attributes are as follows:

$C^{ + } \left( {H_{{S_{O} }} } \right) = \left\{ {23.75^{ \circ } ,5^{ \circ } ,5^{ \circ } ,8.35^{ \circ } ,13.35^{ \circ } ,23.125^{ \circ } } \right\}$, $C^{ - } \left( {H_{{S_{O} }} } \right) = \left\{ {75^{ \circ } ,50^{ \circ } ,78.35^{ \circ } ,78^{ \circ } ,68.125^{ \circ } ,80^{ \circ } } \right\}$.

Step 3 Calculate the cosine similarity between the evaluation values of all alternatives under each attribute and the corresponding positive and negative ideal solutions.

According to Eq. (19), the cosine similarity between $h_{{S_{{O_{ij} }} }}$ and the positive and negative ideal solutions are shown in Table 2:

Table 2 Cosine similarity between $h_{{S_{{O_{ij} }} }}$ and the positive and negative ideal solutions

Step 4 Establish the DHHFL-concordance set, the DHHFL-discordance set and the DHHFL-indifferent set.

According to Eqs. (22, 23 and 24), we obtain the DHHFL-concordance set, the DHHFL-discordance set and the DHHFL-indifferent set as follows:

$J_{C} = \left[ {\begin{array}{*{20}c} - & {1,3,5} & 2 & {3,4,5} \\ {2,4,6} & - & {2,4,6} & {4,5,6} \\ {1,3,5,6} & {1,3,5} & - & {3,5,6} \\ {1,2} & {1,2,3} & {2,4} & - \\ \end{array} } \right]$, $J_{D} = \left[ {\begin{array}{*{20}c} - & {2,4,6} & {1,3,5,6} & {1,2} \\ {1,3,5} & - & {1,3,5} & {1,2,3} \\ 2 & {2,4,6} & - & {2,4} \\ {3,4,5} & {4,5,6} & {3,5,6} & - \\ \end{array} } \right]$, $J_{I} = \left[ {\begin{array}{*{20}c} - & - & 4 & 6 \\ - & - & - & - \\ 4 & - & - & 1 \\ 6 & - & 1 & - \\ \end{array} } \right]$.

Step 5 Calculate the DHHFL-concordance index and construct the corresponding DHHFL-concordance matrix.

The attitude weight vector is $w_{attitude} = \left( {w_{C} ,w_{D} ,w_{I} } \right)^{T} = \left( {1,1,0.7} \right)^{T}$. According to Eq. (25), the DHHFL-concordance matrix $C$ is constructed as follows:

$$ C = \left[ {\begin{array}{*{20}c} - & {0.38} & {0.389} & {0.655} \\ {0.62} & - & {0.62} & {0.6} \\ {0.719} & {0.38} & - & {0.5} \\ {0.405} & {0.4} & {0.54} & - \\ \end{array} } \right] $$

Step 6 Calculate the DHHFL-discordance index and construct the corresponding DHHFL-discordance matrix.

Firstly, the weighted cosine similarity between any two alternatives is shown in Table 3:

Table 3 The weighted cosine similarity between any two alternatives

Then, the DHHFL-discordance matrix $D$ is constructed as follows:

$$ D = \left[ {\begin{array}{*{20}c} - & {1.64} & 1 & {1.43} \\ 1 & - & 1 & 1 \\ {2.05} & {3.27} & - & {2.83} \\ 1 & {1.31} & 1 & - \\ \end{array} } \right] $$

Step 7 Calculate the DHHFL-concordance level and DHHFL-discordance level, then construct the DHHFL-concordance Boolean matrix and DHHFL-discordance Boolean matrix.

Through Eqs. (29 and 31), we obtain $\overline{C} = 0.517$ and $\overline{D} = 1.544$. The DHHFL-concordance Boolean matrix $E$ and DHHFL-concordance Boolean matrix $F$ can be expressed as follows:

$E = \left[ {\begin{array}{*{20}c} - & 0 & 0 & 1 \\ 1 & - & 1 & 1 \\ 1 & 0 & - & 0 \\ 0 & 0 & 1 & - \\ \end{array} } \right]$, $F = \left[ {\begin{array}{*{20}c} - & 0 & 1 & 1 \\ 1 & - & 1 & 1 \\ 0 & 0 & - & 0 \\ 1 & 1 & 1 & - \\ \end{array} } \right]$.

Step 8 Construct the global matrix.

Based on the DHHFL-concordance Boolean matrix and the DHHFL-discordance Boolean matrix, the global matrix $G$ can be expressed as follows:

$$ G = \left[ {\begin{array}{*{20}c} - & 0 & 0 & 1 \\ 1 & - & 1 & 1 \\ 0 & 0 & - & 0 \\ 0 & 0 & 1 & - \\ \end{array} } \right] $$

Step 9 Draw a ranking chart of all alternatives.

The ranking chart $P$ of all alternatives is shown in Fig. 4. From Fig. 4, we can see that $A_{2}$ is the enterprise with the best performance evaluation results.

Fig. 4

The ranking chart of all alternatives

5.3 Comparative analysis

Next, we take solving the problem of traffic congestion assessment (quoted from Wang et al. (2020)) as an example to compare the proposed method with some existing decision-making methods.

Firstly, use the method proposed in this paper to solve this problem.

Step 1 The positive and negative ideal solutions of each attribute are as follows:

$C^{ + } \left( {H_{{S_{O} }} } \right) = \left\{ {8.35^{ \circ } ,68,125^{ \circ } ,8.35^{ \circ } ,25^{ \circ } ,10^{ \circ } } \right\}$, $C^{ - } \left( {H_{{S_{O} }} } \right) = \left\{ {52.85^{ \circ } ,23^{ \circ } ,67.8^{ \circ } ,48.35^{ \circ } ,82.75^{ \circ } } \right\}$.

Step 2 The cosine similarity between evaluation information and the positive and negative ideal solutions are shown in Table 4:

Table 4 Cosine similarity between evaluation information $h_{{S_{{O_{ij} }} }}$ and the positive and negative ideal solutions

Step 3 The DHHFL-concordance set, DHHFL-discordance set, and DHHFL-indifferent set are established as follows:

$J_{C} = \left[ {\begin{array}{*{20}c} - & {1,3,4,5} & {2,3,4,5} & {1,3,5} \\ 2 & - & {2,4} & {2,3,5} \\ 1 & {1,3,5} & - & {1,3,5} \\ {2,4} & {1,4} & {2,4} & - \\ \end{array} } \right]$, $J_{D} = \left[ {\begin{array}{*{20}c} - & 2 & 1 & {2,4} \\ 2 & - & {1,3,5} & {1,4} \\ {2,3,4,5} & {2,4} & - & {2,4} \\ {1,3,5} & {2,3,5} & {1,3,5} & - \\ \end{array} } \right]$, $J_{I} = \left[ {\begin{array}{*{20}c} - & - & - & - \\ - & - & - & - \\ - & - & - & - \\ - & - & - & - \\ \end{array} } \right]$.

Step 4 Calculate the DHHFL-concordance, DHHFL-discordance index and construct the corresponding matrices as follows:

$C = \left[ {\begin{array}{*{20}c} - & {0.8} & {0.76} & {0.62} \\ {0,2} & - & {0.38} & {0.58} \\ {0.24} & {0.62} & - & {0.62} \\ {0.38} & {0.42} & {0.38} & - \\ \end{array} } \right]$, $D = \left[ {\begin{array}{*{20}c} - & {3.73} & {1.68} & {3.34} \\ {3.73} & - & 1 & 1 \\ 1 & {1.35} & - & {1.59} \\ 1 & {1.01} & 1 & - \\ \end{array} } \right]$.

Step 5 Calculate the DHHFL-concordance level and DHHFL-discordance level, $\overline{C} = 0.5$, $\overline{D} = 1.79$. Then the DHHFL-concordance, DHHFL-discordance Boolean matrices are obtained as follows:

$E = \left[ {\begin{array}{*{20}c} - & 1 & 1 & 1 \\ 0 & - & 0 & 1 \\ 0 & 1 & - & 1 \\ 0 & 0 & 0 & - \\ \end{array} } \right]$, $F = \left[ {\begin{array}{*{20}c} - & 0 & 1 & 0 \\ 0 & - & 1 & 1 \\ 1 & 1 & - & 1 \\ 1 & 1 & 1 & - \\ \end{array} } \right]$.

Step 6 The global matrix is as follows:

$$ G = \left[ {\begin{array}{*{20}c} - & 0 & 1 & 0 \\ 0 & - & 0 & 1 \\ 0 & 1 & - & 1 \\ 0 & 0 & 0 & - \\ \end{array} } \right] $$

Step 7 Draw the ranking chart of all alternatives, as shown in Fig. 5:

Fig. 5

The ranking chart of all alternatives

As can be seen from Fig. 5, the ranking of the four cities is $A_{1} PA_{3} PA_{2} PA_{4}$, Chongqing $\left( {A_{1} } \right)$ is the most congested city among the four cities.

Then, we use the existing MADM method about DHHFLTSs to solve this problem, and the ranking results are shown in Table 5, including the DHHFL-MULTIMOORA (Multiple Multi-objective Optimization by Ratio Analysis) method, the classical ORESTE (Organísation, Rangement Et SynThèse de donnéEs relarionnelles in French) method and the DHHFL-ORESTE method.

Table 5 The ranking order obtained by different methods

It can be seen from Table 5 that the ranking results of the cosine similarity-based DHHFL-ELECTRE II method are the same as those of the DHHFL-MULTIMOORA method, but different from those of the classical ORESTE method and the DHHFL-ORESTE method. The specific reasons are as follows:

• (1) The DHHFL-MULTIMOORA method is a decision-making method based on the expected value and variance of DHHFLEs. The decision-making model is established from three aspects of the ratio system, reference point and full multiplicative form, which makes the problem more comprehensively considered. However, when considering these three aspects, they are parallel, that is, they are of the same importance, and the majority is selected as the final conclusion. In other words, the DHHFL-MULTIMOORA method cannot subdivide the relationship between alternatives. If the three measures results obtained by DHHFL-MULTIMOORA method are completely different, the comprehensive ranking cannot be obtained. The cosine similarity-based DHHFL-ELECTRE II method pays more attention to the pairwise comparison between alternatives. In contrast, the calculation steps of the method proposed in this paper are progressive, which can not only subdivide the alternatives, but also avoid conflicting results. Therefore, the DHHFL-ELECTRE II method has more advantages in dealing with problems with more complex information and more alternatives.

• (2) The classical ORESTE method and the DHHFL-ORESTE method are outranking-based decision-making method. Similar to the method proposed in this paper, these method focus on the global preference weak rankings. The latter improves the former in many aspects. For example, the DHHFL-ORESTE method does not always use ranking results to make decisions like the classical method, so it is more suitable to deal with MCDM problems with qualitative information. In addition, the DHHFL-ORESTE method determines the threshold by calculating the boundary value, and the preference intensity indifference threshold has a fixed range. However, in the classical ORESTE method, only by ranking, the value of the threshold is similar to the perfect conflict degree, which is unreliable. Therefore, the DHHFL-ORESTE method proposes the Score-DHHeLiSF to solve the above problems. However, according to our previous analysis, this comparison method has defects. In some cases, the correct comparison results of two DHHFLEs cannot be obtained. This is the biggest reason why the two methods get different results from the method proposed in this paper.

6 Conclusions

In order to improve the shortcomings of the existing comparison methods for comparing DHHFLEs, this paper proposes a new comparison method from the perspective of cosine similarity, that is, the enveloped-based expected value comparison method. On this basis, a cosine similarity measure is proposed to measure measure the similarity of DHHFLEs. Further, based on the idea of ELECTRE method, a cosine similarity-based DHHFL-ELECTRE method II is proposed to solve the MADM problem in double hierarchy hesitant fuzzy linguistic environment.

The innovation of this paper is summarized as follows:

• (1) In this paper, a new DHHFLEs comparison method is proposed to improve the shortcomings of the existing comparison methods.

• (2) This paper presents a cosine similarity measure for DHHFLEs. Different from the existing similarity studies of DHHFLEs, this method innovatively transforms DHHFLEs into unit vectors and obtains the cosine similarity between DHHFLEs, which is not only easy to understand, but also avoids adding information artificially.

• (3) This paper proposes a cosine similarity-based DHHFL-ELECTRE II method. Based on the proposed cosine similarity, the concordance set, discordance set and indifference set are established, and the priority relationship between alternatives is constructed based on these three sets.

This paper further studies the similarity measure of DHHFLTS. In addition to similarity measure, correlation measurement is also an important research direction. Considering that entropy measure is the basis of many decision-making methods, the research on DHHFLEs entropy measure is limited. In the future research, we will strive to study more types of entropy measures, such as entropy measures and cross-entropy measures, in order to improve the research system of DHHFLTS measures.