1 Introduction

Production planning and control (PPC) systems are comprehensive information systems that deal with many tasks within a company, among which managing replenishment orders remains the most important (Olhager and Wikner 2000). MRP (Material Requirements Planning or Material Resource Planning) is a popular PPC system which first appeared in the 1980’s (Dolgui and Prodhon 2007). MRP is based on sales forecasts to build replenishment orders. MRP computes these orders so as to match with forecasted due date schedule. This strategy is called a push strategy since production is triggered based on forecast and not demand then pushed to the customer (Brocato 2010), at the opposite of a pull strategy [implemented in a Kanban system (Junior and Godinho Filho 2010)] where real demand is pulled from customer to trigger production. Once the PPC system generates replenishment orders, these should be executed. PPC systems usually come with execution modules addressing priority between orders. MRP usually uses priority by due dates, leading prioritizing replenishment orders that are due the earliest.

Demand-Driven MRP (DDMRP) is a hybrid push-and-pull system that uses both short-horizon forecasts and real-time observations of stock and customer demand to generate replenishment orders (Damand et al. 2022; Lahrichi et al. 2022). This PPC system has been described and comprehensively explained in two books (Ptak and Smith 2011, 2016). Its main aim is to achieve higher service levels and lower operating costs by hybridizing push systems that are robust but not responsive enough to fluctuations and pull systems that minimize stocks at the expense of poorer customer service levels. Demand-Driven MRP is explained and illustrated by means of an example in the following section.

Demand-Driven MRP is an ongoing topic of research. Since the two seminal publications of the method by the authors Ptak and Smith (2011), Ptak and Smith (2016), many scholars have taken an interest in Demand-Driven MRP. Comprehensive states of the art can be found in Pekarčíková et al. (2019), Bahu et al. (2019), El Marzougui et al. (2020), Azzamouri et al. (2021). We can split Demand-Driven MRP publications into two main categories:

  • Evaluative surveys Within this class of publications, scholars examine the relevance of DDMRP as a new PPC system by simulating an industrial environment (real or fictitious) (Ihme 2015; Shofa and Widyarto 2017; Bayard and Grimaud 2018; Dessevre et al. 2019; Martin 2020; Velasco Acosta et al. 2020; Dessevre et al. 2021; Azzamouri et al. 2022) and potentially comparing it with more prevalent PPC systems (mainly MRP or Kanban) (Favaretto and Marin 2018; Kortabarria et al. 2018; Shofa et al. 2018; Miclo et al. 2019; Thürer et al. 2020). For example, in Thürer et al. (2020), DDMRP is compared with MRP, Kanban, and Optimized Production Technology (OPT). Simulations are based on gradual due dates and bottlenecks (capacity). The study finds out that DDMRP (and Kanban) perform better if no bottleneck capacity is considered, whereas DDMRP (and OPT) achieve good performance if a bottleneck capacity is considered. In Velasco Acosta et al. (2020), DDMRP is simulated on a product structure of four levels with seven references. The study shows that a reduction of 18% and 41% is observed in terms of stock levels and lead times (respectively).

  • Parameterization studies Within this class of publications, scholars put forward algorithms to parameterize Demand-Driven MRP. Indeed, DDMRP relies on numerical parameters that are to be fixed by the user (production manager). Decision support algorithms are needed to help the production manager fix these parameters. In Damand et al. (2022), we conducted a first comprehensive study on algorithmic parameterization of DDMRP. All the parameters (eight in total) were included in the study. A genetic algorithm was developed to fix these parameters while minimizing the stock and maximizing on-time delivery (percentage of customer orders delivered on-time). The study shows that three parameters, namely, the lead time factor, the variability factor and the order peak threshold, were most in need of fixing by means of an optimization algorithm. The remaining parameters were constant overall. The suggested algorithm was tested on a data set containing 60 instances spanning a planning horizon of one year. We retained the three parameters to design a Mixed Integer Linear Programming model (MILP) in Lahrichi et al. (2022). The designed MILP computes the optimal solution to minimize stock and satisfy all demand on time. Optimal solutions were found within a few seconds on a data set with 24 instances spanning a 3-month planning horizon. In Duhem et al. (2023) and Lahrichi et al. (2023), the authors put forward a reinforcement learning algorithm to fix respectively, two and three DDMRP parameters, optimizing stock levels and customer satisfaction. Papers dealing with DDMRP parameterization are summarized in Table 1. Only papers suggesting algorithms are considered in the table. We note that some articles, like Martin (2020) or Dessevre et al. (2019), infer general parameterization rules from simulation. These are not considered in the table.

Table 1 Papers on algorithmic parameterization of DDMRP
Full size table

We note a lack of research with regards to algorithmic parameterization of DDMRP. However, it remains an active area of research, as shown by the recent publication dates. The most widely studied objective functions are minimizing average stock and maximizing the On-time Delivery (OTD) that is the percentage of customer orders delivered on-time.

1.1 Literature gap and contribution of this paper

A PPC system is usually applied within a complex manufacturing environment containing several references competing for bottleneck resources (Thürer et al. 2020). To the best of our knowledge, no paper to date has considered the parameterization of several buffered references with limited capacity within DDMRP, justifying the contribution of our paper. Indeed, all papers dealing with the parametrization of DDMRP consider only one reference. The suggested algorithms cannot be applied to contexts with multiple references since this requires management of capacity given its limited quantity. The presence of several references with a limited capacity delays the replenishment orders and therefore impacts the parameterization decision.

The present paper examines the parameterization of several references. The suggested algorithm computes a vector of parameters for each buffered reference. A simulation DDMRP algorithm generates replenishment orders based on the suggested parameterization. The on-order inventory (i.e., the quantity of stock that has been ordered but not yet delivered) is considered to be limited and cannot exceed a given capacity. Consequently, a priority rule must be used to decide which orders to prioritize given this finite capacity. The priority rule used in this paper is derived from Ptak and Smith (2016). The average stock and the OTD are optimized simultaneously.

In the following section, DDMRP with multiple products and finite capacity is detailed and illustrated by means of an numerical example. Sections 3 and 4 are devoted, respectively, to the problem statement and resolution approach. Section 5 gives the plan of experiments and summarizes the results obtained. The last section of the paper presents concluding remarks and further potential research avenues.

2 Demand-driven MRP with multiple products and finite capacity

Demand-Driven MRP was suggested in Ptak and Smith (2011) and further extended in Ptak and Smith (2016). These books contain the general principles of Demand-Driven MRP and numerical examples allowing to derive the simulation algorithm. However, a few details are left to the appreciation of the reader, especially in the finite capacity case, where no numerical example is given. The working principle of DDMRP presented in this section is inspired from Ptak and Smith (2011, 2016). Demand-Driven MRP works within the three decision levels: strategic, tactical, and operational (see Fig. 1).

Fig. 1
figure 1

DDMRP decision levels

Full size image

Each of the following subsections is dedicated to a different decision level.

2.1 Strategic planning

The first step in Demand-Driven MRP deals with the strategic positioning of buffer stocks within a product structure (BOM, Bill of Materials). More specifically, the references that need to be managed with an inventory (called a buffer stock) need to be decided. All remaining references are managed by JIT (Just-In-Time) with zero stock. The choice of references to be buffered is crucial (Velasco Acosta et al. 2020) for two main reasons:

  • A buffer stock requires an investment and generates operating expenses.

  • A well-positioned buffer stock can lead to a significant reduction in lead times.

Figure 2 shows a 4-level product structure. Three references are chosen to be buffered: REF_X_B, REF_X_B_B and REF_X_C_A. In the figures, the lead times are shown at the top right of the reference.

Fig. 2
figure 2

A product structure with 3 buffered references

Full size image

Buffering a reference makes it immediately available if the buffer stock is replenished. Thus, DDMRP defines the DLT (Decoupled lead time) of a buffered reference as the cumulative lead time necessary to produce the considered reference with its non-buffered sub-references Ptak and Smith (2016). For example (Fig. 2), the DLT of REF_X_B is the sum of the lead times of REF_X_B, REF_X_B_A and REF_X_B_A_A, which makes 8 \((5+1+2)\). REF_X_B_B is not included since it is buffered. This shows how buffer stocks can lead to a reduction of delays.

Some scholars have dealt with the strategic positioning of buffers as a combinatorial optimization problem (Jiang and Rim 2017; Rim et al. 2014; Abdelhalim et al. 2021; Miclo 2016; Lee and Rim 2019). These studies put forward algorithms to select references to be buffered while minimizing operating costs.

Strategic buffer positioning is beyond the scope of this paper. We assume that buffers are already in place and consider parameterizing each buffered reference.

Within DDMRP, the buffer stocks all have the same structure, consisting of three superposed and fictitiously colored zones (Fig. 3).

Fig. 3
figure 3

Stock structure within DDMRP

Full size image

The yellow zone is dimensioned by \(ADU \times DLT\) where ADU is the average daily usage (demand averaged over a given horizon) and DLT is the decoupled lead time. Since DLT is the delay necessary for a given replenishment order to be delivered, the yellow zone represents demand during replenishment time. The red zone represents a safety stock. It is dimensioned with \(ADU \times DLT \times F_{LT}+ADU \times DLT \times F_{LT} \times F_{V}\) where \(F_{LT}\) and \(F_{V}\) are numerical parameters to be fixed by the user. In this paper, these two parameters are fixed by the suggested algorithm. The green zone is dimensioned by \(ADU \times DLT \times F_{LT}\), which aims to further protect the stock. These three zones define the TOR (Top Of Red), the TOY (Top Of Yellow) and the TOG (Top Of Green), as shown in Fig. 3.

2.2 Tactical planning

Tactical planning within Demand-Driven MRP deals with the generation of replenishment orders. DDMRP uses the net flow to decide when to generate an order. Net flow is a concept specific to DDMRP. It represents the quantity in stock (on-hand inventory) plus the amount of stock that has been ordered (released) but not yet delivered (on-order inventory) minus the qualified demand. Qualified demand is another notion specific to DDMRP. It subsumes the demand of the day plus future demand exceeding a given threshold. This threshold is a numerical parameter to be fixed by the user. In this paper, the parameter is fixed by the suggested algorithm and denoted by \(\text {T}_{\text {peak}}\). The peak threshold is expressed as a percentage of the TOR. Future demand is observed within a horizon called the peak horizon and fixed at DLT. The DDMRP simulation algorithm generates a replenishment order on a given day if the net flow \(\le\) TOY. In this case, the quantity of the order is TOG—net flow. Table 2 illustrates order generation using a small numerical example.

Table 2 Order planning within DDMRP
Full size table

2.3 Operational execution

Following the planning of replenishment orders, execution should be carried out carefully to avoid extra delays. Finite capacity prevents orders from being executed according to their planned schedule. A priority rule helps decide which orders should be executed first. Demand-Driven MRP introduces a novel priority rule called priority by buffer status (Ptak and Smith 2016). This priority rule creates a disruption with priority by due date and addresses its weakness. Priority by due date, which is most often used, has some shortcomings, as mentioned in Ptak and Smith (2016):

  • It is a static rule that does not take real-time stock into account.

  • Several orders can have the same due date.

  • Due dates can change which creates an alignment problem with suppliers.

Buffer status is defined as the ratio between on-hand inventory and the TOR (\(\text {Buffer status}=\frac{\text {On-hand inventory}}{\text {TOR}}\%\)). We may note that, unlike planning where order generation is based on the net flow, which is a theoretical concept, order execution is based on the on-hand inventory which is observed in real time. Orders with the lowest buffer status are prioritized.

The buffer status is associated with a code color, making it easier to recognize the priority visually:

  • When the buffer status is inferior to 50%, the system sends a red alert (the stock is critically low, the order comes with a high priority).

  • When the buffer status is between 50 and 100%, the system sends a yellow alert (moderate priority).

  • When the buffer status is greater than 100%, the system sends a green alert.

Even if finite capacity is mentioned in Ptak and Smith (2011, 2016), this notion is never modeled and illustrated through an example. We suggest here a way to take finite capacity into account. We define capacity as a maximum number of SKUs (stock-keeping unit) being processed simultaneously. In other words, capacity is a limitation in the total on-order inventory (Herbots et al. 2007; Hall and Liu 2008).

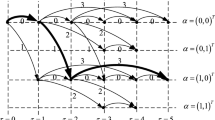
In Table 3, we present an example where the total capacity is 350. At day 1, the on-order inventory is 0 for the three references, which means that the available capacity is 350. This capacity is allocated within the priority order reference 2, reference 3, reference 1 (based on buffer status). Planned orders associated with references 2 and 3 are released in their entirety at day 1, and the remaining capacity \((350 - 109 - 170 = 71)\) is allocated to reference 1. At day 6, the total on-order inventory is \(85 + 0 + 68 = 153\), so the available capacity is \(350 - 153 = 197\). This available capacity is allocated within the priority order “reference 1, reference 3, reference 2” (based on buffer status). All planned orders are released at day 6 as they do not exceed 197 in total.

Table 3 Order planning within DDMRP
Full size table

3 Problem statement

The problem addressed falls within the tactical and operational levels. We assume that the strategic problem involving the choice of references to be buffered has already been resolved. We are given a number of references (products) with associated Decoupled Lead Times (DLT) and we propose fixing the three parameters associated with each buffered reference. The parameters come into play in the planning and execution of replenishment orders and thereafter in the computation of KPIs. The problem can be described as centralized since a single agent parameterizes all references and aggregated KPIs (see Fig. 4).

Fig. 4
figure 4

Centralized parametrization within DDMRP

Full size image

We make a number of assumptions based (in part) on Ptak and Smith (2011, 2016); Damand et al. (2022); Lahrichi et al. (2022):

  • The planning horizon H spans over a year. Parameterization is performed once a year and uses the forecast demand data of the following year. The planning time step is 1 day.

  • A capacity C is considered: the total on-order inventory (i.e., quantity of orders released but not yet finished) cannot exceed C at a given day. C is measured in terms of SKUs (Stock-Keeping Unit).

  • When a replenishment order is planned on day t, it waits to be released based on available capacity and priority relative to other orders. If released on day t, the order finishes at \(t+\)DLT where DLT is the decoupled lead time associated with the reference.

  • The order peak horizon is fixed at DLT for each product as recommended in Ptak and Smith (2016) and confirmed in Damand et al. (2022). Indeed, such an order peak horizon gives just enough time for released orders to be delivered on time for peaks.

  • The ADU (average daily usage) for each product is computed once as the average demand over the planning horizon

Below, we state the multiple products and finite capacity DDMRP parameterization problem :

  • Data

    • A set of products/references and their associated DLTs (Decoupled lead time).

    • The demand data for each product over the considered horizon.

    • The initial stock for each product.

  • Variables

    • The Lead Time (LT) factor, \(F_{LT}\).

    • The variability factor, \(F_{V}\).

    • The order peak threshold, \(T_{Peak}\).

  • Constraints

    • A DDMRP replenishment policy is used for planning the replenishment orders.

    • The buffer status priority rule is used for the execution of replenishment orders.

  • Objectives

    • Minimization of on-hand inventory: the stock is averaged over the planning horizon for each reference then averaged over the references. The objective can be expressed as follows: \(\dfrac{\sum _{i=1}^{p_{max}}\sum _{t=1}^{h_{max}}q_t^{\text {on-hand}}(i)}{p_{max}.h_{max}}\) where \(q_t^{\text {on-hand}}\) is the on-hand inventory of product i at the end of the \(t^\text {th}\) day of the planning horizon, \(h_{max}\) is the number of days of the planning horizon and \(p_{max}\) is the number of products.

    • Maximization of OTD (On-time Delivery): the OTD is computed as the ratio of the number of days with non-negative on-hand inventory with the number of days in the planning horizon. The OTD is calculated for each reference then averaged over the references. The objective can be expressed as follows: \(\dfrac{\sum _{i=1}^{p_{max}}\sum _{t=1}^{h_{max}}{f(t,i)}}{p_{max}.h_{max}} \times 100 \%\) where f is defined as follows:

      $$\begin{aligned} f(t,i) = {\left\{ \begin{array}{ll} 1 &{} \text {if } q_t^{\text {on-hand}}(i) \ge d_t^i \\ 0 &{} \text {otherwise } \end{array}\right. } \end{aligned}$$

      where \(d_t^i\) is the customer demand of product i at day t.

4 Resolution approach

The suggested optimization approach is an extension of the genetic algorithm introduced in Damand et al. (2022). In Damand et al. (2022), the algorithm is developed for a single reference without any capacity constraints. We extend the algorithm here for multiple references with limited capacity.

NSGA-II (Non-dominated Sorting Genetic Algorithm) is a metaheuristic designed for multi-objective optimization (Deb et al. 2002). The algorithm has proven its efficiency in different industrial contexts (Verma et al. 2021; Rahimi et al. 2022). Like any genetic algorithm, NSGA-2 applies cross-over and mutation operators to improve a pool of solutions over successive generations. NSGA-2 uses a specific fitness function based on non-dominated sorting and crowding distance to discriminate between non-dominated solutions.

A vector of size 3.n is used to encode the solution, where n is the number of products (or references). Lead time factor \(F_{LT}\), variability factor \(F_{V}\) and order peak threshold \(T_{Peak}\) are encoded successively in the vector for each product as shown in Fig. 5.

Cross-over between two parent solutions is used to generate one child solution averaging the parameters of its parents, as shown in Fig. 6.

The mutation operator is used to bring diversification to the pool of solutions. A solution is muted by averaging each of its parameters with either the lower bound or the upper bound. A coin toss is performed to choose between the upper bound and the lower bound.

Fig. 5
figure 5

Solution encoding

Full size image
Fig. 6
figure 6

Cross-over scheme

Full size image

Algorithm 1 describes the suggested algorithm. First, the population is initialized with random individuals. The parameters within these individuals are randomly generated between the given upper and lower bounds. Each time a new individual is generated, DDMRP simulation algorithm is applied to evaluate the on-hand inventory and OTD. A deterministic tournament selection is used as a selection mechanism to choose two parent individuals to be reproduced with the cross-over operator. Each individual within the population is muted with a given probability, the resulting individual (mutated) is added to the population while the initial individual is not deleted. Elitism is implemented from a generation to the next by choosing the best half of the population with respect to non-dominated sorting and crowding distance. The algorithm outputs the first front of non-dominated solution with respect to the on-hand inventory and OTD.

Algorithm 1
figure a

Genetic algorithm for the parameterization of DDMRP with multiple products and finite capacity

Full size image

5 Computational experiments

The suggested resolution approach is tested numerically in this section. Computational experiments are performed on a computer equipped with a RAM of 16 GB. Algorithms were developed under JAVA. Data instances used for the experiments are generated by us and are available upon request.

5.1 Experimental design

The experimental design is aimed at testing the algorithm in different configurations. 16 different data instances are generated and 10 references with different DLTs (Decoupled Lead Time) are considered (see Table 4). A data instance consists of 10 demand scenarios (one for each reference).

Table 4 Decoupled lead times
Full size table

The demand scenario spans over an open year (255 days). The same demand data is used for all instances. The 16 instances only differ in terms of capacity. Within the same instance and different products, demand data follow the same normal distribution centered at 1000 with a standard deviation of 100.20% of demand entries are selected to constitute demand peaks within [1500, 2000]. Figure 7 shows the distribution of a given reference.

Fig. 7
figure 7

Demand distribution of a given reference

Full size image

If demand is constant for all references, we can determine the minimum capacity to reach an OTD of 100% . We call this capacity the theoretical capacity (TC) and calculate it as follows:

$$\begin{aligned} \text {Theoretical capacity (TC)} = \sum _{ref \in References} ADU_{ref} \times DLT_{ref} \end{aligned}$$

where \(ADU_{ref}\) and \(DLT_{ref}\) are respectively the average daily usage and the decoupled lead time associated with a given reference ref.

In our case, where the demand is not constant, we use the theoretical capacity as a reference to size the capacity in our instances. Table 5 gives the capacity associated with each instance. We gradually increase the capacity beyond the theoretical capacity to study the behavior of the algorithm in different scenarios.

Table 5 Data instances and capacities
Full size table

The optimization algorithm relies on the lower and upper bounds associated with the parameters. These are given in Table 6. We should recall that the order peak horizon is fixed to the DLT.

Table 6 Parameters lower and upper bounds
Full size table

The genetic algorithm relies on three parameters: the population size, the number of generations, and the mutation probability. An experimental tuning was performed by testing many values and choosing the best set of parameters giving good solutions for a representative sample of instances in a reasonable CPU time. The parameters are given in Table 7. The total CPU time of the suggested algorithm on all data instances is about 11 min (41 s per instance on average).

Table 7 Optimization parameters
Full size table

5.2 Results and discussion

On each instance, the algorithm outputs a number of non-dominated solutions with respect to OTD and average stock.

Table 8 gives the number of non-dominated solutions as well as the OTD and average stock associated with the solution featuring the best OTD.

Table 8 Number of non-dominated solutions, OTD and average stock
Full size table

Table 8 shows that an OTD of 100% can be obtained starting from a capacity greater than the theoretical capacity by 30%. Below this capacity, the OTD seems to be proportional to the capacity.

Table 8 also shows that increasing capacity leads to an increase in average stock. The OTD and average stock (associated to the best OTD solution) reach a steady state starting from instance 5.

Increasing the capacity leads to a reduction in the number of non-dominated solutions obtained. There are several possible explanations for this observation. We can argue that, at low capacity, the problem is very constrained, which makes the interaction between the parameters of different references very acute as well as the interaction between the two objective functions. Capacity at least 30 % greater than the theoretical capacity allows the algorithm to obtain one or two solutions that dominate all the others.

Figure 8 draws the evolution of the number of non-dominated solutions, OTD and average stock related to the capacity.

Figure 9 represents the front of non-dominated solutions associated with instance 5. Six different solutions are obtained. These solutions are close in terms of OTD and average stock.

Figure 10 shows the evolution of non-dominated fronts through successive generations due to the application of cross-over and mutation operators. The data instance used to illustrate this evolution in the figure is instance 4.

Figure 10 demonstrates the effectiveness of the genetic operators allowing a drastic improvement in terms of OTD and average stock from generation 1 to generation 100. The OTD is improved approximately by 15% while the average stock is improved approximately by 16%. The improvement is greater within first generations and diminishes over the generations (generations 100 and 80 are closer to each other than generations 20 and 0). We can also note that the number of non-dominated solutions is greater in advanced generations.

Tables 9 and 10 give the breakdown by reference of OTD and average stock (respectively).

Fig. 8
figure 8

Evolution of the number of non-dominated solutions, OTD and average stock as a function of capacity

Full size image
Fig. 9
figure 9

Front of non-dominated solutions for instance 5

Full size image
Fig. 10
figure 10

Evolution of fronts through successive generations for instance 4

Full size image

Regarding the OTD, we can note that references with the lowest DLT obtain the highest OTD. This is understandable since low lead times allow replenishment orders to be delivered quickly, thereby avoiding stockouts. All references obtain a 100% OTD starting from instance 6.

Table 9 OTD breakdown by reference (best OTD solution)
Full size table
Table 10 Breakdown by reference of average stock in thousands of SKUs (Stock-keeping units) for the best OTD solution
Full size table

We define the release ratio as follows:

$$\begin{aligned} \text {Release ratio} = \frac{Q_\text {released}}{Q_\text {planned}} \times 100\% \end{aligned}$$

where \(Q_\text {planned}\) is the sum of the planned replenishment order quantities and \(Q_\text {released}\) is the sum of the released order quantities. Due to limited capacity, \(Q_\text {released}\) is usually lower than \(Q_\text {planned}\).

Table 11 gives the release ratio associated with the best OTD solution. It shows the following:

  • From instance 0 to instance 4, references with the lowest DLT obtain the highest release ratio. Indeed, a lower DLT gives lower and less frequent planned replenishment orders, which make them more likely to be released.

  • From instance 5 to instance 8, we note that the release ratio almost never reaches 100% despite having an OTD of 100% (Table 9). Indeed, it is possible to have an OTD of 100% without launching all planned orders. This can be put down to the protectiveness of DDMRP planning.

  • From instance 9 to instance 15, a large capacity allows all the planned orders to be launched in their entirety and thus to have release ratios of 100%.

Table 11 Release ratio (best OTD solution)
Full size table

Table 12 gives the parameters obtained by the genetic algorithm. The parameters from the best OTD solution are shown. Since references have growing DLT and instances have growing capacity, the table can help us understand the interplay between the two.

Table 12 Parameters (rounded without floating point) obtained (best OTD solution)
Full size table

From Table 12, it seems that the lead time factor is proportional to the DLT for instances with tight capacity, and inversely proportional for remaining instances.

Table 12 also shows that the capacity is inversely proportional to the lead time factor for references with high DLT and proportional for remaining references.

6 Conclusion and perspectives

This paper presents a first parameterization study for Demand-Driven MRP under finite capacity with multiple references. We included capacity as an on-order capacity and adapted the DDMRP simulation algorithm accordingly using the priority rule by buffer status. Sixteen data instances, each integrating 10 references, were generated to test the suggested algorithm. Different decoupled lead times and different capacities were considered to test the algorithm in different configurations.

Computational experiments found that the suggested algorithm can produce non- dominated solutions within a reasonable time. The solutions obtained usually come with a high OTD. The experiments also estimated the minimum capacity required to reach a 100% OTD. This estimation gives a 30% increase in the theoretical capacity. As expected, experiments establish proportionality between the OTD and capacity. High OTD usually comes at the expense of higher average stock. Experiments also found that references with the lowest DLT obtain the highest OTD. These references also obtain the highest release ratio.

This work adapts an existing approach for infinite capacity DDMRP parameterization to a newly defined problem integrating finite capacity. A natural perspective for the present work is to adapt the other published parameterization approaches for infinite capacity DDMRP to finite capacity, notably, the MILP (mixed integer linear programming) model from Lahrichi et al. (2022).