Modeling and Simulation of a Shock Driving Gas Jet Laden with Dense Extinguishant Particles Through a Tube with a Tail Nozzle

Abstract

In this study, we proposed a new concept of shock wave driving fire extinguishing system (SWDES), which works using a pulsed shock-induced gas-particle jet. We conducted modeling and simulations of shock-induced gas-particle jets through a rectangular tube with a tail nozzle based on a dense discrete phase model. A corrected drag model was developed to take into account gas compressibility and particle volume fraction effects. The aerodynamic and collision forces imposed on particles were determined by a point particle force model and an improved spring-dashpot model, respectively. Based on the validation of numerical method against a previous experiment, a parametric study was performed to explore the effects of type of tail nozzle, incident shock Mach number M_s, initial particle volume fraction φ_p, and particle size d_p on the dimensionless streamwise average velocity v_px,a/u_s, velocity inhomogeneity ξ_vp and dispersity of particles ψ_p. We revealed that the evolution process of the gas-particle jet consists of the first transmitted shock-induced stage and the second pressure-induced stage of gas jet, and identified penetration, spreading and breakup types of pulsed gas-particle jets suited for fire suppression of correspondingly three types of flames.

1 Introduction

Dry powders are environmentally friendly and highly efficient to suppress fire. The fire suppression efficiency of dry powders such as potassium bicarbonate (KHCO₃), sodium bicarbonate (NaHCO₃), and ammonium dihygrogen phosphate (NH₄H₂PO₄) is nearly 2.5 times of alkyl halide, 4 times of carbon dioxide (CO₂), and even 40 times of water or foam [1]. These dry powders are most effective for fire extinguishing of electrical equipment, liquefied natural gas, and flammable metals, etc. Moreover, quick-response dry powder fire extinguishing systems are extremely important for effective fighting against fires in gas wells and spills of oil and petroleum products in man-caused accidents and catastrophes, and in super high buildings. Therefore, they are extensively applied in the real world fire extinguishing.

Dry powder fire suppressants can be discharged towards a flame in continuous or pulsed ways. For a continuous fire extinguishing system, the efficiency mainly depends on the suppressant type and properties (e.g., composition, size, and density), the geometries of injector (geometrical parameters of primary nozzle, mixing duct and tail section), and operating conditions (e.g., motive pressure and mass flow rates of suppressant). In these aspects, extensive investigations have been performed over the last five decades. Liu et al., Ibrahim and Patruni [2, 3] conducted experiments to compare the effectiveness of different fire suppressants, which include magnesium hydroxide (Mg(OH)₂), NaHCO₃, and NH₄H₂PO₄ powders. The results indicated that the Mg(OH)₂ powder performs much more efficiently in fire extinguishing time than the others. Kuang et al. [4] carried out experiments to compare the fire suppression effectiveness of Mg(OH)₂ with two commercial dry powders, and they concluded that the fire extinguishing effectiveness is significantly improved as the powder size is decreased. Lau and Nathan [5] experimentally investigated the effect of Stokes number on particle velocity and concentration distributions in a particle-laden turbulent jet with a particle image velocimetry (PIV). The result revealed that the magnitudes of effective Stokes number in the radial direction are higher than that in the axial direction. Wang et al. [6] conducted a direct numerical simulation to investigate the influence of Stokes number on a particle-laden plane turbulent wall jet. Jebakumar and Abraham [7] carried out two-dimensional axisymmetric CFD simulations using a k–ε turbulence model to analyze the structure of particle-laden jets for Stokes number = 0.3 to 500. Tavangar et al. [8] used a three-dimensional Eulerian–Lagrangian multiphase model coupled with k–w shear stress transport (SST) turbulence model to investigate the horizontal motion of particle-laden jets and analyzed the relation between the jet Reynolds number and Stokes number. Chellappan and Ramaiyan [9] experimentally studied the effects of design parameters and suction position with respect to the motive jet on a gas–solid ejector performance. Abd El-hamid et al. [10] performed a detailed experimental investigation on the effect of the shape of mixing duct with tail section on the ejector performance for an air–solid two-phase ejector. Zhu et al. [11] numerically investigated the effects of the primary nozzle exit position and the geometry of mixing section on the ejector performance. The transport properties of powder ejectors based on single- and double-venturi effect and the influence of nozzle position on the transportation performance were experimentally and numerically investigated with the aid of CFD-DEM coupling method [12]. The effects of different operating variables and the ejector geometry on the performance of ejectors were determined experimentally by Kim et al. [13]. Szabó [14] numerically studied the influence of pressure of the primary gas jet on the final vacuum created by a supersonic gas ejector. Zhang and Chin [15] investigated jet-to-coflow velocity ratio on the particle-laden coflow jet characteristics using a large eddy simulation (LES) approach.

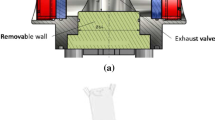
On the other hand, as a representative of pulsed type fire suppression techniques, the condensed aerosol-based fire extinguishing system (CAFES, see Figure 1a) has been introduced since 1960s and developed to the third generation. CAFES generates hot gas accompanied with tiny particulates when a pyrotechnic based aerosol forming composite is ignited electrically or thermally [16]. The generated hot gas pushes the downstream coolant particles to form a jet of aerosol. The aerosol extinguishes fire via physical and chemical mechanisms (inhibition of chain reaction of fire propagating radicals). CAFES has many advantages such as high fire extinguishing efficiency, low Ozone Depletion Potential (ODP) and Global Warming Potential (GWP) values [17], and unnecessity of pressurized canister, etc. Thus, it can be flexibly applied in many applications such as power generation, transportation, storage rooms, heavy industries, battery storage systems, etc., both in fixed and portable ways. However, it also has some obvious disadvantages, which include generation of pathogenic gases (e.g., nitrogen oxides NO_x and carbon monoxide CO), PM 2.5 particulates, and potential risks of burns to eyes and skin due to the hot aerosol [18]. Consequently, CAFES is unsuitable for use in occasions with human activities. Therefore, we propose an alternative pulsed type fire suppression technique, i.e., shock wave driving fire extinguishing system (SWDFES, see Figure 1b), which produces a shock wave when the interface between the pressurized and atmospheric inert gases (e.g., nitrogen N₂ or carbon dioxide CO₂) is open. The produced shock wave and the post-shock high-speed gas flow impinges and accelerates the downstream dry powder fire suppressant, leading to the generation of a particle-laden two-phase jet, which has fire extinguishing effects. The adopted fire suppressants include KHCO₃, Mg(OH)₂, NaHCO₃, and NH₄H₂PO₄ ordinary or superfine dry powders, etc. SWDFES can be designed to be utilized repeatedly if a quick-action solenoid valve is employed to separate the aforesaid inert gases, and meanwhile an auxiliary system is equipped to realize the controllable supply of fire suppressant powders and inert gases. In principle, SWDFES is able to be used for all the applications of CAFES no matter whether there are human activities or not. Viewing from multiphase flow, SWDFES play a role via a particle-laden gas jet driven by a shock wave.

Figure 1

Sketches of (a) CAFES, and (b) SWDFES

After the generated incident shock wave impinges on a cloud of fire suppressant particles, moving reflected and transmitted shock waves, contact surfaces appear, while the particles are accelerated by the incident and transmitted shock waves and the post-shock gas flow. Gas-phase and gas-particle two-phase jets are produced in sequence due to the passage of the transmitted shock wave and the post-shock gas flow through a tail nozzle. During this process, the motion of particles is mainly dependent on the aerodynamic and inter-particle collisional forces, and also affected by wall collisional and turbulent viscous effects. The key difficulty in modeling is to construct the force models and consider these effects appropriately.

In the present modeling, we utilized a dense discrete phase model (DDPM), in which much less particle parcels than the real particles are required to be tracked in velocity, position, and thermal histories. An improved version of [19] spring-dashpot model based on a distinct elemental method (DEM) was employed to model multi-body collisions of particle parcels. Thus, the computational cost can be significantly reduced. In consideration of a remarkably inhomogeneous distribution of pressure and gas acceleration induced by multiple reflections and transmissions of shock waves, pressure-gradient and added-mass force contributions were contained in the aerodynamic force. Because quasi-steady force dominates the motion of particles over the long-time scale, we included its contribution to the aerodynamic force. But we ignored the contribution of viscous-unsteady force due to the complexity of mathematical expression and lack of precise understanding so far [20].

In this study, we conducted an interphase four-way coupled modeling for a shock-induced gas-particle jet through a rectangular tube with a tail nozzle. The numerical method was validated against experiments on shock-particle curtain interaction [21]. Formation mechanisms of two different types of jets were illustrated first. And then, the effects of type of tail nozzle, incident shock Mach number, initial particle volume fraction, and particle size on three newly defined index parameters, which include the streamwise average velocity, velocity inhomogeneity and dispersity of particles, were analyzed. The remainder of this paper is organized as follows. The interphase coupled modeling is delineated in the Sect. 2. The numerical method is then presented in the Sect. 3. Next, in the Sect. 4, we illustrate and analyze the computational results. The main conclusions are given in the Sect. 5 finally.

2 Interphase Coupled Modeling

2.1 Equations for Particle Phase

The DDPM is used for predictions of motion and thermal histories of particle parcels in a Lagrangian framework. Bhattacharya et al. performed analysis of order of magnitude for forces of tens micron-sized particles travelling through a converging–diverging micro-nozzle. It indicated that Magnus force that is associated with rotation of particles should be greatly smaller than other forces such as quasi-steady, added-mass, pressure-gradient, and Saffman forces. Thus, the effect of particle rotation was usually neglected in the related gas particle flows such as in Refs. [21, 22], etc. Therefore, the rotational motion of the particles is also ignored in this modeling due to the small sizes of not greater than O(100 μm) and large translational velocities up to O(100 m/s) of the studied particles.

2.1.1 Aerodynamic Force

Following the previous works by Parmar et al. [23, 24] and Ling et al. [25, 26], the overall aerodynamic force component F_fp,i imposed on a particle utilizes the following point particle force model:

$$F_{fp,i} = F_{qs,i} + F_{am,i} + F_{pg,i}$$

(1)

in which F_qs,i, F_am,i, and F_pg,i represent the quasi-steady (drag), added-mass, and pressure-gradient force components in i direction, respectively. The quasi-steady force component F_qs,i is given as

$$F_{qs,i} = \frac{\pi }{8}d_{p}^{2} \rho_{g} C_{D} \left( {v_{g,i} - v_{p,i} } \right)\left| {{\mathbf{v}}_{g} - {\mathbf{v}}_{p} } \right|$$

(2)

where d_p is the particle diameter. v_g and v_p are gas and particle velocity vectors, respectively. ρ_g denotes the gas density. v_g,i and v_p,i represent the gas phase and particle velocity components, respectively. A corrected model for the drag coefficient C_D, which considers effects of gas compressibility and particle volume fraction, is expressed as

$$C_{D} = f_{v} \left( {\alpha_{p} } \right)\left( {\omega_{1} C_{DC} { + }\omega_{2} C_{DP} } \right)$$

(3)

$$\omega_{1} { = }\frac{1}{2} - \frac{1}{2}\tanh ({\text{Re}}_{p} - 1500),\quad \omega_{2} { = }\frac{1}{2} + \frac{1}{2}\tanh ({\text{Re}}_{p} - 1500)$$

(4)

in which C_DC and C_DP are Clift and Parmar drag coefficients [24, 27] (see Table 1), respectively. In such a form of C_D in Equation (3), we took into account the excellent accuracy of C_DC for low and moderate Re_p and C_DP for large Re_p, and the necessity of particle volume fraction correction for both the drag coefficients owing to the large local particle volume fractions appearing in the gas jet laden with dense particles. The correction factor of particle volume fraction f_v is determined by

$$f_{v} \left( {\alpha_{p} } \right) = \frac{{1 + 2\alpha_{p} }}{{\left( {1 - \alpha_{p} } \right)^{3} }}$$

(5)

Table 1 Summary of the Used Drag Coefficients in the Corrected Model

The particle Reynolds number Re_p and particle Mach number M_p are defined by

$${\text{Re}}_{p} = \rho_{g} \left| {{\mathbf{v}}_{g} - {\mathbf{v}}_{p} } \right|d_{p} /\mu$$

(6)

$$M_{p} = \left| {{\mathbf{v}}_{g} - {\mathbf{v}}_{p} } \right|/c$$

(7)

where μ is the gas dynamic viscosity, and c is the local sound speed.

The added-mass force component F_am,i is determined by

$$F_{am,i} = C_{M} \rho_{g} V_{p} \left( {\frac{{dv_{g,i} }}{dt} - \frac{{dv_{p,i} }}{dt}} \right)$$

(10)

where V_p is the volume of a single particle. For spherical particles, the coefficient C_M is set as 0.5. The pressure-gradient force component F_pg,i is given as

$$F_{pg,i} = - V_{p} \frac{\partial p}{{\partial x_{i} }}$$

(11)

2.1.2 Collisional Force

An improved spring-dashpot model of [19] is used to predict inter-particle collisional forces. The collisional force on a particle parcel between the mth and nth parcels is calculated by

$$F_{pp,i}^{mn} = \left( {K\delta + \lambda \left( {v_{i}^{mn} e_{i}^{mn} } \right)} \right)e_{i}^{mn}$$

(12)

in which δ represents the overlap of the collision pair of particle parcels.$v_{i}^{mn}$ and $e_{i}^{mn}$ denote the pre-collisional relative velocity component between the mth and nth particle parcels and the component of its unit vector, respectively. The spring constant K is estimated as

$$K = \pi \left| {{\mathbf{v}}^{mn} } \right|\rho_{p} D_{p} /\left( {3\xi_{D}^{2} } \right)$$

(13)

where v^mn is relative velocity vector between the mth and nth particle parcels. ξ_D denotes the allowable overlap fraction of diameter. ρ_p is the particle density, and the effective diameter of a particle parcel D_p is simply related to the particle diameter d_p as

$$D_{p} = \sqrt[3]{{N_{p} d_{p} }}$$

(14)

in which N_p is the number of real particles represented by one particle parcel.

The damping coefficient λ in Equation (12) is computed by

$$\lambda = - \sqrt {\frac{{2N_{p} m_{p} K}}{{\pi^{2} + \ln^{2} \eta }}} \ln \eta$$

(15)

where m_p denotes the mass of a single particle. The coefficient of restitution should fall in a range of 0 < η ≤ 1. In this work, we focused on the behavior and characteristics of generated jets. Thus, we set it as a fixed value of η = 0.9 [20].

The overall collisional force component imposed on the nth particle is finally computed by

$$F_{pp,i}^{n} = \frac{1}{{N_{p} }}\sum\nolimits_{l = 0}^{L} {F_{pp,i}^{nl} }$$

(16)

where L is the total number of all the lth particle parcels in contact with the nth particle parcel at this time step.

2.1.3 Particle Equations of Motion and Heat Transfer

In accordance with Newton’s second law, the equations of motion for each particle in the Lagrangian framework is given as

$$m_{p} \frac{{dv_{p,i} }}{dt} = F_{qs,i} + F_{am,i} + F_{pg,i} + F_{pp,i} ,\quad {\text{and}}\quad v_{p,i} = \frac{{dx_{p,i} }}{dt}$$

(17)

where x_p,i denotes the i-direction position coordinate of the particle.

The gas convective heat transfer to a particle is computed by

$$Q_{gp} = {\uppi }\mu c_{pg} d_{p} \left( {T_{g} - T_{p} } \right){\text{Nu}}/{\text{Pr}}$$

(18)

where c_pg is the gas specific heat at constant pressure. T_g and T_p are the gas and particle temperatures, respectively. Prandtl number Pr is given as Pr = 4γ/(9γ − 5) where γ is the ratio of gas specific heats (γ = 1.4 for air). The computation of Nusselt number Nu adopts Ranz and Marshall’s empirical correlation [28].

2.2 Equations for Gas Phase

The equations of the viscous, compressible, and unsteady gas phase flow governing mass, momentum, and energy conservations can be expressed as follows:

$$\frac{\partial }{\partial t}\left( {\varphi_{g} \rho_{g} } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\varphi_{g} \rho_{g} v_{g,i} } \right) = 0$$

(19)

$$\frac{\partial }{\partial t}\left( {\varphi_{g} \rho_{g} v_{g,i} } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\varphi_{g} \rho_{g} v_{g,i} v_{g,i} } \right) = - \frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\varphi_{g} \tau_{eff,ij} } \right) - \frac{{N_{p} }}{{V_{cell} }}\sum\nolimits_{n = 0}^{N} {F_{fp,i}^{n} }$$

(20)

$$\frac{\partial }{\partial t}\left( {\varphi_{g} \rho_{g} e_{g}^{ * } } \right) + \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\varphi_{g} \rho_{g} e_{g}^{ * } + p} \right)v_{g,i} } \right] = \frac{\partial }{{\partial x_{j} }}\left[ {\varphi_{g} \left( {k_{eff} \frac{{\partial T_{g} }}{{\partial x_{j} }}\user2{ + }\tau_{eff,ij} v_{g,i} } \right)} \right] - \frac{{N_{p} }}{{V_{cell} }}\sum\nolimits_{n = 0}^{N} {\left( {G_{fp}^{n} + Q_{fp}^{n} } \right)}$$

(21)

where φ_g is the gas volume fraction. n and N are the number and total number of particle parcels within the current cell. e_g^* is the specific total energy. k_eff is the effective thermal conductivity. $G_{fp}^{n} = F_{fp,i}^{n} v_{g,i}$ is the rate of work on the nth particle parcel caused by the aerodynamic force. $Q_{fp}^{n}$ is the rate of heat transfer to the nth particle parcel from the gas. The effective stress tensor component $\tau_{eff,ij}$ is the sum of the molecular stress tensor $\tau_{m,ij}$ and Reynolds stress tensor $\tau_{t,,ij}$ expressed as follows:

$$\tau_{m,ij} = \mu \left( {\frac{{\partial v_{g,i} }}{{\partial x_{j} }} + \frac{{\partial v_{g,j} }}{{\partial x_{i} }} - \frac{2}{3}e_{ij} \frac{{\partial v_{g,l} }}{{\partial x_{l} }}} \right)$$

(22)

$$\tau_{t,ij} = \mu_{t} \left( {\frac{{\partial v_{g,i} }}{{\partial x_{j} }} + \frac{{\partial v_{g,j} }}{{\partial x_{i} }} - \frac{2}{3}e_{ij} \frac{{\partial v_{g,l} }}{{\partial x_{l} }}} \right) - \frac{2}{3}\rho_{g} ke_{ij}$$

(23)

here μ_t and k are the turbulent viscosity and turbulent kinetic energy, respectively. e_ij is the identity matrix component. The realizable k–ε turbulence model was adopted in this study due to its high reliability and acceptable accuracy in simulations of complex flow fields such as jet flows [29], and transient, compressible, and viscous turbulent flows [30]. The turbulent kinetic energy k and the rate of turbulent dissipation ε transport equations are respectively expressed as follows:

$$\frac{{\partial \left( {\rho _{g} k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho _{g} kv_{{g,i}} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\mu + \frac{{\mu _{t} }}{{\sigma _{k} }}} \right)\frac{{\partial k}}{{\partial x_{i} }}} \right] + G_{k} + G_{b} - \rho _{g} \varepsilon - Y_{M}$$

(24)

$$\frac{{\partial \left( {\rho _{g} \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho _{g} \varepsilon v_{{g,i}} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\mu + \frac{{\mu _{t} }}{{\sigma _{\varepsilon } }}} \right)\frac{{\partial \varepsilon }}{{\partial x_{i} }}} \right] + \rho _{g} \left( {C_{1} S\varepsilon - C_{2} \frac{{\varepsilon ^{2} }}{{k + \sqrt {\nu _{g} \varepsilon } }}} \right) + C_{{1\varepsilon }} \frac{\varepsilon }{k}C_{{3\varepsilon }} G_{b}$$

(25)

where G_k and G_b are the turbulent kinetic energies related to the average velocity gradient and buoyancy, respectively. Y_M is the contribution of pulsating expansion to the total dissipation rate in a compressible turbulent flow. ν_g is the gas kinematic viscosity. Model parameters include C₁ = max[0.43, ξ/(ξ + 5)], ξ = Sk/ε, S = (2S_ijS_ij)^0.5, where S_ij denoting the mean strain rate component, C₂ = 1.9, C_1ε = 1.44, C_3ε = 1.3, σ_k = 1.0 and σ_ε = 1.2, respectively. Actually, an initial value of C₁ = 4.3 was always achieved due to the uniform initial flow fields up- and downstream the incident shock wave. The ideal gas equation of state and relation of φ_g + φ_p = 1 were finally employed to enclose the gas-particle flow equations. Additionally, three-coefficient Sutherland’s law [31] was adopted to consider the effects of temperature on the dynamic viscosity and thermal conductivity of air.

3 Numerical Method and Set-Up

3.1 Numerical Method

ANSYS Fluent V20.2 was adopted as the solver. A pressure-based implicit algorithm that allowed a full pressure–velocity coupling was used for computations of gas-phase parameters [32]. We utilized third-order MUSCL and QUICK schemes [33, 34] to discretize the convective fluxes in the momentum and energy conservation equations and in the turbulence model equations, respectively. A body-force-weighted interpolation scheme was employed to reconstruct the face pressure. The transient formulation used a bonded second-order implicit scheme [22]. The discrete phase particle parcels were tracked on the Lagrangian framework with the time step for gas-phase computations. The particle volume fraction in each cell was computed with a centered-point method, in which the local particle volume fraction is determined by cumulating the number of particle parcel centroids being located in the current cell.

3.2 Problem Set-Up

We conducted numerical simulations of shock-induced gas-particle jets with varying type of tail nozzle, incident shock Mach number, initial particle volume fraction and particle size for a parametric study. Figure 2 shows sketches of (a) the computational domain and (b) boundary conditions. The origin of the Cartesian coordinates corresponds to the center of the exit cross section of the tail nozzle. In order to validate the numerical method, we first adopted a simple geometry, which is a rectangular tube without a tail nozzle in reference of the test section of a shock tube in Ling et al. [21], and a pressure-outlet boundary condition. The side length of rectangular channel and the initial width of particle curtain were fixed as L_s = 2 mm and L_p = 2 mm in cases 1 and 5 to 17. The length of acceleration section was set as L_a = 125L_s and 2L_s in the parametric study cases (7 to 17) and validation cases (1 and 4 to 6), respectively. The remaining geometric parameters include the wall thickness L_t = 0.5L_s, length of tail nozzle L_j = 2L_s, distance from the channel inlet to the upstream side of particle curtain L_f = 125L_s, and outside flow field dimensions L_l = 40L_s and L_w = 10L_s. Structural parameters of three types of tail nozzle are listed in Table 2. The same as in Ling et al.’s experiments [21], we set two pressure monitoring ports P1 and P2 68.6 mm upstream and 64.2 mm downstream of the particle curtain, respectively. In the computations for validation, the adopted soda lime particles have a density of ρ_p = 2520 kg/m³ and specific heat of C_p = 840 J/(kg K). While in the parametric study, we used NH₄H₂PO₄ particles which have a density of ρ_p = 1803 kg/m³ and specific heat of C_p = 1280 J/(kg K). The initial parameters of the gas phase and particle curtains are summarized in Table 3. The initial pressure and temperature downstream the incident shock wave were set as p₁ = 101,325 Pa and T₁ = 300 K, respectively. In order further validate the present numerical method, we performed numerical simulations against the experiment in [35], in which they adopted a 25-mm internal diameter shock tube with a convergent tail nozzle. In fact, the flow channel had a geometry of L_p = 16.7 mm, L_a = 0 and L_j = 160 mm, and the inlet and outlet areas are given in Table 2 (see cases 2–4). The tested SiC particles have a density of ρ_p = 3200 kg/m³ and specific heat of C_p = 445.13 J/(kg K). Incident shock Mach numbers of M_s = 1.385 to 1.783 were achieved by ruptures of aluminum diaphragms due to the pressurization in the driven section. The post-incident shock thermodynamic conditions in these cases were used as elsewhere in this study.

Figure 2

Sketches of (a) computational domain and (b) boundary conditions

Table 2 Structural Parameters in Three Types of Tail Nozzle

Table 3 Summary of Computational Parameters of the Gas and Particle Phases and Particle Species

3.3 Validation of Numerical Method and Mesh Independence

In the present computational procedure, each particle parcel injection position one-to-one corresponds to a cell center. In order to obtain a uniform initial distribution of particle parcels, we used uniform grids in the particle curtain region. The computational domain was discretized with structured hexahedron grids as shown in Figure 3 due to the regular geometry of the flow channel. In accordance with the criterion of y⁺ for a k–ε turbulence model, the minimum grid sizes should fall in the range of around 0.03–0.3 mm. Mesh refinement was used for a sub-domain that includes an inside-tube region between the particle curtain and the tail nozzle outlet and an outside-tube core region of jet so as to obtain sufficiently high resolutions of flow field.

Figure 3

Sketches of global and local structured hexahedron meshes

According to the Courant–Friedrichs–Lewy stability rule, the time step of gas phase τ_g can be estimated by

$$\tau_{g} \le CFL\frac{{\Delta l_{\min } }}{{v_{2} + c_{2} }}$$

(26)

in which v₂ and c₂ are the post-incident shock gas velocity and sound speed, respectively. Based on the adopted minimum grid size of Δl_min = 0.15 mm and Courant number of CFL = 2.5, the time step was estimated as τ_g ≤ 5.2 × 10⁻⁷ s. Actually, we have compared different combinations of time steps (τ_g = 0.1 to 0.5 μs) and Courant numbers (CFL = 1 to 5). A good effect of shock wave capturing was achieved by using a combination of τ_g = 0.1 μs and CFL = 1 (c.f. Figure 4a, b). However, a combination of moderate time step and Courant number was also able to obtain acceptable simulation results. Thus, an actual time step of τ_g = 2.5 × 10⁻⁷ s and a Courant number of CFL = 2.5 were used so as to balance the computational convergence and cost.

Figure 4

Numerically generated Schlieren images (contours of gas density gradient in region without particles) of case 1 at (a) t/(L_p/u_s) = − 4.7 (t = − 18 μs) and (b) t/(L_p/u_s) = 1.3 (t = 5 μs), compared with experimental results [21]

Figure 5a and b present experimental [21] and calculated instantaneous pressures at ports P1 and P2 (denoted by RS and TS), and transient positions of upstream and downstream fronts of the particle curtain (represented by the very rear and leading particles, and denoted by UFP and DFP) for case 1 on different meshes, which correspond to minimum grid sizes of 0.15, 0.25, and 0.3 mm, respectively. It is observed from Figure 5b that the computational transient positions of the UFP and DFP obtained on all the adopted meshes are perfectly consistent with the experimental data. On the other hand, one can find from Figure 5b that all the calculated dynamic pressures agree well with each other except that a very slight deviation from the others is visible when using mesh 3. Besides that, a good agreement of the computational dynamic pressures with the experimental data has been achieved although the latter exhibits fewer fluctuations than the former. These fluctuations induced by dissipative effects are probably due to the following three aspects: (a) non-uniform initial arrangement along the vertical direction of the particle curtain, (b) elastic–plastic deformation of the particle material, and (c) scattering of particles on the bottom floor of the test section in the experiment [21]. However, such effects did not be contained in the modeling. In summary, we believed that the mesh independence had been reached on all the meshes. The setting of mesh 2 was utilized in the subsequent computations in consideration of a balance between the time consumption and computational resolution. Furthermore, the validity of the current numerical method has been demonstrated.

Figure 5

Comparisons of computational (a) instantaneous pressures at monitoring ports, and (b) transient positions of upstream and downstream fronts of the particle curtain on different meshes with experimental data [21]

Figure 6 presents typical high-speed photographs at a series of moments for M_s = 1.385 in [35] and the corresponding simulation results. One can find that the simulation catches the main morphology of particles such as the irregular downstream front of particles (DFP) and non-uniform spatial distribution inside the particles, although the asymmetry of particle spatial distribution was not captured in the simulation due to the adopted an assumption of existing symmetrical planes. Stewart et al. [20] observed a traveling wave structure in the particle concentration downstream of the shock and attributed this instability to the volume fraction dependent drag force. We believe that the asymmetry of particle distribution should be an inevitable result of the development of such instabilities. But this issue is out of the scope of present study and will be boosted in the future. Furthermore, the most downstream 5% in total particles was used for the statistics of the DFP axial positions. We can see that a good agreement of computational results with the experimental data [35], actually only a maximum discrepancy of around 5.67%, can be achieved for all the studied incident shock Mach numbers (c.f. Figure 7). Thus, the validity of the adopted numerical method can be further confirmed.

Figure 6

Typical high-speed photographs (left column) at (a) t = 0, (b) t = 1.125 ms, (c) t = 2.25 ms, (d) t = 3.375 ms and (e) t = 4.5 ms for M_s = 1.385 in Chen et al.’s experiment [35] and the corresponding simulation results (right column)

Figure 7

Comparison of variations of the simulation axial position of downstream front of particles (DFP) with time with Chen et al.’s measured data for different incident shock Mach numbers

4 Results and Analyses

The behavior of shock interaction with a dense particle curtain in a tube was analyzed in detail in [21, 36]. The incident shock wave is reflected and transmitted by the particle curtain. The particles are accelerated by forces induced by the shock-induced aerodynamic force and also might be affected by the collision force between neighboring particles or between particles and side walls. Before the particles enter the tail nozzle with condition-dependent velocities, the leading transmitted shock wave has arrived at the nozzle, where complex reflection and transmission of shock wave happen. As a result, a high pressure level is established upstream the nozzle. The present study focuses on formation mechanisms and characteristics of single gas-phase and gas-particle jets.

4.1 Effect of Tail-Nozzle Type

In order to study the effect of tail-nozzle type, a series of numerical simulations were conducted at M_s = 1.66, φ_p = 21%, d_p = 115 μm, and three different types of tail-nozzle. It is observed from Figure 5a that a bow-shaped leading transmitted shock (TS) is formed outside the tail nozzle in each case. Expansion waves (EW) appear exactly at the exit of the tail nozzle in the convergent nozzle case, while oblique shocks (OS) come into being correspondingly in the Laval and divergent nozzle cases, C.F. Figure 8a. As the leading TS propagates downstream, its front area is gradually increased. As a result, its strength becomes weaker and weaker. Finally, it degrades into an acoustic wave due to successive attenuation. A Mach disk, across which an abrupt decrease of gas velocity is visible, occurs near each nozzle exit. A downstream-moving vortex ring is generated due to the shear effect between the central gas flow and the surrounding stationary air, and thus a shock-induced transient gas jet is produced in each case. The velocity of gas jet and therefore the travelling speed of vortex ring are “convergent” > “Laval” > “divergent” in sequence, C.F. Figure 8b and c.

Figure 8

Instantaneous pressure contour (left), pressure gradient contour (middle), and velocity vector (right) at different moments

The above illustrates the generation mechanism of shock-induced unsteady gas jet that is significantly different from the following one that will be described. It is observed from Figure 9a that after the previous stage of unsteady gas jet, the pressure upstream the tail nozzle maintains a relatively high level at x_p/L_s = − 2, when the very front particle is exactly arriving at the nozzle inlet. Another gas jet is generated due to a high pressure difference between the upstream and downstream of the nozzle, thus it will be referred to as a pressure-driving jet. The convergent nozzle is in an under-expanded state, in which the maximum velocity of gas is reached a little downstream the nozzle exit due to the acceleration of expansion fans emitting from the exit edges of the nozzle. A chain of shock and expansion waves, which discontinuously or rapidly changes the gas flow velocity and pressure, is visible outside the nozzle exit, leading to a more discontinuous and larger outside gas flow field than those of the other two types of nozzle. By contrary, both the Laval and divergent nozzles are in over-expanded states. Moreover, the gas flow obtains earlier and larger acceleration due to gas expansion in the divergent nozzle than that in the Laval nozzle. The gas flows discharged both from the divergent and Laval nozzles are similarly decelerated by a Mach disk immediately downstream each nozzle exit. Driven by such a gas jet, the particles are accelerated to pass through the nozzle. Thus, a gas-particle two-phase jet is produced. Because of the blockage effects caused by the convergent structures both of the convergent and Laval nozzles, the particles exhibit more collective states when moving inside the nozzles than those in the divergent nozzle, in which the particles scatter, keeping a regular stratified structure, c.f. Figure 9b. After the downstream partial particles pass through the nozzle exit, the radial outward velocity components lead to an increase of transverse distribution range of particles. It is intuitively observed from Figure 9c–e that the transverse distribution ranges of particles corresponding to the Laval and divergent nozzles are the largest and smallest, respectively. At x_p/L_s = 6, all or most of the particles have passed through the nozzle, c.f. Figure 9d. The pressure difference upstream and downstream the nozzle begins to recover. Consequently, it induces the regeneration of a pressure-driving gas jet. At x_p/L_s = 12, when almost all the particles have left the core region of jet, each gas jet basically returns back to its original state at x_p/L_s = − 2. In order to conduct a quantitative analysis for the performance of gas-particle jet, we define the following indexes, which include the streamwise average velocity v_px,a, velocity inhomogeneity ξ_vp and dispersion of particles ψ_p:

$$v_{px,a} = \frac{1}{N}\sum\nolimits_{n = 1}^{N} {v_{px}^{n} }$$

(27)

$$\xi_{vp} = \frac{1}{N}\sqrt {\sum\nolimits_{n = 1}^{N} {\left( {v_{px}^{n} - v_{px,a} } \right)^{2} } }$$

(28)

$$\psi_{p} = \frac{1}{{L_{e} N}}\sqrt {\sum\nolimits_{n = 1}^{N} {\left[ {\left( {y_{p}^{n} } \right)^{2} + \left( {z_{p}^{n} } \right)^{2} } \right]} }$$

(29)

where v_px,a reflects the acceleration effect of particles in the jet. ξ_vp indicates the degree of unevenness of particle streamwise velocity. ψ_p represents the transverse distribution range of particles. $v_{px}^{n}$ denotes the streamwise velocity of the nth particle. $y_{p}^{n}$ and $z_{p}^{n}$ are y and z coordinates of the nth particle. L_e is the side length of nozzle exit.

Figure 9

Instantaneous pressure contour (left), gas velocity contour (middle), and particle velocity (right) in different gas-particle jets at different moments. Note that the variable x_p in the captions denotes the position of the very front particle

Figure 10a–c show the dimensionless average streamwise velocity v_px,a/u_s, velocity inhomogeneity ξ_vp and dispersion of particles ψ_p versus dimensionless position of the very front particle for different types of tail nozzle, respectively. Where, the post-incident shock velocity u_s is chosen as the characteristic velocity. It is seen from Figure 10a that the average streamwise velocity v_px,a/u_s is increased with increasing x_p/L_p in the studied range for any of the three types of tail nozzle. The sort of v_px,a/u_s is “divergent” > “Laval” > “convergent” basically at any x_p/L_p although the latter two types of tail nozzle correspond to quite close v_px,a/u_s values at x_p/L_p ≤ 5. One can find from Figure 10b that the velocity inhomogeneity ξ_vp for the Laval nozzle decreases first, and then slightly increases. The ξ_vp for the divergent nozzle slightly decreases first, and then increases, and next decreases very slightly again thereafter. The ξ_vp for the convergent nozzle decreases first, and then significantly increases. The ξ_vp for the convergent nozzle is considerably larger than those for the other two nozzles. It is clear from Figure 10c that the particle dispersion ψ_p always increases with x_p/L_p in the studied range for each tail nozzle. The convergent nozzle has the minimum ψ_p value at any x_p/L_p, while the divergent and Laval nozzles respectively correspond to the maximum value of ψ_p for an x_p/L_p smaller and larger than a value of around 9.

Figure 10

Variations of (a) dimensionless average streamwise velocity, (b) velocity inhomogeneity and (c) dispersion of particles with dimensionless position of the very front particle for different types of tail nozzle

When passing through a nozzle, particles obtain relatively better acceleration due to the considerably larger gas velocities in the divergent nozzle than in the other two. Because the divergent nozzle achieves a relatively continuous outside gas flow field, these particles remain larger and more uniform velocities outside the nozzle. The under-expanded gas flow state corresponding to the divergent nozzle means that the radially outward motion of the particles is limited by the radially inward pressure-gradient forces. Thus, the dispersion of particles trends to increase most slowly and have the potential to obtain the minimum value further downstream although it has the maximum value at the earlier stages, which is mainly due to the monotonously divergent geometrical configuration of nozzle. By contrast, the more discontinuous and larger outside gas velocity field of the convergent nozzle generates the largest particle velocity inhomogeneity and the potential to accelerate particles. However, the blockage effect of the nozzle exit limits the particle acceleration effect at some extent. As a result, only the medium average streamwise velocity is attained by the convergent nozzle. Moreover, monotonously convergent structure of nozzle is beneficial for focusing effect of particles towards the central line. Therefore, the smallest particle dispersion is achieved in the presented range of x_p/L_p. It should also be noted that in the over-expanded gas flow structure, the existing expansion fans, which produce radially outward pressure-gradient forces acting on particles, promote the radially outward motion of the particles. Consequently, it has large possibilities for the convergent nozzle to lose the minimum position of ψ_p as x_p/L_p increases further. The divergent nozzle that generates a better acceleration effect and smaller dispersion of particles under the current operating condition has a stronger ability to penetrate into a burned objective, therefore is more suited for fire extinguishing of such a penetration type of flames. The Laval nozzle that produces the maximum dispersion of particles is more beneficial for fire suppression of spreading type of flames, e.g., combustions of liquid fuels. The convergent nozzle that produces a largest velocity inhomogeneity and moderate average streamwise velocity of particles should be more effective in fire fighting for a distributing type of flames. Correspondingly, these jets are named penetration, spreading, and breakup types of pulsed gas-particle jets in sequence based on the different evolution mechanisms similar to those described in [37]. A reasonable choice of one type of jet can be made according to the different requirements for designs and applications. Absolutely, key factors such as operating condition, particle size and loading state among others probably have significant influence on the fire extinguishing effect.

4.2 Effect of Shock Mach Number

In order to investigate the effect of shock Mach number M_s, we carried out a series of numerical simulations for Laval nozzle gas-particle jets at φ_p = 21%, d_p = 115 μm, and three different M_s. Figure 11a shows pressure-driving gas jets at x_p/L_s = − 2 before particles enter the nozzle. It is observed that as the M_s increases, the upstream pressure of nozzle is increased, the core region of gas jet is stretched along the axial direction, and a chain structure of shock and expansion fans outside the nozzle becomes more and more extended. Thus, the gas velocity is increased and meanwhile the velocity field exhibits more considerably discontinuous changes in the jet. Figure 11b presents situations when particles are travelling inside the nozzle at x_p/L_s = 0 for different M_s. It is found that the relatively high upstream pressure, large velocities not only inside or but also outside the nozzle, and complex velocity field remain with increasing M_s. The pressure, velocity and particle fields for different M_s at x_p/L_s = 0 when almost all the particles have been divorced from the core region of jet are shown in Figure 11c. One can find that all the gas phase fields are quite similar to those at x_p/L_s = − 2 except that the chain structure of shock and expansion fans in each case is enhanced and thus becomes more distinct than its previous state.

Figure 11

Instantaneous pressure contour (left), gas velocity contour (middle), and particle velocity (right) in a Laval nozzle gas-particle jet for different shock Mach numbers at different moments

Figure 12a–c present the dimensionless average streamwise velocity v_px,a/u_s, velocity inhomogeneity ξ_vp and dispersion of particles ψ_p versus dimensionless position of the very front particle in a Laval nozzle gas-particle jet for different M_s, respectively. It is found from Figure 12a that the average streamwise velocity v_px,a/u_s is increased with increasing M_s at any x_p/L_p. One can observe from Figure 12b that each ξ_vp decreases first, and then increases. Furthermore, as the M_s increases, the more significant increase of ξ_vp is achieved. It is seen from Figure 12c that each ψ_p increases with increasing M_s. Meanwhile, the differences among all the ψ_p are quite limited. Only close inspection indicates that when the M_s is increased, the ψ_p trends to increase first and then decrease. However, such a trend of ψ_p with increasing x_p/L_p includes complex non-monotonous variations with respect to M_s.

Figure 12

Variations of (a) dimensionless average streamwise velocity, (b) velocity inhomogeneity and (c) dispersion of particles with dimensionless position of the very front particle in a Laval nozzle gas-particle jet for different shock Mach numbers

The increase of M_s leads to the increase both of the gas velocity and the complexity of flow field. Naturally, both the magnitude of particle velocity and its discontinuity are increased in the jet. As the M_s increases, the difference of gas parameters between different sub-regions, which are divided by shock waves and expansion fans, becomes more and more considerable. Therefore, the velocity of a particle passing through these sub-regions inevitably experiences more dramatic changes. The appearance of the minimum values of ψ_p at x_p/L_p = 8 to 10 should be related to the situation when almost all the particles are located in the core region of jet, thus the ξ_vp is limited. In combination of Figure 12a and c, we surmise that there exists a critical shock Mach number for a given geometry of Laval nozzle, e.g., M_s close to 1.56 in the current cases. Below this critical M_s, the formed chain structure of shocks and expansion fans tends to strengthen the influence of radial component of gas velocity, and therefore to increase the radially outward motion of particles as M_s increases. By contrary, above this critical M_s, the generated chain structure of waves tends to decrease the radially outward motion of particles when the M_s is increased. But anyway, such influence is complicated on account of the complex gas flow field that accompanies shock and expansion waves.

The increase of M_s is able to increase the firing range or penetration depth of extinguishing powders. A large enough M_s above the critical value is advantageous for decreasing the radial while increasing the axial acting ranges. The choice of operating condition close to the critical M_s can maximize the dispersion of fire extinguishant particles.

4.3 Effect of Particle Size

In order to explore the effect of particle size, we performed a series of numerical simulations for Laval nozzle gas-particle jets at M_s = 1.66, φ_p = 21%, and different particle sizes d_p. At x_p/L_s = − 2, the generated pressure-driving gas jets are similar to each other, c.f. Figure 13a. In fact, as the d_p increases, the particle velocity increases, while the gas velocity decreases at this moment. At x_p/L_s = 0, when the very front particle is arriving at the nozzle exit, smaller particle size corresponds to more remarkable aggregation effect inside the nozzle and larger particle velocity at the nozzle exit, c.f. Figure 13b. At x_p/L_s = 12, when almost all the particles have travelled through the core region of jet, it is intuitively observed that the increase of particle size leads to larger particle velocities, larger radial dimension and smaller streamwise dimension of particle field, c.f. Figure 13c.

Figure 13

Instantaneous pressure contour (left), gas velocity contour (middle), and particle velocity (right) in a Laval nozzle gas-particle jet for different particle sizes at different moments

Figure 14a–c exhibit the dimensionless average streamwise velocity v_px,a/u_s, velocity inhomogeneity ξ_vp and dispersion of particles ψ_p versus dimensionless position of the very front particle in a Laval nozzle gas-particle jet for different particle sizes d_p, respectively. It is seen from Figure 14a that the average streamwise velocity v_px,a/u_s is decreased with increasing d_p at any x_p/L_p. One can observe from Figure 14b that each ξ_vp decreases first, and then increases with x_p/L_p. On the other hand, the ξ_vp trends to increase as the d_p is increased, albeit such a trend does not exhibit for relatively small x_p/L_p (i.e., below around 8). Furthermore, the smaller d_p corresponds to the more significant increase of ξ_vp. It is seen from Figure 14c that the ψ_p monotonously increases with both increasing x_p/L_p and d_p.

Figure 14

Variations of (a) dimensionless average streamwise velocity, (b) velocity inhomogeneity and (c) dispersion of particles with dimensionless position of the very front particle in a Laval nozzle gas-particle jet for different particle sizes

When smaller particles with larger velocities pass through basically consistent pressure-driving gas jets, they obtain better streamwise acceleration effects due to larger unit-mass total forces mainly imposed by the gas medium. The decrease of particle size is advantageous for improving the ability to follow the velocity change of gas phase. Thus, the particles exhibit more significant velocity changes. Furthermore, the particles are accelerated more remarkably by the regenerated pressure-driving gas jet. As a result, the particle spatial distribution has both larger streamwise and transverse dimensions. The non-monotonous variation of ξ_vp with d_p for x_p/L_p < 8 is mainly attributed to the complex chain structure of waves produced closely downstream the nozzle exit.

As we can conclude that a larger firing range (or penetration depth) and spatial acting range can generally be achieved by using smaller particle sizes. Therefore, people tend to increase the use of fine and superfine fire suppressant powders to improve the effectiveness of fire suppression. However, the possible adverse effects to people and environment mentioned in the introduction should also be considered in designs and applications of SWDFES.

4.4 Effect of Initial Particle Volume Fraction

In order to examine the effect of initial particle volume fraction, we executed a series of numerical simulations for Laval nozzle gas-particle jets at M_s = 1.66, d_p = 115 μm, and different initial particle volume fractions φ_p. At x_p/L_s = − 2, the produced pressure-driving gas jet corresponding to a smaller φ_p develops a stronger core region of jet due to the larger pressure difference upstream and downstream the nozzle, and thus leading to the generation of a more distinct Mach disk located downstream the nozzle exit, c.f. Figure 15a. Actually, when the φ_p is increased, the particles have increased velocities before entering the nozzle. At x_p/L_s = 0, when the very front particle is arriving at the nozzle exit, for a relatively small case of φ_p = 11%, the void among particles is more remarkable. Especially, the downstream particles are scattered in disordered state. The blockage effect and momentum and energy exchange between gas and particle phases are reduced, thus the gas flow in the divergent section has higher velocities, which aggravate the peeling of the downstream particles off the particle group. On the other hand, the increased void among particles and the disordered scattered distribution of the downstream particles lead to the generation of many slender passages in any directions. As a result, the downstream particles are further dispersed. By contrast, for a relatively large case of φ_p = 31%, the agglomeration of the downstream particles is still evident. The particles squeeze each other more seriously in the convergent section. The void among particles is not large enough to form effective passages to change the moving directions of particles. Therefore, the particles basically remain the original moving states along the axial direction, c.f. Figure 15b. At x_p/L_s = 12, the gas jets for φ_p = 21% and 31% develop the weakest and strongest core regions, respectively. The particles for φ_p = 11% are most seriously scattered with the largest streamwise and transverse dimensions. The particle field for φ_p = 21% has a moderate transverse dimension while a shortest streamwise dimension. The particle field for φ_p = 31% has a moderate streamwise dimension while a smallest transverse dimension, c.f. Figure 15c.

Figure 15

Instantaneous pressure contour (left), gas velocity contour (middle), and particle velocity (right) in a Laval nozzle gas-particle jet for different initial particle volume fractions at different moments

Figure 16a–c give the dimensionless average streamwise velocity v_px,a/u_s, velocity inhomogeneity ξ_vp and dispersion of particles ψ_p versus dimensionless position of the very front particle for different initial particle volume fractions φ_p, respectively. It is observed from Figure 16a that the minimum initial particle volume fraction (i.e., φ_p = 11%) always corresponds to the minimum average streamwise velocity of particles v_px,a/u_s at any x_p/L_p. The v_px,a/u_s corresponding to the moderate φ_p of 21% achieves the maximum value for at x_p/L_p ≤ 10, however is gradually overtaken by that corresponding to the maximum φ_p of 31% thereafter. It is found from Figure 16b that the ξ_vp for φ_p = 11% and 21% always have the maximum and minimum values at any x_p/L_p although the ξ_vp for 21% is caught up with by that for φ_p = 31% after x_p/L_p exceeds 10. Moreover, one can see from Figure 16c that when the φ_p is increased, the smaller ψ_p is always obtained.

Figure 16

Variations of (a) dimensionless average streamwise velocity, (b) velocity inhomogeneity and (c) dispersion of particles with dimensionless position of the very front particle in a Laval nozzle gas-particle jet for different initial particle volume fractions

The particles for smaller φ_p obtain a better acceleration when travelling through the nozzle and the following sub-region of jet with maximum gas velocity due to the stronger pressure-driving jet. On the other hand, a larger φ_p causes a greater possibility of particle collisions between particle and side walls or between neighboring particles due to the very large local particle volume fractions, c.f. Figure 17a–c. As a result, the particle velocities for a larger φ_p are limited at some extent. Thus, a larger φ_p corresponds to a smaller v_px,a/u_s at around x_p/L_p ≤ 10. However, the particles for the largest φ_p are accelerated best in the strongest regenerated pressure-driving jet, therefore the v_px,a/u_s exceeds the remaining ones thereafter. The particles for the smallest φ_p form the particle field with the largest streamwise and transverse dimensions. Therefore, they suffer the largest velocity difference in the jet. In the largest φ_p case, the particle collisions and blockage effect should extend the streamwise dimension of the particle field at some extent, thus leading to a ξ_vp larger than that for φ_p = 21% and even close to that for φ_p = 11%.

Figure 17

Particle volume fraction distributions for different initial particle volume fractions at x_p/L_s = 0

Fire suppressant particles are usually supplied perpendicular to the axial line of the flow channel in a gravity-fed way. The initial particle volume fraction can be controlled by regulating the mass flow rate of fire suppressant. Specially designed leakage slots, which permits rapid open-close operations, are also able to be applied in a loading chamber for the control of the initial particle volume fraction.

5 Conclusions

This paper carried out modeling and simulations of shock-induced gas-particle jets through a rectangular tube with a tail nozzle based on a dense discrete phase model. A point particle force model and an improved spring-dashpot model were employed to calculate the aerodynamic and collision forces exerted on particles, respectively. We revealed the evolution mechanisms of a gas-particle jet, and analyzed the effects of type of tail nozzle, incident shock Mach number M_s, initial particle volume fraction φ_p, and particle size d_p on the dimensionless streamwise average velocity v_px,a/u_s, velocity inhomogeneity ξ_vp and dispersity of particles ψ_p. The main conclusions are drawn as follows:

• (1) The evolution process of the gas-particle jet consists of two different stages: the first stage of transmitted shock-induced gas jet and the second stage of pressure-induced jet. Penetration, spreading, and breakup types of pulsed gas-particle jets, which are suited for fire suppression of correspondingly three types of flames, were identified.

• (2) The v_px,a/u_s and ψ_p are always increased with x_p/L_p (dimensionless position of the very front particle) in the studied range (x_p/L_p ≤ 16). The sort of v_px,a/u_s is virtually always “divergent” > “convergent” > “Laval”. The ξ_vp for the Laval and convergent nozzles decrease first, and then increase. The ξ_vp for the divergent nozzle decreases first, and then increase, and next decreases again. The ξ_vp for the convergent nozzle is considerably larger than those for the other nozzles. The convergent nozzle has the minimum ψ_p value, while the divergent and Laval nozzles respectively occupy the maximum ψ_p when x_p/L_p is below and above about 9.

• (3) For a Laval nozzle, the v_px,a/u_s is increased with M_s. A larger M_s means a more significant increase of ξ_vp. The ψ_p increases first, and then decreases as the M_s is increased. The v_px,a/u_s is decreased with increasing d_p. Both the ξ_vp and ψ_p trend to decrease as d_p is increased. The larger d_p corresponds to the more significant increase of ξ_vp. The minimum φ_p always corresponds to the minimum v_px,a/u_s. The v_px,a/u_s for a moderate φ_p achieves the maximum value for at x_p/L_p ≤ 10, however is gradually overtaken by that for the largest φ_p later. The ξ_vp for φ_p = 11% and 21% always have the maximum and minimum values. Moreover, when the φ_p is increased, the ψ_p is decreased.