Multifactor Portfolio Construction by Factor Risk Parity Strategies: An Empirical Comparison of Global Stock Markets

Abstract

Since the financial crisis in 2008, factor investing has attracted the attention of investment managers and asset owners. A factor-based investment portfolio can enjoy effective diversification and acquire factor risk premiums at lower cost than active managers can. In equity investments, “smart beta” investing has been established as a common investment style and the multifactor strategy has become the most popular in recent years. This study makes an additional contribution to empirical research for risk-based asset allocation in multifactor investing. We verified the effectiveness of the factor risk parity (FRP) strategy by constructing active equity FRP portfolios for four stock markets, Japan, the United States, United Kingdom, and Euro countries. For the Japanese market, four factors considered to be effective in the market were adopted for constructing FRP portfolios. For the other markets, we constructed FRP portfolios by equalizing factor risk contributions between the cyclical and defensive factors. We found that the FRP strategy is a prospective method for capturing factor risk premiums, since it can adequately allocate risk to factors that contribute positive returns in the active FRP portfolios.

1 Introduction

Since the financial crisis in 2008, factor investing focusing on risk factors that are common determinants of assets return dynamics has drawn much attention from investment managers and asset owners. In equity investment, factor indexes called “smart beta,” which employ rule-based approaches for index construction that differ from conventional market capitalization indexes, have been adopted by various types of investors, such as corporations, governments, non-profit organizations, and pension funds. The total assets under management of factor investing are estimated to be more than USD 2 trillion globally (FTSE Russell 2018).

The background to factor investing is summarized as follows. First, since asset class-based diversification have not worked effectively owing to increased correlations among various asset classes during financial crises, the importance of risk diversification of factors has been advocated by numerous studies, such as Clarke et al. (2005), Ang et al. (2009), Bender et al. (2010), Blitz (2012, 2015), Ilmanen and Kizer (2012), Podkaminer (2013), and Ang (2014). Second, it was considered that factor risk premiums could be obtained by constantly acquiring exposure to factors in long-term investment. Third, several academic works have found that a substantial portion of the investment results obtained by active managers could be accounted for by systematic factors and acquired at lower cost by passive investment in factor indexes. Ang et al. (2009) reported that approximately 70% of the active portfolio returns of the Norwegian Government Pension Fund could be explained by exposure to systematic factors. Bender et al. (2014) showed that 80% of active managers’ alphas in the United States (US) market could be attributed to factors. Fourth, since factor correlations are generally lower and more stable than asset correlations are, factor-based diversification can provide superior return-risk characteristics for a portfolio. Ang (2014) compared nutrients and food to illustrate the relationship between factors and assets. An asset can be viewed as a bundle of factors and a food as a bundle of nutrients. On the one hand, as a result of overlapping risk factor exposure, asset classes may have high correlations especially during market turmoil. On the other hand, factors can be considered as unique and essential sources of return and risk, which show consistent behavior of each style with low and stable correlation relationships among factors. Bender et al. (2010) showed that the correlations of 11 style and strategy factors are close to zero, confirming that these factor risk premiums captured unique return characteristics and offered diversification opportunities. Ilmanen and Kizer (2012) examined six risk factors (equity, size, value, momentum, term, and default premiums) defined by long–short portfolio returns and showed that the correlation structure among the factors is stable even in financial crises.

The smart beta strategy has been established as a common investment style, whose concept is to harvest equity risk premiums from identifiable risk factors that are considered to be persistent and prospective in long-term investment. These factors include value, size, and momentum. Initially, a single-factor strategy that aims to invest in a single factor was the mainstream of the smart beta investment. However, as a result of focusing on the diversification benefit among factors, multifactor combination strategies have become the most popular in recent years.¹ According to FTSE Russell (2018), 49% of asset owners that have implemented smart beta investment adopted a multifactor strategy. With growing interest in smart beta investing, various practical questions have been discussed for multifactor portfolio construction.

There are mainly two ways to construct multifactor portfolios. One is a combination approach simply combining single-factor portfolios into one portfolio, the other is a bottom–up approach building a portfolio from the security level. Bender and Wang (2016) argued that a bottom–up approach is superior because of the non-linear cross-sectional interaction effects between factors. Conversely, Chow et al. (2018) recommended a combination approach because of its broad diversification, easier implementation, and transparency from a governance perspective. With the adoption of either approach, it is necessary to consider how to allocate assets to each single factor portfolio or stock. Bender and Wang (2016) compared a rank- and a score-based approach and showed that the latter approach creates a meaningful difference between combination- and bottom–up-based portfolios with the insight that score-based approach preserves the distributional differences and the rank-based approach may rule out the ability to capture the interaction effects among the factors. Alighanbari and Chia (2016) examined six rule- and optimization-based multifactor strategies (equal weight, inverse variance, risk parity, inverse of tracking error, tracking error optimization, and trend following) by the combination approach. Shimizu and Shiohama (2018) studied the effectiveness of a risk-based asset allocation approach in multifactor investing. They presented the multifactor portfolio construction method using the factor risk parity (FRP) based on the bottom–up approach and illustrated empirical results in the Japanese stock market using six fundamental factors, namely, value, size, momentum, low volatility, yield, and quality.²

This study makes following contributions to the empirical research on risk-based asset allocation in multifactor investing. First, we construct FRP portfolios in four global stock markets, Japan, the US, United Kingdom (UK), and Euro countries,³ and show that their performance is superior to that of market capitalization-weighted (MCW) portfolios. Second, we demonstrate that an FRP portfolio can acquire factor risk premiums from risk-allocated factors. From these empirical findings, we conclude that an FRP strategy is a prospective investment strategy that captures factor risk premiums for global equity investments.

The rest of this paper is organized as follows. Section 2 provides an overview of factor investing and FRP strategy. Section 3 describes the factor risk budgeting (FRB) methodology that is utilized for our FRP portfolio construction. Discussions on the concrete FRP portfolio construction methods, including investment universes, observation data, and objective functions, are given in Sect. 4. In Sect. 5, we construct an FRP portfolio in the four stock markets and discuss the empirical results. Finally, Sect. 6 summarizes and discusses some issues arising in FRP portfolio construction.

2 Factor Investing and FRP Strategy

In this section, we provide an overview on factor investing by introducing three types of factors, namely, macroeconomic, statistical, and fundamental factors. The fundamental factor is used for the construction of an FRP portfolio in the subsequent sections. Then we review the FRP strategy. Thereafter, we discuss the volatility of returns as a risk measure.

2.1 Factor Investing

Factor investing is an investment method that constructs portfolios focusing on risk factors common to asset return dynamics. This concept can be traced to the capital asset pricing model (CAPM), which became the foundation for modern portfolio management. In the CAPM, securities have two risk drivers: systematic (market) risk and idiosyncratic risk. Systematic risk is expressed by the sensitivity to the market (“market beta”), or exposure to market risk. The arbitrage pricing theory (APT) introduced by Ross has made the multifactor model widely prevalent. Since the APT did not state explicitly what variables should comprise the factors, extensive empirical research has explored factors in various asset classes.

Factors are often considered as the determinants of price fluctuations common to assets and securities. Ang (2014) regarded factors as drivers of risk premiums inherent in assets and defined an asset as a bundle of factors, leading to his assertion that factor risk generates returns (premiums). Ang et al. (2009) recommended that factors included in portfolios should (1) be justified by academic research; (2) have exhibited significant premiums in the past, which are expected to be maintained in the future; (3) have return history available for “bad periods”; and (4) be implementable in liquid and traded instruments. Ang (2014) stated that factors that satisfy these characteristics with widespread acceptance in practical fields should qualify as benchmarks. For instance, factors derived by using data mining methods are currently categorized in active investment whereas such factors as value and momentum, which were once considered anomalies or alphas, are now accepted as factor risks (beta) with the progress of research and acquisition of the popularity as factor investing strategies.

While Ang (2014) divided factors into macroeconomic and investment-style (fundamental) factors, Connor (1995) grouped factors into the three categories of macroeconomic, statistical, and fundamental, and compared the predictive power of each factor. This study adopts the latter factor category in the following discussion.

The macroeconomic factor model uses observable economic time series, such as economic growth and inflation rates. Chen et al. (1986) adopted industrial production, expected inflation rate, bond risk premium (the return difference between long-term government bonds and corporate bonds rated Baa or lower), and term structure (the return difference between long-term and short-term government bonds) as macroeconomic factors. Ang (2014) stated that stocks perform well when the economic growth rate (real GDP) is high, while government and investment-grade corporate bonds show superior performance when the economic growth rate is low. These findings may be naturally acceptable with our understanding of macroeconomic fluctuations, however the difficulty of utilizing these economic factors in actual modeling has been pointed out.⁴

Principal component analysis (PCA), a statistical method that aims to reduce data dimensions by extracting uncorrelated components from correlated variables, is often used for statistical factor modeling. Studies of portfolio management using PCA-based factors include Meucci (2009) and subsequent research, such as Lohre et al. (2012, 2014), and Poddig and Unger (2012).

Fundamental factors utilize characteristics of securities and return behavior as factors. The most widely discussed factors in equity investment include the original Fama–French–Carhart factors of size, value, and momentum, but a handful of additional factors exist, such as low volatility, quality, and yield.⁵ Generally, fundamental factor returns are not directly observed, since they are inherent in price fluctuations of security sets that have a similar feature. Thus, factor returns are obtained in the time-series cross-sectional regressions of security returns by factor loadings. Another approach defines factor returns as long-short returns of portfolios characterized by some security feature and acquires factor loadings by the regression analysis, like Fama–French’s approach.

Macroeconomic factors have the drawback of poor explanatory power in practical application as Kaya et al. (2012) pointed out. PCA-based factors have desirable characteristics in terms of factor risk diversification because they are true uncorrelated risk sources. However, it is not clear whether they have risk premiums in long-term investment. Therefore, we focus on fundamental factors with ample literature of factor research for portfolio construction in Shimizu and Shiohama (2018). In this study, we adopt the same approach and construct FRP portfolios in global equity markets using six fundamental factors.

2.2 FRP Strategy

While the mean-variance approach advocated by Markowitz in modern portfolio theory has become the foundation of portfolio construction, it is reported that its optimization result suffers from several well-known drawbacks. It is often pointed out that the mean-variance portfolio is so sensitive to its input parameters (a mean vector and covariance matrix), and that predicting expected returns are more difficult than estimating covariance matrixes. In addition, the risk sources for asset allocations of traditional pension funds are tilted toward stocks. Consequently, the portfolio returns are significantly influenced by stock price movements. In response to these dilemmas, Qian (2006) proposed asset risk parity (ARP), which aims to achieve risk diversification by equalizing risk contributions among asset classes without predicting expected returns. Maillard et al. (2010) constructed an ARP portfolio from 13 asset classes, including global stocks, bonds, and commodities, and showed that it outperformed equal-weight and minimum-variance portfolios in terms of the risk-adjusted return.

Even if risk contributions are equalized among asset classes by ARP, risk diversification from the perspective of risk factors is not necessarily achieved. Bhansali et al. (2012) indicated that investment-grade and high-yield corporate bonds have similar factor loadings to equities. The authors showed the risk decomposition among four commercially available ARP portfolios by equity (growth) and bond (inflation) factors, and revealed the existence of biased ARP portfolios in terms of factor risk. To address such criticism, the FRP, which equalizes risk contributions among the factors, is proposed. There are two approaches to implement the FRP strategy, namely, the PCA-based approach and the method based on a regression model.

PCA-based FRP portfolios are constructed by equalizing risk contributions among principal components. Meucci (2009) introduced the entropy-based diversification measure, which shows the diversification or effective number of uncorrelated bets in a portfolio. Subsequent studies using the approach of Meucci (2009) include Lohre et al. (2012), Poddig and Unger (2012), and Lohre et al. (2014). Lohre et al. (2012) constructed the maximum diversification (PCA-based FRP) portfolio for the US stock market and showed that the strategy has more efficient performance compared with equally weighted, minimum-variance, risk parity, and maximum-diversification portfolios. Poddig and Unger (2012) studied the effect of estimation errors on the outcomes of the equally weighted risk contribution (ERC) and the PCA-based FRP portfolios and found that the ERC portfolio is more robust to changes in the input parameters and has a smaller estimation error than the Markowitz approaches, whereas the PCA-based portfolio is more unstable than the classical approaches. Lohre et al. (2014) built multi-asset maximum diversification portfolios and demonstrated that the strategy provides convincing risk-adjusted performance with superior diversification properties to other risk-based investment strategies.⁶

The regression-based approach requires factor returns and loadings to construct an FRP portfolio. In the case in which observable variables are defined as proxy factor returns, securities’ factor loadings are estimated by cross-sectional regressions. Macroeconomic variables and long–short returns between stock portfolios characterized by a certain feature are often used as factors. Roncalli and Weisang (2016) illustrated FRB portfolio construction methods and examined the risk characteristics of strategic asset allocation portfolios based on the three macroeconomic factors: activity (economic growth), inflation, and interest rates. Shimizu and Shiohama (2018) constructed FRP portfolios in the Japanese stock market by using the method of Roncalli and Weisang (2016) and confirmed its effectiveness in the market.

3 FRB Portfolio Construction

The risk parity strategy can be considered as a special case of the risk budgeting approach in which all risk budgets for each source of risk are equal. Therefore, in this section, we first introduce the FRB approach proposed in Roncalli and Weisang (2016), and then consider the construction of an FRP portfolio as its special case. While their approach is based on the total risk basis, here, we discuss active⁷ return and risk basis, since the FRP portfolio we construct can be considered as an active strategy. This is because the FRP portfolio seeks to exceed MCW portfolios by harvesting additional factor risk premiums to market returns.

Hereafter, we use the following notations. The number of assets and factors are denoted by n and m, respectively, assuming $n > m$. The transpose of a matrix or vector $\varvec{z}$ is denoted by $\varvec{z}^T$. The j-th component of a vector $\varvec{z}$ is denoted by $(\varvec{z})_j$.

3.1 Linear Factor Model

We use a standard linear model to express returns of assets. Let $\varvec{A}~(n\times m)$, $\varvec{{f}}~(m\times 1)$, and $\varvec{\varepsilon }~(n\times 1)$ denote a factor loading matrix, a factor return vector, and an idiosyncratic return vector, respectively. Then an asset return vector $\varvec{r}~(n\times 1)$ is expressed as follows:⁸

$$\begin{aligned} \varvec{r} = \varvec{A{f}} + \varvec{\varepsilon }. \end{aligned}$$

(1)

Assuming that factor returns and idiosyncratic returns are uncorrelated, the corresponding covariance matrix for $\varvec{\varSigma }~(n\times n)$ is expressed as

$$\begin{aligned} \varvec{\varSigma } = \text {Var}(\varvec{r}) = \varvec{A} \varvec{\varOmega } \varvec{A}^T + \varvec{D}, \end{aligned}$$

(2)

where $\varvec{\varOmega }~(m\times m)$ is a factor covariance matrix, and $\varvec{D}~(n\times n)$ is an idiosyncratic covariance matrix. Notice that the $\varvec{D}$ is a diagonal matrix whose diagonal elements are the variances of idiosyncratic returns. Let $\varvec{x}$ be an active weight (AW) vector $(n \times 1)$; then, a portfolio’s active return is expressed by using Eq. (1) as follows:

$$\begin{aligned} \varvec{\varPi } = \varvec{x}^T \varvec{r} = \varvec{x}^T \varvec{A{f}} + \varvec{x}^T \varvec{\varepsilon } = \varvec{y}^T \varvec{{f}} + \varvec{\eta }. \end{aligned}$$

(3)

Here, $\varvec{y} = \varvec{A}^T\varvec{x}$ is an active factor exposure (AFE) vector $(m \times 1)$, $\varvec{y}^T\varvec{{f}}$ is the factor effect on the active return, and $\varvec{\eta }=\varvec{x}^T\varvec{\varepsilon }$ is a portfolio’s idiosyncratic active return. Using the covariance matrix in Eq. (2), a portfolio’s active risk $\sigma (\varvec{x})$ is expressed as

$$\begin{aligned} \sigma (\varvec{x}) = \sqrt{ \varvec{x}^T \varvec{\varSigma }\varvec{x} } = \sqrt{ \varvec{x}^T (\varvec{A} \varvec{\varOmega }\varvec{A}^T + \varvec{D})\varvec{x} }. \end{aligned}$$

The risk contribution $RC(F_j)$ of a factor $F_j$ to the active risk is expressed as

$$\begin{aligned} RC (F_j) = \frac{(\varvec{A}^T \varvec{x})_j \cdot (\varvec{A}^+\varvec{\varSigma } \varvec{x})_j}{ \sigma (\varvec{x})}, \end{aligned}$$

where $\varvec{A}^+$ is a Moore–Penrose inverse matrix, which is defined as $\varvec{A}^{+} = \varvec{A}^T (\varvec{AA}^T)^{-1}$ with the assumption that $n > m$. A percentage risk contribution of a factor $F_j$ can be composed as $RC(F_j)/\sigma (\varvec{x})$, and note that $\sum _{j=1}^{m} RC(F_j)/\sigma (\varvec{x}) = 1$. We address this percentage risk contribution as risk allocation of a portfolio and use it in the optimization problem.

3.2 FRB Portfolio Construction

An FRB portfolio matches portfolio risk allocations to risk budgets, which are target risk allocations for each factor. Defining a risk budget for a factor $F_j$ as $d_j$, this condition can be expressed as

$$\begin{aligned} \frac{RC(F_j)}{\sigma (\varvec{x})} =d_j. \end{aligned}$$

While Roncalli and Weisang (2016) utilized the Herfindahl index, Gini coefficients, and Shannon entropy in the optimization to equalize factor risk contributions, in this study, we adopt simple minimizing squared error. Hence, an FRB portfolio can be obtained by solving the following optimization problem:

$$\begin{aligned} \underset{x}{\text {argmin}} \sum _{j=1}^{m} \left( \frac{RC(F_j)}{\sigma (\varvec{x})} -d_j \right) ^2 . \end{aligned}$$

(4)

The risk allocation of factor $F_j$ is optimized to match a factor risk budget $d_j$ by solving this problem. The FRP portfolio construction can be considered as a special case of FRB portfolio in which all factor risk budgets are equal, that is, $d_j=1/m$ for all j.⁹

4 FRP Portfolio Construction by FRB

In this study, we construct FRP portfolios based on the FRB method described in Sect. 3 for the four stock markets, Japan, the US, UK, and Euro. We first define investment universes, the factors that are used as explanatory variables, and risk-allocated factors, then explain the optimization and estimation methods used for the portfolio constructions for each market in detail. Although there are slight differences in portfolio construction methods in each market, our approaches are consistent in every market in terms of constructing FRP portfolios for factors that are considered effective in each market.

4.1 Investment Universe and MCW Portfolio

We construct the three FRP portfolios in the Japanese market. We adopt the constituents in the MSCI Japan, S&P Japan LargeMidCap, and TOPIX 500 indexes as of the end of December 2017 with the complete time-series data for the analysis period (from January 4, 2002 to December 30, 2017). The investment universes for the US, UK, and Euro markets are the constituents in the S&P 500, FTSE 350, and MSCI EMU indexes, respectively as of the end of December 2017 with the complete time-series data. We calculate an MCW portfolio return as an MCW average of stock returns of each investment universe for the performance comparison.

4.2 Factors and Risk Allocation

We use the following six factors, which are considered to be reasonable as explanatory factors in the equity investment: value, size, momentum, low volatility, yield, and quality. Active returns of factor indexes to a market capitalization index are used as proxy factor returns for each market. Table 1 shows the factor indexes corresponding to each factor.

Table 1 List of factor indexes used for factor returns

For the Japanese market, we construct an FRP portfolio by equalizing risk contributions among the four factors (value, size, low volatility, and yield) which are considered effective in the market. Momentum and quality are excluded from the risk-allocated factors in our empirical analysis in the Japanese market because they are considered to be ineffective in the market by previous studies.¹⁰ For the US, UK, and Euro markets, we take a different approach to constructing the FRP portfolios in order to alleviate the difficulty of optimization due to an increase in the number of risk-allocated factors. In particular, we divide the six factors into two factor groups, pro-cyclical and defensive, and we equalize risk contributions between the two groups. The pro-cyclical factor group includes value, size, and momentum, and the defensive factor group includes low volatility, yield, and quality.¹¹

4.3 FRP Portfolio Construction

The objective function and its parameter constraints used for the portfolio construction for the Japanese market are given by

$$\begin{aligned}&\text {minimize}~ \sum _{j=1}^{6} \left( \frac{RC(F_j)}{\sigma (\varvec{x})} -d_j \right) ^2, \\&\text {subject to}~ {\max (-\varvec{{b}}, -\varvec{c})} \le \varvec{x} \le \varvec{c}, ~\varvec{1}^T\varvec{x} =0,\nonumber \\&\begin{pmatrix} \varvec{0} \\ \varvec{-1} \end{pmatrix} \le \begin{pmatrix} (\varvec{A}^T\varvec{x})_{RP} \\ (\varvec{A}^T\varvec{x})_{{\overline{RP}}} \end{pmatrix} \le \begin{pmatrix} \varvec{1} \\ \varvec{1} \end{pmatrix}, \end{aligned}$$

and those for the US, UK, and Euro markets are as follows:

$$\begin{aligned}&\text {minimize}~ \sum _{j=1}^{2} \left( \frac{RC(F_j)}{\sigma (\varvec{x})} -d_j \right) ^2,\\&\text {subject to}~ {\max (-\varvec{{b}}, -\varvec{c})} \le \varvec{x} \le \varvec{c}, ~\varvec{1}^T\varvec{x}=0, ~\varvec{0} \le \varvec{A}^T\varvec{x}\le \varvec{1}, \end{aligned}$$

where

$$\begin{aligned} RC(F_1)=&RC(F_{\text {Value}})+RC(F_{\text {Size}})+RC(F_{\text {Momentum}}),\\ RC(F_2)=&RC(F_{\text {Low volatility}})+RC(F_{\text {Yield}})+RC(F_{\text {Quality}}) . \end{aligned}$$

Here, $\varvec{{b}}~(n \times 1)$ is a benchmark weight vector that satisfies $\varvec{{b}} \ge \varvec{0}$ and $\varvec{1}^T\varvec{{b}}=1$, and $\varvec{c}~(n \times 1)$ is a lower and upper bound vector for AWs. $\varvec{A}^T\varvec{x}(=\varvec{y})$ is the AFE vector given in Eq. (3). For the Japanese market, the AFE vector of the four risk-allocated factors and the other two factors are denoted by $(\varvec{A}^T\varvec{x})_{RP}$ and $(\varvec{A}^T\varvec{x})_{{\overline{RP}}}$, respectively. The risk budget for the risk-allocated four factors is set as $d_j = 1/4$ with the others being 0. The $d_j$ is set as 1/2 for the two factor groups in the risk allocation for the other three markets.

The first constraint indicates the restriction of a short position for a portfolio weight and AW range. The second maintains the sum of AWs to zero. The third constraint imposes a non-negative restriction on the AFE of risk-allocated factors and upper and lower bounds for the AFE’s ranges. This optimization problem with constraints can be solved by using the sequential quadratic programming (SQP) method.¹²

4.4 Estimation and Factor Decomposition

Each stock’s active return is calculated against a market return of each market (MSCI Japan, US, UK, and EMU). The factor loading matrix is estimated based on the 1000-day return observations with 250-day rolling windows.

The factor loading $\beta _{i,j}$ to each factor is estimated by ordinary least squares (OLS) using the following equation expressing an active return of security i at time t by a liner regression model.

$$\begin{aligned} {r_{i, t} -r_{M, t}= \alpha _i + \sum _{j=1}^m \beta _{i,j} f_{j, t}+\varepsilon _{i, t}}, \end{aligned}$$

(5)

where $\alpha _i$ is a constant and $\beta _{i, j}$ is the sensitivity of security i to a factor ${F_j}$, $r_{M, t}$ is a market return, $f_{j, t}$ is the factor return of a factor $F_j$, and $\varepsilon _{i,t}$ is an error term at time t. This multifactor model for active returns can be rewritten in time-series regression form for security i as

$$\begin{aligned} {\varvec{r}_{i} -\varvec{r}_{M} = \varvec{F} \varvec{\theta }_i+\varvec{\varepsilon }_i} \end{aligned}$$

where $\varvec{r}_{i} =(r_{i,1}, \ldots , r_{i,t})^T$ for $i =1,\ldots , n$ and M,

$$\begin{aligned} { \varvec{\theta }_i= \left( \begin{array}{c} \alpha _i \\ \beta _{i,1} \\ \vdots \\ \beta _{i,m} \end{array} \right) = \left( \begin{array}{c} \alpha _i \\ \varvec{\beta }_{i} \end{array} \right) , \text {and}~~ \varvec{F} = \left( \begin{array}{cccc} 1 &{} f_{1, 1} &{} \cdots &{} f_{m, 1} \\ 1 &{} f_{1, 2} &{} \cdots &{} f_{m, 2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} f_{1, T} &{} \cdots &{} f_{m, T} \end{array} \right) . } \end{aligned}$$

Here, we impose the strictly exogenous assumptions on error terms and factors such that $E[\varepsilon _{i,t} |\varvec{f}_{t, j} ]=0$ for all i, j, and t, which is required for unbiased estimation of the OLS estimates $\hat{\varvec{\theta }}_{i}^{\text {(}OLS)}$ and for $\hat{\varvec{A}}$. This assumption seems too strong, since at each time period t, the error term is assumed to be uncorrelated with all lags and leads of the factor variables, but this is critical assumption for the OLS estimators to be unbiased.¹³ The OLS estimates become $\hat{\varvec{\theta }}_i^{\text {(}OLS)} = ({\hat{\alpha }}_i, \hat{\varvec{\beta }}_{i}^T)^T=(\varvec{F}^{T}\varvec{F})^{-1}\varvec{F}^{T}{(\varvec{r}_i-\varvec{r}_M)}$. The sample estimate of $\varvec{A}$ becomes $\hat{\varvec{A}} =(\hat{\varvec{\beta }}_1, \hat{\varvec{\beta }}_2, \cdots, \hat{\varvec{\beta }}_n)^T$.

Since the factor effects on the active return are expressed by $\varvec{y}^T\varvec{{f}}$ in Eq. (3), we can define the factor effect $\varvec{{u}}_t$, which is the factor decomposition of active returns for the FRP portfolios at period t, as

$$\begin{aligned} \varvec{{u}}_t = \varvec{y}^T_{t-1} \varvec{{f}}_t. \end{aligned}$$

This can be estimated as $\hat{\varvec{u}}_t = \hat{\varvec{y}}_{t-1}^T\varvec{f}_t$, where $\hat{\varvec{y}}_t = \varvec{x}_{*, t}^{T}\hat{\varvec{A}_{t}}$, with $\varvec{x}_{*, t}$ being the solution of the active weight vector at time t.¹⁴

5 Empirical Analysis of FRP Portfolio

In this section, we construct FRP portfolios for the four stock markets, Japan, the US, UK, and Euro countries, based on the method described in Sect. 4, and then, we compare the performance of obtained portfolios with MCW portfolios. In each subsection, we first provide a brief overview of the characteristics of the factors in the analysis period, and then, we construct FRP portfolios and discuss the simulation results in detail.

5.1 FRP Portfolio for the Japanese Market

Figure 1 plots the daily cumulative factor returns in the Japanese market from January 4, 2002 to December 30, 2017. Although the factors had cyclical fluctuations during the observation period, value showed the best performance, followed by yield and size. Momentum experienced highly volatile fluctuations during the financial crisis between 2008 and 2009. Quality and low volatility showed an upward trend after the financial crisis.

Fig. 1

Time-series plot of cumulative factor returns for the Japanese market from January 4, 2002 to December 30, 2017

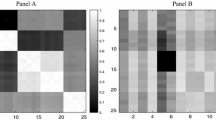
Table 2 shows the correlation matrix of the factor returns during the same period. We observe that factor correlations were generally low, except that between yield and low volatility, which showed a higher correlation than that between other pairs.

Table 2 Factor correlation matrix for the Japanese market from January 4, 2002 to December 30, 2017

Figure 2 plots the factor risk allocation for the obtained portfolios on a monthly basis. It should be noted that factor risks do not total 100% owing to the existence of idiosyncratic risks, with the exception of the re-balancing month at each quarter end. The risk allocations generally remained equalized among the four factors during the backtest period, indicating that the desired FRP portfolio was successfully constructed.

The performance summary of FRP portfolios is shown in Table 3.¹⁵ Among all investment universes, FRP strategies significantly outperformed MCW portfolios. As FRP portfolios were constructed based on an active risk basis, the resulting total risks generally approximated those of MCW portfolios. The portfolio’s active risk was around the 2–3% level. The FRP portfolio’s return-risk ratios improved compared with those of MCW portfolios, and the active return-risk (information) ratios for MSCI Japan, S&P Japan LargeMidCap, and TOPIX 500 were 0.94, 0.72, and 0.73, respectively. The significant Jensen’s $\alpha$s indicate that the FRP portfolios obtained positive returns after being adjusted by market returns. Since our proposed FRP strategy is not constructed to reduce market risks, the market $\beta$ was similar to or slightly lower than that of the MCW portfolio. The portfolios’ turnover rate (the one-way ratio to the portfolio’s market capitalization) was lower than 30%, and thus, it is expected that satisfactory active returns could be obtained by the FRP strategy even after taking transaction costs into account.

Table 3 Summary of the portfolio performances among investment universes for the Japanese market

The fact that FRP portfolios surpassed MCW portfolios indicates that additional risk premiums were obtained by the FRP strategy. We verified this fact by decomposing active returns for each factor effect. Table 4 shows the decomposition of active returns among the factors throughout the backtest period. The risk-allocated factors (value, size, low volatility, and yield) were the principal drivers of positive returns, while either insignificant plus or negative contributions were observed for momentum and quality, which were not included in the factor risk allocation.

Table 4 Active return decompositions among factors for the Japanese market

The monthly AFE plots shown in Fig. 3 verify that the four risk-allocated factors stably derived positive AFEs and contributed to the acquisition of factor risk premiums. Since the AFEs of momentum and quality persisted close to 0, where these factors did not undergo risk allocation, the contributions from these factors remained negligible.

Fig. 2

Time-series plot of active risk allocations among factors for the Japanese market

Fig. 3

Time-series plots of monthly AFE records for the Japanese market

5.2 FRP Portfolio for the US, UK, and Euro Markets

Figure 4 plots the daily cumulative factor returns in US, UK, and Euro stock markets from January 4, 2002 to December 30, 2017. As in the Japanese market, the factors generated positive risk premiums over the long term in the US and Euro markets, while they showed cyclical fluctuations. In particular, momentum and value performed well during the period for both markets. Other factors also followed suit. Although quality was stagnant prior to the financial crisis, it subsequently garnered positive returns. Meanwhile, the factors showed different results for those in the UK market. Specifically, momentum and quality produced favorable returns, while size and low volatility had the same positive trend, whereas value and yield faltered. In particular, yield generated negative factor returns throughout the period.¹⁶

Fig. 4

Time-series plots of cumulative factor returns for the US, UK, and Euro markets from January 4, 2002 to December 30, 2017

Table 5 shows the factor correlation matrix for the three markets during the same period. Similar to the Japanese market, the US market showed a relatively high correlation between yield and low volatility, while in the Euro market, low volatility had higher correlations with size and momentum. Quality was comparatively highly correlated with both momentum and low volatility in the UK and Euro markets. Except for these, factor correlations were generally low lingering within the $\pm 0.5$ range.

Table 5 Factor correlation matrixes for the US, UK, and Euro markets from January 4, 2002 to December 30, 2017

Figure 5 plots the factor risk allocation for the obtained portfolios on a monthly basis. The risk allocations generally have been kept equalized between the pro-cyclical and defensive factors throughout the simulation period, indicating that the desired FRP portfolio was successfully constructed.¹⁷

Fig. 5

Time-series plot of active risk allocations among factors for the US, UK, and Euro markets

Table 6 summarizes the performance of the obtained FRP portfolios for the three markets. As in the case of the Japanese market, the FRP portfolio significantly outperformed the MCW portfolio for all markets. We observe similar results in the Japanese market for total risk, active risk, and market $\beta$. The information ratio in the UK market was 0.67, which was inferior to that for the US (0.97), Euro (0.85), and Japanese (0.80, an average of the three investment universes) markets. This can be explained by the fact that value and yield were sluggish in the UK market during the observation period. While significant Jensen’s $\alpha$s were observed for the three markets, the significance level in the UK market was the lowest among all the universes we analyzed in this study. Since turnover rates for the obtained FRP portfolios were within 40%, satisfactory active returns could also be expected by the strategy for the three markets even after deducting transaction costs.

Table 6 Portfolio performances for the US, UK, and Euro markets

Table 7 shows the decomposition of active returns among the factors. In the US market, the factor effect was about 4.0% whereas the idiosyncratic effect contributed negatively by 1.4%. All the factors generated positive contributions to the active return. In particular, size, momentum, and quality helped to boost the FRP portfolio performances. Similar to the result of the US market, the total factor effect contributed positively in the Euro market, accounting for a large part of the active return. Momentum and quality were positive performance drivers, while size and yield contributed little to the performance. However, the factor decomposition in the UK revealed that value and yield dragged down the portfolio’s performance by their sluggish factor returns, with positive contributions from the other factors.

Table 7 Active return decompositions among factors for the US, UK, and Euro markets

The monthly AFE plots shown in Fig. 6 verified that the six factors stably derived positive AFEs, since non-negative constraints were imposed on AFEs in the portfolio optimization. In the US and Euro markets, the stably positive factor AFEs contributed to the acquisition of factor risk premiums. Although positive AFEs were also acquired for each factor in the UK, the portfolio’s performance lagged behind the other investment universes owing to the positive AFEs for value and yield, of which performances were disappointing during the analysis period.

Fig. 6

Time-series plots of monthly AFE records for the US, UK, and Euro markets

6 Summary and Discussions

In this study, we constructed FRP portfolios for four global stock markets based on fundamental factors and investigated their effectiveness. The obtained FRP portfolios outperformed MCW portfolios, since positive contributions can be obtained from the risk-allocated factors. From these results, we conclude that the FRP strategy is a prospective method for capturing factor risk premiums in global stock markets. Additional empirical contributions and practical implications are as follows.

Factor investing and risk-based asset allocation approaches have been developed both in the investment community and academic field in recent years.¹⁸ Shimizu and Shiohama (2018) introduced the risk parity method, which is one of popular risk-based strategies in factor investing for the Japanese stock market. We extended this method to global stock markets and confirmed its effectiveness. We consider that there is affinity between factor investing and risk-based asset allocation, which arises from the property of undertaking asset allocation without forecasting expected returns, since smart beta strategies seek factor risk premiums by constantly acquiring exposure to factors without any forecasts. Therefore, studies combining these two fields may generate fruitful outcomes.

While we studied the application of the risk parity strategy for factor investing, other risk-based allocations, such as inverse volatility, inverse variance, minimum volatility, and maximum diversification, can be applied to factor investing. In particular, inverse volatility, which is a conditional risk parity for correlation, can provide a more simplified FRP portfolio construction approach. For the estimation of factor exposures, we used a naive approach using OLS regressions by time-series proxy factor returns extracted from factor indexes. The score-based approach that Bender and Wang (2016) examined may provide more stable and consistent factor exposures for each security. We leave these subjects as future research topics.

Additional themes from the viewpoint of risk diversification and management are discussed as follows with three notable considerations and issues that arise in FRP portfolio construction.

First, even when considering asset allocations based on factors, diversification is the overriding principle, that is, investing in low correlated factors that have different economic characteristics. If an FRP portfolio is constructed based on Fama–French–Carhart’s value, size, and momentum, the portfolio is exposed only to pro-cyclical factors and can have substantial draw-downs by the overlapping bad periods of factors. The risk allocations are equalized between cyclical and defensive factors for every investment universe in our FRP portfolio construction. Hence, our approach probably has more desirable characteristics from the viewpoint of risk diversification.

Second, it should be noted that an FRP strategy is not designed to control factor exposures. Cases may occur whereby unintended factor exposures are acquired, or positive exposures to factors in risk allocation are not attained without constraints.

Third, the numerical optimization tends to become complex in the FRP portfolio construction, because the FRP strategy strictly equalizes risk contributions among factors taking factor correlations into account. As Maillard et al. (2010) noted, more computational cost will be required when a portfolio becomes larger. The similar difficulties also arise from increasing the number of factors, whereby it becomes more difficult to obtain optimal solutions that equalize factor contributions strictly. Hence, we took the factor-grouping approach for the portfolio construction in the US, UK, and Euro markets, which simplifies the optimization problem.

Factor investing attempts to analyze portfolio returns and risk sources beyond asset classes with intuitive suggestions for portfolio and risk management. Factor investing has the potential to enhance portfolio efficiency as well as achieve more effective diversification rather than asset class-based investment. It is also beneficial for investors who are not directly engaged in factor investing by providing information about what kinds of factors their portfolios are exposed to and how they would react to changes in market environment. More advanced research into factor investing involving various asset classes can be anticipated in the future.