1 Introduction

In the aftermath of the financial crisis 2007–2009 the previous separation of market risk and credit risk has disappeared. Credit or default risks of trading parties are no longer ignored, even for popular vanilla trades involving mainly market risk. The posting of collateral has been widely adopted in derivative trades. This changes the profile of credit risk of a derivative and usually affects its price. Credit valuation adjustment (CVA) has become the market standard. It reflects the expected value of loss due to possible defaults. In Cesari et al. (2009) an introduction to CVA is given from a practical viewpoint. The book Bielecki et al. (2011) presents several more theoretically oriented perspectives on credit risk including CVA. The literature on CVA is evolving rapidly: papers related to CVA include Brigo and Chourdakis (2009), Burgard and Kjaer (2011), Crépey (2011), Pallavicini et al. (2011), Tang et al. (2011) and Wu (2012).

In this paper, we discuss how to model credit risk under the benchmark approach. Firstly we introduce an affine credit risk model. We then show how to price credit default swaps (CDSs) and introduce CVA as an extension of CDSs. In particular, our model can capture right-way—and wrong-way exposure. This means, we capture the dependence structure of the default event and the value of the transaction under consideration. For simple contracts, we provide closed-form solutions. However, due to the fact that we allow for a dependence between the default event and the value of the transaction, closed-form solutions are difficult to obtain in general. Hence we conclude this paper with a reduced form model, which is more tractable.

Chapter 14 in Baldeaux and Platen (2013) follows closely the current paper, which aims to contribute to the emerging literature by applying the benchmark approach to CVA using a tractable model. The paper is organized as follows: Sect. 2 sets a general framework for financial modeling by introducing some key relationships of the benchmark approach due to Platen (2002), see Platen and Heath (2010). Section 3 describes an affine credit risk model along the lines of results in Filipović (2009). Section 4 discusses the pricing of CDSs under the benchmark approach. CVA is then studied in Sect. 5. An example of CVA in a commodity context is analyzed in Sect. 6. Section 7 presents a reduced form model, which allows to obtain various explicit formulas.

2 Comments on the Benchmark Approach

When modeling and pricing in finance there has been a strong emphasis in theory and practice on risk neutral modeling under an assumed equivalent risk neutral probability measure. The existence of a risk neutral measure is a rather strong assumption, which may not be realistic for longer term contracts, as argued in Platen and Heath (2010). By using the numéraire portfolio (NP) \(S^{{{\delta _*}}}_t\) as numéraire or benchmark, as suggested by Long (1990) and Platen (2002), one can model the market dynamics under the real world probability measure. The defining property of the NP guarantees for all nonnegative portfolios \(S^{{{\delta _*}}}_t\) that their benchmarked value

$$\begin{aligned} \hat{S}^{\delta }_t = \frac{S^{\delta }_t}{S^{{{\delta _*}}}_t} \end{aligned}$$

forms a supermartingale on the given filtered probability space \((\Omega , {\mathcal {A}}, \underline{{\mathcal { A}}}, P)\) with \(\underline{{\mathcal { A}}}= ( {\mathcal {A}}_t )_{t \ge 0}\) satisfying the usual conditions. More precisely, one has

$$\begin{aligned} \hat{S}^{\delta }_t \ge E \left( \frac{S^{\delta }_s}{S^{{{\delta _*}}}_s} \,\bigg |\, {\mathcal {A}}_t \right) \end{aligned}$$

for all \(0 \le t \le s < \infty \). It has been pointed out in Platen and Heath (2010) that one can avoid the classical risk neutral assumptions and can conveniently work in a much wider modeling work. Strong arbitrage in the sense of Platen and Bruti-Liberati (2010) and Platen and Heath (2010) is then automatically excluded. When aiming for the minimal possible price for a replicable, nonnegative benchmarked contingent claim \(\hat{H}_T\), which matures at a bounded stopping time \(T\), is \({\mathcal {A}}_T\)-measurable and integrable such that \(E \left( \hat{H}_T \vert {\mathcal {A}}_T \right) < \infty \), it follows the real world pricing formula

$$\begin{aligned} \hat{V}_t = E \left( \hat{H}_T \,\bigg |\, {\mathcal {A}}_t \right) \end{aligned}$$
(1)

for \(0 \le t \le T < \infty \) for the minimal possible benchmarked price of the claim, see Platen and Heath (2010). This price, when denominated in domestic currency, is then obtained as

$$\begin{aligned} V_t = \hat{V}_t S^{{{\delta _*}}}_t. \end{aligned}$$
(2)

In Du and Platen (2012a) the concept of benchmarked risk minimization has been proposed, which derives the real world pricing formula (1) also for nonhedgeable benchmarked contingent claims. Under this concept the price and the benchmarked profit and loss are minimized when hedging the claim. More precisely, the benchmarked profit and loss is orthogonal to benchmarked traded wealth in the sense that the product of the benchmarked profit and loss with any benchmarked self-financing portfolio forms a local martingale.

In CVA one faces the problem that traditionally one is used to price counterparty credit exposure under an assumed risk neutral probability measure, but crucial information about the likelihood of default of counterparties and their dependencies is available under the real world probability measure. This paper suggests to resolve this issue by considering the problem of CVA entirely under the real world probability measure. This approach provides the advantage that one can employ more realistic models and has not to make assumptions about a putative risk neutral probability measure with respect to credit events. The paper will demonstrate this approach by employing an affine model which permits for various contracts explicit formulas, and yields for other quantities expressions that can be easily evaluated via Monte Carlo methods.

It is important to identify for the given market model the NP or a proxy of the NP. The NP is known to be the growth optimal portfolio of the given investment universe, and maximizes expected logarithmic utility, see Kelly (1956) and Platen and Heath (2010). In practice, the NP can be approximated by a well diversified portfolio, as shown by diversification theorems in Platen and Heath (2010) and Platen and Rendek (2012). A simple, readily available proxy for the NP is a well diversified market index, e.g. the MSCI World total return index.

3 An Affine Credit Risk Model

In this section, we aim to introduce a reasonably realistic, yet tractable model for credit risk. In particular, our model allows for a stochastic interest rate, and a stochastic default intensity, both of which are correlated with the numéraire portfolio (NP). We point out that our model satisfies the assumptions \(\mathbf {(D1)}\) and \(\mathbf {(D2)}\), in Filipović (2009), and hence we can employ the results presented in this reference. For further technical background, we refer the reader to this reference.

We fix a probability space \((\Omega , {\mathcal {A}}, P)\), where \(P\) denotes the real world probability measure. Next, we present a model for the evolution of financial information. We remark that in our model, only having access to market information is not sufficient to decide whether or not default has occurred or not. We now present this model, which is a doubly stochastic intensity based model. We introduce a filtration \(\underline{{ \mathcal {G}}} = \left( {{\mathcal {G}}}_t \right) _{t \ge 0}\), satisfying the usual conditions and set

$$\begin{aligned} {{\mathcal {G}}}_{\infty } = \sigma \left\{ {{\mathcal {G}}}_t, \, t \ge 0 \right\} \subset {\mathcal {A}}, \end{aligned}$$

and a nonnegative \(\underline{{ \mathcal {G}}}\)-progessively measurable process \(\lambda = \left\{ \lambda _t, \, t \ge 0 \right\} \) with the property

$$\begin{aligned} \int ^t_0 \lambda _s ds < \infty , \, P-a.s. \text{ for } \text{ all } t \ge 0. \end{aligned}$$

Next, we fix an exponential random variable \(\phi \) with intensity parameter 1, independent of \({{\mathcal {G}}}_{\infty }\), and we define the random time

$$\begin{aligned} \tau := \inf \left\{ t : \int ^t_0 \lambda _s ds \ge \phi \right\} \end{aligned}$$

assuming values in \((0, \infty ]\). From the independence property of \(\phi \) and \({{\mathcal {G}}}_{\infty }\), we have that

$$\begin{aligned} P \left( \tau > t \, \vert \, {{\mathcal {G}}}_{\infty } \right) = P \left( \phi > \int ^t_0 \lambda _s ds \vert {{\mathcal {G}}}_{\infty } \right) = \exp \left\{ - \int ^t_0 \lambda _s ds \right\} . \end{aligned}$$
(3)

Lastly, we condition both sides in the preceding equation on \({{\mathcal {G}}}_t\) and obtain

$$\begin{aligned} P ( \tau > t \, \vert \, {{\mathcal {G}}}_t) = \exp \left\{ - \int ^t_0 \lambda _s ds \right\} . \end{aligned}$$
(4)

Equations (4) and (3) are consistent with the assumptions \(\mathbf {(D1)}\) and \(\mathbf {(D2)}\) in Filipović (2009), which are hence satisfied in our model. Next, we set

$$\begin{aligned} H_t = {\mathbf{1}_{\left\{ \tau \le t \right\} }}\end{aligned}$$

and \({{\mathcal {H}}}_t = \sigma \left\{ H_s, \, s \le t \right\} \) and set \({\mathcal {A}}_t = {{\mathcal {G}}}_t \vee {{\mathcal {H}}}_t\), the smallest \(\sigma \)-algebra containing \({{\mathcal {G}}}_t\) and \({{\mathcal {H}}}_t\). We remark that the inclusion \({{\mathcal {G}}}_t \subset {{\mathcal {A}}}_t\) is strict, having access to \({{\mathcal {G}}}_t\) does not allow us to decide whether default has occurred by \(t\), i.e. the event \(\left\{ \tau \le t \right\} \) is not included in \({{\mathcal {G}}}_t\), so \(\tau \) is not a \(\underline{{{\mathcal {G}}}}\)-stopping time. We find this realistic, since it means that only by observing financial data such as stock prices and interest rates, one cannot determine whether default has occurred or not, as additional, non-financial factors, can be assumed to be relevant to this decision too. The following lemma is Lemma 12.1 in Filipović (2009).

Lemma 3.1

Let \(t \ge 0\). Then for every \(A \in {\mathcal {A}}_t\), there exists a \( B \in {{\mathcal {G}}}_t\) such that

$$\begin{aligned} A \cap \left\{ \tau >t \right\} = B \cap \left\{ \tau > t \right\} . \end{aligned}$$

We have the following corollary to Lemma 3.1, the proof of which is analogous to the proof of Lemma 12.1 in Filipović (2009).

Corollary 3.1

Let \(t \ge 0\). Then for every \(A \in {\mathcal {A}}_t\), there exists a \( B \in {{\mathcal {G}}}_t\) such that

$$\begin{aligned} A \cap \left\{ \tau \le t \right\} = B \cap \left\{ \tau \le t \right\} . \end{aligned}$$
(5)

The first part of the following lemma is Lemma 12.2 in Filipović (2009), the second part of the next lemma forms part of Lemma 12.5 in Filipović (2009).

Lemma 3.2

Let \(Y\) be a nonnegative random variable and \(\lambda \) and \(\tau \) be as defined above. Then

$$\begin{aligned} E \left( {\mathbf{1}_{ \left\{ \tau > t \right\} }}Y \,\bigg |\, {\mathcal {A}}_t \right) = {\mathbf{1}_{ \left\{ \tau > t \right\} }}\exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( {\mathbf{1}_{ \left\{ \tau > t \right\} }}Y \,\bigg |\, {{\mathcal {G}}}_t \right) , \end{aligned}$$

for all \(t \ge 0\). If \(Y\) is also \({{\mathcal {G}}}_{\infty }\) measurable, then we have

$$\begin{aligned} E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}Y \,\bigg |\, {\mathcal {A}}_t \right) = {\mathbf{1}_{\left\{ \tau \le t \right\} }}E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) . \end{aligned}$$

Proof

The first part of the lemma is proven in Filipović (2009), see the proof of Lemma 12.2. For the second part, let \(A \in {\mathcal {A}}_t\), and note that by Corollary 3.1, there exists a \(B \in {{\mathcal {G}}}_t\) with property (5). We now use the definition of conditional expectation, the fact that \({\mathbf{1}_{\left\{ \tau \le t \right\} }}\mathbf{1}_{A} = {\mathbf{1}_{\left\{ \tau \le t \right\} }}\mathbf{1}_{B}\), that \(Y \in {{\mathcal {G}}}_{\infty }\) and that \(P ( \tau \le t \, \vert \, {{\mathcal {G}}}_{\infty } ) = P ( \tau \le t \, \vert \, {{\mathcal {G}}}_t )\), which follows from Eqs. (4) and (3):

$$\begin{aligned} \int _{A} {\mathbf{1}_{\left\{ \tau \le t \right\} }}Y dP= & {} \int _{B} {\mathbf{1}_{\left\{ \tau \le t \right\} }}Y dP\\= & {} \int _{B} E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}Y \,\bigg |\, {{\mathcal {G}}}_t \right) dP\\= & {} \int _{B} E \left( E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}Y \,\bigg |\, {{\mathcal {G}}}_{\infty } \right) \,\bigg |\, {{\mathcal {G}}}_t \right) dP\\= & {} \int _{B} E \left( Y E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}\,\bigg |\, {{\mathcal {G}}}_{\infty } \right) \,\bigg |\, {{\mathcal {G}}}_t \right) dP\\= & {} \int _{B} E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}\,\bigg |\, {{\mathcal {G}}}_t \right) dP\\= & {} \int _{B} E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) \,\bigg |\, {{\mathcal {G}}}_t \right) dP\\= & {} \int _{B} {\mathbf{1}_{\left\{ \tau \le t \right\} }}E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) dP\\= & {} \int _{A} {\mathbf{1}_{\left\{ \tau \le t \right\} }}E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) dP. \end{aligned}$$

Hence we have

$$\begin{aligned} E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}Y \,\bigg |\, {\mathcal {A}}_t \right)= & {} E \left( {\mathbf{1}_{\left\{ \tau \le t \right\} }}E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) \,\bigg |\, {\mathcal {A}}_t \right) = {\mathbf{1}_{\left\{ \tau \le t \right\} }}E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) .\\ \end{aligned}$$

\(\square \)

The following formula is useful, when considering claims which are independent of default risk. It is an immediate corollary to Lemma 3.2.

Corollary 3.2

Let \(Y\) be a nonnegative random variable which is \({{\mathcal {G}}}_{\infty }\) measurable. Then

$$\begin{aligned} E \left( Y \,\bigg |\, {\mathcal {A}}_t \right) = E \left( Y \,\bigg |\, {{\mathcal {G}}}_t \right) . \end{aligned}$$

We now present our specific model, which is based on affine processes. Firstly, we define the square-root process \(Y = \left\{ Y_t, \, t \ge 0 \right\} \), given by

$$\begin{aligned} d Y_t = ( 1 - \eta Y_t ) dt + \sqrt{Y_t} d W^1_t, \end{aligned}$$

where \(W^1\) is a \(\underline{{{\mathcal {G}}}}\)-Brownian motion and we define the deterministic time-change

$$\begin{aligned} \alpha _t = \alpha _0 \exp \left\{ \eta t \right\} , \end{aligned}$$

and we model the discounted NP as

$$\begin{aligned} {\bar{S}}^{{{\delta _*}}}_t = \alpha _t Y_t. \end{aligned}$$

In this context, the time change can be interpreted as follows. When expressing the discounted NP in units of the time change, we obtain a process which mean-reverts. We now describe the short-rate using the stochastic process

$$\begin{aligned} r_t = a^r_t + b^r Z^1_t + c^r f^r (Y_t), \end{aligned}$$
(6)

where \(a^r_{\cdot }\) is a nonnegative deterministic function of time, \(b^r\) and \(c^r\) are nonnegative constants and \(f^r (x) = x\) or \(f^r(x) = \frac{1}{x}\). The process \(Z^1 = \left\{ Z^1_t, \, t \ge 0 \right\} \) is a square-root process given by

$$\begin{aligned} d Z^1_t = \kappa ^1 ( \theta ^1 - Z^1_t ) dt + \sigma ^1 \sqrt{Z^1_t} d W^2_t, \end{aligned}$$
(7)

where \(\kappa ^1, \theta ^1, \sigma ^1 >0\) and \( 2 \kappa ^1 \theta ^1 > ( \sigma ^1 )^2\), where \(W^2\) is an independent \(\underline{ {{\mathcal {G}}}}\)—Brownian motion. We now introduce the NP, which is given by

$$\begin{aligned} S^{\delta ^*}_t = B_t {\bar{S}}^{{{\delta _*}}}_t, \end{aligned}$$
(8)

where \(B_t = \exp \left\{ \int ^t_0 r_s ds \right\} \). Finally, we introduce a model for the stochastic intensity

$$\begin{aligned} \lambda _t = a^{\lambda }_t + b^{\lambda } Z^1_t + c^{\lambda } f^r(Y_t) + d^{\lambda } Z^2_t, \end{aligned}$$
(9)

where \(\kappa ^2, \theta ^2, \sigma ^2 >0\), \(a^{\lambda }_{\cdot }\) is a nonnegative function of time. The constants \(b^{\lambda }\), \(c^{\lambda }\), and \(d^{\lambda }\) are nonnegative, and \(Z^2 = \left\{ Z^2_t, \, t \ge 0 \right\} \) is a square-root process:

$$\begin{aligned} d Z^2_t = \kappa ^2 (\theta ^2 - Z^2_t ) dt + \sigma ^2 \sqrt{Z^2_t} d W^3_t, \end{aligned}$$

where \(2 \kappa ^2 \theta ^2 > (\sigma ^2 )^2\), and \(W^3\) is an independent \(\underline{{{\mathcal {G}}}}\)-Brownian motion. We conclude that \(\lambda , r, \) and \(S^{\delta ^*}\) are dependent, as they share some of their respective stochastic drivers. Clearly, a joint estimation of the triplet \((Y,Z_1,Z_2)\) is challenging and computationally expensive. A computationally more efficient method is the following: one first estimates the process \(Y\) using data on \({\bar{S}}^{{{\delta _*}}}\), and subsequently, keeping the parameters of \(Y\) fixed, \(Z_1\) from data on \(r\). Lastly, keeping the parameters of \((Y,Z_1)\) fixed, one estimates the parameters of \(Z_2\) from data on \(\lambda \). Of course, this approach will lead to a result that is not as satisfactory as one generated by jointly fitting \((Y,Z_1,Z_2)\), but is computationally more efficient.

We conclude this section with presenting pricing formulas for some standard claims, namely zero coupon bonds and European put options on the NP, where the latter can be interpreteted as a well diversified market index. In Sect. 5, we will study these products in the presence of CVA. We remark that the affine nature of our model together with Laplace transforms derived using Lie symmetry analysis allow us to obtain these explicit derivative pricing formulas, see Baldeaux and Platen (2013). Regarding the zero coupon bond \(P_T(t)\) with maturity \(T>0\) at time \(t \in [0,T]\), we have from the real world pricing formula (1) with (2)

$$\begin{aligned} P_T(t)= & {} S^{{{\delta _*}}}_t E \left( \frac{1}{S^{{{\delta _*}}}_T} \,\bigg |\, {{\mathcal {A}}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( \frac{1}{S^{{{\delta _*}}}_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} \frac{\alpha _t}{\alpha _T} Y_t E \left( \frac{1}{Y_T} \exp \left\{ - \int ^T_t a^r_s ds - b^r \int ^T_t Z^1_s ds - c^r \int ^T_t f(Y_s ) ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} \frac{\alpha _t}{\alpha _T} Y_t \exp \left\{ - \int ^T_t a^r_s ds \right\} E \left( \frac{ \exp \left\{ - c^r \int ^T_t f^r(Y_s) ds \right\} }{Y_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\times \,E \left( \exp \left\{ - b^r \int ^T_t Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) . \end{aligned}$$

We remark that the expectations

$$\begin{aligned} E \left( \frac{ \exp \left\{ - c^r \int ^T_t f^r(Y_s) ds \right\} }{Y_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$

and

$$\begin{aligned} E \left( \exp \left\{ - b^r \int ^T_t Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$

can be computed using Propositions 7.3.8 and 7.3.9 in Baldeaux and Platen (2013), which we recall in the Appendix. Note that \(P_T(t)\) denotes the default free zero coupon bond. We alert the reader to the fact that since the global financial crisis, zero coupon bonds can no longer be regarded as being default free. By allowing zero coupon bonds to become defaultable at some default time \(\tau \) with some potentially random recovery rate, one obtains families of discount curves corresponding to defaultable zero coupon bonds. We refer to Sects. 4 and 5 for details in the context of credit default swaps and recovery rates. Within the current section we focus, for simplicity, on the “single discount curve” of non-defaultable zero coupon bonds. Multi-curve models emerge naturally by taking default events and recovery into account.

Having introduced zero coupon bonds, we now attend to swaps, in particular, we consider a fixed-for-floating forward starting swap settled in arrears. We fix a finite collection of future dates \(T_j\), \(j=0,\ldots ,n\), \(T_0 \ge 0\), and \(T_j - T_{j-1} =: \delta _j >0\), \(j=1, \ldots ,n\). The floating rate \(L(T_j, T_{j+1})\) received at time \(T_{j+1}\) is set at time \(T_j\) by reference to a zero coupon bond for the time period \([T_j, T_{j+1})\), in particular,

$$\begin{aligned} P^{-1}_{T_{j+1}} (T_j) = 1+ \delta _{j+1} L(T_j, T_{j+1}). \end{aligned}$$
(10)

The interest rate \(L(T_j,T_{j+1})\) is the spot LIBOR that prevails at time \(T_j\) for the period of length \(\delta _{j+1}\). A long position in a payer swap entitles the investor to receive floating payments in exchange for fixed payments, so the cash flow at time \(T_j\) is \((L(T_{j-1}, T_j) - \kappa ) \delta _j\). The dates \(T_0, \ldots , T_{n-1}\) are known as reset dates, whereas the dates \(T_1, \ldots , T_n\) are known as settlement dates. The first reset date \(T_0\) is known as the start date of the swap. Since after the global financial crisis zero coupon bonds are no longer regarded as being default free, LIBOR rates cannot be generated using a single discount curve, but should be generated using zero coupon bonds which reflect the appropriate default probabilities and recovery rates. The defaultable zero coupon bonds discussed in this paper for example could be used, see (18) but also Filipović (2009) for recent developments. For \(t \le T_0\), the real world pricing formula (1) gives with (2) the following value for a non-defaultable swap:

$$\begin{aligned} FS_{\kappa ,T_0} (t) := E \left( \sum ^n_{j=1} \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_{T_j}} \left( L(T_{j-1}, T_j) - \kappa \right) \delta _j \,\bigg |\, {\mathcal {A}}_t \right) . \end{aligned}$$
(11)

We now show how to rewrite the value of a swap as the difference of a zero coupon bond and a coupon bearing bond. From Eq. (11), we obtain

$$\begin{aligned} FS_{\kappa ,T_0} (t) = \sum ^n_{j=1} E \left( \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_{T_j}} \left( \frac{1}{P_{T_j} (T_{j-1})} - (1 +\kappa \delta _j) \right) \,\bigg |\, {\mathcal {A}}_t \right) . \end{aligned}$$
(12)

Focussing on the computation of a single term in this sum we obtain

$$\begin{aligned}&E \left( \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_{T_j}} \left( \frac{1}{P_{T_j} (T_{j-1})} - (1 +\kappa \delta _j) \right) \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad =E \left( \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_{T_j} P_{T_{j}} (T_{j-1}) } \,\bigg |\, {\mathcal {A}}_t \right) - ( 1+ \kappa \delta _j ) E \left( \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_{T_j}} \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad =E \left( \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_{T_{j-1}}} \frac{1}{P_{T_j} (T_{j-1})} E \left( \frac{S^{{{\delta _*}}}_{T_{j-1}}}{S^{{{\delta _*}}}_{T_j}} \,\bigg |\, {\mathcal {A}}_{T_{j-1}} \right) \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\qquad -\, ( 1 +\kappa \delta _j ) P_{T_j} (t)\nonumber \\&\quad =P_{T_{j-1}} (t) - (1 + \kappa \delta _j)P_{T_j} (t). \end{aligned}$$
(13)

Substituting Eq. (13) into (12), we obtain

$$\begin{aligned} FS_{\kappa , T_0} (t) = P_{T_0}(t) - \sum ^n_{j=1} c_j P_{T_j} (t), \end{aligned}$$
(14)

where \(c_j=\kappa \delta _j\), \(j=1, \ldots , n-1\) and \(c_n = 1 + \kappa \delta _n\). We remark that Eq. (14) is analogous to equation (13.2) in Musiela and Rutkowski (2005). In Sect. 5, we will show that in the presence of default risk, even a simple linear product like a swap is, in fact, treated like an option on a swap, or a swaption, which we now introduce.

The owner of an option on the above described swap with strike rate \(\kappa \) maturing at \(T=T_0\) has the right to enter at time \(T\) the underlying fixed-for-floating forward starting swap settled in arrears. The real world pricing formula (1) yields with (2) the following price for such a contract:

$$\begin{aligned} PS_{\kappa , T_0} := S^{{{\delta _*}}}_t E \left( \frac{ ( FS_{\kappa , T_0} (T_0) )^+}{S^{{{\delta _*}}}_{T_0}} \,\bigg |\, {\mathcal {A}}_t \right) . \end{aligned}$$
(15)

We remark that, as discussed in Section 13.1.2 in Musiela and Rutkowski (2005), it seems difficult to develop closed form solutions for swaptions. However, as we employ a tractable model, we can easily price swaptions via Monte Carlo methods: from Eq. (15), it is clear that in order to price the swaption, we need to have access to the joint distributions of \(( Y_T, \int ^T_t f^r(Y_s) ds )\) conditional on \(Y_t\), and \((Z^1_T, \int ^T_t Z^1_s ds)\) conditional on \(Z^1_t\). These joint distributions have been derived, for instance, in Sections 6.3 and 6.4 of Baldeaux and Platen (2013), which means that we can price swaptions using an exact Monte Carlo scheme.

For purposes of credit valuation adjustment (CVA), it is convenient to introduce a forward starting swaption: here the expiry date \(T\) of the swaption precedes the initiation date \(T_0\) of the swap, i.e. \(T \le T_0\). The real world pricing formula (1) associates the following value with this contract:

$$\begin{aligned} PS_{\kappa , T_0,T} (t) := S^{{{\delta _*}}}_t E \left( \frac{ ( FS_{\kappa , T_0} (T) )^+ }{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) . \end{aligned}$$

We will return to forward start swaptions when discussing CVA.

Finally, we show how to price a non-defaultable European put option on the NP, where we employ Lemma 8.3.2 of Baldeaux and Platen (2013), see also Filipović (2009), and we explicitly emphasize the dependence on \(Z^1_t\), \(Y_t\) and \(S_t\), which will be relevant when discussing CVA. From Corollary 3.2, we get

$$\begin{aligned} p_{T,K} (t, Z^1_t, Y_t, S_t )= & {} S^{\delta ^*}_t E \left( \frac{(K - S^{\delta ^*}_T)^+}{S^{\delta ^*}_T} \,\bigg |\, {{\mathcal {A}}}_t \right) \\= & {} S^{\delta ^*}_t E \left( \frac{(K - S^{\delta ^*}_T)^+}{S^{\delta ^*}_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} K E \left( \left( \frac{S^{{{\delta _*}}}_t}{S^{{{\delta _*}}}_T} - \frac{S^{{{\delta _*}}}_t}{K} \right) ^+ \,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} K E \left( \left( \exp \left\{ - \ln ( Y(t,T) ) \right\} - \tilde{K} \right) ^+ \,\bigg |\, {{\mathcal {G}}}_t \right) , \end{aligned}$$

where \(\tilde{K} = \frac{S^{{{\delta _*}}}_t}{K}\), \(Y(t,T) = \frac{S^{{{\delta _*}}}_T}{S^{{{\delta _*}}}_t}\). Hence from Lemma 8.3.2 in Baldeaux and Platen (2013), for \(w>1\) and \(\imath \) the imaginary unit, it follows

$$\begin{aligned}&S^{\delta ^*}_t E \left( \frac{(K - S^{\delta ^*}_T)^+}{S^{\delta ^*}_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\quad = \frac{K}{2 \pi } \int _{\mathfrak {R}} E \left( \exp \left\{ ( w + \imath \lambda ) \left( - \ln ( Y(t,T) ) \right) \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \frac{\tilde{K}^{- ( w -1 + \imath \lambda )}}{ (w + \imath ) (w - 1 + \imath \lambda ) } d \lambda . \end{aligned}$$

We now discuss the computation of the above conditional expectation

$$\begin{aligned} E \left( \exp \left\{ ( w + \imath \lambda ) \left( - \ln ( Y(t,T) ) \right) \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) . \end{aligned}$$

From Eq. (6), we have

$$\begin{aligned}&E \left( \exp \left\{ ( w + \imath \lambda ) \left( - \ln ( Y(t,T) ) \right) \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\quad = E \left( \exp \left\{ - (w + \imath \lambda ) \left( \int ^T_t r_s ds + \ln \left( \frac{\alpha _T}{\alpha _t} \right) + \ln (Y_T) - \ln (Y_t) \right) \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\quad = \exp \left\{ - (w + \imath \lambda ) \int ^T_t a^r_s ds - ( w + \imath \lambda ) \ln \left( \frac{\alpha _T}{\alpha _t} \right) \right\} Y^{(w + \imath ) \lambda }_t\\&\qquad \times \, E \left( \exp \left\{ - (w + \imath \lambda ) \int ^T_t b^r Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\qquad \times \,E \left( \exp \left\{ - (w + \imath \lambda ) \int ^T_t c^r f^1 (Y_s) ds \right\} Y^{-( w + \imath \lambda )}_T \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\quad = : f ( \lambda , Z^1_t, Y_t). \end{aligned}$$

Here

$$\begin{aligned} E \left( \exp \left\{ - (w + \imath \lambda ) \int ^T_t b^r Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$

and

$$\begin{aligned} E \left( \exp \left\{ - (w + \imath \lambda ) \int ^T_t c^r f^1 (Y_s) ds \right\} Y^{-( w + \imath \lambda )}_T \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$

can be computed using Propositions 7.3.8 and 7.3.9 in Baldeaux and Platen (2013). Hence, we obtain

$$\begin{aligned}&p_{T,K}(t,Z^1_t, Y_t, S_t) = \frac{K}{2 \pi } \int _{\mathfrak {R}} f( \lambda , Z^1_t, Y_t) \\&\quad \times \exp \left\{ -(w + \imath \lambda ) \left( \int ^T_t a^r_s ds + \ln \left( \frac{\alpha _T}{\alpha _t} \right) \right) \right\} \frac{ ( \tilde{K} )^{-(w - 1 +\imath \lambda )} }{(w + \imath \lambda ) (w - 1 + \imath \lambda )} d \lambda . \end{aligned}$$

The above formulas will be employed in Sect. 5.

4 Pricing Credit Default Swaps Under the Benchmark Approach

We now discuss how to price CDSs. Firstly, we summarize a CDS transaction. Consider two parties: A, the protection buyer, and B, the protection seller. If a third party, say C, the reference company, defaults at a time \(\tau \), where \(\tau \) is between two fixed times \(T_a\) and \(T_b\), B pays A a certain fixed amount, say \(L\). In exchange A pays B coupons at a rate \(R\) at time points \(T_{a+1}, \ldots , T_b\), or until default.

Under the benchmark approach, the techniques from Filipović (2009) can be combined with Laplace transforms. Using the real world pricing formula, the value of this contract to B at a time \(t < T_a\) is given by

$$\begin{aligned} CDS_t:= & {} S^{{{\delta _*}}}_t E \left( \mathbf{1}_{ \left\{ T_a < \tau \le T_b \right\} } R \frac{ \tau - T_{\beta (\tau )-1}}{S^{{{\delta _*}}}_{\tau }} \,\bigg |\, {{\mathcal {A}}}_t \right) \\&+\, S^{{{\delta _*}}}_t \sum ^b_{i=a+1} \alpha _i R E \left( \frac{ \mathbf{1}_{ \left\{ \tau > T_i \right\} } }{S^{{{\delta _*}}}_{T_i}} \,\bigg |\, {{\mathcal {A}}}_t \right) \\&- \,S^{{{\delta _*}}}_t L E \left( \frac{\mathbf{1}_{ \left\{ T_a < \tau \le T_b \right\} }}{S^{{{\delta _*}}}_{\tau }} \,\bigg |\, {{\mathcal {A}}}_t \right) , \end{aligned}$$

where \(\delta _i = T_{i} - T_{i-1}\), and \(T_{\beta (\tau )}\) is the first of the \(T_i\)’s following \(\tau \). The interpretation is clear, the first two terms represent payments from party A to party B, where the first term represents the amount accrued between the last payment before default, made at time \(T_{\beta (\tau ) -1}\), and the default time \(\tau \). The last term represents the payment to be made by \(B\) in case \(C\) defaults. Using the terminology from Filipović (2009), the second term is a zero recovery zero coupon bond, a payment \(R\) is only made at \(T_i\) if default occurs after \(T_i\). The third term is a partial recovery at default zero coupon bond with payment \(L\), and so is the first term, for which the payment at default is \(( \tau - T_{\beta (\tau )-1}) R\).

We firstly value the zero recovery zero coupon bond, where we use Lemma 3.2:

$$\begin{aligned} P^{0}_T(t)&:= S^{{{\delta _*}}}_t E \left( \frac{ {\mathbf{1}_{ \left\{ \tau > T \right\} }}}{S^{{{\delta _*}}}_T} \,\bigg |\, {{\mathcal {A}}}_t \right) \nonumber \\&={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( \frac{ {\mathbf{1}_{ \left\{ \tau > T \right\} }}}{S^{{{\delta _*}}}_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \nonumber \\&={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( \frac{1}{S^{{{\delta _*}}}_T} E \left( {\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {{\mathcal {G}}}_T \right) \,\bigg |\, {{\mathcal {G}}}_t \right) \nonumber \\&={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( \frac{ \exp \left\{ - \int ^T_0 \lambda _s ds \right\} }{S^{{{\delta _*}}}_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \nonumber \\&={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( \frac{\exp \left\{ - \int ^T_t \lambda _s ds \right\} }{ S^{{{\delta _*}}}_T } \,\bigg |\, {{\mathcal {G}}}_t \right) \nonumber \\&= {\mathbf{1}_{ \left\{ \tau > t \right\} }}\frac{ \alpha _t }{\alpha _T} E \left( \frac{Y_t}{Y_T} \exp \left\{ - \int ^T_t ( r_s +\lambda _s ) ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$
(16)
$$\begin{aligned}&={\mathbf{1}_{ \left\{ \tau > t \right\} }}\frac{\alpha _t}{\alpha _T} Y_t \nonumber \\&\quad \times \,E \left( \frac{ \exp \left\{ - \int ^T_t a_s ds - b \int ^T_t Z^1_s ds - d \int ^T_t Z^2_s ds - \int ^T_t f(Y_s) ds \right\} }{Y_T} \,\bigg |\, {{\mathcal {G}}}_t \right) \nonumber \\&= {\mathbf{1}_{ \left\{ \tau > t \right\} }}\frac{\alpha _t}{\alpha _T} Y_t \exp \left\{ - \int ^T_t a_s ds \right\} E \left( \exp \left\{ - b \int ^T_t Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$
(17)
$$\begin{aligned}&\quad \times \, E \left( \exp \left\{ - d \int ^T_t Z^2_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) E \left( \frac{ \exp \left\{ - \int ^T_t f(Y_s) ds \right\} }{Y_T} \,\bigg |\, {{\mathcal {G}}}_t \right) , \end{aligned}$$
(18)

where \(a_t = a^r_{t} + a^{\lambda }_t\), \(b=b^r + b^{\lambda }\), \(d= d^{\lambda }\), and \(f(x) =c^r f^r (x) + c^{\lambda } f^{\lambda } (x)\). We point out that from Eq. (16), one can confirm the observation from Filipović (2009) that when pricing a zero recovery zero coupon bond, as opposed to a zero coupon bond, one replaces the short rate process by \(r_t + \lambda _t\), which results in a lower price. Again, the expected values in Eqs. (17) and (18) can be computed using Propositions 7.3.8 and 7.3.9 in Baldeaux and Platen (2013).

We now turn to the remaining two components of the credit default swap pricing formula. We remark that it suffices to focus on

$$\begin{aligned} S^{{{\delta _*}}}_t E \left( \frac{ \tau - T_{\beta (\tau ) - 1} }{S^{{{\delta _*}}}_{\tau }} \mathbf{1}_{\left\{ T_a < \tau \le T_b \right\} } \,\bigg |\, {{\mathcal {A}}}_t \right) . \end{aligned}$$

From Section 12.3.3.3 in Filipović (2009) we recall that the distribution of \(\tau \), conditional on the event \(\left\{ \tau > t \right\} \) for \(t \le u\), is given by

$$\begin{aligned}&P \left( t < \tau \le u \,\bigg |\, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t \right) \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}\exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( \mathbf{1}_{\left\{ t < \tau \le u \right\} } \,\bigg |\, {{\mathcal {G}}}_{\infty } \right) \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}\exp \left\{ \int ^t_0 \lambda _s ds \right\} \left( \exp \left\{ - \int ^t_0 \lambda _s ds \right\} - \exp \left\{ - \int ^u_0 \lambda _s ds \right\} \right) \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}\left( 1 - \exp \left\{ - \int ^u_t \lambda _s ds \right\} \right) , \end{aligned}$$

which is the regular \({{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t\)-conditional distribution of \(\tau \) given \(\left\{ \tau >t \right\} \). For more details on regular conditional distributions the reader is referred to Section 4.1.4 in Filipović (2009). To obtain the density function, we differentiate with respect to \(u\) to obtain

$$\begin{aligned} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} , \end{aligned}$$
(19)

for \(u \ge t\). We now price the partial recovery at default bond

$$\begin{aligned} P^{p}_T(t) := S^{{{\delta _*}}}_t E \left( \frac{(\tau - T_{\beta (\tau )-1 })}{S^{{{\delta _*}}}_{\tau }} \mathbf{1}_{ \left\{ T_a < \tau \le T_b \right\} } \,\bigg |\, {{\mathcal {A}}}_t \right) . \end{aligned}$$

Using Eq. (19) and the Fubini theorem, we compute

$$\begin{aligned}&S^{{{\delta _*}}}_t E \left( \frac{\tau - T_{\beta (\tau )-1 }}{S^{{{\delta _*}}}_{\tau }} \mathbf{1}_{ \left\{ T_a < \tau \le T_b \right\} } \,\bigg |\, {{\mathcal {A}}}_t \right) \\&\quad = S^{{{\delta _*}}}_t E \left( \frac{f(\tau ) \mathbf{1}_{\left\{ T_a < \tau \le T_b \right\} } }{S^{{{\delta _*}}}_{\tau } } \,\bigg |\, {{\mathcal {A}}}_t \right) \\&\quad = E \left( E \left( f( \tau ) \frac{\alpha _t}{\alpha _{\tau }} \exp \left\{ - \int ^{\tau }_{t} r_s ds \right\} \mathbf{1}_{ \left\{ T_a < \tau \le T_b \right\} } \frac{Y_t}{Y_{\tau }} \,\bigg |\, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t \right) \,\bigg |\, {\mathcal {A}}_t \right) \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}E \left( \int ^{T_b}_{T_a} \tilde{f} (u) \exp \left\{ - \int ^u_t r_s ds \right\} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \frac{Y_t}{Y_u} du \,\bigg |\, {\mathcal {A}}_t \right) \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}\int ^{T_b}_{T_a} \tilde{f} (u) E \left( \exp \left\{ - \int ^u_t r_s ds \right\} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \frac{Y_t}{Y_u} \,\bigg |\, {\mathcal {A}}_t \right) du, \end{aligned}$$

where \(f(x)= (x-T_{\beta (x)-1})\) and \(\tilde{f}(x)= \frac{\alpha _t}{\alpha _x} f(x)\). From Corollary 3.2, we obtain

$$\begin{aligned}&E \left( \exp \left\{ - \int ^u_t r_s ds \right\} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \frac{Y_t}{Y_u} \,\bigg |\, {\mathcal {A}}_t \right) \end{aligned}$$
(20)
$$\begin{aligned}&\quad = E \left( \frac{ \lambda _u \exp \left\{ - \int ^u_t ( r_s + \lambda _s ) ds \right\} Y_t}{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) . \end{aligned}$$
(21)

Hence we conclude that

$$\begin{aligned} P^{p}_T(t) = {\mathbf{1}_{ \left\{ \tau > t \right\} }}Y_t \int ^T_t \tilde{f}(u) E \left( \frac{ \lambda _u \exp \left\{ - \int ^u_t ( r_s + \lambda _s ) ds \right\} }{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) du. \end{aligned}$$

We now discuss how to compute

$$\begin{aligned} E \left( \frac{ \lambda _u \exp \left\{ - \int ^u_t ( r_s + \lambda _s ) ds \right\} }{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) . \end{aligned}$$

Since we have

$$\begin{aligned}&\exp \left\{ - \int ^u_t ( r_s + \lambda _s ) ds \right\} \\&\quad = \exp \left\{ - \int ^u_t a_s ds - b \int ^u_t Z^1_s ds - d \int ^u_t Z^2_s ds - \int ^u_t f(Y_s) ds \right\} \end{aligned}$$

and

$$\begin{aligned} \lambda _u = a^{\lambda }_u + b^{\lambda } Z^1_u + c^{\lambda } f^{\lambda } ( Y_u) + d^{\lambda } Z^2_u, \end{aligned}$$

we have

$$\begin{aligned}&E \left( \exp \left\{ - \int ^u_t a_s ds - b \int ^u_t Z^1_s ds - d \int ^u_t Z^2_s - \int ^u_t f(Y_s) ds \right\} \frac{\lambda _u}{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) \\&\quad = \exp \left\{ - \int ^u_t a_s ds \right\} \left( a^{\lambda }_u E \left( \exp \left\{ - b \int ^u_t Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. \times \, E \left( \exp \left\{ - d \int ^u_t Z^2_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) E \left( \frac{ \exp \left\{ - \int ^u_t f(Y_s) ds \right\} }{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. +\, E \left( b^{\lambda } Z^1_u \exp \left\{ - b \int ^u_t Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) E \left( \exp \left\{ - d \int ^u_t Z^2_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. \times \,E \left( \frac{ \exp \left\{ - \int ^u_t f(Y_s) ds \right\} }{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. +\, E \left( \exp \left\{ - b \int ^u_t Z^1_s ds \right\} \vert {{\mathcal {G}}}_t \right) E \left( d^{\lambda } Z^2_u \exp \left\{ - d \int ^u_t Z^2_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. \times \,E \left( \frac{ \exp \left\{ - \int ^u_t f(Y_s) ds \right\} }{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. +\, E \left( \exp \left\{ - b \int ^u_t Z^1_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) E \left( \exp \left\{ - d \int ^u_t Z^2_s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \right. \\&\qquad \left. \times \, E \left( \frac{ c^{\lambda } f^2(Y_u) \exp \left\{ - \int ^u_t f(Y_s) ds \right\} }{Y_u} \,\bigg |\, {{\mathcal {G}}}_t \right) \right) , \end{aligned}$$

where all expectations can be computed using Propositions 7.3.8 and 7.3.9 in Baldeaux and Platen (2013). We remark that the third term in the CDS valuation formula can be computed as above, in this case \(f(\tau ) = 1\).

5 Credit Valuation Adjustment Under the Benchmark Approach

In this section, we discuss the computation of CVA, in the affine credit risk model introduced in Sect. 3. First, we introduce CVA as an extension of a CDS: assume two parties, A and C, have entered into a series of contracts, the aggregate value of which at time \(t\) is given by \(V_t\). We take the point of view of party A, and say that \(V_t >0\) if the aggregate value of the contracts at time \(t\) is profitable to A, and \(V_t <0\) if the aggregate value of the contracts is profitable to C. For ease of exposition, we assume that party A cannot default but C can, so we discuss unilateral CVA, though of course bilateral CVA can also be discussed under the benchmark approach using the techniques introduced in this paper.

Party A now approaches another party, say B, for protection on its portfolio \(V\) with C over the period \([0,T]\): in case C defaults, B pays the value of the part of the portfolio that is not recovered at the time of default, only if the value of the portfolio is positive to A, i.e. only if \(V_{\tau } >0\), where \(\tau \) denotes the time of default of C. Hence the payment at default is

$$\begin{aligned} ( 1- R) V^+_{\tau }, \end{aligned}$$

where \(R\) is the recovery rate and \(V^+_t := \max (V_t, 0)\). Again, for ease of exposition, we assume that B cannot default. Using the real world pricing formula, we obtain the real world price of this protection as

$$\begin{aligned} CVA_t := (1 - R) S^{{{\delta _*}}}_t E \left( \frac{V^+_{\tau }}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) , \end{aligned}$$
(22)

for \( t \ge 0\). It is crucial for CVA computations, that right-way exposure and wrong-way exposure are taken into account. This requires the modeling of a dependence structure between the portfolio process \(V\) and the time of default, \(\tau \): under the benchmark approach, the value of \(V\) depends on the numéraire, which is the NP, \(S^{{{\delta _*}}}\), and hence its stochastic drivers, \(Y\) and \(Z^1\). However, \(\tau \) can in general also be expected to depend on \(S^{{{\delta _*}}}\): if the NP drops, which affects the value of \(V\), a default of C can be more likely, or less likely, depending on the nature of company C. In the next section, we present an illustrative example including commodities. The exposure is called right-way if the value of \(V\) is negatively related to the credit quality of the counter party and wrong-way is defined analogously, see Cesari et al. (2009). Our specification of \(\lambda \), which takes into account \(Z^1\) and \(Y\) allows us to model this by choosing \(f^{\lambda }(x) =x\) or \(f^{\lambda }(x) = \frac{1}{x}\). This may appear as a somewhat artificial choice. However, it models the dependencies in the right directions and yields tractable formulas. Other choices are possible but would probably not be as tractable as the proposed one. We now consider the valuation of some simple contracts. We remark that, for simplicity, we set \(R=0\) in the remainder of the paper.

Firstly, we assume that \(V_t = S^{{{\delta _*}}}_t\) and that A has bought protection from B for the period \([0,T]\), then

$$\begin{aligned} CVA_t= & {} S^{{{\delta _*}}}_t E \left( \frac{V^+_{\tau }}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t P \left( t < \tau \le T \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( {\mathbf{1}_{ \left\{ \tau > t \right\} }}- {\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( 1 - {\mathbf{1}_{ \left\{ \tau > t \right\} }}{\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) . \end{aligned}$$

Now, we have

$$\begin{aligned} E \left( {\mathbf{1}_{ \left\{ \tau > t \right\} }}{\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right)= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( {\mathbf{1}_{ \left\{ \tau > t \right\} }}{\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( E \left( {\mathbf{1}_{ \left\{ \tau > T \right\} }}\,\bigg |\, {{\mathcal {G}}}_T \right) \,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\exp \left\{ \int ^t_0 \lambda _s ds \right\} E \left( \exp \left\{ - \int ^T_0 \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}E \left( \exp \left\{ - \int ^T_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) , \end{aligned}$$

where we used Lemma 3.2 with \(Y={\mathbf{1}_{ \left\{ \tau > T \right\} }}\) and Eq. (4). Finally,

$$\begin{aligned} CVA_t = {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( 1 - \exp \left\{ - \int ^T_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) , \end{aligned}$$

and we compute

$$\begin{aligned} E \left( \exp \left\{ - \int ^T_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) \end{aligned}$$

as in Sect. 4, since \(\lambda _t\) is a function of affine processes, and the relevant Laplace transforms are given in Propositions 7.3.8 and 7.3.9 of Baldeaux and Platen (2013).

Now assume that \(V_t = P_T(t)\), a zero coupon bond, which we priced in Sect. 3. Again we consider \(CVA\) over the period \([0,T]\)

$$\begin{aligned} CVA_t= & {} S^{{{\delta _*}}}_t E \left( \frac{V^+_{\tau } }{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {{\mathcal {A}}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( E \left( \frac{1}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_{\tau } \right) {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( \frac{ {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\left( S^{{{\delta _*}}}_t E \left( \frac{1}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) - S^{{{\delta _*}}}_t E \left( \frac{ {\mathbf{1}_{ \left\{ \tau > T \right\} }}}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\left( P_T (t) - P^0_T(t) \right) , \end{aligned}$$

so, conditional on the event \(\left\{ \tau > t \right\} \), we have represented CVA as the difference between a zero coupon bond and a zero recovery zero coupon bond. We remind the reader that the latter was priced in Sect. 4.

Next, we discuss the pricing of a European put option in the presence of counterparty risk. Recall that standard European put options were priced in Sect. 3. We use the density function from Eq. (19), the fact that \({\mathbf{1}_{ \left\{ \tau > t \right\} }}\) is \({{\mathcal {A}}}_t\)-measurable, and Corollary 3.2 to obtain

$$\begin{aligned}&\textit{CVA}_t = S^{{{\delta _*}}}_t E \left( \frac{V^+_{\tau }}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad =S^{{{\delta _*}}}_t E \left( \frac{p_{T,K}(\tau , Z^1_{\tau }, Y_{\tau }, S^{{{\delta _*}}}_{\tau } ) }{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad =S^{{{\delta _*}}}_t E \left( \frac{(K - S^{{{\delta _*}}}_T )^+}{S^{{{\delta _*}}}_T} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {{\mathcal {A}}}_t \right) \nonumber \\&\quad =S^{{{\delta _*}}}_t E \left( E \left( \frac{ ( K - S^{{{\delta _*}}}_T )^+ }{S^{{{\delta _*}}}_T} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t \right) \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad =S^{{{\delta _*}}}_t E \left( {\mathbf{1}_{ \left\{ \tau > t \right\} }}\int ^T_t \frac{( K - S^{{{\delta _*}}}_T )^+}{S^{{{\delta _*}}}_T} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} du \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \int ^T_t E \left( \frac{ ( K - S^{{{\delta _*}}}_T )^+ }{S^{{{\delta _*}}}_T} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) du \nonumber \\&\quad ={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \int ^T_t E \left( \frac{S^{{{\delta _*}}}_u}{S^{{{\delta _*}}}_u} E \left( \frac{(K - S^{{{\delta _*}}}_T )^+}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_u \right) \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) du \nonumber \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \int ^T_t E \left( \frac{p_{T,K} (u,Z^1_u, Y_u, S^{{{\delta _*}}}_u) }{S^{{{\delta _*}}}_u} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) du. \end{aligned}$$
(23)

In general, it seems difficult to simplify the above expression further. Essentially, this is due to the fact that our model incorporates wrong-way and right-way exposure, i.e. we allow for dependence between \(\tau \) and \(S^{{{\delta _*}}}\). Hence one would usually employ a Monte Carlo algorithm, see e.g. Cesari et al. (2009). We remark that in Section 6.3 in Baldeaux and Platen (2013), we derived the joint law of \(\left( \int ^u_t Y_s ds, Y_u\right) \), conditional on \(Y_t\), and in Section 6.4 in Baldeaux and Platen (2013), the joint law of \(\left( \int ^u_t \frac{ds}{Y_s}, Y_u\right) \) conditional on \(Y_t\), which are useful in developing respective Monte Carlo algorithms.

We now discuss the pricing of swaps in the presence of counterparty risk. In Sect. 3, we presented the value of a swap as a linear combination of zero coupon bonds. Hence, if market prices of zero coupon bonds are available, a model would not be required to price swaps in practice. In the presence of counterparty risk, this is different, as we now show. We set \(V_t = FS_{\kappa , T_0} (t)\), where \(FS_{\kappa , T_0} (t)\) is defined in Eq. (11), so we consider a swap with start date \(T_0\), and we focus on CVA for the period \([0,T]\) for \(T \le T_0\). We have

$$\begin{aligned} CVA_t:= & {} S^{{{\delta _*}}}_t E \left( \frac{V^{+}_{\tau }}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\= & {} S^{{{\delta _*}}}_t E \left( \frac{ ( FS_{\kappa , T_0} (\tau ) )^+ }{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \,, \end{aligned}$$
(24)

hence the market price of counterparty risk associated with a swap can be interpreted as a forward start swaption with random expiry date \(\tau \). Again, we use the density function from Eq. (19), the fact that \({\mathbf{1}_{ \left\{ \tau > t \right\} }}\) is \({{\mathcal {A}}}_t\)-measurable, and Corollary 3.2 to obtain

$$\begin{aligned}&S^{{{\delta _*}}}_t E \left( \frac{( FS_{\kappa , T_0} (\tau ) )^+}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad = S^{{{\delta _*}}}_t E \left( E \left( {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\frac{ ( FS_{\kappa , T_0} (\tau ) )^+ }{S^{{{\delta _*}}}_{\tau }} \,\bigg |\, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t \right) \,\bigg |\, {\mathcal {A}}_t \right) \end{aligned}$$
(25)
$$\begin{aligned}&\quad ={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( \int ^T_t \frac{ ( FS_{\kappa , T_0} (u) )^+ }{S^{{{\delta _*}}}_u} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} du \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad ={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( \int ^T_t \frac{( FS_{\kappa , T_0} (u) )^+}{S^{{{\delta _*}}}_u} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} du \,\bigg |\, {{\mathcal {G}}}_t \right) \nonumber \\&\quad ={\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \int ^T_t E \left( \frac{( FS_{\kappa , T_0} (u) )^+}{S^{{{\delta _*}}}_u} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) du. \end{aligned}$$
(26)

Hence, as for the European put, we need to resort to Monte Carlo methods to compute Eq. (26). This is due to the fact that accounting for right-way and wrong-way exposure makes it difficult to compute CVA analytically.

6 CVA for Commodities

We now consider counterparty risk for commodities. In particular, we consider the case where the counterparty C is directly affected by the value of the commodity underlying the transaction. For example, say the counterparty C is an airline, in which case it is clear that the company has a large exposure to the price of oil and could be interested in trading forward contracts on oil with company A, which is assumed to be default free. However, in case the price of oil rises, default of company C becomes more likely. Taking into account right-way and wrong-way exposure, it is important to recognize that the value of the commodity impacts both, the value of the transaction \(V\), assumed to be a forward on oil, but also the time of default \(\tau \). We hence model this under the benchmark approach following Du and Platen (2012b). In particular, we use \(S^{i, {{\delta _*}}}_t\) to denote the value of the NP at time \(t\), denominated in units of the \(i\)-th security. A general exchange price, which could be a number of units of currency \(i\) to be paid for one unit of currency \(j\), or a number of units of currency \(i\) to be paid for one unit of commodity \(j\) is then given by

$$\begin{aligned} X^{i,j}_t = \frac{S^{i,{{\delta _*}}}_t}{S^{j,{{\delta _*}}}_t}. \end{aligned}$$
(27)

In this section, currency \(i\) would be the domestic currency and commodity \(j\) the commodity of interest, so \(j\) could correspond to oil and \(i\) to US dollars. In particular, we note that if \(S^{i, {{\delta _*}}}_t\) appreciates or \(S^{j, {{\delta _*}}}_t\) depreciates, then \(X^{i,j}_t\) appreciates, so more units of currency \(i\), say US dollars, have to be paid for one unit of the commodity. We recall the minimal market model (MMM) as applied in Du and Platen (2012b). Though parsimonious, the model is tractable and in particular allows us to incorporate right-way and wrong-way exposure. In particular, we set

$$\begin{aligned} S^{k, {{\delta _*}}}_t = B^k_t Y^k_t A^k_t, \end{aligned}$$
(28)

where \(k \in \left\{ i,j \right\} \) and where

$$\begin{aligned} d Y^k_t = \xi ^k(1 - Y^k_t) dt + \sqrt{ \xi ^k Y^k_t} dW^k_t, \end{aligned}$$

\(k \in \left\{ i,j \right\} \), where \(W^i\) and \(W^j\) are independent \(\underline{{{\mathcal {G}}}}\)-Brownian motions. Furthermore,

$$\begin{aligned} A^k_t = A^k_0 \exp \left\{ \xi ^k t \right\} , \end{aligned}$$

and

$$\begin{aligned} B^k_t = \exp \left\{ \int ^t_0 r^k_s ds\right\} . \end{aligned}$$

Again, we remark that when discounting \(S^{k, {{\delta _*}}}\) and rescaling it using \(A^k\), we obtain a mean-reverting process, \(Y^k\). When considering a currency, say \(i\), \(r^i = \{ r^i_t, \, t \ge 0 \} \) is interpreted as a short rate process, and for commodities \(r^j = \{ r^j_t, \, t \ge 0 \} \) can be interpreted as the convenience yield process. Following Du and Platen (2012b), we set

$$\begin{aligned} r^i_t= & {} a^i + b^{ii} Y^i_t + b^{ij} Y^j_t,\\ r^j_t= & {} a^j + b^{ji} Y^i_t + b^{jj} Y^j_t, \end{aligned}$$

where \(a^i, a^j, b^{ii}, b^{ji}, b^{ij}, b^{jj}\) are nonnegative constants, and \(b^{ij}\) corresponds to the sensitivity of the short rate \(r^i\) to changes in \(Y^j\). In particular, we note that \(S^{i, {{\delta _*}}}\) and \(S^{j, {{\delta _*}}}\) are dependent, as they share common drivers. We are now in a position to price a standard forward contract, and recall the relevant result from Du and Platen (2012b). Recall that at initiation time \(t\), the forward price \(F^{i,j,T}_t\) of one unit of commodity \(j\) to be delivered at time \(T\), denominated in currency \(i\), is chosen so that the forward contract has no value. Using the real world pricing formula (1), we chose \(F^{i,j,T}_t\) so that

$$\begin{aligned} E \left( \frac{(X^{i,j}_T - F^{i,j,T}_t ) }{S^{i,{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) = 0. \end{aligned}$$
(29)

Solving Eq. (29) for \(F^{i,j,T}_t\) produces Theorem 3.1 from Du and Platen (2012b), which we now present.

Theorem 6.1

The real world price at inception time \(t \in [0,T]\) in units of the \(i\)-th currency, for one unit of the \(j\)-th commodity to be delivered at time \(T \in [0, \infty )\) equals

$$\begin{aligned} F^{i,j,T}_t = X^{i,j}_t \frac{P^j_T(t)}{P^i_T(t)}. \end{aligned}$$

We point out that \(P^i_T(t)\) corresponds to a zero coupon bond in currency \(i\), whereas \(P^j_T(t)\) is the time \(t\) value of the delivery of one unit of the \(j\)-th commodity at maturity \(T\), denominated in units of the commodity \(j\) itself. Furthermore, we need to know the value of the forward initiated at time \(t_0\), at an intermediate time, say \(t \in [t_0, T]\). The relevant formula is given in Theorem 3.2 in Du and Platen (2012b), which we now recall.

Theorem 6.2

The real world value \(U^{i,j,t_0,T}_t\) of a forward contract at time \(t\) for one unit of the \(j\)th commodity with initiation time \(t_0\) and maturity date \(T\) equals

$$\begin{aligned} U^{i,j,t_0,T}_t = P^i_T (t) \left( F^{i,j,T}_t - F^{i,j,T}_{t_0} \right) , \end{aligned}$$

when denominated in units of the \(i\)-th currency, \(t_0 \in [0,T]\), \(t \in [t_0, T]\), \(T \in [0, \infty )\).

We remark that for the model introduced in this section, we can derive closed-form solutions for forward prices and the value of forward contracts the way we did in Sect. 3.

Now we want to return to our counterparty risk example. As we had discussed before, the airline is more likely to default if the price of the commodity increases. Hence we propose the following model: we introduce an additional square-root process

$$\begin{aligned} d Z_t = \kappa ( \theta -Z_t) dt + \sigma \sqrt{Z_t} d W^k_t, \end{aligned}$$

where \(W^k\) is a \(\underline{{{\mathcal {G}}}}\)-Brownian motion independent of \(W^i\) and \(W^j\). The default intensity \(\lambda \) is modeled as follows:

$$\begin{aligned} \lambda _t = a^{\lambda }_t + b^{\lambda } Y^i_t + c^{\lambda } \frac{1}{Y^j_t} + d^{\lambda } Z_t, \end{aligned}$$
(30)

where \(b^{\lambda }, c^{\lambda }, d^{\lambda }\) are nonnegative constants and \(a^{\lambda }_{\cdot }\) is a nonnegative function. In particular, we note that if the main driver of \(S^{i, {{\delta _*}}}\), which is \(Y^i\), increases, then \(X^{i,j}_t\) and \(\lambda _t\) increase, i.e. default becomes more likely as the price of the commodity increases. Likewise, as the main driver of \(S^{j, {{\delta _*}}}_t\), which is \(Y^j_t\), decreases, then \(X^{i,j}_t\) and \(\lambda _t\) increase, i.e. default becomes more likely. We now consider \(CVA\) for \(V_t = U^{i,j,t_0,T}_t\) over the period \([0,T]\). We employ the density function from Eq. (19), the fact that \({\mathbf{1}_{ \left\{ \tau > t \right\} }}\) is \({{\mathcal {A}}}_t\)-measurable, and Corollary 3.2 to obtain

$$\begin{aligned}&\textit{CVA}_t =S^{i,{{\delta _*}}}_t E \left( \frac{V^+_{\tau }}{S^{i, {{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{i, {{\delta _*}}}_t E \left( \int ^T_t \frac{ ( U^{i,j,t_0,T}_{u})^+ }{S^{i, {{\delta _*}}}_u} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} du \,\bigg |\, {\mathcal {A}}_t \right) \nonumber \\&\quad = {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{i, {{\delta _*}}}_t \int ^T_t E \left( \frac{( U^{i,j,t_0,T}_u )^+}{S^{i,{{\delta _*}}}_u} \lambda _u \exp \left\{ - \int ^u_t \lambda _s ds \right\} \,\bigg |\, {{\mathcal {G}}}_t \right) du. \end{aligned}$$
(31)

Again, one needs to resort to Monte Carlo methods to compute (31), due to the fact that our model takes into account right-way and wrong-way exposure. We point out that prices of call and put options on futures on commodities were derived in Du and Platen (2012b), which can be used to reduce the cost of Monte Carlo simulation.

7 A Reduced-Form Model

The affine credit risk model presented in Sect. 3 is able to incorporate right-way and wrong-way exposure, and should hence be useful when performing CVA computations. However, as we noticed for many products, Monte Carlo algorithms need to be employed when performing computations. Though from e.g. Cesari et al. (2009) this should be expected, we aim to produce a reduced form model in this section, which is more tractable. The model assumes independence between default risk and financial risk. Though not necessarily satisfied for all transactions relevant to practice, this is a very tractable model and may help to provide reasonable CVA for important cases.

We hence modify the model from Sect. 3 as follows: firstly, we model \(S^{{{\delta _*}}}\) using the MMM, see Platen and Heath (2010), we set

$$\begin{aligned} d Y_t = ( 1- \eta Y_t ) dt + \sqrt{Y_t} dW_t, \end{aligned}$$

where \(W\) is a \(\underline{{{\mathcal {G}}}}\)-Brownian motion and we set

$$\begin{aligned} \alpha _t = \alpha _0 \exp \left\{ \eta t \right\} . \end{aligned}$$

A constant interest rate \(r \ge 0\) is employed for simplicity, so we have

$$\begin{aligned} B_t = \exp \left\{ r t \right\} . \end{aligned}$$

Next, we set \(\lambda _t = \lambda >0\), i.e. we employ a constant default intensity. The assumptions of Section 12.3 in Filipović (2009) are satisfied and we have

$$\begin{aligned} P ( \tau > t \, \vert \, {{\mathcal {G}}}_{\infty } ) = P( \tau > t \, \vert \, {{\mathcal {G}}}_t ) = \exp \left\{ - \lambda t \right\} \end{aligned}$$

and

$$\begin{aligned} P ( t < \tau \le u \, \vert \, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t ) = {\mathbf{1}_{ \left\{ \tau > t \right\} }}\left( 1 - \exp \left\{ - \lambda (u-t) \right\} \right) , \end{aligned}$$

so the conditional density of \(\tau \) given \(\tau >t\) is exponential with parameter \(\lambda \), i.e.

$$\begin{aligned} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\lambda \exp \left\{ - \lambda ( u-t) \right\} . \end{aligned}$$
(32)

This facilitates computations greatly, as we now demonstrate.

Assume that \(V_t \ge 0, \, \forall \, t \in [0,T]\), and that the portfolio \(V\) does not generate any cash flows on the interval \([0,T]\). Furthermore, we assume that \(\frac{V}{S^{{{\delta _*}}}}\) forms an \(( \underline{{\mathcal { A}}}, P)\)-martingale,

$$\begin{aligned} CVA_t= & {} S^{{{\delta _*}}}_t E \left( \frac{V^{+}_{\tau }}{S_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( E \left( \frac{V^{+}_{\tau }}{S_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t \right) \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( \int ^T_t \frac{V^+_u}{S^{{{\delta _*}}}_u} \lambda \exp \left\{ - \lambda ( u-t) \right\} du \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t \int ^T_t E \left( \frac{V^+_u}{S^{{{\delta _*}}}_u} \,\bigg |\, {\mathcal {A}}_t \right) \lambda \exp \left\{ - \lambda (u-t) \right\} du. \end{aligned}$$

Since \(V^+_t = V_t\), one can compute

$$\begin{aligned} S^{{{\delta _*}}}_t E \left( \frac{V^+_u}{S^{{{\delta _*}}}_u} \,\bigg |\, {\mathcal {A}}_t \right)= & {} S^{{{\delta _*}}}_t E \left( \frac{V_u}{S^{{{\delta _*}}}_u} \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( E \left( \frac{V_T}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_u \right) {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( \frac{V_T}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} V_t. \end{aligned}$$

Hence we get

$$\begin{aligned} CVA_t = {\mathbf{1}_{ \left\{ \tau > t \right\} }}V_t \left( 1 - \exp \left\{ - \lambda ( T - t ) \right\} \right) . \end{aligned}$$
(33)

We point out that Eq. (33) can be used e.g. to deal with zero coupon bonds, European call options and swaptions, but not, for example, to deal with swaps, as the latter can assume negative values. We do, however, recall our previous observation that there exists a close link with forward start swaptions, which we now exploit. Set \(V_t = FS_{\kappa , T_0} (t)\) and consider \(CVA\) over the period \([0,T]\), where \(T \le T_0\), then using the density in Eq. (32) we obtain

$$\begin{aligned} CVA_t= & {} S^{{{\delta _*}}}_t E \left( \frac{V^{+}_{\tau }}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( E \left( \frac{V^{+}_{\tau }}{S^{{{\delta _*}}}_{\tau }} {\mathbf{1}_{ \left\{ t < \tau \le T \right\} }}\,\bigg |\, {{\mathcal {G}}}_{\infty } \vee {{\mathcal {H}}}_t \right) \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}S^{{{\delta _*}}}_t E \left( \int ^T_t \frac{V^+_u}{S^{{{\delta _*}}}_u} \lambda \exp \left\{ - \lambda ( u - t) \right\} du \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\int ^T_t S^{{{\delta _*}}}_t E \left( \frac{V^+_u}{S^{{{\delta _*}}}_u} \,\bigg |\, {\mathcal {A}}_t \right) \lambda \exp \left\{ - \lambda (u-t) \right\} du\\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\int ^T_t S^{{{\delta _*}}}_t E \left( \frac{( FS_{\kappa , T_0} (u) )^+}{S^{{{\delta _*}}}_u} \,\bigg |\, {\mathcal {A}}_t \right) \lambda \exp \left\{ - \lambda (u - t) \right\} du\\= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\int ^T_t PS_{\kappa , T_0, u} (t) \lambda \exp \left\{ - \lambda (u - t) \right\} du. \end{aligned}$$

We remark that under the minimal market model (MMM), see Platen and Heath (2010) or Baldeaux and Platen (2013), the value of a forward start swaption amounts to the computation of a one-dimensional integral. From Sect. 3, we recall

$$\begin{aligned} PS_{\kappa , T_0, T} (t)= & {} S^{{{\delta _*}}}_t E \left( \frac{ ( FS_{ \kappa , T_0} (T) )^+ }{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) \\= & {} S^{{{\delta _*}}}_t E \left( \frac{ ( P_{T_0} (T) - \sum ^n_{j=1} c_j P_{T_j} (T) )^+}{S^{{{\delta _*}}}_T} \,\bigg |\, {\mathcal {A}}_t \right) . \end{aligned}$$

For the reduced form model, \(\bar{S}^{{{\delta _*}}}_t = \frac{S^{{{\delta _*}}}_t}{B_t}\) is a time-changed squared Bessel process of dimension four, the transition density of which is known in closed-form, see Platen and Heath (2010):

$$\begin{aligned}&p_4 (\varphi (t),x;\varphi (T),y)\\&\quad = \frac{1}{2(\varphi (T)-\varphi (t))} \left( \frac{y}{x}\right) ^{\frac{1}{2}} \,\exp \left\{ - \frac{x+y}{2(\varphi (T)-\varphi (t))}\right\} \,I_{1} \left( \frac{\sqrt{x\,y}}{\varphi (T)-\varphi (t)}\right) \end{aligned}$$

with \(\varphi (t) = \frac{\alpha _0}{4} ( \exp \left\{ \eta t \right\} - 1)\). Furthermore, it can be shown that

$$\begin{aligned} P_T(t) = \exp \left\{ - r(T-t) \right\} \left( 1 - \exp \left\{ - \frac{\bar{S}^{{{\delta _*}}}_t}{2 ( \varphi (T) - \varphi (t) )} \right\} \right) , \end{aligned}$$

see e.g. Platen and Heath (2010). We define

$$\begin{aligned} f(t,T,y) = \exp \left\{ - r(T-t) \right\} \left( 1 - \exp \left\{ - \frac{y}{2 ( \varphi (T) - \varphi (t) ) } \right\} \right) . \end{aligned}$$

Hence we get

$$\begin{aligned}&PS_{\kappa , T_0, T}(t) = \bar{S}^{{{\delta _*}}}_t \exp \left\{ - r (T -t) \right\} \\&\quad \int ^{\infty }_0 \frac{(f(T, T_0, y) - \sum ^n_{j=1} c_j f(T,T_j,y))}{y} p_4 ( \varphi (t), \bar{S}^{{{\delta _*}}}_t, \varphi (T), y) dy, \end{aligned}$$

and regarding CVA, we obtain

$$\begin{aligned} CVA_t= & {} {\mathbf{1}_{ \left\{ \tau > t \right\} }}\bar{S}^{{{\delta _*}}}_t \int ^T_t \int ^{\infty }_0 \exp \left\{ - ( r +\lambda ) (u-t) \right\} \\&\times \frac{( f(u,T_0,y) - \sum ^n_{j=1} c_j f(u,T_j,y) )^+}{y} p_4 ( \varphi (t), \bar{S}^{{{\delta _*}}}_t, \varphi (u), y ) \lambda dy du. \end{aligned}$$

Hence the CVA associated with a swap can be expressed in terms of a two-dimensional integral, which can be evaluated using Monte Carlo methods. We now illustrate this using the following example, where we choose the following set of parameters for the NP:

$$\begin{aligned} S=2.3, r=0.01, \alpha _0=10.0483, \eta =0.0528. \end{aligned}$$
Fig. 1
figure 1

CVA of a swap for different values of \(\lambda \)

Full size image

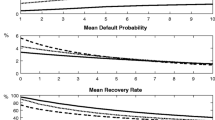
Furthermore, we choose \(T=2\), \(n=3\) and \(T_0=2\), \(T_1=3\), \(T_2=4\), \(T_3=5\) and \(c=0.2\). For \(\lambda =0.05, 0.1, 0.15, 0.2, 0.25, 0.3\) we obtain the values \(0.0440\), \(0.0838\), \(0.1196\), \(0.1521\), \(0.1815\), \(0.2081\), see Fig. 1. The value of the swap at time \(t=0\) with no probability of default is \(0.4703\). We have shown that CVA can be made much better accessible to Monte Carlo methods by employing highly tractable affine models. For economic and other reasons one has often rather clear views on real world default intensities and dependencies. By using the benchmark approach this is sufficient and the models become also more realistic in the long run. Most importantly, one has not to make questionable assumptions, e.g. about “risk neutral” default intensities and “risk neutral” dependencies.