Does decision error decrease with risk aversion?

Abstract

There is substantial evidence that risky decision-making involves a stochastic error process. The literature has adopted different approaches to address this issue, however, risk preferences are not uniquely identified by the most popular methods; decision error is not predicted to monotonically decrease with risk aversion. This paper reports the results of an experiment that elicits risk preferences to identify risk averse individuals and evaluates the frequency the stochastically dominant of two lotteries is chosen. Risk averse subjects exhibit a strong preference for dominant lotteries. More importantly, violations are consistent with stochastic decision error that decreases with risk aversion.

1 Introduction

While expected utility theory has been the dominant approach taken by economists to modeling decision-making under uncertainty for the last half century, it is not beyond criticism. Among the various discrepancies identified in the experimental literature, several studies (Ballinger and Wilcox 1997; Hey 1995; Hey and Orme 1994; Harless and Camerer 1994; Loomes et al. 2002; Wilcox 1993) have reported results that indicate choice under risk involves a stochastic component, which is unaccounted for by any deterministic choice theory.¹ For instance, when faced with repeated trials of choices between risky assets, subjects frequently make contradicting decisions for the same choice pair. This has motivated several different approaches to modeling the stochastic error process, originating from psychophysics (Fechner 1860) and psychometrics (Thurston 1927). To date, the stochastic process has been modeled as a ‘trembling hand’ (Harless and Camerer 1994), traditional white noise (Fechner 1860; Luce 1959), and random preferences (Becker et al. 1963). The most popular models, however, fail to translate what it means to be ‘more risk averse’, as defined by Pratt (1964), to stochastic choice under risk; a more risk averse individual is not necessarily more likely to choose the safer of two assets with equivalent expected returns. On the other hand, less popular approaches not only account for random decision error, but predict that it is decreasing in risk aversion. While this is a theoretically appealing property of stochastic models of risky decision-making, it is still an open empirical question whether this is an accurate depiction of individual behavior.

By far, the most popular approaches to account for stochastic decision error in the literature are the Fechner (1860) and Luce (1959) models.² These models assume that given a choice over two risky assets, an individual chooses their most preferred asset with some probability determined by the difference in expected utilities. The issue that arises is that for commonly adopted specifications of the utility function, such as constant absolute risk aversion (CARA) and constant relative risk aversion (CRRA), the difference in expected utilities is not always monotonically increasing in risk aversion. This can be problematic when these models are used to estimate risk preferences, since risk preferences may not be uniquely identified in such models; such stochastic models of risk preference are not ‘monontone’ (Apesteguia and Ballester 2016). However, this problem can be avoided by incorporating the less popular mean-variance specification of utility into a standard white noise model or by employing a random preference specification of the stochastic error process in conjunction with CARA or CRRA preference specifications.³ In either case, an increase in risk aversion implies a decrease in decision error.

This paper reports the results of an experiment designed to test the hypothesis that an increase in risk aversion should result in a reduction in decision error. To do so, the experimental design exploits the theoretical equivalence of risk aversion and second-order stochastic dominance (Hadar and Russell 1969; Hanoch and Levy 1969; Rothschild and Stiglitz 1970). Herein after stochastic dominance refers to second-order stochastic dominance, as opposed to first-order stochastic dominance. That is, given a choice between two risky assets such that one asset is a mean-preserving spread of the other, an individual with risk averse preferences should prefer the safer asset. Accordingly, the experiment presents subjects with a series of pairwise choices between risky assets where one asset stochastically dominates the other. The key feature of this task is that all risk averse subjects should make the same choice for each lottery pair. Hence, the experiment elicits risk preferences to identify risk averse subjects and their degree of risk aversion. This permits an investigation as to whether the error rate is decreasing in risk aversion.

The most common mechanism used by experimental economists to elicit risk preferences is a multiple price list (MPL) (Andersen et al. 2006).⁴ The MPL requires subjects to make a series of pairwise choices between a risky and a safe option. As subjects proceed through the series, the expected value of the risky option is increased to induce them to switch from the safe to the risky option. The point at which a subject switches provides an interval estimate of the subject’s underlying risk preference. The experiment implemented two formats of the MPL to elicit risk preferences, a probability variation (PV) format and a reward variation (RV) format. Both formats involved a series of 10 decisions between $5 or a lottery. The PV format increased the expected return of the lottery by increasing the probability of a return from 0.10 to 1.0 in increments of 0.10, holding the possible returns constant at $0 or $10. The RV format increased the expected return of the lottery by increasing the high return from $2.00 to $20.00 in $2.00 increments, holding the probability of a return constant at 0.50.⁵ All subjects were given both the PV and RV formats of the MPL. The analysis identifies both the direction and strength of subjects’ risk preferences using their choices in the PV and RV formats of the MPL.

All subjects were also presented with a third MPL that was designed to determine the frequency risk averse subjects choose the stochastically dominant of two risky assets.⁶ In the lottery variation (LV) format, subjects faced a series of 10 pairwise choices between the risky options from the PV and RV formats. Each pair of lotteries had equivalent expected returns but different levels of risk. As subjects proceeded through this series, initially the RV lottery dominated the PV lottery and then vice versa. Thus, risk averse subjects should initially choose the RV lottery for the first four decisions and then switch to choosing the PV lottery for all subsequent decisions. Subjects’ decisions from all three formats of the MPL were then combined to test whether the error rate in the LV format decreased with risk aversion, as elicited by the PV and RV formats.

Overall, most subjects were consistently risk averse both across and within the PV and RV formats.⁷ Moreover, the distribution of choices in the LV format for risk averse subjects was heavily skewed towards a preference for dominant lotteries with the modal pattern of behavior being to choose all 10 dominant lotteries. Hence, risk averse subjects exhibited a strong preference for dominant lotteries, as predicted. Still, there were a substantial amount of discrepancies; only about a third of risk averse subjects chose all 10 dominant lotteries. However, such violations of stochastic dominance are to be expected given a stochastic error component to decision-making. More importantly, there is significant negative correlation between the error rate and the level of risk aversion. Hence, observed behavior supports the adoption of ‘monontone’ stochastic error models of risk preference.

The remainder of the paper is organized as follows. Section 2 presents the theoretical framework to establish testable hypotheses. Section 3 describes the experimental design. Section 4 presents the results from the experimental sessions. Section 5 summarizes the results and discusses their implications.

2 Theoretical framework

For clarity, the following section will briefly discuss the distributional properties required to satisfy stochastic dominance and the associated equivalence to maximizing the value function of an individual with concave preferences. Finally, subjects’ ability to make mistakes is accounted for and it is demonstrated that for a particular specification of the error process, decision error is decreasing in the degree of risk aversion. The theoretical framework provides the necessary foundation to analyze the choices made in the experimental setting.

2.1 Stochastic dominance of Bernoulli random variables

Consider a choice between two risky assets, $k =$ A or B, with equivalent expected returns. The return, R, of each asset is assumed to be a Bernoulli random variable where $R = R_k$ with probability $p_k$ and $R = 0$ with probability $1 - p_k$. The expected return from an asset is $p_kR_k$ and is assumed to be equivalent across assets. Now consider how the rules of stochastic dominance apply to the returns on the two risky assets. Each return has a cumulative distribution function, $F_k(R) = 1 - p_k$ if $0 \le R < R_k$ and $F_k(R) = 1$ if $R \ge R_k$. Following Hadar and Russell (1969) and Rothschild and Stiglitz (1970), asset A is said to stochastically dominate asset B iff

$$ \int\limits _{0}^{R_A} [F_B(R) - F_A(R)]dR \ge 0 \qquad {\text {for\;all\;R, with\,at\,least\,one\,strict\,inequality.}}$$

Thus when $R_B$ exceeds $R_A$ such that the assets have equivalent expected returns, $p_BR_B = p_AR_A$, asset A dominates asset B.

2.2 Concavity of preferences and stochastic dominance

Let agent i’s expected valuation from asset k be $EV_i = p_kV_i(R_k)$, where $V_i(R_k)$ is a monotonically increasing function of $R_k$, $V_i'(R_k) > 0$.⁸ If $V_i(R_k)$ is concave, $V_i''(R_k) < 0$, then agent i is risk averse; if $V_i(R_k)$ is convex, $V_i''(R_k) > 0$, then agent i is risk seeking; if $V_i(R_k)$ is linear, $V_i''(R_k) = 0$, then agent i is risk neutral.

When $R_{B}$ exceeds $R_A$, while each asset still has the same expected return, $E[R] = p_BR_B = p_AR_A$, the expected valuation of asset A is greater than asset B, $EV_{A} > EV_{B}$, for a globally risk averse agent.

Hence, the same condition that generates stochastic dominance generates maximization of the expected valuation for a globally risk averse agent. For equivalent expected returns, the asset with the lower potential return but greater chance of success dominates the other asset and should be preferred by a globally risk averse agent. This is the first hypothesis to be tested.

Hypothesis 1

For equivalent expected returns, if asset k stochastically dominates the alternative when the returns are Bernoulli random variables, then a risk averse agent should choose asset k.

2.3 Accounting for decision error

Hypothesis 1 implies risk averse agents should always satisfy stochastic dominance when choosing between risky assets with equivalent expected returns. A more likely case is that an agent will make mistakes. Previous literature (Ballinger and Wilcox 1997; Blavatskyy 2007; Hey 1995; Hey and Orme 1994; Loomes et al. 2002; McFadden 1974; Wilcox 1993) assumes each agent i maximizes her stochastic expected valuation from asset k, $EV_i(R_k) = p_kV_i(R_k) + \varepsilon _{ik}$, where $\varepsilon _{ik}$ is a stochastic noise parameter. That is, agent i formulates a noisy estimate of her expected valuation. One may think of the noise parameter as capturing the cognitive cost associated with refining one’s estimate of the expected valuation (Smith and Walker 1993). This formulation changes agent i’s decision rule such that she does not always choose the dominant lottery, rather the decision becomes stochastic. If asset A dominates asset B, then an agent will choose asset A iff:

$$EV_i(R_A) = p_AV_i(R_A) + \varepsilon _{iA} > p_BV(R_B) + \varepsilon _{iB} = EV_i(R_B) $$

Then the probability that agent i chooses A can be written as

$$P[p_AV_i(R_A) - p_BV_i(R_B) > \varepsilon _i]$$

(1)

where $\varepsilon _i = \varepsilon _{iB} - \varepsilon _{iA}$ such that $\varepsilon _i \sim (0, \sigma _i)$; adopting the Fechner (1860) model of stochastic choice under risk. The decision rule in Eq. (1) says that the probability an agent chooses the dominant asset is equal to the probability that the difference in expected valuations exceeds the noise. The issue that arises is the difference in expected valuations is not necessarily monotonically increasing in risk aversion.

Fig. 1

Difference in CRRA (left) and mean-variance (right) valuations by risk aversion coefficient

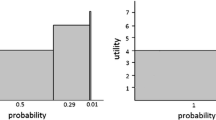
For example, suppose the assumed valuation specification is CRRA preferences, as is common practice in the literature. The left graph in Fig. 1 plots the difference in expected valuations, $|p_{PV}R_{PV}^{1 - r_i} - p_{RV}R_{RV}^{1 - r_i}|$, as a function of the coefficient of CRRA for three of the lottery pairs used in the experiment. The graph demonstrates the difference in expected valuations is not monotonically increasing in risk aversion. Hence, the likelihood a risk averse individual chooses the stochastically dominant of two assets is not necessarily greater for someone with greater aversion to risk using a white noise approach to modeling decision error with CRRA preferences (Wilcox 2011). The same is true for other common specifications of the value function, such as CARA.

An exception to this problem with Fechner white noise models, however, is the case of mean-variance valuations. This can be seen in the right graph in Fig. 1, which plots the difference in mean-variance valuations, $|r_i(p_{PV}(1-p_{PV})R_{PV}^2 - p_{RV}(1-p_{RV})R_{RV}^2)|$, as a function of the coefficient of risk aversion for the same three lottery pairs. The graph demonstrates the difference in mean-variance valuations is monotonically increasing in risk aversion. Hence, risk preferences are uniquely identified when mean-variance preferences are incorporated into a white noise model; such a model is ‘monontone’.⁹ In this case, decision error should decrease with greater aversion to risk. This is the second hypothesis to be tested.

Hypothesis 2

The likelihood of a risk averse agent choosing the stochastically dominant asset increases with the magnitude of risk aversion.

3 Experimental design

Table 1 Decisions for the MPL formats

The experiments were designed to investigate the extent to which risk averse subjects satisfy stochastic dominance when choosing between two lotteries and whether errors are decreasing in risk aversion. Since risk preferences must be identified, subjects were presented with two formats of a risk preference elicitation mechanism, PV and RV, in which they faced a menu of 10 choices between a guaranteed $5 and a lottery (Bruner 2009). In either format, as subjects proceed through the menu the expected return from the lottery increases to induce the subject to switch from the safe to the risky option. The PV format increases the expected return by increasing the probability of a return from 0.10 to 1.0 in increments of 0.10, holding the possible returns constant at $0 or $10. The RV format increases the expected return by increasing the high return from $2.00 to $20.00 in $2.00 increments, holding the probability of a return constant at 0.50.¹⁰ Table 1 presents the decisions for the PV and RV formats. In either format, the point at which a subject switches from the safe to the risky option provides an interval estimate of the subject’s risk preference.

In order to test whether decision error decreases with risk aversion, subjects were also presented with a LV format shown in Table 1. The LV format consisted of a menu of 10 choices between the previously described lotteries in the PV and RV formats. Although the two lotteries had equivalent expected returns for each decision, they differed in their levels of risk. The RV lottery is safer for the first four decisions and the PV lottery is safer for the last five decisions. The analysis required a within-subjects design; subjects were presented with all three decision tasks. As hypothesis 1 indicates, risk averse subjects should choose the dominant lottery for each decision since it has a higher expected valuation. Hypothesis 2 implies that decision error should be decreasing in risk aversion. Hence, the stronger a subject’s revealed risk aversion is in the PV and RV formats, the fewer times they should violate stochastic dominance in the LV format.

Table 2 Experimental design

Sessions consisted of three stages. In each stage, one of the three formats was presented to a subject. Subjects were presented with all three elicitation formats; thus subjects made 30 decisions in the experiment. In order to control for order effects (Harrison et al. 2005), the order in which the three formats were presented was randomized across subjects yielding six orthogonal treatments.¹¹ Table 2 presents the experimental design.

Subjects were informed in advance that they would be making 30 decisions, 10 in each of the three stages. Furthermore, subjects were told that only one of their decisions would determine their earnings in the experiment.¹² After completion of the final stage, subjects were shown the stage and the decision that was selected for payment. Subjects were paid individually in private.

Subjects were recruited by email via the lab’s Online Recruitment System for Experimental Economics (ORSEE) (Greiner 2004). The sessions were programmed and conducted with the software Z-Tree (Fischbacher 2007). Experimental sessions lasted approximately 35 mins. The average earnings were $12 including a $5 show-up fee. A total of 106 subjects participated in the experiment.

4 Analysis and results

Since hypothesis 1 neglects decision error, it implies risk averse subjects should choose the dominant lottery for each decision in the LV format. Alternatively, hypothesis 2 explicitly includes ‘monotonic’ decision error and predicts it should decrease with risk aversion. Thus, the direction and strength of risk preferences must first be determined, using subject’s choices in the PV and RV formats. Then the elicited risk preferences are used to predict behavior in the LV format.

4.1 Elicited risk preferences

Table 3 Risk preference classification based on lottery choices

Since subjects make 10 decisions in each format, it is possible to construct bounds on the implied risk aversion parameter based on the number times the safe option was chosen. Table 3 shows the ranges of the implied risk aversion parameter in columns 2 and 3 for the PV and the RV formats, respectively, assuming CRRA preferences.¹³ Similar to previous findings, the majority of subjects exhibited risk aversion; 76 and 78 % of subjects chose the safe option five or more times in the PV and the RV formats, respectively.¹⁴ Moreover, there are a substantial number of subject whose implied risk aversion parameter is in the decreasing portions of the left graph in Fig. 1.¹⁵

Consistent with a stochastic error process in decision-making, however, there were inconsistencies in elicited risk preferences. 18 subjects behaved inconsistently across formats; nine subjects only exhibited risk aversion in the PV format and another nine subjects only exhibited risk aversion in the RV format. Furthermore, 11 subjects behaved inconsistently within a format by switching from the safe to the risky option more than once.¹⁶ There were 64 subjects that exhibited across both formats and consistently within each format. The remaining 13 subjects exhibited risk loving preferences across both formats.

Nonetheless, probabilistic decision-making implies risk preferences are measured with error.¹⁷ To minimize the associated attenuation bias in the subsequent analysis, the average number of safe choices made across formats is used to identify risk preferences. The implied distribution of risk preferences when the number of safe choices are averaged across the PV and RV formats is reported in the sixth column of Table 3. In this case, 79 out of 106 subjects exhibited risk aversion, averaging 5 or more safe choices.

4.2 Choices in LV format

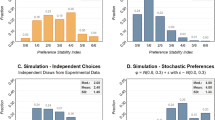
According to hypothesis 1, risk averse subjects should prefer the dominant lottery for each decision in the LV format. Figure 2 presents distributions of the number of dominant lotteries chosen by subjects in the LV format. The upper left graph plots the distribution of choices for all 106 subjects, while the upper right graph plots the distribution for the restricted sample of 79 risk averse subjects. Since the majority of subjects were risk averse, the distributions are quite similar. In either case, the distribution is heavily skewed towards a preference for dominant lotteries with the modal pattern of behavior being to choose all 10 dominant lotteries. So it appears risk averse subjects prefer dominant assets, as predicted. Still, there are a substantial amount discrepancies; only about a third of risk averse subjects choose dominant assets every time.

Fig. 2

Distribution of number of dominant lotteries chosen

According to hypothesis 2, however, noisiness in the expected valuation of lotteries should result in decision error, the likelihood of which should decrease with the degree of risk aversion. To investigate this hypothesis, the restricted sample of risk averse subjects is divided into two sub-samples based on degree of risk aversion. There were 46 subjects that averaged between 5 and 7 safe choices in the PV and RV formats, which are classified as low risk aversion, and 33 subjects that averaged more than 7 safe choices, which are classified as high risk aversion.¹⁸ The lower left and right graphs in Fig. 2 present the distributions of choices for low and high risk aversion subjects, respectively. Not only is the former distribution more dispersed, but it lacks an obvious modal pattern of behavior, whereas nearly half of the high risk aversion subjects chose all 10 dominant lotteries. This is consistent with decisions involving a stochastic error process that is decreasing in risk aversion.

Fig. 3

Error rate across decisions

To explore this possibility further, Fig. 3 plots the error rate in LV lottery choices for low and high risk aversion subjects across decisions. The error rate is calculated as the percentage of times the dominated lottery was chosen. For every decision the error rate is lower for high risk aversion subjects relative to low risk aversion subjects. Thus, not only are high risk aversion subjects less likely to make errors overall, they are less likely to error on any decision.

Fig. 4

Error rate by risk aversion

Figure 4 plots the error rate based on degree of risk aversion (i.e., the average number of safe choices in the PV and RV formats). The numerical labels report the number of subjects that exhibited each behavior. As the trend line indicates, there is a negative correlation between decision error and risk aversion. Figure 4 reports both the Pearson and the Spearman correlation coefficients. The correlation coefficients are both significant and quite similar, suggesting there is a strong inverse relationship between risk aversion and decision error that is not only monotonic, as predicted by hypothesis 2, but also linear, as depicted in Fig. 1.¹⁹

5 Discussion

The question raised at the outset was whether decision error decreases with risk aversion? The results of an experiment designed to answer this question are reported. Risk preferences were elicited and used to explain the error rate of subjects faced with a series of pairwise choices between lotteries with equivalent expected returns but different levels of risk, such that one dominates the other (i.e., one lottery is a mean-preserving spread of the other). The modal pattern of behavior among risk averse subjects was to choose all 10 of the dominant lotteries. Moreover, the distribution of choices for risk averse subjects was skewed towards dominant lotteries. Hence, risk averse subjects displayed a clear preference for dominant lotteries. Still, there were a nontrivial number of violations of stochastic dominance; only about a third of subjects chose all 10 dominant lotteries. However, such violations of stochastic dominance are to be expected given a stochastic error component to decision-making. More importantly, there is significant negative correlation between the error rate and the level of risk aversion, suggesting decision error does indeed decrease with risk aversion.

A related argument put forward by Smith and Walker (1993) regarding decision cost and decision rewards has stimulated the literature to place considerable attention on modeling decision cost and decision error (Blavatskyy 2007; Ballinger and Wilcox 1997; Buschena and Zilberman 2000; Hey 1995; Loomes et al. 2002). Wilcox (1993) exploits heterogeneity in decision costs to demonstrate that error rates increase as the ratio of decision rewards to decision costs declines. This study approaches the problem from the reward side, exploiting heterogeneity in preferences to observe reward heterogeneity, to further demonstrate the error rate increases as the benefit-cost ratio declines. The growing and consistent evidence suggests that the argument made by Smith and Walker (1993) has merit.

The present findings have significant implications when it comes to modeling the stochastic error process in risky decision-making. The literature has modeled the stochastic error process as a ‘trembling hand’ (Harless and Camerer 1994), traditional white noise (Fechner 1860; Luce 1959), and random preferences (Becker et al. 1963). By far, the most popular approach in the literature is a traditional white noise model (Fechner 1860; Luce 1959).²⁰ This approach assumes that given a choice over two risky assets, an individual chooses their most preferred asset with some probability determined by the difference in expected utilities. The issue that arises is that for commonly adopted specifications of the utility function, such as CARA and CRRA, the difference in expected utilities is not always monotonically increasing in risk aversion. So someone who is more risk averse is not necessarily more likely to choose the safer of two risky assets with equivalent expected returns. Not only is this theoretically unappealing, but contradicts the observed behavior in this experiment.

There are two possible remedies to address the issue, as shown by Apesteguia and Ballester (2016), that result in ‘monontone’ stochastic models of risky decision-making. The first is to employ a mean-variance specification of the utility function in a white noise model. Although such a specification is not particularly popular in the economics literature, it is widely adopted in the finance literature. The alternative is to use a random preferences approach to modeling the stochastic error process, which permits more popular specifications of the utility function. Despite the lack of prominence in the literature, random preferences have been used as an alternative to classic microeconometric approach (Loomes and Sugden 1995, 1998; Carbone 1998; Loomes et al. 2002; Wilcox 2011).²¹ Neither approach is obviously superior; both have their advantages. The former is likely to be more familiar and, hence, easier to adopt, while the latter offers more flexibility when choosing the preference function. It remains a matter of choice as to which approach is utilized in future research.