Abstract
Particular gradient elasticity models arise as limits of Mindlin’s micro-structured elastic materials, when the micro-deformation is assumed to be a function of the classical displacement gradient. In this case, the only independent kinematical degrees of freedom in the internal points of the continuum are the classical ones, reflected by the displacement field. The present work addresses a class of gradient elasticity models, including those of Mindlin, in the context of a continuum theory without balance laws of double-forces and without parts of stresses being left indeterminate. This is accomplished by using a non-conventional thermodynamic framework. The resulting models are restated as classical continua with non-classical body and non-classical inertial forces. The new interpretation suggests a definition of the appropriate boundary conditions in a different way than usually done in references addressing this subject. Numerical examples involving the axial motion of a gradient elastic bar possessing micro-stiffness and micro-inertia are studied in detail to illustrate the behavior of the above models.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The micro-structured elastic material of Mindlin [19] or the micromorphic elastic continuum of Eringen (cf. [11] and the references cited there), are examples of continua with more kinematical degrees of freedom than in classical continua. The additional kinematical degrees of freedom are expressed in terms of a micro-deformation field. Accordingly, higher-order stresses, the so-called double-stresses, which are conjugate to the micro-deformation variables, are required in the theory and the classical stresses are not anymore symmetric. But otherwise, it seems that usual thermodynamics is the appropriate framework to address such continua.
For the micro-structured elastic materials it is worthwhile to note that Mindlin [19] established the stress-equations of motion and the related boundary conditions, by employing Hamilton’s variational principle. Characteristic for this principle are the assumed potential and kinetic energies. There are some particular cases of interest, which result as limits when the micro-deformation in micro-structured elastic materials is constrained to be a function of the macro-deformation. Mindlin [19] and Mindlin and Eshel [20] discussed these cases, which we call here Mindlin’s gradient elasticity models, by introducing kinetic energy-density, a new potential energy function, new stresses and volume forces and employing, once again, Hamilton’s principle to establish the stress-equations of motion and the associated boundary conditions. Evidently, Mindlin [19] and Mindlin and Eshel [20] derived the models for the constrained geometry without specifying the kind of the employed forces. From the context it might be presumed that their approach is within a framework with balance laws of double-forces. In any case, like the indeterminate couple-stress elasticity (see Mindlin and Tiersten [21], Muki and Sternberg [22], Alber et al. [1]), parts of the stresses in the resulting models remain indeterminate. It is shown in this paper, that there are alternative ways to establish Mindlin’s gradient elasticity models. What is more important is that, in deriving the resulting models, it will become clear that some terms in the boundary conditions may be different than in Mindlin [19]. Here, we adopt the point of view suggested by Podio-Guidugli [25, 26] and Gurtin et al. [14, Sect. 19] and decompose body forces in inertial and non-inertial forces. On the other hand, it is important to remark that Mindlin’s gradient elasticity models posses in all internal points only classical displacement degrees of freedom. Thus, the question arises, if it is possible to reinterpret/restate Mindlin’s gradient elasticity models as continua without postulating explicitly balance laws of double-forces and with ordinary symmetric stresses. The answer is affirmative, as we shall see in the paper.
Closely related to the above question is the thermodynamical consistency of constitutive theories, which incorporate response functions involving spatial gradients of state variables. In fact, Eringen [9] investigated the limitations which the Clausius-Duhem inequality in conventional thermodynamics places on non-polar materials. He found that the spatial gradients must drop out from the response function for the internal energy. Therefore, a non-conventional thermodynamics is desired, which admits the response functions for energy to account for spatial interactions expressed in terms of gradients. A non-equilibrium thermodynamics allowing to address non-localities over space, and also non-localities over time has been proposed in Alber et al. [1]. We shall employ the non-equilibrium thermodynamic framework of [1] in the present paper, in order to reinterpret Mindlin’s gradient elasticity models. The latter models will be restated as classical continua with body and inertial forces involving non-classical terms. This will further lead us to define the appropriate boundary conditions in a manner different than in most references addressing this subject. Moreover, the non-equilibrium thermodynamic framework is broad enough to include further gradient elasticity theories beyond the one of Mindlin.
The aims of the present paper are: (1) To discuss the boundary conditions in Mindlin’s gradient elasticity models. (2) To address gradient elasticity in the framework of the non-equilibrium thermodynamics introduced in Alber et al. [1] and so to reinterpret/restate Mindlin’s gradient elasticity models. In doing this, we shall demonstrate, that the proposed non-equilibrium thermodynamics is capable of establishing not only Mindlin’s gradient elasticity models, but also new gradient elasticity models, e.g., obeying classical potential relations for the Cauchy stress. The scope of the paper is organized as follows. Section 2 concerns some preliminaries mainly concerning the notation used in this work. Then, in Sect. 3, we give an overview about the features of the non-conventional thermodynamics used in the remainder of the paper. The main issues of Mindlin’s micro-structured elastic materials are summarized in Sect. 4.1. Section 4.2 is devoted to interpreting some forces and stresses in micro-structured materials differently than in Mindlin [19], and to making someone familiar with the notion of inertial forces and body forces acting on micro-structured materials. The consistency of micro-structural materials with conventional thermodynamics is outlined in Sect. 4.3. Sections 4.4 and 4.5 deal with Mindlin’s gradient elasticity models, implied by the micro-structural elasticity for the case of a constrained geometry. First (Sect. 4.4) we review the results given by Mindlin [19] and then (Sect. 4.5) we derive the same results in a way which is convenient for the purposes of subsequent sections. An alternative form for the potential energy function in terms of strain gradient is adopted in Sect. 4.6. Critical remarks concerning Mindlin’s approach are provided in Sect. 4.7. In Sect. 5, we present a class of gradient elasticity models including the ones introduced by Mindlin [19]. Thermodynamical consistency is established on the basis of the non-equilibrium thermodynamics of Sect. 3. All models in the class are characterized by classical symmetric stresses, which are well determined by deformation. The discussions in Sect. 4.7 and the procedure of Sect. 5 lead to specifying boundary conditions different than those in Mindlin [19]. Furthermore, the non-equilibrium thermodynamic framework allows the establishment of gradient elasticity models characterized by classical constitutive laws for the Cauchy stress, denoted as Version 3-models in Sect. 5.2.2. The differences between the various models and the effect of different boundary conditions are discussed in Sect. 6 with reference to the problem of a bar under a dynamic axial load. The paper closes with a list of conclusions in Sect. 7, summarizing the major findings of this work.
2 Preliminaries
Throughout the paper we use the same notation as in Mindlin [19] and Mindlin and Eshel [20], in order to facilitate comparison with these works. The deformations are assumed to be small, so we do not distinguish, as usually done, between reference and actual configuration. Unless explicitly stated, all indices will have the range of integers (\(1,2,3\)), while summation over repeated indices is implied. All tensorial components are referred to a Cartesian coordinate system \(\{x_{i}\}\) in the three-dimensional Euclidean point space, which induces the basis \(\{\mathbf{e}_{i}\}\).
Often a tensor \(\mathbf{A}\) will be identified by its components \(A_{i\cdots j}\). For a second order tensor \(\mathbf{A}\) with components \(A_{ij}\), \(A_{(ij)}\) and \(A_{[ij]}\) are the components of the symmetric and skew-symmetric parts, respectively. The Kronecker-delta is denoted by \(\delta_{ij}\) and the alternating symbol by \(e_{ijk}\). For space and time derivatives we shall use the notations
where \(t\) is time. Explicit reference to space and time variables, upon which functions depend, will be dropped in most part of the paper. As often in physics, we find it convenient in several passages not to distinguish between functions and their values. However, to make things clear, when necessary, we shall give explicitly the set of variables which a function depends upon.
Let ℬ be a material body, which may be identified by the position vectors \(\mathbf{x}=x_{i}\mathbf{e}_{i}\). It is assumed that ℬ is a single component system (no mixture), and that it occupies the space \(V\) in the three dimensional Euclidean point space we deal with. We denote by \(n_{i}\) the components of the outward unit normal vector \(\mathbf{n}\) to the surface \(\partial V\) bounding the space range \(V\). For a function \(f(\mathbf{x}, t)\), with \(\mathbf{x}\in V\cup\partial V\), the normal derivative \(Df\) and the surface derivative \(D_{i}f\) are defined by
for every \(\mathbf{x}\in\partial V\) (see Toupin [27, p. 401] or Mindlin and Eshel [20, p. 112]).
3 Non-conventional Thermodynamic Framework
In this section, we review with some modifications the non-conventional thermodynamic framework proposed in Alber et al. [1].
It is assumed that radiant heating, chemical reactions and electromagnetic effects are absent. Then, the local form of the energy balance for the material body ℬ reads
where \(e\) is the internal energy measured per unit volume, \(w_{st}\) is the stress power per unit volume, and \(\mathbf{q}\) is the energy/heat flux vector. Toupin [27] suggested the possibility for \(\mathbf{q}\) to encapsulate more than heat flux, and this has been in fact elaborated by Dunn and Serrin [8] and Dunn [7].
Fundamental in usual irreversible thermodynamics is the hypothesis of a local equilibrium state. It assumes that each material point of ℬ behaves like a simple homogeneous system in equilibrium, so that absolute temperature \(\theta>0\) and entropy per unit volume \(\eta\) may be assigned to that point. The free energy per unit volume is defined through
and the energy law (4) takes the equivalent form
The second law of thermodynamics is commonly accepted in the form of the Clausius-Duhem inequality
Now consider a class of materials which are sensitive to non-localities in space and time effects. For example, assume the free energy function \(\psi\) to depend, besides on state variables permitted in classical irreversible thermodynamics, also on the spatial gradients of these variables. Since gradient terms indicate neighborhood effects, the hypothesis of a classical local equilibrium state is generally no longer justified. Yet, according to classical irreversible thermodynamics, absolute temperature \(\theta\) and entropy \(\eta\) can be attributed only to equilibrium states. We may proceed conceptually further along the lines of classical irreversible thermodynamics as follows.
The state of each material point of ℬ is assumed at any time to be associated with a homogeneous material system in equilibrium, which we call the generalized associated local equilibrium state or system. Classical thermostatics ensures for the generalized associated equilibrium system the existence of absolute temperature \(\theta(\mathbf{x}, t)\) and entropy \(\eta(\mathbf{x}, t)\), and these are attributed to be the temperature and entropy of the real material at \((\mathbf{x}, t)\). Denote by \(v_{I}\), \(I=1,\ldots,N_{I}\), the components of state variables and by \(\xi_{J}\), \(J=1,\ldots,N_{J}\) the components of time and space derivatives of \(v_{I}\), and assume for the real material
We generally call such functions, as \(\psi()\) on the right hand side of Eq. (8), as response functions. In contrast to Alber et al. [1], time and space derivatives of \(\theta\) are not supposed to be included in \(\xi_{J}\) (this case will be discussed separately elsewhere).
The mass density and the response function of free energy of the generally fictitious local equilibrium system are defined to be the same as for the real material characterized by Eq. (8). For both, the real material and the associated equilibrium state, the free energy \(\psi\) and the internal energy \(e\) are postulated to satisfy Eq. (5). In other words, not only the free energy, but also the internal energy is identical in the two systems. Let \(w_{st}\) be the stress power and \(\mathbf{q}\) the energy/heat flux vector for the real material, so that the energy balance laws (4) and (6) hold for the real material. We will introduce an energy balance for the generalized associated equilibrium system by regarding \(\xi_{J}\) for this (homogeneous) system as new state variables, which are independent of \(v_{I}, \theta\). For example, assume \(\varepsilon_{ij}\) and \(\partial_{k}\varepsilon_{ij}\) to be included as state variables in the response function of \(\psi\), where \(\varepsilon_{ij}\) are the components of the infinitesimal strain tensor \(\boldsymbol{\varepsilon }\). Then, \(\partial_{k}\varepsilon_{ij}\) have to be regarded for the generalized associated local equilibrium state as new, independent kinematical variables. These, again, engender additional, higher-order stresses and hence the stress power \(\overline{w}_{st}\) entering into the energy balance law for the fictitious generalized associated local equilibrium state will be in general different from \(w_{st}\). We denote by \(\partial_{i}\overline{q}_{i}\) the energy/heat flux supply for the associated equilibrium system and postulate for this system the energy balance law
Next define stress power \(w'_{st}\) and energy/heat flux \(\mathbf {q}'\) through
so that, from Eqs. (4) and (9),
Further, assume that \(w'_{st}\) and \(\mathbf{q}'\) can be decomposed in \(N\) parts \(w'_{st(i)}\) and \(\mathbf{q}'_{(i)}\),
and postulate energy/heat transfer into mechanical power through
In order to complete the theory, it remains to specify some constitutive equations for \(w'_{st(i)}\) and \(\mathbf{q}'_{(i)}\). In doing so, it might be that new variables will be involved.
The physical idea behind these equations is that the energy/heat flux difference \(\mathbf{q}'\), between the actual and the generalized local equilibrium state, may be composed of various parts, say \(N\), which can be related to corresponding energy carriers. These carriers provide the opportunity for producing some energy/heat transfer to mechanical power without affecting the internal energy, as manifested by Eqs. (10)–(15). The assumed transfer must be accounted for in the entropy production and hence it is postulated that
or, in view of Eq. (9),
Inequality (16) (respectively (17)) is the Clausius-Duhem inequality for the generalized associated local equilibrium state, which is supposed to apply for the real material as well. Once more it is worth remarking, that the concept of the generalized associated local equilibrium state imposes the existence of absolute temperature and entropy and motivates the introduction of inequality (16) or (17). Otherwise, these inequalities can be exploited by employing known methods in continuum thermodynamics. That means, like in classical irreversible thermodynamics based on the hypothesis of a local equilibrium state, when exploiting the inequality, temporal and space derivatives of the state variables can be elaborated. As mentioned above, throughout the present paper we assume that all response functions do not depend on time and space derivatives of \(\theta\). Then, by using the Coleman-Noll procedure [4, 5], it can be proved that
This potential relation will hold in the remainder of the paper. Concluding, we would like to remark that the main difference of this thermodynamic approach to other approaches on the same subject is the energy transfer equations (10)–(15), which are not postulated in the other theories.
4 Mindlin’s Materials with Micro-structure
Mindlin [19] proposed a theory for linear elastic materials with microstructure (micro-structural elasticity), in which stress-equations of motion are derived by employing Hamilton’s variational principle. The main features of this elasticity theory, which is of fundamental importance for the present paper, and limiting cases, are comprised and discussed in this section in a manner convenient for the remainder of the paper.
4.1 Main Features of Mindlin’s Elasticity with Micro-structure
The micro-structured linear elastic materials introduced by Mindlin [19] are characterized by a micro-continuum attached at each material point \(\mathbf{x}\) of a macro-continuum. In this paper, we call as overall material body (continuum) the macro-continuum together with the attached micro-continua. Using the notation of Mindlin [19], the macro-continuum is characterized by the macro-strain tensor \(\boldsymbol{\varepsilon}(\mathbf{x}, t)\) and macro-mass per unit macro-volume \(\rho_{M}=\rho_{M}(\mathbf{x})\). The micro-continuum is supposed to undergo homogeneous micro-deformations described by the micro-deformation tensor \(\varPsi_{ij}=\varPsi_{ij}(\mathbf{x},t)\). The mass of micro-continuum per unit macro-volume is denoted by \(\rho'=\rho'(\mathbf{x})\). Thus, besides the classical displacements \(u_{i}=u_{i}(\mathbf{x},t)\), the components \(\varPsi_{ij}\) are also independent kinematical degrees of freedom for the micro-structured (overall) material, which possesses mass per unit macro-volume \(\rho\),
On denoting by \(\partial_{i}u_{j}\) the components of the macro-displacement gradient, by \(\boldsymbol{\omega}\) the macro-rotation tensor, by \(\boldsymbol{\gamma}\) the relative deformation tensor and by \(\mathbf{k}\) the micro-deformation gradient tensor (the macro-gradient of the micro-deformation), we have
The additional kinematical degrees of freedom, on the one hand, impose classical stresses to be in general not symmetric, and on the other hand, require the existence of higher-order forces and stresses, the so called double-forces and double-stresses. Mindlin assumed for the overall elastic continuum the existence of a “potential energy” \(W\) per unit macro-volume of the form
and a kinetic energy density \(T\) per unit macro-volume of the form
where \(d^{2}_{kl}\) are components of a material dependent second-order tensor. He defined stresses \(\boldsymbol{\tau}\), \(\boldsymbol{\sigma}\), \(\boldsymbol{\mu}\), through
and on making use of Hamilton’s variational principle, he derived the stress-equations of motion
and the following boundary conditions:
have to be specified on \(\partial V\). He adopted as appropriate the terminology Cauchy stress for \(\boldsymbol {\tau}\), relative stress for \(\boldsymbol{\sigma}\) and double-stress for \(\boldsymbol{\mu}\). Typical components of \(\boldsymbol{\mu}\) have been illustrated in Mindlin [19] and Grentzelou and Georgiadis [13]. A general theory on hyperstress fields on the basis of internal corner and surface contact interactions has been recently developed by Fosdick [12] (cf. also the works of Noll and Virga [24] and Dell ’Isola and Seppecher [6]). In Eq. (30), \(\mathbf{f}\) is the ordinary body force per unit macro-volume, given externally, while the second-order tensor \(\boldsymbol{\phi}\) in Eq. (31), given externally as well, is to be interpreted as a body double-force per unit macro-volume. Also, he assumed \(t_{j}\) in Eq. (32) to represent components of a classical traction vector \(\mathbf{t}\), and \(T_{jk}\) in Eq. (33) to be components of a double-force \(\mathbf{T}\) per unit area.
4.2 Power Balance for Materials with Micro-structure
It is helpful for the aims of this paper to consider the stress-equations of motion (30), (31) as balance laws of forces and double-forces. For the discussions to be given and for the specifications of boundary conditions in gradient elasticity, it is also helpful to decompose, right here, body forces in inertial and non-inertial forces, as suggested by Podio-Guidugli [25, 26] and Gurtin et al. [14, Sect. 19]. To be more specific, we think of
(and not of \(\tau_{ij}\)) to be the components of a non-symmetric Cauchy stress tensor, so that
and hence Eq. (30) takes the form
The vector with components
is referred to as the inertial (body) force, and the vector with components \(f_{j}+i_{j}\) as generalized body force (cf. Podio-Guidugli [25, 26], Gurtin et al. [14, p. 136]). Equation (36) represents the local form of force balance or local balance of linear momentum. Along this line of thought, \(\sigma _{jk}+\phi_{jk}\) in Eq. (31) are components of a body double-force, and this equation may be rewritten as
Equation (38) represents the local form of double-force balance, with \(i_{jk}\) being components of an inertial (body) double-force, and \(\sigma_{jk}\) being the part of \(\varSigma_{jk}\) contributing to the double-force balance. It is evident that the part \(\tau_{jk}=\varSigma _{jk}-\sigma_{jk}\), not contributing to the balance of double-forces, must be symmetric. Otherwise it would contribute to the balance of angular momentum, which is included in Eq. (38). The tensor with components \(\sigma_{jk}+\phi_{jk}+i_{jk}\) is referred to as the generalized body double-force. In interpreting so, we have to take into account that \(\phi_{jk}\) is prescribed externally, whereas \(\sigma _{jk}\) emerges internally from material deformations. Therefore, \(\phi _{jk}\) will contribute to the power expended by external forces, whereas \(\sigma_{jk}\) will contribute to the stress power, i.e., to the power expended on the overall body by internal forces.
For all micro-structured continua (irrespective of constitutive properties) the stresses \(\varSigma_{ij}\), \(\sigma_{ij}\) and \(\mu_{ijk}\) expend stress power \(w_{st}\) per unit macro-volume, internal to the overall continuum, which can be established by considering the power balance. To this end, we multiply Eq. (36) by \(\dot{u}_{j}\), Eq. (38) by \(\dot{\varPsi}_{jk}\), take the integrals over \(V\), add the resulting two equations and perform standard calculations, to obtain
Using the terminology of Gurtin et al. [14, Sect. 19], we define the generalized external power \(W_{\mathit{gen.ext.}}\) to be composed of the power \(W_{\mathit{ext.}}\) expended by external loads and the inertial power \(W_{\mathit{inert.}}\), while \(w_{st}\) is the stress-power per unit macro-volume and the kinetic energy \(\mathcal{T}\) is defined to be given by (cf. Eq. (25))
For later reference, and in view of Eq. (42), note that \(W_{\mathit{gen.ext.}}\) in Eq. (40) may be expressed equivalently in the form
In the case of micro-structural elasticity we have \(w_{st}=\frac {d}{dt}W(\boldsymbol{\varepsilon}, \boldsymbol{\gamma}, \mathbf {k})\) (see Eqs. (22), (27)–(29) and (43)) and from Eq. (40) we conclude that
4.3 Micro-structural Elasticity Discussed in the Framework of Conventional Thermodynamics
For given potential energy \(W(\boldsymbol{\varepsilon}, \boldsymbol {\gamma}, \mathbf{k})\), defined stresses \(\boldsymbol{\tau}, \boldsymbol {\sigma}, \boldsymbol{\mu}\) in Eqs. (27)–(29), and defined kinetic energy density in Eq. (25), Mindlin [19] derived the balance laws in Sect. 4.2, by employing Hamilton’s variational principle. Here, we shall start by postulating the validity of the balance laws in Sect. 4.2 and the existence of a potential energy \(W(\boldsymbol{\varepsilon}, \boldsymbol{\gamma}, \mathbf{k})\). More precisely, we shall assume the existence of a free energy \(\psi\) per unit macro-volume and for the response functions the forms
where \(\nabla\theta\) is the gradient of \(\theta\) (in components \((\nabla\theta)_{i}=\partial_{i}\theta\)). Then, we shall derive the potential relations (27)–(29) as constitutive restrictions imposed by the second law of thermodynamics for isothermal processes. Note that the kinematical state variables \(\boldsymbol{\varepsilon}, \boldsymbol{\gamma}\) and \(\mathbf{k}\) enter into the response function for \(\psi\), and that the rates of these state variables appear in \(w_{st}\) in Eq. (43). The above constitutive modelling, suggests that standard continuum thermodynamics, with \(w_{st}\equiv\overline{w}_{st}\), \(\mathbf {q}\equiv \overline{\mathbf{q}}\) and \(\gamma\equiv\overline{\gamma}\), would be sufficient. Indeed, on substituting (43) in (17), we have
Recall from (18) that
and hence
The Coleman-Noll procedure (see [4, 5]) provides arguments proving that the conditions
are necessary and sufficient for the inequality (54) to be satisfied identically. For isothermal processes with \(\theta=\theta_{0}=\mathit{const.}\) everywhere, we set
and Eqs. (55)–(57) lead to the potential relations (27)–(29), or equivalently to
Alternatively, one might consider the fully recoverable, isothermal case, which is defined by Eq. (59) and the condition \(\theta _{0}\dot{\eta}+\partial_{i}q_{i}=0\). (The fully recoverable case for isothermal processes has been discussed in Truesdell and Toupin [29, Sect. 265A] and Malvern [16, Sect. 5.7].) It turns out, that, for this case, the energy law (6) reduces to Eq. (60), and this, together with (59) and (55)–(57), lead to the potential relations (27)–(29).
In conclusion, elasticity with micro-structure is compatible with conventional thermodynamics and traction boundary conditions necessitate \(t_{j}\) and \(T_{jk}\) to be prescribed on \(\partial V\). Next, we focus attention on particular cases of micro-structured elastic materials, where the micro-deformation is constrained to be a function of the macro-deformation. Especially, we concentrate ourselves on those models, introduced by Mindlin [19], and further investigated in Mindlin and Eshel [20]. (Even more subclasses of micro-structured and micromorphic elasticity models have been introduced in Neff et al. [23].)
4.4 Mindlin’s Gradient Elasticity
Mindlin [19] assumed the constitutive parameters in a micro-structured linear elastic material to be such, that
where the dimensionless parameters \(\alpha,\beta\) are functions of material parameters. It is readily seen, that
Following Mindlin [19], define
It is immediately clear, that, if \(A^{A}_{ij}\) is skew-symmetric, i.e., \(A^{A}_{ij}\equiv A^{A}_{[ij]}\), then
Furthermore, define by \(\tilde{k}_{ijk}\) the gradient of \(\partial_{j}u_{k}\),
Thus,
By virtue of Eqs. (62), (63) and (71), \(\gamma_{ij}\) and \(k_{ijk}\) may be expressed in terms of \(\varepsilon _{ij}\) and \(\tilde{k}_{ijk}\), so that the potential energy \(W\) in Eq. (24) becomes
Mindlin [19] defined new stresses,
He used Eq. (70) in the definition of the kinetic energy density in Eq. (25) and obtained
with
Also, he introduced a new, not further specified, external force vector per unit macro-volume with components \(F_{k}\), and by employing Hamilton’s variational principle, he derived the stress-equations of motion
For sufficient smooth boundary surface \(\partial V\), he found the following associated boundary conditions:
have to be specified on \(\partial V\), where
The normal derivative \(D()\) and the surface derivative \(D_{i}()\) are defined by Eqs. (2) and (3). As only the first and the second displacement gradient of macro-deformation occur in the response function \(\tilde{W}\) in Eq. (72), we refer to the resulting model (72)–(81) as the gradient elasticity model of Mindlin. Another equivalent formulation of the boundary terms (80), (81), suggested by Mindlin [19] and Mindlin and Eshel [20], reads
(For a proof see Appendix A.)
4.5 An Alternative Approach to Establish Mindlin’s Gradient Elasticity Model
It is instructive to establish Mindlin’s gradient elasticity model, induced by the constrains (61)–(63), as a direct consequence of the balance laws in Sect. 4.2 and the power statement (60). In fact, we shall do this by establishing first the stress-equations of motion, secondly the boundary tractions and then we shall compare the results with those provided by Mindlin’s approach.
4.5.1 The Stress-Equations of Motion (Eq. (77))
The constrains (61)–(63) render the power \(\sigma _{ij}\dot{\gamma}_{ij}\) to vanish, so that, by Eqs. (60), (72),
where \(\tilde{\tau}_{ij}\) and \(\tilde{\mu}_{ijk}\) are defined in Eqs. (73), (74). We conclude that
and, in view of Eqs. (71), (84), that
We know from Eq. (69), that \(\tilde{k}_{imn}\) is symmetric in its first two subscripts \(i,m\). Because of this reason and as Eq. (86) has to hold for arbitrary rates \(\dot{\tilde{k}}_{imn}\), we may conclude that
with \(\beta_{rn}\) being components of a second-order tensor, which cannot be specified further in terms of deformation. While \(\tilde{\mu }_{imn}\), given by Eq. (74), can be determined by the deformation, Eq. (87) asserts that the double-stress \(\mu _{ijk}\) will be indeterminate to the extent of the tensor \(\beta_{rn}\). This is similar to the indeterminate couple-stress theory, and related statements can be found in Mindlin and Eshel [20], Mindlin and Thiersten [21], Eringen [10] and Alber et al. [1]. Note that the indeterminacy of \(\mu_{ijk}\) implies, in view of Eq. (38), that \(\sigma_{jk}\) will remain further indeterminate. However, this indeterminacy can be dropped out, as we will see in due course.
The constrained geometry affects the inertial double-force as well. From Eqs. (39) and (70), we see that \(i_{jk}\) reduces to
and after multiplying Eq. (38) by \(h_{jkpq}\),
where
are the components of the reduced body double-forces and inertial double-forces, respectively. (In Eq. (91) use has been made of Eq. (76).) To modify Eq. (89) further, recall that \(\sigma _{(jk)}\equiv 0\), and that \(\sigma_{[jk]}h_{jkpq}=\sigma_{[pq]}\) by virtue of Eq. (68), so that \(\sigma_{jk}h_{jkpq}\equiv\sigma_{pq}\). Thus, from Eq. (89),
or
and, because of Eq. (87),
Next, recall Eq. (85), replace \(\boldsymbol{\varSigma}\) in Eq. (36) by \(\tilde{\boldsymbol{\tau}}+\boldsymbol{\sigma}\) to receive
and use (94) to obtain
This result is nothing but the stress-equations of motion (77), provided that
We will come back to Eq. (96) in Sect. 5.2.1 (cf. Eq. (164)), when we will attempt to interpret the various terms there.
4.5.2 The Boundary Tractions (Eqs. (80), (81))
A convenient way to specify the required boundary conditions, is to write the external power and then to resolve the terms with respect to the rates of the independent kinematical variables. To this end, we start with the stress-equation of motion (96), multiply this by the rate \(\dot{u}_{k}\), take the volume integral over \(V\) and use standard steps to receive
Application once more of the divergence theorem to the second integral on the left-hand side of Eq. (98) and recalling of Eqs. (69), (20), yields
The far right-hand side of Eq. (99) has been expressed in terms of the potential energy function \(\tilde{W}\) by using Eqs. (72)–(74). To accomplish, the second integral on the left-hand side in Eq. (99) must be resolved further, for the rate \(\partial_{j}\dot {u}_{k}\) is not independent of \(\dot{u}_{k}\) on \(\partial V\). To this end, we make use of the integral transformation (B.4) in Appendix B and rearrange terms to prove that Eq. (99) implies (cf. Eq. (46))
We can show (see Appendix B), that Eq. (100) may be also derived from Eqs. (40)–(43), by confining ourselves to the constrained geometry.
The question now reads which is the decomposition of \(W_{\mathit{gen.ext.}}\) for the gradient elasticity model analogous to that one for the micro-structured materials in Eqs. (40)–(46). The answer to this question is very important, for the appropriate definition of \(W_{\mathit{ext.}}\) and its form will suggest the required boundary conditions for traction, as this is the case in Eq. (41) by the first integral on the right-hand side.
The two surface integrals in Eq. (100) do not have to be further resolved, since the rates \(\dot{u}_{k}\) and \(D \dot{u}_{k}\) are independent of each other on \(\partial V\). However, the integrals involving the forces \(\tilde{\phi}_{jk}\) and \(\tilde{i}_{jk}\) require some thought. From a purely formal point of view, there are more than one ways to deal with these integrals. It seems that in the approach of Mindlin [19] the integral involving the inertial term \(\partial_{j}\tilde{i}_{jk}\) is resolved as
while the integral involving the terms \(\partial_{j}\tilde{\phi}_{jk}\) is combined with the integral involving the force \(f_{k}\),
where the definition (97) has been incorporated. This way, it follows from Eq. (100) that
With the aid of Eqs. (75), (37) and (91), it is not difficult to see that
Therefore, Eq. (103) becomes
with the difference power \(W_{\mathit{diff.}}\) being defined as
and with \(\tilde{P}_{k}\), \(\tilde{R}_{k}\) being the same as in Eqs. (82), (83), i.e., in view of Eq. (91),
Obviously, Eq. (106) for Mindlin’s gradient elasticity model corresponds to Eq. (45) for the micro-structured materials. Apparently, motivated by the surface integral in Eq. (107), Mindlin [19] suggested the boundary conditions
have to be given on \(\partial V\). The decomposition (106) with the assumed consequence that the appropriate traction terms on the boundary are given by Eqs. (108), (109), portray an important step in the approach of Mindlin.
It has to be remarked that the decomposition (106) does not correspond to the decomposition (40), or equivalently, the term \(W_{\mathit{diff.}}\) in Eq. (106) does not correspond to the term \(W_{\mathit{ext.}}\) in Eqs. (40), (41). The reason is that \(W_{\mathit{ext.}}\) in Eqs. (40), (41) is independent from inertial terms, whereas \(W_{\mathit{diff.}}\) in Eqs. (107)–(109) includes inertial terms arising from \(n_{j}\tilde{i}_{jk}\). Note that just the term \(W_{\mathit{ext.}}\) in Eqs. (40), (41) is associated to, or even suggests, the traction terms \(t_{j}=n_{i}\varSigma_{ij}\) and \(T_{jk}=n_{i}\mu_{ijk}\) on the boundary \(\partial V\). In every case, the specification of the required boundary tractions as in Eqs. (110), (111) is not a compelling consequence as we shall see in due course (cf. Sect. 4.7 and paragraph “Mindlin’s gradient elasticity without inertial terms in the boundary conditions”). Before doing this, it is of interest to look at Mindlin’s gradient elasticity model when its potential energy function is expressed in terms of \(\varepsilon_{ij}\) and \(\partial _{i}\varepsilon_{jk}\).
4.6 Potential Energy as Function of Strain-Gradient
An equivalent formulation of Mindlin’s gradient elasticity arises by replacing the second gradient \(\tilde{\mathbf{k}}\) given in Eq. (69) by the strain-gradient \(\hat{\mathbf{k}}\) defined as
This approach has been referred to as Form II (cf. [19, 20]) and relies upon the identities
These relations offer the possibility to represent the potential energy \(W\) in Eq. (72) as a function of \(\boldsymbol{\varepsilon}\) and \(\hat{\mathbf{k}}\),
Mindlin [19] and Mindlin and Eshel [20] introduced new stresses
and described the manner \(\hat{\mu}_{ijk}\) and \(\tilde{\mu}_{ijk}\) are connected, i.e.,
Since
the stress-equations of motion (96) (respectively Eq. (77)) become
or equivalently, in view of Eq. (119) and the symmetry property \(\tilde{\mu}_{jki}=\tilde{\mu}_{kji}\),
The equivalent forms for \(W_{\mathit{gen.ext}}\) and \(W_{\mathit{diff.}}\) in Eqs. (100), (106)–(109) read (see Appendix C)
Finally, \(\dot{\mathcal{T}}\) is given as in Eq. (105) and the boundary conditions are equivalent to those in (110), (111), i.e.,
have to be prescribed on \(\partial V\).
4.7 Discussion on Mindlin’s Approach
Mindlin’s micro-structural elasticity, and the reduced gradient elasticity model, are milestones in the development of continuum theories and have motivated numerous subsequent works. Nevertheless, there are some aspects in Mindlin’s gradient elasticity model, which seem to be worthy of discussion. To be more specific, Mindlin [19] assumed the inertial term \(\tilde{i}_{jk}\) to be involved in the boundary conditions in Eqs. (110), (108), which renders the boundary force \(\tilde{P}_{k}\) (respectively \(\hat {P}_{k}\) in Eq. (126)) to be non-objective. In continuum theories non-objective boundary forces are considered as physically unnatural (for related remarks concerning the indeterminate couple stress theory see Eringen [10, Sect. XXIII], who considers non-objective stresses as physically unnatural). It may be that the decision to assume the presence of \(\tilde{i}_{jk}\) in the boundary force \(\tilde{P}_{k}\), originates from the desire to design a theory, where \(W_{\mathit{gen.ext.}}\) is decomposed as in Eq. (106), which corresponds to Eq. (45). Another reason could be the presence of \(\partial_{i}\tilde{i}_{jk}\) in the stress-equations of motion (96) (respectively (122)). If one believes that \(\partial_{i}\tilde{i}_{jk}\) has to be viewed as a flux term, like \(\partial_{j}\tilde{\tau}_{jk}\), then, consequently, \(\tilde{i}_{jk}\) has to be involved in the concomitant boundary conditions for traction. A similar thought, however, would suggest viewing \(\partial _{i}\tilde{\phi}_{jk}\) also as a flux term, and so placing \(\tilde {\phi }_{jk}\) in the boundary conditions for traction as well. Actually, among others, Bleustein [2] in a paper addressing equilibrium cases, assumed body double-forces to be present in the adjoint boundary conditions. On the other hand, in the approach of Mindlin [19], such terms do not occur explicitly in the resulting gradient elasticity model and in particular in the associated boundary conditions, although they are assumed in the equations governing elasticity with micro-structure. It should perhaps be mentioned that the form of traction boundary conditions for special gradient elasticity theories has been addressed in, e.g., Madeo et al. [15]. However, the main focus in this paper and similar ones by Neff and coauthors, is not on the role of inertial and body forces, as it is the case in the present paper.
Since Mindlin’s gradient elasticity has been introduced as a limit of an elastic micro-structured material, it appears at first glance to be reasonable to consider the limiting theory in the context of balances of double-forces. However, it is well known and it has been outlined above, that, in the context of balances of double-forces, parts of the stresses are left indeterminate. It also has to be remarked, that in the limiting case of gradient elasticity, no further degrees of freedom, besides the ones specified by displacements \(u_{k}\), exist in the interior of \(V\). Therefore, the question arises, if it is possible in general to formulate Mindlin’s and other gradient elasticity models in a context without balances of double-forces, without parts of stresses being left indeterminate and with physically acceptable boundary conditions for traction. The answer to this question is closely related to an appropriate interpretation of the involved stresses and forces. Variational methods, like those employed by Mindlin [19], Mindlin and Eshel [20] or [27] and [28] cannot provide this interpretation:
“Since they can be stated without even any concept of internal stresses, virtual work principles like that of TOUPIN …are fundamentally unable ever to tell one what the stresses are in a body to which they apply. This, of course, may be viewed as a strength of these principles, since they are thus compatible with a multiplicity of materials, having different forms of stresses. Our point here, however, is that the most they can do in this regard is to suggest a form for the stress up to a divergence-free term and they can do even this only if one is prepared to adjoin to them Cauchy’s concept of stress and the momentum equations based on it. Thus, TOUPIN’s form …are all suspect to us; each of these …”. This passage in quotes is taken from Dunn and Serrin [8, p. 107].
We shall show in the following, that various gradient elasticity models, including that one of Mindlin, can be well addressed in the context of classical, symmetric Cauchy stresses, without leaving parts of stresses indeterminate. The approach we shall employ, relies upon the conventional balance laws of linear and angular momentum and the non-conventional thermodynamics proposed in Sect. 3. Especially, we shall show that concomitant boundary conditions for traction, not including inertial terms, can be specified on the boundary \(\partial V\). This is the reason we adopted the point of view of Gurtin et al. [14, Sect. 19], namely to deal with inertial forces and generalized external powers, and we announced the equivalent form for the stress-equations of motion in Eq. (122).
5 A Class of Gradient Elasticity Models
Important characteristic features in Mindlin’s gradient elasticity are the existence of the potential energy (115), of the kinetic energy rate (105) and of body forces, body double-forces, inertial forces and inertial double-forces with components \(f_{j},\tilde{\phi}_{jk}, i_{j}\) and \(\tilde {i}_{jk}\), respectively. All these (body) forces can be reflected in the stress-equations of motion (122), (123) by a single body force \(\mathbf{b}\) (generalized body force vector) with components
According to these formulas, \(\mathbf{F}\) and \(\mathbf{I}\) reflect ordinary body and inertial forces in terms of non-classical ones. We shall focus attention on a class of gradient elasticity models, having also the potential energy (115), the kinetic energy rate (105) and the forces (130)–(132) as characteristic features. First we shall postulate the mechanical balance laws for this class of models.
5.1 Mechanical Balance Laws
Consider material bodies which are governed by ordinary balance laws of linear and angular momentum leading to the local forms
In these equations, \(\hat{\varSigma}_{jk}\) are the components of the Cauchy stress tensor.
An immediate consequence of Eq. (133), after multiplying by \(\dot{u}_{k}\), integrating over \(V\), using Eqs. (20), (134) and performing standard steps, is the classical result
which leads to the classical stress power
The left-hand side of Eq. (135) might not be interpreted as generalized external power, because the integrand \(w_{st}=\hat{\varSigma }_{jk}\dot{\varepsilon}_{jk}\) at the right-hand side of Eq. (135) is not equal to \(\frac{d}{dt}\hat{W}(\boldsymbol {\varepsilon }, \mathbf{k})\), i.e., Eq. (135) is not an analogue of Eq. (46). By using Eqs. (132) and (105), it may be seen, that the inertial force \(\mathbf{I}\) expends the power
This law asserts that the inertial power expended on \(V\) is balanced by the negative kinetic energy rate of \(V\) and an inertial power transfer to \(V\) across \(\partial V\). Equation (137) has to be regarded as a non-classical law, the classical ones being characterized by equations of the form \(W_{\mathit{inert.}} = -\dot{\mathcal{T}}\) (cf. Eq. (42)). Similarly, by appealing to Eq. (131), the conventional body force \(\mathbf{F}\) expends the power
According to this law, the power expended on V by \(\mathbf{F}\) is balanced by the sum of power expended within V by ordinary body forces and ordinary double-forces and a power transfer to V across \(\partial V\), caused by the power flux \(\tilde{\phi}_{jk}\dot{u}_{k}\). It should be clear, that Eqs. (130), (137) and (138) furnish
It remains to examine the compatibility with the laws of thermodynamics and to specify the concomitant boundary conditions. We shall do this by employing the non-conventional thermodynamic framework comprised in Sect. 3.
5.2 Gradient Elasticity in the Framework of Non-classical Thermodynamics
Assume that \(\hat{W}(\boldsymbol{\varepsilon}, \hat{\mathbf{k}})\) in Eq. (115) is the isothermal case of a free energy function
We know from Eq. (136) that the stress power has the classical form \(w_{st}=\hat{\varSigma}_{jk}\dot{\varepsilon}_{jk}\). However, we know also (cf. Eringen [9]) that restrictions imposed on non-polar materials by conventional thermodynamics drop out from the response function \(\hat{\psi}\) the strain gradient \(\hat{\mathbf {k}}\). We shall now show, that constitutive models governed by the response function in Eq. (140) can well be addressed in the framework of the non-conventional thermodynamics presented in Sect. 3. The investigations will lead to a broad constitutive structure, including Mindlin’s gradient elasticity.
Suppose that \(w_{st}\) and \(\mathbf{q}\) satisfy Eqs. (9)–(15), with \(N=1\),
and
Assume, moreover, the validity of the Clausius-Duhem-inequality (17), and use Eq. (141) together with \(w_{st}=\hat {\varSigma }_{jk}\dot{\varepsilon}_{jk}\) to obtain
The potential relation in Eq. (18) reads now
Further potential relations are introduced by the definitions
The three Eqs. (140), (144) and (145) yield
or equivalently,
To complete the constitutive structure, assume that, besides the response function for \(\psi\) in Eq. (140), we are given response functions of the form
To proceed further, some constitutive properties for \(w'_{st}\) and \(\mathbf{q}'\) have to be prescribed. Three cases, which always allow the fulfillment of inequality (149), will be addressed in the subsequent sections. The first two are versions of Mindlin’s gradient elasticity subject to different boundary conditions (see Sect. 5.2.1). The third case is substantially different than Mindlin’s gradient elasticity to the point, that the stress tensor obeys a classical potential relation (see Sect. 5.2.2).
5.2.1 Mindlin’s Gradient Elasticity Reinterpreted/Restated
The identity
allows to rewrite inequality (149) in the form
A simple way to satisfy this inequality is to apply the procedure of Maugin [17], suggesting to make the constitutive assumption
Then, \(-\partial_{i} (\hat{\mu}_{ijk}\dot{\varepsilon }_{jk} )-w'_{st}\) cancels out in Eq. (153), and using Coleman-Noll’s arguments [4, 5], it is readily shown that
are necessary and sufficient conditions for inequality (153) to be satisfied always.
In order to satisfy Eq. (143), we make the constitutive assumption
The divergence-free vector \(\mathbf{c}\), not further specified here, may depend on the state variables and their spatial and temporal derivatives. Then, Eq. (142) becomes
while Eq. (143) is satisfied identically. This energy balance law seems to have the same form as that energy law proposed in Dunn and Serrin [8] (see also Dunn [7]), if their interstitial work flux is identified by \(\mathbf{q}'\) and their heat flux by \(\bar{\mathbf{q}}\). However, in difference to the interstitial work flux in [8], the energy flux \(\bar {\mathbf{q}}'\) has to fit the transfer law (143). With regard to the energy law (158), we define the fully recoverable isothermal case through \(\theta=\theta_{0}=\mathit{const.}\) and
so that (cf. Eqs. (136), (141)–(143))
The isothermal version of Eq. (155) is
with
and the balance law (133) becomes
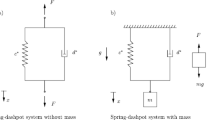
Keeping in mind Eqs. (130)–(132), the balance law (164) is nothing but the stress-equations of motion (122) governing Mindlin’s gradient elasticity model. Recalling that \(\hat{\boldsymbol{\varSigma}}\) is postulated to be a symmetric Cauchy stress tensor, and Eq. (133) to be the balance law of linear momentum, it should be clear that Eq. (161) has to be interpreted as a constitutive law for the Cauchy stress tensor suggested by the thermodynamical restrictions. The stresses \(\hat {\boldsymbol{\tau}}\) and \(\hat{\boldsymbol{\mu}}\) are determined by the deformation according to Eqs. (162) and (163). The mechanical analog of the constitutive law (161) is illustrated in Fig. 1 and consists of two springs in parallel. One spring (corresponding to Eq. (162)) is standard, i.e., its response is described by a classical elasticity law. The other (corresponding to Eq. (163)) is a non-standard spring, which acts only if the strain is non-homogeneous.
Next, take the volume integral of Eq. (160) and use Eq. (135) to obtain
Bearing in mind Eqs. (161), (157), we deduce that
If \(\mathbf{c}\equiv\mathbf{0}\), then, by employing steps similar to those in Sect. 4.5.2, and on comparing with Eq. (124), we can recognize that
where
With the help of Eq. (139), Eq. (167) takes the form
Furthermore, comparison of Eq. (170) with Eqs. (124)–(127), reveals that
with
It has been remarked in the paragraph before Eq. (101), that there are more than one way to resolve \(W_{\mathit{gen.ext.}}\) as a sum of surface integrals and thus to specify the boundary conditions. Here, we will pursue two possibilities, the first one being Mindlin’s original approach to gradient elasticity.
Mindlin’s Gradient Elasticity with Inertial Terms in the Boundary Conditions
The aim is to solve the field equations of linear momentum (133), or equivalently Eq. (164). We presumed in Sect. 4.5.2 that the approach of Mindlin suggests specifying the adjoint boundary conditions on the basis of the surface integral in Eq. (107), or equivalently in Eq. (171). Hence the boundary conditions read
have to be prescribed on \(\partial V\). The presence of the inertial term \(n_{j}\tilde{i}_{jk}\) in the boundary conditions has been commented in Sect. 4.7.
Mindlin’s Gradient Elasticity Without Inertial Terms in the Boundary Conditions
The gradient elasticity model proposed here differs from Mindlin’s original version only in the boundary conditions. Again, the aim is to solve the field equations for linear momentum (133), or equivalently Eq. (164). But now the point of view is adopted that, because \(b_{k}\) or respectively \(F_{k}\) and \({I}_{k}\) are body forces, it is reasonable to postulate that they do not contribute to the boundary conditions for traction. To elucidate, starting from Eqs. (167) and (139),
we have
with
and \(W_{\mathit{inert.}}\) as defined in Eq. (137). We believe that this \(W_{\mathit{ext.}}\) is the appropriate counterpart of \(W_{\mathit{ext.}}\) in Eq. (41) and that the surface integral in Eq. (177) should be the basis for the definition of the appropriate boundary conditions for traction. However, owing to the presence of non-classical inertial terms, we believe that the relation between \(W_{\mathit{inert.}}\) and \(\dot{\mathcal{T}}\) in Eq. (42) should be generalized by that one in Eq. (137). With respect to the surface integral in Eq. (177), we define the boundary conditions as follows:
must be prescribed on \(\partial V\), where \(\hat{P}_{k}^{*}\) and \(\hat{R}_{k}\) are given in Eqs. (168) and (169). We shall refer to Eq. (164), accompanied by the boundary conditions (178) and (179), as Mindlin’s gradient elasticity without inertial terms in the boundary conditions.
Besides the differences in the boundary conditions according to the two possibilities, and the assumption of vanishing vector \(\mathbf{c}\), we have restated the main results of Mindlin’s gradient elasticity, within a scope dealing with classical, symmetric stresses and without postulating balance laws of double-forces. Evidently, if \(\mathbf{c}\) does not vanish, then some effects on the boundary will arise. The effect of the different boundary conditions in Eqs. (173), (174) and (178), (179) is discussed in Sect. 6.4 with reference to one-dimensional examples.
5.2.2 Gradient Elasticity Characterized by Classical Constitutive Laws for the Cauchy Stress
Another simple way to satisfy inequality (149) consists of the constitutive assumption
where \(\hat{\boldsymbol{\mu}}\) is defined in Eq. (147). It is straightforward to prove, on the basis of Coleman-Noll’s arguments [4, 5] and the assumptions (150), (151), that the conditions
are necessary and sufficient for inequality (149) to always hold true. As in the case of Eqs. (161)–(163), the stress tensor \(\hat{\boldsymbol{\varSigma}}\) in Eq. (181) is determined by the deformation. But here, unlike in Eq. (155), \(\hat{\boldsymbol{\varSigma}}\) is equal to \(\hat {\boldsymbol{\tau}}\) and admits a classical potential relation. Also, in contrast to Eq. (164), the field equations to be solved, are now
Generally, further constitutive laws will be needed in order to complete the system of equations. To illustrate, let the region \(V\) be simply connected and make the constitutive assumption that the energy flux vector \(\mathbf{q}'\) is irrotational. Then, there exists a scalar-valued potential \(\phi(\mathbf{x}, t)\), so that
It follows from Eqs. (143) and (180) that \(\phi\) satisfies the Poisson’s equation
The global counterpart of this equation is (cf. Eq. (2))
In analogy to Sect. 5.2.1, define the fully recoverable, isothermal case by \(\theta=\theta_{0}=\mathit{const.}\) and
Then, keeping in mind Eqs. (136), (141)–(143), (180), (185) and (187), we can infer that
Again, take the volume integral of this equation and use (135), to obtain
with \(\hat{t}_{k}\) given in Eq. (134). To proceed further, we have to specify \(D\phi\) on \(\partial V\). In the present paper we make the assumption
where \(\varLambda={\varLambda}(\mathbf{x},t), \mathbf{x}\in\partial V\), is a dimensionless parameter. Note that we do not dispose of \(\varLambda\) arbitrary, as \(\varLambda\) is subject to the constrain (186),
The two Eqs. (189) and (190) yield
Along the line of the last paragraph “Mindlin’s gradient elasticity without inertial terms in the boundary conditions”, and with the second integral on the left-hand side of Eq. (192) being given in Eq. (139), we may deduce the following results:
With respect to the surface integral in Eq. (195), we define the boundary conditions
have to be prescribed on \(\partial V\), where the surface traction \(\hat {\mathbf{K}}\) is given by
and \({\varLambda}\) has to satisfy the constrain (191). Some aspects of this model are discussed in the next section for one-dimensional conditions.
In the following, we denote by Version 1 and Version 2 Mindlin’s gradient elasticity with and without inertial terms in the boundary conditions, respectively, and by Version 3 the models of gradient elasticity exhibiting classical potential relations for the Cauchy stress.
6 One-Dimensional Examples
6.1 Linear, Isotropic Gradient Elasticity
For the examples to be discussed here, we concentrate on the general form of the potential energy function for linear, isotropic material behavior proposed in Mindlin [19] and Mindlin and Eshel [20]. Accordingly, we assume the existence of a potential energy function
so that
where \(\lambda, \mu\) (Lamé constants), \(\hat{a}_{1},\ldots,\hat{a}_{5}\) are material parameters. The assumed isotropy imposes the material dependent tensor \(d^{2}_{jl}\) (see Eqs. (25), (26)) to be a spherical tensor, i.e.,
where \(d\) is a material length. From this and Eqs. (67), (76),
Now, set \(x_{1}=x\) and consider a prismatic, slender bar of length \(L\) and cross section \(A\), orientated along the \(x\)-axis. In accordance with the classical one-dimensional theory, assume a displacement field of the form
This corresponds to vanishing Poisson’s ratio, or equivalently to \(\lambda=0\) and \(2\mu=E\), where \(E\) is the classical Young’s modulus. Then,
where \(\hat{g}\) represents a material length and is given by
All the other components of \(\boldsymbol{\varepsilon}, \hat {\boldsymbol {\tau}}\) and \(\hat{\mathbf{k}}\) are vanishing. Besides \(\hat{\mu}_{111}\), the components \(\hat{\mu}_{122}\), \(\hat {\mu }_{133}\), \(\hat{\mu}_{212}\) and \(\hat{\mu}_{313}\) are also non-vanishing, but they play no role neither in the field equations nor in the boundary conditions. From Eqs. (91), (203)–(205),
where the parameter \(h\) describes a material length and is given by
Since \(\tilde{i}_{22},\tilde{i}_{33}\) are functions of \(x\) only, their derivatives with respect to \(x_{2},x_{3}\) vanish and so these terms do not affect the field equations either. For simplicity we assume vanishing body forces \(\mathbf{F}\), so that, from Eqs. (130)–(132), (211),
In what follows, we concentrate ourselves first on Versions 1 and 2 of Mindlin’s gradient elasticity and then on the gradient elasticity Version 3 exhibiting classical potential relations for the Cauchy stress.
6.2 Versions 1 and 2 of Gradient Elasticity Models
With the results from the last section, it is not difficult to verify, that
is the only non-trivial equation which follows from Eq. (164). Invoking Eqs. (208), (209) in Eq. (215),
This equation has been established previously and studied intensively, e.g., in [30] and [18].
In order to specify the boundary conditions, we must first specify the components \(\hat{P}_{k}\), \(\hat{P}_{k}^{*}\) and \(\hat{R}_{k}\) (cf. Eqs. (173), (174) and (178), (179)). For the one-dimensional bar the only non-vanishing component of the normal vector \(\mathbf{n}\) is \(n_{1}=\pm1\). Therefore (see Eqs. (2), (3))
Since \(u\) and \(\hat{\mu}_{ijk}\) depend on \(x\) only, we have on the one hand
and on the other hand
Among the components \(\hat{\mu}_{11k}\) only \(\hat{\mu}_{111}\) is non-vanishing, so that
All together, we have from Eqs. (168), (169) and (172)
where use has been made of Eqs. (208), (209) and (211). In what regards the boundary planes parallel to the \(x\)-axis, it can be seen, that in all cases, the assumed geometry implies \(u_{2}=u_{3}=Du_{2}=Du_{3}=0\). Therefore, homogeneous boundary conditions on these planes are satisfied trivially. On the \(x_{2}-x_{3}\) boundary planes at \(x=0\) and \(x=L\), the assumed geometry imposes the conditions \(u_{2}=u_{3}=Du_{2}=Du_{3}=0\), so that the only non-trivial boundary conditions to be prescribed are
at \(x=0\) and \(x=L\).
Now consider the bar with length \(L\) to be fixed at its left end (\(x=0\)) and subjected to a given dynamic axial load of amplitude \(P_{0}\), harmonically varying with time, at its right end (\(x=L\)). Thus, we have the following
Classical boundary conditions:
where \(\omega=\mathit{const.}\) is the operational frequency and \(P_{0}=\mathit{const.}\) the amplitude of the axial load. The other two non-classical boundary conditions are assumed to be a vanishing force \(\hat{R}\) at \(x=0\) and a harmonically varying with time strain \(Du\equiv u_{,x}\) at \(x=L\). Thus, we have the following
Non-classical boundary conditions:
where \(\varepsilon_{0}=\mathit{const.}\) is a prescribed strain value. In solving the boundary value problem (216), (227)–(230), it is convenient to use the classical velocity of propagation of axial elastic waves
the dimensionless variables
the dimensionless parameters
and the dimensionless stress
Thus, we may rewrite Eq. (216) in the dimensionless form
The form of the loading conditions (228) suggests making the ansatz
for the solution of (235). Hence, (235) yields
This is a linear, ordinary differential equation with constant coefficients. Its eigenvalues are
where
Therefore, the general solution of Eq. (237) can be given in the form
and the boundary conditions (227), (229) and (230) reduce to
The boundary conditions (228), in view of Eqs. (222), (223) and the employment of the ansatz (236), yield
The last two equations can be presented in a unified manner through
Equation (248), on account of (242), becomes
Equations (243), (244), (245) and (250) form a linear system for the constants \(C_{1}\), \(C_{2}\), \(C_{3}\) and \(C_{4}\):
where the coefficients \(A_{ij}\) \((i,j=1,2,3,4)\) can be found explicitly in Appendix D.
The solution depends on \(\xi_{1}\), \(\xi_{2}\) and \(\zeta\), which in turn must be calculated from Eqs. (239)–(241), (249).
Of particular interest is the case \(\bar{g}\equiv0\). For this case, we deduce from Eq. (235) that
and from Eqs. (236) and (237) that
This has to be supplemented only with the classical boundary conditions (cf. Eqs. (237), (248))
with \(\zeta\) given in Eq. (249). In order to provide an insight into the consequences of \(\bar{g}=0\), it suffices to focus on \(1-\bar{h}^{2}\bar{\omega}^{2}>0\). Then, the eigenvalues of this linear ordinary differential equation (253) are
and the general solution is
This, together with the ansatz (236) and the boundary conditions (254) yield
and hence
Classical elasticity is recovered from these equations for \(\bar{h}=0\), implying \(\zeta=1\).
6.3 Version 3 of Gradient Elasticity Models
From the results in Sect. 6.1, we may deduce that Eq. (183), for vanishing body force \(\mathbf{F}\) (see Eq. (214)), reduces to
Appealing to Eqs. (208) and (231)–(234), we obtain
For uniaxial problems like those in the last section, the boundary conditions (197), (198) take the form
With regard to Eqs. (208), (231)–(234), we find from Eq. (262) that
We observe that Eq. (260) is identical to Eq. (252). Thus, its solution (with the assumption of \(1-\bar{h}^{2}\bar{\omega }^{2}>0\)) will be also given by Eq. (256). The boundary condition (261) imposes \(B=0\), so that
Assuming the potential \(\phi\) to be a function of \(x,t\), i.e., \(\phi =\phi(x,t)\), we conclude from Eq. (185) that
or, in dimensionless form,
where \(\bar{\phi}\) denotes the dimensionless potential
The solution (264) and the ansatz (236) furnish
and hence, after inserting it into Eq. (266),
We may integrate this equation with respect to \(\bar{x}\) between \(\bar {x}=0\) and \(\bar{x}=1\), to obtain
which corresponds to Eq. (186). The assumption (190) takes now the form
From the condition (261) we infer that \(u_{,t}(0,t)=0\) and therefore \(\phi_{,x}(0,t)=0\). Equation (271) can be written in dimensionless form,
or, with regard to Eq. (268),
All together, we deduce from Eq. (270) that
which may be solved to obtain \(\varLambda(1,\bar{t})\) in the form
Finally, we use Eqs. (276) and (268) in Eq. (263) to obtain
and solve it for \(C\):
With \(C\) being determined in Eq. (278), the predicted responses for \(\bar{U}(x)\) follow from Eq. (264).
6.4 \(\bar{U}(\bar{x})\)-Responses Predicted by the Gradient Elasticity Models
Various distributions \(\bar{U}(\bar{x})\) are displayed in Figs. 2–15. In all cases, we have chosen \(\varepsilon_{0}=0.0075\) and \(\bar{\tau }_{0}=0.015\). The other parameters are given in the figures. In comparing the various gradient models, we denote by V1, V2, V3 and Cl. the models or their responses according to Version 1, Version 2, Version 3 and Classical elasticity, respectively.
The discussion on boundary conditions with and without inertial terms is referred to V1 and V2, and can be best illustrated when gradient effects are solely due to inertia, i.e., for \(\bar{g}=0\). Such cases are displayed in Figs. 2, 3, 4, 5 for \(\bar{\omega}=1.4; 2; 3; 4\), i.e., for values away from the natural frequencies of free vibrations of the classical bar with fixed-free boundary conditions in order to avoid resonance. These natural frequencies are determined from \(\cos\bar{\omega}=0\), with solutions \(\bar{\omega}_{1}=\frac {\pi }{2}=1.57, \bar{\omega}_{2}=\frac{3\pi}{2}=4.71, \bar{\omega }_{3}=\frac {5\pi}{2}=7.85,\ldots{}\). It can be seen in Fig. 2, that for \(\bar {\omega}=1.4\) the \(\bar{U}\) values according to V1 and V2 are larger than those due to the classical solution and that the responses due to V2 are larger than those due to V1. But this is no more true for \(\bar {\omega}=2; 3; 4\). The general tendency which can be stated in all Figs. 2–5 is that, the V1-responses are always closer to the \(\bar {x}\)-axis, than the corresponding V2 responses. In addition, it is observed that the values of \(\bar{U}\) increase for increasing \(\bar {h}\) when \(\bar{\omega}=1.4\) and \(\bar{\omega}=2\). For \(\bar {\omega }=3\) and 4, \(\bar{U}\) exhibits oscillations around the value \(\bar {U}=0\), especially for high values of \(\bar{h}\), indicating that higher modes dominate the response.
The other particular case, where gradient effects are solely due to the strain energy, arises for \(\bar{h}=0\). Then, all distributions due to V1 and V2 are identical. Such distributions are displayed in Figs. 6–9. The general observation, which can be made, is that the distributions \(\bar{U}(\bar{x})\) tend to be closer to the classical one, the smaller the value of \(\bar{g}\). It is also observed, that for low frequencies, as in Fig. 6 where \(\bar{\omega}=1.4\), the stiffening effect of gradient elasticity increases with increasing values of \(\bar {g}\), i.e., decreasing absolute values of \(\bar{U}\) with increasing \(\bar{g}\). However, the opposite happens for \(\bar{\omega }=2.0\) (see Fig. 7), while for \(\bar{\omega}=3.0;4.0\) (see Figs. 8, 9) the effect of higher modes on the response is apparent. It may be concluded, that in general the stiffening effect of gradient elasticity is dependent on the frequency \(\bar{\omega}\).
Comparing, e.g., Fig. 2 with Fig. 6, we may recognize that the two particular cases \(\bar{g}=0\) and \(\bar{h}=0\) cause distributions which, with respect to the classical one, have the tendency to be opposite. Therefore, it might be expected that, when both parameters \(\bar{g}\) and \(\bar{h}\) are not vanishing, their effect will be controversial. In fact, this is confirmed in Figs. 10 and 11. Thus, Fig. 10, for \(\bar {\omega}=1.4\), clearly shows that for both V1 and V2 models, increasing values of \(\bar{h}\) (up to \(\bar{h}=0.2\)) increases the response, which approaches the classical one (Cl.). However, for \(\bar{h}=0.3\), the response surpasses the classical one. A similarly strange behavior is shown in Fig. 11 for \(\bar{\omega}=2.0\). Here, for both models V1 and V2 and low values of \(\bar{h}\) (\(\bar{h}=0.01, 0.1\)), the absolute values of the responses are larger than the classical one (Cl.). However for \(\bar{h}=0.2, 0.3\), the absolute values decrease and become much smaller than the classical one (Cl.).
Concerning responses predicted by V3, it is of interest first to compare them with the classical one (Cl.). Figures 12 and 13 illustrate this comparison for \(\bar{\omega}=1.4\) and \(\bar{\omega}=2\). We see in Fig. 12, that, for the chosen values \(\bar{g}\), the smaller the \(\bar{g}\), the closer the \(\bar{U}(\bar{x})\)-responses to that of Cl. (stiffening effect). Also, all \(\bar{U}(\bar{x})\)-responses are below the classical response (Cl.). This is no more true in Fig. 13, where for higher values of \(\bar{g}\), the constant in Eq. (278) can change the response sign from the negative to the positive regime. Evidently, this is related to the fact, that for given \(\bar{g}\), there are frequencies \(\bar{\omega}\) making the denominator in Eq. (278) zero. Thus for decreasing values of \(\bar{g}\) (\(\bar{g}=0.2;0.1\)) the amount of the response decreases and approaches the classical one (Cl.) in the negative regime, while for increasing values of \(\bar{g}\) (\(\bar{g}=0.3-0.4\)) the response decreases in the positive regime. Similar aspects apply also to responses according to V3 with \(\bar {h}\ne0\), see Figs. 14 and 15.
Finally, one can observe that for the cases exhibiting the stiffening effect (Figs. 6, 12), which is associated with nonzero micro-stiffness (\(\bar{g}\ne0\)), the absolute values of responses due to V3 are larger than those due to the other two models.
7 Conclusions
On the basis of the preceding developments, the following conclusions can be briefly stated.
-
(1)
Using a non-conventional thermodynamic framework, Mindlin’s gradient elasticity theory has been reinterpreted/restated in the context of a continuum theory without assuming explicitly balance laws of double-forces and without leaving parts of stresses indeterminate. It should, however, be emphasized, that double-stresses are present in several constitutive relations of all three models and additionally they are involved in the energy transfer law (143).
-
(2)
The above theoretical study resulted in three versions of gradient elasticity theory: one with inertia in its boundary conditions coinciding with Mindlin’s gradient elasticity (model V1); one without inertia in its boundary conditions (model V2) and one exhibiting classical potential relations for the Cauchy stress (model V3).
-
(3)
On the basis of the problem of the axial motion of a gradient elastic bar fixed at the one end and subjected to an axial load harmonically varying with time at its other end, the three above mentioned versions of gradient elasticity theory have been compared and the effects of the micro-stiffness and micro-inertia on the predicted responses have been determined.
-
(4)
It has been found from the above analyses and comparison studies that the response strongly depends not only on the combination of values of micro-stiffness and micro-inertia coefficients \(\bar{g}\) and \(\bar{h}\), but also on the operational frequency \(\bar{\omega}\). High values of \(\bar{\omega}\) make things complicated as the contribution of higher modes is significant. For the particular case of low frequency \(\bar{\omega}=1.4\) and for vanishing micro-inertia, \(\bar{h}=0\), there is a clear stiffening effect caused by \(\bar{g}\): it can be recognized that for increasing values of \(\bar {g}\) the responses \(\bar{U}\) decrease in all cases and in particular the responses \(\bar{U}\) due to V3 are smaller than those due to the other two models, meaning V3 is stiffer than the other two models.
References
Alber, H.-D., Hutter, K., Tsakmakis, Ch.: Nonconventional thermodynamics, indeterminate couple stress elasticity and heat conduction. Contin. Mech. Thermodyn. (2014). doi:10.1007/s00161-014-0406-1
Bleustein, J.L.: A note on the boundary conditions of Toupin’s strain-gradient theory. Int. J. Solids Struct. 3, 1053–1057 (1967)
Brand, L.: Vector and Tensor Analysis. Wiley, New York (1948)
Coleman, B.D.: Thermodynamics of materials with memory. Arch. Ration. Mech. Anal. 17, 1–46 (1964)
Coleman, B.D., Noll, W.: The thermodynamics of elastic materials with heat conduction and viscosity. Arch. Ration. Mech. Anal. 13, 167–178 (1963)
Dell ’Isola, F., Seppecher, P.: Edge contact forces and quasi-balanced power. Meccanica 32, 33–52 (1997)
Dunn, J.E.: Interstitial working and a nonclassical continuum thermodynamics. In: Serrin, J. (ed.) New Perspectives in Thermodynamics, pp. 187–222. Springer, Berlin (1986)
Dunn, J.E., Serrin, J.: On the thermodynamics of interstitial working. Arch. Ration. Mech. Anal. 88, 95–133 (1985)
Eringen, A.C.: A unified theory of thermomechanical materials. Int. J. Eng. Sci. 4, 179–202 (1966)
Eringen, A.C.: Theory of micropolar elasticity. In: Liebowitz, H. (ed.) Fracture—An Advanced Treatise, vol. I Microscopic and Macroscopic Fundamentals, pp. 621–729. Academic Press, New York (1968)
Eringen, A.C.: Microcontinuum Field Theories: I. Foundations and Solids. Springer, New York (1999)
Fosdick, R.: A generalized continuum theory with internal corner and surface contact interactions. Contin. Mech. Thermodyn. (2015). doi:10.1007/s00161-015-0423-8
Grentzelou, C.G., Georgiadis, H.G.: Uniqueness for plane crack problems in dipolar gradient elasticity and in couple-stress elasticity. Int. J. Solids Struct. 42, 6226–6244 (2005)
Gurtin, M.E., Fried, E., Anand, L.: The Mechanics and Thermodynamics of Continua. Cambridge University Press, New York (2010)
Madeo, A., Ghiba, I.-D., Neff, P., Münch, I.: Incomplete traction boundary conditions in the Grioli-Koiter-Mindlin-Toupin indeterminate couple stress model (2015). arXiv:1505.00995v1 [math-ph]
Malvern, L.E.: Introduction to the Mechanics of a Continuous Medium. Prentice Hall International, Englewood Cliffs (1969)
Maugin, G.A.: Internal variables and dissipative structures. J. Non-Equilib. Thermodyn. 15, 173–192 (1990)
Metrikine, A.V.: On causality of the gradient elasticity models. J. Sound Vib. 297, 727–742 (2006)
Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16, 51–78 (1964)
Mindlin, R.D., Eshel, N.N.: On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 4, 109–124 (1968)
Mindlin, R.D., Tiersten, H.F.: Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 11, 415–448 (1962)
Muki, R., Sternberg, E.: The influence of couple-stresses on singular concentrations in elastic solids. Z. Angew. Math. Phys. 16, 611–648 (1965)
Neff, P., Ghiba, I.-D., Madeo, A., Placidi, L., Rosi, G.: A unifying perspective: the relaxed linear micromorphic continuum (2013). arXiv:1308.3219v3 [math-ph]
Noll, W., Virga, E.G.: On edge interactions and surface tension. Arch. Ration. Mech. Anal. 111, 1–31 (1990)
Podio-Guidugli, P.: Inertia nd invariance. Ann. Mat. Pura Appl. (4) CLXXII, 103–124 (1997)
Podio-Guidugli, P.: A primer in elasticity. J. Elast. 58, 1–104 (2000)
Toupin, R.A.: Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 11, 385–414 (1962)
Toupin, R.A.: Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 17, 85–112 (1964)
Truesdell, C., Toupin, R.A.: The classical field theories. In: Flügge, S. (ed.) Handbuch der Physik, vol. III/1. Springer, Berlin (1960)
Tsepoura, K.G., Papargyri-Beskou, S., Polyzos, D., Beskos, D.E.: Static and dynamic analysis of a gradient-elastic bar in tension. Arch. Appl. Mech. 72, 483–497 (2002)
Acknowledgements
The first two authors acknowledge with thanks the Deutsche Forschungsgemeinschaft (DFG) for partial support of this work under Grant TS 29/8-1.
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article can be found at http://dx.doi.org/10.1007/s10659-016-9585-2.
Appendices
Appendix A
In order to prove the equivalence between Eqs. (80) and (82) it is convenient to start from Eq. (80), written in the form
with
Focussing attention on \(U_{k}\),
and since \(\tilde{\mu}_{ijk}=\tilde{\mu}_{jik}\) (cf. Eq. (74)),
Now, we make use of definitions (2), (3) in the two last terms of the right-hand side of Eq. (A.4) and receive
Thus, \(U_{k}\) becomes
The desired proof follows by substituting the result (A.6) into Eq. (A.1) and then comparing with Eq. (82).
Appendix B
Let \(V\) be a region in \(\mathbb{R}^{3}\), bounded by a close, smooth surface \(\partial V\), and let \(A_{ij}\), \(u_{i}\) be sufficient smooth fields. Then, the integral transformation
applies (see [3, p. 222]). By Eqs. (2), (3), we have
and by using this in Eq. (B.1)
or equivalently
We shall employ this integral transformation in order to derive Eq. (100) from (40)–(43).
It is easily seen from Eqs. (43), (60) and (84), that, for the constrains (61)–(71), the right-hand side of Eq. (40) reduces to the right-hand side of (100). Thus, we have to show that the left-hand side of (40),
reduces to \(W_{\mathit{gen.ext}}\) in Eq. (100). We use the relations \(t_{j}=n_{i}(\tau_{ij}+\sigma_{ij})=n_{i}\tilde{\tau }_{ij}+n_{i}\sigma _{ij}\), \(T_{jk}=n_{i}\mu_{ijk}\), and Eqs. (70), (39), (90) and (91) to obtain, from Eq. (B.5),
The second integral can be recast, by using first equation (92),
and then Eq. (87),
The third integral in Eq. (B.6) can be recast by appealing first to Eq. (87),
and then to Eq. (B.4),
On adding the two equations (B.8) and (B.10),
In view of the well known symmetry (cf. [3, p. 286])
we have
and, therefore, the integral on the far right-hand side in Eq. (B.11) vanishes. The final result reads
By the divergence theorem,
The three equations (B.6), (B.14) and (B.15) yield
and the proof is accomplished.
Appendix C
The aim is to express \(W_{\mathit{gen.ext.}}\) and \(W_{\mathit{diff.}}\) in Eqs. (106)–(109),
in terms of the stresses \(\hat{\tau}_{jk}\), \(\hat{\mu}_{ijk}\).
It is not difficult to see, by recalling to the symmetries \(\tilde{\mu }_{ijk}=\tilde{\mu}_{jik}\), \(\hat{\mu}_{ijk}=\hat{\mu}_{ikj}\), and Eqs. (B.12), (2), (3), (74), (119), that
Therefore,
Also
After substituting Eqs. (C.6), (C.7) and (116) into Eq. (C.2),
which has the desired form.
Appendix D
Explicit expressions of the coefficients \(A_{ij}\) \((i,j=1,2,3,4)\) of Eq. (251):
Rights and permissions
About this article
Cite this article
Broese, C., Tsakmakis, C. & Beskos, D. Mindlin’s Micro-structural and Gradient Elasticity Theories and Their Thermodynamics. J Elast 125, 87–132 (2016). https://doi.org/10.1007/s10659-016-9572-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-016-9572-7
Keywords
- Gradient elasticity
- Mindlin’s micro-structured materials
- Micromorphic continuum
- Symmetric Cauchy stress
- Non-classical inertia
- Non-classical body forces
- Micro-inertia
- Non-equilibrium thermodynamics
- Vibrations
- Micro-stiffness
- Non-classical boundary conditions