Mixing rates in stably stratified flows with respect to the turbulent froude number and turbulent scales

Abstract

In this analysis the quantification of diapycnal diffusivity $K_\rho$ in stratified flows such as those found in the ocean and atmosphere is explored. There are two simplifications that are routinely made when estimating mixing rates in stably stratified flows. First, a constant value is commonly assumed for the (irreversible) mixing coefficient $\Gamma$. Second, dissipation rates of turbulent kinetic energy $\epsilon$ are inferred using either the Thorpe (or Ellison) length scales or from microstructure measurements using the isotropy assumption. Data from three independent direct numerical simulations of homogeneous stratified turbulence are used as a testbed to highlight impacts of these assumptions on estimates of $K_\rho$. A systematic analysis compares the inferred diffusivities to exact DNS diffusivities as a function of the turbulent Froude number $Fr_t$. Use of a constant $\Gamma$ results in an under-prediction of $K_\rho$ by up to a factor of 5 for strongly stratified conditions (low $Fr_t$) and an over-prediction of $K_\rho$ by up to two orders of magnitude in weakly stratified conditions (high $Fr_t$). The use of inferred dissipation rates $\epsilon$ based on the assumption of isotropy results in an over-prediction of $K_\rho$ by a factor of 2 for low $Fr_t$ (which is within the instrumentation error) and converges on the exact $K_\rho$ for $Fr_t \ge 1$. However, the use of kinematic length scales, such as the Thorpe or Ellison scales, to infer $\epsilon$ result in significant errors. The implications of these findings are applied in a simple demonstration to show how these tools can be used for improved estimates of mixing rates in stably stratified flows.

1 Introduction

Diapycnal mixing is the molecular diffusion of density across isopycnals (surfaces of constant density) [7, 34]. In stably stratified flows, such as those found in the ocean and atmosphere, diapycnal mixing is essential for maintaining the circulation driving currents and the resulting overturning events, creating mixing of different fluid masses and transport of nutrients [33]. However, there are numerous challenges for direct measurement of pertinent quantities needed to determine the diapycnal diffusivity $K_\rho$ which provides the pathway for estimating turbulent heat/mass fluxes in both atmospheric and oceanic flows. These include instrumentation that collects subsets of turbulence data, data collected in only the vertical dimension (as profiles) and an inability to make reliable measurements near boundaries [12, 15, 35, 44]. Widely used instrumentation for oceanic measurement that are directly mounted to a buoy or ship include ADCPs (acoustic Doppler current profilers) and CTD (conductivity-temperature-depth) probes. Another common autonomous instrument is the VMP (vertical microstructure profiler) which is released from the surface and collects data while free-falling through the ocean. Thus, by necessity, a number of indirect methods are commonly used for quantifying $K_\rho$ (e.g. Osborn [34]). Under the assumptions of statistical homogeneity and stationarity, the diapycnal diffusivity is commonly obtained from the turbulent kinetic energy equation using the gradient diffusion hypothesis as $K_{\rho }=\Gamma \epsilon /N^2$, where $\Gamma =R_f/(1-R_f)$ is called the irreversible mixing coefficient, $\epsilon$ is the turbulent kinetic energy dissipation rate, and N is the buoyancy frequency associated with the background stratification. $R_f=\epsilon _{PE}/(\epsilon _{PE}+\epsilon )$ is known as the diapycnal mixing efficiency, or flux Richardson number. The dissipation rate of turbulent potential energy is given by $\epsilon _{PE}=N^2\epsilon _\rho (d\bar{\rho }/dz)^{-2}$, where the rate of dissipation of the density (scalar) variance is $\epsilon _\rho =\kappa \overline{(\nabla \rho ^\prime )^2}$. Here $\rho ^\prime$ is the density (scalar) fluctuation and $\kappa$ defines the molecular diffusivity of density (scalar). See Ivey and Imberger [18], Peltier and Caulfield [37], Venayagamoorthy and Stretch [45],Venayagamoorthy and Koseff [44] for detailed discussions of $\epsilon _{PE}$. The turbulent kinetic energy dissipation rate $\epsilon$ is defined

$$\begin{aligned} {\epsilon =\nu \left\langle \frac{\partial u_i}{\partial x_j}\left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) \right\rangle ,} \end{aligned}$$

(1)

where the angle bracket, $\langle \rangle$, represent the ensemble average, $u_i$ is the fluctuating velocity vector, $\nu$ is the kinematic viscosity, and i, $j=1,2,3$. $\epsilon$ can be directly calculated from DNS results (along with other relevant flow quantities) and when calculated is used as the ‘true’ value as compared to the value estimated using the main simplifying assumptions investigated in this analysis.

The three main parameters that are used in the calculation of the diffusivity $K_\rho$ are $\Gamma$, $\epsilon$, and N. In Sect. 3.1 the assumption of a constant (irreversible) mixing coefficient $\Gamma _c=0.2$ is discussed. Implications of estimates of the dissipation rates of turbulent kinetic energy, $\epsilon$, using an assumption of local flow isotropy (as is done in the field when using microstructure data) and indirectly by inference from kinematic flow scales are examined in Sect. 3.2. The combined impact of the simplifications and assumptions made in quantifying $K_\rho$ is discussed in Sect. 3.3. Using three independent direct numerical simulation (DNS) data sets the implications of common assumptions are systematically investigated with careful consideration to implications for estimating turbulent diffusivities from field measurements. We ‘sample’ the DNS data, applying the common assumptions and compare the resulting values for $K_\rho$ to the values determined directly from the DNS. Section 3.4 provides a brief discussion on improving estimates of diapycnal diffusivity from available measurements. The third parameter used for estimating $K_\rho$ is N, the buoyancy frequency. Estimating the background density stratification against which turbulence must work to mix fluids of different densities in the field is not trivial. Investigation of this parameter is beyond the scope of the present analysis and is an area for further investigation. The interested reader is referred to Arthur et al. [1] for a detailed discussion on how the computation of N could impact estimates of diapycnal mixing in stratified flows.

Despite the numerous studies pertaining to prevalent issues with estimating diapycnal diffusivity, to the best of our knowledge, no study has been done to systematically explore and pinpoint the consequences of these assumptions on mixing estimates in this manner. Thus, the main aim of this research is to bring to focus how these common assumptions and practices associated with estimating diapycnal diffusivity could have a significant impact on mixing estimates in stratified flows. These simple procedures provide a demonstration of not only the impact but illuminates how simple procedures combined with knowledge from the literature can possibly be used to improve these estimates moving forward.

2 Simulations and data sources

This work is a direct extension of the work presented in Garanaik and Venayagamoorthy [9] (hereafter GV19). The work of GV19 present a simple and robust parameterization of $\Gamma$ in stratified flow using results of 3 distinct DNS simulation data sets covering conditions of forced, sheared and decaying stratified turbulence. Using estimates of kinematic length scales obtained from the DNS data, the turbulent Froude number $Fr_t$ can be determined for a flow, which in turn can be used to inform the state of mixing. The three different independent DNS data sets presented in GV19 are also used to test the arguments presented within this analysis. The first set of DNS is initially presented in Garanaik and Venayagamoorthy [8] and solve the Navier–Stokes equations with the Boussinesq approximation for stably stratified homogeneous decaying homogeneous turbulent flows. These types of simulations are used to study transient or episodic turbulent flow behavior such as breaking internal waves in the oceans. The second data set analyzed was the high resolution forced DNS of stratified turbulence completed by Maffioli et al. [25]. To achieve stationary turbulence an isotropic forcing (body force) was imposed in the majority of these simulations, however, in a subset of these simulations two-dimensional vortical forcing was imposed in order to achieve flow conditions where the buoyancy Reynolds number $Re_B=\epsilon /\nu N^2$ is greater than 10 within a stratified flow regime. $\nu$ is the kinematic viscosity. The third data set used for this analysis is presented in Shih et al. [40]. This DNS has the relatively lower resolution of $128^3$ grid points but introduce the effects of background shear. Simulations present evolution of homogeneous turbulence forced by a mean shear and a constant background stratification. Each publication where the data has been initially presented, Garanaik and Venayagamoorthy [8], Maffioli et al. [25], Shih et al. [40], can be consulted for further details of the respective simulations. These simulations are useful for illustration of these concepts as they represent simulated conditions of decaying, forced and sheared flows highlighting that the results are similar for all three of these different flow conditions.

3 Results

The ratio between the turbulent diapycnal diffusivity ($K_\rho$) and the molecular diffusivity ($\kappa$) is denoted here as $\hat{\kappa }=(K_\rho /\kappa )$. This is a useful non-dimensional way to represent $K_\rho$ especially when applied to DNS data, to clearly show the magnitude of the diapycnal diffusivity relative to its molecular counterpart. We note that $\hat{\kappa }$ can be defined using $\epsilon _{PE}$, N and $\kappa$ and cast in terms of relevant non-dimensional parameters that define $K_\rho$ where $Pr = \nu /\kappa$ is the molecular Prandtl number and $Re_B$,

$$\begin{aligned} \hat{\kappa }=\frac{K_\rho }{\kappa }=\frac{\epsilon _{PE}}{N^2 \kappa }=\Gamma Re_B Pr. \end{aligned}$$

(2)

In much of this analysis results are plotted using the diffusivity ratio as defined in Eq. 2. If the turbulent diffusivity ratios are computed using the common assumptions and then normalized using the ‘true’ turbulent diffusivity (values calculated directly from DNS results without assumptions), the result necessarily becomes the ratio of the estimated turbulent diffusivity to the ‘true’ turbulent diffusivity $\hat{\kappa }_{(estimated)}/{\hat{\kappa }_\rho }=(K_{(estimated)}/\kappa )/(K_\rho /\kappa )=K_{(estimated)}/K_\rho$, where the $\rho$ subscript denotes the DNS directly calculated diffusivity without the inclusion of any assumptions.

3.1 Application of a constant irreversible mixing coefficient $\Gamma$

In the oceanic setting the irreversible mixing coefficient $\Gamma$ is often assumed to have the constant value of $\Gamma _c=0.2$ [2, 34]. Validity of assuming that this parameter has a constant value has been challenged and debated [12, 16, 23, 29, 38]. Various parameterizations for the mixing efficiency have been proposed [27, 29, 31, 32] but despite this in the ocean a constant value of 0.2 for $\Gamma$ is commonly assumed for estimating diapycnal diffusivities. Assumption of a constant irreversible mixing coefficient oversimplifies diapycnal mixing as the turbulent diffusivity should depend on the magnitudes of turbulence and stratification in a flow, Maffioli and Davidson [24], Venayagamoorthy and Koseff [44]. The definition of the irreversible mixing coefficient given by $\Gamma =\epsilon _{PE}/\epsilon$ is used for the present analysis. Although it is worth noting that other definitions exist that may give a different value of $\Gamma$ (see, e.g. Garrett [11], Howland et al. [14], Lewin and Caulfield [21]). GV19 used direct numerical simulations (DNS) of homogeneous stratified turbulence to clearly show that the value of the irreversible mixing coefficient is not a constant but instead has a strong functional dependence on the magnitude of the turbulent Froude number, $Fr_t = \epsilon /Nk$, where k is turbulent kinetic energy. $Fr_t$ has proved to be a robust parameter for determining the particular state of a stratified flow, i.e., at low values of $Fr_t$, the flow is strongly influenced by buoyancy effects and conversely at high $Fr_t$ by turbulence. This is evident when its definition is cast as a competition of the buoyancy timescale ($N^{-1}$) to the turbulence decay time scale ($T_L=k/\epsilon$). As pointed out by GV19, $Fr_t$ can be used as a diagnostic indicator of the local state of evolution of a stably stratified flow. GV19 also used scaling arguments to show how $Fr_t$ can be determined from the Ozmidov ($L_O$) and Ellison ($L_E$) which may be directly derived from field measurements.

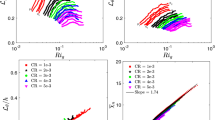
In order to clearly highlight the implication of the constant $\Gamma _c=0.2$ assumption, Fig. 1 shows the diffusivity ratio calculated using a constant irreversible mixing coefficient, $\Gamma _c=0.2$, normalized by the diffusivity ratio calculated using the ‘true’ turbulent diffusivity, $K_\rho$, as taken from the DNS. These values are plotted as a function of the turbulent Froude number and colored by the buoyancy Reynolds number, $Re_B=\epsilon /\nu N^2$, where $\nu$ is the kinematic viscosity. The impact of the constant assumption for $\Gamma$ becomes striking. For $Fr_t \ge 1,$ the assumption of $\Gamma _c=0.2$ results in estimates for the diffusivity ratio up to two orders of magnitude greater than the diffusivity determined directly from the turbulent quantities. As the buoyancy effects increase, the difference between $\hat{\kappa }_c$ and $\hat{\kappa }_\rho$ decreases until they are equivalent as $Fr_t$ approaches unity. Below $Fr_t < 1$, $\hat{\kappa }_c$ under predicts $\hat{\kappa }_\rho$ and reaches a constant value that is about 3 to 6 times less than the exact value $\hat{\kappa }_\rho$ as calculated directly from the DNS. In summary it is clear from this data analysis that an assumption of a constant $\Gamma =0.2$ is not accurate because the mixing efficiency is a dynamic variable that is strongly dependent on the flow conditions as has been pointed out previously by a number of studies such as GV19 and Mashayek et al. [28], recently. It is clear that the assumption of a constant $\Gamma$ does have a significant and differing impact on estimates of turbulent diffusivity depending on competition between the stratification and turbulence in a given flow. The axis at the top of Fig. 1 references the direct relationship between $Fr_t$ and $L_E/L_O$ as shown in GV19 and is discussed in detail in Sect. 3.4.

Fig. 1

Plot of the diffusivity ratio calculated using a constant irreversible mixing coefficient, $\Gamma _c=0.2$, normalized by the diffusivity ratio calculated using the ‘true’ turbulent diffusivity, $K_\rho$, for the Garanaik and Venayagamoorthy [9] DNS. Assuming $\Gamma _c=0.2$ results in an under-prediction of the turbulent diffusivity for strongly stratified flows $Fr\ll \mathcal {O}(1))$ and an over-prediction for weakly stratified turbulence $Fr\gg \mathcal {O}(1)$. All data are colored by their corresponding values of the buoyancy Reynolds number, $Re_B$

3.2 Application of an inferred kinetic energy dissipation rate $\epsilon$

The rate of dissipation of turbulent kinetic energy, $\epsilon$, is often inferred in one of two ways. The first method is to directly infer $\epsilon$ from microstructure measurements that typically use shear probes to measure one or two out of the nine turbulent components of the fluctuating velocity gradient tensor of a three-dimensional velocity field [43, 46]. To do this, the assumption of local (small-scale) isotropy is invoked [4, 8]. Whenever this assumption is made in this analysis it is denoted $\epsilon _{1D}$. This one-dimensional kinetic energy dissipation rate is computed using the volume integrated DNS data. Gregg et al. [12], Itsweire et al [17] and Garanaik and Venayagamoorthy [8] show that the isotropy assumption for the kinetic energy dissipation rate is valid for stratified flows when the turbulent Froude number, $Fr_t \ge 1$. However, when the flow is strongly stratified (typically for $Fr_t < 1$), then the isotropy assumption starts to break down especially when the buoyancy Reynolds number is very small. Increased stratification limits the component of the velocity field in line with the stratification and results in a non-isotropic velocity field [10, 13, 22].

The second method indirectly infers a kinetic energy dissipation rate through an equivalency assumption between derived kinematic length scales namely: the Ozmidov length scale [36] and Thorpe length scale [42]. The Ellison length scale [6] has also been used as an alternative to the Thorpe length scale given that they have been found to track each other quite well [17, 30]. The Thorpe length scales are determined from instantaneous vertical density profiles (typically using CTD casts from a ship or mooring) or from VMP dropped from a ship. Using such one-dimensional profiles, both the Thorpe ($L_{Th}$) and Ellison ($L_E$) scales provide a statistical measure of the vertical distance travelled by fluid parcels in order to achieve a position of equilibrium [5, 6, 42, 43, 47]. The Ozmidov length scale is a kinematic length scale that is often used to define the size of an isotropic large eddy scale that is unaffected by buoyancy in stratified turbulence. Thus, based on the grossly simplifying assumption that the Thorpe scale ($L_{Th}$) is equivalent to the Ozmidov scale ($L_O=(\epsilon /N^2)^{1/2}$), the rate of dissipation of turbulent kinetic energy is inferred (i.e. $\epsilon _{Th}=L_{Th}^2N^3$). Mater et al. [30] presented arguments that $L_O$ and $L_{Th}$ are only equivalent for flow conditions with a turbulent Froude number of order 1. Smyth and Moum [41] showed that the ratio of the Thorpe and Ozmidov length scales can be used to estimate the age or evolution of a turbulent event. The analysis of GV19 rigorously showed that the ratio of the Ellison (or Thorpe) and Ozmidov length scales can be used to infer both the local state of turbulence and the mixing efficiency in stably stratified turbulent flows. These three length scales see widespread application given that they can be readily calculated from measured field data but also see widespread use in analysis of numerical simulations [3, 19, 20].

Figure 2a shows the three inferred dissipation rates of turbulent kinetic energy, $\epsilon _{1D}$, $\epsilon _{L_E}$ and $\epsilon _{Th}$ derived from the Garanaik and Venayagamoorthy [8] DNS data using analogous processes that would be used to derive an estimate of the kinetic energy dissipation rate from a one-dimensional microstructure profile, the Ellison scale and the Thorpe scale from measured field data, respectively. Each of these inferred kinetic energy dissipation rates are normalized by the exact dissipation rates $\epsilon$ obtained directly from the DNS, and plotted as a function of the turbulent Froude number. Results calculated by indirect inference using the Ellison and Thorpe scales, while are not exact, closely track each other confirming the analysis of Itsweire et al [17] and Mater et al [30]. In Fig. 2a for small values of the turbulent Froude number ($Fr\ll \mathcal {O}(1))$, the inferred rates of dissipation of kinetic energy derived from the kinematic length scales are approximately 15–18 times larger than $\epsilon$. Above $Fr_t\sim 1$, $\epsilon _{L_E}$ and $\epsilon _{Th}$ under-predict $\epsilon$ resulting in a ratio close to zero. Results show that an assumption of isotropy does not have a significant impact, over-predicting the kinetic energy dissipation rate by a factor of two for strongly stratified conditions ($Fr_t<<1$). This over-prediction decreases as $Fr_t$ increases becoming functionally equivalent to the exact dissipation rates above $Fr_t > 1$, for weakly stratified flow conditions. The over-prediction visible in this plot is a result of the stratification of the flow and the resulting anisotropy of the flow at low magnitudes of $Fr_t$. This clearly shows that using the Thorpe or Ellison scale for estimations of $\epsilon$ oversimplifies the strength of the anisotropic structures in strongly stratified flows.

Fig. 2

Subplot a show rates of dissipation of turbulent kinetic energy inferred using an assumption of local isotropy ($\epsilon _{1D}$), derived from the Ellison length scale ($\epsilon _{L_E}$) or derived from the Thorpe length scale ($\epsilon _{Th}$) all normalized by the true kinetic energy dissipation rate $\epsilon$. These normalized kinetic energy dissipation rates are plotted as a function of the turbulent Froude number $Fr_t$ and colored by the corresponding values of the buoyancy Reynolds number ($Re_B$). The second subplot, b shows the impact of the different assumed kinetic energy dissipation rates on the turbulent diffusivity through plots of the normalized diffusivity ratio. The plots demonstrate that using one-dimensional kinetic energy dissipation rates (e.g. from field microstructure measurements) give more accurate estimates than those inferred using the Ellison of Thorpe length scales

Figure 2b shows the results of using $\epsilon _{1D}$, $\epsilon _{L_E}$ and $\epsilon _{Th}$ in calculations of normalized turbulent diffusivity ratio for the Garanaik and Venayagamoorthy [8] data. If $\epsilon _{1D}$ is used the over-predictions remain much less than an order of magnitude for flows at low $Fr_t$ and becomes equivalent at high $Fr_t$ which indicates that anisotropic effects of stratification are not dominant/important when $Fr_t > 1$. Using $\epsilon _{L_E}$ in calculations of the turbulent diffusivity amplifies the differences shown in Fig. 2a. In the strongly stratified flow regimes ($Fr_t<\mathcal {O}(0.1)$) the turbulent diffusivity is up to one order of magnitude greater than $\hat{\kappa }_\rho$. For $Fr_t>\mathcal {O}(1)$ the turbulent diffusivity calculated using $\epsilon _{L_E}$ ($\sim \epsilon _{Th}$) results in an under-prediction of the turbulent diffusivity by up to three orders of magnitude for $Fr_t \approx 10$. This is a result of the inferred $\epsilon _{L_E}$ and $\epsilon _{Th}$ having very small magnitudes compared to the true dissipation rates for weakly stratified flow conditions. This result has important implications in the field when only CTD profiles are used to infer mixing rates in a weakly stratified turbulent flow field since any large overturns would essentially be cancelled out by small values of the background density gradients resulting in low mixing even though the turbulence is potentially strong. DNS data of Maffioli et al [25] and Shih et al. [39] show similar trends and are omitted from Fig. 2 for clarity.

3.3 Application of a constant mixing coefficient combined with an inferred kinetic energy dissipation rate

As pointed out previously, it is common practice to use a constant mixing coefficient combined with an inferred kinetic energy dissipation rate in estimating the turbulent diffusivity. The next step in this analysis is to investigate how the two common assumptions explored in the previous two sections influence estimates of turbulent diffusivity in stratified flow when combined rather than in isolation. Figure 3 shows estimated turbulent diffusivities calculated with these two combined assumptions. All data are plotted as a function of the turbulent Froude number and colored by the buoyancy Reynolds number. Figure 3a shows the magnitudes of the diffusivity ratio calculated with a constant irreversible mixing coefficient $\Gamma _c=0.2$ and a one-dimensional kinetic energy dissipation rate $\epsilon _{1D}$, for both the Garanaik and Venayagamoorthy [8] and Maffioli et al. [25] data, normalized by $\hat{\kappa }_\rho$. Results for the diffusivity ratio calculated using a kinetic energy dissipation rates derived from the Ellison kinematic length scale $\epsilon _{L_E}$ in combination with $\Gamma _c=0.2$ are presented in Fig. 3b for all three data sets. These results are also normalized by $\hat{\kappa }_\rho$

Fig. 3

Plots illustrating the combined impact of a constant mixing coefficient and inferred rates of dissipation of turbulent kinetic energy as a function of turbulent Froude number, $Fr_t$. a Diffusivity ratios calculated using (i) isotropic assumption in conjunction with (ii) a constant $\Gamma _c = 0.2$ and b diffusivity ratios calculated using (i) inferred dissipation rates from Ellison scale in conjunction with (ii) a constant $\Gamma _c = 0.2$. Diffusivity ratios calculated using the combined irreversible mixing coefficient and kinetic energy dissipation rate assumptions used for estimation of the turbulent diffusivity are shown in normalized by $\hat{\kappa }_\rho$. All data is colored by the buoyancy Reynolds number, $Re_B$

As clearly illustrated in Fig. 3a for the case where $\Gamma _c$ is combined with $\epsilon _{1D}$ the estimated turbulent diffusivity over-predicts the true diffusivity by up to two orders of magnitude for $Fr_t>\mathcal {O}(1)$. For $Fr_t<\mathcal {O}(1)$ the estimated diffusivity under-predicts the true value by 2-3 times the true value. The turbulent diffusivity is over-predicted in flows dominated by buoyancy effects (low $Fr_t$) by up to one order of magnitude and under-predicted by almost two orders of magnitude for flows with low stratification when $\Gamma _c$ and $\epsilon _{L_E}$ are both used, as illustrated in Fig. 3b. These results show that while these assumptions may be acceptable for flow regimes with $Fr_t\sim \mathcal {O}(1)$, for flow regimes that are characterized by a turbulent Froude number outside this narrow intermediate range, the combination of these two assumptions will lead to predictions of turbulent diffusivities that are much different than the actual flow diffusivities especially in cases where a kinematic length scale ($L_E\sim L_{Th}$) is used to estimate the kinetic energy dissipation rate.

As could be predicted based on observing the data trends in Figs. 1 and 2 the combination of $\Gamma _c$ and $\epsilon _{1D}$ results in an estimate of turbulent diffusivity for flows with $Fr_t<\mathcal {O}(1)$ that is not significantly different from the true magnitude. Under-prediction of the turbulent diffusivity created by $\Gamma _c$ is mostly offset by the over-prediction created by using $\epsilon _{1D}$ in strongly stratified flow regimes. For $Fr_t>\mathcal {O}(1)$ the assumption of $\Gamma _c$ dominates the estimates creating an over-prediction that reaches up to two orders of magnitude. The nearly constant turbulent diffusivity shown in Fig. 3a for the more strongly stratified flows is simply a result of combining the two different assumptions and is not a physical characteristic of the flow. We have used data and analysis driven by the physics of the controlling equations applied in the DNS to show that while these common assumptions may be acceptable when using microstructure measurements ($\sim 2-3$ times difference) it has been traditionally made for the wrong reasons. Pieces of this analysis, such as the differences in assuming a one-dimensional kinetic energy dissipation rates from field measurements, have been discussed in other settings but this analysis brings these ideas together within a framework for understanding assumptions used for computing the turbulent diffusivity. Such a systematic analysis that breaks down and analyzes the impact of each of these parameters on estimates of the turbulent diffusivity has not been shown previously.

3.4 Implications for improved estimates of mixing in stratified turbulence

In the light of these issues, the question then is how can this information be used to improve estimates? Here we discuss how best to leverage these insights to improve estimates of mixing even when only limited physical measured data are available. Use of scaling insights developed from physically based arguments in combination with careful consideration of the assumptions made will directly incorporate consideration of the relevant flow physics and limit unnecessary approximations. The turbulent Froude number as used in this analysis is a useful parameter for indicating the local state of turbulence (GV19) and as a measure of the competition between the turbulence and buoyancy time scales in stratified flows [30]. In the proceeding analysis $Fr_t$ will be used directly in determining the best estimate of $K_\rho$, however it is worth noting here that the results up to this point would not be influenced by completing the analysis as a function of $Re_B$ instead of $Fr_t$. While the $Fr_t$ parameter is useful for flow classification and theoretical analysis, it is difficult to calculate from field measurements, hence the prevalent and persistent use of $Re_B$, but it turns out that it does not need to be explicitly determined for improved estimates. For example, GV19 show that through robust scalings based on the flow physics $Fr_t$ can estimated using the ratio between $L_E$ and $L_O$ (see their Fig. 3).

Analysis in Sect. 3.1 clearly corroborates the assertion that the irreversible mixing coefficient can not be assumed constant as has been discussed in many recent publications [9, 21, 25, 26, 28]. Determination of the best estimate of the irreversible mixing coefficient can be determined using scaling presented by these sources. For example the scaling arguments presented in GV19 using the ratio of $L_O$ and $L_E$, and in particular, the scaling results presented in Fig. 4 of GV19 allows for determination of a value of $\Gamma$ that is best for the measured flow conditions given a ratio of $L_E$ to $L_O$. Similarly, Mashayek et al [28] present a scaling range of the irreversible mixing coefficient that is similarly based on a ratio of kinematic length scales $L_O$ to $L_{Th}$, defined by Eq. 3

$$\begin{aligned} \Gamma =A\frac{\left( \frac{L_O}{L_{Th}}\right) ^{-1}}{1+\left( \frac{L_O}{L_{Th}}\right) ^{1/3}}.\qquad \qquad \frac{2}{5}\le A\le \frac{2}{3} \end{aligned}$$

(3)

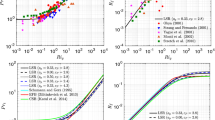
While $L_E$ and $L_{Th}$ are derived differently, in this analysis if it is assumed $L_E\sim L_{Th}$ the results of GV19 and Mashayek et al. [28] can be compared by replacing $L_{Th}$ in Eq. 3 with $L_E$. Results in Fig. 2a, b show tracking between the results derived from these two kinematic length scales. Figure 4 here shows Fig. 4 from GV19 combined with the parameterization of $\Gamma$ from a modified form of Eq. 3. The two results show remarkable agreement which would be expected since the asymptotic scalings found in Mashayek et al. [28] are the exact inverse of the scaling relationships found by GV19. The inverse relationship is due to the inverse ratio of the kinematic scales used by the two analyses. For the most stratified flow ($L_E/L_O\ge 0.2$) the relationship breaks down as it is outside of the range defined for application of Eq. 3. As noted in GV19 a constant $\Gamma \sim 1/3$ can be assumed for flows with high stratification. Since the Ozmidov scale $L_O=\left( \epsilon /N^3\right) ^{1/2}$ can not be directly calculated using data measured from the field, we use the inferred $\epsilon _{1D}$ to get the best estimate of $L_O$ based on the results from Sect. 3.2. The parameterization of $\Gamma$ given by Eq. 3 includes a parameterization constant A with a defined range. This variation necessarily creates a range in the possible values of $\Gamma$ resulting from application of the equations.

Fig. 4

Figure 4 shows a recreation of the Fig. 4 from GV19 [9] in combination with the parameterization (modified) for the irreversible mixing coefficient $\Gamma$ presented in Mashayek et al.  [28] noting that the variation in parameterization constant A results in a variation range contained between the dashed lines. The parameterization of of the irreversible mixing coefficient $\Gamma$ has been modified by replacing the Thorpe length scale, $L_{Th}$, with the Ellison length scale, $L_E$. Parameterization calculated using an Ozmidov length scale, $L_O$, calculated using and a one-dimensional kinetic energy dissipation rate, $\epsilon _{1D}$ can also be applied. In addition, note that despite the criticism articulated by Mashayek et al. [28] of the $\Gamma$ parameterization in GV19 there is in fact no functional difference between the two parameterizations, as shown

Analysis in Sect. 3.2 clearly shows that an assumption of local isotropy for the estimation of the rate of dissipation of kinetic energy dissipation using microstructure measurements may be reasonable. Using $\epsilon _{1D}$ only will bias turbulent diffusivity estimates by factor of 2-3 times as compared to multiple orders of magnitude if $\epsilon _{L_E}$, or similarly $\epsilon _{Th}$, is used. This again underscores how the common assumption of the equivalency between the Thorpe and Ozmidov scales to infer dissipation rates of turbulent kinetic energy is fundamentally flawed.

From the analysis presented herein improved estimates of the turbulent diffusivity $K_\rho$ can be made when limited data sets are all that are available. The two main considerations are choosing the appropriate irreversible mixing coefficient $\Gamma$ and dissipation rate of kinetic energy $\epsilon$. Determining the best $\epsilon$ is simple and straightforward. Analysis in Sect. 3.2 clearly illustrates that inferring the dissipation rate of kinetic energy from one component of the velocity gradient tensor is superior to inferring from either the Ellison of Thorpe kinematic length scales. $\epsilon _{1D}$ is available from data measured in the field and should be used in place of $\epsilon$ when estimating $K_\rho$. For example simple parameterizations of $\Gamma$ as a function of $L_E/L_O$ are presented in GV19 and in Mashayek et al. [28]. When $\epsilon _{1D}$ is used in calculating $L_O$ the estimates for $\Gamma$ given by these two methods will be functionally equivalent except when $L_E/L_O>\mathcal {O}(2)\sim Fr_t<\mathcal {O}(0.1)$. In this case $\Gamma \approx 1/3$ should be applied as presented in GV19. Note that $Fr_t$ can also be determined using $L_E/L_O$ as shown in the results presented in Fig. 3 of GV19. These considerations in inferring $\epsilon$ and $\Gamma$ for use in estimating the diapycnal diffusivity $K_\rho$ will greatly improve estimates of mixing in stably stratified turbulence as illustrated in Fig. 5. This figure clearly shows the impact of applying these recommended procedures will have on achieving better estimates of the turbulent diffusivity.

Fig. 5

Plot graphically illustrating how estimates of diapycnal diffusivity can be improved by using a one-dimensional kinetic energy dissipation rate $\epsilon _{1D}$ in combination with the estimates of the irreversible mixing coefficient using parameterizations provided by GV19 $\sim$ Mashayek et al. [28] for $Fr_t>O(0.1)$ and $\Gamma =1/3$ for $Fr_t\le O(0.1)$

4 Concluding remarks

The analyses presented here provide a systematic, yet simple, evaluation of the most common assumptions used in applications when estimating the diapycnal diffusivity from limited data sets. DNS data of homogeneous stratified turbulence have been used in a manner that takes into direct consideration how the data from field measurements are used. Use of a constant value for the irreversible mixing coefficient combined with indirect inference of the kinetic energy dissipation rate from either the Thorpe (or Ellison) scale results in significant error in the estimations of the turbulent diffusivity. When compared to values calculated directly from the DNS data an assumption of local isotropy from microstructure measurements combined with a determination of a irreversible mixing coefficient value from a suitable parameterizations should result in more accurate estimates as clearly illustrated by the example application shown in Fig. 5.