An empirical parametrization of internal seiche amplitude including secondary effects

Abstract

An internal wave is a propagating disturbance within a stable density-stratified fluid. The internal seiche amplitude is often estimated through theories that describe the amplitude growth based on the Bulk Richardson number (Ri). However, most theoretical formulations neglect secondary effects that may influence the evolution of internal seiches. Since these waves have been pointed out as the most important process of vertical mixing, influencing the biogeochemical fluxes in stratified basins, the wrong estimation may have several impacts on the prediction of the system dynamics. This research paid particular attention to the importance of secondary effects that may play a major role on the basin-scale internal wave amplitude, especially related to the interaction between internal waves and lake boundaries, internal wave depth, and mixing processes due to turbulence. Based on a set of methods, which include auto- and cross-correlations, spectral analysis, and mathematical models, we analyzed the effect of total water depth, wind-resonance, and higher vertical modes on the amplitude growth. We based our analysis on underwater temperature measurements and meteorological data obtained from two small thermally-stratified basins, complemented with numerical simulations. We introduce here a new parametrization which takes into account the total water depth (H), lake length (L), epilimnion thickness ($h_e$), as well as the resonance effect. We observed that the rate of amplitude growth decreases compared to linear theory when $Ri~h_e/L\le 1$. In these cases, we suggests that previous theories overestimate the internal seiche amplitude, neglecting the instabilities generated near the wave crest due to weak stability and wave interactions. However, under shallow thermocline conditions, due to extra pressure in the upper layer, the vertical displacement may be higher than that predicted by the linear theory.

1 Introduction

Internal gravity waves are a propagating disturbance within a stable density-stratified fluid, and have been observed to have great impact on many stratified ecosystems, such as atmosphere [50], ocean [56], lakes, and reservoirs [23]. In closed stratified systems, generally called basins, such as lakes and reservoirs, the most common type of waves is the basin-scale internal wave which is often formed due to the wind stress at the water surface [55]. Herein, the wind introduces kinetic energy at the water surface, and the wind stress pushes the surface water to the leeward shore, causing a small surface displacement. If the wind stress is applied for sufficient time, the horizontal pressure gradient rises, and the hypolimnion water is accelerated towards the upwind direction, resulting in an internal tilt of the thermocline (Fig. 1). When the wind stops, the tilted layer flows back towards equilibrium. However, as momentum is considerable the equilibrium position can be overshot, resulting in a rocking motion around the nodal point, which characterizes the evolution of a basin-scale internal wave (BSIW), a stationary wave.

Fig. 1

A wind-induced stationary internal wave in a stratified basin. Left: Tilting of surface and interface, due to wind stress. Right: Oscillatory motion of surface and interface after wind stopped at one half of the wave period. Dashed lines indicate surface and interface location right after wind stopped

Basin-scale internal waves have been studied extensively since the Twentieth century. New field and laboratory measurement techniques have provided a better understanding of internal wave patterns, revealing the strong influence on the system dynamics. Studies have pointed out that wind-induced BSIWs are responsible for benthic boundary layer resuspension [11]. Furthermore, there is evidence that up to $40\%$ of the hypolimnic volume may be exchanged after a passage of a BSIW in stratified lakes [52]. Wind-induced internal seiches are capable of moving back and forth between the reservoir boundaries without appreciable damping. In addition, the energy deposited into such long internal seiches is transformed through a down-scale energy cascade across the spectrum of internal waves [8], increasing the system mixing, and consequently, affecting significantly the water quality of these ecosystems. Internal waves produced in stratified systems have direct consequences on nutrients [32], microorganisms [36], and chemical substance fluxes [9].

Normally, BSIWs are classified by nodal points on the vertical (V) and horizontal (H) components, VnHm, in which n and m are the number of nodes of each component (Fig. 2). Higher vertical internal seiche modes were rarely reported for large lakes. However, there is a growing evidence that the formation of higher vertical modes is more evidenced in small lakes where the metalimnion takes up a relatively larger proportion of the total lake depth than in large closed basins [39]. In addition, there is evidence that the higher vertical modes are also correlated to unequal differences of density between layers, wind resonance, and basin asymmetry [35].

Fig. 2

Schematic view of various internal wave modes in a closed basin: a V0H1, b V1H1, c V2H1 and d V1H2. The mode for n = 0 is related to the pure surface (barotropic) mode. The black dots ($\cdot$) represent nodal points

Previous theories of the dynamics of BSIWs have shown that the internal seiche amplitude is inversely proportional to the ratio of the buoyancy frequency and the vertical wind shear [6, 42, 44], which is often described by the Bulk Richardson number (Ri),

$$\begin{aligned} Ri = \frac{g'h_e}{\kappa u_*^2}, \end{aligned}$$

(1)

in which $g'$ is the reduced gravity $(=g\Delta \rho /\rho )$, $\kappa \approx 0.4$ is the Von Kármán constant, $h_e$ is the epilimnion thickness at the deepest point, and $u_*$ is the friction velocity of the wind. Although many studies have investigated internal seiches excited during summer seasons due to the stratification conditions, higher amplitude internal waves have been detected during periods of weak thermal-stratification [2].

Current theories and descriptions of internal wave dynamics [6, 42, 44] have shown good agreement with field observations under some conditions, especially for high Bulk Richardson numbers [48]. However, the motion of the basin-scale internal waves is not well understood yet. The theories formulated to describe the evolution of BSIWs just take the thickness and density of an immiscible two-layer system and the wind intensity into account. Based on that, the theories show that the weaker the stratification, the higher will be the internal wave. However, the evolution of BSIWs can be modified by secondary effects, such as the influence of mixing due to higher turbulence production, interaction between internal wave and lake surface and lake bathymetry, wind resonance, and systems with multi-layer or continuous stratification, which may favor the formation of higher vertical modes. Furthermore, only specific case studies analyzed their internal wave characteristics [40, 47, 54]. Studies are missing on analysis of universal features or common processes that cause the excitation of BSIWs and their evolution, and this holds especially for BSIWs generated during periods of low Bulk Richardson number.

This study therefore aimed to compare field observations and numerical simulations with previously established theories that predict the height of BSIWs based on dimensionless variables [42, 44]. This paper highlights the differences between BSIWs generated in different conditions, and exploring the reasons of these differences. Based on this analysis, we suggest a new empirical parametrization which includes the contribution of internal seiche interaction with lake boundaries. The analysis is based on Ri and internal seiches detected in two real thermally-stratified basins (Vossoroca reservoir and Harp Lake) and additionally generated in a three-dimensional numerical model, considering different meteorological and underwater temperature conditions.

2 Methods

To identify internal wave patterns, we used spectral analysis of different isotherms and pycnocline variations. From the governing equation of motion, internal wave periods were estimated. To highlight and observe the universality of BSIWs, internal seiches were analyzed in two different thermally-stratified basins, a dendritic reservoir in the subtropics and a nondendritic lake in a temperate climate. We also simulated the formation of BSIWs in a three-dimensional numerical model under different density stratifications and pycnocline depths. We combined all parameters and stratification structures obtained from Vossoroca Reservoir, Harp Lake, and the numerical simulations, in a single diagram, through a new parametrization.

2.1 Site description and data collection

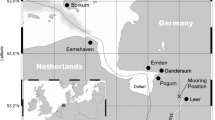
Vossoroca Reservoir (25$^{\circ }$ 49$^{\prime }$ 31$^{\prime \prime }$ S, 49$^{\circ }$ 3$^\prime$ 60$^{\prime \prime }$ W) is a small and dendritic-shaped reservoir located $30~{{\text {km}}}$ from Curitiba, capital of Paraná state in southern Brazil. The reservoir presents a shoreline development index of 6.2 (ratio of the length of the shoreline to lake area) and has two long narrow arms $300~{{\text {m}}}$ wide oriented to the southeast and southwest with length of $3.25~{{\text {km}}}$ and $2.72~{\text {km}}$, respectively. The reservoir, shown in Fig. 3 (left), has a volume of $35.7~10^6~{\text {m}}^3$, a maximum depth of $17~{\text {m}}$, an average depth of approximately $6~{\text {m}}$, and surface area of $510~{\text {ha}}$. The wind action over the reservoir is essentially driven by the regional topography to northeast direction with an average magnitude of $3.6~{{\text {m/s}}}$. Winds stronger than $5.5~{{\text {m/s}}}$ are rare in the region, lasting only few minutes and never greater than $7.3~{\text {m/s}}$.

We compare the results obtained from Vossoroca Reservoir with those obtained from Harp Lake. Harp Lake (45$^{\circ }$ 22$^\prime$ 45$^{\prime \prime }$ N, 79$^{\circ }$ 08$^\prime$ 08$^{\prime \prime }$ W), which has been monitored by Dorset Environmental Science Centre (DESC) [58,59,60], is a small, square-shaped lake located in south-central Ontario, Canada. The lake, shown in Fig. 3 (right), is an oligotrophic lake with an area of $71.38~{\text {ha}}$, volume of $9.5~\text {million m}^3$, maximum depth of $37.5~{\text {m}}$, and average depth of approximately $13.3~{\text {m}}$. The Harp Lake presents a shoreline development index of 1.7. The wind does not present a dominant direction as observed in Vossoroca Reservoir, presenting wind speed average of $3.0~{\text {m/s}}$, with a maximum of $5.4~{\text {m/s}}$.

Fig. 3

Maps of Vossoroca reservoir (left), and Harp Lake (right), with depth contours and locations of observation points (green: meteorological station, red: platform with thermistor chain), and in and outflows (arrows)

The vertical temperature structure of Vossoroca Reservoir corresponds to a holomictic (i.e. polymictic) lake, whilst Harp lake is a dimictic lake that is covered by ice during the winter. In Vossoroca reservoir, periods with weaker stratification start in autumn (after April), and the system is completely mixed only in July. In summer, around December, the temperature difference between bottom and surface reaches $10~^{\circ }{\text {C}}$. The relatively simple bathymetry of Vossoroca Reservoir and the constant wind direction leads to standing internal wave activities [12]. This study amplifies the previous study by adding a multi-layer model and a complete analyses along the whole year of 2012 and 2013.

Differently from Vossoroca reservoir, in Harp Lake, the thermal stratification starts after April (spring in the northern hemisphere), and the system is strongly stratified in July with $\Delta T = 20~^{\circ }{\text {C}}$. Between the northern winter period, December and March, the lake is ice-covered. Although studies have identified internal waves in ice-covered lakes [10], the excitation mechanism during the winter season is not due to wind forcing on the water surface. As our goals in this study is to compare results between Vossoroca Reservoir and Harp Lake, the consideration of internal waves in ice-covered season was beyond the scope of this study. Thus, we just investigate the internal wave activity during summer and autumn for Harp Lake.

Water temperature, water level, solar radiation, wind speed and direction were recorded during 2010 to 2015. Wind direction and velocity were measured in Vossoroca reservoir and Harp Lake by a Young wind monitor with accuracy of $\pm ~2^{\circ }$ and $\pm ~3^{\circ }$, respectively, both with $\pm ~0.3~{\text {m/s}}$ of speed accuracy. Solar radiation was measured in Vossoroca Reservoir and Harp Lake by a Campbell Scientific CMP3-L Pyranometer with accuracy of $\pm ~1~{\text {W/m}}^2$ and a Kipp & Zonen Solar Radiation CMP6 Sensors with accuracy of $5~\text {to}~20~\upmu {\text {V/W/m}}^2$, respectively. The meteorological station recorded data at 30-min and 10-min interval in Vossoroca and Harp, respectively.

A thermistor chain was deployed at both basins, at the deepest point (Fig. 3). The chains were equipped in Vossoroca reservoir and Harp Lake with seven thermistors LM 35 with sampling frequency of 10-min and 28 Campbell Scientific thermistors with a sampling rate of 10-min, respectively. Both thermistor chains have an accuracy of $\pm ~0.1~^{\circ }{\text {C}}$. We analyzed internal seiche formation through water temperature and meteorological data from 2012 to 2015, and we chose different sub-periods to identify baroclinic activity during different seasons and thermal conditions.

2.2 Data treatment

We calculated density profiles based on the last version of the equation of state proposed by Commission et al. [29]. We neglected the contribution of salinity to density since salinity levels in those freshwater bodies were insignificant. Moreover, we also ignored the effect of pressure on water density since we considered the flow as incompressible [33]. Although, as stated by Wüest and Lorke [57], dissolved substances may affect water density, however, relevant substance concentrations were insignificant, too.

For the definition of the pycnocline depth and the metalimnion thickness, we used the weight approach proposed by Read et al. [37]. This technique adds a weight to adjacent measurements, improving the initial guess that the pycnocline is located at the midpoint depth between two measurements that present the highest temperature change. In addition, for Vossoroca reservoir, we compared, during sporadic campaigns, once or twice a month, temperature profiles obtained from the thermistor chain with CTD (Conductivity, Temperature, and Density) profiles obtained by a Sontek CastAway probe. The isotherms were obtained through linear interpolations from water temperature data [30].

2.3 Numerical simulation

We conduced a total of 32 numerical simulations in a rectangular basin to simulate the formation of a BSIW in a two-layer thermally stratified rectangular tank of $4~{\text {km}}$ long and $500~{\text {m}}$ wide with a constant water depth of $15~{\text {m}}$ (Figure 4a). These dimensions were chosen based on general dimension of Vossoroca reservoir. We covered a range of density differences of $0.04~{\text {kg/m}}^3\le \Delta \rho \le 2.32~{\text {kg/m}}^3$, which correspond to temperature difference of $0.25~^\circ {\text {C}}$ to $11~^\circ {\text {C}}$. The density range used were chosen based on values of Ri. For all simulation, the initial temperature of the lower layer was assumed to be constant and equal to $15~^\circ {\text {C}}$. We changed the ratio $h_e/H$ from 0.13 to 0.73, in which $h_e$ is the upper layer thickness and H is the total water depth ($H=15~{\text {m}}$).

Fig. 4

a Sketch of the numerical experiment and b the wind event responsible to excite a BSIW for all numerical simulations. Red bar indicates the period of homogeneous wind

We used the Delft3D-FLOW model [15], which is capable of simulating the hydrodynamics of shallow water system, such as coastal waters, rivers, lakes, reservoirs, and estuarine areas, providing a detailed analysis of the spatial and temporal variations of physical mixing and transport processes in water bodies. This model has been widely used to analyze the hydrodynamics of stratified water basins and the biological effects in these ecosystem. Moreover, evidences show that the Delft3D model might successfully reproduce the formation and evolution of basin-scale internal waves in stratified lakes [16]. The model solves the unsteady Reynolds-averaged Navier–Stokes equations and the hydrostatic assumption for heat and momentum transfer across the tank through a finite difference approach with an ADI numerical scheme. The model uses a multi-directional upwind scheme to solve the horizontal advection equation [45]. For a better analysis of the dynamics of BSIWs, we neglected the heat transfer at the water surface, as well as through internal heating by radiation. Thus, there is no heat energy source or sink considered. In addition, we did not consider the Coriolis effect, which could favor the occurrence of Kelvin and Poicaré internal waves in large lakes or higher vertical baroclinic modes. We used the $k-\epsilon$ turbulent closure scheme [38], in which turbulent kinetic energy and energy dissipation was estimated by the transport equation.

Simulations were performed on a $90~{\text {m}}\times 90~{\text {m}}$ horizontal grid with 50 fixed layers equally spaced in depth providing a vertical resolution of $30~{\text {cm}}$. We used a z-grid in the vertical direction and an orthogonal grid in the horizontal plane. The depth of each layer was defined in the center of each cell, whereas the velocity field was defined in the middle of the cell side. To satisfy the Courant–Friedrichs–Lewy (CFL) stability condition, a time step of 1 min was used in all simulations. The formation of basin-scale internal waves was obtained through an initial stress boundary condition at the free surface that was kept equal for all simulations. We considered one wind event with maximum peak of $4.5~{\text {m/s}}$ blowing in the west direction for $\approx 4~{\text {h}}$ (Fig. 4b). No inflows or outflows were considered.

2.4 Spectral analysis

To identify the periodicity and evolution within the measured data, we used Wavelet and Fourier transforms. The spectral analysis of isotherms was used to determine the number of standing wave modes, the depth variation of each mode, and its energy distribution.

The spectral analysis was applied to the time series of wind speed, solar radiation, and the depth of different isotherms. Power spectral densities were applied to overlapping data segments using the Hamming window function. Then, firstly, we obtained the traditional fast Fourier transform (FFT), which provided time-averaged pictures of the frequency distribution. Since we did not know exactly what is the internal wave period range that could be excited in the stratified system, we used four different window sizes (5 days, 1 day, 12 h, and 1 h) to analyze the spectrum. This technique was used to improve the confidence interval for the spectral power at short time periods. To analyze more details in frequency spectral variance, we reduce the window size to average more numbers of segments, and tried to balance the frequency resolution and the internal wave peak variance.

We used $50\%$ of overlapping for the Hamming procedure [22]. Secondly, through the ratio of sampling frequency and the mean-square power spectrum, which is obtained through the Fourier transform of the auto-covariance function, we obtained the power spectral density (PSD).

We obtained the coherence and phase shift of isotherms and meteorological data to identify energetic peaks in the temperature spectrum that could indicate resonance between wind-forced oscillations and the internal seiche modes, and the excitation of higher vertical baroclinic motions. We compute the coherence between two signals using the mean-square power spectrum of these signals and the cross power spectrum.

Finally, we applied the wavelet technique in different isotherms since this solves the variations of frequency content with time, improving the temporal resolution [51]. We applied the discrete time continuous wavelet transform (DT-CWT) to the isotherms. We used the Morlet basic wavelet function since it consists of a plane wave modulated by a Gaussian function, improving considerably the temporal resolution.

2.5 Internal seiche model

All results from the processed field observations and the numerical simulations will be compared also to a simplified seiche model to check its performance and accuracy for the presented multi-scale cases.

We used a multi-layer hydrostatic linear model with free surface and the shallow water assumption ($H~\ll ~\lambda$) based on Mortimer [34] three-layer model. We computed the wind fetch based on the geographic wind direction and the basin length. As mentioned before, if the wind stress is applied for sufficient time, the setup height at the lake end can increase and, consequently internal waves can develop. Therefore, we compared the wind stress and the direction of the wind to identify the direction and predicted periodicity of internal seiches. We computed the mean internal seiche period by averaging all the fetch vectors within 20 degree from the main wind direction, considering the pycnocline shore for V1H1 mode.

Based on the governing equation of motion for x-direction with N layers and considering a hydrostatic expansion of the total pressure in terms of interfacial displacements, the inviscid, linearized momentum equation becomes

$$\begin{aligned} \frac{\partial u_j}{\partial t} = -g \displaystyle \sum ^{N}_{k=1}\Bigg (\frac{ \rho _{k(j)}}{\rho _j} \frac{\partial }{\partial x}(\zeta _k + \zeta _{k+1})(-1)^{k+1}\Bigg ), \end{aligned}$$

(2)

where $\zeta _k$ is the interfacial displacement of layer k, except for $\zeta _1$ that represents the surface displacement, $\rho _{k(j)}$ is the density of the layer k when $k<j$, whilst for $k>j$, the $\rho _{k(j)}$ assumes the value of j, in which j is just a counter increment.

The linearized mass-conservation equation for layer j can be obtained through the Taylor expansion and the linearization procedure ($a_j~\ll ~\lambda$), which results to

$$\begin{aligned} \frac{\partial }{\partial t}((\zeta _j + \zeta _{j+1})(-1)^{k+1}) + H_j \frac{\partial u_j}{\partial x} = 0, \end{aligned}$$

(3)

where $H_j$ is the total depth until layer j.

Combining Eqs. 2 and 3 to eliminate u, give us the wave equation:

$$\begin{aligned} \frac{\partial ^2}{\partial t^2} (\zeta _j + \zeta _{j+1}) = -g H_j \displaystyle \sum ^{N}_{k=1}\Bigg (\frac{ \rho _{k(j)}}{\rho _j} \frac{\partial ^2}{\partial x^2}(\zeta _k + \zeta _{k+1})\Bigg ). \end{aligned}$$

(4)

Assuming that $\zeta _j+\zeta _{j+1}\equiv ~f(x,t)=X(x)\cos (\omega ~t)$, Eq. 4 reduces to a second-order linear ordinary differential equation, which is a classical Sturm–Liouville eigenvalue problem for N layers.

Finally, combining the horizontal eigenvalue problem with the phase speed ($c_n=\sqrt{g\beta _n}$) yields the dispersion relation

$$\begin{aligned} \omega ^2_{n,m}= g \beta _n k^2, \end{aligned}$$

(5)

in which $\beta$ represents the eigenvalues, k is the wavenumber, $\omega$ is the angular frequency of the internal wave, and n and m are the number of nodes of vertical and horizontal components, respectively.

Finally, since higher vertical modes frequently have frequencies near the inertial frequency, which normally results in the formation of a Poicaré internal seiche, we computed the deviation caused by Earth rotation correcting the angular frequency based on techniques for shallow water influenced by rotation [49]. Based on recommendations made by Hutter et al. [27], since the higher vertical modes present subjective layer thickness, we also obtained the model sensitivity to evaluate internal wave period changes due to layer thickness change. For numerical simulations, since our system was stratified just in two layers, we only calculated the periodicity for fundamental basin-scale internal waves.

2.6 Characteristic parameters

Although many procedures have been proposed to detect the excitation of baroclinic motion, our particular attention was devoted to understand the relationship between basin-scale internal wave amplitude and the thermal stratification stability of the stratified basins. Often this analysis is conducted through the estimation of the dimensionless Richardson number (Ri), which may be expressed through Eq. 1.

We compared the results obtained from Harp Lake, Vossoroca reservoir, and numerical simulations with mathematical theories proposed by Spigel and Imberger [44] and Shintani et al. [42]. Spigel and Imberger [44] formulated a linear approach to predict the amplitude of fundamental internal seiches based on the Ri. The linear approach is described by the following expression:

$$\begin{aligned} Ri = \frac{a~L}{2~h_e^2}, \end{aligned}$$

(6)

where a is the amplitude of the basin-scale internal wave, $h_e$ is the epilimnion depth, L is the length of the reservoir aligned to the wind at the pycnocline depth,

Recently a nonlinear approach has been proposed by Shintani et al. [42]. The theory presents an upward curvature of the interface due to the nonlinear effects, which tends to deviate from linear theory for small Ri ($\approx 3$). The nonlinear solution may be estimated by the empirical fitting function,

$$\begin{aligned} Ri = \frac{8L}{9h_e}\Bigg ( 1 + \tan \Bigg (\frac{\pi }{2}\Bigg (1-\frac{a}{h_e}\Bigg )^{1/0.57}\Bigg )^{1/0.81}\Bigg ), \end{aligned}$$

(7)

in which a is the amplitude of the basin-scale internal wave.

Based on results obtained from Vossoroca reservoir, Harp Lake, and numerical simulations during periods of different meteorological conditions, density profiles, basin morphology, we correlated the spectral energy of internal seiche and amplitude of basin-scale internal wave to Ri, to understand the relationship between the system instability and internal seiche amplitude, highlighting a more complex classification for basin-scale internal seiches. Finally, based on these analyses, we could understand better the condition that favors the excitation of higher amplitude internal waves, and how it affects the internal wave evolution.

3 Results and discussions

3.1 Spectral analysis and seiche model

For Vossoroca, the basin-scale internal waves were excited in early spring in the Southern Hemisphere, during the month of September 2012. The selected sub-period is comprised between September 15 and 25, 2012. Although the first half of September has presented a strong oscillation near the thermocline, the system presented higher Ri, with daily wind events $<1~{\text {m/s}}$ and thermal stratification of $\Delta T \approx 4~^{\circ }{\text {C}}$ (Fig. 5). During the selected sub-period the temperature difference increased to $\Delta T \approx 8~^{\circ }{\text {C}}$, and the mean daily wind speed increased to $1.3~{\text {m/s}}$, presenting higher wind changes. Since the increase of the thermal stratification was compensated by the mean daily wind rise, the daily Ri decreased in the sub-period from $10^6$ to $10^3$. The selected period is likely to excite dominant internal seiches that should be susceptible to a nonlinear degeneration [7, 44]. During the entire period of analysis the wind presented a small diurnal component that could favor the formation of forced internal seiche [5]. However, due to low energy associated with the diurnal wind component, the internal wave of mode two was dominant in the stable interior layer.

Fig. 5

Overview of field data from Vossoroca reservoir during September 2012 (Vossoroca reservoir; 01/09–29/09). a Wind speed and direction, b wind speed time difference (WSTD), and c thermal structure showing temperatures in colors and the thermocline position as a white solid line. The water surface elevation is represented by the blue solid line

The spectral analyses for that period (Fig. 6a) shows a significant peak, with spectral energy higher than the mean red noise spectrum for the time series at a $95\%$ confidence level. The peak is observed in the $16~^{\circ }{\text {C}}$ isotherm $\approx ~2~{\text {m}}$ below the thermocline. Since the coherence between the $16~^{\circ }{\text {C}}$ isotherm and the wind intensity is notably low ($<50\%$), the excited internal wave is not apparently affected by wind resonance effects. Considering that the generated internal wave has higher frequency compared to the diurnal component of the wind (often the most energetic component), diurnal forced internal wave could be excited in the system [5]. However, apparently due to the small amount of energy associated to diurnal components of the wind, forced oscillatory motions have not been observed with diurnal period.

Fig. 6

Spectral analyses of Vossoroca reservoir during September 2012: a Power spectral density of the isotherms of $18.5~^{\circ }{\text {C}}$ and $16~^{\circ }{\text {C}}$ (Vossoroca reservoir; 15/09–25/09). The dashed lines show the mean red noise spectrum for the time series, where spectral peaks above this line are significantly different from noise at a $95\%$ confidence level. Horizontal color boxes indicate the theoretical period for different vertical modes. b Coherence between $16~^{\circ }{\text {C}}$ isotherm and wind speed

The multi-layer hydrostatic linear model with free surface and shallow water assumption was applied to predict the first three vertical internal wave modes (Fig. 6a). The model results match with the first two vertical modes, indicating the occurrence of an internal seiche of $16~{\text {h}}~30$ period (Fig. 6a).

The out-of-phase response between isotherms, a typical characteristic of higher vertical modes, can be evidenced by the phase analysis between the 16 and $18.5~^{\circ }{\text {C}}$ isotherm time series (Fig. 7a). The $16~{\text {h}}~30$ period is also observed in $18.5~^{\circ }{\text {C}}$ isotherm with spectral energy higher than the mean red noise spectrum for the time series at a $95\%$ confidence level (Fig. 6a). The $90^{\circ }$ out of phase response between the $16~^{\circ }{\text {C}}$ and $18.5~^{\circ }{\text {C}}$ isotherm time series suggests that they belong to different layers. This observation corroborates with previous results from Vossoroca reservoir [12]. Although both isotherms present oscillatory motion compatible with evolution of internal seiches, the deeper interface apparently has more oscillations with higher energy compared to the $18.5~^{\circ }{\text {C}}$ isotherm. Since the water density difference is lower in deeper region, the same energy input may generate a higher displacement of the $16~^{\circ }{\text {C}}$ isotherm compared to a upper interface (Fig. 7b).

Fig. 7

Isotherm, phase, and wavelet analyses of Vossoroca reservoir during September 2012. a Phase analyses of two pairs of isotherms (phase was just plotted for coherence above the $95\%$ confidence level). b $16~^{\circ }{\text {C}}$ and $18.5~^\circ {\text {C}}$ isotherm time series. c Wavelet analyses of the $16~^{\circ }{\text {C}}$ isotherm (Vossoroca reservoir; 15/09–25/09)

The variation due to internal seiche activity presented a total vertical displacement of approximately $1.0~{\text {m}}$ in the $16~^{\circ }{\text {C}}$ isotherm, $6\%$ of the total depth. The wavelet analyses (Fig. 7c) shows that the V2H1 internal seiche was generated at the end of September 16. The internal wave action lasted for four days and was completely damped on September 22.

Higher horizontal modes have not been observed to be excited given the small size of Vossoroca reservoir. Often higher vertical modes are more susceptible to be excited in large lakes with irregular bathymetry. In addition, the formation of higher horizontal modes due to wind resonance effects during this period of analysis are unlikely to occur since detected internal seiches in Vossoroca reservoir often have periods lower than the diurnal component of the wind.

For time being this section highlighted only one period of basin-scale internal wave activity, however, other periods are summarized in the supplementary material. In addition, one period from Harp Lake is presented in details in “Appendix B”, similar to what has been provided here for Vossoroca reservoir.

3.2 General comparison

All data for Vossoroca and Harp were processed in a similar way, and compared to each other with respect to the seiche amplitude for different Ri. Fig. 8 illustrates the obtained results for different methods to compute Ri, described as follows.

All isotherms time-series were filtered in terms of spectral analysis to reveal the total vertical displacement associated to each frequency band. The internal seiche amplitude was estimated through the total vertical displacement in the internal seiche frequency. The internal wave amplitude is directly associated to the daily Ri number of the analyzed period (Fig. 8a). The overall result, more clear for V1H1 internal seiche mode observed in Vossoroca reservoir, shows an inversely proportional relationship between internal wave amplitude and Ri number. This suggests, as observed by previous studies [28, 42] that internal seiche amplitude grows exponentially with the decrease of stability. This is true unless the Ri reaches a critical value, $Ri_{\text {crit}} \sim L/2~h_e$. In this case, interface shear accompanied by large interface displacements that may cause a complete vertical mixing during a strong wind episode [44]. This type of regime has been observed during the transition between mixed and weakly stratified periods in Vossoroca reservoir, in the beginning of May.

Fig. 8

Internal seiche amplitude of the most energetic isotherm versus a the daily Ri, b filtered $Ri_{\text {duration}}$ using only periods with winds capable to generate internal waves, and c filtered $Ri_{\text {direction}}$ using only periods with winds in directions capable to generate internal waves. Linear regression was obtained for each basin

Although we have detected a similar trend in all analyzed periods, data from Harp Lake presented a slight deviation compared to Vossoroca reservoir. Given the lake characteristics, we suggest that the disturbance, mainly observed in Harp Lake, was due to the improper estimation of the mean wind energy available to excite basin-scale internal waves. As non-homogeneous wind events are predominant in Harp Lake, the mean wind velocity of the period is not a good representation of the wind that contributes to the formation of basin-scale internal waves. Recent studies have pointed out that filtering the friction velocity of the wind, $u_*$, can improve significantly the accuracy of some numerical models to predict internal seiches in deep lakes [18]. However, the filtering process is just used to compute the wind energy available to excite internal seiches, and does not represent a reduction of the wind strength.

We filtered the $u_*$ based on the duration of the wind event that could excite basin-scale internal waves [41]. Herefore, we firstly applied a duration filter, which consists of discarding wind events with duration lower than 1/4 of the internal wave period, an essential condition for internal seiche activity [21]. In addition, since heterogeneous direction of wind events may also be incapable to generate internal seiches, we also applied a filter based on wind direction. The Ri was estimated considering the fraction of the time that wind direction was in the same quarter of a circle, considering just events longer than $25\%$ of the wave period. Both processes improved considerably the correlation between Ri and the internal wave displacement (Fig. 8b and c). Differences between Harp Lake and Vossoroca reservoir are due to basin length of each basin.

3.3 Numerical simulations and spatial variations

Given the innumerable variables that may affect the evolution of basin-scale internal waves in real lakes, the complete description of the generation and evolution of these waves may be difficult considering data from just a pair of thermistor chains deployed in different locations of two different lakes. To overcome the difficulty to describe the evolution of BSIWs in stratified lakes, we firstly provide a detailed description of the dynamics of BSIW simulated through a numerical model. The baroclinic response due to the wind event is easily detected in the numerical results (See “Appendix A”). To describe the BSIW evolution of all simulations, the results from the numerical model were also processed using spectral analyses and the additional treatment applied to the data from field observations.

Often in thermal-stratified lakes, the Ri is written considering an aspect ratio that takes into account the length of the stratified basin L [42]. This parametrization preserves the main aspects of the Ri number, including an additional influence of the wind fetch. The non-dimensional parameter is written as $Ri~h_e/L$, in which $h_e$ is the epilimnion thickness.

The results of the numerical simulations are shown in Fig. 9, where the internal wave amplitude (a) or the non-dimensional internal wave amplitude (b) have been plotted against the non-dimensional time (using the internal wave period $T_{V1H1}$ for normalization). The results show good agreement to theoretical results obtained by [42, 44], which predicted that the vertical displacement due to BSIWs increases as the non-dimensional parameter $Ri~h_e/L$ becomes lower (Fig. 9a). Although this trend is observed in most numerical simulations, we observed a distinct behavior for cases with $h_e/H=0.13$ (see arrow in Fig. 9a).

Fig. 9

Numerical simulations results: Evolution of the generated basin-scale internal waves. a internal wave amplitude, and b non-dimensional internal wave amplitude, plotted against the non-dimensional time (using the internal wave period $T_{V1H1}$ for normalization) for different stratification conditions and pycnocline depths. The arrow indicates the anomaly of the run with $h_e/H=0.13$. The red region in (b) indicates the same interval analyzed in (a)

We suggest that when the pycnocline is too shallow (small $h_e/H$), the BSIW evolution may be different due to the increase of pressure in the upper layer, which may result in an additional acceleration of the tilted interface when it is returning to the equilibrium position. The faster downward movement is characterized by a temporal displacement of the internal seiche trough, which can be observed in Fig. 9a. This phenomenon is similar to wave shoaling, increasing non-linearity aspects, resulting a higher dissipation of energy. The interaction between wave crest and water surface increases energy dissipation of the BSIW resulting in a short-period activity.

Internal seiches dissipate energy in the interior of stratified basins by viscous forces or due to a down-scaling energy cascades that transfer energy to high-frequency internal wave fields of various modal structures [1]. The dissipation process reduces the energy of internal seiche, that may be damped after some periods of oscillation. This is evidenced in all numerical simulations, in which some are shown in Fig. 9b.

Although the damping of basin-scale internal waves present a substantial contribution of boundary layer dissipation [43], we show a strong influence of the system stability through those numerical results. The rate of energy decay is also a function of the bulk Richardson number. Although the internal seiche amplitude is higher for periods of weaker stability conditions, we observe that the seiche motion decays faster the more energy it contains, which is exemplified in Fig. 10a. This conclusion agrees well with observations in Lake Alpnach [19, 20]. We observed that for $Ri~h_e/L = 0.35$, internal seiche of $\approx ~3~{\text {m}}$ of amplitude was rapidly dampened, in which more than $80\%$ of its energy was dissipated after the first wave period. On the other hand, considering a more stable system ($Ri~h_e/L=2.32$), an $1~{\text {m}}$ internal seiche was completely dissipated after only 10 wave periods. One reason to the fast energy dissipation can be related to higher turbulent production generated on large amplitude waves and their interaction with boundaries.

Fig. 10

Numerical simulations results: Initial displacement of the generated basin-scale internal waves. a Decay of the non-dimensional internal seiche amplitude (using the initial displacement for normalization) as a function of the non-dimensional time (using the internal wave period $T_{V1H1}$ for normalization). b $Ri~h_e/L$ as a function of non-dimensional time in which $80\%$ of internal wave energy is dissipated

The relationship between $Ri~h_e/L$ and the internal seiche decay is characterized by an exponential function that fits well to our numerical observation with $h_e/H \ge 0.3$. For $h_e/H = 0.13$ (dotted lines in Fig. 10a), a disturbance during the internal seiche dissipation may be attributed to the asymmetrical temporal evolution of the excited internal seiche. Although, according to our observations, we may suggest that this interference reduced the energy dissipation, we actually observed a smaller decay rate due to the increase of wave amplitudes due to non-linearity. Eventually, after some periods, this interaction results in a faster energy decay by an increase of local mixing.

Even though the difficulty to analyze the influence of secondary wind events on internal wave evolution makes the analysis harder, some field observations have suggested a slower energy decay compared to our numerical results (Fig. 10b). We suggest that since real lakes are susceptible to continuous wind events, secondary storms may contribute to energize the internal waves fields, reducing the rate of energy decay. This phenomenon may be correlated to the amplification of internal seiches due to resonance events, typically observed in lakes [5, 35].

Although field observations are rarely capable to describe in detail the dynamics and evolution of BSIWs in real lakes, the initial responses due to a wind event have been extensively detected in many stratified lakes and reservoirs [1, 34, 53]. Even though these field and numerical observations are well represented by theoretical results [48], those present higher variation for different thermocline depth conditions (Fig. 11a). For shallow systems, when the internal seiche displacement is susceptible to reach the lake surface, the variation is completely different from up- and down-wind regions. In the up-wind region, the internal wave growth is limited by the water surface, whilst in down-wind part, the thermocline can erode downward the lake bottom as a strong jet due to an additional pressure at upper layer. As observed, the water surface interaction creates a faster dissipation of energy due to turbulence production, and the displacement oscillates during a shorter period of time. However, the strong jet can potentially intensify the vertical transport of substances, and may also have a strong effect on water quality.

Fig. 11

a Maximum basin-scale internal wave displacement normalized by the thermocline depth $h_e$ at downwind regions, where the initial displacement is characterized by a downward movement. The horizontal dashed black curve indicates the limit boundaries to direct interaction between water surface and internal seiche at upwind region. b The longitudinal temperature profile during the wind event ($3~{\text {h}}$ of simulation time) showing the strong erosion of thermocline at downwind region (Simulation: Run 23). The white dashed line indicates the unperturbed thermocline depth and the blue dashed line the theoretical displacement according to linear theory

As observed in Fig. 11, when $Ri~h_e/L \le 3$, depending on the $h_e/H$ condition, the internal seiche amplitude does not grow as described by previous theoretical results [42, 44, 48]. The internal seiche amplitude is higher than predicted by linear theory when the thermocline is near the water surface ($h_e/H \approx 0.2$). The thermocline feels an extra pressure at downwind region due to the interaction of physical barrier imposed by the lake surface and the internal seiche. This increase of pressure pushes the thermocline deeper (Fig.11b). Rapidly after the first wave motion, the BSIW seems to be degenerated into a bore that propagates back and forth (For more detail, see “Appendix A”). The observation agrees well with the degeneration regime described by [25], that falls into the supercritical flow regime.

In the other hand, when the thermocline is located in deeper regions ($h_e/H > 0.6$), the bottom condition may also play an important role on increasing mixing at the wave trough. The linear theory does not include an higher order influence that can be observed in simulated cases due to the extra pressure at the epilimnion layer. Although when the $Ri~h_e/L$ gets lower nonlinear interactions tend to increase the internal seiche amplitude [42] and the extra pressure may also have a relevant contribution depending on the $h_e/H$ condition, mixing activity due to the low thermal stability can have a significant role on the internal seiche growth, reducing their amplitude and accelerating their energy dissipation due to turbulence production.

As observed in Fig. 11a and differently from mathematical theories derived by [44] and [42], numerical results show an influence of the total water depth and a higher order contribution of the upper layer thickness. The shallower the interface of the BSIWs, the higher the energy transferred to the internal wave field. However, when $Ri~h_e/L$ gets really small, the weaker system stability may play an addition role on the internal seiche amplitude. The deeper the tilted interface, the lower will be the energy that will reach the internal wave field. We suggest that part of the energy is lost by mixing and less energy is available to excite basin-scale internal waves. In other words, less energy is transferred to deeper regions.

3.4 Parametrization

The parametrization proposed here takes the reservoir depth into consideration and an higher order contribution of Ri, water length and thermocline depth. The parametrization is based on simulation results from $h_e/H = 0.1$ to 0.8 ($h_e = 2$ to $12~{\text {m}}$). The parametrized equation that best fits to the numerical observations is given by

$$\begin{aligned} \frac{\zeta _o}{h_e} = \xi ~\exp \Bigg (\frac{-(Ri~h_e-k_2~L)^2}{2~(L~f)^2}\Bigg ), \end{aligned}$$

(8)

in which Ri is the bulk Richardson number, $h_e$ is the epilimnion thickness, L is the reservoir length, $\xi =0.1$ is the constant that defines the lowest internal wave energy that can be predicted by the parametrization, $k_1=6$ is an universal constant obtained empirically, and f is a non-dimensional function of $h_e/H$, which describes a higher order influence of $h_e/H$ on internal seiche amplitude:

$$\begin{aligned} f(h_e/H) = g(h_e/H)~\exp \Bigg (\frac{(h_e/H)^2}{k_3}\Bigg ), \end{aligned}$$

(9)

where $k_2=0.125$ is an universal constant (obtained empirically) and g is a sub-function of $h_e/H$. The $g(h_e/H)$ was estimated empirically considering all simulated cases. We applied two best approximations: a linear ($g(h_e/H) = -3.021~h_e/H + 2.6674$) and a third-order polynomial function ($12.156~h_e/H^3 - 15.714~h_e/H^2 +2.8426~h_e/H + 2.0846$) (Fig. 12).

Fig. 12

a Variation of g as a function of $h_e/H$ for all simulated cases. Black dots represent the empirical parameter defined considering all simulated $h_e/H$ condition. Red curves indicate different functions to describe the variability of $g(h_e/H)$ (linear and a third order polynomial regressions). b Maximum vertical displacement associated with internal seiche. Solid curve is derived from parametrized equation (Eq. 8) for different $h_e/H$ conditions applying the third-order polynomial equation to describe the g function, expressed with distinct colors. The result using the linear equation for g is presented in “Appendix A”. Marks indicate the simulated results from different $h_e/H$ conditions

The $\xi$ constant limits the minimal energy of the BSIW, which impose that Eq. 8 should be applied just when the wave amplitude is at lest $10\%$ of epilimnion thickness. For small internal wave energy ($\zeta _o/h_e \le 0.1$), the system should be stable enough and far from the boundaries, that higher order influences of $h_e/H$ and turbulent production at wave crest and trough do not have any additional influence on wave energy. Thus, for $Ri~h_e/L > 5$, the linear theory is a satisfactory approximation to predict internal wave amplitude.

The universal constants $k_1$ and $k_2$, which were determined empirically trough numerical iterations, are independent of $h_e/H$ conditions and apparently valid for all simulated cases.

The parametrization (Eq. 8) shows a better prediction of internal seiche amplitude compared to linear theory (Fig. 13a), suggesting that for most lakes and reservoir that are under $h_e/H = 0.1$ to 0.8 conditions the equation should work well to describe the internal seiche amplitudes. For all tested $h_e/H$ conditions the parametrization showed a better prediction of internal seiche amplitude, mainly for cases when the internal seiche interacts with the lake boundaries (Fig. 13b). The observed data suggest a mean error reduction of more than $50\%$ related to the linear theory. In critical $h_e/H$ conditions, the parametrization reduced the error in $90\%$ compared to the linear theory.

Fig. 13

a Comparison between theoretical (linear and parametrized equation) and internal seiche amplitude detected in simulations. b Error percentage with respect to $h_e/H$

The energy from a wind event that passes the surface boundary layer is susceptible to favor the excitation of basin-scale internal waves in the stable interior layer interior. We suggest that when the thermocline is shallow under low $Ri~h_e/L$, the wave crest is susceptible to reach the water surface. The change in pressure caused by this phenomenon pushes the wave to deeper regions, which leads to a higher vertical transport at downwind regions. However, when $Ri~h_e/L$ is lower, the turbulence production at higher vertical displacement and the interaction with lake boundaries start to play a crucial role on the initial internal wave growth, which may result in lower vertical displacement due to turbulence production. This decrease of amplitude may collapse when $Ri~h_e/L$ is too low so that the vertical displacement may result in turbulent mixing that is not supported by the stratification condition, leading to a complete mixing of the lake. We observed in some simulated cases a rapid stratification break due to high turbulence production. These cases are summarized in “Appendix A”.

The parametrization equation (Eq. 8) describes the distribution of internal wave energy for different values of Ri he/L as a Gaussian function (Fig. 12b). However, the higher order contribution of epilimnion layer and the interaction between internal seiche and lake boundaries play a crucial role on describing the maximum internal seiche displacement. The variability observed as a function of $h_e/H$ controls the standard deviation of the Gaussian function, which is parametrized by Eq. 9.

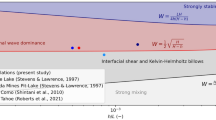
Comparing the parametrization with field observations conducted in Vossoroca reservoir and Harp Lake we observe that the linear theory underestimated in the majority of cases the internal wave amplitude for larger Richardson number ($Ri~h_e/L>3$) (Fig. 14a). The higher vertical displacement may be due to the resonance effect caused by the wind forcing frequency [3]. When the forcing frequency matches one of the natural frequencies of the basin scale internal wave modes, resonant amplification may occur [4]. For both basins and modes, the initial amplitude was approximately $30\%$ larger than that predicted by the linear theory, except for $Ri~h_e/L<5$ that presented different behavior depending on the $h_e/H$ condition, which we suggest to occur due to the mixing and boundary effects discussed previously.

Fig. 14

a Maximum vertical displacement associated with internal seiche normalized by the epilimnion thickness against $Ri~h_e/L$. Data points include values from simulations, Harp lake, Vossoroca reservoir, and many other lakes from the literature [13, 14, 17, 24, 31, 46, 48] b Normalization of Eq. 8 (dashed line represents the result from theoretical parametrization) incorporating the function f to demonstrate their variability against $Ri~h_e/L$

Although field observations suggest that wind resonance apparently affects the internal wave amplitude independently of the $Ri~h_e/L$ (increasing the wave amplitude by $\approx ~20\%$), we observe that for a very stable system ($Ri~h_e/L > 10$) probably the effect is much less. In this condition, observations suggest that the $\xi$ in Eq. 8 must be a function of other variables based on wind resonance. Physically, this condition may indicate that when the system becomes more stable, wind resonance does not affect strongly the internal seiche amplitude, however a new parametrization is required in order to better predict the growth rate for different $Ri~h_e/L$.

Another observation is that the proposed parametrization also incorporates the linear theory at $Ri~h_e/L=5$, for higher $Ri~h_e/L$ the linear theory is more adequate to represent the internal seiche amplitude. For $Ri~h_e/L < 5$ we observe a reduction of the internal seiche amplitude when $Ri~h_e/L$ gets lower, Fig. 14. For different $h_e/H$ condition we may observe an increase of the internal seiche amplitude at downwind region for shallow thermocline, which fits better to the proposed parametrization that takes into account the total water depth of the system and interaction of internal seiche and lake boundaries.

Although we do not observe a clear evidence that resonance occurs exactly when internal seiche periodicity matches a frequency of the wind component, as shown in Fig. 15a, we detected good correlation between the total spectral energy of a specific wind frequency bandwidth (0.5 to 1.5 of the internal wave period) with the growth of amplitude due to resonance effects (Fig. 15b). This conclusion agrees well with laboratory results conducted by Boegman and Ivey [5] that showed that wind frequencies between 0.8 and 1.2 of the fundamental basin-scale internal wave period may amplify the internal wave amplitude due to resonance effects.

Fig. 15

Amplitude growth due to resonance effect against a the peak of the power spectral density of the wind intensity at the internal seiche period and b the integration of the wind spectrum for wind frequencies between 0.5 to 1.5 of the internal wave period per bandwidth frequency

In addition, our analysis shows that the wind fluctuations with higher spectral energy can also be responsible for generating higher amplitude internal waves and also favor the occurrence of higher vertical modes. This characteristics are also evidenced in Fig. 14, in which higher vertical modes detected in Vossoroca reservoir and Harp Lake deviate more from the theoretical results.

As also observed in Fig. 15b, the correlations fit well just for a determined basin and internal wave mode. Considering different modes and basins, the correlation patterns are altered. This suggests that the amplification of the internal wave can be directly correlated to resonance effects for data obtained in a same basin for a single mode, but for different modes and basins this correlation differs, probably influenced by basin length and internal wave periodicity. This conclusion indicates that resonance effects may introduce additional variables into equation 8, which suggests that it should be a function of wave mode and wavelength, characterized by the basin length L. Since L is already incorporated into parametrization $Ri~h_e/L$, we may assume that L introduces an additional influence on the internal seiche amplitude depending on the resonance efficiency.

In general, this parametrization presents satisfactory results and could be applicable to small to medium lakes under different boundary and meteorological conditions. Some limitations and precautions related to the parametrization are highlighted below:

The parametrization just takes into account linear internal seiches that are not influenced by Coriolis effect, and could not be applied on large lakes where Poicarè and Kelvin internal waves are susceptible to be excited.

The parametrization equation does not take into account the bathymetry irregularity, since the simulation was performed in smooth bed conditions. Although the Vossoroca is a dendritic reservoir, its bathymetry is not much irregular, similar to Harp Lake bathymetry. The comparison between results from simulation and different lakes presented good results. However, the parametrization should be applied with precautions on stratified basin with irregularly bathymetry conditions.

Finally, we did not consider the influence of river discharges in the formation of basin-scale internal waves. This interaction is not well understood yet, but apparently could have only minor effect on the internal wave formation since mixing process just takes place close to rivers. Vossoroca is a dendritic reservoir, its bathymetry is not much irregular, similar to Harp Lake bathymetry and the simulation performed here. The parametrization should be applied with precautions on stratified basin with irregularly bathymetry.

4 Conclusion

In the light of recent field observations of basin-scale internal waves, previously established theories often fail to estimate the initial amplitude of internal seiches in thermally-stratified basins during determined conditions. As evidenced by a series of observations, theoretical models [42, 44] often fail to describe the BSIW amplitude during periods of $Ri~h_e/L < 2$. Since basin-scale internal waves have been pointed as one of the most important process of vertical mixing and horizontal transport, the wrong estimation of internal seiche amplitude may have several impacts on the water transport.

The result of this study revealed that secondary effects, which are not incorporated by these theories, play a major role under determined meteorological conditions on the dynamics of basin-scale internal waves. We observed that the interaction of internal seiche with lake boundaries (surface water and lake bathymetry) is an important variable that has been neglected by the previous theories. We have demonstrated through numerical modelling and field observation analysis that the shallower the BSIW, the higher the energy transferred to the internal wave field, exciting higher internal waves. However, simultaneously, when $Ri~h_e/L$ gets lower, a larger part of the energy is lost by mixing and less energy is available to excite basin-scale internal waves, resulting in a internal seiche with smaller amplitude.

In addition, we observed that wind-resonance effects favor the excitation of higher vertical modes in small lakes and reservoirs since diurnal winds have similar period of higher vertical modes. The resonance effect increases the energy of the BSIW significantly, leading to higher amplitude waves. This may indicate an additional dependence of other variables on the proposed parametrization.

For further analysis we suggested the proposed parametrization should be tested to different conditions of low $Ri~h_e/L$. Observations here indicate a stratification break which is strongly influenced by both parameters, $h_e/H$ and Richardson number. Although it fitted well to describe the reduction of energy for weakly stable systems, we may observe a critical influence of the wind-resonance. Based on the analysis of resonance efficiency, the parametrization may include new variables related to the wind resonance to better predict the BSIW amplitude. The influence of wind-resonance during period of high stability may also be better tested, to describe more appropriately the low efficiency observed here. In addition, future studies could better explore the influence of modes and basin length on the wind-resonance efficiency.

Finally, although the parametrization has presented positive outcomes for the majority of conditions, we may suggest a deeper investigation on influence of other variables such as: Coriolis effect, lake topography irregularities, and interaction with secondary flows.

Appendices

Numerical simulations

This appendix contains detailed parameters used to simulate the evolution of basin-scale internal waves in Delft3D. In addition, Tables 1 and 2 presents general data and processed results from all 32 simulated cases, including general parameters of boundary conditions, theoretical results for vertical displacement and degeneration regime.

We used the three-dimensional hydrodynamic model Delft3D-FLOW, which solves the shallow water equations using the hydrostatic assumption [15]. Although Delft3D model may fails to reproduce the internal wave breaking and most of degeneration regimes, it has already been used to describe internal seiche in real lakes and reservoir [16].

The implemented model operated in a horizontal Cartesian grid cells of $90~{\text {m}}\times 90~{\text {m}}$ and 50 fixed layers, with no heat flux at water surface. For the turbulence closure scheme, vertical eddy diffusivity and viscosity was calculated by a $k-\epsilon$ model. The coefficients of background vertical and horizontal viscosity and diffusivity were considered as calibration coefficients and were kept fixed during the simulation. Considering the stability condition, specified by the Courant–Friedrichs number, we used a time step of 1 min to simulate approximately 10 days.

Although Delft3D fails to describe most of the degeneration process of BSIW, Fig. 16 highlights the evolution of the internal bore generated after the degeneration of the basin-scale internal wave detected in simulation 23 (Fig. 11b). The degeneration regime evidenced in the simulation matches with theoretical results [25, 26].

Table 1 Summary of collected data from simulated cases $h_e$ and H indicate the epilimnion and total water depth, respectively

Fig. 16

Internal bore generated as a result of the degeneration process of basin-scale internal wave (Simulation: Run 23)

Table 2 Summary of processed results from simulated cases

Harp lake

For time being this section highlights only one period of basin-scale internal wave activity in Harp Lake. Other periods are summarized in the supplementary material. For Harp Lake, the basin-scale internal waves were excited in summer and spring in the North Hemisphere. The highlighted sub-period is comprised between September 16 and October 20, 2013.

We selected the period from 25th of September to 4th of October since it presented low Ri due to the strong wind events, with mean wind speed $> 3.5~{\text {m/s}}$ and peaks that reached almost $6~{\text {m/s}}$. Homogeneous wind events presented duration of approximately $11~{\text {h}}$ blowing $169~^\circ$ North. The thermal stratification was constant during the period, $\Delta T \approx 15~^{\circ }{\text {C}}$. The strong wind events decreased the Ri from $10^6$ to $10^3$, which lead to the formation of basin-scale internal waves. According to the criteria established by [44], the reduction of Ri value leads to a lake regime of internal seiche dominance. Although it is not a full proof of their existence, this theory gives indication of their generation.

Considering the analyzed period, oscillatory motion was observed mainly in the $8~^{\circ }{\text {C}}$ isotherm, located approximately $1~{\text {m}}$ below the mean thermocline depth ($\approx 7~{\text {m}}$ above the water surface). The first event occurred between September 28 and 30, whilst the second and stronger one was detected in the last five days of the analyzed sub-period, from 1st to 5th of October, 2013. The first one presents mean wind intensity of $2.7~{\text {m/s}}$, whereas the second one a mean wind speed of $3.5~{\text {m/s}}$ (Fig. 17a). Both periods present low Ri and, according to [44], were susceptible to internal seiche formations. Although the Ri does not account the wind direction to analyze the excitation of internal waves, the period presents homogeneous wind events, with mean wind direction to $120^\circ$ and $270^\circ$ North, respectively. Stronger wind events provided higher oscillations, with vertical displacement reaching $1.2~{\text {m}}$, whilst the first period presented maximum vertical displacement of $0.6~{\text {m}}$.

Fig. 17

Thermal and wind speed condition in Harp Lake. a Isotherms time-series in height above the bottom (h.a.b.). b Wind speed time series (Harp Lake; 25/09–04/10)

Figure 18a shows results of the multi-layer hydrostatic linear model with free surface and the power spectral density of isotherms time series. The power spectral density of $8~^{\circ }{\text {C}}$ isotherm shows two prominent peaks (Fig. 18a). Peak (I) and (II) are above the mean red noise spectrum, presenting period of $5~{\text {h}}~30$ and $4~{\text {h}}~30$, respectively. Both periods are close and compatible with the first two vertical modes. Both modes showed similar results since the thermal structure of Harp Lake during this period of analysis is characterized by a thin metalimnion (Fig. 18c).

The $4~{\text {h}}~30$ peak (Fig. 18a; peak I), has lower spectral energy compared to the peak (II), that has periodicity of $5~{\text {h}}~30$. It indicates that the $4~{\text {h}}~30$ fluctuation occurred between September 28 and 30 due to wind event of $2.7~{\text {m/s}}$. The phase analysis indicates that the $8~^{\circ }{\text {C}}$ and $12~^{\circ }{\text {C}}$ isotherms propagates out-of-phase (Fig. 18b), suggesting the occurrence of a higher baroclinic internal wave. The out-of-phase structure may also be observed through Fig. 17b from 1st to 5th of October. However, the detection of the out-of-phase structure is harder for the first period, since the internal seiche amplitude is lower. In both periods the V2H1 mode was more pronounced below the thermocline, in the $8~^{\circ }{\text {C}}$ isotherm, and barely detectable at the $10~^{\circ }{\text {C}}$ isotherm.

Fig. 18

a Power spectral density of the isotherms of $12~^{\circ }{\text {C}}$ and $8~^{\circ }{\text {C}}$. Dashed lines show the mean red noise spectrum for the time series, indicating significant peaks at a $95\%$ confidence level. b spectral phase analyses considering just coherence higher than $80\%$ (Harp Lake; 25/09–05/10), c Vertical temperature profile obtained from Harp Lake in 2nd of October 2013 at 5 a.m., d Zoom-in view of the temperature profile with a second profile $2~{\text {h}}$ late, which is approximately half of the internal seiche period. At $22~{\text {m}}$ above the bottom the water becomes warmer, which leads to a erosion of the $12~^{\circ }{\text {C}}$ isotherm due to internal seiche passage. However, $2~{\text {m}}$ bellow that point, the water becomes colder due to the elevation of the $8~^{\circ }{\text {C}}$ isotherm, that was caused by the oscillation of the second interface, clearly out-of-phase with the $12~^{\circ }{\text {C}}$ isotherm. e a sketch of the V2 mode is presented in (d)

The second vertical mode affects the vertical temperature profile as shown in Fig. 18d, generating vertical displacement in opposite directions. This motion occurs repeatedly, as illustrated schematically in Fig. 18e, until the complete internal seiche dissipation.