1 Introduction

The remarkable and intensive efforts of the scientific community for precise forecasting are not yet effective due to the complexity of the earthquake generation process. Our restricted knowledge of its underlying mechanisms and the limited duration of the earthquake catalogs highlight the necessity for the development of stochastic models, which lie between physics-based models that ignore statistics and pure statistical models without taking into account physics (Vere-Jones et al. 2005). Among them, self-exciting point processes, introduced by Hawkes (1971) and Hawkes and Oakes (1974), form a large family of procedures that are successfully used in many fields, such as Ecology, Forestry and Finance and many other fields. In this class of processes the arrival time of an event increases the probability of a next one to occur. Regarding earthquake generation, this class of models is based on the assumption that earthquakes tend to occur in clusters. The Epidemic Type Aftershock Sequences (ETAS) model is a particular form of Hawkes processes for modeling earthquake occurrence in time and space (Ogata 1988, 1998). Since its development, the ETAS model and its modifications have been popular for short-term earthquake forecasts (e.g. Console et al. 2003; Zhuang et al. 2004; Marzocchi and Lombardi 2009; Davoudi et al. 2018). Mohler et al. (2011) developed a model based on the analogy of the aftershock and criminal behavior. Meyer et al. (2012) introduced a spatio-temporal point process model for the diffusion of an infectious disease. Information diffusion modeling is also feasible through self-exciting processes (Wu and Huberman 2007; Zipkin et al. 2016). The memory over time is pointed out, i.e. the fact that retweeting in Twitter is increased when the content is fresh. Memory is introduced in the autoregressive conditional duration model (ACD) (Engle and Russell 1998) for exploring transaction data based on the dependence of the conditional intensity to past durations.

Another class of such processes is the self-correcting ones, where the occurrence of an event has an inhibitory effect by decreasing the probability of new events appearance. The equivalent model in Seismology is the Stress Release Model (SRM), introduced by Vere-Jones (1978), which transfers Reid’s elastic theory (Reid 1910) in a stochastic framework. In this model, the occurrence of an earthquake provokes release of energy- and thus a period of quiescence-, which is then re-accumulated until the occurrence of the next event, i.e. earthquakes generation decreases the amount of strain present at the locations along the fault where rupture grows. The first applications were performed by Zheng and Vere-Jones (1991, 1994) who used historical catalogs from China, Iran and Japan, and showed that the SRM clearly performs better than the Poisson model with better fit obtained when the whole region is subdivided into smaller parts. Liu et al. (1998) proposed an extended version of the model where interactions between subareas are allowed. In the new model, called Linked Stress Release Model (LSRM), the earthquake occurrence in a subarea can cause either damping or excitation in the adjacent subareas through stress transfer. Liu et al. (1999) and Lu et al. (1999) applied the LSRM in North China and Japan, respectively and found that the LSRM fits better the data than independent SRMs applied in the subareas. Lu and Vere-Jones (2000) when applied the LSRM in North China and New Zealand, pointed out the differences in different tectonic regimes. They concluded that the complexity of the plate boundary region of New Zealand favors the use of the LSRM instead of different independent models since extra parameters are incorporated, such as different loading rates. On the contrary, in the intraplate region of North China the LSRM is not clearly preferred and modest interactions between subregions are evidenced.

Using an example from Taiwan, Bebbington and Harte (2001) focused on the statistical features of the model. The same authors (Bebbington and Harte 2003) conducted an extensive study regarding the procedures for identifying and evaluating the best model, the optimization methods as well as the model sensitivity to the determination of the subregions and the possible catalog errors. Information gains (Bebbington 2005) and entropy score (Harte and Vere-Jones 2005) were studied as methods for quantifying the model predictability. Technical issues were also raised by Kuehn et al. (2008), who performed numerical simulations in order to investigate the effect of coupling among different subareas in the occurrence probability distributions. The LSRM was applied in Romania by Imoto and Hurukawa (2006) who compared its performance with other renewal models, in which the interevent time distribution follows the Brownian Passage Time model, the Log-normal, the Weibull and the Gamma following the Working Group on California Earthquake Probabilities. They concluded that the SRM is the most suitable for the long-term hazard assessment in the study area. Rotondi and Varini (2007), Varini and Rotondi (2015) and Varini et al. (2016) applied the model in Italy adopting a Bayesian approach.

In Greece the first application of the SSRM was performed by Rotondi and Varini (2006) in the western part of the Corinth Gulf. In the same area Mangira et al. (2017) applied the LSRM and suggested an alternative type for the conditional intensity function, of Weibull-type form instead of an exponential. Mangira et al. (2018) revisited the area by investigating not only the interactions between the subareas but rather inserting them by incorporating in the model knowledge from Coulomb stress changes calculations. In the area of Central Ionian Islands Votsi et al. (2011) investigated through LSRM possible interactions between two subregions, namely Kefalonia and Lefkada. The results are in accordance with those of Mangira et al. (2017) regarding the kind of interactions between Kefalonia and Lefkada Islands since in both studies the transfer parameters are estimated to be positive and thus there are indications for slight damping between the two subareas.

In the original form of the SSRM, the conditional intensity function depends on the entire history of the seismicity process, meaning that an earthquake occurrence results from all previous seismicity. Aiming to improve the performance of the model and reduce the computational burden, a “constrained-memory” point process is introduced where only the \(m\) most recent arrival times and magnitudes are comprised in the conditional intensity function. An earthquake occurrence is no longer dependent on all previous ones; this influence stops at some degree which is defined as the memory of the point process. The memory order, \(m\), is investigated in moderate magnitude seismicity (\(M \ge 5.2\)) of the Corinth Gulf, by considering different numbers of steps backwards in time to find out the optimal that better fits the observations.

2 Study area and data

The Corinth Gulf’s seismotectonics and seismicity have been widely studied since the area consists one of the most rapidly deforming rifts worldwide (Briole et al. 2000; Papanikolaou and Royden 2007; Chousianitis et al. 2015). The rift has the shape of an asymmetric half-graben trending WNW- ESE with the southern footwall being uplifted (Armijo et al. 1996). The major fault segments associated with frequent strong (\(M \ge 6.0\)) earthquakes are principally the north dipping faults that margin the Gulf to the south.

The lack of continuity of the faults seems responsible for the fact that the maximum magnitude recorded or ever reported hardly exceeds 6.8 (Jackson and White 1989). Intense microseismic activity, clustered both in time and space, is apparent in the region, mainly located in the western part of the Gulf (Pacchiani and Lyon-Caen 2010; Mesimeri et al. 2016, 2018).

The high level of seismicity is testified both by historical and instrumental records (Papazachos and Papazachou 2003). Recently one of the most intense sequences occurred in 1981, in the eastern part of the Corinth Gulf in Alkyonides Bay and has motivated numerous studies (e.g. Jackson et al. 1982; King et al. 1985; Hubert et al. 1996; Hatzfeld et al. 2000). The western part has also experienced destructive earthquakes near Galaxidi in 1992 (Hatzfeld et al. 1996) and Aigion in 1995 (Bernard et al. 1997). The last strong earthquake (\(M\) 6.4) occurred in the northwestern Peloponnese on 8 June 2008 and provided the opportunity of studying an area not known for accommodating strong earthquakes before (Karakostas et al. 2017). Two moderate magnitude earthquakes (\(M5.5\) and \(M5.4\)), occurred in January 2010 close to Efpalio in the western part of the Corinth Gulf, are the last two events included in the dataset. They are separated temporally only by 4 days and spatially at a distance of about 5 km on two adjacent fault segments, that were probably simultaneously close to failure (Karakostas et al. 2012; Sokos et al. 2012; Ganas et al. 2013).

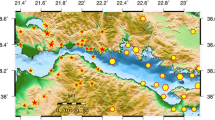
The data used for the current study are taken from the catalog compiled by the Geophysics Department of the Aristotle University of Thessaloniki (Aristotle University of Thessaloniki Seismological Network 1981) based on the recordings of the Hellenic Unified Seismological Network (HUSN). In order to obtain a complete dataset with as many events as possible, our catalog comprises 61 events with Mth = 5.2 shown on the map that occurred from the 1st of January 1911 since the 31st of December 2017 (Fig. 1). The same study area and dataset was used by Mangira et al. (2017) and Mangira et al. (2018) for the application of the LSRM and modifications. The data will now be employed for a comparison between the original SSRM and the suggested CM-SRM.

Fig. 1
figure 1

Seismicity map showing all earthquakes with \(M \ge 5.2\) that occurred in the Corinth Gulf since 1911. Orange and magenta circles depict earthquakes with \(5.2 \le M < 5.5\) and \(5.5 \le M < 6.0\) and yellow asterisks the ones with \(M \ge 6.0\)

Full size image

3 Formulation of the model

The SRM incorporates simple yet fundamental ideas in a stochastic framework. It constitutes a stochastic expansion of elastic rebound theory, according to which the elastic strain is accumulated on a fault or fault segment due to long-term tectonic loading and is released when the fault is slipped during an earthquake when a certain stress level is surpassed. Strictly speaking, the stress is transferred or relieved and not released; yet it is the most common term used in all relevant works and known among scientists, thus also adopted here. The basic variable,\(X\left( t \right)\), refers to the stress level, which is an unobserved quantity that increases linearly between earthquakes and then drops suddenly when an event occurs, expressed as

$$X\left( t \right) = X\left( 0 \right) + \rho t - S\left( t \right),$$
(1)

where \(X\left( 0 \right)\) is the stress level at the initial time \(t = 0\), \(\rho\) is the loading rate, which is considered constant, and \(S\left( t \right)\) refers to the accumulated stress release during \(\left( {0, t} \right)\), i.e.,\(S\left( t \right) = \mathop \sum \limits_{{i:t_{i} < t}} S_{i}\) where \(t_{i}\) is the occurrence time of the \(i\)-th event and \(S_{i}\) the stress released due to the \(i\)-th event.

The stress released during an earthquake is inferred from its magnitude according to empirical relations. Assuming that the energy released is described by the cumulative Benioff’s strain (Bufe and Varnes 1993), the stress difference can be written as

$$S_{i} = 10^{{0.75\left( {M_{i} - M_{th} } \right)}} ,$$
(2)

where \(M_{i}\) is the magnitude of the \(i\)-th event and \(M_{th}\) is the magnitude threshold.

The data form a point process which is uniquely defined by the conditional intensity function (c.i.f.),\(\lambda^{*} \left( t \right)\), or hazard function, i.e., the instantaneous occurrence probability (Daley and Vere-Jones 2003). The simplest and most common form for the hazard function is an exponential one given by

$$\lambda^{*} \left( t \right) = \exp \left\{ {Z\left( t \right)} \right\} = exp\left\{ {\mu + \nu {\rm X}\left( t \right)} \right\} = \exp \left\{ {\mu + \nu \left[ {{\rm X}\left( 0 \right) + \rho t - S\left( t \right)} \right]} \right\} = \exp \left\{ {a + b\left( {t - cS\left( t \right)} \right)} \right\},$$
(3)

where \(a = \mu + \nu X\left( 0 \right)\), \(b = \nu \rho\) and \(c = 1/\rho\) are the parameters to be estimated. This estimation is achieved by maximizing the log-likelihood function. Given the observations \(\left\{ {t_{1} , t_{2} , \ldots ,t_{N\left( T \right)} } \right\}\) in a time period \(\left[ {0, T} \right]\), the likelihood function \({\text{L}}\) can be written as (Daley and Vere-Jones 2003)

$${\text{L}} = \Big( \mathop \prod \limits_{{{\text{i}} = 1}}^{{{\text{N}}\left( {\text{T}} \right)}} \lambda^{ *} \left( {{\text{t}}_{\text{i}} } \right) \Big)\exp \left( { - \mathop \smallint \limits_{0}^{\text{T}} \lambda^{ *} \left( {\text{u}} \right){\text{du}}} \right),$$

and the logarithm of the likelihood is given by

$$logL = \mathop \sum \limits_{i = 1}^{N\left( T \right)} { \log }\left( {\lambda^{*} \left( {t_{i} } \right)} \right) - \mathop \smallint \limits_{0}^{T} \lambda^{*} \left( u \right)du,$$
(4)

where \(N\left( T \right)\) stands for the total number of events over the time interval \(\left[ {0,T} \right].\)

Defining the c.i.f. is a convenient and intuitive way of specifying how the present depends on the past in an evolutionary point process. In the aforementioned form, the c.i.f. depends on the entire history of the process since for the occurrence probability of a subsequent earthquake, which is expressed through the c.i.f., at some point \(t\), we take into account all the previous earthquakes occurred during (0,\(t\)). In order to find a more realistic and practical model that describes the seismogenesis, we introduce a constrained-memory point process where only the m most recent arrival times are present in the conditional intensity function. The hazard function has the form \(\lambda^{*} \left( t \right) = \exp \left\{ {Y\left( t \right)} \right\}\), where

$$Y\left( t \right) = \left\{ {\begin{array}{ll} {a + b\left( {t - \mathop \sum \limits_{{i:t_{i} < t}} cS_{i} } \right), \quad 0 \le t \le t_{m} } \\ {a + b\Big(\left( {t - t_{{j - m + 1}} } \right) - \mathop \sum \limits_{{i:t_{{j - m + 1}} \le t_{i} < t_{{j + 1}} }} cS_{i} \Big), \quad t_{j} < t \le t_{{j + 1}}, \, j = m,~ \ldots ,n - 1~} \\ {a + b\Big(\left( {t - t_{{n - m + 1}} } \right) - \mathop \sum \limits_{{i:t_{{n - m + 1}} \le t_{i} }} cS_{i} \Big), \quad t > t_{n} } \\ \end{array} } \right.,$$
(5)

where \(n = N\left( T \right)\) stands for the total number of events of the study period. The first branch of relation (5) is equivalent to the relation (3), since for number of steps less than the degree of memory investigated, the c.i.f. is exactly the same as in the classical form of the SRM. In that case, \(Y\left( t \right)\) coincides with \(Z\left( t \right)\) given in (3). The third branch of the relation (5) refers to time greater than the occurrence time of the last earthquake, i.e., to time interval from the last event until the end of the study period. By the second branch of (5) the concept of the Constrained Memory SRM (CM-SRM) is described. According to this relation, we go back in time as many steps as the degree of memory and without taking into account all the earthquakes that occurred since the beginning of the study. It should be noted that the number \(m\) could not take a larger value than the number of events. The energy released when an event occurs depends upon not only the earthquake magnitude but also on the magnitudes of the \(m\) previous earthquakes and the total duration of the time intervals taken into account before the occurrence of the earthquake. \(Y\left( t \right)\) is influenced by the time that the m-th previous event occurred as the relevant time interval defines the amount added in the second branch of the Formula (5). If there is relevant quiescence, the time intervals are large, and \(Y\left( t \right)\) is increased. \(Y\left( t \right)\) depends also on the magnitudes of the m previous events through the amount that is extracted in Formula (5). If the magnitudes of the \(m\) previous events are large then a large amount of energy is released and a significant drop of \(Y\left( t \right)\) and consequently of \(\lambda^{*} \left( t \right)\) is observed. The difference of the two competitive models, the SSRM and the CM-SRM, lies upon the way that the past events influence the current earthquake occurrence. The CM-SRM incorporates the SSRM in the case where it is supposed that the degree of the memory of the point process equals the number of the events that are included in the dataset.

For each degree of memory that is investigated, a different model is developed. The estimation of the parameters is still carried out by means of the maximum log-likelihood function (4). Then the comparison between the competing models that are characterized by different extent of memory and the qualification of the most suitable one is performed by means of the Akaike Information Criterion (AIC; Akaike 1974).

In the classical SSRM the occurrence probability at any point \(t\) depends on the whole history. In the constrained SRM, this is not the case. In order to estimate the parameters and find the degree of memory, all the data are used. The novelty of the new model lies in the fact that after computing the degree of memory, there is no need to go back at the initial time of the catalog since we assume that the occurrence of the subsequent event is not affected by all the previous events occurred in the past but only by some recent ones. The proposed method thus, appears to have less computational burden than the one employing the classical SSRM since when the memory is computed the whole history is no longer used but rather some steps backwards. It is worth to emphasize that the computational gain refers only to future evaluations of the model. Computing the memory is not trivial and should be examined separately for each investigated dataset. The different study area as well as the magnitude threshold could demand and/or favor the use of different steps backwards. It is anticipated that the higher the magnitude threshold, the smaller is the memory of the proposed model because large earthquakes are supposed to be independent and not influenced by the previous seismicity. The computational gain is achieved in comparison with the classical SSRM as soon as the memory of the process is detected.

4 Application of the constrained-memory SRM

For the parameters estimation, a quasi–Newton method, the Broyden–Fletcher–Goldfarb– Shanno (BFGS) method (Fletcher 1987) is adopted. It should be noted that when stochastic modeling is engaged, mathematical tools should be used with caution in order to be combined with the geophysical meaning. A set of estimated parameters which gives the maximum of the log-likelihood function but does not reflect the physical meaning of the process should be rejected. In other words, the optimum set of parameters is the one that gives the maximum of the log-likelihood function, without violating the physical meaning of the process; apparently, this procedure is equivalent to constrain optimization of the log-likelihood function.

In our case, the parameters \(b = \nu \rho\) and \(c = 1/\rho\) of the relation (5) should be positive since the loading rate \(\rho\) and the parameter \(\nu\), depending upon the heterogeneity and the strength of the crust in the study area, take only positive values. For that reason,\(b\) and \(c\) are transformed and reparametrized as exponential functions. The Fisher information matrix is then used in order to calculate the standard errors through the evaluation of second derivatives of the log likelihood. Through this technique the amount of information provided by the estimated parameters is measured and the bounds on the variance of estimators are found. Although the parameter a, representing the initial stress value, is known to be particularly sensitive, the same a for each subinterval has been assumed in order to achieve a simplified model. It should be noted that keeping the same a may be a heavy assumption but the choice is inevitable in order not to have as many parameters as the data. For the construction of the confidence intervals asymptotic normality of the maximum likelihood estimation is employed, obtained through the central limit theorem under a large sample size.

Different steps are tested in an attempt to find the most appropriate model version that better describes the observations. For memory order of 1 up to 12, the estimated parameters are given in Table 1. Despite the fact that the differences are slight, the maximum of the log-likelihood function is obtained for m = 6 steps (Fig. 2). As expected, some degree of memory is encouraged. The memory of the point process for moderate earthquakes cannot be very small, 1 or 2 steps. That means the occurrence of every earthquake would depend only on the last event and that would lead to a renewal process, which is not suitable for moderate seismicity.

Table 1 Constrained-memory SRM’s estimated parameters for different degrees of memory
Full size table
Fig. 2
figure 2

Maximum likelihood under the Constrained SRM versus different steps backwards

Full size image

Figure 3 shows the conditional intensity functions versus time for various steps backwards along with the temporal distribution of the Corinth Gulf seismicity. In many time-points the behavior of conditional intensity functions are similar and the curves coincide. This is due to the fact that the values of some parameters are very close. For example, the parameter \(c\) is related to the loading rate \(\rho\), such that \(c = 1/\rho\), that defines the slope of the curve. In most cases \(c\) takes similar values and for this reason the increasing trend is almost the same.

Fig. 3
figure 3

Conditional intensity functions of the Constraint SRM versus time for various steps backwards

Full size image

As previously mentioned, the best model among the competing ones is, according to the AIC, the one having memory six (magenta line in Fig. 3). A different feature in the plots of the c.i.f. that are derived from the CM-SRM may be observed in Fig. 3 shedding light on the concept of the model. The occurrence of an earthquake may be accompanied by a jump up rather than a drop in contrast to what is observed in the case of the SSRM. This depends on the change of the data that form the memory of the process, e.g. the loading rate, the time intervals between events and the magnitude of the upcoming earthquake.

In Fig. 4 a comparison is made between the optimal model and the SSRM. Regarding the variation of the curve, the maximum value and drop for \(\lambda^{*} \left( t \right)\) is related to the Mw5.8 event of the 5th of September 1953. Going back in time at the genesis of the 6th previous event means the 29th April 1928 event is attained. This is the reason why the value of the c.i.f. is that high, the fact that a long time interval has passed (the amount we add in Formula (5)) while, on the contrary, the energy released is not a large amount (the amount we extract in Formula (5)), since the last 6 events were moderate (with magnitudes 5.2, 5.6, 5.3, 5.2, 5.2, 5.5). One more point worth to be mentioned where relatively large discrepancy from the SSRM is observed is in 1981 when the compound sequence of three strong (\(M \ge 6.3\)) events occurred very close in time (10 days). The value of the c.i.f. is not very high, approximately equal to 0.5. This is explained by the fact that going six steps back actually means that we are still in 1981. The curve, thus, cannot increase very much after taking also into account the large amount of energy released mainly due to the three main shocks. This means that in the aforementioned case one-year earthquake activity describes a large–scale process. The shortage of catalogs results in limitations regarding the performance of the models, but the restricted knowledge of the underlying mechanisms motivates the adoption of alternative options that may improve or support the existing ones.

Fig. 4
figure 4

Conditional intensity functions of the optimal Constrained SRM (m = 6) and the Simple SRM

Full size image

Comparing the estimated parameters of the SSRM and the CM-SRM, it can be seen that their differences actually are due to the \(c\) value (Table 2). The small c value in the proposed model indicates that the stress drop is not very much affected by the earthquake magnitude since the amount of energy released is multiplied by a very small number. Based on our computations, as it is shown in Table 1, the parameter a does not alter significantly when testing different degrees of memory backward ranging between (− 0.76, − 0.55) for the first 12 steps that have been examined. The value of the optimal model, a = − 0.752, is compatible with the value of a derived from the original SRM, a = − 0.789.

Table 2 Estimated parameters, standard errors and 90% confidence intervals for the SSRM and the 6-memory CM-SRM
Full size table

5 Model fitting

The model evaluation is performed by means of the second-order information criterion (AICc), which constitutes a modification of AIC for small sizes (Hurvich and Tsai 1989). Burnham and Anderson (2002) recommend its use when the ratio of the number of observations to the number of parameters is less than 40. In the constrained-memory SRM convergence is achieved for \(logL = - 94.877\), whereas in the SSRM \(logL = - 94.796\), with the difference very slightly favoring the SSRM. The number of parameters in the case of the CM-SRM is four since m is added in the parameters space. This factor, thus, moderately weakens the use of the CM-SRM. Specifically, AICc for the CM-SRM is equal to 198.469, whereas AICc in the case of the SSRM is equal to 196.013.

For the model evaluation residual analysis is also performed. This concerns a class of methods applied on spatiοtemporal point process models that provide graphical ways which may reveal where one model achieves better results than another or where a model does not fit with the data. Thinned residuals, applied in this work, are based on the technique of random thinning, which was first introduced by Lewis and Shedler (1979) and Ogata (1981) aiming at simulating spatiotemporal point processes and extended by Schoenberg (2003) for model evaluation (Bray and Schoenberg 2013).We suppose that the data {\(t_{i}\)} are generated by the estimated \(\lambda^{*} \left( t \right)\). Time transformation is used in order to test the model goodness-of-fit. Specifically, we consider the integral \(\tau_{i} = \mathop \smallint \limits_{0}^{{t_{i} }} \lambda^{*} \left( t \right)dt\) . This means {\(t_{i}\)} are transformed into {\(\tau_{i}\)}. It is known that the sequence of {\(\tau_{i}\)} derives from a stationary Poisson process of intensity equal to 1. The concept of the residual analysis is that if the compensator used for the transformation is that of the true model, then the transformed process will be unit-rate Process (Daley and Vere-Jones 2003). Otherwise, a systematic deviation would mean that a crucial factor is not taken into account in the proposed model, maybe due to the model complexity. In practice, if the fitted model adequately describes the data, it means that a large discrepancy from the unit-rate Poisson Process is not observed (red dashed line in Fig. 5). The advantage of the residual analysis is that a qualitative evaluation of the goodness-of-fit can be easily achieved through visual display. Nevertheless, in the current case the analysis does not clearly favor the application of any of the two competing models, and both seem to adequately fit the data.

Fig. 5
figure 5

Residual analysis of the constrained SRM with m = 6 steps memory (left) and the SSRM (right)

Full size image

6 Discussion and concluding remarks

Summarizing, the moderate magnitude (\(M \ge 5.2\)) earthquake occurrence in the Corinth Gulf (Greece), one of the most active regions in the Mediterranean Sea, is modeled through a new version of the Stress Release Model (SRM), the constrained-memory Stress Release Model (CM-SRM). As in the original formulation, the model combines a gradual increase of the strain energy due to slow continuous tectonic loading and a sudden release due to earthquake occurrence (stick—slip behavior).

For modeling the time-dependent seismicity, stochastic processes that are totally determined by the conditional intensity function (c.i.f.), are engaged. Studying the behavior of the c.i.f. consists a way for figuring out how the present is influenced by the past in an evolutionary process. An exponential type is implied, as proposed by previous researchers (e.g. Bebbington and Harte 2003 and references therein), that differs in that the c.i.f. does no longer depend on the whole history of the process. An “m -memory” point process is introduced where only the m most recent arrival times are taken into account in the c.i.f.. The memory is investigated, as to the number of steps backwards we should go, how many events in the past affect the occurrence of the subsequent event. The evaluation and selection of the most appropriate model is then performed by means of the maximum value of the log-likelihood function.

Adopting a constrained—memory SRM leads to different behavior of the conditional intensity function. The level of energy just before an earthquake occurrence, expressed through the “stress” level, is determined by the earthquake magnitude as well as by the occurrence time of the m-th previous event. For example, adopting 3-steps memory would mean that the occurrence time of each event is controlled by the magnitude and thus, the energy released in the last three events, and also by the time elapsed since the occurrence of the 3 previous events. If there is a relative quiescence and the last 3 events are of moderate magnitude, then the c.i.f. will get a large value. On the contrary, if tight clustering of strong events is observed, then the value of the hazard function will be quite low.

In this study, going back in time by six steps is found to be the most appropriate model that better describes moderate (\(M \ge 5.2\)) earthquake occurrence, which is indicative of a memory with long-range dependence. This model is then compared with the SSRM, i.e., the model that in every step takes into account the entire history, by means of the second-order AIC and the residual analysis. Despite the fact that the maximum value of the log-likelihood function for the two competitive models is almost the same, their difference is determined by the additional parameter of the suggested model. The residual analysis does not clearly indicate any of the two, since in both contrasting plots the residual processes derived from time transformation do not seem to deviate from the unit-rate Poisson and are indistinguishable.

The new model is suggested as an alternative option of the SSRM. The results revealed the significance of the memory investigation in the point process. Since they are comparable with those of the SSRM, having estimated the parameters and the degree of memory, the application of the model can be performed by avoiding using all the past information. Instead of knowing the whole history of the process, it seems adequate to get knowledge of just a few events backwards. It is plausible to assume that a moderate event of \(M \ge 5.2\) is not really affected by an event that occurred deeply in time, but rather by those that occurred in the most recent past. The computational burden thus is reduced as soon as the memory is found. The model could particularly serve as a basis for data simulation. In that way, a CM-SRM for a particular region and magnitude threshold that is proved to provide satisfactory fit can be alternatively used instead of the original SSRM with comparable results. In a further work, investigation of the memory of the point process by changing the magnitude threshold of the dataset used is worthy, in order to test whether the same number of steps backwards are sufficient. Synthetic catalogs could be particularly employed in order to further examine the c parameter’s variability through the application of the model in large datasets in an attempt to diminish the standard errors. Modeling through the constrained-memory SRM earthquake occurrence in other tectonic regimes could also give insight if the proposed model still adequately fits the data. Finally, the model might be expanded by incorporating interactions between adjacent subareas as in the case of the LSRM.