1 Introduction

Mathematics educators, researchers, and policymakers widely agree that fostering student perseverance in making sense of problems is highly consequential for supporting students’ participation with conceptually rich mathematics activities in fluent and flexible ways (Bass & Ball, 2015; DiNapoli & Miller, 2022; Hiebert & Grouws, 2007; Sengupta-Irving & Agarwal, 2017; SRI International, 2018; Warshauer, 2015a; Weltman, 2020). Indeed, within a U.S. context, “make sense of problems and persevere in solving them” is the first of eight mathematical practices deemed essential for teachers to inculcate in their students as outlined in the Common Core State Standards for Mathematics (CCSS-M; National Governors Association, 2010). Notwithstanding, research has corroborated that too often students struggle in mathematics classrooms with few opportunities for making sense of the underlying structure of mathematical concepts (e.g., Stein et al., 2017; Warshauer, 2015a). These findings highlight the need to better articulate connections between the notions of perseverance and sensemaking in mathematics classroom, with an explicit orientation away from a narrow conception of perseverance as mere persistence in hard work.

Regrettably, perseverance has the potential to be taken up by students, practitioners and policymakers in harmful ways, by placing undue blame on students for not possessing the disposition to take on challenging material. We find this logic problematic because it reifies false notions of meritocracy that hard work directly leads to success in math (Gresalfi & Hand, 2019; Mcgee, 2016; Rubel & Ehrenfeld, 2020; Weltman, 2020). This pernicious logic provides a narrow framework to suggest that struggling students need only work harder or ‘‘toughen up.” For example, Weltman, (2020) found that such notions of perseverance held significant explanatory power for teachers’ rationalization of failed cases of learning. Those who succeed are typecast as hardworking while others are deemed incompetent or lazy (Gresalfi & Hand, 2019; Horn, 2007). This is a burden projected onto students’ mathematical identities that even successful students, especially from historically excluded groups, manage daily (McGee, 2015).

In this paper, we work towards supporting teachers in shifting these classroom realities by clarifying instructional mediators that explicitly move student expectations beyond mere persistence and bridge perseverance and mathematical sensemaking. To clarify our terminology, we refer to sensemaking as making connections among mathematical facts, procedures, ideas, concepts, and students’ existing knowledge (Hiebert, 1997; Hiebert & Grouws, 2007; National Council of Teachers of Mathematics, 2009; Palatnik & Koichu, 2017). In addition, we adopt and further develop researchers’ distinction between the notions of persistence and perseverance, marking persistence as one component of the broader notion of perseverance in mathematics classrooms.

Secondly, we address discrepancies in how teachers and teacher educators define and operationalize ideas around perseverance. Perseverance has been conceptualized differently across seemingly distinct research traditions making it difficult to provide practitioners and teacher educators with a clear path towards supporting student growth. We attend to this discord by providing a conceptual framework that ties the various traditions of mathematics education research together to support teachers’ facilitation of perseverance. In particular, this framework underscores how dispositional, metacognitive, and contextual-interactive traditions inform instructional mediators of perseverance practices and dispositions and foster mathematical sensemaking. We argue that they conjointly specify a holistic and generative lens for teaching and teacher learning, towards facilitating perseverance and sensemaking in their classrooms.

Finally, there is a dearth of research on how teachers and teacher educators make sense of perseverance (for an exception, see Weltman, 2020). To be clear, our work with teachers in the field inspired us to clarify a conceptualization of perseverance that would be productive for teachers and teacher educators in supporting student sensemaking. Hence, we ground our conceptual work on perseverance in empirical data. We describe the unfolding logic of our inquiry as linear (from conceptual to empirical) for the sake of clarity. However, as is common in qualitative analyses, we refined earlier conceptual phases as our empirical analysis deepened and vice versa (Horn & Kane, 2015; Strauss & Corbin, 1998). In other words, we moved between our related conceptual goals and empirical questions to inform our conceptual framework and empirical findings.

We offer a conceptual framework that offers pedagogical direction for practitioners and a research baseline for teacher educators who are in search of ways to operationalize and facilitate perseverance in mathematics classrooms. We begin by reviewing the perseverance-related research that informed our conceptual framework for operationalizing perseverance towards sensemaking followed by reviewing the framework itself. We then use the framework to analyze a case study of a middle school mathematics teacher whose explicit goal was to support students’ perseverance, in relation to the first CCSS-M Standard. Classroom findings show the teacher repeatedly provided students with conceptual challenges yet offered scaffolds that minimized sensemaking opportunities. Our analysis of the post-class debrief suggests that teachers’ and teacher educators’ learning opportunities were limited by their reliance on a colloquial understanding of perseverance as persistence, overlooking explicit connections between students’ perseverance and their mathematical sensemaking. We conclude by discussing the framework and its potential utility for supporting teachers and teacher educators in interpreting, making sense of, and operationalizing perseverance.

2 Prior research on perseverance in mathematics education

The centrality of perseverance in mathematics education is evidenced in both research and policy documents (Bass & Ball, 2015; Hiebert & Grouws, 2007; Kilpatrick et al., 2001; National Governors Association, 2010; Sengupta-Irving & Agarwal, 2017; Warshauer, 2015a; Weltman, 2020). Yet, it is often unclear what is meant by perseverance, how teachers take it up, and how it is connected to other central ideas in mathematics education. In this section, we first elaborate on the distinction we adopt between the notions of perseverance and persistence followed by a review of prior research, detailing how the multiple yet complementary perspectives on perseverance—dispositional, metacognitive, and contextual-interactive—might be coordinated.

2.1 Distinguishing perseverance and persistence

Expecting students to continue in absolute obstinance absent instructional support can often exacerbate barriers to mathematics learning (Barnes, 2021; Star, 2015). For this reason, several mathematics education scholars have drawn distinctions between persistence as continuing and doing the same thing in the face of unanticipated obstacles from perseverance as changing one’s approach or seeking additional resources to address such obstacles (Bass & Ball, 2015; DiNapoli & Miller, 2022; Middleton et al., 2015). For example, Middleton et al., (2015) defined perseverance as entailing “a pattern of relatively consistent decisions over time” constituted by both persistence and a sense of when and how to “amend one’s plan” (p. 5). Whereas persistence has the quality of a “stubborn resistance to or a lack of change,” (Bass & Ball, 2015, p. 4), perseverance is marked by a cyclical and active practice of engaging and re-engaging with difficult mathematical challenges by employing a range of strategies (DiNapoli & Miller, 2022). We see a convergence around the ways these scholars and the CCSS-M authors use the term perseverance in relation to making sense of the problem with a focus on how students move “through barriers” by employing and changing up their strategies. To be clear, supporting students’ capacities to alter their approaches—to learn how to become unstuck—offers educators a tangible target for fostering students’ perseverance. The distinction between perseverance and persistence is productive because it shifts the focus on perseverance away from a student characteristic toward supporting teacher agency in designing efficacious learning environments.

2.2 Complementary theoretical perspectives on perseverance

As a starting point for organizing the review, we drew on a relatively recent collection of articles on this topic, funded by the Spencer Foundation, in which perseverance was discussed in terms of identity, attitude, and agency (Berry & Thunder, 2015; Middleton et al., 2015), metacognitive self-regulation and executive functioning (Clements & Sarama, 2015; Middleton et al., 2015), and practices-in-context (Bass & Ball, 2015; Taylor, 2015). In this collection of papers, perseverance is characterized across the perspectives of (1) students’ dispositions to (2) students’ regulation of their own thinking during a problem-solving session and (3) students’ participation within social spaces of learning. Although rooted in different traditions, we consider them to be incommensurable rather than incompatible (Sfard, 2007). In fact, these perspectives interact in multiple and complex ways. For example, students’ dispositions towards mathematics learning are inextricably connected to the social norms within mathematics classrooms that determine the nature and characterization of mathematical success which in turn shapes how, if at all, students engage with their peers to solve demanding tasks. Hence, we argue that when brought together, the three perspectives shape one another in generative ways—multiplicative as opposed to additive.

Below we address each category incorporating related key research, subsequently explicating our own conceptual framework. Following Kennedy’s, (2007) distinction between conceptual and systematic reviews of literature (see also Chen & Horn, 2022), rather than searching for an answer to a specific empirical question (as systematic reviews do), we synthesized different ways that researchers conceptualized perseverance. In reviewing articles, we began with the Spencer Foundation collection and followed up with relevant references from these articles, and so forth. In order to consolidate the review with newer and more diverse research, and to assess the validity of the three perspectives on perseverance, we then located additional peer-reviewed articles using the following search terms in the ERIC database: “perseverance” OR “productive struggle” in the title AND “mathematics education” anywhere in the article. This search yielded 24 articles from 18 peer-reviewed journals.

As our search terms imply, scholarly work on productive struggle greatly informed this work. However, our choice to center perseverance rather than productive struggle is rooted in challenging narrow uptakes of perseverance in relation to the first Common Core Standards of Mathematical Practice and our commitment to practitioners’ sensemaking about circulating instructional resources (Ehrenfeld, 2022).

2.3 Dispositional perspectives on perseverance

Across the corpus, the first of three perspectives represents the association between perseverance and students’ attitudes and mindset. Dweck’s (2006) work on fixed versus growth mindset has gained traction across education as it offers teachers a tangible framework for students to see themselves as capable learners. Dweck and others (Boaler, 2015; Livy et al., 2018) have argued that shifting teachers’ and students’ attention to their growable mathematical proficiency can in turn facilitate their sustained efforts in problem-solving. Indeed, one experimental study (Bettinger et al., 2018) showed how introducing students to a growth mindset contributed to extended time on tasks. At the same time, a growth mindset combats the perception that certain students simply come pre-wired for mathematics.

Students’ dispositions are entangled with notions of hard work alongside sensemaking throughout influential documents such as in Adding It Up (Kilpatrick et al., 2001) where a productive mathematical disposition is defined as a “habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy” (p. 116). They further elaborate mathematical proficiency as contingent upon students' opportunities “to make sense in mathematics, to recognize the benefits of perseverance, and to experience the rewards of sense making in mathematics,” (p. 131). In other words, perseverance as a dispositional attribute should be coupled with sense making.

Beyond the notions of growth mindset and productive dispositions, constructs such as mathematical identity, students’ agency, and mathematical relevancy have been substantially examined in mathematics education but the explicit relationship to perseverance has been limited. A couple of exceptions are two studies from the Spencer collection revealing the ways in which high levels of agency (Berry & Thunder, 2015), identity-related beliefs, and personal interests (Middleton et al., 2015) significantly support learners’ tendency to persevere. The messages students receive and the narratives students hold about themselves as mathematical learners are consequential for perseverance. While research and policy on students’ dispositions show promise for fostering perseverance through positioning students as capable learners, alone such disposition is insufficient.

2.4 Metacognitive perspectives on perseverance

From a metacognitive perspective, sustained participation is largely rooted in students’ understanding about and regulation of their own thinking and strategic knowledge (Clements & Sarama, 2015; Schneider & Artelt, 2010; Schoenfeld, 1987, 1992). Hence, moving beyond students’ attitudes and willingness to persist, metacognitive research examines how well students are able to reflect on and regulate their cognitive activity, at times in relation to emotional responses such as anxiety or joy (Barnes, 2019, 2021; Clements et al., 2016; Jiang et al., 2021). Specifically, researchers have shown a significant positive correlation between metacognitive knowledge and motivation towards mathematical activity over time (Schneider & Artelt, 2010).

The CCSS-M first Standard of Mathematical Practice cited in the introduction, “make sense of problems and persevere in solving them,” to a great degree takes a learner perspective on perseverance as a set of metacognitive practices. It highlights what mathematically proficient students do when they solve problems: look for entry points, analyze givens and goals, and monitor progress as well as change course, if necessary. It lays out a constellation of practices offering little, if any, direction on how to actualize them.

From a teaching perspective on metacognitive heuristics, Bass & Ball, (2015) contrasted one scaffold to another that proved to be more successful with transfer. The former involved reducing the complexity of the task through hinting as a way of supporting students’ advancement with the problem; whereas, the latter directed students’ engagement with general practices in support of perseverance for future problems: “A distinctly different kind of instructional support is to make visible the techniques, strategies, and tools that are in general useful to accomplishing a complex practice” (p. 19). In short, honing in on explicitly building up students’ toolkit is key in developing their ability to monitor, sustain, and manage decisions about which strategies to pursue or abandon at any point in the problem-solving experience (Barnes, 2019; DiNapoli & Miller, 2022; Thom & Pirie, 2002).

2.5 Contextual-interactive perspectives on perseverance

A third view for understanding perseverance foregrounds the role of instructional contexts, focusing on interactions and materials that support opportunities for students to persevere. For example, researchers have underscored the role of tasks (Hiebert & Grouws, 2007; Stein et al., 1996; Taylor, 2015), peer and student–teacher interactions (Bass & Ball, 2015; Sengupta-Irving & Agarwal, 2017; Stein et al., 2017; Warshauer, 2015a, b), as well as conceptual resources such as translanguaging (Morales & diNapoli, 2018) and scaffolding prompts (DiNapoli & Miller, 2022).

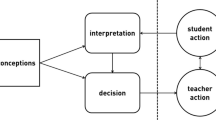
This third view substantiates perseverance as both an individual and collective endeavor (Bass & Ball, 2015; Sengupta-Irving & Agarwal, 2017; Weltman, 2020). For example, Sengupta-Irving & Agarwal, (2017) conceptualized perseverance in problem solving contexts as collective enterprise. They built on Hiebert & Grouws, (2007) distinction between (unproductive) struggle as “needless frustration or extreme levels of challenge created by nonsensical or overly difficult problems,” (p. 367) from the more productive meaning of struggle as efforts to make sense of mathematical ideas that are not well formed yet within reach. Extending this work, Sengupta-Irving & Agarwal, (2017) demarcated the inner and outer bounds of students’ collaborative Zone of Proximal Development (ZPD; Goos et al., 2002; Vygotsky, 1978), discerning productive from ineffectual cases of group problem-solving (see Fig. 1). In productive cases of perseverance, the task, peers, and the teacher facilitated student collaborative participation within their ZPD (“productive struggle”). Conversely, ineffectual cases occurred when either the task was beyond the groups’ grasp and therefore, beyond their collaborative ZPD (“unnecessary struggle”) or when the task was deemed too easy, apparent, or procedural (“no struggle”).

Fig. 1
figure 1

Struggle and students’ collaborative ZPD (reproduced with permission from Sengupta-Irving & Agarwal, 2017)

Full size image

Indeed, supporting students’ perseverance with sensemaking as a primary outcome requires us to pay close attention to the teacher’s role in tuning appropriate levels of challenge and support (i.e., scaffolds) that enable students to make progress on tasks. For example, Stein et al., (1996) found that rich tasks often become “non-problems” when teachers over-scaffold by specifying explicit next steps or doing them for students. Indeed, teachers struggle to facilitate without leading “so much that students abandon their own sense-making…” (Hiebert, 1997, p. 29). Thus, mediating perseverance practices and dispositions towards bolstering conceptual understanding has proved to be both challenging and worthwhile.

Our overarching pragmatic goal in this study is to provide guidance on how to couple perseverance in solving problems with opportunities to make sense of the conceptual underpinnings of mathematics by bringing together the dispositional, metacognitive, and contextual-interactive perspectives on perseverance.

3 Conceptual framework

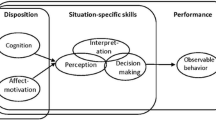
In this section, we describe our conceptual framework for fostering perseverance practices and dispositions to advance mathematical sensemaking. First, building on prior literature (e.g., Bass & Ball, 2015), we refer to perseverance as a set of domain-specific dispositions and practices, collective and individual, that can be mediated by teachers in specific problem-solving contexts towards mathematical sensemaking. Second, we elaborate on the guidance that the dispositional, metacognitive, and contextual-interactive perspectives provide through three respective instructional mediators: positioning students as capable sensemakers, making problem-solving heuristics explicit, and facilitating student participation within their collective Zone of Proximal Development (ZPD) through interactions and lesson materials.

3.1 A framework for bridging perseverance and sensemaking

A major impediment for supporting teachers in learning how to couple perseverance with sensemaking is the seemingly distinct meanings used across different traditions of research. This inconsistency makes it difficult to operationalize pedagogical goals around perseverance. We address this gap by providing a conceptual framework (Fig. 2) that ties the three perspectives (dispositional, metacognitive, and contextual-interactive) together under the goal of understanding pedagogical mediators that create the conditions for bridging perseverance and sensemaking. We then illustrate the framework with an empirical case study of classroom teaching accompanied by teachers’ collaborative sensemaking about perseverance.

Fig. 2
figure 2

Conceptual framework: bridging perseverance and sensemaking

Full size image

At the core of our conceptual framework is the notion that there are several instructional mediators that can influence how students engage mathematics problems in order to make sense of them. The thick, green arrows demarcate a productive cycle of perseverance and sensemaking when the mediators present themselves in positive ways. As we reviewed, first, research on identity, agency, and attitude pointed to the importance of providing students with resources to position them as capable learners. Second, metacognitive research pointed to the importance of providing students with explicit heuristics to make decisions about which strategies to pursue or abandon at various phases of their problem-solving experience. Finally, the contextual-interactive research pointed out the importance of using local resources (such as the task, peers, and the teacher) in ways that facilitate students’ collective participation within their collaborative ZPD: learning that is neither beyond the students’ grasp nor too easy, apparent, or procedural.

In contrast to the productive cycle, the dashed line that directly connects persistence to sensemaking represents colloquial understandings of perseverance. These understandings suggest (often implicitly) that continuous persistence eventually leads to sensemaking. The literature review, as well as the empirical sections below, show that in the absence of appropriate identity, metacognitive, and interactional resources to make sense of the underlying mathematical ideas, students’ potential to make sense of mathematics can be limited. Hence, our conceptual framework underscores the various mediators aligned with the three perspectives that direct students’ perseverance towards sensemaking and away from narrow understandings of the term as mere persistence.

Significantly, we aim to challenge false notions of meritocracy that are prevalent within mathematics education (Gresalfi & Hand, 2019; Mcgee, 2016; Rubel & Ehrenfeld, 2020; Weltman, 2020) by laying bare ways to connect perseverance with sensemaking. We find it imperative to caution against drawing on perseverance to apply undue blame on students and, instead, interrogate the ways in which our instruction and support of teachers can foster perseverance practices and dispositions in learning and doing mathematics.

In the rest of the paper, we build on the case of the teacher, Ezio (all teacher names are pseudonyms), to examine our overarching research question: how might we support teachers and teacher educators to interpret, make sense of, and operationalize perseverance practices and dispositions? Specifically, we use the conceptual framework to understand both the focal teacher’s attempt to operationalize his pedagogical goals around perseverance in his classroom and our own attempts as teacher educators to support him in doing so. To clarify, the lesson and video-based debrief preceded our articulation of the conceptual framework. In fact, the primary motivation for seeking a clearer conceptualization of perseverance was our emerging understanding of ways in which we fell short in supporting the focal teacher, Ezio, in fostering a more productive view of perseverance in the lesson debrief. We conflated persistence with perseverance and neglected to draw out explicit mediators that shift perseverance towards sensemaking.

4 Methods

To answer our overarching conceptual research question, we divided it into two analytic sub-research questions (SRQ). We answer these analytic questions by utilizing the conceptual framework for the case of Ezio: How did Ezio facilitate his students’ perseverance during the Tower of Hanoi task in his classroom? (SRQ1) What opportunities did the teachers have (or not) to develop a more comprehensive view of perseverance in the lesson debrief? (SRQ2).

4.1 Research context

This analysis comes from a larger research-practice partnership with a professional development organization (PDO), where we used video to support secondary mathematics teacher teams in improving their practice (Project SIGMa; Horn & Garner, 2022). Through this partnership, we worked with teacher teams from six schools, visiting each team 2–5 times per year according to their needs and capacity. Our visit protocol began with the teacher sharing their inquiry focus ahead of the observation. The research team then video-taped the lesson using both a point-of-view (goPro) and wide-angle lens camera (Swivl) as well as microphones placed at four student groups. Upon reviewing the recordings, the team identified clips that supported both the teacher’s question(s) and ones we found promising for supporting their growth towards ambitious and equitable instruction. Finally, a few days after the lesson, the teacher, their school-based colleagues, and members of the research team met to view and discuss the clips.

The topics raised during the 32 debriefs across the project began with teachers’ questions of interest and often shifted to additional topics that emerged. Conversational topics ranged across problems of practice that included discourse facilitation, planning and curriculum, groupwork facilitation, math-specific topics, social-emotional aspects of teaching, and more (Horn & Garner, 2022).

Prior to our visit with Ezio and at our request, he sent an email with his plan to use the Tower of Hanoi task; he wanted students to work with a non-linear function as an intentional contrast to the linear patterns they had been investigating. Prior to the class, Ezio asked us to look at group dynamics to determine if certain students were dominating. After recording the lesson, we met with Ezio and Veronica (his peer) 4 days later to debrief the lesson at which point Ezio shared that a central reason for choosing the Tower of Hanoi task was to support students in learning how to persevere. He added, “It is one of the standards. I totally agree with that standard.” To be clear, at this point, we had not developed the conceptual framework for perseverance. As previously stated, a primary motivation for this study and for seeking a clearer conceptualization of perseverance for teaching and teacher learning was our analysis of the debrief conversation revealing ways we fell short in supporting Ezio’s learning how to foster perseverance.

4.2 Data sources

Primary data sources for this analysis include the 90-min video-recorded classroom session and the 81-min videotaped debrief of the lesson with three members of the research team––the two authors of this paper and Ilana Horn (Lani in the transcripts). The first author of this paper, Patty, a teacher educator with over 15 years of teaching and professional development experience, facilitated the conversation with Ezio and Veronica. The other researchers, Nadav and Lani, primarily filmed and took field notes but on occasion participated in the conversation.

4.3 Case selection: focal teacher

The lesson and debrief conversation analyzed here are focused on Ezio, a veteran, middle-school teacher with over 17 years of experience. Ezio demonstrated strong content knowledge during his teaching and in professional development workshops, underscored by his undergraduate and graduate mathematics degrees.

We argue that Ezio’s classroom teaching in this episode is similar to what Stein et al., (2017) framed as high Students Opportunities to Struggle (SOS) and low Explicit Attention to Concepts (EAC), the predominant profile in their corpus of 256 teachers. This profile typifies those teachers moving beyond memorization-based mathematics teaching to teaching that promotes engagement with conceptually rich materials like working in small groups on the Tower of Hanoi task. By examining Ezio’s discernment of perseverance, our analysis offers insights into this prevalent profile, revealing ways PD providers and teacher educators can better address learning within this transitional category of teaching.

4.4 The lesson

The class episode under study featured animated talk, boisterous laughter, and wooden manipulatives in action. The classroom was decorated with mathematical phrases, posters, and books. In short, it appeared a vibrant environment in which to learn and do math. Ezio’s queries prior to filming centered around student group dynamics. Notwithstanding, in the debrief, Ezio revealed that perseverance was an explicit goal for the featured task, the Tower of Hanoi. The 90-min lesson was replete with intensive mathematical work by 31 eighth graders. It was built around two mathematical tasks: a warm up with visual patterns representing a linear function (around 30 min), and the Tower of Hanoi (around 60 min). The episode discussed here is focused on the second task.

4.5 Focal task: “Tower of Hanoi”

The Tower of Hanoi activity consists of three poles and a varying number of rings in different sizes (see Fig. 3), arranged on one pole. The goal of the task is to move all the rings, one at a time, from the initial pole to either of the two remaining poles, while avoiding the placement of a larger ring onto a smaller one in the least number of moves. For example, 3 rings can be transferred with a minimum of 7 moves. In the focal lesson, students were given the manipulative with 5 rings and tasked to find the general rule for determining the minimal number of moves for any given number of rings [f(n) = 2n-1]. Prior to the lesson, students had only been working with linear patterns. Ezio chose the Tower of Hanoi for two reasons: first, to distinguish between linear vs non-linear patterns (as explained in his email before class). And second, he wanted students to experience a challenging problem with which to persevere (as he explained in the lesson debrief). The Tower of Hanoi was a good fit to his goals given its non-linear structure and the conceptual challenges it entails.

Fig. 3
figure 3

Illustration of the Tower of Hanoi kit with three poles and four rings

Full size image

4.6 Methods of analysis

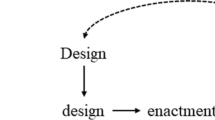
Our overall methods represent an iterative process of analyzing data sources to understand how Ezio made sense of, designed for, enacted, and reflected on perseverance. In the analysis of the classroom lesson, we illustrate Ezio’s design and enactment of the task in light of our conceptual framework, detailing the relationship between students’ consistent engagement and their limited sensemaking opportunities. First, we segmented classroom events and the unfolding temporal organization of the classroom (Ball & Bass, 2015; Jordan & Henderson, 1995), which we labelled as two cycles of conceptual challenges and scaffolds that proceduralized students’ work. We then explored the relationship between perseverance and sensemaking through the three mediators provided by the framework.

In the analysis of the lesson debrief, we report teachers’ video-based collaborative reflections about the lesson. We follow Horn and Kane’s (2015), emphasis on opportunities to learn in professional conversations. As they do, we attend to teachers’ epistemic stances, problem frames and representations of practice to reveal how teachers make sense of and improve upon their instruction through interaction. Briefly, epistemic stances are notions of what can be known, how so, and why it matters (Goodwin, 2007; Hall & Horn, 2012). Problem frames are implicit or explicit aspects of communication by which teachers index particular lenses when discussing problems of practice (Horn, 2007; Louie, 2016; Vedder-Weiss et al., 2018). Representations of practice are different aspects of teaching made visible in teacher conversations through simulated classroom dialogue, video-based representations, and other communicative means (Hall & Horn, 2012; Hall & Jurow, 2015; Little, 2003).

Thus, we examined Ezio’s epistemic stances as he aspired to promote perseverance in his classroom and looked at Ezio’s opportunities to make sense of the notion of perseverance (Horn & Kane, 2015). We used our conceptual framework as well as methods of frame analysis (Goffman, 1974) to understand how we collectively took up Ezio’s problems of practice indexing particular problem frames, some more productive than others for teacher learning (Vedder-Weiss et al., 2018). Using these analytic tools we first show Ezio’s epistemic stance on positioning students as sensemakers, and then show how the teachers and teacher educators relied on a colloquial understanding of perseverance, limiting the teachers’ learning opportunities.

5 Results

Below we share our analysis of Ezio’s classroom events from the filmed lesson and the ensuing debrief conversation with respect to perseverance. Our analysis revealed how, in our role as teacher educators, we both provided and missed opportunities to support Ezio in re-imagining perseverance in his classroom. Taken together, our empirical findings highlight the utility of our conceptual framework (Fig. 2) as a clearer conceptualization of perseverance with the potential to offer teachers and teacher educators an actionable resource for fostering students’ perseverance.

5.1 Classroom excerpt: cycles of conceptual challenges and scaffolds

In this section, we explain classroom events with a particular aim of understanding Ezio’s implementation of the task and the emerging relationships between perseverance and sensemaking. We show how Ezio’s conceptual challenges pushed students beyond their collaborative ZPD, and how he supported students to engage with these conceptual challenges, arguably at the expense of making sense of the mathematical ideas.

Generally speaking, in our initial analysis of classroom events during the Tower of Hanoi task, we identified 7 main segments (see Table 1) clustered as two repeated cycles. Each cycle consists of a conceptual challenge, a whole class scaffold to support overcoming each challenge, and groupwork monitoring to validate the scaffold.

Table 1 Segments of classroom activities
Full size table

5.1.1 First challenge: “How Do You Know That’s the Fewest?”

Ezio introduced the Tower of Hanoi and circulated among groups to ensure all student pairs understood the task. As students began to collect and annotate their initial empirical results, Ezio circulated around the groups asking them “how do you know that’s the fewest [number of moves]?” He repeatedly asked this question without waiting for—or following up with—students for a response. Students seemed to interpret it as an invitation to continue to explore the problem empirically (i.e., trying to move rings in fewer moves). We account for this question as the first challenge. We base our claim that responding was beyond students’ ZPD (Fig. 4) on two pieces of evidence. First, neither students nor the teacher attempted to consider a response to the question; that is, students did not attempt to answer it either among themselves or directly to Ezio upon posing it and Ezio never circled back to see if students had answered the question. Second, from our experience as teachers, the mathematical complexity of understanding the fewest moves after a few empirical tries is beyond the initial reach of most middle schoolers without adequate scaffolding.

Fig. 4
figure 4

(Reproduced from Buenrostro & Ehrenfeld, 2019. Curved arrows added by authors on top of the figure from Sengupta-Irving & Agarwal, 2017)

Cycles of conceptual challenges and scaffolds

Full size image

5.1.2 First scaffold: the “Cheat”

Ezio followed his line of inquiry up with a whole-class scaffold where he explained and demonstrated the “cheat.” The cheat represented the recursive nature of the task, allowing one to easily determine the fewest number of possible moves for any number of rings, n, given the result for n-1. For example, as Ezio illustrated to his students, one can determine the least number of moves for 4 rings by building on the least number of moves for 3 rings. First, by moving the top three rings altogether which “costs” f(3) moves. Second, by moving the largest forth ring to an empty pole which “costs” one move. And finally, by moving the three smaller rings on top of the larger one which again “costs” f(3), and altogether f(4) = 2f(3) + 1 and generally, f(n) = 2f(n − 1) + 1.

We want to be explicit regarding the assumptions under which we consider this teaching move to be an over-scaffold (Fig. 4); explaining to students the recursive rule is over-scaffolding if the teacher aims for student discovery of mathematical ideas, as was the case here. It is also an over-scaffold in the sense that it forecloses new ways to solve the problem and divergent ways of making sense of the mathematical structure. Upon explaining the “cheat,” Ezio circulated among several groups prompting them to replicate the “cheat,” asking questions such as “If you know [the number of moves for] 4 [rings], how can you determine the number of moves for 5?”.

The over-scaffold is demonstrative of the tendency for some teachers to reduce the complexity of the task (Hiebert, 1997; Stein et al., 1996). Note that an alternative approach would have been to support students in articulating the cheat themselves perhaps by focusing on solutions to n = 1, 2, 3 rings instead of 7 (see later our discussion in the lesson debrief of Polya’s (1945/2004) heuristic “solve a simpler problem first”).

5.1.3 Second challenge: “What if I Want to Know For a Hundred Rings?”

Having students demonstrate the recursive rule via the cheat meant that students knew how to calculate the minimal number of moves for any number of rings, given the result of the previous step. At this point, Ezio introduced to them what we account for as the next conceptual challenge. As the following short example illustrates, when students explained to Ezio the recursive pattern, he asked them to determine the minimal number of moves for 100 rings, implicitly asking for a closed-form solution:

Student: From the last step you multiply by two and you add one.

Ezio: True, that’s one pattern. Right. Okay but wait a minute. What if I want to know for a hundred rings?

Indeed, this is where students largely got stuck.

5.1.4 Second scaffold: synthetic manipulation

In response to students’ struggle to find the closed-form solution, Ezio redirected students to use a scaffold in the form of a table (distributed on a hand-out) where they could determine the number of minimal moves for n rings into the function only by way of a synthetic manipulation. As one example, for n = 3 rings, students were instructed to (a) find the minimal number of moves (7), (b) add one (8), (c) do prime factorization (2 × 2 × 2), and (d) write the final power form [f(n) = 23]. Students were then asked to find a relationship between the final power form [f(n) = 2n] and the function [f(n) = 2n − 1]. Again, we view this as an over-scaffold (Fig. 4) in the sense that it did not prompt, or even suggest, new strategies to solve the problem while making sense of its mathematical structure. Rather, it guided students procedurally and almost directly to generating the function. Notably, we recognize that finding a closed solution is an ambitious instructional goal in middle school, and indeed one that Ezio “wasn’t expecting [students] to come up with.”

5.1.5 Bridging persistence and sensemaking: using the lens of the three mediators

Our analysis yielded two cycles of conceptual challenges and scaffolds. That is, in each of these cycles, Ezio’s questioning functioned to place students between moments of struggle beyond reach and moments of no struggle, which we interpreted as over-scaffolds (Fig. 4). With regard to persistence (one component of perseverance), it worked. Our analysis as well as our experience as visitors in the classroom showed students consistently engaged in intensive mathematical work with one another. From a sensemaking perspective, we find the design and enactment of students’ perseverance worked against creating opportunities to make sense of mathematical ideas (see Fig. 5).

Fig. 5
figure 5

The conceptual framework as a lens to understand perseverance in Ezio’s lesson. Note: the unproductive struggle and students’ limited sensemaking opportunities are represented by the right-side arrow in red and explained through the lens of the three mediators

Full size image

Drawing on the three mediators of perseverance practices and dispositions outlined in our conceptual framework, we assert that Ezio did position students as capable learners, intentionally giving them the time and space to collaborate and engage with a conceptually rich mathematical problem. It is notable that students repeatedly moved the rings trying to reproduce the minimal number of moves until they felt confident to move onto the subsequent number of rings. However, notably absent were explicit problem-solving heuristics (including visual representations and records of their work) that could have supported sensemaking both in the focal lesson and in students’ future work. That is, students needed tools to determine whether they had indeed generated the minimal number of moves beyond reproducing the same number of moves through trial and error. Finally, the interactions and lesson materials as carried out by way of “the cheat” and the synthetic manipulation as laid out in the handout bypassed students making sense of the structure of the task with their group partners foregoing participation within a collaborative ZPD. Coming up against the seemingly insurmountable challenges, students initially appeared to have few, if any, resources to draw from, and were then strongly scaffolded towards a solution path. These cycles of challenges and over-scaffolds stood at odds with mathematical sensemaking.

5.2 Debrief conversation: “I Want Them to Learn How to Persevere”

During the debrief, we learned with more clarity that Ezio believed a task such as the Tower of Hanoi afforded his students opportunities to learn how to persevere. Ezio’s stated goal of teaching his students to persevere became a main theme in the conversation and in the subsequent analysis. To study teachers’ learning opportunities in the debrief conversation, we follow Horn & Kane, (2015) by focusing on Ezio’s epistemic stances about perseverance and the ways participants collectively framed problems of practice.

The presence and absence of the three mediators in Ezio’s classroom (see Fig. 5) provided the video-based conversations with important substrates for learning. Indeed, when we investigated Ezio’s epistemic stance about perseverance, ideas about the value of positioning students as capable problem solvers (mediator #1) came up strongly. In addition, when we investigated participants’ collective framing of the problems of practice—how to support students’ exploration of the task structure—problem-solving heuristics (mediator #2) and classroom interactions and materials (mediator #3) both came up as well. However, we did not explicitly connect the ways in which the three mediators work together to support (or constrain) students’ perseverance. Moreover, by conflating perseverance and persistence, we diminished opportunities to scrutinise possible relationships between students’ perseverance and their sensemaking.

5.2.1 Ezio’s epistemic stance about perseverance: positioning students as capable problem solvers (mediator #1)

As we began watching the first video clip during the debrief, Ezio asked Patty to pause the clip to share his intentionality behind choosing the Tower of Hanoi task, “I like the Tower of Hanoi, a personal belief I have…I just don’t know how to do it., but I think Tower of Hanoi at least gets you there.” He explained that “sooner or later [students] hit a mathematics problem where they hit a wall…I think everybody hits that wall.” Ezio asserted that everyone will hit this inevitable wall wherein all learners eventually confront a seemingly insurmountable concept or mathematics problem. He described this moment as a critical juncture for all mathematical learners, including himself:

When they reach that breaking point and they snap, those who give up, that's it. They're done with math […] while those who continue the struggle, even if they take a break but eventually get back to it, they're the ones who will succeed in math [...] We all hit that breaking point. It's just learning how to overcome that breaking point.

Drawing on his own beliefs about learning mathematics, Ezio posited that students who persevere learn “how to overcome that breaking point.” This suggests that from Ezio’s perspective all students can succeed if they learn how to persevere, noting perseverance as a standard (CCSS-M) worthy of intentionality:

I think the Tower of Hanoi is complex enough, at least in a middle school. I want them to learn how to persevere. It is one of the standards. I totally agree with that standard. I don't feel like I do a good job of teaching them how to persevere over those obstacles. [The] Tower of Hanoi at least gives me the opportunity to focus in on that.

We center Ezio’s epistemic stance to illustrate that he presented his students with a complex task knowing they would struggle. He articulated this to us in an email prior to our classroom visit and he reiterated this in the debrief conversation, “I wasn’t expecting them to come up with the actual equation.” Accordingly, their knowledge of working with a linear structure would not work here, making way to discover something different. He positioned them as developmentally ready to expand on their knowledge of function types. His expectations were high, presenting them with high school level material; the Tower of Hanoi is a 12th grade task in other curricula (e.g., IMP Year Four).

In sum, Ezio’s reasoning for choosing this particular task drew both on the institutional discourse of the standards and on his own epistemic stance of how students can become stronger mathematical learners. Ezio attempted to support students for a longer trajectory in mathematics. Beyond getting through the content of the task, his intentions were to support students in learning how to overcome obstacles in preparation for mathematical challenges yet to come. In this sense, Ezio’s prognosis rests on the assumptions that, (1) perseverance is learnable, (2) his students are capable (mediator #1), and, (3) he is responsible for creating the right conditions for students to learn how to overcome breaking points.

5.2.2 Framing practices in support of students’ sensemaking: problem-solving heuristics (mediator #2) and classroom interactions (mediator #3)

Because they had just completed a unit on linear functions, Ezio believed it was an appropriate time to introduce students to non-linear structures like the Tower of Hanoi. As classroom observers, we witnessed students eagerly trying to reproduce the fewest moves over and over again to analyze the task structure. We, the researchers, framed this problem of practice as one of facilitating students towards unearthing the task structure as a pathway to make sense of the problem. After observing a video clip of Ezio’s interactions with small groups, Patty asked him to reflect on his first recurring question of “how do you know [x] number of moves is the minimum?” This question posed by Ezio to students seemingly directed students to make sense of the underlying structure of the function at play in the task.

Patty: You kept throwing this question to a lot of groups of ‘you need to be asking yourself, how do you know, it’s a minimum number of moves, right?

Ezio: Right, I threw that out, but I never asked them. No one had shown me that they know it was…Oh that was one thing I was hoping. As they were moving their rings, I didn’t hear anyone say, ‘Well, I’ve reached the halfway point.’ When they move that final ring, right around there is kind of the halfway point so it should be more than double that. I didn’t hear anyone making that conclusion..

Ezio recognized that he kept asking groups the same question (i.e., the conceptual challenge) without requiring students to produce a response (“I threw that out but I never asked them [to respond]”). It bears noting that Ezio wanted students to conclude with a sense of the structure (i.e., the halfway point). However, understanding that the number of moves doubles (the function is represented with 2n + 1) was a conceptual leap for students. Patty suggested that students needed a way to explore how to consistently produce the least number of moves as a precursor to sorting out the structure. She noted, “students didn’t really have a way to talk about the things you were raising.” In response, Ezio’s co-teacher, Veronica, affirmed this framing of the problem:

They’re coming up with strong conclusions, but like you said, you didn't hear the verbalization as to why. Ezio gave a probing question. Well, how do you know 19? How do you know 17? Clearly it's not 19 [because] they got 17. He is pushing their thinking, but it’s that next level of verbalizing, the why [that is missing].

To this point, Patty offered the problem-solving heuristic of “solve a simpler problem first” strategy (Polya, 1945/2004) as a way to support students in investigating how to consistently produce 7 moves from 3 rings. By finding a systematic way to produce 7 moves (which students were consistently doing), students could be poised to identify an underlying pattern that could then be extended to the subsequent number of rings. This heuristic could have served as a mediator for Ezio to direct students’ collective inquiry towards the underlying structure of the Tower of Hanoi.

Ezio and Veronica took this idea as their main takeaway from the conversation. For example, in the latter part of the debrief conversation, Ezio commented, “I totally agree with you. It was too much too fast… If I had just focused on the three, pause, okay.” Similarly, Veronica noted:

I do feel like just given the environment that Ezio and I work in, teaching the strategies and really having them verbalize strategies, for me, is pushing me as a teacher. [...] Getting them to do problem solving strategies and how and the why, I would say that's an area where I'm trying to grow.

We see evidence here of a significant teacher learning opportunity as Veronica indicated. She understood that asking students to justify (verbalization of the why) was a professional goal of hers. Veronica identified problem-solving heuristics as an area of growth that was stretching her professionally and the next level of teaching to which she aspired.

5.2.3 Conflating perseverance and persistence: “We Saw a Lot of Perseverance”

Upon sharing the scaffold and having it received well by both Ezio and Veronica, Patty transitioned to discuss Ezio’s primary goal of supporting students’ perseverance. However, as evidenced in the following excerpt, we all conflated it with persistence.

Patty: I would say to your desire to have students persevere, I think we saw a lot of perseverance, a lot of perseverance. That was my perspective, right?

Lani: Definitely.

Ezio: Right, but-

Patty: You didn't really see kids giving up, even though-

Veronica: You didn't have groups just setting it aside.

From both Veronica’s and the researchers’ perspectives, students were persistent in working through the problem. However, we conflated persistence with the broader notion of perseverance in mathematics classrooms (Middleton et al., 2015), foregoing the centrality of sensemaking.

Patty transitioned from the previous exchanges about positioning students as capable problem solvers (mediator #1), problem-solving heuristics (mediator #2), and classroom interactions (mediator #3) to establish students’ perseverance: “I would say to your desire to have students persevere, I think we saw a lot of perseverance, a lot of perseverance,” to which Lani confirmed, “Definitely.” Patty and Veronica followed up with comments related to students not giving up nor “just setting [the task] aside.” Nadav followed (not shown in the transcription above) by confirming that students worked hard. Across this episode, we all affirmed students’ persistence in working on the task for close to 60 min as evidence of fulfillment of Ezio’s goal to teach students how to persevere. In other words, we framed perseverance as mere persistence, disconnected from themes about mediating student sensemaking which are central to a comprehensive notion of perseverance in mathematics classrooms. In this sense, our own conceptualization and the teachers’ learning about perseverance was limited.

6 Discussion and implications

Our overarching conceptual research question was How might we support teachers and teacher educators to interpret, make sense of, and operationalize perseverance practices and dispositions? We attended to this question by providing a framework for bridging perseverance and sensemaking in mathematics teaching and teacher learning. Disentangling perseverance from persistence enabled us to expose pedagogical mediators that can support students’ sensemaking, place agency within the purview of the teacher, and minimize deficit orientations towards students. The conceptual framework we suggest (Fig. 2) ties together the various perspectives and their corresponding mediators that bolster sustained work towards sensemaking, and, it makes explicit the resources consonant with pedagogical goals around perseverance. As illustrated in the debrief conversation, we touched on various themes as largely disparate resources: positioning students as capable, the desire to facilitate perseverance, using heuristics as scaffolds, and the role of questioning in interaction. Notwithstanding, these resources in this context interacted in complex ways to support and constrain students’ learning.

Furthermore, our conceptual question was coupled with analytic sub-research questions (SRQ) that illustrated the framework and its utility with empirical data (Fig. 5). First, we asked, How did Ezio facilitate his students’ perseverance during the Tower of Hanoi task in his classroom? (SRQ1) The main classroom findings were that students consistently engaged in intensive work (i.e., persisted) with limited sensemaking opportunities. We explained classroom events through the three mediators: students were positioned as capable learners, explicit problem-solving heuristics were absent, and the interactions and lesson materials as carried out facilitated cycles of participation that vacillated between too challenging and proceduralized.

Then, we asked, What opportunities did the teachers have (or not) to develop a more comprehensive view of perseverance in the lesson debrief? (SRQ2) Debrief findings show that as teacher educators, we provided the teachers with several learning opportunities around the three mediators. For example, Ezio reiterated that the “solve a simpler problem first” strategy could have supported students in engaging with the task conceptually. He identified this as the key takeaway for this particular task, and as such, we were unable to attend directly to his larger query of how to support students’ perseverance. Veronica connected the scaffold as a step in the right direction towards her own professional learning around supporting students’ verbalization of their reasoning and justification. We believe a conceptual framework distinguishing perseverance from persistence and explicating the mediating factors between perseverance and sensemaking could have made the notion of perseverance more visible and learnable, providing Ezio and Veronica with the tools to attend more consistently to fostering perseverance in their classrooms over time.

Despite the burgeoning conversations within education broadly and mathematics classrooms specifically, little research has investigated how mathematics teachers interpret, design for, and enact ideas around perseverance in math classrooms, and how teacher educators can better support them. Here, we focused on the ways teachers and teacher educators made sense of perseverance, in light of Ezio’s lesson, instructional resources such as CCSS-M, and his asset-based orientation toward his students. We argue that our conceptual framework can be a starting point to support teachers and teacher educators in interpreting, making sense of, and operationalizing perseverance practices and disposition by attending to the various mediating perspectives and resources available.

6.1 Implications for teacher learning and further research

Given the prominence of mathematics classrooms that yield unproductive opportunities to struggle (Stein et al., 2017; Warshauer, 2015a), we believe that teacher educators could benefit from a conceptual framework that makes explicit the mediators for bridging perseverance and sensemaking. Indeed, conceptual frameworks have shown promise in supporting teacher sensemaking about perseverance towards a collaborative learning process (Warshauer et al., 2019; Weltman, 2020). In a similar vein, we offer our conceptual framework to teacher educators and researchers as a lens for facilitating teacher conversations about perseverance in generative ways. We believe that establishing such a framework is both important and timely, given that perseverance and associated terms such as productive struggle have experienced more prominence in practitioner journals, professional development workshops, and even program themes (e.g., the 2021 Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA 43); Spitzer et al., (2021)).

Finally, we suggest our framework as a departure point for future work and acknowledge its limitations. The paper is built on a single case study of a single cycle that included the lesson and a lesson debrief. In addition, the task of the Tower of Hanoi, although rich and conceptual, is not a typical problem-solving activity. Consequently, further empirical research on teachers’ and teacher educators’ sensemaking of the notion of perseverance is greatly needed. A potentially productive path for future research is to consider how teacher educators use the conceptual framework offered here, beyond our suggestions, to further investigate and specify mediators between perseverance and sensemaking. Our interest in such research stems from our belief that pedagogical ideas are dynamic and gain their meanings from the specific context of use. Conceptual frameworks need to be sufficiently porous to account for teachers’ sensemaking and localized contexts yet specific enough to support specific learning trajectories. Our conceptualization of perseverance for teaching and teacher learning aims at simultaneously supporting teachers’ sensemaking about the notion of perseverance and bolstering students’ sensemaking about mathematical ideas, in the rich and generative meaning of the word.