1 Introduction

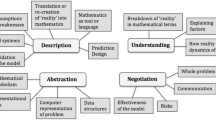
School mathematics has been described as an outcome of didactic transposition processes (Chevallard, 1991) by which mathematical knowledge having a pre-existence outside school is being adapted to become teachable to students in school. This transposition of knowledge from one institution to another is affected by constraints within the target institution and different actors and interests influencing the process.Footnote 1 To characterise possible sources of the didactic transposition of mathematical modelling one would need to investigate how it is conceptualised and used in out of school contexts such as, for example, everyday situations, workplaces, research institutions, media and policy debates. How and to what extent these types of practices influence the different levels of the didactic transposition process (see Fig. 1) is not only a matter of content goals and pedagogical principles but also of ideology (Bernstein, 2000).

Fig. 1
figure 1

The didactic transposition process (Bosch & Gascón, 2006, p. 56)

Full size image

In relation to Fig. 1, mathematical modelling as a professional taskFootnote 2 in non-educational settings can be considered a part of the scholarly knowledge of mathematical modelling. This is where mathematical models are constructed in different types of professional institutions. The teaching activities in the classroom (constituting the taught knowledge), however, generally do not relate directly to this institutional level but to the “teaching text” (Bosch & Gascón, 2006, p. 56) comprised by national and local curriculum texts as well as textbooks and other teaching material—the knowledge to be taught. The transposition of scholarly knowledge into knowledge to be taught is, as indicated above, regulated by the different types of constraints and criteria for knowledge production that exist in the educational institution, as well as ideology regarding what knowledge is valued (Bernstein, 2000; Chevallard, 1991).

While educational research on mathematical modelling is extensive, not much attention has been paid to empirical investigations of its scholarly knowledge from the perspective of didactic transposition processes. The fact that mathematical modelling as an educational task has been realised in different ways in different national curricula (e.g., Ärlebäck, 2009; Blomhøj & Hoff Kjeldsen, 2006; Schmidt, 2012), may indicate a weak influence from its scholarly knowledge on these processes. When shaped mainly by educational stakeholders rather than authentic practices, modelling in school may become school modelling, losing parts of its raison d’être (cf. Chevallard, 2006). Dierdorp, Bakker, van Maanen, and Eijkelhof (2014) argue that students find education more meaningful and useful when it draws on “problems in authentic professional practices” (p. 3), also when those problems are “educationalized” (p. 4), that is didactically transposed. Empirically based descriptions of scholarly knowledge of mathematical modelling would provide a viable knowledge base for curriculum development, as well as more specifically for developing teaching and learning approaches for the enculturation of students into future professional activities as constructors and users of models (cf. Drakes, 2012; Gainsburg, 2003) and for teachers’ and students’ critical reflection on actual modelling work (cf. Jablonka, 2007).

To characterise how mathematical models are developed and used in different contexts requires an “epistemological analysis and empirical research of mathematical practices” (Jablonka, 2007, p. 197). In this paper we present research that we use as a basis for an epistemological analysis of the construction of mathematical models by professional model constructorsFootnote 3 in their workplaces. The focus of our investigation is on how mathematical models are developed as a professional task with the aim to characterise some aspects of scholarly knowledge of mathematical modelling. The analysis has been guided by the following research question:

  • How can mathematical modelling by professional mathematical model constructors be characterised?

Before describing our empirical investigation, which took place in Sweden, we will provide a background of research based theoretical and empirical descriptions of models and modelling of relevance for our study, including the notion of a mathematical model, the use of computers in modelling, and modelling in the workplace.

2 Mathematical models

In mathematics educational research literature, definitions of mathematical model often include two systems (sometimes called the mathematical world and the extra-mathematical world) and a mapping between them, so that the mathematical system can describe, explain, construct or predict behaviours in the other system (e.g., Lesh & Doerr, 2003, p. 10; Niss, Blum, & Galbraith, 2007, p. 4). The appropriateness of a definition depends on the purpose of its use. For the purpose of our study focussing on professional mathematical modelling (scholarly knowledge), we will refer to the following definition.

A mathematical model is a triplet (S, Q, M) where S is a system, Q is a question relating to S, and M is a set of mathematical statements M = {Σ1, Σ2, …, Σ n } which can be used to answer Q. (Velten 2009, p. 12)

The system (S) can be any field of inquiry (e.g., climate, tax system, educational measurement) and the question (Q) sets the goal or purpose for developing the mathematical statements (M). A rationale for providing the type of formal definition as the one given is that it “helps us to understand the nature of mathematical models” and “allows us to talk about mathematical models in a concise way” (Velten, 2009, p. 12).

In terms of the available knowledge of the structure of the system, a mathematical model is called phenomenological, when its construction is “based on experimental data only, using no a priori information about S” and mechanistic when “some of the statements in M are based on a priori information about S” (p. 35). The terms black box models and white box models are used for these extreme cases, respectively, while grey box models refer to the common case when the modeller has some a priori information about the system. Black box models are also referred to as empirical models or data-driven models.Footnote 4

Velten (2009, p. 40) made a classification of models across the black box / white box spectrum, as shown in Fig. 2. The diagram is based on relations between type of system (S), ordered according to levels of a priori knowledge about the system, type of purpose or goal with the modelling activity (Q), and type of corresponding mathematical statements (M).

Fig. 2
figure 2

A classification of models between black and white boxes (Velten, 2009, p. 40); the abbreviation AEs refers to algebraic equations, DEs to differential equations

Full size image

Figure 2 illustrates that scholarly knowledge of mathematical modelling may be distributed in terms of (S, Q, M) between different categories of model constructors. The diagram serves as an illustration of a set of fields of inquiries related to professional mathematical modelling and as a tool for analysing mathematical models in terms of black, grey and white boxes.

3 Mathematical modelling and computer support

The relation between mathematical modelling and technology is a topic of an ongoing discussion in the mathematics education research literature (Blum, Galbraith, Henn, & Niss, 2007; Greefrath, 2011; Jablonka & Gellert, 2007; Kaiser & Sriraman, 2006; Williams & Goos, 2013). A common description of the mathematical modelling process is the modelling cycle (Geiger & Frejd, 2015), organised in many different ways depending on research aim (Borromeo Ferri, 2006; Jablonka, 1996; Perrenet & Zwaneveld, 2012). These cycles are split into two domains—reality (the extra-mathematical world) and mathematics (the mathematical world)—including five up to seven sub processes of “moves” within and between the domains (Kaiser, Blomhøj, & Sriraman, 2006; see Fig. 3). This can be seen as an ideal description of modelling; while engaged in a modelling activity, that students “move” between reality and mathematics and back to reality in a cyclic process has not been verified in empirical observations (Ärlebäck, 2009; Borromeo Ferri, 2006; Oke & Bajpai, 1986). The role of technology in modelling is not often depicted in modelling cycles but an attempt has been made for example in Siller and Greefrath (2010), where an extra technology world is connected to the mathematical world. Seeing this approach as “restricted”, Greefrath (2011) outlines a more integrated approach to better capture the complexity of the role of computers in mathematical modelling. Figure 3 illustrates how the use of digital tools may support investigation, experimentation, visualization, simulation, algebraization, calculation, and control at different phases of the modelling cycle (Greefrath, 2011, p. 303).

Fig. 3
figure 3

A modelling cycle integrating the influence of digital tools (Greefrath, 2011, p. 303; based on Blum & Leiss, 2007)

Full size image

Williams and Goos (2013), taking an activity-theoretical perspective, point to this complexity of a modelling activity and argue for the necessity of a fusion of technology and mathematics: “mathematics is always mediated by the technology” (p. 554). According to their wide definition of technology it “includes the instruments, techniques and organisation that often embed mathematics ‘materially’ in tools and methods involved in practical activity” (p. 552). The perspective of Williams and Goos acknowledges mathematics, technology, and an activity-or-problem-context, as three connected dimensions of mathematical modelling. This approach to modelling also incorporates what Noss, Bakker, Hoyles and Kent (2007, p. 370) describe as techno-mathematical literacies. Seeing mathematical modelling, within this perspective, as the work or activity of constructing mathematical models, a model always has a goal or purpose. This view of mathematical modelling in our exploration of constructors’ modelling work offers us a broad perspective that considers the interdependence of modelling, mathematics and computer support embedded in a social context.

4 Mathematical modelling in the workplace

Mathematical models are frequently used/developed in the workplace for different purposes and in a variety of contexts (Hoyles, Wolf, Molyneux-Hodgson, & Kent, 2002; Hunt, 2007; SIAM, 2012; Van der Valk, Van Driel, & De Vos, 2007; Wake, 2007) and have been described as providing an interface between mathematics and a workplace (Sträßer, Damlamian, & Rodrigues, 2012). Workplace mathematics is generally more complex and situation dependent than school mathematics, including specific technologies and social, political and cultural dimensions that are not found in educational settings (e.g., Harris, 1991; Noss & Hoyles, 1996; Wedege, 2010).

Much research on workplace mathematics has focused on operators (e.g., Noss & Hoyles, 1996; Triantafillou & Potari, 2010; Wake, 2007; Williams & Wake, 2007b). Examples of research on constructors of mathematical models are found in Drakes (2012) and Gainsburg (2003). Gainsburg’s study included the construction of mathematical models in structural engineering, and identified three critical parts in the modelling process: the understanding of the underlying physical phenomena, mathematizing, and keeping track of what has been modelled and justify the complex models. The mathematizing was influenced by the access of technology and performed by the selection of a pre-defined model, the adaption of a model or the creation of a model, based on an understanding of the phenomenon. Another observation was that “communication is a critical part of structural engineering […] their work is highly collaborative and they frequently engage in verbal practices” (p. 259) with colleagues inside and outside the firm. That communication is crucial is similar to findings in the study by Drakes (2012) which investigated “how mathematical modelling is perceived by novice, intermediate and expert modellers” (p. iv). The work of the expert modellers with modelling problems included exploration, research and data gathering, identification of relevant information and underlying processes involved, simplification, and collaboration. Also after different types of validations of their models, they emphasised that no “correct” but only consistent or reasonable solutions exist. In both these studies, constructors of mathematical models emphasise aspects such as communication, collaboration (including division of labour), personal experience and technology to identify relevant information and verify solutions as important in their work.

5 The empirical study

5.1 Theoretical considerations

Even if we brought some theoretical as well as empirically based knowledge relevant for our research interest into our investigation, as outlined above, our relation to the empirical field was predominantly explorative in the sense that we had no specific expectations of how professional model constructors would characterise their work. Wedege (2010) suggests observations and interviews as a research method to capture the complexity of workplace mathematics. Drakes (2012) and Gainsburg (2003) are both examples of such studies, employing grounded theory related approaches for the analysis of their data. Grounded theory inspired approaches are frequently used for analysing qualitative data, in particular in exploratory studies, to develop insights that are representative of the data; it handles large data sets in a systematic, transparent and conceptually oriented approach (Bryman, 2004; Strauss & Corbin, 1998). For the interview study of a predominantly exploratory character that we chose to conduct, this kind of approach was deemed more appropriate than a top-down theoretical approach. It enabled us to explore and conceptualise the latent patterns and structures of the modelling activities of professional mathematical model constructors through a well defined process of constant comparison. These patterns and structures would then be compared to existing theoretical descriptions of mathematical modelling.

To be able to answer our research question, How can mathematical modelling by professional mathematical model constructors be characterised?, it needed to be operationalized into more specific questions. For this purpose, we found the critical questions developed by Jablonka (1996, 1997) for analysing mathematical models highly relevant to our research aim and useful for developing and structuring the guiding questions for the semi-structured interviews. According to Jablonka (1997), a key issue for someone working with mathematical modelling is to judge the quality of the model, which can be evaluated in terms of its usefulness and its effectiveness. Usefulness refers to the extent at which a model is suitable for a particular context, including taking into account “intended, actual and possible consequences of the implementation or usage”, and effectiveness to the extent at which a model can “fulfil the special purpose for which it was constructed” (p. 42).

Another aspect of the research question relates to the overall structure of the modelling activities. Our specific research questions were thus formulated:

  • How do professional mathematical model constructors describe their work in terms of goals, assumptions, communication/collaboration, computer support, established models, validation, and evaluation of risks involved in using the models?

  • How are their mathematical modelling activities structured?

5.2 Participants

The selection of the sample (see Table 1) was based on the rationale of having a variety of model constructors from different sectors—public service, private firms and universities—with different areas of expertise. While some of the participants were known to the authors, or recommended to be invited by colleagues or interview participants, three participants were found on a web search. Eventually nine persons were invited to participate and all accepted. They had a PhD in mathematics or other disciplines and were working professionally with mathematical modelling, most of them employed since more than 15 years in their present positions at universities or larger companies in Sweden. In Table 1 the participants are categorised by their main professional discipline.

Table 1 The sample of nine interviewees with their background information described with respect to sector, being employed in universities (U) or in companies (C), area of PhD degree, and expertise
Full size table

5.3 Data analysis

We set up the three hypothetical phases of pre-construction, construction and post-construction to structure our interview questions and the data analysis, as described in Table 2.

Table 2 Three phases of analysis of mathematical model constructions
Full size table

The interview questions, aiming at exploring these different phases of the constructors’ work and to provide background information, are listed in Appendix with information about which phases they focus on. The audio taped interviews, conducted in spring 2013, lasted between 40 and 90 min and were fully transcribed before the analysis.

The method of analysis originates from an iterative process to develop open codes, axial codes and selective coding, inspired by the coding procedure of grounded theory (e.g., Boeije, 2010; Bryman, 2004; Strauss & Corbin, 1998). Open codes refer to organising pieces of text into discrete categories, based on the content. The axial codes are compiled through linking the open codes. Selective coding includes the integration and refining of the axial codes into a general characterisation of the phenomena investigated.

To develop open codes the authors collaborated to enhance reliability and used memos, written records of analysis, thoughts and ideas (Bryman, 2004), to develop a common understanding. Fragments of the transcribed interviews were labelled with codes, names for categories, related to some phenomena. The categories are specific in terms of properties and dimensions. Properties relate to the characteristics or attributes of a category and dimensions to the location of a property along a continuum or range (Bryman, 2004).

We will illustrate the open coding and the use of memos with an example from an interview excerpt related to questions 6 and 8 (see Appendix):

Often these are people [clients] that have been thinking about the problem […] and feel a bit unsure and they want some help with the mathematical part, but I can feel, as a mathematical modeller, you have to clarify to yourself at least if, the whole problem, it is not enough with only this last part, I think. For me it is important that I feel that it is the correct form, that they have ended up with the correct problem. To identify the problem, the problem formulation, to identify the problem is a very long and slow, often long, long and slow process, and important so that you really look at the correct problem, that you have the correct quantities, the correct thing. This requires quite a lot of communication, precise communication back and forth. (Various)

Memo [categories of open codes marked with italics]: The first two lines indicate that: People (clients) initiate the modelling process by giving the problem to the modeller. The word “often”, seems to address that it is frequently occurring that the clients have thought about the problem for a while, but need some mathematical support, because they “feel a bit unsure and they want some help with the mathematical part”. The modeller actually wants to start the modelling process one step earlier than the client thought was necessary to make sure that this mathematical problem is the right one given the underlying actual phenomena. The modeller argues that “identify the problem is a very long and slow” process, but that the process is necessary to “clarify to yourself”. The last line in the excerpt indicates that communication between the modeller and the clients is frequently occurring and constitutes an essential part of the identification of the problem.

The re-formulated research question guided our axial analysis together with memos and the use of diagrams. The open coding categories were compared, contrasted and discussed in terms of properties and dimensions to fit in a bigger puzzle and relations between categories were visualized in diagrams. For example, as in the excerpt above and in other fragments of texts, all modellers described that the construction of models requires communication between clients and constructors, which was visualized in diagrams by arrows between clients and constructors. However, the dimension relating to this axial category in terms of the frequency of communication varied between the model constructors. Other properties relating to the initial conversations between clients and some constructors include issues such as to clarify, identify and re-formulate a problem to be solved.

The selective coding process included connecting and generalizing the relations between the axial coding categories that were visualized in diagrams to give insights about the flow of the model constructors’ work to develop general characterisations of constructors’ modelling activity.

5.4 Credibility of the research

The selection of our interview participants aimed at providing a variety of contexts that reflect scholarly knowledge of mathematical modelling. Some other areas for mathematical modelling in workplaces (see e.g., Hoyles et al., 2002; SIAM, 2012), could have resulted in differently structured modelling activity schemes. It may also happen that similar modelling problems are handled in different ways by different work teams. An indicator of external validity is, however, that some of the findings in this study reflect outcomes from previous research (e.g., Drakes, 2012; Gainsburg, 2003) and theoretical descriptions of mathematical modelling (e.g., Velten, 2009).

As part of the ethical considerations regarding the participants, and to improve validity, respondent validation was used (Bryman, 2004); the participating modellers were invited to comment on a draft version of this paper. The four participants responding commented on specific formulations, for example that “count on future cash flows” should be “simulate future cash flows”, but no overall critic on the result was raised. Nor did they give suggestions about specialised literature where similar results already have been discussed.

According to Bryman (2004) there is a consensus among researchers that many factors impact the result based on qualitative research methods inspired by grounded theory, such as the reliability of the coding and the researchers’ own scientific and general knowledge. The reliability of the coding in this study has built on discussions and final agreement between the two authors. As an example of the influence of the researchers’ knowledge, communication was included in interview question 8 as we expected it to be an important part of the modelling activity; that it was identified as an open code was, however, also due to the fact that the participants actually found it important.

One limitation of the study is that the research literature reviewed relates mainly to mathematics education, with only a few titles relating to modelling in science education or specialised literature on mathematical modelling. An ethnographic study observing professional modellers in authentic work situations might have provided more differentiated descriptions of their work but as our interest was on scholarly knowledge we found interviews more appropriate. The broad variety of areas and expertise represented in our sample was selected to cover a fairly wide range of scholarly knowledge of mathematical modelling, though we cannot generalize all our findings to other professional model constructors or systems to model.

6 Results

The selective coding process generated a general characterisation of the modelling work of professional mathematical model constructors in three differently structured modelling activities. In data-generated modelling the models are developed principally from quantitative data drawing on no or only some assumed knowledge of the system being modelled, while in theory-generated modelling the models are developed based on established theory.Footnote 5 In the third activity, model-generated modelling, the development of new models is based on already established models. In the following subsections the three types of modelling activities will be described in more depth, supported by interview quotes and visualized in diagrams as modelling activity schemes. In the Section 7.2, these activities will be compared and contrasted to theoretical and empirical descriptions of mathematical modelling from the literature.

6.1 Data-generated modelling

The data analysis led us to the identification of one type of modelling activity in which seven of the professional modellers were engaged: the work of gathering, interpreting, synthesizing, and transforming data as the main underlying base for identifying variables, relationships and constraints about a phenomenon used in the model development process. We call this activity data-generated modelling. As it also may include drawing on data relating to some particular structures explicitly known in the system that is modelled, it can result in both, black-box and grey-box models (cf. Fig. 2).

6.1.1 Pre-construction phase

The constructors get orders/problems from clients. Clients can be consumers from other companies and government agencies, or employers and supervisors within the firm. The goals, as illustrated in Table 3, are to describe and simulate a phenomenon in order to be able to predict (to make prognoses about the future), design (improving objects), or construct (objects). As an example, a supervisor asks a model constructor to assess the bank’s risks of “a portfolio of life insurance contracts, where… the customer is guaranteed to get some refund” (Banking). The goal is therefore to predict the banks’ risks and potential returns of the money they invest, but implicitly the aim is also to describe the current situation and to simulate the future. The models are developed to serve as basis for decision making concerning who and to what interest rates the bank should offer loans to customers while making a profit for the bank. In data-generated modelling, the models will be used for several purposes, such as measurement instruments, algorithms for investments, and traffic routes. In all cases the constructors of the models set up the specific goals and define the criteria for the mathematical activity, even though there is a dialogue with those who “own” the problem. The results related to the pre-construction phase are summarised in Table 3, where the goal together with the problem correspond to the question (Q) in Fig. 2.

Table 3 Results of the pre-construction phase of data-generated modelling
Full size table

6.1.2 Construction phase

The structure of the data-generated modelling activity visualized in Fig. 4, is generated from the analysis of the interview protocols. The modelling activity scheme depicts three actors (Client, Constructor and Expert) involved in the construction activity. The term “Client” was described in the previous paragraph; “Constructor” refers to the (interviewed) model constructor; and “Expert” is a person with specialised knowledge relevant for the modelling problem. Regular arrows visualize the flow of the activity, whereas the dotted arrows are used to illustrate that communication takes place between the different actors. Rectangles and ellipses illustrate vital aspects, emphasised by the participants, for the activity.

Fig. 4
figure 4

Modelling activity scheme of data-generated modelling

Full size image

The constructors receive the problem from clients, depicted in Fig. 4 as the introduction of the problem (Problem). The communication between the constructor and clients is emphasised in the interviews as a central part in the process of clarifying, adapting and reformulating the problem (Re-formulate), as exemplified in the excerpt illustrating the open coding process in the Section 5.3.

The clients need a model that is useful for a particular purpose and some of the communication partly serves to establish how accurate the model needs to be. The communication between the constructor and other experts, however, is more often addressing the extent to which a model can fulfil its purpose, the effectiveness of the model, by discussing what the problem really is about. Larger projects often include interdisciplinary competencies (Biology, Traffic, Aircraft industry) and are too large and time consuming to be handled by one person (Bank), thus requiring communication between experts. Communication and collaboration are also emphasised as constructive tools:

You need to communicate about these things to get them up to the surface, to speed up the thoughts and to avoid mistakes. (Scheduling)

The data may originate from different sources—from the clients, experiments, observations, surveys or statistics from data archives within the company, or from external resources like government agencies. According to all interviewees categorised as working with data-generated modelling, data is treated as a fundamental aspect of the construction phase and has therefore been located in the centre of Fig. 4.

When we work with a set of data it must be good enough so that we will be able to, so to speak, that we will be able to make some claim. (Biology)

Issues about data always come up. Absolutely, it is very important. (Banking)

It is very important and you may work until death trying to control the quality of that [the data] […] we had loads of data […] but when we started to look at it lots of errors were found […] there we put down much work to get something out that could be used. (Traffic)

The excerpts indicate that control of data quality is something taken very seriously by the constructors. Data and its quality influence how the model is going to be constructed; the data frame the specific problem formulation (Re-formulate), and are, together with computer support, used to identify processes, variables, conditions, and constrains of the phenomena. Conditions, constraints, process and facts may also be found in communication with clients and experts or analytically found. The quality of data is validated using computer support (statistical and visualization programs) and/ or by expertise and working experience:

[…] you often have a filter that compares this data point [closing price] with the previous, and if the jump is too big it sends an automatic email or something to some person who then goes in to check if this is really correct or is it an error that has occurred […] when you go through data and see if it looks reasonable, if you see then some odd trends or something else, you go back and ask people who were there when the data was collected, how did this product look then (Banking)

There are no general principles [for data control], nothing … you can only make lots of controls of the reasonableness. (Scheduling)

When the processes, variables, parameters, conditions, and constraints are identified the model is formulated in mathematical terms and computer codes. The model is calibrated with data within this computer environment. Thus, computer support plays a major role in the construction (see Fig. 4), which is also the case for the evaluation/ simulation process when in- and outputs are tested, validated and compared with given data, outcomes of experiments or expert opinions.

The following excerpt about pensions (Insurance) illustrates the issue of determining an acceptable solution, also depicted in Fig. 4, based on data and one role of simulation.

So often you simulate different pension scenarios at the same time as you simulate different outcomes from the asset portfolio, and from there you calculate, by optimization, a strategic allocation. […] it is often the board that take the final decision on this allocation. But there is always a mathematical model in the background. (Insurance)

The board, expert opinions, and clients’ interests must be taken into consideration by the constructors, in dialogues about evaluating and assessing the usefulness and effectiveness of the models as well as in the process of determining an acceptable solution. All constructors emphasised that a modelling process does not end up with only one solution. An acceptable or reasonable solution is grounded on discussions with expert opinions and use of statistics (Insurance), the relation to instructions from the finance inspection (Banking), the most frequent (Biology), the closest measure to an optimum (Scheduling), or good fit with experiments (Aircraft industry). Validation methods used include statistical methods such as ANOVA (Biology), back testing on old data (Banking), and plotting (Scheduling).

6.1.3 Post-construction phase

The constructors all agreed that there are risks attached to the use of their models, for example that people will lose money.

Of course there are risks of using models and sometimes one talks about model risks and that is exactly that you have missed something, that you use the model in a context where it should not be used. Or you use it even if the conditions are not fulfilled, or that the assumptions maybe worked when you made the model […] you had incorporated assumptions that you were not even aware of because it was taken for granted somehow […] the customer has paid money today to get it back as a pension after twenty years and when you get there no money is left. (Banking)

According to this modeller, there is a range of potential risks involved when using models, not only due to a “blind” trust in the model. Such view was confirmed also in the technical sector. There may also be ethical problems due to the new information that the use of the models may present.

If I look at it from the perspective of the animals and an optimiser, then this farm […] should not be allowed to have cows he should have pigs […] this slaughter house you should not place here as it would create very long animal transports. (Biology)

Suddenly you take away the power from people that used to have power, to be able to construct schedules for themselves, and this power is now given to outsiders. (Scheduling)

Other ethical considerations were also expressed, for example that you cannot build ethnicity into mathematical models for loans. These ethical considerations also illustrate that influences from society beyond clients or experts may or may not affect that actual modelling work. The Biology modeller, in the citation above, seems not to let possible effects on farmers influence the model. However, the Bank modeller seems to have let regulations about not using ethnicity information affect the model (an example of constraints in Fig. 4).

6.2 Theory-generated modelling

A second type of activity, represented by two of the interviewed modellers, is the work of setting up new equations based on already theorised and established physical equations. This is followed by the activation of computer resources for computational purposes to solve the new equations with aim to get information about the ‘theorised’ equations (i.e., to develop a theory). We call the activity theory-generated modelling, in which white-box models are constructed.

6.2.1 Pre-construction phase

The initial “trigger” and the goals in theory-generated modelling are similar to data-generated modelling. The problems come from clients inside or outside the firm or from own research, and the goals are to describe, simulate, predict, design, and construct an object. Examples are to predict the climate change, including describing the current situation and simulating the future. The theory-generated activity is also similar to the data-generated activity in that the constructor sets up the goal and the criteria for the mathematical activity. In Table 4 the findings from the pre-construction phase of the activity are summarized.

Table 4 Results of the pre-construction phase of theory-generated modelling
Full size table

6.2.2 Construction phase

The structure of the theory-generated activity is different from the data-generated activity as visualized in Fig. 5. When the problem is introduced (illustrated with a one way arrow from the client in Fig. 5), there is less dialogue between the client and the constructor in the theory-generated activity than in the data-generated activity, because the physical equations (the theorised equations) that control and influence the problem situation are known from the start.

Fig. 5
figure 5

Modelling activity scheme of theory-generated modelling

Full size image

Briefly, the problems consist of sets of differential equations (theorised equations), developed by some physicist, that need to be solved:

More or less I know the equations that influence these materials I’m looking at. The problem then is that they cannot be fully solved exactly, so you have to do some type of mathematical modelling […] In my case there is a mathematical modelling activity also in the very calculations. To get these material values and material properties, we have to model our equations further and include approximations. (Physics)

My competence consists of translating mathematics to a computer model that will emulate the ‘real’ mathematical model […] the mathematical model is already well-known, but how to solve it on a computer and how to move from the continuous to the discrete finite quantity, it is a challenge for me. (Climate)

Both constructors re-formulate the problems (setting up mathematical models of equations with approximations). Communication between constructor and other experts sometimes takes place, in particular for the constructor working with climate models, as the division of labour at his company is based on different competencies. There they work collaboratively, often in pairs, to develop the optimal way to solve a problem. After the re-formulation of the given task, the model constructors translate the mathematical model to a computer model, solve the computer model and interpret and evaluate the result, and finally evaluate the validity of the computer model.

To do climate simulations one needs to select data and make qualitative mathematical reasoning about input values, such as present climate, geographic location, vegetation characteristics, and earth revolution speed. In order to minimize problematic data the modellers use many different series of large amounts of measurements provided by satellites. It is possible to verify and control the computer model, because some expected values are known, but it is difficult in practice with computer codes to actually get these values, according to the climate modeller. This part he described as a key aspect of his vocation and a bit frustrating, because the computer programs he constructs do not always behave as expected. The results that the climate team produce are predictions, and therefore the validity of the results, the acceptable solution, is based on historical data and climate trends.

Also in the construction and design of models for new material the computer is used as the main tool:

The computer is our big tool, not the least when it comes to solving these quantum mechanics equations, regardless the levels of approximations, it is terribly difficult […] that is also an area where the use of extremely powerful computers provides a much better prediction power. (Physics)

Examples of data for in-puts to the computerised model for designing materials include the geometry of crystal structure, natural constants like the speed of light, the electron charge, which are used in equations that need to be solved (e.g., the Schrödinger equations). The out-puts may be in terms of energies. The result may be compared with experiments, which is one way to deal with validity.

Similar to the case of the data-generated modelling, the clients’ main interest in an acceptable solution is its usefulness, whereas the communication with other experts is more focused on the effectiveness of the models.

6.2.3 Post-construction phase

The physics and the climate constructors described, in coherence with the other model constructors, that there are risks involved in using their models:

If you start using our results right off in a critical application then you may be in trouble. The fact that we use approximations and have uncontrollable sources of error, even if we gradually decrease them, they do exist. […] (Physics)

And if you take this as an absolute truth and use it, well for something, I would certainly not bet my life on it that it is correct. One must understand a little that it comes from a model. (Climate)

In both excerpts the risk of using model out-puts without awareness of errors potentially inherent in the models is described.

6.3 Model-generated modelling

A third type of activity that we could categorize based on the analysis of our data is a part of all constructors’ work. In model-generated modelling models are constructed by identifying situations on which some mathematics or some established mathematical models can be directly applied. The activity concerns the interplay of mathematical / theoretical considerations (e.g., on the type of model or form of a formula or equation), some empirical aspects in which the mathematical model is confronted with data, and some application elements in which the model’s behaviour and the real phenomena are confronted. Both grey box and white box models result from this activity. The pre- and post-phases of this activity will only be briefly discussed, as they are similar to the previous two types of activities.

6.3.1 Pre-construction phase

The underlying aim/purpose, problems, use of models, defining the goal and defining the criteria are similar to the data-generated and theory-generated activity as displayed in Tables 3 and 4. However, the activity of applying already defined models is a consequence of the modellers’ working experiences or collaboration with others and serves another ‘implicit’ purpose, which is to save working time (i.e., to solve tasks by using standardized routines). The application of pre-defined models may also be used to solve specific parts of the problem/project.

6.3.2 Construction phase

One of the model constructors, Biology, explicitly emphasises the application of mathematics as a way to work whereas the other modellers stress the use of already defined models. The structure of model-generated modelling is visualized in Fig. 6.

Fig. 6
figure 6

Modelling activity scheme of model-generated modelling

Full size image

The following excerpt, about spread of diseases between oak trees, illustrates modelling work as an application of mathematics. After mentioning the application of differential equations in different contexts, the modeller goes on:

There are often disturbances such as climate, weather and wind and so on. […] How can you describe such disturbance, well Fourier transformations are really good and you can then rewrite anything as a sum of sine functions. […] This has been used by people at the department of systems control […] Basically it is knowledge about mathematical methods that do the work, and sometimes you start with the problem and then you add a method […] It is basically the same thing if bugs fly between oak trees or if animals are transported in trucks. (Biology)

Differential equations here define the starting point of the activity. One way to deal with differential equations, according to the Biology modeller, is the use of Fourier transformations, which in Fig. 6 is depicted as identifying which models and how existing models can be adapted. Communication takes place with other experts (i.e., control engineers) with more experience in the area. The Biology modeller applies Fourier transformations on the problem about disturbances, which includes a set of data. With use of computer support he sets up a model and calibrates the model structure to conform to the data variability. The model is evaluated and validated with help of statistical methods and the set of outcomes is discussed with clients and other experts for identifying an acceptable solution.

Another common activity in the modelling work within this category is the application of already defined models to solve problems.

This part of developing models can be a large or a small part of our projects. We can use an already defined traffic simulation model. (Traffic)

There are many tools constructed, so we do not build everything ourselves, instead you often start with something already existing and if you have a special product you may write some scripts that you put into the program. (Banking)

To apply already developed models is a part of all the constructors’ work, either due to limitation of time or because there exist models that take care of types of standardized problems. All constructors also emphasise that they use computers and software that include some types of established models. The use of the already defined models stems from the working experience or is an outcome of communication with other experts. The excerpts also show that standardized models might need to be adapted due to evaluation and validation of the outcome of the application. Discussions with clients and other experts about the usefulness and the effectiveness of the applied model may take place as a consequence of the validation process. The issue of what constitutes an acceptable solution is based on the same statements as found in data-generated or theory-generated modelling.

6.3.3 Post-construction phase

Solving the problems based on model-generated modelling involves similar risks as data-generated and theory-generated modelling, since the underlying goals and problems are similar.

7 Summary and discussion

7.1 Summary of results

To answer to our research question, How can mathematical modelling by professional mathematical model constructors be characterised?, we conducted an analysis based on interviews with nine professional model constructors that led us to the characterisation of three main types of modelling activities in which the different modellers were engaged, as summarized in Table 5.

Table 5 Three types of mathematical modelling
Full size table

Model construction is usually teamwork, in particular for larger projects, and the use of computer support is central. Our results therefore concur with Williams and Goos (2013) regarding the interdependence of mathematical modelling and technology embedded in a social context. The goals describe, simulate, predict, design, and construct are part of the three activities. Communication between different actors (clients and other experts) is by all constructors pointed at as a vital part of the work. The communication with clients mainly involved discussions about the usefulness of the models, while communication with other experts often addressed the models’ effectiveness. Expert opinions are also in some cases (Insurance, Banking, Scheduling) used for the validation of the models. Other examples of validation methods include statistics and back testing on old data (Insurance, Banking, Biology, Climate), and good fit with experiments (Aircraft industry, Physics). All model constructors stated that there are always risks involved in the use of their models and that clients and others should be aware that it is “just” models and critically reflect upon that fact.

7.2 Discussion

Our study took its starting point in existing theoretical and empirical descriptions of mathematical modelling (e.g., Drakes, 2012; Gainsburg, 2003; Jablonka, 1996; Velten, 2009). However, as not much research attention has been paid to the construction phase of mathematical models (Morrison & Morgan, 1999), our interview study had a predominantly explorative character. Nevertheless, the literature includes several terms related to those representing the modelling activities summarized in Table 5, allowing an interpretation of both confirmation and differentiation. The term data-driven modelling (or empirical modelling; see Velten, 2009, p. 35) refers to the activity of developing models that do not build on specific assumptions or a priori knowledge about the studied system but only on data from empirical observations (Bissell & Dillon, 2000, p. 5; Solomatine & Ostfeld, 2008, pp. 17–18). Our category data-generated modelling is broader in the sense that it also includes modelling data from a system of which there exists some a priori knowledge of its structure. Such knowledge is not always made explicit, as pointed out by Morrison and Morgan (1999): “models which look at first sight to be constructed purely from data often involve several other elements” (p. 15). Theory-generated modelling has similarities to computational modelling, which has been defined as “the use of mathematics, physics and computer science to study the behavior of complex systems by computer simulation” (NIBIB, 2013, p. 1). A system studied by computational models “is often a complex nonlinear system for which simple, intuitive analytical solutions are not readily available” (Wikipedia, n.d.). Some examples are weather forecasts, earthquake simulations, and molecular protein folding. The two constructors in our dataset also explicitly described an overall aim to contribute to the development of theory about the equations they solved. In a similar vein, Van der Velde (2007) writes that “computational models are […] epistemological tools. They help to fix the conceptual and terminological foundations of a discipline” (p. 207). Our third type of mathematical modelling, model-generated modelling, often serves as a sub-activity within a larger modelling activity (cf. Gainsburg, 2003).

Comparing the outcomes from our study with the systems (fields of inquiry) in Fig. 2 (Velten, 2009), data-generated modelling produced black box and grey box models within social, economic, biological, and physical systems in alignment with Velten’s classification. The white box models constructed through theory-generated modelling related to climate and physics may be placed close to mechanical systems. However, the grey and white box models derived in model-generated modelling are not easy to directly relate to the systems in Fig. 2 as they often are integrated with the other modelling activities. The five goals listed in the summary above, driving the different modelling activities described in our study, are similar to four of the five questions (Q) in Fig. 2. Our categories construct and design, though, are used across systems. The category speculation in Fig. 2 was not found; psychological systems were not represented in our sample.

Some of these outcomes reflect findings reported in Drakes (2012) and Gainsburg (2003), as for example the key roles of communication, collaboration, and division of labour for modelling work. In contrast to our epistemological approach, however, these studies employ a cognitive approach with a focus on challenges, skills and understandings. The modelling activity schemes outlined in Figs. 4, 5 and 6 attempt to specify the relations between different aspects of the modelling activity described by the modellers, and differentiate the communication and collaboration between the actors involved in the process. Compared to the previous studies, another difference is that our sample was selected to focus mainly on contexts where the scholarly knowledge of mathematical modelling could be studied. The activity schemes also illustrate, as a background component, the key and complex role of computer support in all three types of modelling activity (cf. Greefrath, 2011, and Fig. 3; Williams & Goos, 2013).

Based on our selection principles for the sample and the rich data provided by the extensive interviews, along with alignment to results from previous research studies and theoretical descriptions of models in professional literature, it may be argued that the descriptions of three types of mathematical modelling summarized in Table 5 and their diagrammatic representations in Figs. 4, 5, and 6 represent central parts of the scholarly knowledge of mathematical modelling. While the terms data-driven (or empirical) and computational modelling more refer to the type of mathematical model being developed, our study provides a typology and characterization of mathematical modelling activities among professional model constructors as well as a characterization of their work in terms of the structure of the construction process of the model, as visualized in the modelling activity schemes and detailed in the examples. Further research is needed, however, to refine and establish these types of modelling as a part of the scholarly knowledge of mathematical modelling, as well as to describe other types that should form part of this knowledge.

7.3 Educational relevance

In didactic transposition theory (Bosch & Gascón, 2006; Chevallard, 1991) it is assumed that knowledge diffused in schoolFootnote 6 has a pre-existence outside school, ultimately as scholarly knowledge within the field of knowledge production. To be available for learners in school, scholarly knowledge needs to be adapted or transposed to school institutions by different actors including policy makers, educators and educational researchers, curriculum developers, textbook authors and teachers. In this process the source is, however, not only scholarly knowledge but also knowledge involved in a diversity of practices outside school, and certainly also previously transposed knowledge from school mathematics as writing a new curriculum partly involves re-writing the old curriculum. The outcome of the present study, a characterisation of scholarly knowledge of mathematical modelling, is one possible starting point for the didactic transposition of mathematical modelling into school mathematics as it is scholarly knowledge that provides the principles of the field.

The literature, as well as our study, indicate major differences between modelling work in educational and non-educational contexts. Much of the professional modellers’ work is based on knowledge and experiences reaching far beyond what can be found in a secondary mathematics classroom (cf. Jablonka, 2007; Williams & Goos, 2013). There are also major differences between the professional and the educational contexts in terms of objectives and consequences of the modelling activity (cf. Dierdorp et al., 2014, p. 4; Wake, 2014, p. 272). For example, in the classroom mathematical models constructed by students are seldom put to use in a context of practice, or in other ways involve risks. Another difference relates to the division of labour that is common in professional practices with specialised competencies. These major differences between modelling work in educational and non-educational contexts seem to entail that mathematical modelling in school becomes an unrealistic utopia in terms of coherence to non-educational professional practice. That this comment could be made also about mathematics in general, points to the necessity of having access to a viable account of the scholarly knowledge for the purpose of not losing out its key elements during a didactic transposition process influenced by different stakeholders.

There are also different views among teachers and researchers in mathematics education on what constitutes mathematical modelling (Frejd, 2011; Sriraman & Kaiser, 2006). This suggests that a standardized knowledge of mathematical modelling has not yet been established in the educational community. Here, our characterization of the constructors’ modelling work may contribute to the didactic transposition process by being a source of information about central components and processes used by the professional model constructors. Taking Sweden as an example, model-generated modelling seems to be an activity which resembles activities (be it in a very simplified form) described and used at the didactic transposition levels of knowledge to be taught and taught knowledge at upper secondary school; the “modelling ability” to be taught includes the goal to use models, and textbook descriptions of modelling as well as assessment of modelling in national course tests emphasise the use of, and sometimes adaptions of already defined models (Frejd, 2011, 2013). In educational research literature on mathematical modelling, examples and projects that include simple versions of (parts of) data-generated modelling are common (see e.g., Blum et al., 2007). Theory-generated modelling presents more of a challenge or “inaccessible phenomena” (Gainsburg, 2003, p. 263) to work with in school mathematics.

While scholarly knowledge of modelling construction may be one source for the didactic transposition of mathematical modelling, as indicated above there are also actors influencing this process driven more by ideological and economic/political agendas than characteristics of scholarly knowledge or other authentic modelling practices. These actors may be policy makers referring to PISA league tables as an argument for curricular reform without providing analyses of how mathematical modelling is conceptualised and operationalized in the PISA framework. Therefore, to continue a path where mathematics education is built on the principle that knowledge taught in classrooms is to be useful for everyday life, society and workplaces (cf. Wake, 2012), requires more empirical research to seek evidence of how and what mathematical knowledge and abilities, including mathematical modelling, are used and valued as important in these contexts.