1 Introduction

Before presenting this study, we first report the reflection from two experienced mathematics teachers on professional development programs in Taiwan about the power of an experienced mathematics teacher educator-researcher (MTE-R), to whom we refer hereinafter with the pseudonym X, the major focus of this study.

Flora: In the first 5 years, my teaching mainly focused on being acquainted with the materials such as textbooks….After becoming familiar with the materials, I thought teaching should be easy for me. However, it seems to become a blind alley for me now…Every time when I saw students’ frustrated faces, I felt no sense of achievement.…This was why I joined the programs…I felt amazed when X gave us suggestions and comments on those tasks we designed during the programs…He can always find the educational values in our designs and lead us to experience those values….His power is far beyond my expectations. [Interview data].

AdamFootnote 1: …Before attending the workshops, I did not pay attention to check if students know what they are doing and which role mathematics can play in their learning….Now, my experience in the professional development programs made me realize that the core of mathematics learning lies in how much students participate in the learning rather than how well teachers teach students. That is, students can communicate their ideas with teachers and learn mathematics…Now I realize the goal should be set on students’ abilities to think about mathematics actively and to learn mathematics from different perspectives. [Interview data].

The reflection above shows the reason for selecting X as the major focus of the investigation in this study in which we aimed to explore how the experienced MTE-R demonstrated his influential power to facilitate teacher professional development (TPD) programs. The research specifically focused on unveiling the ways that X put his research and practice knowledge to the fore and acted upon it (Mason & Spence, 1999). For teacher educators, as explained by Watson and Mason (2007), initiating at-the-moment actions is much more complex than the clear distinction between subject content knowledge and pedagogical content knowledge, and “understanding how being knowledgeable about mathematics teaching influences classroom actions and knowing to act in the moment through having pertinent possibilities come to mind” (p. 209). Initiating at-the-moment actions to facilitate TPD necessitates the consideration of pertinent possibilities from different perspectives as well as dialectics between practice and theory (García, Sánchez, Escudero, & Llinares, 2006).

The educative power of initiating at-the-moment actions has not been clearly investigated yet. Previous researchers have examined the learning of teacher educators by a self-study approach (e.g., Loughran & Russell, 2009), showing that the learning of teacher educators involves a continuing search for appropriate and effective actions (e.g., Kremer-Hayon & Zuzovsky, 1995). Some researchers have also investigated types of knowledge that teacher educators require (e.g., Chauvot, 2009; Peled & Hershkovitz, 2004) and the strategies that can be used to facilitate the growth of beginning teacher educators (e.g., Harrison & McKeown, 2008; Jaworski & Wood, 2008; Murray & Male, 2005; Zaslavsky & Leikin, 2004). An alternative is to examine how the nature of educators’ work shapes their understanding of teaching, their expectations of teacher education, and their identities as mathematics teacher educators (Loughran, 2011). MTE-Rs need not only profound knowledge to educate mathematics teachers and the ability to conduct research but also the competence to initiate at-the-moment actions for exploiting knowledge in practice. Thus, the main research goal of this study is to explore the features specific to X’s educative power that have contributed to gaining deep insights into what educative power is, the strategies that can better facilitate TPD, and suggestions for the development of educative power.

2 Conceptual framework

Jaworski (2001) coined the term educative power to capture the engendering role of teacher educators originating from both mathematical power and pedagogical power. Mathematical power refers to the ability to discern mathematical relationships, logical reasoning, and effective use of mathematical techniques (Schoenfeld, 1992). Pedagogical power is constructed based on mathematical power, referring to the ability to draw on whatever knowledge is needed to solve pedagogical problems (Cooney, 1994). With respect to educative power, it pertains to the ability to draw on knowledge that is required to improve the mathematical and pedagogical power of teachers (Zaslavsky, Chapman, & Leikin, 2003). Thus, students have to develop mathematical power to solve mathematical problems, whereas mathematics teachers need pedagogical power to solve both mathematical and pedagogical problems. Analogically, mathematics teacher educators need educative power to solve mathematical, pedagogical, and educative problems (Tsamir, Tirosh, Dreyfus, Barkai, & Tabach, 2009). In other words, mathematical power is the core in mathematics education for students, mathematics teachers, and mathematics teacher educators.

The relationship among the three types of power makes it reasonable to build up a framework for educative power using the existing conceptual constructs of mathematical power. The constructs in this study were adopted from the framework developed by National Assessment of Educational Progress (NAEP) (Orrill & French, 2002). NAEP created the framework to assess students’ mathematics performances considering three perspectives: mathematics content strands (e.g., geometry and spatial sense), mathematical abilities (e.g., problem solving), and mathematical power. Specifically, the mathematical power elaborated by NAEP refers to communication, reasoning, and connection, which are characterized as students’ overall competencies in communicating ideas about and through mathematics, in logical reasoning, as well as making connections between ideas within and outside of mathematical world.

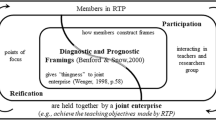
As mathematical power is the core for mathematics teacher educators to solve educative problems, we suppose that educative power of initiating at-the-moment actions for the facilitation of teacher professional development (TPD) also involves the components of mathematical power—communication, reasoning, and connection—which become the reasonable constructs for conceptualizing the framework in this study. It is noted that the features of the three components are still under investigation. Additionally, similar to the framework for assessing student mathematics proficiency which involves three dimensions, we also consider another two dimensions in order to capture the nuances of educators’ ability to initiate at-the-moment actions. The first dimension has to do with the dual role—as both a facilitator and a learner—that teacher educators have to play. The role-playing in the reciprocal facilitator-learner relationship requires complexity in knowledge involving students, teachers, and educators. The second dimension considers a bridge between research and practice in relation to the facilitation of TPD. Of importance is the development of educative power through the transformation from research to practice and vice versa. The conceptual framework of educative power in this study is shown in Fig. 1.

Fig. 1
figure 1

The conceptual framework of educative power

Full size image

For the reciprocal facilitator-learner relationship, researchers have pointed out that the expertise of mathematics teacher educators is nested in different roles they play: learning mathematics as a student, learning to teach mathematics as a teacher, learning to teach mathematics teachers as a teacher educator, and learning to teach mathematics teacher educators as a mentor (Lin, 2010; Tzur, 2001; Zaslavsky & Leikin, 2004). In addition to mathematics teacher educators’ knowledge for facilitating TPD, Mason (2008) pointed out that mathematics should be viewed as the core to challenge students, teachers, and teacher educators. In this regard, the expertise of MTE-Rs relies on how to consider the knowledge specific to the three tiers of participants and how to properly facilitate TPD through communication, reasoning, and connection.

Regarding the bridge between research and practice for facilitating TPD, this has been one of the challenges for teacher education. For example, while theories offer lenses that could be used to analyze teaching and learning (e.g., Cooney, 1995; Lerman, 2001), they do not offer clear recipes or guidance for teaching practice. Thus, mathematics teachers might not be able to make sense of theories unless those theories are contextualized in realistic narratives or cases. Moreover, pedagogical problems often involve a wide range of complexity which increases the demands of explicit suggestions on teacher educators while they might not have any at hand. Currently, researchers tended to bridge the gap between theory and practice by proposing a variety of sources and strategies. One approach is the use of cultural tools (e.g., tasks, cases, narratives) as mediators for teachers to make sense of theories (Jaworski, 2006; Markovits & Smith, 2008; Stein, Smith, Henningsen, & Silver, 2000; Watson & Sullivan, 2008; Yoshida, 2008). An alternative is to use an intermediate framework and design tools for connecting and contextualizing theories within the design of teaching sequences (Hjalmarson & Diefes-Dux, 2008; Ruthven, Laborde, Leach, & Tiberghien, 2009). The educative power of MTE-Rs is developed through engaging in both teaching and research (Adler, 1993; Jaworski, 2001; Peled & Hershkovitz, 2004). Adler (1993) argued that teacher educators are practicing researchers using reflective inquiry into practice as a form of research to overcome “obstacles to academic respectability” (p. 165) that teacher educators face. Peled and Hershkovitz (2004) further used the term “researchive power” (p. 321) to describe how MTE-Rs broaden their theoretical knowledge through designing tasks to facilitate TPD. However, more fundamental issues still lie in teacher educators’ power to initiate at-the-moment actions that can bridge research and practice for helping teachers to solve a wide range of their complex teaching problems.

In sum, educative power of MTE-Rs is conceptualized as a fundamental basis which supports MTE-Rs to initiate at-the-moment actions through communication, reasoning, and connection with the consideration of both research and practice, as well as different facilitator-learner relationships with respect to educators, teachers, and students.

3 Method

3.1 Study design

Both self-study approach (Loughran, 2004) and case-study method (Merriam, 1998; Yin, 1994) were applied in this study to investigate the educative power of X, an experienced MTE-R. A self-study approach was adopted as it satisfies an individual’s desire to better understand the nature of teaching and teaching about teaching. Self-study approach is useful for the exploration of features specific to X’s power; however, this approach might lack objectivity as the self-study participant is confined to providing rigorous and valid responses to all the inquiries in the complex world (Loughran, 2007).

For this reason, we also employed a case-study method by which X’s educative power can be tracked, triangulated, and validated to keep the study informative and objective. To do so, a team including X and four researchers, R1 to R4, participated in this study. All of them were MTE-Rs and had their specific interest in research and practice. X had been the supervisor of R1 and R4. R3 was studying his PhD supervised by X. R2 was a postdoctoral student working for an integrated project directed by X. For R1 to R4, X was a case in this study to investigate the educative power with respect to the three proposed constructs. Case-study methodology allows researchers to understand complex instances through description and contextual analysis in which multiple sources of evidence are used (Yin, 1994). In the research team, R2 and R3 were responsible for observing and interviewing the teachers who participated in the teacher professional development (TPD) programs. R1 and R4, who did not attend the observation or conduct the interview, were responsible for asking critical questions and discussing with R2 and R3 the critical instances that can reveal the educative power of X. X discussed with the four researchers his reflection on his educative power in facilitating TPD and his reading of teachers’ interview data. The integration of work in this case study conducted by the four researchers and the self-study implemented by X was to strive for a heuristic understanding of the features specific to the three constructs that can better describe the educative power of X. The integration is also valuable as it could validate the findings by triangulating the diverse sources of data including those from the observations of TPD programs, the interviews, and X’s self-reflection.

3.2 Participants

Whereas a number of studies have focused on the development or knowledge of novice teacher educators (e.g., Chauvot, 2009; Zaslavsky & Leikin, 2004; Zeichner, 2005), the major focus in this study was the experienced MTE-R, X, who had more than 30 years experience researching in mathematics education and teaching prospective secondary teachers. Both research and teaching experiences had enabled him to initiate at-the-moment actions to facilitate TPD. X specifically believed that the core of educative power lies in the capabilities of enhancing teachers’ professional knowledge, enriching teachers to see diverse perspectives on teaching, encouraging teachers to fulfill their potential, and enlightening them to experience the essence of teaching and learning. To this end, X usually grasped the key ideas from research and checked the ideas with teaching contexts. He then reified the ideas into thinking models which allowed him to generalize the models to a variety of teaching contexts. This process enabled X the capability of initiating at-the-moment actions that tie well to both research and practice. Other researchers and teachers in the TPD programs were also participants in this study.

3.3 Design-based TPD programs for experienced mathematics teachers

The context of this study was in Taiwan. It has been acknowledged that Taiwanese students often lack confidence and take negative attitudes toward the learning of mathematics even though they consistently out-perform students in other countries in cross-national comparisons (e.g., Mullis, Martin, Foy, & Arora, 2012; OECD, 2010). One key reason for this specific educational phenomenon in Taiwan is the examination-driven and traditional exposition which mainly focuses on drills and routine practice (Lin & Tsao, 1999). Lin (2009) pointed out that Taiwanese teachers often think that traditional exposition is necessary for getting high scores, so students’ learning is limited to surface understanding and quick responses. To improve such an instructional situation, we need to enhance students’ mathematical power and teachers’ instruction. Thus, the aim of the TPD programs was to develop teachers’ competence in designing tasks that can inspire students to think (communicate, reason, and connect) about mathematics actively in the examination-driven learning environment.

The TPD programs were planned by a team of five researchers (including X) and directed by X. The team proposed a hypothetical learning cycle (see Fig. 2) based on Simon’s (1995) idea of hypothetical learning trajectory and used the cycle to arrange learning activities for mathematics teachers. The hypothetical learning cycle involves four stages: evaluating tasks given by the educator, discussing challenging pedagogical problems specific to each individual mathematics teacher, designing tasks, and testing the potential of the tasks according to students’ responses. The study reported here was the implementation of four design-based TPD programs—developed based on this hypothetical learning cycle—for experienced mathematics teachers, most of whom worked in northern regions of Taiwan.

Fig. 2
figure 2

A hypothetical learning cycle

Full size image

The first program is reported here as an example. First, X presented the educational problems existing in Taiwan and invited the participating teachers to express and discuss their perspectives on active thinking in learning mathematics. Then, X introduced types of strategies and examples that can be used to enhance students’ active thinking. Meanwhile, teachers were also asked to evaluate the task examples according to their perspectives on active thinking. Second, the teachers expressed their own pedagogical challenges when enhancing students’ active thinking and discussed the challenges with X and other participating teachers. Third, the teachers were required to design tasks individually or collaboratively and then discussed their designs with X and other participating teachers during the program or by e-mail exchanges. Fourth, participating teachers also needed to enact the tasks with their students to obtain feedback for refining the tasks accordingly.

Each of the four programs lasted for one semester and each program had six 3-h meetings in a semester. Since the diverse backgrounds of the participating experienced teachers might influence their learning progression, the programs were organized flexibly. The first two programs had about 30 experienced junior high school mathematics teachers (their average teaching experience was 15 years); eight of them continued to participate in the third and fourth programs. Most of the participating teachers were also teacher consultants who were responsible for offering suggestions to school mathematics teachers when they encountered pedagogical challenges.

3.4 Data collection and analysis

Data were collected from several sources during the implementation of the four TPD programs for exploring the educative power of X: the videotape corpus of the TPD programs, X’s self-reflection, interviews with X and participating teachers, and written materials (e.g., e-mail exchanges between X and the teachers as well as teachers’ written reports of their designing processes). The videotape corpus allowed us to analyze how X interacted with the participating teachers. The data from X’s self-reflection enabled us to understand the ways in which he implemented and facilitated the TPD programs. To better understand his educative power, we also interviewed X for him to explain his intentions in initiating at-the-moment actions by way of a series of questions: (1) How do you communicate with teachers? (2) How do you reason in your at-the-moment actions with the participating teachers? (3) How do you connect research and practice to frame your facilitating strategies? Those questions allowed the research team to identify the features specific to communication, reasoning, and connection respectively. Additionally, the data of the interviews with the participating teachers and the written materials made it possible for the research team to further clarify and triangulate the actions initiated by X and the reasons supporting his actions. The processes of data collection—especially those involving X’s reflection and comments on participating teachers’ queries and designed tasks—provided us a basis for exploring X’s educative power situated in a variety of interactive contexts.

For data analysis, three stages were implemented to secure the features specific to the three constructs, respectively. The first stage was to probe the meanings of the educative power that X demonstrated when facilitating the TPD programs. During this stage, R2 and R3 presented what they observed in the first two TPD programs and discussed critical instances with R1 and R4. Meanwhile, the four researchers also interviewed X with the three proposed questions to elicit his study on the three constructs. When the interpretations of the critical instances made by the four researchers and X’s notes or reflection were consistent, the team further discussed the deep meaning of educative power. If the data were not consistent, the team interviewed the participating teachers for further clarification.

For the second stage, the goal was to formulate the features specific to the three constructs. To accomplish this goal, R1 proposed the features by connecting the educative power with the meanings derived from the first stage and theories in the related literature. This mapping process enabled the formulation of the features that can better elaborate the core of the educative power of X. Additionally, the proposed features were further revised and validated by the team based on both supporting instances and counter instances that R2 and R3 intentionally identified from their observations of the following two TPD programs. Regarding the third stage, R1 and R2 attempted to secure and define the features based on the meanings and theories identified. In addition, X revised some theoretical explanations used to elaborate how he connected the meanings with theories for evaluating the tasks designed by participating teachers drawing on his self-study.

4 Findings

Based on analyses through the three stages described in methodology section, we intentionally select episodes which can well illustrate the features of X’s educative power in relation to communication, reasoning, and connection. We acknowledge that the three constructs were interrelated in this study; thus, any episode would involve all the constructs. The goal here is to highlight the features specific to each construct in X’s educative power.

4.1 Communication using an approach of creating educative phenomenology

To help readers understand the feature associated with communication, we present in this paper interview data, workshop data, and X’s reflection to show how X communicated with participating teachers to facilitate their professional development.

Adam: …In the past, I thought active thinking was just an activity that led students to “apply different mathematics knowledge to solve a variety of mathematics problems.” But now, I change my mind….I think my teaching goal should be shifted to help students develop mathematics knowledge and consider a mathematics problem from different perspectives. [Interview transcript]

After Adam had changed his viewpoint on mathematics teaching and learning, he designed several tasks. One of the tasks was to explore the essence of the ratio concept. As shown in Appendix A, the task involves a variety of real-life contexts in which students have opportunities to perceive the essence of comparisons. For example, problem A3 asks which glass of water is sweeter when one glass has 3 sugar cubes and the other has 5. It is noteworthy that the problem does not provide sufficient information to determine the sweetness of the water; thus, students themselves have to figure out the need for using the ratio concept and other quantitative information for the comparisons.

X treated the task regarding the essence of the ratio concept as a good learning opportunity not only for Adam but also for other participating teachers. Before Adam presented his task, X asked other participating teachers to reflect on their own perspectives on the ratio concept. During group discussions, Gina, one of the participating teachers, said:

Gina: …you always need exact numbers when making comparisons…once I know the ratio for students passing a certain exam in each class…For example, one is 4/5 and another is 1/5…I could evaluate which class performed better…

X: Gina used an empirical example to express what the essence of ratio is that she had in mind…Adam, do you agree?

Adam: I should further explain myself…when I created the task, I did not want to discuss specific values of ratio…Rather, my aim was to help students understand what ratio concept is. If students could clearly identify ratio, then they should have better sense of the concept…. [Workshop transcript]

Gina’s reflection showed that she considered ratio from a calculation perspective. Unless exact numbers are given, one cannot calculate the ratio and make comparisons. At that moment, X did not directly explain to Gina what the essence of the ratio concept is and its relation to calculations. On the contrary, he treated this as a learning opportunity for teachers to make sense of the essence of the ratio concept. To this end, X asked Adam how he would respond to Gina’s reflection on the ratio concept. X expressed that in doing so I could facilitate professional development of different participating teachers by comparing their different perspectives on the ratio concept. The discussions continued for a while. Then, X summarized the points and made their connection to the relevant theories.

X: …Ratio is developed to describe different sensorial feelings, such as touch, seeing, taste, smell, and hearing. You want students to be conscious of when and why the ratio concept is needed…You should scaffold students in making sense of the concept and reasoning it out in real contexts…this is the so-called quantitative reasoning in the literature… [Workshop data]

X’s communication with the participating teachers afforded them opportunities to explore the essence of the ratio concept and how the essence can be enculturated (Bishop, 1991); moreover, X implicitly communicated to them the theoretical conception, enculturation, by bringing their attention to realize the essence of mathematics with personal feelings. As Watson and Mason (2007) stated that “unless the phenomena of teaching and learning can become real for teachers, they are unlikely to make sense to them” (p. 211), X’s communication with the participating teachers enabled them to perceive the essence of the ratio concept and its realization for student learning. Furthermore, X suggested to Adam how to refine the task he had designed in the workshop. X said:

X: …you [Adam] already grasped the essence of ratio as it was used to describe the feelings by existing quantitative representation…or in situations when existing quantitative representation could not describe any feelings…Basically, you already had two types of tasks that allowed students to experience the essence of ratio…I think you can design another type of problem which does not include any quantity…In this situation, students can concentrate more on observing the objects in contexts and describing their feelings…I suggest you to include this in the first part of your design. [Workshop transcript]

To understand how X initiated at-the-moment actions for communication, the notion of didactical phenomenology was adapted. According to Freudenthal (1983), didactical phenomenology in realistic mathematics education emphasizes where mathematical ideas are developed and rooted so that the meaningfulness and the utility of mathematics can be ensured. Similarly, we use the term educative phenomenology to refer to realistic situations in which relevant didactical ideas can be developed and realized. Let us take the above episode as an example. Educative phenomenology in the episode refers to the communication—between X and the participating teachers—that had enabled X to facilitate those teachers in developing and realizing the essence of ratio and how it could be enculturated. Two characteristics specific to X’s communication in this episode have to be highlighted. First, while considering teachers as active learners actively engaged in constructing their knowledge for teaching, X put effort into establishing the norm where teachers could discuss and learn how to teach to prompt students to actively think about mathematics. During the teacher professional development (TPD) programs, X paid attention to identify situations where educative phenomenology could be developed. When no such situations were accessible, X then shared his prior educative or teaching experiences with the participating teachers to enable their understanding of didactical ideas. For X, communication helped teachers not only to figure out solutions to their own pedagogical problems but also to learn about other teachers’ pedagogical problems through participation in the discussions.

Second, during communication, X had to consider both the essence of mathematical tasks along with their enactment in classrooms, and the theories that could be used to support the development of the tasks and TPD. X usually guided the participating teachers to reflect on mathematical meanings and processes in their designed tasks and discussed how the tasks can enhance student learning. Communication using an approach of creating educative phenomenology requires MTE-Rs to perceive teachers’ understandings of and perspectives on the essence of mathematics and student learning as well as didactic ideas about the mediation between mathematics and students. Teacher educators also have to decide when, and what kind of, educative phenomenology needs to be created in order to facilitate TPD.

4.2 Reasoning by mapping teachers’ ideas onto emergent models to solve problems in educative challenges

We present here X’s reflection and feedback on Zhuang’s design of a task to reveal how X reasoned in encountering his educative challenges when facilitating TPD. Zhuang designed a task by which he expected to help students understand the formula of multiplying square roots \( \sqrt{a}\times \sqrt{b}=\sqrt{ab} \) and to correct their misconception of \( \sqrt{2}+\sqrt{2}=\sqrt{4} \). To do so, Zhuang used a paper-folding activity (see Appendix B) to help students recognize the existence of \( \sqrt{2} \) and understand \( \sqrt{2}+\sqrt{2}=\sqrt{8} \) through observing the relations between the sides of a big square with an area of eight units and those of a small square with an area of two units. However, the instructional strategy Zhuang proposed did not ultimately succeed in meeting his expectations at the end. Students agreed that \( \sqrt{2}+\sqrt{2}=\sqrt{8} \) is correct when observing the relation of the sides in diagrammatic representation but their answers changed to \( \sqrt{2}+\sqrt{2}=\sqrt{4} \) when doing calculation problems. For the pedagogical challenge Zhuang encountered, X first presumed the possible reasons behind this problem and figured out relevant theories that can be used to explain the students’ inconsistent responses to two kinds of representation: diagrammatic representation and the written symbolic representation. X said the following:

X: “While I was thinking what kinds of comments would be helpful for Zhuang to solve his pedagogical problem in the professional development program, the ideas of mathematical contradiction and cognitive conflict suddenly came to my mind….I concluded that mathematics contradiction does not necessarily lead to the consequence of cognitive conflict for students….I mapped Zhuang’s pedagogical problem onto the theory of cognitive conflict and a quasi-empirical perspective on mathematical contradiction….They both allowed me to offer suggestions to Zhuang’s task design.” [Interview transcript]

X used the theory of cognitive conflict (Fischbein, 1978) and a quasi-empirical perspective (Lakatos, 1986) to support his reasoning in solving the pedagogical problem encountered by Zhuang. The analysis allowed Zhuang to understand the reason for students’ inconsistent responses. According to X’s notes, he reflected that the theories can only explain the reasons for students’ unexpected responses but is insufficient to solve Zhuang’s pedagogical problem. Thus, X further referred to the historical development of irrational numbers (mathematics) and approximation in relation to students’ conception of number (cognition) which can facilitate Zhuang to formulate a solution to his pedagogical problem.

X: “It appears that Zhuang wanted to correct students’ errors by the mathematical contradiction between diagrammatic and symbolic representations in which the foundation lies in mathematical legitimacy. However, he did not really perceive the reasons accounting for students’ errors…. Zhuang should incorporate both epistemological analysis and mathematical legitimacy to create the design; otherwise, the task cannot help students understand the mathematics in coherence and correct their errors….Representation theory and its transformation are important for Zhuang to revise the task…The notion of didactical situation can also help Zhuang frame his task….One of my graduate students also designed a task to conjecture the Pythagorean Theorem in this way.” [Self-reflection]

Representation theory and its transformation (Brenner et al., 1997; Lesh, Post, & Behr, 1987) were also the theories that X applied to reason out students’ inconsistent responses. Representation theory showed that the same mathematical concept embodied in different representations can be treated differently by students (Behr, Lesh, Post, & Silver, 1983). It is likely that Zhuang’s students treated \( \sqrt{2} \) in diagrammatic representation as an object without numerical meaning. In this regard, \( \sqrt{2} \) in diagrammatic representation cannot be calculated. Zhuang’s students might not develop the ability to transform their understanding between different representations and realize the underlying mathematical concepts (Lesh et al., 1987). Thus, mathematical contradiction between diagrammatic representation and written symbolic representation could not provoke students’ cognitive conflict and enhance their learning. X further pointed out that the students’ error in thinking of \( \sqrt{2}+\sqrt{2}=\sqrt{4} \) could be viewed as a case similar to the error pattern 2a + 5b = 7ab (Hart, 1981). Hart used the mathematical sentence as an example to elaborate a variety of students’ cognitive behaviors by calculating familiar numbers, ignoring unfamiliar parts, and then incorporating both together as the final answer. Let us take \( \sqrt{2}+\sqrt{2}=\sqrt{4} \) as an example. Students might calculate 2 + 2 = 4 by ignoring the unfamiliar square root notation and then take the notation back after obtaining the calculated answer of 4. X facilitated participating teachers to understand how the specific error can be the pattern generalized to the learning of a broader range of mathematical content areas and be the principle in guiding the design of instructional tasks. Realizing this error pattern is particularly important for mathematics teachers because it helps them identify reasons for students’ various errors associated with the pattern and enables them to develop follow-up diagnostic teaching plans to correct the errors.

Additionally, X’s reflection showed that he adopted the notion of didactical situation which states that knowledge is the result of students’ adaptation to situations in which they justify the knowledge by making it more or less effective (Brousseau, 1997). In line with this notion, teaching becomes the devolution for students from didactical situations to adidactical situations through which students can overcome their epistemological obstacles. In this regard, X suggested to Zhuang that the theory of didactical situation and adidactical situation could be the intermediate framework and design tool, respectively (Ruthven et al., 2009), for structuring and refining his tasks.

To address the capability of dealing with at-the-moment challenges, the notion of emergent models from realistic mathematics education is borrowed to interpret X’s ways of reasoning and thinking. In realistic mathematics education, emergent refers both to “the character of the process by which models emerge within RME,Footnote 2 and to the process by which these models support the emergence of formal mathematical knowledge” (Gravemeijer, 1999, p. 175).

Similarly, emergent for educative power means both the character of the process by which models of educative phenomena emerge within educative practice and the process by which these models support the emergence of theories of teaching and learning. Consequently, the key feature of the emergent model is its attribute of generalizability for applying one model of one educative phenomenon to reason in a broader range of educative phenomena. The emergent models that X used in the episode to facilitate TPD included cognitive conflict theory, quasi-empirical perspective, historical development of irrational number, approximation in relation to students’ sense of number, and didactical situation. X reflected that he developed the emergent models starting from both teaching practices and theoretical ideas obtained from the relevant literature. Then, he gradually generalized the models through iterative practice (teaching) and research (studying). Those models which entail rich educative phenomenology allowed him to reason out solutions to educative problems he encountered when facilitating TPD. Additionally, X also expected that reasoning in solving problems in educative challenges based on emergent models can be perceived by teachers so that they know how to search for proper theoretical models and adopt them to reason out solutions for their own pedagogical problems.

Cochran-Smith (2004) used the term “working the dialectic” (p. 2) to highlight the relationship of scholarship and practice. She pointed out that dialectics plays an important role in overcoming the tensions faced by teacher educator-researchers when constructing knowledge from practice and then making that knowledge accessible and usable in other contexts. Generally speaking, MTE-Rs are familiar with conducting research and planning TPD programs. However, MTE-Rs, especially novices, may not be so effective and efficient in handling their at-the-moment challenges when facilitating TPD. The nature of dialectics allows MTE-Rs to transform research into their practice and at the same time increase their educative and researchive power (García et al., 2006; Peled & Hershkovitz, 2004). In this paper, we deliberately report the ways in which X reasoned based on his emergent models and then formulated strategies to solve problems in his educative challenges.

4.3 Connection between research and practice by coordination

Connection in mathematical power emphasizes the ability to unite within and across the domains of mathematical content as well as the mathematical proficiencies. For pedagogical power, Byrd and McIntyre (1999) indicated that the connection should focus on the link within and between research and practice. Similarly, connection in educative power also emphasizes the connection between research and practice. Here we use the term “coordination” in particular to highlight the approach that X used to initiate his at-the-moment actions for connecting between research and practice.

Coordination is aligned with dialectics mentioned above, but it further highlights the debates of pertinent possibilities in facilitating TPD by considering both research and practice as well as different reciprocal facilitator-learner relationships involving educators, teachers, and students. X had to consider his roles as a teacher educator who facilitated TPD, as a teacher who was also a learner in TPD programs, as a facilitator in classrooms, and as a student who had the responsibilities to learn mathematics in class. In TPD programs, X usually felt tension as he did not have enough time to comprehensively reflect on relevant theories before providing feedback to participating teachers. In such situations, X first paid attention to teachers’ pedagogical problems and then connected those problems with relevant theories which would be helpful. When reasoning about pertinent possibilities, X always took the effectiveness of classroom teaching as the top priority and then facilitated teachers in understanding the theories which can be the thinking models for generalizing learning to a broader range of teaching contexts. We use the following example to illustrate this point.

Adam designed a task with the aim to help students make sense of the sum of infinite series by a paper-scissors-stone game. The underlying mathematical concept of the game is probability. Adam created this task because the curriculum at middle school level did not introduce the convergent property of infinite series. After Adam had shared his design with others, some participating teachers criticized the task by claiming that it did not demonstrate mathematical rigor. One teacher even suggested Adam should use an alternative strategy by observing the areas of a series of triangles, that is, each of the following triangles was to be constructed by connecting the midpoints of all sides of the previous one. During the debate, with the focus on mathematical rigor but in a way different from those teachers’ comments, X pointed out that the value of Adam’s design was to help students make sense of the meaning of the sum of infinite series (Appendix C) as follows:

X: Instead of focusing on geometry, analyses, or formal infinity, Adam tried to introduce the sum of infinite series by applying combinatorial thinking to create his design. Because of the real context of the game and the use of probability conception [of students], the task makes it possible for students to make sense of the sum of infinite series.…You want students to think beyond intuition when learning mathematics, you have to first admit that intuition cannot be avoided.…Students can obtain the meaning of the sum as a result of the game, and that of the continuous calculating processes of an infinite series.…students build up the equilibrium between the sum and the calculating processes of an infinite series. This can be viewed as a kind of situational thinking: students have to reason with what they experience in realistic contexts in order to obtain solutions…The design is worthy of follow-up teaching experiments… [Workshop transcript]

The above example shows how X reasoned out a solution to the problem in the debate about Adam’s task by coordinating both research and practice. From the mathematics perspective, the comments made by other teachers were reasonable as the design approach did not take mathematical rigor into consideration. However, from the learning perspective, Adam’s task provided opportunities for students to make sense of the meaning of the sum of infinite series in realistic contexts. The coordination of pertinent possibilities with respect to research and practice as well as different facilitator-learner relationships allowed X to provide suggestions about Adam’s design and, at the same time, facilitate professional growth of other participating teachers.

We use one more example here to show how X created a task by coordinating research and practice as well as different reciprocal facilitator-learner relationships. In the programs, Jing did not make every effort to design his tasks as he stated that he needed good examples to imitate and to learn. He used his unsuccessful task-design experiences to make this claim. Jing aimed to create a task which allows students to conjecture the completing the square method for solving quadratic equations. Jing tried several approaches but the tasks he designed did not offer many opportunities for students to make conjectures and looked quite similar to the formulas in textbooks. At that moment, X decided to guide Jing to design a task by considering different facilitator-learner relationships as follows:

X: …you have to set up your design goal first…If your goal is to let students conjecture the completing the square method, you should let students know why they need this method…you can direct students to recognize that not all quadratic equations can be factored by a cross method…Students need a new method to find the roots of quadratic equations…if students can calculate the roots for x2, then they can also acquire that for (x + a)2…Additionally, students can also use numerical examples to check the equation and then formulate the method…Formulating the completing the square method and checking the method by some examples are essential in conjecturing. [Workshop data]

The above transcript shows how X provided suggestions to refine Jing’s task based on coordination of different reciprocal facilitator-learner relationships. Regarding this educator-teacher relationship, X evaluated Jing’s learning situation in programs and identified that it was the time for him to provide more support and good examples to guide Jing’s learning. Specifically, X decided to show Jing and other teachers how to create a task which offers opportunities for students to conjecture a mathematical formula actively. Regarding the relationship between teachers and students, X considered different perspectives on student learning (e.g., motivation, prior knowledge, learning trajectory) and incorporated those perspectives into the design of the conjecturing task. According to X’s notes, he reflected that the use of inquiry-based approach helped him understand his educative problems and formulate solutions accordingly (Adler, 1993), and this is one reason why he could coordinate different facilitator-learner relationships for connecting between research and practice. Coordinating research and practice as well as different reciprocal facilitator-learner relationships to create the conjecturing task surprised all the participating teachers as they originally thought that a mathematical formula was not the material that can be used to design conjecturing tasks. Flora said the following:

Flora: I feel amazed when X gives suggestions and comments on these tasks created by us…No matter what quality the task was, he could always find its connotative value and provide useful comments for refinement…I always thought the quality of the tasks couldn’t be improved in the past. If a task had bad quality, no matter how hard you worked on it, it wouldn’t become a better one….Nevertheless, X’s suggestions and comments changed my thinking. I start to believe that every task has its own value and can be gradually modified into better work….This is why I adore X. He can always find the educational value of every design and direct us to be conscious of it….I believe his power is far beyond my expectations. [Interview transcript]

By coordination, X was able to become aware of teachers’ pedagogical problems and provide proper suggestions accordingly. Coordination enabled X to connect research and practice for the facilitation of TPD. X further elaborated the philosophy guiding his teaching as follows:

X: The philosophy that guides my teaching is the dictum in the Book of Rites Footnote 3: harmony, easy attainment, and thoughtfulness. For me, teaching is to guide but not to push, to strengthen but not to suppress, and to inspire but not just to give answers…When facilitating teacher growth, I first discard my knowledge about research but just focus on how I can inspire teachers, strengthen their competence, and scaffold them in solving their own pedagogical problems. I expect to nurture teachers with their competence so that they know how to search and solve their own pedagogical problems in the future. [Self-reflection]

5 Reflecting remarks

In this paper, we report the educative power of an MTE-R by elaborating how he initiated at-the-moment actions to facilitate teacher professional development (TPD) programs. Based on the conceptual framework and mixed approaches of self-study and case study, we identify three key features of the MTE-R’s educative power: (1) communication using an approach of creating educative phenomenology, (2) reasoning by mapping teachers’ ideas onto emergent models to solve problems in educative challenges, and (3) connection between research and practice by coordination. Our exploration goes beyond previous studies focusing on types of knowledge that teacher educators require (e.g., Chauvot, 2009; Zeichner, 2005) or those studies investigating professional development of teacher educators through the interplay between research and practice (e.g., Jaworski, 2001; Peled & Hershkovitz, 2004; Zaslavsky et al., 2003). This is because we have analyzed in-depth the at-the-moment actions initiated by the experienced MTE-R through communication, reasoning, and connection. Our use of both self-study and case-study methods has allowed for the articulation and validation of at-the-moment actions as well as the MTE-R’s thinking to support his actions. Moreover, the following paragraph shows what other MTE-Rs could learn from the findings about X.

The episode about the MTE-R’s communication with the ratio concept reveals that he emphasized the essence of mathematics and treated it as the core for developing tasks. The episode about the formula of completing the square for solving quadratic equations illustrates how student learning became the foundation for him to reason out solutions to teacher’s pedagogical problems. The episodes used to exemplify the connection between research and practice further articulate how the learning of both teachers and students was considered in his facilitation. He intuitively diagnosed weaknesses and strengths of teachers’ learning and then formulated proper at-the-moment actions with the concern for both the essence of mathematics and the learning of teachers and students. The theories and research are the foundation for him to reflect on and to examine the appropriateness of his actions for both teachers and students. He expected to facilitate participating teachers to establish thinking models that can be generalized to solving pedagogical problems situated in a broader range of teaching contexts.

Although we do not restrict the conceptual framework in Taiwan as we expect it would become universally available, further research is required to examine the generality of the conceptual framework and to investigate how the educative power actually influenced TPD as well as how teachers gain access to MTE-Rs’ theoretical bases. Investigating educative power from the perspectives of both teachers and educators makes it possible to articulate how TPD programs can be planned in more efficient ways and formulate the principles for facilitating the professional development of both teachers and educators, especially when previous studies have found that there is difficulty in improving the pedagogy of teacher educators (e.g., Korthagen, Kessels, Koster, Lagerwerf, & Wubbels, 2001). In a way similar to the relationship between student and teacher—that can vary because of the differences in culture and society—the effectiveness of strategies with which MTE-Rs use to facilitate TPD very much depends on teachers’ learning objectives and their learning styles. It can also be the case that teachers’ learning objectives are determined by their students (Runesson & Marton, 2002). Thus, the extent to which educative power can effectively facilitate TPD is of interest. Regarding X, he also led TPD programs in other countries/regions such as Korea and Macau of China. In Korea, for example, X collaborated with a professor of a Korean university to design and implement TPD programs. Under their collaboration, the cultural and societal differences can be considered and tackled. His influential educative power, particularly the features of communication and connection, can be again confirmed by the following quote from the Korean professor’s reflection:

“…his ability to shed light on essential but ignore points by teachers.…his disposition to respect teachers’ potential.…If there are seemingly kinds of ruptures happened, then he smoothly wheeled the interactions to alternative ones that could deal with the same issues but looking different.”

Researchers have highlighted reflective enquiry as the research approach for MTE-Rs to integrate both research and practice (e.g., Adler, 1993). On the one hand, MTE-Rs have to develop research by conjecturing and evaluating theoretical ideas. On the other, they also need to facilitate TPD in practice. The combination of both roles as researchers and educators is the key to nurturing educative power of MTE-Rs, enabling their development of pedagogy of teacher education, theoretical knowledge, and practical knowledge (Loughran, 2006). Those types of knowledge for teacher education necessitate not only the dialectics between research and practice (Cochran-Smith, 2005; García et al., 2006) but also coordination through the debates of pertinent possibilities and the consideration of different reciprocal facilitator-learner relationships involving educators, teachers, and students. Based on our findings, we believe that coordination may enable MTE-Rs to transform their tensions by connecting research and practice to strategies of supporting TPD.

Finally, of importance is the philosophy of the experienced MTE-R in this study: to guide teachers but not to push, to strengthen their competence but not to suppress, and to inspire them to think and challenge problems actively instead of just to give them the answers. To facilitate TPD in line with this philosophy, the MTE-R had a variety of contextualized narratives about teaching practices to which important theories are applied. Because of those rich narratives, the MTE-R was able to create educative phenomenology to facilitate teachers in developing the meaningfulness and the utility of didactical ideas for their students’ learning. For the MTE-R, those narratives are generative and can be used to solve a variety of educative problems. In particular, the MTE-R took those educative challenges as opportunities to reflect on and coordinate his research and practices. Whereas researchers have reported the dilemmas that teacher educators often face in their practices (Cabaroglu & Tillema, 2011; Tillema, 2004), our study shows how the MTE-R transformed educative challenges involving dilemmas and tensions into the driving forces for self-growth in professional development. The MTE-R in the study not only offered solutions to break the limitations in facilitating TPD in practice but also accommodated the practical contexts to overcome the restraints in research. In addition, it is worthy of further research to explore how MTE-Rs deal with dilemmas and tensions in practice and such relation to their educative power.