Acquiring knowledge without retaining it is a fruitless venture, yet it characterizes the experience of many college students. College students learn large amounts of information in their classes but may quickly lose their ability to recall much of it…Although the consequences may sometimes be limited to disappointment and a sense of time wasted, they may at other times be more profound and even career path-altering. Success in some disciplines depends on students possessing a cumulative body of knowledge and is thwarted by poor retention of foundational content…Because excellence in science, technology, engineering, and mathematics is deemed critical for the USA’ success in the twenty-first-century global economy (White House, n.d.), poor retention of mathematics may also undermine national priorities (Hopkins et al. 2016, p. 854).

As highlighted in the quote above, improving knowledge retention is a perennial issue of practical importance, and mathematics is no exception. One learning technique that is particularly promising for enhancing knowledge retention is successive relearning (Bahrick 1979), which involves practicing to-be-learned content until a designated level of mastery is achieved in each of multiple practice sessions. Although a relatively small number of studies have investigated successive relearning, these studies have consistently demonstrated impressive effects of successive relearning on long-term retention of target content. Based on these outcomes, we have advocated for successive relearning as an effective technique for enhancing durable learning (Rawson and Dunlosky 2011, 2013; Rawson et al. 2013; Rawson et al. 2018). However, the onus of establishing generalizability—and the limits thereof—for a prescribed learning technique falls heavily on proponents of that technique. Notably, the kinds of to-be-learned content targeted in prior work have been limited to verbal learning tasks (i.e., learning of foreign language vocabulary or key-term definitions). Additionally, the practice and final test items have been identical in almost all prior studies, and no evidence exists for whether successive relearning supports transfer to novel tokens of a type. Does successive relearning also improve learning for other kinds of educationally relevant content and when practice and final test questions are not identical? In particular, does the documented potency of successive relearning extend to the learning of mathematical procedures?

Prior Research on Successive Relearning

Successive relearning involves practicing until a particular level of mastery (referred to as the criterion level) is met, and then repeating the same practice across multiple learning sessions (e.g., Bahrick 1979). Thus, successive relearning combines two highly effective learning techniques—practice testing and spaced practice (for recent reviews of these two techniques, see Rowland 2014; Wiseheart et al. 2019). Although part of the power of successive relearning is derived from spacing (for relevant evidence, see Rawson and Dunlosky 2011), successive relearning and spaced practice are not identical. That is, successive relearning does involve sessions that are distributed across multiple sessions, but each session also includes using retrieval practice with feedback until a specific criterion (e.g., one correct response) is met. By contrast, research on spacing has almost exclusively demonstrated the spacing effect within a single session, by comparing practice that is massed in time versus spread over a longer interval within a study session. Moreover, the majority of research on the spacing effect has not included retrieval practice—that is, all trials for target items typically involve restudy rather than practice tests (for a detailed review, see Rawson and Dunlosky 2011). Put differently, successive relearning always involves spaced practice, but spaced practice does not always constitute successive relearning. And, in the few cases where retrieval practice has been spaced across time, it rarely involves successive relearning (which requires practicing to criterion). One example is research using in-class quizzes (i.e., a form of retrieval practice), which can improve student achievement (for a review, see McDaniel and Little 2019). Although this research highlights the potency of retrieval practice in authentic classrooms, it has not involved criterion learning in multiple sessions and hence is not relevant to estimating the potency of successive relearning.

To date, eight published studies have investigated the effects of successive relearning on long-term retention (Bahrick 1979; Bahrick et al. 1993; Bahrick and Hall 2005; Rawson and Dunlosky 2011, 2013; Rawson et al. 2013, 2018; Vaughn et al. 2016). All of these studies involved verbal learning tasks (i.e., learning either foreign language vocabulary or key-term definitions) and used the same basic methodology. During an initial learning session, learners are presented with a list of to-be-learned items (e.g., foreign language translation word pairs, such as maison-house) for cued recall practice trials followed by restudy as needed until each target is correctly recalled. This procedure is then repeated in one or more subsequent relearning sessions, such that each item is correctly recalled multiple times across sessions. Long-term retention is typically assessed via a final cued recall test administered days or weeks after the last learning session.

These prior studies have involved two kinds of experimental manipulation, either (a) comparing different successive relearning schedules to one another, or (b) comparing successive relearning to single-session learning. As an example of a study comparing different relearning schedules, Bahrick (1979) had students practice English-Spanish word pairs until each item was correctly recalled once in either three or six learning sessions that were each separated by either 1 or 30 days. Performance on a final cued recall test 1 month later was greater with more versus fewer learning sessions and with longer versus shorter lags between sessions.

The comparison of greater interest for present purposes concerns the advantage of successive relearning over single-session learning, an effect referred to as relearning potency (Rawson et al. 2018). Several prior studies have included conditions that afford examination of relearning potency (Bahrick 1979; Bahrick and Hall 2005; Rawson and Dunlosky 2011, 2013; Rawson et al. 2018; Vaughn et al. 2016). The most rigorous design involves equating the overall criterion level (i.e., the total number of times an item is correctly recalled during practice) and also equating the retention interval (i.e., the interval between the end of practice and final test); the key manipulation concerns whether the overall criterion level is achieved in a single practice session versus distributed across two or more separate sessions. For example, Bahrick and Hall (2005, Experiment 1) had students practice Swahili-English word pairs until each item was correctly recalled either four times in one session (i.e., single-session learning) or one time in each of four sessions (i.e., successive relearning). Performance on a final cued recall test 2 weeks later was substantially greater after successive relearning versus single-session learning (76 versus 31%). Vaughn et al. (2016) also had students practice Swahili-English word pairs until each item was correctly recalled either four times in one session or one time in four sessions; the relearning potency effect on final cued recall 1 week later was impressive (74 versus 28%). The other studies involving the learning of foreign language vocabulary have also shown sizeable advantages of successive relearning over single-session learning (Bahrick 1979; Rawson et al. 2018).

Fewer experiments involving key-term definitions have included conditions that afford examination of relearning potency. In Rawson and Dunlosky (2011, Experiment 2), students practiced key-term definitions until each definition was correctly recalled either three times in one session or one time in each of three sessions. On a final cued recall test 2 days later, the advantage of successive relearning over single-session learning was modest (73 versus 67%). This study was replicated by conditions in Rawson and Dunlosky (2013, Experiments 1–2). Although not reported in the original article, we reanalyzed data from those experiments and found similarly modest benefits of successive relearning over single-session learning (74 versus 65% in Experiment 1; 83 versus 73% in Experiment 2). These findings hint at the possibility that the sizeable advantages of successive relearning over single-session learning demonstrated with foreign language learning may not generalize to all kinds of academic content.

Finally, all prior studies have included final tests that were identical to the practice tests (e.g., cued recall during both practice and final test for the same foreign language word pairs or the same key-term definitions). Rawson et al. (2013) also examined performance on course exam questions that tapped the key-term definitions that were practiced in the context of the experiment, but this study did not include conditions comparing successive relearning to single-session learning (in brief, successive relearning was compared with restudy only or self-regulated learning conditions). Rawson and Dunlosky (2011, 2013) also administered final multiple-choice tests of the practiced key-term definitions but not under conditions affording a comparison of successive relearning to single-session learning with retention interval held constant. Thus, no evidence exists on whether relearning potency effects obtain with non-identical final test questions. Likewise, no evidence exists for whether successive relearning supports transfer to novel tokens of a type, which is particularly relevant to content domains such as mathematics.

Relearning Potency Effects on Learning of Mathematics

What then are the prospects for relearning potency in mathematics? To revisit, successive relearning is defined by two key functional components, mastery learning and distributed practice (i.e., practicing until a designated level of success is achieved in each of multiple sessions). Note that the mastery learning component of successive relearning mimics the learning-to-criterion algorithms instantiated in some autotutor programs for mathematics. For example, Assessment and Learning in Knowledge Spaces (ALEKS) is a learning system that has been used to teach mathematics to millions of K-12 and college-level students globally (https://www.aleks.com/about_aleks/overview). During learning, ALEKS continues to present students with practice problems for a given topic until they can consistently solve problems correctly (e.g., at least three correct responses for a given problem type). However, ALEKS does not require that these criterion trials be distributed across different learning sessions. The primary question of interest in the current research concerns the degree to which distributing criterion across sessions matters.

Examining relearning potency requires comparison of two conditions in which the overall criterion level is equated but the distribution of practice is manipulated, such that the overall criterion level is achieved either in a single session or across multiple sessions. No prior research on the learning of mathematical procedures has included the requisite design, because prior studies have involved non-mastery learning with a fixed amount of practice (i.e., equating the number of trials and allowing the level of success achieved during practice to vary). Furthermore, only a few of these non-mastery studies have manipulated the distribution of practice within versus across sessions. Some of these studies have demonstrated advantages of distributing fixed amounts of practice across sessions versus a single session (Chen et al. 2018; Lyle et al. 2020; Nazari and Ebersbach 2019; Rohrer and Taylor 2007), although the benefits of distributing practice of mathematical procedures across sessions do not always obtain (e.g., Rohrer and Taylor 2006).

More generally, some meta-analytic outcomes suggest that the effects of distributed practice decrease as the conceptual difficulty of the learning task increases (Donovan and Radosevich 1999; Wiseheart et al. 2019). By comparison, whereas the relearning potency effects documented with simple verbal learning task (foreign language vocabulary) are sizeable, effects with more complex verbal materials (key-term definitions) are modest. Thus, one might also expect modest relearning potency effects for the learning of complex mathematical procedures. Additionally, the extent to which relearning potency effects generalize to non-practiced questions or tokens is unknown. Importantly, real-world evaluation of the learning of mathematical procedures typically involves transfer. That is, when learning how to solve a particular type of problem, students are given different problems to solve during practice versus on the final test. Even practice of mathematical procedures involves solving different problems on each practice trial, rather than repeating the same practice test questions as in verbal learning tasks that involve retrieval of a target from a cue (e.g., maison-???).

Finally, recent evidence from research investigating the impact of retrieval practice while solving problems also suggests that successive relearning may have a relatively minor impact in the present context (e.g., Leahy et al. 2015; van Gog et al. 2015). Consider outcomes from van Gog et al. (2015), who had students learn to solve problems that involved troubleshooting electrical circuits. Students studied worked examples and then had a chance either to solve similar problems (i.e., a testing group as in the current research) or to study the solutions to those problems. Across four experiments, final performance was typically not better when students solved problems than when they studied problems. Testing may have been relatively inert because of a mismatch between the problems that are tested and the different versions (or tokens) of each problem that comprise the criterion test (as in the present research). In such cases, the testing itself may not help students to fully understand the problem schema and hence any performance gains are limited to the specific problems that were practiced. Note, however, that this prior research on testing and problem solving did not involve successive relearning (i.e., going until the problems were correctly solved, and doing so during multiple sessions), so whether testing will be relatively inert when used to successively relearn to solve problems is unknown.

In sum, no prior research has directly investigated relearning potency in the learning of mathematical procedures. Outcomes from indirectly relevant literature are somewhat mixed, and no evidence exists concerning the effects of relearning potency when practice and final test questions are not identical. Thus, the extent to which relearning potency effects generalize to the learning of mathematical procedures is an open question.

Overview of Current Research

In three experiments, we examined the extent to which the documented potency of successive relearning extends to the learning of mathematical procedures. During initial learning, undergraduates studied an instructional text explaining how to solve four interrelated types of probability problems (independent or dependent events in which event order was relevant or irrelevant). During the practice phase, students were presented with practice problems until they correctly solved three problems of each type. The key manipulation concerned when these correct problem solutions took place. In the successive relearning group, students engaged in practice until one problem of each type was correctly solved in each of three different practice sessions. In the single-session group, students engaged in practice until three problems of each type were correctly solved in a single practice session. Both groups completed a final test involving novel problems 1 week after the end of practice.Footnote 1

The primary outcome concerns performance on the final test. Our a priori prediction was that a relearning potency effect would obtain, such that final test performance would be greater in the successive relearning group than in the single-session group. The open question concerned the magnitude of the effect—would the effect be sufficiently strong to be of practical relevance? Estimating relearning potency effects is important for practical purposes, because successive relearning is logistically more difficult for students to implement than single-session learning. In particular, successive relearning places greater demands on students for effective time management, organization, and planning of practice sessions. Additionally, achieving a desired level of mastery will typically require more practice trials when distributed across versus within session, due to a greater degree of forgetting between sessions versus between trials all contained within a single session. Is the relearning potency effect sufficient to warrant these additional costs?

Experiment 1

Methods

Participants and Design

Participants were randomly assigned to one of two groups, defined by the schedule of practice (successive relearning or single session). The targeted sample size was 102, based on an a priori power analysis conducted using G*Power 3.1.9.2 (Faul et al. 2007) for one-tailed independent-samples planned comparisons with power set at .80, α = .05, and d = 0.50; we oversampled to allow for some attrition. The sample included 115 undergraduates who participated for course credit (mean age = 19 years, 75% female, 47% freshmen, and mean self-reported college GPA = 3.42, based on the subset of 64 participants who provided demographic information).

Materials

The materials used here were modified and expanded versions of the material set used by Foster et al. (2018). The pretest included 10 of the 13 pretest questions used by Foster et al. (2018), originally developed by Groβe and Renkl 2007); we excluded one item with ceiling-level performance and two items with floor-level performance in Foster et al. (2018). The pretest questions covered a broad range of probability principles and thus estimated general knowledge of probability.

The instructional text (1357 words) introduced four specific types of probability problem. We chose to use four types of problem to ensure variability in performance and to increase the generalizability of any outcomes. Each problem involved the probability of two events in which the order of the two events either did or did not matter and that had either independent or dependent probabilities. A sample problem of each type is shown in Table 1. The text explained each type of problem, described the procedure used to solve each type of problem, and stepped through examples of each problem type. The text concluded by notifying participants that on each trial during the practice phase, they would first need to decide which type of problem each practice item involved and then solve the problem.

Table 1 Sample problems from materials used in Experiments 1–3
Full size table

Materials for the practice phase included 68 practice problems (17 isomorphic problems for each of the four types). These problems were divided into three subsets, with 36 problems (9 of each type) for practice during the initial learning session, 20 problems (5 of each type) for practice in the first relearning session, and 12 problems (3 of each type) for practice in the second relearning session. Differential allocation of practice problems across sessions was based on the expectation that the number of practice trials needed to achieve criterion would decrease across sessions.

Materials for the final test included an additional 12 isomorphic problems (3 of each type). Practice and final test problems were isomorphic in that all problems involved the same structures (probability of two events in which the order of the two events either did or did not matter and that had either independent or dependent probabilities, depending on problem type) but differed in their surface features (for examples, the materials are available at https://osf.io/uz2vf).

Procedure

During Session 1, all participants first completed the pretest. The ten questions were presented one at a time in a fixed order. Participants were given scratch paper and a calculator to use during problem solving. Participants were given up to 8 min to complete the pretest.

After completing the pretest (or after time expired), all participants were then told that they would next study a text that would explain four types of probability problems and how to solve each type. They were informed that after studying the text, they would be asked to solve practice problems until they reached a pre-specified level of accuracy (although they were not told at this point specifically what their target accuracy would be) and thus were encouraged to study the text carefully to help them perform well during practice. Participants were also told that the text would remain on the screen for a minimum of 6 min but that they could choose to continue studying for additional time if needed. Participants then advanced to a screen with a scrolling text field containing the instructional text. At the end of 6 min, a “done studying” button appeared on the screen that participants could click when ready to advance to the practice phase, along with a text field informing participants that they could continue to study if they wanted.

When participants indicated they were done studying, they advanced to an instruction screen that explained the practice task. They were told that they would first be asked to identify what type of problem it was and then to solve the problem. Participants were provided with scratch paper and a calculator and told that they could use these during the solution phase. Participants were also told to enter responses as a decimal, up to four decimal places, without rounding. At this point, they were also given group-specific instructions about how many problems of each type they would need to correctly answer (one for the successive-relearning group or three for the single-session learning group). They were also told that to receive credit, they would need to answer both parts of the question correctly (i.e., correct identification and then correct solution).

On each practice trial, a problem was presented at the top of the screen along with the prompt “What type of problem is described in this scenario?” and four multiple-choice alternatives (irrelevant-order independent events, irrelevant-order dependent events, relevant-order independent events, relevant-order dependent events). The order of response options was randomized anew on each trial, and participants clicked a button next to a response to indicate their choice. The problem scenario remained on the screen but the multiple-choice question was replaced with a feedback message, either “Correct!” or “Incorrect. This problem type is [correct answer].” Feedback was self-paced, and participants clicked a button when they were ready to solve the problem. On the next screen, the problem scenario remained at the top of the screen, along with a text field in which participants entered their solution, a reminder to enter their response as a decimal up to four places without rounding, and a button to click when they were ready to submit their answer. After submitting an answer, the problem scenario remained on the screen along with a feedback message, either “Correct!” or “Incorrect. The correct formula and solution for this problem is [correct formula and solution].” Feedback was self-paced, and participants clicked a button when they were ready to advance to the next problem.

Concerning the order in which problems were presented during practice, one of the nine problems for each type was assigned to each of nine mini-blocks, with assignment of problem to mini-block randomized anew for each participant. The order of the four problems (one of each type) within each mini-block was also then randomized anew. Note that this procedure for ordering problems involved interleaving the different types of problem across practice; blocking functionally would have involved massed practice and would increase the chances that participants retrieved the same solution from short-term memory, which would have increased the chances of floor-level performance on the delayed criterion test. On each trial, the computer tracked whether both parts of the question had been answered correctly. Once a participant reached their assigned criterion level for a given problem type, all other problems of that type were removed from the remaining mini-blocks. In the single-session group, the three correct responses did not need to be on consecutive trials. If a participant did not reach their assigned criterion level by the ninth mini-block, practice problems were repeated starting over with the first mini-block. All participants had up to 55 min to complete Session 1. The practice phase ended once a participant reached their assigned criterion or after time expired.

Participants who reached criterion were then asked to make category learning judgments (CLJs). They were shown the names of the four problem types one at a time in random order; for each one, they were asked to indicate their confidence that they would be able to correctly answer questions about that problem type in 1 week, using a slider on a continuous scale with end points labeled “0% confident” and “100% confident.” Participants were then asked to provide basic demographic information.

To equate the expectation of completing four sessions, all participants in both groups were asked to return for three more sessions, each separated by 1 week. Participants in the single-session learning group completed the final test during Session 2 and then completed unrelated tasks (not reported here) during Sessions 3 and 4. Participants in the successive relearning group engaged in relearning during Sessions 2 and 3 and then completed the final test in Session 4. Each relearning session began with practice task instructions similar to those provided in Session 1, notifying participants that they would again be presented with practice problems of each type until they correctly answered one problem for that type. The procedure for practice trials during relearning was the same as in Session 1, except that the practice list involved five mini-blocks of problems in the first relearning session and three mini-blocks in the second relearning session.

The procedure for the final test was the same for both groups. Participants were given scratch paper and a calculator. Final test problems were presented one at a time, with order randomized anew for each participant. The final test was self-paced with no time limit. The procedure for administering each question was the same as during practice trials, except that no feedback was provided.

Results and Discussion

Data for four participants were excluded from analyses due to evidence of non-compliance with task instructions during the initial learning session (number of practice trials more than 3 SDs above group mean coupled with mean response times less than 5 s, suggesting they were rapidly clicking through trials without attempting to answer the questions). Twelve other participants did not return for the final test session. Outcomes reported below are based on data from 99 participants who completed the final test session (n = 49 in the relearning group, n = 50 in the single-session group). Pretest performance was similar for the relearning group (M = 35%, SE = 4) and the single-session group (M = 31%, SE = 3), t(97) = 0.82. On the final test, Cronbach’s α was .65 for the problem-type identification portion of the final test questions and .84 for the problem solution portion of the final test questions.

For all three experiments, a priori directional predictions were evaluated via planned comparisons with one-tail tests (Greenland et al. 2016; Judd and McClelland 1989; Rosenthal and Rosnow 1985; Tabachnik and Fidell 2001). Cohen’s d values were computed using pooled standard deviations (Cortina and Nouri 2000).

Criterion Level During Learning Sessions

As an important preface, the method was designed to equate the total criterion level achieved in each of the two groups (i.e., each group achieving three correct practice trials per problem type), with the key difference between groups concerning the schedule in which those correct trials were achieved (either one in each of three sessions in the successive relearning group or three in one session for the single-session group). However, two aspects of the methods unintentionally led to the successive relearning group achieving a higher functional criterion level during practice (to foreshadow, we modified methods to sidestep this limitation in Experiments 2 and 3). First, a participant needed to answer both parts of a question correctly (i.e., correct problem type identification and correct problem solution) for that trial to be counted as correct. However, participants often responded correctly on one but not both parts of a question. As a result, the functional criterion level achieved for the two parts of the questions was often higher than the nominal criterion. Second, participants had up to 55 min to complete the initial learning session, but a disproportionate number of participants in the single-session group timed out before achieving the nominal criterion of three trials in which both parts of the question were answered correctly (60% in the single-session group versus 22% in the relearning group who timed out in Session 1).Footnote 2 The unintended consequence of these two factors was that the functional criterion level achieved for each part of the questions was lower in the single-session group than in the relearning group (see Table 2), although both groups achieved at least three correct responses on average for each part of the final test questions.

Table 2 Functional criterion levels achieved in each group for each portion of the practice problems in Experiments 1–3
Full size table

These differences in functional criterion would be problematic if a marked advantage obtained for successive relearning over single-session learning on the primary outcomes of interest. However, despite the unlevel playing field, successive relearning did not emerge as the decisive winner for durable and efficient learning, as described further below. Thus, outcomes of Experiment 1 are still informative.

Relearning Potency Effects on Final Test Performance

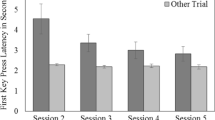
In Fig. 1, performance both for correctly identifying problems (left side of each panel) and for correctly solving each problem (right side of each panel) are presented. Note that the guessing rate for correctly identifying each problem is well above chance (i.e., guessing rate of 25% for the four-alternative multiple-choice questions), and most important, the guessing rate for correctly solving problems would be close to zero (and hence guessing would not influence problem solution performance, the focal outcome measure in the present research). As is apparent from inspection of Fig. 1, the benefits of relearning for final test performance were modest at best. The relearning group did not outperform the single-session group on the problem-type identification portion of each final test question, t(97) = 1.00, p = .319, d = − 0.20 (95% CI − 0.60, 0.19). Furthermore, the advantage of relearning over the single-session group for the problem solution portion of the final test questions was relatively small, t(97) = 1.84, p = .035, d = 0.37 (95% CI − 0.03, 0.77). Thus, the sizeable effects of relearning over single practice session demonstrated with simpler verbal materials were attenuated in the mathematics domain examined here.

Fig. 1
figure 1

Performance on the final test for each practice group in Experiments 1–3. Each question on the final test included two parts: (a) identification of which type of problem was described in the problem scenario, followed by (b) computation of the solution to the problem. Error bars report standard errors of the mean

Full size image

Secondary Outcomes

The mean number of practice trials completed per problem type in each practice session is reported in Table 3. Four values more than 3 SDs above the group mean were excluded from analyses, including for two participants (one in each group) for trials in the initial learning session and for two participants in the relearning group for trials in the first relearning session. Overall efficiency was lower in the relearning group than in the single-session group. The bottom row of Table 3 reports means for the total number of practice trials completed per problem type across learning sessions in the two groups. The total number of trials required to reach criterion was greater in the relearning group than in the single-session group, t(92) = 4.04, p < .001, d = 0.83 (95% CI 0.42, 1.26).

Table 3 Mean number of practice trials completed per problem type in each group for each session in Experiments 1–3
Full size table

Although not of primary interest for present purposes, we report outcomes for the category learning judgments (CLJs) for interested readers. CLJ magnitude was greater in the single-session group (M = 76%, SE = 4) than in the relearning group (M = 68%, SE = 3), t(56) = 1.68, p = .098, d = 0.46 (95% CI − 0.07, 0.97).

Experiment 2

The purpose of Experiment 2 was to provide a close replication of Experiment 1, with two methodological modifications (described below) intended to more closely match the functional criterion level achieved in the two practice groups.

Methods

Participants and Design

The targeted sample size was 102, based on the same a priori power analysis as in Experiment 1. The sample included 90 undergraduates who participated for course credit (mean age = 20 years, 81% female, 38% freshmen, and mean self-reported college GPA = 3.29, based on the subset of 79 participants who provided demographic information).Footnote 3 Participants were randomly assigned to one of two groups, defined by the schedule of practice (relearning or single session).

Materials and Procedure

The materials and procedure for Experiment 2 were the same as in Experiment 1, except for two key changes. First, participants had up to 85 min to complete the initial learning session. Extending session length reduced the number of participants who timed out before reaching criterion (14% in the single-session group and 3% in the relearning group). Second, during all learning sessions, the computer only tracked whether the problem solution portion of each question was answered correctly to determine when participants had reached their assigned criterion level. In the task instructions, participants were simply told that they would continue to be presented with practice problems until they correctly answered one or three questions (depending on group assignment) for each problem type, but they were not told that scoring would be based only on the second part of each question.

Results and Discussion

Data for one participant were excluded from analyses due to evidence of non-compliance with task instructions during the initial learning session (number of practice trials more than 3 SDs above group mean coupled with mean response times less than 5 s). Eleven other participants did not return for the final test session, and two additional participants in the relearning group missed one relearning session. Outcomes reported below are based on data from the remaining 76 participants (n = 34 in the relearning group, n = 42 in the single-session group). Pretest performance was similar for the relearning group (M = 29%, SE = 4) and the single-session group (M = 33%, SE = 4), t(74) = 0.83. Cronbach’s α was .76 for the problem-type identification portion of the final test questions and .81 for the problem solution portion of the final test questions.

Criterion Level During Learning Sessions

As intended, the methodological changes in Experiment 2 yielded a closer match of the functional criterion level achieved in each practice group (see Table 2). To revisit, nominal criterion in Experiment 2 was based only on whether the problem solution portion of each question was answered correctly. The two groups did not differ in the actual criterion level achieved across sessions for the problem solution portion of the practice questions, t(74) = 0.45; the trend for the problem-type identification portion of the practice questions was not significant, t(74) = 1.20, p = .233.

Relearning Potency Effects on Final Test Performance

As is apparent from inspection of Fig. 1, the benefits of relearning for final test performance were once again modest. The relearning group and the single-session group performed similarly on the problem-type identification portion of each final test question, t(74) = 0.42, d = 0.10 (95% CI − 0.35, 0.55). Furthermore, the advantage of relearning over the single-session group for the problem solution portion of the final test questions was relatively small, t(74) = 1.22, p = .113, d = 0.28 (95% CI − 0.17, 0.73).

Secondary Outcomes

The mean number of practice trials completed per problem type in each practice session is reported in Table 3. Six values more than 3 SDs above the group mean were excluded from analyses, including for four participants (two in each group) for trials in the initial learning session, for one participant in the relearning group for trials in the first relearning session, and for one participant in the relearning group for trials in the second relearning session. The bottom row of Table 3 reports means for the total number of practice trials completed per problem type across learning sessions in the two groups. Overall efficiency in the relearning group and the single-session group was similar, t(69) = 0.19.

CLJ magnitude was similar for the single-session group (M = 67%, SE = 2) and the relearning group (M = 67%, SE = 3), t(67) = 0.23.

Experiment 3

Experiment 3 was conducted to replicate key findings from Experiments 1 and 2 and to explore the kinds of error that participants make while solving problems, which may provide insight into why students struggled to master these probability problems. In particular, during the problem solution phase of each trial in Experiments 1–2, participants were provided with scratch paper and a calculator that they could use to write out and solve equations. In Experiment 3, participants were not given paper or calculator and instead entered information into an equation template on the computer screen. They then clicked a button when they were ready for the computer to calculate the answer to the equation they set up (see the screenshot in Fig. 2). This modification was intended to serve two purposes. First, when participants solved problems in Experiments 1–2, at least some of their errors may have been due to mathematical errors (e.g., multiplying fractions incorrectly) rather than reflecting errors in setting up the equations properly. The modified response format in Experiment 3 circumvents such errors by only requiring participants to set up the equation. Second, this modification permitted exploratory analyses of the kinds of error that participants make during the problem solution phase of each trial, which we describe further and report in the “Exploratory Analysis of Error” section that follows Experiment 3.

Fig. 2
figure 2

Screenshot of the problem solution task in Experiment 2

Full size image

Methods

Participants and Design

The targeted sample size was 204, based on an a priori power analysis for detecting group effects on final test performance. For performance on the problem solution portion of final test trials, the pooled estimate across Experiments 1–2 is d = 0.35; based on this effect size estimate, the target n is 204 for a one-tailed independent-samples planned comparison with power set at .80 and α = .05. We oversampled to allow for some attrition. The sample included 226 undergraduates who participated for course credit (mean age = 20 years, 80% female, 51% freshmen, and mean self-reported college GPA = 3.28, based on the subset of 224 participants who provided demographic information). Participants were randomly assigned to one of two groups, defined by the schedule of practice (relearning or single session).

Materials and Procedure

The materials and procedure for Experiment 3 were the same as in Experiment 2, except for two key changes. First, we revised the instructional text that participants studied at the beginning of Session 1 to align with the modified task structure that they would be completing on practice and final test trials. The major revisions involved (a) additional explanation of how the denominator values depend on whether the events in a problem are dependent or independent, (b) additional explanation that all of the problems in this study involve two events and thus equations for irrelevant-order problems are multiplied by two, and (c) task instructions explaining that during problem solving, they would be asked to fill in numerator and denominator values into the equation and then indicate if it needed to be multiplied by two. We also made other minor revisions to the text to improve the clarity of the prose. Second, on the problem solution phase of all trials during practice and during the final test, students were prompted to fill in the appropriate equation values and indicate the appropriate multiplier for that problem, as depicted in Fig. 2.

Results and Discussion

Only one participant timed out before reaching criterion in Session 1. Twenty-seven participants did not return for the final test session, and two additional participants in the relearning group missed one relearning session. Outcomes reported below are based on data from the remaining 197 participants (n = 97 in the relearning group, n = 100 in the single-session group). Pretest performance was similar for the relearning group (M = 29%, SE = 2) and the single-session group (M = 29%, SE = 2), t(195) = 0.06. Cronbach’s α was .60 for the problem-type identification portion of the final test questions and .59 for the problem solution portion of the final test questions.

Criterion Level During Learning Sessions

Outcomes are reported in Table 2. To revisit, nominal criterion was based only on whether the problem solution portion of each question was answered correctly. The two groups did not differ in the actual criterion level achieved across sessions for the problem solution portion of the practice questions, t(195) = 1.33; the trend favoring the relearning group for the problem-type identification portion of the practice questions was significant, t(195) = 3.04, p = .003.

Relearning Potency Effects on Final Test Performance

As is apparent from inspection of Fig. 1, the benefits of relearning for final test performance were once again modest at best. The relearning group and the single-session group performed similarly on the problem-type identification portion of each final test question, t(195) = 0.89, d = 0.13 (95% CI − 0.15, 0.41). Furthermore, the advantage of relearning over the single-session group for the problem solution portion of the final test questions was small, t(195) = 1.71, p = .045, d = 0.24 (95% CI − 0.04, 0.52).

Secondary Outcomes

The mean number of practice trials completed per problem type in each practice session is reported in Table 3. Five values more than 3 SDs above the group mean were excluded from analyses, including for two participants in the single-session group for trials in the initial learning session, for two participants in the relearning group for trials in the first relearning session, and for one participant in the relearning group for trials in the second relearning session. The bottom row of Table 3 reports means for the total number of practice trials completed per problem type across learning sessions in the two groups. Overall efficiency in the relearning group and the single-session group was similar, t(190) = 0.73.

CLJ magnitude was similar for the single-session group (M = 57%, SE = 2) and the relearning group (M = 61%, SE = 2), t(194) = 1.17.

Exploratory Analysis of Errors

The current task involved learning and retaining basic solution rules for a given type of problem and then correctly applying those rules to particular token problems of that type. Errors may have arisen because learners did not use the correct solution rules when attempting to solve a token problem of a given type (because they either misunderstood or did not remember the relevant rules). Alternatively, errors may have arisen when learners used the correct solution rules but failed to extract the relevant information from the word problem and/or made calculation errors. To what extent were the errors during practice because learners had not yet mastered the solution rules (versus other sources of error)?

The modified response format in Experiment 3 afforded diagnosis of errors that arose because learners were not using the correct solution rules. To explain the logic of this analysis, we briefly revisit relevant aspects of the methodology. First, the instructional text that participants studied at the outset of Session 1 stated that all of the problems in this study involved two events and accordingly explained why equations for irrelevant-order problems are multiplied by two (and why equations for relevant-order problems are not). Likewise, the text also explained why the two denominator values in the equation would be the same for independent events (due to replacement, versus different denominator values for dependent events not involving replacement). During practice, each problem solution phase was immediately preceded by problem identification with correct-answer feedback; thus, participants always knew the correct problem type when setting up the formula during the problem solution phase. Trials in which they did not correctly apply one or both of the corresponding rules would indicate they had not yet adequately learned the rules for each problem type. For each participant in each practice session, we computed (a) the total number of practice trials in which their answer during the problem solution phase was incorrect, (b) the number of these trials in which they misapplied the multiply-by-two rule, including trials in which they selected not to multiply for an irrelevant-order problem or selected to multiply by two for a relevant-order problem, and (c) the number of trials in which they misapplied the denominator rule, including trials in which they entered different denominator values for an independent-event problem or entered the same denominator values for a dependent-event problem (note for this third variable, we only examined whether the entered values were same or different, regardless of whether they were the correct values). As is evident from inspection of Table 4, a non-trivial number of incorrect trials in each session and in both groups involved these kinds of conceptual errors. We consider the implications of these errors in “General Discussion.”

Table 4 Total number of trials involving an incorrect answer during the problem solution phase, and the number of those trials involving misapplication of a corresponding solution rule for a given problem type in Experiment 3
Full size table

General Discussion

Prior research has consistently demonstrated the potency of successive relearning, which has produced impressive levels of retention for different kinds of verbal learning tasks in the laboratory (e.g., Bahrick 1979; Rawson and Dunlosky 2011; Rawson et al. 2018) and in authentic educational settings (Rawson et al. 2013). In embarking on the present research, we expected that these practically relevant outcomes would likely generalize to learning mathematical procedures and would boost students’ learning and retention of how to correctly solve probability problems. But, consistent with the adage that all good things must come to an end, the current research revealed an important empirical boundary condition to the potency of successive relearning. Namely, in contrast to the sizeable relearning potency effects demonstrated in prior research, the advantage of successive relearning over single-session learning in the current research was modest at best. To provide the most precise estimate of the magnitude of this effect, Table 5 reports the outcomes of an internal meta-analysis (Braver et al. 2014) for performance on the problem solution portion of the final test questions across Experiments 1, 2, and 3, which is the primary learning outcome of interest.Footnote 4 The combined estimate indicates a significant but small advantage of successive relearning over single-session learning (pooled d = 0.28, 95% CI = 0.08, 0.49).

Table 5 Outcomes of internal meta-analysis for problem solution performance on final test
Full size table

Why was the relearning potency effect for mathematical procedures so weak? By definition, successive relearning involves the re-learning of information that has already been learned to a designated level of mastery during a prior study session (Bahrick 1979). In research on successive relearning, mastery during a given session is typically operationalized as correct responses on practice test questions. However, a correct response on one or more practice questions may not always be a valid indicator that the target information has been sufficiently well learned or mastered. For the successive relearning groups in the current study, practice for a given procedure terminated after one correct response. Thus, a possibility is that students had not fully learned the procedures prior to their first correct response, and hence practice may have been terminated before mastery was achieved during the initial learning session. If so, practice during the relearning sessions may have reflected a continuation of initial learning rather than relearning per se.

To evaluate this possibility, we conducted a series of exploratory analyses. To the extent that the first correct response during initial practice indicates that a target procedure has been learned, responses to subsequent practice questions for that procedure in the same session should have a high probability of also being correct. To evaluate this assumption, we analyzed data for participants in the single-session groups, who continued to answer practice questions for each procedure after their first correct responses for each problem type. As reported in Table 6, after the first correct response for a given problem type, participants correctly answered the next question for that problem type with a likelihood of about 43–55%. Even after the second correct response for a given problem type, participants did not consistently answer the next question correctly (50–59%). Parallel outcomes for the successive relearning groups are reported in the bottom half of Table 6. These outcomes suggest that the first correct response for a given problem type is likely not indicative of the student having fully learned that procedure. If so, then terminating practice after one correct response for learners in the successive relearning group may have meant that practice was stopped before functional mastery was achieved. As a result, “relearning” sessions may have involved a continuation of initial acquisition rather than relearning per se.

Table 6 Mean performance on the problem solution portion of practice test questions for the trial after a first correct response and after a second correct response for a given problem type
Full size table

These analyses also provide insight into why relearning potency effects were less robust for learning mathematical procedures than for the simple verbal material (foreign language vocabulary) used in prior research. In particular, the same nominal criterion of one correct response likely reflects different levels of functional mastery for these two kinds of target content. To provide a point of comparison with the outcomes reported in Table 6, we reanalyzed data from two experiments reported in Vaughn et al. (2016) involving foreign language learning. After the first correct response during practice for a given item, participants were 89% likely to answer correctly on the next trial for that item.

Not only was the relearning potency effect weaker for math versus simple verbal learning, but also the absolute level of performance achieved in the relearning group in the present experiments was not particularly impressive for practical purposes. In prior studies, we based prescriptive conclusions not only on the relative advantage of successive relearning over single-session learning but also on the arguably impressive levels of absolute retention achieved. For example, after two relearning sessions of Lithuanian-English translation equivalents, college students could recall about 80% of them 1 week later (Rawson et al. 2018, Experiment 2, Lag 47 group). Students then relearned any items that had not been correctly recalled, and 1 month later, their retention was about 70% correct recall. The relearning potency effects demonstrated in research using key-term definitions are weaker (Rawson and Dunlosky 2011, 2013); however, this weaker effect occurs not because the successive relearning group showed poor absolute levels of retention but instead because the single-session learning group had relatively good retention. These outcomes contrast the weak relearning potency effect in the present research, which arose because the absolute level of performance in the successive relearning group was relatively poor.

As noted above, one explanation for the poor retention in the present experiments is simply that when students correctly solved a given practice problem, it did not necessarily indicate that they had learned the corresponding mathematical procedure well. The exploratory analysis of conceptual errors in Experiment 3 (Table 4) suggests that students are struggling in part because they are not understanding the solution rules for a given type of problem and/or are not retaining those rules. Of course, students’ poor performance could result from both of these factors across problem types. These possibilities suggest different approaches to increasing the potency of successive relearning for improving students’ ability to learn, retain, and use mathematical procedures to solve probability problems (and more generally, other kinds of math problems in which different problem types require the application of different forms of equations). For instance, if students are struggling because they do not understand the rules, then prior to engaging in problem-solving practice, they may benefit from studying worked examples that highlight the relationship between relevant content in a problem and how the rule for that type of problem is applied (for a review of the literature on worked examples, see van Gog et al. 2019). Combining the use of worked examples with successive relearning could be instantiated in multiple ways, but one promising approach may be to use a fading approach to transition from full worked examples to problem-solving practice (for the benefits of using fading worked examples, see Foster et al. 2018; Renkl et al. 2002; Renkl et al. 2004). For instance, during the first practice trial for each problem type, a student would study a worked example. During the next trial for a problem of that type, only part of the example would be worked out, and the student would need to solve the remainder of the problem. If they answered incorrectly, they would need to study the entire worked example, but if they answered correctly, then less of the worked example would be provided during the next trial for that problem type, and so on. A challenge for future research will be to explore how best to combine these strategies—successive relearning with fading worked examples—to produce the highest levels of retention for solving math problems.

If students do understand the rules but are not retaining them, then successive relearning of the rules themselves may boost their retention, which in turn may improve problem-solving performance. In this case, in each study session, students would be prompted with a problem type and would need to retrieve the correct rule until they can correctly retrieve the rules. Of course, if some combination of the aforementioned factors is limiting students’ progress in this domain, an approach that involves combining these techniques may produce the largest gains (for discussion of combining techniques, see Miyatsu et al. 2019, Table 2). For instance, the rules could be successively relearned, and such learning could be interleaved with problem solving that is supported with worked examples when students incorrectly solve a problem. Discovering which techniques—or combinations of them—promote the greatest boost to students’ problem solving in this domain is an important challenge for future research.

In summary, the present research is the first to evaluate the degree to which successive relearning across sessions boosts performance (as compared with learning within a single session) for solving mathematics problems. In contrast to prior research on successive relearning that involved simple verbal materials, the benefits of successive relearning over single-session learning were small, and the overall retention after practice did not reach a practical level of significance. The current work provides an important foundation for future research on how to improve successive learning for mathematical procedures (either alone or in combination with other strategies) to achieve high levels of retention that have practical relevance to student achievement.