Abstract
Nowadays, Web services allow interoperability among distributed software applications deployed on different platforms and architectures which in effect plays a major role in electronic businesses. Web services allow organizations to carry out certain business activities automatically and in a distributed fashion. However, in some circumstances, a single service is not able to perform a certain task and it becomes imperative to compose two or more services in order to complete it. Thus, a key research challenge in this field is the problem of automatic service composition. Several approaches exist that tackle the problem of automatic service composition, however, the task of generating provably correct Web service compositions still remains a challenging and complex task. In this paper, we develop a formal framework for modeling Web service compositions based on Supervisory Control Theory (SCT) of discrete-event systems. We model services that exchange messages and exhibit nondeterministic behaviours. The objective is to synthesize a supervisor which interacts with a given set of Web services through messages to guarantee that a given specification is satisfied. A key novelty of this work is the application of control theory to service-oriented computing and the incorporation of run-time input into the supervisor generation process. First, we describe a novel supervisory control framework for automated composition of Web services. The framework employs Labelled Transition Systems equipped with guards and data variables to model Web services and provides a technique to synthesize a controller. We model the interactions of services asynchronously and we use the guards and data variables to allow us to express certain preconditions which are then propagated from the system requirements through the overall composite service. Second, we develop a set of algorithms to generate a controller satisfying a given functional requirement also specified as a Labelled Transition System equipped with guards and data variables. Besides the standard disabling and enabling of events, the generated controller in our framework has the ability to enforce certain events based on run-time information to drive the system towards its goal. In addition, the controller is able to impose restrictions on the kind of data that can be sent or received by services. This includes the automatic generation of stronger guards or preconditions which impose restrictions on which path to take during execution. Lastly, we state a theorem capturing the existence of a controller and provide a proof to demonstrate the correctness of the proposed approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Today, we are undergoing a major paradigm shift in software development as a result of the emergence of the World Wide Web. This has brought about the Service-Oriented Computing (SOC) paradigm which aims to encapsulate software components and expose them as services through network-accessible, platform and language independent interfaces. The most widely adopted software design pattern in SOC for realizing the SOC model into an architecture is known as Service-Oriented Architecture (SOA) (Erl 2004), which in essence is a logical way of organizing and developing distributed software systems by providing services to end-user applications or to others, and whose interface descriptions can be published and discovered. The most widely used implementation of SOA are Web services (Papazoglou et al. 2007).
The vision underpinning Web services can be fully achieved if we envision a collaboration between a community of numerous service providers and service consumers who interact in order to achieve certain business goals. Thus, one of the key functionalities of Web services is service composition, which seeks to create, select and integrate pre-existing services to develop new value-added services and applications. Hence, it promotes the rapid development of software systems by reducing the cost and effort for developing new services from scratch. Furthermore, the output of a service composition (i.e., composite service) could serve as the input (atomic service) for further service compositions (re-usability). A typical motivating example of a Web service composition is given as follows. Consider a group of business clients who are going on a business trip and want to make a reservation for a flight ticket, a hotel room and a car for a particular destination and a period of time. There exist only an airline reservation Web service, a hotel reservation Web service and a car rental Web service separately. Clearly, we want to combine these Web services rather than implementing a new one.
Several approaches have been proposed that attempt to address the problem of automatic service composition and most of these techniques are motivated by the works in AI (Artificial intelligence) planning and cross-enterprise workflow techniques (Zou et al. 2014; Kazhamiakin et al. 2013; Bertoli et al. 2010; Klusch and Gerber 2005; Hatzi et al. 2015; Portchelvi and Venkatesan 2015; Rodríguez et al. 2016). However, the task of generating provably correct Web service compositions still remains a challenging and complex task.
In this paper, we develop the formal framework Supervisor Aware Service Composition Architecture (SASCA) for modeling Web service composition based on Supervisory Control Theory (SCT) of Discrete-Event Systems (DES). Discrete-Event Systems control theory is a branch of control theory that models behaviours as sequences of discrete events instead of continuous functions of time. The classical Ramadge-Wonham approach to the supervisory control problem (SCP) (Cassandras and Lafortune 2008; Wonham and Ramadge 1987; Ramadge and Wonham 1987), is defined as follows: given a plant \({\mathcal G}\) modeled in the form of a state-transition system which captures the behaviours of the process to be controlled according to some possible events, given a set of specifications \({\mathcal L}\) which describes the legal sequences of events of the plant, synthesize a supervisor \({\mathcal S}\) so that \({\mathcal S}\) restricts \({\mathcal G}\) in such a way that all its executions satisfy \({\mathcal L}\) and such that \({\mathcal S}\) is minimally restrictive. We believe that SCT of DES is a well suited technique for tackling the problem of automated service composition. In addition, existing tools and algorithms of DES can be adapted to address this problem. With respect to other service composition approaches, Supervisory Control Synthesis has several benefits which are as follows. It results in a correct-by-construction control synthesis, and the generated controller is minimally restrictive by preventing a system behaviour only if it violates the system requirements. It also relies on automata theory to provide a well-defined syntax and semantics for modeling systems which could be very useful for specifying services. In addition, DES provides various techniques (e.g., how to model system requirements) that can be used to model various business logics and requirements in a dynamic environment. Supervisory control theory (SCT) has been applied to software systems such as concurrency in multithreaded programs and component based software systems. Notable ones are the work by Dragert et al. (2008) and Auer et al. (2014) and the work by Wang et al. (2009) and Wang et al. (2010). Here we apply SCT to address the problem of Web service composition. To the best of our knowledge our work is the first of its kind to deal with the problem of Web services composition.
The approach we propose employs a variant of Labelled Transition Systems (LTSs) which is equipped with guards, and data variables to model a given set of Web services specified in WS-BPEL (Andrews et al. 2003). We refer to this variant LTS as a Service Labelled Transition System (SLTS) which we formally defined below (Definition 2). To this end, we provide an SCT modeling formalism based on SLTSs and then we describe a novel technique to synthesize a composition satisfying a given functional requirement (data and control flow) also specified as SLTS. That is, the problem of synthesizing a composition can be reduced to the problem of supervisor synthesis when the available services and a goal specification represent the plant and the legal language (desired behaviour), respectively, in DES. In this way, the problem of orchestrating data and control flow requirements can be achieved using the notion of controllability in DES where the supervisor enacts control by disabling and enabling certain actions in order to enforce the given goal. The inputs to the system are the set of Web services specified in WS-BPEL and the requirements also specified as SLTSs. Internally, we represent these Web services using SLTSs, Next, the proposed supervisory control framework based on SLTSs is applied to synthesize a controller that ensures that the given composition requirements are satisfied. A key novelty of this work is the application of control theory to service-oriented computing and the incorporation of run-time input into the supervisor generation process. The contributions that we make in this paper are as follows:
- (I)
We provide a novel supervisory control framework for automated composition of Web services, which uses Labelled Transition Systems augmented with guards and data variables to model a given set of Web service specifications in industrial standard languages like WS-BPEL. The framework models the interactions of services asynchronously and uses guards and data variables to express certain preconditions which are then propagated from the system requirements through the composite service. We provide insight into how to express and define functional requirements (data and control flow) for a composition, and we provide a formalism for the problem of automated composition based on controller synthesis.
- (II)
We develop a set of algorithms based on the formalism provided to generate a controller satisfying a given functional requirement also specified as SLTSs. Beyond the standard disabling and enabling of events, the generated controller in our framework has the ability to enforce certain events based on run-time information to drive the system towards its goal. In addition, the controller is able to impose restrictions on the kind of data or variables that can be sent or received by the services. This includes the automatic generation of stronger guards or conditions which impose restrictions on which path to take during execution.
- (III)
We demonstrate the correctness of our approach by stating a theorem on the existence of a controller and providing a proof for this theorem.
The rest of the paper is organized as follows. First, in Section 2, we provide a brief introduction to the standard supervisory control theory of DES and then, we will describe informally the problem of automated service composition by means of an illustrative example in the travel domain. In Section 3, we present the formal language and various definitions that will serve as the basis for our formalism. In Section 4, we develop the service composition framework based on the formalism provided in Section 3. We present the set of algorithms for composition synthesis in Section 5 and in Section 6, we provide proofs for our formalism. In Section 7 we discuss the relevant related work and in Section 8 we provide some concluding remarks and an overview of future work.
2 Background
2.1 Discrete-event systems
In this section, we give a brief overview of the supervisory control theory of DES (Cassandras and Lafortune 2008; Wonham and Ramadge 1987; Ramadge and Wonham 1987). We start with a brief summary of the notion of formal languages.
2.1.1 Preliminaries
We define Σ∗ as the set of all possible strings over some finite alphabetΣ, including the empty string 𝜖 of length zero. A language\(\mathcal {L}\) over Σ is any subset of Σ∗. In particular {𝜖}, Σ and Σ∗ are languages. Let s ∈Σ∗, a string t ∈Σ∗ is a prefix of s if s = tu for some u ∈Σ∗ (where tu is the concatenation of the strings t and u). The prefix-closure of a language \(\mathcal {L}\subseteq {\Sigma }^{*}\), denoted by \(\overline {\mathcal {L}}\) consists of all the prefixes of all strings in \(\mathcal {L}\), i.e., \(\overline {\mathcal {L}} = \{s\in {\Sigma }^{*}~|~\exists t\in {\Sigma }^{*}, st \in \mathcal {L}\}\). A language \(\mathcal {L}\) is said to be prefixed-closed if \(\mathcal {L}= \overline {\mathcal {L}}\).
A DES is usually represented by a finite automaton defined as G = (Σ,Q,q0,δ,Qm), where Q is a finite set of states, q0 ∈ Q is the initial state, δ is a partial function called the transition function” such that δ : Σ × Q → Q, and Qm ⊆ Q is the set of marked state. In DES Σ is the finite alphabet of events. We extend the transition function δ to strings (words) by defining it inductively as follows: δ : Σ∗× Q → Q is such that δ(𝜖,q) = q, δ(sσ,q) = δ(σ,δ(s,q)), with σ ∈Σ and s ∈Σ∗. The language generated by G is \(\mathcal {L}(G)=\{s \in {\Sigma }^{*}~|~ \delta (s,q_{0}) \text {~is defined}\}\). This represents all the possible event sequences that some process G can go through (i.e., the sequences need not terminate at marked states). On the other hand, the marked language of G is \(\mathcal {L}_{m}(G)=\{s \in \mathcal {L}(G)~ |~ \delta (s,q_{0}) \in Q_{m}\}\). The marked language describes the subset of event sequences that represents the completion of some tasks. For more details, we can refer the text by Cassandras and Lafortune (2008).
2.1.2 Supervisory control theory of DES
Although there are many variations and embellishments of SCT, the standard Ramadge–Wonham Theory (Wonham and Ramadge 1987; Ramadge and Wonham 1987) considers a DES modeled at an untimed level of abstraction which relies on feedback control to restrict the system so as to achieve a given set of specifications. In this framework, the process (system) to be modeled which is characterized by sequences of actions or events is assumed to be behaving undesirably in some way; such a process called the plant \(\mathcal {G}\) is modeled with a DES as defined above (Section 2.1.1). Events are represented by the transitions in \(\mathcal {G}\), and the language generated \(\mathcal {L}(\mathcal {G})\) represents the behaviour of \(\mathcal {G}\). That is, the language \(\mathcal {L}(\mathcal {G})\) contains strings that may be unacceptable because they violate some rules or nonblocking conditions that we wish to impose on the system. The undesirable behaviour could be sequences of transitions in \(\mathcal {G}\) that result in deadlock or livelock, or inadmissible states. To this end, the behaviour of \(\mathcal {G}\) is not satisfactory and must be controlled by restricting the behaviour to a subset of \(\mathcal {L}(\mathcal {G})\). A supervisor \(\mathcal {S}\) is introduced in order to restrict the behaviour of \(\mathcal {G}\).
In the basic model, the event set Σ of \(\mathcal {G}\) is partitioned into two disjoint sets, namely, the set of controllable eventsΣc, meaning an event in Σ that can be disabled and the set of uncontrollable eventsΣuc, meaning an event in Σ that cannot or should not be prevented from occurring. According to Cassandras and Lafortune (2008), an event might be modeled as uncontrollable because it is inherently unpreventable or it models a change of sensor readings not due to a command; it cannot be prevented due to hardware or actuation limitations; or it is modeled as uncontrollable by choice, as an example when the event has high priority and thus should not be disabled, or when the event represents the tick of a clock. Ideally, a supervisor is given by a function \(S : \mathcal {L}(\mathcal {G})\rightarrow 2^{\Sigma }\) that maps the sequence of generated events to a subset of controllable events to be disabled. The synchronous product of \(\mathcal {S}\) and \(\mathcal {G}\) is the marked language denoted by \(\mathcal {L}_{M}(\mathcal {S}/ \mathcal {G})\) that represents the behaviour of the plant \(\mathcal {G}\) under supervision of \(\mathcal {S}\). The work by Wonham and Ramadge (1987) states the necessary and sufficient conditions for the existence of a supervisor. In this framework, a specification given as a finite automaton provides the desired behaviour of the plant, and is called the legal language\(\mathcal {E}\). A plant \(\mathcal {G}\) is called controllable with respect to a specification \(\mathcal {E}\) if for any string s from the prefix closure of \(\mathcal {E}\), there are no uncontrollable events e that could be generated by \(\mathcal {G}\) at the state reached by s, such that se would not be in the prefix closure of \(\mathcal {E}\). That is, if something cannot be prevented, it must be legal. The Supervisory Control Architecture addressed by this work assumes that the plant spontaneously generates all events and the role of the supervisor is to enable/disable controllable events (since \(\mathcal {S}\) is not allowed to ever disable a feasible uncontrollable event). The supervisor \(\mathcal {S}\) guarantees not only deadlock-freedom (nonblocking) and adherence to the specification \(\mathcal {E}\), but also minimal restrictiveness. These formal guarantees set DES apart from approaches like AI planning (Zou et al. 2014; Kazhamiakin et al. 2013).
2.2 Service composition problem
In this section, we present the composition problem by means of an example. The example described here is a modified version of a well-known example for illustrating Web service composition in the business domain. As mentioned above, the service composition problem comes into play when a request to a service (component service) is not satisfied by a single service and then multiple services are identified and constructed into a new service (composite service) to satisfy the request or the desired functionality through orchestrating the services involved.
Let us consider a Travel Reservation and Purchase System (TRPS) that offers customers travel packages by allowing customers to make a reservation for a specified airline and to make payment in order to reserve the flight. All interactions are managed by Web services. The objective of TRPS can be attained by composing an Airline Service, a Bank Service, a Hotel Service and an On-line Customer Interface Service. We assume that these services are represented in WS-BPEL. The main challenge is how to compose these services so that the user can directly ask the combined service to reserve and purchase a ticket satisfying some given system requirements. In the following, we will provide an informal description of these services.
Airline Service: The Flight service is designed to receive requests for booking a specified flight for a given date and location. It checks an internal database for flight availability, and sends an offer with a cost and a flight schedule in response to the client’s request. The client can either accept or refuse the offer; if the client decides to accept the offer, the TRPS will book the flight and provide additional information such as an electronic ticket.
Bank Service: The Bank service is designed to receive a request to check that a credit card, debit card or money order can be used to make a payment and provides an option for its clients to check their current balance or withdraw from the account to make a payment for a purchase. The transaction may fail if the card provided is not valid or if there are not sufficient funds in the client’s accounts.
Hotel Service: The Hotel service accepts requests for providing information on available hotels for a given date and a given location. It checks for the availability of hotels and selects a specific hotel based on the client’s request and returns an offer with a cost and other hotel information. The external service that invoked the Hotel service can choose to refuse or accept the offer. In case of acceptance, the hotel proceeds with the booking and sends a confirmation message to the client.
On-line User Interface Service: This service serves as a customer interface through which the client can interact with TRPS. It receives input messages from the user and in return sends output messages to the user and also facilitates interactions among the available services.
The following is a typical sequence of events that can take place when making a reservation using the above services. The customer makes a travel reservation by sending a request through the On-line User Interface Service to TRPS. The request is received by TRPS which may specify the type of airline (e.g., KLM, Delta or Air Canada), the location and the time of travel as well as the details of the hotel the customer wants. The Travel Reservation and Purchase System checks for the availability of a flight based on the information provided by the customer and a given system requirement, and returns an offer to the customer if available, otherwise a failure message is generated. In case an offer is sent to the customer, he or she may decide to accept or cancel the offer. In the event that the customer accepts to purchase the ticket, then TRPS proceeds to check the customer’s credit card or authenticates his or her debit card or any other means of payment and finally transfers an appropriate amount of funds from the client’s bank account to the airline’s bank account. Composing these services must take into account certain business constraints such as the following: (1) The Hotel service should not be booked if the flight is not available, (2) The client can make payment using either a debit card or a credit card but not money order payment, (3) The composed service should process only flight reservations involving KLM or Delta Airlines but not Air Canada, and (4) The customer must accept the offer before his or her bank account is charged.
3 Service and supervisory control theory representation
In this section, we first give a quick description of the two industry standard languages used in specifying services, namely WS-BPEL and WSDL. Next, we present the formal details of a Service Labelled Transition system including its properties. The specification of an SLTS allows us to model and manipulate data conveniently, and to support compact representation. That is, it is sufficient to specify systems or processes that store and exchange data information.
3.1 Specification of services using the WS-BPEL and the WSDL languages
Basically, a Web service (Nath et al. 2014; Zhong et al. 2014) is a collection of executable functions which is available in the form of a Web resource. Each Web service is identified by a name, a unique location (URL) and a set of operations. These operations are specified by their names and input and output types. The information about these operations is available in the form of a syntactic description using a Web Service Description Language. In the following, we give a brief overview of the two main standard languages used in specifying services; the reader may refer to the existing literature (Alves et al. 2007; Andrews et al. 2003; Christensen et al. 2001; Silva and Rosa 2006; Crasso et al. 2010) for further details.
Web Service Description Language (WSDL) (Christensen et al. 2001; Silva and Rosa 2006; Crasso et al. 2010) is an XML-based interface description language for describing network services (e.g., ingoing and outgoing messages, and data types) in the form of the functionality it offers. Services are represented as network endpoints (or ports) and the network provides a model for representing the communication between multiple services. In addition, WSDL provides a mechanism for Web services to be located (e.g., using a URL), and exchanges messages using well-defined protocols. In this model, operations and messages are described abstractly, and then an endpoint is defined by binding it to a concrete network protocol and a specified message format. The data format specifications for a particular port type along with a concrete protocol constitutes a reusable binding, where the messages and operations are bound to the protocol and the format. A Web Service Description Language is often used in combination with SOAP (Gudgin et al. 2007) and an XML Schema (Domain 2017) to provide Web services over the Internet.
Web Service Business Process Execution Language (WS-BPEL) (Alves et al. 2007; Andrews et al. 2003) is an XML-based executable language designed to enable the coordination and composition of a set of Web services. It is described using Web Service Description Language WSDL and in an XML data format. Web Service Business Process Execution Language is an orchestration language, thus, it specifies an executable process in which messages are exchanged among different systems via a central controller, where the participants are represented using a state transition model. Web Service Business Process Execution Language is a behavioural extension of WSDL using a workflow-based approach. It uses control and data flow links to express relationships between multiple invocations. It models the flow of a Web service as a process which is a net-based concurrent description connecting activities that can send (receive) messages to (from) an external Web service provider. A process can be specified using a set of basic activities (e.g., receive, reply, invoke and assign) and structured activities (e.g., while, if, pick, sequence and flow).
3.2 Formal specification of services: the service labelled transition system (SLTS)
In this paper, we assume that each WS-BPEL/WSDL of a Web service is formally represented as a Service Labelled Transition System. In the literature, this formal language is often referred to as a guarded automaton (Fu et al. 2004). It is essentially an Extended Finite State Machine (EFSM) (Teixeira et al. 2015) without an update function or an action language. The formal model we present here consists of a set of states which model the dynamism of a system. The evolution of the system from one state to another is determined by its current state and the evaluation of a guard of a transition. We consider a set of data variables or data parameters V over a given finite domain D. Guards are predicates or Boolean expressions over data variables. We denote the set of predicates or Boolean expressions by \(\mathcal {B}\), which is evaluated with respect to the valuation function \(f_{d}: \mathcal {B}\rightarrow \) {true, false}. The atomic propositions are derived from the comparison predicates {<,=,>} and the constants true or false over variables. Boolean expression are constructed using the standard set of logical operators {¬,∧,∨, ⇒} denoting logical negation, conjunction, disjunction, and implication. Formally, we define a guard as follows (i.e., the grammar of a guard):
Definition 1
A guard \(g \in \mathcal {B}\) over variables V is inductively defined as follows:
A guard is an atomic proposition if and only if it is either true or false, an equality, or an inequality. Definition 1 can be extended to include quantifiers (∃,∀) and other logical operators. For more details on predicate logic the reader should refer to the text by Kumar et al. (1993).
We distinguish among three kinds of events, namely, input actions, which represent the reception of messages, output actions, which represent messages sent to external services, atomic actions which may modify the value of a variable arbitrarily. More specifically, the events or actions of an SLTS consist of the following:
Input and Output Messages: We denote a reception of a message as \(?m({\overrightarrow {x}})\) and an emission of message as \(!m({\overrightarrow {x}})\), where m is the name of the message also known as the message header, and x is the set of variables. The symbols ? and ! are used to denote the direction of messages. Variables are local to a service and only one service can modify a variable.
Atomic Operations: Operations such as function invocations are denoted by nameOperation(I::O) with input parameters I and output parameters O. Atomic operations are indivisible functions that can modify the variables in a service. The atomic operations/functions that we consider here are similar to atomic processes defined in OWL-S and BPEL, which can access and modify the variables of a Web service. OWL-S defines an atomic process as a non-decomposable Web-accessible program. It is executed by a single (e.g., http) call, and returns a response. There is no need for an extended conversation or interaction between the atomic operation and the calling program or agent. We assume that these atomic functions are local to a given service. The atomic operation, e.g., function(i1,i2 :: o1,o2) takes as inputs a set of variables {i1,i2} and returns a set of variables {o1,o2} as output. The effects that the atomic operation has on its output variables are not visible to the entire system. It can be observed that there are many cases where it will not make sense to assume static information about Web services. In a dynamic environment, Web services information may change while the Web service procedure is operating at runtime. Typical examples are the following: whether a product is in stock, how much it will cost or how much has been bid for it, what the weather is like, what time a train or airplane will arrive, what seats are available for an airplane or a concert, what shipping facilities are available for a shipping request, all of which are unknown before runtime. The output of an atomic function in our model depends on the time and the circumstances of invocation. That is, the output of the atomic operation depend not only on the available input, but also on the current state of the whole system. In addition, we assume that the service providers keep details about the atomic operations secret. For example, if a service solves sophisticated routing problems, the service provider does not want the description of the service to reveal how the results are computed. Due to the nondeterministic nature of atomic operations, we treat them as black-box events.
Formally, we define an SLTS as follows:
Definition 2
A Service Labelled Transition System is modeled by a tuple \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F}, V, \mathcal {B})\) where
\(\mathcal {S}\) is a finite set of states;
\(\mathcal {S}^{0} \subseteq \mathcal {S}\) is the set of initial states;
Σ = \(\mathcal {I}\) ∪ \(\mathcal {O}\) ∪ \(\mathcal {A}\) is the set of events (i.e, set of actions), where \(\mathcal {I},\)\(\mathcal {O},\)\(\mathcal {A}\) denote the set of input messages; \((?m({\overrightarrow {x}}))\), outputs messages \((!m({\overrightarrow {x}}))\) and atomic operations, respectively, and \(\mathcal {I}\) ∩ \(\mathcal {O} = \emptyset \), \(\mathcal {I}\) ∩ \(\mathcal {A} = \emptyset \), \(\mathcal {O}\) ∩ \(\mathcal {A} = \emptyset \);
\({\Gamma } \subseteq \mathcal {S} \times (\mathcal {I} \cup \mathcal {O} \cup \mathcal {A}) \times {\mathcal {B}}\times \mathcal {S}\) is the transition relation;
\(\mathcal {S}^{F} \subseteq \mathcal {S}\) is the set of final states;
V = {v1,...,vn} is a finite set of data variables over a given domain D = D1 × D2 ×… × Dn;
\({\mathcal {B}}\) is the set of predicates called guards (\(g \in \mathcal {B}\)) over a subset of the variables in V.
We employ infix notation and we write  as shorthand for (s,e,g,s′) ∈Γ. A tuple
as shorthand for (s,e,g,s′) ∈Γ. A tuple  is a transition in \(\mathcal {G}_{W}\), where e ∈Σ, and g is a guard in \({\mathcal {B}}\), a condition or a predicate defined over variables and formulas. The absence of an explicit guard on a transition means that the condition is always true. The dynamics of an SLTS depends on the current state of the system and on the valuation of the transition guards with respect to the current value of a variable. The truth value of a guard on a transition must evaluate to true in order for the transition to be allowed to occur.
is a transition in \(\mathcal {G}_{W}\), where e ∈Σ, and g is a guard in \({\mathcal {B}}\), a condition or a predicate defined over variables and formulas. The absence of an explicit guard on a transition means that the condition is always true. The dynamics of an SLTS depends on the current state of the system and on the valuation of the transition guards with respect to the current value of a variable. The truth value of a guard on a transition must evaluate to true in order for the transition to be allowed to occur.
In the sequel, let Σ∗ denote the set of all finite strings of the form α1α2...αn of events from Σ, including the empty string 𝜖.
The possible behaviour of an SLTS is modeled by the set of executions. The execution or the run of an SLTS is a sequence of transitions  such that
such that  and the trace of the run is given by α0α1α2...αn− 1. An SLTS may contain both finite and infinite runs. The language generated by an SLTS, denoted by \(\mathcal {L}(\mathcal {G}_{w}),\) is the set of words
and the trace of the run is given by α0α1α2...αn− 1. An SLTS may contain both finite and infinite runs. The language generated by an SLTS, denoted by \(\mathcal {L}(\mathcal {G}_{w}),\) is the set of words  where s0
where s0 denotes a multi-step transition relation which is defined inductively as a finite sequence of applications of a transition relation which produces a state y that a sequence of events leads to from the initial state s0 and g′ denotes a sequence of guards.
denotes a multi-step transition relation which is defined inductively as a finite sequence of applications of a transition relation which produces a state y that a sequence of events leads to from the initial state s0 and g′ denotes a sequence of guards.
The formal language that we define here differs from extended finite state automata (Teixeira et al. 2015) in that we do not require an update function. Hence, in some cases it becomes impossible to track the values of variables in our model. That is, there is no action language, but we assume the updating of variables is done internally, which makes it difficult to track the values of variables.
We distinguish between two kinds of transitions, the first one is a static transition which does not depend on a variable; the guard of this transition is always true and is triggered when the event on the transition takes place. The second type of transition is a dynamic transition
which does not depend on a variable; the guard of this transition is always true and is triggered when the event on the transition takes place. The second type of transition is a dynamic transition which has non-trivial guards that depend on a variable which is fired only if the guard on the transition evaluates to true and the event has occurred. For example, in Fig. 2a, the transition s1
which has non-trivial guards that depend on a variable which is fired only if the guard on the transition evaluates to true and the event has occurred. For example, in Fig. 2a, the transition s1 is a static transition whereas the transition
is a static transition whereas the transition  is a dynamic transition.
is a dynamic transition.
Definition 3
Subguards
Let g1 and g2 be two guards. We call g2 a subguard of g1 denoted by g2 ≤ g1, if g2 is stronger than g1, i.e., g1 ∧ g2 = g2.
In order to model behaviours common to two or more SLTSs, we define product in such a way that an event can be executed only if it can be executed by all the SLTSs involved. This will allow us to model multiple requirements of a system. For example, given SLTS1 and SLTS2 specifying certain given system requirements, an event is allowed to occur only if it is allowed in both SLTSs.
Definition 4
Product
Given two SLTSs \(\mathcal {G}_{W_1} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_1, \mathcal {B}_1)\) and \(\mathcal {G}_{W_{2}} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2}, {\Gamma }_{2},\mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2})\) their product is given by \(\mathcal {G}_{W_{1}} \times \mathcal {G}_{W_{2}} = (\mathcal {S}_{1} \times \mathcal {S}_{2},\mathcal {S}^{0}_{1} \times \mathcal {S}^{0}_{2},\mathcal {I}_{1}\cup \mathcal {I}_{2}, \mathcal {O}_{1}\cup \mathcal {O}_{2}, \mathcal {A}_{1}\cup \mathcal {A}_{2}, {\Gamma }_{1}\times {\Gamma }_{2}, \mathcal {S}^{F}_{1} \times \mathcal {S}^{F}_{2}, V_{1}\cup V_{2}, \mathcal {B}_{1}\cup \mathcal {B}_{2})\) such that the transition relation Γ1 ×Γ2 is defined as follows.
In the product, the transitions of two SLTSs must always synchronize on shared events Σ1 ∩Σ2, where Σ1 = (\(\mathcal {I}_{1}\cup \mathcal {O}_{1} \cup \mathcal {A}_{1}\)) and Σ2 = (\(\mathcal {I}_{2}\cup \mathcal {O}_{2} \cup \mathcal {A}_{2}\)). That is, the product of two SLTSs captures the intersection of their behaviours.
Analogous to the standard SCT where the legal language is a sublanguage of the plant, in our framework we use the notion of a simulation relation to describe the relationship between a system (plant) and a given specification, both modeled as SLTSs.
Definition 5
Simulation Relation with Guards
Given two SLTSs \(\mathcal {G}_{W_1} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_1, \mathcal {B}_1)\) and \(\mathcal {G}_{W_{2}} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2}, {\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2}), \mathcal {G}_{W_{2}}\) simulates \(\mathcal {G}_{W_{1}}\) if there exists a relation \(R\subseteq \mathcal {S}_{1} \times \mathcal {S}_{2}\) such that ∀(s1,s2) ∈ R,
- 1.
if \(s_{1} \in \mathcal {S}^{0}_{1}\) then \(s_{2} \in \mathcal {S}^{0}_{2}\);
- 2.
if
 then \(\exists s_{2}^{\prime }, \exists g^{\prime }\) such that
then \(\exists s_{2}^{\prime }, \exists g^{\prime }\) such that  and g1 ≤ g′ and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\).
and g1 ≤ g′ and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\).
That is, we say \(\mathcal {G}_{W_{2}}\) simulates \(\mathcal {G}_{W_{1}}\) denoted by \(\mathcal {G}_{W_{1}} \preceq \mathcal {G}_{W_{2}}\) if every transition taken by \(\mathcal {G}_{W_{1}}\) can be matched by a corresponding transition in \(\mathcal {G}_{W_{2}}\). In essence, when the two SLTSs are represented as their respective execution trees, \(\mathcal {G}_{W_{1}} \preceq \mathcal {G}_{W_{2}}\) means that \(\mathcal {G}_{W_{1}}\) is a subtree of \(\mathcal {G}_{W_{2}}\).
Definition 6
Bisimulation Relation
Given two SLTSs \(\mathcal {G}_{W_1} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_1, \mathcal {B}_1)\) and \(\mathcal {G}_{W_{2}} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2}, {\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2}),\) a bisimulation relation is a binary relation \(R\subseteq \mathcal {S}_{1} \times \mathcal {S}_{2}\) such that for all (s1,s2) ∈ R, it holds that:
- 1.
\(s_{1} \in \mathcal {S}^{0}_{1}\) if and only if \( s_{2} \in \mathcal {S}^{0}_{2}\);
- 2.
if
 for \(g_{1}\in \mathcal {B}_{1}\) and \(s_{1}^{\prime }\in \mathcal {S}_{1}\), then \( \exists g_{2}\in \mathcal {B}_{2}\) and \(\exists s_{2}^{\prime }\in \mathcal {S}_{2}\) such that
for \(g_{1}\in \mathcal {B}_{1}\) and \(s_{1}^{\prime }\in \mathcal {S}_{1}\), then \( \exists g_{2}\in \mathcal {B}_{2}\) and \(\exists s_{2}^{\prime }\in \mathcal {S}_{2}\) such that  g1 ⇔ g2 and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\);
g1 ⇔ g2 and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\); - 3.
if
 for \(g_{2}\in \mathcal {B}_{2}\) and \(s_{2}^{\prime }\in \mathcal {S}_{2}\), then \(\exists g_{1}\in \mathcal {B}_{1}\) and \(\exists s_{1}^{\prime } \in \mathcal {S}_{1}\), such that
for \(g_{2}\in \mathcal {B}_{2}\) and \(s_{2}^{\prime }\in \mathcal {S}_{2}\), then \(\exists g_{1}\in \mathcal {B}_{1}\) and \(\exists s_{1}^{\prime } \in \mathcal {S}_{1}\), such that  g1 ⇔ g2 and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\).
g1 ⇔ g2 and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\).
The SLTS \(\mathcal {G}_{W_{1}}\) and \(\mathcal {G}_{W_{2}}\) are called bisimilar if there exists a bisimulation relation between \(\mathcal {G}_{W_{1}}\) and \(\mathcal {G}_{W_{2}}\), which we will denote as \(\mathcal {G}_{W_{1}}\) ≈ \(\mathcal {G}_{W_{2}}\).
3.3 WS-BPEL to SLTS
In our framework, we assume that Web services are described in WS-BPEL; based on this we automatically extract the SLTS models. Formally, we model a service as an SLTS as defined above. We also assume that the available Web services are published and reside in a repository in which we select the required services that meet a given functionality. The focus of this paper is on the problem of automated Web service composition, thus the issue of discovery and the selection of services is beyond the scope of this paper.
Given a WS-BPEL specification of a process, a translation technique (not discussed here) is used to systematically translate this process into a corresponding SLTS. For instance, the WS-BPEL basic constructs such as receive, reply, invoke (or assign) are translated into the input, output and atomic operation transitions of a corresponding SLTS, respectively, while the structured constructs (while, if, flow, pick) are mapped into the conditions or guards of their respective transitions of the SLTS in a systematic fashion.
We model input messages and atomic functions as uncontrollable since we cannot control inputs from the user. We assume that no service can deny an input action from other services, while it is completely up to the service to control its outputs. On the other hand, output messages from the system are modeled as controllable. In the context of Web services a guard (g) represents the preconditions on variables.
Figure 1 shows the SLTS representations of the four component services of TRPS example introduced in Section 2.2.
3.4 Highlights of the proposed method
In the following, we will highlight some of the relevant concepts that are pertinent to the proposed technique. Our approach lies between the event-based supervisory control (Wonham and Ramadge 1987) and state-avoidance control problem (Gall et al. 2005). However, our approach extends the basic control capabilities in these approaches as follows. Apart from the supervisor being able to prevent certain events from occurring by properly disabling and enabling controllable events, the supervisor is also able to prevent the system from reaching certain sets of states designated as forbidden states by using run-time information of variables in the system. This is due to the fact that some of the events in our model are black-box (atomic actions) in nature and may exhibit non-deterministic properties. We deal with this non-determinism through model refinement and the adaptation of event enforcement supervisory control theory (Diekmann and Weidemann 2013). Therefore, the generated supervisor not only restricts the behaviour of the plant, but also has the opportunity to actively enforce certain events. In addition, the generated supervisor is able to restrict the system by assigning stronger guards to data variables. This allows us to control the data a service can send or receive.
The use of run-time information in our model is inspired by the fact that the services we model are nondeterministic and partially controllable. That is, the outputs of a service cannot be predicted a priori and some of the internal computations of a service are hidden from other external services. For example, the information whether there are still seats available on a flight cannot be known until run-time or whether there is enough cash in a customer bank account will only be available at run-time. Due to non-determinism and the black box nature of some of the events in our model, the use of the classic supervisory control theory in many cases will result in an empty controller or an overly restrictive controller.
Intuitively, in order to model services using supervisory control theory, we need to provide support for (i) message exchanges, (ii) data and variables, (iii) conditions, and (iv) information or data that may not be known until runtime.
Let us illustrate the above discussion with the following example. Consider Fig. 2 which models an airline reservation system and its specification. For now we are not interested in the formal details of this example; we will deal with this in subsequent sections. Figure 2a represents an airline system (plant) which upon accepting a request, checks the availability of an airline and returns an offer if it is available. Assume that Fig. 2b is the system requirements to be met. The specification permits the plant to do everything except for the transition from state s4 to s5 where there is a restriction on what branch to take based on the value of the variable. Assume the transitions labeled checkAirlinesAvail(date, loc::av) and processBooking() are not controllable. Now, at state s4 of S2 (Fig. 2b) the specification allows the plant to transition to state s5 only if the value of the variable av is either KLM or Delta; anything else is not allowed. The use of the classic DES will never allow the plant to reach state s4 which implies that the system will receive a request but will never return a response, which does not make much sense in the service domain. In other words, modeling the service composition problem using the standard SCT could result in an overly restrictive controller. The use of supervisory control based on extended finite state machines would also not work, since the value of the variable av is unknown and can not be tracked until state s4. The event checkAirlinesAvail(date, loc::av) is assumed to be black-box, i.e., the effect that it has on variables are not known.
4 Supervisor aware service composition architecture (SASCA)
4.1 Controller synthesis for service composition
In this section, based on the representation of services using SLTSs, we formalize the problem of composing Web services, and we describe its solution by means of supervisory control theory of SLTS. Our model of synthesized Web services relies on message passing, interaction with data and actions. The composition problem that we consider here is as follows: given a set of available services \(\mathcal {G}_{W_{1}}, \mathcal {G}_{W_{2}}, \hdots , \mathcal {G}_{W_{n}}\) and a set of specifications \(\mathcal {T}^{W}\) representing the goal (or desired) service over the same environment (same set of atomic actions), we would like to construct a controller \(\mathcal {C}\) satisfying some controllability and nonblocking constraints which interacts with the available services to satisfy the specification \(\mathcal {T}^{W}\). Thus, \(\mathcal {C}\) serves as a controller that restricts the system in such a way that all its executions satisfy \(\mathcal {T}^{W}\) and so that \(\mathcal {C}\) is minimally restrictive. In addition to requiring that the generated controller satisfies the controllability and nonblocking criteria, the controlled system is also free of errors that may result from communication among component services. We assume that both the available services and the goal service are expressed as SLTSs as defined above. Figure 3 shows the basic architecture diagram for the SASCA framework. The inputs to the system are the set of component Web services specified in WS-BPEL and the requirements are specified as SLTSs. We then provide a translator to generate the SLTSs representations from the WS-BPEL descriptions of the available services. The diagram shows the important internal representations from when the input enters the system to when a controller is generated. The framework also depicts an intermediate preprocessing step of the plant to achieve a more refined model suitable for composition synthesis. The final output of the synthesis is a WS-BPEL executable file. In the rest of this section, we explain the different parts of the figure; the core details of our approach including relevant definitions and theorems are discussed.
4.2 Asynchronous communication and system to be controlled
In our formalism, we use asynchronous communication to model the interaction among the available services. Synchronous semantics requires that during a message exchange, the sender and the receiver have to synchronize the send and receive actions, and the sender blocks until a reply is received. However, in the domain of Web services where component services are dynamically discovered and plugged in to obtain a composite service (loosely coupled), using synchronous semantics may go a long way to limit the applicability of our model. Hence, in this paper we assume that Web services interact in an asynchronous fashion. Asynchrony can be achieved by employing unbounded memory to store the variables and parameters exchanged among component services. However, in this work the way we model service interactions does not take into consideration how the messages are stored and retrieved. Asynchrony eliminates the situation where the sender halts its process and wait for a reply from the receiver. The asynchronous semantics that we adopt here make implementation easier compared to synchronous semantics, however, it is very hard to reason about communication systems modeled using asynchronous semantics. In general, modeling the composition of communicating systems could result in various undesirable behaviours such as unspecified receptions and non-executable interactions of the system (Zafiropulo et al. 1980; Brand and Zafiropulo 1983). We will refer to these undesirable communication properties as communication errors.
The framework we propose has two inputs as shown in Fig. 3, the composition requirements \(\mathcal {T}^{W}\) and the set of component Web services with SLTSs as \(\mathcal {G}_{W_{1}}, \mathcal {G}_{W_{2}}, \hdots , \mathcal {G}_{W_{n}}\). The set of available services \(\mathcal {G}_{W_{1}}, \mathcal {G}_{W_{2}}, \hdots , \mathcal {G}_{W_{n}}\) evolves independently, but together they form a combined system \(\mathcal {G}_{W}\) whose behaviours we need to control. The individual component services cannot communicate among themselves; in order to exchange messages a controller is generated to mediate the interactions among component services. In the supervisory control domain, \(\mathcal {G}_{W}\) models the plant which represents the set of possible behaviors. As a first step in the composition process we obtain \(\mathcal {G}_{W}\) by combining the set of available services whose SLTSs is given by \(\mathcal {G}_{W_{1}}, \mathcal {G}_{W_{2}}, \hdots ,\mathcal {G}_{W_{n}}\) by means of an Asynchronous Parallel Composition which captures the notion of asynchronous communication (Honda and Tokoro 1991; Milner 1989).
Definition 7
Asynchronous Parallel Composition
Given two SLTSs \(\mathcal {G}_{W_1} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_1, \mathcal {B}_1)\) and \(\mathcal {G}_{W_{2}} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2}, {\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2})\) their asynchronous parallel composition is given by \({G}_{W_{1}} \parallel {G}_{W_{2}} = (\mathcal {S}_{1} \times \mathcal {S}_{2},\mathcal {S}^{0}_{1} \times \mathcal {S}^{0}_{2},\mathcal {I}_{1}\cup \mathcal {I}_{2}, \mathcal {O}_{1}\cup \mathcal {O}_{2}, \mathcal {A}_{1}\cup \mathcal {A}_{2},{\Gamma }_{1}\parallel {\Gamma }_{2}, \mathcal {S}^{F}_{1} \times \mathcal {S}^{F}_{2}, V_{1}\cup V_{2}, \mathcal {B}_{1}\cup \mathcal {B}_{2})\) such that the transition relation Γ1 ∥Γ2 is defined as follows.
Definition 7 can be extended to n services by observing that it is associative, i.e., \((\mathcal {G}_{W_{1}}\parallel \mathcal {G}_{W_{2}})\parallel \mathcal {G}_{W_{3}}= \mathcal {G}_{W_{1}}\parallel (\mathcal {G}_{W_{2}}\parallel \mathcal {G}_{W_{3}})\) (this is true only up to isomorphism). Therefore, without ambiguity we can write \(\mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}\) to represent the composition of multiple Web services. The definition of asynchronous parallel composition given above is defined so that individual services are allow to make independent moves. In addition, We assume that the available services do not interact among themselves; any form of communication is through the supervisor. Hence, we require that the input (output) messages of a service are disjoint from the inputs (output) of another service. That is, no two services can have the same name for message headers with the same direction of messages. Atomic operations are local to a service. Generally, variables of a service have local scope and hence, each service refers to different internal variables. We assume that the component services participation in a composition are designed in such a way that conflicts in variables names are avoided.
Given a set of available services, forming the asynchronous parallel composition \(\mathcal {G}_{W}=\mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}\) could result in communication errors. This leads us to the second step of our composition process in the next section.
4.3 Preprocessing design errors
Applying Definition 7 to combine the available services may result in two main communication errors: cases where messages are sent to a service but it is unable to receive them and cases where a service expects a message which another service is unable to provide. That is, given the system to be controlled which represents the asynchronous parallel composition of available services \(\mathcal {G}_{W} = \mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}, \mathcal {G}_{W}\) may contain the following errors as defined below. We want the combined set of services to be free from communication errors. Consider for instance an airline service that provides several functionalities and is able to receive requests to book different kinds of flights from customers including book_KML, book_Air_Canada, book_Ethiopian_airline and so on. In this situation, the airline service may be providing more functionalities than what a particular client service actually needs. Therefore, it will be necessary to make the airline service cooperate with the client service by restricting its set of messages to a subset of the client’s request.
The work by Zafiropulo et al. (1980) and Brand and Zafiropulo (1983) presents various communication errors. One such communication error discussed in the work by Zafiropulo et al. unspecified reception (Zafiropulo et al. 1980; Brand and Zafiropulo 1983) which is a situation where one service can send a message at a reachable state, but other services are not able to receive it. That is, the SLTS description of a service contains an emission that cannot be consumed by the related component services involved in the composition. Consider Fig. 4a and b, S1 and S2 can communicate based on the message headers requestFlight and flightOffer, however when S2 is in state s1, it is capable of sending an additional message !searchFlight which cannot be consumed by S1. Another communication error presented by Zafiropulo et al. is non-executable interactions which refer to a situation in which one service is able to receive a message that has not already been sent by some other service. This results in additional unmatched receptions. For instance, in Fig. 4, when S1 and S3 are combined by asynchronous parallel composition, the combined system will be stuck at a state in which S1 will be waiting on the reception of ?flightOffer at state s1 while S3 will be waiting on either the reception of ?searchFlight or ?requestHotel which is not being sent by any of these services. In the following we present a variant of the notion of communication errors as used in this paper.
Given an SLTS, for every output transition  there must exist at least one run containing the state s′ of t such that this run contains a corresponding reception or input transition t′, and t precedes t′. The assumption is that once a message is sent there is a possibility that it will be consumed if a specific run or execution is taken based on the state of the system. Similarly, for every input transition
there must exist at least one run containing the state s′ of t such that this run contains a corresponding reception or input transition t′, and t precedes t′. The assumption is that once a message is sent there is a possibility that it will be consumed if a specific run or execution is taken based on the state of the system. Similarly, for every input transition  if there exists at least one run containing state s of t such that there is a corresponding output transition t′ in this run, and t is preceded by t′. Furthermore, for a run r containing an output transition t of message header m and at least one corresponding input transition t′ of message header m, we require that the number of output transitions with message header m and the number input transition with message header m be equal. We assume that the run r is the run to be taken if the transition t is to be consumed, hence we need to ensure that the number of sends with message header m is equal to the number of receives with message header m.
if there exists at least one run containing state s of t such that there is a corresponding output transition t′ in this run, and t is preceded by t′. Furthermore, for a run r containing an output transition t of message header m and at least one corresponding input transition t′ of message header m, we require that the number of output transitions with message header m and the number input transition with message header m be equal. We assume that the run r is the run to be taken if the transition t is to be consumed, hence we need to ensure that the number of sends with message header m is equal to the number of receives with message header m.
In this paper, we will limit the notion of communication errors to an SLTS with finite number of runs. Let the length \(p \in \mathbb {N}\) of a run  sn be the number of transitions from the initial state s0 to the end state sn.
sn be the number of transitions from the initial state s0 to the end state sn.
Now, define an SLTS \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F},V, \mathcal {B})\) to depthp to be an SLTS with finite runs such that the length of every run  sn in \(\mathcal {G}_{W}\) is (1) equal to p or (2) sn is a final state such that n ≤ p + 1 or (3) sn has no successor state and n ≤ p + 1.
sn in \(\mathcal {G}_{W}\) is (1) equal to p or (2) sn is a final state such that n ≤ p + 1 or (3) sn has no successor state and n ≤ p + 1.
Definition 8
Communication-Error Free SLTSs to Depth p
An SLTS \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F},V, \mathcal {B})\) is said to be communication-error free to depth \(p \in \mathbb {N}\) if all the following holds:
- (1)
for each output transition
 there exists a run r of length p or less such that
there exists a run r of length p or less such that  of \(\mathcal {G}_{W}\) such that the input transition
of \(\mathcal {G}_{W}\) such that the input transition 
- (2)
for each input transition
 there exists a run r up to length p such that
there exists a run r up to length p such that 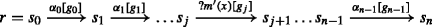 of \(\mathcal {G}_{W}\) such that the output transition
of \(\mathcal {G}_{W}\) such that the output transition  is in r and i < j.
is in r and i < j. - (3)
for each run r of length p or less that ends in a terminal state and that contains an output transition
 and at least one input transition
and at least one input transition  of message header m″, then the number of output transitions of message header m″ must be equal to the number of input transitions of message header m″ in r.
of message header m″, then the number of output transitions of message header m″ must be equal to the number of input transitions of message header m″ in r.
In other words, in (1) for each output transition  there must exist a run r of length p that contains a corresponding input transition
there must exist a run r of length p that contains a corresponding input transition  Γ such that the output transition t precedes the input transition t′; in (2) for each input transition
Γ such that the output transition t precedes the input transition t′; in (2) for each input transition  there must exist a run r of length p or less that ends in a terminal state that contains a corresponding output transition
there must exist a run r of length p or less that ends in a terminal state that contains a corresponding output transition  such that the output transition t′ precedes the input transition t; and (3) for every run of length p that ends in a terminal state containing an output transition
such that the output transition t′ precedes the input transition t; and (3) for every run of length p that ends in a terminal state containing an output transition  and at least one corresponding input transition for
and at least one corresponding input transition for  then for every transition of message header m″, the number of sends of m″ (output transitions of message header (m″)) is equal to the number of receives of m″ (input transitions of message header m″).
then for every transition of message header m″, the number of sends of m″ (output transitions of message header (m″)) is equal to the number of receives of m″ (input transitions of message header m″).
Consider the plant in Fig. 5. In what follows, we consider whether this SLTS is communication-error free up to depth six. For example, (i) the transition from s0 to s1 satisfies condition (1) since the run containing the transition from s2 to s7 contains a corresponding input transition and this run also satisfies condition (3). However, one should note that even though the run from s0 to s6 and containing state s5 does not contain a reception of the input transition from s0 to s1, condition (1) is still met by the transition from s0 to s1, since there exists another run (namely the one that goes through s7) that does contain a reception of message m1(x) (in other words, a run may contain an output transition without a corresponding reception but will be considered valid for condition (1) so long as there exists another run satisfying this condition); (ii) the transition from s1 to s2 also meets condition (1) since there is at least one run passing through state s2 containing a corresponding input transition, however the run passing through state s2 and state s3 does not satisfy condition (3), since the number of the output messages m2 is more than the number of input messages m2 on this run; (iii) the transition from s0 to s9 does not satisfy condition (1), since no sequence of transitions contains the reception of message m4, (iv) the transition from s9 to s10 meets condition (1) but the run containing it that goes to s6 and has transition ?m6(x) does not satisfy condition (3) since the number of sends of m6 is more than the number of receives of m6; and (v) the transition from s11 to s6 with message header m7 does not satisfy condition (2) and the run containing it too does not meet condition (3). In conclusion, the SLTS is not communication-error free to depth six.
Also, if we had considered whether that same plant is communication-error free up to depth three then we would see that, for example, the run that goes from state s0 to s1 to s2 to s7 will not satisfy condition (2) since that run does not contain a message reception of the transmission !m2(x).
As another example, consider the plant \(\mathcal {G}_{W}\) in Fig. 6 which is communication-error free to depth two. There is only one run that ends at a terminal state and that has at least one output transition and at least one input transition and also has two or fewer transitions and that is the run from s0 to s1 that has !m1(x)?m1(x), which satisfies Definition 8.
In order to ensure the system we design is communication-error free to some depth p, we perform a prefiltering step as part of our composition generation process to refine the system to be controlled. Given the SLTS \(\mathcal {G}_{W}\) representing asynchronous parallel composition of the available services, we perform a refinement or preprocessing on \(\mathcal {G}_{W}\) to get a communication-error free SLTS. We denote a plant which is a valid SLTS or the refined plant as Ref(\(\mathcal {G}_{W}\)). This preprocessing step removes transitions not satisfying Definition 8 from the original plant. This does not affect the functionality of the system, since we want to consider a communication-error free to depth p set of communicating services. That is, once the services are composed, input (output) messages that are not consumed by other services will become useless and may obstruct system progress. We make the following assumption before ending this section. (i) We do not assume the existence of any specific technique for message queuing and buffering, we assume that asynchronous communication is correctly implemented such that all problems and complications associated with asynchrony have been properly tackled. For example, if a service A sends the same message say m three times to service B, but service B can only accept only one of those messages at a time, then the implementation of the asynchronism should ensure that only one of the messages m is consumed by B and there rest are discarded, accordingly; (ii) We assume that the services we model do not result in nontermination during communication. That is, the services that we consider are guaranteed to terminate during execution and as such, no service can keep sending a message infinitely and no service will wait for the reception of a particular message forever. Even though, we model loops (e.g., self loops) in our framework, we assume that after some finite number of iteration of a loop at a given state of a service, it will eventually progress to a final state or to a state where it terminates;
4.4 Composition requirements
The composition requirements are also given as SLTSs which specify the possible accepted interactions that must hold in the composition. We require that the system requirements to be satisfied be clearly specified in terms of its input/output messages and atomic operations that would be made available to other services. We also assume that the SLTSs of the specification are also communication-error free to depth \(p \in \mathbb {N}\) by Definition 8. There could be multiple specifications. In that case, we use product to put them together. Intuitively, a supervisor in this case will be one that guarantees that all specifications are achieved. We assume that the designer of the specification is aware of the set of services available and must specify the specification in such a way that it is simulated by the combined services. In the case that the specification cannot be simulated by the plant, then further refinement must be done. Using our approach, it is possible that no composition exists to satisfy a given specification due to incomplete specification or the specification provided by the composition designer results in a failure of a composition. It may be of interest to find an approximate “solution”. More precisely, in the case where a composition does not exist, one may be interested in understanding which parts of the specification cannot be realized and which can. Realistically, the composition designer would have to reconstruct the specification and find another specification to do the work. As part of the composition synthesis algorithms that we provide, we seek to aid the reconstruction of a given specification when a composition cannot be met due to a failure caused by the specification using an iterative refinement technique that refines the specification until a composition can be generated. In the worst case, the refinement will result in an empty specification which will lead to an empty composition.
In this framework, specification can take one of the following forms: (i) A composition requirement can specify a set of constraints on the ordering of events and actions. A typical example of these constraints in our flight booking system is that the credit card of the user must be verified by the Bank service before a booking confirmation is delivered to the customer. Another ordering requirement could be that the Flight service must confirm flight availability before the hotel is booked. In other words, the hotel should not be booked if the flight cannot be booked. A simple SLTS specification expressing this composition requirement is depicted in Fig. 7a. We assume that self loops would be used at certain states to indicate that other transitions are allowed to occur at those states. (ii) Another form of composition requirement is to specify stronger guards that limit the values that can be taken by a variable or a data parameter from a given domain. This can be used to restrict the values of a variable that can be sent or received by services. In Fig. 7b, the SLTS specifies that the airline service from our running example can accept reservations for only KLM and Delta ((av = KLM) ∨ (av = Delta)) but not Air Canada. This specification restricts the values of the variable av. Hence, a correct composition must not allow Air Canada reservations to be made. Figure 7c also specifies the kind of payment that can be made by a client to the Travel Reservation and Purchase System. The SLTS specifies that the system can only accept payment made by credit card or debit card. (iii) One can also explicitly specify a set of forbidden states that the system should not reach during execution. For example, a specification that specifies that the cost of a product c should not exceed a limit m, i.e., c < m implies that c ≥ m leads to an unsafe state.
4.5 Controller synthesis
In this section, we study how to synthesize a controller that will ensure that the system's behaviour satisfies the given requirements. We assume that the system to be controlled is given by the asynchronous parallel composition of the available services \(\mathcal {G}_{W_{1}}\) ∥ \(\mathcal {G}_{W_{2}}...\parallel \)\(\mathcal {G}_{W_{n}}\) and the system requirements (target service) are given by \(\mathcal {T}^{W}\). Now, we require that the asynchronous parallel composition of the available services simulates the goal services. That is, \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\). In the case that it does not simulate the goal service we perform refinement on the target services. The following definition specifies the product operation with refinement to safe (good) and forbidden (bad) states.
Definition 9
Composition Refinement
Given two SLTSs \(\mathcal {G}_{W_1} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_1, \mathcal {B}_1)\) and \(\mathcal {T}^{W} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2}, {\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2})\) representing the plant and the specification respectively, we can compute their product as well as refine the plant with respect to the specification in such a way that the behaviour not allowed by the specification ends in bad or forbidden states in the plant. A bad or forbidden state is a state reachable in \(\mathcal {G}_{{W_{1}}}\) but not in \(\mathcal {T}^{W}\). The composition refinement of the plant and the specification denoted by \(\mathcal {G}_{{W_{1}}}\times _{ref}\mathcal {T}^{W}\) is given by \(\mathcal {C}^{0} = (\mathcal {S}_{1} \times (\mathcal {S}_{2} \cup \{ s^{\text {Bad}}\}), \mathcal {S}^{0}_{1} \times \mathcal {S}^{0}_{2},\mathcal {I}_{1}\cup \mathcal {I}_{2}, \mathcal {O}_{1}\cup \mathcal {O}_{2}, \mathcal {A}_{1}\cup \mathcal {A}_{2}, {\Gamma }_{1}\times {\Gamma }_{2}, \mathcal {S}^{F}_{1} \times \mathcal {S}^{F}_{2}, V_{1} \cup V_{2}, \mathcal {B}_{1} \cup \mathcal {B}_{2})\), where sBad denotes a bad or forbidden state and the transition relation Γ1 ×Γ2 is defined as follows.
- (1)

- (a)
 , if the conditions in (1) are true and exists no state \(s_{2}^{\prime \prime }\) such that
, if the conditions in (1) are true and exists no state \(s_{2}^{\prime \prime }\) such that 
- (a)
- (2)
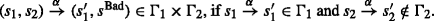
The first item (1) of the definition creates two new transitions in \(\mathcal {C}^{0}\) (the refined SLTS) with the same events but different guards. Intuitively, The first transition given by  replaces the guards of \(\mathcal {C}^{0}\) with that of the specification and the resultant state is a state allowed by both the plant and the specification. The second transition in (a) given by
replaces the guards of \(\mathcal {C}^{0}\) with that of the specification and the resultant state is a state allowed by both the plant and the specification. The second transition in (a) given by  is essentially the same as the former, however the guard of the latter transition is g1 ∧¬g2 which results in a new state allowed by the plant but unsafe in the specification. Note that (a) is only true if the preceding conditions in (1) is true and that a similar transition with an event α and guard g1 ∧¬g2 is not in the specification. The second item (2) of the definition creates a new transition in \(\mathcal {C}^{0}\) if an event is allowed by the plant but not legal in the specification.
is essentially the same as the former, however the guard of the latter transition is g1 ∧¬g2 which results in a new state allowed by the plant but unsafe in the specification. Note that (a) is only true if the preceding conditions in (1) is true and that a similar transition with an event α and guard g1 ∧¬g2 is not in the specification. The second item (2) of the definition creates a new transition in \(\mathcal {C}^{0}\) if an event is allowed by the plant but not legal in the specification.
Now the set of states of \(\mathcal {C}^{0}\) is given by Y =\(\mathcal {S}_{1} \times (\mathcal {S}_{2} \cup \{ s^{\text {Bad}}\})\). A state (s1,s2) ∈ Y is said to be forbidden if s2 = sBad. That is, it is a bad state. We denote \(\mathcal {S}^{\text {Bad}}\) as the set of bad states of \(\mathcal {C}^{0}\). That is the set of states reachable in \(\mathcal {G}_{{W_{1}}}\) but not in \(\mathcal {T}^{W}\). The state (s1,s2) ∈ Y is safe if s2≠sBad. States that are not in \( \mathcal {S}^{\text {Bad}}\) are called safe or good states denoted by \(\mathcal {S}^{Good}_{\mathcal {C}^{0}}\). Now, by strengthening the guards of \(\mathcal {C}^{0}\) with respect to the plant so that forbidden states in \(\mathcal {C}^{0}\) are not reachable we obtain a new SLTS which we will call a safe SLTS of \(\mathcal {C}^{0}\). We show how to strengthen the guards of \(\mathcal {C}^{0}\) later on in Algorithm 5 of Section 5.
We assume that the set of events Σ is partitioned into three disjoint subsets namely, controllable events Σc ⊆ Σ, uncontrollable Σuc ⊆ Σ and enforceable events Σf ⊆ Σ . Controllable events can be disabled by the controller while uncontrollable events cannot be prevented from occurring. In addition, the enforceable events are special events that can be enforced by the controller. Enforceable events are able to be “forced” to preempt both controllable and uncontrollable events at run-time but not static transitions. As mentioned earlier, input messages and atomic functions are modeled as uncontrollable events, whereas output messages from the system are modeled as controllable events. In addition, some output messages are marked as enforceable events at design time. The notion of preemption can be understood if we look at Fig. 8. Suppose that in the plant in Fig. 8a the event α is enforcible and the event β is uncontrollable. To capture the intention that when the system is in state s0 there is time for transition α to be forced to occur before β uncontrollably occurs, we can introduce a new transition 𝜖 and imagine that instead of transition β exiting directly from state s0, the event 𝜖 exits s0 followed by β, as seen in Fig. 8b. The concept of preemption presented here is similar to the work by Wonham and Cai (2019).
We do not assume any relationship between the set of controllable and enforceable events at this moment. The notion or the intent of control in this framework involves the following techniques. Firstly, the generated controller prevents the system from firing or taking a particular path that violates the control requirement and secondly, it also prevents the system from reaching states designated as forbidden. In order to achieve the above control goals the supervisor enacts control based on the following three control criteria:
- 1.
Disabling of controllable events on a transition (static transition);
- 2.
Assignment of stronger guards to controllable transitions (transitions whose events are controllable);
- 3.
Enforcement of enforceable events.
To develop our control synthesis algorithms and strategies, we assume that the system evolves from one state to another based on the kind of transitions (static or dynamic transitions) at a given state. Thus, it is imperative to study the kind of transitions at a given state. We will explore the notion of control based on whether the transition is static or dynamic, or whether the values of the variable used on the transition can be tracked or not. Once, we have generated \(\mathcal {C}^{0}\) from Definition 9, we will iteratively pare down \(\mathcal {C}^{0}\) until it satisfies the requirements.
- Static Transition Case::
-
Given a static transition (i.e., a transition with the trivial guard “true”), if this transition is associated with a controllable event which is allowed by the plant \(\mathcal {G}_{W}\) but that violates system requirements, then we assume that this transition will be disabled by the supervisor. However, if the event associated with this transition is an uncontrollable event, then we must ensure that this static transition does not occur in the plant. For a static transition if the specification does not allow it, we will not allow the system to reach a state where it can occur.
- Dynamic Transition Case (Dynamic Type 1 Transition): :
-
Let \(\mathcal {G}_{W_{1}} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1},\mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1}, {\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_{1}, \mathcal {B}_{1}\)) and \(\mathcal {G}_{W_2} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2},{\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_2, \mathcal {B}_2)\) be two Web services, and suppose that the transition
 is an emission of a variable v1 from \(G_{W_{1}}\) to \(G_{W_{2}}\) and
is an emission of a variable v1 from \(G_{W_{1}}\) to \(G_{W_{2}}\) and  is reception of v1 by \(G_{W_{2}}\). Now, suppose that the variable v1 (the content of the message !m(v1)) has not been modified from its original value assigned by the transition t1, it means that the value of v1 will remain the same when \(G_{W_{2}}\) receives the message ?m(v1) on the transition t2.
is reception of v1 by \(G_{W_{2}}\). Now, suppose that the variable v1 (the content of the message !m(v1)) has not been modified from its original value assigned by the transition t1, it means that the value of v1 will remain the same when \(G_{W_{2}}\) receives the message ?m(v1) on the transition t2.
This implies that we can easily track the value of the variable v1 in the message from the service that sent it to the receiving service. Now, at the state that this variable is being used, if there is a condition on a transition (t2) from this state that imposes a restriction on the set of values the variable can take, then we need to make sure that the guard on t1 is never true for those values to prevent the system from reaching an illegal state. Hence, the supervisor can enact control by restricting the value of the variable at the sending service side before it would be received by the receiving service. The control strategy employed to deal with this kind of transition is to assign stronger guards to a controllable transition. Hence, we generate the guard g1 ∧¬g2 and attach it to the transition t1. In our example above, the Bank service Fig. 1c can accept a debit card, credit card or money order as a means of payment, but the specification in Fig. 7c prevents a payment with money order. To satisfy this constraint, we put a condition on the transition of the service that will send a request for payment to the Bank service not to send a request for money order payment.
- Dynamic Nondeterministic Transition Case (Dynamic Type 2 Transition): :
-
This case deals with atomic operations whose output value is unknown until runtime. This introduces an issue of nondeterminism into our model. Since the values of the variable are unknown until runtime we cannot treat this case in the same way as the previous case. During design time we will classify certain events (e.g., failure message events) as enforceable events. If such a transition does not exist we will introduce a new transition into the plant and the specification. To be able to prevent transitions that may cause a specification violation and that have guards containing outputs of atomic operations, we will rely on enforceable events to preempt uncontrollable events from happening when the output of the variable from atomic operations violates a specification. That is, if a failure could occur in the system due to values associated to atomic operations, then enforceable transitions are used to preempt the failure. This can be done by modification of the plant (Diekmann and Weidemann 2013; Wonham and Cai 2019). Consider Fig. 1a, the transition from state S2 to S3 labeled with checkAirlinesAvail(date,loc :: av) has an output variable av which can take KLM, AirCanada or Delta as its values. The operation checkAirlinesAvail(date,loc :: av) is assumed to be black-box, so we do not know which value it will assign to av. Now, the specification in Fig. 7b limits the values that av can take to only KLM and Delta. To ensure that the transition from state S3 to S4 in Fig. 1a is never taken when the value of av is AirCanada, we mark the transition
 in Fig. 1a as an enforceable transition. The value of av is monitored so that this enforceable transition can be used to preempt other transitions at runtime when the value of av violates a specification. This kind of situation is very common in SOA applications. For instance, the WS-BPEL language provides certain constructs such as Fault Handler and Event Handler to deal with unexpected failures that may occur at runtime. Example 1 below further illustrates the notion of event enforcement.
in Fig. 1a as an enforceable transition. The value of av is monitored so that this enforceable transition can be used to preempt other transitions at runtime when the value of av violates a specification. This kind of situation is very common in SOA applications. For instance, the WS-BPEL language provides certain constructs such as Fault Handler and Event Handler to deal with unexpected failures that may occur at runtime. Example 1 below further illustrates the notion of event enforcement.
Example 1
Event Enforcement
Consider the plant \(\mathcal {G}_{W}\) in Fig. 9 which at the initial state can emit a message !m1(x). The emission of this message transmits a variable x which is consumed by the transition from state s1 to s2. Now, the transition from state s2 to s3 uses the variable x as an input to the atomic operation atomop1(x :: y). This atomic operation performs some internal computation and outputs the variable y to be used in the next state. As stated above, all output transitions are controllable while all input and atomic operation transitions are uncontrollable.
Now, consider a specification on \(\mathcal {G}_{W}\), which states that every transition in \(\mathcal {G}_{W}\) is allowed except that the value of y is constrained to the set y ∈{β,γ}. Given this requirement, it means that \(\mathcal {G}_{W}\) must not be allowed to take the uncontrollable transition from s3 to s5 (i.e., y cannot be equal to λ). At this point, the problem is how to get to state s3 without firing the uncontrollable transition from s3 to s5 and also noting that (i) the value of y cannot be altered until \(\mathcal {G}_{W}\) is in state s2, and (ii) y is the output of the atomic operation atomop1(x :: y) and that the internal computation of atomop1(x :: y) is not known (i.e., atomop1(x :: y) is a black box and how the value of y is computed is not known and cannot be modified). To this end, all we can do is to take whatever value of y that is produced by atomop1(x :: y) at runtime.
The solution we provide is to ensure that there is an enforceable event exiting state s3 which will be used to preempt the uncontrollable transition from s3 to s5 at runtime. In more detail, the variable x and y will be monitored at runtime to ensure that once y = λ the enforceable transition from s3 to s7 will be triggered to preempt the transition s3 to s5. In the case that there is no enforceable outgoing event from state s3 then at design time, we add a new enforceable transition to \(\mathcal {G}_{W}\) which is triggered when the value of y turns out to be λ.
Definition 10
Controlled System
Let \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F}, V, \mathcal {B})\) be the an SLTS of a given plant, and let \(\mathcal {C} = (\mathcal {S}_{\mathcal {C}}, \mathcal {S}^{0}_{\mathcal {C}}, \mathcal {I}_{\mathcal {C}}, \mathcal {O}_{\mathcal {C}}, \mathcal {A}_{\mathcal {C}},{\Gamma }_{\mathcal {C}}, \mathcal {S}^{F}_{\mathcal {C}}, V_{\mathcal {C}}, \mathcal {B}_{\mathcal {C}})\) represent the controller of \(\mathcal {G}_{W}\). The controlled system \(\mathcal {C}\otimes \mathcal {G}_{W}\) representing the behaviour of \(\mathcal {G}_{W}\) when constrained (controlled) by \(\mathcal {C}\) is given by \(\mathcal {C} \otimes \mathcal {G}_{W} = (\mathcal {S}_{\mathcal {C}} \times \mathcal {S},\mathcal {S}^{0}_{\mathcal {C}} \times \mathcal {S}^{0},\mathcal {I}_{\mathcal {C}}\cup \mathcal {I}, \mathcal {O}_{\mathcal {C}}\cup \mathcal {O}, \mathcal {A}_{\mathcal {C}}\cup \mathcal {A}, {\Gamma }_{\mathcal {C}}\times {\Gamma }, \mathcal {S}^{F}_{\mathcal {C}} \times \mathcal {S}^{F}, V_{\mathcal {C}}\cup V, \mathcal {B}_{\mathcal {C}}\cup \mathcal {B})\) where:
In other words, a transition is possible in the plant if it is also possible in the controller transition system, which implies that the guards are true and the transition can be fired.
Definition 11
(Controlled System and Specification) Let m be the message header of the output message !m and the input message ?m. Let \(\mathcal {H}\) be the set of message headers of a given SLTS. Given a controlled system \(\mathcal {C}\otimes \mathcal {G}_{W} =(\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, V_{1},\mathcal {B}_{1}) \) and a specification \(\mathcal {T}^{W}= (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2}, {\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2})\) a simulation relation between \(\mathcal {C}\otimes \mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) is a relation \(R\subseteq \mathcal {S}_{1} \times \mathcal {S}_{2}\) such that ∀(s1,s2) ∈ R,
if
 in Γ1 and \(m\in \mathcal {H}\) then
in Γ1 and \(m\in \mathcal {H}\) then  and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\) or
and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\) or  and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\), and
and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\), andif
 and \( \alpha \in \mathcal {A}_{1}\) then
and \( \alpha \in \mathcal {A}_{1}\) then  and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\).
and \((s_{1}^{\prime }, s_{2}^{\prime }) \in {R}\).
4.6 Controllability
The original setting of supervisory control theory considers language-based controllability (Cassandras and Lafortune 2008; Wonham and Ramadge 1987) which assumes the underlying automata to be deterministic. Language-based controllability was subsequently extended to provide a stronger notion of controllability called state-controllability (Miremadi et al. 2008; Fabian and Lennartson 1996; Zhou and Kumar 2007) for non-deterministic discrete-events systems. In this work, we rely on a notion similar to state-based controllability to capture the concept of controllability of SLTS in our model.
For a given SLTS \(\mathcal {T}^{W}\) specification which is simulated by a given plant \(\mathcal {G}_{W}\), a reachable state (p,q) in \(\mathcal {G}_{W} \times \mathcal {T}^{W}\) is uncontrollable if the following holds: (1) if an uncontrollable transition labeled with α (static transition) can be fired from the state p in the plant but not from the state (p,q) in \(\mathcal {G}_{W} \times \mathcal {T}^{W}\); and (2) if an uncontrollable transition labeled with α and a guard g1 can be fired in \(\mathcal {G}_{W}\) at state p and this same uncontrollable transition labeled with α but a different guard g2 is possible at (p,q) in the \(\mathcal {G}_{W} \times \mathcal {T}^{W},\) then whenever g1 evaluates to true for a given set of values of a variable v, g2 does not always evaluate to true for the same values of v. That is, g1 does not imply g2. This implies that the uncontrollable transition at (p,q) leads to a forbidden state.
Let  denote that there exists at least one state s′ such that
denote that there exists at least one state s′ such that  and denote
and denote  as the set of enabled static transitions of the state \(s \in \mathcal {S}\) of the SLTS P. Similarly, let
as the set of enabled static transitions of the state \(s \in \mathcal {S}\) of the SLTS P. Similarly, let  denote that there exists a guard g and at least one state s′ such that
denote that there exists a guard g and at least one state s′ such that  and let
and let  represent the set of dynamic transitions enabled at state s of the SLTS P.
represent the set of dynamic transitions enabled at state s of the SLTS P.
Definition 12
Controllability
Given two SLTSs \(\mathcal {G}_{W} = (\mathcal {S}_{1}, \mathcal {S}^{0}_{1}, \mathcal {I}_{1}, \mathcal {O}_{1}, \mathcal {A}_{1},{\Gamma }_{1}, \mathcal {S}^{F}_{1}, {V}_{1}, \mathcal {B}_{1} )\) and \(\mathcal {T}^{W} = (\mathcal {S}_{2}, \mathcal {S}^{0}_{2}, \mathcal {I}_{2}, \mathcal {O}_{2}, \mathcal {A}_{2},{\Gamma }_{2}, \mathcal {S}^{F}_{2}, V_{2}, \mathcal {B}_{2} )\), representing the plant and the specification, respectively, such that \(\mathcal {T}^{W} \preceq \ \mathcal {G}_{W}\). Let \(R_{(\mathcal {T}^{W}\preceq \mathcal {G}_{W})}\) denote the simulation relation between \(\mathcal {T}^{W}\) and \(\mathcal {G}_{W}\). A pair of states \((p,q) \in R_{(\mathcal {T}^{W}\preceq \mathcal {G}_{W})}\subseteq \mathcal {S}_{1} \times \mathcal {S}_{2}\) is controllable if the following holds:
- 1.
Static Controllability:
$$\forall \delta \in {\Sigma}_{uc} : \delta \in E^{\mathcal{S}}_{\mathcal{G}_{W}}(p) \implies \delta \in E^{\mathcal{S}}_{(\mathcal{G}_{W} \times \mathcal{T}^{W})}((p,q))$$ - 2.
Dynamic Controllability:
$$ \begin{array}{@{}rcl@{}} &\forall \delta \in {\Sigma}_{uc} : (\delta, g_{1}) \in E^{\mathcal{D}}_{\mathcal{G}_{W}}(p) \implies (\exists g_{2}\in \mathcal{B}_{2}: (\delta, g_{2} )\in E^{\mathcal{D}}_{(\mathcal{G}_{W}\times \mathcal{T}^{W})}((p,q))\land (g_{1} \implies g_{2}))\\ &{\kern36pt}\lor~ (\exists \delta^{\prime}, \exists g_{3} \in \mathcal{B}_{2}: (\delta^{\prime},g_{3})\in E^{\mathcal{D}}_{(\mathcal{G}_{W}\times \mathcal{T}^{W})}((p,q)) \land (g_{3}=\text{true})\land~(\delta^{\prime} \in {\Sigma}_{f})) \end{array} $$
\(\mathcal {T}^{W}\) is said to be state controllable with respect to\(\mathcal {G}_{W}\) if all reachable states of \(\mathcal {G}_{W}\times \mathcal {T}^{W}\) are state controllable. According to Definition 12, uncontrollable transitions that are enabled in the reachable states of the plant state q by following the same trace, must also be enabled at the corresponding reachable state (p,q) of \(\mathcal {G}_{W}\times \mathcal {T}^{W}\). Thus, we say \(\mathcal {T}^{W}\) is controllable if: (1) δ is uncontrollable and δ is the current static transition event enabled in \(\mathcal {G}_{W}\) implies that δ is also enabled at the corresponding state of \(\mathcal {G}_{W}\times \mathcal {T}^{W}\); and (2) δ is a dynamic uncontrollable event and a guard g1 is possible at the current state of \(\mathcal {G}_{W}\) then, it implies that there exists a corresponding uncontrollable dynamic transition and a guard g2 in \(\mathcal {G}_{W}\times \mathcal {T}^{W}\) such that g2 is true only if g1 is true, or there exists an enforceable transition δ′ that can preempt any uncontrollable transition in the current enabled state.
Now, let \({g_{n}^{A}}(v)\) denote a guard gn with a variable v whose values depend on an output of an atomic operation A of a given transition system (e.g., in Fig. 10, A = func1(x :: y),v = y,gn = (y < 10)). We state the following corollary as a consequence of controllability of a given plant and a specification. Here we will assume that a guard depends on only one variable.
Corollary 1 below states that given a plant \(\mathcal {G}_{W}\) and a specification \(\mathcal {T}^{W}\), if a dynamic type 2 transition, say T, is enabled at a state p of the plant \(\mathcal {G}_{W}\) but not at a corresponding state (p,q) of the specification \(\mathcal {T}^{W}\) then, for the state (p,q) to be state controllable it implies that there must exist an enforceable transition also enabled at (p,q) to preempt T.
Corollary 1
Let\(\mathcal {G}_{W} = (\mathcal {S}_{\mathcal {G}_{W}}, \mathcal {S}^{0}_{\mathcal {G}_{W}}, \mathcal {I}_{\mathcal {G}_{W}}, \mathcal {O}_{\mathcal {G}_{W}}, \mathcal {A}_{\mathcal {G}_{W}}, {\Gamma }_{\mathcal {G}_{W}}, \mathcal {S}^{F}_{\mathcal {G}_{W}}, V_{\mathcal {G}_{W}}, \mathcal {B}_{\mathcal {G}_{W}})\)and\(\mathcal {T}^{W} = (\mathcal {S}_{\mathcal {T}^{W}}, \mathcal {S}^{0}_{\mathcal {T}^{W}}, \mathcal {I}_{\mathcal {T}^{W}}, \mathcal {O}_{\mathcal {T}^{W}}, \mathcal {A}_{\mathcal {T}^{W}}, {\Gamma }_{\mathcal {T}^{W}}, \mathcal {S}^{F}_{\mathcal {T}^{W}}, V_{\mathcal {T}^{W}}, \mathcal {B}_{\mathcal {T}^{W}}\))denote a plant and its specification, respectively, andlet\((p,q)\in \mathcal {S}_{\mathcal {G}_{W}}\times \mathcal {S}_{\mathcal {T}^{W}}\).If\(\exists \delta \in {\Sigma }_{uc}, \exists g^{A}(v) \in \mathcal {B}: (\delta , g^{A}(v)) \in E^{D}_{\mathcal {G}_{W}}(p)\)but\(\nexists (g^{A}(v))^{\prime } \):\((\delta ,(g^{A}(v))^{\prime }) \in E^{D}_{\mathcal {T}^{W}}(p,q),\)andgA(v) ∧ (gA(v))′satisfiable, then if (p,q) is state controllable then there must existsδ′∈Σfand a guardg″such\((\delta ^{\prime },g^{\prime \prime }) \in E^{D}_{\mathcal {T}^{W}}(p,q)\).
Proof
The proof follows from the second part of definition 12 where the transition is a dynamic type 2 transition with guard \({g_{n}^{A}}(v)\). □
Example 2
Illustration of Corollary 1
Consider the plant service \(\mathcal {G}_{W}\) in Fig. 11 and the target service \(\mathcal {T}^{W}\) of Fig. 12.  is a dynamic type 2 transition whose guard (y < 10) has a variable whose values depends on the output of the atomic operation func1(x :: y).
is a dynamic type 2 transition whose guard (y < 10) has a variable whose values depends on the output of the atomic operation func1(x :: y).
Since \(\mathcal {T}^{W}\) does not allow T at state S2, and \(\mathcal {T}^{W}\) is state controllable with respect to \(\mathcal {G}_{W}\), then there must exist an enforceable transition T′ also enabled at state S2 which is given by  to preempt T at runtime.
to preempt T at runtime.
The control solution that we seek in our approach requires that the system does not reach a state from which the only exiting transitions lead to unsafe states. We formalize this in the following definition. Recall from Definition 9 that \(\mathcal {S}^{\text {Bad}}\) denotes a set of bad or forbidden state.
In the following we specify what a legitimate controller is. Given a plant modeled by an SLTS \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F}, V, \mathcal {B})\), a legitimate controller \(\mathcal {C}\) for \(\mathcal {G}_{W}\) is one that can (i) dynamically enable or disable static controllable transitions of \(\mathcal {G}_{W}\); (ii) can assign stronger guards to dynamic type 1 transitions; and (iii) enforce enforceable transitions to preempt dynamic type 2 transitions.
Formally, we define a legitimate controller as follows.
Definition 13
Legitimate Controller
Given a plant modeled by an SLTS \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F}, V, \mathcal {B})\), a legitimate controller \(\mathcal {C}\) for \(\mathcal {G}_{W}\)is such that for all reachable states (p,q) in \(\mathcal {C}\otimes \mathcal {G}_{W}\) if:
- 1.
\(\forall \delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}(p) \) and \(\delta \notin E^{\mathcal {S}}_{(\mathcal {G}_{W} \otimes \mathcal {C})}((p,q))\) ⇒ δ ∈Σc,
- 2.
\(\forall \delta \in {\Sigma }_{uc}, g\in \mathcal {B}\) and \((\delta , g) \in E^{\mathcal {D}}_{\mathcal {G}_{W}}(p) \) then ∃g′ in \(\mathcal {C}\) such g′≤ g and \((\delta , g^{\prime } )\in E^{\mathcal {D}}_{(\mathcal {G}_{W}\otimes \mathcal {C})}((p,q))\),
- 3.
\(\forall \delta \in {\Sigma }_{uc}: \exists {g_{1}^{A}}(v) \in \mathcal {B}\) and \((\delta , {g_{1}^{A}}(v)) \in E^{D}_{\mathcal {G}_{W}}(p)\) then
- (a)
\(\exists {g_{2}^{A}}(v)\) such that \((\delta , {g_{2}^{A}}(v)) \in E^{D}_{\mathcal {G}_{W}\otimes \mathcal {C}}(p,q),\) and \({g_{1}^{A}}(v)\land {g_{2}^{A}}(v)\) satisfiable or
- (b)
∃δ′∈Σf and ∃g″ such that \((\delta ^{\prime },g^{\prime \prime }) \in E^{D}_{\mathcal {G}_{W}\otimes \mathcal {C}}(p,q) \) and g″ = true.
- (a)
The control solution that we seek in our approach requires that the system does not reach a state from which the only exiting transitions lead to unsafe states. We formalize this in the following definition.
Definition 14
Non-blocking
Let \(\mathcal {G}_{W} = (\mathcal {S}, \mathcal {S}^{0}, \mathcal {I}, \mathcal {O}, \mathcal {A},{\Gamma }, \mathcal {S}^{F},V, \mathcal {B})\) be an SLTS, a state s is non-blocking if there exists a sequence w and a sequence of guards g″ such that  and \(s^{\prime } \in \mathcal {S}^{F}\backslash \mathcal {S}^{\text {Bad}}\), where \(\mathcal {S}^{\text {Bad}}\) is the set of unsafe (bad) states. An SLTS \(\mathcal {G}_{W}\) is nonblocking if every reachable state of \(\mathcal {G}_{W}\) is nonblocking.
and \(s^{\prime } \in \mathcal {S}^{F}\backslash \mathcal {S}^{\text {Bad}}\), where \(\mathcal {S}^{\text {Bad}}\) is the set of unsafe (bad) states. An SLTS \(\mathcal {G}_{W}\) is nonblocking if every reachable state of \(\mathcal {G}_{W}\) is nonblocking.
A controller is minimally restrictive in the sense that it interferes with the progress of the system only when the violation of the specification is otherwise inevitable. It is natural to require that a controller restricts the plant as little as possible. We formalize this qualitative property in the following definition using the pre-order notion implied by simulation relation.
Definition 15
Minimally Restrictive Controller
Given a plant \(\mathcal {G}_{W}\) and a specification \(\mathcal {T}^{W}\), a controller \(\mathcal {C}\) for \(\mathcal {G}_{W}\) satisfying \(\mathcal {T}^{W}\) is minimally restrictive if there does not exist a controller \(\mathcal {C}^{\prime }\) for \(\mathcal {G}_{W}\) such that \(\mathcal {C} \otimes \mathcal {G}_{W} \preceq \mathcal {C}^{\prime }\otimes \mathcal {G}_{W}\).
The composition problem that we consider is as follows. Given a set of available services \(\mathcal {G}_{W_{1}},\mathcal {G}_{W_{2}},...,\mathcal {G}_{W_{n}}\) and a set of specifications \(\mathcal {T}^{W}\) representing the goal service over the same environment (same set of messages and atomic actions), we would like to construct a controller \(\mathcal {C}\) such that the \(\mathcal {C} \otimes (\mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}\)) is simulated by \(\mathcal {T}^{W}\) satisfying some controllability and nonblocking constraints. Thus, \(\mathcal {C}\) serves as a controller that interacts with the uncontrolled system in such a way that all its executions satisfy \(\mathcal {T}^{W}\) and that \(\mathcal {C}\) is minimally restrictive. That is, we seek to generate an SLTS which interacts with the system \(\mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}\) to satisfy the specification \(\mathcal {T}^{W}\). In addition to requiring that the generated controller satisfies controllability and nonblocking criteria, the controlled system is also free of errors that may result from communication among component services. We formalize this in the following problem statement.
Definition 16
Composition Problem
Let \(\mathcal {G}_{W_{1}}, \mathcal {G}_{W_{2}}, \hdots ,\mathcal {G}_{W_{n}}\) be a set of SLTSs and let \(\mathcal {T}^{W}\) be the composition requirements. The composition problem is to find a non-blocking, communication-error free to depth \(p\in \mathbb {N}\) and minimally restrictive controller \(\mathcal {C}\) such that \(\mathcal {C} \otimes (\mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}) \preceq \mathcal {T}^{W}\).
The definition implies that the controller constrains the plant such that every transition that can be taken by the controlled system \(\mathcal {C}\) ⊗ (\(\mathcal {G}_{W_{1}} \parallel \mathcal {G}_{W_{2}}...\parallel \mathcal {G}_{W_{n}}\)) can also be taken in the specification. The intuition is that controllability will be necessary and sufficient to solve the composition problem as formulated in Section 6.
5 Composition synthesis algorithm
In this section, we provide the core details of our approach by presenting a set of algorithms that can be used to generate a composition. The composition generation technique proposed in our framework is an incremental process. Algorithm 1 presents a step-by-step process that can be used to build a non-blocking and communication error free to depth \(p\in \mathbb {N}\) controller for a given system that ensures that the controllability condition is met. The algorithm takes the set of available component services and a goal service specifying the functional requirements as inputs. The algorithm first refines the plant \(\mathcal {G}_{W}\) by removing communication errors to a given depth p which is given by Line 2. Once the plant has been transformed into its communication-error free SLTS form, we check whether the target service is simulated by the plant \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\) (Line 3). The function simulationCheck(\(\mathcal {G}_{W},\mathcal {T}^{W}\)) is an implementation of the simulation relation given in Definition 5. The function simulationCheck(\(\mathcal {G}_{W},\mathcal {T}^{W}\)) takes \(\mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) as inputs, and checks if \(\mathcal {G}_{W}\) simulates \(\mathcal {T}^{W}\). It returns “true” if \(\mathcal {G}_{W}\) simulates \(\mathcal {T}^{W}\) and false if \(\mathcal {G}_{W}\) does not simulate \(\mathcal {T}^{W}\). In the case that a simulation relation exists between the plant and the target service, we then make adjustments to the plant to include a special event that will enable the controller to enforce enforceable events at runtime. This is given at Line 4 of Algorithm 1. The algorithm then computes the composition refinement (given by Definition 9) of the plant and the target service to get a new SLTS \(\mathcal {C}^{0}\) upon which further minimization steps will be performed (Line 5).

The next step of the algorithm (repeat until loop Lines 7-12) then performs various reductions on \(\mathcal {C}^{0}\). Line 9 performs static controllability minimization which is given by Algorithm 3. Line 10 eliminates blocking states and states from which only bad states are reachable. In Line 11 of the algorithm we perform dynamic controllability minimization and generate stronger guards to ensure that all executions of the \(\mathcal {C}^{0}\) lead to safe states. Lines 7-12 performs a fixed point computation on \(\mathcal {C}^{0}\) and terminates when a fixed point is reached (i.e., if \(\mathcal {C}^{k} ==\mathcal {C}^{k-1}\)). Finally, we refine \(\mathcal {C}^{K}\) by removing communication errors from \(\mathcal {C}^{k}\). To ensure that the generated controller is able to communicate with the available services, we reverse the direction of the messages of \(\mathcal {C}^{k}\) in Line 14. This implies that an input message ?m(x) in \(\mathcal {C}^{k}\) will become an output message !m(x) and vice versa. The message header m does not change, it is only the directions of the message that change. In the event that the algorithm does not find a simulation relation between the plant and the target service we iteratively refine the target service until a simulation relation is found.
Algorithm 2 converts a given SLTS into its communication-error free form to the depth p as given in Definition 8. The input to this algorithm is the asynchronous parallel composition of the available services \(\mathcal {G}_{W}\). Algorithm 2 traverses the SLTS to eliminate transitions that results in communication errors to depth p. Lines 6-14 implement the first part of Definition 8. At Lines 6-14, given a state sj of \(\mathcal {G}_{W}\), if there is an output transition  exiting state sj then Line 9 of the algorithm checks that there exists a run r of length p or less such that a corresponding input transition
exiting state sj then Line 9 of the algorithm checks that there exists a run r of length p or less such that a corresponding input transition  is in r such that t′ is preceded by t . In the event that there is no such r Algorithm 2 (Line 2) eliminates the transition t. Similarly, Lines 16-26 remove transitions that do not meet the second condition of Definition 8. Lines 30-49 of Algorithm 2 implement condition (3) of Definition 8. For each output transition
is in r such that t′ is preceded by t . In the event that there is no such r Algorithm 2 (Line 2) eliminates the transition t. Similarly, Lines 16-26 remove transitions that do not meet the second condition of Definition 8. Lines 30-49 of Algorithm 2 implement condition (3) of Definition 8. For each output transition  in \(\mathcal {G}_{W}\) and for each run r containing at least a corresponding input transition
in \(\mathcal {G}_{W}\) and for each run r containing at least a corresponding input transition  , Lines 33-46 check that the number of sends of the message m is equal to the number of receives of the message m. If during the traversal of the run r, we encounter a send of m (Line 34), then messageCounter is incremented, if we encounter a receive of m (Line36), then messageCounter is decremented; if that makes messageCounter negative, the input transition z is eliminated at Line 39 (because there are more receives than sends in r). When we reach the end of r and messageCounter is greater than 0, we eliminate t at Line 44 (because r contains more sends that receives). However, when we reach the end of r and the counter for messageCounter is 0, then r satisfies condition (3) of Definition 8. Algorithm 2 of Line 3-51 iterate until Definition 8 is satisfied.
, Lines 33-46 check that the number of sends of the message m is equal to the number of receives of the message m. If during the traversal of the run r, we encounter a send of m (Line 34), then messageCounter is incremented, if we encounter a receive of m (Line36), then messageCounter is decremented; if that makes messageCounter negative, the input transition z is eliminated at Line 39 (because there are more receives than sends in r). When we reach the end of r and messageCounter is greater than 0, we eliminate t at Line 44 (because r contains more sends that receives). However, when we reach the end of r and the counter for messageCounter is 0, then r satisfies condition (3) of Definition 8. Algorithm 2 of Line 3-51 iterate until Definition 8 is satisfied.


Algorithm 3 constructs a static controllable SLTS and iteratively creates new transitions that lead to bad states from a given SLTS. The input to this algorithm is the plant, and the composition refinement of the plant and the target service \(\mathcal {C}^{k}\). In the first iteration of the repeat until loop \(\mathcal {C}^{k}\) is given by \(\mathcal {C}^{0}\). The set of states of \(\mathcal {C}^{k}\) is partitioned into safe states \(\mathcal {S}^{Good}_{\mathcal {C}^{k}}\) and bad states \(\mathcal {S}^{Bad}_{\mathcal {C}^{k}}\). For a given state p in \(\mathcal {G}_{W}\) and a corresponding state in \((p,q) \in \mathcal {C}^{k}\), if a static uncontrollable transition is enabled at state p but not in (p,q) (this is given by the first and second for loops), first the algorithm creates a new bad state \( s^{\text {Bad}} \in \mathcal {S}_{\mathcal {C}^{k}}\) and all dynamic transitions leading to (p,q) are diverted to sBad (Lines 6-10). This keeps the structure of dynamic transitions. Second, the uncontrollable state is eliminated including all outgoing transitions (Lines 11-13). Finally, unreachable states and associated transitions are also eliminated at Line 15.


Algorithm 4 presents a technique to deal with unsafe states and blocking states. This algorithm takes an SLTS \(\mathcal {C}^{k}\) as its input. \(\mathcal {C}^{k}\) is assumed to be the SLTS obtained after some iterations of the repeat until loop in Algorithm 1 (Lines 7-11). Specifically, \(\mathcal {C}^{k}\) is the output of Algorithm 3. The iteration of the first for loop statement collects and stores all states from which no marked state is reachable or from which only bad states can be reached (Lines 6-10). The algorithm stores these states in the buffer BlockandUnsafe. For each state in BlockandUnsafe, Lines 12-16 of the algorithm create a new bad state sBad and assign any dynamic transition that leads to a state in BlockandUnsafe to sBad. This is done to preserve the structure of dynamic transitions as done in Algorithm 3. Finally, Lines 18-24 eliminate all states and transitions collected in Lines 6-10. That is, all states in BlockandUnsafe and all associated transitions that lead to a state in BlockandUnsafe are removed.

Algorithm 5 presents an approach that can be used to compute a safe and dynamic controllable SLTS of a given system. This algorithm implements the second part of the definition of controllability given in Definition 12. It involves the generation and attachment of stronger guards to transitions and the collections of variables to be monitored at runtime as well as the removal of dynamic uncontrollable states and transitions.
First, we assume that the set of variables is partitioned into trackable and non-trackable variables. Trackable variables (which we will call deterministic variables because their occurrence is deterministic) are those variables whose values do not change from where they were declared to where they are being used, whereas non-trackable (which we will call nondeterministic variables because their occurrence is nondeterministic) variables are those whose values we cannot predict from when they were declared to when they are used. Specifically, trackable variables are associated with dynamic type 1 transitions while non-trackable variables are associated with dynamic type 2 transitions. Non-trackable variables are the output of atomic operations.
Define the depth-first traversal function  which returns the set of input transitions ΓDFS that occur along any run that leads to state s from the initial state of \(\mathcal {C}^{k}\), subject to the constraint that we consider only runs in which there is no repetition of transitions and states allowed, other than one repetition of a state if it is the start and end state of a loop. The function
which returns the set of input transitions ΓDFS that occur along any run that leads to state s from the initial state of \(\mathcal {C}^{k}\), subject to the constraint that we consider only runs in which there is no repetition of transitions and states allowed, other than one repetition of a state if it is the start and end state of a loop. The function  returns the set of input transitions that have d as an input variable for message m. The DFS function can be implemented using any shortest path or graph traversal algorithm, such as Dijkstra’s Algorithm. As an example, consider the system \(\mathcal {C}^{k}\) in Fig. 13,
returns the set of input transitions that have d as an input variable for message m. The DFS function can be implemented using any shortest path or graph traversal algorithm, such as Dijkstra’s Algorithm. As an example, consider the system \(\mathcal {C}^{k}\) in Fig. 13,  will return
will return 
 . Note that the transition
. Note that the transition  is included in ΓDFS even though the state s2 is repeated in a run from s0 to s3 because the state s2 is repeated only once, in a single pass through the loop. Since we do not consider runs in which loops appear more than once,
is included in ΓDFS even though the state s2 is repeated in a run from s0 to s3 because the state s2 is repeated only once, in a single pass through the loop. Since we do not consider runs in which loops appear more than once,  will not have to traverse an infinite number of runs.
will not have to traverse an infinite number of runs.
Now, Algorithm 5 starts by collecting all transitions that lead to bad states from a given state (Lines 13-27). In these steps we keep track of transitions that lead to a bad state based on the evaluation of nondeterministic variables (Lines 14-19), this is given by the first if statement. The else statement after the if statement keeps track of transitions that lead to an unsafe state due to the evaluation of deterministic variables (Lines 20-27). The next step of the algorithm strengthens the guards of each transition (Lines 30-38). Now, given that the value of deterministic variables can be tracked implies that we can trace back to where it was originally defined from where it is being used in order to strengthen the guard.

Given a transition which leads to a bad state due to deterministic variable (z =  , we check specific sequences of transitions or paths of \(\mathcal {C}^{k}\) to locate where it was declared first
, we check specific sequences of transitions or paths of \(\mathcal {C}^{k}\) to locate where it was declared first  using the function DFS and then we strengthen the guards which is given by taking the conjunction of the current guard on the transition and the negation of the guard of where it is being used
using the function DFS and then we strengthen the guards which is given by taking the conjunction of the current guard on the transition and the negation of the guard of where it is being used  . Lines 40-53 of the algorithm check every state that has a transition that leads to a bad state due to nondeterministic variables for enforceable transitions. In the case that an enforceable transition is enabled at this state, we save the variable for runtime monitoring (Lines 42-44). The runtime monitoring involves equipping the generated controller with additional capability to be able to track a given variable for certain values and then trigger certain actions based on the values of this variable. On the other hand, if there is no enforceable transition enabled at this state, the algorithm (Line 46) first creates a new state in \(\mathcal {S}^{Bad}_{\mathcal {C}}\) and diverts all dynamic transitions to it as done in Algorithm 3. Next, we completely eliminate the entire state and all transitions associated with this state from \(\mathcal {C}^{k}\).
. Lines 40-53 of the algorithm check every state that has a transition that leads to a bad state due to nondeterministic variables for enforceable transitions. In the case that an enforceable transition is enabled at this state, we save the variable for runtime monitoring (Lines 42-44). The runtime monitoring involves equipping the generated controller with additional capability to be able to track a given variable for certain values and then trigger certain actions based on the values of this variable. On the other hand, if there is no enforceable transition enabled at this state, the algorithm (Line 46) first creates a new state in \(\mathcal {S}^{Bad}_{\mathcal {C}}\) and diverts all dynamic transitions to it as done in Algorithm 3. Next, we completely eliminate the entire state and all transitions associated with this state from \(\mathcal {C}^{k}\).

Once the iteration of the repeat until loop of Algorithm 1 has terminated, all states in \(\mathcal {S}^{Bad}_{\mathcal {C}}\) would been made unreachable and there is no need to keep them. Hence, Algorithm 6 is called to remove all bad states and transitions in the set of bad states \(\mathcal {S}^{Bad}_{\mathcal {C}}\). Algorithm 6 iterates over the set of states in \(\mathcal {S}^{Bad}_{\mathcal {C}}\) and eliminates all states in \(\mathcal {S}^{Bad}_{\mathcal {C}}\) including associated transitions.

Once all the issues relating to controllability and non-blocking have been dealt with, the next stage of the algorithm is to reverse the directions of the messages of the resulting controller. This is done to allow for communication between the plant and the controller. This ensures that an output message in the plant’s transition system can be consumed by an input message in the controller’s transition system and vice versa. Given an SLTS \(\mathcal {C}\) as the input to Algorithm 7, it reverses the direction of the messages of \(\mathcal {C}\). That is, given an input (output) message ?m(x), Algorithm 7 will change it to and output (input) message !m(x) and vice versa.
A composition generation process may fail if the given plant cannot simulate its specification. Algorithm 8 iteratively pares down a given specification so that it can be simulated by a given plant. The algorithm takes \(\mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) as inputs such that there is no simulation relation between \(\mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) and returns a new specification \(\mathcal {T}^{W^{\prime }}\) that can be simulated by \(\mathcal {G}_{W}\). Line 2 of Algorithm 8 defines a maximal relation R given by the cross product of the states of \(\mathcal {G}_{W}\) and \(\mathcal {T}^{W}\). Now, Line 6 of the algorithm iterates over each pair of reachable states (t1,si) ∈ R such that there exists a transition  and then checks for the following three cases where a plant may fail to simulate a given specification.
and then checks for the following three cases where a plant may fail to simulate a given specification.
There is no matching transition at state si of the plant. In this case the transition

 will be removed (Lines 8-9).
will be removed (Lines 8-9).There exists a transition
 and (ti,si) ∈ R but the guard g1 is not a subguard of g2, i.e., g1 ≤ g2. In this case the guard on \(\mathcal {T}^{W}\) is strengthened to that of \(\mathcal {G}_{W}\) (Lines 11-12).
and (ti,si) ∈ R but the guard g1 is not a subguard of g2, i.e., g1 ≤ g2. In this case the guard on \(\mathcal {T}^{W}\) is strengthened to that of \(\mathcal {G}_{W}\) (Lines 11-12).There exists a transition
 and g1 ≤ g2 but (ti,si)∉R. In this case the transition
and g1 ≤ g2 but (ti,si)∉R. In this case the transition  is eliminated (Lines 13-15).
is eliminated (Lines 13-15).
The algorithm terminates when all transitions that prevent the specification from being simulated by the plant have been dealt with, i.e., \(\mathcal {T}^{W} == \mathcal {T}^{W^{\prime }}\).

Algorithm 9 is a procedure to modify a given SLTS to include a special transition (𝜖 transition) which we will call a “timeout” transition which will be used at runtime to provide the generated controller the ability to be able to preempt certain dynamic type 2 transitions (which we will call preemptable transitions) using enforceable transitions. Self-loops are treated in a similar way. The technique presented here is identical to that in the work by Wonham and Cai (2019).

Example 3 below is a small example to illustrate how Algorithm 1 works.
Example 3
Consider the plant \(\mathcal {G}_{W}\) (assumed to be the asynchronous parallel composition of some given services) in Fig. 14a and the specification \(\mathcal {T}^{W}\) in Fig. 14b as the input to Algorithm 1. As noted above input and function invocation transitions are considered as uncontrollable and output transitions are controllable (i.e., !msg1(x),!msg3(var),!msg2(z) ∈Σc, ?msg1(x), ?msg2(z), ?msg3(var), atom3(x), atom1(x,y), atom2(y,v), atom3(x), ?fail() ∈Σuc, !fail() ∈Σf). Clearly, \(\mathcal {G}_{W}\) simulates \(\mathcal {T}^{W}\). We will consider generating a communication-error free controller to depth five based on the fact that the longest run without loops from the initial state of the plant to a terminal states has depth five. Hence, we choose p to be 5. Line 5 of Algorithm 1 computes the composition refinement \(\mathcal {C}^{0}\) which is represented in Fig. 14c. Applying the rest of Algorithm 1 (Lines 7-22) to \(\mathcal {C}^{0}\) gives the following (where we will only consider steps of the algorithm that are relevant to this example):
- 1.
(Algorithm 1 Lines 7-12) within the repeat until loop we have the following steps:
- (a)
k = 1 means we will pass \(\mathcal {C}^{0}\) to the three functions within the repeat until loop (Algorithm 1 Lines 7-12)
- (i)
Static Controllability (Line 9 Algorithm 1)
Starting from the initial state of \(\mathcal {C}^{0}\) every state of \(\mathcal {C}^{0}\) satisfies the static controllability condition except for state (s5,t5) where there is an uncontrollable static transition
 enabled in the plant but not at the corresponding state (s5,t5) of \(\mathcal {C}^{0}\). This implies that state (s5,t5) and the associated transitions
enabled in the plant but not at the corresponding state (s5,t5) of \(\mathcal {C}^{0}\). This implies that state (s5,t5) and the associated transitions  and
and  will be eliminated from \(\mathcal {C}^{0}\) (Lines 12-14 of Algorithm 3). This produces the SLTS in Fig. 14d
will be eliminated from \(\mathcal {C}^{0}\) (Lines 12-14 of Algorithm 3). This produces the SLTS in Fig. 14d - (ii)
Blocking states (Line 10 Algorithm 1)
At this stage no state of the \(\mathcal {C}^{0}\) in Fig. 14d is blocking, we proceed to the next step.
- (iii)
Dynamic Controllability (Line 11 Algorithm 1)
At this stage of the algorithm, there are three transitions that lead to bad states
 (BAD2),
(BAD2),  in the \(\mathcal {C}^{0}\) of Fig. 14d. By applying the next step of the algorithm we have the following.
in the \(\mathcal {C}^{0}\) of Fig. 14d. By applying the next step of the algorithm we have the following.
Strengthening and Attachment of Guards (Lines 30-38 of Algorithm 5)
The two uncontrollable transitions
 (BAD1) and (s1,t1)
(BAD1) and (s1,t1)  are dynamic type 1 transitions since the values of the variables x and var can be tracked from where they were declared. Hence, at this stage the algorithm strengthens the guards of these transitions so that the state BAD1 and BAD3 are made unreachable by attaching the guard ¬(3 ≤ x < 7) and var∉{db} to the transition
are dynamic type 1 transitions since the values of the variables x and var can be tracked from where they were declared. Hence, at this stage the algorithm strengthens the guards of these transitions so that the state BAD1 and BAD3 are made unreachable by attaching the guard ¬(3 ≤ x < 7) and var∉{db} to the transition  and the transition
and the transition  , respectively. The resultant SLTS is given in Fig. 14e.
, respectively. The resultant SLTS is given in Fig. 14e.Event Enforcement and Collection of Runtime Variable (Lines 40-50 of Algorithm 5)
The transition
 is a dynamic type 2 transition since the variable y depends on the output of the atomic operation atom1(x,y) which cannot be tracked. This step of the algorithm will check for the enforceable transition
is a dynamic type 2 transition since the variable y depends on the output of the atomic operation atom1(x,y) which cannot be tracked. This step of the algorithm will check for the enforceable transition  and save the variable y to be monitored at runtime and then enforce !fail() when y=a, to prevent BAD2 from being reached.
and save the variable y to be monitored at runtime and then enforce !fail() when y=a, to prevent BAD2 from being reached.
- (i)
- (b)
k = 2 means we will pass \(\mathcal {C}^{1}\) (Fig. 14e) to the three functions in the repeat until loop (Algorithm 1 Lines 7-12)
- (i)
Static Controllability (Line 9 Algorithm 1)
Again starting from the initial state of \(\mathcal {C}^{1}\) (Fig. 14e) every state of \(\mathcal {C}^{1}\) satisfies the static controllability condition except for state (s3,t3) where there is an uncontrollable static transitions
 enabled in the corresponding state of the plant but not at the state (s3,t3) of \(\mathcal {C}^{1}\). This implies that state (s3,t3) and the associated transitions
enabled in the corresponding state of the plant but not at the state (s3,t3) of \(\mathcal {C}^{1}\). This implies that state (s3,t3) and the associated transitions 
 and
and  will be eliminated from \(\mathcal {C}^{1}\) (Lines 12-14 of Algorithm 3).
will be eliminated from \(\mathcal {C}^{1}\) (Lines 12-14 of Algorithm 3). - (ii)
Blocking states (Line 10 Algorithm 1)
Now, because in the previous step the transition from state (s7,t7) to state (s3,t3) was eliminated, state (s7,t7) becomes a blocking state since it is not a final state and does not lead to a final state. Given this we have the following steps:
create a new state BAD4 and assign any dynamic transition leading to state (s7,t7) to BAD4 (Algorithm 4 Lines 13-15)
then eliminate (s7,t7) (Algorithm 4 Lines 18-24)
The results of (i) and (ii) are shown in the diagram in Fig. 14f.
- (iii)
Dynamic Controllability (Line 11 Algorithm 1)
A new bad state BAD4 was added to \(\mathcal {C}^{1}\) and needs to be made unreachable. (Note that all other BAD states are still unreachable.) We have the following step:
Strengthening and Attachment of Guards (Lines 30-38 of Algorithm 5)
 is an uncontrollable dynamic type 1 transitions since the values of the variable var can be tracked from when it was declared. Hence, at this stage the algorithm strengthens the guard of this transition so that the state BAD4 is made unreachable by attaching the guard var∉{cr} to the transition
is an uncontrollable dynamic type 1 transitions since the values of the variable var can be tracked from when it was declared. Hence, at this stage the algorithm strengthens the guard of this transition so that the state BAD4 is made unreachable by attaching the guard var∉{cr} to the transition  (shown Fig. 14f).
(shown Fig. 14f).
- (i)
- (c)
k = 3 means we will pass \(\mathcal {C}^{2}\) (Fig. 14f) to the three functions in the repeat until loop.
Iterating over the repeat until loop again will return the same SLTS shown in Fig. 14f, i.e., \(\mathcal {C}^{3}= \mathcal {C}^{2}\), hence the loop terminates.
- (a)
- 2.
Line 13 of Algorithm 1
Now once the loop terminates, the next stage is to remove all the bad states (BAD1, BAD2, BAD3, BAD4) from \(\mathcal {C}^{3}\) by calling Algorithm 6. In addition, all transitions in and out of these bad states are removed.
- 3.
Line 14 of Algorithm 1
\(\mathcal {C}^{3}\) is not communication-error free since the transition
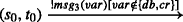 (s1,t1) can emit the message !msg3(var) but there is no matching input transition in \(\mathcal {C}^{3}\) to consume it, hence this step eliminates
(s1,t1) can emit the message !msg3(var) but there is no matching input transition in \(\mathcal {C}^{3}\) to consume it, hence this step eliminates  from \(\mathcal {C}^{3}\). Next, the if statement at Line 15 requires that the execution goes back to Line 7, but in this example when we go back to Line 7 the result remains the same.
from \(\mathcal {C}^{3}\). Next, the if statement at Line 15 requires that the execution goes back to Line 7, but in this example when we go back to Line 7 the result remains the same. - 4.
Line 16 of Algorithm 1,
This step reverses the messages of \(\mathcal {C}^{2}\) producing the final output \(\mathcal {C}\) as shown in Fig. 14g.
The task of labeling an existing transition as enforceable transition or creating a new enforceable transition in the controlled system to be used to preempt dynamic type 2 transitions is mostly dependent on the domain and the designer perspective. In addition, in choosing the target state of an enforceable transition is dependent on the current state of the system and the domain being modeled. That is, in case there is a failure as a result unsuspected output of a dynamic type 2 transition, what state should the system go to; should the system transition to the initial state, should the system try to do the previous transition again and so on. In Example 3 the choosing of the enforceable transition was trivial since the plant already had a transition  that lead to the initial state and because this example had no domain restriction.
that lead to the initial state and because this example had no domain restriction.
We have applied Algorithm 1 to various small examples. Also, Algorithm 1 has been manually applied to the flight booking example introduced earlier. The asynchronous parallel composition forming the plant of this example has 150 states and 3410 transitions while computing the composition refinement of the plant and the specification yielded a transition system \(\mathcal {C}^{0}\) with 175 states and 3945 transitions. Applying Lines 6-16 of the algorithm to \(\mathcal {C}^{0}\) will further reduce the number of states and transitions. We hope to automate the process in the near future.
5.1 Termination arguments
For a complete proof of termination including an analysis of the computational complexities of Algorithm 1, the reader can refer to the dissertation by Atampore (2017, p. 189). In general, to prove that Algorithm 1 terminates, one would have to show that each of the other algorithms (i.e., Algorithms 2 to 9) called by Algorithm 1 terminate and finally show that Algorithm 1 terminates (by showing that every loop and recursive call terminates by providing the necessary termination arguments). In what follows, we present a brief argument to show that Algorithm 1 terminates in a finite number of steps. We consider three cases.
- (1)
Lines 8-11 in Algorithm 1 (inside repeat until loop):
Algorithm 3
The outer loop in Line 3 loops over the states of the plant \(\mathcal {G}_{W}\) and the specification \( \mathcal {T}^{W}\), respectively. This loop terminates since the set of states of \(\mathcal {G}_{W}\) and that of \(\mathcal {T}^{W}\) are finite. The two inner loops in Line 4 and Line 6 iterate over the set of static and dynamic transitions of \(\mathcal {C}^{k}\), respectively. Since these sets are finite it implies that these two inner loops terminate. More importantly, the for loop in Lines 6–11 loops over the set of states of \(\mathcal {C}^{k}\) and creates new states and transitions which are added to \(\mathcal {C}^{k}\). The creation of new states and transitions is bounded by the size of the set of states in \(\mathcal {C}^{k}\). In the worst case, the creation of these new states and transitions will stop after looping over the entire set of states \(\mathcal {C}^{k}\) which is finite.
Algorithm 4
This algorithm has three main for loops. In the worst case each loop is bounded by the size of the set of states in \(\mathcal {C}^{k}\) which is finite. The first for loop searches for all states and transitions that result in blocking and collects them into a buffer. It terminates when all transitions and states leading to blocking have been collected. The second for loop in this function creates new states to preserve the structure of dynamic transitions and terminates when all new states have been created. In the worst case the addition of new states and transitions is bounded by the size of the set of states in \(\mathcal {C}^{k}\) which is finite and hence will eventually terminate. The last nested for loop iterates over the set of states and transition of \(\mathcal {C}^{k}\) and eliminates all blocking states and transitions collected in the previous steps. This loop terminates when all blocking states have been eliminated from the states of \(\mathcal {C}^{k}\).
Algorithm 5
In this algorithm, the iterations in Lines 13–27 perform a search on the set of states and transitions of \(\mathcal {C}^{k}\) and collect all the states and transitions that lead to bad states based on whether the value of a given variable can be modified or not from when it was declared to when it was used. Since the set of states and associated transitions of \(\mathcal {C}^{k}\) is finite, the iterations will eventually terminate. This is because there will be a step in the iteration in Lines 13–27 where there will be no more transitions that lead to bad states to collect. In other words, the loop start at Line 14 terminates since the set of states of \(\mathcal {C}^{k}\) is finite and the inner loop starting from Line 14 is bounded by the number of transitions in \(\mathcal {C}^{k}\) which ends in a bad state which is finite. This implies that this inner loop also terminates.
In the iteration in Lines 29–36, there are four main for loops. The outermost loop (Line 30) loops over the set of bad states BS collected from the previous step and then the second outer loop iterates over the set of transitions that leads to bad states also collected in the previous steps. These two loops terminate since the set of states they iterate over is finite.
The function DFS as defined above returns the set of input transitions that need to be strengthened and then in Line 32 the algorithm strengthens these guards. By definition DFS traverses over finite number of runs and hence terminates. The iteration over ΓDFS at Line 32 terminates since the number of transitions ΓDFS return by the function DFS is finite
Lines 38–49 of this algorithm have two loops which search for all the variables that must be monitored at runtime and collect them into an array called runtimeVariable. These iterations terminate when all the variables to be monitored at runtime have been collected and stored.
- (2)
Lines 7-12 in Algorithm 1 (repeat until loop): We show that the repeat until loop in Lines 7–12 terminates too. Now, since for every iteration of the repeat until loop (a) Line 9 checks the static controllability condition on some \(\mathcal {C}^{k}\) and removes some states and transitions, it also adds certain bad states and transitions, as shown above the addition of bad states and transitions stops after a certain finite number of iterations; (b) Line 10 checks for blocking conditions and eliminates blocking states and associated transitions, this line also adds bad states and transitions to \(\mathcal {C}^{k}\) which is bounded by the number of states in \(\mathcal {C}^{k}\) and (c) Line 11 checks for the dynamic controllability conditions and strengthened guards that do not satisfy these conditions as well as removing states and transitions which do not satisfy the second item of Definition 12. More specifically, every iteration of the repeat until loop either adds or removes states and transitions to \(\mathcal {C}^{k}\). Let us consider these two cases in more detail.
- (i)
Addition of bad states and transitions that leads to bad states: In all the cases that bad states and transitions with bad terminal states are created and added to \(\mathcal {C}^{k}\), a state or a transition violates one of the three conditions (a), (b) and (c) and therefore must be removed, and in the event of removing it a new bad state and a transition resulting in a bad state is added. That is, good states and their associated transitions are systematically replaced with bad states and transitions ending in bad states. In the worst case, after a certain finite number of iterations of the repeat until loop, all good states and associated transitions will be replaced with bad states and transitions ending in bad states. At this point, there will be no more good states and associated transitions to replace and \(\mathcal {C}^{k}\) will remain the same.
- (ii)
Removal of states and transition from\(\mathcal {C}^{k}\): The iteration of the repeat until loop also removes states, in the worst case all states will be removed and \(\mathcal {C}^{k}\) will become empty or left with only bad states and transitions which ends in bad states. At this point \(\mathcal {C}^{k}\) will remain unchanged in the iteration of the repeat until.
After a finite number of iterations, \(\mathcal {C}^{k}\) is bound to remain unchanged as it verifies the above conditions (a), (b) and (c) and a fixed point will be reached. Thus, we will eventually have \(\mathcal {C}^{k}= \mathcal {C}^{k-1}\) which terminates the repeat until loop in Line 12. Therefore, we conclude that Algorithm 1 terminates in a finite number of steps.
- (i)
- (3)
All other lines of Algorithm 1 (Lines 2–6 and Lines 13–22): The number of iterations is never increased by execution of the loop body.
6 Proof of correctness (soundness and completeness)
In this section, we present two theorems and provide proofs that proves the correctness of our approach. Theorem 1 and Theorem 2 show that there exists a controller which solves the composition problem stated in Definition 16. We will start with various definitions and then we will state the main theorem of the section and finally provide a constructive proof for the theorem.
6.1 Proof of controller existences
Before we prove the theorems let us consider the following lemma resulting from observations made from the construction of the controller \(\mathcal {C}\) by Algorithm 1. Let \(\mathcal {S}_{\mathcal {C}}\) and \(\mathcal {S}_{\mathcal {C}^{0}}\) denote the set of states of \(\mathcal {C}\) and \(\mathcal {C}^{0}\), respectively. Also, let \(\mathcal {S}_{\mathcal {C}^{0}}\backslash \mathcal {S}^{Bad}_{\mathcal {C}^{0}} =\{s\mid s\in \mathcal {S}_{\mathcal {C}^{0}} \wedge s\notin \mathcal {S}^{Bad}_{\mathcal {C}^{0}} \}\). In the proofs that follow, we will refer to bad states \(\mathcal {S}^{Bad}_{\mathcal {C}}\) as states that are not reachable in the specification or that violate controllability or nonblocking conditions. Also, during the construction of \(\mathcal {C}\) by Algorithm 1, new states are created. These states are also marked as bad states, since they do not satisfy either some controllability or nonblocking conditions.
The first lemma says that in constructing \(\mathcal {C}\), a state in the resulting SLTS \(\mathcal {C}\) is a state in the original \(\mathcal {C}^{0}\) and is not a bad state.
Lemma 1
Given a controller \(\mathcal {C}\) generated by Algorithm 1 such that \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\operatorname {ref}}\mathcal {T}^{W}\) , then \(\mathcal {S}_{\mathcal {C}} \subseteq \mathcal {S}_{\mathcal {C}^{0}}\backslash \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\) .
Proof
The proof is done constructively.
Algorithm 1, Line 5, \(\mathcal {C}\) is initially given by \(\mathcal {C}^{0} = \mathcal {G}_{W}\times _{\operatorname {ref}}\mathcal {T}^{W}\) and \(\mathcal {S}_{\mathcal {C}^{0}}=\mathcal {S}^{Good}_{\mathcal {C}^{0}}\cup \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\). This implies that at this stage in the construction of \(\mathcal {C}\) by the algorithm, the set of states of \(\mathcal {C}\) is equal to the set of states of \(\mathcal {C}^{0}\). That is, \(\mathcal {S}_{\mathcal {C}} = \mathcal {S}_{\mathcal {C}^{0}}\) which means \(\mathcal {S}_{\mathcal {C}}=\mathcal {S}^{Good}_{\mathcal {C}^{0}}\cup \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\). Let \(\mathcal {C}^{k}\) denote the resultant SLTS obtained after some k iterations of the repeat until loop of Algorithm 1 on \(\mathcal {C}^{0}\). Now to show that \(\mathcal {S}_{\mathcal {C}} \subseteq \mathcal {S}_{\mathcal {C}^{0}}\backslash \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\), we prove the following:
- (i)
Upon termination of Algorithm 1, all the states in \(\mathcal {S}^{Bad}_{\mathcal {C}^{0}}\) have been made unreachable and eliminated and hence would not be in the final output \(\mathcal {C}\) of Algorithm 1,
- (ii)
All new bad states created by the algorithm are made unreachable and eliminated before the algorithm terminates.
To show (i), let \(q \in \mathcal {S}^{Bad}_{\mathcal {C}}\) and suppose that \(\exists p \in \mathcal {S}_{\mathcal {C}^{0}}, \exists \delta \in {\Sigma }\) and \(\exists g\in \mathcal {B}\) such that the transition  in \(\mathcal {C}^{0}\), then in the first iteration of the repeat until of Algorithm 1 loop one of the following holds:
in \(\mathcal {C}^{0}\), then in the first iteration of the repeat until of Algorithm 1 loop one of the following holds:
- (a)
if δ ∈Σuc then
in the case that t is static Lines 11-13 of Algorithm 3 will eliminate t which implies that q is also eliminated.
in the case that t is a dynamic type 1 transition, then the guard g will be strengthened by Algorithm 5 in Lines 30-38. Hence, q becomes unreachable from any good state and finally deleted at Line 13 of Algorithm 1.
in the case that t is a dynamic type 2 transition then by Corollary 1, Algorithm 5 Lines 40-51 will ensure that there is an enforceable transition also enabled at state p to preempt t at runtime. Hence, state q becomes unreachable and is later deleted at Line 13 of Algorithm 1.
- (b)
if δ ∈Σc then in all cases t (static or dynamic transition) deleted at Line 13 of Algorithm 1.
The proof of (ii) is as follows: during the construction of \(\mathcal {C}\), Algorithm 1 creates completely new bad states in the process of constructing \(\mathcal {C}\) (Lines 7-9 of Algorithm 3, Lines 12-15 of Algorithm 4 and Line 46 of Algorithm 5). However, these new bad states are also treated and deleted in the same way as in (i) before the termination of Algorithm 1.
From (i) and (ii) it is clear that by the time Algorithm 1 terminates the set of bad states of its final output \(\mathcal {C}\) will be empty, i.e., \(\mathcal {S}^{Bad}_{\mathcal {C}} = \emptyset \), and some of the states in \(\mathcal {S}^{Good}_{\mathcal {C}^{0}}\) may have been converted into bad states and removed too. This means that the set of states of \(\mathcal {C}\) is only a subset of \(\mathcal {S}^{Good}_{\mathcal {C}^{0}}\). Thus, \(\mathcal {S}_{\mathcal {C}} \subseteq \mathcal {S}_{\mathcal {C}^{0}}\backslash \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\). □
In the following lemma we show that a state \(s \in \mathcal {S}_{\mathcal {C}^{0}}\backslash \mathcal {S}_{\mathcal {C}}\) is either a bad state in \(\mathcal {C}^{0}\) or was made bad at the kth iteration of the repeat until loop of Algorithm 1 over \(\mathcal {C}^{0}\).
Lemma 2
Given that \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\operatorname {ref}}\mathcal {T}^{W}\) and \(s \in \mathcal {S}_{\mathcal {C}^{0}}\backslash \mathcal {S}_{\mathcal {C}}\) , then one of the following holds:
-
(1)
\(s\in \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\) ,
-
(2)
\(s\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\)where\(\mathcal {C}^{k}\)isthe SLTS obtained after some k iterations of therepeat untilloop ofAlgorithm1.
Proof
Let a state s in \(\mathcal {C}^{0}\) be s = (s1,t1), where s1 is a state in \(\mathcal {G}_{W}\) and t1 is a state in \(\mathcal {T}^{W}\) or a new bad state introduced during the construction of \(\mathcal {C}^{0}\).
Now, we know in Line 5 of Algorithm 1 that \(\mathcal {C}\) is initially given by \(\mathcal {C}^{0} = \mathcal {G}_{W}\times _{\operatorname {ref}}\mathcal {T}^{W}\) and \(\mathcal {S}_{\mathcal {C}^{0}}=\mathcal {S}^{Good}_{\mathcal {C}^{0}}\cup \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\).
Suppose the algorithm has executed until (but not including) Line 7 and let \(s\in \mathcal {C}^{0}\). We distinguish the following two cases:
- (a)
Case 1: s is not allowed in\(\mathcal {T}^{W}\) (i.e., t1not in\(\mathcal {T}^{W}\)). By construction of \(\mathcal {C}^{0}\) from Definition 9, then we have that \(s\in \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\), since states not in \(\mathcal {T}^{W}\) but in \(\mathcal {G}_{W}\) are those that end up in \(\mathcal {S}^{Bad}_{\mathcal {C}^{0}}\). Additionally, after some iteration of the repeat until loop and then further processing (Lines 13–22) by the algorithm of the resultant SLTS will not change s being in a bad state to a good state other than the removal of s in Line 13 (i.e., the call to the function removeUnsafeState) from the final output \(\mathcal {C}\) of the algorithm.
- (b)
Case 2: s is allowed in\(\mathcal {T}^{W}\) (i.e., t1is in\(\mathcal {T}^{W}\) ). Then, we have that \(s\in \mathcal {S}^{Good}_{\mathcal {C}^{0}}\) (\(s\notin \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\)). Now, if after one iteration, \(\mathcal {C}^{1}\) does not equal \(\mathcal {C}^{0}\) then the repeat until loop will continue and given that \(s\notin \mathcal {S}_{\mathcal {C}}\) (by (D1)), implies that s might have been removed or changed into a bad state in some \(\mathcal {C}^{k-1}\) through one of the following steps in the iteration of the repeat until loop at Lines 9–11.
- (i)
Line 9: The checking for static controllability could result in removing or changing a good state s in \(\mathcal {C}^{k-1}\) to a bad state in \(\mathcal {C}^{k}\), which implies that \(s\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\).
- (ii)
Line 10: The procedure unsafeStateMinimization removes states not satisfying nonblocking conditions or changes some good states into bad states, s might have been one of these states which will result in \(s\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\).
- (iii)
Line 11: The procedure in this line at some point strengthens guards of \(\mathcal {C}^{k-1}\) based on dynamic controllability and once a guard is strengthens some states may become unreachable or bad and later removed, s might have been one of these states in \(\mathcal {C}^{k}\).
Additionally, the steps from Lines 13–22 of the algorithm will not change a bad state s into a good state other the removal of s in Line 13 (removeUnsafeState) from the final output of the algorithm.
- (i)
□
In the following lemma we show that the set of good states of \(\mathcal {C}\) is a subset of the set of good states of \(\mathcal {C}^{0}\).
Lemma 3
Given a controller \(\mathcal {C}\) generated by Algorithm 1 such that \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\operatorname {ref}} \mathcal {T}^{W}\) , then \(\mathcal {S}^{Good}_{\mathcal {C}}\subseteq \mathcal {S}^{Good}_{\mathcal {C}^{0}}\) .
Proof
The proof of this lemma is similar to that of Lemma 1 and so we omit it here. □
Lemma 4
Given a controller \(\mathcal {C}\) for a plant \(\mathcal {G}_{W}\) , if \(\mathcal {C}\) satisfies the definition of state controllability with respect to \(\mathcal {G}_{W}\) (Definition 12) then \(\mathcal {C}\) is legitimate.
Proof
We prove by contradiction, suppose that \(\mathcal {C}\) is not a legitimate controller, then a reachable state (p,q) in \(\mathcal {C}\otimes \mathcal {G}_{W}\) such that
- 1.
\(\exists \delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}(p) \) and \(\delta \notin E^{\mathcal {S}}_{(\mathcal {C}\otimes \mathcal {G}_{W})}((p,q))\) but δ∉Σc, which implies that δ ∈Σuc. We can rewrite the above as \(\exists \delta \in {\Sigma }_{uc} : \delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}(p)\) but \(\delta \notin E^{\mathcal {S}}_{(\mathcal {C}\otimes \mathcal {G}_{W})}((p,q))\), which does not satisfy the definition of static controllability and contradicts the fact that \(\mathcal {C}\) is controllable or
- 2.
∃δ ∈Σuc, \(g\in \mathcal {B}\) such that \((\delta , g) \in E^{\mathcal {D}}_{\mathcal {G}_{W}}(p) \) but \(\nexists g^{\prime }\) in \(\mathcal {C}\) such g′≤ g and \((\delta , g^{\prime } )\in E^{\mathcal {D}}_{(\mathcal {C}\otimes \mathcal {G}_{W})}((p,q))\), which results in a contradiction that \(\mathcal {C}\) is satisfies the definition of controllability (Definition 12) or
- 3.
\(\exists \delta \in {\Sigma }_{uc}: \exists g^{A}(v) \in \mathcal {B}, (\delta , g^{A}(v)) \in E^{D}_{\mathcal {G}_{W}}(p)\) but
- (a)
\(\nexists (g^{A}(v))^{\prime } \) such that \((\delta , (g^{A}(v))^{\prime }) \in E^{D}_{\mathcal {C}\otimes \mathcal {G}_{W}}(p,q)\) and gA(v) ∧ (gA(v))′ satisfiable and
- (b)
\(\nexists \delta ^{\prime } \in {\Sigma }_{f}\) and \(\nexists g^{\prime \prime }\) such that \((\delta ^{\prime },g^{\prime \prime }) \in E^{D}_{\mathcal {C}}(p,q) \) and g″ = true, which results in a contradiction that \(\mathcal {C}\) is satisfies the definition of controllability (Definition 12).
- (a)
□
Theorem 1
Given a system modeled by an SLTS \(\mathcal {G}_{W}\) and a specification \(\mathcal {T}^{W}\) defined by \(\mathcal {T}^{W} \preceq \mathcal {G}_{W}\) , there exists a controller \(\mathcal {C}\) such that \(\mathcal {C} \otimes \mathcal {G}_{W} \approx \mathcal {T}^{W}\) iff \(\mathcal {T}^{W}\) is state controllable with respect to \(\mathcal {G}_{W}\) .
Proof
Let \(\mathcal {G}_{W} = (\mathcal {S}_{\mathcal {G}_{W}}, \mathcal {S}^{0}_{\mathcal {G}_{W}}, \mathcal {I}_{\mathcal {G}_{W}}, \mathcal {O}_{\mathcal {G}_{W}}, \mathcal {A}_{\mathcal {G}_{W}},{\Gamma }_{\mathcal {G}_{W}}, \mathcal {S}^{F}_{\mathcal {G}_{W}}, V_{\mathcal {G}_{W}}, \mathcal {B}_{\mathcal {G}_{W}})\) , \(\mathcal {C} = (\mathcal {S}_{\mathcal {C}}, \mathcal {S}^{0}_{\mathcal {C}}, \mathcal {I}_{\mathcal {C}}, \mathcal {O}_{\mathcal {C}_{W}}, \mathcal {A}_{\mathcal {C}},{\Gamma }_{\mathcal {C}}, \mathcal {S}^{F}_{\mathcal {C}}, V_{\mathcal {C}}, \mathcal {B}_{\mathcal {C}})\) and \(\mathcal {T}^{W} = (\mathcal {S}_{\mathcal {T}^{W}}, \mathcal {S}^{0}_{\mathcal {T}^{W}}, \mathcal {I}_{\mathcal {T}^{W}}, \mathcal {O}_{\mathcal {T}^{W}}, \mathcal {A}_{\mathcal {T}^{W}}, {\Gamma }_{\mathcal {T}^{W}}, \mathcal {S}^{F}_{\mathcal {T}^{W}}, V_{\mathcal {T}^{W}}, \mathcal {B}_{\mathcal {T}^{W}}\)). Recall that \(R_{(\mathcal {T}^{W}\preceq \mathcal {G}_{W})}\) denotes the simulation relation between \(\mathcal {T}^{W}\) and \(\mathcal {G}_{W}\), also, let R(≈) denote the bisimulation relation between the controlled system \(\mathcal {C}\otimes \mathcal {G}_{W}\) and the specification \(\mathcal {T}^{W}\).

We prove the two parts of the definition of controllability as follows.
- 1.
Static Controllability:

We prove by contradiction:
Let \((s_{n}, t_{n}) \in R_{(\mathcal {T}^{W}\preceq \mathcal {G}_{W})}\subseteq \mathcal {S}_{{\mathcal {G}_{W}}}\times \mathcal {S}_{\mathcal {T}^{W}}\).
Suppose that (sn,tn) is not state controllable (static), then it implies that \(\exists s_{n}^{\prime }, \exists \delta _{n}\in {\Sigma }_{uc}\) such that
 but there exists no \(t_{n}^{\prime } \in \mathcal {S}_{\mathcal {T}^{W}}\) such that
but there exists no \(t_{n}^{\prime } \in \mathcal {S}_{\mathcal {T}^{W}}\) such that 
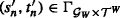 , which implies that
, which implies that  .
.Now, since \(\mathcal {C} \otimes \mathcal {G}_{W} \approx \mathcal {T}^{W}\), this implies that for ((c,v),tn)) ∈ R(≈),

 . That is, \(\nexists c^{\prime }\in \mathcal {S}_{\mathcal {C}}\), \(\nexists v^{\prime }\in \mathcal {S}_{\mathcal {G}_{W}}\) such that the transition
. That is, \(\nexists c^{\prime }\in \mathcal {S}_{\mathcal {C}}\), \(\nexists v^{\prime }\in \mathcal {S}_{\mathcal {G}_{W}}\) such that the transition 

Next, we show that v = sn. Let
 be a path in \(\mathcal {T}^{W}\). Since \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\), there exists a path in \(\mathcal {G}_{W}\) leading to sn, namely
be a path in \(\mathcal {T}^{W}\). Since \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\), there exists a path in \(\mathcal {G}_{W}\) leading to sn, namely 
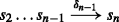 .
.Then δ0δ1…δn labels path that leads to (c,v) in \(\mathcal {C} \times \mathcal {G}_{W}\) (since \(\mathcal {C}\times \mathcal {G}_{W}\approx \mathcal {T}^{W}\)). That is, δ0δ1…δn leads to c in \(\mathcal {C}\) and δ0δ1…δn leads to v in \(\mathcal {G}_{W}\). Since, \(\mathcal {G}_{W}\) is deterministic and δ0δ1…δn leads to sn in \(\mathcal {G}_{W}\), v = sn.
Therefore we have \(\delta _{n}\notin E^{\mathcal {S}}_{\mathcal {C}\otimes \mathcal {G}_{W}}(c,s_{n})\), but since
 , this means \(\delta _{n}\notin E^{\mathcal {S}}_{\mathcal {C}}(c)\). That is, \(\mathcal {C}\) disables δn which contradicts the fact that δn ∈Σuc, as a legitimate controller will not disable uncontrollable events. Hence, (sn,tn) must be state controllable.
, this means \(\delta _{n}\notin E^{\mathcal {S}}_{\mathcal {C}}(c)\). That is, \(\mathcal {C}\) disables δn which contradicts the fact that δn ∈Σuc, as a legitimate controller will not disable uncontrollable events. Hence, (sn,tn) must be state controllable. - 2.
Dynamic Controllability:

Similarly, we prove by contradiction as follows:
Let \((s_{n}, t_{n}) \in R_{(\mathcal {T}^{W}\preceq \mathcal {G}_{W})}\subseteq \mathcal {S}_{{\mathcal {G}_{W}}}\times \mathcal {S}_{\mathcal {T}^{W}}\).
Suppose that (sn,tn) is not state controllable (dynamic), then it implies that \(\exists s_{n}^{\prime } \in \mathcal {S}_{\mathcal {G}_{W}}, \exists \delta _{n}\in {\Sigma }_{uc}\) and a guard \(g_{1}\in \mathcal {B}_{\mathcal {G}_{W}}\) such that
 , but
, but
- (a)
\(\nexists t_{n}^{\prime } \in \mathcal {S}_{\mathcal {T}^{W}}\) and \(\nexists g_{2}\in \mathcal {B}_{\mathcal {T}^{W}}\) such that
 and (g1 ⇒ g2), which implies that
and (g1 ⇒ g2), which implies that  , and
, and - (b)
\(\nexists t_{m} \in \mathcal {S}_{\mathcal {T}^{W}}\), \(\nexists \delta _{n}^{\prime } \in {\Sigma }_{f}\) and \(\nexists g_{3}\) such that
 and g3=true, \(s_{m}\in \mathcal {S}_{\mathcal {G}_{W}}\), which implies that
and g3=true, \(s_{m}\in \mathcal {S}_{\mathcal {G}_{W}}\), which implies that  .
.
Now, since \(\mathcal {C} \otimes \mathcal {G}_{W} \approx \mathcal {T}^{W}\), this implies that for ((c,v),tn)) ∈ R(≈),
- (a)
\(\nexists c^{\prime }\in \mathcal {S}_{\mathcal {C}}\) and \(\nexists g_{2}\) such that the transition
 , where \(v,v^{\prime } \in \mathcal {S}_{\mathcal {G}_{W}}\) and
, where \(v,v^{\prime } \in \mathcal {S}_{\mathcal {G}_{W}}\) and - (b)
\(\nexists c^{\prime \prime } \in \mathcal {S}_{\mathcal {C}}\), \(\nexists \delta _{n}^{\prime } \in {\Sigma }_{f} \) and \(\nexists g_{3}\in \mathcal {B}_{\mathcal {G}_{W}}\), such that
 , where \(v,v^{\prime } \in \mathcal {S}_{\mathcal {G}_{W}}\).
, where \(v,v^{\prime } \in \mathcal {S}_{\mathcal {G}_{W}}\).
Next, we show that v = sn. Let
 be a path in \(\mathcal {T}^{W}\). Since \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\), there exists a path in \(\mathcal {G}_{W}\) leading to sn, namely
be a path in \(\mathcal {T}^{W}\). Since \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\), there exists a path in \(\mathcal {G}_{W}\) leading to sn, namely 
 .
.Then δ0δ1…δn labels path that leads to (c,v) in \(\mathcal {C} \times \mathcal {G}_{W}\) (since \(\mathcal {C}\times \mathcal {G}_{W}\approx \mathcal {T}^{W}\)). That is, δ0δ1…δn leads to cn in \(\mathcal {C}\) and δ0δ1…δn leads to v in \(\mathcal {G}_{W}\). Since, \(\mathcal {G}_{W}\) is deterministic and δ0δ1…δn leads to sn in \(\mathcal {G}_{W}\), v = sn.
Therefore we have
- (1)
\((\delta _{n}, g_{2})\notin E^{\mathcal {D}}_{\mathcal {C}\otimes \mathcal {G}_{W}}(c,s_{n})\), this implies
 but
but 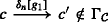 such that g1 ⇒ g2, which means \((\delta _{n},g_{2}) \notin E^{\mathcal {D}}_{\mathcal {C}}(c)\). This implies that \(\mathcal {C}\) disables δn by strengthening the guard g2 (making it stronger than g1) which contradicts the fact that a legitimate controller cannot strengthen guards of transition with uncontrollable events δn ∈Σuc. As a legitimate controller can only strengthen the guard of an controllable transitions. Hence, (sn,tn) must be state controllable and
such that g1 ⇒ g2, which means \((\delta _{n},g_{2}) \notin E^{\mathcal {D}}_{\mathcal {C}}(c)\). This implies that \(\mathcal {C}\) disables δn by strengthening the guard g2 (making it stronger than g1) which contradicts the fact that a legitimate controller cannot strengthen guards of transition with uncontrollable events δn ∈Σuc. As a legitimate controller can only strengthen the guard of an controllable transitions. Hence, (sn,tn) must be state controllable and
- (2)
\((\delta _{n}^{\prime }, g_{3}^{\prime })\notin E^{\mathcal {D}}_{\mathcal {C}\otimes \mathcal {G}_{W}}(c,s_{n})\) implies that \((\delta _{n}^{\prime }, g_{3}^{\prime })\notin E^{\mathcal {D}}_{\mathcal {C}}(c)\) but since
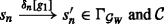 and \(\mathcal {C}\) cannot disable δn or since case (1) is not true then it implies that \(\mathcal {C}\) is not a legitimate controller in this case. That is a legitimate controller must enforce enforceable transitions if case (1) does not hold.
and \(\mathcal {C}\) cannot disable δn or since case (1) is not true then it implies that \(\mathcal {C}\) is not a legitimate controller in this case. That is a legitimate controller must enforce enforceable transitions if case (1) does not hold.
- (2)

Given that \(\mathcal {T}^{W}\) is controllable with respect to \(\mathcal {G}_{W}\), choose \(\mathcal {C}\) to be the SLTS given by \(\mathcal {T}^{W}\). This implies that the controlled system \(\mathcal {C}\otimes \mathcal {G}_{W}=\mathcal {T}^{W}\otimes \mathcal {G}_{W}\) and given that \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\) implies that \(\mathcal {T}^{W}\otimes \mathcal {G}_{W}\) is bisimilar to \(\mathcal {T}^{W}\).
- (a)
Note that since \(\mathcal {T}^{W}\) is controllable it implies that \(\mathcal {C}\) is controllable which means \(\mathcal {C}\) is legitimate by Lemma 4 □
Now, Theorem 1 above assumes that the specification \(\mathcal {T}^{W}\) is state controllable with respect to \(\mathcal {G}_{W}\), however, if \(\mathcal {T}^{W}\) is not controllable with respect to \(\mathcal {G}_{W}\), then Algorithm 1 can be used to construct a controller \(\mathcal {C}\) that is minimally restrictive and limits the plant behaviour to meet some (but not all) of the specification \(\mathcal {T}^{W}\). In the following lemma we show that the controller synthesized by Algorithm 1 is legitimate.
Lemma 5
If \(\mathcal {C}\) is a controller generated by Algorithm 1, then \(\mathcal {C}\) is legitimate.
Proof
We prove by contradiction, suppose that \(\mathcal {C}\) is not a legitimate controller, then ∃(p,q) a reachable state in \(\mathcal {C}\otimes \mathcal {G}_{W}\) such that
- 1.
\(\exists \delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}(p) \) and \(\delta \notin E^{\mathcal {S}}_{(\mathcal {C}\otimes \mathcal {G}_{W})}((p,q))\) but δ∉Σc, which implies that δ ∈Σuc. We can rewrite the above as \(\exists \delta \in {\Sigma }_{uc} : \delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}(p)\) but \(\delta \notin E^{\mathcal {S}}_{(\mathcal {C}\otimes \mathcal {G}_{W})}((p,q))\), which implies that \(\delta \notin E^{\mathcal {S}}_{\mathcal {C}}((q))\) by definition of ⊗. Line 14 of Algorithm 3 would have eliminated the state q and its associated transitions from \(\mathcal {C}\), hence a contradiction, or
- 2.
∃δ ∈Σuc, \(g\in \mathcal {B}\) such that \((\delta , g) \in E^{\mathcal {D}}_{\mathcal {G}_{W}}(p) \) but \(\nexists g^{\prime }\) in \(\mathcal {C}\) such g′≤ g and \((\delta , g^{\prime } )\in E^{\mathcal {D}}_{(\mathcal {C}\otimes \mathcal {G}_{W})}((p,q))\), which does not satisfy the definition of dynamic controllability (Definition 12) hence, Line 33 of Algorithm 5 would have strengthened the guard g since \((\delta , g) \notin E^{\mathcal {D}}_{\mathcal {C}}(p)\) or the state p would have resulted in a bad state and been eliminated at Lines 7-8 of Algorithm 6 to make \(\mathcal {C}\) controllable. Hence, a contradiction as \(\mathcal {C}\) satisfies the definition of controllability (Definition 12), or
- 3.
\(\exists \delta \in {\Sigma }_{uc}: \exists g^{A}(v) \in \mathcal {B}, (\delta , g^{A}(v)) \in E^{D}_{\mathcal {G}_{W}}(p)\) but
- (a)
\(\nexists (g^{A}(v))^{\prime } \) such that \((\delta , (g^{A}(v))^{\prime }) \in E^{D}_{\mathcal {C}\otimes \mathcal {G}_{W}}(p,q)\) and gA(v) ∧ (gA(v))′ satisfiable and
- (b)
\(\nexists \delta ^{\prime } \in {\Sigma }_{f}\) and \(\nexists g^{\prime \prime }\) such that \((\delta ^{\prime },g^{\prime \prime }) \in E^{D}_{\mathcal {C}}(p,q) \) and g″ = true. Conditions (a) and (b) do not meet the definition of dynamic controllability (Definition 12) hence, Lines 39-42 of Algorithm 5 would have ensured that either δ′ is enabled at state q or at Line 46 of Algorithm 5 the state q would have been eliminated, resulting in a contradiction.
- (a)
□
Lemma 6
Given a plant\(\mathcal {G}_{W}\)anda specification\(\mathcal {T}^{W}\),if a static transition is a transition in \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\text { ref}}\mathcal {T}^{W}\) such that \(q\in \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\), then it implies that \(\delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}\) but \(\delta \notin E^{\mathcal {S}}_{\mathcal {T}^{W}}\).
is a transition in \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\text { ref}}\mathcal {T}^{W}\) such that \(q\in \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\), then it implies that \(\delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}\) but \(\delta \notin E^{\mathcal {S}}_{\mathcal {T}^{W}}\).
Proof
The proof of this lemma follows from the construction of \(\mathcal {C}^{0}\) (Line 5 of Algorithm 1), where a transition in \(\mathcal {G}_{W}\) but not in \(\mathcal {T}^{W}\) results in a bad state in \(\mathcal {C}^{0}\) (Definition 9). □
Let \(\mathcal {C}^{k}\) be the SLTS obtained after some iterations of the repeat until loop in Algorithm 1 (Lines 8-13). The following lemma states that if a transition in \(\mathcal {C}^{k}\) leads to a bad state then it implies that this transition is enabled in the plant but not in \(\mathcal {C}^{k}\)
Lemma 7
Given a plant\(\mathcal {G}_{W}\)anda specification\(\mathcal {T}^{W}\),if is a transition in some \(\mathcal {C}^{k}\) such that \(q\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\), then it implies that \(\delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}\) but \(\delta \notin E^{\mathcal {S}}_{\mathcal {C}^{k}}\), where \(\mathcal {C}^{k}\) is the SLTS obtained after some iterations of the repeat until loop in Algorithm 1 (Lines 8-13).
is a transition in some \(\mathcal {C}^{k}\) such that \(q\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\), then it implies that \(\delta \in E^{\mathcal {S}}_{\mathcal {G}_{W}}\) but \(\delta \notin E^{\mathcal {S}}_{\mathcal {C}^{k}}\), where \(\mathcal {C}^{k}\) is the SLTS obtained after some iterations of the repeat until loop in Algorithm 1 (Lines 8-13).
Proof
The proof of this lemma follows from Lemma 6 and the fact that a transition  which leads to a bad state (i.e., \(q\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\)) is only created in \(\mathcal {C}^{k}\) by Algorithm 1 if this transition is allowed in \(\mathcal {G}_{W}\) but not in \(\mathcal {C}^{k}\). That is, transitions that are forbidden in \(\mathcal {G}_{W}\) end up in bad states in \(\mathcal {C}^{k}\). □
which leads to a bad state (i.e., \(q\in \mathcal {S}^{Bad}_{\mathcal {C}^{k}}\)) is only created in \(\mathcal {C}^{k}\) by Algorithm 1 if this transition is allowed in \(\mathcal {G}_{W}\) but not in \(\mathcal {C}^{k}\). That is, transitions that are forbidden in \(\mathcal {G}_{W}\) end up in bad states in \(\mathcal {C}^{k}\). □
Note that from the above, \(\mathcal {C}^{k}\) eventually becomes \(\mathcal {C}\) without bad states.
Lemma 8
The controller generated by Algorithm 1 has no bad states.
Proof
The proof follows from the fact that in the construction of \(\mathcal {C}\) by Algorithm 1, the set of bad states and transitions in and out of bad states are removed at Line 13 of Algorithm 1, thus \(\mathcal {C}\) has no bad states. □
Theorem 2
Given a system modeled by an SLTS\(\mathcal {G}_{W}\)anda specification\(\mathcal {T}^{W}\)with\(\mathcal {T}^{W}\) ≼ \(\mathcal {G}_{W}\),Algorithm1 generates a controller\(\mathcal {C}\)suchthat\(\mathcal {C}\) ⊗ \(\mathcal {G}_{W}\) ≼ \(\mathcal {T}^{W}\).
Proof
The proof is done constructively,
Let \(\mathcal {G}_{W} = (\mathcal {S}_{\mathcal {G}_{W}}, \mathcal {S}^{0}_{\mathcal {G}_{W}}, \mathcal {I}_{\mathcal {G}_{W}}, \mathcal {O}_{\mathcal {G}_{W}}, \mathcal {A}_{\mathcal {G}_{W}},{\Gamma }_{\mathcal {G}_{W}}, \mathcal {S}^{F}_{\mathcal {G}_{W}}, V_{\mathcal {G}_{W}}, \mathcal {B}_{\mathcal {G}_{W}})\) and \(\mathcal {T}^{W} = (\mathcal {S}_{\mathcal {T}^{W}}, \mathcal {S}^{0}_{\mathcal {T}^{W}}, \mathcal {I}_{\mathcal {T}^{W}}, \mathcal {O}_{\mathcal {T}^{W}}, \mathcal {A}_{\mathcal {T}^{W}}, {\Gamma }_{\mathcal {T}^{W}}, \mathcal {S}^{F}_{\mathcal {T}^{W}}, V_{\mathcal {T}^{W}}, \mathcal {B}_{\mathcal {T}^{W}}\)).
Let \(Composer(\mathcal {G}_{W},\mathcal {T}^{W})\) denote the transition system obtained from \(\mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) by applying Algorithm 1 (i.e., the final output of Algorithm 1). Let \(\mathcal {C}= Composer(\mathcal {G}_{W},\mathcal {T}^{W})\).
We will denote the set of states of \(\mathcal {C}^{0}\) as \(\mathcal {S}_{\mathcal {C}^{0}}\) and the set of transitions of \(\mathcal {C}^{0}\) as \({\Gamma }_{\mathcal {C}^{0}}\). Let \(\mathcal {S}^{Good}_{\mathcal {C}^{0}}\) and \(\mathcal {S}^{Bad}_{\mathcal {C}^{0}}\) denote the set of good states of \(\mathcal {C}^{0}\) and the set of bad states of \(\mathcal {C}^{0}\), respectively. Let \(\mathcal {C}^{0} \backslash \mathcal {S}^{Bad}_{\mathcal {C}^0}\) denote the SLTS obtained after removing the set of bad states \(\mathcal {S}^{Bad}_{\mathcal {C}^{0}}\) from \(\mathcal {C}^{0}\), i.e., \(\mathcal {C}^{0}\) excluding the set of bad states. We will assume similar notation for \(\mathcal {C}\).
We make the following observations. In Algorithm 1, \(\mathcal {C}\/\) is initially computed from \(\mathcal {G}_{W}\times _{\text { ref}}\mathcal {T}^{W}\) (Line 5) and then certain reduction steps are further performed on it. By definition, \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\text { ref}}\mathcal {T}^{W}\) in Line 5 of Algorithm 1 (definition of composition refinement). The states of \(\mathcal {C}^{0}\) are partitioned into the set of good states and the set of bad states, respectively. That is, \(\mathcal {S}_{\mathcal {C}^{0}}=\mathcal {S}^{Good}_{\mathcal {C}^{0}}\cup \mathcal {S}^{Bad}_{\mathcal {C}^{0}}\). The set of good states and transitions leading to good states of \(\mathcal {C}^{0}\) lie in \(\mathcal {T}^{W}\). Specifically, \(\mathcal {C}\/\) is obtained from \(\mathcal {C}^{0}\) after removing certain transitions and bad states.
The proof of this theorem entails showing that given a controller \(\mathcal {C}\) generated by Algorithm 1 and \(\mathcal {T}^{W} \preceq \mathcal {G}_{W}\), then \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\) holds. This is presented formally in the gray box below.
Example 4
First let us illustrate the proof of Theorem 2 by an example (i.e., given that \(\mathcal {C}=Composer(\mathcal {G}_{W},\mathcal {T}^{W})\) and \(\mathcal {T}^{W} \preceq \mathcal {G}_{W}\), show that \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\)). Let the SLTS in Fig. 14a and b represent the plant and the specification, respectively. It can be verified that \(\mathcal {T}^{W}\preceq \mathcal {G}_{W}\). Figure 14c is the result of computing the composition refinement (\(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\text { ref}}\mathcal {T}^{W}\)) of the SLTSs in Fig. 14a and b, respectively. Now it can be seen that \(\mathcal {C}^{0}\) is made up of good states and bad states. Our proof to the theorem will be in two parts. The first part of the proof will be to show that \((\mathcal {C}^{0}\otimes \mathcal {G}_{W})\) simulates \(\mathcal {T}^{W}\) when the transitions 
 (BAD3)) have been eliminated from \(\mathcal {C}^{0}\) and the bad states made unreachable. It can be seen that the controller \(\mathcal {C}\) in Fig. 14g has no transitions that lead to bad states and it can also be easily verified that \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\) which will constitute the proof of the second part. That is, the second part of the proof will be to show that \(\mathcal {C}\) generated from \(\mathcal {C}^{0}\) by Algorithm 1 has no bad states and has no transitions that lead to bad states and, hence, satisfies \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\).
(BAD3)) have been eliminated from \(\mathcal {C}^{0}\) and the bad states made unreachable. It can be seen that the controller \(\mathcal {C}\) in Fig. 14g has no transitions that lead to bad states and it can also be easily verified that \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\) which will constitute the proof of the second part. That is, the second part of the proof will be to show that \(\mathcal {C}\) generated from \(\mathcal {C}^{0}\) by Algorithm 1 has no bad states and has no transitions that lead to bad states and, hence, satisfies \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\).
Let \(\mathcal {C}\otimes \mathcal {G}_{W} = (\mathcal {S}_{\mathcal {C}\otimes \mathcal {G}_{W}}, \mathcal {S}^{0}_{\mathcal {C}\otimes \mathcal {G}_{W}}, \mathcal {I}_{\mathcal {C}\otimes \mathcal {G}_{W}}, \mathcal {O}_{\mathcal {C}\otimes \mathcal {G}_{W}}, \mathcal {A}_{\mathcal {C}\otimes \mathcal {G}_{W}}, {\Gamma }_{\mathcal {C}\otimes \mathcal {G}_{W}}, \mathcal {S}^{F}_{\mathcal {C}\otimes \mathcal {G}_{W}}, V_{\mathcal {C}\otimes \mathcal {G}_{W}}, \mathcal {B}_{\mathcal {C}\otimes \mathcal {G}_{W}})\) denote the controlled system when \(\mathcal {G}_{W}\) is under control of \(\mathcal {C}\).

The proof will proceed as follows. Firstly, in (a) we define a relation R and show that R is a simulation relation between \((\mathcal {C}^{0}\otimes \mathcal {G}_{W})\) and \(\mathcal {T}^{W}\) when \(\mathcal {C}^{0}\) is restricted to having only good states, i.e., \((\mathcal {C}^{0} \backslash \mathcal {S}^{Bad}_{\mathcal {C}^0}\otimes \mathcal {G}_{W})\preceq \mathcal {T}^{W}\). Secondly, in (b) we shall further define another relation \(R\upharpoonright \mathcal {S}_{\mathcal {C}}\), a subset of R and establish that \(R\upharpoonright \mathcal {S}_{\mathcal {C}}\) is a simulation relation between \((\mathcal {C}\otimes \mathcal {G}_{W})\) and \(\mathcal {T}^{W}\) if \(\mathcal {C}\) is generated without bad states and transitions that lead to bad states. Finally, in (c) we shall show that actually \(\mathcal {C}\) has no bad states and has no transitions that lead to bad states.
We define the relation

- (a)
We will start by showing that R is a simulation relation between \(\mathcal {C}^{0}\otimes \mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) when the states of \(\mathcal {C}^{0}\otimes \mathcal {G}_{W}\) are constrained to only good states, i.e., \(\mathcal {T}^{W}\) simulates \(((\mathcal {C}^{0} \backslash \mathcal {S}^{Bad}_{\mathcal {C}^0})\otimes \mathcal {G}_{W})\).
Consider (((sn,tn),sn),tn) ∈ R and \((s_{n},t_{n}) \in \mathcal {S}^{Good}_{\mathcal {C}^{0}}\), and suppose
 for some δn ∈Σ and \((s_{n+1},t_{n+1}) \in \mathcal {S}^{Good}_{\mathcal {C}^{0}}\), then by definition of ×ref used in the construction of \(\mathcal {C}^{0}\) it implies that \(\exists t_{n+1} \in S_{\mathcal {T}^{W}}, \exists g_n^{\prime } \in \mathcal {B}_{\mathcal {T}^{W}}\)such that
for some δn ∈Σ and \((s_{n+1},t_{n+1}) \in \mathcal {S}^{Good}_{\mathcal {C}^{0}}\), then by definition of ×ref used in the construction of \(\mathcal {C}^{0}\) it implies that \(\exists t_{n+1} \in S_{\mathcal {T}^{W}}, \exists g_n^{\prime } \in \mathcal {B}_{\mathcal {T}^{W}}\)such that , where \(g_n=g_n^{\prime }\) and therefore (((sn+ 1,tn+ 1),sn+ 1),tn+ 1) ∈ R.
, where \(g_n=g_n^{\prime }\) and therefore (((sn+ 1,tn+ 1),sn+ 1),tn+ 1) ∈ R.This is because from the definition of \(\mathcal {C}^{0}=\mathcal {G}_{W}\times _{\text {ref}}\mathcal {T}^{W}\), every transition that leads to a good state in \(\mathcal {C}^{0}\) from (sn,tn) can be matched by \(\mathcal {T}^{W}\). This implies that R is a simulation relation between \(((\mathcal {C}^{0} \backslash \mathcal {S}^{Bad}_{\mathcal {C}^0})\otimes \mathcal {G}_{W})\) and \(\mathcal {T}^{W}\).
As in Example 4 if we eliminate all bad states and their associated transitions

 from \(\mathcal {C}^{0}\) of Fig. 14c and combine it with the plant in Fig. 14a we get a system that is simulated by the specification in Fig. 14b.
from \(\mathcal {C}^{0}\) of Fig. 14c and combine it with the plant in Fig. 14a we get a system that is simulated by the specification in Fig. 14b.Now in (b) and (c) we prove the following claim:
$$ \mathcal{C}\otimes\mathcal{G}_{W}\preceq\mathcal{T}^{W} $$ - (b)
(Transitions of \(\mathcal {C}\) that lead to good states from good states)
Based on the results obtained in (a), we want to show that \(\mathcal {T}^{W}\) also simulates \(\mathcal {C}\otimes \mathcal {G}_{W}\) based on the fact that \(\mathcal {C}\) is constructed from \(\mathcal {C}^{0}\) and that \(\mathcal {C}\) has no bad states, i.e., \( \mathcal {S}^{Bad}_{\mathcal {C}}= \emptyset \).
From Algorithm 1, \(\mathcal {C}\) is built from \(\mathcal {C}^{0}\) by making bad states unreachable and removing all transitions that lead to bad states.
- (i)
We define another relation \(R\upharpoonright \mathcal {S}_{\mathcal {C}}\) a projection on the states of \(\mathcal {S}_{\mathcal {C}}\) into R given by:
$$ R\upharpoonright\mathcal{S}_{\mathcal{C}} = R\backslash\{(((s_{n},t_{n}),s_{n}),t_{n}) \mid ((s_{n},t_{n}),s_{n}) \notin \mathcal{S}_{\mathcal{C}\otimes\mathcal{G}_{W}}\}$$i.e., the set of pairs in R excluding those not in \(\mathcal {S}_{\mathcal {C}\otimes \mathcal {G}_{W}}\).
We also note that \((R\upharpoonright \mathcal {S}_{\mathcal {C}} )\subseteq R\)
- (ii)
Now we are ready to show that \(R\upharpoonright \mathcal {S}_{\mathcal {C}}\) is a simulation relation between \(\mathcal {C}\otimes \mathcal {G}_{W}\) and \(\mathcal {T}^{W}\) if no transition in \(\mathcal {C}\) leads to a bad state.
Consider\((((s_n, t_n),s_n),t_n) \in R\upharpoonright \mathcal {S}_{\mathcal {C}}\) for some states \(((s_n,t_n),s_n) \in S_{\mathcal {C}\otimes \mathcal {G}_{W}}\) and \(t_n\in S_{\mathcal {T}^{W}}\), and \((s_n, t_n) \in \mathcal {S}^{Good}_{\mathcal {C}}\), then from (i) we have that (((sn,tn),sn),tn) ∈ R.
Now suppose

(by the construction of \(\mathcal {C}\) from \(\mathcal {C}^{0}\) and Lemma 1 and Lemma 2; also, note that gn could be a subguard or different from \(g_n^{\prime }\) since Line 33 of Algorithm 5 could modify \(g_n^{\prime }\) giving gn)

That is, \(R\upharpoonright \mathcal {S}_{\mathcal {C}}\) is a simulation relation between \((\mathcal {C} \backslash \mathcal {S}^{Bad}_{\mathcal {C}})\otimes \mathcal {G}_{W}\) and \(\mathcal {T}^{W}\). So now we have that every transition that leads to a good state from a good state in \(\mathcal {C}\otimes \mathcal {G}_{W}\) can be simulated by \(\mathcal {T}^{W}\). Hence, we only have left to show that \(\mathcal {C}\) has no bad states and has no transitions that lead to bad states from a good state.
- (i)
- (c)
(No bad states and associated transition in \(\mathcal {C}\))
Here, we show that all bad states and associated transitions are eliminated from \(\mathcal {C}\) during the construction of \(\mathcal {C}\) from \(\mathcal {C}^{0}\).
For example, the synthesis of the controller \(\mathcal {C}\) in Fig. 14g from \(\mathcal {C}^{0}\) in Fig. 14c resulted in the elimination of all transitions that lead to bad states and transitions that violate controllability (Definition 12).
Now consider
 (2)
(2)and \((s_{n+1},t_{n+1}) \in \mathcal {S}^{Bad}_{\mathcal {C}}\)
In cases I, II, III and IV below, we show that the final output of Algorithm 1 given by \(\mathcal {C}\) has no bad states and and associated transitions. That is, if \( \mathcal {C}\) is the output of Algorithm 1, then it means that the execution of the repeat loop (Lines 8–12 of Algorithm 1) on \(\mathcal {C}\) should not modify it. Hence, assuming t exists in \(\mathcal {C}\), it suffices to prove that t would be removed by this loop to contradict the existence of t
- (I)
Case 1 (Static controllability)
We assume that t is a static transition which leads to a bad state in \(\mathcal {C}\) and we consider the case where t is uncontrollable and the case where t is controllable. If t is uncontrollable, it implies that t violates the definition of static controllability by the construction of \(\mathcal {C}^{0}\). Thus, applying Algorithm 1 to \(\mathcal {C}\) would eliminate t, contradicting the assumption that t is in \(\mathcal {C}\).
A similar situation prevails in the case that t is a controllable transition and leads to a bad state. It follows that t is not allowed in \(\mathcal {C}\), because the construction would have removed the bad state and all transitions leading to it. Hence, it contradicts the hypothesis that t is in \(\mathcal {C}\). We formally prove the above two cases in the following two steps, respectively.
Suppose that t is a static transition where gn = true. Then, from (2) we have

- (a)
if δn ∈Σuc
$$ \begin{array}{@{}rcl@{}} &&\implies t~\text{violates the definition of static controllability } \end{array} $$(i.e., since \((s_{n+1},t_{n+1}) \in \mathcal {S}^{Bad}_{\mathcal {C}}\), means t is enabled in \(\mathcal {G}_{W}\) but not in \(\mathcal {C}\) by the construction of \(\mathcal {C}^{0}\) and by Lemma 7)

This can be seen from the construction of \(\mathcal {C}\) by Algorithm 3 (Lines 3-15), where any uncontrollable transition t enabled at sn in \(\mathcal {G}_{W}\) but not enabled at a corresponding state (sn,tn) of \(\mathcal {C}\) will lead to the elimination of (sn,tn) from the states of \(\mathcal {C}\) (Line 14). The state (sn,tn) will not even exist in the set of states of \(\mathcal {C}\).
- (b)
If δn ∈Σc,
$$ \begin{array}{@{}rcl@{}} &&{}\implies t \text{is a static controllable transition that is allowed in}~ \mathcal{G}_{W} \text{but not}\\ &&\text{in}~\mathcal{C}~\text{since} ~(s_{n+1},t_{n+1}) \in \mathcal{S}^{Bad}_{\mathcal{C}} \text{and by Lemma~7}\\ &&{}\implies \text{it will be a contradiction to say that~} t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$If t leads to a bad state, it means it is not allowed in \(\mathcal {C}\), which means it will not appear in \(\mathcal {C}\otimes \mathcal {G}_{W}\) by Lemma 8. This leads to a contradiction.
- (a)
- (II)
Case 2 (Dynamic controllability 1, stronger guards generation)
Here we assume that t is a dynamic type 1 transition which leads to a bad state in \(\mathcal {C}\) and we consider the case where t is uncontrollable and the case where t is controllable. In the case that t is an uncontrollable transition, it implies that t is either not allowed in \(\mathcal {C}\) at all or it allowed but the guards on both transitions are not satisfied by the construction of \(\mathcal {C}^{0}\). It follows that Algorithm 1 would have strengthened the guard on t during the construction of \(\mathcal {C}\) and making the guard on t stronger, which implies that the state (sn+ 1,tn+ 1) is not reachable. It follows that t is not a valid transition. Hence, it would be a contradiction if it holds that t is in \(\mathcal {C}\). A similar scenario holds in the case that t is a controllable transition and leads to a bad state. It follows that t is not allowed in \(\mathcal {C}\) at all or the guards on both transitions do not agree. Thus, t is not in \(\mathcal {C}\otimes \mathcal {G}_{W}\). We formally prove the above two cases in the following two steps, respectively.
Suppose that t is a dynamic type 1 transition
Then, from (2) we have,

- (a)
if δn ∈Σuc(e.g., in Example 4 take t to be the transition
 of Fig. 14c)$$ \begin{array}{@{}rcl@{}} && \implies t~\text{violates the definition of dynamic 1 controllability}\\ &&\text{i.e., since} (s_{n+1},t_{n+1}) \in\mathcal{S}^{Bad}_{\mathcal{C}}, t \text{is allowed in} \mathcal{G}_{W} \text{but not in} C \text{by} \\ &&\text{the construction of } \mathcal{C}^{0}\\ &&\implies \text{the guard} g_{n} \text{of~} \mathcal{C} \text{would have been strengthened and}\\ &&\text{transition}~t \text{eliminated}\\ &&\implies \text{it will be a contradiction to say that} t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$
of Fig. 14c)$$ \begin{array}{@{}rcl@{}} && \implies t~\text{violates the definition of dynamic 1 controllability}\\ &&\text{i.e., since} (s_{n+1},t_{n+1}) \in\mathcal{S}^{Bad}_{\mathcal{C}}, t \text{is allowed in} \mathcal{G}_{W} \text{but not in} C \text{by} \\ &&\text{the construction of } \mathcal{C}^{0}\\ &&\implies \text{the guard} g_{n} \text{of~} \mathcal{C} \text{would have been strengthened and}\\ &&\text{transition}~t \text{eliminated}\\ &&\implies \text{it will be a contradiction to say that} t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$By Algorithm 5 (Lines 30-38), the guards of \(\mathcal {C}\/\) are strengthened, in particular the guard gn on

 will never be true and the state (sn+ 1,tn+ 1) will be eliminated. Hence, it will be a contradiction to say that \(t \in {\Gamma }_{\mathcal {C}\otimes \mathcal {G}_{W}}\)
will never be true and the state (sn+ 1,tn+ 1) will be eliminated. Hence, it will be a contradiction to say that \(t \in {\Gamma }_{\mathcal {C}\otimes \mathcal {G}_{W}}\) - (b)
if δn ∈Σc,
$$ \begin{array}{@{}rcl@{}} && \implies \text{Since} (s_{n+1},t_{n+1}) \in\mathcal{S}^{Bad}_{\mathcal{C}} \text{means the controllable transition} t \\ &&\quad\text{is allowed in} \mathcal{G}_{W}\\ && \text{~~~~but not in} \mathcal{C} \qquad\text{i.e., the guard} g_{n} \text{is allow in} \mathcal{G}_{W} \text{but not in} \mathcal{C} \end{array} $$(i.e., a controllable transition that leads to a bad state in \(\mathcal {C}\) means either the transition is in \(\mathcal {C}\) but the guards are not satisfied for all values or the transition is not in \(\mathcal {C}\) at all)
$$ \begin{array}{@{}rcl@{}} &&\implies t \text{will not appear in} C \text{by Lemma~8}\\ &&\implies \text{it will be a contradiction to say that~} t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$
- (a)
- (III)
Case 3 (Dynamic controllability type 2, event enforcement)
Suppose that t is a dynamic type 2 transition which leads to a bad state in \(\mathcal {C}\). In this particular case (Case 3) the guard on t has a variable whose value depends on the output of an atomic operation (e.g., in Fig. 10). We consider separately the case where t is uncontrollable and the case where t is controllable.
In the case that t is an uncontrollable transition, it implies t does not satisfy the definition of dynamic controllability (event enforcement), since (sn+ 1,tn+ 1) is a bad state in \(\mathcal {C}\). Now by controllability of event enforcement, there must exist another enforceable transition, say t′, also enabled at the same state as t to be used to preempt t during runtime. This means that (sn+ 1,tn+ 1) is unreachable. It follows that t is not a valid transition in \(\mathcal {C}\). This contradicts the hypothesis that t is in \(\mathcal {C}\).
Similarly, consider the case that t is a controllable transition and leads to a bad state. It follows that t is not allowed in \(\mathcal {C}\) but in \(\mathcal {G}_{W}\). Hence, it contradicts the hypothesis that t is in \(\mathcal {C}\). We formally prove the above two cases in the following two steps, respectively.
Recall that \(g_n^A(v)\) denote a guard gn with a variable v whose values depend on an output of an atomic operation A of a given transition system. Suppose that t is a dynamic type 2 transition where \(g_n= g_n^A(v)\). Then, from (2) we have,

- (a)
If δn ∈Σuc(e.g., in Example 4 take t to be the transitions
 of Fig. 14c).
of Fig. 14c).

by Corollary 1, i.e., from the controllability of dynamic transition of type 2 using event enforcement. Otherwise Algorithm 5 (Lines 47-48) would have eliminated
 from \(\mathcal {C}\). Since there is an enforceable event \(\delta _{n}^{\prime }\) also enabled at state (sn,tn) of the controller, the state (sn+ 1,tn+ 1) is not reachable because \(\delta _{n}^{\prime }\) would be used to preempt t at runtime.
$$ \begin{array}{@{}rcl@{}} &&\implies \text{it will be a contradiction to say that}~ t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$
from \(\mathcal {C}\). Since there is an enforceable event \(\delta _{n}^{\prime }\) also enabled at state (sn,tn) of the controller, the state (sn+ 1,tn+ 1) is not reachable because \(\delta _{n}^{\prime }\) would be used to preempt t at runtime.
$$ \begin{array}{@{}rcl@{}} &&\implies \text{it will be a contradiction to say that}~ t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$This can be seen from Lines 39-51 of Algorithm 5, if there is a state (sn,tn) in the set of states of \(\mathcal {C}\) with a transition t whose guard is given by \({g_{n}^{A}}(v)\) and leads to a bad state, it implies that there must be an enforceable transition t′ exiting (sn,tn), otherwise the state (sn,tn) is removed from the states of \(\mathcal {C}\). Hence, it will be a contradiction to say that \(t \in {\Gamma }_{\mathcal {C}\otimes \mathcal {G}_{W}}\). Algorithm 5 monitors the variable v at runtime and ensures that \(\delta _{n}^{\prime }\) is enforced.
- (b)
If δn ∈Σc,

i.e., a dynamic type 2 controllable transition that leads to a bad state in \(\mathcal {C}\) means it is not allowed to occur by the construction of \(\mathcal {C}^{0}\)
$$ \begin{array}{@{}rcl@{}} &&\implies t \text{will not appear in} C \text{by Lemma 8}\\ &&\implies \text{it will be a contradiction to say that}~ t\in{\Gamma}_{\mathcal{C}\otimes\mathcal{G}_{W}} \end{array} $$
- (a)
- (IV)
Finally, in the computation of \(\mathcal {C}\) by Algorithm 1 (Line 13), any new transition that was created as a result of the checking for controllability is removed.
- (I)
From cases I, II, III, IV, we have shown that any transition \(t \in {\Gamma }_{\mathcal {C}^{0}}\) that leads to a bad state is eliminated from the set of transitions of \({\mathcal {C}^{0}}\) upon termination of Algorithm 1. Thus, the final output of Algorithm 1 given by \(\mathcal {C}\) has no bad states and has no transitions that lead to a bad state. This implies that every transition in the controlled system \(\mathcal {C}\otimes \mathcal {G}_{W}\) leads to a good state which can be matched by \(\mathcal {T}^{W}\). Hence, \(\mathcal {C}\otimes \mathcal {G}_{W}\preceq \mathcal {T}^{W}\).
□
Additionally, we speculate that the controller \(\mathcal {C}\) generated by Algorithm 1 is minimally restrictive. We believe this because we have shown that the controller \(\mathcal {C}\) generated by Algorithm 1 is minimally restrictive in a comparable model in the dissertation by Atampore (2017) (pages 175-189).
7 Related work
In this section, we will discuss related work and highlight the differences between existing work and our work. As there exists an extensive body of work on automatic service composition, due to space limitations we discuss only the work most relevant to ours. The reader may also refer to our technical report (Atampore et al. 2016) for further details.
We will start by looking at works that apply supervisory control theory to the SOC paradigm. As stated earlier in this paper, supervisory control theory has been applied to software systems such as concurrency in multithreaded programs and component based software systems (Dragert et al. 2008; Auer et al. 2014; Wang et al. 2009, 2010).
7.1 DES and services
With respect to applying DES to SOA, the work of Wang and Nazeem (2011) investigates the use of supervisory control in the artifact-centric design paradigm. They present a framework to synthesize an artifact-centric process from a given set of artifacts such that a correct execution is guaranteed by properly handling uncontrollable events. However, this work relies on the standard SCT which utilizes finite state machines for modeling. In addition, this approach does not deal with data and how messages are actually exchanged among component services. Another related work is the paper by Balbiani et al. (2008) which applies a variant of supervisory control theory in which system requirements are specified in modal logic to model an abstract form of service composition where non-deterministic communicating automata are used to represent Web services. The composition synthesis problem considered here is, given a community of services and a goal service, to synthesize a mediator such that the triplet client/mediator/community is equivalent to the goal service. The composition problem considered in their paper is restricted to synthesizing a specification (mediator) that realizes a given goal, but does not show how to actually orchestrate the services in terms of data and control flow requirements during execution time.
7.2 AI and service composition
Next, we look at work that employs AI planning techniques. A lot of AI planning based approaches have been proposed to solve the problem of automatic service composition. Kazhamiakin et al. (2013), Bertoli et al. (2010), Pistore et al. (2005b), Hoffmann et al. (2014), and Bucchiarone et al. (2014) present a model-checking based planning approach that uses transition systems to model Web services that communicate by exchanging messages. The authors adapt symbolic model-checking techniques into planning in order to deal effectively with non-determinism, partial observability, and complex goals. They use these techniques to find a parallel composition of all the available services and then synthesize a controller that ensures that the composed service satisfies the given requirement by controlling it. That is, given a set of available services \(\mathcal {W} = {\mathcal {W}_{1},\mathcal {W}_{2},...,\mathcal {W}_{n}}\) and ρ describing the goal specification, they compute a controller (plan) \(\mathcal {W}_{c}\) such that \(\mathcal {W}_{c}\)\(\rhd ({\mathcal {W}_{1}\parallel \mathcal {W}_{2}...\parallel \mathcal {W}_{n}}) \models \rho \), where ∥ is the composition operator. Their work converts OWL-S processes to state transition systems and then goals are expressed using a requirement specification language called EAGLE. Both the state transition systems and the goals are fed into an MBP planner. Even though this approach can produce correct plans, it suffers from scalability problems partly due to the way goals are expressed. Raik et al. (2012) and Pistore et al. (2005a) tried to solve the scalability issues in the aforementioned approach by defining an appropriate model for providing a knowledge level description of the component services which uses BPEL workflows instead of OWL-S process models. The work has been incorporated into a well-known automated service composition project called the ASTRO framework (Marconi et al. 2008). The main difference between the work by Pistore et al. and our work is that Pistore et al. make use of AI techniques in generating a controller while in our work we make use of supervisory control theory. In addition, our approach makes use of Labelled Transition Systems augmented with guards and variables while the approach by Pistore et al. make use of State Transition Systems.
Another AI planning approach is the work by Rao et al. (2006) which presents a mixed initiative framework for semantic Web service discovery and composition which does not attempt to automate all decisions, but assumes that the users should retain close control over many decisions while having the ability to selectively delegate tedious aspects of their tasks. They used an AI planning algorithm known as GraphPlan to build their composition engine which combines rule-based reasoning on OWL ontologies with Jess (a rule engine and scripting environment for Java platforms) and planning functionalities. The main use of planning here is to provide suggestions of composition schemata to the user, instead of enforcing decisions which form the ultimate goal of this work.
Wu et al. (2007) also employed graph-based planning to solve the service composition problem. The approach considers both process heterogeneity and data heterogeneity problems. They implemented their own definition of an abstract semantic Web service built on top of SAWSDL and WSDL-S. Then, they extended GraphPlan that automatically generates the control flow of a Web process. The system automatically generates an executable BPEL process from a given specification of the initial state, the goal state and a semantically annotated Web service description in SAWSDL. Data mediation is done using assignment activities in BPEL or by a data mediator which may be embedded in a middleware. At runtime the data mediator converts the available service into the format of the input message of the operation which is invoked when called by the BPEL process.
Sirin et al. (2004) attempt to leverage the Hierarchical Task Network (HTN) planning techniques for the automated composition of semantic Web services. The authors are motivated to use this technique based on the fact that the concept of task decomposition in HTN planning is very similar to the concept of composite process decomposition in OWL-S process ontology. They built a system that translates OWL-S service descriptions into SHOP2 (a domain-independent HTN planning system for HTN) (Nau et al. 2003) and then they provided a method to automatically synthesize a feasible composition plan. The system is also capable of executing information-providing Web services during the planning process. They went ahead to prove the correctness of their algorithm/approach by showing the correspondence to the situational calculus semantics of OWL-S.
Peer (2005) shows how the Partial Order Planner known as Versatile Heuristic Partial Order Planner (VHPOP) can be combined with re-planning algorithm for automatic service composition. They provide their own definition of semantic Web services which is then translated into PDDL as an input for VHPOP. The PDDL description of the Web service is fed into VHPOP as well as a set of links between tasks to avoid. One or more plans are automatically generated which may be partially defined. During runtime, execution is done one step at a time since the generated plan(s) does not necessarily ensure correct execution. Hence, if a plan fails, a re-planning is performed and a new plan is produced, given the conditions of the failure; however, if the execution of a plan is successful, there is no need to re-plan and one can move on to the next task.
Klusch and Gerber (2005) present an approach similar to that of Peer. However, they built their framework on OWL-S descriptions rather than developing their own ontology service language. Similarly, the OWL-S descriptions are converted into PDDL descriptions and then fed into their AI planner. They used a hybrid AI planner known as Xplan which combines the benefits of both graph based planning and HTN. Their approach increases planning efficiency in two ways. The graph-plan based FastForward-planner always finds a composition/solution if it exists in the action state space, whereas HTN planning provides decomposition planning techniques. In addition, their planner supports re-planning components which automatically updates or reacts to changes during the composition planning process.
Recently, Sohrabi and McIlraith (2009) presented an approach that supports customization, optimization and regulation enforcement during composition construction time by incorporating preferences and regulations into HTN planning. This work builds on the work in McIlraith and Son (2002) by extending and customizing Golog (Ferrein et al. 2009) to support personalized constraints and nondeterminism in sequential executions and then, they redesigned ConGolog, the interpreter of Golog to take care of these changes. Interestingly, this development took place alongside the development of the definition of OWL-S and was one of the first works to use semantic Web services as an input to planners through translation to PDDL.
Continuing in the AI approaches, Zou et al. (2014) use numerical temporal planning to tackle the problem of dynamic Web service composition which considers quality of service properties. One unique feature of this approach is that it does not rely on existing predefined workflows but it automatically generates temporal and numeral specifications from a composition task. This approach is basically made up of two steps. Firstly, a quality of service aware composition task is translated into a PDDL which is further transformed into a cost-sensitive temporally-expressive planning problem. This stage presents the service composition problem as a numeral planning problem involving time and cost optimization. Finally, the temporally expressive planning problem is solved using a SAT-based cost planning solver developed by the group. This solver deals with logical reasoning, temporal planning and optimization of composition. Other recent works using AI planning to deal with Web service composition can be found in the literature (Rodriguez-Mier et al. 2011; Fayyad et al. 2015; Na-Lumpoon et al. 2014; Abdullah and Xining 2013; Niewiadomski et al. 2014). However, most of the AI planning techniques assume that the behaviour of services is deterministic and, hence, these approaches fail when unexpected events occur (Bartalos and Bieliková 2011).
7.3 Other categories of service composition approaches
Other categories of Web service composition approaches are those that exploit transition systems and formal modeling languages such as Petri nets, UML and FSMs to model service composition. In the following paragraphs we discuss a number of them.
One of the earliest works in this category is by Berardi et al. (2005a, 2005b, 2005c, 2008) who present a formal framework in which execution trees are used to describe the exported behaviour of services (an abstraction for its possible executions). These execution trees are represented using Finite State Machines. In the approach, a service is modeled using two schemata, an external and internal schema which are represented using FSMs. The external schema specifies the exported behaviour (externally-visible) of services, whereas the internal schema contains information on which service instances execute a given action within the community of services. Their approach reduces the problem of composition synthesis into the satisfiability of a suitable formula of Deterministic Propositional Dynamic Logic (DPDL). That is, both the FSM models of the available services and the target service are encoded into DPDL, and a target service exists if and only if the set of formulas are satisfiable and then an FSM is automatically synthesized. The resulting FSM is further translated into a BPEL process and executed in a BPEL engine.
Pathak et al. (2008) propose a Framework for Modeling Service Composition and Execution (MoSCoE) where both the available services and the goal service exhibit infinite-state behaviour. The approach employs Symbolic Transition Systems (STSs) to model services that are associated with guards over infinite domain variables. They use refinement analysis to guide users to refine their composition goal in the case of a failure. Typically, the framework consists of three steps, abstraction, composition and refinement. Both component services and the goal service are described using UML state machines and are translated into STSs. To this end, they apply their composition algorithms to synthesize a composition if it exists. In the case that it does not exist, the users refine their requirements and then try again.
Skogan et al. (2004) also proposed an approach for semantic Web service composition using Model-Driven Development (MDD). UML is used to model Web services. They first translate WSDL descriptions into UML models. This allows existing services to be modeled using UML platforms designed for building compositions. They apply MDD techniques to generate a composition based on the UML models of the Web services, which in turn can be translated into executable BPEL specifications. Furthermore, this paper presents an open-source implementation that realizes their technique.
Jingjing et al. (2014) solve the service composition problem using timed automata. A formal model built on timed automata is used to model Web services and provides an approach for automatic Web service composition. They implemented an algorithm that automatically generates a timed automaton model for each Web service interface which are all put together by synchronizing them through their branches and end tags. In this case, the equivalent graph is a topology which connects each Web service interface by an equivalence relation. The algorithm has been implemented in a composition automation engine which uses the Web service interface description language (WSIL). The Web service interface description language is a context-free grammar language developed to describe Web service interfaces. The engine is basically a compiler which takes inputs in the form of WSIL and produces outputs via semantic analysis in the form of a graph or an equivalent tree for Web service interface. The equivalent tree represents a data structure without loops which can be obtained by performing a breadth-first traversal of the equivalent graph described above. The output is then verified with a verification tool known as UPPAAL.
The work of Wang et al. (2014) presents an approach in which conditional branch structures are used to model the problem of service composition. This approach supports user preferences as well as the ability to adapt to changes in a dynamic real-world environment. In order to model conditional branch structures accurately, they employ activity diagrams in UML to represent the dependencies in composite services. They consider two types of user preferences during composition synthesis. “One type is that a user prefers a class of services over another according to certain conditions (e.g., Lucy prefers to go by air over car, if the driving time is greater than 4 hours). The other type is that the user assigns priorities over services with similar functionalities” (Wang et al. 2014). Based on these user preferences and a set of services (each specified by an activity diagram) they provide an algorithm that generates all the feasible composite services.
In another direction, the work by Yang et al. (2014) adopts the extended BDI (Belief-Desire-Intention) logic to deal with the problem of Web service composition in the case where a user’s goal is not consistent with the composition goal. The Belief-Desire-Intention model is used to specify a service’s belief, desire and intention, which are mapped into the environment of BDI, the goal of the web service (and user) and composition schemes respectively. A process model is then used to characterize the results. In order to allow for dynamic evolution of their workflow, they use AgentSpeak(L) (a communication language) to express it.
Khoumsi (2013) casts the service composition problem as a control problem using a simple input-output automata-based method. The problem is to synthesize an orchestrator Orch from a given set of Web service S1,...,Sn and a desired goal S0 such that Orch coordinates the available services to achieve S0. However, this approach is limited to only the input and output parameter descriptions of services and does not capture the behavioural constraints of services.
In a nutshell, relative to supervisory control theory, none of the above approaches is able to prevent a system from violating its requirements or guarantees that the system requirement would always be satisfied until a violation occurs.
8 Conclusion and future work
In this paper, we have developed a supervisory control framework for modeling Web service composition. We have provided a formalism based on SLTS and have also formalized the problem of Web service composition. We have described a technique to generate a composition from a given set of Web services and a specification specified as SLTS.
In future work, we will show that the controller \(\mathcal {C}\) generated by Algorithm 1 is in fact, minimally restrictive. In this framework, we assume full observability of events but it will be of great interest to model partial observability aspects of services. That is, sometimes a service could progress from one state to another after executing some sequence of internal events or actions which cannot be observed by the controller. Hence, a new control mechanism is needed in order to prevent the system from violating any system requirements. Another direction is to research into how non-functional requirements could be incorporated into the framework. One can also look into how to efficiently represent the SLTSs for our formalism using data structures such as BDDs and process algebra and to also provide a prototype and evaluations of the proposed approach. Another general extension of our approach could be the use use decentralized control of DES to model automated choreography synthesis Web services.
References
Abdullah A, Xining l (2013) An efficient I/O based clustering HTN in web service composition. In: International conference on computing, management and telecommunications (ComManTel), Ho Chi Minh City, pp 252–257
Alves A, Arkin A, Askary S, Barreto C, Bloch B, Curbera F, Ford M, Goland Y, Guizar A, Kartha N, Kevin CL, Khalaf R, König D, Marin M, Mehta V, Thatte S, Rijn D, Yendluri P, Yiu A (2007) Web services business process execution language version 2.0, OASIS Standard. http://docs.oasis-open.org/wsbpel/2.0/OS/wsbpel-v2.0-OS.html. [Online; accessed 10 Mar 2017]
Andrews T, Curbera F, Dholakia H, Goland Y, Klein J, Leymann F, Liu K, Roller D, Smith D, Thatte S, Trickovic I, Weerawarana S (2003) Business process execution language for web services version 1.1. http://msdn.microsoft.com/en-us/library/ee251594(v=bts.10).aspx#feedback. [Online; accessed 10 Mar 2017]
Atampore F (2017) Towards provably correct services: automated service composition via supervisory control synthesis. Ph.D. thesis, School of Computing, Queen’s University, Ontario
Atampore F, Dingel J, Rudie K (2016) A controller synthesis framework for automated service composition. Tech. Rep. 2016-630, School of Computing, Queen’s University, Kingston, Ontario, Canada. http://sites.cs.queensu.ca/tr/
Auer A, Dingel J, Rudie K (2014) Concurrency control generation for dynamic threads using discrete-event systems. Sci Comput Program 82:22–43
Balbiani P, Cheikh F, Feuillade G (2008) Composition of interactive web services based on controller synthesis. In: IEEE Congress on services - Part I. IEEE Computer Society, pp 521–528
Bartalos P, Bieliková M (2011) Automatic dynamic web service composition: a survey and problem formalization. Comput Inform 30(4):793–827
Berardi D, Calvanese D, De Giacomo G, Hull R, Lenzerini M, Mecella M (2005a) Modeling data & processes for service specifications in Colombo. In: Proceedings of the open interop workshop on enterprise modeling and ontologies for interoperability (EMOI-INTEROP’05) co-located with CAiSE’05 conference. Portugal
Berardi D, Calvanese D, De Giacomo G, Hull R, Mecella M (2005b) Automatic composition of web services in Colombo. In: Proceedings of the thirteenth Italian symposium on advanced database systems, (SEBD). Brixen-Bressanone (near Bozen-Bolzano), Italy, pp 8–15
Berardi D, Calvanese D, De Giacomo G, Hull R, Mecella M (2005c) Automatic service composition based on behavioural descriptions. Int J Coop Informa Syst 14(4):333–376
Berardi D, Cheikh F, Giuseppe GD, Patrizi F (2008) Automatic service composition via simulation. Int J Found Comput Sci 19(2):429–451
Bertoli P, Pistore M, Traverso P (2010) Automated composition of web services via planning in asynchronous domains. Artif Intell: Int J 174(3–4):316–361
Brand D, Zafiropulo P (1983) On communicating finite-state machines. J ACM 30(2):323–342. https://doi.org/10.1145/322374.322380
Bucchiarone A, de Sanctis M, Pistore M (2014) Domain objects for dynamic and incremental service composition. In: Service-oriented and cloud computing - third European conference, ESOCC, Manchester, pp 62–80
Cassandras C, Lafortune S (2008) Introduction to discrete-event systems, 2nd edn. Springer, US
Christensen E, Curbera F, Meredith G, Weerawarana S (2001) Web services description language (WSDL), Version 1.1. http://www.w3.org/TR/wsdl. [Online; accessed 6-Jan-2017]
Crasso M, Rodríguez JM, Zunino A, Campo M (2010) Revising WSDL documents: why and how. Internet Comput IEEE 14(5):48–56
Diekmann R, Weidemann D (2013) Event enforcement in the context of the supervisory control theory, Miȩdzyzdroje, Poland
Domain WUW (2017) XML schema. https://www.w3.org/XML/Schema. [Online; Accessed 20 Aug 2017]
Dragert C, Dingel J, Rudie K (2008) Generation of concurrency control code using discrete-event systems theory. In: Proceedings of the 16th ACM international symposium on foundations of software engineering (SIGSOFT), vol FSE-16. ACM, New York, pp 146–157
Erl T (2004) Service-oriented architecture: a field guide to integrating XML and web services. Prentice Hall, New Jersey
Fabian M, Lennartson B (1996) On non-deterministic supervisory control. In: Proceedings of the 35th IEEE conference on decision and control, vol 2. IEEE, Kobe, pp 2213–2218
Fayyad M, Kamel A, Salah A (2015) ACUAI framework for automatic composition of web services using gaming AI. In: Fifth international conference on digital information and communication technology and its applications (DICTAP). Lebanese University, Lebanon, pp 1–6
Ferrein A, Schiffer S, Lakemeyer G (2009) Embedding fuzzy controllers in golog. In: IEEE International conference on fuzzy systems, FUZZ-IEEE’09. IEEE, Jeju Island, pp 894–899
Fu X, Bultan T, Suc JJ (2004) Analysis of interacting BPEL web services. In: Proceedings of the 13th international conference on world wide web, (WWW ’04). ACM, New York, pp 621–630, DOI https://doi.org/10.1145/988672.988756, (to appear in print)
Gall TL, Jeannet B, Marchand H (2005) Supervisory control of infinite symbolic systems using abstract interpretation. In: Proceedings of the 44th IEEE conference on decision and control and european control conference (CDC-ECC ’05). IEEE Control Systems Society, Melia Sevilla, pp 30–35
Gudgin M, Hadley M, Mendelsohn N, Moreau J, Nielsen HF, Karmarkar A, Lafon Y (2007) Simple object access protocol, Version 1.1. http://www.w3.org/TR/soap/. [Online; accessed 20 Aug 2017]
Hatzi O, Nikolaidou M, Vrakas D, Bassiliades N, Anagnostopoulos D, Vlahavas I (2015) Semantically aware web service composition through AI planning. Int J Artif Intell Tools 24(01):1450,015. https://doi.org/10.1142/S0218213014500158. http://www.worldscientific.com/doi/abs/10.1142/S0218213014500158
Hoffmann J, Bertoli P, Helmert M, Pistore M (2014) Message-based web service composition, integrity constraints, and planning under uncertainty: a new connection. Computing Research Repository, arXiv:1401.3470
Honda K, Tokoro M (1991) An object calculus for asynchronous communication. In: Proceedings of the European conference on object-oriented programming (ECOOP), LNCS 512. Springer, Geneva, pp 133–147
Jingjing H, Wei Z, Pesic M, Xing Z, Dongfeng Z (2014) Web service composition automation based on timed automata. Appl Math Inf Sci: Int J 8 (4):2017–2024
Kazhamiakin R, Marconi A, Pistore M, Raik H (2013) Data-flow requirements for dynamic service composition. In: Proceedings of the IEEE 20th international conference on web services. IEEE, Santa Clara, pp 243–250
Khoumsi A (2013) A simple formal method to synthesize an orchestrator in web service composition. In: American control conference (ACC). USA, Washington, DC, pp 107–112
Klusch M, Gerber A (2005) Semantic web service composition planning with OWLS-XPlan. In: Proceedings of the 1st international association for the advancement of artificial intelligence (AAAI) fall symposium on agents and the semantic web, Technical Report FS-05-01. AAAI Press, Arlington, pp 55–62
Kumar R, Garg V, Marcus SI (1993) Predicates and predicate transformers for supervisory control of discrete event dynamical systems. IEEE Trans Autom Control 38(2):232–247
Marconi A, Pistore M, Traverso P (2008) Automated composition of web services: the ASTRO approach. IEEE Data Eng Bull Issues 31(3):23–26
McIlraith SA, Son TC (2002) Adapting golog for composition of semantic web services. In: Fensel D, Giunchiglia F, McGuinness DL, Williams MA (eds) Proceedings of the eights international conference on principles and knowledge representation and reasoning (KR-02). Morgan Kaufmann, Toulouse, pp 482–496
Milner R (1989) Communication and concurrency. Prentice Hall International, Upper Saddle River
Miremadi S, Åkesson K, Lennartson B (2008) Extraction and representation of a supervisor using guards in extended finite automata. In: Proceedings of the 9th international workshop on discrete event systems, (WODES 08). IEEE, Gothenburg, pp 193–199
Na-Lumpoon P, Fauvet MC, Lbath A (2014) Toward a framework for automated service composition and execution. In: 8th International conference on software, knowledge, information management and applications (SKIMA). Kathmandu, Nepal, pp 1–8
Nath K, Dhar S, Basishtha S (2014) Web 1.0 to web 3.0 - evolution of the web and its various challenges. In: International conference on optimization, reliabilty, and information technology (ICROIT). IEEE, Faridabad, pp 86–89
Nau D, Au T, Ilghami O, Kuter U, Murdock JW, Wu D, Yaman F (2003) SHOP2: an HTN planning system. J Artif Intell Res 20(1):379–404
Niewiadomski A, Penczek W, Skaruz J (2014) A hybrid approach to web service composition problem in the planICS framework. In: Irfan A, Muhammad Y, Xavier F, Carme Q (eds) Mobile web information systems, lecture notes in computer science, vol 8640. Springer International Publishing, pp 17–28
Papazoglou MP, Traverso P, Dustdar D, Leymann F (2007) Service-oriented computing: state of the art and research challenges. IEEE Comput 40(11):38–45
Pathak J, Basu S, Lutz RR, Honavar V (2008) MOSCOE: an approach for composing web services through iterative reformulation of functional specifications. Int J Artif Intell Tools 17(1):109–138
Peer J (2005) A POP-based replanning agent for automatic web service composition. In: Proceedings of the second european conference on the semantic web: research and applications, ESWC’05. Springer, Berlin, pp 47–61
Pistore M, Marconi A, Bertoli P, Traverso P (2005a) Automated composition of web services by planning at the knowledge level. In: Proceedings of the nineteenth international joint conference on artificial intelligence. Professional Book Center, Edinburgh, pp 1252–1259
Pistore M, Traverso P, Bertoli P, Marconi A (2005b) Automated synthesis of composite BPEL4WS web services. In: Proceedings of the IEEE international conference on web services (ICWS’05). IEEE Computer Society, Orlando, pp 293–301
Portchelvi V, Venkatesan VP (2015) A goal-directed orchestration approach for agile service composition. Int J Inf Technol Comput Sci (IJITCS) 7(3):60–67
Raik H, Bucchiarone H, Khurshid N, Marconi A, Pistore M (2012) ASTRO-CAptEvo: dynamic context-aware adaptation for service-based systems. In: Proceedings of the IEEE Eighth World congress on services, SERVICES ’12. IEEE Computer Society, Washington, DC, pp 385–392
Ramadge PJ, Wonham WM (1987) Supervisory control of a class of discrete event processes. SIAM J Control Optim (SICON) 25(1):206–230. https://doi.org/10.1137/0325013
Rao J, Dimitrov D, Hofmann P, Sadeh NM (2006) A mixed initiative approach to semantic web service discovery and composition: SAP’s guided procedures framework. In: IEEE International conference on web services (ICWS’06). IEEE Computer Society, Chicago, pp 401–410
Rodríguez G, Soria A, Campo M (2016) Artificial intelligence in service-oriented software design. Eng Appl Artif Intell 53:86–104. http://www.sciencedirect.com/science/article/pii/S0952197616300677
Rodriguez-Mier P, Mucientes M, Lama M (2011) Automatic web service composition with a heuristic-based search algorithm. In: IEEE International conference on web services (ICWS). USA, Washington DC, pp 81–88
Silva FO, Rosa PF (2006) The quest for the web services stack: a fast trip. In: Proceedings of the 6th international conference on web engineering, ICWE ’06. ACM, New York, pp 93–94
Sirin E, Parsia B, Wu D, Hendler J, Nau D (2004) HTN planning for web service composition using SHOP2. Web Sem: Sci Services Agents World Wide Web 1(4):377–396. International Semantic Web Conference 2003
Skogan D, Grønmo R, Solheim I (2004) Web service composition in UML. In: Proceedings of the eighth IEEE international enterprise distributed object computing conference, EDOC ’04. IEEE Computer Society, Washington, DC, pp 47–57
Sohrabi S, McIlraith SA (2009) Optimizing web service composition while enforcing regulations. In: Proceedings of the 8th international semantic web conference, ISWC ’09. Springer, Berlin, pp 601–617, DOI https://doi.org/10.1007/978-3-642-04930-9_38, (to appear in print)
Teixeira M, Malik R, Cury J, de Queiroz M (2015) Supervisory control of DES with extended finite-state machines and variable abstraction. IEEE Trans Autom Control 60(1):118–129
Wang Y, Nazeem A (2011) Artifact-centric business process synthesis framework using discrete event systems theory. Tech. rep., HP Laboratories
Wang Y, Lafortune S, Kelly T, Kudlur M, Mahlke S (2009) The theory of deadlock avoidance via discrete control. In: Proceedings of the 36th annual SIGPLAN-SIGACT symposium on principles of programming languages (POPL’09), New York, pp 252–263
Wang Y, Cho H, Liao H, Nazeem A, Kelly T, Lafortune S, Mahlke S, Reveliotis S (2010) Supervisory control of software execution for failure avoidance: experience from the Gadara project. In: Raisch J, Giua A, Lafortune S, Moor T (eds) Proceedings of the international workshop on discrete event systems (WODES’10), vol 43. International Federation of Automatic Control, Technische Universität, Berlin, pp 259–266
Wang P, Ding Z, Jiang C, Zhou M (2014) Automated web service composition supporting conditional branch structures. Enterprise Inf Syst 8(1):121–146. https://doi.org/10.1080/17517575.2011.584132
Wonham WM, Cai K (2019) Supervisory control of discrete-event systems. Springer International Publishing, pp XX–489
Wonham WM, Ramadge PJ (1987) On the supremal controllable sublanguage of a given language. SIAM J Control Optim 25(3):637–659
Wu Z, Ranabahu A, Gomadam K, Sheth AP, Miller JA (2007) Automatic composition of semantic web services using process and data mediation. Technical report, Kno.e.sis Center, Wright State University, Dayton, Ohio USA
Yang J, Zhou X, Wang J, Zhu X (2014) A novel method for web service composition based on extended BDI. In: IEEE 11th International conference on networking, sensing and control, (ICNSC’14). IEEE, Miami, pp 310–315, DOI https://doi.org/10.1109/ICNSC.2014.6819644, (to appear in print)
Zafiropulo P, West C, Rudin H, Cowan D, Brand D (1980) Towards analyzing and synthesizing protocols. IEEE Trans Commun 28(4):651–661
Zhong N, Chen J, Ma J, Yao Y, Liu J, Huang R, Li W, Huang Z, Gao Y, Cao J (2014) WaaS-wisdom as a service. Intell Syst IEEE PP(99):1–1. https://doi.org/10.1109/MIS.2014.19
Zhou C, Kumar R (2007) Control of nondeterministic discrete-event systems for simulation equivalence. IEEE Trans Autom Sci Eng 4(3):340–349
Zou G, Lu Q, Chen Y, Huang R, Xu Y, Xiang Y (2014) QoS-aware dynamic composition of web services using numerical temporal planning. IEEE Trans Serv Comput 7(1):18–31
Acknowledgments
We are grateful to the anonymous reviewers of the original version of this paper. Their comments significantly improved our approach.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Atampore, F., Dingel, J. & Rudie, K. A controller synthesis framework for automated service composition. Discrete Event Dyn Syst 29, 297–365 (2019). https://doi.org/10.1007/s10626-019-00282-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-019-00282-0






 then
then  and g1 ≤ g′ and
and g1 ≤ g′ and  for
for  g1 ⇔ g2 and
g1 ⇔ g2 and  for
for  g1 ⇔ g2 and
g1 ⇔ g2 and 






 there exists a run r of length p or less such that
there exists a run r of length p or less such that  of
of 
 there exists a run r up to length p such that
there exists a run r up to length p such that 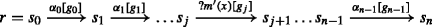 of
of  is in r and i < j.
is in r and i < j. and at least one input transition
and at least one input transition  of message header m″, then the number of output transitions of message header m″ must be equal to the number of input transitions of message header m″ in r.
of message header m″, then the number of output transitions of message header m″ must be equal to the number of input transitions of message header m″ in r.



 , if the conditions in (1) are true and exists no state
, if the conditions in (1) are true and exists no state 
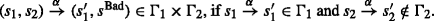

 is an emission of a variable v1 from
is an emission of a variable v1 from  is reception of v1 by
is reception of v1 by  in Fig.
in Fig. 



 in Γ1 and
in Γ1 and  and
and  and
and  and
and  and
and 




 will be removed (Lines 8-9).
will be removed (Lines 8-9). and (ti,si) ∈ R but the guard g1 is not a subguard of g2, i.e., g1 ≤ g2. In this case the guard on
and (ti,si) ∈ R but the guard g1 is not a subguard of g2, i.e., g1 ≤ g2. In this case the guard on  and g1 ≤ g2 but (ti,si)∉R. In this case the transition
and g1 ≤ g2 but (ti,si)∉R. In this case the transition  is eliminated (Lines 13-15).
is eliminated (Lines 13-15). enabled in the plant but not at the corresponding state (s5,t5) of
enabled in the plant but not at the corresponding state (s5,t5) of  and
and  will be eliminated from
will be eliminated from  (BAD2),
(BAD2),  in the
in the  (BAD1) and (s1,t1)
(BAD1) and (s1,t1)  are dynamic type 1 transitions since the values of the variables x and var can be tracked from where they were declared. Hence, at this stage the algorithm strengthens the guards of these transitions so that the state BAD1 and BAD3 are made unreachable by attaching the guard ¬(3 ≤ x < 7) and var∉{db} to the transition
are dynamic type 1 transitions since the values of the variables x and var can be tracked from where they were declared. Hence, at this stage the algorithm strengthens the guards of these transitions so that the state BAD1 and BAD3 are made unreachable by attaching the guard ¬(3 ≤ x < 7) and var∉{db} to the transition  and the transition
and the transition  , respectively. The resultant SLTS is given in Fig.
, respectively. The resultant SLTS is given in Fig.  is a dynamic type 2 transition since the variable y depends on the output of the atomic operation atom1(x,y) which cannot be tracked. This step of the algorithm will check for the enforceable transition
is a dynamic type 2 transition since the variable y depends on the output of the atomic operation atom1(x,y) which cannot be tracked. This step of the algorithm will check for the enforceable transition  and save the variable y to be monitored at runtime and then enforce !fail() when y=a, to prevent BAD2 from being reached.
and save the variable y to be monitored at runtime and then enforce !fail() when y=a, to prevent BAD2 from being reached. enabled in the corresponding state of the plant but not at the state (s3,t3) of
enabled in the corresponding state of the plant but not at the state (s3,t3) of 
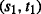 and
and  will be eliminated from
will be eliminated from  is an uncontrollable dynamic type 1 transitions since the values of the variable var can be tracked from when it was declared. Hence, at this stage the algorithm strengthens the guard of this transition so that the state BAD4 is made unreachable by attaching the guard var∉{cr} to the transition
is an uncontrollable dynamic type 1 transitions since the values of the variable var can be tracked from when it was declared. Hence, at this stage the algorithm strengthens the guard of this transition so that the state BAD4 is made unreachable by attaching the guard var∉{cr} to the transition  (shown Fig.
(shown Fig. 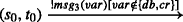 (s1,t1) can emit the message !msg3(var) but there is no matching input transition in
(s1,t1) can emit the message !msg3(var) but there is no matching input transition in  from
from 




 but there exists no
but there exists no 
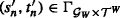 , which implies that
, which implies that  .
.
 . That is,
. That is, 

 be a path in
be a path in 
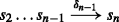 .
. , this means
, this means 
 , but
, but
 and (g1 ⇒ g2), which implies that
and (g1 ⇒ g2), which implies that  , and
, and and g3=true,
and g3=true,  .
. , where
, where  , where
, where  be a path in
be a path in 
 .
. but
but 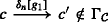 such that g1 ⇒ g2, which means
such that g1 ⇒ g2, which means 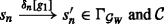 and
and 
 for some δn ∈Σ and
for some δn ∈Σ and  , where
, where 
 from
from 





 of Fig.
of Fig. 
 will never be true and the state (sn+ 1,tn+ 1) will be eliminated. Hence, it will be a contradiction to say that
will never be true and the state (sn+ 1,tn+ 1) will be eliminated. Hence, it will be a contradiction to say that 
 of Fig.
of Fig. 
 from
from 