1 Introduction

The discrete logarithm problem is one of the most fundamental hard problems used in public-key cryptography. In general, the (interval) multi-dimensional discrete logarithm problem is defined as follows [9].

Definition 1

Let G be a multiplicative abelian group. The \(d-\)dimensional discrete logarithm problem is: Given \(g_1,\ldots ,g_d,h\in G\) and \(N_1,\ldots ,N_d\in {\mathbb {N}}\) to find \(a_i\in [0,N_i)\text { for } 1\le i\le d\), if exists, such that

$$\begin{aligned} h = g_1^{a_1}g_2^{a_2}\ldots g_d^{a_d}. \end{aligned}$$

Suppose \(N_i, 1\le i\le d\) are all even and let \(N = N_1\times N_2\times \cdots \times N_d\).

When \(d=1\), this is the classical version of discrete logarithm problem, whose hardness underpins the security of many cryptographic schemes, like key exchange [5], public-key encryption [3, 6] and digit signature [16, 22]. The multi-dimensional discrete logarithm problem also arises in certain scenarios, such as computing the group order of some curves over finite fields [15, 17], using the GLV method to accelerate computations over elliptic curves [13], constructing electronic cash scheme [2] and election scheme [4].

To solve the multi-dimensional discrete logarithm problem, one can adapt Shank’s baby-step-giant-step algorithm [24]. By extending the algorithm to the d-dimensional situations, Matsuo et al. [17] obtain a method with \(O(\sqrt{N})\) time complexity and \(O(\sqrt{N})\) space complexity.

To reduce the space complexity, it is helpful to design algorithms with the aids of pseudorandom walks. For the 1-dimensional DLP, Pollard designed kangaroo algorithm [20], which requires \(O(\sqrt{N})\) group operation and only constant storage under heuristic assumptions. Van Oorschot and Wiener [25] proposed a variant of the kangaroo method using distinguished point technique. Galbraith, Pollard and Ruprai [12, 21] considered 3 and 4 variants of kangaroo algorithm. The complexity of 4 kangaroo variant is \(1.715\sqrt{N}\) \((\approx 0.968\sqrt{\pi N})\). However, it is not known how to adapt these algorithms to high-dimensional DLP. One can see more details in [9].

Gaudry and Schost [14] gave a low-memory algorithm for solving 2-dimensional DLP, which can be generalized to general multi-dimensional cases. The basic idea of the algorithm is to find collisions between different types of pseudorandom walks (usually called tame walks and wild walks) with the help of distinguished points.

Some variants of the Gaudry–Schost algorithm have been proposed following different lines. One line of research considers improving the Gaudry–Schost algorithm when the underling group G has efficient endomorphisms such as point inversion over elliptic curves [11, 18, 19, 26]. Another line of research focuses on improving the time complexity by adjusting parameters without assuming extra structure of the group. In particular, Galbraith and Ruprai [7] proposed an improvement to the original Gaudry–Schost algorithm in multi-dimensional situations, which takes specific sizes of the tame and wild regions such that the overlap of the tame and wild regions equal to N/3 in the 1-dimensional case. Besides, Galbraith, Pollard and Ruprai [12, 21] considered 3-set and 4-set variants of the Gaudry–Schost algorithm for the 1-dimensional case. The complexity of original 3-set and 4-set variant of Gaudry–Schost algorithm is \(1.044\sqrt{\pi N}\) and \(0.982\sqrt{\pi N}\) respectively, and the latter can be improved to \(1.661\sqrt{N}(\approx 0.937\sqrt{\pi N})\).

1.1 Our results

In this work, we concentrate on solving multidimensional discrete logarithm by refining the Gaudry–Schost algorithm. We follow the second line of research and systemically study the impact of general tame and wild regions on the Gaudry–Schost algorithm. We give two variants to improve the expected time complexity of the original algorithm under certain heuristic assumptions.

First, we extend Galbraith–Ruprai’s method in a more general setting. We introduce a variable \(\beta \), and take both sizes of tame and wild sets to be \((1-2\beta )N\) and give the corresponding complexity with respect to the parameter \(\beta \). In this setting the overlap of the tame and wild sets is a function depending on \(\beta \) and the discrete logarithm. Then we find the optimal \(\beta \) and the corresponding average complexity in the 1-dimensional case. Galbraith and Ruprai used \(\beta =1/6\), and our calculations show that \(\beta =71/270 \approx 0.263\) is the optimal value. Since distinct dimensions are independent of each other, the result of the d-dimensional case is the d-th power of the 1-dimensional case. The comparison of heuristic expected time complexity for the d-dimensional discrete logarithms is summarized in Table 1.

Table 1 Comparison of the expected time complexity for Algorithm 1
Full size table

Second, we consider another variant where the tame set is fixed and the wild set is varying. The intuition about this variant is as follows. The average running time of the Gaudry–Schost algorithm is badly affected by the cases where the solution to the DLP instance is near the edges of the tame set. These instances lead to the worst case running time. So the idea of Sect. 4 of the paper is to study a variant that increases the proportion of instances where the algorithm behaves like the best case, and reduces the proportion of instances that are “edge" cases. Taking a very small wild set allows to do this. Specifically, the size of the wild set is set to be \(\alpha N\), where \(0<\alpha \le 1\) is a constant. And the average complexity under certain heuristic assumptions is \(((3-2\sqrt{2})\alpha +1)\sqrt{\pi N}\). Taking \(\alpha \) close to zero (and large enough N that the boundary effects do not cause difficulties) leads to an algorithm with running time close to \(\sqrt{\pi N}\). As shown by Galbraith and Holmes [10], one would not expect to beat \(\sqrt{\pi N}\) using an algorithm with two sets (one tame and one wild). The only known way to beat this bound is to use more than 2 types of walk, as was done by Galbraith–Pollard–Ruprai [12] and Bernstein–Lange [1]. Hence the algorithm in the paper should be essentially optimal for any algorithm based on two sets and without using inversion in the group.

The comparison of expected time complexity is summarized in Table 2.

Table 2 Comparison of the expected time complexity for Algorithm 2
Full size table

In summary, the variants of this work perform better for higher dimensional case in average case. Note that the algorithm of [12] is still the-state-of-art in the 1-dimensional case.

Paper organization The rest of the paper is organized as follows. In Sect. 2, we briefly recall the Gaudry–Schost algorithm and the Galbraith–Ruprai algorithm. In Sect. 3, we describe our first improvement which adjusts both the tame and wild sets. In Sect. 4, we propose another improvement that keeps the tame region and adjusts the wild region. In Sect. 5, we conclude the paper.

2 Preliminary

Denote [0, N] the set of \(\{0,\ldots ,N\}\), and \(\# A\) the number of the set A.

2.1 The Gaudry–Schost algorithm

The basic idea of the Gaudry–Schost algorithm [14] is as follows. There are two subsets of the group, one is called “tame set” and the other is called “wild set”. The algorithm runs pseudorandom walks alternatively in these two sets. Once a collision of walks between two different types is found, the discrete logarithm problem instance is solved. To reduce the space overhead, the algorithm uses the distinguished points which are stored in an easy-searched structure such as a binary tree.

In the original Gaudry–Schost algorithm, the tame set and wild set are defined as follows.

Definition 2

Let the notation be as the Definition 1 and assume that \( h = g_1^{a_1}g_2^{a_2}\ldots g_d^{a_d}\). Define the tame set T and the wild set W.

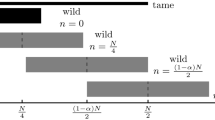
$$\begin{aligned} \begin{aligned} T =&\{(m_1,m_2,\ldots ,m_d)\in {\mathbb {Z}}^d:0\le m_i<N_i \text { for } 1\le i\le d\},\\ W =&(a_1-N_1/2,\ldots ,a_d-N_d/2) + T \\ =&\{(a_1-N_1/2+m_1,\ldots ,a_d-N_d/2+m_d)\in {\mathbb {Z}}^d:0\le m_i<N_i \text { for } 1\le i\le d\}. \end{aligned} \end{aligned}$$

When \(d=2\), the tame and wild sets are illustrated in Fig. 1.

Fig. 1
figure 1

Tame set and Wild set when \(d = 2\)

Full size image

The pseudorandom walk is defined as follows: First choose \(n_{s} >\log (\max {N_i})\) random d-tuple integers \(-M< m_{ij} <M\) for \(i = 1,\cdots ,d, j = 0,\ldots ,n_{s}-1 \), where M is a fixed upper bound of each walk. Then precompute elements \(w_j = g_1^{m_{1j}}g_2^{m_{2j}}\ldots g_d^{m_{dj}}\) for \(0\le j < n_{s}\). Moreover, choose a selection function \(S:G\rightarrow \{0,1,\ldots ,n_{s}-1\}\). The pseudorandom walk function is defined as follows:

$$\begin{aligned} walk(g,x_1,\ldots ,x_d) = (gw_{S(g)},x_1+m_{1S(g)},\ldots ,x_d+m_{dS(g)}). \end{aligned}$$

Tame walks are started at random a point \((x_1,\ldots ,x_d)\) in T for

$$\begin{aligned} (g_1^{x_1}g_2^{x_2}\ldots g_d^{x_d},x_1,\ldots ,x_d), \end{aligned}$$

and wild walks are started at a random point \((x'_1,\ldots ,x'_d)\) in W for

$$\begin{aligned} (hg_1^{x'_1}g_2^{x'_2}\ldots g_d^{x'_d},x'_1,\ldots ,x'_d). \end{aligned}$$

The algorithm iterates these two types of walks respectively until a distinguished element in G is visited, then stores the data \((g,x_1,\ldots ,x_d)\) and the type of walk in the database. When a distinguished point is visited, the walk is restarted at a uniformly chosen point. Once two different type walks hit the same distinguished point, the multi-dimensional DLP is solved.

The complexity analysis of the Gaudry–Schost algorithm is based on birthday paradox results. We recall the following result, whose proof can be found in [23].

Theorem 1

If one samples uniformly at random from a set with size M, alternatively records the element in two different lists, then the expected number of samples before an element exists in two lists is \(\sqrt{\pi M} + O(1)\).

Note that collisions between tame set and wild set only occur in the region \(L=T\cap W\). The analysis of the time complexity of the Gaudry–Schost algorithm and its variants including our improvement is based on some heuristic assumptions.

  1. 1.

    First, the elements are sampled uniformly, which means that pseudorandom walks and true random walks are indistinguishable.

  2. 2.

    Second, distinguished points are sufficiently common.

  3. 3.

    Third, the walks do not go outside the tame and wild sets.

One can see more details in [9].

Theorem 2

[14] Let the notation be as Definition 1 and assume the heuristic assumptions hold. Then the expected number of group operation of d-dimensional Gaudry–Schost algorithm is

$$\begin{aligned} ((4-2\sqrt{2})^d+o(1))\sqrt{\pi N} \end{aligned}$$

in the average case.

2.2 Galbraith–Ruprai’s improvement

In order to improve the Gaudry–Schost algorithm, Galbraith and Ruprai [7] considered smaller tame and wild set and different shape of the wild set. They gave a variant of the Gaudry–Schost algorithm with lower expected time complexity.

One interesting feature of the Galbraith–Ruprai’s variant is that the size of the overlap of the two sets is set to be a fixed constant. Thus the expected running time in the best case, worst case and average case are all equal. For simplicity, we adapt Galbraith–Ruprai’s variant in the setting where the interval is [0, N) instead of \([-N/2,N/2]\), and describe the 1-dimensional case in the following.

Define the tame set \(T'\) and wild set \(W'\) as follows:

$$\begin{aligned} T'= & {} \left[ \frac{1}{6}N,\frac{5}{6}N\right] \\ W'= & {} \left[ a_1-\frac{N}{2},a_1-\frac{N}{6}\right] \bigcup \left[ a_1+\frac{N}{6},a_1+\frac{N}{2}\right] \end{aligned}$$

Since the value of \(a_1\) is ranging from 0 to N, the size of the overlap part \(L' = T'\cap W'\) is equal to N/3 all the time. The improved algorithm proceeds in the same way as the original algorithm in other parts. The \(T'\) and \(W'\) in the \(1-\) dimensional case is illustrated in Fig. 2.

Fig. 2
figure 2

Tame and wild set of [7] in the 1-dimensional case when \(a_1 = \frac{N}{2}\)

Full size image

The time complexity of Galbraith–Ruprai’s variant is analyzed under similar assumptions as in the analysis of the original Gaudry–Schost algorithm.

Theorem 3

(Galbraith and Ruprai [7]) Let notations be the same as Definition 1. The expected number of group operations in the average and worst-case for d-dimensional improved Gaudry–Schost algorithm is

$$\begin{aligned} \left( \frac{2^d}{3^{d/2}}+o(1)\right) \sqrt{\pi N} \end{aligned}$$

For the sake of completeness, we sketch the method of proof in [7], which will be used later.

Proof

Note that \(\#T' = \#W' = (\frac{2}{3})^d N\). Recall \(L' = T'\cap W'\). It is easy to verify that \(\# L'=N/3^d\) all the time. To find a collision in \(L'\), the expected number of sampled elements from \(L'\) is \(\sqrt{\pi \# L'}+O(1)\) by Theorem 1. To sample \(\sqrt{\pi \# L'}+O(1)\) group elements in \(L'\), it is necessary to sample \(\# T'/\# L'\) elements in \(T'\) and \(W'\). Hence, the number of group elements to be chosen is

$$\begin{aligned} \frac{\# T'}{\# L'}\left( \sqrt{\pi \#L'}+O(1)\right) = \sqrt{\pi }(\#T'+o(1))(\#L')^{-1/2}. \end{aligned}$$

Taking the value of \(\# T'\text { and }\#L'\) into the formula above, the expected running time of improved Gaudry–Schost algorithm is

$$\begin{aligned} \left( \frac{2^d}{3^{d/2}}+o(1)\right) \sqrt{\pi N}. \end{aligned}$$

\(\square \)

3 First improvement to the Gaudry–Schost algorithm

In this section, we show our first variant of the Gaudry–Schost algorithm with improved expected time complexity. Inspired by the work [7], we explore the impact of shape and size of the tame and wild sets.

Suppose we are given \(g,h\in G\) and \(N\in {\mathbb {N}}\) such that \(h=g^a,0\le a<N\). We can rewrite it as \(h=g^{xN},0\le x<1\). In the 1-dimensional situation, our algorithm’s tame and wild sets are defined as follows:

$$\begin{aligned} T:= & {} [\beta N,(1-\beta )N],\\ W:= & {} \left[ xN -\frac{N}{2}+\beta N-\frac{1-2\beta }{4}N,xN -\frac{N}{2}+\beta N+\frac{1-2\beta }{4}N\right] \bigcup \\&\quad \left[ xN -\frac{N}{2} +(1-\beta )N-\frac{1-2\beta }{4}N,xN -\frac{N}{2} +(1-\beta )N+\frac{1-2\beta }{4}N\right] , \end{aligned}$$

where the parameter \(\beta \) is a constant in [0, 1/2). Note that Galbraith–Ruprai’s variant takes \(\beta =\frac{1}{6}\). The tame and wild sets are illustrated in Fig. 3. We use A, B to represent the left and right endpoints of set T. \(C(E) \text { and } D(F)\) are the left and right endpoints of sets \(W_{1}\) and \(W_2\) respectively.

Note that \(\# T=\# W=(1-2\beta )N\), \(\# W_1 = \# W_2 = \frac{1}{2}\#T\). By symmetry, we assume that x ranges from 0 to 1/2.

For example, we consider the special situation when \(x = 1/2\). The tame and wild sets are depicted in Fig. 3. In this situation,

$$\begin{aligned} W_1= & {} \left[ \beta N-\frac{1-2\beta }{4}N,\beta N+\frac{1-2\beta }{4}N\right] ,\\ W_2= & {} \left[ (1-\beta )N-\frac{1-2\beta }{4}N,(1-\beta )N+\frac{1-2\beta }{4}N\right] . \end{aligned}$$
Fig. 3
figure 3

Tame and wild set in our algorithm when \(h = g^{\frac{1}{2}x}\)

Full size image

Next we analyze different general situations in detail according to the value of \(\beta \) and x in the 1-dimensional case. Because distinct dimensions are independent of each other, the d-dimensional result is the d-th power of the 1-dimensional result.

3.1 \(0\le \beta \le 1/6\)

This situation is illustrated in Fig. 4.

Fig. 4
figure 4

Depiction when \(x=1/10,\beta = 1/8\)

Full size image

When \(0\le \beta \le 1/6\), \(\#L(\beta ) =\frac{1}{2}\#T(\beta ) = \frac{1-2\beta }{2}N\) when \(x\in [0,1)\). Following the method of proof in Theorem 3, the expected number of group operations is

$$\begin{aligned} \frac{\#T}{\#L}\left( \sqrt{\pi \#L}+O(1)\right) = \sqrt{\pi }(\#T+o(1))(\#L)^{-1/2} \end{aligned}$$
(1)

under heuristic assumptions. Taking \(\# T(\beta ) = (1-2\beta )N\) and \(\# L(\beta ) = \frac{1-2\beta }{2}N\) into the formula (1), the expected running time is approximately

$$\begin{aligned} \sqrt{2(1-2\beta )\pi N}. \end{aligned}$$

This function decreases in \(\beta \), so when \(\beta = \frac{1}{6}\), we minimize the expected running time, which is

$$\begin{aligned} \frac{2}{\sqrt{3}}\sqrt{\pi N} \approx 1.155\sqrt{\pi N}. \end{aligned}$$

3.2 \(1/6< \beta <3/10\)

This situation is depicted in Fig. 5.

Fig. 5
figure 5

Depiction when \(x=1/10,\beta = 1/4\)

Full size image

There are three possibilities for the size of L as follows. \(\# L\) is a function depending on variables \(\beta \) and x, so we write \(\#L\) as \(\#L(\beta ,x)\).

$$\begin{aligned} \# L(\beta ,x) = {\left\{ \begin{array}{ll} \frac{5}{4}(1-2\beta )N-\frac{N}{2}+xN, &{} 0\le x<\frac{1}{2}-\frac{3}{4}(1-2\beta ), \\ \frac{1-2\beta }{2}N, &{} \frac{1}{2}-\frac{3}{4}(1-2\beta )\le x<\frac{1}{2}+\frac{3}{4}(1-2\beta ),\\ \frac{5}{4}(1-2\beta )N+\frac{N}{2}-xN, &{} \frac{1}{2}+\frac{3}{4}(1-2\beta )\le x<1. \end{array}\right. } \end{aligned}$$

The size of tame and wild sets is also \((1-2\beta )N\). Taking the values into formula (1), we get the expected running time is approximately

$$\begin{aligned} \begin{aligned} \sqrt{\pi }\#T(\#L(\beta ,x))^{-1/2} =&\, \sqrt{\pi N}(1-2\beta )\left( \int _{0}^{\frac{1}{2}-\frac{3}{4}(1-2\beta )}\frac{dx}{\sqrt{\frac{5}{4}(1-2\beta )-\frac{1}{2}+x}} +\right. \\&\left. \int _{\frac{1}{2}-\frac{3}{4}(1-2\beta )}^{\frac{1}{2}+\frac{3}{4}(1-2\beta )}\frac{dx}{\sqrt{\frac{1-2\beta }{2}}} +\int _{\frac{1}{2}+\frac{3}{4}(1-2\beta )}^{1}\frac{dx}{\sqrt{\frac{5}{4}(1-2\beta )~+~\frac{1}{2}-x}} \right) \\&= \sqrt{\pi N}(1-2\beta )\left( 7\sqrt{\frac{1}{2}-\beta }-4\sqrt{\frac{3}{4}-\frac{5}{2}\beta }\right) \\&= \sqrt{\pi N}f(\beta ). \end{aligned} \end{aligned}$$
(2)

The graph of \(f(\beta )\) is shown in Fig. 6. Solving

$$\begin{aligned} f'(x) = (1/2-x)\left( \frac{10}{\sqrt{\frac{3}{4}-\frac{5}{2}x}} - \frac{7}{\sqrt{\frac{1}{2}-x}}\right) -14\sqrt{\frac{1}{2}-x} + 8\sqrt{\frac{3}{4}-\frac{5}{2}x} = 0, \end{aligned}$$

we get that \(f(\beta )\) takes the minimum value when \(\beta = 71/270\), which is

$$\begin{aligned} (f(\beta )\times \sqrt{\pi N})\approx 1.039\sqrt{\pi N} \end{aligned}$$

and the expected running time in the worst case is \(\frac{128}{75}\sqrt{5\pi N/6} \approx 1.558\sqrt{\pi N}\) under \(\beta = 71/270\).

Fig. 6
figure 6

The graph of \(f(\beta )\)

Full size image

3.3 \(3/10\le \beta <1/2\)

When \(3/10\le \beta <1/2\), this situation is depicted in Fig. 7.

Fig. 7
figure 7

Depiction when \(x=1/10,\beta = 2/5\)

Full size image

In this situation, there are five possibilities of \(\#L(\beta ,x)\) as follows.

$$\begin{aligned} \# L(\beta ,x) = {\left\{ \begin{array}{ll} 0, &{}0\le x<\frac{1}{2}-\frac{5}{4}(1-2\beta ),\\ \frac{5}{4}(1-2\beta )N-\frac{N}{2}+xN, &{} \frac{1}{2}-\frac{5}{4}(1-2\beta )\le x<\frac{1}{2}-\frac{3}{4}(1-2\beta ), \\ \frac{1-2\beta }{2}N, &{} \frac{1}{2}-\frac{3}{4}(1-2\beta )\le x<\frac{1}{2}+\frac{3}{4}(1-2\beta ),\\ \frac{5}{4}(1-2\beta )N+\frac{N}{2}-xN, &{} \frac{1}{2}+\frac{3}{4}(1-2\beta )\le x<\frac{1}{2}+\frac{5}{4}(1-2\beta ),\\ 0, &{}\frac{1}{2}+\frac{5}{4}(1-2\beta )\le x<1. \end{array}\right. } \end{aligned}$$

When \(\beta \ge 3/10\), note that this algorithm cannot solve some discrete logarithm problem instances. Precisely, this method can only solve DLP instance \(h=g^x\) for \(x\in [\frac{1}{2}-\frac{5}{4}(1-2\beta ),\frac{1}{2}+\frac{5}{4}(1-2\beta )]\). So the expected average-case complexity is infinity for this case.

In conclusion, the minimum expected running time of our algorithm is \(1.039\sqrt{\pi N}\) in the average case for the 1-dimensional case achieved when \(\beta = 71/270\). Because distinct dimensions are independent of each other, the d-dimensional result is the d-th power of the 1-dimensional result. We can analyse the high-dimensional situations based on the result of the 1-dimensional case. The expected running time is \(1.039^d\sqrt{\pi N}\) in the average case in the d-dimensional case when \(\beta \) is equal to 71/270 in all dimensions.

4 Second improvement to the Gaudry–Schost algorithm

In this section, we demonstrate another variant to improve the Gaudry–Schost algorithm. In particular, we fix the tame set and change the size of the wild set. This idea has been applied by [26] to improve the Galbraith–Ruprai algorithm [8] which utilizes equivalent classes to accelerate the Gaudry–Schost algorithm. The analysis is similar to that of [26]. For completeness, we include the analysis below.

Since the size of the tame set is not equal to that of the wild set, analysis of the complexity in this improvement relies on [10], where Galbraith and Holmes consider non-uniform birthday problem. It is equivalent to consider placing colored balls in urns, which the probability of putting balls into the urns depends on the color of the balls. And this model can be used in some variant of discrete logarithm problems [8, 26]. We recall the main theorem [10, Theorem 1] in the following.

Assumption 1

[10] (Color selection). Assume that there are balls which has \({\mathcal {C}}\) different colors. For \(c = 1,2,\ldots ,{\mathcal {C}}\), \(r_{k,c}\) denote the probability of the k-th ball has the color c. This probability is independent of other balls. For each c, \(q_c\) denote the average value of \(r_{k,c}\), \(q_c := \lim _{n\rightarrow \infty }n^{-1}\sum _{k=1}^{n}r_{k,c}\). Assume \(q_c\) exists and \(q_1\ge q_2\ge \cdots \ge q_{{\mathcal {C}}}>0\). Let \(b_{n,c} := q_c - n^{-1}\sum _{k=1}^{n}r_{k,c}\). Assume there is a constant K such that \(|b_{n,c}|\le K/n\) for all c.

Assumption 2

[10] (Urn selection). Assume there are \(R\in {\mathbb {N}}\) distinct urns. If the k-th ball has the color c and it is placed in the urn a, the probability will be denoted as \(q_{c,a}(R)\). There exists \(d>0\) such that \(0\le q_{c,a}\le d/R\) for all c and a. And there are \(\mu ,\nu >0\) such that the size of the set \(S_R = \{1\le a\le R:q_{1,a},q_{2,a}\ge \mu /R\}\) is no less than \(\nu R\).

Let \(A_R\) be the limiting probability that balls are given different colors but assigned to the same urn.

$$\begin{aligned} A_R = \sum _{c=1}^{{\mathcal {C}}}q_c\left( \sum _{c'=1,c'\ne c}^{{\mathcal {C}}}q_{c'}\left( \sum _{a=1}^{R}q_{c,a}q_{c',a}\right) \right) . \end{aligned}$$

Theorem 4

[10] Under these two assumptions and the definition of \(A_R\), then the expected number of assignments before there are two balls which are different colors placing into the same urn is

$$\begin{aligned} \sqrt{\frac{\pi }{2A_R}}+O(R^{1/4}) \end{aligned}$$

In this section, we focus on the case that there are only two colors, denoted by “t(tame)” and “w(wild)”. And assume that the elements in the tame set and wild set are sampled uniformly and alternatively, so \(q_t\) and \(q_w\) are equal to 1/2.

4.1 The 1-dimensional case

We first consider the 1-dimensional case to illustrate our idea.

Suppose we are given \(g,h\in G\) and \(N \in {\mathbb {N}}\), and we want to find an integer \(0\le a < N\) such that \(h = g^a\). We rewrite it as \(h = g^{xN},0\le x<1\). Define the tame set

$$\begin{aligned} T = [0,N], \end{aligned}$$

and the wild set

$$\begin{aligned} W = \left[ xN-\frac{\alpha N}{2},xN+\frac{\alpha N}{2}\right] , \end{aligned}$$

where \(\alpha \) is a parameter which belongs to [0, 1]. \(\# T = N\) and \(\# W = \alpha N\).

The difference between our second improvement and the original Gaudry–Schost algorithm is that we reduce the size of the wild set. The other parts follow the same.

The size \(\# L=\#(T\cap W)\) can be divided into three cases according to x as follows.

$$\begin{aligned} \# L(x) = {\left\{ \begin{array}{ll} (\frac{1}{2}\alpha +x)N, &{} 0\le x<\frac{1}{2}\alpha , \\ \alpha N, &{} \frac{1}{2}\alpha \le x< 1-\frac{1}{2}\alpha , \\ (1+\frac{1}{2}\alpha -x)N, &{} 1-\frac{1}{2}\alpha \le x<1. \end{array}\right. } \end{aligned}$$
  1. (1)

    When \(0\le x<\frac{1}{2}\alpha \), the \(R = N+\frac{\alpha }{2}N-xN\). And the probability \(q_{t,a} = 1/N\) for \(a\in T\), the \(q_{w,a}\) is equal to \(1/\alpha N\) for \(a\in W\) and equal to 0 otherwise. Using the Theorem 4, we can compute

    $$\begin{aligned} A_R = \frac{1}{2}\frac{1}{N}\frac{1}{\alpha N}\left( \frac{1}{2}\alpha + x\right) N = \frac{\alpha +2x}{4\alpha N} \end{aligned}$$

    and the complexity is \(\sqrt{\frac{2\pi \alpha N}{\alpha +x}} + O(N^{1/4})\).

  2. (2)

    When \(\frac{1}{2}\alpha \le x < 1-\frac{1}{2}\alpha \), the \(W\subseteq T\). Then the \(R=N, q_{t,a} = 1/N\) and \(q_{w,a} = 1/\alpha N\) for \(a\in W\). The \(A_R\) can be computed in the same way

    $$\begin{aligned} A_R = \frac{1}{2}\frac{1}{N}\frac{1}{\alpha N}\alpha N = \frac{1}{2N} \end{aligned}$$

    and the corresponding complexity is \(\sqrt{\pi N} + O(N^{1/4})\).

  3. (3)

    When \(1-\frac{1}{2}\alpha \le x \le 1\), the \(R = xN + \frac{\alpha }{2}N\). In this case, \(q_{t,a} = 1/N\) for \(a\in T\) and \(q_{w,a} = 1/\alpha N\) for \(a\in W\). Then

    $$\begin{aligned} A_R = \frac{1}{2}\frac{1}{N}\frac{1}{\alpha N}\left( 1+\frac{\alpha }{2}-x\right) N = \frac{2-2x+\alpha }{4\alpha N} \end{aligned}$$

    The complexity is \(\sqrt{\frac{2\pi \alpha N}{2-2x+\alpha }} + O(N^{1/4})\).

In total, under the heuristic assumptions, the average complexity of this algorithm before a tame-wild collision is

$$\begin{aligned} \int _{0}^{\frac{\alpha }{2}}\sqrt{\frac{2\pi \alpha N}{\alpha +x}}dx + \int _{\frac{\alpha }{2}}^{1-\frac{\alpha }{2}}\sqrt{\pi N}dx + \int _{1-\frac{\alpha }{2}}^{1}\sqrt{\frac{2\pi \alpha N}{2-2x+\alpha }}dx + O(N^{1/4}). \end{aligned}$$

which is

$$\begin{aligned} ((3-2\sqrt{2})\alpha + 1)\sqrt{\pi N} + O(N^{1/4}). \end{aligned}$$

For the worst case(x = 0 or 1), the expect complexity is

$$\begin{aligned} \sqrt{2\pi N} + O(N^{1/4}). \end{aligned}$$

Note the average case complexity tends to \(\sqrt{\pi N}\) when the parameter \(\alpha \) tends to \(0^+\). However, when \(\alpha \) is small enough, the second term \(O(N^{1/4})\) will be large and it will affect the average complexity. We explain this situation briefly. The analysis of our algorithm is under the heuristic assumptions and it uses pseudorandom walks. When \(\alpha \rightarrow 0\), the size of W tends to be small and the pseudorandom walks will travel beyond the boundary of the set. So when we use this conclusion, we can choose the corresponding \(\alpha \) for the different N. By choosing \(\alpha = 0.1\), the heuristic average complexity can be computed as \(1.0171\sqrt{\pi N} + O(N^{1/4})\), which is better than the result \(1.15\sqrt{\pi N}\) [7].

4.2 High dimensional case

For the d-dimensional case, all d-dimensions are independent, so the method of analysis in the 1-dimensional case can be applied in the same way. Under the heuristic assumptions, the expected average complexity is approximately

$$\begin{aligned} ((3-2\sqrt{2})\alpha + 1)^d \sqrt{\pi N} + O(N^{1/4}), \end{aligned}$$

where \(\alpha >0\) is a constant. For instance, when \(\alpha = 0.1\), the expected average complexity complexity is \(1.0171^d\sqrt{\pi N}\), which is better than the result in [7]. Note that the expected worst case complexity is \(2^{\frac{d}{2}}\sqrt{\pi N}\).

5 Conclusion

The Gaudry–Schost algorithm and its variants are state-of-the-art low memory algorithms for solving interval multi-dimensional discrete logarithm problem. One feature of the Gaudry–Schost algorithm is that there are many parameters to adjust. In this work, we present two improvements to the Gaudry–Schost algorithm by adjusting the tame and wild regions. The first variant makes both the tame and wild sets vary and determines the optimal value. The second variant fixes the tame set and varies the wild set and calculates the optimal choice. Both variants achieves better average case time complexity for the multidimensional case under certain heuristic assumptions. In particular, the second method is asymptotically optimal.