A new class of metrics for learning on real-valued and structured data

Abstract

We propose a new class of metrics on sets, vectors, and functions that can be used in various stages of data mining, including exploratory data analysis, learning, and result interpretation. These new distance functions unify and generalize some of the popular metrics, such as the Jaccard and bag distances on sets, Manhattan distance on vector spaces, and Marczewski-Steinhaus distance on integrable functions. We prove that the new metrics are complete and show useful relationships with f-divergences for probability distributions. To further extend our approach to structured objects such as ontologies, we introduce information-theoretic metrics on directed acyclic graphs drawn according to a fixed probability distribution. We conduct empirical investigation to demonstrate the effectiveness on real-valued, high-dimensional, and structured data. Overall, the new metrics compare favorably to multiple similarity and dissimilarity functions traditionally used in data mining, including the Minkowski ($L^p$) family, the fractional $L^p$ family, two f-divergences, cosine distance, and two correlation coefficients. We provide evidence that they are particularly appropriate for rapid processing of high-dimensional and structured data in distance-based learning.

1 Introduction

The development of domain-specific learning algorithms inevitably requires choices regarding data preprocessing, data representation, training, model selection, or evaluation. One such requirement permeating all of data mining is the selection of similarity or distance functions. In a supervised setting, for example, the nearest neighbor classifiers (Cover and Hart 1967) and kernel machines (Shawe-Taylor and Cristianini 2004) critically depend on the selection of distance functions. Similarly, the entire classes of clustering techniques rely on the distances that are sensible for a particular domain (Tan et al. 2006). Modern applications further require that distance functions be fast to compute, easy to interpret, and effective on high-dimensional data.

We distinguish between distances and distance metrics; i.e., functions that impose constraints on the general notion of distance (Deza and Deza 2013). Although restrictions to metrics are not required in data mining (Ben-David and Ackerman 2009; Ting et al. 2016), a number of algorithms rely on the existence of metric spaces either explicitly or implicitly. Metric-associated benefits include well-defined point neighborhoods, advanced indexing through metric trees, provable convergence, guarantees for embedding, and intuitive result interpretation. Satisfying metric properties is therefore desirable and generally leads to computational speed-ups and better inference outcomes (Moore 2000; Elkan 2003; Kryszkiewicz and Lasek 2010; Hamerly 2010; Baraty et al. 2011).

In this work we present a new class of metrics on sets, vectors, and functions that satisfy all of the aforementioned properties. We identify well-known special cases and then show how these distance functions can be adapted to give rise to information-theoretic metric spaces on sets of directed acyclic graphs that are used as class labels in high-cardinality structured-output learning. We prove useful properties of the new metrics and then carry out experiments to assess their suitability in real-life applications. The new metrics exhibited good intuitive behavior and performed favorably against all similarity and dissimilarity functions evaluated in this work, including the Euclidean distance, cosine distance, Pearson’s correlation coefficient, Spearman’s rank correlation coefficient, and others.

The remainder of this paper is organized as follows. In Sect.  2 we give a motivating example for this work and state the contributions. In Sects. 3 and 4 we present new metrics and prove useful theoretical properties. In Sect. 5 we carry out empirical evaluation on several types of data. In Sect. 6 we introduce metrics on ontologies and evaluate their performance on problems in computational biology. Sections 5 and 6 also give performance insights and discuss computational complexity. In Sect. 7 we summarize the related work. Finally, in Sect. 8 we draw conclusions considering both theoretical and empirical findings of our study.

2 Motivation and contributions

2.1 A motivating example

The selection of distance functions and understanding of their behavior is fundamental to data mining. Inference algorithms such as k-nearest neighbor (KNN) classification and K-means clustering rely directly on user-provided distance functions and are among the most popular techniques in the field (Wu and Kumar 2009). Although both algorithms permit the use of any distance measure, they are generally used with the Euclidean distance.¹ There is ample evidence, however, that Euclidean distance displays undesirable properties in high-dimensional spaces, leading to a body of theoretical and practical work towards understanding its properties (Beyer et al. 1999; Hinneburg et al. 2000; Aggarwal et al. 2001; Radovanović et al. 2010). Other distances; e.g., fractional distances or cosine typically improve the performance in practice. However, these distances are not metrics (e.g., they violate triangle inequality), and so applications using them relinquish theoretical guarantees reserved only for distance metrics. For example, well-known accelerations for K-means clustering only apply to metric spaces (Elkan 2003; Hamerly 2010).

In an ideal application, one would select a distance function with good theoretical and practical characteristics. Surprisingly, however, we are not aware of any distance metric that performs competitively in high-dimensional spaces against best non-metric distances and other dissimilarities. One is therefore left with a balancing act between performance accuracy and theoretical guarantees, a choice that ultimately hinges on a practitioner’s intuition and experience. This work aims to address this situation by proposing a class of distance metrics that, among other benefits, also perform well in high-dimensional spaces.

2.2 Contributions

As discussed above, the motivation for this work is to addresses important needs of a typical data mining pipeline through theoretical and practical contributions. In particular,

(i) We introduce a new class of distance metrics across different data types, including sets, vector spaces, integrable functions, and ontologies.

(ii) We identify several important special cases of these metrics, also across different data types. This unexpected unification provides new insights and connections between data mining applications.

(iii) We analyze theoretical properties of the new metrics and show connections with the Minkowski family and f-divergences. This analysis gives inequalities that can be used to provide guarantees in further theoretical studies (e.g., lower risk bounds).

(iv) We empirically evaluate the performance of the new metrics against many other distance functions. While our metrics fare well on all types of data, the main distinction is shown on sparse high-dimensional data in text mining applications.

(v) We extend the class of distance metrics to ontologies (directed acyclic graphs) drawn from a fixed probability distribution. We demonstrate that these metrics have natural information-theoretic interpretation and can be used for evaluation of classification models in structured-output learning; in particular, when the output of a classifier is a subgraph of a large directed acyclic graph.

(vi) We evaluate distance metrics on ontologies in two bioinformatics case studies. The first application demonstrates the intuitive nature of new distances by comparing protein sequence similarity against similarity of their molecular and biological functions. The second application clusters several species based solely on biological functions of their proteins, defined via Gene Ontology (Ashburner et al. 2000) annotations, and shows that such clustering can recover the evolutionary species tree obtained from protein sequences.

3 Theoretical framework

3.1 Background

Metrics are a mathematical formalization of the everyday notion of distance (Goldfarb 1992). Given a non-empty set X, a function $d:X\times X\rightarrow {\mathbb {R}}$ is called a metric if

• 1. $d(a,b) \ge 0$ (nonnegativity)

• 2. $d(a,a) = 0$ (reflexivity)

• 3. $d(a,b) = 0 \; \Leftrightarrow \; a=b$ (identity of indiscernibles)

• 4. $d(a,b) = d(b,a)$ (symmetry)

• 5. $d(a,c) \le d(a,b) + d(b,c)$ (triangle inequality)

for all $a,b\in X$. A non-empty set X endowed with a metric d is called a metric space (Deza and Deza 2013).

Although these conditions do not provide the minimum set that defines a metric (e.g., 1 follows from 4 and 5), they are stated to explicitly point out important properties of distance functions and enable us to distinguish between various types of distances. For example, there exists a historical distinction between the general notion of distance (conditions 1, 2, and 4) and that of a metric (Deza and Deza 2013), though there are inconsistencies in the more recent literature. Examples of distances that do not satisfy metrics requirements include cosine distance, fractional $L^p$ distances, one minus a Pearson’s correlation coefficient, etc. Furthermore, functions such as some f-divergences may not even satisfy the symmetry requirement and are generally referred to as dissimilarities or divergences.

In Sects. 3.2–3.4 we will introduce new metrics on sets, vectors, and integrable functions. Each metric will have a real-valued parameter $p \ge 1$, with the possibility that $p = \infty$. All proofs can be found in Electronic Supplementary Materials.

3.2 Metrics on sets

We start with the simplest case and define two new metrics on finite sets. Both will be extended to more complex situations in subsequent sections.

3.2.1 Unnormalized metrics on sets

Let X be a non-empty set of finite sets drawn from some universe U. We define a function $d^{p}:X\times X\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d^{p}(A,B) = (|A {\setminus } B|^p+|B{\setminus } A|^p)^\frac{1}{p}, \end{aligned}$$

(1)

where $|\cdot |$ denotes set cardinality, $A{\setminus } B = A \cap B^c$ with $B^c = \{x|x\in U \text { and } x \notin B\}$, and $p \ge 1$ is a parameter mentioned earlier.

Theorem 3.1

$(X, d^p)$ is a metric space.

The symmetric distance on sets is a special case of $d^{p}$ when $p=1$ and it converges to the bag distance as $p \rightarrow \infty$ (Deza and Deza 2013).

3.2.2 Normalized metrics on sets

Let X again be a non-empty set of finite sets drawn from some universe. We define a function $d_N^{p}:X\times X\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d_N^{p}(A,B) = \dfrac{(|A {\setminus } B|^p+|B {\setminus } A|^p)^\frac{1}{p}}{|A\cup B|}, \end{aligned}$$

(2)

if $|A\cup B| \ne 0$ and zero otherwise.

Theorem 3.2

$(X, d_N^{p})$ is a metric space. In addition, $d_N^{p}:X \times X \rightarrow [0,1]$.

Observe that the Jaccard distance is a special case of $d_N^{p}$ when $p=1$.

3.2.3 Relationship to Minkowski distance

Although the new metrics have a similar form to the Minkowski ($L^p$) distance on binary set representations, they are generally different. Take for example $A=\left\{ 1,2,4\right\}$ and $B=\left\{ 2,3,4,5\right\}$ from a universe of $k=5$ elements. A sparse set representation results in the following encoding: ${\mathbf {a}}=\left( 1,1,0,1,0\right)$ and ${\mathbf {b}}=\left( 0,1,1,1,1\right)$. The Minkowski distance of order p between ${\mathbf {a}}$ and ${\mathbf {b}}$ is defined as

$$\begin{aligned} d^p_{\text {M}}({\mathbf {a}},{\mathbf {b}})=\left( {\textstyle \sum _{i=1}^{k}}\left| a_i-b_i\right| ^{p}\right) ^{\nicefrac {1}{p}} = \left\| {\mathbf {a}}-{\mathbf {b}}\right\| _{p}, \end{aligned}$$

(3)

and $p\ge 1$. Substituting the numbers into Eq.  (3) gives $d_{\text {M}}^{1}({\mathbf {a}},{\mathbf {b}})=3$ and $d^{1}(A,B)=3$; $d^{2}_{\text {M}}({\mathbf {a}},{\mathbf {b}})=\sqrt{3}$ and $d^{2}(A,B)=\sqrt{5}$, etc. In fact, $d_{\text {M}}^{p}({\mathbf {a}},{\mathbf {b}})\ne d^{p}(A,B)$ for all $p > 1$.

3.3 Metrics on vector spaces

We define a version of our metrics on the vector space ${\mathbb {R}}^k$, where $k \in {\mathbb {N}}$ is the dimension of the space. Let ${\mathbf {x}}=(x_1,x_2, \ldots ,x_k)$ and ${\mathbf {y}}=(y_1,y_2, \ldots ,y_k)$ be any two points in ${\mathbb {R}}^k$.

3.3.1 Unnormalized metrics on vectors

We define a function $d^{p}: {\mathbb {R}}^k \times {\mathbb {R}}^k \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d^{p}({\mathbf {x}},{\mathbf {y}}) = \Bigg (\Big (\sum _{i:x_i \ge y_i}x_{i}-y_{i}\Big )^{p}+\Big (\sum _{i:x_i<y_i}y_{i}-x_{i}\Big )^{p}\Bigg )^{\frac{1}{p}}. \end{aligned}$$

(4)

Theorem 3.3

$({\mathbb {R}}^k, d^{p})$ is a metric space.

When $p=1$ the distance from Eq. 4 is equivalent to the Manhattan (cityblock) distance.

3.3.2 Normalized metrics on vectors

We define a function $d_N^{p}: {\mathbb {R}}^k \times {\mathbb {R}}^k \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d_N^{p}({\mathbf {x}},{\mathbf {y}})=\frac{d^{p}({\mathbf {x}},{\mathbf {y}})}{\sum _{i=1}^{k}\max (|x_{i}|,|y_{i}|,|x_{i}-y_{i}|)}. \end{aligned}$$

(5)

Theorem 3.4

$({\mathbb {R}}^k,d_N^{p})$ is a metric space. In addition, $d_N^{p}:X \times X \rightarrow [0,1]$.

As mentioned above, the new metrics $d^{p}$ and the Minkowski distance $d_{\text {M}}^p$ on ${\mathbb {R}}^k$ are different for $p>1$. However, we were able to establish a strong equivalence between the two in Sect. 4. Therefore, many useful properties of the class of Minkowski distances also hold for the metrics $d^{p}$. For instance, the completeness of $({\mathbb {R}}^k,d_{\text {M}}^p)$ implies that $({\mathbb {R}}^k,d^{p})$ is also complete.

We alert the reader that we used the same symbol $d^{p}$ in Eqs. 1 and 4 and $d_N^{p}$ in Eqs. 2 and 5, but believe it should not present interpretation problems. For example, Eq. 5 is not the Jaccard distance when $p=1$, but rather its analog in real-valued vector spaces, as defined in this work. We shall continue this notation pattern in the next section.

3.4 Metrics on integrable functions

We now extend the previously introduced metrics to integrable functions and show that the space of the integrable functions equipped with the new metrics is complete.

3.4.1 Unnormalized metrics on functions

Let $L({\mathbb {R}})$ be a set of integrable functions on ${\mathbb {R}}$. We define $d^{p}: L({\mathbb {R}}) \times L({\mathbb {R}}) \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d^{p}(f,g) = \left( \left( \int (f-g)^{+}\,dx\right) ^p+\left( \int (f-g)^{-}\,dx\right) ^p\right) ^\frac{1}{p}, \end{aligned}$$

(6)

where $f^+ = \max (f,0)$, $f^- = \max (-f,0)$.

Theorem 3.5

$(L({\mathbb {R}}),d^{p})$ is a metric space.

The well-known $L^1$ distance is a special case of $d^{p}$ when $p=1$.

3.4.2 Normalized metrics on functions

Let $L({\mathbb {R}})$ again be a set of bounded integrable functions on ${\mathbb {R}}$ and $d^{p}$ the distance function from Eq. 6. We define $d_N^{p}: L({\mathbb {R}}) \times L({\mathbb {R}}) \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d_N^{p}(f,g) = \dfrac{d^{p}(f,g)}{\int \max (|f|,|g|,|f-g|)\,dx}. \end{aligned}$$

(7)

Theorem 3.6

$(L({\mathbb {R}}),d_N^{p})$ is a metric space. In addition, $d_N^{p}:L({\mathbb {R}})\times L({\mathbb {R}})\rightarrow [0,1]$.

Observe that the Marczewski–Steinhaus (1958) distance is a special case of $d_N^{p}$ when $p=1$.

Theorem 3.7

$(L({\mathbb {R}}),d^{p})$ and $(L({\mathbb {R}}),d_N^{p})$ are complete metric spaces.

3.4.3 Geometric interpretation of the new distances

We illustrate the geometry of new distances in Fig.  1. Consider two functions f(x) and g(x). Let $A_{f>g}$ be the total area (volume) of the space between f and g where $f > g$ and $A_{f<g}$ be the area where $g > f$. Our unnormalized distance corresponds to the $L^p$ norm of the vector $(A_{f>g}, A_{f<g})$. The similarity between f and g depends on the balance of $A_{f>g}$ and $A_{f<g}$ as a function of p.

Fig. 1

Geometry of the new distances between two functions $f(x)=\sin (x)$ and $g(x)=\cos (x)$ over $[0,2\pi ]$. The blue area corresponds to $A_{f>g}$, whereas the red area corresponds to $A_{f<g}$. The vertical lines visualize the normalization factor from Eq. 7 (Color figure online)

3.4.4 Scaling

The objects from the input space X may sometimes have interpretable bounded norms; e.g., $M = \max _{f\in X}\int |f(x)|dx < \infty$. One example is that $\int f(x)dx=1$ for every f in a space of probability densities, when the normalized distance from Eq. 7 reaches maximum at $\root p \of {2}/2$. In these situations it is possible to further scale Eq. 2, Eq. 5 and Eq. 7 to the full [0, 1] interval by multiplying the proposed distances by $2/\root p \of {2}$. For probability distributions and $p=2$, this corresponds to multiplying the distance from Eq. 7 by $\sqrt{2}$.

4 Connections with other dissimilarity measures

4.1 Equivalence with Minkowski distances

In the previous section we noted that our various metrics reduce to certain well-known metrics when the parameter p is either 1 or $\infty$.

In the case of our unnormalized metrics on vector spaces from Eq. 4, we can establish a stronger relationship with the Minkowski distance for $p\ge 1$ and $p=\infty$.

Proposition 4.1

The new metric $d^{p}$ and the Minkowski distance $d_{\text {M}}^p$ on ${\mathbb {R}}^k$, when they share the same parameter p, where $p\ge 0$ or $p=\infty$, are equivalent metrics; that is, there exist positive constants $\alpha$ and $\beta$ such that for all ${\mathbf {x}},{\mathbf {y}}\in {\mathbb {R}}^k$ it holds that

$$\begin{aligned} \alpha d^{p}({\mathbf {x}},{\mathbf {y}}) \le d_{\text {M}}^p({\mathbf {x}},{\mathbf {y}}) \le \beta d^{p}({\mathbf {x}},{\mathbf {y}}). \end{aligned}$$

(8)

This proposition can be proved by invoking Hölder’s inequality and some algebraic manipulations (Electronic Supplementary Materials).

4.2 Comparisons with f-divergences for probability distributions

Suppose P and Q are probability distributions for some random variables defined on a Lebesgue-measurable set in ${\mathbb {R}}$ with probability densities h and g in $L({\mathbb {R}})$ respectively. Then $d^{p}(h,g)$ or $d_N^{p}(h,g)$ provide a measure of dissimilarity between h and g. In comparison, an f-divergence of P with respect to Q is the expectation of f(dP / dQ) under the distribution Q (Csiszár 1967) with regularity constraints on f. Replacing f(t) by $\frac{1}{2}|t-1|$, $(1-\sqrt{t})^2$ or $t\log (t)$ gives the total variation ${\text {TV}}(P,Q)$, the Hellinger distance H(P, Q), or the Kullback-Leibler (KL) divergence $D_{\text {KL}}(P||Q)$, respectively (Liese and Vajda 2006).

The total variation and the Hellinger distance are metrics while the KL divergence is not. However, the KL divergence $D_{\text {KL}}(P||Q)$ is meaningful as it measures the information theoretic divergence when P is the true underlying distribution for the model in hand and Q is the presumed distribution in model development. The information theoretic bounds on compressibility and relationship to maximum-likelihood inference of $D_{\text {KL}}(P||Q)$ are well understood (Cover and Thomas 2006).

When $p=1$, our distance on probability densities h and g is equivalent to the total variation of their distributions P and Q as $d^{p}(h,g) = 2{\text {TV}}(P,Q)$. Based on this equality we are able to establish the relationships between $d^{p}(h,g)$ to their corresponding KL divergence and Hellinger distance.

Proposition 4.2

Let P and Q be probability distributions with respect to some real random variables with probability densities h and g in $L({\mathbb {R}})$, respectively. For any $p\ge 1$ it holds that

$$\begin{aligned} d^{p}(h,g)\le \sqrt{2\min (D_{\text {KL}}(P||Q),D_{\text {KL}}(Q||P))}. \end{aligned}$$

The result directly follows from Pinsker’s inequality (Pinsker 1964) and the symmetry of metrics. Interestingly, the converse does not hold. That is, there exist sequences of probability density functions $\{h_n\}$ and $\{g_n\}$ such that $d^{p}(h_n,g_n) \rightarrow 0$ but $D_{\text {KL}}(P_n||Q_n) \rightarrow \infty$.

Proposition 4.3

Under the same conditions as in Proposition 4.2, it holds that

$$\begin{aligned} 2H(P,Q)^2 \le d^{p}(h,g)\le 2\sqrt{2} H(P,Q). \end{aligned}$$

The conclusion follows from $H(P,Q)^2 \le {\text {TV}}(P,Q)\le \sqrt{2}H(P,Q)$; see LeCam (1973).

Proposition 4.2 and Proposition 4.3 (up to a multiplicative constant) also apply to $d_N^{p}(h,g)$ as $\frac{1}{2}d^{p}(h,g) \le d_N^{p}(h,g)\le d^{p}(h,g)$ since h and g are densities. These inequalities can prove useful in establishing lower risk bounds in applications that directly minimize the new distances as opposed to f-divergences (Guntuboyina 2011).

5 Empirical investigation

5.1 Classification-based evaluation

The performance of the new metrics was first evaluated through classification experiments on thirty real-valued (low dimension) and ten text-document (high dimension) data sets. Classification on each data set was carried out by applying the KNN algorithm (Cover and Hart 1967) with different underlying distance measures. These distances were then compared based on the estimated performance of their corresponding classifiers. Classification accuracy (the fraction of correctly classified data points) was estimated though a five-fold cross-validation in all experiments. Parameter K was selected from $\{1, 3, 5, \ldots , \lceil \sqrt{n}\,\rceil \}$, where n is the data set size, using a leave-one-out procedure on the training partition. The selected K was then used to classify data points from the test partition.

The new metrics were compared to the following distances: (1) Minkowski ($L^p$) family; (2) fractional $L^p$ distances; i.e., Minkowski distances with $0<p<1$; (3) normalized $L^p$ distances; i.e., $\left\| {\mathbf {x}}-{\mathbf {y}}\right\| _{p}/(\left\| {\mathbf {x}}\right\| _{p}+\left\| {\mathbf {y}}\right\| _{p})$; (4) cosine distance; (5) one minus Pearson’s and Spearman’s correlation coefficient; (6) f-divergences; i.e., Hellinger distance and total variation; and (7) the fractional equivalent of all our metrics ($f^p$ and $f^p_N$, $0<p<1$). Note that all Minkowski distances, Hellinger distance, and total variation (applicable only to nonnegative inputs) are metrics. However, all fractional distances, all normalized $L^p$ distances (except when $p=2$, when it is a metric), cosine distance, and one minus the correlation coefficient are not metrics. For example, the cosine distance on ${\mathbb {R}}^k - \left\{ 0 \right\} ^k$ violates the identity of indiscernibles and the triangle inequality. For all $L^p$ and $d^p$ distances, we varied p from $\{1, 2, 4, 8, 16, 32, \infty \}$ and for fractional distances from $\{ \nicefrac {1}{2}, \nicefrac {1}{4}, \nicefrac {1}{8}, \nicefrac {1}{16}, \nicefrac {1}{32} \}$.

The evaluation on high-dimensional data was carried out using tf-idf encoding (Tan et al. 2006) on ten text document data sets. The first data set was constructed in this work by using abstracts from five life sciences journals with the task of predicting the journal each paper was published in. The remaining data sets included webkb from Cardoso-Cachopo (2007); 20NewsGroups downloaded via scikit-learn library; MovieReview from Pang and Lee (2004); farm-ads, NIPS, Reuters and TTC-3600 from the UCI Machine Learning Repository and two data sets extracted from the literature (Dalkilic et al. 2006; Greene and Cunningham 2006). Each data set was treated as a multi-class classification problem; see Electronic Supplementary Materials.

To compare distances $d_1$ and $d_2$ on a particular data set, we scored a “win” to the one with the higher estimated accuracy or assigned half a win to each in case of a tie. We then counted the number of wins in a “tournament” where each distance was pairwise-compared with all its competitors on each data set. The expectation is that a better distance will lead to higher classification performance and more wins.

Figure 2 shows the number of wins per text data set with the variation assessed by bootstrapping. That is, the set of data sets was sampled with replacement 1000 times from which wins and losses were counted as described above. We find that normalized distance functions outperformed their unnormalized counterparts; i.e., as a group, the $d_N^p$ metrics show the best performance, with the maximum reached when $p=1$. However, the performance of $d_N^1$ is not significantly better than that of $d_N^2$ ($P=0.0547$ using binomial test on the number of wins and $P = 0.0578$ using Friedman’s test on estimated accuracies). The $d^p$ and $d_N^p$ metrics generally outperformed their $L^p$ counterparts. Interestingly, the normalized $L^1$ distance, and one minus Spearman correlation coefficients show excellent performance on tf-idf data as shown in Fig. 2. However, neither of these functions is a metric. Therefore, the $d_N^p$ metrics are the only group that provide both high performance accuracy and theoretical guarantees reserved for metric spaces. Specifically, $d_N^1$ performs significantly better than the best metrics, i.e., the normalized Euclidean metric on these high-dimensional data sets ($P = 9.77 \times 10^{-4}$ using bionomial test on the number of wins; $P = 0.0016$ using Friedman test on estimated accuracies). In fact, $d_N^1$ outperformed the normalized Euclidean metric on each data set. In addition, there is no significant difference among $d_N^1$ and the two top-performing non-metrics: one minus Spearman correlation coefficient and the normalized cityblock ($P = 0.7037$ using Friedman’s test on accuracies with the null hypothesis being “there is no difference in performance among these three methods”). Additional results obtained by varying data types (low dimensional dense real-valued versus high-dimensional sparse text data), and data normalization procedures (z-score, min-max, unit) are provided in Electronic Supplementary Materials.

Fig. 2

Comparison between distance functions on text document data. The upper panel shows the performance comparison of the new metrics against all other metrics. The lower panel shows the comparison between the new metrics and all other non-metrics. The functions are color coded as follows: $L^p$ family (light blue), normalized $L^p$ family (dark blue), $d^p$ family (light green), normalized $d^p$ family (dark green); f-divergences (light yellow), cosine distance and the correlation coefficients (light red). All metrics are labeled by an asterisk (Color figure online)

The evaluation on low-dimensional data was performed over thirty real-valued data sets from the UCI Machine Learning Repository (Lichman 2013). All data sets and results are summarized in Electronic Supplementary Materials, with the main conclusion that metrics generally outperform non-metrics and that $p=1$ and $p=2$ are the most useful parameter choices. The new distances are competitive with the Minkowski family.

Overall, the following results stand out. First, metrics have generally outperformed non-metrics and fractional distances did not provide the expected improvement on high-dimensional data. The $d^p$ distances outperformed their $L^p$ counterparts over all $p>1$ (they are identical for $p=1$). As expected, the cosine distance worked well on high-dimensional data, but surprisingly the two correlation coefficients were as good. Finally, when averaged over the two groups of data (Figures for real-valued data are in Electronic Supplementary Materials), $d^1_N$ and $d^2_N$ are the best performing metrics, with on par performance with the top non-metric distance functions. These results provide compelling evidence that the new metrics fare well against all competing distances.

Fig. 3

Hubness in low- and high-dimensional data sets. The upper panels show the distribution of $N_5$ for simulated data sets with the standard normal distribution ($n=10000$, $k \in \left\{ 3, 100\right\}$). The lower panels show the distribution of $N_5({\mathbf {x}})$ for the spambase ($n=4601$, $k = 57$) and bbc ($n=2225$, $k = 9635$) data sets (Color figure online)

5.2 Hubness and concentration in high-dimensional spaces

Recent work has shown that high-dimensional data sets suffer from the effect of hubness. That is, as the data dimensionality increases, a smaller fraction of points tend to find themselves as nearest neighbors of many other points in the data set, whereas a larger fraction of points tend to be within no one’s nearest neighbors (Radovanović et al. 2010). This effect underlies the poor performance of traditional distance functions in high-dimensional spaces (Beyer et al. 1999).

Fig. 4

Scatter plots and Spearman’s correlation coefficient ($\rho _s$) of $N_5({\mathbf {x}})$ against the distance to the geometric mean of the data sets. Simulated data sets were generated i.i.d. following a standard Gaussian distribution and contained 10,000 points. From left to right: the dimensionality of the data set k chosen from $\{3, 20, 100\}$. From top to bottom, we show three dissimilarity functions: Euclidean, cosine and $d_N^2$ (Color figure online)

Fig. 5

Concentration effects in simulated data sets generated from a zero-mean Gaussian distribution with unit covariance matrix. Each data set contained 1000 points (Color figure online)

We investigated the effect of hubness for the $d^p$ and $d^p_N$ metrics on both simulated and real data. Following Radovanović et al. (2010), for every data point ${\mathbf {x}}$ we first counted the number of other points in the data set such that ${\mathbf {x}}$ was within their K closest neighbors, $N_K({\mathbf {x}})$. We then plot the distribution of $N_5({\mathbf {x}})$ on an i.i.d. Gaussian data and two real-life data sets from the collection used in this work (Fig.  3). We find that the $d^p_N$ metrics show similar hubness effects and resilience to high dimension as the cosine distance, while at the same time being a metric. There do not exist similar normalizers for the $L^p$ family, except when $p=2$ (Deza and Deza 2013). We next plot the relationship between $N_5({\mathbf {x}})$ of each data point and its distance from the geometric mean of the data set (Fig. 4). We observe that, unlike the Euclidean distance, cosine and $d_N^p$ do not show strong correlation with increasing dimensionality and the hubness effect as a long tail in $N_5({\mathbf {x}})$ has been largely alleviated.

Finally, we investigated concentration effects for $d^p$ and $d_N^p$ metrics on simulated data and compare with other representative distances. Figure 5 reaffirms the comparable behavior between $d_N^p$ and cosine distances.

5.3 Performance insights

A potential factor contributing to the success of the $d_N^{p}$ metrics on the tf-idf data could be the lack of translational invariance. We call a metric d on Xtranslation-invariant if $d(x,y) = d(x+z,y+z)$ for all $x,y,z \in X$. A number of classical metrics fall into this group, such as all norm-induced metrics; e.g., Minkowki distances. The normalized metric $d_N^{p}$ is not translation-invariant as demonstrated by a simple example that $\forall p>1, d_N^{p}(0,1)\ne d_N^{p}(1,2)$. This effect, however, is important for quantifying distance in semantic data such as text documents. To illustrate this, consider the following bag-of-words features of two pairs of article abstracts in ${\mathbb {R}}^k$ for $p=1$; $d_N^{p}((1,0,\ldots ,0),(0,\ldots , 0)) =1$ while $d_N^{p}((100,100,\ldots ,100),(99,100,\ldots ,100)) = 1/(100k)$. The two pairs of elements have equal Minkowski distance of 1, but the elements $(100,100,\ldots ,100)$ and $(99,100,\ldots ,100)$ are more related as they share a large number of words. The normalized metric $d_N^{p}$ captures that strong similarity by incorporating built-in information of the data as indicated by the results on text data (Fig. 2). The tf-idf data studied here can also be viewed as ontological data with a trivial structure, the concept of which will be introduced in Sect. 6.

5.4 Computational efficiency

Computing the Minkowski distance of order p between two k-dimensional vectors requires $2k-1$ additions and k exponentiations, before calculating the p-th root. Our unnormalized metric from Eq. 4 requires $2k-1$ additions, k comparisons to a 0, and only 2 exponentiations. Since exponentiation is slow, especially for larger p, the new metric is faster to compute. Both classes of metrics have the same asymptotic complexity of O(k).

6 Application to ontologies

Modern classification approaches increasingly rely on ontological output spaces (Grosshans et al. 2014; Movshovitz-Attias et al. 2015). An ontology ${\mathcal {O}}=(V,E)$ is a directed acyclic graph with a set of vertices (concepts) V and a set of edges (relational ties) $E\subset V\times V$. A news article, for instance, covering aspects of sports injuries might be labeled by the term “sports”, “medicine”, but also “sports medicine” that is a subcategory of both sports and medical articles. Similarly, a protein associated with the terms “transferase” and “oxidoreductase” could also be associated with a more general term “enzyme”. In terms of class labels, a news article or a protein function can be seen as a consistent subgraph$F\subseteq V$ of the larger ontology graph. By saying consistent, we mean that if a vertex v belongs to F, then all the ancestors of v up to the root(s) of the ontology must also belong to F. This consistency requirement follows from the transitive relationships specified on edges that are commonly used; e.g., is-a and part-of. In some domains such as computational biology, a subgraph F corresponding to an experimentally characterized protein function (its biological activity) contains 10–100 nodes, whereas the ontology graph consists of 1000–10000 nodes (Robinson and Bauer 2011). We will use the terms consistent subgraph and ontological annotation interchangeably. In the context of proteins, we will also refer to them as protein function.

Before we introduce metrics on ontological annotations, we briefly review relevant theoretical concepts. Suppose that the underlying probabilistic model according to which ontological annotations have been generated is a Bayesian network structured according to the ontology ${\mathcal {O}}$ (Clark and Radivojac 2013; Jiang et al. 2014). That is, we consider that each concept in the ontology is a binary random variable and that the graph structure specifies the conditional independence relationships in the network. Then, using the standard Bayesian network factorization we write the marginal probability for any consistent subgraph F as

$$\begin{aligned} P(F)=\prod _{v\in F}P(v|\mathrm {Parents}(v)), \end{aligned}$$

where $P(v|\mathrm {Parents}(v))$ is the probability that node v is part of an ontological annotation given that all of its parents are part of the annotation. Due to consistency, the marginalization can be performed in a straightforward manner from the leaves of the network towards the root. This marginalization is reasonable in open-world domains such as molecular biology because some activities are never tested and those that are might not be fully observable. Thus, treating nodes not in F as unknown and marginalizing over them is intuitive. Observe that each conditional probability table in this (restricted) Bayesian network needs to store a single number; i.e., the concept v can be present only if all of its parents are part of the annotation. If any of the parents is not a part of the annotation F, v is guaranteed to not be in F.

6.1 Metrics on ontologies

We express the information content of a consistent subgraph F as

$$\begin{aligned} i(F)&=\log \frac{1}{P(F)} ={\textstyle \sum }_{v\in F}ia(v), \end{aligned}$$

where $ia(v) = -\log P(v|\mathrm {Parents}(v))$ is referred to as information accretion (Clark and Radivojac 2013). This term corresponds to the additional information inherent to the node v under the assumption that all its parents are already present in the annotation of the object.

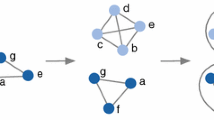
We can now compare two ontological annotations F and G. For the moment, suppose that annotation G is a prediction of F. We use the term misinformation to refer to the cumulative information content of the nodes in G that are not part of the true annotation F; i.e., it gives the total information content along all incorrect paths in G. Similarly, the remaining uncertainty gives the overall information content corresponding to the nodes in F that are not included in the predicted graph G (Fig. 6). More formally, misinformation (mi) and remaining uncertainty (ru) are defined as

$$\begin{aligned} mi(F,G)=\sum _{v\in G{\setminus } F}ia(v)\,\,\, \text {and} \,\,\, ru(F,G)=\sum _{v\in F{\setminus } G}ia(v). \end{aligned}$$

Fig. 6

Illustration of the calculation of the remaining uncertainty and misinformation for two proteins with their ontological annotations: F (true, blue) and G (predicted, red). The circled nodes contribute to the remaining uncertainty (blue nodes, left) and misinformation (red node, right) (Color figure online)

Let now X be a non-empty set of all consistent subgraphs generated according to a probability distribution specified by the Bayesian network. We define a function $d^{p}:X\times X\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d^{p}(F,G)=\left( ru^{p}(F,G)+mi^{p}(F,G)\right) ^{\frac{1}{p}}. \end{aligned}$$

(9)

We refer to the function $d^{p}$ as semantic distance. Similarly, we define another function $d_N^{p}:X\times X\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} d_N^{p}(F,G)=\frac{\left( ru^{p}(F,G)+mi^{p}(F,G)\right) ^{\frac{1}{p}}}{\sum _{v\in F\cup G}ia(v)}. \end{aligned}$$

(10)

We refer to the function $d_N^{p}$ as normalized semantic distance.

Theorem 6.1

$(X, d^{p})$ is a metric space.

Theorem 6.2

$(X, d_N^{p})$ is a metric space. In addition, $d_N^{p}: X \times X \rightarrow [0,1]$.

6.2 Indirect evaluations using ontological annotations for proteins

Evaluating dissimilarity measures between consistent subgraphs is difficult because ontological annotations are usually class labels rather than attributes, and this excludes a classification-based benchmarking performed in Sect. 5. Therefore, we use an indirect approach and assess the quality of the proposed semantic distance between ontological annotations using domain knowledge on the set of proteins for which both an amino acid sequence and an ontological annotation were available to us.

Fig. 7

Indirect evaluation of semantic distance between ontological annotations. Distance comparisons are color-coded for the three Gene Ontology domains. In each domain, three boxes from light to dark show the distribution of pairwise distances ($d_N^{2}$) between proteins within different sequence similarity groups: [0, 1 / 3), [1 / 3, 2 / 3) and [2 / 3, 1]; see Electronic Supplementary Materials for details related to sequence similarity calculation. Each box is sampled, with $N=5000$, from all human-mouse protein pairs. All paired differences are statistically significant based on the t-test after Bonferroni correction (Color figure online)

In the first experiment, we take a set of protein pairs from the UniProt database (Bairoch et al. 2005) and compare their sequence similarity to ontological distance with a biologically justified expectation that more similar sequences will be associated with more similar ontological annotations. Figure 7 shows this relationship for three separate concept hierarchies in the Gene Ontology: Molecular Function Ontology (MFO), Biological Process Ontology (BPO) and Cellular Component Ontology (CCO). We split the protein pairs in each ontology into three groups based on their sequence similarity and then measured distances between their ontological annotations. As expected, we observed significant differences between each pair of sequence similarity groups in each ontology. Statistical tests give P-values close to zero on each data set.

In the second experiment we perform clustering of organisms based on the ontological annotations of their proteins; i.e., we ignore protein sequences and attempt to reconstruct the species tree using protein functions only. We considered five species for which we could extract a sufficient number of ontological annotations (Homo sapiens, Mus musculus, Saccharomyces cerevisiae, Arabidopsis thaliana and Escherichia coli), each species effectively being a set of protein functions. Hierarchical clustering on these groups of ontological annotations (one group for each species) was used to form an evolutionary tree; for simplicity, we refer to the tree derived solely from functional information as a functional phylogeny. A good distance measure is expected to provide the same evolutionary tree as the one that has been determined by evolutionary biologists based on DNA or protein sequences. Such studies are difficult among distantly related species (such as those studied here) for two reasons. First, researchers must be able identify single-copy genes shared by all species to build such trees from. Given that the species studied here share a common ancestor more than 1 billion years ago, there are very few such genes; e.g., see Wu et al. (2011). Second, even if appropriate sequences are identified, they may not be informative for deep phylogenetic relationships, as multiple substitutions at individual nucleotides or amino acids effectively over-write evolutionary relatedness. For these reasons, we hoped that a tree based on function would provide more data with which to answer questions about phylogenetic relationships.

Using the Molecular Function and Cellular Component functional annotations of the Gene Ontology, our clustering approach did recover the correct relationships among species (Fig.  8, left tree). This result is gratifying, especially as we might expect many similar functions to be present in the single-celled organisms (E. coli and S. cerevisiae). However, using the Biological Process annotations did not result in the correct phylogeny, as the positions of S. cerevisiae and A. thaliana were reversed (Fig. 8, right tree).

The accuracy of the molecular function and cellular component annotations and the inaccuracy of the biological process annotations are consistent with the higher level of functional conservation for the less abstract annotations (Rogers and Ben-Hur 2009; Nehrt et al. 2011), as greater conservation of function could result in more phylogenetic signal within this ontology. As a reminder, this algorithm only produces an unrooted topology among the species. It is up to the experimenters to root the tree with some expert knowledge, as we have done here.

Fig. 8

Functional phylogenetic trees for H. sapiens, M. musculus, S. cerevisiae, A. thaliana and E. coli in the Molecular function and Cellular component ontologies (left, correct) and the Biological process ontology (right, incorrect). See Electronic Supplementary Materials for further details

7 Related work

7.1 Metric learning and data-dependent dissimilarities

Learning distance metrics has emerged as one of the important topics in machine learning and data mining (Xing et al. 2003). In this approach, a metric itself depends on a set of parameters that are learned with respect to a specific problem, data set and algorithm at hand; e.g., KNN (Weinberger and Saul 2009), K-means (Bilenko et al. 2004), sometimes under constraints such as sparseness. The most studied metric in this field is the Mahalanobis metric

$$\begin{aligned} d({\mathbf {x}},{\mathbf {y}}) = \sqrt{({\mathbf {x}}-{\mathbf {y}})^T{\mathbf {A}}({\mathbf {x}}-{\mathbf {y}})}, \end{aligned}$$

where ${\mathbf {x}},{\mathbf {y}} \in {\mathbb {R}}^k$ and ${\mathbf {A}} \in {\mathbb {R}}^{k\times k}$, which usually leads to convex formulations. This approach has important merits such as application-specific optimality. However, there is insufficient theoretical understanding related to the consistency of metric learning (Bellet et al. 2013) as well as scalability issues caused by either large parameter space or the data set size (Yang and Jin 2006; Weinberger and Saul 2009). In contrast, default metrics, though not tailored for specific problems, are immediately available and usually present the first line of attack to a specific learning task. Incorporating the $d^p$ metrics into the metric learning framework might be an interesting research direction.

Data-dependent dissimilarities provide another interesting direction in data mining. Dissimilarities such as shared nearest neighbor distance (Jarvis and Patrick 1973) and mass-based dissimilarity (Ting et al. 2016) have been shown to overcome clustering problems related to sample spaces with varying densities or identification of local effects such as local anomalies. Although such functions have notable benefits when combined with particular learning algorithms (e.g., density-based clustering), they require further understanding and performance characterization in a range of different applications; for example, under sample selection bias.

7.2 Default metrics

A body of research exists on handcrafting domain-specific distance functions (Deza and Deza 2013). Distances on strings (Yujian and Bo 2007; Li et al. 2004), rankings (Kumar and Vassilvitskii 2010; Hassanzadeh and Milenkovic 2014), or graphs (Cao et al. 2013) have been actively researched in information retrieval, computational biology, computer vision, etc. Similarly, metrics on probability distributions have long been theoretically studied (Zolotarev 1983). Different metrics emerge for different reasons: some originated in functional analysis, such as the $L^p$ metric and the uniform metric, yet others due to their special properties; e.g., the Hellinger distance which admits decomposition under certain conditions (Zolotarev 1983). One application for such metrics is in stochastic programming and stability analysis in related problems (Rachev and Römisch 2002). They are also used in statistical inference (Rao 1973) or applied to measure the within- and between-population diversity in economics, genetics, etc. (Rao 1982).

7.3 Kernel-induced distances

Given an input space X, kernels are defined as symmetric positive semi-definite similarity functions $k:X\times X\rightarrow {\mathbb {R}}$ (Shawe-Taylor and Cristianini 2004). The theoretical properties guarantee an existence of a Hilbert space in which the kernel can be equivalently computed as an inner product of the images of the original objects as well as a globally optimal solution (unique if positive definite) when combined with optimizers such as support vector machines. Over the past three decades, kernels have been used ubiquitously with a number of applications in supervised and unsupervised learning (Shawe-Taylor and Cristianini 2004). As expected, there exist connections between kernels and distances; e.g., the transformation

$$\begin{aligned} d(x,y)=\sqrt{k(x,x)+k(y,y)-2k(x,y)},\qquad \forall x,y\in X \end{aligned}$$

has been proposed as a general kernel-induced distance (Schölkopf 2000). Several other transformations are possible such as $d(x,y)=1-k(x,y)$ for unit-normalized kernels that is equivalent to the cosine and correlation distances used in this work. Neither transformation, however, guarantees that the resulting distances satisfy metric properties; e.g., for $x=(0,1)$ and $y=(0,2)$ it follows that both equations violate the identity of indiscernibles (Sect. 3.1) for the cosine similarity. On the other hand, $d(x,y)=1-k(x,y)$ does guarantee a metric property for the Jaccard distance on sets. Therefore, while a thorough treatment and use of kernel-to-distance transformations have been out of scope for this study, we believe that both theoretical and empirical studies are necessary to further understand the properties and performance of these transformations.

8 Conclusions

This work was motivated by the desire to develop a family of metrics for learning across different domains, especially on high-dimensional and structured data that characterize many modern applications. Overall, we believe that the class of functions proposed in this work present sensible choices in various fields and believe that their good theoretical properties and strong empirical performance will play a positive role in their adoption.