Constrained distance based clustering for time-series: a comparative and experimental study

Abstract

Constrained clustering is becoming an increasingly popular approach in data mining. It offers a balance between the complexity of producing a formal definition of thematic classes—required by supervised methods—and unsupervised approaches, which ignore expert knowledge and intuition. Nevertheless, the application of constrained clustering to time-series analysis is relatively unknown. This is partly due to the unsuitability of the Euclidean distance metric, which is typically used in data mining, to time-series data. This article addresses this divide by presenting an exhaustive review of constrained clustering algorithms and by modifying publicly available implementations to use a more appropriate distance measure—dynamic time warping. It presents a comparative study, in which their performance is evaluated when applied to time-series. It is found that k-means based algorithms become computationally expensive and unstable under these modifications. Spectral approaches are easily applied and offer state-of-the-art performance, whereas declarative approaches are also easily applied and guarantee constraint satisfaction. An analysis of the results raises several influencing factors to an algorithm’s performance when constraints are introduced.

1 Introduction

Time-series are becoming more readily available with the introduction of mobile sensing devices, satellite constellations, wearable devices, and health monitors, to name but a few. Contemporary time-series data mining problems are therefore characterised by increasingly large volumes of data.

This complicates time-series classification because of the complexity of collecting reliable ground truth (or reference) data and the definition of thematic classes. As such, unsupervised clustering is often employed, which offers a solution based upon the data alone. These approaches, however, ignore expert knowledge and intuition (that is to say to the potential thematic classes), and do not offer the possibility for an expert to propose modifications to the clustering.

Constrained clustering (also known as semi-supervised clustering) is the process of introducing background knowledge (also known as side information) to guide a clustering algorithm. The background knowledge takes the form of constraints that supplement the information derived from the data through a distance metric, for a (generally small) subset of the data. A constrained algorithm attempts to find a solution that balances the data derived information with that derived from the user constraints. As such these approaches offer a new tool for time-series clustering which, to the best of our knowledge, has not been applied to the domain.

This paper addresses this through the following three contributions.

• A review of constrained clustering methods, including single algorithm approaches and collaborative and ensemble approaches, which define an interaction between algorithms.

• Adapting a sample of these algorithms for use in time-series analysis and describes the properties of others which prevents their adaptation to time-series analysis.

• An evaluation of these adapted methods on publicly available time-series data (Chen et al. 2015), which gives insight into the factors that influence their performance in constrained clustering.

As such, this article offers insight into the different formulations of constrained clustering algorithms and how they can be adapted to be used in time-series clustering. The algorithms are selected from implementations that are publicly available. Some algorithms can be directly applied by inputting a dissimilarity/similarity matrix calculated using an appropriate dissimilarity measure, others require modification of the algorithm itself to integrate the measure. The evaluation is performed using nine different datasets and forty constraint cases for each dataset.

The remainder of this paper is organised as follows. Section 2 presents some background on clustering, user-constraints, and time-series clustering. Section 3 presents a comprehensive review of the literature on constrained clustering. Section 4 describes the modification of publicly available implementations for use in time-series clustering, and a comparative study of these algorithms using standard datasets. Section 5 analyses and discusses these results and discusses the limitations of existing approaches when applied to time-series data. Finally the conclusions of the study are drawn in Sect. 6.

2 Background

2.1 Cluster analysis

Let $\mathcal {O}$ be a set of instances (data points) $\{o_1,\ldots ,o_n\}$ and $d(o_i,o_j)$ a dissimilarity (or a similarity) measure between any two instances $o_i$ and $o_j$. The similarity or dissimilarity between instances can be computed from their features or given by a similarity graph. Partition clustering involves finding a partition of $\mathcal {O}$ into K non-empty and disjoint groups called clusters, $C_1,\ldots ,C_K$, such that instances in the same cluster are very similar and instances in different clusters are different. The homogeneity of the clusters is usually formalised by a optimisation criterion, and clustering aims at finding a partition that optimises the given objective. For distance-based clustering, different optimisation criteria exist, the most popular are (Hansen and Jaumard 1997):

• minimising the maximal diameter of the clusters,

• minimising the maximal radius of the clusters,

• maximising the minimal split between clusters,

• minimising the sum of stars,

• minimising the within-cluster sum of dissimilarities (WCSD),

• minimising the within-cluster sum of squares (WCSS).

All of these criteria, except the minimal split, are NP-Hard. Finding a partition by maximising the minimal split between clusters is polynomial (Delattre and Hansen 1980) but becomes NP-Hard under user constraints (Davidson and Ravi 2007). As for the maximal diameter criterion, the problem is polynomial with 2 clusters ($K=2$), but is NP-Hard with more than 3 clusters ($K\ge 3$) (Hansen and Delattre 1978). The NP-Hardness of the WCSS criterion in general dimensions when $K=2$ is proved in (Aloise et al. 2009).

Similarity-based clustering uses data in the form of an undirected and weighted similarity graph, $G=(V,E)$, where each vertex, $v\in V$, represents a data point and each edge between two vertices, $v_i$ and $v_j$, has a non-negative weight $w_{ij}$. Spectral clustering aims to find a partition of the graph such that the edges between different groups have a very low weight and the edges within a group have high weight. Given a cluster $C_i$, a cut measure is defined by the sum of the weights of the edges that link an instance in $C_i$ and an instance not in $C_i$. The two most common optimisation criteria are (Luxburg 2007):

• minimising the ratio cut, which is defined by the sum of $\tfrac{{{\mathrm{cut}}}(C_i)}{|C_i|}$,

• minimising the normalised cut, which is defined by the sum of $\tfrac{{{\mathrm{cut}}}(C_i)}{{{\mathrm{vol}}}(C_i)}$, where ${{\mathrm{vol}}}(C_i)$ measures the degrees of the nodes belonging to $C_i$.

These criteria are also NP-Hard. Spectral clustering algorithms solve relaxed versions of those problems: relaxing the normalised cut leads to normalised spectral clustering and relaxing the ratio cut leads to unnormalised spectral clustering.

2.2 User constraints

In practice, a user may have some requirements for, or prior knowledge about, the final solution. For instance, the user can have some information on the label of a subset of objects (Wagstaff and Cardie 2000). Because of the inherent complexity of clustering optimisation criteria, classic algorithms always find a local optimum. Several optima may exist, some of which may be closer to the user requirement. It is therefore important to integrate prior knowledge into the clustering process and several studies have demonstrated the importance of this kind of domain knowledge in data mining processes (Anand et al. 1995). Prior knowledge is expressed by user constraints to be satisfied by the clustering solution. The subject of these user constraints can be the instances or the clusters (Basu et al. 2008).

Instance-level constraints are the most widely used type of constraint and were first introduced by Wagstaff and Cardie (2000). Two kinds of instance-level constraints exist: must-link (ML) and cannot-link (CL). An ML constraint between two instances $o_i$ and $o_j$ states that they must be in the same cluster: $\forall k \in \{1,\dots ,K\}$, $o_i \in C_k \Leftrightarrow o_j \in C_{k}$. A CL constraint on two instances $o_i$ and $o_j$ states that they cannot be in the same cluster: $\forall k \in \{1,\dots ,K\}$, $\lnot (o_i \in C_k\wedge o_j\in C_k)$. In semi-supervised clustering, this information is available to aid the clustering process and can be inferred from class labels: if two objects have the same label then they are linked by an ML constraint, otherwise by a CL constraint. Supervision by instance-level constraints is however more general and more realistic than class labels. Using knowledge, even when class labels may be unknown, a user can specify whether pairs of points belong to the same cluster or not (Wagstaff et al. 2001).

Cluster-level constraints define requirements on the clusters, for example:

• the number of clusters K;

• their absolute or relative maximal or minimal size;

• their maximum diameter, i.e. clusters must have a diameter of at most $\gamma$;

• their split, i.e. clusters must be separated by at least $\delta$ [note that although the diameter or split constraints state requirements on the clusters, they can be expressed by a conjunction of cannot-link constraints or must-link constraints, respectively (Davidson and Ravi 2005)];

• the $\epsilon$-constraint, introduced in Davidson and Ravi (2005), demands that each object $o_i$ has in its neighborhood of radius $\epsilon$ at least one other object in the same cluster.

See Fig. 1 for an example of these constraints.

Fig. 1

Examples of ML, CL, $\delta$, $\gamma$, and $\epsilon$ constraints

Mechanisms to integrate these constraints into the clustering process can be categorised into three different approaches:

• enforcing constraints by guiding clustering algorithms during their process or by modifying the objective function;

• learning the distance function using metric learning;

• declarative and generative methods.

By far the most common constraints to be used in clustering are must-link and cannot-link constraints. This is because they can be intuitively derived from user inputs without in-depth knowledge of the underlying clustering process and feature space. As such, the review will focus on algorithms that explicitly model these constraints.

2.3 Time-series clustering

Time-series increase the complexity of clustering due to the properties of the data. Almost all clustering algorithms use a distance function based upon the norm of two vectors $L_p$ (Manhattan, $L_1$; Euclidean, $L_2$; and Maximum, $L_\infty$). This implies a fixed mapping between points in two time-series and as such, norm based distances are sensitive to noise, misalignment in time (however small) (Keogh and Kasetty 2003), and are unable to correct for sub-sequence, i.e. non-linear, time shifts (Wang et al. 2013). Dynamic time warping (DTW) (Sakoe and Chiba 1971, 1978) on the other hand is a dissimilarity measure that finds an optimal alignment between two time series by non-linearly warping them. As such, it overcomes the limitations of norm based distances when applied to time-series. Furthermore, certain types of clustering algorithms, for example k-Means, calculate centroids during their optimisation, which is not a trivial task in the case of time-series due to the misalignments discussed previously. The DTW Barycenter Averaging (DBA) algorithm (Petitjean et al. 2011) overcomes this limitation by iteratively refining an initial estimate of the average sequence (usually taken to be a random sample of the time-series being averaged), in order to minimise its squared DTW measure to the sequences being averaged. As such, classical constrained clustering implementations require modification to use the DTW measure and DBA averaging (if required) before being applied to time-series. Other considerations when working with time-series are that the dimensionality of the data can be very large, which means that the sampling of the input space can be sparse.

For an in-depth background on time-series clustering the following reviews are recommended: (Keogh and Kasetty 2003; Laxman and Sastry 2006; Kavitha and Punithavalli 2010; Antunes and Oliveira 2001; Liao 2005; Rani and Sikka 2012; Aghabozorgi et al. 2015). Keogh and Lin (2005) define two categories of time-series clustering:

• Whole clustering: “The notion of clustering here is similar to that of conventional clustering of discrete objects. Given a set of individual time series data, the objective is to group similar time series into the same cluster” (Keogh and Lin 2005).

• Subsequence clustering: “Given a single time series, sometimes in the form of streaming time series, individual time series (subsequences) are extracted with a sliding window. Clustering is then performed on the extracted time series subsequences” (Keogh and Lin 2005).

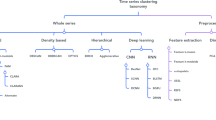
They then proceed to demonstrate that subsequence clustering is “meaningless” because “clusters extracted from these time series are forced to obey a certain constraints that are pathologically unlikely to be satisfied by any dataset, and because of this, the clusters extracted by any clustering algorithm are essentially random” (Keogh and Lin 2005). A typical goal in time-series analysis is to cluster the data using the full time-series and this is the most direct application of existing constrained clustering approaches. Therefore this review will focus on ‘Whole Clustering’.

It should be noted that DTW is not the only available method for measuring dissimilarity between time-series. It is, nevertheless, often found that alternative dissimilarity measures are not significantly better than DTW in real-world datasets (Ding et al. 2008; Wang et al. 2013; Lines and Bagnall 2015; Bagnall et al. 2017) (the reader is referred to these references for a comprehensive review and comparison of the alternatives). To simplify the presented work it will therefore focus on DTW.

3 Constrained clustering methods

This section presents a review of partitional constrained clustering methods. These range from algorithmic approaches to declarative approaches, from using the constraints to guide the search process to using them to learn a metric before and/or during searching, and from constructing a clustering directly from the dataset to constructing a clustering from a set of given clusterings. The algorithms that exist in the literature, and which are reviewed herein, are summarised in Table 1. The methods that are used in the experimental section of this paper will be discussed in more depth in Sect. 4.

Table 1 Categorisation of methods found in the literature

3.1 k-Means

In this type of approach, the clustering algorithm or the objective function is modified so that user constraints are used to guide the algorithm towards a more appropriate data partitioning. Most of these works consider instance-level must-link and cannot-link constraints. The extension is done either by enforcing pairwise constraints or by using pairwise constraints to define penalties in the objective function. A survey on partitional and hierarchical clustering with instance level constraints can be found in (Davidson and Basu 2007).

In the category of enforcing pairwise constraints, the first work proposed a modified version of COBWEB (Fisher 1987) that tends to satisfy all the pairwise constraints, named COP-COBWEB (Wagstaff and Cardie 2000). Subsequent work extended the k-Means algorithm to instance-level constraints. The k-Means algorithm starts with initial assignment seeds and assigns objects to clusters in several iterations. At each iteration, the centroids of the clusters are computed and the objects are reassigned to the closest centroid. The algorithm converges and finds a solution which is a local optimum of the within-cluster sum of squares (WCSS or distortion). To integrate must-link and cannot-link constraints, the COP-KMeans algorithm by Wagstaff et al. (2001) extends the k-Means algorithm by choosing a reassignment that does not violate any constraints at each iteration.¹ This greedy behavior without backtracking means that COP-KMeans may fail to find a solution that satisfies all the constraints even when such a solution exists. Basu et al. (2002) propose two variants of k-Means, the Seed-KMeans and Constrained-KMeans algorithms, which allow the use of objects labeled as seeds: the difference between the two being the possibility of changing the class centers or not. In both approaches, it is assumed that there is at least one seed for each cluster and that the number of clusters is known. The seeds are used to overcome the sensitivity of the k-Means approaches to the initial parameterisation.

Incorporating must-link and cannot-link constraints makes clustering algorithms sensitive to the assignment order of instances and therefore results in consequent constraint-violation. To address the issue of constraint violation in COP-KMeans, Tan et al. (2010) (ICOP-KMeans) and Rutayisire et al. (2011) propose a modified version with an assignment order, which is either based on a measure of certainty computed for each instance or a sequenced assignment of cannot-linked instances. MLC-KMeans (Huang et al. 2008) takes an alternative approach by introducing assistant centroids, which are calculated using the points implicated by must-link constraints for each cluster, and which are used to calculate the similarity of instances and clusters.

For high-dimensional sparse data, the SCREEN method (Tang et al. 2007) for constraint-guided feature projection was developed, which can be used with a semi-supervised clustering algorithm. This method considers an objective function to learn the projection matrix, which can project the original high-dimensional dataset into a low-dimensional space such that the distance between any pair of instances involved in the cannot-link constraints are maximised while the distance between any pair of instances involved in the must-link constrains are minimised. A spherical k-Means algorithm is then used to try to avoid violating cannot-link constraints.

Other methods uses penalties as a trade-off between finding the best clustering and satisfying as many constraints as possible. Considering a subset of instances whose label is known, Demiriz et al. (1999) modifies the clustering objective function to incorporate a dispersion measure and an impurity measure. The impurity measure is based on Gini Index to measure misplaced known labels. The CVQE (constrained vector quantization error) method (Davidson and Ravi 2005) penalizes constraint violations using distance. If a must-link constraint is violated then the penalty is the distance between the two centroids of the clusters containing the two instances that should be together. If a cannot-link constraint is violated then the penalty is the distance between the cluster centroid the two instances are assigned to and the distance to the nearest cluster centroid. These two penalty types together with the distortion measure define a new differentiable objective function. An improved version, linear-time CVQE (LCVQE) (Pelleg and Baras 2007), avoids checking all possible assignments for cannot-link constraints and its penalty calculations takes into account coordinates of the involved instances in the violated constraint. The method PCK-Means (Basu et al. 2004a) formulated the goal of pairwise constrained clustering as minimising a combined objective function, defined as the sum of the total squared distances between the points and their cluster centroids WCSS, and the cost incurred by violating any pairwise constraints. The cost can be uniform but can also take into account the metric of the clusters, as in the MPCK-Means version that integrates both constraints and metric learning. Lagrangian constrained clustering (Ganji et al. 2016) also formulates the objective function as a sum of distortion and the penalty of violating cannot-link constraints (must-link constraints are used to aggregate instances into super-instances so they are all satisfied). This method uses a Lagrangian relaxation strategy of increasing penalties for constraints which remain unsatisfied in subsequent clustering iterations. A local search approach using Tabu search was developed to optimise the objective function, which is the sum of the distortion and the weighted cost incurred by violating pairwise constraints (Hiep et al. 2016). Grira et al. (2006) introduced the cost of violating pairwise constraints into the objective function of Fuzzy CMeans algorithm. Li et al. (2007) use non-negative matrix factorisation to perform centroid-less constrained k-Means clustering (Zha et al. 2001).

Hybrid approaches integrate both constraint enforcing and metric learning (see Sect. 3.2) into a single framework: MPCK-Means (Bilenko et al. 2004), HMRF-KMeans (Basu et al. 2004b), semi-supervised kernel k-Means (Kulis et al. 2005), and CLWC (Cheng et al. 2008). Bilenko et al. (2004) define an uniform framework that integrates both constraint-based and metric-based methods. This framework represents PCK-Means when considering a constraint-based factor and MPCK-Means when considering both constraint-based and metric-based factors. Semi-supervised HMRF k-Means (Basu et al. 2004b) is a probabilistic framework based on Hidden Markov Random Fields, where the semi-supervised clustering objective minimises both the overall distortion measure of the clusters and the number of violated must-link and cannot-link constraints. A k-Means like iterative algorithm is used for optimising the objective, where at each step the distortion measure is re-estimated to respect user-constraints. Semi-supervised kernel k-Means (Kulis et al. 2005, 2009) is a weighted kernel-based approach, that generalises HMRF k-Means. The method can perform semi-supervised clustering on data given either as vectors or as a graph. It can be used on a wide class of graph clustering objectives such as minimising the normalised cut or ratio cut. The framework can be therefore applied on semi-supervised spectral clustering. Constrained locally weighted clustering (CLWC) (Cheng et al. 2008) integrates the local distance metric learning with constrained learning. Each cluster is assigned to its own local weighting vector in a different subspace. The data points in the constraint set are arranged into disjoint groups (chunklets), and the chunklets are assigned entirely in each assignment and weight update step.

Beyond pairwise constraints, Ng (2000) adds suitable constraints into the mathematical program formulation of the k-Means algorithm to extend the algorithm to the problem of partitioning objects into clusters where the number of elements in each cluster is fixed. Bradley et al. (2000) avoid local solution with empty clusters or clusters having very few points by explicitly adding k minimal capacity constraints to the formulation of the clustering optimisation problem. This work considers that the k-Means algorithm and the constraints are enforced during the assignment step at each iteration. Banerjee and Ghosh (2006) proposed a framework to generate balanced clusters, i.e. clusters of comparable sizes. Demiriz et al. (2008) integrated a minimal size constraint to k-Means algorithm. Considering two types of constraints, the minimum number of objects in a cluster and minimum variance of a cluster, Ge et al. (2007) proposed an algorithm that generates clusters satisfying them both. This algorithm is based on a CD-Tree data structure, which organizes data points in leaf nodes such that each leaf node approximately satisfies the significance and variance constraint and minimises the sum of squared distances.

3.2 Metric learning

Metric learning aims to automatically learn a metric measure from training data that best discriminates the comprising samples according to a given criterion. In general, this metric is either a similarity or a distance (Klein et al. 2002). Many machine learning approaches rely on the learned metric; thus metric learning is usually a preprocessing step for such approaches.

In the context of clustering, the metric can be defined as the Mahalanobis distance parameterised by a matrix M, i.e. ${\mathbf {d_M}}(o_i,o_j) = \Vert o_i - o_j\Vert _M$ (Bellet et al. 2015). Unlike the Euclidean distance, which assumes that attributes are independent of one another, the Mahalanobis distance enables the similarity measure to take into account correlations between attributes. Learning the distance ${\mathbf {d_M}}$ is equivalent to learning the matrix M. For ${\mathbf {d_M}}$ to satisfy distance proprieties (non-negativity, identity, symmetry, and the triangle inequality) M should be a positive semi-definite real-valued matrix.

To guide the learning process, two sets are constructed from the ML and CL constraints: the set of supposedly similar—must-link—pairs ${{\mathrm{Sim}}}$, and the supposedly dissimilar—cannot-link—pairs ${{\mathrm{Dis}}}$, such that

• ${{\mathrm{Sim}}}= \{(o_i,o_j)\ |\ o_i \text { and } o_j \text { should be as similar as possible}\}$,

• ${{\mathrm{Dis}}}= \{(o_i,o_j)\ |\ o_i \text { and } o_j \text { should be as dissimilar as possible}\}$.

It is also possible to introduce unlabeled data along with the constraints to prevent over-fitting.

The ways of using cannot-link constraints in [11, 13] are not well justified too, because a similarity of 0 between two cannot-link objects in the input space does not mean that the two objects tend to belong to different categories

Several proposals have been made to modify (learn) a distance (or metric) taking into account this principle. We can cite works on the Euclidean distance and shortest path (Klein et al. 2002), Mahanalobis distance (Bar-Hillel et al. 2005, 2003; Xing et al. 2002), Kullback-Leibler divergence (Cohn et al. 2003), string-edit distance (Bilenko and Mooney 2003), and the Laplacian regularizer metric learning (LRML) method for clustering and imagery (Hoi et al. 2008, 2010).

Yi et al. (2012) describe a metric learning algorithm that avoids the high computational cost implied by the positive semi-definite constraint. Matrix completion is performed on the partially observed constraints and it is observed that the completed similarity matrix has a high probability of being positive semi-definite, thus avoiding the explicit constraint.

3.3 Spectral graph theory

Spectral clustering is a non-supervised method that takes as input a pre-calculated similarity matrix (graph) and aims to minimise the ratio cut criterion (Luxburg 2007) or the normalised cut criterion (Shi and Malik 2000). Spectral clustering is often considered superior to classical clustering algorithms, such as k-Means, because it is capable of extracting clusters of arbitrary form (Luxburg 2007). It has also been shown that algorithms that build partitions incrementally (like k-Means and EM) are prone to be overly constrained (Davidson and Ravi 2006). Moreover, spectral clustering has polynomial time complexity. The constraints can be expressed as ML/CL constraints or in the form of labels, these can be taken into account either as “hard” (binary) constraints or “soft” (probabilistic) constraints. The method allows the user to specify a lower bound on constraint satisfaction and all points are assigned to clusters simultaneously, even if the constraints are inconsistent.

Kamvar et al. (2003) first integrated ML and CL constraints into spectral clustering.² This is achieved by modifying the affinity matrix by setting ML constrained pairs to maximum similarity, 1, and CL constrained pairs to minimum similarity, 0. This has been extended to out-of-sample points and soft-constraints through regularisation (Alzate and Suykens 2009). Li et al. (2009) point out, however, that a similarity of 0 in the affinity matrix does not mean that the two objects tend to belong to different clusters.

Wang and Davidson (2010a), Wang et al. (2014) introduce a framework for integrating constraints into a spectral clustering. Constraints between N objects are modelled by a matrix Q of size $N \times N$, such that

$$\begin{aligned} Q_{ij} = Q_{ji} = {\left\{ \begin{array}{ll} +1, &{}\text { if } {{\mathrm{ML}}}(i,j),\\ -1, &{}\text { if } {{\mathrm{CL}}}(i,j),\\ 0, &{}\text { otherwise,} \end{array}\right. } \end{aligned}$$

(1)

upon which a constraint satisfaction measure can be defined. Soft constraints can be taken into account by allowing real values to be assigned to Q or by allowing fuzzy cluster membership values. Subsequently, the authors introduce a method to integrate a user-defined lower-bound on the level of constraint satisfaction (Wang and Davidson 2010b). Work has also been described that allows for inconsistent constraints (Rangapuram and Hein 2012).

Based on the Karush–Kuhn–Tucker (Kuhn and Tucker 1951) conditions, an optimal solution can then be found by first finding the set of solutions satisfying all constraints and then using a brute-force approach to find the optimal solution from this set.

These approaches have been extended to integrate logical combinations of constraints (Zhi et al. 2013), which are translated into linear equations or linear inequations. Furthermore, instead of modifying the affinity matrix using binary values, Anand and Reddy (2011) propose to modify the distances using an all-pairs-shortest-path algorithm such that the new distance metric is similar to the original space.

Lu and Carreira-Perpiñán (2008) state that an affinity matrix constructed using constraints is highly informative but only for a small subset of points. To overcome this limitation they propose a method to propagate constraints (in a method that is consistent with the measured similarities) to points that are not directly affected by the original constraint set. These advances are proposed for the two-class problem (multi-class extension is discussed but is computationally inefficient), multi-class alternatives have been proposed (Lu and Ip 2010; Chen and Feng 2012; Ding et al. 2013).

Several works (Zhang and Ando 2006; Hoi et al. 2007; Li et al. 2008; Li and Liu 2009) use the constraints and point similarities to learn a kernel matrix such that points belonging to the same cluster are mapped to be close and points from different clusters are mapped to be well-separated.²

Most recently, progress has been made in introducing faster and simpler formulations, while providing a theoretical guarantee of the quality of the partitioning (Cucuringu et al. 2016).

3.4 Ensemble clustering

The abundance of clustering methods presented in this review can be explained by the ill-posed nature of the problem. Indeed, each clustering algorithm is biased by the objective function used to build the clusters. Consequently, different methods can produce very different clustering results from the same data. Furthermore, the same algorithm can produce different results depending upon its parameters and initialisation. Ensemble clustering methods aim to improve the overall quality of the clustering by reducing the bias of each single algorithm (Hadjitodorov and Kuncheva 2007). An ensemble clustering is composed of two steps. First, multiple clusterings are produced from a set of methods having different points of view. These methods can be different clustering algorithms (Strehl and Ghosh 2002) or the same algorithm with different parameter values or initialisations (Fred and Jain 2002). The final result is derived from the independently obtained results by applying a consensus function.

Constraints can be integrated in two manners: each learning agent integrates them in its own fashion; or applying them in the consensus function. The former approach faces an important dilemma: either favor diversity or quality. High quality is desired, but the gain of ensemble clustering is derived from diversity (thus avoiding biased solutions). Clustering from constrained algorithms tends to have a low variance, which implies low diversity (Yang et al. 2017), especially when using the same set of constraints. Therefore the advantage of ensemble clustering is limited.

Implementations of the first approach exist (Yu et al. 2011; Yang et al. 2012). For example Iqbal et al. (2012) develop the semi-supervised clustering ensembles by voting (SCEV) algorithm, in which diversity is balanced by using different types of semi-supervised algorithms (i.e. constrained k-Means, COP-KMeans, SP-Kmeans, etc.). In the first step each semi-supervised agent computes a clustering given the data and the set of constraints. It then combines all the results using a voting algorithm after having relabeled and align the different clustering results. The authors propose to integrate a weight for each agents’ contributions into the voting algorithm. This weight is a combination of two sub-weights, the first one is defined a priori, based upon the expert’s trust of each agent according to the data (i.e. seeded k-Means is more efficient for noise, COP-Means and constraints are more efficient if the data is noise free), the second is also user defined but based upon the user’s feedback on the clustering result. As such, the algorithm allows more flexibility and user control over the clustering.

The second approach focuses on applying constraints in the consensus function (Al-Razgan and Domeniconi 2009; Xiao et al. 2016; Dimitriadou et al. 2002). These algorithms start by generating the set of clusterings from the clustering agents. The constraints are then integrated in the consensus function, which can be divide into four steps:

• 1. generate a similarity matrix from the set of clusterings;

• 2. construct a sparse graph from this similarity matrix using the CHAMELEON algorithm—an edge is constructed between two vertices if the value in the similarity matrix is greater than zero for the corresponding elements;

• 3. partition the graph into a large number of sub-clusters using the METIS method;

• 4. merge the sub-clusters using an agglomerative hierarchical clustering approach by finding the most similar pair of sub-clusters.

Constraints are integrated during partitioning. Cannot-link constraints are used as priorities for the split operation—sub-clusters that contains a CL constraints are partitioned until the two elements in the constraint are allocated to two different clusters.

3.5 Collaborative clustering

Collaborative clustering is similar to ensemble clustering, but considers that the information offered by different sources and different clusterings are complementary (Kittler 1998). An important problem encountered by ensemble clustering is the difficulty of computing a consensual result from different clusterings that have a wide range of numbers of clusters—the correspondence between each cluster is not a trivial problem (Forestier et al. 2010a).

Collaborative clustering consists in making multiple clustering methods collaborate to reach an agreement on a data partitioning. While ensemble clustering (and consensus clustering (Monti et al. 2003; Li and Ding 2008)) focuses on merging clustering results, collaborative clustering focuses on iteratively modifying the clustering results by sharing information between them (Wemmert et al. 2000; Gançarski and Wemmert 2007; Pedrycz 2002). In consequence it extends ensemble clustering by adding a refinement step before the unification of the results. For instance, in Samarah (Wemmert et al. 2000; Gançarski and Wemmert 2007) each clustering algorithm modifies its results according to all the other clusterings until all the clusterings proposed by the different methods are strongly similar.³ Thus, they can be more easily unified through a voting algorithm (for example).

Three stages for integrating user constraints in the collaborative process can be identified (Forestier et al. 2010a): (1) generation of the final result (by labeling the clusters of the final result using label constraints); (2) directly in the collaborative clustering (in order to guide the collaborative process); and (3) using constrained agents. Integrating user constraints into the learning agents (3) is complex because it requires extensive modification of each of the clustering methods involved. The complexity of integrating constraints in the collaboration (2) depends on how information is exchanged between the learning agents. Integrating the constraints after collaboration (1), however, does not interfere in the collaborative process, which makes it easier to implement.

Samarah (Forestier et al. 2010a) is based on the principle of mutual and iterative refinement of multiple clustering algorithms. This is achieved by generating a set of initial results (using different algorithms, or the same but with different parameter values), refining these results according to the constraints, and combining them. During the refinement stage, each result is compared with the set of results proposed by the other methods, the goal being to evaluate the similarity between the different results in order to observe differences in the clusterings. Once these differences (named conflicts) are identified, the objective is to modify the results to reduce these differences and the number of constraints violations, i.e. resolving the conflicts (Forestier et al. 2010b). These are resolved by either merging clusters, splitting clusters, or re-clustering clusters iteratively. This step can be seen as a questioning each result according to the information provided by the other actors in the collaboration and the background knowledge. After multiple iterations of refinement [in which a local similarity criterion is used to evaluate whether the modifications of a pair of results is relevant (Forestier et al. 2010a)], the results are expected to be more similar than before the collaboration began. During the third and final step, the refined results are combined to propose a final and unique result (which is simplified due to the similarity of the results).

At level (3), the background knowledge is not used directly by the collaborative process but by each collaborative agent. A simple implementation of this approach is to replace the learning agents by constraints clustering methods. This naive approach results in a loss of diversity (as discussed in relation to ensemble clustering), making the collaborative process irrelevant and increasing error rates (Domeniconi and Al-Razgan 2008). To address this, a hybrid approach, that integrates constraints in levels (2) and (3), has been proposed by Domeniconi and Al-Razgan (2008).

The approach uses a set of constrained learning agents that also collaborate using constraints. Multiple instances of the constrained locally adaptive clustering (CLAC) algorithm, which is derived from the LAC method (Domeniconi et al. 2007), are used. Before each iteration, a chunklet graph is constructed with the constraints. This is achieved by grouping data points according to the ML constraints and adding edges according to the CL constraints. A new set of centroids is deduced from this chunklet graph, with a set of associated weights, by assigning vertices in the graph to the appropriate centroid without violating any ML or CL constraints. These set of new centroids and associated weights are then used as initialisation parameters for the learning agents.

The exchange of knowledge through the agents is achieved by adding new constraints at the end of each iteration. These constraints are built to highlight features shared between the majority of clusterings and by selecting those most relevant.

3.6 Declarative approaches

These approaches offer the user a general framework to formalise the problem by choosing an objective function and explicitly stating the constraints. They enable the modeling of different types of user constraints and the search for an exact solution—a global optimum that satisfies all the user constraints. The frameworks are usually developed using a general optimisation tool, such as integer linear programming (ILP), SAT, or constraint programming (CP). While the other approaches usually focus on instance-level must-link and cannot-link constraints, declarative approaches using CP or ILP allow direct integration of cluster-level constraints. They also allow for the integration of different optimisation criteria within the same framework, while other approaches are usually developed for one particular optimisation criterion.

3.6.1 SAT

Considering constrained clustering problems with $K=2$, a SAT based framework has been proposed (Davidson et al. 2010). Based on $K=2$, the assignment of objects into clusters is represented by a Boolean variable $x_i$ for each object i. This framework integrates different constraints such as must-link, cannot-link, maximum diameter and minimum split. Using binary search, the framework offers both single objective optimisation and bi-objective optimisation. Several single optimisation criteria are integrated: minimising the maximal diameter, maximising the minimal split, minimising the difference between diameters, minimising the sum of diameters.

Optimising multiple objectives, the framework considers minimising the diameter and maximising the split either in a way such that one objective is used as a constraint and the other is optimised under that constraint, or by combining them in a single objective which is the ratio of diameter to split. Approximation schemes are also developed to reduce the number of calls in binary search, in order to make the framework more efficient.

3.6.2 Constraint programming

Problem modeling in CP consists in formalizing the problem into a Constraint Satisfaction Problem (CSP) or a Constraint Optimisation Problem (COP). A CSP is a triple $\langle X, {{\mathrm{Dom}}}, C\rangle$ where X is a set of variables, ${{\mathrm{Dom}}}(x)$ for each $x\in X$ is the domain of x and C is a set of constraints, each one expresses a condition on a subset of X. A solution of a CSP is a complete assignment of values from ${{\mathrm{Dom}}}(x)$ to each variable $x\in X$ that satisfies all the constraints of C. A COP is a CSP with an objective function to be optimised. An optimal solution of a COP is a solution of the CSP that optimises the objective function.

In general, solving a CSP or a COP is NP-Hard. Nevertheless, the methods used by the CP solvers enable us to efficiently solve a large number of real-world applications. They rely on constraint propagation and search strategies (Rossi et al. 2006).

A CP-based framework for distance-based constrained clustering has been developed by Dao et al. (2013).⁴ This framework enables the modeling of different constrained clustering problems, by specifying an optimisation criterion and by setting the user constraints. The framework is evolved by improving the model and by developing dedicated propagation algorithms for each optimisation criterion (Dao et al. 2017). In this model, the number of clusters K does not need to be fixed beforehand, only bounds are needed $K_{\min }\le K \le K_{\max }$ and the model has three components: partition constraints, user constraints, and objective function constraints.

In order to improve the performance of CP solvers, different search strategies are elaborated for each criterion. For example, a CP-based framework using repetitive branch-and-bound search has been developed (Guns et al. 2016) for the WCSS criterion.

Another interest of the declarative framework is the bi-objective constrained clustering problem. This problem aims to find clusters that are both compact (minimising the maximal diameter) and well separated (maximising the split), under user constraints. In Dao et al. (2017) it is shown that to solve this problem, the framework can be used by iteratively changing the objective function and adding constraints on the other objective value. This framework has been extended to integrate user constraints on properties, in order to make clustering actionable (Dao et al. 2016).

3.6.3 Integer linear programming

Different frameworks using Integer Linear Programming (ILP) have been developed for constrained clustering. Using ILP, constrained clustering problems must be formalized by a linear objective function subject to linear constraints. In the formulation of clustering such as the one used in CP-based approaches, a clustering is defined by an assignment of instances to clusters. ILP-based approaches use a formulation that is orthogonal to this: a clustering is considered to be a subset of the set of all possible clusters.

In this formulation, the first constraint states that each instance must be covered by exactly one cluster (the clustering is therefore a partition of the instances) and the second states that the clustering is formed by K clusters. Deciding whether a cluster is kept in the final solution is exponential w.r.t. the number of instances. The candidate number of clusters in principle is exponential w.r.t. the number of instances. As such, two kinds of ILP-based approaches have been developed for constrained clustering: (1) use a column generation approach, where the master problem is restricted to a smaller set $T'\subseteq T$, where T is the set of all possibles non-empty clusters, and columns (clusters) are incrementally added until the optimal solution is proved (Babaki et al. 2014); and (2) restrict the cluster candidates on a subset $T'\subseteq T$ and define the clustering problem on $T'$ (Mueller and Kramer 2010; Ouali et al. 2016).

The first type of approaches use column generation to handle the exponential number of possible clusters. To handle this aspect, an ILP-based column generation approach for unconstrained minimum sum of squares clustering was introduced in Merle et al. (1999) and improved in Aloise et al. (2012). Column generation iterates between solving the restricted master problem and adding one or multiple columns. A column is added to the master problem if it can improve the objective function. If no such column can be found, one is certain that the optimal solution of the restricted master problem is also an optimal solution of the full master problem.

The column generation approach has been extended to integrate anti-monotone user constraints in (Babaki et al. 2014). A constraint is anti-monotone if it is satisfied on a set of instances S and satisfied on all subsets $S'\subseteq S$. For instance maximal capacity constraints are anti-monotone but minimal capacity constraints are not.

Another approach to handle the exponential number of cluster candidates is to restrict them on a smaller subset. In some clustering settings such as conceptual clustering, the candidates can usually be taken in a smaller subset $T'$. Considering a constrained clustering problem on a restricted subset $T'$, Mueller and Kramer (2010) and Ouali et al. (2016) develop ILP-based frameworks that can integrate different kinds of user constraints.

3.7 Miscellaneous

Shental et al. (2013) argue that the EM procedure allows for constraints to be integrated in a principled way, instead of heuristically, and present a Gaussian mixture model approach. Lu and Leen (2005) extend this by relaxing the requirement for hard constraints.

Handl and Knowles (2006) address the difficulty of selecting a single clustering objective function and therefore propose a multi-objective evolutionary algorithm to optimise compactness, connectedness, and constraint satisfaction.

Zhu et al. (2016) modify the split function of random forests to include constraints and therefore introduce the constraint propagation random forest, which can deal with noisy constraints.

4 Constrained clustering for time-series

General constrained clustering algorithms have been reviewed in the previous section, and what now remains is to describe their application to time-series. In most cases, this involves modifying the algorithm to use an alternative dissimilarity measure. The modified algorithms are then evaluated by applying them to several publicly available datasets.

4.1 Algorithm adaptation

A subset of the reviewed algorithms were chosen based upon the public availability of implementations and their ability to be modified to use the DTW measure, enabling them to be applied to time-series analysis. Where possible, the initial implementations were taken from, and all modifications were validated with, the originating authors.

Spectral clustering algorithms take as their input a similarity matrix. This simplifies their application to time-series data as the similarity matrix can be pre-computed using DTW and the methods require no, or little, modification. In the case of spectral methods, the form of the Laplacian matrix needs consideration. In the presented evaluation, fully connected graphs were used and similarity was calculated using the Gaussian function, such that

$$\begin{aligned} s_{ij} = \exp \left( \frac{-d_{ij}}{2\sigma ^2}\right) , \end{aligned}$$

(2)

where $d_{ij}$ is the DTW dissimilarity between points i and j and $\sigma$ controls the widths of the neighbourhoods, its value was optimised on each training set using a grid search (as were the number of principal components). The algorithms modified using this methodology were: Adjacency Matrix Modification (Kamvar et al. 2003), Constrained 1-Spectral Clustering (Rangapuram and Hein 2012), Constrained Clustering via Spectral Regularization (CCSR) (Li et al. 2009), CSP (Wang et al. 2014), and Guaranteed Quality Clustering (Cucuringu et al. 2016).

Declarative approaches can take as their input either the data points or a dissimilarity matrix, depending upon the objective function used. The declarative approach found for this study is CPClustering (Dao et al. 2017), which takes the pre-computed DTW dissimilarity matrix and therefore does not need modification.

k-Means based algorithms are more involved to apply to time-series as they iteratively calculate distances to cluster centroids and update these centroids. This implies that the algorithm itself needs to be modified to integrate the DTW measure and to use DBA to calculate the cluster centroids. The COP-KMeans (Wagstaff et al. 2001), LCVQE (Pelleg and Baras 2007), MPCK-Means (Bilenko et al. 2004), Tabu search (Hiep et al. 2016), and MIP-KMeans (Babaki 2017) were modified to incorporate these changes.

Metric learning approaches are inherently tied to the distance metric upon which they are based. Therefore, modifying them for use with time-series (i.e. difference distance measures) implies the development of novel algorithms to tackle the problem. This was deemed outside the scope of this study. Similarly, it is unclear how probabilistic methods such as the Constrained EM algorithm (Shental et al. 2013) could be modified to use alternative distance measures and averaging techniques as it is not obvious how these would affect the probability estimates needed for their application.

Collaborative approaches offer several means to integrate constraints. In this study the Samarah (Forestier et al. 2010a) algorithm was modified to use pairwise constraints in the collaborative process (detailed in the following subsection) and DTW based k-Means agents.

Of these modified implementations, only a few were found to be suitable to include in the study due to various reasons. The implementation by Wang et al. (2014) is formulated for two class problems (although authors describe how the method can be extended to multi-class problems in their article). That by Cucuringu et al. (2016) was modified but did not converge on all the datasets. Constrained 1-Spectral Clustering (Rangapuram and Hein 2012) and MIP-KMeans (Babaki 2017) were too slow once modified to use DTW and DBA. The implementation of Tabu search is heavily optimised for the Euclidean distance to make it computationally feasible (Hiep et al. 2016) and these efficiencies do not hold when using a similarity measure such as DTW. LCVQE Pelleg and Baras (2007) updates the centroids heuristically using a formulation which does not have an obvious extension to DTW. MPCK-Means (Bilenko et al. 2004) implements metric learning, as such it is intrinsically tied to norm based distance metrics. A declarative approach using ILP (Babaki et al. 2014) is publicly available and was modified, however, it was either too slow (even though it does not require repetitive distance calculations and averaging) or did not converge.

Implementations of these modified algorithms are available from https://sites.google.com/site/tomalampert/code.

4.2 Evaluated algorithms

After modification and initial evaluation, the following algorithms were used in the remainder of this study: COP-KMeans (Wagstaff et al. 2001) (k-Means), Spec (Kamvar et al. 2003) (spectral), CCSR (Li et al. 2009) (spectral), CPClustering (Dao et al. 2017) (declarative), and Samarah (using three k-Means agents) (Forestier et al. 2010a) (collaborative).

These have been reviewed in the previous section but before proceeding to analysing their performance, the manner in which each algorithm uses constraints will first be analysed. This is summarised in Fig. 2a, b. At one end of the spectrum of constraint use (Fig. 2a) is COP-KMeans, which uses constraints to validate assignments, at the other end is CPClustering, which explicitly forms the clusters according to the constraints, and between these two extremes are Spec, CCSR, and Samarah, which determine the assignment of points according to a balance of the information derived from the constraints and the distance measure. From the point of view of constraint satisfaction (Fig. 2b), CPClustering and COP-KMeans are found at the end of the spectrum where constraints are guaranteed to be satisfied, and Spec, CCSR, and Samarah are found at the other end, where there is no guarantee of constraint satisfaction.

Fig. 2

Spectra describing the evaluated algorithms. a Constraint use, b constraint satisfaction

4.2.1 COP-KMeans

COP-KMeans represents the simplest approach for using constraints in the spectrum and is described in Algorithm 1. As with the (unconstrained) k-means algorithm, clustering is performed according to the distance function. The algorithm tries to extend the partial assignment in such a way that all the constraints are satisfied. If the partial assignment cannot be extended, and without a backtracking mechanism, the algorithm fails. In this way COP-KMeans can be considered a heuristic method that tries to enforce the constraints. COP-KMeans is the most involved of the evaluated algorithms to adapt to time-series clustering. It is necessary to integrate the DTW measure in line 4 of Algorithm 1 to calculate the closest clusters for each point, i.e. the cluster centroid with the smallest distance to the point. In addition to this, it is necessary to integrate the DBA algorithm in line 7 to calculate the updated cluster centroids. DBA is a heuristic which aims to minimise the sum of squared DTW distances of the set of time-series and the resulting average sequence. It should be noted that the convergence of k-Means is only guaranteed with the Euclidean distance metric. Since DBA is non-deterministic, this guarantee does not hold, nevertheless, the effects of the non-deterministic averaging process are minimal and therefore on average the cost function decreases at each iteration.

4.2.2 Spec

On the other hand, spectral clustering methods form a balance between the information derived from the distance function and the constraint set, and therefore do not impose a hard requirement for constraints to be fulfilled. The most basic method is that presented by Kamvar et al. (2003), which is described in Algorithm 2. The goal of spectral clustering is to find a partition of the graph defined by the Laplacian matrix (line 6) such that the edges between different groups have very low weights (which means that points in different clusters are dissimilar from each other) and the edges within a group have high weights (which means that points within the same cluster are similar to each other), this is achieved by taking the eigenvalue decomposition of the Laplacian and clustering the rows into ‘blocks’, or clusters, (line 9) (Luxburg 2007). Constraints are integrated by modifying the affinity matrix (lines 3 and 4). As such must-linked points are made more similar than any other pair of points in the data set and therefore their graph edges are weighted maximally, increasing the probability for them to be within the same partition of the graph. Conversely, cannot-linked points are made more dissimilar than any pair of points in the data set and therefore their graph edges are weighted minimally, decreasing the probability for them to be within the same partition of the graph.

The Spec algorithm is adapted for use with the DTW dissimilarity measure by simply constructing the distance matrix (B in Algorithm 2) from the output of the the DTW algorithm, such that

$$\begin{aligned} B_{ij} = \text {DTW}(o_i, o_j). \end{aligned}$$

(3)

4.2.3 CCSR

Rather than modifying the affinity matrix to integrate ML and CL constraints, Li et al. (2009) propose to bias the spectral embedding towards one that is as consistent with the pairwise constraints as possible. This is inspired by the observation that “the spectral embedding consists of the smoothest eigenvectors of the normalised Laplacian on the graph, and adapting it to accord with pairwise constraints will in effect propagate the pairwise constraints to unconstrained objects” (Li et al. 2009). Algorithm 3 describes this process, which constructs a spectral embedding that minimises the cost function

$$\begin{aligned} \mathcal {L}(F) = \sum _{i=1}^{n}\left( \mathbf{y}_i^T \mathbf{y}_i - 1\right) ^2 + \sum _{(i,j) \in \text {ML}} \left( \mathbf{y}_i^T \mathbf{y}_j - 1\right) ^2 + \sum _{(i,j) \in \text {CL}} \left( \mathbf{y}_i^T \mathbf{y}_j - 0\right) ^2 \end{aligned}$$

(4)

via semidefinite programming (SDP), where $F = (\mathbf{y}_1, \dots , \mathbf{y}_n)^T$ is the data representation. The minimum of $\mathcal {L}$ should result in a representation in which objects are close to the unit sphere (the first term), i.e. data is normalised; must-link constrained objects are close to each other (the second term); and cannot-link constrained objects are far apart (the second term).

As with the Spec algorithm, the only change necessary for the algorithm’s application to time-series is to construct the distance matrix B using the DTW measure, Eq. 3.

4.2.4 Samarah

Samarah (Forestier et al. 2010a) iteratively refines the output of multiple clustering agents to promote agreement on their solutions. This process is described in Algorithm 4.

At its core, the algorithm finds conflicts (differences between the output of two agents) and attempts to resolve them. A quality criterion is used to evaluate whether the modifications are relevant or not (line 8 of Algorithm 4). In unsupervised clustering, this criterion is a combination of the similarity between the clusterings and the quality of each clustering, e.g. inertia, the number of clusters, or the cluster size ratio. For semi-supervised clustering, this criterion is extended to ensure that constraints are represented when resolving conflicts and in this way a wide range of background knowledge can be integrated.

It requires a function to be defined that measures the satisfaction of the prior knowledge in agent n’s solution ($\mathcal {R}^n$) on the range [0, 1]. In the case of must-link and cannot-link constraints, the criterion measures the fraction of respected constraints, such that

$$\begin{aligned} Q(\mathcal {R}^n)=\frac{1}{|\text {ML}|+|\text {CL}|} \left( \sum _{(i,j)\in \text {ML}}{v_\text {ML}(\mathcal {R}^c,i,j)}+\sum _{(i,j)\in \text {CL}}{v_\text {CL}(\mathcal {R}^c,i,j)}\right) , \end{aligned}$$

where

$$\begin{aligned} v_{ML}(\mathcal {R}^c,i,j) = {\left\{ \begin{array}{ll} 1, &{}\text {if } o_i \in C^c_k \text { and } o_j \in C^c_{k},\\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} v_{CL}(\mathcal {R}^c,i,j) = {\left\{ \begin{array}{ll} 1, &{}\text {if } o_i \in C^c_k \text { and } o_j \notin C^c_{k},\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

This modification causes a balance between the background knowledge and the distance metric to be sought during conflict resolution, for example a modification that causes a large improvement in either the similarity or the overall quality can be approved even if the fraction of satisfied constraints decreases.

For use in time-series clustering, it is necessary to modify each agent to use the DTW measure. In the case of k-Means agents, the same modifications as those described for the COP-KMeans algorithm are required.

4.2.5 CPClustering

Different from the other methods which are algorithmic, CPClustering is a declarative approach, where problem and constraints are expressed as a constraint optimisation problem (COP). The COP, which can be viewed as the definition of the search space, is then solved using a constraint programming solver. The main principle of constraint programming is to explore the search space using constraint propagation and search. Propagating a constraint c means removing from the domain of the variables involved by c some or all of the values that cannot be part of a solution of c. In this way constraints are used to prune the search space. All the constraints of the COP are propagated until a stable state if found. If in this state, the domain of one variable becomes empty, then the state is a failure and the solver backtracks. If the domain of each variable becomes a singleton, then a solution is reached. Otherwise the solver takes one variables whose domain is not singleton, split its domain to create subproblems and continues proceeding on each subproblem. The choice of variables and the way to create as well as to order subproblems can be defined by a search strategy. For instance, for an optimisation problem with an objective function F to be minimised, a branch-and-bound mechanism is integrated: each time a solution is reached, its objective value f is computed, and the solver backtracks with a new added constraint $F<f$, which enforces that next solution must be better than the current. The last solution found is therefore the best one.

Using constraint programming, CPClustering models a constrained clustering problem as a constraint optimisation problem. The assignment of objects to clusters is modeled by a variable $G_i$ for each object $o_i$. The domain of each variable $G_i$ is the set $\{1,\ldots ,K\}$, so an assignment $G_i=c$ means that object $o_i$ is grouped into cluster c. A complete assignment of all the variables $G_i$ therefore defines a partition. To break symmetries between partitions, other conditions are imposed using CP constraints:

• the first object must be in the first cluster,

• an object $o_i$ is assigned to a new cluster c iff cluster $c-1$ contains an object $o_j$ such that $j<i$.

In this model, must-link and cannot-link constraints are expressed in a natural way. A must-link constraint on two objects $o_i$, $o_j$ is expressed by the constraint $G_i=G_j$, a cannot-link constraint is expressed by $G_i\ne G_j$. CP solvers are extendable, which means new constraints along with their propagation algorithm can be added. Exploiting this advantage, CPClustering is reinforced with new and dedicated constraints for the principal clustering objective function (Dao et al. 2017). For instance, for a clustering problem that minimises the maximal diameter of the clusters, a variable D is introduced in the model. This variable represents the maximal diameter of the clusters. Therefore, any two objects $o_i$, $o_j$ whose distance is larger than D must be in different clusters. This is expressed by the relation

$$\begin{aligned} \forall \ i,j\in \{1,\ldots ,N\},\quad d(o_i,o_j)>D \longrightarrow G_i\ne G_j, \end{aligned}$$

which is encapsulated by a new constraint $\text {diameter}(D,G,d)$. In this relation, the distance measure between objects are represented by d. This distance measure can be either Euclidean or DTW, therefore CPClustering can be used with both without modification (by pre-computing the distance matrix, e.g. Eq. 3).

By the principle of constraint programming, all the must-link and cannot-link constraints are satisfied by the returned solution.

4.3 Methodology

Several datasets were chosen to evaluate the algorithms so that they represent typical time-series clustering problems. The UCR repository (Chen et al. 2015) is a standard repository that enables comparative results to be published. A subset of the repository that have a large number of samples and a moderate number of classes were chosen to reflect the characteristics of challenging problems and are described in Table 2.

Table 2 Subset of the UCR repository used for experimentation

Constraints were generated by taking pairs of points randomly and generating a must-link or cannot-link constraint depending upon whether they belonged to the same class or not. Different sizes of constraint sets were considered: 5, 10, 15, and $50\%$ of the number of points N in the dataset (they represent a very small fraction of the total number of possible constraints, which is $\tfrac{1}{2}N(N-1)$). Ten repetitions of each constraint set size were generated, as such each experiment was repeated ten times, each with a different random subset of constraints (all algorithms are evaluated using the same random constraint sets). Finally, the algorithms were executed with no constraints for comparison.

Because these algorithms are applied as semi-supervised approaches, reference data in the form of training or validation sets do not exist and therefore optimising parameter values proves difficult. This does not pose too much of a problem for k-Means based algorithms (COP-KMeans and Samarah’s agents) because the cost function under DBA globally decreases (or remains the same) at each iteration, and therefore choosing a sufficiently large number of iterations mitigates the problem (in these experiments a value of 100 was taken). The same approach cannot be taken for spectral approaches (Spec and CCSR), however, as their parameters ($\sigma$ in Equation (2) and the number of eigenvectors) need to be specifically chosen for each problem. Unfortunately, these cannot be intuitively selected and the algorithm’s performance is highly dependent upon these values (Ng et al. 2001). To enable the spectral methods to be included in the study, the unrealistic use case was chosen in which these parameters were optimsed by grid search on the training sets included in the UCR datasets with 5% constraints. To determine the value of the constraints the same parameter values were used for each constraint size (including unconstrained). Being parameter free, the CPClustering is the only method that can be applied without these considerations.

All samples were normalised to have unit length. The adjusted Rand index (ARI) (Hubert and Arabie 1985) and constraint satisfaction (Sat.) metrics are used to evaluate performance. The presented results represent the mean of ten repetitions of each experiment (each with a different random set of constraints) and are rounded to three decimal places.

Finally, to measure the amount of agreement between the underlying objective function and search bias of the algorithms and the constraints, the algorithms were evaluated with no constraints (i.e. unconstrained) and then the fraction of satisfied constraints was determined using the $50\%$ constraint sets. This is referred to as consistency or Con.—the inverse of inconsistency (Wagstaff et al. 2006) or informativeness (Davidson et al. 2006)—and measures the constraints that an algorithm is able to correctly determine using its default bias.

4.4 Results

As a sanity check, the effect of the distance measure on cluster (as defined by the ground truth) distribution was evaluated using the mean silhouette score (Rousseeuw 1987). This score varies between $-1$ and 1 and evaluates cluster overlap such that

$$\begin{aligned} s(i) = \frac{b(i)-a(i)}{\max \{a(i),b(i)\}}, \end{aligned}$$

(5)

where a(i) is the average dissimilarity of point i with all other points within the same cluster and b(i) is the lowest average dissimilarity of point i to each of the clusters to which it is not assigned. This can be averaged over all points in a dataset to calculate its silhouette score. Higher scores indicate that points belong to clusters in which the other points are similar, and are dissimilar to the points in the next closest cluster. The results, which are presented in Table 3, show that the DTW measure results in clusters that are more distinct than those obtained when using the Euclidean distance measure in five out of the nine datasets. The mean difference in scores when DTW results in more separated clusters is 0.122, compared to 0.027 with Euclidean. Therefore DTW, in general, results in more separated clusters. It should be noted that DTW was used without a locality constraint, which can speed up its calculation and increase performance on unseen data (Lines and Bagnall 2015); however, adding this constraint introduces an additional parameter.

Table 3 Silhouette scores of the time-series datasets (test sets)

The unconstrained performance of the algorithms is presented first to determine a baseline. These results are presented in Appendix A, Table 8, in addition to their consistencies, in Table 9. It is seen that Spec outperforms all other algorithms in most datasets, sometimes by large margins, e.g. ECG5000 and UWaveGestureLibraryAll. The overall ranking of algorithms in terms of how many datasets (in parentheses) in which they achieved the highest ARI is: Spec (7), COP-KMeans (2), CCSR (0), Samarah (0), and CPClustering (0). It is also found that it is the most consistent of all the algorithms. The overall ranking of algorithms in terms of how many datasets (in parentheses) they achieved the highest consistency is: Spec (6), COP-KMeans (2), CCSR (1), Samarah (0), and CPClustering (0).

Due to the added computational complexity of integrating DTW and DBA into COP-KMeans and Samarah’s underlying k-Means algorithms, not all of the experiments completed within a reasonable amount of time, the absence of these results are marked by a dash in the tables. These datasets represent the longest of the evaluated time-series. Furthermore, several constraint sets iterations resulted in a constraint violations during the COP-KMeans clustering process and these results are marked in the tables (with the number of completed iterations mentioned in the table caption).

The mean ARIs and Constraint Satisfaction results for the constrained clustering experiments are presented in Appendix A, Tables 10, 11, 12, 13, 14, 15, 16, 17 and 18 and are summarised in Tables 4 and 5.

Table 4 ARI difference between unconstrained clustering and constrained clustering (Constrained ARI–Unconstrained ARI) for each constraint fraction averaged over all datasets, standard deviations in parentheses

The Spec algorithm outperforms all other algorithms in five of the datasets in each constraint fraction. This is unsurprising because it outperforms all other algorithms in five datasets in the unsupervised setting, indicating that it has a strong baseline performance. Analysing the average ARI changes (Constrained ARI–Unconstrained ARI) for each algorithm for each constraint fraction (Table 4) reveals that not all algorithms benefit from the introduction of constraints. CCSR benefits the most, resulting in an $\sim 0.262$ increase in ARI performance. Interestingly, adding more constraints does not directly result in an increase in average ARI. In some cases (Spec and CPClustering), adding constraints leads to a small decrease in ARI; however, all of the standard deviations are greater than the change in ARI. Taking CCSR as an example, in six of the datasets (ECG5000, FacesUCR, MALLAT, TwoPatterns, UWaveGestureLibraryX, and UWaveGestureLibraryAll) a large increase in ARI and an associated increase in constraint satisfaction is observed, indicating that the algorithm has benefited from the additional information. In the remaining datasets, however, either no increase or a decrease is observed. CPClustering and COP-KMeans, on the other hand, guarantee full constraint satisfaction, resulting in a large increase in constraint satisfaction from the unconstrained case, however, this is not associated with significant increases in ARI and in some cases a decrease. This indicates that these algorithms focus on correctly clustering the points bound by constraints at the expense of correctly clustering the remaining data. It is therefore clear that simply adding constraints does not always lead to an increase in performance for all algorithms and all datasets, instead several influencing factors seem to be at play.

Table 5 Constraint satisfaction difference between unconstrained clustering and constrained clustering (Satisfaction–mean consistency) for each constraint fraction averaged over all datasets, standard deviations in parentheses

5 Discussion

This section offers further analysis of the results and discusses implications that arise from them.

5.1 Analysis of the results

A multiple linear regression analysis was performed to uncover the factors that influence the change in clustering performance when constraints are introduced. Several parameters that could influence the change in clustering performance were identified:

• Consistency when an algorithm tends to satisfy constraints using its default bias (i.e. unconstrained clustering), adding constraints should not considerably affect clustering performance;

• Silhouette score when the clusters in a dataset overlap, adding constraints should lead to an increase in clustering performance;

• Unconstrained ARI when an algorithm has a high baseline performance in unconstrained clustering, the benefit of constraints should be diminished;

• Algorithm certain algorithms may benefit from the introduction of constraints more than others.

Each algorithm’s mean unconstrained ARI performance was subtracted from its constrained ARI performance samples, which formed the dependent variable of the analysis (1782 samples in total). The categorical predictor representing the algorithms was encoded by dummy variables and the remaining predictors were mean centred to allow interpretation of the intercept as the base group (the Spec algorithm). An initial correlation analysis revealed that Consistency and Unconstrained ARI are strongly correlated ($r=0.724$ and $p=6.533\mathrm {e}{-289}$, the significance threshold was set at 0.01). As Consistency is a pairwise measure of the performance in a subset of the data, while ARI is a pointwise measure of performance for the whole dataset they both capture similar information and therefore Unconstrained ARI was removed from the analysis.

The result of the regression analysis is presented in Table 6 and the added variable plot for the model is presented in Fig. 3. The model has a root-mean-squared error (RMSE) of 0.125, $R^2=0.549$, Adjusted $R^2=0.548$, F-Statistic$~=360$, and $p=1.020\mathrm {e}{-302}$ (significance threshold was set at 0.01). As is intuitive, consistency has a large negative influence on ARI difference, indicating that, when all other factors remain constant, the higher consistency an algorithm has in an unsupervised setting, the less increase in ARI will result when adding constraints. This corroborates that which was found by Wagstaff et al. (2006). This analysis, however, uncovers additional facets to the problem. It was found earlier that certain algorithms react more favourably to the introduction of constraints, Spec and CPClustering negatively and CCSR and Samarah positively. Unexpectedly, however, the dataset’s silhouette score has a moderate positive correlation with ARI difference. This may be explained by considering what happens when a point that is subject to an ML constraint is surrounded by points belonging to another cluster (i.e. has a low, or negative, silhouette score). An algorithm is biased to cluster the ML constrained points together. This may, however, also have the effect of biasing any points similar to (therefore close to) a point linked by an ML constraint to be assigned to the same cluster, which in a dataset with a low silhouette score is more likely to be an incorrect assignment.

Table 6 ARI difference multiple linear regression coefficients (significance threshold was set at 0.01)

Fig. 3

Added variable plot for the whole model (Color figure online)

5.2 Constraint influence

It has been discussed that adding the maximum number of constraints does not necessarily lead to an increase in clustering accuracy. This implies that it is necessary to consider methods to measure the usefulness of constraints to determine whether they should be included or not. These measures fall into two categories, those that are dependent upon the clustering algorithm, and those that are not.

Davidson et al. (2006) demonstrate that constraints improve performance when they are both informative (algorithm dependent) and coherent (algorithm independent).

5.2.1 Algorithm dependent measures

In the case of algorithm dependent measures, Wagstaff et al. (2006) show that there is a strong negative correlation between inconsistency (also referred to as informativeness (Davidson et al. 2006)) and accuracy. Inconsistency is defined as “amount of information in the constraint set that the algorithm cannot determine on its own” (Davidson et al. 2006) and has been measured in this study as consistency (the inverse of inconsistency). In the experiments presented herein a negative correlation between ARI difference and consistency has been found and it is true that, in general, when a high consistency is found, adding constraints does not improve performance (or sometimes decreases performance)—for example, see Table 10 Spec; Table 11 Spec, CCSR, and Samarah; Table 12 Spec, CCSR, and Samarah—and when a low consistency if measured, performance increases—for example, see Tables 10, 15, and 16 CCSR.

5.2.2 Algorithm independent measures

Measures in the second category attempt to quantify the amount of information contained within a set of constraints independent of the clustering algorithm and are therefore dependent upon the distance measure used. Coherence is one such measure, which quantifies “the amount of agreement between the constraints themselves, given a metric that specifies the distance between points” (Davidson et al. 2006).

To measure coherence, vectors are constructed between two points that are joined by ML and CL constraints. The constraints are coherent if the vectors are orthogonal to each other, and incoherent if they are parallel (and overlap). This is a useful measure when considering the Euclidean distance metric, however, it is not obvious how this concept can be extended to DTW, which does not define vector projection, and therefore new measures to quantify the usefulness of constraints should be developed and is an open research question.

Table 7 Average ML distance to average CL distance ratio and constraint coherence measured in 2D multi-dimensional scaling representations

We must instead indirectly measure some of the properties of the constraint set in order to gain some insight into the effect of using DTW. Table 7 presents the following measures, taken when using Euclidean distance and DTW dissimilarity:

• ML/CL Dist. Ratio—the ratio of the average distance between must-link pairs and cannot-link pairs, a value less-then one means that ML pairs are closer together then CL pairs;

• MDS Coherence—the constraint coherence (Davidson et al. 2006) measured within a two dimensional multidimensional scaling (MDS) (Kruskal 1964) representation of the distance matrix.

It is unlikely that the MDS representations of the distance matrices capture the necessary aspects of the original space in which the time-series exist (vector angles, exact point distances, etc.) to directly measure constraint coherence. These measurements should therefore only be used to observe any trends that become apparent in order to understand the dissimilarity measure’s effect on constraints. Furthermore, embedding DTW dissimilarities into a Euclidean space will be less accurate than when embedding Euclidean distances. The figures in Table 7 represent the average of the measures taken over all 40 constraints sets generated in the previous section.

The method for calculating constraint coherence that exists in the literature (Davidson et al. 2006) was found to miss some of the cases when constraints overlap, and therefore a new formulation was developed. This is presented in Appendix B and follows the principle of the original description (Davidson et al. 2006).

It is clear that in five out of the nine datasets, the ML/CL distance ratio is lower when using DTW than when using Euclidean distance, in one dataset it is the same, and in three datasets Euclidean is lower but the differences are very small in comparison. This trend is mirrored when analysing the MDS coherences, the DTW measure increases constraint coherence when compared to the Euclidean distance in all but two of the datasets. In addition to the 2D MDS results presented in Table 7, the experiments were repeated using 3–10 dimensional representations and the same relative results were found in all cases except that DTW resulted in the highest coherence in the InsectWingbeatSound dataset when more than three dimensions were used. The trend of these results is in line with the silhouette scores presented in Table 3: the datasets with the largest differences in DTW’s favour are those in which the constraints appear to be most faithfully represented.

To illustrate the data behind these figures, the dataset in which DTW has the most effect on the constrained points is presented in Fig. 4. It clearly shows that when using the DTW distance, points under must-link constraints are more clustered (Fig. 4a) when compared to the Euclidean embedding (Fig. 4b), in fact in the Euclidean embedding there is no distinction between clusters of points having the same label. This is confirmed when analysing the cannot-link constraints, they clearly define separate clusters when using the DTW similarity measure (Fig. 4c) and when using the Euclidean distance they are randomly distributed (Fig. 4d).

Fig. 4

Constraints represented by the point distances embedded in 2D space using multidimensional scaling. The original distance matrices were calculated using DTW (a) and (c), and Euclidean (b) and (d). a DTW: must-link constraints, b Euclidean: must-link constraints, c DTW: cannot-link constraints, d Euclidean: cannot-link constraints (Color figure online)

5.3 Challenges

This study has focused on using constraints in time-series clustering, however, there exists numerous challenges related to capturing these constraints. For example, it is necessary to study and detail the thematic constraints (i.e. the opinions of the expert) that have to be captured to guide the process.

These thematic constraints can be extremely broad and have to be translated into actionable constraints. In the current state of knowledge, a limited number of actionable constraints into which thematic constraints can be translated exist: ML, CL, label, number of clusters k, and size. The following observations are therefore translatable: “these two objects seem to be of the same nature”; “these two ensembles of objects are of the same nature” (ML constraints between all the pairs of objects of the two sets); “these three sets are completely different” (CL constraint on all the pairs of objects from the three sets); “this object is of type X” (labeling constraint); and “a cluster cannot represent more than 20% of the data” (cluster size constraint).

Nevertheless, generating actionable constraints from a set of data points can rapidly lead to a significant increase in both combinatorial complexity and the scope of the constraints. For example, a constraint “of the same nature” on two sets of size $N_1$ and $N_2$, will generate $\frac{1}{2}(N_1(N_1-1) + N_2(N_2-1)+N_1N_2)$ ML constraints. Resulting in a very large number of constraints, which could prevent the use of declarative methods. Another example is a constraint that states two sets of size $N_1$ and $N_2$ are “of different nature”. Depending on the context this constraint can correspond to a disjunction of several sets of constraints.

The following two problems are therefore identified. For each problem we give some direction on how it can be tackled.

• How should algorithms be modified to enable them to deal with large constraint sets?

  • Reduce the size of the model by limiting the number of considered objects, for example by sampling and/or by identifying irrelevant objects.

  • Relax the optimality of the solution using a threshold on the execution time (with no guarantees of the quality of the final result).

  • Using local search instead of global search.

• How can the number of constraints be reduced or limited without loss of quality (i.e. define a minimal set of constraints)?

  • Sample the constraints and/or sample the objects under constraint.

  • Identify informative constraints (some progress has been made in this direction, as discussed in the previous subsection).

6 Conclusions

To recapitulate, this manuscript has presented a background of constrained clustering in relation to time-series clustering. A comprehensive review of general constrained clustering algorithms has been presented and several publicly available implementations were modified to use the DTW dissimilarity measure and DBA averaging method. A comparative study of these approaches applied to publicly available data has been conducted and the results analysed. This investigation has been concluded by a discussion of the issues raised.

It has been shown that integrating DTW and DBA averaging method allows classic constrained clustering algorithms to be effectively used for time-series. Nevertheless, the lack of backtracking in COP-KMeans means that if a constraint violation is unavoidable in the current iteration the algorithm fails, a problem that becomes more pronounced as more constraints are added. Furthermore, when iterative algorithms are in question, the execution time can become prohibitive when long time-series are to be analysed. Methods that take a distance-matrix as their input (such as spectral clustering and declarative approaches) are more effective in this case. Within these methods, spectral algorithms offer superior performance, however, this is dependent upon the correct choice of parameter values, which is not possible in a semi-supervised setting. Declarative approaches are easier still, having no parameters and omit the need of calculating cluster centers, and therefore expensive averaging computations, however, performance is lacking. In terms of constraint satisfaction, both COP-KMeans (if a solution is returned) and CPClustering guarantee to fulfill all the constraints.

By analysing the results of applying the modified algorithms to time-series datasets, several factors that influence the effectiveness of constraints have been identified, namely coherence and cluster overlap. These results have highlighted the need for measures of constraint usefulness. The current definition of constraint coherence, which may indicate whether a constraint set will increase performance or not, is dependent of the distance measure used and cannot be extended to metrics without a definition of orthogonality (e.g. DTW). Furthermore, links between cluster overlap and ARI offer new directions of research.

Appendices

Appendix A: Full metric scores

See Tables 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18.

Table 8 Unconstrained mean ARI

Table 9 Mean consistency (measured using 50% constraint sets)

Table 10 Performance on ECG5000

Table 11 Performance on ElectricDevices

Table 12 Performance on FacesUCR

Table 13 Performance on InsectWingbeatSound

Table 14 Performance on MALLAT

Table 15 Performance on StarLightCurves

Table 16 Performance on TwoPatterns

Table 17 Performance on uWaveGestureLibraryX

Table 18 Performance on UWaveGestureLibraryAll

Appendix B: Constraint coherence

As described in Davidson et al. (2006): “We consider all constraint pairs composed of an ML and a CL constraint (pairs composed of the same constraint type cannot be contradictory). To determine the coherence of two constraints, a and b, we compute the projected overlap of each constraint on the other”.

Let $\mathbf {a}$ and $\mathbf {b}$ be vectors connecting the points constrained by a, i.e. $(a_1,a_2)$, and b, i.e. $(b_1,b_2)$, respectively. We first project the points bound by constraint a onto the line that is defined by the points bound by constraint b, such that

$$\begin{aligned} a'_1= & {} ((a_1 - b_1) \cdot \mathbf {e}) \mathbf {e} + b_1,\\ a'_2= & {} ((a_2 - b_1) \cdot \mathbf {e}) \mathbf {e} + b_1, \end{aligned}$$

where

$$\begin{aligned} \mathbf {e} = \frac{\mathbf {b}}{|\mathbf {b}|}. \end{aligned}$$

The points $a'_1$, $a'_2$, $b_1$, and $b_2$ now all exist in the 1D space described by the basis vector $\mathbf {e}$, and as such are projected into this 1D space, such that

$$\begin{aligned} a''_i = a'_i \mathbf {e}, \quad b''_i = b_i \mathbf {e}, \quad \text {where }\ i \in \{1,2\} . \end{aligned}$$

The 1D points of each constraint are then sorted such that $a''_1 \le a''_2$ and $b''_1 \le b''_2$. With this assumption satisfied, the overlap of constraint a on constraint b becomes

$$\begin{aligned} o_a^b = \max \left\{ 0, \min \{a''_2,b''_2\} - \max \{a''_1, b''_1\}\right\} . \end{aligned}$$

Two constraints are coherent if there is no overlap between them, such that

$$\begin{aligned} \text {coh}_{cm} = {\left\{ \begin{array}{ll} 1, \quad \text {if }\ o_c^m = 0\ \text { and }\ o_m^c = 0,\\ 0, \quad \text {otherwise,} \end{array}\right. } \end{aligned}$$

and the coherence of a set of constraints is defined to be the fraction of coherent constraints within the set, such that

$$\begin{aligned} \text {COH}(C) = \frac{\sum _{c \in C_{\text {CL}}, m \in C_{\text {ML}}}\text {coh}_{cm}}{|C_{\text {CL}}||C_{\text {ML}}|}. \end{aligned}$$