1 Introduction

Following the 2008 launch of Bitcoin by Satoshi Nakamoto, additional cryptocurrencies, including Ethereum, have emerged. Due to their spectacular market capitalization increase, referred to as (ElBahrawy et al., 2017), these digital assets now have a significant impact on the global financial landscape, attracting the attention of investors, regulators, public institutions, and the academic community. Cryptocurrencies exhibit heteroscedasticity, just like traditional financial time series, making it difficult to forecast their volatility, a crucial component of risk management.

The existing models of estimating and forecasting realized volatility can be mainly divided into two categories: statistical models and machine-learning models. It is known that the selection of parameters such as training set size, the type of window, and window size affect the forecasting performance in both models (Di-Giorgi et al., 2023). Additionally, it has been determined that using different RV measures affects the accuracy of volatility forecasting (Chen & Jin, 2023). The reason for selecting MedRV as an alternative to RV, as also noted by (Andersen et al., 2012), is its finite-sample robustness for jumps and small returns.

Furthermore, concerning the robustness of the models, it has been observed that the choice of training set size affects the forecasting performance in both the GARCH-type and machine learning models (Souto & Moradi, 2024). Another important issue in forecasting volatility is the preference for popular rolling and expanding windows. In this study, not only has the effective rolling window approach for addressing structural changes in the dataset been considered but also the expanding window approach, which effectively employs the information from all observations using the entire available data. Although both approaches have their unique advantages, it has been observed that different studies such as (Zhang et al., 2020; He et al., 2021) and (Gillitzer & McCarthy, 2019) choose different approaches. Besides using different forecasting window types, the literature also shows that the selection of forecasting window size leads to different forecasting performances (Inoue et al., 2017; Li et al., 2023).

In studies (Khaldi et al., 2019; Amirshahi & Lahmiri, 2023), comparing the forecasting performance of GARCH-type models with machine learning models in volatility forecasting, a limited number of GARCH-type models were considered and their performance was examined under specific error distributions. The difference between this and other studies on volatility forecasting is that it considers not only the performance of 11 different GARCH-type models using six different error distributions, but also compares the predictive power of deep learning models. This allows for investigation of more models, and the examination of the effect of many different parameters on the forecasting accuracy of the models during the modeling and forecasting processes. However, this study is limited on three fronts. The first concerns how investors and academics decide on the selection of different parameters in the process of modeling volatility. From the forecasting perspective, the models with different parameter configurations may provide different forecasting outcomes. The second limitation concerns the financial markets, especially those dealing with cryptocurrencies like Bitcoin, Ethereum, and Binance Coin, which are very volatile and affected by multiple external factors. Unexpected events or sudden market changes may impact the accuracy of volatility forecasts which might not have been captured. To overcome this limitation and achieve more accurate forecasts, the rolling window approach has been used to capture the structural changes. The final limitation concerns the selection of data with different characteristics. The key parameters can change the forecasting results when using other financial instruments. To address this shortcoming, the returns on three different cryptocurrencies have been used.

This study contributes to the existing academic literature in three ways. First, it finds that GARCH-type models with heavy-tailed distributions can adjust well to volatility changes in three cryptocurrency prices and provide better forecast accuracy in all error metrics than the assumption of normality for errors. Second, the sensitivity of GARCH-type models and deep learning models to various parameters, such as test and training sizes, window type, window size, measures of RV, and error measure selection, provides valuable insights. This can make it easier for practitioners and academicians to comprehend how robust the predictive performance of the models is in different scenarios. Finally, using two different methods to calculate RV to test the forecasting abilities of 11 GARCH-type models with different error distributions and deep learning models gives different results, depending on the error metrics used. This range of evaluation metrics provides a way for the forecasters to understand how accurately the models forecast volatility patterns.

The remainder of the paper is organized as follows. Section 2 reviews the literature. Section 3 describes the data and methodology. Section 4 presents the empirical results and discusses the main results. Section 5 concludes the paper and outlines the future work.

2 Literature

Empirically, the volatility of cryptocurrency returns has emerged as an ongoing and significant topic in financial literature. The volatility dynamics of cryptocurrencies, especially Bitcoin, have been extensively examined, as is evident in the literature. The majority of studies in the literature currently focus on analyzing Bitcoin, while limited research targets other cryptocurrencies. It is essential to note that other digital currencies play a significant role as speculative assets.

GARCH-type models, such as GARCH (Gronwald, 2014), Threshold GARCH (TGARCH) (Bouoiyour & Selmi, 2015, 2016), and Exponential GARCH (EGARCH) (Dyhrberg, 2016), were employed to model and forecast Bitcoin’s volatility. In a similar vein, Bouoiyour and Selmi (2016) compared various GARCH-type models and recommended using asymmetrical TGARCH models. In the study by Maciel (2021), the one-, five-, and ten-steps ahead forecasts for the volatility of six leading digital coins were conducted. It was concluded that the MS-GARCH model exhibited good forecasting accuracy.

Panagiotidis et al. (2022) stated that the MS-GARCH model exhibited superior prediction accuracy compared to standard GARCH models in forecasting cryptocurrency volatility. Moreover, the significance of the EGARCH model was emphasized through the internal evaluation of the GARCH models. After researching forecasting Bitcoin price volatility, Bergsli et al. (2022) concluded that the EGARCH and APARCH models performed better. The study by Kumar et al. (2024) demonstrated that among GARCH models, the IGARCH model had the best forecasting performance for Bitcoin volatility. Fung et al. (2022) found that the asymmetric GARCH models with heavy-tailed distributions have the best goodness-of-fit properties among 254 cryptocurrencies. Naimy et al. (2021) found that different GARCH models showed varying levels of performance in forecasting the volatility of six cryptocurrencies depending on the specific cryptocurrency used.

Conversely, machine learning methodologies have been extensively used across various domains, including the forecasting of cryptocurrency prices. Although GARCH models are still the most often used model for volatility forecasting, deep learning algorithms are becoming more popular as effective and reliable alternatives. When considering machine learning models, the Artificial Neural Networks (ANN) model has been employed for forecasting financial markets by using the lags as inputs (Adhikari & Agrawal, 2014; Lahmiri, 2016, 2018; Lei, 2018). Phaladisailoed et al. (2018) have forecasted Bitcoin prices using machine learning models and deep learning methods. Recently, Akyildirim et al. (2021) has employed various machine learning methods, including support vector machines (SVM), logistic regression, ANN, and random forest, to forecast cryptocurrency returns. Mallqui and Fernandes (2019) employed the ANN and SVM models, with the findings indicating that the SVM model outperformed in out-of-sample forecasting. García-Medina and Aguayo-Moreno (2024) have shown that among GARCH models and deep learning models, multilayer perceptron (MLP) models provide the best predictive results. The study by Murray et al. (2023) investigated the forecasting performance of deep learning models for forecasting cryptocurrency prices. Their results showed that the LSTM model had the best forecasting performance for all the cryptocurrencies used.

The literature indicates that different methodologies exhibit varying degrees of superiority when analyzed in the context of modeling and forecasting price volatility. The main cause of this variation is attributed to the dynamic parameter selection made during the studies’ analyses.

3 Data and Methodology

3.1 Data

In this study, data from three cryptocurrencies, namely Bitcoin, Ethereum, and Binance Coin, were utilized. As of the data acquisition date, which was in December 2021, these cryptocurrencies were among the top three in terms of market capitalization. The closing prices of these cryptocurrencies were obtained through the Binance application programming interface (API) using the Python programming language. Two datasets were downloaded for each cryptocurrency, one containing daily data and the other containing five-minute data. While the five-minute data was solely used to calculate realized volatility, the daily data was used to construct a return series, and the models were applied using this series. The formula used to calculate the return series is provided below, where \(p_t\) represents the value of the daily closing price at time t.

$$\begin{aligned} r_t=\ \log {\left( \frac{p_t}{p_{t-1}}\right) } \end{aligned}$$
(1)

The data used in the study were divided into two separate sets: training and testing. The models were trained on the training set, and their prediction performance was measured on the testing set. To investigate whether the prediction performance varied with different dataset sizes, three different train-test ratios were employed: 70:30, 80:20, and 90:10. The number of observations in both the training and testing sets for each dataset, along with other details, is further explored in this section.

Table 1 Descriptive statistics of three cryptocurrency datasets
Full size table

For the case of Bitcoin, the daily closing prices from 18th August 2017 to 31st December 2021 were used. Figure 1 is a graph of this series. Upon examination of the graph, it can be seen that Bitcoin’s price remained relatively stable until the end of 2020, after which it exhibited an increasing trend. It can also be noted that its volatility was relatively high.

Fig. 1
figure 1

The plot of the Bitcoin price series

Full size image

In the context of Bitcoin, the 70:30 train-test ratio results in 480 observations in the testing set, the 80:20 ratio results in 320 observations, and the 90:10 ratio results in 160 observations.

Table 1, presents the descriptive statistics of the datasets used in the study. For Bitcoin, given that the mean values for both daily and five-minute data are greater than their respective median values, and the positive skewness coefficients, it can be inferred that these distributions are right-skewed. The positive skewness values indicate that these distributions are more peaked compared to a normal distribution. Furthermore, the returns exhibit a positive mean. The negative skewness coefficient and the high kurtosis coefficient indicate that the distribution properties commonly observed in financial time series are also applicable to Bitcoin.

Line and histogram graphs of the returns are provided in Figs. 2 and 3. The line graph illustrates that times of high volatility are followed by high volatility and, similarly, times of low volatility are followed by low changes. This clustering of volatility is a characteristic feature often observed in financial time series and is a positive sign that the series can be modeled using a GARCH model.

Fig. 2
figure 2

Histogram of Bitcoin return series

Full size image
Fig. 3
figure 3

The plot of Bitcoin return series

Full size image

The data for Ethereum covers the period from 17th August 2017 to 31st December 2021. The line graph of Ethereum’s price, as shown in Fig. 4, indicates that it reached a peak in early 2018, followed by a decline until early 2019. Similar to Bitcoin, Ethereum exhibited a relatively stable trend until the end of 2020, after which it began an upward trend.

Fig. 4
figure 4

The plot of the Ethereum price series

Full size image
Fig. 5
figure 5

Histogram of Ethereum return series

Full size image
Fig. 6
figure 6

The plot of Ethereum return series

Full size image

The number of observations in the testing set for Ethereum, at 70:30, 80:20, and 90:10 train-test ratios, mirrors the same values as the Bitcoin dataset: 480, 320, and 160, respectively.

Similar to Bitcoin, the mean values of the price series exceed their respective medians, and the positive skewness and kurtosis coefficients suggest that Ethereum’s price distribution is right-skewed and peaked. The return series for Ethereum shares similarities with Bitcoin in terms of mean returns. However, the standard deviation of Ethereum’s returns is larger than that of Bitcoin. The Ethereum return distribution also exhibits a thick-tailed characteristic.

Figures 5 and  6 present line and histogram graphs of the Ethereum return series. The line graph illustrates volatility clustering, while the histogram reflects the sharpness of the distribution and the length of the left tail, consistent with financial time series characteristics.

The third and final cryptocurrency used in the study was Binance Coin, with daily closing prices covering the period from 6th November 2017 to 31st December 2021. The line graph in Fig. 7 depicts its price behavior, showing a similar pattern to the other two cryptocurrencies, with a relatively stable trend until late 2020, followed by an increasing trend.

Fig. 7
figure 7

The plot of the Binance Coin price series

Full size image
Fig. 8
figure 8

Histogram of Binance Coin return series

Full size image
Fig. 9
figure 9

The plot of Binance Coin return series

Full size image

The testing set for Binance Coin consists of 455 observations at a 70:30 ratio, 303 observations at an 80:20 ratio, and 152 observations at a 90:10 ratio. The mean values of the price series exceed their respective medians, and the positive skewness and kurtosis coefficients suggest that Binance Coin’s price distribution is right-skewed and peaked. However, the return series for Binance Coin differs from the other datasets, as it exhibits larger mean and standard deviation values. Additionally, Binance Coin has the largest difference between its maximum and minimum values. The skewness coefficient suggests that this distribution is right-skewed, contrary to the others.

Figures 8 and  9 display line and histogram graphs of Binance Coin’s return series, showing volatility clustering similar to Bitcoin and Ethereum. The process of empirical research discussed in Fig. 10 is summarized to better understand the impact of different parameters adapted during the modeling phase of datasets on the forecasting performance of the models.

Fig. 10
figure 10

Research Architecture

Full size image

3.2 The GARCH Models

In the study by Engle (1982), volatility is modeled as a function of past errors using the United Kingdom inflation series. With the ARCH model introduced in this work, the volatility was modeled as not constant but varying depending on past values. The return series of a financial asset can be calculated as follows:

$$\begin{aligned} r_t = \mu + \varepsilon _t \ \end{aligned}$$
(2)

The error term \(\varepsilon _t\) can be expressed as the product of the time-dependent standard deviation term \(\sigma _t\) and the stochastic term \({z}_t\):

$$\begin{aligned} \varepsilon _t = \sigma _t {z}_t \ \end{aligned}$$
(3)

Here, \({z}_t\) is a random variable with a zero mean and unit variance. The conditional variance is given in Eq. (4):

$$\begin{aligned} \sigma _t^2 = \omega + \sum _{i=1}^{p} \alpha _i \varepsilon _{t-1}^2 \ \end{aligned}$$
(4)

This formulation represents the equation of the ARCH model. In this equation, when \(\omega > 0\) and \(\alpha _i \ge 0\), the condition for the positivity of variance is satisfied. The ARCH model is effective in capturing volatility clustering.

In the study by Bollerslev (1986), the GARCH model was introduced by incorporating lagged values of conditional variance into the ARCH model. The superiority of this model over the ARCH model lies in its ability to model autocorrelation in the series with fewer parameters.

In this study, 11 different versions of the GARCH model were employed. The equations for the utilized GARCH models are provided in Table 2.

In a standard GARCH model, the assumption that the error term follows a normal distribution may not always hold true, given the characteristic features such as fat tails, high kurtosis values, and skewness, often observed in financial time series. To address this limitation, alternative distributions like the student-t distribution (std) or the generalized error distribution (ged) have been considered (Bollerslev, 1987; Nelson, 1991). This study aims to identify the most suitable distribution for the error terms in GARCH models by exploring six different distributions: normal distribution (norm), skewed normal distribution (snorm), student-t distribution, skewed student-t distribution (sstd), generalized error distribution, and skewed generalized error distribution (sged).

Table 2 The equations of GARCH models
Full size table

3.3 Deep Learning Models

3.3.1 Artificial Neural Networks

ANN is a machine learning method that was inspired by the human brain and has gained popularity over time. It was initially proposed in the study by McCulloch and Pitts (1943) as a non-parametric model. A single-hidden-layer ANN can approximate any linear or non-linear continuous function (Hornik et al., 1989), making it widely used in solving classification, prediction, regression, and pattern recognition problems across various fields such as medicine, engineering, physics, biology, finance, marketing, and more.

The artificial neurons in an ANN exhibit similarities to biological neurons. In a biological neuron, the dendrites receive signals. Subsequently, these signals are sent to the cell body for processing. When the stimulation surpasses a certain threshold, the signal is transmitted to the next neuron through axons. In an artificial neuron, this threshold is modeled with the help of an activation function. Various functions, such as linear, sigmoid, hyperbolic tangent, or rectified linear units, can be selected as activation functions. The perceptron model, introduced by Rosenblatt (1958), is a single-neuron model and is the simplest form of ANN. The mathematical representation of perceptron is given in Eq. (5):

$$\begin{aligned} y=\psi \left( b+\sum _{i=1}^{n}{w_iX_i}\right) \end{aligned}$$
(5)

In this equation, y represents the predicted value, \(\psi\) denotes the activation function, b is the bias term, \(w_i\) represents the weights learned by the model, and \(X_i\) denotes the inputs. ANN is formed by grouping artificial neurons in layers and connecting them one after the other. The outputs of the artificial neurons in the previous layer become the inputs of the artificial neurons in the next layer. In an ANN model, there are three types of layers: the input layer, hidden layer(s), and output layer. The input layer is where neurons that receive inputs from the external world are located. The hidden layer processes the data, and a model may have multiple hidden layers. The output layer is where the final prediction value is generated. An MLP is calculated as follows:

$$\begin{aligned} y= \psi \left( b_2+\sum _{k=1}^q w_{ok} \theta \left( b_1+\sum _{j=1}^m w_{kj} \phi \left( \ldots \, \delta \left( b_0+\sum _{i=1}^n w_{li} X_i \right) \right) \right) \right) \end{aligned}$$
(6)

where \(\psi\), \(\theta\), \(\phi\), \(\delta\), are activation functions, \(b_0\), \(b_1\), and \(b_2\) are bias terms, \(w_{ok}\) is the weight from neuron k in the last hidden layer to the output neuron. o and n are the number of inputs.

3.3.2 Long Short-Term Memory

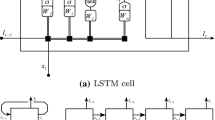
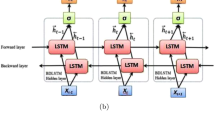
The LSTM model, proposed in the work by Hochreiter (1997), is an extension of the recurrent neural network (RNN) model, which is used for modeling sequential data. LSTM provides a solution to the vanishing gradient problem that arises during the training of RNN models using the backpropagation algorithm (Bengio et al., 1994). This model has been successfully applied in various domains such as machine translation, speech recognition, and prediction (Goodfellow et al., 2016). LSTM incorporates gates in its structure to control the flow of information. These gates enable the learning of which information to forget and which to remember during the training process. Sigmoid activation functions are employed in these gates, producing an output between zero and one. A zero output implies that no information passes through the gate, while a one output signifies that all information is allowed to pass. There are three types of gates in the LSTM model: input, forget, and output gates. In the input gate, the determination of which information to add to the cell state takes place. The forget gate plays a role in deciding which information should be erased from the cell state, and the output gate is responsible for determining which information should be produced as output. The LSTM model can be expressed using the following formulas:

$$\begin{aligned} f_t= & {} \sigma \left( W_f x_t + U_f h_{t-1} + b_f\right) \end{aligned}$$
(7)
$$\begin{aligned} i_t= & {} \sigma \left( W_i x_t + U_i h_{t-1} + b_i\right) \end{aligned}$$
(8)
$$\begin{aligned} \tilde{C_t}= & {} \tanh \left( W_c x_t + U_c h_{t-1} + b_c\right) \end{aligned}$$
(9)
$$\begin{aligned} C_t= & {} f_t C_{t-1} + i_t \tilde{C_t} \end{aligned}$$
(10)
$$\begin{aligned} o_t= & {} \sigma \left( W_o x_t + U_o h_{t-1} + b_o\right) \end{aligned}$$
(11)
$$\begin{aligned} h_t= & {} o_t \tanh \left( C_t\right) \end{aligned}$$
(12)

In this given context, \(\sigma\) symbolizes the sigmoid function. The forget gate is denoted as \(f_t\), the input gate as \(i_t\), the output gate as \(o_t\), the cell stated as \(C_t\), the candidate cell stated as \({\tilde{C}}_t\), the hidden stated as \(h_t\), and the input a time step t, as \(x_t\). The weight matrices corresponding to the forget, input, cell state, and output gates are labeled as \(W_f\), \(W_i\), \(W_c\), and \(W_o\), while the corresponding matrices for the gates are represented by \(U_f\), \(U_i\), \(U_c\), and \(U_o\). Additionally, the bias terms associated with the forget, input, cell state, and output gates are denoted by \(b_f\), \(b_i\), \(b_c\), and \(b_o\) respectively.

3.3.3 Convolutional Neural Networks

When dealing with multidimensional data such as images, ANNs tend to be computationally inefficient. Considering pixels in image data as individual variables, an ANN model requires a neuron for each variable in the input layer. Consequently, the computation involves calculating thousands of weights just in the first layer. Convolutional neural networks (CNNs) offer a more efficient computational approach to image-like data by automatically extracting features and reducing dimensions through convolution and pooling layers (Lecun et al., 1998). In the convolutional layer, a smaller-sized filter traverses the input tensor using sliding windows and conducting element-wise multiplication and summation. The result forms a new matrix, and this matrix is referred to as a feature map. Another specialized layer in the CNN architecture is the pooling layer. Commonly situated after the convolutional layers, its primary function is subsampling. There are generally two types of pooling: max pooling and average pooling. In max pooling, a sliding window, similar to the convolutional layer, is applied, and the new matrix’s element is the maximum value in the window. Similarly, in average pooling, the average of these values is calculated. The convolution layer formula is given in Eq. (13):

$$\begin{aligned} Y_{i,j} = \phi \left( \sum _{r=0}^{R-1}\sum _{c=0}^{C-1} W_{r,c} X_{i+c, j+r} + b \right) \end{aligned}$$
(13)

The feature map’s intersection at row i and column j is expressed as \(Y_{i,j}\), and the corresponding value in the input matrix at row \(i+c\) and column \(j+r\) is denoted as \(X_{i+c, j+r}\). The activation function applied to this operation is \(\phi\), and the convolution kernel’s weight at row r and column c is represented as \(W_{c,r}\). R and C are the height and width of the convolutional kernel, respectively. Additionally, the bias associated with the convolution kernel is denoted by b. Finally, the selection of hyperparameters used in deep learning models is provided in Table 3.

Table 3 Hyperparameters of deep learning models
Full size table

3.4 Realized Volatility

Volatility, unlike directly observable variables such as price or volume, requires the calculation of realized volatility for meaningful comparison. In the context of this study, two distinct realized volatilities, computed using five-minute data, were examined. These methodologies included the square of five-minute returns as proposed in Andersen and Bollerslev (1998) and the median realized volatility, as outlined in Andersen and Bollerslev (1998). The calculation involved summing the squares of five-minute returns, as per the formula provided in Eq. (14).

$$\begin{aligned} {RV}_t=\sum _{i=1}^{M}r_{t,i}^2 \end{aligned}$$
(14)

The formula for median realized volatility is given in Eq. (15).

$$\begin{aligned} {MedRV}_t=\frac{\pi }{6-4\sqrt{3}+\pi }\left( \frac{M}{M-2}\right) \sum _{i=2}^{M-1}{med\left( \left| r_{t,i-1}\right| ,\ \left| r_{t,i}\right| ,\left| r_{t,i+1}\right| \right) }^2 \end{aligned}$$
(15)

3.5 Loss Functions

The study by Patton (2011) highlighted the robustness of MSE and QLIKE loss functions in the face of noise in realized volatility calculations. In this study, the out-of-sample predictive capabilities of models were evaluated using not only these two metrics but also three additional loss functions, these being HMSE, MAPE, and MASE. The formulations for these loss functions are detailed below.

$$\begin{aligned} MSE= & {} \frac{1}{n}\sum _{t=1}^{n}\left( \sigma _t^2-{{\hat{\sigma }}}_t^2\right) ^2 \end{aligned}$$
(16)
$$\begin{aligned} HMSE= & {} \frac{1}{n}\sum _{t=1}^{n}\left( \frac{\sigma _t^2-{{\hat{\sigma }}}_t^2}{\sigma _t^2}\right) ^2 \end{aligned}$$
(17)
$$\begin{aligned} MAPE= & {} \frac{1}{n}\sum _{t=1}^{n}\left| \frac{\sigma _t^2-{{\hat{\sigma }}}_t^2}{\sigma _t^2}\right| \end{aligned}$$
(18)
$$\begin{aligned} MASE= & {} mean\left( \frac{\left| e_t\right| }{\frac{1}{n-1}\sum _{t=2}^{n}\left| \sigma _t^2-{{\hat{\sigma }}}_t^2\right| }\right) \end{aligned}$$
(19)
$$\begin{aligned} QLIKE= & {} \frac{1}{n}\sum _{t=1}^{n}\left( \frac{\sigma _t^2}{{{\hat{\sigma }}}_t^2}-\log {\left( \frac{\sigma _t^2}{{{\hat{\sigma }}}_t^2}\right) -1}\right) \end{aligned}$$
(20)

3.6 Rolling and Expanding Window

In addition to applying the GARCH models with a fixed training set range, rolling and expanding window techniques were employed with varying window values. These techniques involved updating the model parameters at specified intervals. In the expanding window approach, the initial point remains fixed, and the training set continuously expands. For instance, when forecasting \(y_t\), the training set is \(y_0\), \(y_1\),..., \(y_{t-1}\), and when estimating \(y_{t+1}\), it becomes \(y_0\), \(y_1\),..., \(y_t\).

Conversely, the rolling window technique maintains a constant training set size but shifts it with each prediction. For example, when forecasting \(y_t\), the training set is \(y_0\), \(y_1\),..., \(y_{t-1}\), and when forecasting \(y_{t+1}\), it shifts to \(y_1\), \(y_2\),..., \(y_t\).

4 Empirical Results and Discussion

In this study, 11 different GARCH models and three different DL algorithms were compared in terms of out-of-sample forecasting performance for each cryptocurrency, considering various parameters. During the comparisons, the impact of factors such as model type, error distribution, the rolling window method, window size, realized volatility formula and train-test ratio was also examined. Models such as sGARCH, IGARCH, EGARCH, GJR-GARCH, APARCH, TGARCH, AVGARCH, NGARCH, NAGARCH, csGARCH, and ALLGARCH were analyzed under normal, skewed normal, student-t, skewed student-t, generalized error, and skewed generalized error distributions. The ARCH (p) and GARCH (q) parameters for GARCH models were set to one. The models were applied with window sizes of 3, 5, 10, 15, 30, and 45 in both rolling and expanding window techniques, in addition to the fixed training set interval settings. They were also implemented with train-test ratios of 70:30, 80:20, and 90:10. The total number of applied GARCH models was 7722.

ANN, CNN, and LSTM were used as DL algorithms. These models use lagged values of realized volatility as input, with lag values ranging from one to 10. The DL models had two hidden layers, and the number of neurons in the hidden layers took values ranging from 20 to 200 in increments of 20. The DL models were separately applied for the squares of five-minute returns and the median realized volatility formulas. A total of 54000 DL models were considered. As a result, the total number of GARCH and DL models obtained in this study was 61722. This study utilized Python version 3.7.12 and R version 4.0.5 as the programming languages.

Tables 4, 6, 8, 10, and 12 present the frequency of selection for GARCH models and error distributions across various scenarios based on the MSE, HMSE, MAPE, MASE, and QLIKE loss functions, respectively. A comprehensive set of 234 scenarios was generated by combining different data sets, train-test ratios, rolling window methods, and realized volatility formulas. In Tables 5, 7, 9, 11, and 13, the best performing model, error distribution, rolling window and loss function values for these loss functions according to three data sets and three train-test ratios are given.

4.1 Empirical Results

Analysis of Table 4 reveals that the csGARCH model demonstrated a notable preference for the MSE loss function. Among the various error distributions considered, the ged stood out as the most commonly chosen distribution. However, it is noteworthy that within the specific framework of the csGARCH model, the sged gained prominence as the preferred choice.

Table 4 Number of selections of GARCH models and error distributions by MSE
Full size table

According to the results presented in Table 5, it can be seen that the ALLGARCH model, employed with sged error distribution and a rolling window of 45 in the Bitcoin dataset at a 70:30 train-test ratio, demonstrated the optimal performance with values of 0.000017 and 0.0000141 for both realized volatility formulas. Similarly, for the 80:20 ratio, the TGARCH-sged model was selected, while for the 90:10 ratio, the csGARCH-ged and ALLGARCH-snorm models were chosen. The performance of the selected models for other scenarios can be seen in Table 5.

Table 5 MSE values of selected models
Full size table

When the results are examined based on the HMSE loss function, it can be seen that the most frequently chosen model was AVGARCH, and the most frequently selected distributions were std and sstd. The AVGARCH model yielded the best results 22 times when modeled with the snorm error distribution. This number was equal to the number of selections when the TGARCH model was modeled under the sged distribution. The sGARCH model, on the other hand, demonstrated notably poor performance, both in terms of MSE and HMSE, being the least frequently chosen model. Furthermore, Table 6 shows that another model exhibiting poor performance was the APARCH model.

Table 6 Number of selections of GARCH models and error distributions by HMSE
Full size table

Additionally, in Table 7, it is evident that the AVGARCH model was the selected model in scenarios involving BTC 80:20, BTC 90:10, BNB 80:20, and BNB 90:10.

Table 7 HMSE values of selected models
Full size table

The results obtained from the MAPE were similar to those obtained by MSE. As can be seen in Table 8, the csGARCH model demonstrated superior performance in 87 out of 234 scenarios, while the ged distribution yielded the best results in 86 instances. In terms of model distribution combinations, the csGARCH and sged combination was selected more frequently than other combinations. Contrary to the outcomes in MSE and HMSE, the sGARCH models did not emerge as the worst models according to MAPE; instead, the IGARCH and TGARCH models exhibited the poorest performance. Table 8 indicates that the snorm distribution corresponded to the least favorable error distribution.

Table 8 Number of selections of GARCH models and error distributions by MAPE
Full size table

Based on the MAPE values presented in Table 9, the csGARCH-sged model was chosen for the BTC 70:30 scenario, the NGARCH-sged model for the 80:20 scenario, and the GJR-GARCH-sstd model for the 90:10 scenario. In the Ethereum dataset, the GJR-GARCH model was the optimal choice in four out of six scenarios, while the APARCH model was favored in the remaining two scenarios. ALLGARCH, AVGARCH and EGARCH models were among the selected models in the Binance Coin data set.

When the results are examined according to MASE, a different pattern emerges compared to the previous findings. While the ALLGARCH model yields the best results in 76 scenarios, the norm distribution, characterized by the best-performing error distribution, offers the most favorable distribution in more than half of the total scenarios. In contrast to the previous results, the sGARCH model has not been selected in any scenarios. The models not chosen include the NGARCH and NAGARCH models.

Table 9 MAPE values of selected models
Full size table

The results presented in Table 10 parallel those in Table 11. The ALLGARCH model has proven to be the best-performing model in scenarios such as BTC 80:20 and 90:10, ETH 80:20, and BNB 80:20.

Table 10 Number of selections of GARCH models and error distributions by MASE
Full size table

Finally, when the results are scrutinized using the QLIKE loss function, similar to the findings in MASE, the ALLGARCH model is prominent. The subsequent best-performing model is the csGARCH model, which yields the best results for MSE and MAPE. The csGARCH model, when modeled using sged error distribution, outperforms other models according to these three loss functions. When considering all the loss functions, it can be seen that different models and error distributions come to the forefront. However, among the applied 11 GARCH models, the csGARCH and ALLGARCH models are more frequently selected compared to other models, indicating their superior performance.

Table 11 MASE values of selected models
Full size table
Table 12 Number of selections of GARCH models and error distributions by QLIKE
Full size table

The ALLGARCH model yielded the optimal results in five out of six models within the BTC dataset, whereas in the ETH dataset, the GJR-GARCH, NGARCH, APARCH, and NAGARCH models are among the selected models. In the case of BNB, involving the EGARCH, GJR-GARCH, and AVGARCH, Table 12 shows that the ALLGARCH models were among the models selected in different scenarios. These scenarios and the corresponding QLIKE values can be seen in Table 13.

Upon scrutiny of the results up to this point, it seems challenging to identify a superior model or error distribution that is consistent across all scenarios. The optimal model appears to vary based on the utilized dataset, the train-test ratio, the rolling window technique, the realized volatility formula, and the loss function applied.

Within the scope of this study, another question to be addressed is which rolling window method and window size are more suitable for forecasting the volatility of cryptocurrencies. For this, models were applied with 13 different rolling window approaches. The results for the various data sets and train-test ratios are presented in Tables 14 through 22. Additionally, the interpretation of whether the results vary according to the formula for realized volatility can be gleaned from these tables.

Table 13 QLIKE values of selected models
Full size table
Table 14 Loss functions of rolling window methods on BTC dataset with a 70:30 train-test ratio
Full size table

The results obtained utilizing a 70:30 train-test ratio in the Bitcoin dataset are presented in Table 14. According to this table, the expanding window method was not selected. The results for the squares of five-minute returns and median realized volatility formulas remain unchanged. Additionally, in three out of five loss functions, the rolling window 45 has been chosen.

In the scenario modeled with an 80:20 train-test ratio in Bitcoin, the results exhibit some variations. In Table 15, the results exhibit consistency across the two RV formulas, as indicated by MAPE, MASE, and MSE. However, this consistency is not observed concerning HMSE and QLIKE.

Table 15 Loss functions of rolling window methods on BTC dataset with a 80:20 train-test ratio
Full size table
Table 16 Loss functions of rolling window methods on BTC dataset with a 90:10 train-test ratio
Full size table

In the final scenario of the Bitcoin dataset, the training set encompasses 90% of the entire data and the rest is reserved for testing. Table 16 reveals that, for the first realized volatility formula based on the square of five-minute returns, rolling window 45 emerged as the optimal method in terms of HMSE and MAPE loss functions. Similarly, for the median realized volatility formula, rolling Window 45 demonstrated superiority in HMSE, MAPE, and MSE loss functions. Interestingly, the MASE loss function identified the method employing a fixed training set interval as yielding the best results in both formulas. However, it is noteworthy that the MSE and QLIKE functions exhibited inconsistency across the two RV formulas. Notably, in this scenario, no expanding window methods were chosen for either formula.

In the scenario where the entire dataset of Ethereum was partitioned into 70% for training and 30% for testing, an inclination toward rolling window methods, particularly with smaller window sizes such as three and five, can be seen. For both realized volatility formulas, the optimal method based on HMSE, MASE, and MSE loss functions is rolling window 3. However, concerning MAPE, one-step-ahead proves to be the superior approach. Additionally, the outcomes, akin to those in the Bitcoin dataset, exhibit inconsistency among realized volatility formulas in terms of QLIKE. As depicted in Table 17, expanding window methods, akin to the 80:20 scenario in the Bitcoin dataset, manifest inferior performance compared to rolling window methods.

Table 17 Loss functions of rolling window methods on ETH dataset with a 70:30 train-test ratio
Full size table

Although the loss functions other than QLIKE indicate the same method for the two formulas at the 80:20 train-test ratio for the ETH dataset, a different method was chosen for each loss function. For instance, in the case of the rolling window 5 method, the HMSE value is 0.9912, representing the lowest value. On the other hand, for the MAPE, the minimum value belongs to rolling window 30 with 1.1612 in Table 18.

Table 18 Loss functions of rolling window methods on ETH dataset with a 80:20 train-test ratio
Full size table
Table 19 Loss functions of rolling window methods on ETH dataset with a 90:10 train-test ratio
Full size table

In the final Ethereum scenario, the loss functions calculated using the squared five-minute returns and the median realized volatility pointed to the same rolling window methods. Despite rolling window 5 being selected based on HMSE, other loss functions consistently indicated rolling window 45 as the optimal method. This outcome stands out as the most robust and reliable result across different scenarios. Additionally, this scenario marks the third instance where rolling window 45 has consistently delivered superior results across multiple loss functions. Table 19 highlights that the expanding window method, in contrast, failed to yield the best outcomes in any of the examined loss functions.

The results obtained with a train-test ratio of 70:30 for the third and final dataset, the Binance Coin dataset, are presented in Table 20. According to these results, for the one-step-ahead, the HMSE and QLIKE values were calculated as 0.6091 and 0.4998, respectively, in the first formula, and 0.6087 and 0.5525 in the second formula, establishing it as the superior method. In terms of MAPE, the first formula yielded the lowest value on rolling window 3, while the second formula achieved this on expanding window 5. The MASE and MSE error metrics, on the other hand, dictated the selection of the expanding window 3 and rolling window 30 methods.

Table 20 Loss functions of rolling window methods on BNB dataset with a 70:30 train-test ratio
Full size table

In Table 21, in the second scenario of the Binance Coin dataset, the expanding window 3 method was chosen concerning MAPE and MASE loss functions. The calculated value of the HMSE based on the square of five-minute returns for rolling window 45 was 0.9867, representing the minimum value. Meanwhile, the corresponding value for the median of realized volatility was computed as 0.9859. While rolling window 30 gave the best results in terms of MSE and QLIKE in the first formula, QLIKE got the smallest value in rolling window 5 in the second formula.

Table 21 Loss functions of rolling window methods on BNB dataset with a 80:20 train-test ratio
Full size table
Table 22 Loss functions of rolling window methods on BNB dataset with a 90:10 train-test ratio
Full size table

Table 22, which is the final table displaying the results of rolling window approaches, contains the results of the models applied in Binance Coin with a train-test ratio of 90:10. In this table as well, the rolling window 45 method has been identified as the most effective approach in terms of HMSE, MAPE, MSE, and QLIKE metrics. Meanwhile, rolling window 10 has been determined to be the optimal method concerning the MASE metric.

When a general overview is taken of rolling window methods, it can be stated that as the size of the training set increases, there is a tendency for the loss functions to indicate the same method. Furthermore, it is possible to assert that expanding window methods exhibit poorer performances compared to rolling windows. Models with a window size of 45 in the rolling window methods, especially, demonstrate improved performance as the training set grows. Examination of whether the performances of rolling window methods vary according to realized volatility calculations reveals that, except for QLIKE, there are no frequent inconsistencies across loss functions.

Within the scope of the study, another question under investigation is whether DL methods exhibit superior performance compared to GARCH models. To examine the results from this perspective, heatmaps for various scenarios are provided in Figs. 11, 12, 13, 14, 15, 16, 17, 18, and 19. The heatmaps depict the loss functions of 11 GARCH models and three DL models separately for the squares of five-minute returns and the median realized volatility formulas. For ease of interpretability in the heatmaps, the loss function values were normalized using the minimum-maximum approach, scaling the values to a range between zero and one.

The performance of models with a 70:30 train-test ratio on the Bitcoin dataset is illustrated in Fig. 11. DL models demonstrated superior performance compared to GARCH models in the left graph. Particularly, the ANN model was selected as the optimal model in terms of loss functions other than QLIKE. However, the selected model for QLIKE was LSTM. In the second realized volatility formula, contrary to the first one, EGARCH was the model that gave the best results based on HMSE.

Fig. 11
figure 11

Heatmap of loss functions on BTC dataset 70:30 train-test ratio

Full size image

When examining the loss functions calculated in the Bitcoin dataset with an 80:20 train-test ratio, it can be seen that the ANN model exhibited superior performance compared to other models. The CNN model was selected as the best model based on the first realized volatility formula, based on the HMSE and QLIKE. Another notable observation in Fig. 12 was the discrepancy in the LSTM model’s performance, where it was identified as the worst model in terms of QLIKE in the first graph but the best model in the second. This underscores how much the realized volatility formula and loss functions can change the results when evaluating the models.

Fig. 12
figure 12

Heatmap of loss functions on BTC dataset 80:20 train-test ratio

Full size image

In the last scenario in the Bitcoin data set, a train-test ratio of 90:10 was adopted. According to the findings illustrated in Fig. 13, the AVGARCH model was selected for both realized volatility formulas based on the HMSE criterion. Regarding the QLIKE criterion, the CNN model emerged as the optimal choice, whereas the ALLGARCH model was exclusively chosen based on the MSE in the first graph. In contrast, in the second graph, the ANN model was selected instead of the ALLGARCH model. For the remaining combinations of realized volatility formulas and loss functions, the ANN model was chosen as the optimal one.

Fig. 13
figure 13

Heatmap of loss functions on BTC dataset 90:10 train-test ratio

Full size image

In Fig. 14, regarding Ethereum, with a train-test ratio of 70:30, it can be seen that as you go to the lower parts of the graphs where the DL algorithms are located, the colors become lighter, that is, the loss functions take smaller values. EGARCH was selected in terms of HMSE only in the first formula. For the first formula, two of the remaining loss functions took the smallest value in ANN, one in the LSTM and one in the CNN model. For the second formula, while the first four loss functions pointed to ANN, CNN was the best model only in terms of QLIKE.

Fig. 14
figure 14

Heatmap of loss functions on ETH dataset 70:30 train-test ratio

Full size image

The results in Fig. 15 are indicative of the superiority of DL algorithms over GARCH models. In the first graph, the model selected as the best in terms of HMSE, MASE, and MSE was the ANN. In the second graph, it was also chosen as the optimal model based on the MAPE. Regarding the QLIKE, the CNN model was selected in both graphs. LSTM was identified as the DL model selected in the first graph in terms of MAPE.

Fig. 15
figure 15

Heatmap of loss functions on ETH dataset 80:20 train-test ratio

Full size image

Figure 16 shows the loss functions of the models in the final scenario for the Ethereum data set. The superiority of the ANN model can be observed in various metrics in both graphs. In the left graph, ANN was selected as the best model based on MAPE, MASE, MSE, and QLIKE. In the right graph, ANN was chosen as the optimal model considering MAPE, MASE, and MSE. GJR-GARCH is only selected in terms of HMSE in the first graph. In the second graph, CNN emerged as the best model regarding QLIKE.

Fig. 16
figure 16

Heatmap of loss functions on ETH dataset 90:10 train-test ratio

Full size image

Similar results were obtained in the Binance Coin dataset as in the Bitcoin and Ethereum datasets. Figure 17 depicts the results of the models applied with a 70:30 train-test ratio. In both formulations, the HMSE value points to the EGARCH model, while the MASE value indicates the csGARCH model. For the first formulation, the CNN model was chosen in terms of MAPE, and the LSTM model was selected for MSE and QLIKE. However, in the second formulation, CNN yielded superior results in terms of MSE compared to the LSTM model.

Fig. 17
figure 17

Heatmap of loss functions on BNB dataset 70:30 train-test ratio

Full size image

In the examination of the loss functions in the 80:20 scenario of Binance Coin, no GARCH model was selected in the evaluation made using the square of the five-minute returns. Among the DL models, CNN demonstrated superior performance in terms of HMSE, MSE, and QLIKE, as depicted in Fig. 18 on the left. However, due to minor discrepancies among the loss functions, when considering the median realized volatility, some alterations were observed in the selected models. For instance, on the left, CNN was chosen for HMSE, MSE, and QLIKE, while on the right, ANN was selected for HMSE, and LSTM was chosen for MSE. No changes occurred in the results for other loss functions.

Fig. 18
figure 18

Heatmap of loss functions on BNB dataset 80:20 train-test ratio

Full size image

In the last scenario, the models were applied to the Binance Coin dataset in such a way that the training set comprised 90% of the total data. In this scenario, as depicted in Fig. 19, DL models exhibited superior performance regarding loss functions other than HMSE. MAPE, MSE, and QLIKE attained their lowest values in the LSTM model in the first formulation. The ANN emerged as the optimal model for MASE in both formulations, while in the second formulation, CNN took the place of LSTM.

Fig. 19
figure 19

Heatmap of loss functions on BNB dataset 90:10 train-test ratio

Full size image

Examining the graphs comparing GARCH models and DL algorithms, it can be seen that the performance of the DL algorithms surpasses that of the GARCH models in numerous scenarios. However, it can be said that the optimal model varies according to the train-test ratio, error function, and realized volatility formula.

4.2 Discussion

According to widely held views, the impact of various parameters, such as forecasting window size, the selection of rolling or expanding windows, the computation of RV measure, and the type of error metric measure, on GARCH-type models under different distributions and deep learning models is a well-known fact. These parameters significantly influence the modeling of volatility and consequently the predictive performance of the models. To strengthen our findings, we conducted an analysis to determine how the best predictive power of 11 GARCH-type models under six different error distributions, and ANN, LSTM, and CNN models perform across different parameters for three cryptocurrency prices, BTC, ETH, and BNB.

The results show that when forecasting out-of-sample returns, considering all five different error measures, the most selected GARCH-type model is the csGARCH model, followed by the ALLGARCH model. Additionally, in terms of error distributions, when examining the five different error measures, the most selected distribution is the ged, followed by the sged distribution.

Considering the two measures used for calculating realized variance and the results involving GARCH-type models, as stated in (Liu et al., 2015), by using 5-minute RV yields, there are more accurate forecast results compared to MedRV across all error measures. However, when considering deep learning models, it has been determined that MedRV is selected more frequently and achieves higher forecast accuracy compared to 5-minute RV.

Another important finding is that the selection of training size improves the forecasts. Considering three different training sizes of 70:30, 80:20, and 90:10, it has been found that both deep learning models and GARCH-type models have higher forecast accuracy when the training/test ratio is 90:10. This result also aligns with the findings of the study conducted by Ewees et al. (2020).

The selection of forecasting window type tested in both GARCH-type models and deep learning models confirms that the rolling forecasting window approach provides better forecasting performances for three returns. Finally, as stated in the study by Wang et al. (2023), it has been found that deep learning models outperform GARCH-type models in forecasting the volatility of the three returns.

5 Conclusion and Future Work

In recent years, the market capitalization of cryptocurrencies has grown significantly, and they have attracted a lot of interest. Since the first digital money, Bitcoin, was created, there are now many more types. A growing number of businesses and institutions are accepting cryptocurrencies as a result of their rising popularity, which has increased their use in various financial activities. However, compared to other financial assets, cryptocurrencies are more volatile; thus, accurate volatility forecasts are crucial for efficient risk management in the market.

In this study, the volatilities of the three cryptocurrencies with the highest market capitalization were forecasted, and models exhibiting the best out-of-sample forecasting performances were reported. Additionally, the performances of rolling window methods were examined, and whether the results varied across different train-test ratios, realized volatility formulas and loss function combinations was investigated. Eleven distinct GARCH models were considered under six different error distributions. Each GARCH model was implemented using two sliding window techniques with six different lengths. DL algorithms, including ANN, LSTM, and CNN, were modeled with varying delays in series and different numbers of neurons in hidden layers. All the models were applied using three train-test ratios: 70:30, 80:20, and 90:10. Furthermore, two different realized volatility formulas and five different loss functions were employed to examine the results. In total, considering all the datasets and scenarios, a total of 61722 models were implemented within the scope of the study.

When the GARCH models are compared with each other, it can be seen that consistently identifying a superior model or error distribution across all scenarios is challenging. Results vary based on the utilized data set, the train-test ratio, the rolling window technique, the realized volatility formula, and the loss function. Upon examination of results based on rolling window methods, it is generally noted that the performance of the expanding window method is worse than the rolling window method. The most frequently chosen window size is 45. Another finding derived from the performance of the rolling window methods is that the QLIKE loss function is more sensitive to the selected realized volatility formula compared to other loss functions.

When examining the results of DL algorithms, it can be seen that the model with the best performance was ANN, followed by the second-best model, LSTM. CNN, on the other hand, exhibited the poorest performance among the DL algorithms. The outcomes displayed partial differences in terms of the applied volatility formulas. However, when the median realized volatility formula was employed, lower loss functions were obtained compared to the five-minute squared returns formula. Finally, upon comparing the performances of all employed DL algorithms and GARCH models, the DL algorithms exhibited a superior performance. Furthermore, it is noteworthy that the results vary based on the utilized train-test ratio, realized volatility formula, and loss functions, necessitating distinct examinations for each scenario.

In future work, the forecasting performance of hybrid models, created by combining various commonly used models, can be explored and analyzed. Additionally, the accuracy of forecasts could be improved by developing a combining algorithm with a dynamic structure for combining forecasts from different models.