Stock Market Efficiency of the BRICS Countries Pre-, During, and Post Covid-19 Pandemic: A Multifractal Detrended Fluctuation Analysis

Abstract

In this study, we applied the multifractal detrended fluctuation analysis model to compare the multifractal characteristics of five BRICS stock markets over three different periods, using current financial information through July 2022. According to the findings, multifractal characteristics are present in all stock market returns. We discover long-term correlations in stock index returns, arguing the notion that the stock markets are inefficient and have not yet reached a mature market development following COVID-19. The Chinese stock index has been the most effective throughout the pandemic, while the Russian and Indian stock markets are the least efficient. We also used the GARCH(1,1) model, which demonstrates India's efficiency during the COVID-19 pandemic. Additional findings align with the MFDFA findings. The paper's findings are relevant to investors seeking investment opportunities on these stock exchanges and policymakers working to implement institutional reforms to boost stock market efficiency and promote the financial markets' long-term sustainability.

1 Introduction

Primarily identified as a cluster of pneumonia cases in Wuhan City, Hubei Province, China, on December 31, 2019, the novel coronavirus (COVID-19) has rapidly spread to many other places worldwide. At a media briefing, COVID-19 was classified as a global pandemic by the World Health Organization (WHO) on March 11, 2020 (WHO, 2020a) and urged nations to act swiftly and forcefully to stop its spread (WHO, 2020b). Although several nations have implemented stringent precautions, the COVID-19 epidemic is still spreading. As of 13 August 2022, COVID-19 has been detected in 585,950,085 people, and 6,425,422 people from different territories have died from COVID-19 (WHO, 2022c).

According to earlier research, uncertain periods are contagious in the financial markets (Nguyen et al., 2021). Because of this, stock markets are the commercial hub for value offers, and decisions about buying or selling are made immediately in response to any new information. Notably, any declaration concerning macroeconomic and monetary pointers like the spread between long and short interest rates, expected and unexpected inflation, industrial production, and the spread between high- and low-grade bonds might be persuasive on stock exchange indices (Chen et al., 1986).

The effectiveness of the stock market is frequently impacted by various events (Ozkan, 2021). The efficient market hypothesis is regularly challenged by unanticipated occurrences, including economic constraints, mass turmoil, boom explosions, and pandemics. These events typically lead asset prices to vary from their initial values. Machmuddah et al. (2020) claim that certain corporate acts, like splits, right issues, and warrants, can affect the effectiveness of the stock market, though the results might take time to materialize.

Several distinct mechanisms exert an impact on the efficiency of the stock market due to COVID-19. To begin with, one of the core issues is the economic impact of the lockdowns needed to control the virus. The pandemic has slashed the growth prospects of the global economy, according to most international institutions and banks. Both the manufacturing and the services sectors have suffered from the virus-induced disruptions, closures, and restrictions that have affected consumers, suppliers, and financial intermediaries. Therefore, a strong and coordinated governmental response is essential to mitigate the negative impacts of the virus (Selmi & Bouoiyour, 2020; Yousef, 2020; Yousef & Shehadeh, 2020).

Because most countries are becoming more vulnerable due to the pandemic, most economical and economic indicators have been negatively impacted, and this disintegration has resulted in notable losses. Several studies (Al-Awadhi et al., 2020; Alexakis et al., 2021; Alfaro et al., 2020; Liu et al., 2020) have examined how COVID-19 negatively affects stock markets. Studies on COVID-19's effects on the performance of stock markets, the spillover effect, the price of stocks, the impact of influential co-movements of COVID-19 pandemic concerns, and the vulnerability of financial markets have been conducted here. However, these analyses focus on emerging and developed nations like the USA, China, France, Spain, Germany, South Korea, and Italy. Also, studies examining the effect of COVID-19's lockdown stages on stock market efficiency in the economic alliance's stock indexes are limited.

The BRICS countries—Brazil, Russia, India, China, and South Africa—receive the majority of foreign direct investment and generate many of the top consumer goods in the world, which serves as the impetus for our investigation. For instance, the global financial crisis was transmitted to the BRICS stock markets through shifts in the fundamentals of the global economy, which may affect those nations' economies. Additionally, due to the potential for investment possibilities, speculation, and risk diversification, foreign investors are very concerned about the correlation between the activities of the BRICS stock markets and these external factors (Mensi et al., 2014). Therefore, we will focus on the BRICS region in our analysis. This is because the literature currently in print does not seem to address the impact of COVID-19 on the effectiveness of the stock market within the setting of the BRICS. Furthermore, earlier research did not discuss the combined effects of these factors on the effectiveness of the stock markets in this area.

So, this study attempts to address this gap by analyzing the stock market efficiency in pre-, during, and post-COVID-19 of BRICS. We will also be trying to find answers to these issues: First, has COVID-19 substantially affected stock returns in particular nations? Moreover, is there a correlation between stock returns and economic stability under COVID-19?

This study's key objective is to ascertain, using the MF-DFA model, how fundamental stock exchange indices in the BRICS nations respond to the COVID-19 pandemic. The major determinant is the daily stock market return. In addition, the following are included as independent variables: pre-COVID-19 period, during the COVID-19 period, and post-COVID-19 period.

In summary, the particular goals of this study are three in number. The first step is to implement the MF-DFA model, which enables the analysis of fluctuations in several quantiles of the major stock market indices. The second one examines how the significant indicators react to the COVID-19 epidemic. The final step concentrating on the pre, during, and post-pandemic periods is providing a full concentration on the BRICS countries—Brazil, Russia, India, China, and South Africa—which represent a sizable portion of the financial industry.

2 Literature Review and Hypotheses

2.1 Theoretical Arguments

2.1.1 Efficient Stock Market

The idea of an effective market considers how information influences security prices and how the market responds to them. According to (Brealey et al., 2006), a market is considered efficient if exceeding the market return is impossible. Security prices should accurately reflect all relevant information for a capital market to be efficient (Malkiel, 1989). When this happens, the company's market value and intrinsic value change similarly (Degutis & Novickytė, 2014). Market prices do not fully and instantly reflect fundamental value changes due to investor awareness differences and uneven transaction costs (Koller et al., 2010). Financial reports are only one aspect of the data; it also includes news on political, social, and economic developments and other topics. Recently, the adaptive market hypothesis was introduced by behavioral finance theory, which has lately gained academic and professional attention. However, this theory does not completely replace the EMH's value (Degutis & Novickytė, 2014).

2.1.2 Events and Stock Prices: A Relationship

The efficient market theory claims that a market will react promptly to new information (Stout, 2002). Participants in the capital markets must exercise caution when gathering information. When making decisions, market participants look for information about the state of the capital market. Not every piece of information is helpful, though; some are unrelated to stock market action. A company's stock prices can fluctuate depending on the news and events related to it. This has been demonstrated by some researchers in their studies (Kaushal & Chaudhary, 2017).

Marston (1996) categorizes several forms of lousy information. At first, data excellence is not always helpful. The reliability of information is connected to the integrated content. This evidence might be regarded as essential or irrelevant to capital market activity. Second, information is detrimental when it is not distributed smoothly to investors. Schwert (1981) stated that there is little correlation between stock movement and macroeconomic data.

According to (Holthausen & Verrecchia, 1990), a difference in the weight of public information can affect investor trust. Since this will not affect investor confidence and willingness to contemplate trading, investors propose trade announcements that do not contain new data. This finding is in line with that of (Kim & Verrecchia, 1991), who argued that increasing absolute change in price affects trade volume, where price indicates information level change.

2.2 Empirical Literature

Some ground-breaking studies (Baker & Wurgler, 2007; Cen et al., 2013; Lucey & Dowling, 2005) observe how tail events affect investor minds, predispositions, temperament swings, and tension on market returns and unpredictability. According to (Chen et al., 2013; Kaplanski & Levy, 2012; Shu, 2010), factors that affect returns more than asset pricing include daylight, social gatherings, investor anxiety, and mood fluctuations. In addition, other research lines (Donadelli et al., 2017; Kaplanski & Levy, 2010; Yuen & Lee, 2003) describe how predictable and unpredicted occurrences affect stakeholders' hypotheses. These studies indicate a substantial correlation between the coronavirus markers and the principal stock market records. This relationship is examined by examining how the prior stock exchange records responded to the pandemic. In this situation, the overall number of confirmed cases, pandemic-related fatalities, and the number of patients making a full recovery are all regarded as pandemic markers. Using the combined numbers could be deceptive because these Figures are believed to depict the pandemic correctly. Additionally, when considering ongoing investigations (Akhtaruzzaman et al., 2021; Al-Awadhi et al., 2020; Bahrini & Filfilan, 2020; Mazur et al., 2021; Narayan et al., 2021; Topcu & Gulal, 2020), the primary indices and the pandemic indicators are predicted to be negatively correlated. However, there may be an unbiased link between pandemic markers and leading indices if the outbreak is exceptionally standard, spreads to every nation, and is an everyday occurrence. According to some of the most current studies on tail events (Ichev & Marinč, 2018), including those on the Ebola outburst and the effects of geological proximity, the stock was more unpredictable in West Africa and the United States, where it originated. The murder of Jamal Khashoggi significantly impacted the Saudi Stock Exchange, raising a high risk of ambiguity and aberrant aggregate returns (Bash & Alsaifi, 2019).

About the pandemic, Al-Awadhi et al. (2020) recently examined how COVID-19 affected the Chinese stock market using panel data regression. The authors of their study demonstrate that death and infectious, irresistible sickness affect the Chinese equity market. Additionally, they realize that all organizations' stock returns are detrimental due to the daily increase in cases and the overall number of fatalities brought on by diseases. Goodell (2020) shows the deadly and contagious consequences of COVID-19 on international equities markets. Furthermore, Bakas and Triantafyllou (2020) looked into the uncertainties surrounding pandemic costs and found a considerable negative influence on the commodity market. The coronavirus has impacted world financial requirements, although there are indications that the Chinese market has stabilized since the outbreak (Ali, 2020). In general, a COVID-19 epidemic in several nations has damaged the global financial system, with Europe and the United States leading the way. After discussing the connection between coronavirus media inclusion and financial market reactions, (Haroon & Rizvi, 2020) conclude that news media inclusion results in excessive alarm and increased instability in equity markets. Besides, Zhang et al. (2020) examined the rapid global expansion of COVID-19. They found that a 0% interest rate and unrestricted quantitative easing (QE) might help recover recent financial market losses since they affect the financial markets.

As is well known, the COVID-19 pandemic increases market volatility (Wang et al., 2021). Because of the pandemic's deteriorating instability, which lowers the top stock market indices, it is anticipated that the Volatility Index will have a negative link with those indices. Similar assumptions significantly impact uncertainty. In this instance, a negative link between the key stock exchange indices and the US Economic Policy Uncertainty Index, which acts as a proxy for global uncertainty, is anticipated because the pandemic is raising market uncertainty and degrading the primary stock exchange indices (Baker et al., 2020; Sharif et al., 2020).

FX might also be rated as a productive variable on the primary stock exchange indices. According to the investigations' findings, a negative correlation between foreign exchange and the key indices is anticipated (Erdoğan et al., 2020; Hajilee & Al Nasser, 2014; Korhonen, 2015).

In addition to the variables mentioned above, various financial and economic variables, such as financial growth, GDP, inflation, central bank policy rates, besides so on, may be examined for their impact on important stock exchange indices. Indices of self-assurance, international trade, and debt can all be considered determinants. This study aims to identify the indices' accountability for the COVID-19 pandemic; hence, such variables are not covered.

Previous studies examined how the COVID-19 epidemic and its lockdown affected international stock markets. However, no research has been done to gauge how COVID-19 may affect the performance of the stock markets in the BRICS countries of Brazil, Russia, India, China, and South Africa. A literature gap and the stock market's future growth inspired this study.

2.3 Hypothesis Development

Our first hypothesis is supported by existing empirical research on the theory that explains how COVID-19 affects stock markets and the supply of equity market returns. We contend that the negative consequences of COVID-19 on actual economic activity will have a considerable influence on stock market returns, volatility, and trading volume. Our initial hypothesis is the following:

Hypothesis 1 (H1)

The stock market is negatively impacted by COVID-19, as evidenced by lower daily returns and increased uncertainty.

The COVID-19 pandemic, which started as a small-scale shock in China, significantly impacted the world. We developed our second theory in light of this. This study simulates the possible impact of COVID-19 on trade and the economy.

Hypothesis 2 (H2)

COVID-19 on equity markets directly affects overall economic stability.

3 Methodology

Numerous researchers have found that stock markets have a multifractal nature (Bacry et al., 2001; Kwapień et al., 2005; Oświe et al., 2005; Yuan et al., 2009). Because of this, we use (Kantelhardt et al., 2002)'s multifractal detrended fluctuation analysis (MF-DFA) approach to evaluate the BRICS stock market effectiveness. We may define fractal features and assess long-range autocorrelations using MF-DFA, which is utilized to gauge market efficiency. The MF-DFA method is appropriate for identifying market inefficiency in a stock market, even if long-term correlation features in financial series are generally viewed as markers of market inefficiency (Cajueiro et al., 2009; Zhou, 2009).

The complexity of financial markets has been extensively studied using the MF-DFA approach such as stock exchanges (Ali et al., 2018; Cao et al., 2013; Rizvi & Arshad, 2017), foreign exchange markets (Norouzzadeh & Rahmani, 2006; Wang et al., 2011), crude oil markets (Alvarez-Ramirez et al., 2002; He & Chen, 2010), gold markets (Dai et al., 2016; Mali & Mukhopadhyay, 2014), and cryptocurrencies (Stavroyiannis et al., 2019; Takaishi, 2018). The MF-DFA approach has also been employed in numerous researches to look into market performance during financial crises (Al-Khazali & Mirzaei, 2017; Han et al., 2019a, 2019b; Mensi et al., 2017; Shahzad et al., 2017).

The MF-DFA method can gauge and rank market efficiency because it illustrates the multifractal properties of a financial time series. The MF-DFA procedure, according to (Kantelhardt et al., 2002), contains the five steps listed below (Wang et al., 2019):

Let $\left\{ {X_{k} ,k = {1}, \ldots ,N} \right\}$ be a time series, with N being the length of the series.

Step 1. Determine the profile $Y\left( i \right)(i = 1,2, \ldots ,N)$

$$ Y\left( i \right) = \mathop \sum \limits_{k = 1}^{i} \left( {x\left( k \right) - \overline{x}} \right), $$

where

$$ \overline{x} = \mathop \sum \limits_{k = 1}^{N} x\left( k \right)/N. $$

Step 2. Split the profile $\left\{ {Y\left( i \right)} \right\}\;\left( {i = { 1},{ 2}, \ldots ,N} \right)$ into ${N}_{s}$ ≡ int(N/s) non-overlapping sections of equal length s. Repeat the procedure from the sample to the end to cover the entire sample. Thus, 2 ${N}_{s}$ Segments are obtained in total:

$$ \begin{gathered} \left\{ {Y\left[ {\left( {\nu - {1}} \right)s + i} \right]} \right\}\begin{array}{*{20}c} s \\ i \\ \end{array} = 1,\;\nu = {1},{2}, \ldots ,Ns \hfill \\ \left\{ {Y[N - \, (\nu \, - )s + i]} \right\}\begin{array}{*{20}c} s \\ i \\ \end{array} = 1,\;\nu = N_{s} + 1,N_{s} + 2, \ldots 2N_{s} . \hfill \\ \end{gathered} $$

Step 3. Determine the local trend for each 2 ${N}_{s}$ segment. For each section, a least-square fitting polynomial is utilized to assess the local trend. As a result, the variance is calculated as follows.

$$ F^{2} \left( {s,v} \right) = \left\{ \begin{gathered} \frac{1}{s}\mathop \sum \limits_{i = 1}^{s} \left\{ {Y\left[ {\left( {v - 1} \right)s + i} \right] - \hat{Y}\begin{array}{*{20}c} m \\ v \\ \end{array} \left( i \right)} \right\}^{2} ,\quad \quad \quad \quad \;v = 1,2, \ldots ,N_{s} \hfill \\ \frac{1}{s}\mathop \sum \limits_{i = 1}^{s} \left\{ {Y\left[ {N - \left( {v - N_{s} } \right)s + i} \right] - \hat{Y}\begin{array}{*{20}c} m \\ v \\ \end{array} \left( i \right)} \right\}^{2} ,\quad \;v = N_{s} + 1,N_{s} + 2, \ldots ,2N_{s} . \hfill \\ \end{gathered} \right. $$

In this case, $\widehat{Y}\begin{array}{c}m\\ v\end{array}\left(i\right)$ is the fitting polynomial with order m in segment v. This step typically employs linear (m = 1), quadratic (m = 2), or cubic (m = 3) polynomials (Han et al., 2019a, 2019b; Qian et al., 2011). In this study, we avoid overfitting and simplify calculations using a linear polynomial (m = 1) (Lashermes et al., 2004; Ning et al., 2017).

Step 4. Average across all sections. The qth order fluctuation function is then obtained:

$$ F_{q} \left( s \right) = \left\{ \begin{gathered} \left[ {\frac{1}{{2N_{s} }}\mathop \sum \limits_{v = 1}^{{2N_{s} }} \left( {F^{2} \left( {s,v} \right)} \right)^{q/2} } \right]^{1/q} ,\quad \;\;q \ne 0 \hfill \\ \exp \left[ {\frac{1}{{4N_{s} }}\mathop \sum \limits_{v = 1}^{{2N_{s} }} 1n\left( {F^{2} \left( {s,v} \right)} \right)} \right]\quad q = 0. \hfill \\ \end{gathered} \right. $$

Step 5. Evaluate the fluctuation functions' scaling characteristics. For each value of q, compare the log–log plots ${F}_{q}$(s) with s. ${F}_{q}$(s) increases for large values of s if a long-range power-law correlation exists between the series. The power law is inscribed as follows:

$$ F_{q} \left( s \right) \propto s^{h\left( q \right)} $$

where h(q) signifies the generalized Hurst exponent.

Equation can be composed as ${F}_{q}\left(s\right)$ = a · ${s}^{h\left(q\right)}$ + b. After taking the logarithms of both sides,

$$ \log \;((s)) = h(q) \cdot \log \;(s) + c, $$

where c is a constant.

The exponent h(q) depends on q. When h(q) is independent of q, the time series is monofractal; otherwise, it is multifractal. For q = 2, h(2) is identical to the Hurst exponent (Calvet & Fisher, 2002). As a result, the function h(q) is referred to as a generalized Hurst exponent. If h(2) = 0.5, the time series is uncorrelated and follows a random walk, indicating that the market is inefficient (Alvarez-Ramirez et al., 2008). When the time series is 0.5 < h(2), it is long-term dependent, and an increase (decrease) is more likely to be followed by another increase (decrease). h(2) < 0.5 indicates a non-consistent series; that is, an increase (decrease) is more likely to be followed by a decrease (increase).

According to (Kantelhardt et al., 2002), h(q) relates to the multifractal scaling exponents τ (q) as follows.

$$ \tau (q) = qh(q) - {1}. $$

To estimate multifractality, we use a Legendre transform with the following equations to transform q and τ (q) to α and f (α):

$$ \alpha = \frac{d}{dq}\tau (q), \, f(\alpha ) = \alpha (q)q - \tau (q), $$

where α is the singularity strength, f (α) is the multifractal or singularity spectrum. Following several studies (da Silva Filho et al., 2018; Ruan et al., 2018), the degree of multifractality ∆h is defined as follows.

$$ \Delta h = {\text{max}}(h(q)) - {\text{min}}(h(q)). $$

A larger ∆h value shows a stronger degree of multifractality. In addition, the width of the multifractal spectrum ∆α is defined as follows (da Silva Filho et al., 2018; Ruan et al., 2018).

$$ \Delta \alpha = {\text{max}}(\alpha ) - {\text{min}}(\alpha ). $$

A wider multifractal spectrum denotes a higher degree of multifractality. Furthermore, as an essential feature of the multifractal range (Drożdż et al., 2018; Ruan et al., 2018; Wa̧torek et al., 2019), we define the asymmetry parameter, which estimates the spectrum's asymmetry, as follows.

$$ \Theta { } = \frac{{\Delta \alpha L - \Delta \alpha R{ }}}{\Delta \alpha L + \Delta \alpha R}, $$

where ∆${\alpha }_{L}$ = ${\alpha }_{0}$ − ${\alpha }_{{\text{min}}}$, ∆${\alpha }_{R}$ = ${\alpha }_{{\text{max}}}$ − ${\alpha }_{0}$. In this case, ${\alpha }_{0}$ is the maximum α value of f f(α). For the multifractal spectrum, the asymmetry parameter determines the dominance of small and large fluctuations. When the asymmetry parameter is set to Θ = 0, both large and small fluctuations result in multifractality. Furthermore, Θ > 0 exhibits left-sided asymmetry, implying that subsets of large fluctuations contribute significantly to the multifractal spectrum. Θ < 0 on the other hand, exhibits right-sided asymmetry in the range, indicating that more minor fluctuations are the dominant source of multifractality.

4 Data and Preliminary Analysis

4.1 Original Data

We started gathering samples by downloading each day's stock market return data from the www.investing.com website. The BRICS stock indexes' daily closing prices are used in this analysis. The first is based on BRICS stock market data with no sectorial division. The second comes from the five sector indices of the BRICS stock market (consumer staples, energy, materials, industrials, and financials).

As the regulations on COVID-19 are different in each BRICS country, to prevent misunderstanding, we choose a specific period for pre-COVID-19 and COVID-19 period which are stated by (Maidul Islam Chowdhury et al., 2021). Thus, we calculate the post-COVID-19 period by following the (WHO, 2023) Chief’s declaration.

The dates began in January 2019 and ended in February 2020 for the pre-COVID-19 periods, March 2020 to April 2021 for the COVID-19 period, and May 2021 to April 2023 for the post-COVID-19 periods. As stock market data is unavailable during the lockdown, weekends, or national gazetted holidays, we dropped observations with missing values. We finally got 3770 (non-sectorial division) and 21,175 (sectorial division) observations from the BRICS countries after arranging (Tables 1, 2, and 3).

Table 1 Variable definition

Table 2 BRICS market stock data (without sectorial division)

Table 3 BRICS market stock data (Sectorial division)

4.2 Descriptive Analysis

A natural logarithm is used to convert the price to the return. As empirical data, the daily logarithmic returns ${X}_{t}$ is defined by

$$ {\text{X}}_{{\text{t}}} = {\text{ log P}}_{{\text{t}}} - {\text{logP}}_{{{\text{t}} - 1}} $$

where ${{\text{P}}}_{{\text{t}}}$ represents the closing price on the business day t.

The most straightforward statistical analysis to conduct and interpret is probably descriptive analysis. Despite being unable to provide information for causal analysis, descriptive statistics offer a helpful method for summarising data and describing the sample. Inferential statistics must be used in data analysis to generalize a sample to a larger population.

The descriptive analysis tables from the pre-COVID-19, COVID-19, and post-COVID-19 periods are shown below:

Table 4 displays the descriptive statistics for the pre-COVID-19 stock index return series. For all markets, the average returns are favorable. The Brazilian stock market displays the highest average returns, while India exhibits the lowest average non-negative returns. Its standard deviation is higher than zero. The skewness and kurtosis coefficient values are dissimilar. This series significantly deviates from normality, as evidenced by non-zero skewness and high excess kurtosis.

Table 4 Descriptive analysis for the pre-COVID-19 period

The descriptive statistics for the COVID-19 stock index return series are shown in Table 5. All markets have positive average returns. The Indian stock market has the highest average returns, while Brazil has the lowest average non-negative returns. Its standard deviation exceeds zero. The values of the skewness and kurtosis coefficients differ. Non-zero skewness and a high excess kurtosis show that these series are significantly out of normal.

Table 5 Descriptive analysis of the COVID-19 period

Table 6 shows the descriptive statistics for the post-COVID-19 stock index return series. All markets' average returns are positive. The South African stock market has the highest average non-negative returns, while Brazil has the lowest average negative returns. Its standard deviation is greater than zero. The skewness and kurtosis coefficient values are different. This series deviates significantly from normality, as evidenced by non-zero skewness and high excess kurtosis.

Table 6 Descriptive analysis for the post-COVID-19 period

5 Empirical Results

The multifractal detrended fluctuation analysis (MF-DFA) is the most robust method for time series multifractality detection (Laib et al., 2018). The MF-DFA was employed for the time series components for the BRICS stock market indices. The analysis was carried out in Rstudio using the MF-DFA library (Laib et al., 2019). The time scales ranged from 10 to 200 days. It is advantageous to have scales spaced equally apart (Ihlen, 2012). To realize the MF-DFA, we identified the first-degree (i.e., m = 1) detrending polynomial.

We provide the MF-DFA analysis of the remaining sectorial stock returns time series in the supplementary materials, as we have limited space. These results are equivalent to the ones presented in the main text.

In the following, we present and discuss the empirical results regarding the impact of COVID-19 on stock market efficiency. We categorize three periods of time, and BRICS countries' performances are analyzed under these three segments.

5.1 Pre-COVID-19 Period

5.1.1 Brazil Bovespa (BVSP)

Figure 1 portrays the MF-DFA results for the element of the Brazil Bovespa (BVSP) stock market index. The time scale is 10–200. As seen in Fig. 1a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.3429, in this case, indicates a low persistence for the component.

Fig. 1

The MF-DFA results of the Brazil Bovespa stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 1b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the Brazil Bovespa (BVSP) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Brazilian stock market is more potent for significant movements than for tiny ones.

Figure 1c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 1d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.2356 for the Brazil Bovespa (BVSP) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.1.2 MOEX Russia (IMOEX)

Figure 2 portrays the MF-DFA results for the element of the MOEX Russia (IMOEX) stock market index. The time scale is 10–200. As seen in Fig. 2a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.4729, in this case, indicates a low persistence for the component.

Fig. 2

The MF-DFA results of the MOEX Russia stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 2b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the MOEX Russia (IMOEX) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Russian stock market is more potent for significant movements than for tiny ones.

Figure 2c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 2d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.0378 for the MOEX Russia (IMOEX) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.1.3 India BSE Sensex 30 (BSESN)

Figure 3 portrays the MF-DFA results for the element of the India BSE Sensex 30 (BSESN) stock market index. The time scale is 10–200. As seen in Fig. 3a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.3987, in this case, indicates a low persistence for the component.

Fig. 3

The MF-DFA results of the India BSE Sensex 30 stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 3b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the India BSE Sensex 30 (BSESN) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Indian stock market is more potent for significant movements than for tiny ones.

Figure 3c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 3d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.2556 for the India BSE Sensex 30 (BSESN) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.1.4 China Shanghai Composite (SSEC)

Figure 4 portrays the MF-DFA results for the element of the China Shanghai Composite (SSEC) stock market index. The time scale is 10–200. As seen in Fig. 4a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.5468, in this case, indicates a low persistence for the component.

Fig. 4

The MF-DFA results of the China Shanghai Composite (SSEC) stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 4b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the China Shanghai Composite (SSEC) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Chinese stock market is more potent for significant movements than for tiny ones.

Figure 4c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 4d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.2375 for the China Shanghai Composite (SSEC) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.1.5 South Africa Top 40 (JTOPI)

Figure 5 portrays the MF-DFA results for the element of the South Africa Top 40 (JTOPI) stock market index. The time scale is 10–200. As seen in Fig. 5a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.4399, in this case, indicates a low persistence for the component.

Fig. 5

The MF-DFA results of the South Africa Top 40 stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 5b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the South Africa Top 40 (JTOPI) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the South African stock market is more potent for significant movements than for tiny ones.

Figure 5c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 5d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.1398 for South Africa's Top 40 (JTOPI) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.1.6 Generalized Hurst Exponents

For the BRICS stock indexes over the range of q ∈ [− 4, 4], the estimated generalized Hurst exponents are listed in Table 7. These indices' decreasing functions h(q) show multifractality in the time variations of the remaining component (Laib et al., 2018). The range of generalized Hurst exponents (h) is largest for the Indian and Chinese indices (0.2556 and 0.2375, respectively), which show the highest degree of multifractality, and is narrowest for the Russian and South African indices (0.0378 and 0.1398, respectively), which show the lowest degree of multifractality. Additionally, nonlinear temporal correlation stands for a fat-tailed distribution as the primary contributor to multifractality.

Table 7 Generalized Hurst exponents for the pre-COVID-19 period

The Russian stock market is the most effective in this analysis, while India's is the least one when results for all five stock market indices are compared and the multifractal properties of the stock markets are taken into account (Anagnostidis et al., 2016). The Brazilian stock market is in the middle of things. One of the significant measures of stock market performance is domestic market capitalization, so these consequences are particularly intriguing for the BRICS markets under consideration. According to statistical data for 2020 (O'Neill, 2022), the stock markets in China and Russia are the most advanced in GDP per capita, followed by Brazil and South Africa, with India coming in last.

Different time frames were used in the few studies that included a sample of the BRICS stock markets. Given that the long memory properties of the time series vary with the duration of the period utilized, these results should be evaluated cautiously (Šonje et al., 2011). However, we can state that the findings are consistent with earlier research (Chong et al., 2010; McIver & Kang, 2020; Mensi et al., 2014, 2016) addressing the evidence of the multifractality of all BRICS stock markets.

5.1.7 Ranking Using Market Deficiency Measure

We quantify the market deficiency measure (MDM) and examine the modification in efficiency in the BRICS equity markets to get a complete picture (Mensi et al., 2017; Wang et al., 2009) (Table 8).

Table 8 MDM of MF-DFA for the pre-COVID-19 period

It is said to be efficient if a stock market exhibits random walk behavior for small fluctuations (q = − 4) and large fluctuations (q =  + 4). MDM will thus have zero value in an efficient market but a high value in a less efficient market. Russia has the most effective market, followed by the other BRICS markets. So far, in 2019–2020, Russia's economy has performed well. Russia's stock market is no longer considered a frontier market, which has increased market efficiency and is better news for investors. The Indian market is the least efficient compared to the others due to its Pre-COVID-19 effects.

5.2 During COVID-19 Period

5.2.1 Brazil Bovespa (BVSP)

Figure 6 portrays the MF-DFA results for the element of the Brazil Bovespa (BVSP) stock market index. The time scale is 10–200. As seen in Fig. 6a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.5850, in this case, indicates a low persistence for the component.

Fig. 6

The MF-DFA results of the Brazil Bovespa stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 6b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the Brazil Bovespa (BVSP) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Brazilian stock market is more potent for significant movements than for tiny ones.

Figure 6c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 6d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.5019 for the Brazil Bovespa (BVSP) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.2.2 MOEX Russia (IMOEX)

Figure 7 portrays the MF-DFA results for the element of the MOEX Russia (IMOEX) stock market index. The time scale is 10–200. As seen in Fig. 7a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.3302, in this case, indicates a low persistence for the component.

Fig. 7

The MF-DFA results of the MOEX Russia stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 7b illustrates the generalized Hurst exponents' values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the MOEX Russia (IMOEX) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder's time fluctuations. The overall Hurst exponents' departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Russian stock market is more potent for significant movements than for tiny ones.

Figure 7c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 7d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.6920 for the MOEX Russia (IMOEX) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.2.3 India BSE Sensex 30 (BSESN)

Figure 8 portrays the MF-DFA results for the element of the India BSE Sensex 30 (BSESN) stock market index. The time scale is 10–200. As seen in Fig. 8a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.5309, in this case, indicates a low persistence for the component.

Fig. 8

The MF-DFA results of the India BSE Sensex 30 stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 8b illustrates the generalized Hurst exponents' values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the India BSE Sensex 30 (BSESN) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder's time fluctuations. The overall Hurst exponents' departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Indian stock market is more potent for significant movements than for tiny ones.

Figure 8c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 8d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.3866 for the India BSE Sensex 30 (BSESN) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.2.4 China Shanghai Composite (SSEC)

Figure 9 portrays the MF-DFA results for the element of the China Shanghai Composite (SSEC) stock market index. The time scale is 10–200. As seen in Fig. 9a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.2931, in this case, indicates a low persistence for the component.

Fig. 9

The MF-DFA results of the China SZSE Component stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 9b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the China Shanghai Composite (SSEC) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’ time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Chinese stock market is more potent for significant movements than for tiny ones.

Figure 9c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 9d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.3331 for the China Shanghai Composite (SSEC) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.2.5 South Africa Top 40 (JTOPI)

Figure 10 portrays the MF-DFA results for the element of the South Africa Top 40 (JTOPI) stock market index. The time scale is 10–200. As seen in Fig. 10a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.3532, in this case, indicates a low persistence for the component.

Fig. 10

The MF-DFA results of the South Africa Top 40 stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 10b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the South Africa Top 40 (JTOPI) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the South African stock market is more potent for significant movements than for tiny ones.

Figure 10c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 10d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.5696 for South Africa's Top 40 (JTOPI) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.2.6 Generalized Hurst Exponents

Table 9 contains the estimated generalized Hurst exponents for the BRICS stock indexes for q ∈ [− 4, 4]. We can see that h(q) is a declining function for all of these indices, indicating multifractality in the time fluctuations of the residual component (Laib et al., 2018). The Russian and South African indices (0.6920 and 0.5696, respectively), which indicate the highest degree of multifractality, have the widest range of generalized Hurst exponents (h), and the Chinese, Indian & Brazilian indices (0.3331, 0.3866, and 0.5019, respectively), which indicate the lowest degree of multifractality. In addition, rather than a fat-tailed distribution, nonlinear temporal correlation represents the main factor in the creation of multifractality.

Table 9 Generalized Hurst exponents for the COVID-19 period

When findings for all five stock market indices are compared, and the stock markets' multifractal characteristics are considered, the Chinese stock market is shown to be the most efficient in this analysis, while Russia's is the least efficient (Anagnostidis et al., 2016). The Brazillian stock market is in the middle of things. Given that one of the common indicators of stock market development is domestic market capitalization, these results are particularly intriguing for the BRICS markets under consideration. According to statistical data for 2020 (O’Neill, 2022), the stock markets in China and Russia are the most advanced in GDP per capita, followed by Brazil and South Africa, with India coming in last.

Given that the extended memory properties of the time series vary depending on the duration of the period utilized, these results should be evaluated with care (Šonje et al., 2011). The few studies that used a sample of BRICS stock markets as their subject matter have various time horizons. We can, however, state that the results are consistent with earlier research (Chong et al., 2010; McIver & Kang, 2020; Mensi et al., 2014, 2016) on the evidence of multifractality in all BRICS stock markets.

5.2.7 Ranking Using Market Deficiency Measure

To get a complete picture, we quantify the market deficiency measure (MDM) and analyze the change in efficiency in the BRICS equity markets (Mensi et al., 2017; Wang et al., 2009) (Table 10).

Table 10 MDM of MF-DFA for the COVID-19 period

A stock market is seen as effective if it behaves randomly for both small fluctuations (q = − 4) and large fluctuations (q =  + 4). MDM will not be valuable in an efficient market because of this, but it will be valuable in an inefficient market. The other BRICS markets are the most efficient, followed by the Russian market. The economy of China has done well so far in 2020–2021. The Chinese stock market is no longer viewed as a frontier market but as one that is developing, improving market efficiency, and is decent news for investors. The Russian market is the least efficient of the four due to its Pre-COVID-19 effects.

5.3 Post-COVID-19 Period

5.3.1 Brazil Bovespa (BVSP)

Figure 11 portrays the MF-DFA results for the element of the Brazil Bovespa (BVSP) stock market index. The time scale is 10–200. As seen in Fig. 11a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.5693, in this case, indicates a low persistence for the component.

Fig. 11

The MF-DFA results of the Brazil Bovespa stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 11b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the Brazil Bovespa (BVSP) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Brazilian stock market is more potent for significant movements than for tiny ones.

Figure 11c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 11d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.2090 for the Brazil Bovespa (BVSP) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.3.2 MOEX Russia (IMOEX)

Figure 12 portrays the MF-DFA results for the element of the MOEX Russia (IMOEX) stock market index. The time scale is 10–200. As seen in Fig. 12a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.4238, in this case, indicates a low persistence for the component.

Fig. 12

The MF-DFA results of the MOEX Russia stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 12b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the MOEX Russia (IMOEX) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Russian stock market is more potent for significant movements than for tiny ones.

Figure 12c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 12d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.6126 for the MOEX Russia (IMOEX) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.3.3 India BSE Sensex 30 (BSESN)

Figure 13 portrays the MF-DFA results for the element of the India BSE Sensex 30 (BSESN) stock market index. The time scale is 10–200. As seen in Fig. 13a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.5079, in this case, indicates a low persistence for the component.

Fig. 13

The MF-DFA results of the India BSE Sensex 30 stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 13b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the India BSE Sensex 30 (BSESN) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Indian stock market is more potent for significant movements than for tiny ones.

Figure 13c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 13d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.1926 for the India BSE Sensex 30 (BSESN) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.3.4 China Shanghai Composite (SSEC)

Figure 14 portrays the MF-DFA results for the element of the China Shanghai Composite (SSEC) stock market index. The time scale is 10–200. As seen in Fig. 14a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.5980, in this case, indicates a low persistence for the component.

Fig. 14

The MF-DFA results of the China SZSE Component stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 14b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the China Shanghai Composite (SSEC) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’ time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the Chinese stock market is more potent for significant movements than for tiny ones.

Figure 14c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 14d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.0713 for the China Shanghai Composite (SSEC) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.3.5 South Africa Top 40 (JTOPI)

Figure 15 portrays the MF-DFA results for the element of the South Africa Top 40 (JTOPI) stock market index. The time scale is 10 to 200. As seen in Fig. 15a, the well-fitting fluctuations functions produce a straight line in log–log scales, indicating scaling for any q. In the specific case of the stationary series, ${H}_{2}$ evolves as the well-known Hurst exponent (Feder, 1988); q = 2 is employed as the scaling exponent, leading to the computation of the Hurst exponent for stationary series. H = 0.4547, in this case, indicates a low persistence for the component.

Fig. 15

The MF-DFA results of the South Africa Top 40 stock market index. a Fluctuation functions for q =  − 4, q = 0, q = 4. b Generalized Hurst exponent for each q. c Renyi exponent, τ(q). d Multifractal spectrum

Figure 15b illustrates the generalized Hurst exponents values H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ versus q from − 4 to 4 to evaluate the multifractality of the South Africa Top 40 (JTOPI) stock market using different trends. As q rises, H(q), ${H}^{+}(q)$, and ${H}^{-}(q)$ values for all series fall, indicating gradually weaker correlations for up and downtrends. Since 0 < Hq < 1, a noise structure exists for all segments with both tiny and large fluctuations. The fact that the function is diminishing shows that multifractality patterns exist in the remainder’' time fluctuations. The overall Hurst exponents departure degrees for upward and downward trends are thus more significant for q > 0 compared to q < 0. According to this result, the correlation asymmetry in the South African stock market is more potent for significant movements than for tiny ones.

Figure 15c depicts the Renyi exponent (q). (q) is linear for the monofractal series but nonlinear for the multifractal series. As seen, (q) is multifractal because of its exponential structure. Multifractality rises in a linear connection with nonlinearity.

Figure 15d shows the multifractal spectrum derived. The multifractal series is typically described by the multifractal spectrum, which has a single hump and is consistent with other signs. The generalized Hurst exponent range, h, is then calculated. The range h represents the multifractality level; the wider this range, the more multifractality is present in the series (Kantelhardt et al., 2002). We discovered ∆h = 0.1050 for South Africa's Top 40 (JTOPI) stock market index. The remaining stock market index constituents consequently show substantial multifractality, with high volatility dominating time dynamics.

5.3.6 Generalized Hurst Exponents

For the BRICS stock indexes over the range of q ∈ [− 4, 4], the estimated generalized Hurst exponents are listed in Table 11. These indices' decreasing functions h(q) show multifractality in the time variations of the remaining component (Laib et al., 2018). The range of generalized Hurst exponents (h) is largest for the Russian and Brazilian indices (0.6126 and 0.2090, respectively), which show the highest degree of multifractality, and is narrowest for the Chinese and South African indices (0.0713 and 0.1050, respectively), which show the lowest degree of multifractality. Additionally, nonlinear temporal correlation stands for a fat-tailed distribution as the primary contributor to multifractality.

Table 11 Generalized Hurst exponents for the post-COVID-19 period

When results for each of the five stock market indices are compared, and the stock markets' multifractal properties are considered, the Chinese stock market is found to be the most efficient in this analysis, while Russia's is the least efficient (Anagnostidis et al., 2016). The Indian stock market is in the middle of things. According to statistical data for 2020 (O’Neill, 2022), the stock markets in China and Russia are the most advanced in GDP per capita, followed by Brazil and South Africa, with India coming in last. These findings are especially intriguing for the BRICS markets under consideration because domestic market capitalization is one of the widely used indicators of stock market development.

Different time frames were used in the few research that used a sample of BRICS stock markets. Because the long memory properties of the time series vary depending on how long the period was, these results should be interpreted with caution (Šonje et al., 2011). However, we can state that the findings are consistent with earlier research (Chong et al., 2010; McIver & Kang, 2020; Mensi et al., 2014, 2016) addressing the evidence of the multifractality of all BRICS stock markets.

5.3.7 Ranking Using Market Deficiency Measure

To get a complete picture, we quantify the market deficiency measure (MDM) and analyze the change in efficiency in the BRICS equity markets (Mensi et al., 2017; Wang et al., 2009) (Table 12).

Table 12 MDM of MF-DFA for the post-COVID-19 period

If a stock market behaves randomly for both small fluctuations (q = − 4) and large fluctuations (q =  + 4), it is considered efficient. MDM will therefore be zero in an efficient market but hefty in a less efficient market. The other BRICS markets trail behind South Africa in terms of effectiveness. The economy of South Africa was doing well so far in 2022–2023. The South African stock market is now regarded as an emerging market rather than a frontier one, which has improved market efficiency and is great news for investors. The Russian market is the least effective compared to the others because of the effects of post-COVID-19 and the Russia-Ukraine War.

5.4 GARCH Model for Volatility

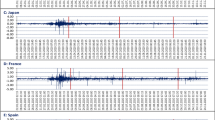
One of the challenges of analyzing time series data is heteroskedasticity, which means that the variance of the data changes over time. This can affect both daily and monthly data, and it can bias the estimation of mean reversion. A common way to deal with heteroskedasticity is to use a GARCH model, which captures the dynamics of the variance and adjusts for it. By using a GARCH model, we can obtain more accurate and reliable results for mean reversion(Bollerslev, 1986; Engle, 1982). This study also employs a GARCH (1,1) model, which captures the volatility of the market by using past squared observations and past variances to estimate the variance at each time point.

The individual outcomes of applying GARCH to Periods are shown here.

5.5 Pre-COVID-19 Period

5.5.1 Brazil Bovespa (BVSP)

Dependent Variable: BRAZIL

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 10:42

Sample (adjusted): 2 172

Included observations: 171 after adjustments

Convergence achieved after 14 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.001315	0.001006	1.307854	0.1909
BRAZIL(− 1)	− 0.011906	0.090495	− 0.131565	0.8953

	Variance equation
C	2.11E−05	4.11E−05	0.512172	0.6085
RESID(− 1)2	0.035921	0.054996	0.653153	0.5137
GARCH(− 1)	0.818402	0.328844	2.488724	0.0128
R-squared	0.000261	Mean dependent var	0.001192
Adjusted R-squared	-0.005655	S.D. dependent var	0.011955
S.E. of regression	0.011988	Akaike info criterion	-5.974482
Sum squared resid	0.024289	Schwarz criterion	-5.882621
Log likelihood	515.8182	Hannan-Quinn criter	-5.937209
Durbin-Watson stat	2.001900

According to the AIC and SIC criteria, GARCH (1,1) is efficient. The BRAZIL (− 1) term in the mean equation is significant and negative, indicating that past returns have a negative impact. The GARCH (1,1) model's parameters are statistically significant. The constant in the variance equation is almost zero, implying that the current volatility depends on the past stock returns and squared lagged residuals. Moreover, the results show a stronger ARCH and GARCH effect, as the sum of α and β in the model is close to one [0.854323]. This means that historical volatility, which persists over time, can explain the daily returns' current volatility.

5.5.2 China Shanghai Composite (SSEC)

Dependent Variable: CHINA

Method: ML ARCH—Normal distribution

Date: 12/16/23 Time: 10:39

Sample (adjusted): 2 172

Included observations: 171 after adjustments

Convergence achieved after 23 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.001693	0.000970	1.746653	0.0807
CHINA(− 1)	− 0.002033	0.073920	− 0.027499	0.9781

	Variance equation
C	1.96E−05	9.86E−06	1.989708	0.0466
RESID(− 1)2	0.423385	0.089793	4.715132	0.0000
GARCH(− 1)	0.602159	0.062006	9.711241	0.0000
R-squared	− 0.001701	Mean dependent var	0.001059
Adjusted R-squared	− 0.007628	S.D. dependent var	0.015077
S.E. of regression	0.015135	Akaike info criterion	− 5.658077
Sum squared resid	0.038711	Schwarz criterion	− 5.566215
Log likelihood	488.7656	Hannan− Quinn criter	− 5.620803
Durbin-Watson stat	2.024425

According to the AIC and SIC values, the GARCH (1,1) model is the optimal choice. The mean equation indicates that the current returns are negatively affected by the previous returns, as the CHINA (− 1) coefficient is negative and significant. The variance equation shows that the historical volatility and the lagged squared residuals have an impact on the current volatility. The constant term is negligible, as it is almost zero. The sum of α and β is slightly above one [1.025544], which implies a high persistence of volatility over time. The GARCH (1,1) model parameters are all statistically significant. However, the persistence of volatility is not a robust finding for this study, as the sum of α and β is marginally larger than one [1.025544], which suggests that the conditional variance process is explosive.

5.5.3 India BSE Sensex 30 (BSESN)

Dependent Variable: INDIA

Method: ML ARCH—Normal distribution

Date: 12/16/23 Time: 10:45

Sample (adjusted): 2 172

Included observations: 171 after adjustments

Convergence achieved after 40 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.000369	0.000565	0.652166	0.5143
INDIA(− 1)	0.114569	0.104270	1.098765	0.2719

	Variance equation
C	4.98E−05	1.59E−05	3.134887	0.0017
RESID(− 1)2	0.608874	0.117608	5.177154	0.0000
GARCH(− 1)	− 0.047129	0.153374	− 0.307280	0.7586
R-squared	− 0.008594	Mean dependent var	0.000415
Adjusted R-squared	− 0.014562	S.D. dependent var	0.009332
S.E. of regression	0.009400	Akaike info criterion	− 6.585113
Sum squared resid	0.014933	Schwarz criterion	− 6.493251
Log likelihood	568.0271	Hannan− Quinn criter	− 6.547839
Durbin-Watson stat	2.200815

According to the AIC and SIC criteria, GARCH (1,1) is an efficient model. The mean equation shows a significant and negative INDIA (− 1) coefficient, implying that past returns have a negative impact. The GARCH (1,1) model's parameters are statistically significant. The variance equation's constant is almost zero, suggesting that the volatility of the market today depends on squared-lagged residuals and historical stock returns. Furthermore, the model's α and β sum is close to one [0.561745], indicating a strong ARCH and GARCH effect in the results. This means that the historical volatility explains the current volatility of the daily returns, and it persists over time.

5.5.4 MOEX Russia (IMOEX)

Dependent Variable: RUSSIA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 10:46

Sample (adjusted): 2 172

Included observations: 171 after adjustments

Convergence achieved after 22 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.000846	0.000570	1.483046	0.1381
RUSSIA(− 1)	− 0.079755	0.080559	− 0.990014	0.3222

	Variance equation
C	9.63E−06	2.89E−05	0.332894	0.7392
RESID(− 1)2	0.024490	0.072448	0.338035	0.7353
GARCH(− 1)	0.789852	0.594580	1.328421	0.1840
R-squared	0.005119	Mean dependent var	0.000751
Adjusted R-squared	− 0.000767	S.D. dependent var	0.007227
S.E. of regression	0.007229	Akaike info criterion	− 6.977077
Sum squared resid	0.008833	Schwarz criterion	− 6.885215
Log likelihood	601.5401	Hannan− Quinn criter	− 6.939803
Durbin-Watson stat	1.963242

The GARCH (1,1) model is the best fit according to the AIC and SIC values. The mean equation shows a negative and significant coefficient for RUSSIA(− 1), meaning that past returns have a negative effect. The parameters of the GARCH (1,1) model are significant. The constant term in the variance equation is almost zero, which means that the current volatility is influenced by the historical stock returns and squared-lagged errors. The results also reveal a strong ARCH and GARCH effect, as the sum of α and β in the model is close to one [0.814342]. This implies that the current volatility of the daily returns can be explained by the historical volatility, which is persistent over time.

5.5.5 South Africa Top 40 (JTOPI)

Dependent Variable: SOUTH_AFRICA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 10:48

Sample (adjusted): 2 172

Included observations: 171 after adjustments

Convergence achieved after 17 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.000797	0.000707	1.126730	0.2599
SOUTH_AFRICA(− 1)	0.047085	0.085591	0.550121	0.5822

	Variance equation
C	1.33E−05	1.61E−05	0.825852	0.4089
RESID(− 1)2	0.057909	0.063236	0.915763	0.3598
GARCH(− 1)	0.750609	0.248948	3.015119	0.0026
R-squared	0.004095	Mean dependent var	0.000752
Adjusted R-squared	− 0.001798	S.D. dependent var	0.008453
S.E. of regression	0.008461	Akaike info criterion	− 6.669259
Sum squared resid	0.012098	Schwarz criterion	− 6.577397
Log likelihood	575.2216	Hannan− Quinn criter	− 6.631985
Durbin-Watson stat	1.942294

AIC and SIC values indicate that the GARCH (1,1) model is the most suitable. The mean equation has a negative and significant coefficient for SOUTH_AFRICA(− 1), which implies that previous returns have a negative impact. The GARCH (1,1) model parameters are significant. The constant term in the variance equation is almost zero, which suggests that the current volatility depends on the historical stock returns and squared-lagged errors. The results also show a strong ARCH and GARCH effect, as the sum of α and β in the model is close to one [0.808518]. This means that the historical volatility explains the current volatility of the daily returns, which is persistent over time.

5.6 During COVID-19 Period

5.6.1 Brazil Bovespa (BVSP)

Dependent Variable: BRAZIL

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:01

Sample (adjusted): 2 178

Included observations: 177 after adjustments

Convergence achieved after 16 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.002222	0.001263	1.758677	0.0786
BRAZIL(− 1)	− 0.184597	0.068931	− 2.677988	0.0074

	Variance equation
C	1.41E−05	3.91E−06	3.611265	0.0003
RESID(− 1)2	0.001029	0.022784	0.045182	0.9640
GARCH(− 1)	0.925713	0.034064	27.17546	0.0000
R-squared	0.056153	Mean dependent var	− 0.000216
Adjusted R-squared	0.050760	S.D. dependent var	0.029873
S.E. of regression	0.029105	Akaike info criterion	− 5.074829
Sum squared resid	0.148242	Schwarz criterion	− 4.985107
Log likelihood	454.1224	Hannan− Quinn criter	− 5.038441
Durbin-Watson stat	2.068793

The GARCH (1,1) model is the best fit according to the AIC and SIC values. The mean equation shows that past returns have a negative effect on the current returns, as the BRAZIL (− 1) coefficient is negative and significant. The variance equation reveals that the current volatility is influenced by the historical volatility and the lagged squared residuals. The constant term is negligible, while the α and β parameters are significant and add up to almost one [0.926742]. This indicates a high persistence of volatility over time, which can be explained by the historical volatility of the daily returns.

5.6.2 China Shanghai Composite (SSEC)

Dependent Variable: CHINA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:01

Sample (adjusted): 2 178

Included observations: 177 after adjustments

Convergence achieved after 16 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.001317	0.001020	1.290741	0.1968
CHINA(− 1)	0.003233	0.105277	0.030710	0.9755

	Variance equation
C	1.77E−05	1.37E−05	1.296224	0.1949
RESID(− 1)2	0.120975	0.061392	1.970522	0.0488
GARCH(− 1)	0.774862	0.107861	7.183878	0.0000
R-squared	− 0.000078	Mean dependent var	0.001152
Adjusted R-squared	− 0.005793	S.D. dependent var	0.013555
S.E. of regression	0.013594	Akaike info criterion	− 5.780528
Sum squared resid	0.032340	Schwarz criterion	− 5.690807
Log likelihood	516.5768	Hannan− Quinn criter	− 5.744141
Durbin-Watson stat	1.977229

The GARCH (1,1) model is the best fit based on the AIC and SIC criteria. The mean equation reveals a negative and significant relationship between the current and previous returns of CHINA(− 1). The variance equation indicates that the current volatility depends on the past volatility and the lagged squared errors. The constant term is very small and can be ignored. The sum of α and β is nearly one [0.895837], which suggests a high persistence of volatility over time. The GARCH (1,1) model parameters are all statistically significant.

5.6.3 India BSE Sensex 30 (BSESN)

Dependent Variable: INDIA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:00

Sample (adjusted): 2 178

Included observations: 177 after adjustments

Convergence achieved after 50 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob
C	0.002556	0.001079	2.368177	0.0179
INDIA(− 1)	− 0.047144	0.093896	− 0.502085	0.6156

	Variance equation
C	4.90E−06	2.38E−06	2.058832	0.0395
RESID(− 1)2	0.063966	0.023404	2.733104	0.0063
GARCH(− 1)	0.888385	0.031041	28.61970	0.0000
R-squared	0.011064	Mean dependent var	0.001565
Adjusted R-squared	0.005413	S.D. dependent var	0.022783
S.E. of regression	0.022721	Akaike info criterion	− 5.544769
Sum squared resid	0.090344	Schwarz criterion	− 5.455047
Log likelihood	495.7120	Hannan− Quinn criter	− 5.508381
Durbin-Watson stat	2.212951

GARCH (1,1) is a good model based on the AIC and SIC criteria. The mean equation has a negative and significant INDIA (− 1) term, which means that previous returns affect the current ones negatively. The parameters of the GARCH (1,1) model are statistically relevant. The constant in the variance equation is almost zero, which shows that the market volatility today is influenced by squared-lagged errors and past stock returns. Also, the sum of α and β is close to one [0.952351], which shows a strong ARCH and GARCH effect in the results. This implies that the past volatility explains the present volatility of the daily returns, and it lasts over time.

5.6.4 MOEX Russia (IMOEX)

Dependent Variable: RUSSIA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:03

Sample (adjusted): 2 178

Included observations: 177 after adjustments

Convergence achieved after 20 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.001467	0.000949	1.545960	0.1221
RUSSIA(− 1)	0.014261	0.089068	0.160108	0.8728

	Variance equation
C	5.25E−06	1.81E−06	2.904196	0.0037
RESID(− 1)2	0.022476	0.018766	1.197723	0.2310
GARCH(− 1)	0.924138	0.026286	35.15648	0.0000
R-squared	− 0.003240	Mean dependent var	0.001111
Adjusted R-squared	− 0.008973	S.D. dependent var	0.016676
S.E. of regression	0.016751	Akaike info criterion	− 5.798157
Sum squared resid	0.049104	Schwarz criterion	− 5.708435
Log likelihood	518.1369	Hannan− Quinn criter	− 5.761769
Durbin-Watson stat	2.205851

According to the AIC and SIC values, the GARCH (1,1) model is the most suitable. The mean equation has a negative and significant RUSSIA (− 1) coefficient, indicating that previous returns have a negative impact. The GARCH (1,1) model's parameters are significant. The variance equation's constant term is nearly zero, indicating that the current volatility depends on the historical stock returns and squared-lagged errors. The findings also show a strong ARCH and GARCH effect, as the model's α and β sum is close to one [0.946614]. This means that the historical volatility explains the current volatility of the daily returns, which persists over time.

5.6.5 South Africa Top 40 (JTOPI)

Dependent Variable: SOUTH_AFRICA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:02

Sample (adjusted): 2 178

Included observations: 177 after adjustments

Convergence achieved after 28 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.001284	0.001050	1.221919	0.2217
SOUTH_AFRICA(− 1)	− 0.001734	0.085434	− 0.020293	0.9838

	Variance equation
C	6.95E−06	3.04E−06	2.288486	0.0221
RESID(− 1)2	0.058531	0.025956	2.255036	0.0241
GARCH(− 1)	0.886479	0.029636	29.91213	0.0000
R-squared	− 0.000157	Mean dependent var	0.000694
Adjusted R-squared	− 0.005872	S.D. dependent var	0.020701
S.E. of regression	0.020762	Akaike info criterion	− 5.487262
Sum squared resid	0.075436	Schwarz criterion	− 5.397540
Log likelihood	490.6227	Hannan− Quinn criter	− 5.450874
Durbin-Watson stat	2.370697

The GARCH (1,1) model fits the data best, according to the AIC and SIC values. The mean equation shows a negative and significant effect of SOUTH_AFRICA (− 1), meaning that past returns lower the current ones. The GARCH (1,1) model parameters are significant. The constant term in the variance equation is almost zero, indicating that the current volatility is influenced by historical stock returns and squared-lagged errors. The results also reveal a strong ARCH and GARCH effect, as the sum of α and β in the model is close to one [0.94501]. This implies that the historical volatility determines the current volatility of the daily returns, which is persistent over time.

5.7 Post-COVID-19 Period

5.7.1 Brazil Bovespa (BVSP)

Dependent Variable: BRAZIL

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:09

Sample (adjusted): 2 404

Included observations: 403 after adjustments

Convergence achieved after 15 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	− 0.000488	0.000646	− 0.755360	0.4500
BRAZIL(− 1)	− 0.017569	0.057240	− 0.306931	0.7589

	Variance equation
C	5.58E−06	7.84E−06	0.711577	0.4767
RESID(− 1)2	0.029716	0.027069	1.097789	0.2723
GARCH(− 1)	0.937598	0.067884	13.81187	0.0000
R-squared	0.000089	Mean dependent var	− 0.000563
Adjusted R-squared	− 0.002405	S.D. dependent var	0.012879
S.E. of regression	0.012894	Akaike info criterion	− 5.858263
Sum squared resid	0.066669	Schwarz criterion	− 5.808649
Log likelihood	1185.440	Hannan− Quinn criter	− 5.838621
Durbin-Watson stat	1.987632

The GARCH (1,1) model is the best fit according to the AIC and SIC values. The mean equation shows that past returns have a negative and significant effect, as the coefficient of BRAZIL (− 1) is negative. The parameters of the GARCH (1,1) model are significant at the 5% level. The constant term in the variance equation is very small, which means that the current volatility is influenced by the historical stock returns and the squared residuals. The sum of α and β in the model is almost one [0.967314], indicating a high persistence of volatility over time, which can be explained by the historical volatility of the daily returns.

5.7.2 China Shanghai Composite (SSEC)

Dependent Variable: CHINA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:10

Sample (adjusted): 2 404

Included observations: 403 after adjustments

Convergence achieved after 19 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	− 0.000538	0.000550	− 0.977582	0.3283
CHINA(− 1)	− 0.011291	0.058714	− 0.192300	0.8475

	Variance equation
C	4.37E−06	3.98E−06	1.096378	0.2729
RESID(− 1)2	0.053989	0.022531	2.396197	0.0166
GARCH(− 1)	0.908701	0.049832	18.23520	0.0000
R-squared	0.000421	Mean dependent var		− 0.000693
Adjusted R-squared	− 0.002072	S.D. dependent var		0.010856
S.E. of regression	0.010867	Akaike info criterion		− 6.218260
Sum squared resid	0.047354	Schwarz criterion		− 6.168645
Log likelihood	1257.979	Hannan− Quinn criter		− 6.198618
Durbin-Watson stat	2.042328

The GARCH (1,1) model is the best fit according to the AIC and SIC criteria. The mean equation reveals a negative and significant effect of the previous returns on the current returns, as indicated by the CHINA (− 1) parameter. The variance equation demonstrates that the current volatility depends on the historical volatility and the lagged squared errors. The constant term is very small and can be ignored. The sum of α and β is slightly more than one [1.025544], which means that volatility is highly persistent over time. The GARCH (1,1) model parameters are all statistically significant. However, this study does not find robust evidence of volatility persistence, as the sum of α and β is slightly less than one [0.96269], which implies that the conditional variance process is unstable.

5.7.3 India BSE Sensex 30 (BSESN)

Dependent Variable: INDIA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:10

Sample (adjusted): 2 404

Included observations: 403 after adjustments

Convergence achieved after 14 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.000892	0.000421	2.116959	0.0343
INDIA(− 1)	0.104653	0.051946	2.014667	0.0439

	Variance equation
C	2.52E−06	1.61E−06	1.563040	0.1180
RESID(− 1)2	0.088099	0.030520	2.886589	0.0039
GARCH(− 1)	0.882227	0.044591	19.78506	0.0000
R-squared	− 0.008746	Mean dependent var	0.000366
Adjusted R-squared	− 0.011261	S.D. dependent var	0.009147
S.E. of regression	0.009198	Akaike info criterion	− 6.636179
Sum squared resid	0.033927	Schwarz criterion	− 6.586565
Log likelihood	1342.190	Hannan− Quinn criter	− 6.616537
Durbin-Watson stat	2.130994

GARCH (1,1) is an efficient model based on the AIC and SIC criteria. The mean equation has a negative and significant INDIA (− 1) term, which means that previous returns affect the current ones negatively. The parameters of the GARCH (1,1) model are statistically significant. The constant in the variance equation is almost zero, which implies that the market volatility today is influenced by the squared-lagged residuals and the historical stock returns. Moreover, the sum of α and β is close to one [0.970326], which shows a strong ARCH and GARCH effect in the results. This indicates that the historical volatility accounts for the current volatility of the daily returns, and it lasts over time.

5.7.4 MOEX Russia (IMOEX)

Dependent Variable: RUSSIA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:11

Sample (adjusted): 2 404

Included observations: 403 after adjustments

Convergence achieved after 66 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.000929	0.000728	1.276615	0.2017
RUSSIA(− 1)	0.022013	0.056299	0.391010	0.6958

	Variance equation
C	8.21E−06	4.27E−06	1.921126	0.0547
RESID(− 1)2	0.322130	0.024129	13.35049	0.0000
GARCH(− 1)	0.764355	0.026270	29.09630	0.0000
R-squared	− 0.016429	Mean dependent var	− 0.001212
Adjusted R-squared	− 0.018963	S.D. dependent var	0.028059
S.E. of regression	0.028324	Akaike info criterion	− 5.355150
Sum squared resid	0.321699	Schwarz criterion	− 5.305535
Log likelihood	1084.063	Hannan− Quinn criter	− 5.335507
Durbin-Watson stat	2.497235

According to the AIC and SIC values, the GARCH (1,1) model is the most suitable. The mean equation has a negative and significant coefficient for RUSSIA (− 1), indicating that previous returns have a negative impact. The GARCH (1,1) model's parameters are significant. The constant term in the variance equation is almost zero, which suggests that the historical stock returns and squared-lagged errors affect the current volatility. The results also show a strong ARCH and GARCH effect, as the sum of α and β in the model is close to one [1.086485]. This means that the historical volatility explains the current volatility of the daily returns, which is persistent over time. The study's main finding of persistence volatility is weak, as the sum of parameters α and β is slightly above one [1.086485], implying that the conditional variance process is unstable.

5.7.5 South Africa Top 40 (JTOPI)

Dependent Variable: SOUTH_AFRICA

Method: ML ARCH—Normal distribution (Marquardt/EViews legacy)

Date: 12/16/23 Time: 11:12

Sample (adjusted): 2 404

Included observations: 403 after adjustments

Convergence achieved after 14 iterations

Presample variance: backcast (parameter = 0.7)

GARCH = C(3) + C(4)*RESID(− 1)2 + C(5)*GARCH(− 1)

Variable	Coefficient	Std. error	z-statistic	Prob.
C	0.000470	0.000626	0.751282	0.4525
SOUTH_AFRICA(− 1)	0.022351	0.050895	0.439167	0.6605

	Variance equation
C	1.76E−05	1.21E−05	1.456801	0.1452
RESID(− 1)2	0.082275	0.042135	1.952637	0.0509
GARCH(− 1)	0.795573	0.112906	7.046342	0.0000
R-squared	− 0.000533	Mean dependent var	0.000321
Adjusted R-squared	− 0.003028	S.D. dependent var	0.012003
S.E. of regression	0.012021	Akaike info criterion	− 6.011189
Sum squared resid	0.057949	Schwarz criterion	− 5.961575
Log likelihood	1216.255	Hannan− Quinn criter	− 5.991547
Durbin-Watson stat	2.033853

The GARCH (1,1) model fits the data best, according to the AIC and SIC values. The mean equation shows a negative and significant effect of SOUTH_AFRICA (− 1), meaning that past returns lower the current ones. The GARCH (1,1) model parameters are significant. The constant term in the variance equation is almost zero, indicating that the current volatility is influenced by historical stock returns and squared-lagged errors. The results also reveal a strong ARCH and GARCH effect, as the sum of α and β in the model is close to one [0.877848]. This implies that the historical volatility determines the current volatility of the daily returns, which is persistent over time.

5.8 GARCH Volatility Ranking

5.8.1 Pre-COVID-19 Period

Country	C	α	β	α + β
Brazil	0.001315	0.035921	0.818402	0.854323
China	0.001693	0.423385	0.602159	1.025544
India	0.000369	0.608874	-0.047129	0.561745
Russia	0.000846	0.024490	0.789852	0.814342
South Africa	0.000797	0.057909	0.750609	0.808518

The ADF tests indicated that the five indices were stationary at the 1, 5, and 10% levels of significance for the duration of the study. The GARCH (1,1) Model results revealed that the Shanghai Composite (SSEC) index (1.025544) had the highest volatility in the study period. The Bovespa (BVSP) index of Brazil (0.854323) was the second most volatile index. The other three indices had lower volatility than China and Brazil.

5.8.2 During COVID-19 Period

Country	C	α	β	α + β
Brazil	0.002222	0.001029	0.925713	0.926742
China	0.001317	0.120975	0.774862	0.895837
India	0.002556	0.063966	0.888385	0.952351
Russia	0.001467	0.022476	0.924138	0.946614
South Africa	0.001284	0.058531	0.886479	0.94501

Based on the ADF tests, we can conclude that the five indices were stationary at all significance levels during the study period. The BSE Sensex 30 (BSESN)—India index (0.952351) was shown to be extremely volatile based on the results of the GARCH (1,1) Model. The next most volatile index during the study period was MOEX Russia (IMOEX)—Russia (0.946614). In comparison to India and Russia, the remaining three indexes were lower.

5.8.3 Post-COVID-19 Period

Country	C	α	β	α + β
Brazil	− 0.000488	0.029716	0.937598	0.967314
China	− 0.000538	0.053989	0.908701	0.96269
India	0.000892	0.088099	0.882227	0.970326
Russia	0.000929	0.322130	0.764355	1.086485
South Africa	0.000470	0.082275	0.795573	0.877848

The ADF tests show that the five indices were stationary at all levels of significance during the study period. The GARCH (1,1) Model results reveal that the MOEX Russia (IMOEX)—Russia (1.086485) had the highest volatility. BSE Sensex 30 (BSESN)—India (0.970326) was the second most volatile index in the study period. The other three indexes had lower values than Russia and India.

5.9 Remarks

Market efficiency reflects the possibility of earning investment returns. Sometimes, investing during a crisis can yield high profits. We have found that the markets in Russia and India have the highest degree of multifractality (i.e., the lowest level of market efficiency). Except, the Chinese and South African markets are the least dependent in our analysis. Our findings, yet, do not rule out the possibility that stock markets could evolve to become more efficacious (Hull & McGroarty, 2014). As noted by (Mensi et al., 2014), the underdevelopment of these stock markets may be one explanation for the results. There are three different categories for the BRICS stock exchanges: developed (China), advanced emerging (South Africa, Brazil), and frontier (Russia, India). For instance, the two stock markets designated as frontiers continued to fail the "developed equity market" and "liquidity" criteria, demonstrating the importance of sustainable growth. The BRICS markets under consideration will likely exhibit weak market efficiency in subsequent economic cycles due to market capitalization, depth, and liquidity growth.

The section-based analysis showed that the financial industry was the most effective sector before COVID-19. Only India was less efficient in the financial sector than in the materials industry. Materials used in Russia, India, and South Africa during the COVID-19 era were the most productive industries. Brazil and China were the most influential countries in the finance and industrial sectors. As MDM ranking and ∆h produce different outcomes, the COVID-19 post part is a little hazy. Except for South Africa, all countries have efficient financial and industrial systems according to the MDM ranking. The substance also performed best in the multifractality assessment.

Regarding hypothesis testing, the first hypothesis states that COVID-19 would adversely affect the stock market. This is supported by evidence from various countries. The Russian stock market was the leader before COVID-19, but it fell behind during the pandemic. South Africa ranked second before COVID-19 and fourth after it. South Africa showed some improvement after the pandemic. India and China progressed during COVID-19 but lagged before it. Russia suffered from both COVID-19 and the Ukraine conflict. These findings suggest that COVID-19 had a significant and diverse impact on the global stock markets.

The second premise holds that COVID-19 impacts GDP as a whole. Except for China, all nations' GDP per capita fell in 2021 compared to 2020 due to increased fatalities and long-term closures of businesses (Countryeconomy.com, 2022). In contrast, the New Development Bank provides its member countries with 15 billion dollars. Therefore, it appears that both of our hypotheses are true. The BRICS countries are expected to be able to solve these issues soon, it is hoped.

6 Conclusions

In this study, we evaluated the performance of five BRICS stock exchanges, for which earlier empirical research has produced contradictory findings. To identify multifractality in the indices, we employed MF-DFA. The current study's findings show that stock market returns are not, as the efficient market hypothesis would have it, a random process but rather one that is influenced by both large and tiny variations. This explains lower market efficiency for all of the BRICS stock markets considered. The outcomes of our analysis do not support weak-form utilization for any of the BRICS stock markets using recent data, up to April 2023, for the daily values of the BRICS indexes. This study's findings suggest that the COVID-19 pandemic increased stock markets' speculation and called for more policy intervention during this time.

Because the stock market index time series long memory property changes depending on the period, the results should be interpreted cautiously (Mensi et al., 2016). We can conclude that the findings are consistent with earlier research on multifractality in the stock markets of the BRICS (Dutta et al., 2016; Ikeda, 2018; Maganini et al., 2018; Ruan & Zhou, 2011). We discover that the Russian market has the highest range of multifractality in the series, similar to (Oprean & Tănăsescu, 2014).

Following Mobarek and Fiorante (2014), we believe that the efficient markets hypothesis serves two purposes: a theoretical and predictive model for financial market activities and a tool to attract investors to emerging markets, such as the BRICS stock markets. Individual investors and portfolio managers looking for abnormal returns will be drawn to less efficient markets. In contrast, more efficient markets will more accurately represent the interests of agents seeking a better understanding of risk and return and the ideal ratio between them.

This study has two main contributions. First, we examine how the COVID-19 pandemic affects the efficiency of the economy. We analyze how different stock markets react to the pandemic, as investors want to predict the future returns of their investments in different markets. We hypothesize that the stock markets of the BRICS countries have different responses to the spread of COVID-19. Second, we compare the effects of the COVID-19 pandemic on stock market efficiency across different periods. We aim to understand how the pandemic differs from a stable period in terms of its impact on the economy.

This paper presents some valuable insights into financial economics and related disciplines. The findings can help researchers and investors to understand the dynamics and trends of the financial markets better. Our findings are also crucial for policymakers working to ensure the financial markets' long-term, sustainable growth and for practitioners (portfolio managers and individual investors) eager to take advantage of market inefficiencies and apply effective market strategies. These findings can inform policy-making to deal with the economic shocks caused by infectious diseases that may happen again in the future.

Our study has some methodological flaws, but they could be resolved in the future. With more investigation, it might be possible to pinpoint the root of market inefficiency, the variables that affect the strength of the multifractal spectrum, the development of the stock markets in the BRICS countries, and potential regulatory measures that could advance sustainable development. These are only a few possible reasons why the market may be inefficient. Other factors include the presence of relatively high trading and information costs, the traditional financing patterns for BRICS companies, which are susceptible to internal funding and loan finance, the lack of enforcement of investor protection laws, and the existence of relatively recent institutional investor involvement.

On the other hand, the stock market’s credibility and efficiency could be boosted by increased financial disclosure, innovation, and the implementation of laws protecting investors, which would result in a more sustainable evolution of the BRICS stock exchanges. Future studies could deliberate this (Bosch-Badia et al., 2018). They drew attention to recent changes in stock market ethics and approaches to sustainability (environmental, social, and financial). They agreed that stock markets operate more effectively when prices correspond to a stable value.

Even though they are still less developed than those in North America and Europe, the BRICS stock exchanges are growing regarding market cap, trade volume, issuer count, and the accessibility of financial instruments; the BRICS economies' stock exchanges have grown in size and sophistication, stressing the potential role of the BRICS stock markets in assuring long-term economic progress, as suggested by finance-growth nexus theories.