Correlation Structure and Evolution of World Stock Markets: Evidence from Pearson and Partial Correlation-Based Networks

Abstract

We construct a Pearson correlation-based network and a partial correlation-based network, i.e., two minimum spanning trees (MST-Pearson and MST-Partial), to analyze the correlation structure and evolution of world stock markets. We propose a new method for constructing the MST-Partial. We use daily price indices of 57 stock markets from 2005 to 2014 and find (i) that the distributions of the Pearson correlation coefficient and the partial correlation coefficient differ completely, which implies that the correlation between pairs of stock markets is greatly affected by other markets, and (ii) that both MSTs are scale-free networks and that the MST-Pearson network is more compact than the MST-Partial. Depending on the geographical locations of the stock markets, two large clusters (i.e., European and Asia-Pacific) are formed in the MST-Pearson, but in the MST-Partial the European cluster splits into two subgroups bridged by the American cluster with the USA at its center. We also find (iii) that the centrality structure indicates that outcomes obtained from the MST-Partial are more reasonable and useful than those from the MST-Pearson, e.g., in the MST-Partial, markets of the USA, Germany, and Japan clearly serve as hubs or connectors in world stock markets, (iv) that during the 2008 financial crisis the time-varying topological measures of the two MSTs formed a valley, implying that during a crisis stock markets are tightly correlated and information (e.g., about price fluctuations) is transmitted quickly, and (v) that the presence of multi-step survival ratios indicates that network stability decreases as step length increases. From these findings we conclude that the MST-Partial is an effective new tool for use by international investors and hedge-fund operators.

1 Introduction

With the rapid expansion and globalization of economic activity has come a significant correlation increase in world financial markets. Although this interaction among financial markets promotes an optimal allocation of global financial and economic resources, it also allows the spread of financial crises that cause world market deterioration. In 2007, for example, the US subprime mortgage crisis started in US mortgage lenders and investment banks but then spread to insurance companies, commercial banks, and savings institutions, rapidly swept across global financial markets, and resulted in global financial turmoil. Being able to describe and understand correlations in complex financial market systems can thus help market participants and regulators access market information as they make economic policy. It also can help market participants understand the formation mechanism of financial asset prices, i.e., it can aid in the optimization allocation and risk management of financial assets.

Previous research has proposed numerous analytical methods for describing correlations in financial markets, one of the most popular being the correlation-based financial network.¹ This widely-used method measures correlations among the elements (e.g., stock markets) of the financial system, treating stock markets as nodes and correlations among them as edges that connect the nodes. The existing literature provides a variety of correlation-based network methods of constructing a filtered network for investigating its potential structure. The correlation-based network methods tend to fall into three categories according to the way they measure correlation.

• (i) Pearson correlation-based network methods construct and measure the network using Pearson correlation coefficients. The pioneering work is done by Mantegna (1999) who propose a minimum spanning tree (MST) for investigating the correlation structure of financial markets. Tumminello et al. (2005) extend the MST by designing a planar maximally-filtered graph (PMFG), which is a new technique for filtering out information from a complex system (e.g., a financial system). Boginski et al. (2005) propose the correlation threshold (CT) or market graph (MG) method that uses a specified CT to construct a financial network. Pearson correlation-based network approaches have been widely applied to various financial systems (see, e.g., Onnela et al. 2003, 2004; Kwapień et al. 2009; Aste et al. 2010; Gilmore et al. 2010; Tse et al. 2010; Song et al. 2011; Buccheri et al. 2013; Vizgunov et al. 2014; Wang and Xie 2015, 2016; Birch et al. 2016).

• (ii) Partial correlation-based network approaches compute and filter a network using partial correlation coefficients. Because financial markets are complex systems that consist of interwoven heterogeneous agents (Mantegna and Stanley 2000; Podobnik et al. 2011; Kwapień and Drożdż 2012; Qian et al. 2015), the correlation between two financial agents is often affected by other financial agents, i.e., two interacting financial agents may also be correlated with other financial agents. For example, the Chinese and Hong Kong stock markets may also be influenced by the US stock market or by European stock markets. If we remove any effects of the US and European stock markets hidden in the correlation between the Chinese and Hong Kong stock markets we get the “net” (or “pure”) correlation between the two markets. The partial correlation coefficient quantifies the “net” correlation between any two financial agents by measuring the relation between two financial agents and discounting the effects of any other financial agents. Using a partial correlation measure, Kenett et al. (2010) determine correlation dependency (or correlation influence) and propose (i) a partial correlation threshold network (PCTN) that is an extension of the CT or MG method, and (ii) a partial correlation planar maximally filtered graph (PCPG) that is an adaptation of the PMFG approach. These two partial correlation-based networks are also called dependency networks by Kenett et al. (2012a) and have been widely applied to financial markets (see, e.g., Kenett et al. 2012b, 2015).

• (iii) Other correlation-based network methods estimate and build a network using other correlation or similarity measures (Brida and Risso 2010; Wang et al. 2012, 2013a; Matesanz and Ortega 2014). For example, Brida and Risso (2010) propose the tool of symbolic time series analysis to acquire a metric distance between two different stocks and use it to build a MST network for studying the structure of the 30 largest North American companies. Wang et al. (2012) use a dynamic time wrapping method to measure the similarity between two financial agents and combine it with the MST to construct a system of foreign exchange networks. Matesanz and Ortega (2014) employ phase synchronization coefficients and the MST to investigate the nonlinear co-movements of foreign exchange markets during the Asian currency crisis.

Although different correlation-based network methods of analyzing the correlation structure of financial markets have been proposed in the literature, the MST is the preferred and most frequently used because it is simple, robust, and clear as it visualizes the linkages.

Our goal here is to study the correlation structure and evolution of world stock markets using Pearson and partial correlation-based MST methods to construct world stock market networks and to investigate their structure and dynamics. We use these two MST methods because in the literature much use is made of the Pearson correlation-based network to study the correlation structure and evolution of world stock markets. For example, Coelho et al. (2007) use the Pearson correlation-based MST to construct a dynamic network of 53 stock markets during the period 1997–2006 and find that the network tends to become increasingly compact. Gilmore et al. (2008) employ the Pearson correlation-based MST method to study the evolution of linkages in European stock markets and find that the French stock market occupies the center. Eryiǧit and Eryiǧit (2009) investigate the correlation structure of world stock markets using the Pearson correlation-based MST and PMFG and obtain a result that agrees with Gilmore et al. (2008) that the French stock market is the most important node in both the MST and PMFG networks. Liu and Tse (2012) study the correlation structure of world stock markets during the period 2006–2010 using the dynamic Pearson CT method and find that the behavior of stock markets in different countries is synchronous. Although network approaches have produced many new well-documented descriptions of the correlation structure and evolution of world stock markets, no research has done this using a partial correlation-based network, and thus our use of the partial correlation-based MST method is a new application. As a part of our study we will also compare the Pearson and partial correlation-based MSTs.

There are three ways of estimating the partial correlation coefficient. The first is the liner regression method, which is a tedious way of solving two associated linear regression problems, obtaining the residuals, and computing the correlation between the residuals. The second is the iterative method, which is a computationally expensive way, e.g., when the Pearson correlation coefficient is the 0-order partial correlation coefficient, the nth-order partial correlation coefficient is calculated from three ($n-1$)th-order partial correlation coefficients. The third is matrix inversion, which is simple and effective and allows the computing of all partial correlation coefficients. The matrix inversion procedure constructs the Pearson correlation matrix, computes its inverse matrix, and calculates the partial correlation coefficients between any two variables. Kenett et al. (2010, 2012a, b, 2015) choose the second way of estimating the partial correlation coefficients and use the correlation influence values to construct the PCTC and PCPG networks. Strictly speaking, the PCTC and PCPG networks are the influence network. The network linkages are the influences of one node on another, but not the “net” correlation between the two nodes (markets). Thus unlike in Kenett et al. (2010, 2012a, b, 2015), choosing the third way of quantifying partial correlation coefficients between any two financial variables and transforming them into distances that follow Euclidean axioms as in Mantegna (1999) would be novel and a contribution to the literature.

The empirical data for our study are daily closing price indices of 57 stock markets during the period from 2005 to 2014. Following the construction of the MST proposed by Mantegna (1999), we obtain two correlation matrices by computing the Pearson and partial correlation coefficients between any two stock markets, and transform the two correlation matrices into two corresponding distance matrices whose elements fulfill the three axioms of Euclidean distance. We next transform the two distance matrices into two world stock market networks filtered using the Pearson and partial correlation-based MST methods. We designate the two networks MST-Pearson and MST-Partial. We also use the Pearson and partial correlation-based hierarchical trees (HTs) associated with the corresponding MSTs to study the hierarchical structure of world stock markets. Finally we use a rolling window to build time-varying MST-Pearson and MST-Partial networks and examine the evolution of world stock markets. We also investigate the differing topological properties between the MST-Pearson and MST-Partial networks.

In summary, we have made four contributions.

• (i) In studying the 57 stock markets that fall into the three categories of developed market, emerging market, and frontier market, we extend the previous research that is primarily focused on a few developed or emerging markets (see, e.g., the G7 stock markets investigated by Erb et al. 1994, six developed markets studied by Solnik et al. 1996, and the US market and nine Asian markets examined by Chiang et al. 2007) and that does not take into full consideration all possible correlations across different stock markets. Understanding the correlation structure and dynamics across different national stock markets is crucial in constructing globally diversified portfolios for international investors and hedge-fund operators and monitoring the market risk for regulators and policy-markers. Thus our investigation of the interactions across 57 stock markets from a network perspective adds to the existing literature and provides a fuller picture of the interactive behavior of world stock markets for market participants and regulators.

• (ii) Our study is the first to analyze the correlation structure and evolution of world stock markets using Pearson and partial correlation-based networks. Previous studies used only the Pearson correlation-based network. Thus our work is a comparative study that uses a new perspective (the partial correlation-based network) to investigate the correlation structure of world stock markets.

• (iii) Unlike previous partial correlation-based networks (e.g., PCTN and PCPG), we use a new method of constructing partial correlation-based networks. We design the partial correlation-based MST network to analyze the “net” correlation structure of the world stock markets. In addition, our proposed construction method also can be applied to other filtered networks, e.g., PMFG and CT.

• (iv) We find that the MST-Partial, which has a structure that differs from the MST-Pearson, enhances the study of correlation structure in financial markets. Using empirical results, we argue that the outcomes obtained from the MST-Partial network are more useful than those from the MST-Pearson network. This is the case because when we remove the influences of other stock markets, the correlation between any two stock markets is “net.” Thus the MST-Partial is a “net” network that provides a “net” correlation structure for analyzing world stock markets.

The rest of this paper is organized as follows. In the next section, we describe the empirical data and methodologies. In Sect. 3, we show the main empirical results of the MST-Pearson and MST-Partial networks. We provide a discussion and some conclusions in Sect. 4.

Table 1 57 counties (regions) and respective symbols

2 Data and Methodology

2.1 Data

Over the past decade world stock markets have experienced the US subprime crisis, the 2008 financial crisis, and the European debt crisis. This has been an unusually active period, and in our study we follow Bonanno et al. (2000), Coelho et al. (2007) and Liu and Tse (2012) and use data comprising 57 Morgan Stanley Capital International (MSCI) daily closing price indices during the period 3 January 2005–31 December 2014. As in Coelho et al. (2007) and Gilmore et al. (2008), we list indices in US dollars, reflecting the perspective of international investors and hedge-fund operators. They comprise 57 stock market indices in 57 countries and regions across seven areas of the world: seven African indices, 13 Asian indices, 24 European indices, six Latin American indices, three Middle Eastern indices, two North American indices, and two Oceanian indices. Table 1 lists the 57 countries and regions and their respective symbols. The data are obtained from the website of MSCI (https://www.msci.com/end-of-day-data-search). We define the daily stock market or country index returns i to be $r_{i}(t)=\ln P_{i}(t)-\ln P_{i}(t-1)$, where $P_{i}(t)$ and $P_{i}(t-1)$ are values of stock price index i on day t and t–1, respectively. There are 2607 observations for each return series during the period investigated.

2.2 Methodology

To construct Pearson and partial correlation-based MSTs for world stock markets we calculate the Pearson correlation coefficients between all pairs of daily returns of the 57 stock market indices. The Pearson correlation coefficient between any two stock markets i and j is defined

$$\begin{aligned} C_{ij} = \frac{\langle \mathbf{r}_i \mathbf{r}_j \rangle - \langle {\mathbf{r}}_i \rangle \langle {\mathbf{r}}_j \rangle }{\sqrt{\langle {\mathbf{r}}_i^2 - \langle {\mathbf{r}}_i \rangle ^2\rangle \langle {\mathbf{r}}_j^2 - \langle {\mathbf{r}}_j \rangle ^2\rangle }}, \end{aligned}$$

(1)

where $\mathbf{r}_{i}$ and $\mathbf{r}_{j}$ are vectors of return series of stock markets i and j respectively, and $\langle \cdot \rangle$ is the time average over the period investigated.

Then the Pearson correlation matrix C is

$$\begin{aligned} {\mathbf{C}} = \left[ \begin{array}{cccc} C_{11} &{} \quad C_{12} &{} \quad \cdots &{} \quad C_{1N} \\ C_{21} &{} \quad C_{22} &{} \quad \cdots &{} \quad C_{2N} \\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots \\ C_{N1} &{} \quad C_{N2} &{} \quad \cdots &{} \quad C_{NN} \\ \end{array}\right] , \end{aligned}$$

(2)

where $C_{ij}$ ranges from $-1$ to 1 and N is the number of stock markets, which in our case is $N=57$. If two stock markets i and j are each correlated with other stock markets, the correlation between these two markets computed by Eq. (1) may introduce spurious correlation information, which we exclude by introducing a partial correlation coefficient. We use the matrix inversion method to calculate this partial correlation coefficient, the first step of which is computing the inverse matrix of C given by

$$\begin{aligned} {\mathbf{{C}}^{\prime }} = {\mathbf{{C}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {C_{11}^{\prime }}&{} \quad {C_{12}^{\prime }}&{} \quad \cdots &{} \quad {C_{1N}^{\prime }}\\ {C_{21}^{\prime }}&{} \quad {C_{22}^{\prime }}&{} \quad \cdots &{} \quad {C_{2N}^{\prime }}\\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots \\ {C_{N1}^{\prime }}&{} \quad {C_{N2}^{\prime }}&{} \quad \cdots &{} \quad {C_{NN}^{\prime }} \end{array}} \right] . \end{aligned}$$

(3)

For any two stock markets i and j, the partial correlation coefficient is

$$\begin{aligned} C_{ij}^{*} = - \frac{{C_{ij}^{\prime }}}{{\sqrt{C_{ii}^{\prime }C_{jj}^{\prime }} }}, \end{aligned}$$

(4)

where the coefficient $C_{ij}^*$ is the “net” correlation between stock markets i and j, the value that emerges when all influences from other stock markets are excluded. The partial correlation matrix C $^*$ is thus

$$\begin{aligned} {\mathbf{C}}^*= \left[ {{\begin{array}{*{20}c} {C_{11}^*} &{} \quad {C_{12}^*} &{} \quad \cdots &{} \quad {C_{1N}^*} \\ {C_{21}^*} &{} \quad {C_{22}^*} &{} \quad \cdots &{} \quad {C_{2N}^*} \\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots \\ {C_{N1}^*} &{} \quad {C_{N2}^*} &{} \quad \cdots &{} \quad {C_{NN}^*} \\ \end{array}}} \right] . \end{aligned}$$

(5)

As proposed by Mantegna (1999), we can link the stock markets in the MST network by transforming the correlation matrix into a distance matrix. Following Mantegna (1999), we covert the element $C_{ij}$ ($C_{ij}^*)$ in the correlation matrix C $(\mathbf{C}^{*})$ into a distance metric between each pair of stock markets i and j, and this is given by

$$\begin{aligned} d_{ij} = \sqrt{2(1 - C_{ij} )}, \quad \mathrm{or} \; d_{ij}^{*} = \sqrt{2(1 - C_{ij}^{*})}, \end{aligned}$$

(6)

where $d_{ij}$ ($d_{ij}^*$) varies from 0 to 2 and stratifies the three axioms of the Euclidean distance (i) $d_{ij}=0$ if and only if $i=j$, (ii) $d_{ij}=d_{ji}$, and (iii) $d_{ij} \le d_{ik}+ d_{kj}$.² When the distance is short the correlation is high, and vice versa. Thus we can use elements $d_{ij}$ and $d_{ij}^*$ to form two $N\times N$ distance matrices D and $\mathbf{D}^{*}$.

The MST network is a graph constructed by linking N nodes (stock markets) with $N-1$ edges such that the sum of all edge distances is the minimum, i.e., the MST network uses the $N-1$ linkages to extract the most important information from the correlation matrix. We use the Kruskal’s algorithm (1956) to apply the distance matrices D and $\mathbf{D}^{*}$ in constructing the MST-Pearson and MST-Partial networks. There are fours steps in the construction of the Kruskal’s algorithm.

• (i) Place the $N(N-1)/2$ elements from the distance matrix in increasing order.

• (ii) Select the element (e.g., a pair of stock markets) with the shortest distance and add the edge to the graph.

• (iii) Select the next-shortest element and add the edge such that the new graph is still a tree.

• (iv) Repeat (iii) until all stock markets are linked in the graph.

Mantegna (1999) and Mantegna and Stanley (2000) specify the construction of the MST in detail.

Fig. 1

Probability density functions (PDFs) of correlation coefficients for the world stock markets over the period 2005–2014. The left and right panels respectively show the PDFs of Pearson correlation coefficients $\{C_{ij};i<j\}$ and partial correlation coefficients $\{C_{ij}^*;i < j\}$

Table 2 Descriptive statistics of Pearson correlation coefficients $\{C_{ij};i<j\}$ and partial correlation coefficients $\{C_{ij}^*;i < j\}$

3 Empirical Results

3.1 Statistics of Pearson and Partial Correlation Coefficients

Prior to analyzing the MST-Pearson and MST-Partial networks, we investigate the probability density functions (PDFs) of $N(N-1)/2$ elements $\{C_{ij};i<j\}$ in the Pearson correlation matrix C and elements $\{C_{ij}^*;i < j\}$ in the partial correlation matrix $\mathbf{C}^{*}$. Figure 1 provides graphs of the two PDFs. Table 2 provides the descriptive statistics of Pearson correlation coefficients $\{C_{ij};i<j\}$ and partial correlation coefficients $\{C_{ij}^*;i < j\}$. From Fig. 1 and Table 2 we see that the two PDFs differ completely. The PDF of Pearson correlation coefficients $\{C_{ij};i<j\}$ is a nonsymmetrical distribution with a large positive value at its center that deviates from a Gaussian-like shape. Like the correlation distribution reported in Drożdż et al. (2001) and Wang and Xie (2015), the distribution of $\{C_{ij};i<j\}$ is bimodal, indicating that the distribution may be derived from two independent markets and that the MST-Pearson network has a minimum of two large independent clusters. The PDF of partial correlation coefficients $\{C_{ij}^*;i < j\}$ has a non-Gaussian shape with a high degree of kurtosis and a long right tail. Table 2 shows that for each distribution the Jarque–Bera statistic rejects the null hypothesis of Gaussian distribution at the 1 % significance level. By comparing the mean, maximum, and minimum values of the two distributions, we conclude that the partial correlations between world stock market pairs are smaller than the Pearson correlations, indicating that correlations between world stock market pairs are significantly influenced by other stock markets.

Fig. 2

(Color online) MST-Pearson network of 57 stock indices in the world stock markets obtained from the Pearson correlation matrix computed by all daily index returns during the period 2005–2014. In the network, the length of the edge between two nodes stands for the relative distance between two nodes. The longer the edge, the father the distance between two nodes, and the smaller the correlation between two stock markets is. The color and shape of the symbols represent the geographical distribution of the host country (region) of the stock market. African stock markets are orange circles, Asian are cyan diamonds, European are yellow squares, Latin American are blue triangles, Middle Eastern are green diamonds, North American are red circles, and Oceanian are magenta squares

3.2 Results of MSTs and HTs

Figures 2 and 3 show the MST-Pearson and MST-Partial networks of 57 world stock market indices acquired from the Pearson correlation matrix and the partial correlation matrix estimated using all daily index returns over the period 2005–2014. In both figures, the colors and shapes of the symbols indicate the geographical distribution of the host country (region) of the stock market, i.e., the host countries (regions) from the same geographical location are coded using the same color and shape. The length of an edge shown in the figure reflects the relative distance between the two corresponding nodes. For example, in Fig. 2 the FRA–DEU length is shorter than the FRA-NOR length, indicating that the distance between FRA and DEU is less than the distance between FRA and NOR. It also indicates that the correlation between the French stock market and the German stock market is greater than between the French stock market and the Norwegian stock market.

Figure 2 shows a MST-Pearson network comprised of two large clusters, one Western and one Eastern, and this suggests that stock markets tend to cluster according to their geographical distribution. There are two clusters in the Western cluster, the European cluster with the French stock market (FRA) at its center and the American cluster that includes stock markets in North America and Latin America. The Eastern cluster is the Asia-Pacific cluster and it has two centers, the Singapore stock market (SGP) and the Australian stock market (AUS). The African stock markets (e.g., KEN, NGA, MUS, and TUN) deviate from this network clustering, their distribution is dispersed, and they do not form clusters. This may be because the economies of many African countries are underdeveloped and the capital markets are dominated by frontier markets.

Fig. 3

(Color online) MST-Partial network of 57 stock indices in the world stock markets obtained from the partial correlation matrix computed by all daily index returns during the period 2005–2014. In the network, the length of the edge between two nodes stands for the relative distance between two nodes. The longer the edge, the father the distance between two nodes, and the smaller the correlation between two stock markets is. The color and shape of the symbols represent the geographical distribution of the host country (region) of the stock market. African stock markets are orange circles, Asian are cyan diamonds, European areyellow squares, Latin American are blue triangles, Middle Eastern are green diamonds, North American are red circles, and Oceanian are magenta squares

The distances between stock markets in the European cluster are smaller than in the American cluster and the Asia-Pacific cluster, which suggests that correlations between the European stock markets are stronger than in other regional stock markets. The MST-Pearson network indicates an surprising linkage among ten stock markets, i.e., CAN in North America, GBR in Europe, ZAF in Africa, AUS and NZL in Oceania, and SGP, IND, LKA, MYS, and PAK in Asia. The host countries of all ten of these stock markets are member states of the Commonwealth of Nations, indicating that their capital markets may be influenced by shared common values and goals. As indicated by Coelho et al. (2007), it is surprising that the USA stock market, the largest stock market in the world, is not the hub in the MST-Pearson network and is only a bridge between CAN and the Latin American cluster. This may be because the strong correlations among the 21 European stock markets lessen the influence of the USA stock market. By removing the influences of other stock markets (most of which will be from the same geographical location) on the correlations, the MST-Partial network reveals the “net” correlation structure of world stock markets.

Figure 3 shows that the structure of the MST-Partial network differs from the structure of the MST-Pearson network. The biggest difference is that the Western cluster is broken into three clusters, two in the European cluster and one in the American cluster comprising North America and Latin America.³ The European cluster has one stock market cluster in Western and Southern Europe and the other in Northern, Central, and Eastern Europe. The American cluster with the USA stock market at its center bridges the two European clusters, indicating that the USA stock market is the actual hub and has the dominant market position. In the MST-Partial network, the Asia-Pacific cluster is more highly concentrated and has three subsets, (i) a big sub-cluster with SGP at its hub, (ii) an Oceanian cluster consisting of AUS and NZL, and (iii) a cluster comprised of JPN, KOR, and TWN. Two Middle Eastern stock markets, i.e., the Lebanese stock market (LBN) and the Jordanian stock market (JOR), link with the Egyptian stock market (EGY), again indicating that geographical distribution strongly influences network architecture.

Fig. 4

(Color online) Hierarchical trees (HTs) of 57 stock indices in the world stock markets during the period 2005–2014. a and b respectively show the HT-Pearson and HT-Partial obtained from the Pearson and partial correlation matrices estimated by all daily index returns. The color of symbols represents the geographical distribution of the host country (region) of the stock market. African stock markets are orange, Asian are cyan, European are yellow, Latin American are blue, Middle Eastern are green, North American are red, and Oceanian are magenta

In addition to our use of the MST-Pearson and MST-Partial networks to investigate the hierarchical structure of world stock markets, we also use the hierarchical tree (HT). We construct the HT using an ultrametric distance metric that fulfills the first two properties of the Euclidean distance, and also the ultrametric inequality (${\hat{d}_{ij}} \le \max \{ {\hat{d}_{ik}},{\hat{d}_{kj}}\}$), which is stronger than the triangular inequality of the Euclidean distance. Mantegna (1999) and Mantegna and Stanley (2000) provide a detailed introduction to HT. Using Pearson and partial correlation matrices, we obtain two HTs, i.e., HT-Pearson and HT-Partial of world stock markets during the period 2005–2014 (see Fig. 4).

Figure 4a shows at least four hierarchical clusters of linked stock markets in the HT-Pearson. The first is a European cluster that encompasses most European markets. The distance between FRA and DEU is the smallest in the HT-Pearson, indicating that the relationship between the French and German markets is the strongest of all world stock markets. The second is the North American cluster composed of CAN and USA. The third is the Latin American cluster that consists of BRA and MEX. These two clusters are closely linked and constitute an American cluster. The fourth is the Asia-Pacific cluster comprising two sub-clusters, (i) the HKG, CHN, SGP, AUS, and NZL cluster, and (ii) the KOR and TWN cluster. Other Asian stock markets, including MYS, IDN, and IND, also connect to the Asia-Pacific cluster.

Figure 4b shows that (i) the HT-Partial is more hierarchical than the HT-Pearson, (ii) the distances among stock markets are more uniformly distributed, and (iii) more hierarchical clusters are formed in the HT-Partial than in the HT-Pearson. The distance between HKG and CHN in the HT-Partial is the smallest, indicating the tight economic relationship between Hong Kong and the Chinese mainland. We designate this kind of tight relationship a “twin market.” Other twin markets in the HT-Partial include FRA–DEU, CAN–USA, AUS–NZL, ITA–ESP, KOR–TWN, HUN–POL, FIN–SWE, and HRV–SVN. International investors and hedge-fund operators should take co-movements between twin markets into consideration when making portfolio decisions. Except for the two frontier markets LKA and PAK, the rest of the Asian and Oceanian markets form three hierarchical clusters, (i) one composed of most Asian stock markets, (ii) the Oceanian cluster with AUS and NZL, and (iii) one composed of JPN, KOR, and TWN, which is similar to that in the MST-Partial network. The union of European stock markets presented in the HT-Pearson is split into at least five clusters bridged by the American cluster that includes the North American cluster (USA and CAN) and the Latin American cluster (MEX, BRA and PER). This indicates once again that the European and American stock markets are correlated and that the USA stock market is prominent world-wide. In addition to the big cluster with centers in FRA and DEU, the European clusters also include the North European cluster (FIN, SWE, NOR, and RUS), the Central European cluster (CZE, HUF and POL), and other small clusters. A cluster with EGP, JOR, and LBN is formed in the HT-Partial. Overall, the HT-Partial shows more hierarchical clusters and includes more information about world stock markets than the HT-Pearson.

3.3 Scale-Free Structure of MSTs

Scale-free networks, pioneered by Barabási and Albert (1999), are networks with a distribution that follows a power law. They found that many real networks (e.g., the World Wide Web) are scale-free. If a node i has k edges in a network, then k is designated the degree of node i. The degree distribution p(k) is the probability that a node will have k edges and is also the ratio between the number of nodes with k edges and the total number nodes in the network. If the degree distribution p(k) of a network has a power-law tail, i.e.,

$$\begin{aligned} p(k)\sim {k^{ - \alpha }}, \end{aligned}$$

(7)

the network is scale-free or has a scale-free structure (Albert and Barabási 2002). Scale-free structures are widespread in financial networks, e.g., stock market networks (Vandewalle et al. 2001; Onnela et al. 2003) and foreign exchange networks (Górski et al. 2008; Kwapień et al. 2009; Wang et al. 2013a).

Fig. 5

The CDFs P(k) of node degree for MST-Pearson and MST-Partial networks. The tail power-law fitting is estimated by the method of Clauset et al. (2009). If the p value is larger than 0.1, the power-law hypothesis can be accepted for the empirical data; otherwise, reject it. The estimated power-law exponents for the node degree distributions of MST-Pearson and MST-Partial networks are 2.76 and 3.26, respectively. Both their p values (>0.1) accept the power-law hypothesis, meaning that the MST-Pearson and MST-Partial networks are scale-free networks

To study the scale-free structure of MST-Pearson and MST-Partial networks we use an analytical tool proposed by Clauset et al. (2009) that combines the maximum-likelihood estimation method of fitting a power-law with the Kolmogorov-Smirnov (KS) test for goodness-of-fit and confidence-interval. Figure 5 is a graph of the distributions of node degree for the MST-Pearson and MST-Partial networks. Note that when the estimated p value is greater than 0.1, the power-law hypothesis for the empirical data stands. Clauset et al. (2009) provide a detailed explanation of p value. Figure 5 shows that the power-law exponents are 2.76 and 3.26 for the two MSTs and the corresponding p values are greater than 0.1, indicating that the MST-Pearson and MST-Partial networks are scale-free networks.⁴ In general, the closer the value of the power-law exponent $\alpha$ is to 1.0, the longer the tail of the distribution, and the larger the proportion of the distribution in the tail. Thus the degree distribution with $\alpha =2.76$ in the MST-Pearson network has a greater proportion of tail distribution than the degree distribution $\alpha =3.26$ for the MST-Pearson network, and this is in accord with the graphic results shown in Figs. 2 and 3. This is because the MST-Pearson network is more compact than the MST-Partial network, e.g., the degree of FRA in the former network is greater than in the latter.

3.4 Centrality Structure of MSTs

To measure the relative influence of stock markets, we analyze the centrality structure of MST-Pearson and MST-Partial networks using centrality measures—influence strength, betweenness centrality, and closeness centrality—to quantify the centrality structure of the MSTs.

The influence strength (IS) of a node is the sum of the correlations of the node with all other connected nodes (Kim et al. 2002), i.e.,

$$\begin{aligned} S(i) = \sum \limits _{j \in {\varGamma } _i} {\rho _{ij}}, \end{aligned}$$

(8)

where S(i) is the influence strength of node i and $\rho _{ij}$ the correlation coefficient between nodes (stock markets) i and j. Here $\rho _{ij}$ represents the Pearson and partial correlation coefficients, and ${\varGamma }_{i}$ represents the neighbors of node i.

The betweenness centrality (BC) of a node quantifies the importance of a node when it is positioned between other nodes in the network. The betweenness centrality B(i) of node i is defined (Freeman 1977)

$$\begin{aligned} B(i) = \sum \limits _{k \ne i \ne h} {\frac{\sigma _{kh} (i)}{\sigma _{kh}}}, \end{aligned}$$

(9)

where $\sigma _{kh}(i)$ is the number of shortest paths between nodes (stock markets) k and h that run through node (stock market) i, and $\sigma _{kh}$ is the total number of shortest paths between k and h.

The betweenness centrality (BC) of an edge is similar to the definition of BC for a node, i.e., it is the number of shortest paths passing through the edge in the network (Girvan and Newman 2002).

Table 3 The top five markets of MST-Pearson and MST-Partial networks according to values of influence strength (IS), betweenness centrality (BC), and closeness centrality (CC)

The closeness centrality (CC) of a node is the reciprocal of its farness. The farness of a node is defined as the sum of all the shortest path lengths from the node to all other nodes in the network. On average, the larger the closeness centrality of a node, the closer the node is to other nodes (Tabak et al. 2010). For a node i in a network with N nodes, the closeness centrality C(i) is

$$\begin{aligned} C(i) = \frac{1}{\sum \nolimits _{j = 1}^N {l_{ij}} }, \end{aligned}$$

(10)

where $l_{ij}$ is the shortest path length from node i to node j.

We calculate the influence strength, betweenness centrality, and closeness centrality values for each node in the MST-Pearson and MST-Partial networks. Table 3 shows the top five markets (nodes) of the MST-Pearson and MST-Partial networks ranked by their corresponding values.

In the MST-Pearson network four markets, including two European markets (France and UK), one Asian market (Singapore), and one Oceanian stock market (Australian), are always among the top five irrespective of how they are measured. The betweenness centrality and closeness centrality of the South African stock market also perform well. Somewhat surprisingly, the stock markets of the USA (the biggest economic entity), Germany (the economic engine of Europe), and Japan (with a huge economy and world-wide trading volume) never rank in the top five.

In the MST-Partial network the French market occupies the top position irrespective of how it is measured. This may be because the headquarters of the World Federation of Exchanges (WFE) is located in Paris, and this would allow other markets to have co-movements with the French stock market. Note that the USA, German, and Japanese stock markets appear in the top-five ranking, that the USA and German markets are particularly strong, and that the Swiss and Canadian stock markets are also influential and important.

To determine the influence of edges in the MSTs, we compute the values of the edge betweenness centrality in MST-Pearson and MST-Partial networks. Table 4 shows the top five market–market edges in the two MSTs. A network edge with a large betweenness centrality value links two parts of the network. For example, if we remove or break the edge between AUS and ZAR in the MST-Pearson network shown in Fig. 2, the network splits into Western and Eastern clusters. Table 4 shows that, with the exception of FRA, all nodes (markets) on edges in the MST-Pearson network are member states of the Commonwealth of Nations, but that in the MST-Partial network the USA, DEU, FRA, CHE, CAN and JPN markets are the world stock market connectors, a result more in line with our expectations.

Table 4 The top five edges (market–market) of MST-Pearson and MST-Partial networks according to values of the edge betweenness centrality (BC)

3.5 Dynamic Structure of MSTs

To study the evolution of world stock markets, we use a rolling window to analyze the dynamic structure of MSTs. We divide the empirical data from the period 2005–2014 into T windows $t=1, 2, \ldots , T$, with a window width L, i.e., there are L observations of the daily returns from each stock market in the window. Following Wang and Xie (2015), we set window width L to 260 trading days (approximently one trading year) and fix the window step length to one trading day. In each window we calculate the Pearson and partial correlation matrices and obtain two corresponding MSTs. The T MST-Pearson and MST-Partial networks we get we use in investigating the time-varying structure of world stock markets.

In our study of the dynamic structure of the MSTs we focus on (i) the topological properties of the network, and (ii) the linkage survival ratio in the network. Following Onnela et al. (2003) and Wang et al. (2012, 2014), we introduce three measures—normalized tree length, average path length, and mean occupation layer—to analyze the topological properties of the MSTs.

The normalized tree length (NTL) is the average distance of the network at time t (Wang et al. 2012), i.e.,

$$\begin{aligned} \text{ NTL }(t) = \frac{1}{N - 1}\sum \limits _{d_{ij}^t \in {\varTheta }_{t} } {d_{ij}^t}, \end{aligned}$$

(11)

where $d_{ij}^t$ is the distance between nodes i and j at time t, ${\varTheta }_t$ denotes the set of all edges of the network at time t, and $N-1$ is the number of edges.

The average path length (APL) can be used to analyze the network density and is defined

$$\begin{aligned} \text{ APL }(t) = \frac{2}{N(N - 1)}\sum \limits _{i < j} {l_{ij}^t}, \end{aligned}$$

(12)

where $l_{ij}^t$ is the shortest path between nodes i and j in the network at time t.

The mean occupation layer (MOL) proposed by Onnela et al. (2003) is used to characterize the spread of nodes in the network and is defined

$$\begin{aligned} \text{ MOL }(t,v_c^t ) = \frac{1}{N}\sum \limits _{i = 1}^N {\text{ Lev }(v_i^t )}, \end{aligned}$$

(13)

where $v_c^t$ and $v_i^t$ are the central node c and node i, respectively, in the network at time t, and $\text{ Lev }(v_i^t )$ is the difference in level between nodes i and c at time t when the level of the central node c is set at zero.

Fig. 6

Time-varying normalized tree length (NTL) of MST-Pearson and MST-Partial networks. The top and bottom panels respectively show the corresponding results for MST-Pearson and MST-Partial, and the same below

Fig. 7

Time-varying average path length (APL) of MST-Pearson and MST-Partial networks

Fig. 8

Time-varying mean occupation layer (MOL) of MST-Pearson and MST-Partial networks

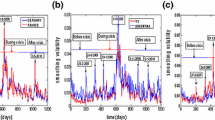
Figures 6, 7 and 8 show the time-varying results of NTL, average path length, and mean occupation layer in the MST-Pearson and MST-Partial networks. Figure 6 shows that all the dynamic values of the NTL in the MST-Partial are greater than in the MST-Pearson, which is the case because the partial correlations between stock markets are smaller than the Pearson correlations. The NTL curves of the two networks both show that during the 2008 financial crisis the values of NTL were clearly lower than average and that there was a valley formed in each curve. Because lower values of NTL correspond to higher correlations across stock markets, these NTL results show evidence of the usually used phase “correlations jump to one” when describing the behavior of financial asset prices during the financial crisis (Papenbrock and Schwendner 2015). During the 2008 financial crisis trigged by the US subprime mortgage crisis, and especially after the bankruptcy of the financial giant Lehman Brothers on 15 September 2008, many stocks and other assets in the USA market declined dramatically in value or even became illiquid (Papenbrock and Schwendner 2015), and this behavior was transmitted to other stock markets and led to increasing correlations across national stock markets. Our finding adds to the literature that financial crises and market crashes usually lead to an increase in correlations (or co-moments) across stock markets (see, e.g., Erb et al. 1994; Solnik et al. 1996; Wang et al. 2011; Rizvi et al. 2015).⁵ The NTL curve of the MTS-Pearson network during the period from Q4 2010 to the end of 2011 shows another significant valley. We also find this fluctuation behavior in the NTL curve of the MST-Partial network during the period July–August 2011. This “July–August-2011 stock market drop” was the worst period in the European debit crisis across the USA, Europe, Middle East, and Asia. The S&P 500 index of the USA fell 6.7 % on 8 August 2011, the FTSE MIB index of Italy fell 24.7 % from 19,491 points on 21 July 2011 to 14,676 points on 10 August 2011, and the FTSE 100 index of the UK dropped 1100 points (about 18.6 %) from above 5900 points on 26 July 2011 to below 4800 points on 9 August 2011. Two reasons for this stock market crash were fears generated by (i) the European debit crisis spreading to Spain, Portugal, and Italy, and (ii) the downgrading of the credit ratings of such countries as the USA and France. These factors increased market coordination and the correlations across stock markets. In 2012 the NTL curves of the two networks exhibited an opposite pattern, i.e., an increasing trend in the MST-Pearson network and a decreasing trend in the MST-Partial network, indicating that the correlation across stock markets declined but the “net” correlation increased. Although bailout procedures were utilized, e.g., a € 120 billion stimulus package passed by the EU and a $430 billion contributed to the IMF by the G20 to halt the contagion, the 2012 world economy was still in crisis and thus the “net” correlation across stock markets increased. More recently both NTL curves have increased and reached the 2005 level, suggesting that the world economy is in recovery and international investors can benefit from global portfolio diversification.

Figure 7 shows that on average the dynamic values of the average path length (APL) in the MST-Partial are larger than in the MST-Pearson, indicating that the MST-Partial requires more intermediary markets to transmit price fluctuations from one market to another than the MST-Pearson. As in the NTL curves, the APL curves of the two MSTs show a sharp fluctuation during the 2008 financial crisis, especially in the MST-Partial network, and the APL reaches its minimum. This finding once again suggests that stock markets are more highly correlated during a crisis and price fluctuations and other information more quickly delivered. Figure 8 shows that in the mean occupation layer (MOL) the dynamic values of the MST-Partial are on average higher than in the MST-Pearson. The MOL curves of the two MSTs also form a valley during the 2008 financial crisis. The smaller MOL value during the crisis means that the transmission of price fluctuations and other information from the central market (node) to other markets (nodes) requires fewer intermediate markets than during more stable periods. Surprisingly, the APL and MOL curves during the European debt crisis are dynamic irrespective of macroeconomic or political events. In summary, the 2008 financial crisis greatly influenced world stock market networks, increased the correlations among them, and made them more sensitive to changes in market price.

Fig. 9

Single-step survival ratios (SSRs) of MST-Pearson and MST-Partial networks

Fig. 10

Multi-step survival ratios (MSRs) of MST-Pearson and MST-Partial networks, where the step length $\delta$ is set to be five trading days (i.e., a 5-day trading week)

We next use the multi-step survival ratio (MSR) and the single-step survival ratio (SSR), measurements proposed by Onnela et al. (2003), to quantify MST edge evolution. The MSR is the ratio between the number of common edges found in successive MSTs and the total number of edges in the MST, i.e.,

$$\begin{aligned} \text{ MSR }(t,\delta ) = \frac{1}{N - 1}\left| {E(t) \cap E(t - 1) \cap \cdots \cap E(t - \delta )} \right| , \end{aligned}$$

(14)

where $\delta$ is the step length and E(t) the set of edges in the MST at time t. For small and large $\delta$ values, MSR ($t,\delta$) quantifies the short-term and long-term MST stability, respectively (Sensoy and Tabak 2014). The larger the survival ratio, the more stable the MST. When $\delta =1$, the MSR reduces to the SSR, i.e.,

$$\begin{aligned} \text{ SSR }(t) = \frac{1}{N - 1}\left| {E(t) \cap E(t - 1)} \right| . \end{aligned}$$

(15)

Fig. 11

Multi-step survival ratios (MSRs) of MST-Pearson and MST-Partial networks, where the step length $\delta$ is set to be 20 trading days (i.e., a 20-day trading month)

Fig. 12

Multi-step survival ratios (MSRs) of MST-Pearson and MST-Partial networks, where the step length $\delta$ is set to be 60 trading days (i.e., a 60-day trading quarter)

Fig. 13

Multi-step survival ratios (MSRs) of MST-Pearson and MST-Partial networks, where the step length $\delta$ is set to be 260 trading days (i.e., a 260-day trading year)

Figure 9 shows the single-step survival ratios (SSRs) of MST-Pearson and MST-Partial networks. Note that the SSR trends in both MSTs are similar and that the SSR values are very high. We find that the average SSR values in the MST-Pearson and MST-Partial are 0.93 and 0.96, respectively, indicating that most linkages survive from one time to the next and that the MSTs in the short term are stable. We then quantify the robustness of the edges by measuring the MSR using different step lengths. We set the MSR step length at a 5-day trading week, a 20-day trading month, a 60-day trading quarter, and a 260-day trading year and examine the stability of the MST-Pearson and MST-Partial networks. Figures 10, 11, 12 and 13 show the results from four different MSRs for the two MSTs. Note that the MSR curves of the two MSTs show the same trend across different step lengths. Note also that increasing the step length intensifies the MSR curves of the two MSTs, suggesting that the MST edges become less stable over time. For example, when the step length is 5 days, the average values of the two MSTs are 0.89 and 0.82, respectively, indicating that 50 linkages in the MST-Pearson network and 46 linkages in the MST-Partial network are identical over 5 days. If we increase the step length to 260 days, however, the average values are 0.22 and 0.13, respectively, suggesting that only 12 linkages in the MST-Pearson and 7 linkages in the MST-Partial networks are identical over one year. Thus international investors and hedge-fund operators should make timely adjustments in their portfolios if they are to avoid or reduce risk.

4 Discussion and Conclusions

In this study we use a complex-network approach to investigate the correlation structure and evolution of world stock markets. Our empirical data are daily price indices of 57 stock markets during the 2005–2014 period, and we construct MST-Pearson and MST-Partial networks. We examine Pearson and partial correlation coefficient statistics, the clustering structure of MSTs, the scale-free structure of MSTs, and the centrality structure of MSTs. We also analyze the hierarchical structure of world stock markets using HTs. As a comparative study, we analyze the topological properties between the MST-Pearson and MST-Partial networks. Finally, we construct time-varying MSTs and use them to study the dynamic structure of MSTs.

Studying the correlation structure and evolution of world stock markets we found (i) that comparing the distributions of Pearson and partial correlation coefficients reveals that the two distributions have fat tails but are totally different, indicating that correlations between two stock markets are greatly influenced by other markets, (ii) that the structure of the MST-Pearson and MST-Partial networks also differs, i.e., the former is more compact than the latter, (iii) that two large stock market clusters (European and Asia-Pacific) form in the MST-Pearson network according to their geographical distribution, and that in the MST-Partial network the European cluster splits into two parts and that they are bridged by the American cluster with the USA at its center, (iv) that the HT-Partial is more hierarchical than the HT-Pearson and more hierarchical clusters are grouped in the former than in the latter, (v) that the degree distributions of both the MST-Pearson and MST-Partial networks show a power-law tail, indicating that the two MST networks are scale-free, (vi) that the centrality measurement results indicate that the ranking of influential markets presented in the two MSTs differ, i.e., in the MST-Pearson network the USA, DEU, and JPN markets are not listed the top five but in the MST-Partial network they are, (vii) that during the 2008 financial crisis the time-varying topological measures of MST-Pearson and MST-Partial networks form a valley, which implies that during crises the world stock markets are tightly correlated and price changes and other information quickly transmitted, and (viii) that increasing the step length decreases the multi-step survival ratio (MSR) values of the two MSTs, indicating that the linkage stability in the two MSTs decreases as step length increases.

We have not taken into consideration non-synchronous trading in world stock markets, and that will be a useful focus for future study. We leave this topic for future study because to the best of our knowledge there is no effective way of eliminating the non-synchronous trading effect. For example, weekly data are usually used to fix the time-zone differences in the study of world stock markets, but trading activities and decisions are heterogeneous and change across days or even hours and minutes (i.e., across different time horizons) and thus weekly data lose information contained in daily data. Eryiǧit and Eryiǧit (2009) find that the weekly MST network is somewhat similar to—but still differs from—the daily MST network. In the well-known work on contagion among stock markets by Forbes and Rigobon (2002), the authors employ the rolling-average 2-day returns of each stock market index to control for the non-synchronous trading effect and find no significant difference between daily returns and rolling-average 2-day returns. This finding is confirmed by Chiang et al. (2007) who study financial contagion with a dynamic conditional-correlation model. But they point out that using rolling-average 2-day returns can easily produce serial auto-correlations and ignores the daily-based announcement effect. Another way of fixing the problem of data asynchronous due to time-zone differences is to lag daily prices or returns of stock market indices (see, e.g., Sheng and Tu 2000). The 57 world stock markets can be divided into three time-zone regions, (i) Asian-Pacific, (ii) European-African, and (iii) American. When measuring the correlations between two stock markets from different regions simultaneously take into consideration three cases, i.e., Asian-Pacific and European-African, Asian-Pacific and American, and European-African and American, and lag one time series of two stock markets by 1 day in each case. A correlation matrix only allows us two choices, however, to lag or not to lag,⁶ which is why Sandoval (2014) uses an enlarged correlation matrix among all original and lagged time series⁷ to analyze the correlation structure of world stock markets. Based on the random matrix theory (RMT), a large body of research (see, e.g., Laloux et al. 1999; Plerou et al. 1999; Kwapień and Drożdż 2012; Zhou et al. 2012; Wang et al. 2013b; Meng et al. 2014, 2015; Dai et al. 2016) finds that the empirical correlation matrix for financial data contains a great deal of random noise. Thus the enlarged correlation matrix would introduce more random noise into the network and make the analysis more complex. Thus finding a way of eliminating the non-synchronous trading effect in the study of world stock markets is a topic worth researching.

Our new perspective described here can be a useful tool for international investors and hedge-fund operators as they make portfolio decisions and for regulators and policy-markers as they assess the market stability and formulate economic policy. Modern investment theory such as the mean-variance model proposed by Markowitz (1952) indicates that investors should hold a diversified portfolio in order to balance risk and optimize returns. Thus international investors investing in more than one stock market would obtain benefits from global portfolio diversification. The correlation structure across different assets is at the root of the optimization problem in the mean-variance model. Previous research shows that a correlation-based network can improve optimal investment strategy. For example, Onnela et al. (2003) find that stocks in a portfolio with minimum risk usually are located in the “leaves” of the MST-Pearson network. Tola et al. (2008) show that the network-filtered correlation matrices used in the mean-variance model can improve the reliability of portfolios. Thus our proposed MST-Partial network offers a new tool for portfolio optimization. Highly correlated stock markets during financial crises lower any potential gains from international portfolio diversification, but the “twin market” (e.g., the HKG–CHN) found in the MST-Partial network offers new opportunities for pair trading. If the highly correlated twin markets show two different trends (i.e., one moves up and the other moves down), for example, investors can go long on the underperforming one, go short on the overperforming one, and close the positions when the correlations between the two return to normal. If market regulators and policy-markers understand the correlation structure and the corresponding clustering structure of stock markets observed in correlation-based networks, they can improve their global and regional policy coordination and deal with extreme market volatility and the co-movements in world stock markets. Information on the evolution of correlation-based networks and their dynamic topological features would enable them to assess market stability and monitor risk.

Appendix

See Figs. 14 and 15 for the triangle inequality verification of the partial correlation-based distance metric $d_{ij}^{*}$.

Fig. 14

Histogram of $\{H_{ikj}\}$ and its descriptive statics for 57 stock market indices during the period from 2005 to 2014

Fig. 15

Minimums of $\{H_{ikj}^{t}\}$ for dynamic MST-Partial networks of 57 stock market indices using rolling windows