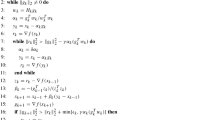1 Introduction

Recently [13], Oviedo proposed a low-cost method for the minimization of large-scale convex quadratic functions, which is based on a smoothing technique combined with a one-step delayed gradient method. For gradient-type methods, smoothing techniques were previously developed [1, 11], as well as delayed schemes [7, 12]. A skillful combination of these independent ideas produces the so-called delayed weighted gradient method (DWGM), which exhibits an impressive fast convergence behavior that compares favorable with the conjugate gradient (CG) method [13]. Moreover, we have observed that in exact arithmetic DWGM also exhibits finite termination, which is a well-known property of the CG method, as well as the Conjugate Residual (CR) method, in the convex quadratic case [14]. Nevertheless, from the same initial guess, DWGM produces a different sequence of iterates to converge (or to terminate) at the same solution obtained by the CG or the CR method (see Table 1, Fig. 1 below). In this work we will establish several properties of the DWGM method, including its surprising finite termination for convex quadratics.

The rest of this document is organized as follows. In Sect. 2, we briefly describe the DWGM algorithm and list the convergence properties established in [13]. In Sect. 3, we describe and establish the additional properties concerning the orthogonality relationships that exist among the involved sequence of vectors produced by the DWGM algorithm, and we also establish the key results concerning finite termination and optimality of the gradient norm. In Sect. 4, we present some final remarks and perspectives.

2 DWGM algorithm

Let us consider the minimization of the strictly convex quadratic function

$$\begin{aligned} f(x) = \frac{1}{2} x^{T} A x - b^{T}x, \end{aligned}$$
(2.1)

where \(b\in \mathbb {R}^n\), \(A\in \mathbb {R}^{n\times n}\) is a symmetric and positive definite (SPD) matrix. Since A is SPD and the gradient \(g(x)\equiv \nabla f(x) = Ax-b\), then the global solution of (2.1) is the unique solution \(A^{-1}b\) of the linear system \(A x = b\). For large n, many low-cost iterative methods have been proposed and analyzed, and in particular some of the so-called gradient-type methods have shown to be very competitive since they show an impressive fast linear convergence; see, e.g., [2,3,4,5,6, 9]. They can all be seen as improved extensions of the classical steepest descent method. From a starting point \(x_0 \in \mathbb {R}^n\), the well-known steepest descent (or gradient) method is given by the iteration

$$\begin{aligned} x_{k+1} = x_k - \lambda _k g_k, \end{aligned}$$

where \(g_k = g(x_k)\) and \(\lambda _k\) is the minimizer of \(f(x_k - \lambda g_k)\). Therefore, if \(g_k \ne 0\),

$$\begin{aligned} \lambda _k = \frac{g_k^T g_k}{g_k^T A g_k}. \end{aligned}$$
(2.2)

This classical low-cost method is globally convergent but its rate of convergence is very slow in most practical cases.

We focus our attention on the DWGM method, that can be viewed as a special gradient-type method. Following the development in [13], the DWGM algorithm is now presented.

figure a

Notice that the iterations in Algorithm DWGM are stopped when the 2-norm of the gradient at \(x_k\) is less than or equal to a preestablished small tolerance \(\varepsilon >0\). Note also that in addition to the sequence of iterates \(\{x_k\}\), the algorithm DWGM generates an auxiliary sequence \(\{y_k\}\), and two associated gradient-type sequences given by

$$\begin{aligned} g_k = A x_k - b \;\;\; \text{ and } \;\;\; r_k = A y_k - b. \end{aligned}$$
(2.3)

Finally, we note that at every k, the scalar \(\beta _k\) is chosen at Step 7 to guarantee that \(g_{k+1}^T(r_k - g_{k-1})=0\), and the scalar \(\alpha _k\) is chosen at Step 4 to minimize the gradient norm along the negative gradient direction, as explained in [13, p. 731]; see also [5].

In [13], it is established that \(\beta _k\ge 0\) for all k, that the sequence \(\{\Vert g_k\Vert _2\}\) is monotonically decreasing, and moreover that the sequence \(\{g_k\}\) converges to zero q-linearly when k goes to infinity, which implies that the sequence \(\{x_k\}\) converges to the unique global minimizer of f(x). Furthermore, from the proof of Lemma 1 in [13], if \(g_k \ne 0\) we notice that

$$\begin{aligned} \Vert r_{k}\Vert _2^2 = \Vert g_{k}\Vert _2^2 - \alpha _k g_k^TAg_k, \end{aligned}$$

and also that

$$\begin{aligned} \Vert g_{k+1}\Vert _2 \le \Vert r_{k}\Vert _2 < \Vert g_{k}\Vert _2\le \Vert r_{k-1}\Vert _2. \end{aligned}$$
(2.4)

Since \(\alpha _k\) can be seen as an inverse Rayleigh quotient of A evaluated at the vector \(A^{1/2}g_k\), where \(\Vert g_{k}\Vert _2\ne 0\), then for all k

$$\begin{aligned} { 0<\frac{1}{\lambda _{\max }(A)} \le \alpha _k \le \frac{1}{\lambda _{\min }(A)} < \infty }, \end{aligned}$$
(2.5)

where \(\lambda _{\min }(A)\) and \(\lambda _{\max }(A)\) are the smallest and largest eigenvalues of A, respectively.

3 Additional properties of DWGM

Let us recall that, in exact arithmetic, the A-orthogonality of the set of all search directions plays a fundamental role in the finite termination of the CG method. Similarly, the A-orthogonality of the set of all residual vectors plays a fundamental role in the finite termination of the CR method see, e.g., [14]. We note that a similar A-orthogonality is not imposed on any of the vector sets used by DWGM, however it also exhibits finite termination for convex quadratic functions, as can be observed in Table 1 and Fig. 1. In order to establish this important fact we need a few preliminary results, which include a few unexpected A-orthogonality relationships.

Lemma 1

In Algorithm DWGM

(a) \(\beta _0 = 1\), and hence \(x_1 = y_0\) and \(g_1 = r_0\).

The following equalities hold for all \(k\ge 0\)

(b) \(r_k^TAg_k = 0\).

(c) \(r_k^T r_k = r_k^T g_k\).

(d) \(g_{k+1}^T(r_k - g_{k-1}) = 0\).

Proof

(a) Since \(g_{-1}=g_0\), using the definition of \(\beta _k\) at Step 7 and \(\alpha _k\) at Step 4, combined with the equality at Step 6, we obtain

$$\begin{aligned} \beta _0 = g_0^T(g_0 - r_0)/\Vert g_0 - r_0\Vert _2 = \alpha _0 (g_0^Tw_0)/\alpha _0^2 \Vert w_0\Vert _2^2= g_0^TAg_0/(\alpha _0\, g_0^TA^2g_0) = 1. \end{aligned}$$

Now, using \(\beta _0 = 1\) in Steps 8 and 9, it follows that \(x_1 = y_0\) and \(g_1 = r_0\).

(b) Combining Steps 6, 4, and 3, we have

$$\begin{aligned} r_k^TAg_k = (g_k - \alpha _k A g_k)^TAg_k = g_k^TAg_k - \alpha _k(g_k^TA^2g_k) = 0. \end{aligned}$$

(c) Using Step 6 and (b) we obtain

$$\begin{aligned} r_k^Tr_k - r_k^Tg_k = r_k^T(r_k - g_k) = -\alpha _k (r_k^T A g_k) = 0. \end{aligned}$$

(d) Follows from the definition of \(\beta _k\) at Step 7 and simple algebraic manipulations. \(\square\)

We note that the choice of \(\alpha _k\) accounts for \(r_k^TAg_k = 0\) for all \(k\ge 0\), which is an A-orthogonality result that will play a key role in the rest of this section.

Table 1 Gradient norm at each iteration (Iter i) of DWGM, CG, and CR, from the same initial point, for the minimization of a strictly convex quadratic function when \(n=5\), and the eigenvalues of A are given by \(\lambda _i = i\), for \(1\le i \le 5\)
Full size table
Fig. 1
figure 1

Convergence history of DWGM, CG, and CR, from the same initial point, for the minimization of a strictly convex quadratic function. On the left, \(n=11\) and we use the following distribution of eigenvalues of A: \(\lambda _1=0.1\), \(\lambda _i=i\) for \(2\le i \le 10\), and \(\lambda _{11}=1000\). On the right, \(n=60\) and we use the following distribution of eigenvalues of A: \(\lambda _1=0.1\), \(\lambda _i=i\) for \(2\le i \le 59\), and \(\lambda _{60}=6000\)

Full size image

Lemma 2

Algorithm DWGM generates the sequence of gradient vectors \(\{g_k\}\) such that for all \(k\ge 1\),

$$\begin{aligned} g_{k}^TA g_{k-1} = 0. \end{aligned}$$

Proof

Using (a) and (b) from Lemma 1, it follows that \(g_1 = r_0\) and \(g_1^TAg_0 = r_0^TAg_0 = 0\), and the result holds for \(k=1\). Let us now assume, by induction on k, that \(g_{k}^TA g_{k-1} = 0\) up to \(k={\hat{k}}\ge 2\), and consider the next iteration. Hence, we need to show that \(g_{{\hat{k}}+1}^TA g_{{\hat{k}}} = 0\). Using Step 9, (b) from Lemma 1, and noticing that by the inductive hypothesis \(g_{{\hat{k}}-1}^TA g_{{\hat{k}}} = 0\), we have

$$\begin{aligned} g_{{\hat{k}}+1}^TA g_{{\hat{k}}} = (g_{{\hat{k}}-1} + \beta _{{\hat{k}}} (r_{{\hat{k}}} - g_{{\hat{k}}-1}))^TAg_{{\hat{k}}} = (1-\beta _{{\hat{k}}})g_{{\hat{k}}-1}^TA g_{{\hat{k}}} + \beta _{{\hat{k}}} r_{{\hat{k}}}^TA g_{{\hat{k}}} = 0, \end{aligned}$$

and the result is established. \(\square\)

Lemma 3

In Algorithm DWGM the following statements hold for all \(k\ge 1\)

  1. (a)

    \(g_k^Tr_{k-1} = g_k^Tg_{k-1}\).

  2. (b)

    \(g_{k-1}^Tr_{k} = g_{k-1}^Tg_k\).

  3. (c)

    \(g_k^Tr_{k-1} = g_{k-1}^Tr_{k}\).

  4. (d)

    \(\Vert g_{k-1} - r_{k}\Vert _2^2 = \Vert g_{k-1} - g_{k}\Vert _2^2 - [(g_k^TAg_{k})^2/g_k^TA^2g_{k}]\).

  5. (e)

    \(g_{k+1}^T(g_k - g_{k-1}) = 0\).

Proof

(a) Using Steps 4 and 6 and Lemma 2, we have

$$\begin{aligned} g_k^T(r_{k-1} - g_{k-1}) = - \alpha _{k-1} g_k^TAg_{k-1} = 0. \end{aligned}$$

(b) Similar to the proof of (a),

$$\begin{aligned} g_{k-1}^T(r_{k} - g_{k}) = - \alpha _{k} g_{k-1}^TAg_{k} = 0. \end{aligned}$$

(c) The result is obtained directly from (a) and (b).

(d) Using Step 4 and 6 of the DWGM algorithm and Lemma 2, we have

$$\begin{aligned} \Vert g_{k-1} - r_{k}\Vert _2^2&= \Vert g_{k-1} - g_{k} + \alpha _{k}Ag_{k}\Vert _2^2 \\&= \Vert g_{k-1} - g_{k}\Vert _2^2 + 2(g_{k-1} - g_{k})^T\alpha _{k}Ag_{k} + \alpha _{k}^2g_{k}^TA^2g_{k} \\&= \Vert g_{k-1} - g_{k}\Vert _2^2 - 2\alpha _{k}g_{k}^TAg_{k} + \alpha _{k}^2g_{k}^TA^2g_{k} \\&= \Vert g_{k-1} - g_{k}\Vert _2^2 - [(g_k^TAg_{k})^2/g_k^TA^2g_{k}]. \end{aligned}$$

(e) Combining Step 6 of the DWGM algorithm, (d) from Lemmas 1 and 2, it follows that

$$\begin{aligned} g_{k+1}^T(g_{k} - g_{k-1}) = g_{k+1}^T( r_{k} + \alpha _{k}Ag_{k} - g_{k-1}) = g_{k+1}^T(r_{k}- g_{k-1}) + \alpha _{k}g_{k+1}^TAg_{k} = 0. \end{aligned}$$

\(\square\)

Lemma 4

In Algorithm DWGM the following statements hold for all \(k\ge 1\)

(a) \(g_{k+1}^Tg_{k+1} = g_{k+1}^Tg_{k} = g_{k+1}^Tg_{k-1}\).

(b) \(\Vert g_{k-1} - g_{k}\Vert _2^2 = g_{k-1}^T(g_{k-1}- g_{k})\)

(c) \(\beta _k = g_{k-1}^T(g_{k-1}- g_{k})/\left( \Vert g_{k-1} - g_{k}\Vert _2^2 - [(g_k^TAg_{k})^2/g_k^TA^2g_{k}]\right) >1\).

Proof

(a) Combining Steps 3, 6, and 9 of the DWGM algorithm, we get

$$\begin{aligned} g_{k+1}^Tg_{k+1} = g_{k+1}^T(g_{k-1} + \beta _k (g_k - g_{k-1} - \alpha _k Ag_k)) = g_{k+1}^Tg_{k-1} + \beta _k g_{k+1}^T(g_k - g_{k-1}) - \alpha _k g_{k+1}^TAg_k. \end{aligned}$$

From (e) in Lemma 3, \(g_{k+1}^T(g_k - g_{k-1})=0\), and from Lemma 2 we have that \(g_{k+1}^TAg_k=0\), and so \(g_{k+1}^Tg_{k+1} = g_{k+1}^Tg_{k-1}\). Now, using again (e) in Lemma 3, we obtain that

$$\begin{aligned} g_{k+1}^Tg_{k-1} = g_{k+1}^Tg_{k}. \end{aligned}$$

(b) From (a) we obtain \(g_{k}^T(g_k - g_{k-1})=0\), and hence

$$\begin{aligned} 0 = (g_{k} - g_{k-1} + g_{k-1})^T(g_k - g_{k-1}) = \Vert g_{k} - g_{k-1}\Vert _2^2 - g_{k-1}^T(g_{k-1} - g_{k}), \end{aligned}$$

which implies that \(\Vert g_{k-1} - g_{k}\Vert _2^2 = g_{k-1}^T(g_{k-1}- g_{k})\).

(c) First, by Cauchy-Schwarz inequality and (2.4), we obtain

$$\begin{aligned} g_{k-1}^Tg_k \le \Vert g_{k-1}\Vert _2 \Vert g_k\Vert _2 < \Vert g_{k-1}\Vert _2^2 = g_{k-1}^Tg_{k-1}, \end{aligned}$$

and hence, using (b) in Lemma 3, we have that \(g_{k-1}^T(g_{k-1} - r_k) = g_{k-1}^T(g_{k-1} - g_k) >0\). Therefore, the numerator at Step 7 of the DWGM algorithm is positive and \(\beta _k>0\). Now, combining Step 7 of the DWGM algorithm with (b) and (d) in Lemma 3 we get

$$\begin{aligned} \beta _k = \frac{g_{k-1}^T (g_{k-1} - r_k)}{\Vert g_{k-1} - r_k\Vert _2^2} = \frac{g_{k-1}^T (g_{k-1} - g_k)}{\left( \Vert g_{k-1} - g_{k}\Vert _2^2 - [(g_k^TAg_{k})^2/g_k^TA^2g_{k}]\right) }. \end{aligned}$$
(3.1)

Since \(\beta _k>0\) and \(g_{k-1}^T (g_{k-1} - g_k)>0\), we obtain that the denominator in (3.1) must be also positive. As a consequence

$$\begin{aligned} 0< (g_k^TAg_{k})^2/g_k^TA^2g_{k} < \Vert g_{k-1} - g_{k}\Vert _2^2, \end{aligned}$$

and we conclude using (b) that in (3.1) the numerator is strictly bigger than the denominator and both are positive, which establishes that \(\beta _k>1\). \(\square\)

In what follows we will establish some key A-orthogonality results, which will be obtained simultaneously using an inductive argument.

Theorem 5

Algorithm DWGM generates the sequences \(\{g_k\}\) and \(\{r_k\}\) such that

(i) For \(k\ge 2\), \(g_{k}^TA g_j = 0\;\;\; \text{ for } \text{ all } \;\;\; -1\le j\le k-2\).

(ii) For \(k\ge 2\), \(r_{k}^TA g_j = 0\;\;\; \text{ for } \text{ all } \;\;\; -1\le j\le k-2\).

Proof

Concerning (i), since \(g_0 = g_{-1}\), \(g_1 = r_0\) and \(\alpha _0 > 0\) (see (2.5)), using (e) from Lemma 3 and Steps 4 and 6 of the DWGM algorithm we obtain

$$\begin{aligned} g_2^TAg_{-1} = g_2^TAg_0 = g_2^T(g_0 - r_0)/\alpha _0 = g_2^T(g_0 - g_1)/\alpha _0 = 0, \end{aligned}$$
(3.2)

and the result is obtained for \(k=2\). Concerning (ii), since \(\alpha _k > 0\) for all k [see (2.5)], using (e) in Lemma 3, (a) in Lemma 1, Step 6 (twice), Lemma 2, and (3.2), it follows that

$$\begin{aligned} r_2^TAg_0&= \frac{1}{\alpha _0}r_2^T(g_0-r_0) = -\frac{1}{\alpha _0}r_2^T(g_1 -g_0) + 0 = -\frac{1}{\alpha _0}r_2^T(g_1 -g_0) + \frac{1}{\alpha _0}g_2^T(g_1 - g_0) \\&= \frac{1}{\alpha _0}(g_2 - r_2)^T(g_1 - g_0) = \frac{\alpha _2}{\alpha _0} g_2^TA(g_1 - g_0) = \frac{\alpha _2}{\alpha _0} [g_2^TAg_1 - g_2^TAg_{-1}] = 0. \end{aligned}$$

Since \(r_2^TAg_{-1} = r_2^TAg_0 = 0\), the result is established for \(k=2\).

Let us now assume, by induction on k, that (i) and (ii) hold up to \(k={\hat{k}} \ge 3\), and consider the next iteration. Hence, we need to show that \(g_{{\hat{k}}+1}^TA g_{j} = 0\), and also that \(r_{{\hat{k}}+1}^TA g_{j} = 0\) , for all \(-1 \le j\le {\hat{k}}-1\).

For \(-1\le j\le {\hat{k}}-2\), using Lemma 2, Step 9 of the DWGM algorithm, and the inductive hypothesis associated with (i) and (ii), we have that

$$\begin{aligned} g_{{\hat{k}}+1}^TA g_{j} = (g_{{\hat{k}}-1} + \beta _{{\hat{k}}}(r_{{\hat{k}}} - g_{{\hat{k}}-1}))^TAg_j = (1-\beta _{{\hat{k}}})g_{{\hat{k}}-1}^TA g_{j} + \beta _{{\hat{k}}} r_{{\hat{k}}}^TA g_{j} = 0. \end{aligned}$$

For \(j = {\hat{k}}-1\), using Step 6, adding and subtracting \(g_{{\hat{k}}-2}\), and then using the fact that \(r_{{\hat{k}}-1} - g_{{\hat{k}}-2} = (g_{{\hat{k}}}-g_{{\hat{k}}-2})/\beta _{{\hat{k}}-1}\) (from Step 9 of DWGM algorithm), we get

$$\begin{aligned} g_{{\hat{k}}+1}^TA g_{{\hat{k}}-1}&= \frac{1}{\alpha _{{\hat{k}}-1}}g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}-1} - r_{{\hat{k}}-1}\Big ) = -\frac{1}{\alpha _{{\hat{k}}-1}}g_{{\hat{k}}+1}^T\Big (r_{{\hat{k}}-1} - g_{{\hat{k}}-2} + g_{{\hat{k}}-2} - g_{{\hat{k}}-1}\Big ) \\&= -\frac{1}{\alpha _{{\hat{k}}-1}}\left[ \frac{1}{\beta _{{\hat{k}}-1}}g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}}-g_{{\hat{k}}-2}\Big ) + g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}-2}-g_{{\hat{k}}-1}\Big ) \right] . \end{aligned}$$

Adding and subtracting \(g_{{\hat{k}}+1}^Tg_{{\hat{k}}-1}\), using (e) from Lemma 3, and Step 9, we obtain

$$\begin{aligned} g_{{\hat{k}}+1}^TA g_{{\hat{k}}-1}&= -\frac{1}{\alpha _{{\hat{k}}-1}}\left[ \frac{g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}}-g_{{\hat{k}}-1}\Big ) + g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}-1}-g_{{\hat{k}}-2}\Big )}{\beta _{{\hat{k}}-1}} + g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}-2}-g_{{\hat{k}}-1}\Big ) \right] \\&= \gamma _{{\hat{k}}} g_{{\hat{k}}+1}^T\Big (g_{{\hat{k}}-1}-g_{{\hat{k}}-2}\Big ) = \gamma _{{\hat{k}}}\Big [\Big (1- \beta _{{\hat{k}}}\Big )g_{{\hat{k}}-1} + \beta _{{\hat{k}}} r_{{\hat{k}}}\Big ]^T\Big (g_{{\hat{k}}-1}-g_{{\hat{k}}-2}\Big ), \end{aligned}$$
(3.3)

where \(\gamma _{{\hat{k}}}= (\beta _{{\hat{k}}-1}-1)/(\alpha _{{\hat{k}}-1}\,\beta _{{\hat{k}}-1})\) is a well-defined positive number. Finally, from (a) in Lemma 4 we have that \(g_{{\hat{k}}-1}^T(g_{{\hat{k}}-1}-g_{{\hat{k}}-2})=0\) and also that \(g_{{\hat{k}}}^T(g_{{\hat{k}}-1}-g_{{\hat{k}}-2})=0\), and hence using (3.3) combined with Step 6, Lemma 2, and the inductive hypothesis, yields

$$\begin{aligned} g_{{\hat{k}}+1}^TA g_{{\hat{k}}-1}&= \gamma _{{\hat{k}}}\beta _{{\hat{k}}}\, r_{{\hat{k}}}^T(g_{{\hat{k}}-1}-g_{{\hat{k}}-2}) = \gamma _{{\hat{k}}}\beta _{{\hat{k}}}\, (g_{{\hat{k}}} - \alpha _{{\hat{k}}}Ag_{{\hat{k}}})^T(g_{{\hat{k}}-1}-g_{{\hat{k}}-2}) \\&= \gamma _{{\hat{k}}}\beta _{{\hat{k}}}\alpha _{{\hat{k}}}\,g_{{\hat{k}}}^TA(g_{{\hat{k}}-2}-g_{{\hat{k}}-1}) = \gamma _{{\hat{k}}}\beta _{{\hat{k}}}\alpha _{{\hat{k}}}\,[g_{{\hat{k}}}^TAg_{{\hat{k}}-2} - g_{{\hat{k}}}^TAg_{{\hat{k}}-1}] = 0, \end{aligned}$$

and (i) is established for all \(k\ge 2\) and for \(-1\le j\le k-2\).

Concerning (ii), for \(-1\le j\le {\hat{k}}-1\), using Step 9 of the DWGM algorithm, Lemma 2, (i) which has now been established, and that \(\beta _k>1\) for all k, we obtain

$$\begin{aligned} r_{{\hat{k}}+1}^TA g_{j} = \frac{1}{\beta _{{\hat{k}}+1}}[g_{{\hat{k}}+2} + (\beta _{{\hat{k}}+1} -1)g_{{\hat{k}}}]^TAg_j = \frac{1}{\beta _{{\hat{k}}+1}}g_{{\hat{k}}+2}^TAg_j + \frac{\beta _{{\hat{k}}+1} -1}{\beta _{{\hat{k}}+1}}g_{{\hat{k}}}^TAg_j = 0, \end{aligned}$$

and (ii) is also established. \(\square\)

Summing up, combining (b) from Lemma 1 with (ii) from Theorem 5, it follows that \(r_k^TAg_j = 0\) for \(j=k\) and for \(j \le k-2\). In other words, for all k, \(r_k\) is A-orthogonal to all previous gradient vectors except to \(g_{k-1}\). Moreover, combining Lemma 2 with (i) from Theorem 5, it follows that for all k, \(g_k\) is A-orthogonal to all previous gradient vectors, i.e., for all \(k\ge 1\)

$$\begin{aligned} g_k^TAg_j = 0 \;\;\; \text{ for } \text{ all } \;\;\; j\le k-1. \end{aligned}$$
(3.4)

We are now ready to show the finite termination of the DWGM algorithm.

Theorem 6

For any initial guess \(x_0 \in \mathbb {R}^n\), Algorithm DWGM generates the iterates \(x_k\), \(k\ge 1\), such that \(x_n = A^{-1}b\).

Proof

From (3.4) we have that the n vectors \(g_k\), \(0\le k\le n-1\), form an A-orthogonal set, and hence they form a linearly independent set of n vectors in \(\mathbb {R}^n\). Therefore, the next vector \(g_n\in \mathbb {R}^n\) must be zero to be able to keep the A-orthogonality with all the previous gradient vectors. Thus, \(Ax_n = b\) and hence \(x_n = A^{-1}b\). \(\square\)

Fig. 2
figure 2

Convergence history of DWGM, CG, and CR, from the same initial point, for the minimization of a strictly convex quadratic function, when \(n=1000\) and the matrix A has only 5 distinct eigenvalues, equally distributed in the interval [10, 1000], each one repeated 200 times

Full size image

It is worth noticing that in exact arithmetic the final termination of DWGM, as in the CG and CR methods, is related to the number of distinct eigenvalues of the matrix A, and not to the dimension of A. In Fig. 2 this fact is illustrated on a strictly convex quadratic function, with \(n=1000\) and for which the matrix A has only 5 distinct eigenvalues. Indeed, we can observe that the three methods terminate in 5 iterations. A key observation, before establishing this important result, is that for each k the gradient vector \(g_k\) generated by DWGM belongs to the Krylov subspace \({{\mathcal {K}}}_{k+1}(A,g_{0})\) (to be defined in our next lemma) that only depends on the matrix A and the initial gradient vector \(g_0\).

Lemma 7

In Algorithm DWGM, for all \(k\ge 1\)

$$\begin{aligned} g_k \in {{\mathcal {K}}}_{k+1}(A,g_{0}) := span\{g_{0},Ag_{0},A^{2}g_{0},\ldots ,A^{k}g_{0}\}. \end{aligned}$$

Proof

For \(k=1\), using (a) in Lemma 1, we have \(g_1=r_0 = g_0 - \alpha _0 Ag_0\), and so \(g_1 \in span\{g_{0},Ag_{0}\}\). Let us now assume, by induction on k, that for all \(1\le j \le k\)

$$\begin{aligned} g_j \in {{\mathcal {K}}}_{j+1}(A,g_{0}) = span\{g_{0},Ag_{0},A^{2}g_{0},\ldots ,A^{j}g_{0}\}, \end{aligned}$$

and consider \(g_{k+1}\). From Step 9 and Step 6 of the DWGM algorithm, we have

$$\begin{aligned} g_{k+1} = (1-\beta _k)g_{k-1} + \beta _{k}r_{k} = (1-\beta _k)g_{k-1} + \beta _{k}g_k - \beta _{k}\alpha _k A g_k. \end{aligned}$$

By the inductive hypothesis, \(g_{k-1} \in {{\mathcal {K}}}_{k}(A,g_{0})\), \(g_{k} \in {{\mathcal {K}}}_{k+1}(A,g_{0})\), and so \(Ag_k \in {{\mathcal {K}}}_{k+2}(A,g_{0})\). Consequently, \(g_{k+1} \in {{\mathcal {K}}}_{k+2}(A,g_{0})\) and the result is established. \(\square\)

Krylov spaces are closely related to polynomials. In fact, for any nonzero vector \(z\in \mathbb {R}^n\) and any positive integer m, it is clear that

$$\begin{aligned} {{\mathcal {K}}}_{m}(A,z) := span\{z,Az,A^{2}z,\ldots ,A^{m-1}z\} = \{q(A)z\,:\, q\in {{\mathcal {P}}}_{m-1}\}, \end{aligned}$$

where \({{\mathcal {P}}}_{m-1}\) denotes the space of all polynomials of degree at most \(m-1\). Let us recall that the minimal polynomial of z with respect to A is the nonzero monic polynomial \({\widehat{q}}\) of lowest degree such that \({\widehat{q}}(A)z=0\). The results stated in our next theorem are well-known and we present them here without a proof; for a complete discussion on the connection between Krylov spaces and polynomials see, e.g., [15, Ch. VI] and [16, Ch. 4].

Theorem 8

The Krylov subspace \({{\mathcal {K}}}_{m}(A,z)\) is of dimension m if and only if the degree of the minimal polynomial \({\widehat{q}}\) of z with respect to A is greater than or equal to m. Moreover, if \(\eta\) is the degree of the the minimal polynomial \({\widehat{q}}\) of z with respect to A, then \({{\mathcal {K}}}_{\eta }(A,z)\) is invariant under A and \({{\mathcal {K}}}_{m}(A,z)={{\mathcal {K}}}_{\eta }(A,z)\) for all \(m\ge \eta\).

We note that, based on Theorem 8, the degree of the minimal polynomial \({\widehat{q}}\) can also be characterized as the smallest positive integer \(\eta\) such that \({{\mathcal {K}}}_{\eta }(A,z)= {{\mathcal {K}}}_{\eta +1}(A,z)\). In particular, the relation between Krylov subspaces and the minimal polynomial of the initial gradient vector \(g_0\) has played a fundamental role to study the finite termination of the CG and CR methods when the matrix A has only \(p<n\) distinct eigenvalues; see e.g., [10, 14]. It will also play a key role to study the finite termination of the DWGM algorithm at iteration p.

Theorem 9

If A has only \(p<n\) distinct eigenvalues, then for any initial guess \(x_0 \in \mathbb {R}^n\) Algorithm DWGM generates the iterates \(x_k\), \(k\ge 1\), such that \(x_p = A^{-1}b\).

Proof

Since A is symmetric and positive definite, the eigenvalues \(\lambda _i\), \(1\le i \le p\), are positive and the associated eigenvectors \(v_i\), \(1\le i \le n\), can be chosen to form an orthonormal set. Without loss of generality we can assume that the eigenvectors \(\{v_1,\ldots ,v_{i_{1}}\}\) are associated with \(\lambda _1\), the eigenvectors \(\{v_{i_{1}+1},\ldots ,v_{i_{2}}\}\) with \(\lambda _2\), and so on, until finally the eigenvectors \(\{v_{i_{p-1}},\ldots ,v_{n}\}\) are associated with \(\lambda _p\), where \(1\le i_{1}< \cdots <i_{p-1}\le n\). Clearly, the set of eigenvectors form a basis in \(\mathbb {R}^n\), and so there exist real scalars \(\gamma _i\), \(1\le i\le n\), such that

$$\begin{aligned} g_0 = \sum _{j=1}^{i_1}\gamma _j v_j + \sum _{j=i_{1}+1}^{i_{2}}\gamma _j v_j + \cdots + \sum _{j=i_{p-1}}^{n}\gamma _j v_j = \sum _{i=1}^p {\widehat{w}}_i, \end{aligned}$$

where \({\widehat{w}}_1 = \sum _{j=1}^{i_1}\gamma _j v_j\), \({\widehat{w}}_2 = \sum _{j=i_{1}+1}^{i_{2}}\gamma _j v_j\), and so on until \({\widehat{w}}_p= \sum _{j=i_{p-1}}^{n}\gamma _j v_j\). Hence, \(g_0 \in span\{{\widehat{w}}_1, {\widehat{w}}_2,\ldots , {\widehat{w}}_p\}\). Moreover, for any \(1\le j\le p\), \(A{\widehat{w}}_j = \lambda _j {\widehat{w}}_j\), and so the subspace \(span\{{\widehat{w}}_1, {\widehat{w}}_2,\ldots , {\widehat{w}}_p\}\) is invariant under A. Furthermore, for any \(0\le k\le p-1\), \(A^k g_0 = \sum _{i=1}^p \lambda _i^k {\widehat{w}}_i\) and we obtain the following column-wise matrix equality

$$\begin{aligned} \left[ \begin{array}{cccc} | & | & & | \\ g_0 & Ag_0 & \cdots & A^{p-1}g_{0} \\ | & | & & | \\ \end{array} \right] = \left[ \begin{array}{cccc} | & | & & | \\ {\widehat{w}}_1 & {\widehat{w}}_2 & \cdots & {\widehat{w}}_p \\ | & | & & | \\ \end{array} \right] \left[ \begin{array}{cccc} 1 & \lambda _1 & \cdots & \lambda _1^{p-1} \\ \vdots & \vdots & & \vdots \\ 1 & \lambda _p & \cdots & \lambda _p^{p-1} \\ \end{array} \right] . \end{aligned}$$
(3.5)

We note that the second matrix on the right hand side of (3.5) is a real \(p\times p\) Vandermonde’s matrix, whose determinant is given by \(\prod _{1\le i<j\le p}(\lambda _j - \lambda _i)\); see, e.g., [8, Sect. 6.1]. Since the p eigenvalues of A are distinct, we conclude that it is a nonsingular matrix. Hence, the column space of the two \(n\times p\) matrices in (3.5) are equal, which implies that

$$\begin{aligned} {{\mathcal {K}}}_{p}(A,g_{0}) := span\Big \{g_{0},Ag_{0},A^{2}g_{0},\ldots ,A^{p-1}g_{0}\Big \} = span\Big \{{\widehat{w}}_1, {\widehat{w}}_2,\ldots , {\widehat{w}}_p\Big \}. \end{aligned}$$

Consequently, \({{\mathcal {K}}}_{p}(A,g_{0})\) is also invariant under A, which in turn implies from Theorem 8 that the degree of the the minimal polynomial \({\widehat{q}}\) of \(g_0\) with respect to A is p. Therefore, combining (3.4) and Lemma 7, it follows that the only way for the vector \(g_p\) to be A-orthogonal to all the previous gradient vectors while being in \({{\mathcal {K}}}_{p}(A,g_{0})\) is that \(g_p=0\). Thus, \(Ax_p = b\) and we obtain that \(x_p = A^{-1}b\). \(\square\)

In addition to the A-orthogonality results shown in Theorem 5, we can also study the A-orthogonality of the current gradient \(g_k\) with all the previously explored search directions. As can be noticed from Step 8 of the DWGM algorithm, the search direction to move from \(x_k\) to the next iterate is not given explicitly, instead it is given the direction to move from \(x_{k-1}\) to \(x_{k+1}\), which uses the auxiliary vector \(y_k\). Nevertheless, we can consider the vector \(x_k - x_{k-1}\) as the search direction to move from \(x_{k-1}\) to \(x_{k}\). Notice that for any \(1\le j\le k\),

$$\begin{aligned} g_k^TA\big (x_j - x_{j-1}\big ) = g_k^T\Big [\big (Ax_j - b\big ) - \big (Ax_{j-1} - b\big )\Big ] = g_k^T\big (g_j - g_{j-1}\big ). \end{aligned}$$

Using this equality, our next result establishes the mentioned A-orthogonality.

Theorem 10

Algorithm DWGM generates the sequences \(\{g_k\}\) such that for \(k\ge 2\)

$$\begin{aligned} g_k^T\big (g_j - g_{j-1}\big )= 0\;\;\; \text{ for } \text{ all } \;\;\; 1\le j\le k. \end{aligned}$$
(3.6)

Proof

Let us notice, from (e) in Lemma 3, that \(g_2^T(g_1 - g_0) = 0\), and so the result is obtained for \(k=2\). Let us now assume, by induction on k, that (3.6) holds up to \(k={\hat{k}} \ge 3\), and consider the next iteration. Hence, we need to show that \(g_{{\hat{k}}+1}^T( g_{j}- g_{j-1})= 0\) for all \(-1 \le j\le {\hat{k}}+1\).

When \(j={\hat{k}}\), the result follows directly from (e) in Lemma 3, and when \(j={\hat{k}}+1\), the result follows directly from (a) in Lemma 4. Now, if \(j\le {\hat{k}}-2\), using Steps 6 and 9 of the DWGM algorithm, the inductive hypothesis on (3.6), Lemma 2, and (i) from Theorem 5, we have

$$\begin{aligned} g_{{\hat{k}}+1}^T\big (g_{j}- g_{j-1}\big )&= \big [\big (1-\beta _{{\hat{k}}}\big )g_{{\hat{k}}-1} + \beta _{{\hat{k}}}r_{{\hat{k}}}\big ]^T\big (g_{j}- g_{j-1}\big ) = \beta _{{\hat{k}}}r_{{\hat{k}}}^T\big (g_{j}- g_{j-1}\big ) \\&= \beta _{{\hat{k}}}\big (g_{{\hat{k}}} - \alpha _{{\hat{k}}}Ag_{{\hat{k}}}\big )^T\big (g_{j}- g_{j-1}\big ) = -\alpha _{{\hat{k}}}\beta _{{\hat{k}}}g_{{\hat{k}}}^T A\big (g_{j}- g_{j-1}\big ) \\&= -\alpha _{{\hat{k}}}\beta _{{\hat{k}}}\Big [\Big (g_{{\hat{k}}}^T Ag_{j}\Big ) - \Big (g_{{\hat{k}}}^T Ag_{j-1}\Big )\Big ] = 0. \end{aligned}$$

Finally, when \(j={\hat{k}}-1\), using Steps 6 (twice) and 9 of the DWGM algorithm, (d) from Lemmas 1, 2, and (i) from Theorem 5, we obtain

$$\begin{aligned} g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}-1}- g_{{\hat{k}}-2}\big )&= g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}-1}- r_{{\hat{k}}} + r_{{\hat{k}}} - g_{{\hat{k}}-2}\big ) = g_{{\hat{k}}+1}^T\big (r_{{\hat{k}}} -g_{{\hat{k}}-2}\big ) \\&= g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}} - \alpha _{{\hat{k}}}Ag_{{\hat{k}}} - g_{{\hat{k}}-2}\big ) = g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}}- g_{{\hat{k}}-2}\big ) \\&= g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}-2} + \beta _{{\hat{k}}-1}\big (r_{{\hat{k}}-1}-g_{{\hat{k}}-2}\big ) - g_{{\hat{k}}-2}\big ) = \beta _{{\hat{k}}-1}g_{{\hat{k}}+1}^T\big (r_{{\hat{k}}-1}-g_{{\hat{k}}-2}\big ) \\&= \beta _{{\hat{k}}-1}g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}-1}-g_{{\hat{k}}-2} - \alpha _{{\hat{k}}-1}Ag_{{\hat{k}}-1}\big ) = \beta _{{\hat{k}}-1}g_{{\hat{k}}+1}^T\big (g_{{\hat{k}}-1}-g_{{\hat{k}}-2}\big ). \end{aligned}$$

Therefore, \((\beta _{{\hat{k}}-1} -1)g_{{\hat{k}}+1}^T(g_{{\hat{k}}-1}-g_{{\hat{k}}-2})=0\). Since \(\beta _k> 1\) for all \(k\ge 1\) [(c) in Lemma 4], we conclude that \(g_{{\hat{k}}+1}^T(g_{{\hat{k}}-1}- g_{{\hat{k}}-2}) = 0\), and (3.6) is established. \(\square\)

Let us recall that the step length \(\alpha _k\) is obtained in the DWGM algorithm to guarantee that the gradient norm is minimized along the negative gradient direction to obtain \(y_k\); see [13, p. 731]. Our next result establishes, using Theorem 10, that the gradient norm at iteration k actually attains the minimum possible value on the linear manifold (subspace if \(x_0=0\)) of dimension k generated by all the search directions that have been explored so far:

$$\begin{aligned} V_k = \left\{ x\in \mathbb {R}^n\, : \, x= x_0 + \sum _{j=1}^{k} \eta _j (x_j - x_{j-1}) \; \text{ and } \; \eta _j \in \mathbb {R}, \; \text{ for } \; 1\le j\le k\right\} . \end{aligned}$$

In that sense, the gradient norm in the DWGM algorithm plays a similar role to the one played by the objective function in the CG method. Indeed, in the CG method (starting at \(x_0=0\)) the step length is chosen to guarantee that the function value f(x) is minimized along the k-th search direction, but in reality based on the orthogonality of the gradient with all the previous search directions, the function value attains the minimum value on the entire explored subspace.

Corollary 11

In Algorithm DWGM, for all \(k\ge 1\), the iterate \(x_k\) is obtained such that \(\Vert g_k\Vert _2\) is the minimum possible value of \(\Vert \nabla f(x)\Vert _2\) on \(V_k\).

Proof

Let us notice that the minimization of \(\Vert \nabla f(x)\Vert _2 = \Vert Ax - b\Vert _2\) subject to \(x\in V_k\) is equivalent to the unconstrained minimization of

$$\begin{aligned} G(\eta ) \equiv \left\Vert A(x_0 + \sum _{j=1}^{k} \eta _j (x_j - x_{j-1})) - b\right\Vert _2^2 = \left\Vert \sum _{j=1}^{k} \eta _j (g_j - g_{j-1}) + g_0\right\Vert _2^2, \end{aligned}$$
(3.7)

where \(\eta =(\eta _1,\ldots ,\eta _k)^T \in \mathbb {R}^k\). Notice that the objective function \(G(\eta )\) is clearly a strictly convex function in \(\mathbb {R}^{k}\). Hence, (3.7) has a unique solution, say \(\eta ^* \in \mathbb {R}^{k}\), and let us define \(R(\eta ^*) = (\sum _{j=1}^{k} \eta _j^* (g_j - g_{j-1}) + g_0)\in \mathbb {R}^n\). Since \(G(\eta )\) is strictly convex, the necessary optimality conditions

$$\begin{aligned} \frac{\partial G(\eta )}{\partial \eta _j} = R(\eta ^*)^T(g_j - g_{j-1}) = 0, \; \text{ for } \; 1\le j \le k, \end{aligned}$$

are also sufficient. Hence, it follows that \(R(\eta ^*)\) is orthogonal to the subspace generated by the vectors \(\{g_k - g_{k-1}, \ldots , g_1 - g_{0}\}\). From Theorem 10 we have that \(g_k\) is also orthogonal to the subspace generated by \(\{g_k - g_{k-1}, \ldots , g_1 - g_{0}\}\). Moreover, notice that choosing \(\eta \in \mathbb {R}^k\) such that \(\eta _j = 1\) for \(1\le j \le k\), we obtain that \(x_k \in V_k\) and \(R(\eta )= g_k\). Therefore, by the uniqueness of the solution of (3.7) we obtain that \(g_k=R(\eta ^*)\in \mathbb {R}^n\). Using now the equivalence of the two minimization problems stated above, we have that the iterate \(x_k\) in algorithm DWGM can be written as

$$\begin{aligned} x_k = x_0 + \sum _{j=1}^{k} \eta _j^* (x_j - x_{j-1}), \end{aligned}$$

and the result is established. \(\square\)

4 Conclusions and perspectives

We have discussed and established several properties of the DWGM algorithm, originally developed and analyzed in [13], which add understanding to the surprisingly good behavior of the method. In particular, we have shown the A-orthogonality of the gradient vector at the current iteration with all the previous gradient vectors, which yields the finite termination of the method for the minimization of strictly convex quadratics. We have also established the A-orthogonality of the gradient vector at the current iteration with all the previously explored directions, including the current one, which shows that the method guarantees at each iteration that the norm of the current gradient is optimal on the entire explored linear manifold. We have also studied the finite termination in \(p<n\) iterations when the \(n\times n\) Hessian matrix has only p distinct eigenvalues, as it also happens for the CG and CR methods. This result clearly motivates the use of preconditioning strategies when solving large-scale symmetric and positive definite linear systems.

An advantage of the DWGM algorithm is that it does not impose any of the established A-orthogonality results in its algorithmic steps and as a consequence its extension to the local minimization of non-quadratic functions is appealing, as observed by Oviedo-Leon [13]. Another advantage for the possible extension of the DWGM algorithm to the non-quadratic case is the tendency to outperform the CG method when low accuracy in the gradient norm is required, which could be a key issue in practical applications.