1 Introduction

Sociology believes that the formation of social phenomenons on the basic of community rather than the individual [1]. Over the past decades, the study of social community occupies a mainly important space in social computing. Social community, which refers to a set of vertexes, results in inner interaction closer than that with the outer sets. Particularly, recently, with the increasing popularity of social networking application, the development is most pronounced in the structure complexity of social network [2]. Current technology promotes social network methodology from data collection, to network construction, to network dynamics, to network analysis, to results interpretation, etc., [3]. To better understand social network, a large number of approaches are proposed to capture network properties [4,5,6]. Similarity measure is one such method, with previous publications exploring the similarity of two vertexes [7,8,9] and vertex feature values [10, 11]. The analysis of inner-vertices relationship is, however, still limited, from the point of view of structure or property. It is hard to extract a proper description for the community scope. Few articles have been published on this aspect. Similarity measure will still have the challenges owing to the increasing complicated social network. For this reason, many current applications use similarity measure as a secondary approach or as a tool to study network structure via similarity analysis. Vertex similarities, however, still have the potential to be beneficial for network analysis, such as the nodes affected by each other.

To solve the above issue, this study proposes a multi-similarity method (MSM) for social network analysis, depicts the similarity-based method in combination with clustering algorithms for data collection, interprets the detection into community properties, and obtains a better working performance by providing the processing steps via laboratory setup.

The research contributions of this paper can be summarized as follows:

  1. a.

    Multi-similarity method (MSM): this study devises a multi-similarity method for graph topological structure and vertex feature capture which is based on six types of similarity properties.

  2. b.

    Similarity measure evaluation: define the properties of multi-similarity vertex in the network, and qualitatively identify the methodology design on similarity detection.

  3. c.

    Community detection: an optimized architecture combining MSM with K-means clustering algorithm is defined. The proposed method is utilized in a manner similar to the spectral clustering algorithm.

This paper presents similarity measure-related background knowledge and clustering algorithms in Sect. 2; illustrates the overall community structure in Sect. 3; shows the multi-similarity design concept and assessing indexes in Sect. 4; describes the community detection method devise process in Sect. 5; experimental results achieved in this study and the analysis in Sect. 6, and finally presents the research significances and future expectation and planning in Sect. 7.

2 Background and relate work

This section introduces the basic knowledge of similarity measure and clustering algorithms, so as to facilitate the depiction of subsequent methodology.

2.1 Similarity measure

Traditional similarity measure is characterized by Jaccard similarity based on neighbor vertexes [12]. Vertexes that share similar connection tend to settle in the same community. The more mutual friends of the two vertices, the more similar they appear to be. Jaccard similarity means that the similarity of two-pairs object is the common neighbor number, Jaccard similarity shows that \(v_j\) and \(v_i\) are more similar if they have more common neighbors, and \(Jaccard(v_i,v_j)\) increased with the increasing number of common friends. However, the Jaccard similarity equals 1 when the two have common friends; otherwise, the value of similarity is 0. This arbitrary detection method is certainly extreme and cannot correctly show the relationship between the two points of social networks.

The SimRank, which is based on neighbor over arbitrary graphs, plays an important role in similarity scoring [13]. The equation \(s(v_i,v_j)\) denotes that the similarity between \(v_i\) and \(v_j\) is the average value of the similarity between the neighbor vertexes of \(v_i\) and the neighbor vertexes of \(v_j\). Just like Jaccard similarity, the SimRank metric value is 1 only for computing relation of the vertex and itself, otherwise is 0. Whereas, for SimRank, the more in-neighbors of vertex \(v_i\) and \(v_j\) is, the smaller the similarity between \(v_i\) and \(v_j\) [14] is. In other words, the SimRank score only accommodates the paths with equal length from a common source vertex, other paths for vertex-pairare fully ignored [15]. The optimized SimRank is Simrank++ [16], which improves the former approach in two ways: defining the evidence score as an increasing function of common and keeping the similarity score consistent with the weights on the graph [9].

2.2 Clustering algorithm

Previous work highlights the function of K-means algorithm in community discovery [17]. K-means is a general used clustering algorithm for expectation maximization. The K-means clustering is employed for determining the initial cluster center, measuring the similarity between object and cluster center and resolving the objection function. On the foundation of expectation maximization, algorithms with Jaccard similarity, Cosine or SimRank, are developed to conduct community discovery [13].

Spectral clustering algorithm, in line with adjacency matrix or Laplapcian matrix feature vector, is established for searching the minimum cut in network. The parameter involved is merely similarity matrix, which modifies sparse data processing effectively. For this reason, many current applications use K-means clustering as a secondary tool to complement similarity measure. The realization of spectral clustering algorithm is affected by the specific similarity matrix. Different matrix will definitely lead to different clusters. Thus, using an appropriate matrix is the key to address the problem [18].

Table 1 Symbols definition and their descriptions
Full size table

3 Overview of network structure

This section will completely introduce the overall structure of the network, as well as features and relations of internal vertexes. As shown in Table 1, we describe the symbols definition and their descriptions about network structure.

In general, a number of parameters are required to characterize the network structure. An example of the social network is defined as a undirected graph \(G=(V,F,E,W)\) where V is the set of all the vertices, F is the feature set of these vertices, E is the set of undirect links and W is the relationship density for every community with the number of vertexes \(n\ge 1\). Thus, a community containing M features can be defined as:

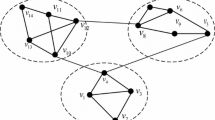
$$\begin{aligned} \mathbf {F(v)}=(f_{1}, f_{2},\ldots , f_{M}),\, f_i \in [0,1], i=1, 2,\ldots M \end{aligned}$$

As shown in Fig. 1, the network we adopted has all the feature probability values ranging from 0 to 1. According to the aforementioned principle, the greater the value is, the stronger the correlation is. The value of vertex v3 on features 1 and features 2 are 0.2 and 0.1, respectively, which is shown as (0.2, 0.1).

Fig. 1
figure 1

An example of network architecture

Full size image

The value of the similarity between vertexes in Fig. 1 depends on the situation between their features and their relationships. Node v1 is directly connected to v7 and v8, so does v2, thereby v1 and v2 are named as common neighbor nodes for v7 and v8. Correspondingly, v2 and v7 have non-common neighbor nodes or exclusive neighbor nodes where v8 is exclusive neighbor for v2, as well as v1, v3 and v4 for v7. Thus, a path between exclusive vertexes v2 and v7 is formed as v2-v8-v1-v7. Therefore, three types of relationships exist within the structure, which are direct connection, common neighbor connection and exclusive vertexes connection.

Supposing that we divide the social network into k unconnected community, where \(C_i=(V_i, F_i, E_i, W_i )\)\(i=1,2,\ldots , k\), \(V=\cup _{i=1}^{i=k} V_i\), and \(V_i \cap V_j=\phi \) when \(i \ne j\), the purpose of the function is to address high-quality and efficient community results.

4 Multi-similarity method (MSM)

This section depicts the multi-similarity method design process on the foundation of vertex similarities and relations. The method constructing together with the effectiveness evaluation is facilitated by proposed similarity properties.

4.1 Similarity properties index

In order to understand the similarity measure design with social network, it is required to study the natural characteristics of similarity. On the foundation of research [13,14,15,16, 19,20,21], a generalized similarity properties of the vertex are summarized as follows.

  1. p1

    The similarity between the vertexes should be related to a commonneighbor, and increases with the number of common neighbors.

  2. p2

    A larger number of similar features leads to increased similarity between vertexes. Granovetter [22] proposed that the more common the feature are between vertices are, the more similarities in the vertexes cluster exist.

  3. p3

    Similarity should be normalized to the scale of [0,1], while the upper and lower bounds of the value should make practical sense.

  4. p4

    The value of the upper and lower bounds of similarity must be reasonable.

  5. p5

    The similarity is consistent with the weights on the graph.

  6. p6

    The value of similarity is related to the path.

Accordingly, the aforementioned properties are used for similarity measure method design. However, when distributed vertex have multiple features, the multi-similarity based method with this principle is required.

4.2 Multi-similarity method (MSM)

On the basic of para.3, the direct connection, common neighbor connection and exclusive vertexes connection are represented by \(s_l\), \(s_c\) and \(s_e\), respectively. In the process of calculating, we emphasize the influence of the feature metric between vertexes and the relationship density of the user. The aforementioned properties, which are reflected in the three-similarity computing, are utilized for working performance evaluation.

4.2.1 Similarity based on direct connection

A similarity exists between two directly connected vertexes, which is related to their own features and the strength of connections. We use a continuous function to depict the processing of vertex feature and relationship density. Generally, the relationship density is the main factor for analysis while the vertex feature is the supplement factor, since the feature of social network users is often cross domain. If their features are alike, the effect of vertex features on the relationship density is positive and vice versa. Thus, a combination of the Gauss function is added to the feature metric of vertexes as well as the density to describe the correlation. Similarity based on direct linked edge is calculated as follows:

$$\begin{aligned} {s_l(v_i,v_j)=\frac{w_{ij}e^{-\gamma ||\mathbf {F(v_i)} -\mathbf {F(v_j)}||}}{w^{'}(v_i,v_j)}} \end{aligned}$$
(1)

together with

$$\begin{aligned} w^{'}(v_i,v_j)= & {} \sum _{a_k\in N(v_i)}w(a_k,v_i)\\&+\sum _{b_k\in N(v_j)}w(b_k,v_j)-w(v_i,v_j) \end{aligned}$$

where \(\gamma \) is a parameter that determines the influenced speed of vertex feature to the vertex relationships, \(N(v_i)\) is directed neighbor of vertex \(v_i\), \(w(a_k,v_i)\) is weight value expressed as the relation number of the two vertexes and \(\mathbf {F(v_i)}\) is feature vector of vertex \(v_i\). The similarity of the vertex feature will inevitably influence the relationship between them.

4.2.2 Similarity based on direct common neighbor

Influenced by social factors, in a social group, individual relation usually varies on the common neighbor as well as their features. If the features between two vertexes do not change (i.e., the two vertexes are the same), they will be more influenced by the relation density between the two vertexes. A continuous function is applied to depict the process of features and relations. The function in vertex \(v_i\) is described as:

$$\begin{aligned} g(v_i)=\sum _{a_k\in N(v_i)\cap N(v_j)}w(a_k,v_i)e^{-\gamma ||\mathbf {F(a_k)}-\mathbf {F(v_i)}||} \end{aligned}$$
(2)

The Jaccard similarity between \(v_i\) and \(v_j\) is

$$\begin{aligned} s(v_i,v_j)=\frac{|N(v_i) \cap N(v_j)|}{|N(v_i) \cup N(v_j)|} \end{aligned}$$
(3)

Then similarity based on direct common neighbors is

$$\begin{aligned} { s_c(v_i,v_j)\!=\! \frac{g(v_i,v_j)}{w^{'}(v_i,v_j)} } \end{aligned}$$
(4)

The connection relation factor between the vertexes and the features factors of the vertexes are considered. For common neighbors we have \(g(v_i, v_j)=g(v_i)+g(v_j)\) where \((v_i, v_j)\) is weight value sum of direct neighbor vertexes \(v_i\) and \(v_j\). For exclusive neighbors, \(g^{'}(v_i,v_j)=\sum _{a_k\in N(v_i)}w(a_k,v_i)+\sum _{b_k\in N(v_j)}w(b_k,v_j)-g(v_i,v_j)\) of \((v_i, v_j)\) where \((v_i, v_j)\) is the value sum of non-common directed neighbor vertexes \(v_i\) and \(v_j\).

4.2.3 Similarity based on exclusive vertexes

The influence of similarity from neighbors is of maximum weight. On the other hand, the effect of exclusive neighbors is studied by using the ideas of Simrank through three steps of random walk strategy, whose similarity is

$$\begin{aligned} s_e(v_i, v_j)=\frac{\sum _{{ev}_i \in EN(v_i),{ev}_j \in EN(v_j)}{s(v_i, ev_i)s({ev}_i,{ev}_j)s({ev}_j,v_j)}}{|EN(v_i)|\times |EN(v_j)|} \end{aligned}$$
(5)

in line with \(EN(v_i)=N(v_i)-N(v_i)\cap N(v_j)\).

4.2.4 Similarity evaluation

The similarity value represents the homogeneity between specific vertexes within the social network. According to the preceding analysis, the formula is defined as follows:

$$\begin{aligned} s(v_i,v_j)= & {} a \cdot s_l(v_i,v_j)+b \cdot s_c(v_i,v_j) \nonumber \\&{}+(1-a-b)\cdot s_e(v_i,v_j) \nonumber \\&{}a \in [0,1],b \in [0,1] \end{aligned}$$
(6)

According to Eq. (6), the outcome of multi-similarity method caters to the requirements of the evaluation indexes. Since Due to the utilization of Jaccard method, values \(s _l\) and \(s_c\) are consistent with the definition of common neighbor in P1. The less the value of \(||\mathbf {F(v_i)}-\mathbf {F(v_j)}||\) is, the more the values of \(s _l\) and \(s_c\) reach. Meanwhile, \(s_e\) is the similarity value of SimRank based on Jaccard similarity, which is also satisfied with P1 and P2. Further, for each \(s(v_i,v_j)\in [0,1]\), the similarity between the vertex and itself is either 1 and no or 0, which results in the \(s(v_i,v_j)\) meets the qualification of P3 and P4. Likewise, based on Eqs. (1)–(6), the \(s(v_i,v_j)\) is proportional to the weight value, which is exactly in accordance with P5. In addition, P6 refers to the path of computing, in line with the random walk for the similarity measure algorithm implementation in this research.

Including some derivation details to justify the design theory on multi-similarities, positive results at this stage indicated that the strategy could indeed be effective in network interpretation. Specifically, the evaluation indexes are capable of generating measurable vertex responses of community detection algorithm design.

Table 2 Similarity value among vertexes given Fig. 1 using Eq. (6)
Full size table

5 Community detection algorithm

This section describes the community detection algorithm devised based on MSM. The algorithm is conducted on similarity matrix denoting the relative similarity of vertexes in social network. To accurately identify the social network, the input data is formulated through spectral clustering, the community is detected by K-means clustering and the outcomes optimized via modularity algorithm.

5.1 Detection based on K-means clustering

The architecture of community detection contains two main steps:

  1. 1.

    Establishing the clustering center based on graph clustering with parameter determination and initialization.

  2. 2.

    Constructing the objective function with the similarity method to detect community.

5.1.1 Clustering center initialization

To start with, spectral clustering algorithm is utilized to perform graph representation on similarity matrix eigenvalues of the social network. For the deployment of K-means clustering, the number of clusters K and the controlling parameter \(\gamma \) are selected. At this stage, the clustering center has significant impact on clustering outcome. Generally, the center is selected randomly thus the outcome is inevitably unstable. For the purpose of community detection, the user multi-similarity value, based on PageRank [23] algorithm, is set as the initial center. Probability value of vertexes \((v_i,v_j)\) as well as the influence rank value of vertex \(v_i\) is showed as

$$\begin{aligned} P_{v_iv_j}= & {} \frac{s(v_i,v_j)}{\sum _{v_i \in N(v_u)} {s(v_u,v_i)} }\nonumber \\ I_{v_i}= & {} \sum _{v_u \in N(v_i) }{I_{v_u}P_{v_uv_i}} \end{aligned}$$
(7)

where k seeds are the k maximum of I.

figure e

5.1.2 Objection function

In our algorithm, the distance value is objection function in terms of the topological structure and feature attributes of vertexes. In particular, the distance between vertexes is related to the proposed similarity method, which is illustrated as:

$$\begin{aligned} F_{objection}=\sum _{i=1}^{k}\sum _{p\in C_i}d(p,c_i)^2 \end{aligned}$$
(8)

where initial distance \(d(i,j)=1-s(i,j)\) while the distance value is updated by

$$\begin{aligned} d(p,c_i)=1-\frac{\sum _{p\in C_i}s(i,p)}{|m_i|} \end{aligned}$$
(9)

where \(|m_i|\) is the number of vertexes in \(C_i\). \(c_i\) is the center of cluster \(C_i\). Referring to the vertexes in Fig. 1, the relations among nodes are presented in Table 2. For the purpose of clustering, the similarities between each node and itself is 1 while for exclusive one is 0. Based on K-means clustering algorithm, a larger value denotes a closer relation of the vertexes.

The time complexity of the similarity method, which makes the three-step distance strategy is O(NET). The memory allocation is mainly related to the number of edges. The clustering outcomes are optimized according to minimum modularity value, which results in a high inner-community similarity and a low external one. This approaches capable of dealing with medium and large-scale graphs. The pseudo code of proposed method is presented in Algorithm 1.

5.2 Evaluation of working performance

We tend to use the state-of-art technologies for working performance evaluation. However, current processing has to be adjusted to fit the proposed graph. For this reason, modularity, SSE (sum of the squared error) and density are recommended as criteria.

5.2.1 Modularity

Modularity has been proved highly effective in practice for community evaluation [24]. For clustering result estimation, an improved module is defined as:

$$\begin{aligned} Q=\frac{1}{||W||}\sum _{c=1}^{c=k}\sum _{i,j\in C_c}(w_{ij}e^{-\gamma ||\mathbf {F(v_i)}-\mathbf {F(v_j)}||}-\frac{p_ip_j}{||W||}) \end{aligned}$$
(10)

where \(||W||=\sum _{i=1}^{i=N}\sum _{j=1}^{j=N}w_{ij}\), \(p_i=\sum _{j=1}^{j=N}w_{ij}e^{-\gamma ||\mathbf {F(v_i)}-\mathbf {F(v_j)}||}\), N is the number of vertexes, considering the difference between the community density and expectation value, the modularity characterizes the network. The greater the modularity value is, the more concentrated the vertexes within the community are.

5.2.2 SSE (sum of the squared error)

SSE uses Euclidean distance to assess the cluster quality from the perspective of data feature. A smaller value of SSE indicates a better-selected center of the cluster. The sum of the squared error based on the data feature between vertexes is

$$\begin{aligned} SSE=\sum _{i=1}^{k}\sum _{v_j\in C_i}||F(v_j)-F(c_i)||^2_2 \end{aligned}$$
(11)

5.2.3 Density

The density function is the most significant specification representing the clustering. Destiny stands for the ratio between edges in the cluster and total edges in the graph, which lies in the interval of [0,1]. According to Eq. (12), the greater the density value, the stronger the connection of the edge in the clusters.

$$\begin{aligned} Density=\frac{\sum _{i=1}^{i=k}\sum _{v_j,v_c\in C_i}{||E(v_j,v_c)||}}{||E||} \end{aligned}$$
(12)

6 Experiments

This section shows the implemented methodology for community detection. The laboratory establishing integrates K-means [25], spectral clustering [26] and modularity [24] algorithm for clustering. In order to demonstrate method effectiveness, three evaluation parameters modularity [24], sum of squared error (SSE), and density [20] are employed.

6.1 Dataset description

We conducted experiments on two real datasets and a synthetic dataset. The DBLP network dataset has 5000 users with 12,796 links between these vertexes having two attributes. The other one is political blog network of 1490 web blogs with 19,090 links containing one attribute, which is named as Pblog in the following parts. Details are given in Table 3.

Table 3 Data sets information
Full size table

6.2 Experimental procedures

Experiments were performed on the experimental targets with different topological densities. Before the compiling of the algorithm, typical parameters \( \gamma \), a and b are quantified based on the natural characteristics of target community, which are set as 0.8, 0.4 and 0.4, respectively. To quantify the clustering, the aforementioned indexes are presented for estimation.

Aiming at evaluating the working performances of the proposed method, experiments with traditional approaches are carried out subsequently: Sa-clustering [22] , W-clustering [27] and KSNAP [28] algorithm are employed to deal with the same targets.

6.3 Results and analysis

The evaluation indexes on synthetic dataset are exhibited in Figs. 2, 3, 4, and 5. In general, a lower value of variable \(\gamma \) results in a lower modularity. The curve of \(\gamma \) appears to be smoother with the variation of SSE and density. According to Fig. 3, the k-means and spec-cluster combined algorithm brings improved density values.

Fig. 2
figure 2

Curve graphs show feature weight factor \(\gamma \) and cluster number k versus modularity is analysed on synthetic dataset

Full size image
Fig. 3
figure 3

Curve graphs show feature weight factor \(\gamma \) and cluster number k versus SSE is analysed on synthetic dataset

Full size image
Fig. 4
figure 4

Curve graphs show feature weight factor \(\gamma \) and cluster number k versus density is analysed on synthetic dataset

Full size image

In Figs. 6, 7, and 8 we can see that our proposed similarity method combined with the k-means and spec-cluster algorithm yields improved density values.

Fig. 5
figure 5

The histograms describe no. of cluster number k versus moudularity, SSE, and density on synthetic dataset in three kinds of cluster algorithm: k means (k means community detection algorithm based on MSM), spec-cluster (spectral clustering algorithm based on the MSM), and modularity (modularity maximization cluster algorithm)

Full size image
Fig. 6
figure 6

No. of cluster number k versus modularity on pblog dataset (the first figure) and DBLP dataset (the second figure), using three kinds of cluster algorithm: k means (k means community detection algorithm based on MSM), spec-cluster (spectral clustering algorithm based on the MSM), and modularity (modularity maximization cluster algorithm)

Full size image
Fig. 7
figure 7

No. of cluster number k versus SSE on pblog dataset (the first figure) and DBLP dataset (the second figure), using three kinds of cluster algorithm: k means (k means community detection algorithm based on MSM), spec-cluster (spectral clustering algorithm based on the MSM), and modularity (modularity maximization cluster algorithm )

Full size image
Fig. 8
figure 8

No. of cluster number k versus density on pblog dataset (the first figure) and DBLP dataset (the second figure), using three kinds of cluster algorithm: k means (k means community detection algorithm based on MSM), spec-cluster (spectral clustering algorithm based on the MSM), and modularity (modularity maximization cluster algorithm)

Full size image

As can be seen from the results as Figs. 6, 7, and 8, the proposed method dose have a better implementation compared to other models. In the analysis of modularity, the similarity measure-based algorithm gains a larger value in clustering (Fig. 6), which is because of the optimization of vertexes distance during pre-processing. Meanwhile, since the initial cluster vertex and vertex features are formulated, the SSE value for K-means tends to be the best outcome (Fig. 7). Further, with the increasing of k, the value of density reduces, especially for K-means algorithm (Fig. 8), which generate a more desirable clustering outcome.

Besides, on the basic of the same vertex feature and topology structure, the resolution of different processing on the density are tested. The proposed detection algorithm obtained the best value of density by selecting four different K values, and the results are shown in Figs. 8, and 9, which is stronger than that of other methods. Under the condition of K = 3, the density reaches its best performance. Results in other cases are slightly better than the traditional technique results when processing separately.

7 Concluding remarks

In this paper, a multi-similarity-based method for community detection is described. The approach is basically obtained via the optimization of similarity measure as well as the analysis of social network. The method presented is improved with the combination of clustering algorithms. Specific properties are put forward for methodology design and interpretation. Results indicate that the working performance of a structured community detection is estimated by three variables.

Firstly, by investigating the characteristic of social network, the community structure is depicted as the detecting target. This analysis also illustrates the similarity relation of inner and external vertexes. The application of similarity measure is provided with the property indexes for similarity-based method evaluation.

Secondly, the devise of the similarity-based detection algorithm is provided. Based on the address of three different relations, the algorithm is formulated. The multi-similarity vertexes can be effectively detected due to the satisfactory of detection algorithm to the evaluation indexes.

Thirdly, the community detection method is optimized with the integration of K-means clustering, spectral clustering and modularity algorithm. The input data is formulated as well as the initialization of clustering is revised, which offers an efficient center selecting procedure.

The paper also presented a laboratory architecture for effectiveness certification. A better working performance is obtained on community datasets by highlighting the results of the three criteria. In addition, all experiments are conducted on traditional clustering algorithms while results are carefully analyzed with density function.

Fig. 9
figure 9

No of cluster number k versus density. Cluster density is analysed on pblog dataset using three kinds of cluster algorithm: proposed, KSNAP, and W-Cluster. “proposed” is the community detection algorithm of kmeans in Algorithm 1

Full size image

This study introduces a new social network detection opportunity to communities of multi-similarities, which also facilitate the design processes. A detection strategy like this, even if imperfect, may allow users to point in complex communities in social networks.

Future work should address more sophisticated situations where large-scale and multiple data a represented to explore whether the current multi-similarity-based method can be extended to a more complex community.