Outage probability of SSTS for distributed antenna systems over Rayleigh fading channels in multi-cell environment

Abstract

In this paper, downlink outage probability for distributed antenna systems (DAS) in multicell environment is proposed, while based on maximum desired signal criterion, a single selection transmission scheme (SSTS) is proposed. Usually, adopting central limit theorem (CLT) method, the component of interference plus noise is considered as a fixed-variance Gaussian random variable in most papers. However, the aforementioned method does not reflect the effect of short-term fading on interference and its usage is in the constraints of restrictive conditions. To relax the constraints, non-central limit theorem (NCLT) is introduced, which treats the variance of interference plus noise as a changeable-variance random variable influenced by short-term fading. It is assumed that channels are independent identical Rayleigh fading with propagation path-loss, and the closed-form expression of outage probability for DAS is derived. Finally, simulation results demonstrate the validity of theoretical analysis.

1 Introduction

In wireless communications, the conflict between the continuous improved quality of experience (QoE) and the lagged performance of current cellular networks becomes more and more obvious. This is because the improved QoE requires much higher data rates for support, which can be realized by more available spectrum resource. However, the spectrum resource utilized by cellular networks constrained is more and more precious, and there are no additional spectrum resources assigned to cellular networks. Distributed antenna systems (DAS) has been introduced as a key technology for next generation communications for expanding coverage and increasing sum rates. Different from a conventional antenna system (CAS) which has centralized antennas at the center location, in DAS, distributed antenna (DA) ports which are physically connected with each other via dedicated channels are separated geographically throughout a cell. Therefore, the access distance for each user along with the transmit power and co-channel interference can be reduced in DAS, which results in improved overall performance [1]. Recently, the distributed antenna system (DAS) has been regarded as a promising technique for the design of future network architectures, since it has great potential for capacity improvement and coverage extension [2, 3]. It also meets the increasing demand for high spectral efficiency and good coverage [4,5,6]. Distributed antenna systems (DAS) as a feasible technology are first proposed and adopted to cover any dead spots in indoor wireless communications [7]. However, the application scope of DAS has been expanded to other domains, such as better coverage, increased battery life, as well as improved signal-to-interference plus noise (SINR) at receiver [8].

An overview of distributed wireless communication systems (DWCS) and the corresponding advantages for it were described in [9]. Similar to DWCS, the configuration of remote antenna units (RAUs) in DAS is geographically distributed, in order to bridge the distance between transmitter and receiver, which can improve communication quality [10], while the antenna units within conventional co-located antenna systems (CAS) are centralised at a fixed location. In DAS, a central processing unit (CPU) is configured to provide high speed and reliable data transmission for each cell. The communication channels between CPU and RAUs are realized through optical fibre, exclusive frequency link, and so on. According to the configuration of DAS, it is considered to be cooperative communications, as an recently developed technique in the next few years [11, 12].

Adopting the central limit theorem (CLT) method, the system performance of DAS has been analyzed for the most existing works [8, 10, 13, 14]. For the CLT method, interference plus noise of communications is assumed as fixed-variance Gaussian noise, when propagation path-loss and transmitted power are given. In other words, the interference power of communication for DAS is treated as a constant. The disadvantages of CLT method in DAS is that the role of short-term fading on interference cannot be employed. The precondition for CLT method is that the number of interference and noise items is sufficient, but in most cases this condition is not satisfied. If interference plus noise terms are sparse, the analytical result does output an error, and it should not be neglected. Therefore, we propose a non-central limit theorem (NCLT) method to overcome the aforementioned limitations in this paper. Compared with CLT method, the interference power as well as the variance of it in DAS are treated as random variable simultaneously for the proposed NCLT method. For NCLT method, the effect of short-term fading on the variance of interference power can be shown, while the CLT method is not. So NCLT method can evaluate the system performance more practically and accurately in comparison with the CLT method. For NCLT method, many scholars have conducted a lot of researches. Channels between CPU and RAUs assumed to suffer from Rayleigh fading, the capacity, bit error rate (BER) and outage probability for blanket transmission scheme (BTS, i.e., all of the RAUs within cell broadcast data) in DAS have been studied [15]. While Choi et al. have done research on the capacity of DAS with Gaussian fading for channels between mobile terminals (MTs) and RAUs [16].

Another challenge for future information and communication (ICT) technologies is to reduce the power consumption. Against power-saving, Vereecken et al. [17] introduced sleep modes for communication nodes. On the basis of maximum desired signal criterion, a single selection transmission scheme (SSTS) is proposed to reduce energy, in which one of the RAUs is chosen for transmission and the rest of RAUs are sleeping. As far as we know, the studies of system performance of DAS for SSTS are few. Adopting CLT method, we have analyze the capacity and outage probability of DAS for SSTS, where the interference plus noise is regarded as fixed-variance Gaussian noise [18]. Adopted NCLT method, the BER for SSTS has been analyzed in [19]. However, the studies of the outage probability for SSTS does not, hence we do research on outage probability for SSTS with NCLT method.

In this paper, the main contributions are summarized as follows: (1) the interference power as well as its variance in DAS are treated as random variable simultaneously. The effect of short-term fading on the corresponding variance is embodied. So this NCLT method is more practical and accurate to evaluate the system performance of DAS. (2) An SSTS strategy is proposed on the basis of maximum desired signal criterion. Downlink outage probability of DAS for the proposed SSTS is investigated and the closed-form expressions of it are derived under no shadowing conditions, while the corresponding approximate analytical expressions for shadowing conditions are also given.

The rest of paper is organized as follows: the DAS model is described in Sect. 2. The outage probability of SSTS for DAS is derived in Sect. 3. Section 4 discusses some practical concerns, and provides numerical results together with some discussions. Finally, the key conclusions from this research are summarised in Sect. 5.

Notation: scalar, vectors, and matrices are represented by lowercase plain-font letters, lowercase bold-font letters, and uppercase bold-font letters throughout the paper, respectively. $(\cdot )^\mathrm{H}$ and $\hbox {E}_\mathrm{h}[\cdot ]$ denote the conjugate transpose matrix and the expectation to h, respectively. $\hbox {f}_\mathrm{X}$(x) represents the probability density function (PDF) against random variable X. ln ($\cdot$) and log $_{10}(\cdot )$ are the nature logarithm and common logarithm, respectively.

2 System and channel model

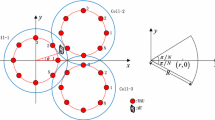
In each reference cell, a CPU located in a fixed position is configurated in DAS. The communication channels between CPU and the RAUs in the corresponding cell are connected via dedicated wire. However, the CPUs from different cell are independent with each other. As shown in Fig. 1, the Wyner’s planar cellular deployment is introduced in this paper [14, 20]. For Wyner model, arbitrarily cell can receive the signal from the two adjacent cells, which is referred to as inter-cell interference. In actual deployment, coverage, user number as well as other environmental factors are taken into consideration for the RAUs number of each cell [21].

Fig. 1

Configuration of a distributed antenna system

In cellular system, each cell coverage in DAS is usually circular, and the RAUs in the corresponding cell are located on a red circle, which is called circular layout (CL) [22, 23]. Therefore, the coverage of cell is expressed by a circle with radius R, while the radius of another circle RAUs located on and uniformly distributed, is r. As shown in Fig. 1, the number of RAUs within each cell is N, and its corresponding coverage region is represented by solid lines. The coverage region of RAUs is congruent sector, and the central angles for that of it is $2\uppi /N$, as depicted in Fig. 1 [24]. Each RAU in the cell is located on the bisector of the central angle.

The following hypotheses are made for this paper:

• All of the RAUs and mobile terminals (MTs) support one omni-directional antenna. MT located in Cell i is designated as MT$_{i}$, while the index of RAUs within each cell is labeled by RAU$_{j}$, and the angle between objective cell centre, MT, and the horizontal is denoted as theta as depicted in Fig. 1.

• Within each cell, only one MT is active, which can be realised by adopting time-division multiple access (TDMA) techniques. Moreover, the channels between MTs and RAUs suffer from block fading, i.e. the fading coefficients for channels keep unchanged within a packet interval and vary among different packets.

2.1 Linear Wyner architecture

Arbitrary one cell is chosen as the object of study and denoted as Cell 1. The corresponding two adjacent cells around Cell 1 are labeled as Cell 2 and Cell 3 respectively. The transmitted power for the $i\mathrm{th}$ RAU in the $j\mathrm{th}$ cell is written as $P_{i}$, j(i = 1, ..., N; j = 1, 2, 3); as a consequence, the total transmitted power of each cell in DAS is the same, i.e., $P=\sum \limits _{i=1}^N {P_{i,j} }$. For the $j\mathrm{th}$ cell, the distances between MT and RAUs are written as $d_{i},_{j}$, and the corresponding propagation path-loss is written as $L_{i,j} =Kd_{i,j}^{-\alpha }$, where $\alpha$ is the path-loss exponent, K is a unitless constant depending on antenna characteristics and average channel attenuation. From the perspective of simplicity, we set $K=1$.

2.2 Channel model and received signal

For each cell in DAS, all of the distributed antennas (DAs) broadcast signal to the corresponding active MT with blanket transmission scheme (BTS), and vice versa. In objective cell, the discrete time-base band signal received at MT for BTS is written as:

$$\begin{aligned} y=\sqrt{S_s }{} \mathbf{h}^{\left( 1 \right) }{} \mathbf{x}^{\left( 1 \right) }+\sqrt{S_s }\sum _{j=2,3} {\mathbf{h}^{\left( j \right) }\mathbf{x}^{\left( j \right) }} +n \end{aligned}$$

(1)

where

$\mathbf{h}^{\left( j \right) }=\left[ {\sqrt{S_s }h_{1,j} ,\cdots ,\sqrt{S_s }h_{N,j} } \right]$denote channel vector in the $j^\mathrm{th}$ cell, $h_{i,j}$is the short-term fading between the active MT in the $j^\mathrm{th}$ cell and the $i^\mathrm{th}$ RAU in the corresponding cell, and it is assumed to suffer from independent identical Rayleigh fading. While $L_{i,j}$ denotes the corresponding propagation path-loss.

$\mathbf{x}^{\left( j \right) }=\left[ {x_{1,j} ,\cdots ,x_{N,j} } \right] ^{T}$is the transmitted signal vector from all of the RAUs in the $j^\mathrm{th}$ cell, $x_{i,j}$ is the corresponding transmitted signal from the $i^\mathrm{th}$ RAU, and the average power for that of it is $\mathrm{E}\left[ {\left| {x_{i,j} } \right| ^{2}} \right] =P_{i,j}$.

n is the additive Gaussian noise with variance $E\left[ {nn^{H}} \right] =\sigma _n^2$, which is assumed to be independent of signal $\hbox {x}_{1,j}$.

Here, s characterises the shadowing effect, whose probability density function (PDF) is expressed as log-normal distribution [25]:

$$\begin{aligned} f_{S_s } \left( s \right) =\frac{\xi }{\sqrt{2\pi }\sigma s}\exp \left[ {-\frac{\left( {10\lg s-\mu } \right) ^{2}}{2\sigma ^{2}}} \right] \end{aligned}$$

(2)

where $\xi ={10}/{\left( {\ln 10} \right) },\mu \,$(in dB) and $\sigma$ (in dB) denote the mean and standard deviation for $10\log _{10} s$, respectively. Meanwhile, from the perspective of simplicity, the channels between RAUs and MTs are assumed to be independent identically distributed shadow fading. According to the aforementioned equation, it can be derived that $S=1$ is the means of no shadowing.

3 Closed-form of outage probability for STSS

In the following section, we will derive the closed-from expressions of outage probability for shadowing scenarios as well as the corresponding approximate expressions for shadowing case under downlink cellular DAS environment. It is assumed that the channel state information can be obtained at the receiver.

The proposed SSTS method in this paper is on the basis of the maximum desired signal criterion. For this selection scheme, the channel with feature of the largest signal intensity is selected to transmit signal, while the remainder of channels in the objective cell is sleep to save energy. Moreover, the selection of channel between active MT and RAUs from adjacent cells (Cell j, j = 2, 3) is random. In this case, the received signal at the active MT is given by:

$$\begin{aligned} y_1= & {} \underbrace{\sqrt{S_s L_{k,1} }h_{k,1} x_{k,1} }_{\mathrm{desired\;signal}}\nonumber \\&+\,\underbrace{\sqrt{S_s L_{q,2} }h_{q,2} x_{q,2} +\sqrt{S_s L_{l,3} }h_{l,3} x_{l,3} }_{\mathrm{interfernce}}+\underset{\textit{noise}}{n} \end{aligned}$$

(3)

where $k=\arg \max _{i\in \left\{ {1,\cdots ,N} \right\} } \left\{ {z_{i,1} } \right\} , q$ and l are randomly selected from $D=\left\{ {1,\cdots ,N} \right\}$, respectively.

According to Eq. (3), the signal to interference plus noise ratio (SINR) at the MT in objective cell is written as:

$$\begin{aligned} \gamma =\frac{L_{k,1} P_{k,1} \left| {h_{k,1} } \right| ^{2}}{L_{q,2} P_{q,2} \left| {h_{q,2} } \right| ^{2}+L_{l,3} P_{l,3} \left| {h_{l,3} } \right| ^{2}+{\sigma _n^2 }/{S_s }} \end{aligned}$$

(4)

The interference plus noise and its variance are treated as random variable simultaneously, which is different from the most existing works adopted CLT method. For CLT method, the variance is considered as constant rather than a random variable.

Since $h_{i,j}$ follows the Rayleigh distribution, the PDF of $\left| {h_{i,j} } \right| ^{2}L_{i,j} P_{i,j}$ is an exponential distribution with mean value $L_{i,j} P_{i,j}$.

The received desired signal at MT from all of the RAUs within Cell 1 are denoted by $Z=\left\{ {z_{1,1} ,\cdots ,z_{N,1} } \right\}$, where $z_{i,1} =\left| {h_{i,1} } \right| ^{2}L_{i,1} P_{i,1}$. The expected values of the elements in Z are re-denoted as $\Omega =\left\{ {\overline{z} _1 ,\cdots ,\overline{z} _{\left| D \right| } } \right\}$, in which $\left| D \right|$ is the cardinality of D. Let $z_{\max } =\mathop {\max }\limits _{i\in \left\{ {1,\cdots ,N} \right\} } \left\{ {z_{i,1} } \right\}$, so Eq. (4) can be rewritten as:

$$\begin{aligned} \gamma =\frac{z_{\max } }{L_{q,2} P_{q,2} \left| {h_{q,2} } \right| ^{2}+L_{l,3} P_{l,3} \left| {h_{l,3} } \right| ^{2}+{\sigma _n^2 }/{S_s }} \end{aligned}$$

(5)

The maximum desired signal can be indexed by $z_{\max } =\mathop {\max }\limits _{i\in \left\{ {1,\cdots ,N} \right\} } \left\{ {z_{i,1} } \right\}$, and its corresponding PDF can be derived and given as [14]:

$$\begin{aligned} f_{z_{\max } } \left( z \right) =\frac{d}{dz}\left[ {\prod _{i=\left\{ {1,\cdots ,\left| D \right| } \right\} } {\left( {1-\exp \left( {-\frac{z}{\overline{z} _i }} \right) } \right) } } \right] \end{aligned}$$

(6)

Let $\Omega _{vu}$denote the vth u-subset of the set $\Omega$, i.e., the vth subset of $\Omega$ which includes exactly u elements $\Big ( u=1,\cdots ,\left| D \right| ,v=1,\cdots ,\Big ( {\mathop {\left| D \right| }\limits _u } \Big ) \Big )$. The elements from $\Omega$ are denoted by $\eta _{u,v,w} \left( {w=1,\cdots ,u} \right)$. In consideration of the relationship between $\overline{z} _i$ and $\eta _{u,v,w}$, the product in Eq. (6) can be expanded with the proposed method in [26]:

$$\begin{aligned}&\prod _{i\in D} {\left( {1-\exp \left( {-\frac{z}{\overline{z} _i }} \right) } \right) } \nonumber \\&\quad =1-\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\prod _{w=1}^u {\exp \left( {-\frac{z}{\eta _{u,v,w} }} \right) } } } \nonumber \\&\quad =1-\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\exp \left( {-z\sum _{v=1}^u {\eta _{u,v,w} } } \right) } } \nonumber \\&\quad =1-\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\exp \left( {-\lambda _{uv} z} \right) } } \end{aligned}$$

(7)

According to the Eqs. (7) and (6), the PDF of $z_{max}$ can be readily written as follows:

$$\begin{aligned} f_{z_{\max } } \left( z \right) =\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\left[ {\lambda _{uv} \exp \left( {-\lambda _{uv} z} \right) } \right] } } \end{aligned}$$

(8)

The outage probability is defined as the received SINR less than a given threshold value $\gamma _{th}$ at MT.

$$\begin{aligned} P_{out} =\Pr \left( {\gamma <\gamma _{th} } \right) =1-\Pr \left( {\gamma >\gamma _{th} } \right) \end{aligned}$$

(9)

With reference to [27, 28], the right-hand part of Eq. (9) is given by:

$$\begin{aligned}&\Pr \left( {\gamma>\gamma _{th} } \right) \nonumber \\&\quad =\Pr \left( {\frac{z_{\max } }{L_{q,2} P_{q,2} \left| {h_{q,2} } \right| ^{2}+L_{l,3} P_{l,3} \left| {h_{l,3} } \right| ^{2}+{\sigma _n^2 }/{S_s }}>\gamma _{th} } \right) \nonumber \\&\quad =\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\exp \left( {-{\lambda _{uv} \gamma _{th} \sigma _n^2 }/{S_s }} \right) } } \;\times \nonumber \\&\quad \quad \left( {\frac{1}{\lambda _{uv} \gamma _{th} L_{q,2} P_{q,2} +1}\frac{1}{\lambda _{uv} \gamma _{th} L_{l,3} P_{l,3} +1}} \right) \end{aligned}$$

(10)

The detailed derivation of Eq. (10) is given in Appendix A.

3.1 No shadowing scenario $\left( {S_s =1} \right)$

The closed-form expression of outage probability at MT is given as:

$$\begin{aligned} P_{out}^{NS}= & {} \Pr \left( {\gamma <\gamma _{th} } \right) =1-\Pr \left( {\gamma >\gamma _{th} } \right) \nonumber \\= & {} 1-\sum _{u=1}^{| D |} {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\exp \left( {-\lambda _{uv} \gamma _{th} \sigma _n^2 } \right) } }\nonumber \\&\quad \left( {\frac{1}{\lambda _{uv} \gamma _{th} L_{q,2} P_{q,2} +1}\frac{1}{\lambda _{uv} \gamma _{th} L_{l,3} P_{l,3} +1}} \right) \end{aligned}$$

(11)

3.2 Shadowing scenario

Taking shadowing effect into consideration, we can rewrite the outage probability as follows:

$$\begin{aligned} P_{out}^S =\int _0^\infty {P_{out}^{NS} } f_{S_s } \left( s \right) ds \end{aligned}$$

(12)

It is hard to get the closed-form expression for Eq. (12), therefore, the Gauss-Hermite integral [25] is introduced to approximate, and the final result is given as:

$$\begin{aligned}&P_{out}^S \simeq 1-\frac{1}{\sqrt{\pi }}\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}} \times \nonumber \\&\quad \sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\left( {\frac{1}{\lambda _{uv} \gamma _{th} L_{q,2} P_{q,2} +1}\frac{1}{\lambda _{uv} \gamma _{th} L_{l,3} P_{l,3} +1}} \right) } \; \nonumber \\&\quad \times \sum _{w=1}^{N_w } {H_w \exp \left( {-\frac{\lambda _{uv} \gamma _{th} \sigma _n^2 }{10^{{\left( {\sqrt{2}\sigma t_w +\mu } \right) }/{10}}}} \right) } \end{aligned}$$

(13)

where $t_w$ denotes the base point,$H_w$ denotes the weight factor, and $N_w$ is the order of the introduced Hermite polynomial (see also Appendix B).

In comparison with the results for the NCLT method, herein, the closed-form expression of outage probability with the CLT method is given. For CLT method, the interference plus noise is considered as constant when given propagation path-loss and transmitted power.

The SINR at MT is given by [13]:

$$\begin{aligned} \gamma _{CLT} =\frac{z_{\max } }{\delta _z^2 } \end{aligned}$$

(14)

where $\delta _z^2 =L_{q,2} P_{q,2} \left| {h_{q,2} } \right| ^{2}+L_{l,3} P_{l,3} \left| {h_{l,3} } \right| ^{2}+\sigma _n^2$.

So, the PDF of $\gamma _{CLT}$ is given as:

$$\begin{aligned} f_{\gamma _{CLT} } =\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\left[ {\frac{\lambda _{uv} }{\delta _z^2 }\exp \left( {-\frac{\lambda _{uv} \gamma }{\delta _z^2 }} \right) } \right] } } \end{aligned}$$

(15)

According to Eqs. (14–15), we can get the outage probability of MT as:

$$\begin{aligned} \begin{array}{l} P_{out-CLT} =\Pr \left( {\gamma <\gamma _{th} } \right) \\ =\sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}\sum _{v=1}^{\left( {\mathop {\left| D \right| }\limits _u } \right) } {\left[ {1-\exp \left( {-\lambda _{uv} \gamma _{th} } \right) } \right] } } \\ \end{array} \end{aligned}$$

(16)

4 Simulation Results and Discussion

To verify the accuracy of the aforementioned analytical results, computer Monte-Carlo simulation is introduced in the following section. The distance between active MT and the objective cell centre is re-designated as d, which is normalised (i.e., $0<d\le 1)$ for the convenience of analysis. It is assumed that in Cell-1 the moving route for MT-1 is from RAU-1 in the direction of $\theta$ to the cell edge, as shown in Figure 1. Furthermore, the reminder of simulation parameters are set as follows in Table 1.

Table 1 Simulation Parameters

Along the direction $\theta = 0 {^{\circ }}$, the outage probability of SSTS in DAS versus the normalised distance d from the initial position (i.e., the objective cell centre) to the cell boundary, is depicted in Fig. 2. The analytical results by the NCLT method as well as the CLT method are clearly different, this is because the impact of short-term fading plays important role in the process of outage probability analysis. In comparison with NCLT method, interference plus noise is treated as a fixed-variance Gaussian noise when given propagation path-loss and transmitted power. The disadvantage of CLT method is that the impact of short-term fading is neglected. Therefore, it is more accurate to describe the outage probability with NCLT method.

Fig. 2

Outage probability versus the normalised distance as $\theta = 0$ (r = 0.65)

Fig. 3

Outage probability versus the signal-to-noise ratio as $\theta =0$; d = 0.9 (r = 0.65)

Moreover, the outage probability of a DAS is higher than that of its surroundings when the MT is located at a cell centre as well as a cell edge, because the distance between MT and the selected RAU becomes greater. As the MT moves to the location of $d = 0.65$, the outage probability is lower, this is because the distance between the selected RAU and MT is nearer. It can be demonstrated from Fig. 2 that the theoretical analysis results throughout the paper is correct, this is because the simulation results and analytical results are in excellent agreement.

The outage probability of MT versus the signal-to-noise ratio (SNR) as d = 0.9, $\theta = 0$ is depicted in Fig. 3. It can be seen from Fig. 3 that the difference between no-shadowing and shadowing scenarios as well as between SSTS and BTS methods are obvious, this is because the shadowing fading has bad effect on the outage probability, which is the nature property of shadowing. Moreover, the outage probability of SSTS is better compared with BTS, this is because the advantage of selection diversity is embodied and the inter-cell interferences reduce. It can also be demonstrated from Fig. 3 that the theoretical analysis results throughout the paper is correct, the explanation for this is the same as Fig. 2.

Fig. 4

Outage probability versus the path-loss exponent $\alpha$ as r = 0.5, d = 0.65

In the direction of $\theta$ = 0, the outage probability versus path-loss exponent $\alpha$ is depicted in Fig. 4, as the position of MT is located at d = 0.65 together with r = 0.5. The outage probability performance decreases along with $\alpha$ increases, which is in conformity with the definition of propagation path-loss $L=d^{-\alpha }$. Therefore, the larger the value of $\alpha$, the lower the propagation path-loss. It can be obtained from Fig. 4 that the outage probability of SSTS in DAS by NCLT method is more accurate than the counterpart by CLT method, because the impact of short-term fading on interference can be embodied. Moreover, it can be seen that the outage probability of SSTS in DAS outperforms the corresponding BTS scenario, the explanation for this is the same as Fig. 2.

Fig. 5

Outage probability versus the angle $\theta$ as r = 0.65; d = 1.0 (NCLT)

Fig. 6

Outage probability versus the normalised distance for different number of RAUs as r = 0.65 (NCLT)

In Fig. 5, the outage probability versus$\theta$ for MT along the cell edge is plotted. The trends in SSTS and BTS are similar. There is a vertex around $\theta ={-\pi }/6$, because the RAU from Cell 3 is near the MT and has an effect on system performance. It is the same as vertex at $\theta ={-\pi }/6$. It has three valleys around $\theta ={-\pi }/4,0,\pi /4$, respectively, because it exits from three RAUs in Cell 1 at the range $\theta \in \left( {{-\pi }/3,\pi /3} \right)$. As the MT moves, the RAU closest to the MT is selected. Therefore, the number of valleys matches the number of RAUs in the corresponding range. Moreover, it can be seen from Fig. 5 that shadowing fading has an adverse effect on outage probability, which is an shadowing’ innate property of itself.

Fig. 7

Outage probability versus the normalised distance for SSTS and BTS at r = 0.65 (NCLT)

The outage probability of SSTS in DAS versus the number of RAUs N is depicted in Fig. 6. It can be seen that the outage probability is lower than the surroundings when MT located at d = 0.65, because the RAU around d = 0.65 is chosen to transmit the signal with MT. Correspondingly, the communication distance between the selected RAU and MT becomes small, which can reduce outage probability. It also can be seen that the number of RAUs (N) has greatly influences on outage probability.

The outage probability of a DAS versus d with r = 0.65 is shown in Fig. 7. The whole transmitted power in each cell is the same for both SSTS and BTS in case of simulation. For SSTS, the outage probability is lower than that of BTS, this is because the reduced inter-cell interference and selection diversity play important roles. From Fig. 6, we see that, at the same outage probability, SSTS consumes less power than that of BTS. So, from the point of energy efficiency, SSTS offers better advantages compared to BTS.

Fig. 8

Outage probability versus the normalised distance for SSTS at r = 0.65 (NCLT)

The outage probability of DAS versus d as r = 0.65, $\theta = 0$ is illustrated in Fig. 8. The threshold values $\gamma _{th} = 6.45,7.45,8.45$ dB are selected as research object. With the values of threshold become large, the outage probability of DAS is worse, which is consistent with the definition of it.

5 Conclusions

In this paper, the interference power as well as its variance in DAS are considered as a random variable for the proposed NCLT method, when the propagation path-loss and transmitted power are given. For the proposed NCLT method, the effect of short-term fading on interference plus noise can be embodied, which can describe the outage probability more accurately. So this proposed NCLT method is more practical and accurate to evaluate the system performance of DAS. Moreover, an SSTS for DAS is proposed on the basis of the maximum desired signal criterion. Downlink outage probability of DAS for the proposed SSTS is investigated and the closed-form expressions of it are derived under no shadowing conditions, while the corresponding approximate analytical expressions for shadowing conditions are also given. Finally, it can be concluded that the proposed NCLT method is more accurate to describe outage probability when compared with CLT method. In the near future, many interesting issues on basis of this work are worth further investigation. Orthogonal frequency-division multiple access (OFDMA) as an important interference cancellation technology can be introduced to improve the system performance of DAS. Nakagami-m fading channel is more general in practice, and the closed-expression for DAS can be derived when channels suffer from this fading. Hence, it is meaningful to investigate the application of OFDMA and Nakagami-m fading to DAS in future work.

Appendices

Appendix A: derivation of Eq. (10)

$$\begin{aligned}&\Pr \left( {\gamma>\gamma _{th} } \right) \nonumber \\&\quad =\Delta \Pr \left( {\frac{z_{\max } }{L_{q,2} P_{q,2} \left| {h_{q,2} } \right| ^{2}+L_{l,3} P_{l,3} \left| {h_{l,3} } \right| ^{2}+\sigma _n^2 /S_s }>\gamma _{th} } \right) \nonumber \\&\quad =\int _{t_2 =0}^\infty {\int _{t_3 =0}^\infty {\Pr \left( {z_{\max } >\gamma _{th} \left( {t_2 +t_3 +\sigma _n^2 /S_s } \right) } \right) } }\nonumber \\&\times \exp \left( {\frac{-t_2 }{L_{q,2} P_{q,2} }} \right) \exp \left( {\frac{-t_3 }{L_{l,3} P_{l,3} }} \right) dt_2 dt_3 \nonumber \\&\quad =\Delta \sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}}\sum _{u=1}^{\left( \left( {\mathop {\left| D \right| }\limits _u } \right) \right) }\int _{t_2 =0}^\infty \int _{t_3 =0}^\infty \exp \left( -\lambda _{uv} \gamma _{th} \right. \nonumber \\&\quad \left. \left( {t_2 +t_3 +\sigma _n^2 /S_s } \right) \right) \nonumber \\&\times \exp \left( {\frac{-t_2 }{L_{q,2} P_{q,2} }} \right) \exp \left( {\frac{-t_3 }{L_{l,3} P_{l,3} }} \right) dt_2 dt_3 \nonumber \\&\quad =\Delta \sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}} \nonumber \\&\times \sum _{u=1}^{\left( \left( {\mathop {\left| D \right| }\limits _u } \right) \right) } \exp \left( {-\lambda _{uv} \gamma _{th} \sigma _n^2 /S_s } \right) \nonumber \\&\quad \int _{t_2 =0}^\infty {\int _{t_3 =0}^\infty {\hbox {!`}\exp \left( {\frac{-\lambda _{uv} \gamma _{th} L_{q,2} P_{q,2} -1}{L_{q,2} P_{q,2} }} \right) } } \nonumber \\&\quad \times \exp \left( {\frac{-\lambda _{uv} \gamma _{th} L_{l,3} P_{l,3} -1}{L_{l,3} P_{l,3} }t_3 } \right) dt_2 dt_3 \nonumber \\&\quad =\Delta \sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}} \sum _{u=1}^{\left( \left( {\mathop {\left| D \right| }\limits _u } \right) \right) } {\exp \left( {-\lambda _{uv} \gamma _{th} \sigma _n^2 /S_s } \right) } \nonumber \\&\times \left[ {\frac{L_{q,2} P_{q,2} }{\lambda _{uv} \gamma _{th} L_{q,2} P_{q,2} +1}\frac{L_{l,3} P_{l,3} }{\lambda _{uv} \gamma _{th} L_{l,3} P_{l,3} +1}} \right] \nonumber \\&\quad =\Delta \sum _{u=1}^{\left| D \right| } {\left( {-1} \right) ^{u-1}} \sum _{u=1}^{\left( \left( {\mathop {\left| D \right| }\limits _u } \right) \right) } {\exp \left( {-\lambda _{uv} \gamma _{th} \sigma _n^2 /S_s } \right) } \nonumber \\&\quad \left( {\frac{1}{\lambda _{uv} \gamma _{th} L_{q,2} P_{q,2} +1}\frac{1}{\lambda _{uv} \gamma _{th} L_{l,3} P_{l,3} +1}} \right) \end{aligned}$$

(17)

$$\begin{aligned} where{\begin{array}{ll} &{} \Delta \\ \end{array} }=\frac{1}{L_{q,2} P_{q,2} }\frac{1}{L_{l,3} P_{l,3} } \end{aligned}$$

Appendix B: Gauss-Hermite quadrature

The Gauss-Hermite formula is expressed as [29]:

$$\begin{aligned} \int _{-\infty }^{+\infty } {\exp \left( {-x^{2}} \right) } f\left( x \right) dx= & {} \sum _{i=1}^n {H_i } f\left( {x_i } \right) +R_n\nonumber \\\simeq & {} \sum _{i=1}^n {H_i } f\left( {x_i } \right) \end{aligned}$$

(18)

where n is the order of Hermite polynomial (the number of sample points utilized for the approximation). The value $x_{i}$ is the roots of the Hermite polynomial$H_n \left( x \right) {\begin{array}{ll} &{} {\left( {i=1,\cdots ,n} \right) } \\ \end{array} }$ and the associated weights $H_{i}$ are given as:

$$\begin{aligned} H_i =\frac{2^{n-1}n!\sqrt{\pi }}{n^{2}\left[ {H_{n-1} \left( {x_i } \right) } \right] ^{2}} \end{aligned}$$

(19)

The Hermite polynomial $H_n \left( x \right)$is written as [28]:

$$\begin{aligned} \begin{array}{l} H_n \left( x \right) =\left( {-1} \right) ^{n}\exp \left( {x^{2}} \right) \frac{d^{n}}{dx^{n}}\left( {\exp \left( {-x^{2}} \right) } \right) {\begin{array}{ll} &{} {or} \\ \end{array} } \\ H_n \left( x \right) =2^{n}x^{n}-2^{n-1}\left( {{\begin{array}{l} n \\ 2 \\ \end{array} }} \right) x^{n-1}+ \\ 2^{n-2}\cdot 1\cdot 3\cdot \left( {{\begin{array}{l} n \\ 4 \\ \end{array} }} \right) x^{n-4}-2^{n-3}\cdot 1\cdot 3\cdot 5\cdot \left( {{\begin{array}{l} n \\ 6 \\ \end{array} }} \right) x^{n-6}+\cdots \\ H_0 \left( x \right) =1 \\ \end{array} \end{aligned}$$

(20)

The remainder in Eq. (15) is given as:

$$\begin{aligned} R_n =\frac{n!\sqrt{\pi }}{2^{n}\left( {2n} \right) !}f^{\left( {2n} \right) }\left( \xi \right) {\begin{array}{ll} &{} {\left( {-\infty<\xi <\infty } \right) } \\ \end{array} } \end{aligned}$$

(21)

where $\xi$ is arbitrarily chosen and $f^{\left( n \right) }\left( x \right)$ is the $n^{\mathrm{th}}$ derivative of f(x).

The precision of the Gauss-Hermite approximation is dominated by n. If the number of sample points (n) is insufficient, the approximate and exact curves do not match exactly. On the contrary, the larger n, the more accurate the approximation obtained.