Orbit covariance propagation via quadratic-order state transition matrix in curvilinear coordinates

Abstract

In this paper, an analytical second-order state transition matrix (STM) for relative motion in curvilinear coordinates is presented and applied to the problem of orbit uncertainty propagation in nearly circular orbits (eccentricity smaller than 0.1). The matrix is obtained by linearization around a second-order analytical approximation of the relative motion recently proposed by one of the authors and can be seen as a second-order extension of the curvilinear Clohessy–Wiltshire (C–W) solution. The accuracy of the uncertainty propagation is assessed by comparison with numerical results based on Monte Carlo propagation of a high-fidelity model including geopotential and third-body perturbations. Results show that the proposed STM can greatly improve the accuracy of the predicted relative state: the average error is found to be at least one order of magnitude smaller compared to the curvilinear C–W solution. In addition, the effect of environmental perturbations on the uncertainty propagation is shown to be negligible up to several revolutions in the geostationary region and for a few revolutions in low Earth orbit in the worst case.

1 Introduction

Due to uncertainties in orbit determination and modeling, the orbit of an object is not deterministic but has always a stochastic component. While for most applications it may be sufficient to consider only the nominal trajectory, in some cases it is mandatory to analyze the effect of the possible deviations around it. One important example is the evaluation of the risk of collision between two orbiting objects. Even if the nominal trajectories do not lead to an impact, the orbit errors of both objects may induce a collision. The probability of collision for a pair of objects is low, but since the population of satellites and space debris is large and growing every year, the total risk cannot be neglected. In fact there are several examples of collisions in the past, like the 2009 Iridium–Cosmos collision (Newman et al 2009) or the non-catastrophic damage sustained by the solar panels of the European satellite Copernicus Sentinel-1A in August 2016 (Kuchynka et al 2017). The assessment of the risk of collision between two orbiting objects in low Earth orbit (LEO) requires the knowledge of the covariance matrices of both objects propagated up to the collision epoch (see García-Pelayo and Hernando-Ayuso 2016 and references therein). In geostationary orbits (GEO), where conjunctions occur throughout a much larger timescale, these matrices may even need to be propagated throughout the conjunction duration to properly evaluate collision probabilities (Chan 2008, pp. 153–171). An example of potential collision in GEO was presented by Lee et al (2012).

Several approaches are possible for propagating the orbit uncertainty. A distinction can be made between linear and nonlinear methods. The former are usually faster but may lack accuracy, especially for large uncertainties or large propagation periods, while the latter are more computationally intensive, but as a merit, they usually allow retaining more details of the real phenomena. The linear methods are based on considering a linearized solution to the equations of motion. If a linear solution is available and the orbit uncertainty can be modeled as a Gaussian distribution for the initial epoch, the predicted distribution will also be Gaussian. However, the validity of modeling the real distribution by a Gaussian depends on the variables used to express it: Some sets of variables remain closer to a Gaussian distribution than others (Junkins et al. 1996, b; Folcik et al 2011). In particular, the use of curvilinear coordinates and orbital elements was found to be advantageous with respect to an approach based on Cartesian coordinates (Junkins et al. 1996), as the along-track error is effectively projected onto the orbit, instead of being tangent to it.

In spite of their limitations, Cartesian coordinates have been widely used for uncertainty propagation. One of the most elementary techniques is to employ the Clohessy–Wiltshire (C–W) linear solution. Melton (2000) improved the C–W solution considering reference elliptical orbits using a series expansion on the eccentricity. He also proposed using an angular variable to increase accuracy. However, in his method the relation between the angular variable and the Cartesian coordinates was linearized; thus, variations of the angular variable are no longer contained inside the orbit. More recently, Lee et al. (2014) presented a semi-analytical method (it requires solving Kepler’s equation) for propagating the covariance matrix expressed in Cartesian coordinates, which is based on the Yamanaka–Ankersen state transition matrix (Yamanaka and Ankersen 2002) and consequently valid for elliptical orbits. Again, the method does not allow one to project the along-track error along the curved orbital path.

The use of curvilinear coordinates is especially interesting for propagating the orbit uncertainty because variations in the angular variable lead to a time delay, preserving the orbit shape. This fact allows one to accurately propagate uncertainties over a much larger time span when compared with Cartesian methods. Alfriend et al (2009) and Geller and Lovell (2017) presented the equations of motion using cylindrical coordinates in linear and full form, respectively. Bombardelli et al. (2017) presented the solution for the Keplerian relative motion expressed in curvilinear coordinates. In their work, the latter authors provided the exact solution as an infinite convergent series, a linear solution which can be regarded as an improved version of the C–W solution and a single-frequency quadratic solution among others. Other authors have employed spherical coordinates (see Lane and Axelrad 2006 for example) or elliptical curvilinear coordinates (Hill et al 2008; Coppola and Tanygin 2015 among others).

In this paper, the results of Bombardelli et al. (2017) are revisited in Sects. 2 and 3 and then extended to a double-frequency quadratic solution in Sect. 4. A linearization technique around such solution is then applied to obtain a new analytical state transition matrix, valid for orbits with small eccentricity ($e<0.1$ approximately). The STM is then employed as a straightforward means to propagate the state uncertainty along the orbit. The domain of validity of the proposed method is investigated by comparing the analytically propagated uncertainty with numerical results obtained using a Monte Carlo method and accounting for all relevant environmental perturbations. Test cases in LEO and GEO are considered.

2 Curvilinear coordinates

The relative motion of a Follower object (F) with respect to a Chief (C) spacecraft which moves in a circular orbit can be conveniently described using curvilinear coordinates. This motivated the works of Alfriend et al (2009), Geller and Lovell (2017) and Bombardelli et al. (2017) among others. In the following, we employ a similar approach to Bombardelli et al. (2017) and reproduce the key equations for completeness.

We will employ the Chief orbital radius and the inverse of the mean motion as unit of length and time, respectively. Let ${\mathcal {I}} \left\langle \varvec{i}, \varvec{j}, \varvec{k}\right\rangle$ be the Earth-centered reference frame where we set $\varvec{k}$ perpendicular to the Chief orbital plane and $\varvec{i}$ pointing to the Chief at the initial epoch $\tau = 0$. A non-inertial reference system ${\mathcal {C}}$ ${ \left< \varvec{i}', \varvec{j}', \varvec{k}' \right> }$ is defined as the Chief local vertical local horizontal reference frame. This Chief-centered system’s axes are oriented such that $\varvec{k}'$ is parallel to $\varvec{k}$ and $\varvec{j}'$ is parallel to the Chief orbital velocity vector. The reference systems ${\mathcal {I}}$ and ${\mathcal {C}}$ are shown in Fig. 1.

Fig. 1

Relative motion geometry and curvilinear coordinates

The position of the Follower relative to the Chief and its velocity relative to the frame ${\mathcal {C}}$ can be written as

$$\begin{aligned} \varvec{r}' = x \varvec{i}' + y \varvec{j}' + z \varvec{k}', \end{aligned}$$

(1)

$$\begin{aligned} \varvec{v}' = \dot{x} \varvec{i}' + \dot{y} \varvec{j}' + \dot{z} \varvec{k}'. \end{aligned}$$

(2)

After introducing the curvilinear coordinates of the Follower, $\rho$ and $\theta \in \left( -\pi , \pi \right]$

$$\begin{aligned} \rho&= -1 + \sqrt{ \left( x + 1 \right) ^2 + y^2 } ,\end{aligned}$$

(3)

$$\begin{aligned} \theta&= {{\mathrm{atan2}}}\left( y, 1 + x \right) , \end{aligned}$$

(4)

the relative position and velocity components can be expressed as a function of the curvilinear coordinates and its time-derivatives as

$$\begin{aligned}&x = -1 + \left( 1 + \rho \right) \cos \theta , \end{aligned}$$

(5)

$$\begin{aligned}&y = \left( 1 + \rho \right) \sin \theta , \end{aligned}$$

(6)

$$\begin{aligned}&\dot{x} = \dot{\rho } \cos \theta - \dot{\theta } \left( 1 + \rho \right) \sin \theta , \end{aligned}$$

(7)

$$\begin{aligned}&\dot{y} = \dot{\rho } \sin \theta + \dot{\theta } \left( 1 + \rho \right) \cos \theta . \end{aligned}$$

(8)

We note that the presented curvilinear coordinates can also describe the absolute position of the Follower in cylindrical coordinates $( 1 + \rho , \theta + \tau , z)$.

The absolute position, velocity and acceleration of the Follower can be written as:

$$\begin{aligned} \varvec{r}= & {} \varvec{r}_C + \varvec{r}', \end{aligned}$$

(9)

$$\begin{aligned} \varvec{v}= & {} \varvec{v}_C + \varvec{v}' + \varvec{\omega }_C \times \varvec{r}', \end{aligned}$$

(10)

$$\begin{aligned} \varvec{a}= & {} \varvec{\omega }_{\mathcal {C}} \times \left( \varvec{\omega }_{\mathcal {C}} \times \varvec{r}' \right) + 2 \varvec{\omega }_{\mathcal {C}} \times \varvec{v}' + \varvec{a}_C + \varvec{a}' = {-} \frac{\varvec{r}}{r^3} , \end{aligned}$$

(11)

where $\varvec{r}_C$, $\varvec{v}_C$ and $\varvec{a_C}$ are the known position, velocity and acceleration vectors of the Chief, $\varvec{\omega }_{\mathcal {C}}$ is the angular velocity vector of the reference system ${\mathcal {C}}$, and $\varvec{v}'$ and $\varvec{a}'$ are the time-derivatives of Eqs. (1) and (2), respectively. Note that in the right-hand side of Eq. (11), the gravitational parameter becomes unity in the system of units defined above and therefore is omitted. After some manipulations of the equations, we obtain:

$$\begin{aligned} \begin{aligned} \ddot{\rho } - 2 \dot{\theta } - 3\rho&= a_{i\rho } + a_{g\rho },\\ \ddot{\theta } + 2 \dot{\rho }&= a_{i\theta },\\ \ddot{z} + z&= a_{gz}, \end{aligned} \end{aligned}$$

(12)

where the nonlinear terms, which do not depend on $\theta$, can be divided into inertial accelerations ($a_{i\rho }$ and $a_{i\theta }$) and gravitational accelerations ($a_{g\rho }$ and $a_{gz}$). The nonlinear accelerations obey:

$$\begin{aligned} \begin{aligned} a_{i\rho }&= \dot{\theta }^2 \left( 1 + \rho \right) + 2 \dot{\theta } \rho ,\\ { a_{g\rho }}&{ = -2 \rho + 1 - \frac{1 + \rho }{\left[ \left( 1+\rho \right) ^2 + z^2 \right] ^{3/2}},}\\ a_{i\theta }&= \frac{ 2 \dot{\rho } \left( \rho - \dot{\theta } \right) }{1 + \rho },\\ a_{gz}&= z - \frac{z}{\left[ \left( 1+\rho \right) ^2 + z^2 \right] ^{3/2}}. \end{aligned} \end{aligned}$$

(13)

Finally, we introduce for later use the curvilinear state vector

$$\begin{aligned} \varvec{c} = \left( \rho , \theta , z, \dot{\rho }, \dot{\theta }, \dot{z} \right) ^\top . \end{aligned}$$

(14)

3 Curvilinear Clohessy–Wiltshire

The homogeneous solution to the system of differential equations of Eq. (12) corresponds to the case in which the nonlinear accelerations are negligible. Analyzing the nonlinear accelerations reveals that this will happen when

$$\begin{aligned} \left( \vert \rho _0 \vert , \vert z_0 \vert , \vert \dot{\rho }_0 \vert , \vert \dot{\theta }_0 \vert , \vert \dot{z}_0 \vert \right) \ll 1 . \end{aligned}$$

Eq. (12) reduces then to:

$$\begin{aligned} \begin{aligned} \ddot{\rho } - 2 \dot{\theta } - 3\rho&= 0\\ \ddot{\theta } + 2 \dot{\rho }&= 0\\ \ddot{z} + z&= 0. \end{aligned} \end{aligned}$$

(15)

The homogeneous equations have the same structure of the Cartesian Clohessy–Wiltshire (C–W) equations after replacing the Cartesian y coordinate with $\theta$. However, Eq. 15 have a larger domain of validity compared to the Cartesian C–W due to the fact that $\theta$, unlike y, does not play any role in the nonlinear terms (see Eq. (13)) and need not to be small for the preceding linearization to be valid. The homogeneous solution with initial conditions $\varvec{c}_0$ at epoch $\tau = 0$ reads:

$$\begin{aligned} \varvec{c} ={\varvec{\varPhi }_{\mathrm{CW}}} \varvec{c}_0 \end{aligned}$$

(16)

with

$$\begin{aligned} \varvec{\varPhi }_{\mathrm{CW}} = \begin{bmatrix} 4 - 3 \cos \tau&\quad 0&\quad 0&\quad \sin \tau&\quad 2(1-\cos \tau )&\quad 0 \\ 6(-\tau +\sin \tau )&\quad 1&\quad 0&\quad 2(-1+\cos \tau )&\quad -3\tau +4\sin \tau&\quad 0 \\ 0&\quad 0&\quad \cos \tau&\quad 0&\quad 0&\quad \sin \tau \\ 3 \sin \tau&\quad 0&\quad 0&\quad \cos \tau&\quad 2\sin \tau&\quad 0 \\ 6(-1+\cos \tau )&\quad 0&\quad 0&\quad -2\sin \tau&\quad -3+4\cos \tau&\quad 0 \\ 0&\quad 0&\quad -\sin \tau&\quad 0&\quad 0&\quad \cos \tau \\ \end{bmatrix}. \end{aligned}$$

(17)

4 Quadratic solution

Bombardelli et al. (2017) presented a single-frequency, quadratic solution to the relative motion using curvilinear coordinates. A careful inspection of the general solution reveals that the double-frequency terms, which were previously neglected, are also of quadratic order.

First, we report the exact solution in curvilinear coordinates as a function of the orbital elements of the Follower (normalized semi-major axis a, eccentricity e, inclination i, right ascension of the ascending node $\varOmega$, argument of periapsis $\omega$ and true anomaly $\nu$)

$$\begin{aligned} \begin{aligned} \rho =&-1 + \frac{a (1 - e^2)}{1 + e\cos \nu } \sqrt{1- \sin ^2 i \ \sin ^2 (\omega + \nu )} \, ,\\ \theta =&- \tau + \varOmega + {{\mathrm{atan2}}}\Big ( \cos i \ \sin (\omega + \nu ), \ \cos (\omega + \nu ) \Big ), \\ z =&\frac{a (1 - e^2)}{1 + e\cos \nu } \sin i \ \sin (\omega +\nu ) . \end{aligned} \end{aligned}$$

(18)

In this equation, $\nu$ is related to the eccentric anomaly E by

$$\begin{aligned} \cos \nu = \frac{\cos E - e}{1 - e \cos E} , \qquad \sin \nu = \frac{\sqrt{1 - e^2}\sin E}{1 - e \cos E} , \end{aligned}$$

(19)

which in turn is related to the normalized time $\tau$ by Kepler’s equation:

$$\begin{aligned} M = M_0 + n \tau = E - e \sin E, \end{aligned}$$

(20)

where M is the mean anomaly and n is the normalized mean motion. Even if a closed-form solution to the relative motion is available, Eq. (18) requires solving Kepler’s equation for each epoch so it cannot be considered completely analytical. However, it is possible to expand $\cos \nu$ and $\sin \nu$ in series as a function of the eccentricity using $J_j$, the Bessel function of the first kind and order j. Following (Battin 1999, p. 210), Eq. (19) can be expanded as

$$\begin{aligned} \begin{aligned} \cos \nu =&-e + \frac{2\left( 1-e^2\right) }{e}\sum _{j=1}^\infty J_j(je) \cos jM,\\ \sin \nu =&2\sqrt{ 1 - e^2} \sum _{j=1}^\infty \frac{1}{j} \frac{\text {d} J_j(je) }{ \text {d} e} \sin jM. \end{aligned} \end{aligned}$$

(21)

Equation (21) can be substituted into Eq. (18) after applying the angle sum trigonometric identities. We can express a, e, i, $\varOmega$, $\omega$, $M_0$ and n in Eqs. (18–21) as a function of the initial curvilinear coordinates $\varvec{c}_0$ (see the online Appendix for these expressions or Bombardelli et al. (2017) for a detailed derivation).

The obtained equations provide the exact solution to the relative motion as a function of $\varvec{c}_0$ and $\tau$, but involve convoluted expressions and infinite summations. With the help of a symbolic manipulator, we expand them in series of the initial curvilinear coordinates. After neglecting terms of order ${\mathcal {O}}( \varvec{c}_0^3)$ and higher, the double-frequency quadratic solution is obtained as

$$\begin{aligned} \rho (\tau ) \simeq&\ \rho _{\text {const}} + \rho _{C\tau } \cos n \tau + \rho _{S\tau } \sin n \tau + \rho _{C2\tau } \cos 2n \tau + \rho _{S2\tau } \sin 2n \tau , \end{aligned}$$

(22)

$$\begin{aligned} \theta (\tau ) \simeq&\ \theta _{\text {const}} + \theta _{C\tau } \cos n \tau + \theta _{S\tau } \sin n \tau + \theta _{C2\tau } \cos 2n \tau + \theta _{S2\tau } \sin 2n \tau + \theta _{\text {sec}} \tau , \end{aligned}$$

(23)

$$\begin{aligned} z (\tau ) \simeq&\ z_{\text {const}} + z_{C\tau } \cos n \tau + z_{S\tau } \sin n \tau + z_{C2\tau } \cos 2n \tau + z_{S2\tau } \sin 2n \tau , \end{aligned}$$

(24)

where the coefficients and the normalized mean motion n are quadratic functions of $\varvec{c}_0$. The triple-frequency terms were found to be at most of cubic order and thus are not included.

The normalized mean motion obeys

$$\begin{aligned} n \simeq 1 -6 \rho _0- 3 \dot{\theta }_0- \frac{3}{2} \left( z_0^2 + \dot{z}_0^2 + \dot{\rho }_0^2 - 5 \rho _0^2 \right) . \end{aligned}$$

(25)

The coefficients for $\rho$ and $\dot{\rho }$ in Eqs. (22, 29) are given by

(26)

For the angular variable, the corresponding expressions are:

$$\begin{aligned} \begin{aligned}&\theta _{\text {const}} = \theta _0-2 \dot{\rho }_0+ \frac{1}{2} \dot{\rho }_0\rho _0+ \dot{\rho }_0\dot{\theta }_0- 2 z_0\dot{z}_0,\\&\theta _\text {sec} = (n - 1),\\&\theta _{C\tau } = 2 \dot{\rho }_0- 8 \dot{\theta }_0\dot{\rho }_0- 6 \dot{\rho }_0\dot{\theta }_0+ 2 z_0\dot{z}_0,\\&\theta _{S\tau } = 4 \dot{\theta }_0+ 6 \rho _0+ 6 \rho _0^2 + 12 \rho _0\dot{\theta }_0+ 4 \dot{\rho }_0^2 + 2 \dot{\theta }_0^2 + 2 \dot{z}_0^2 + z_0^2 ,\\&\theta _{C2\tau } = \frac{15}{2} \rho _0\dot{\rho }_0- \frac{1}{2} z_0\dot{z}_0+ 5 \dot{\theta }_0\dot{\rho }_0,\\&\theta _{S2\tau } = \frac{45}{4} \rho _0^2 + 15 \rho _0\dot{\theta }_0+ \frac{1}{4} z_0^2 - \frac{5}{4} \dot{\rho }_0^2 + 5 \dot{\theta }_0^2 - \frac{1}{4} \dot{z}_0^2 . \end{aligned} \end{aligned}$$

(27)

The coefficients of the quadratic formula for the out-of-plane motion read:

$$\begin{aligned} \begin{aligned}&z_{\text {const}} = \frac{3}{2} \dot{\rho }_0\dot{z}_0- 3z_0\dot{\theta }_0- \frac{9}{2} \rho _0z_0,\\&z_{C\tau } = z_0+ 3 \rho _0z_0- 2 \dot{\rho }_0\dot{z}_0+ 2 \dot{\theta }_0z_0,\\&z_{S\tau } = \dot{z}_0+ 3 \rho _0\dot{z}_0+ \dot{\rho }_0z_0+ \dot{\theta }_0\dot{z}_0,\\&z_{C2\tau } = \frac{3}{2} \rho _0z_0+ z_0\dot{\theta }_0+ \frac{1}{2} \dot{\rho }_0\dot{z}_0,\\&z_{S2\tau } = \frac{3}{2} \dot{z}_0\rho _0- \frac{1}{2} z_0\dot{\rho }_0+ \dot{\theta }_0\dot{z}_0. \end{aligned} \end{aligned}$$

(28)

The following expressions provide the time-derivative of the curvilinear coordinates

$$\begin{aligned} \dot{\rho } (\tau ) \simeq&\ n \left( -\rho _{C\tau } \sin n \tau + \rho _{S\tau } \cos n \tau \right) + 2n \left( -\rho _{C2\tau } \sin 2n \tau + \rho _{S2\tau } \cos 2n \tau \right) , \end{aligned}$$

(29)

$$\begin{aligned} \dot{\theta } (\tau ) \simeq&\ n \left( - \theta _{C\tau } \sin n \tau + \theta _{S\tau } \cos n \tau \right) +2n \left( - \theta _{C2\tau } \sin 2n \tau + \theta _{S2\tau } \cos 2n \tau \right) + {\theta }_\text {sec} , \end{aligned}$$

(30)

$$\begin{aligned} \dot{z} (\tau ) \simeq&\ n \left( - z_{C\tau } \sin n \tau + z_{S\tau } \cos n \tau \right) + 2 n \left( - z_{C2\tau } \sin 2n \tau + z_{S2\tau } \cos n 2\tau \right) . \end{aligned}$$

(31)

5 Linearization around the quadratic solution (QuadLin)

Let $\varvec{c}_\text {nom}$ be the nominal orbit with initial conditions $\varvec{c}_0 = \left( \rho _0, \theta _0, z_0, \dot{\rho }_0, \dot{\theta }_0, \dot{z}_0\right) ^\top$. The nominal orbit can be calculated using the quadratic solution $\varvec{q}$:

$$\begin{aligned} \varvec{c}_\text {nom} = \varvec{q} \left( \varvec{c}_0 \right) . \end{aligned}$$

(32)

Another orbit $\varvec{c}$ very close to the previous one will have as initial conditions

$$\begin{aligned} \varvec{c}_0 + {\delta } \varvec{c}_0 = \left( \rho _0+ \delta \rho _0, \theta _0+ \delta \theta _0, z_0+ \delta z_0, \dot{\rho }_0+ \delta \dot{\rho }_0, \dot{\theta }_0+ \delta \dot{\theta }_0, \dot{z}_0+ \delta \dot{z}_0\right) ^\top , \end{aligned}$$

(33)

and the quadratic formula will yield

$$\begin{aligned} \varvec{c} = \varvec{q} \left( \varvec{c}_0 + {\delta } \varvec{ c}_0 \right) . \end{aligned}$$

(34)

It is possible to expand $\varvec{q}$ in Taylor series around $\varvec{c}_0$. The zeroth-order term is simply $\varvec{c}_\text {nom}$, which corresponds to the evolution of the nominal orbit and can be calculated with a more accurate method if necessary. If the difference between the orbits is very small, the linear terms will provide a sufficiently accurate approximation

$$\begin{aligned} \begin{aligned} \varvec{c} =&\, \varvec{c}_\text {nom} + \left. \frac{\partial \varvec{q} }{\partial \varvec{c}_0 } \right| _{\varvec{c}_0}\ \delta \varvec{ c}_0 +\dots ,\\ \delta \varvec{ c} =&\, \varvec{c} - \varvec{c}_\text {nom}\simeq \varvec{\varPhi }(\tau , \tau _0) \delta \varvec{ c}_0 . \end{aligned} \end{aligned}$$

(35)

The matrix $\left. \frac{\partial \varvec{q}}{\partial \varvec{c}_0 } \right| _{\varvec{c}_0}$ constitutes a state transition matrix (STM) $\varvec{\varPhi }(\tau , \tau _0)$ for the Keplerian relative motion. $\varvec{\varPhi }(\tau , \tau _0)$ corresponds to an approximate solution, since it was developed from the truncated quadratic solution, and as a consequence, it deviates from the real solution by cubic and higher- order terms.

The first row of $\varvec{\varPhi }(\tau , \tau _0)$ reads

$$\begin{aligned} \begin{aligned} \left. \frac{\partial \rho }{ \partial \varvec{c}_0} \right| _{\varvec{c}_0} =&[\begin{array}{llllll} {\varPhi }_{\rho \rho },&{\varPhi }_{\rho \theta },&{\varPhi }_{\rho z} ,&{\varPhi }_{\rho \dot{\rho }} ,&{\varPhi }_{\rho \dot{\theta }} ,&{\varPhi }_{\rho \dot{z}} \end{array}] \\ =&\Bigg \{ \frac{\partial \rho _{\text {const}} }{ \partial \varvec{c}_0} + \left( \frac{\partial \rho _{C\tau } }{ \partial \varvec{c}_0} + \rho _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( n \tau \right) + \left( \frac{\partial \rho _{S\tau } }{ \partial \varvec{c}_0} - \rho _{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( n \tau \right) \\&+ \left( \frac{\partial \rho _{C2\tau } }{ \partial \varvec{c}_0} + 2\rho _{S2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( 2n \tau \right) + \left( \frac{\partial \rho _{S2\tau } }{ \partial \varvec{c}_0} - 2\rho _{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( 2n \tau \right) \Bigg \}_{\varvec{c}_0}, \end{aligned} \end{aligned}$$

(36)

where the partial derivatives are given by the row vectors

and

The row corresponding to the angular variable $\theta$ can be calculated as

$$\begin{aligned} \begin{aligned} \left. \frac{\partial \theta }{ \partial \varvec{c}_0} \right| _{\varvec{c}_0} =&\begin{bmatrix} {\varPhi }_{\theta \rho },&{\varPhi }_{\theta \theta },&{\varPhi }_{\theta z} ,&{\varPhi }_{\theta \dot{\rho }} ,&{\varPhi }_{\theta \dot{\theta }} ,&{\varPhi }_{\theta \dot{z}} \end{bmatrix} \\&=\Bigg \{ \frac{\partial \theta _{\text {const}} }{ \partial \varvec{c}_0} + \frac{\partial n }{ \partial \varvec{c}_0} \tau \\&+ \left( \frac{\partial \theta _{C\tau } }{ \partial \varvec{c}_0} + \theta _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( n \tau \right) + \left( \frac{\partial \theta _{S\tau } }{ \partial \varvec{c}_0} - \theta _{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( n \tau \right) \\&+ \left( \frac{\partial \theta _{C2\tau } }{ \partial \varvec{c}_0} + 2 \theta _{S2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( 2n \tau \right) + \left( \frac{\partial \theta _{S2\tau } }{ \partial \varvec{c}_0} - 2 \theta _{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( 2n \tau \right) \Bigg \}_{\varvec{c}_0} \end{aligned} \end{aligned}$$

(39)

together with

The out-of-plane row of the STM is governed by

$$\begin{aligned} \begin{aligned} \left. \frac{\partial z }{ \partial \varvec{c}_0} \right| _{\varvec{c}_0}=&\begin{bmatrix} {\varPhi }_{z \rho },&{\varPhi }_{z \theta },&{\varPhi }_{z z} ,&{\varPhi }_{z \dot{\rho }} ,&{\varPhi }_{z \dot{\theta }} ,&{\varPhi }_{z \dot{z}} \end{bmatrix} \\ =&\Bigg \{ \frac{\partial z_{\text {const}} }{ \partial \varvec{c}_0} + \left( \frac{\partial z_{C\tau } }{ \partial \varvec{c}_0} + z_{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( n \tau \right) + \left( \frac{\partial z_{S\tau } }{ \partial \varvec{c}_0} - z_{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( n \tau \right) \\&+ \left( \frac{\partial z_{C2\tau } }{ \partial \varvec{c}_0} + 2 z_{S2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( 2n \tau \right) + \left( \frac{\partial z_{S2\tau } }{ \partial \varvec{c}_0} - 2 z_{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( 2n \tau \right) \Bigg \}_{\varvec{c}_0}, \end{aligned} \end{aligned}$$

(41)

where we set

Finally, the last three rows of $\varvec{\varPhi }(\tau , \tau _0)$ can be obtained as the $\tau$ derivative of the first three rows

$$\begin{aligned} \left. \frac{\partial \dot{\rho } }{ \partial \varvec{c}_0 } \right| _{\varvec{c}_0}= & {} \frac{\text {d} }{ \text {d} \tau } \left( \left. \frac{\partial \rho }{ \partial \varvec{c}_0} \right| _{\varvec{c}_0} \right) = \begin{bmatrix} {\varPhi }_{\dot{\rho } \rho },&{\varPhi }_{\dot{\rho } \theta },&{\varPhi }_{\dot{\rho } z} ,&{\varPhi }_{\dot{\rho } \dot{\rho }} ,&{\varPhi }_{\dot{\rho } \dot{\theta }} ,&{\varPhi }_{\dot{\rho } \dot{z}} \end{bmatrix} \nonumber \\= & {} \Bigg \{ n \left( \frac{\partial \rho _{S\tau } }{ \partial \varvec{c}_0} - \rho _{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( n \tau \right) - \rho _{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \sin \left( n \tau \right) \nonumber \\&- n \left( \frac{\partial \rho _{C\tau } }{ \partial \varvec{c}_0} + \rho _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( n \tau \right) + \rho _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \cos \left( n \tau \right) \nonumber \\&+ 2n \left( \frac{\partial \rho _{S2\tau } }{ \partial \varvec{c}_0} - 2\rho _{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( 2n \tau \right) - 2\rho _{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \sin \left( 2 n \tau \right) \nonumber \\&- 2n \left( \frac{\partial \rho _{C2\tau } }{ \partial \varvec{c}_0} + 2\rho _{2S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( 2n \tau \right) + 2\rho _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \cos \left( 2n \tau \right) \Bigg \}_{\varvec{c}_0} \end{aligned}$$

(43)

$$\begin{aligned} \begin{aligned} \left. \frac{\partial \dot{\theta } }{ \partial \varvec{c}_0 } \right| _{\varvec{c}_0} =&\frac{\text {d} }{ \text {d} \tau } \left( \left. \frac{\partial \theta }{ \partial \varvec{c}_0} \right| _{\varvec{c}_0} \right) = \begin{bmatrix} {\varPhi }_{\dot{\theta } \rho },&{\varPhi }_{\dot{\theta } \theta },&{\varPhi }_{\dot{\theta } z} ,&{\varPhi }_{\dot{\theta } \dot{\rho }} ,&{\varPhi }_{\dot{\theta } \dot{\theta }} ,&{\varPhi }_{\dot{\theta } \dot{z}} \end{bmatrix} \\ =&\Bigg \{ \frac{\partial n }{ \partial \varvec{c}_0} + n \left( \frac{\partial \theta _{S\tau } }{ \partial \varvec{c}_0} - \theta _{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( n \tau \right) - \theta _{C_\tau } \frac{\partial n }{ \partial \varvec{c}_0} \sin \left( n \tau \right) \\&- n \left( \frac{\partial \theta _{C\tau } }{ \partial \varvec{c}_0} + \theta _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( n \tau \right) + \theta _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \cos \left( n \tau \right) \\&+ 2n \left( \frac{\partial \theta _{S2\tau } }{ \partial \varvec{c}_0} - 2 \theta _{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( 2n \tau \right) - 2 \theta _{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \sin \left( 2 n \tau \right) \\&- 2n \left( \frac{\partial \theta _{C2\tau } }{ \partial \varvec{c}_0} + 2 \theta _{S2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( 2n \tau \right) + 2 \theta _{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \cos \left( 2n \tau \right) \Bigg \}_{\varvec{c}_0} \end{aligned} \end{aligned}$$

(44)

$$\begin{aligned} \begin{aligned} \left. \frac{\partial \dot{z} }{ \partial \varvec{c}_0 } \right| _{\varvec{c}_0} =&\frac{\text {d} }{ \text {d} \tau } \left( \left. \frac{\partial z }{ \partial \varvec{c}_0} \right| _{\varvec{c}_0} \right) = \begin{bmatrix} {\varPhi }_{\dot{z} \rho },&{\varPhi }_{\dot{z} \theta },&{\varPhi }_{\dot{z} z} ,&{\varPhi }_{\dot{z} \dot{\rho }} ,&{\varPhi }_{\dot{z} \dot{\theta }} ,&{\varPhi }_{\dot{z} \dot{z}} \end{bmatrix} \\ =&\Bigg \{ n \left( \frac{\partial z_{S\tau } }{ \partial \varvec{c}_0} - z_{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( n \tau \right) - z_{C\tau } \frac{\partial n }{ \partial \varvec{c}_0} \sin \left( n \tau \right) \\&- n \left( \frac{\partial z_{C\tau } }{ \partial \varvec{c}_0} + z_{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( n \tau \right) + z_{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \cos \left( n \tau \right) \\&+ 2n \left( \frac{\partial z_{S2\tau } }{ \partial \varvec{c}_0} - 2 z_{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \cos \left( 2n \tau \right) - 2 z_{C2\tau } \frac{\partial n }{ \partial \varvec{c}_0} \sin \left( 2 n \tau \right) \\&- 2n \left( \frac{\partial z_{C2\tau } }{ \partial \varvec{c}_0} + 2 z_{2S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \tau \right) \sin \left( 2n \tau \right) + 2 z_{S\tau } \frac{\partial n }{ \partial \varvec{c}_0} \cos \left( 2n \tau \right) \Bigg \}_{\varvec{c}_0}. \end{aligned} \end{aligned}$$

(45)

The covariance matrix is the second-order moment of the uncertainty distribution, and when expressed in curvilinear coordinates, it takes the form

$$\begin{aligned} \varvec{C}(\tau ) = \text {E} \left[ \delta \varvec{c}(\tau ) \, \delta \varvec{c}^\top (\tau ) \right] , \end{aligned}$$

(46)

where $\text {E}$ is the estimation operator. By use of Eq. (35), the covariance matrix can be calculated as

$$\begin{aligned} \varvec{C}(\tau ) = \varvec{\varPhi } \left( \tau , \tau _0 \right) \varvec{C}_0 \, \varvec{\varPhi }^\top \left( \tau , \tau _0 \right) . \end{aligned}$$

(47)

Fig. 2

Relative motion in the ${\mathcal {C}}$ frame: Full view (left) and zoom (right)

Fig. 3

$\rho$ standard deviation error (GEO)

Fig. 4

$\dot{\rho }$ standard deviation error (GEO)

Fig. 5

$\theta$ standard deviation error (GEO)

Fig. 6

$\dot{\theta }$ standard deviation error (GEO)

Fig. 7

z standard deviation error (GEO)

6 Results

In this section, we first apply the proposed STM to the uncertainty propagation problem of a piece of space debris orbiting in the GEO region with respect to an active satellite. We propagate the covariance matrix of the relative state using the curvilinear C–W and the QuadLin STM. To assess whether the Gaussian distributions associated with these matrices are representative of the dynamics of the problem, we compare them to high-fidelity numerical simulations considering Luni-Solar, $J_2$ and $C_{2,2}$ perturbations. To this end, the initial uncertainty region is sampled and propagated via direct integration of the equations of motion. The covariance matrix is then estimated at every epoch from the samples. The evolution of the samples is also compared to the result of applying the STM to the relative initial states. A comparison with the work of Melton (2000) is also included.

An example in LEO using a fictitious reference orbit is also presented following the same procedure as in the GEO example.

6.1 Application to the GEO region

An active GEO satellite whose orbit is known with arbitrary accuracy is considered as the Chief. The unit of length is set as the orbital radius, approximately equal to 42164 km. The unit of time is equal to $86400/(2\pi )$ s, which is approximately 13751 s. In these units, the Earth’s gravitational parameter is unity and the GEO orbital period is $2\pi$. The ratio of the unit of distance to the unit of length is equal to the velocity of a satellite in GEO orbit, around 3.066 km s$^{-1}$.

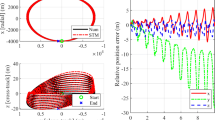
The motion of a nearby piece of space debris or a non-maneuverable, non-cooperative object was studied using the linearization method presented in the previous section. The initial relative state was set imposing $\rho _0 = -0.0003$, $\dot{\rho }_0 = 0.001$, $\theta _0 = 10.55 ^\circ$, $e = 0.01$ and $i = 0^\circ$. Figure 2 shows the nominal relative motion between both bodies in the ${\mathcal {C}}$ reference frame. The relative orbit was propagated for 8 days. The nominal orbits do not intersect, but the orbit uncertainty could lead to a collision.

Fig. 8

$\dot{z}$ standard deviation error (GEO)

Fig. 9

Uncertainty dispersion in the $\Delta \theta$–$\Delta \rho$ plane at an intermediate epoch (GEO, $\tau = 2.81$ days)

Fig. 10

Uncertainty dispersion in the $\Delta \theta$–$\Delta \rho$ plane at an intermediate epoch (GEO, $\tau = 8.00$ days)

The relative position and velocity uncertainty at the initial epoch were assumed to follow independent isotropic Gaussian distributions expressed in Cartesian coordinates, with $\sigma _\text {pos} = 10^{-4}$ and $\sigma _\text {vel} = 10^{-5}$. In non-normalized units, these values correspond to 4.2 km and 3 cm s$^{-1}$ approximately. As the uncertainty is small, an initial Gaussian distribution in curvilinear coordinates was generated from the initial distribution in Cartesian coordinates using a linear mapping based on the Jacobian of Eqs. (3, 4) and its time-derivatives. Here we exploit the fact that linear transformations preserve Gaussianity, and because the uncertainty region is small, higher-order terms can be neglected. From this point onwards, we refer to the uncertainty distribution in curvilinear coordinates.

Fig. 11

Angular-radial uncertainty clouds including Melton’s method at an early epoch (GEO, $\tau = 0.80$ days)

Fig. 12

Angular-radial uncertainty clouds including Melton’s method at an intermediate epoch (GEO, $\tau = 2.81$ days)

The covariance matrix was propagated employing the curvilinear C–W solution and the linearization around the quadratic solution (QuadLin). To assess the validity of the method, a validation against a Monte Carlo simulation (M-C) was performed. For each of N samples in the initial distribution, the orbit was propagated using the curvilinear C–W solution, the QuadLin solution and a high-fidelity numerical solution including Luni-Solar, $J_2$ and $C_{2,2}$ perturbations. Finally, for each time step, the mean orbit was estimated as

$$\begin{aligned} \left\langle \varvec{c}(\tau ) \right\rangle = \frac{1}{N}\sum _{i=1}^{N} \varvec{c}_i(\tau ) , \end{aligned}$$

(48)

and the covariance matrix was estimated as

$$\begin{aligned} \varvec{C}(\tau ) = \frac{1}{N-1} \sum _{i=1}^{N} \Big ( \varvec{c}_i(\tau ) - \left\langle \varvec{c}(\tau ) \right\rangle \Big ) \Big ( \varvec{c}_i(\tau ) - \left\langle \varvec{c}(\tau ) \right\rangle \Big )^\top . \end{aligned}$$

(49)

Figures 3, 4, 5, 6, 7 and 8 show the standard deviation absolute errors with respect to the high-fidelity numerical M-C simulations. The blue lines correspond to the curvilinear C–W solution, and the green dashed lines represent the QuadLin method. When considering second-order terms in the covariance propagation, the absolute error is reduced by one to two orders of magnitude.

Fig. 13

Average position error including comparison with Melton’s method (GEO)

One can gain some insight into the performance of the methods by looking at the samples of the M-C simulations. The uncertainty point clouds are identical at the initial epoch for the three compared methods. However, at an intermediate epoch (Fig. 9), the C–W solution shows a considerable deviation on the $(\Delta \theta , \Delta \rho )$ plane. This effect is multiplied for later epochs as can be seen in Fig. 10. In both figures, the QuadLin method is able to reproduce the covariance evolution with a higher fidelity. The M-C points show a slight “banana” shape, which suggests that the real uncertainty distribution starts to depart from Gaussianity owing to nonlinear effects. The result in all cases shows improvement compared to the curvilinear C–W method.

Fig. 14

$\rho$ standard deviation error (LEO, $i=98^\circ$)

Fig. 15

$\rho$ standard deviation error (LEO, $i=45^\circ$)

Fig. 16

z standard deviation (LEO, $i=98^\circ$)

Fig. 17

z standard deviation (LEO, $i=45^\circ$)

Additionally, a comparison against Melton’s method (Melton 2000) was performed. Numerical simulations reveal that out-of-plane motion accuracy is similar between the proposed and Melton’s method. The $\theta$ error remains smaller for Melton’s method as it considers the high-fidelity nonlinear expression for the normalized mean motion n, instead of its second-order expansion. However, Melton’s method is not able to reproduce with high fidelity the nonlinear motion in the radial direction. Figures 11 and 12 show this effect: For early epochs, Melton’s method presents a small error, but the accuracy degrades as the covariance grows larger. This could be caused by the definition of Melton’s angular variable as a linear function of the transversal distance, which makes the orbit error to be tangent to the orbit instead of curved along the orbit. We note, however, that Melton’s method was probably not developed with long-term propagation in mind, and his approximation yields high accuracy for small errors and short propagation times.

Finally we consider the position error with respect to the Monte Carlo result, averaged over the samples for each epoch (see Fig. 13). The QuadLin method shows the best accuracy for almost every epoch. The only exception is for very short propagation arcs (smaller than 0.1 days), when the three compared methods provide results with error of the same order of magnitude. For the proposed method, the maximum average error is around 5 km. This is about one order of magnitude smaller when compared with the Curvilinear C–W solution and Melton’s method.

6.2 Application to the LEO region

We consider an uncontrolled object following an elliptical orbit in the LEO region with $a=7000$ km and $e=0.01$. We set for simplicity $\varOmega = \omega = \nu _0 = 0^\circ$. We study two cases with different inclination: 98 and $45^\circ$. The former is commonly used for sun-synchronous orbits, while the latter is characterized by a stronger perturbation that induces a higher precession of the orbital plane. The position standard deviations are taken as 10, 362 and 12 m in the cross-track, along-track and out-of-plane directions, respectively, following the values reported in Bombardelli and Hernando-Ayuso (2015). The velocity covariance is set as isotropic with standard deviation of $10^{-3}$ m s$^{-1}$. The orbit and the covariance matrix are propagated for 8 orbits as in the previous GEO case. We employ here a fictitious circular reference orbit with the same energy and whose orbital plane and in-plane angular position coincide with that of the initial osculating orbit.

The in-plane covariance propagation for both inclinations provides good accuracy using the QuadLin method: The second-order terms correspond to a correction to the curvilinear C–W solution. We show for example the radial standard deviation errors (Fig. 14 for $i=98^\circ$, and Fig. 15 for $i=45^\circ$).

On the other hand, the out-of-plane orbit uncertainty is strongly affected by the orbital plane precession induced by the $J_2$ perturbation. Figures 16 and 17 show the time-evolution of $\sigma _z$. In the case of $i=98^\circ$, the covariance prediction is accurate up to two revolutions. The range of validity reduces nearly by half for $i=45^\circ$.

7 Conclusions

A double-frequency, quadratic-order analytical solution to the relative motion with respect to a reference circular orbit, expressed in curvilinear coordinates, was presented and employed as a fast and efficient tool for covariance propagation. The covariance propagation can be performed analytically starting from a new analytical state transition matrix constructed around the quadratic solution.

The proposed covariance propagation method was compared with other linear covariance propagation methods using GEO and LEO orbits and accounting for all main perturbations. An improvement between one and two orders of magnitude was observed when comparing the accuracy of the proposed method with a curvilinear Clohessy–Wiltshire model and a previous model proposed by Melton.

As for the range of validity of the method, two main limitations appear. The first is related to the eccentricity of the nominal orbit, which should be low enough ($e < 0.1$) in order not to exceed the range of validity of the quadratic solution. The second concerns the effect of environmental perturbations, which is only negligible as long as secular effects do not accumulate beyond a limit threshold. For near-geostationary orbits, this corresponds to a maximum propagation time span of around 8 orbits assuming position and velocity uncertainties of the order of km and cm s$^{-1}$, respectively. Beyond this point, the orbit covariance in curvilinear coordinates tends to depart from Gaussianity. On the other hand, the linear uncertainty propagation in LEO is limited to a few orbits owing mainly to the $J_2$-induced orbital plane precession, which directly affects the covariance propagation error in the direction orthogonal to the initial reference plane. Ways to mitigate these effects will be explored in the future.