Direct and indirect capture of near-Earth asteroids in the Earth–Moon system

Abstract

Near-Earth asteroids have attracted attention for both scientific and commercial mission applications. Due to the fact that the Earth–Moon $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points are candidates for gateway stations for lunar exploration, and an ideal location for space science, capturing asteroids and inserting them into periodic orbits around these points is of significant interest for the future. In this paper, we define a new type of lunar asteroid capture, termed direct capture. In this capture strategy, the candidate asteroid leaves its heliocentric orbit after an initial impulse, with its dynamics modeled using the Sun–Earth–Moon restricted four-body problem until its insertion, with a second impulse, onto the $\hbox {L}_{2}$ stable manifold in the Earth–Moon circular restricted three-body problem. A Lambert arc in the Sun-asteroid two-body problem is used as an initial guess and a differential corrector used to generate the transfer trajectory from the asteroid’s initial obit to the stable manifold associated with Earth–Moon $\hbox {L}_{2}$ point. Results show that the direct asteroid capture strategy needs a shorter flight time compared to an indirect asteroid capture, which couples capture in the Sun–Earth circular restricted three-body problem and subsequent transfer to the Earth–Moon circular restricted three-body problem. Finally, the direct and indirect asteroid capture strategies are also applied to consider capture of asteroids at the triangular libration points in the Earth–Moon system.

1 Introduction

As a focus for new research, near-Earth asteroids (NEAs) have attracted significant attention for scientific mission applications (Zimmer 2013; Hasnain et al. 2012; Brophy et al. 2012b). Moreover, there is a growing commercial interest in NEA resources (Tronchetti 2014; Andrews et al. 2015). While they may make close approaches to the Earth and represent a potential impact threat, NEAs can provide opportunities to exploit in situ resources for future space exploration.

The idea of capturing small NEAs with relatively low energy has been investigated in detail in recent work (Sanchez and McInnes 2011; Hasnain et al. 2012; Sanchez et al. 2012). In these studies, periodic orbits around the Sun–Earth $\hbox {L}_{1}$ and $\hbox {L}_{2}$ libration points are regarded as potential parking orbits for captured asteroids, since the Sun–Earth $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points are natural gateways to other systems, e.g., the Earth–Moon (EM) system (Koon et al. 2000). Among those small NEAs, a new class of NEAs, termed the easily retrievable objects (EROs), was proposed by Yárnoz et al. (2013). These are NEAs which can be captured into periodic orbits around the $\hbox {L}_{1}$ and $\hbox {L}_{2}$ libration points in the Sun–Earth circular restricted three-body problem (CRTBP) with the total $\Delta v$ cost below $500\, \hbox {ms}^{-1}$. Moreover, Ceriotti and Sanchez (2016) proposed a strategy to control such EROs retrieval trajectories to solve the problems caused by uncertainties in asteroid mass and injection maneuvers.

Periodic orbits around the libration points and the invariant manifolds associated with them have generated significant interest in NEAs exploration missions, including the NEA flyby (Gao 2013), NEA capture (Yárnoz et al. 2013) and the spacecraft reusability for NEA exploration (Zimmer 2013). Moreover, periodic orbits with unstable characteristics can be utilized to design low-energy ballistic transfers (Lo and Parker 2004; Davis et al. 2011). Again, these orbits can also serve as parking orbits for captured NEAs (Sanchez et al. 2012; Mingotti et al. 2014a). Meanwhile, invariant manifolds have been utilized as the basic mathematical tool to design low-energy transfer trajectories between different multi-body systems, e.g., the Earth–Moon and Sun–Earth systems (Koon et al. 2000, 2011; Howell and Kakoi 2006). During such transfers, the spacecraft or the candidate NEA should first be inserted onto the stable manifold associated with the target periodic orbit around the libration point of interest. Once inserted onto the stable manifold, it will be asymptotically captured without further active maneuvers. A successful application of this method is the design of the Hiten-like mission trajectory (Koon et al. 2001). A further example of trajectory design includes transfer between libration point orbits (LPOs) within a restricted three-body system and transfer trajectories in multi-body dynamical systems (Qi and Xu 2016). Missions including Genesis, WMAP, Triana, ISEE-3 and WIND have utilized the circular restricted three-body problem to design transfers to and from LPOs in the Sun–Earth system. Moreover, the patched circular restricted three-body problem was introduced by Koon et al. (2000) and has been used to design low-energy transfer trajectories from the Earth to the Moon (Koon et al. 2000, 2001; Sousa-Silva and Terra 2016). Based on the patched restricted three-body problem approximation, the bi-circular restricted four-body model was proposed to design the low-cost Earth–Moon transfer trajectories (Koon et al. 2011; Topputo 2013).

Based on ballistic capture mechanics in the restricted three-body problem, transfers between NEAs and LPOs have also been investigated in recent years (Yárnoz et al. 2013; Mingotti et al. 2014a; Farquhar et al. 2004; Zimmer 2013; Wang et al. 2013; Gao 2013). For example, Mingotti et al. (2014a) proposed the use of low-thrust propulsion to capture NEAs to a target periodic orbit around the Sun–Earth $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points by using the stable manifolds associated with the target periodic orbit. Farquhar et al. (2004) regard the Sun–Earth $\hbox {L}_{2}$ libration point as a potential parking orbit and gateway station for missions to NEAs and Mars. Delivering NEA resources to a LPO at the $\hbox {L}_{2}$ point could therefore provide efficient logistic support. In order to lower the cost of space exploration missions, Zimmer (2013) studied reusability by stationing spacecraft on periodic orbits at the Sun–Earth $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points between NEA missions. In related work, a differential correction method was proposed to design flyby trajectories from a Lissajous orbit of the CHANG’E 2 spacecraft to the asteroids Toutatis and 2010 JK1 (Wang et al. 2013).

The Earth–Moon libration points are also key to the future of deep space exploration. In 2010, the two ARTEMIS spacecraft became the first vehicles to operate in the vicinity of an Earth–Moon libration point, operating successfully in this dynamical regime from August 2010 through July 2011 (Folta et al. 2011). In 2011, NASA released a report on Earth–Moon libration point missions as part of ‘The Global Exploration Roadmap’ (Hufenbach et al. 2011). NASA has identified the Earth–Moon $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points as potential locations of interest for future human space exploration (Olson 2012). Meanwhile, NASA has also proposed a potential future mission, the Near-Earth Asteroid Redirect Mission (ARM), to rendezvous with and then capture a small near-Earth asteroid (later a boulder from a near-Earth asteroid) (Brophy et al. 2012a). Given that final placement of the captured asteroid in the vicinity of the Earth may incur an impact risk, it is prudent to place the retrieved asteroid in an orbit from which it could only impact the Moon. Lunar orbits, or possibly regions near the Earth–Moon Lagrange points, would therefore be one of preferred locations, although there is additional work required on this matter. Besides, the Earth–Moon $\hbox {L}_{2}$ point is also regarded as a candidate gateway for future space missions, since spacecraft on periodic orbits around the Earth–Moon $\hbox {L}_{2}$ point can easily achieve low-energy transfers to the vicinity of the Moon and the vicinity of the Sun–Earth $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points (Lo and Ross 2001; Alessi et al. 2009; Davis et al. 2010). Therefore, capturing asteroids and inserting them directly at the Earth–Moon $\hbox {L}_{1}$ and $\hbox {L}_{2}$ points may be of significant benefit for future space exploration by providing in situ resources. In addition, due to the fact the triangular points in the Earth–Moon system are stable, the propellant required to maintain a captured NEA at such a location is modest (Salazar et al. 2012). For this reason, it may also be of interest to capture an NEA and place it on a periodic orbit around the triangular $\hbox {L}_{4}$ and $\hbox {L}_{5}$ points in the Earth–Moon system. Furthermore, due to the fact that the Earth–Moon $\hbox {L}_{4}$ and $\hbox {L}_{5}$ points can be used as a parking orbit for travel to and from cislunar space, O’Neill (1974) proposed to build space colonies at these points where captured NEAs could provide material for these large structures. Accordingly, DeFilippi (1977) studied station-keeping strategies at Earth–Moon $\hbox {L}_{4}$ point.

Mingotti et al. (2014b) proposed the patched circular restricted three-body problem as a model, which consists of the Sun–Earth and the Earth–Moon CRTBP systems, to capture NEAs onto target periodic orbits around the Earth–Moon $\hbox {L}_{2}$ point. However, this would require a significant duration for the asteroid to be asymptotically captured onto periodic orbits around the Sun–Earth $\hbox {L}_{1}$ or $\hbox {L}_{2}$ points, compared to the traditional hyperbolic approach (Sanchez et al. 2012). For this reason, we propose a new type of lunar asteroid capture, termed direct capture. In this capture strategy, an initial impulse will modify the asteroid’s orbit and a second impulse will insert it onto the stable manifold associated with the Earth–Moon $\hbox {L}_{2}$ periodic orbits directly. Then, the asteroid will be asymptotically captured onto the target periodic orbit around the $\hbox {L}_{2}$ point in Earth–Moon system. The transfer trajectories from the asteroid’s orbit to the stable manifold associated with the Earth–Moon $\hbox {L}_{2}$ periodic orbits are modelled by the Sun–Earth–Moon restricted four-body problem. It should be noted that the patched three-body problem is an approximation of the Sun–Earth–Moon four-body problem and it is decomposed into the Earth–Moon CRTBP and Sun–Earth CRTBP. The Sun–Earth–Moon restricted four-body problem incorporates the perturbation of the Moon into the Sun–Earth CRTBP.

In this paper, the CRTBP is used to compute the stable manifolds associated with periodic orbits in the Earth–Moon system and then the Moon–Sun three-body sphere of influence (3BSOI) is utilized as the boundary between the Sun–Earth–Moon restricted four-body problem and the Earth–Moon CRTBP. Then, the target points on the stable manifolds are transformed to the Sun-centered inertial frame. The three-dimensional orbital element space of candidate NEAs is then obtained to select candidate NEAs which can be captured with a total cost under $500\, \hbox {ms}^{-1}$. After calculating the approximate approach date and departure date, a Lambert arc in the Sun-centered two-body problem is utilized to estimate the first impulse to the target points from the candidate asteroid’s orbit. Based on the initial guess of the first impulse, a differential correction method is then used to design the transfer trajectory to the target points from the candidate asteroid’s orbit in the Sun–Earth–Moon restricted four-body problem. Results show that the direct asteroid capture strategy needs a shorter flight time compared to an indirect asteroid capture, which couples together the Sun–Earth CRTBP and the Earth–Moon CRTBP.

The paper is organized as follows. Section 2 presents a set of dynamical models, including the Earth–Moon restricted three-body problem and the Sun–Earth–Moon restricted four-body problem; Sect. 3 considers periodic orbits (Lyapunov orbits and halo orbits) around the Earth–Moon $\hbox {L}_{2}$ point and the stable manifolds associated with those periodic orbits; Sect. 4 proposes the concept of direct capture of NEAs in the Earth–Moon CRTBP and describes the detailed design procedure to calculate the transfer trajectory of an asteroid from its initial orbit to the stable manifolds associated with Earth–Moon $\hbox {L}_{2}$ periodic orbits; finally, these results are optimized using the NSGA-II algorithm; Sect. 5 considers the calculation of the indirect capture of NEAs in the Earth–Moon system by using the patched restricted three-body problem which consists of the Sun–Earth CRTBP system and Earth–Moon CRTBP system; Sect. 6 investigates the direct and indirect capture of NEAs to the triangular points in the Earth–Moon CRTBP system.

2 Dynamical models

2.1 Circular restricted three-body problem

To describe the motion of captured NEAs in the Earth–Moon system, the model of the circular restricted three-body problem (CRTBP) is adopted. Assuming that Earth and Moon are in a circular orbit around their common center-of-mass, the motion of NEAs in the rotating frame, which is centered at the barycenter of the Earth and Moon system, is defined by

$$\begin{aligned} \left\{ {{\begin{array}{l} {\ddot{x}-2\dot{y}=\frac{\partial \Omega }{\partial x}} \\ {\ddot{y}+2\dot{x}=\frac{\partial \Omega }{\partial y}} \\ {\ddot{z}=\frac{\partial \Omega }{\partial z}} \\ \end{array} }} \right. , \end{aligned}$$

(1)

where

$$\begin{aligned} \Omega (x,y,z,\mu )=\frac{1}{2}\left[ \left( x^{2}+y^{2}\right) +\mu (1-\mu )\right] +\frac{1-\mu }{r_1 }+\frac{\mu }{r_2 } \end{aligned}$$

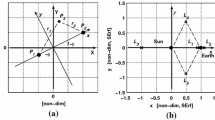
and $r_1 =[(x+\mu )^{2}+y^{2}+z^{2}]^{1/2}$, $r_2 =[(x-1+\mu )^{2}+y^{2}+z^{2}]^{1/2}$ are the magnitudes of the position vectors to the Earth and Moon, scaled by the distance between the Earth and Moon; $\mu$ is the non-dimensional mass ratio of the Earth and Moon. The coordinates of the Earth and Moon in the rotating frame are $[-\mu , 0, 0]$ and $[1 - \mu , 0, 0]$, respectively, as shown in Fig.  1. The unit of time is chosen such that the orbital period of the Earth and Moon about their barycenter is $2\uppi$.

For the CRTBP, the Jacobi constant J is (Koon et al. 2011)

$$\begin{aligned} 2\Omega (x,y,z,\mu )-(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2})=J. \end{aligned}$$

(2)

The five libration points, $\hbox {L}_{\mathrm{i}}, (i = 1, 2 \ldots 5)$ can be obtained from Eq. (1), shown in Fig. 1. The mass parameter assumed for the Earth–Moon model is $\mu = 1.2155650 \times 10^{-2}$.

Fig. 1

Earth–Moon CRTBP with five libration points and Jacobi constant contours

2.2 Sun–Earth–Moon restricted four-body problem model

When designing transfer trajectories from the initial asteroid orbit to the stable manifolds in the Earth–Moon CRTBP system, we assume that the motion of the asteroid is governed by the gravity of the Sun, Earth and Moon. It is also assumed that the motion of the Moon with respect to the Earth and the motion of the Earth with respect to the Sun are described by the two-body problem. Here, the Sun-centered inertial frame is used to describe the Sun–Earth–Moon restricted four-body system such that

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\ddot{{\varvec{r}}}=}-\frac{\mu _{_{\text {Sun}}} }{r^{3}}{\varvec{r}}-\frac{\mu _{_\text {Earth}} }{r_{\textit{ea}}^{3}}({\varvec{r}}-{\varvec{r}}_{{\varvec{e}}} )-\frac{\mu _{_\text {Moon}} }{r_{\textit{ma}}^{3}}({\varvec{r}}-{\varvec{r}}_{{\varvec{e}}} -{\varvec{r}}_{{\varvec{m}}} )} \\ {{\ddot{{\varvec{r}}}}_{{\varvec{e}}} {=}-\frac{\mu _{_\text {Sun}} }{r_{\textit{es}} ^{3}}{\varvec{r}}_{{\varvec{e}}} } \\ {{\ddot{{\varvec{r}}}}_{{\varvec{m}}} {=}-\frac{\mu _{_\text {Earth}} }{r_{\textit{me}} ^{3}}{\varvec{r}}_{{\varvec{m}}} } \\ \end{array} }} \right. , \end{aligned}$$

(3)

where

$$\begin{aligned} r_{\textit{ea}} =\left\| {{{\varvec{r}}}-{{\varvec{r}}}_{{{\varvec{e}}}} } \right\| ,r_{\textit{ma}} =\left\| {{{\varvec{r}}}-{{\varvec{r}}}_{{\varvec{e}}} -{{\varvec{r}}}_{{\varvec{m}}} } \right\| ,r_{{\textit{es}}} =\left\| {{{\varvec{r}}}_{{\varvec{e}}} } \right\| ,r_{{\textit{me}}} =\left\| {{{\varvec{r}}}_{{\varvec{m}}} } \right\| , \end{aligned}$$

where r is the position vector of the asteroid with respect to the Sun; ${{\varvec{r}}}_{{{\varvec{e}}}}$ is the position vector of the Earth with respect to the Sun in the two-body problem; ${{\varvec{r}}}_{{\varvec{m}}}$ is the position vector of the Moon with respect to the Earth in the two-body problem and it is initialized with a state of the Moon with respect to the Earth from the real ephemeris, shown in Fig. 2. The motion of all four bodies is assumed to be in the same plane. In addition, $\mu _{{\text {Sun}}}$, $\mu _{{\text {Earth}}}$ and $\mu _{{\text {Moon}}}$ are the gravitational parameters of the Sun, Earth and Moon, respectively. The gravitational parameters assumed for this model are $\mu _{{\text {Sun}}}= 1.3271244\times 10^{11}\, \hbox {km/s}^{2}$, $\mu _{\text {Earth}}= 3.9860044\times 10^{5}\, \hbox {km/s}^{2}$ and $\mu _{{\text {Moon}}}= 4.9048695\times 10^{3}\, \hbox {km/s}^{2}$.

Fig. 2

Geometry of the Sun–Earth–Moon restricted four-body problem

3 Periodic orbits and invariant manifolds

3.1 Earth–Moon $\mathbf{L}_{2}$ periodic orbits

Families of periodic orbits around the collinear libration points $\hbox {L}_{1}$ and $\hbox {L}_{2}$ in the CRTBP have been studied extensively (Richardson 1980; Gómez 2001). There are two key classes of periodic orbits: halo orbits and Lyapunov orbits. The initial states of such periodic orbits can be computed by utilizing the differential correction method (Howell and Pernicka 1987), based on Richardson’s third order approximation (Richardson 1980); we then follow this process by numerical continuation to generate a series of periodic orbits with increasing or decreasing Jacobi constant J, as shown in Fig. 3, where the unit of length is the Earth–Moon distance (EM unit).

Fig. 3

a Planar Lyapunov orbits with Jacobi constant [2.99533289, 3.17205221] and b halo orbits with Jacobi constant [3.06733209, 3.15211497] around $\hbox {L}_{2}$ point in the Earth–Moon system

3.2 Invariant manifolds

Invariant manifolds associated with periodic orbits around the collinear $\hbox {L}_{1}$ and $\hbox {L}_{2}$ libration points are trajectories which asymptotically approach or depart these target periodic orbits (Koon et al. 2011). The stable manifold $W^{S}$ associated with a periodic orbit consists of all trajectories that reach this target periodic orbit along the periodic orbit’s stable eigenvector. The unstable manifold $W^{U}$ associated with a periodic orbit includes all possible trajectories that depart from this target orbit along the target orbit’s unstable eigenvector. Therefore, the stable manifold in the CRTBP can be calculated by propagating backward from an initial condition as follows

$$\begin{aligned} {\varvec{X}}_{S} ={\varvec{X}}_{0} \pm \varepsilon {\varvec{V}}_{S} \end{aligned}$$

(4)

and the unstable manifold can be computed by propagating forward from the following initial condition

$$\begin{aligned} {\varvec{X}}_{U} ={\varvec{X}}_{0} \pm \varepsilon {\varvec{V}}_{U}, \end{aligned}$$

(5)

where ${\varvec{V}}_{S} /{\varvec{V}}_{U}$ are the stable/unstable eigenvectors of the monodromy matrix evaluated at a point ${\varvec{X}}_{0} =[x_{0} ,y_{0} ,z_{0} ,\dot{{x}}_{0} ,\dot{{y}}_{0} ,\dot{{z}}_{0} ]^{T}$ on the periodic orbit. The parameter $\varepsilon$ represents the magnitude of the perturbation, in the direction of the stable/unstable eigenvectors, between the periodic orbit and the initial condition of the stable/unstable manifolds. Gómez et al. (1991) suggest values of $\varepsilon$ corresponding to non-dimensional position displacements of order $10^{-6}$ (corresponding to about 0.38 km in the position and about $10^{-6}\, \hbox {km/s}$ in the velocity in the Earth–Moon system). We refer to the backward propagation time as the stable manifold transfer time $t_{{\textit{sm}}}$ and the forward propagation time as the unstable manifold transfer time $t_{{\textit{um}}}$.

A Poincaré section can replace a continuous dynamical system with a discrete dynamical system. Here, the Poincaré section is defined by the angle $\uptheta \, (\uptheta > 0)$, shown in Fig. 4.

Fig. 4

Stable manifolds associated with Lyapunov orbits around the Earth–Moon $\hbox {L}_{2}$ point

Then, the stable manifolds on the Poincaré section in the Earth–Moon rotating system can be defined as

$$\begin{aligned} X_{{\textit{EM}}}^{ro} (J,\theta )= & {} \left\{ (x,y,z,\dot{x},\dot{y},\dot{z})\in W^{S}\left| y=(x+\mu )\tan \theta ,\right. \right. \nonumber \\&\left. \left. 2\Omega (x,y,z,\mu )-(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2})=J \right. \right\} . \end{aligned}$$

(6)

The superscript “ro” and the subscript “EM” in Eq. (6) denote the rotating frame and Earth–Moon system, respectively.

3.3 Coordinate transformation

The position of the Moon in an Earth-centered inertial frame can be described by the angle $\upbeta$, shown in Fig. 5. We denote the states of the EM $\hbox {L}_{2}$ stable manifold in the Earth–Moon rotating frame and in the Earth-centered inertial frame by ${\varvec{X}}_{{\textit{EM}}}^{ro}$ and ${\varvec{X}}_{E}^{{\textit{in}}}$ respectively. Thus, we have the transformation

$$\begin{aligned} {\varvec{X}}_{E}^{in} ={\varvec{R}}(\beta )\left( {\varvec{X}}_{EM}^{ro} +[\mu ,0,0,0,0,0]^{T}\right) ,\beta \in [0,2\pi ], \end{aligned}$$

(7)

where

$$\begin{aligned} {{\varvec{R}}}(\beta )=\left[ {{\begin{array}{cccccc} {\cos \beta }&{} \quad {-\sin \beta }&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0 \\ {\sin \beta }&{} \quad {\cos \beta }&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0 \\ 0&{} \quad 0&{} \quad 1&{} \quad 0&{} \quad 0&{} \quad 0 \\ {-\sin \beta }&{} \quad {-\cos \beta }&{} \quad 0&{} \quad {\cos \beta }&{} \quad {-\sin \beta }&{} \quad 0 \\ {\cos \beta }&{} \quad {-\sin \beta }&{} \quad 0&{} \quad {\sin \beta }&{} \quad {\cos \beta }&{} \quad 0 \\ 0&{} \quad 0&{} \quad 0&{} \quad 0&{} \quad 0 &{} \quad 1 \\ \end{array} }} \right] \end{aligned}$$

and the state of the EM $\hbox {L}_{2}$ stable manifold in the Sun-centered inertial frame is then defined by

$$\begin{aligned} {\varvec{X}}_{S}^{{\text {in}}} ={\varvec{X}}_{{\varvec{e}}} +{\varvec{X}}_{E}^{{\text {in}}}, \end{aligned}$$

(8)

where ${\varvec{X}}_{{\varvec{e}}} =[{\varvec{r}}_{{\varvec{e}}} ;{\dot{{\varvec{r}}}}_{{\varvec{e}}} ]$

Fig. 5

Geometry of the Moon in the inertial frame which is centered at the barycenter of the Earth–Moon system

4 Direct capture of near-Earth asteroids in the Earth–Moon system

4.1 Concept of direct capture

The basic concept of direct capture of NEAs is through the following strategy:

• (1) With an initial maneuver $\Delta {{\varvec{v}}}_{1}$, the candidate asteroid leaves its orbit and is modelled in the Sun–Earth–Moon restricted four-body system, shown in Fig. 6a;

• (2) After a second maneuver $\Delta {{\varvec{v}}}_{2}$, the candidate asteroid inserts onto the stable manifold associated with the periodic orbit around the EM $\hbox {L}_{2}$ point and will be asymptotically captured onto it, shown in Fig. 6b.

The total cost of capturing the NEA onto the stable manifold associated with the periodic orbit around the EM $\hbox {L}_{2}$ point is therefore calculated as

$$\begin{aligned} \Delta v=\left\| {\Delta {\varvec{v}}_{{\varvec{1}}} } \right\| +\left\| {\Delta {\varvec{v}}_{{\varvec{2}}} } \right\| . \end{aligned}$$

(9)

Fig. 6

Direct capture of near-Earth asteroid: a initial impulse $\Delta v_{1}$ for the asteroid to leave its orbit; b second impulse $\Delta v_{2}$ to insert the asteroid onto the stable manifold associated with the periodic orbit around the Earth–Moon $\hbox {L}_{2}$ point

Thus, for each candidate NEA, there are 5 variables to describe the sequence of maneuvers as follows:

• $T_{0}$: departure date when the first impulse $\Delta {{\varvec{v}}}_{\mathbf{1}}$ is applied to the candidate asteroid and the asteroid leaves its initial orbit;

• $T_{f}$: approach date corresponding to the date when the candidate asteroid inserts onto the EM $\hbox {L}_{2}$ stable manifold with the second impulse $\Delta {{{\varvec{v}}}}_{2}$;

• J: Jacobi constant of the final periodic orbit around EM $\hbox {L}_{\mathbf{2}}$;

• $t_{p}$: time determining the state on the target periodic orbit around EM $\hbox {L}_{2}$ where the EM $\hbox {L}_{2}$ stable manifold is propagated backward from $t_p \in [0,T_p ]$ where $T_{p}$ is the period of the final periodic orbit;

• $t_{{\textit{sm}}}$: stable manifold transfer time determining the target point where the second impulse is applied.

4.2 Differential correction

A heliocentric two-body Lambert arc with two impulsive maneuvers can be used to provide an initial guess, where the first impulse is applied and the asteroid transfers to the Earth–Moon system. It will be assumed that the initial state of the asteroid is ${{\varvec{X}}}_{{{\varvec{i}}}} =[x_i ,y_i ,z_i ,\dot{x}_i ,\dot{y}_i ,\dot{z}_i ]^{T}$ after the first impulse, the state of the target point is ${{\varvec{X}}}_{{{\varvec{f}}}} =[x_f ,y_f ,z_f ,\dot{x}_f ,\dot{y}_f ,\dot{z}_f ]^{T}$ and the final state of the Lambert arc is ${{\varvec{X}}}_{{{f}}}^{\prime } =[x_f^{\prime } ,y_f^{\prime } ,z_f^{\prime } ,\dot{x}_f^{\prime } ,\dot{y}_f^{\prime } ,\dot{z}_f^{\prime } ]^{T}$, before the second impulse, as shown Fig. 7. Then, we can seek conditions for $\delta {\varvec{r}}_{{\varvec{f}}} =[\delta x_{f} ,\delta y_{f} ,\delta z_{f} ]^{T}=[x_{f} -x_{f}^{'} ,y_{f} -y_{f}^{'} ,z_{f} -z_{f}^{'} ]^{T}=\mathbf 0$ by correcting the initial velocity vector $\delta {\varvec{v}}_{{\varvec{i}}} =[\delta \dot{{x}}_{i} ,\delta \dot{{y}}_{i} ,\delta \dot{{z}}_{i} ]^{T}$.

Fig. 7

Differential correction with an initial guess using a Lambert transfer

We assume that the Sun–Earth–Moon restricted four-body system in Eq. (3) can be represented by a set of nonlinear equations of motion in the general form

$$\begin{aligned} {\dot{{\varvec{X}}}}={{f}}({\varvec{X}},t), \end{aligned}$$

(10)

where

$$\begin{aligned} {\varvec{X}}=[x,y,z,\dot{{x}},\dot{{y}},\dot{{z}}]^{T}. \end{aligned}$$

We then label the solution ${\varvec{X}}_{\mathrm {0}}(t)$ as the reference trajectory of Eq. (10). Defining the relationship between the reference trajectory ${{\varvec{X}}}_{\mathrm {0}}(t)$ and a nearby trajectory ${{\varvec{X}}}(t)$, as

$$\begin{aligned} {\varvec{X}}(t) = {\varvec{X}}_{0} (t)+\delta {\varvec{X}}(t) \end{aligned}$$

(11)

and expanding about the reference solution in a Taylor series generates a set of linear equations, such that

$$\begin{aligned} \delta {\dot{{{{{\varvec{X}}}}}}}={{\varvec{A}}}(t)\delta {\varvec{X}}, \end{aligned}$$

(12)

where ${\varvec{A}}(t)=\left. {\frac{\partial {\varvec{f}}}{\partial {\varvec{X}}}} \right| {\begin{array}{c} \\ {{\varvec{X}}_{0} } \\ \end{array} }$. The general solution to the above equation is

$$\begin{aligned} \delta {\varvec{X}}(t)=\Phi (t,t_{0} )\delta {\varvec{X}}(t_{0} ), \end{aligned}$$

(13)

where the state transition matrix is found from

$$\begin{aligned} \dot{{\Phi }}(t,t_{0} )={\varvec{A}}(t)\Phi (t,t_{0} ),\Phi (t_{0} ,t_{0} )={\varvec{I}}. \end{aligned}$$

Then, we can obtain

$$\begin{aligned} {\varvec{A}}(t)=\frac{\mathrm{d}{\varvec{f}}({\varvec{X}},t)}{\mathrm{d}{\varvec{X}}}=\left[ {{\begin{array}{*{20}c} {{\varvec{0}}} &{} \quad {{\varvec{I}}} \\ \Psi &{} \quad {{\varvec{0}}} \\ \end{array} }} \right] , \end{aligned}$$

(14)

where $\Psi =\left[ {{\begin{array}{*{20}c} {\frac{\partial \ddot{{x}}}{\partial x}} &{} {\frac{\partial \ddot{{x}}}{\partial y}} &{} {\frac{\partial \ddot{{x}}}{\partial z}} \\ {\frac{\partial \ddot{{y}}}{\partial x}} &{} {\frac{\partial \ddot{{y}}}{\partial y}} &{} {\frac{\partial \ddot{{y}}}{\partial z}} \\ {\frac{\partial \ddot{{z}}}{\partial x}} &{} {\frac{\partial \ddot{{z}}}{\partial y}} &{} {\frac{\partial \ddot{{z}}}{\partial z}} \\ \end{array} }} \right]$.

The differential correction can therefore be written as

$$\begin{aligned} \delta {\varvec{X}}_{{\varvec{i}}} =\Phi ^{-1}\delta {\varvec{X}}_{{\varvec{f}}}, \end{aligned}$$

(15)

where $\delta {\varvec{X}}_{{\varvec{i}}} =[0,0,0,\delta \dot{{x}}_{i} ,\delta \dot{{y}}_{i} ,\delta \dot{{z}}_{i} ]^{T},\delta {\varvec{X}}_{{\varvec{f}}} =[\delta x_{f} ,\delta y_{f} ,\delta z_{f} ,0,0,0]^{T}$.

The differential correction in Eq. (15) starts with the initial state ${{\varvec{X}}}_{{{\varvec{0}}}}$ which is based on the Lambert arc, and then the process is repeated until $\delta {\varvec{r}}_{{\varvec{f}}} =[\delta x_{f} ,\delta y_{f} ,\delta z_{f} ]^{T}$ is equal to 0 within some small tolerance.

4.3 Target point filter

After the first impulse, the asteroid leaves its orbit and it is modelled by the Sun–Earth–Moon restricted four-body problem until the asteroid is captured onto the Earth–Moon $\hbox {L}_{{2}}$ stable manifold. When the asteroid inserts onto the invariant manifold, the asteroid’s motion is modelled by the Earth–Moon CRTBP problem. We have defined the patching of these two systems such that they match at the Moon–Sun three-body sphere of influence (3BSOI). Using an analytical approximation, the 3BSOI is a sphere centered at the Moon with a radius given by

$$\begin{aligned} R_{{\text {SOI}}} =a(\mu _{{\text {Moon}}} / \mu _{{\text {Sun}}} )^{2/5} \approx 159200km, \end{aligned}$$

(16)

where a is the distance between the Sun and the Earth, equal to 1AU. That is, once the asteroid is inserted into the target point on the stable manifold inside the 3BSOI of radius $R_{\mathrm {SOI}}$, the asteroid is regarded to be asymptotically captured into a bound orbit around the Earth–Moon $\hbox {L}_{{2}}$ point. Therefore, as shown in Fig. 8, the target points on the stable manifolds should be chosen such that

$$\begin{aligned} \sqrt{(x-1+\mu )^{2}+y^{2}+z^{2}} \le R_\mathrm{SOI}. \end{aligned}$$

(17)

Fig. 8

Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifolds inside the 3BSOI

According to the definition of the Moon–Sun 3BSOI, we can determine the search domain of the stable manifold transfer time $t_{{\textit{sm}}}$. Given one stable manifold which is determined by J and $t_{p}$, we define $t_{{\text {3BSOI}}} (J,t_{p} )$ as the stable manifold transfer time $t_{\textit{sm}}$ when the stable manifold intersects the 3BSOI for a first time. Therefore, for the stable manifolds associated with a periodic orbit with Jacobi constant J, the required set of $t_{{\text {3BSOI}}}$ can be written as

$$\begin{aligned} \Gamma (J)=\mathop {\cup }\limits _{t_{p} \in [0,T_{p} ]} \left\{ {t_{{\text {3BSOI}}} (J,t_{p} )} \right\} , \end{aligned}$$

(18)

and we define the maximum value of the set $\Gamma (J)$ as

$$\begin{aligned} t_{{\text {threshold}}} (J)=\mathop {\max }\limits _{t_{p} \in [0,T_{p} ]} \{\Gamma (J)\}. \end{aligned}$$

(19)

Fig. 9

$t_{{\text {threshold}}}$ with different Jacobi constants J a stable manifold associated with EM $\hbox {L}_{{2}}$ Lyapunov orbits; b stable manifold associated with EM $\hbox {L}_{{2}}$ halo orbits

Therefore, $t_{\text {threshold}} (J)$ is the maximum stable manifold transfer time of the stable manifolds associated with the periodic orbit with Jacobi constant J. Therefore, it can be utilized to determine the search domain of the stable manifold transfer time $t_{\textit{sm}}$. Figure 9 shows $t_{\text {threshold}}$ with different Jacobi constants J. In general, $t_{\text {threshold}}$ decreases when the Jacobi constant J increases and small values of J lead to large $t_{\text {threshold}}$. Since the Jacobi constant J is unknown, we have to select a limited range of the stable manifold flight time $t_{\textit{sm}}$ to fit the stable manifolds of all periodic orbits. Therefore, it is found that $t_{\textit{sm}}$ should be selected in the range [0, 9.7] for Lyapunov orbits, or [0, 7.4] for halo orbits.

4.4 Candidate asteroid selection

To obtain appropriate candidate asteroids, the JPL Small-Body Database will be used, which represents the current catalog of near-Earth objects (NEOs). It is necessary to immediately exclude NEAs with a semi-major axis or inclination much larger than the Earth’s.

With the target point filter, the target point on the stable manifold which is determined by the parameters J, $t_{p}$ and $t_{\textit{sm}}$ can be written as

$$\begin{aligned} P_{t} (J,t_{p} ,t_{\textit{sm}} )=\left\{ {\left( {x,y,z,\dot{{x}},\dot{{y}},\dot{{z}}} \right) \in W^{s}\vert \sqrt{(x-1+\mu )^{2}+y^{2}+z^{2}} \le R_\mathrm{SOI} } \right\} . \end{aligned}$$

(20)

Then, the set of the target points on the stable manifolds can be obtained when we vary J, $t_{p}$ and $t_{\textit{sm}}$. Let K be the set of the target points which can be written as

$$\begin{aligned} {\mathbf{K}}=\left\{ {P_{t} (J,t_{p} ,t_{\textit{sm}} )\vert \, J_{\min } \le J\le J_{\max } ,0\le t_{p} \le T_{p} ,0\le t_{\textit{sm}} \le t_{\text {threshold}} } \right\} , \end{aligned}$$

(21)

where $J_{\min } =2.99533289$, $J_{\max } =3.17205221$ and $t_{\text {threshold}} =9.7$ for the planar Lyapunov orbits, while $J_{\min } =3.06733209$, $J_{\max } =3.15211497$ and $t_{\text {threshold}} =7.4$ for the halo orbits.

Now that the set of target points is known, and it is possible to calculate the three-dimensional orbital element space (the semi-major axis, eccentricity and inclination (a, e, i)) of the candidate NEAs which can be captured onto Earth–Moon $\hbox {L}_{\mathrm {2}}$ periodic orbits under a certain $\Delta v$ threshold. The design procedure is presented as follows,

• (1) Given one approach date $T_{f}$, transform the set of target points K to the Sun-centered inertial frame by using Eqs. (7) and (8) and then obtain the three-dimensional orbital element space of the target points in the Sun-centered inertial frame, shown in Fig. 10;

• (2) Add an impulse $\Delta {\varvec{v}}_{\mathbf {2}} =\left\| {\Delta {\varvec{v}}_{\mathbf {2}} } \right\| \cdot [\cos p_{2} \cos q_{2} ,\cos p_{2} \sin q_{2} ,\sin p_{2} ] (\left\| {\Delta {\varvec{v}}_{\mathbf {2}} } \right\| \le \Delta v , p_{2} \in [0,\pi ], q_{2} \in [0,2\pi ])$ at these target points on the EM $\hbox {L}_{\mathrm {2}}$ stable manifolds and propagate these states backwards (with propagation time T(days)) in the Sun–Earth–Moon restricted four-problem model and then obtain the final states;

• (3) Add another impulse $\Delta {\varvec{v}}_{\mathbf {1}} =\left\| {\Delta {\varvec{v}}_{\mathbf {1}} } \right\| \cdot [\cos p_{1} \cos q_{1} ,\cos p_{1} \sin q_{1} ,\sin p_{1} ]$ ( $\left\| {\Delta {\varvec{v}}_{\mathbf {1}} } \right\| \le \Delta v-\left\| {\Delta {\varvec{v}}_{\mathbf {2}} } \right\|$ , $p_{1} \in [0,\pi ]$ , $q_{1} \in [0,2\pi ]$ ) at these final states and then calculate the three-dimensional orbital element space (a, e,i) of these states after $\Delta {{\varvec{v}}}_{\mathrm {\mathbf {1}}}$ is added;

• (4) Vary the approach date $T_{f}$, propagation time T ($T\in [0,1000{\begin{array}{*{20}c} {days} \\ \end{array} }])$, two impulses $\Delta {{\varvec{v}}}_{\mathrm {\mathbf {1}}}$ and $\Delta {{\varvec{v}}}_{\mathrm {\mathbf {2}}}$ and obtain the three-dimensional orbital element space (a, e, i) of the candidate NEAs that can potentially be captured under the $\Delta v$ threshold.

Fig. 10

Given $T_{f}=63000\, \hbox {[MJD]}$, the three-dimensional orbital element space of target points on the stable manifolds associated with EM $\hbox {L}_{{2}}$ Lyapunov orbits (red) and halo orbits (black)

According to the design procedure above, the three-dimensional orbital element space of candidate NEAs is plotted in Figs. 11 and 12 for transfers to the EM $\hbox {L}_{\mathrm {2}}$ stable manifolds with a $\Delta v$ threshold of $500\, \hbox {ms}^{\mathrm {-1}}$, as used by Yárnoz et al. (2013). With a free phase, any asteroid with orbital elements inside these regions can be captured with a total $\Delta v$ cost below $500\, \hbox {ms}^{\mathrm {-1}}$. With this filter, the candidate asteroids are listed in Table 1.

Fig. 11

Three-dimensional orbital element space of the stable manifold associated with EM $\hbox {L}_{{2}}$ Lyapunov orbits with a $\Delta v$ threshold of $500\, \hbox {ms}^{{-1}}$

Fig. 12

Three-dimensional orbital element space of the stable manifold associated with EM $\hbox {L}_{{2}}$ halo orbits with a $\Delta v$ threshold of $500\, \hbox {ms}^{{-1}}$

4.5 Approach date and departure date guess

For a candidate asteroid, there exists a date when the asteroid has its closest approach to the Earth. Here, we define this date as the moment of minimum distance (MOMD) between the asteroid and the Earth. The distance between the candidate asteroid and the Earth can be calculated by propagating the candidate asteroid’s initial state forward in the Sun–Earth–Moon restricted four-body problem and then the MOMD can be obtained, an example of which is shown in Fig. 13. Since we are interested in low-cost transfers with a total $\Delta v$ cost below $500\, \hbox {ms}^{{-1}}$, the first impulse should be smaller than this value and then the asteroid’s new orbit after the first impulse can be considered to be proximal to its former orbit. Therefore, we can still estimate the date when the asteroid’s closest approach to the Earth is nearby the MOMD. Therefore, the approximate range of approach date can be written as

$$\begin{aligned}{}[{\hbox {MOMD}}-T_{{\text {period}}} ,{\hbox {MOMD}}+T_{{\text {period}}} ], \end{aligned}$$

(22)

where $T_{{\text {period}}}$ is the asteroid’s orbit period about the Sun.

Table 1 Orbital elements of the candidate near-Earth asteroids

Fig. 13

Approach date guess by using MOMD (2014WX202)

The Lambert arc in the two-body problem with two impulses can now be used as an initial guess of the departure date when the first impulse is applied and the asteroid transfers toward the target point in the Earth–Moon system. There are 2 variables in this problem: the departure date $T_{\mathrm {0}}$ and the transfer time $T_{{\text {fly}}}$ (or the approach date $T_{f})$. Then, the total cost of the Lambert transfer can be calculated as

$$\begin{aligned} \delta {{v}}=\left\| {\delta {{{\varvec{v}}}}_{\mathbf {1}} } \right\| +\left\| {\delta {{{\varvec{v}}}}_{\mathbf {2}} } \right\| , \end{aligned}$$

(23)

where $\delta {{{\varvec{v}}}}_{\mathbf {1}}$, $\delta {{{\varvec{v}}}}_{\mathbf {2}}$ are the first impulse and second impulses, respectively.

Since we only consider the influence of the Sun’s gravity here, the total $\delta v$ cost must be different from the result in the Sun–Earth–Moon restricted four-body model. However, we can still use the first Lambert impulse $\delta {\varvec{v}}_{\mathbf {1}}$ to guess the first impulse $\Delta {\varvec{v}}_{\mathbf {1}}$ in Sun–Earth–Moon restricted four-body model. Since we expect to find an asteroid which can be captured directly with $\Delta v\le 500\, \hbox {ms}^{{-1}}$, here we set $500\, \hbox {ms}^{{-1}}$ as a threshold for $\delta {\varvec{v}}_{\mathbf {1}}$ and then guess the departure date $T_{\mathrm {0}}$. As shown in Fig. 8, the target points are defined in a limited region around the Moon (3BSOI). Thus, there should be only a marginal difference between the first impulse of the Lambert to the Moon and the first impulse of the Lambert arc to the target points. Therefore, for simplification, the target position for the Lambert arc is assumed to be the center of the Moon, in order to provide a guess in the search domain of the departure date $T_{\mathrm {0}}$, shown in Fig. 14.

Fig. 14

The first impulse $\delta v_{\mathrm {1}}$ (ms$^{\mathrm {-1}})$ as a function of $T_{\mathrm {0}}$ and $T_{f}$ (2014WX202)

4.6 Design procedure

The process of calculating the transfer trajectories from the candidate asteroid’s orbit to the EM $\hbox {L}_{\mathrm {2}}$ stable manifold is as follows:

• (1) Select one target asteroid among the list of candidate asteroids (e.g., 2014WX202) in Table 1;

• (2) Guess the range of the approach date using Eq. (22);

• (3) Assume that the Moon is the target position for the Lambert arc from the candidate asteroid’s orbit and then guess the search domain of departure date $T_{0}$ and approach date $T_{f}$, corresponding to the first impulse $\left\| {\delta {\varvec{v}}_{\mathbf {1}} } \right\| \le 500\,\hbox {ms}^{\mathrm {-1}}$, as shown in Fig. 15;

• (4) Given a Jacobi constant J, $t_{\mathrm {p}}$ and $t_{\textit{sm}}$, the target point on the EM $\hbox {L}_{\mathrm {2}}$ stable manifolds are determined and then transformed to the Sun-centered inertial frame by using Eqs. (7) and (8);

• (5) The Lambert arc in the Sun-centered two-body problem is utilized to design the transfer to the target points from the candidate asteroid’s orbit, and so the first impulse can be estimated;

• (6) Based on the initial guess of the first impulse, the differential correction in Eq. (15) is utilized to design the transfer trajectory to the target point from the candidate asteroid’s orbit.

Then, we can obtain the capture trajectory for a candidate asteroid to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ periodic orbit, as shown in Fig. 15.

Fig. 15

Given $T_{\mathrm {0}}= 63310\, \hbox {[MJD]}, T_{f}= 63954\hbox {[MJD]}, J = 3.14658338, t_{\mathrm {p}}= 0.66, t_{\textit{sm}} = 5.0$, direct capture trajectory (phase I) for 2014WX202 to an Earth–Moon $\hbox {L}_{\mathrm {2}}$ north halo orbit and stable manifold (phase II) associated with the target halo orbit in the J2000 Sun-cantered inertial frame

4.7 Optimization and discussion

For each candidate NEA, feasible approach dates are assumed in the interval 2016–2050. The orbital elements of the candidate asteroids are assumed to be valid until their next close approach to the Earth. Thus, for each candidate asteroid, there are 5 variables: ($T_{\mathrm {0}}$, $T_{f}$, J, $t_{p}$, $t_{\textit{sm}})$. These transfer trajectories between the candidate asteroid initial orbits and the stable manifolds can be searched using NSGA-II, a global optimization method which is based on a multi-objective evolutionary algorithm (Deb et al. 2002), using the total $\Delta v$ cost as the objective function. Then, transfers obtained with NSGA-II can be locally optimized with sequential quadratic programming (SQP), implemented in the function fmincon in MATLAB. Therefore, we find that 6 NEAs that can be captured with a total $\Delta v$ cost of less than $500\, \hbox {ms}^{{-1}}$, shown in Table 2. It can be seen that the optimal departure date for a given NEA is almost the same for different target periodic orbits around the Earth–Moon $\hbox {L}_{{2}}$ point (i.e., halo orbits and Lyapunov orbits), as well as the approach date.

Comparing the direct capture strategy to Earth–Moon libration point orbits (LPOs) and the capture strategy into Sun–Earth LPOs in prior studies (Yárnoz et al. 2013; Sánchez and Yárnoz 2016), we note that the one of the obvious differences between these two capture strategies is the flight time along the stable manifolds. That is, the direct capture of the asteroids into the Earth–Moon (LPOs) needs a much shorter flight time along the stable manifolds associated with Earth–Moon LPOs, while the capture onto Sun–Earth LPOs requires a longer time for the asteroid to be asymptotically captured through utilizing the stable manifolds associated with the Sun–Earth LPOs.

Without utilizing the Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifolds, the transfer trajectory of the direct capture of the NEAs to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ target periodic orbit is also modeled in the Sun–Earth–Moon restricted four-body problem. The Lambert arc in the Sun-asteroid two-body problem is used as an initial guess, and then the differential correction is used to calculate the transfer trajectory from the asteroid’s initial obit to Earth–Moon $\hbox {L}_{\mathrm {2}}$ target periodic orbit. The optimal results of the direct capture of the NEAs to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ target periodic orbit without utilizing the Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifolds are shown in Table 3. Comparing the results in Tables 2 and 3, it can be seen that direct capture using the stable manifolds is cheaper than direct capture without utilizing the stable manifolds. It can be concluded that the Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifolds can provide greater opportunities to achieve cheaper NEA capture.

Table 2 Results of optimal direct capture of asteroid to EM $\hbox {L}_{2}$ periodic orbits using the stable manifolds

Table 3 Results of optimal direct capture of asteroid to EM $\hbox {L}_{2}$ periodic orbits without using the stable manifolds

5 Indirect capture of near-Earth asteroids to Earth–Moon $\mathbf{L}_{\mathrm {2}}$ periodic orbits

Another type of lunar capture of NEAs will be termed indirect capture. In this capture strategy, the asteroid capture trajectories are designed in a patched three-body model which consists of the Sun–Earth (SE) and Earth–Moon (EM) systems (Mingotti et al. 2014b), based on the work of Sanchez and McInnes (2011), Sanchez et al. (2012) and Yárnoz et al. (2013). As an approximation of the Sun–Earth–Moon four-body problem, the patched three-body model can be decomposed into the Sun–Earth CRTBP system and the Earth–Moon CRTBP system. It is assumed that the Earth–Moon CRTBP system is coplanar with the Sun–Earth CRTBP system. Thus, asteroid capture trajectories can be accomplished by patching together the unstable manifolds in the Sun–Earth CRTBP system and the stable manifolds in the Earth–Moon CRTBP system. It should be noted that the patching points of the two invariant manifolds are defined by the chosen Poincaré section (angle $\gamma$), shown in Fig. 16. The design procedure for the indirect capture of NEAs by using these patched three-body problems can be divided into three parts as follows;

• (1) With the initial impulse $\Delta {{\varvec{v}}}_{\mathrm {1}}$, the asteroid leaves its orbit and is injected onto the stable manifolds associated with the Sun–Earth $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ points with the second impulse $\Delta {{\varvec{v}}}_{\mathrm {2}}$. These two impulsive burns can be solved by using the Lambert arc in the two-body problem (Yárnoz et al. 2013);

• (2) After the NEA inserts onto the stable manifolds, it will be asymptotically captured onto a periodic orbit around the Sun–Earth $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ point; the asteroid will be on the periodic orbit until it reaches the point where the Sun–Earth unstable manifold is propagated forward from; then, the asteroid leaves the periodic orbit by utilizing the unstable manifold and then approaches the injection plane between the Sun–Earth unstable manifold and the Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifolds;

• (3) With the third impulse $\Delta {{\varvec{v}}}_{\mathrm {3}}$, the NEA inserts onto the Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifold and will be asymptotically captured onto a periodic orbit around the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point.

Fig. 16

Indirect asteroid capture in the patched three-body problem with the Poincaré section shown

In this problem, there are 9 variables as follows:

• $T_{\mathrm {0}}$: departure date when the first impulse $\Delta {{\varvec{v}}}_{\mathrm {1}}$ is applied to the candidate asteroid and the asteroid leaves its orbit;

• $T_{f}$: approach date corresponding to the date when the candidate asteroid inserts into the SE (Sun–Earth) $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ stable manifolds with the second impulse $\Delta {{\varvec{v}}}_{\mathrm {2}}$;

• $t_{\textit{sm}}$: SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ stable manifold transfer time;

• $J_{\mathrm {SE}}$: Jacobi constant of target periodic orbit around SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$;

• $t_{p1}$: time determining the point on the target periodic orbit around SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ where the SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ stable manifold is propagated backward from;

• $t_{p2}$: time determining the point on the target periodic orbit around SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ where the SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ unstable manifolds is propagated forward from;

• $\gamma$: angle determining the injection plane where the SE $\hbox {L}_{\mathrm {1}}/\hbox {L}_{\mathrm {2}}$ unstable manifold and EM $\hbox {L}_{\mathrm {2}}$ stable manifold are patched together with the third impulse $\Delta {{\varvec{v}}}_{{{\varvec{3}}}}$;

• $J_{\mathrm {EM}}$: Jacobi constant of EM target periodic orbit;

• $t_{p3}$: time determining the point on the target periodic orbit around EM $\hbox {L}_{\mathrm {2}}$ where the EM $\hbox {L}_{\mathrm {2}}$ stable manifold is propagated backward from.

These 9 variables can be divided into two parts: ($T_{\mathrm {0}}$, $T_{f}, {{t}}_{\textit{sm}}$, $J_{\mathrm {SE}}$, $t_{p1})$ and ($J_{\mathrm {SE}}$, $t_{p2}$, $\gamma$, $J_{\mathrm {EM}}$, $t_{p3})$, corresponding to those associated with capturing the asteroid onto the Sun–Earth stable manifold (Part I) and those associated with patching together the Sun–Earth unstable manifold and Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifold (Part II), respectively. However, there exists a time constraint between the two parts. That is, once the variables ($T_{\mathrm {0}}$, $T_{f}, {{t}}_{\textit{sm}}$, $J_{\mathrm {SE}}$, $t_{p1,}t_{p2}$, $\gamma )$ are given, the Sun–Earth unstable manifold is propagated forward until it reaches the Poincaré section (angle $\gamma$) and then the Sun–Earth unstable transfer time $t_{um}$ is determined; accordingly, the position of the Moon is determined.

Fig. 17

a Unstable manifolds of Sun–Earth $\hbox {L}_{\mathrm {2}}$ Lyapunov orbit $(J=3.0008289345)$ and b their integration time to the same Poincaré section $(x = 1-\mu _{\mathrm {se}})$ with varying ${\varepsilon } {\in } {[0.4}\times {10}^{{-6}}, {2}\times {10}^{{-6}}{]}$

It should be noted that small values of $\varepsilon$ in Eq. (5) can result in large integration times when calculating the unstable manifolds. Figure 17b shows that the integration time of the Sun–Earth unstable manifolds to the same Poincaré section clearly changes when we vary the value of $\varepsilon$. This means even given the values of ($t_{\mathrm {0}}, t_{f}, {{t}}_{\textit{sm}}, J_{\mathrm {SE}}, t_{p1,}t_{p2}, \gamma )$, the position of the Moon can be anywhere along its orbit, as long as an appropriate value of $\varepsilon$ is selected. Therefore, we can introduce a variable $\vartheta (0\le \vartheta < 2\pi )$ determining the position of the Moon, shown in Fig. 17a and the variables of Part II are extended to $(J_{\mathrm {SE}}$, $t_{p2}$, $\gamma$, $J_{\mathrm {EM}}$, $t_{p3}$, $\vartheta )$. The common parameter between the two parts is the Jacobi constant $J_{\mathrm {SE}}$ of the target periodic orbit in the Sun–Earth system. Part II can then be optimized by using NSGA-II. During each step in optimizing Part II, there is a specific value of $J_{\mathrm {SE}}$ and given this value, Part I can be optimized by using the function fmincon in MATLAB. Therefore, this problem can be optimized with total $\Delta v$ cost as the objective function. The results of the indirect capture of the NEAs are listed in Table 4 and the optimal capture trajectory for 2014WX202 to an Earth–Moon $\hbox {L}_{\mathrm {2}}$ Lyapunov orbit is shown in Fig.  18. It should be noted that in Tables 4 and 5, 2L, 2H, 1L, 1H are short for the planar Lyapunov orbit around $\hbox {L}_{\mathrm {2}}$, the halo orbit around $\hbox {L}_{\mathrm {2}}$, the planar Lyapunov orbit around $\hbox {L}_{\mathrm {1}}$ and the halo orbit around $\hbox {L}_{\mathrm {1}}$, respectively.

Fig. 18

Indirect capture trajectory for 2014WX202 to Earth–Moon $\hbox {L}_{\mathrm {2}}$ Lyapunov orbit in the Sun–Earth rotating frame: a the transfer trajectory of Part I, b the transfer trajectory of Part II

Table 4 Results of optimal indirect capture of asteroids to Earth–Moon $\hbox {L}_{2}$ periodic orbits

Table 5 Results of optimal indirect capture of asteroids to Earth–Moon $\hbox {L}_{2}$ periodic orbits without using the Earth–Moon stable manifolds

Comparing the results in Tables 2 and 4, we find that the direct capture to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point needs a shorter flight time and so chemical propulsion may be preferred for this capture strategy. On the other hand, the indirect asteroid capture always needs a much longer flight time. Therefore, low-thrust propulsion can be more easily applied to the indirect capture strategy. For comparison, the optimal results of the indirect capture of NEAs to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ target periodic orbit without utilizing the Earth–Moon $\hbox {L}_{\mathrm {2}}$ stable manifolds are shown in Table 5. It is assumed that the transfer trajectories for indirect asteroid capture can be designed by patching the Sun–Earth unstable manifolds and the Earth–Moon $\hbox {L}_{\mathrm {2}}$ periodic orbits directly. Comparing the results in Tables 4 and 5, we can find that the indirect capture strategy using the Earth–Moon stable manifolds can easily achieve cheaper captures.

From Tables 4 and 5, we find that it is cheapest to patch together the Sun–Earth Lyapunov unstable manifold and Earth–Moon Lyapunov stable manifold than to patch other combinations of the Sun–Earth unstable manifolds and Earth–Moon stable manifolds, e.g. the Sun–Earth halo unstable manifold and Earth–Moon halo stable manifold. This is because in the patched three-body problem it is assumed that the motion of all four bodies is in the same plane. Patching the Sun–Earth Lyapunov unstable manifold and Earth–Moon Lyapunov stable manifold together is a planar problem, and we do not need to consider the z-component of the manifolds. Therefore, we have more opportunities to patch the Sun–Earth Lyapunov unstable manifold and Earth–Moon Lyapunov stable manifold together, while there are only two intersection points between one Sun–Earth halo unstable manifold and one Earth–Moon halo stable manifold, as well as one Sun–Earth halo unstable manifold and one Earth–Moon Lyapunov stable manifold, one Sun–Earth Lyapunov unstable manifold and one Earth–Moon halo stable manifold, shown in Fig.  19.

Fig. 19

Projection of SE $\hbox {L}_{\mathrm {2}}$ manifolds $(J=3.000738)$ and EM $\hbox {L}_{\mathrm {2}}$ manifolds $(J=3.00095, \vartheta =0.5\pi )$ on Poincaré section $(x = 1-\mu _{\mathrm {se}})$ in the Sun–Earth rotating frame

6 Direct and indirect capture of near-Earth asteroids to triangular points in the Earth–Moon system

In the ideal CRTBP model, the triangular points $\hbox {L}_{\mathrm {4}}/\hbox {L}_{\mathrm {5}}$ are stable. Even when we take the eccentricity of the lunar orbit and the influence of the solar radiation pressure into account, the instability of the triangular points is still much milder than that of the collinear points (Zhang and Hou 2015). This means that station-keeping does not require significant energy. Therefore, the vicinity of the triangular points in Earth–Moon system could be a preferred location for captured NEAs. However, the stability properties of the triangular points are also a disadvantage because there are no dynamical structures such as the stable or unstable invariant manifolds associated with the triangular points which can be utilized to design low-cost transfer trajectories.

The linearized solution in the $x-y$ plane around triangular points can be expressed as (Szebehely 1967; Zhang and Hou 2015):

$$\begin{aligned} \left\{ {{\begin{array}{ll} {\xi =C_{1} \cos \theta _{1} +C_{2} \cos \theta _{2} } \\ {\eta =m_{1} C_{1} \cos \theta _{1} +n_{1} C_{1} \sin \theta _{1} +m_{2} C_{2} \cos \theta _{2} +n_{2} C_{2} \sin \theta _{2} } \\ \end{array} }} \right. , \end{aligned}$$

(24)

where

$$\begin{aligned} m_{i}= & {} -\Gamma _{i} \Omega _{xy}^{0} ,n_{i} =-2\omega _{i} \Gamma _{i} ,\Gamma _{i} =\frac{1}{\omega _{i}^{2}+\Omega _{yy}^{0} }\theta _{i} =\omega _{i} t+\varphi _{i}\quad (i=1, 2)\\ \Omega _{xy}= & {} \frac{\partial }{\partial y}\Big (\frac{\partial \Omega }{\partial x}\Big ),\Omega _{yy} =\frac{\partial ^{2}\Omega }{\partial y^{2}},\omega _{1} \cong \frac{27}{4}\mu ,\omega _{2} \cong 1-\frac{27}{8}\mu ,\Omega _{yy} =\frac{\partial ^{2}\Omega }{\partial y^{2}},\omega _{2} \cong 1-\frac{27}{8}\mu \end{aligned}$$

and $\Omega _{xy}^{0},\Omega _{yy}^{0}$ are the values of $\Omega _{xy}$, $\Omega _{yy}$ at the triangular points, respectively.

There are two kinds of periodic orbits around the triangular points: long-period orbits and short-period orbits which are defined by the components $\omega _{\mathrm {1}}$ and $\omega _{\mathrm {2}}$, respectively (Szebehely 1967). The coefficients $C_{\mathrm {1}}, C_{\mathrm {2}}$ correspond to the amplitudes of the short periodic orbit and long periodic orbit, respectively. In addition, $\varphi _{i}(i = 1, 2)$ represents the initial phase angle. Generally speaking, the short-period orbits are much more stable than the long-period orbits, under given perturbations. Therefore, we choose the short-period orbits as the target orbit with $C_{\mathrm {1}} = 0$ and $C_{\mathrm {2}} \le 0.2$ (Zhang and Hou 2015), shown in Fig. 20.

Fig. 20

Short-period orbit around the triangular points $\hbox {L}_{\mathrm {4}}/\hbox {L}_{\mathrm {5}}$ in the Earth–Moon system $(C_{\mathrm {1}}=0, C_{\mathrm {2}}\le 0.2)$

Fig. 21

Two types of asteroid capture strategies to the Earth–Moon triangular points: a direct capture; b indirect capture

Similar to the direct/indirect asteroid capture to periodic orbits around the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point, there also exist two types of asteroid capture strategies and so we can still apply the design procedures of Sects. 3, 4 to design the direct/indirect capture of asteroids to the triangular points. However, different to the transfers to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ periodic orbits, there are no dynamical structures such as invariant manifolds associated with periodic orbits around the triangular points in the Earth–Moon system. Therefore, transfer trajectories for direct asteroid capture can be designed from the candidate NEA’s orbit to the short-period orbits around the Earth–Moon $\hbox {L}_{\mathrm {4}}/\hbox {L}_{\mathrm {5}}$ points directly, shown in Fig. 21a. For the indirect capture strategy, we can patch the unstable manifolds of the Sun–Earth system with the short-period orbit around the Earth–Moon $\hbox {L}_{\mathrm {4}}/\hbox {L}_{\mathrm {5}}$ points, shown in Fig. 21b.

Similar to the optimization of the direct/indirect capture trajectories to the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point, the direct/indirect capture trajectories to the Earth–Moon triangular points can again be optimized by using NSGA-II (Deb et al. 2002) followed by sequential quadratic programming (SQP) which is implemented in the function fmincon in MATLAB. The results of direct and indirect capture of asteroids to the triangular points in the Earth–Moon system are shown in Tables 6 and 7. It can be seen that the direct asteroid capture method needs a shorter flight time, while the indirect asteroid capture method can achieve lower-cost asteroid capture. Compared to the results of Tables 2 and 5, we can find that without invariant manifolds associated with the triangular points, it requires much more energy (i.e., $\Delta v_{\mathrm {2}})$ to insert the candidate asteroids into the short-period orbits around the Earth–Moon triangular points. The optimal direct and indirect capture trajectories for 2014WX202 to the Earth–Moon triangular $\hbox {L}_{\mathrm {4}}$ point are shown in Fig. 22. It should be noted that in Table 7, 2L is short for the planar Lyapunov orbit around $\hbox {L}_{\mathrm {2}}$.

Table 6 Results of optimal direct capture of asteroids to the Earth–Moon triangular point

Table 7 Results of optimal indirect capture of asteroids to the Earth–Moon triangular point

Fig. 22

a Optimal direct capture trajectory for 2014WX202 to the Earth–Moon $\hbox {L}_{\mathrm {4}}$ periodic orbit in the J2000 Sun-cantered inertial frame; b Optimal indirect capture trajectory for 2014WX202 to Earth–Moon $\hbox {L}_{\mathrm {4}}$ periodic orbit in Sun–Earth rotating system

7 Conclusion

The low-energy capture of near-Earth asteroids is of significant interest for both scientific and commercial purposes. It is a logical stepping stone toward more ambitious missions for space exploration in the future.

As a candidate gateway station, and an ideal location for interplanetary transfers, the Earth–Moon $\hbox {L}_{\mathrm {2}}$ libration point is of great importance for future deep space exploration. Capturing asteroids and inserting them into periodic orbits around the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point offers in situ resources to support such ventures. Therefore, the patched restricted three-body problem has been used to investigate the capture of asteroids into periodic orbits around the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point. However, using an indirect capture strategy via the Sun–Earth $\hbox {L}_{\mathrm {2}}$ point the transfer duration is long due to the time required for the asteroid to move along the stable manifold in the Sun–Earth system.

Therefore, we propose a direct asteroid capture method to capture asteroids into periodic orbits around the Earth–Moon $\hbox {L}_{\mathrm {2}}$ point from the asteroid’s heliocentric orbit directly. An initial impulse is used to transfer the candidate asteroid to the appropriate stable manifold where it is then inserted directly onto the stable manifold in the Earth–Moon circular restricted three-body problem with a second impulse. Thus, the asteroid will be asymptotically captured onto a target periodic orbit around the $\hbox {L}_{\mathrm {2}}$ point in Earth–Moon system. On the other hand, due to the stability of the triangular points in the CRTBP model, the vicinity of the triangular points in Earth–Moon system could be another preferred location for captured NEAs. The direct/indirect strategies are also applied to design the direct/indirect capture of asteroids to the triangular points. Since there are no invariant manifolds associated with periodic orbits around the triangular points, transfer trajectories for direct asteroid capture can be designed from the candidate NEA’s orbit to the short-period orbits around the Earth–Moon $\hbox {L}_{\mathrm {4}}/\hbox {L}_{\mathrm {5}}$ points directly and the indirect capture is designed by patching the unstable manifolds of the Sun–Earth system with the short-period orbit around the Earth–Moon $\hbox {L}_{\mathrm {4}}/\hbox {L}_{\mathrm {5}}$ points. Comparing the results of the two methods, we find that the direct asteroid capture strategy requires a shorter flight time, while the indirect asteroid capture strategy can always achieve a cheaper capture of NEAs in terms of energy requirements.