Improved initialization conditions and single impulsive maneuvers for $\hbox {J}_{2}$-invariant relative orbits

Abstract

The determination of the initial conditions for long-term bounded relative motion under natural perturbations is an important theme in satellite cluster flight. Considering the most significant perturbation of the geopotential, namely, the $\hbox {J}_{2}$ term, many researchers have proposed $\hbox {J}_{2}$-mitigating initial conditions for satellite-bounded relative motion. To improve the existing $\hbox {J}_{2}$-invariant conditions, two new methods for finding the correction factor are presented in this paper. In these two methods, Method 1 is obtained by minimizing the possible maximum drift in the along-track relative motion. However, Method 2 is designed by nullifying the rates of change of the bounds of the relative motion. Then the geometric character, such as the self-intersection of the $\hbox {J}_{2}$-invariant relative orbits, is discussed. The conditions of 0, 1 and 2 (the possible maximum number) self-intersection points are also derived. Then, using Gauss’s equations of planetary motion, an analytical optimal single-impulsive maneuver is deduced to guarantee the secular bounded relative motion under $\hbox {J}_{2}$, too. Some numerical simulations are performed to validate the corresponding theoretical predictions. The results demonstrate that the proposed methods enhance performance for achieving the bounded relative motion under $\hbox {J}_{2}$ effects and can be used for future satellite cluster flight missions.

1 Introduction

Using multiple satellites to carry out space tasks is a recent hot topic in the field of spacecraft science and engineering. To this end, a group of satellites can be organized in a formation, a constellation, or, as was recently proposed, a cluster (Alfriend et al. 2010). Here, cluster flight has been identified as one of the most advanced satellite flying techniques since it is usually performed in a very flexible way. Hence, unlike the traditional formation or constellation, the satellites in a cluster need not always be operated in a tightly controlled geometrical shape. Instead, the relative distance between satellites in the cluster should be maintained within a given range, for example, dozens of kilometers (Brown and Eremenko 2006).

It has been found that the bounded relative motion in an unperturbed Keplerian orbit must be such that the semimajor axes of the two satellites are equal (Vallado 1997). In reality, the relative distance between two satellites may increase over time if no control is performed. The main role among the perturbations is played by the $\hbox {J}_{2}$ zonal harmonic. Many works have dealt with this subject of nullifying or restraining the $\hbox {J}_{2}$ effects on the satellite relative motion. Schaub and Alfriend (1999; 2001) proposed a set of first-order constraints on the initial conditions to mitigate the $\hbox {J}_{2}$ secular effects for satellite relative motion. These $\hbox {J}_{2}$-invariant conditions are obtained by nullifying the mean $\hbox {J}_{2}$-induced angular drift rates of the two satellites. Some years later, Gurfil (2007) extended the results of Schaub and Alfriend (2001) and obtained a set of more general $\hbox {J}_{2}$-invariant conditions. These new conditions are deduced by using a nonosculating description of the planetary motion equations under the concept of gauge-velocity (Gurfil 2004). Nearly at the same time, a method of canonical modeling of spacecraft relative motion via epicyclical orbital elements was presented (Kasdin et al. 2005; Kasdin and Kolemen 2005). By inspecting the $\hbox {J}_{2}$ effects on the Cartesian coordinates of the satellite relative motion, they derived a set of initial conditions that guarantee bounded formations when both satellites are in equatorial orbits. Similarly, in the case of a leader satellite in an equatorial orbit, Biggs and Becerra (2005) also presented a method to mitigate the $\hbox {J}_{2}$ effects for satellite relative motion using the targeting method in chaos dynamics.

Recently, Martinusi and Gurfil (2011) proposed a set of new quantities, namely, radial periodicity and orbital angle, for satellite relative motion, which was first introduced by Arnold et al. (2006). Using the commensurability conditions of radial periods and orbital angles between two satellites, a closed-form solution for the $\hbox {J}_{2}$-invariant relative motion in the equatorial plane was determined. The proposed methodology was also extended to cases of nonequatorial orbits and high-order even zonal harmonics. Shortly afterward, according to the results in Gurfil (2004), Martinusi and Gurfil (2014) further derived analytical single-impulsive maneuvers for guaranteeing bounded relative motion under $\hbox {J}_{2}$. Unlike the concept of nullifying the rates of differential orbital elements or matching the periods of motion between two satellites, Koon and Marsden (2001) used the Routh transformation to develop a method of determining the $\hbox {J}_{2}$-invariant relative orbits. By distinguishing the differences between orbital period and ascending node period, a differential correction algorithm to search the $\hbox {J}_{2}$-invariant orbits was also proposed (Xu and Xu 2007; Xu et al. 2012). Rather than using orbital elements, the researchers performed their analysis based on the Hamiltonian expressed in Cartesian coordinates and used invariant manifolds to indicate the asymptotic behavior of the invariant orbit. Moreover, some researchers also suggest finding the partial $\hbox {J}_{2}$-invariant conditions for spacecraft formations to reduce fuel consumption (Breger et al. 2006). Except for the analytic corrections for achieving $\hbox {J}_{2}$-invariant relative orbits, other researchers have used numerical methods. Vadali et al. (1999) used the first-order condition of Schaub and Alfriend (1999) as the initial guess for searching numerically more accurate $\hbox {J}_{2}$-invariant relative orbits. Similarly, Yan and Alfriend (2006) and Sabatini et al. (2009) also proposed numerical methods to search for $\hbox {J}_{2}$-invariant relative orbits.

In the aforementioned approaches, the initial conditions suggested by Schaub and Alfriend (2001) and Gurfil (2007) have analytical expressions and clear physical meanings. Other works are either limited to special orbits (for example, an equatorial orbit) or in numerical form. Since the initial conditions of Schaub and Alfriend (2001) are a set of first-order constraints, it is worth improving these conditions to achieve better performance in nullifying $\hbox {J}_{2}$ effects. Yan and Alfriend (2006) present a set of second-order analytic initial conditions for achieving $\hbox {J}_{2}$ invariant. However, considering the complexity of the method of Yan and Alfriend (2006), the present paper aims to improve the first-order analytic conditions of Schaub and Alfriend (2001) by adding an additional correction factor. Hence, the original constraints of $\delta \dot{\bar{{\Omega }}}={0},\, \delta \dot{\bar{{M}}}+\delta \dot{\bar{{\omega }}}={0}$ in Schaub and Alfriend (2001) are replaced by the improved constraints of $\delta \dot{\bar{{\Omega }}}={0,}\quad \beta \cdot \delta \dot{\bar{{M}}}\,+\,\delta \dot{\bar{{\omega }}}={0}$, where ${\beta }$ is the proposed correction factor. If a proper correction factor is sought, then the performance of $\hbox {J}_{2}$ invariant can be enhanced. To find the proper correction factor, two methods are used in this paper, Method 1 and Method 2. In these two methods, both correction factors depend on the eccentricity. While Method 1 is derived by minimizing the possible maximum drift of the along-track relative motion, Method 2 is obtained by nullifying the rates of the maximum bounds of satellite relative motion. Here the bounds’ model is originated from a newly developed theory, proposed by the same authors (Dang et al. 2014a). The same authors (Dang et al. 2014b) use the bounds’ model to derive a set of $\hbox {J}_{2}$-invariant conditions. However, the results in this paper are more accurate than those in Dang et al. (2014b) because the latter work ignores some effects of small items. Then the effects of the $\hbox {J}_{2}$ mitigation are compared between the two new methods on the one hand and the method of Schaub and Alfriend (2001) on the other. According to the analysis, it was found that the correction factor approached 1 when the eccentricity approached 0. This is consistent with Schaub and Alfriend (2001) when the leader satellite is in a circular orbit. It has also been proven that the two new methods can lead to less drift than the method of Schaub and Alfriend (2001).

Considering the strict $\hbox {J}_{2}$-invariant conditions (Alfriend et al. 2010), which require that the differential semimajor axis, differential eccentricity, and differential mean anomaly be zero, it could still be used in future space missions, and this paper further explores the character of the relative orbit geometry and the configuration of the follower satellite flying around the leader in the $\hbox {J}_{2}$-invariant relative orbits. The same method proposed by Jiang et al. (2008) for studying the self-intersection phenomenon is adopted in this paper. It has been found that, as for the strict $\hbox {J}_{2}$-invariant relative motion, the self-intersection may occur both in the three-dimensional space and $x$–$y$, $y$–$z$, and $z$–$x$ planes with respect to LVLH frame. The number of self-intersection points is further studied. It has been found that, in most cases, there may be at most two self-intersection points.

To achieve the boundedness of relative motion by imposing $\hbox {J}_{2}$-invariant constraints, the analytical derivation of single impulsive maneuvers is also formulated. This derivation is based on Gauss’s variational equations. Some numerical simulations are conducted to validate the methods. The results are consistent with theoretical predictions.

To summarize, the present approach makes three main contributions: (1) it improves $\hbox {J}_{2}$-invariant conditions where a correction factor is employed; (2) it sets out the conditions for self-intersection of the $\hbox {J}_{2}$-invariant orbits; and (3) it introduces an impulsive control to correct the semimajor axis, eccentricity, and inclination to achieve bounded relative motion.

2 Satellite relative motion described by differential orbital elements

The equations of satellite relative motion presented in Dang et al. (2014b) are reorganized here. For simplicity and compactness, some necessary modifications are also made.

2.1 Relation between differential mean anomaly and differential true anomaly

Starting from the Keplerian equation

$$\begin{aligned} M=E-e\sin E, \end{aligned}$$

(1)

the variation of the eccentric anomaly is determined to be

$$\begin{aligned} \delta E=\frac{\delta M+\sin E\delta e}{1-e\cos E}, \end{aligned}$$

(2)

and using the correlation between the eccentric anomaly $E$ and the true anomaly $f$, it is also obtained (Schaub and Junkins 2009) that

$$\begin{aligned} \delta f=\frac{\left( {1-e^{2}} \right) \delta E+\sin E\delta e}{\sqrt{1-e^{2}}\left( {1-e\cos E} \right) }. \end{aligned}$$

(3)

Then, replacing ${\delta E}$ in Eq. (3) with Eq. (2) will naturally lead to the relation of ${\delta M}$ and ${\delta f}$:

$$\begin{aligned} \delta f=\frac{\left( {1-e^{2}} \right) \delta M+\left( {2-e\cos E-e^{2}} \right) \sin E\delta e}{\sqrt{1-e^{2}}\left( {1-e\cos E} \right) ^{2}}, \end{aligned}$$

(4)

which is equal to the following equation:

$$\begin{aligned} \delta f=\frac{1}{1-e^{2}}\left[ {\frac{1}{\sqrt{1-e^{2}}}\left( {1+e\cos f} \right) ^{2}\delta M+\left( {2+e\cos f} \right) \sin f\delta e} \right] . \end{aligned}$$

(5)

2.2 Satellite relative motion expressed by differential orbital elements

For convenience, a new but essentially slightly improved satellite relative motion equation will be introduced. Firstly, recall one available solution of the satellite relative dynamics described by the leader’s position and the differential orbital elements of the follower relative to the leader. Here, the leader is defined as the reference satellite, and the follower is another tracking satellite. From Gim and Alfriend (2003) it can be seen that

$$\begin{aligned} \left\{ {\begin{array}{l} x=\delta r, \\ y=r\left( {\delta \theta +\cos i\delta \Omega } \right) , \\ z=r\left( {\sin \theta \delta i-\cos \theta \sin i\delta \Omega } \right) , \\ \end{array}} \right. \end{aligned}$$

(6)

where $x,\, y$, and $z$ are the position vector’s coordinates of the follower relative to the leader. Note here that these coordinates are all described in the LVLH frame of the leader. $r$ is the magnitude of the position vector of the leader; ${\theta }$, ${i}$, and ${\Omega }$ are respectively the arguments of latitude, orbital inclination, and longitude of the ascending node of the leader. Recall that ${\theta } = \hbox {f} + {\omega }$, with ${\omega }$ being the argument of the perigee. A quantity with a prefix ${\delta }$ represents its variation.

From the expression of $r = r(a, e,f(e))$ in the Kepler problem

$$\begin{aligned} r=\frac{a\left( {1-e^{2}} \right) }{1+e\cos f}, \end{aligned}$$

(7)

the variation of the radial distance, ${\delta r}$, is obtained as

$$\begin{aligned} \delta r=\frac{\left( {1-e^{2}} \right) }{1+e\cos f}\delta a-a\frac{2e+\left( {1+e^{2}} \right) \cos f}{\left( {1+e\cos f} \right) ^{2}}\delta e+a\frac{\left( {1-e^{2}} \right) }{\left( {1+e\cos f} \right) ^{2}}e\sin f\delta f. \end{aligned}$$

(8)

By substitution of Eq. (8) into Eq. (6), the solution of satellite relative motion can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} x=\frac{1-e^{2}}{1+e\cos f}\delta a-a\cos f\delta e+\frac{ae\sin f}{\sqrt{1-e^{2}}}\delta M, \\ y=\frac{a\left( {1-e^{2}} \right) }{1+e\cos f}\left( {\delta \omega +\cos i\delta \,\Omega } \right) +\frac{a\left( {2+e\cos f} \right) \sin f}{1+e\cos f}\delta e+\frac{a\left( {1+e\cos f} \right) }{\sqrt{1-e^{2}}}\delta M, \\ z=\frac{a\left( {1-e^{2}} \right) }{1+e\cos f}\sin \left( {f+\omega } \right) \delta i-\frac{a\left( {1-e^{2}} \right) }{1+e\cos f}\cos \left( {f+\omega } \right) \sin i\delta \,\Omega , \\ \end{array}} \right. \end{aligned}$$

(9)

where Eq. (9) is the same as that in Schaub (2002, 2004); Schaub and Alfriend (2001), in which more deduction details can be found.

2.3 An equivalent algebraic form

For simplicity, the preceding solution of satellite relative motion, which is in trigonometric form of the true anomaly, will be transformed into parametric and algebraic forms. Using the same notations as in Jiang et al. (2008, 2007), a new variable, $s$, is introduced here that depends on the true anomaly,

$$\begin{aligned} s=\tan \left( {f/{2}} \right) ,\quad f\in \left[ {{0},{2}\pi } \right) . \end{aligned}$$

(10)

The substitution $s=\tan \left( {f/{2}} \right)$ introduces a singularity for $f = (2k + 1){\pi }$, where $k$ is an integer, namely, when the leader satellite passes through the apogee. This is because the mapping from $f$ to $s$ in Eq. (10) is not continuous at the point $f = {\pi }$. It can be found that $s$ tends to $+ \infty$ as $f$ tends to ${\pi }^{-}$; however, $s$ tends to $- \infty$ as $f$ tends to ${\pi } ^{+}$. Combining the two values $+ \infty$ and $- \infty$ into one value $\infty$, one can make this mapping continuous and one-to-one (Jiang et al. 2008).

It is clear that

$$\begin{aligned} \sin f&= \frac{{2}s}{{1}+s^{{2}}}, \end{aligned}$$

(11)

$$\begin{aligned} \cos f&= \frac{{1}-s^{{2}}}{{1}+s^{{2}}}. \end{aligned}$$

(12)

Thus, using the equalities of Eqs. (11) and (12), the solution of satellite relative motion from Eq. (9) may be rewritten as

$$\begin{aligned} \left\{ {\begin{array}{l} x=c_1 +c_{6} -\frac{{2}ec_{6} }{\left( {1-e} \right) s^{2}+1+e}+\frac{2\left( {ec_2 s-c_1 } \right) }{s^{2}+1}, \\ y=\left( {1-e} \right) c_2 +c_3 +\frac{2\left( {c_1 s+ec_2 } \right) }{s^{2}+1}+\frac{2\left( {c_1 s-ec_3 } \right) }{\left( {1-e} \right) s^{2}+1+e}, \\ z=-c_5 +\frac{2\left( {c_4 s+c_5 } \right) }{\left( {1-e} \right) s^{2}+1+e} ,\\ \end{array}} \right. \end{aligned}$$

(13)

where

$$\begin{aligned} \left\{ {\begin{array}{l} c_1 =a\delta e, \\ c_2 ={a\delta M}\big /{\sqrt{1-e^{2}}}, \\ c_3 =a\left( {1+e} \right) \left( {\delta \omega +\delta \,\Omega \cos i} \right) , \\ c_4 =a\left( {1-e^{2}} \right) \left( {\delta i\cos \omega +\delta \,\Omega \sin \omega \sin i} \right) , \\ c_5 =a\left( {1+e} \right) \left( {\delta i\sin \omega -\delta \,\Omega \cos \omega \sin i} \right) , \\ c_{6} =\left( {{1+}e} \right) \delta a. \\ \end{array}} \right. \end{aligned}$$

(14)

It should be noted that the coefficients $c_{1} \sim c_{5}$ are the same as those in Jiang et al. (2008, 2007). However, $c_{6}$ is a new coefficient when ${\delta a}$ is not zero.

3 Preliminary remarks on model of bounds of satellite relative motion

To obtain the conditions for $\hbox {J}_{2}$-invariant relative orbits, it is necessary to introduce the bounds’ model of satellite relative motion. The results here are a modified version of those presented in Dang et al. (2014a, b). For completeness, some existing results in Dang et al. (2014a, b) are reorganized and simplified here again.

3.1 Bounds of satellite relative motion without perturbation

Suppose that the real perturbation has vanished and the semimajor axes of two satellites are the same. Then the relative motion will be bounded and periodic. Hence, the follower satellite flies around the leader in a confined space that is determined by the initial orbital elements of the two satellites. The confined space can be described by six parameters that are respectively the minimum and maximum values of the radial, along-track, and cross-track coordinates of the relative motion, namely, $x_{\mathrm{min}},\, x_{\mathrm{max}},\, y_{\mathrm{min}},\, y_{\mathrm{max}},\, z_{\mathrm{min}}$, and $z_{\mathrm{max}}$, which are called the bounds of the relative motion. Naturally, the relative motion coordinates of the follower cannot exceed the aforementioned bounds. Since they are functions of the differential orbital elements of the two satellites, the instantaneous bounds will change with the differential orbital elements. It is evident that the differential orbital elements will vary because of the perturbations or the nonequal semimajor axes of the two satellites. This means that if the perturbations exist or the semimajor axes of the two satellites are different, then the bounds will drift with time. Consequently, the relative motion becomes unbounded. Nevertheless, the instantaneous bounds of the relative motion can be obtained at any time. If the perturbations and the differential semimajor axes are zero from some time, then the relative motion will be bounded from that time.

To obtain the expressions of the instantaneous bounds, which are functions of the instantaneous orbital elements of two satellites, one need simply calculate the partial derivative of each coordinate with respect to the variable $s$. Once the extreme value points are found, the corresponding maximum and minimum coordinates will be found by examining the sign of the second-order partial derivatives. Here, the maximum and minimum values are the upper and lower bounds, respectively. When Eq. (13) is used, the calculated bounds are first-order. It must be noted that the bounds in this paper are in the sense of instantaneous, which means the relative motion will stay in the space constrained by the instantaneous bounds if the orbital elements of the two satellites are no longer changing from this specific time.

Unlike in Dang et al. (2014a), which tackles only the periodic relative motion, that is to say, ${\delta a} = 0$, this paper will solve a more general problem. As for the new scenario, i.e., ${\delta a} \ne 0$, it is clear that the only change occurs in the expression of the radial directional relative motion. Hence, it is only necessary to find the new expression of the bounds for radial directional relative motion. Considering the small eccentricity, the radial directional relative motion can be simplified to

$$\begin{aligned} x\approx c_1 +c_{6} -\frac{\frac{{2}ec_{6} }{1-e}}{s^{2}+{1}}+\frac{2\left( {ec_2 s-c_1 } \right) }{s^{2}+1}. \end{aligned}$$

(15)

The partial derivative of $x$ with respect to $s$ is

$$\begin{aligned} \frac{\partial x}{\partial s}=-2\frac{ec_2 s^{2}-2\left( {c_1 +\frac{e}{{1}-e}c_{6} } \right) s-ec_2 }{\left( {s^{2}+1} \right) ^{2}}. \end{aligned}$$

(16)

To search for critical points to find the extrema, let ${\partial x}/{\partial s}={0}$; then two extreme value points will be found:

$$\begin{aligned} \left\{ {\begin{array}{l} s_{1} =\frac{\left( {{1}-e} \right) c_{1} +ec_{6} }{e\left( {{1}-e} \right) c_{2} }+\frac{{1}}{{1}-e}\sqrt{\left[ {\left( {{1}-e} \right) c_{1} +ec_{6} } \right] ^{{2}}+\left[ {e\left( {{1}-e} \right) c_{2} } \right] ^{{2}}} ,\\ s_{2} =\frac{\left( {{1}-e} \right) c_{1} +ec_{6} }{e\left( {{1}-e} \right) c_{2} }-\frac{{1}}{{1}-e}\sqrt{\left[ {\left( {{1}-e} \right) c_{1} +ec_{6} } \right] ^{{2}}+\left[ {e\left( {{1}-e} \right) c_{2} } \right] ^{{2}}} .\\ \end{array}} \right. \end{aligned}$$

(17)

Checking the second-order partial derivatives of the two preceding extreme value points, the following bounds for the radial relative motion can be determined:

$$\begin{aligned} x_{\hbox {max,min}} =c_{1} +c_{6} \pm \left[ {\sqrt{\left( {ec_{2} } \right) ^{2}+\left( {c_{1} +\frac{e}{{1}-e}c_{6} } \right) ^{2}}\mp \left( {c_{1} +\frac{e}{{1}-e}c_{6} } \right) } \right] , \end{aligned}$$

(18)

where $c_{{1,2,6}}$ are given in Eq. (14). Note that if the extremum occurs at $f = 180^{\circ }$, and thus $s = \infty$, then the maximum and minimum values of $x$ will be the same, namely, $x_{\max } =x_{\min } =c_1 +c_{6}$.

Here, Eq. (18) gives the bounds for the radial relative motion. When ${\delta a} = 0$, Eq. (18) will naturally degenerate into the one presented in Dang et al. (2014a).

In the same manner, the bounds of the along-track and cross-track relative motions can also be determined:

$$\begin{aligned} y_{\max ,\min }&= \left( {1-e} \right) c_2 +c_3\nonumber \\&\pm \, \frac{1}{1-e}\frac{\left( {2-e} \right) ^{2}c_1^2 }{\sqrt{\left( {2-e} \right) ^{2}c_1^2 +e^{2}\left[ {\left( {1-e} \right) c_2 -c_3 } \right] ^{2}}\mp e\left[ {\left( {1-e} \right) c_2 -c_3 } \right] },\quad \quad \quad \end{aligned}$$

(19)

$$\begin{aligned} z_{\max ,\min }&= -c_5 \pm \frac{c_4 }{\left( {1-e} \right) \left[ {\sqrt{\frac{1+e}{1-e}+\left( {\frac{c_5 }{c_4 }} \right) ^{2}}\mp \frac{c_5 }{c_4 }} \right] }. \end{aligned}$$

(20)

3.2 Effects of nonzero differential semimajor axis

It is clear that when ${\delta a} \ne 0$, the differential mean anomaly will linearly increase with time $t$ (Schaub 2002, 2004; Schaub and Alfriend 2001):

$$\begin{aligned} \delta M=\delta M_0 +\delta \dot{M}\cdot t=\delta M_0 +\sqrt{\frac{\mu }{a^{3}}}\frac{\delta a}{a}t. \end{aligned}$$

(21)

If perturbations are ignored, the leader’s orbital elements and the other five differential orbital elements of the follower with respect to the leader will be constant. In this case, ${\delta a} \ne 0$ will lead to an increase of the bounds in the $x$ and $y$ directions. Therefore, the bounded relative motion strongly demands that ${\delta a} = 0$.

In the following sections, only the effect of the dominant perturbation, namely, the $\hbox {J}_{2}$ second zonal harmonic, will be taken into account. When the $\hbox {J}_{2}$ perturbation is considered, however, ${\delta a} = 0$ is not necessary to obtain a bounded relative motion. This phenomenon has already been noticed by Schaub and Alfriend (2001).

3.3 Effects of $\hbox {J}_{2}$ perturbation

The variational equations for the mean orbital elements in the presence of $\hbox {J}_{2}$ perturbations are as follows (Battin 1999; Schaub and Junkins 2003):

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{\bar{{a}}}={0}, \\ \dot{\bar{{e}}}={0}, \\ \dot{\bar{{i}}}={0}, \\ \dot{\bar{{\Omega }}}=-\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{2}}\cos i, \\ \dot{\bar{{\omega }}}=\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{2}}\left( {{2}-\frac{{5}}{{2}}\sin ^{{2}}i} \right) , \\ \dot{\bar{{M}}}=\mu ^{\frac{{1}}{{2}}}a^{-\frac{{3}}{{2}}}+\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-\frac{{3}}{{2}}}\left( {{1}-\frac{{3}}{{2}}\sin ^{{2}}i} \right) . \\ \end{array}} \right. \end{aligned}$$

(22)

Here, the term ${\gamma }$ is defined as

$$\begin{aligned} \gamma =\frac{{3}}{{2}}J_{2} R_e^{2} \mu ^{\frac{{1}}{{2}}}, \end{aligned}$$

(23)

where ${\mu }$ is Earth’s gravity constant, $R_{e }$ the mean equatorial radius.

The variations of the mean elements’ derivatives can be deduced based on Eq. (22) as follows (Schaub 2002, 2004; Schaub and Alfriend 2001):

$$\begin{aligned} \left\{ {\begin{array}{l} \delta \dot{\bar{{a}}}={0}, \\ \delta \dot{\bar{{e}}}={0}, \\ \delta \dot{\bar{{i}}}={0}, \\ \delta \dot{\bar{{\Omega }}}=\frac{\partial \dot{\bar{{\Omega }}}}{\partial a}\delta a+\frac{\partial \dot{\bar{{\Omega }}}}{\partial e}\delta e+\frac{\partial \dot{\bar{{\Omega }}}}{\partial i}\delta i ,\\ \delta \dot{\bar{{\omega }}}=\frac{\partial \dot{\bar{{\omega }}}}{\partial a}\delta a+\frac{\partial \dot{\bar{{\omega }}}}{\partial e}\delta e+\frac{\partial \dot{\bar{{\omega }}}}{\partial i}\delta i, \\ \delta \dot{\bar{{M}}}=\frac{\partial \dot{\bar{{M}}}}{\partial a}\delta a+\frac{\partial \dot{\bar{{M}}}}{\partial e}\delta e+\frac{\partial \dot{\bar{{M}}}}{\partial i}\delta i, \\ \end{array}} \right. \end{aligned}$$

(24)

where the partial derivatives of $\partial y/\partial x \,(y=\dot{\bar{{\Omega }}},\dot{\bar{{\omega }}},\dot{\bar{{M}}},\, x = a, e, i)$ can be found in the “Appendix”. The results in the “Appendix” indicate that all these partial derivatives are constant. This means that the resulting rates of the mean elements’ variations are constant, too.

From Eq. (24) it is concluded that, under a $\hbox {J}_{2}$ perturbation, only the variations of the angular elements, namely, ${\delta \Omega }, \,{\delta \omega }$, and ${\delta M}$, vary with time and their rate of variation is constant, which is a key element in the following discussion.

4 Improved initialization conditions for $\hbox {J}_{2}$-invariant relative orbits

In this section, two new sets of $\hbox {J}_{2}$-invariant conditions (called Method 1 and Method 2) for satellite relative motion are derived. These two sets of conditions are obtained by introducing a correction factor for the original constraints of the initial conditions suggested by Schaub and Alfriend (2001). In Method 1, the correction factor is designed to minimize the greatest possible drift in the $y$ direction in a whole period. In Method 2, however, the correction factor is obtained by nullifying the rates of change of the bounds of the relative motion in the $y$ direction. The concept of Method 2 was once also used in one of our earlier works (Dang et al. 2014b). However, the derivations in this paper are more comprehensive, and the resulting new $\hbox {J}_{2}$-invariant conditions are more accurate than those of (Dang et al. 2014b) since the latter ignores some small items. In addition, some equations in the present version of the paper are reorganized in a more elegant way.

4.1 Strict conditions

According to the preceding discussion, it is possible to find a way to cancel the $\hbox {J}_{2}$ effects for the relative orbits by nullifying the rates of ${\delta \Omega }$, ${\delta \omega }$, and ${\delta M}$. These three rates are linear functions of the other three variations, namely, ${\delta a}$, ${\delta e}$, and ${\delta i}$. Hence, a natural approach is to consider

$$\begin{aligned} \delta \dot{\bar{{\Omega }}}={0,}\quad \delta \dot{\bar{{M}}}={0},\quad \delta \dot{\bar{{\omega }}}={0}, \end{aligned}$$

(25)

which is equivalent to

$$\begin{aligned} \delta a={0,}\quad \delta e={0},\quad \delta i={0}. \end{aligned}$$

(26)

This solution can also be found in (Schaub and Alfriend 2001), as a general result of $\hbox {J}_{2}$-invariant relative orbits. The preceding conditions for generating the $\hbox {J}_{2}$-invariant relative orbits are also called three constraints in (Alfriend et al. 2010). It is clear that this condition is a very strict way of keeping the bounded relative motion under the $\hbox {J}_{2}$ perturbation in a long time period. Nevertheless, there is no doubt that this strict condition is one of the best ways of generating $\hbox {J}_{2}$-invariant relative motion. The features of this kind of $\hbox {J}_{2}$-invariant relative motion will be discussed in the next section.

4.2 Loose conditions

Considering the limits of the preceding strict conditions for $\hbox {J}_{2}$-invariant relative orbits, several sets of loose conditions were proposed. The main idea is to nullify as much as possible the rates of the elements’ variations between two satellites. One way to do this, called two constraints in Alfriend et al. (2010), which is first presented in Schaub and Alfriend (2001), is to nullify the rates of the right ascension and the mean argument of latitude, namely,

$$\begin{aligned} \delta \dot{\bar{{\Omega }}}={0,}\quad \delta \dot{\bar{{M}}}+\delta \dot{\bar{{\omega }}}={0}. \end{aligned}$$

(27)

This proposition is relatively intuitive. It can be confirmed that the varying term in cross-track relative motion is only ${\delta \Omega }$. Therefore, nullifying the rate of ${\delta \Omega }$ is quite justifiable. However, there is a problem with the other equality in Eq. (27) because in mathematical expressions related to relative motion there is no sign showing that these two terms, i.e., ${\delta M}$ and ${\delta \omega }$, always appear in a directly additive way. To improve the conditions shown in Eq. (27), a correction factor in this paper is introduced that leads to the following new constraints:

$$\begin{aligned} \delta \dot{\bar{{\Omega }}}={0,}\quad \beta \cdot \delta \dot{\bar{{M}}}+\delta \dot{\bar{{\omega }}}={0}, \end{aligned}$$

(28)

where ${\beta }$ is a positive constant. It is clear that when ${\beta } = 1$, the new constraints will be degraded into those of Schaub and Alfriend (2001).

For any selected value of ${\beta }$, Eq. (28) can be transformed into the following equations using the relations shown in Eq. (24):

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial \dot{\bar{{\Omega }}}}{\partial a}\delta a+\frac{\partial \dot{\bar{{\Omega }}}}{\partial e}\delta e+\frac{\partial \dot{\bar{{\Omega }}}}{\partial i}\delta i=0, \\ \left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial a}+\frac{\partial \dot{\bar{{\omega }}}}{\partial a}} \right) \delta a+\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial e}+\frac{\partial \dot{\bar{{\omega }}}}{\partial e}} \right) \delta e+\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial i}+\frac{\partial \dot{\bar{{\omega }}}}{\partial i}} \right) \delta i=0 ,\\ \end{array}} \right. \end{aligned}$$

(29)

which can be directly solved to generate the solutions of ${ \delta a}$ and ${\delta i}$ expressed as functions of ${\delta e}$:

$$\begin{aligned} \delta a=\frac{\left\{ {\frac{\partial \dot{\bar{{\Omega }}}}{\partial e}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial i}+\frac{\partial \dot{\bar{{\omega }}}}{\partial i}} \right) -\frac{\partial \dot{\bar{{\Omega }}}}{\partial i}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial e}+\frac{\partial \dot{\bar{{\omega }}}}{\partial e}} \right) } \right\} }{\left\{ {\frac{\partial \dot{\bar{{\Omega }}}}{\partial i}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial a}+\frac{\partial \dot{\bar{{\omega }}}}{\partial a}} \right) -\frac{\partial \dot{\bar{{\Omega }}}}{\partial a}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial i}+\frac{\partial \dot{\bar{{\omega }}}}{\partial i}} \right) } \right\} }\delta e, \end{aligned}$$

(30)

$$\begin{aligned} \delta i=\frac{\left\{ {\frac{\partial \dot{\bar{{\Omega }}}}{\partial e}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial a}+\frac{\partial \dot{\bar{{\omega }}}}{\partial a}} \right) -\frac{\partial \dot{\bar{{\Omega }}}}{\partial a}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial e}+\frac{\partial \dot{\bar{{\omega }}}}{\partial e}} \right) } \right\} }{\left\{ {\frac{\partial \dot{\bar{{\Omega }}}}{\partial a}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial i}+\frac{\partial \dot{\bar{{\omega }}}}{\partial i}} \right) -\frac{\partial \dot{\bar{{\Omega }}}}{\partial i}\left( {\beta \frac{\partial \dot{\bar{{M}}}}{\partial a}+\frac{\partial \dot{\bar{{\omega }}}}{\partial a}} \right) } \right\} }\delta e. \end{aligned}$$

(31)

Substituting the values of the partial derivatives of $\partial y/ \partial x \,(y=\dot{\bar{{\Omega }}},\dot{\bar{{\omega }}},\dot{\bar{{M}}},\, x = a, e, i)$ in the “Appendix” into the preceding Eqs. (30) and (31), the relations among ${ \delta a}$, ${\delta i}$, and ${\delta e}$ can be determined:

$$\begin{aligned} \delta a=f_{ae} \cdot \delta e,\quad \delta i=f_{ie} \cdot \delta e, \end{aligned}$$

(32)

where

$$\begin{aligned} f_{ae}&= \frac{2e\eta \left( {4+3\beta \eta } \right) \left( {1+5\cos ^{2}i} \right) J_2 R_e^2 a}{\beta \left[ {-4a^{2}\eta ^{7}+7J_2 R_e^2 \eta ^{4}\left( {1+3\cos ^{2}i} \right) } \right] +7J_2 R_e^2 \eta ^{3}\left( {1+5\cos ^{2}i} \right) },\end{aligned}$$

(33)

$$\begin{aligned} f_{ie}&= \frac{\beta e\cos i\left( {16a^{2}\eta ^{3}-7J_2 R_e^2 \left( {1-3\cos ^{2}i} \right) } \right) }{\beta \left[ {4a^{2}\eta ^{5}-7J_2 R_e^2 \eta ^{2}\left( {1+3\cos ^{2}i} \right) } \right] \sin i-7J_2 R_e^2 \eta \left( {1+5\cos ^{2}i} \right) \sin i},\quad \quad \end{aligned}$$

(34)

and $\eta =\sqrt{1-e^{2}}$.

Because $J_{2} \approx 10^{-3}$, the results of Eqs. (33) and (34) can be simplified to

$$\begin{aligned} \delta a&= -\frac{J_2 }{2L^{4}\eta ^{6}}\frac{4+3\beta \eta }{\beta }\left( {1+5\cos ^{2}i} \right) ae\delta e, \end{aligned}$$

(35)

$$\begin{aligned} \delta i&= \frac{4e}{\eta ^{2}\tan i}\delta e, \end{aligned}$$

(36)

where $L=\sqrt{a/{R_e }}$.

It should be noted that when the correction factor ${\beta } = 1$, the results of Eqs. (35) and (36) will be degraded into those of (Schaub and Alfriend 2001). In addition, $e = 0$ leads to ${\beta } = 1$. To obtain a proper correction factor to achieve better performance for mitigating the $\hbox {J}_{2}$ effects on relative motion, two methods are proposed as follows.

4.3 Method 1

In Method 1, the best correction factor is found by minimizing the possible maximum drift in the $y$ direction. To this end, the drift of the $y$-directional motion should first be expressed analytically. From Eq. (9) it can be seen that the total drift of $y$ in one orbital period is different for the different true anomaly $f_{0}$:

$$\begin{aligned} \Delta y\left( {f_0 } \right)&= y\left( {f_0 +2\pi } \right) -y\left( {f_0 } \right) \nonumber \\&= \frac{a\left( {1-e^{2}} \right) }{1+e\cos f_0 }\left( {\Delta \delta \omega +\cos i\Delta \delta \, \Omega } \right) +\frac{a\left( {1+e\cos f_0 } \right) }{\sqrt{1-e^{2}}}\Delta \delta M, \end{aligned}$$

(37)

where ${\Delta \delta \omega }$, ${\Delta \delta \,\Omega }$, and ${ \Delta \delta M}$ are the changes in ${\delta \omega }$, ${ \delta \,\Omega }$, and ${\delta M}$ in an orbital period:

$$\begin{aligned} \Delta \delta \omega&= \int _{f_0 }^{f_0 +2\pi } {\frac{\delta \dot{\bar{{\omega }}}}{\dot{f}}df} ,\nonumber \\ \Delta \delta M&= \int _{f_0 }^{f_0 +2\pi } {\frac{\delta \dot{\bar{{M}}}}{\dot{f}}df} ,\quad \Delta \delta \,\Omega =\int _{f_0 }^{f_0 +2\pi } {\frac{\delta \,\dot{\bar{{\Omega }}}}{\dot{f}}df}, \end{aligned}$$

(38)

$$\begin{aligned} \dot{f}&= \frac{h}{r^{2}}=\frac{\sqrt{\mu }\left( {1+e\cos f} \right) ^{2}}{a^{3/2}\eta ^{3}}. \end{aligned}$$

(39)

Since $\delta \dot{\bar{{\Omega }}}=0$ is one of the constraints, the drift of ${\Delta y}(f_{0})$ can be simplified to

$$\begin{aligned} \Delta y\left( {f_0 } \right) =\frac{a\left( {1-e^{2}} \right) }{1+e\cos f_0 }\Delta \delta \omega +\frac{a\left( {1+e\cos f_0 } \right) }{\sqrt{1-e^{2}}}\Delta \delta M. \end{aligned}$$

(40)

Substituting Eq. (38) into Eq. (40) and considering the fact that $\delta \dot{\bar{{\omega }}}$ and $\delta \dot{\bar{{M}}}$ are constants in the sense of secular time, we obtain the following equation:

$$\begin{aligned} \Delta y\left( {f_0 } \right) =\frac{a\left( {1-e^{2}} \right) }{1+e\cos f_0 }\delta \dot{\bar{{\omega }}}\cdot f_\Delta +\frac{a\left( {1+e\cos f_0 } \right) }{\sqrt{1-e^{2}}}\delta \dot{\bar{{M}}}\cdot f_\Delta , \end{aligned}$$

(41)

where

$$\begin{aligned} f_\Delta =\int _{f_0 }^{f_0 +2\pi } {\frac{1}{\dot{f}}df} =\int _0^{2\pi } {\frac{1}{\dot{f}}df}. \end{aligned}$$

(42)

Substituting Eq. (28) into Eq. (41) leads to

$$\begin{aligned} \Delta y\left( {f_0 } \right) =-\frac{a\left( {1-e^{2}} \right) }{1+e\cos f_0 }\beta \cdot \delta \dot{\bar{{M}}}\cdot f_\Delta +\frac{a\left( {1+e\cos f_0 } \right) }{\sqrt{1-e^{2}}}\delta \dot{\bar{{M}}}\cdot f_\Delta . \end{aligned}$$

(43)

For the given ${\beta }$, by solving Eq. (28) with the relations found in the “Appendix”, the following result is obtained:

$$\begin{aligned} \delta \dot{\bar{{M}}}={3}J_2 \sqrt{\mu }a^{-\frac{{3}}{{2}}}\left( {{R_e }/a} \right) ^{2}e\eta ^{-6}\left( {1+5\cos ^{2}i} \right) \beta ^{-1}. \end{aligned}$$

(44)

Hence, the drift of $y$ can be written as

$$\begin{aligned} \Delta y\left( {f_0 } \right) =-\frac{a\left( {1-e^{2}} \right) }{1+e\cos f_0 }\delta \dot{\bar{{M}}}_s \cdot f_\Delta +\frac{a\left( {1+e\cos f_0 } \right) }{\sqrt{1-e^{2}}}\delta \dot{\bar{{M}}}_s \beta ^{-1}\cdot f_\Delta , \end{aligned}$$

(45)

where

$$\begin{aligned} \delta \dot{\bar{{M}}}_s ={3}J_2 \sqrt{\mu }a^{-\frac{{3}}{{2}}}\left( {{R_e }/a} \right) ^{2}e\eta ^{-6}\left( {1+5\cos ^{2}i} \right) \end{aligned}$$

(46)

From Eq. (43) it is found that for any fixed $f_{0}$ there is a relevant correction factor that can make the drift of ${\Delta y}$ at this true anomaly be zero:

$$\begin{aligned} \beta \left( {f_0 } \right) =\frac{\left( {1+e\cos f_0 } \right) ^{2}}{\left( {1-e^{2}} \right) ^{3/2}}. \end{aligned}$$

(47)

It is clear that there is not a sole correction factor that can make all drifts of ${\Delta y}$ at any true anomaly be zero. Therefore, a best correction factor should minimize the possible maximum drift:

$$\begin{aligned} \mathop {\min }\limits _\beta \mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| . \end{aligned}$$

(48)

The maximum value of ${\vert }{\Delta y}(f_{0}){\vert }$ with the given ${\beta }$ can be solved by analyzing the derivatives of ${\Delta y}(f_{0})$ with respect to $f_{0}$:

$$\begin{aligned} \Delta {y}'\left( {f_0 } \right) =\frac{d\Delta y}{df_0 }=-\frac{a\left( {1-e^{2}} \right) e\sin f_0 }{\left( {1+e\cos f_0 } \right) ^{2}}\delta \dot{\bar{{M}}}_s \cdot f_\Delta -\frac{ae\sin f_0 }{\sqrt{1-e^{2}}}\delta \dot{\bar{{M}}}_s \beta ^{-1}\cdot f_\Delta . \end{aligned}$$

(49)

Since ${\beta }$ is a positive value (close to 1), there are two extreme value points from Eq. (49):

$$\begin{aligned} f_{01} =0,\quad f_{02} =\pi . \end{aligned}$$

(50)

Then, substituting these two values into Eq. (45) results in two extreme values of ${\Delta y}$:

$$\begin{aligned} \Delta y\left( {f_{01} } \right) =\frac{a\delta \dot{\bar{{M}}}_s \cdot f_\Delta }{\sqrt{1-e^{2}}}\left( {\frac{1+e}{\beta }-\left( {1-e} \right) \sqrt{1-e^{2}}} \right) , \end{aligned}$$

(51)

$$\begin{aligned} \Delta y\left( {f_{02} } \right) =\frac{a\delta \dot{\bar{{M}}}_s \cdot f_\Delta }{\sqrt{1-e^{2}}}\left( {\frac{1-e}{\beta }-\left( {1+e} \right) \sqrt{1-e^{2}}} \right) . \end{aligned}$$

(52)

Therefore, we have

$$\begin{aligned}&\mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| \nonumber \\&\quad =\frac{a\left| {\delta \dot{M}_s } \right| \cdot f_\Delta }{\sqrt{1-e^{2}}}\max \left( {\left| {\frac{1+e}{\beta }-\left( {1-e} \right) \sqrt{1-e^{2}}} \right| ,\quad \left| {\frac{1-e}{\beta }-\left( {1+e} \right) \sqrt{1-e^{2}}} \right| } \right) .\quad \quad \quad \end{aligned}$$

(53)

Careful analysis leads to the solution of Eq. (48):

$$\begin{aligned} \beta =\frac{1}{\sqrt{1-e^{2}}}, \end{aligned}$$

(54)

which is the best correction factor for mitigating $\hbox {J}_{2}$ effects for the $y$-directional maximum drift. The correction factor expressed by Eq. (54) and the constraints in Eqs. (32) and (34) are formed the Method 1.

When $\beta =\frac{1}{\sqrt{1-e^{2}}}$, the greatest drift in the $y$ direction is calculated to be

$$\begin{aligned} \mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =\frac{1}{\sqrt{1-e^{2}}}} =2\frac{a\left| {\delta \dot{\bar{{M}}}_s } \right| \cdot f_\Delta }{\sqrt{1-e^{2}}}e\sqrt{1-e^{2}}. \end{aligned}$$

(55)

Similarly, the greatest drift of $y$ can be obtained when ${\beta } = 1$, which corresponds to the method of Schaub and Alfriend (2001):

$$\begin{aligned} \mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =1} =\frac{a\left| {\delta \dot{\bar{{M}}}_s } \right| \cdot f_\Delta }{\sqrt{1-e^{2}}}\left( {1+e-\left( {1-e} \right) \sqrt{1-e^{2}}} \right) . \end{aligned}$$

(56)

Subtracting Eq. (56) from Eq. (55), it is found that

$$\begin{aligned} \mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =1} -\mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =\frac{1}{\sqrt{1-e^{2}}}} \!=\!\frac{a\left| {\delta \dot{\bar{{M}}}} \right| \cdot f_\Delta }{\sqrt{1\!-\!e^{2}}}\left( {1\!+\!e} \right) \left( {1\!-\!\sqrt{1\!-\!e^{2}}} \right) \!>\!0. \end{aligned}$$

(57)

This means Method 1 reduces more drift than the method of Schaub and Alfriend (2001) and, hence, enhances the effects of the $\hbox {J}_{2}$ invariant.

4.4 Method 2

When the analytic bounds (in Sect. 3) for relative motion are obtained, one will naturally guess that if the bounds under a $\hbox {J}_{2}$ perturbation are constant, then the related relative motion will also be $\hbox {J}_{2}$-invariant. Using this concept, the conditions for $\hbox {J}_{2}$-invariant relative orbits can be found. To this end, the rates of the upper bounds, which represent the size of the relative motion, are first calculated as

$$\begin{aligned} \dot{x}_{\max }&= \frac{\hbox {d}x_{\max } }{\hbox {d}t}=\frac{\partial x_{\max } }{\partial \delta M}\delta \dot{\bar{{M}}}+\frac{\partial x_{\max } }{\partial \delta \omega }\delta \dot{\bar{{\omega }}}+\frac{\partial x_{\max } }{\partial \delta \,\Omega }\delta \dot{\bar{{\Omega }}}=a\xi _x \delta \dot{\bar{{M}}}, \end{aligned}$$

(58)

$$\begin{aligned} \dot{y}_{\max }&= \frac{\hbox {d}y_{\max } }{\hbox {d}t}=\frac{\partial y_{\max } }{\partial \delta M}\delta \dot{\bar{{M}}}+\frac{\partial y_{\max } }{\partial \delta \omega }\delta \dot{\bar{{\omega }}}+\frac{\partial y_{\max } }{\partial \delta \, \Omega }\delta \dot{\bar{{\Omega }}}\nonumber \\&= a\left( {\xi _{y1} \delta \dot{\bar{{M}}}+\xi _{y2} \delta \dot{\bar{{\omega }}}+\xi _{y2} \cos i\delta \,\dot{\bar{{\Omega }}}} \right) , \end{aligned}$$

(59)

$$\begin{aligned} \dot{z}_{\max }&= \frac{dz_{\max } }{\hbox {d}t}=\frac{\partial z_{\max } }{\partial \delta M}\delta \dot{\bar{{M}}}+\frac{\partial z_{\max } }{\partial \delta \omega }\delta \dot{\bar{{\omega }}}+\frac{\partial z_{\max } }{\partial \delta \,\Omega }\delta \,\dot{\bar{{\Omega }}}=a\xi _z \delta \,\dot{\bar{{\Omega }}}, \end{aligned}$$

(60)

where

$$\begin{aligned} \xi _x&= \frac{{1}}{{1}-e}\frac{e^{{2}}\frac{1-e}{1+e}\delta M}{\sqrt{e^{{2}}\frac{1-e}{1+e}\left( {\delta M} \right) ^{{2}}+\left[ {\left( {{1}-e} \right) \delta e+e\left( {{1+}e} \right) \frac{\delta a}{a}} \right] ^{{2}}}}, \end{aligned}$$

(61)

$$\begin{aligned} \xi _{y1}&= \frac{1}{\sqrt{1-e^{2}}}\left\{ {1+\frac{e^{2}\left[ {\sqrt{\frac{1-e}{1+e}}\delta M-\left( {1+e} \right) \left( {\delta \omega +\delta \Omega \cos i} \right) } \right] }{\sqrt{\left( {2-e} \right) ^{2}\delta e^{2}+e^{2}\left[ {\sqrt{\frac{1-e}{1+e}}\delta M-\left( {1+e} \right) \left( {\delta \omega +\delta \Omega \cos i} \right) } \right] ^{2}}}} \right\} ,\nonumber \\ \end{aligned}$$

(62)

$$\begin{aligned} \xi _{y2}&= \frac{1+e}{1-e}\left\{ {1-2e-\frac{e^{2}\left[ {\sqrt{\frac{1-e}{1+e}}\delta M-\left( {1+e} \right) \left( {\delta \omega +\delta \Omega \cos i} \right) } \right] }{\sqrt{\left( {2-e} \right) ^{2}\delta e^{2}+e^{2}\left[ {\sqrt{\frac{1-e}{1+e}}\delta M-\left( {1+e} \right) \left( {\delta \omega +\delta \Omega \cos i}, \right) } \right] ^{2}}}} \right\} \nonumber \\ \end{aligned}$$

(63)

$$\begin{aligned} \xi _z&= e\cos \omega \sin i+\frac{\delta \Omega \sin ^{2}i}{\sqrt{\delta i^{2}+\delta \Omega ^{2}\sin ^{2}i}}. \end{aligned}$$

(64)

It is clear that when $\delta \,\dot{\bar{{\Omega }}}$, $\delta \dot{\bar{{\omega }}}$, and $\delta \dot{\bar{{M}}}$ are all zero, the rates of the three upper bounds will be zero, which will further make the bounds be constant. Note that for a relative motion with a size less than the order of hundreds of kilometers, the quantities of ${\delta a}/a$, ${\delta e}$, ${\delta i}$, ${\delta \,\Omega }$, ${\delta \omega }$, and ${\delta M}$ will be less than 0.01. Consequently, ${\vert } {\xi }_{x}{\vert } < < 1$, ${\vert } {\xi }_{z}{\vert } < < 1$, ${\vert } {\xi } _{y1} {\vert } \approx 1$, and ${\vert } {\xi } _{y2} {\vert } \approx 1$ will usually hold. Therefore, the contribution of $\delta \dot{\bar{{M}}}$ in the $x$ direction will be far less than that in the $y$ direction. That is to say, when looking for the $\hbox {J}_{2}$-invariant conditions, the $x$ direction’s motion can be ignored justifiably in comparison to the $y$ direction’s motion. Therefore, the following constraints will lead to improved loose conditions for $\hbox {J}_{2}$-invariant relative orbits:

$$\begin{aligned} \dot{y}_{\max } ={0,}\quad \dot{z}_{\max } ={0}. \end{aligned}$$

(65)

Taking into account the results of Eqs. (59) and (60), the following conditions can be easily derived from Eq. (65):

$$\begin{aligned} \delta \, \dot{\bar{{\Omega }}}={0,}\quad \beta \cdot \delta \dot{\bar{{M}}}+\delta \dot{\bar{{\omega }}}={0}, \end{aligned}$$

(66)

where

$$\begin{aligned} \beta =\frac{\xi _{y1} }{\xi _{y2} }. \end{aligned}$$

(67)

By a careful quantitative analysis, it can be quickly determined that

$$\begin{aligned} \left( {2-e} \right) ^{2}\delta e^{2}>>e^{2}\left[ {\sqrt{\frac{1-e}{1+e}}\delta M-\left( {1+e} \right) \left( {\delta \omega +\delta \Omega \cos i} \right) } \right] ^{2}. \end{aligned}$$

(68)

This can be verified by noticing that ${\delta e}$, ${\delta M}$, ${\delta \omega }$, and ${\delta \,\Omega }$ have nearly the same order, and $e$ is usually less than 0.1. Hence, the coefficients ${\xi }_{y1 }$ and ${\xi }_{y2 }$ can be simplified to

$$\begin{aligned} \xi _{y1}&\approx \frac{1}{\sqrt{1-e^{2}}}, \end{aligned}$$

(69)

$$\begin{aligned} \xi _{y2}&\approx \frac{\left( {1+e} \right) \left( {1-2e} \right) }{1-e}. \end{aligned}$$

(70)

Then the correction coefficient ${\beta }$ can be calculated as

$$\begin{aligned} \beta =\frac{1-e}{1-e-2e^{2}}\frac{1}{\sqrt{1-e^{2}}}. \end{aligned}$$

(71)

The correction factor in Eq. (71) and the conditions of Eqs. (32) and (34) are formed the Method 2. By some simple manipulation, the following relation can be obtained:

$$\begin{aligned} \mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =\frac{1-e}{1-e-2e^{2}}\frac{1}{\sqrt{1-e^{2}}}} =2\frac{a\left| {\delta \dot{\bar{{M}}}_s } \right| \cdot f_\Delta }{\sqrt{1-e^{2}}}e\left( {1+e^{2}} \right) \sqrt{1-e^{2}}, \end{aligned}$$

(72)

Hence, we have

$$\begin{aligned} \mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =\frac{1-e}{1-e-2e^{2}}\frac{1}{\sqrt{1-e^{2}}}} <\mathop {\max }\limits _{f_0 \in \left[ {0,2\pi } \right) } \left| {\Delta y\left( {f_0 } \right) } \right| _{\beta =1}. \end{aligned}$$

(73)

This indicates that Method 2 can also lead to less drift than the method of Schaub and Alfriend (2001).

4.5 Examples

In this section, some examples are presented to validate the preceding $\hbox {J}_{2}$-invariant conditions. To this end, let the initial mean orbital elements of the leader be

$$\begin{aligned} a=8378\,\hbox {km},\, i=48^{\circ }, \Omega =30^{\circ }, \omega =60^{\circ }, M_0 =40^{\circ }, \end{aligned}$$

where the eccentricity is selected in the range of [0,0.05]. Here the upper limit of the eccentricity $e=0.05$ in the simulations is selected so as to satisfy the realistic perigee altitude. Generally, the effect of atmospheric drag will come into play if the altitude of the orbit is below approximately 700 km. To make the $\hbox {J}_{2}$-only model realistic, and hence to verify the developed $\hbox {J}_{2}$-mitigating methods in this paper, a lower limit of the perigee altitude is set at 1,500 km. Then, using the relation of $H_{p} = a(1 - e) - R_{e}$, where $H_p =1,\!500\,\hbox {km}$, the upper limit of the eccentricity is calculated to be approximately 0.05.

The initial differential mean orbital elements of the follower are set at

$$\begin{aligned} \delta \, \Omega =0.05^{\circ },\delta \omega =0.01^{\circ }, \delta M_0 =-0.02^{\circ }, \end{aligned}$$

where ${\delta e}$ will be valued from 0.005 to 0.05 at intervals of 0.005, and ${\delta a}$ and ${\delta i}$ will be computed accordingly using Eqs. (32)–(34) with the suggested correction factors.

The relative motion of two satellites with an eccentricity of 0.01 and a differential eccentricity of 0.01 is propagated for 20 orbital periods. The results are presented in what follows. Here, Fig. 1 illustrates the histories of the relative motion using the $\hbox {J}_{2}$-invariant conditions of Method 1 in this paper. It can be seen that the resulting relative motion is bounded. This validates the proposed new methods.

Fig. 1

Histories of relative motion trajectories using Method 1 $(e=0.0{1},\, \delta e=0.0{1})$

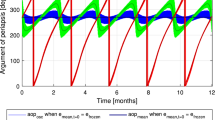
To compare the new $\hbox {J}_{2}$-invariant methods and the methods introduced by Schaub and Alfriend (2001), some extended simulations are conducted. The results of 10 groups’ simulations with 20 orbital periods are recorded and compared with each other. The results are shown in Figs. 2, 3, and 4. Here, in each figure, the drifts in a single direction are presented. The horizontal axis represents the eccentricity of the leader satellite. The vertical axis denotes the drifts of radial, along-track, and cross-track relative motion.

Fig. 2

Drifts of $x$ direction in 20 orbital periods when applying the different $\hbox {J}_{2}$-invariant conditions

Fig. 3

Drifts of $y$ direction in 20 orbital periods when applying the different $\hbox {J}_{2}$-invariant conditions

From Figs. 2 and 4 it can be seen that the drifts in the radial and cross-track relative motion using the three $\hbox {J}_{2}$-invariant methods are nearly the same. As for the drifts in the along-track relative motion (Fig. 3), the drifts of Methods 1 and 2 are always less than the method of Schaub and Alfriend (2001). These results demonstrate that the two improved methods for mitigating $\hbox {J}_{2}$ effects for relative motion are definitely effective. From the simulation results it can be seen that Method 2 yields the least drift compared to the other two methods. But in fact the difference between Methods 1 and 2 is very slight. Therefore, either of them can be used for future cluster flying missions to mitigate $\hbox {J}_{2}$.

Fig. 4

Drifts of $z$ direction in 20 orbital periods when applying the different $\hbox {J}_{2}$-invariant conditions

5 Geometric character of strict $\hbox {J}_{2}$-invariant relative motion

Although the strict $\hbox {J}_{2}$-invariant conditions are too rigid, they support the existence of a significant number of situations in which periodic relative motion is achieved. Because of the periodicity of the strict $\hbox {J}_{2}$-invariant relative orbits, the relevant geometric shape will exhibit some interesting characteristics, such as self-intersection. Here, a curve is defined as self-intersected if it passes through a point no less than twice, and this point is accordingly termed the self-intersection point of the curve (Jiang et al. 2008). In the next section, the self-intersection conditions for strict $\hbox {J}_{2}$-invariant relative orbits are analyzed.

5.1 Criterion of self-intersection

Jiang et al. (2008) gave the criterion of self-intersection when the relative motion is periodic and each satellite is in a Keplerian orbit. When satellites are not affected by perturbations, the periodic relative motion is achieved if and only if ${\delta a} = 0$. However, when $\hbox {J}_{2}$ effects are considered, the periodicity will further require that ${\delta e} = 0$ and ${\delta i} = 0$, which corresponds to the strict $\hbox {J}_{2}$-invariant conditions. Hence, the self-intersection conditions can be determined using the same criterion developed in Jiang et al. (2008). However, because the $\hbox {J}_{2}$-invariant relative motion is a special periodic relative motion, the self-intersection conditions are worth exploring more thoroughly.

When imposing the strict $\hbox {J}_{2}$-invariant conditions, the relative motion equations will become

$$\begin{aligned} \left\{ {\begin{array}{l} x=\frac{2ec_2 s}{s^{2}+1}, \\ y=\left( {1-e} \right) c_2 +c_3 +\frac{2ec_2 }{s^{2}+1}+\frac{-2ec_3 }{\left( {1-e} \right) s^{2}+1+e}, \\ z=-c_5 +\frac{2\left( {c_4 s+c_5 } \right) }{\left( {1-e} \right) s^{2}+1+e} ,\\ \end{array}} \right. \end{aligned}$$

(74)

where the coefficients $c_{2} \sim c_{5 }$ have the same expressions as mentioned in Sect. 2.

According to the definition of self-intersection, if the relative motion trajectory expressed by a set of single-parameter equations self-intersects, there must be at least two different values of the parameter mapping the same set of coordinates. Therefore, if space self-intersection occurs, there must be two different values of $s$, say $s_{1 }$ and $s_{2}$, satisfying

$$\begin{aligned} \left\{ {\begin{array}{l} x\left( {s_1 } \right) =x\left( {s_2 } \right) , \\ y\left( {s_1 } \right) =y\left( {s_2 } \right) , \\ z\left( {s_1 } \right) =z\left( {s_2 } \right) . \\ \end{array}} \right. \end{aligned}$$

(75)

By solving the above three equations together, it is obtained that the space self-intersection can be occurred only in the following conditions:

$$\begin{aligned} c_2=\frac{\left( 1-e\right) \left[ 1+2\left( \frac{c_{4}^{2}e^{2}}{c_{5}^{2}{\left( 1-e\right) }^{2}}-1\right) \right] }{\left( 1+e^{2}\right) +2\left( 1-e^{2}\right) \left( \frac{c_{4}^{2}e^{2}}{c_{5}^{2}{\left( 1-e\right) }^{2}}-1\right) } c_{3}\cup \frac{c_{4}^{2}e^{2}}{c_{5}^{2}{\left( 1-e\right) }^{2}} >1. \end{aligned}$$

(76)

It is also noticed that ${c_{4}^{2}e^{2}}\big /\left[ {c_{5}^{2}{\left( 1-e\right) }^{2}}\right] =e^{2}\tan \omega ^{2}$ by the definition of the strict $\hbox {J}_{2}$-invariant orbits. This means, if $e^{2}\tan \omega ^{2}\le 1$, there will not be any possibility to have a spatial self-intersection point. This condition strongly depends on the parameters of the leader satellite. Therefore, the interest of this paper will focus on the projected self-intersection. The only case that will be discussed in this paper is the self-intersection in the $y$–$z$ projected plane. The self-intersection phenomena in other two projected planes, i.e. $x$–$y$ projected plane and $x$–$z$ projected plane can be studied using the similar methods here.

To find the corresponding conditions, let $y(s_{1}) = y(s_{2})$ and $z(s_{1}) = z(s_{2})$ to obtain

$$\begin{aligned}&\left[ {c_2 \left( {1-e^{2}} \right) -c_3 \left( {1-e} \right) } \right] \left( {s_1^2 +s_2^2 } \right) +\left[ c_2 \left( {1-e} \right) ^{2}\right. \nonumber \\&\quad \left. -\,c_3 \left( {1-e} \right) \right] s_1^2 s_2^2 +c_2 \left( {1+e} \right) ^{2}-c_3 \left( {1-e} \right) =0, \end{aligned}$$

(77)

$$\begin{aligned}&c_5 \left( {1-e} \right) \left( {s_1 +s_2 } \right) +c_4 \left( {1-e} \right) s_1 s_2 -c_4 \left( {1+e} \right) =0. \end{aligned}$$

(78)

Using the same technique as in Jiang et al. (2008), define two new variables,

$$\begin{aligned} m=s_1 +s_2 ,\quad n=s_1 \cdot s_2. \end{aligned}$$

(79)

Then the first condition for the existence of self-intersection is

$$\begin{aligned} m^{2}-4n>0. \end{aligned}$$

(80)

Substituting Eq. (79) into Eq. (77) results in

$$\begin{aligned} n_{1,2}&= \frac{-q\pm \sqrt{q^{2}-4pg}}{2p}, \end{aligned}$$

(81)

$$\begin{aligned} m_{1,2}&= \frac{c_4 }{c_5 }\left( {-n_{1,2} +\frac{1+e}{1-e}} \right) , \end{aligned}$$

(82)

where

$$\begin{aligned} p&= \left\{ {\left[ {c_2 \left( {1-e^{2}} \right) -c_3 \left( {1-e} \right) } \right] \left( {\frac{c_4 }{c_5 }} \right) ^{2}+\left[ {c_2 \left( {1-e} \right) ^{2}-c_3 \left( {1-e} \right) } \right] } \right\} , \end{aligned}$$

(83)

$$\begin{aligned} q&= -2\left[ {c_2 \left( {1-e^{2}} \right) -c_3 \left( {1-e} \right) } \right] \left[ {\left( {\frac{c_4 }{c_5 }} \right) ^{2}\frac{1+e}{1-e}+1} \right] , \end{aligned}$$

(84)

$$\begin{aligned} g&= \left[ {c_2 \left( {1-e^{2}} \right) -c_3 \left( {1-e} \right) } \right] \left( {\frac{1+e}{1-e}\cdot \frac{c_4 }{c_5 }} \right) ^{2}+\left[ {c_2 \left( {1+e} \right) ^{2}-c_3 \left( {1-e} \right) } \right] . \end{aligned}$$

(85)

It is clear that the existence of real $m$ and $n$ is determined by the following condition:

$$\begin{aligned} q^{2}-4pg\ge 0. \end{aligned}$$

(86)

It has been found that the number of self-intersections on the $y$–$z$ projected plane, namely, $l$, can be represented by

$$\begin{aligned} l=\left\{ {\begin{array}{l} 0:\quad \Delta _1 <0\cup \left( {\Delta _1 \ge 0\cap \Delta _2 \le 0\cap \Delta _3 \le 0} \right) , \\ 1:\quad \left( {\Delta _1 =0\cap \Delta _2 =\Delta _3 >0} \right) \cup \left( {\Delta _1 >0\cap \Delta _2 >0\cap \Delta _3 \le 0} \right) \\ \quad \quad \quad \cup \left( {\Delta _1 >0\cap \Delta _2 \le 0\cap \Delta _3 >0} \right) , \\ 2:\quad \Delta _1 >0\cap \Delta _2 >0\cap \Delta _3 >0, \\ \end{array}} \right. \end{aligned}$$

(87)

where

$$\begin{aligned} \Delta _1&= q^{2}-4pg, \end{aligned}$$

(88)

$$\begin{aligned} \Delta _2&= m_1^2 -4n_1, \end{aligned}$$

(89)

$$\begin{aligned} \Delta _3&= m_2^2 -4n_2. \end{aligned}$$

(90)

To explore the details of the preceding criterion represented by Eq. (87), use the notation

$$\begin{aligned} k_1 =\frac{c_2 }{c_3 },\quad k_2 =\frac{c_4 }{c_5 }. \end{aligned}$$

(91)

Then $q^{2} - 4{pg} = 0$ is equal to the following conditions:

$$\begin{aligned} k_1 =\frac{k_2^2 }{k_2^2 \left( {1+e} \right) +1-e} \end{aligned}$$

(92)

and it is easy to determine that

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta _1 >0:\quad k_1 >k_1^0, \\ \Delta _1 \le 0:\quad k_1 \le k_1^0, \\ \end{array}} \right. \end{aligned}$$

(93)

where $k_{1}^{0}$ is expressed as

$$\begin{aligned} k_1^0 =\frac{k_2^2 }{k_2^2 \left( {1+e} \right) +1-e}. \end{aligned}$$

(94)

According to the proof of the sign criterion of ${\Delta }_{3 }$ (see next section for details), we have

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta _3 >0:\quad \left| {k_{2} } \right| >k_2^0 \cap k_1^0 <k_1 <k_1^{*}, \\ \Delta _3 \le 0:\quad \left| {k_{2} } \right| \le k_2^0 \cup \left( {\left| {k_{2} } \right| >k_2^0 \cap k_1^{*} \ge k_1 } \right) , \\ \end{array}} \right. \end{aligned}$$

(95)

where $k_{1}^{*}$ is expressed by Eq. (109) and $k_{2}^{0}$ takes the following form:

$$\begin{aligned} k_2^0 =\frac{{1}-e}{e}. \end{aligned}$$

(96)

Thus far, the self-intersection conditions have been obtained, which are represented by Eq. (87), together with Eqs. (93) and (95).

5.2 Analysis of sign criterion of ${\Delta }_{3}$

In this section, the sign criterion of ${\Delta }_{3 }$ will be analyzed in detail. To this end, the expression of ${\Delta }_{3}$ is rewritten as

$$\begin{aligned} \Delta _3 =k_2^2 \left( {-\frac{1}{2}x+\frac{1+e}{1-e}}, \right) ^{2}-2x \end{aligned}$$

(97)

where

$$\begin{aligned} x=\frac{2\left( {k_2^2 \left( {1+e} \right) +1-e} \right) \left( {k_1 \left( {1+e} \right) -1} \right) -4e\sqrt{k_2^2 \left( {k_1 \left( {1+e} \right) -1} \right) +k_1 \left( {1-e} \right) }}{k_2^2 \left( {k_1 \left( {1-e^{2}} \right) -\left( {1-e} \right) } \right) +k_1 \left( {1-e} \right) ^{2}-\left( {1-e} \right) }. \end{aligned}$$

(98)

Two roots of ${\Delta }_{3} = 0$ can be expressed as

$$\begin{aligned} x_1^{*}&= 2\left( {\frac{2}{k_2^2 }+\frac{1+e}{1-e}} \right) -2\sqrt{\left( {\frac{2}{k_2^2 }+\frac{1+e}{1-e}} \right) ^{2}-\left( {\frac{1+e}{1-e}} \right) ^{2}} \end{aligned}$$

(99)

$$\begin{aligned} x_2^{*}&= 2\left( {\frac{2}{k_2^2 }+\frac{1+e}{1-e}} \right) +2\sqrt{\left( {\frac{2}{k_2^2 }+\frac{1+e}{1-e}} \right) ^{2}-\left( {\frac{1+e}{1-e}} \right) ^{2}}. \end{aligned}$$

(100)

It can be seen that ${\Delta }_{3 }$ can be formed by subtracting the linear function $y_2 =\frac{2}{k_2^2 }x$ from the quadratic function $y_1 =\left( {-\frac{1}{2}x+\frac{1+e}{1-e}} \right) ^{2}$ and further multiplying by the coefficient of $k_{2}^{2}$. Usually, these two curves have a changing trend with the variable $x$ like those in Fig. 5. Thus, if $x$ is always in the set of $(x_{1}^{*},x_{2}^{*})$, then $y_{1 }$ will be less than $y_{2 }$, and consequently, ${\Delta }_{3} < 0$ holds. If not, there is ${\Delta }_{3} > 0$. The proof will be completed in two steps.

Fig. 5

Changing trends of $y_{1 }$ and $y_{2 }$ with respect to the variable $x(k_{2} = 2, e = 0.05)$

Step 1 Prove that for any value of $k_{2}$ there is $x < x_{2}^{*}$.

Let $z_{2}(k_{1}) = x - x_{2}^{*}$; then from the expression of $x$ it is known that

$$\begin{aligned} z_2 \left( \infty \right) =x\left( {k_1 =\infty } \right) -x_2^{*} =-\frac{4\left( {\sqrt{\frac{k_2^2 \left( {1+e} \right) +\left( {1-e} \right) }{\left( {1-e} \right) }}+1} \right) }{k_2^2 }<0. \end{aligned}$$

(101)

Taking the derivative of $z_{2 }$ with respect to $k_{1 }$ leads to

$$\begin{aligned} \frac{\partial z_2 }{\partial k_1 }=\frac{e\left( {k_2^2 \left( {1+e} \right) +1-e} \right) \left( {\sqrt{k_2^2 \left( {k_1 \left( {1+e} \right) -1} \right) +k_1 \left( {1-e} \right) }-1} \right) ^{2}}{\left( {1-e} \right) \left( {k_2^2 \left( {k_1 \left( {1+e} \right) -1} \right) +k_1 \left( {1-e} \right) -1} \right) ^{2}\sqrt{k_2^2 \left( {k_1 \left( {1+e} \right) -1} \right) +k_1 \left( {1-e} \right) }}. \end{aligned}$$

(102)

Since it is known that $k_1 >\frac{k_2^2 }{k_2^2 \left( {1+e} \right) +1-e}$ when ${\Delta }_{1} > 0$, it can be determined that the quantity under the square root sign is positive, and hence, the preceding equation is well defined. Furthermore, because $k_{2}^{2}(1 + e) + 1 - e > 0$, the following results are obtained:

$$\begin{aligned} \frac{\partial z_2 }{\partial k_1 }>0. \end{aligned}$$

(103)

Then, from Eqs. (101) and (103), for all possible values of $k_{1 }$ and $k_{2}$, there are $z_{2} < 0$ and $x < x_{2}^{*}$.

Step 2 Prove that for any value of $k_{2}$ there is $x_{1}^{*} < x$.

Let $z_{1}(k_{1}) = x - x_{1}^{*}$, and taking the derivative of $z_{1 }$ with respect to $k_{1 }$ results in

$$\begin{aligned} \frac{\partial z_1 }{\partial k_1 }=\frac{\partial z_2. }{\partial k_1 }>0 \end{aligned}$$

(104)

It is necessary to first check the signs of the function $z_{1}(k_{1})$ at the two ends of the variable $k_{1}$. At $k_{1} = \infty$, we have

$$\begin{aligned} z_1 \left( \infty \right) =x\left( {k_1 =\infty } \right) -x_1^{*} =\frac{4\left( {\sqrt{\frac{\left( {1+e} \right) }{\left( {1-e} \right) }k_2^2 +1}-1} \right) }{k_2^2 }>0. \end{aligned}$$

(105)

When $k_1 =k_{1}^{0}$, we have

$$\begin{aligned} z_1 \left( {k_{1}^{0} } \right)&= x\left( {k_1 =k_{1}^{0} } \right) -x_1^{*} =-\frac{{2}e}{k_{2}^{2} \left( {{1}-e^{{2}}} \right) }\left( {\sqrt{k_2^2 \left( {1+e} \right) +\left( {1-e} \right) }-\sqrt{{1}-\hbox {e}}} \right) \nonumber \\&\quad \left( {\sqrt{k_2^2 \left( {1+e} \right) +\left( {1-e} \right) }-\frac{\sqrt{{1}-\hbox {e}}}{e}} \right) , \end{aligned}$$

(106)

where the expression of $k_{1}^{0}$ is represented by Eq. (94).

It may be concluded that

$$\begin{aligned} \left\{ {\begin{array}{l} z_1 \left( {k_{1}^{0} } \right) \ge \hbox {0:}\quad \left| {k_{2} } \right| \le k_{2}^{0}, \\ z_1 \left( {k_{1}^{0} } \right) <\hbox {0:}\quad \left| {k_{2} } \right| >k_{2}^{0}, \\ \end{array}} \right. \end{aligned}$$

(107)

where the expression of $k_{2}^{0}$ is represented by Eq. (96).

When $z_1 \left( {k_{1}^{0} } \right) \ge {0}$ or, equivalently, $\left| {k_{2} } \right| \le k_{2}^{0}$, then because $\frac{\partial z_1 }{\partial k_1 }>{0}$, it can be obtained that for any values satisfying $k_1 >k_{1}^{0}$ there will be $z_1 \left( {k_{1} } \right) >{0}$. Therefore, if $\left| {k_{2} } \right| \le k_{2}^{0}$, then there is $x > x_{1}^{*}$.

When $z_1 \left( {k_{1}^{0} } \right) <{0}$ or, equivalently, $\left| {k_{2} } \right| >k_{2}^{0}$, then, because $z_1 \left( \infty \right) >{0}$ and $\frac{\partial z_1 }{\partial k_1 }>{0}$, there must be a value $k_{1}^{*}$ satisfying

$$\begin{aligned} \left\{ {\begin{array}{l} z_1 \left( {k_1 } \right) \ge 0:\quad \forall k_1 \ge k_{1}^{*} ,\\ z_1 \left( {k_1 } \right) <0:\quad \forall k_1 <k_{1}^{*} .\\ \end{array}} \right. \end{aligned}$$

(108)

Imposing $z_1 \left( {k_{1}^{*} } \right) ={0}$ allows us to obtain

$$\begin{aligned}&k_{1}^{*} =\frac{{2}\sqrt{{1}\!-\!e}\sqrt{k_{2}^{2} \left( {{1}+e} \right) +\left( {{1}\!-\!e} \right) }\left( {k_{2}^{2} +\left( {{1}\!-\!e} \right) } \right) \!-\!k_{2}^{4} \!-\!k_{2}^{2} \left( {{3}+e} \right) \left( {{1}\!-\!e} \right) \!-\!{2}\left( {{1}\!-\!e} \right) ^{{2}}}{\!-\!\left( {{1}\!-\!e} \right) \left( {k_{2}^{2} \left( {{1+}e} \right) +\left( {{1}\!-\!e} \right) } \right) \left( {\sqrt{k_{2}^{2} \left( {{1}+e} \right) +\left( {{1}\!-\!e} \right) }\!-\!\sqrt{{1}\!-\!e}} \right) ^{{2}}},\nonumber \\ \end{aligned}$$

(109)

$$\begin{aligned}&k_{1}^{*} \!-\!k_{1}^{0}\nonumber \\&\quad =\frac{\!-\!{2}e\sqrt{{1}\!-\!e}\sqrt{k_{2}^{2} \left( {{1}+e} \right) +\left( {{1}\!-\!e} \right) }\left( {k_{2}^{2} \!-\!\frac{{1}\!-\!e}{e}} \right) \!-\!e^{{2}}k_{2}^{4} \!-\!k_{2}^{2} \left( {{1}+{3}e} \right) \left( {{1}\!-\!e} \right) \!-\!{2}\left( {{1}\!-\!e} \right) ^{{2}}}{\!-\!\left( {{1}\!-\!e} \right) \left( {k_{2}^{2} \left( {{1\!+\!}e} \right) +\left( {{1}\!-\!e} \right) } \right) \left( {\sqrt{k_{2}^{2} \left( {{1}\!+\!e} \right) +\left( {{1}\!-\!e} \right) }\!-\!\sqrt{{1}\!-\!e}} \right) ^{{2}}}\!\ge \! {0}.\nonumber \\ \end{aligned}$$

(110)

Therefore, when $\left| {k_{2} } \right| >\frac{{1}-e}{e}$, if $k_{1}^{0} \le k_{1} < k_{1}^{*}$, then $z_{1}(k_{1}) < 0$ or, equivalently, $x < x_{1}^{*}$. Otherwise, if $k_{1}^{*} \le k_{1}$, then $z_{1}(k_{1}) > 0$ and, consequently, $x > x_{1}^{*}$.

Summarizing the arguments in Steps 1 and 2, the proof is complete.

5.3 Examples

It can be found that the self-intersection number depends on the relation between $k_{1}$ and $k_{2}$. The relation is usually affected by the value of the eccentricity. Assume that the eccentricity is 0.05. The following example will demonstrate how to find the self-intersection number by checking the relation between $k_{1}$ and $k_{2}$. According to Eq. (93), the sign of ${\Delta }_{1}$ can be determined first. If ${\Delta }_{1} < 0$, then it can be affirmed that there is no self-intersection in this set of orbital elements. If ${\Delta }_{1} \ge 0$, then one should use Eqs. (89) and (95) to further check the sign of ${\Delta }_{2 }$ and ${\Delta }_{3}$, respectively. As for the case where $e=0.05$, the relevant results are illustrated in Figs. 6 and 7. In Fig. 6, it can be seen that the possible self-intersection points are located in the right part of the curve of ${\Delta }_{1} = 0$. However, the one self-intersection point is very sparse. Only in a narrow band close to $k_{1} = 1$ is the one self-intersection point up. The conditions for two self-intersection points are more rigorous than that of one self-intersection point, which is shown in the band between the two curves of $k_{10 }$ and $k_{1}^{*}$ in Fig. 7.

Fig. 6

Conditions of zero or one self-intersection point

Fig. 7

Conditions of two self-intersection points

Three cases representing zero, one, and two self-intersection points with an eccentricity of 0.05 are shown below. The conditions and corresponding results are reported in Table 1. According to the requirements for $k_{1 }$ and $k_{2 }$ in Table 1, the orbital elements are selected for two satellites to generate the relative motion numerically. Then the resulting projected curves in the $y$–$z$ plane are shown in Fig. 8. It is clear that the zero, one, and two self-intersection points are consistent with the predictions from the criteria.

Table 1 Different cases of self-intersection for $\hbox {J}_{2}$-invariant periodic relative orbits

Fig. 8

Numerical simulation results of self-intersection for $\hbox {J}_{2}$-invariant periodic relative orbit. a Numerical results under conditions of Case 1. b Numerical results under conditions of Case 2. c Numerical results under conditions of Case 3

6 Optimal single-impulsive maneuvers for $\hbox {J}_{2}$-invariant relative motion

The preceding sections make clear that to achieve $\hbox {J}_{2}$-invariant relative motion, the three differential orbital elements, namely, ${\delta a}$, ${\delta e}$, and ${\delta i}$, should satisfy some constraints. When real differential orbital elements violate these constraints, the necessary control should be conducted to modify the current states of the follower. In this section, a set of analytic impulsive maneuvers for $\hbox {J}_{2}$-invariant relative motion will be derived.

6.1 Single-impulsive maneuvers for given differential orbital elements

It is known that for a given orbital element’s differences, the desired impulsive velocity vector $\Delta {{{\mathbf {v}}}}=\left[ {\Delta v_x ,\Delta v_y ,\Delta v_z } \right] ^{T}$ can be determined using the well-known Gaussian form of planetary motion equations. Here the control goal is simply to achieve bounded relative motion, not a specific formation. Hence, we only consider the possible changes in the semimajor axis, eccentricity, and inclination; the three functions that are used here are

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta a=\frac{2a^{2}}{h}\left( {e\sin f\Delta v_x +\frac{p}{r}\Delta v_y } \right) , \\ \Delta e=\frac{1}{h}\left\{ {p\sin f\Delta v_x +\left[ {\left( {p+r} \right) \cos f+re} \right] \Delta v_y } \right\} , \\ \Delta i=\frac{r\cos \left( {f+\omega } \right) }{h}\Delta v_z, \\ \end{array}} \right. \end{aligned}$$

(111)

where ${\Delta a}$, ${\Delta e}$, and ${\Delta i}$ are the expected changes in the orbital element differences for the semimajor axis, eccentricity, and inclination, respectively. These terms can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta a=\delta a^{+}-\delta a^{-} ,\\ \Delta e=\delta e^{+}-\delta e^{-}, \\ \Delta i=\delta i^{+}-\delta i^{-} ,\\ \end{array}} \right. \end{aligned}$$

(112)

where the superscripts $+$ and $-$ respectively represent the quantity that is expressed after and before the maneuver.

By some manipulation, the relevant expected velocity vector can be obtained:

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta v_x =-\frac{h}{2p}\frac{1+e-\left( {1-e} \right) s^{4}}{s\left( {1+s^{2}} \right) }\frac{\Delta a}{a}-\frac{h}{2p\left( {1-e^{2}} \right) }\frac{\left[ {1+e+\left( {1-e} \right) s^{2}} \right] ^{2}}{s\left( {1+s^{2}} \right) }\Delta e, \\ \Delta v_y =-\frac{h}{2p}\frac{1+e+\left( {1-e} \right) s^{2}}{1+s^{2}}\frac{\Delta a}{a}+\frac{eh}{p\left( {1-e^{2}} \right) }\frac{1+e+\left( {1-e} \right) s^{2}}{1+s^{2}}\Delta e, \\ \Delta v_z =-\frac{h}{p}\frac{1+e+\left( {1-e} \right) s^{2}}{\cos \omega \cdot s^{2}+2\sin \omega \cdot s-\cos \omega }\Delta i, \\ \end{array}} \right. \end{aligned}$$

(113)

where the variable $f$ has been replaced by the variable $s$ through the relation of Eq. (10). Note that when $s$ tends to infinity, the velocity increment requirement in the radial direction will be infinite, which violates the physical fundamentals. Hence, to avoid this difficulty, the control imposing time should not be selected when the mean anomaly is $180^{\circ }$, which corresponds to $s = \pm \infty$.

6.2 Optimal single-impulsive maneuvers for $\hbox {J}_{2}$-invariant relative motion

When using the strict conditions for $\hbox {J}_{2}$ invariant, the required control can be obtained by substituting Eqs. (112) and (114) into the aforementioned velocity vector expression of Eq. (113):

$$\begin{aligned} \delta a^{+}={0,}\quad \delta e^{+}={0},\quad \delta i^{+}={0}. \end{aligned}$$

(114)

When using the improved conditions for achieving the $\hbox {J}_{2}$-invariant relative motion, the expected orbital elements should satisfy the following constraints:

$$\begin{aligned} \left\{ {\begin{array}{l} \delta a^{+}=f_{ae} \left( {a,e,i} \right) \cdot \delta e^{+}, \\ \delta i^{+}=f_{ie} \left( {a,e,i} \right) \cdot \delta e^{+}, \\ \end{array}} \right. \end{aligned}$$

(115)

where $f_{ae}(a, e, i)$ and $f_{ie}(a, e, i)$ are described by Eqs. (32)–(34).

Then the resulting expected changes in the differential orbital elements are

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta a=f_{ae} \left( {a,e,i} \right) \cdot \delta e^{+}-\delta a^{-}, \\ \Delta e=\delta e^{+}-\delta e^{-}, \\ \Delta i=f_{ie} \left( {a,e,i} \right) \cdot \delta e^{+}-\delta i^{-}. \\ \end{array}} \right. \end{aligned}$$

(116)

Substituting these results into Eq. (106) yields

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta v_x =m_{11} \delta e^{+}+m_{12}, \\ \Delta v_y =m_{21} \delta e^{+}+m_{22},\\ \Delta v_z =m_{31} \delta e^{+}+m_{32}, \\ \end{array}} \right. \end{aligned}$$

(117)

where

$$\begin{aligned} \left\{ {\begin{array}{l} m_{11} =-\frac{h}{2p}\frac{1+e-\left( {1-e} \right) s^{4}}{s\left( {1+s^{2}} \right) }\frac{f_{ae} \left( {a,e,i} \right) }{a}-\frac{h}{2p\left( {1-e^{2}} \right) }\frac{\left[ {1+e+\left( {1-e} \right) s^{2}} \right] ^{2}}{s\left( {1+s^{2}} \right) }, \\ m_{12} =\frac{h}{2p}\frac{1+e-\left( {1-e} \right) s^{4}}{s\left( {1+s^{2}} \right) }\frac{\delta a^{-}}{a}+\frac{h}{2p\left( {1-e^{2}} \right) }\frac{\left[ {1+e+\left( {1-e} \right) s^{2}} \right] ^{2}}{s\left( {1+s^{2}} \right) }\delta e^{-}, \\ m_{21} =-\frac{h}{2p}\frac{1+e+\left( {1-e} \right) s^{2}}{1+s^{2}}\frac{f_{ae} \left( {a,e,i} \right) }{a}+\frac{eh}{p\left( {1-e^{2}} \right) }\frac{1+e+\left( {1-e} \right) s^{2}}{1+s^{2}}, \\ m_{22} =\frac{h}{2p}\frac{1+e+\left( {1-e} \right) s^{2}}{1+s^{2}}\frac{\delta a^{-}}{a}-\frac{eh}{p\left( {1-e^{2}} \right) }\frac{1+e+\left( {1-e} \right) s^{2}}{1+s^{2}}\delta e^{-}, \\ m_{31} =-\frac{h}{p}\frac{1+e+\left( {1-e} \right) s^{2}}{\cos \omega \cdot s^{2}+2\sin \omega \cdot s-\cos \omega }f_{ie} \left( {a,e,i} \right) , \\ m_{32} =\frac{h}{p}\frac{1+e+\left( {1-e} \right) s^{2}}{\cos \omega \cdot s^{2}+2\sin \omega \cdot s-\cos \omega }\delta i^{-}. \\ \end{array}} \right. \end{aligned}$$

(118)

To find the velocity vector with the smallest quantity or, equivalently, we calculate

$$\begin{aligned} \mathop {\min }\limits _{\delta e^{+}} \left\| {\Delta {{{\mathbf {v}}}}} \right\| . \end{aligned}$$

(119)

Taking the partial derivative of $\left\| {\Delta {{{\mathbf {v}}}}} \right\|$ with respect to ${\delta e}^{-}$ leads to

$$\begin{aligned} \frac{\partial \left\| {\Delta {{{\mathbf {v}}}}} \right\| }{\partial \delta e^{+}}=\frac{\left( {m_{11} \delta e^{+}+m_{12} } \right) m_{11} +\left( {m_{21} \delta e^{+}+m_{22} } \right) m_{21} +\left( {m_{31} \delta e^{+}+m_{32} } \right) m_{31} }{\left\| {\Delta {{{\mathbf {v}}}}} \right\| }, \end{aligned}$$

(120)

and nullifying the derivative allows us to obtain

$$\begin{aligned} \delta e^{+}=-\frac{m_{11} m_{12} +m_{21} m_{22} +m_{31} m_{32} }{m_{11}^2 +m_{21}^2 +m_{31}^2 }. \end{aligned}$$

(121)

The preceding expression for ${\delta e}^{+}$ is the condition for finding the optimal velocity vector. But note that the constraint $0 \le e + {\delta e}^{+} \le 1$ must be satisfied. Once ${\delta e}^{+}$ is obtained, then the relevant ${\delta a}^{+}$ and ${\delta i}^{+}$ can be further calculated using Eq. (108). Finally, the optimal single-impulsive maneuvers can be built up by substituting these quantities into Eq. (106) or (112). It is worth noting that the preceding optimal single-impulsive maneuvers may be further optimized by searching for the proper maneuver time or, equivalently, the variable $s$. If this is done, then a numerical optimal algorithm, such as a genetic algorithm (Goldberg 1989; Renner and Ekart 2003), can be used.

6.3 Examples

Assume that the leader and follower are initially in the states expressed by the orbital elements and differential orbital elements as

$$\begin{aligned} a&= 8378\,\hbox {km},\, \quad e = 0.01,\, i = 48^{\circ }, \,{\Omega } = 30^{\circ },\, {\omega } = 60^{\circ },\, M_{0} = 40^{\circ },\\ {\delta } a^{-}&= 1400\,\hbox {m}, {\delta } e^{-} = 0.01, {\delta } i^{-} = 0.01^{\circ }, \,{\delta \Omega }^{-} = 0.05^{\circ },\,{\delta \omega }^{-} = 0.01^{\circ }, \,{\delta } M_{0}^{-} = - 0.02^{\circ }. \end{aligned}$$

Using Eq. (116) and Method 2 with a genetic algorithm, the optimal control imposing time is $M=121^{\circ }$, and the expected differential eccentricity is

$$\begin{aligned} \delta e^{+}=0.0102. \end{aligned}$$

Then, according to Eq. (117), the impulsive velocity vector in the inertial frame should be

$$\begin{aligned} \Delta {{{\mathbf {v}}}}=\left[ {\begin{array}{l} -0.0001 \\ 0.6135 \\ 2.6951 \\ \end{array}} \right] \hbox {m}/\hbox {s}. \end{aligned}$$

The evolution of the relative distance between the two satellites before the maneuver is depicted in the left panel of Fig. 9. It can be clearly seen that the relative distance is divergent with time. The relative distance after the maneuver is shown in the right panel of Fig. 9. It is found that the relative distance for 100 days after the maneuver remains bounded between 80 and 180 km. This demonstrates the effectiveness of the control method for $\hbox {J}_{2}$-invariant relative motion.

Fig. 9

Relative distance histories: left no maneuver is performed; right after impulsive maneuvers

7 Conclusion

Through an analysis of the relative motion equation and the bounds expression, two new sets of improved initial conditions (Methods 1 and 2) for bounded relative motion under $\hbox {J}_{2}$ perturbation are obtained. In these two methods, different correction factors for the original $\hbox {J}_{2}$-invariant constraints are designed. Method 1 is obtained by minimizing the possible maximum drift in along-track motion. However, Method 2 is designed by nullifying the maximum bounds’ rate in the along-track motion. These two new methods are compared to those proposed by other researchers in mitigating the $\hbox {J}_{2}$ effects for satellite relative motion using numerical simulations. The simulation results revealed that Method 2 performed better than the others. The self-intersection phenomenon of strict $\hbox {J}_{2}$-invariant relative motion is also discussed. The conditions of zero, one, and two self-intersection points are derived. To achieve $\hbox {J}_{2}$ invariant, the approach of optimal single impulsive maneuvers is also derived. Simulations of satellite relative motion in 100 days are performed. The results show that, compared to the uncorrected initial conditions, the initial conditions after the impulsive maneuvers can lead to a bounded relative motion under $\hbox {J}_{2}$ perturbation. In the future, more perturbations, such as atmospheric drag, should be considered to obtain the general bounded relative motion. Furthermore, when the validity range of the bounds theory is expanded in the future, the $\hbox {J}_{2}$-invariant conditions may be needed to make more improvements.

Appendix: Orbital elements’ variation under \(\hbox {J}_{2}\) perturbation

The variations of the mean elements under a $\hbox {J}_{2}$ perturbation are as follows:

$$\begin{aligned} \frac{\partial \dot{\bar{{\Omega }}}}{\partial a}&= \frac{{7}}{{2}}\gamma a^{-\frac{{9}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{2}}\cos i, \end{aligned}$$

(122)

$$\begin{aligned} \frac{\partial \dot{\bar{{\Omega }}}}{\partial e}&= -{4}e\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{3}}\cos i, \end{aligned}$$

(123)

$$\begin{aligned} \frac{\partial \dot{\bar{{\Omega }}}}{\partial i}&= \gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{2}}\sin i, \end{aligned}$$

(124)

$$\begin{aligned} \frac{\partial \dot{\bar{{\omega }}}}{\partial a}&= -\frac{{7}}{{2}}\gamma a^{-\frac{{9}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{2}}\left( {{2}-\frac{{5}}{{2}}\sin ^{{2}}i} \right) ,\end{aligned}$$

(125)

$$\begin{aligned} \frac{\partial \dot{\bar{{\omega }}}}{\partial e}&= {4}e\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{3}}\left( {{2}-\frac{{5}}{{2}}\sin ^{{2}}i} \right) , \end{aligned}$$

(126)

$$\begin{aligned} \frac{\partial \dot{\bar{{\omega }}}}{\partial i}&= -{5}\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-{2}}\sin i\cos i, \end{aligned}$$

(127)

$$\begin{aligned} \frac{\partial \dot{\bar{{M}}}}{\partial a}&= -\frac{{7}}{{2}}\gamma a^{-\frac{{9}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-\frac{{3}}{{2}}}\left( {{1}-\frac{{3}}{{2}}\sin ^{{2}}i} \right) -\frac{{3}}{{2}}\sqrt{\mu }a^{-\frac{{5}}{{2}}}, \end{aligned}$$

(128)

$$\begin{aligned} \frac{\partial \dot{\bar{{M}}}}{\partial e}&= {3}e\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-\frac{{5}}{{2}}}\left( {{1}-\frac{{3}}{{2}}\sin ^{{2}}i} \right) ,\end{aligned}$$

(129)

$$\begin{aligned} \frac{\partial \dot{\bar{{M}}}}{\partial i}&= -{3}\gamma a^{-\frac{{7}}{{2}}}\left( {{1}-e^{{2}}} \right) ^{-\frac{{3}}{{2}}}\sin i\cos i. \end{aligned}$$

(130)