Lattice-preserving Flower Constellations under $J_2$ perturbations

Abstract

2D Lattice Flower Constellations (2D-LFCs) are stable in the Keplerian model. This means that a flower constellation maintains its structure (the lattice) at any instant of time. However, this is not necessarily true when the $J_2$ harmonic is included in the gravitational potential of the Earth. This paper deals with the new theory of Lattice-preserving Flower Constellations, which shows how 2D-LFC can be designed in such a way that the relative displacement of the orbital parameters of its satellites is invariant even under the presence of the $J_2$ effect. This is achieved following two different procedures: the first consists of the modification of the semi-major axis of all the satellites in a 2D-LFC slightly to control their orbital period, and the second consists of the modification of the values for the eccentricity and inclination, so that the perturbations result in motion that still preserves the lattice of the flower constellation. The proposed theory of Lattice-preserving Flower Constellations validates the theory of 3D Lattice Flower Constellations and has a wide range of potential applications.

1 Introduction

The instantaneous position and velocity of a satellite orbiting around the Earth is determined by six orbital parameters: semi-major axis $(a)$, eccentricity $(e)$, inclination $(i)$, argument of perigee $(\omega )$, right ascension of the ascending node $(\varOmega )$, and mean anomaly $(M)$. In a 2D Lattice Flower Constellation (Avendaño et al. 2013) all the satellites have the same $a, e, i, \omega$, and the pairs $(\varOmega ,M)$ lie on a lattice given by three integer parameters $N_o, N_{ so }, N_c$ (details can be found in Sect. 2.1). The constellation determined by these parameters is denoted $LFC (N_o,N_{ so },N_c,a,e,i,\omega ,\varOmega ,M)$.

In the Keplerian model, the evolution of the orbital parameters of the satellites of a 2D-LFC is very simple because all the parameters remain constant, except for the mean anomaly $M$ that increases linearly at the same rate $n=\sqrt{\mu /a^3}$ for all the satellites, where $\mu$ refers to the Earth gravitational parameter.

$$\begin{aligned} LFC (N_o,N_{ so },N_c,a,e,i,\omega ,\varOmega ,M) \overset{t/\text {Kepler}}{\longrightarrow } LFC (N_o,N_{ so },N_c,a,e,i,\omega ,\varOmega ,M+nt).\quad \end{aligned}$$

(1)

Hidden in Eq. (1) there is a remarkable fact about flower constellations in the Keplerian model that motivates part of this work: LFCs remain LFCs! In the $(\varOmega ,M)$-space, the lattice moves rigidly upwards at constant velocity $n$, thus preserving the structure of the LFC.

In this paper we reflect on whether something similar can happen when the Keplerian potential is perturbed with the $J_2$ term. When a LFC is propagated under the effect of $J_2$, the only way LFC should remain as such would be if $J_2$ perturbs all the satellites in exactly the same way. Therefore, we seek the existence of $a(t),\,e(t),\, i(t),\, \omega (t),\,\varOmega (t),\, M(t)$, such that

$$\begin{aligned}&LFC (N_o,N_{ so },N_c,a,e,i,\omega ,\varOmega ,M) \nonumber \\&\quad \overset{t/J_2}{\longrightarrow } LFC (N_o,N_{ so },N_c,a(t),e(t),i(t),\omega (t),\varOmega (t),M(t)). \end{aligned}$$

(2)

The aim of this paper is to find LFCs satisfying Eq. (2), named Lattice-preserving Flower Constellations. This property, which is automatically satisfied if an averaged $J_2$ potential function is used, is in the general case not trivial at all. However, recent studies have used this property as their starting point, such as the theory of 3D Lattice Flower Constellations (Davis et al. 2013) and the $J_2$ propelled orbits (Mortari et al. 2014), neglecting the effects of the non-secular components of the potential entirely. This work extends those previous results to include the full expression of the $J_2$ perturbation.

One may think that the relative trajectories of the satellites in a lattice-preserving flower constellation are time invariant and that they will preserve the initial configuration. However, the relative trajectories degenerate due to the perturbative effects. The aim of this article is to preserve the FC symmetric configurations under perturbations. This property is achieved through the proper selection of the orbital elements of the satellites in the FC. We do not intend to modify slightly the orbital elements to get certain orbital behavior such as frozen orbits, Sun-synchronous or repeating ground track orbits, we only pursue the preservation of the symmetric configuration of the FCs under the perturbation caused by the zonal harmonic $J_2$.

In this paper we first summarize the theory of 2D Lattice Flower Constellations and we review the fundamentals of satellite motion under the gravitational potential of the Earth. Then, we introduce the main problem, and we study in detail the secular and non-secular components of the orbital elements as a function of the initial conditions. Finally, we present our main results and we give a complete example of a Lattice-preserving Flower Constellation.

2 Fundamentals

In this section we introduce the tools that we will use throughout the paper: the theory of 2D Lattice Flower Constellations, and the equations of motion of a satellite under the gravitational potential of the Earth.

2.1 2D Lattice Flower Constellation theory

In the original theory, flower constellations (Mortari et al. 2004; Mortari and Wilkins 2008; Wilkins and Mortari 2008) were defined as a set of $N_{ sat }$ satellites following the same (closed) trajectory with respect to a rotating reference frame. This was substantially improved with the 2D Lattice Flower Constellation theory (Avendaño et al. 2013) making the definition independent from any reference frame (inertial or rotating) and making the theory work with a minimal parametrization.

A 2D Lattice Flower Constellation (2D-LFC) is described by three integer and six continuous parameters. The first three are $(N_o, N_{ so }, N_c)$, where $N_o$ is the number of inertial orbits, $N_{ so }$ is the number of satellites per orbit, and $N_c \in [0, N_o -1]$ is a phasing parameter. The location of all the satellites of a 2D-LFC corresponds to a lattice in the $(\varOmega ,M)$-space (Avendaño and Mortari 2009), which can be regarded as a 2D torus (both axes, $M$ and $\varOmega$, are modulo $2\pi$), and coincides with all the solutions of the following system of equations:

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} N_o &{} 0 \\ N_c &{} N_{ so } \\ \end{array} \right) \left( \begin{array}{c} \varOmega _{ij} - \varOmega _{00} \\ M_{ij} - M_{00} \\ \end{array} \right) = 2\pi \left( \begin{array}{c} i \\ j \\ \end{array} \right) , \end{aligned}$$

(3)

where $i = 0, \ldots , N_o - 1, j = 0, \ldots , N_{ so } - 1$, and $N_c \in [0, N_o - 1]$. Indices $(i, j)$ represent the $j$th satellite on the $i$th orbital plane.

The other six parameters are $\varOmega _{00}$ and $M_{00}$, which locate the satellite $(0,0)$, the semi-major axis $(a)$, the eccentricity $(e)$, the inclination $(i)$, and the argument of perigee $(\omega )$, which are the same for all the satellites in the constellation.

2.2 Satellite motion

The motion of a satellite orbiting around the Earth is completely determined by the potential function $V(\mathbf{r })$, which accounts for the gravitational interaction between the two bodies. The equations of motion are obtained by taking the partial derivatives of $V(\mathbf{r })$,

$$\begin{aligned} \ddot{\mathbf{r }} = - \nabla V(\mathbf{r }). \end{aligned}$$

(4)

Since the Earth is non-symmetric, the potential of an aspherical body must be obtained first. The potential function (Vallado 2001, p. 509) is usually split into two parts, the Keplerian part (spherical) and the perturbative part (aspherical):

$$\begin{aligned} V(\mathbf{r }) = V_{ Kepler } + R. \end{aligned}$$

(5)

If we only consider the $J_2$ effect, which is the coefficient corresponding to the first harmonic of the Earth’s gravitational potential, the previous equation can be simplified into:

$$\begin{aligned} V(\mathbf{r })&= V_{ Kepler } + R_{J_2}\nonumber \\&= -\frac{\mu }{r} + J_2 \left( \frac{r_{\oplus }}{r} \right) ^2 P_2 \left( sin (\phi _{ sat }) \right) . \end{aligned}$$

(6)

where $r_{\oplus }$ is the Earth radius, $P_2$ is the 2nd-order Legendre Polynomial and $\phi _{ sat } \in [-\pi /2, \pi /2]$ represents the latitude of the satellite.

The second order equation described in Eq. (4) can be expressed as a first order system of equations:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\mathbf{r }}(t) = \mathbf{v }(t),\\ \dot{\mathbf{v }}(t) = - \nabla V(\mathbf{r }(t)), \end{array}\right. \end{aligned}$$

(7)

where $\mathbf{r }(t)$ and $\mathbf{v }(t)$ represent the position and velocity of the satellite at time $t$, respectively. The system presented in Eq. (7) has six differential equations of order one. Given the initial position and velocity, the solution of the system at time $t$ is presented through the state vector at time $t, \mathbf{r }(t)$ and $\mathbf{v }(t)$.

Once the state vector is known, the classical orbital elements $(a,e,i,\omega ,\varOmega ,M)$ can be determined. In the Keplerian motion, a satellite has constant orbital elements except the mean anomaly $M$. Then, the evolution of them over time can be represented as a straight line, since $M$ increases linearly: $M(t) = nt$. The perturbative effects (aspherical body, solar radiation pressure, etc.) cause deviations from the two-body (Keplerian) motion. Consequently, the orbital elements are no longer constant. However, the model can be considered instantaneously as a Keplerian model, i.e. at each instant of time it is possible to describe the movement as a Keplerian motion, using six orbital elements which depend on time. These parameters are named osculating elements; $a(t), e(t), i(t), \omega (t), \varOmega (t)$ and $M(t)$, whose evolution follow Lagrange planetary equations (Abad 2012, p. 194), presented in Eq. (8):

$$\begin{aligned} \begin{aligned} \dot{a}&= -\frac{2}{n a} \frac{\partial R}{\partial M}, \\ \dot{e}&= \frac{\sqrt{1-e^2}}{n a^2 e} \frac{\partial R}{\partial \omega } - \frac{1-e^2}{n a^2 e} \frac{\partial R}{\partial M}, \\ \dot{i}&= \frac{1}{n a^2 \sqrt{1-e^2} \sin (i)} \frac{\partial R}{\partial \varOmega } -\frac{\cos (i)}{n a^2 \sqrt{1-e^2} \sin (i)} \frac{\partial R}{\partial \omega }, \\ \dot{\omega }&= -\frac{\sqrt{1-e^2}}{n a^2 e} \frac{\partial R}{\partial e} + \frac{\cos (i)}{n a^2 \sqrt{1-e^2} \sin (i)} \frac{\partial R}{\partial i}, \\ \dot{\varOmega }&= -\frac{1}{n a^2 \sqrt{1-e^2} \sin (i)} \frac{\partial R}{\partial i}, \\ \dot{M}&= n + \frac{2}{n a} \frac{\partial R}{\partial a} + \frac{1-e^2}{n a^2 e} \frac{\partial R}{\partial e}. \end{aligned} \end{aligned}$$

(8)

where $R$ represents the perturbing part of the potential presented in Eq. (5). Analytical investigations of the oblateness effects of a central body on a satellite has shown that certain elements, such as $\omega , \varOmega , M$, experience secular variations and periodic variations (short and long period variations). Other elements such as $a,e,i$ are possessed of only periodic variations and, hence, they only vary about their mean values.

3 Problem formulation

We assume that the sectorial and tesseral harmonics of the potential function are zero, and the potential function have only zonal harmonic terms. As a first approximation, we only consider the $J_2$ effect since it is almost 1000 times larger than the next coefficient $J_3$.

In order to use Lagrange planetary equations we should determine the potential function in terms of the orbital elements. For that purpose, the latitude of the satellite can be rewritten as $\sin (\phi _{ sat }) = z/r$, where $z = r \sin (i) \sin (\omega + f)$ and $f$ represents the true anomaly. Thus, the expression of the potential function given in Eq. (6) can be expressed in terms of the orbital elements:

$$\begin{aligned} V(a,e,i,\omega ,\varOmega ,f)&= V_{ Kepler } + R_{J_2}\nonumber \\&= -\frac{\mu }{r} + \frac{\mu }{r} J_2 \left( \frac{r_{\oplus }}{r} \right) ^2 \frac{1}{2} \left( 3 \sin ^2(i) \sin ^2(\omega + f) -1 \right) . \end{aligned}$$

(9)

The standard approach is to consider an averaged perturbed potential $\overline{R_{J_2}}$ over an orbital period, instead of the full expression of $R_{J_2}$, to focus on the non-periodic variations (secular terms) of the orbital parameters (Battin 1999, p. 504).

$$\begin{aligned} \overline{R_{J_2}} = \frac{1}{2\pi }\int _0^{2\pi }R_{J_2}(a,e,i,\omega ,\varOmega ,M)dM=\frac{\mu J_2 r_{\oplus }^2 (2-3\sin ^2i)}{4a^3(1-e^2)^{3/2}}. \end{aligned}$$

(10)

Lagrange planetary equations show the variation of the osculating orbital elements of any satellite. As we indicate in Sect. 2.2 each osculating orbital element has a secular and non-secular component. In the particular case where the potential function is averaged over the mean anomaly, as in Eq. (10), we observe that the slopes of the osculating orbital parameters are given by:

$$\begin{aligned} \dot{a}&= 0,&\dot{\omega }(a,e,i)&= \frac{3}{4}J_2\left( \frac{r_{\oplus }}{a(1-e^2)}\right) ^2 n \left( 5\cos ^2i -1\right) , \nonumber \\ \dot{e}&= 0,&\dot{\varOmega }(a,e,i)&= -\frac{3}{2}J_2\left( \frac{r_{\oplus }}{a(1-e^2)}\right) ^2 n \cos i, \nonumber \\ \dot{i}&= 0,&\dot{M}(a,e,i)&= n\left[ 1+\frac{3}{4}\sqrt{1-e^2}J_2\left( \frac{r_{\oplus }}{a(1-e^2)}\right) ^2\left( 3\cos ^2i -1\right) \right] . \end{aligned}$$

(11)

Applying these formulas to the case of FCs, we see that all the satellites suffer exactly the same perturbation due to $\overline{R_{J_2}}$, since all the satellites have the same $a, e$, and $i$. The initial configuration is changing because of the rotation of the right ascension of the ascending node. However, all the satellites experience the same rate of change and, consequently, they are perturbed in the same way preserving the initial symmetric configuration. This shows that, for the case of the averaged perturbed potential, the conclusion of Eq. (2) is valid and a lattice-preserving flower constellation is obtained.

However, as we show in Sect. 4, when the propagation is done with the full expression of $R_{J_2}$, the osculating elements show a slightly different behavior: each parameter has a secular component (a linear function), represented by $a_{ sec }(t), e_{ sec }(t), i_{ sec }(t), \omega _{ sec }(t), \varOmega _{ sec }(t), M_{ sec }(t)$ and a non-secular component (small oscillations with average zero), represented by $a_{ non {\text {-}}{ sec }}(t), e_{ non {\text {-}}{ sec }}(t), i_{ non {\text {-}}{ sec }}(t), \omega _{ non {\text {-}}{ sec }}(t), \varOmega _{ non {\text {-}}{ sec }}(t), M_{ non {\text {-}}{ sec }}(t)$. Consequently, each orbital element can be considered as the sum of its secular component and its non-secular component, $a(t) = a_{ sec }(t) + a_{ non {\text {-}}{ sec }}(t)$, etc.

Using Lagrange planetary equations and the full expression of $R_{J_2}$ is possible to obtain the variation of the orbital elements over time (Guochang 2008, p. 71):

$$\begin{aligned} \dot{a}&= -\frac{6d \sqrt{1-e^2}}{na^4} \left\{ \frac{-e}{(1-e^2)} \frac{a^4}{r^4} \sin f \left[ \frac{3}{2} \sin ^2i (1-\cos 2u) -1\right] + \frac{a^5}{r^5} \left[ \sin ^2i \sin 2u \right] \right\} , \nonumber \\ \dot{e}&= -\frac{3d(1-e^2)^{\frac{3}{2}}}{na^5e}\left\{ \frac{-e}{(1-e^2)} \frac{a^4}{r^4} \sin f \left[ \frac{3}{2} \sin ^2i (1-\cos 2u) -1\right] + \frac{a^5}{r^5} \left[ \sin ^2i \sin 2u \right] \right\} \nonumber \\&\quad +\,\frac{3d\sqrt{1-e^2}}{n a^5e} \sin ^2i \sin 2u, \nonumber \\ \dot{i}&= -\frac{3d}{2na^5\sqrt{1-e^2}} \frac{a^3}{r^3} \sin 2i \sin 2u, \nonumber \\ \dot{\omega }&= -\frac{3d \sqrt{1-e^2}}{na^5e} \left\{ \frac{a^4}{r^4} \cos f \left[ \frac{3}{2} \sin ^2i (1-\cos 2u) -1\right] \right. \nonumber \\&\quad +\,\left. \frac{a^3}{r^3} \left[ \sin ^2i \sin 2u \frac{2 + e \cos f}{1-e^2} \sin f \right] \right\} \nonumber \\&\quad +\,\frac{3d}{na^5 \sqrt{1-e^2}} \frac{a^3}{r^3} \left[ \cos ^2i (1-\cos 2u) \right] , \nonumber \\ \dot{\varOmega }&= -\frac{3d}{na^5 \sqrt{1-e^2}} \frac{a^3}{r^3} \left[ \cos i (1-\cos 2u) \right] , \nonumber \\ \dot{M}&= n - \frac{6d}{na^5} \frac{a^3}{r^3} \left[ \frac{3}{2} \sin ^2i (1-\cos 2u) -1\right] \nonumber \\&\quad +\,\frac{3d(1-e^2)}{na^5e} \left\{ \frac{a^4}{r^4} \cos f \left[ \frac{3}{2} \sin ^2i (1-\cos 2u) -1\right] \right. \nonumber \\&\quad +\,\left. \frac{a^3}{r^3} \left[ \sin ^2i \sin 2u \frac{2 +e\cos f}{1-e^2} \sin f\right] \right\} . \end{aligned}$$

(12)

where $d = \mu J_2 r_{\oplus }^2 / 2$ and $u = \omega + f$. In this situation, the only way we can preserve the configuration for a FC, and consequently satisfy Eq. (2), would be by showing that:

• (a) The slopes of the secular components of the osculating elements depend only on the initial $a, e, i, \omega$, hence, the slopes would be the same for all satellites. In this way, the initial configuration of the constellation and its symmetries are time preserving.

• (b) The non-secular components are negligible (within a certain tolerance).

In the following section we show that the slopes of the secular components of the osculating elements do not depend on $\varOmega$. However, they depend on the initial mean anomaly of each satellite, which is a major problem since the satellites in a FC have different values of $M$. To avoid it, we develop a corrector method based on the correction of the semi-major axis of the satellites by a few kilometers, in such a way that the secular part of the osculating elements of each satellite will have the same slope. Thus, the secular part can be controlled in a FC.

As the second requirement, we describe the non-secular component of a satellite and we study the dependency with respect to the initial orbital elements of the satellite. We will find different regions where the non-secular component of a satellite is minimized.

4 Secular and non-secular perturbation of the osculating elements

The osculating elements have three different kinds of terms (see Sect. 2.2); polynomial terms in the variable $t$, terms of sine and cosine of the variables $\omega , \varOmega$, and $i$, which cause a periodic oscillation with long period, and terms of sine and cosine of the variable $M$, which are named short periodic terms (Escobal 1976, p. 362).

In this paper, we only make a distinction between the first kind of terms (secular) $a_{ sec }(t),\, e_{ sec }(t),\, i_{ sec }(t),\, \omega _{ sec }(t),\, \varOmega _{ sec }(t),\, M_{ sec }(t)$ and the sum of the last two terms corresponding to the short and long periodic variations (non-secular) $a_{ non {\text {-}}{ sec }}(t), e_{ non {\text {-}}{ sec }}(t), i_{ non {\text {-}}{ sec }}(t), \omega _{ non {\text {-}}{ sec }}(t), \varOmega _{ non {\text {-}}{ sec }}(t), M_{ non {\text {-}}{ sec }}(t)$. When the potential is perturbed only with the $J_2$ term, the secular components of the osculating elements show a linear secular behavior.

In this section we analyze how the $J_2$ term affects a satellite orbiting around the Earth. As an example we select random initial orbital elements for a satellite; $a = 26{,}544.2976$ km, $e = 0.1046, i = 36.3356^{\circ }, \omega = \varOmega = M = 0^{\circ }$. This satellite has an orbital period of approximately $12$ h. We integrate the system of Eq. (12) applying a fourth order Runge Kutta, with fixed step $\delta t = 1.0$ s during 10 orbital periods.

It should be highlighted that secular variations are associated with a continuous change of the orbital elements, long period variations are fluctuations of the elements about the secular variation line, and short period variations are bounded fluctuations superimposed on the long period variations. Figure 1a–c shows the evolution (secular and periodic variations) of the semi-major axis, eccentricity and inclination over time, respectively. It is possible to observe that the secular perturbation of these parameters are equal to zero and it is possible to recognize the oscillations produced by the non-secular component. The semi-major axis oscillates about $2.5$ km, the eccentricity about $10^{-4}$ and the inclination around $0.0034^{\circ }$ each orbital period. Figure 1d, e shows the evolution of the argument of perigee and the right ascension of the ascending node, respectively. In these cases we observe a secular and non-secular behavior in each parameter. Finally, Fig. 1f shows the evolution of the mean anomaly over time and we observe a small oscillation besides a secular behavior. Note that instead of a line, the plot has a sawtooth shape due to the modular nature of angular values. For the sake of clarity, the non-secular component of $M$ during an orbital period has been plotted separately in Fig. 2c.

Fig. 1

Evolution of the semi-major axis ($a$), eccentricity ($e$), inclination ($i$), argument of perigee ($\omega$), right ascension of the ascending node ($\varOmega$) and mean anomaly ($M$) during 10 orbital periods

Fig. 2

The large variation that $\omega$ and $M$ present in near-circular orbits. Initial conditions are: $a = 26{,}544.2976$ km, $i = 36.3356^{\circ }, \omega = \varOmega = M = 0^{\circ }$

To determine the secular component of an osculating element $q \in \{ a, e, i, \omega , \varOmega , M \}$, we use linear interpolation over the data set consisting of the pairs $(t, q(t))$ obtained by propagating Eq. (12) with the full expression of the potential $R_{J_2}$. For the angular parameters $\omega , \varOmega$, and $M$, we add or subtract multiples of $2 \pi$ before the linear interpolation, to handle the non-linearity created by their $2 \pi$ modular behavior. In Table 1, we compare the slopes of the secular components of the osculating elements computed with our linear interpolation and the ones that would be obtained if the propagation were done using the averaged potential $\overline{R_{J_2}}$. The difference between both propagations is very small along one orbital period but it is not bounded for a long time period propagation. Since we are interested in accurate results, we disregard the averaged potential $\overline{R_{J_2}}$ in favor of the full expression of $R_{J_2}$.

Table 1 Comparison of the slopes of the secular components of the osculating elements propagating with $\overline{R_{J_2}}$ and $R_{J_2}$

There are cases that require a special treatment. When the eccentricity approaches zero, there is a large variation in $\omega$. Actually, when $e = 0$ the argument of perigee is undefined. In the previous example we consider a non-circular orbit ($e = 0.1046$) and we observe that the argument of perigee oscillates around $10^{-3}$ rad due to the non-secular component (see Fig. 1d). However, if we change the eccentricity to $e = 10^{-4}$, we observe that the secular and non-secular components of the argument of perigee are extremely high, as we illustrate in Fig. 2a. Besides, in Fig. 2b we have removed the secular variations to emphasize the non-secular component of the argument of perigee over a single period. We observe that the non-secular component of the argument of perigee oscillates about $2$ rad in one orbital period, thus proving the large variation that $\omega$ presents in near-circular orbits.

Note that Figs. 1f and 2a may present a similar behavior. Both of them have a remarkable secular component and the plots have a sawtooth shape. Nevertheless, in the case of the mean anomaly (Fig. 1f), we plot its non-secular component in one orbital period in Fig. 2c and we observe that it is rather small (order ${\approx }10^{-4}$), while in the case of the argument of perigee, as we observe in Fig. 2b, the non-secular component is 10,000 times larger.

Another situation that requires special treatment is when $i\approx 0$ or $i\approx \pi$, but these cases are out of consideration due to the impossibility to control or even define the secular part of these parameters (Abad 2012, p. 144).

4.1 Dependence of secular component of the osculating elements in terms of the initial conditions

As we mentioned before secular variation are associated with a continuous drift of the orbital elements. The secular component of the orbital elements is a linear function. The slopes of these linear functions $\dot{a}_{ sec }(t), \dot{e}_{ sec }(t), \dot{i}_{ sec }(t), \dot{\omega }_{ sec }(t), \dot{\varOmega }_{ sec }(t)$, and $\dot{M}_{ sec }(t)$ measure the rate of change of the secular component of each orbital element. Hence, we can ensure that the condition given in Eq. (2) is equivalent to have all the satellites the same values of $\dot{a}_{ sec }(t), \dot{e}_{ sec }(t), \ldots , \dot{M}_{ sec }(t)$.

The expression for the gravitational potential including only the $J_2$ term is symmetric to rotations about the $z$-axis. Consequently, two satellites with same orbital parameters, except the value of the right ascension of the ascending node, have an identical evolution over time but rotated about the z-axis. That is, the slopes of the secular component of the osculating elements do not depend on $\varOmega$, or in other words, they depend only on the initial $a, e, i, \omega$, and $M$.

We have numerically analyzed the dependency of the slopes of the secular components of the osculating elements with respect to the initial mean anomaly. The outline of the procedure is the following:

• 1. We consider an initial set of 100 satellites. The orbital parameters $(a,e,i,\omega )$ of each satellite are selected at random in a region of interest. Taking into account that we have already shown that the slopes do not depend on the value of right ascension of the ascending node, we have set this value to zero for all the satellites (i.e. $\varOmega =0^{\circ }$).

• 2. The mean anomaly $M \in [0,2 \pi ]$ is discretized with a step of $7.35^{\circ }$ for each one of the $100$ satellites. Thus, each satellite has $51$ different possible values for the mean anomaly.

• 3. Finally, each set of initial conditions is propagated using Eq. (12) with a fourth order Runge Kutta during approximately $370$ days, with a time step of $20$ s.

The solution of the above process yields a similar behavior for all the satellites. We illustrate these results with one particular example. We take, for instance, the satellite whose initial orbital elements are $a = 26,215.017$ km, $e = 0.090394, i = 85.9507^{\circ }, \omega = 208.5061^{\circ }$, and $\varOmega = 0^{\circ }$. The values of the mean anomaly vary between $0^{\circ }$ and $360^{\circ }$ with a step about $7.35^{\circ }$. Table 2 shows how the slopes of the secular components of the osculating elements change depending on the value of the mean anomaly.

Table 2 Slopes of the secular components of the osculating elements in function of the initial mean anomaly

If we only vary the value of the initial mean anomaly we observe that the slopes of the semi-major axis are in all cases equal up to order $10^{-11}$ km/s. Meaning that, after 370 days, independently of the initial value of the mean anomaly, the secular variation of the semi-major axis will be $<$1 m ($0.3197$ m). The slopes of the eccentricity have, in all the cases, the same value up to order $10^{-14}$ s$^{-1}$. After 370 days, the variation of the eccentricity will be $3.1968\times 10^{-7}$. It means that the variation of the initial mean anomaly does not affect substantially the slopes of the eccentricity. The slopes of the inclination, $i_{ sec }(t)$ are equal up to order $10^{-16}$ rad/s. That is, after one year (370 days), the variation will be around $10^{-9}$ rad, independently of the initial value of the mean anomaly. We observe that the slopes of $\omega _{ sec }(t)$ and $\varOmega _{ sec }(t)$ have approximately the same value when we change the mean anomaly. These slopes coincide up to order $10^{-11}$ rad/s, in other words, after 370 days, the variation of these elements will be $3.1968 \times 10^{-4}$ rad. All this shows that $a_{ sec }(t), e_{ sec }(t)\,i_{ sec }(t),\,\omega _{ sec }(t)$, and $\varOmega _{ sec }(t)$ do not significantly depend on the initial value of $M$.

However, the slopes of $M_{ sec }(t)$ are sensitive to the variation of the initial mean anomaly. They show a difference of order $5.1608 \times 10^{-8}$ rad/s, which represent a difference of about $94^{\circ }$ in 370 days of propagation. This extreme difference comes from the fact that the orbital periods of the satellites are not equal. The slope of $M_{ sec }(t)$ is equal to $n$, which is the mean motion of a satellite,

$$\begin{aligned} \dot{M}_{ sec }(t) = n = \frac{2 \pi }{T_p}, \end{aligned}$$

where $T_p$ is the Keplerian orbital period of the satellite (related with the semi-major axis). We take from Table 2 two different values for the mean anomaly $M^8 = 0.8975$ rad and $M^{48} = 5.8985$ rad, which correspond to the 8th and the 48th set of parameters that we tested. Those values have been selected because, in those cases, the value of $\dot{M}_{ sec }$ reaches a minimum $\dot{M}_{ sec }^{8} = 1.487122 \times 10^{-4}$ rad/s and a maximum $\dot{M}_{ sec }^{48} = 1.487638 \times 10^{-4}$ rad/s.

Despite having the same orbital parameters, except for the value of $M$, the orbital periods of the satellites are, $T_p^8 = 42250.6175$ s and $T_p^{48} = 42235.9602$ s, respectively. They differ by approximately 14.65 s, meaning that after 370 days (about 740 orbital periods) there will be an offset close to $11{,}118.9743$ s between both satellites, which corresponds to the $94^{\circ }$ of difference that we obtained above.

4.2 Dependence of non-secular component of the osculating elements in terms of the initial conditions

In this section we analyze the non-secular component of the osculating elements. We consider an initial set of orbital elements ($a, e, i, \omega , \varOmega , M$) and we integrate the system of Eq. (12) applying a fourth order Runge Kutta to determine their evolution over time (osculating elements). Furthermore, for each osculating element $q \in \{a,e,i,\omega ,\varOmega ,M\}$, we obtain its secular and non-secular part by linear interpolation as explained before.

In the two body problem it is easy to compute the position and velocity vectors from the orbital elements. Then, we can compute at time $t$ “the real position” $(\mathbf{r }_{J_2} (t))$ and “the approximate or linear position” $(\mathbf{r }_{ sec } (t))$, through the osculating elements $a(t),\, e(t),\, i(t),\, \omega (t), \varOmega (t),\, M(t)$, and the secular component of the osculating elements $a_{ sec }(t),\, e_{ sec }(t),\, i_{ sec }(t), \omega _{ sec }(t),\, \varOmega _{ sec }(t),\, M_{ sec }(t)$, respectively.

The real position of the satellite, $\mathbf{r }_{J_2} (t)$, considers the secular and non-secular terms of the osculating elements, while the approximate position, $\mathbf{r }_{ sec } (t)$, only takes into account the secular terms. Then, the distance:

$$\begin{aligned} ||\mathbf{r }_{J_2} (t) - \mathbf{r }_{ sec } (t) || \end{aligned}$$

represents the deviation of the satellite from its real position due to the non-secular perturbations. We compute this deviation at each instant of time and consider the maximum value experienced,

$$\begin{aligned} \varDelta (a,e,i,\omega , \varOmega , M) = \max _t ||\mathbf{r }_{J_2} (t) - \mathbf{r }_{ sec } (t) ||, \end{aligned}$$

(13)

which represents, as a function of the initial conditions, the maximum deviation due to the non-secular components of the osculating elements.

Our goal is to determine the best values for the initial orbital elements to reduce the deviation of the reference satellite [$(i,j) = (0,0)$]. To find those regions, we first study numerically the dependency of the deviation on the initial orbital elements, and then, we search for the best initial conditions.

We introduce below the procedure followed to study the deviation dependency regarding the semi-major axis. We follow a similar procedure for the other orbital elements:

• Generate randomly the initial orbital elements of 100 satellites, except the semi-major axis.

• For each satellite, the semi-major axis is discretized in the region [18000, 29000] km with a step of 500 m. Then, each satellite has 22 potential values for the semi-major axis.

• For each of the 100 satellites, it is possible to compute the maximum deviation experienced in terms of the semi-major axis, and to infer the dependency between them. Each set of initial conditions is propagated using Eq. (12) with a fourth order Runge Kutta during approximately 370 days, with a time step of 20 s.

Hence, we observe in Fig. 3a that the deviation is inversely proportional to the semi-major axis. This is due to the fact that the $J_2$ effect diminishes as we move away from the Earth. Figure 3b illustrates that the deviation is almost constant until the eccentricity reaches the value $e=0.15$, and then it grows exponentially as the value of $e$ increases. Regarding the inclination, we observed that there is always a value for the inclination which minimizes the deviation, as Fig. 3c illustrates. Notice that, the inclination varies in the range $[0^{\circ },90^{\circ }]$ because the results in the interval $[90^{\circ },180^{\circ }]$ will be exactly the same since we are dealing with the same orbit but in retrograde motion.

Fig. 3

Dependency of the maximum deviation, $\varDelta (a,e,i,\omega , \varOmega , M)$, with respect to the semi-major axis, eccentricity and inclination

As it is explained above, the deviation does not depend on the right ascension of the ascending node. Besides, the deviation varies $<$150 m as we change the argument of perigee and, in the case of the mean anomaly it varies $<$10 m.

The previous study shows that the main contribution to the deviation comes from initial $a, e$, and $i$. To reduce the deviation it is sufficient to increase $a$ as much as possible, reduce $e$ to the interval $[0,0.15]$, and choose the optimal value of the inclination corresponding to the chosen $a$ and $e$.

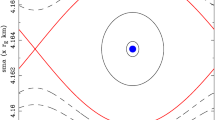
In mission planning it would be useful that, given the semi-major axis, we were able to compute the range of values for $e$ and $i$ such that they reduce as much as possible the deviation of the satellites. For that purpose, we designed an algorithm that, given the semi-major axis, the argument of perigee, the right ascension of the ascending node and the mean anomaly of a satellite, computes and plots the deviation in terms of the eccentricity and the inclination. Figure 3d shows the output of the algorithm for a certain example whose initial data are: $a = 29600.1$ km, $\omega = 0^{\circ }, \varOmega = 0^{\circ }$, and $M=0^{\circ }$.

On the other hand, we explore the maximum deviation that a satellite can experience. For that purpose, we consider the worst initial conditions. We select a satellite whose semi-major axis is $a \ge 18{,}000.0$ km and the eccentricity is $e \le 0.15$ (following Fig. 3a, b). Varying the argument of perigee, the right ascension of the ascending node and the mean anomaly we obtain that the deviation may increase at most $160$ m. Then, we vary the inclination in a range $[0^{\circ }, 90^{\circ }]$. The maximum deviation obtained will correspond to the worst possible case. Summarizing:

• The deviation remain equal for the variation of $\varOmega$.

• The deviation increases about $160$ m when we vary the value of $\omega$ and $M$.

• When the worst semi-major axis and eccentricity are selected, and we change the inclination in the range $[0^{\circ }, 90^{\circ }]$, the deviation is bounded by $5$ km.

Therefore, we have numerically proved that the maximum deviation is ${<}5$ km. Consequently, if a tolerance of a few kilometers ($5$ km) is acceptable for the deviation, then almost all initial conditions are valid to design a lattice-preserving flower constellation since we only need to control the secular motion.

5 Design of Lattice-preserving Flower Constellations

A flower constellation of $N_{ sat }$ satellites has the same semi-major axis, eccentricity, inclination and argument of perigee for each satellite. The right ascension of the ascending node and the mean anomaly of each satellite is determined by Eq. (3). Our goal is to select suitable initial conditions for all the satellites in the flower constellation so that the perturbations result in motion that preserves the structure of flower constellation.

5.1 Correction of semi-major axis

The procedure to have the same secular motion all the satellites in a flower constellation is obtaining the same slopes of the secular component of the osculating elements for all the satellites. We show below that this can be achieved by a slight change to default value of the semi-major axis of each satellite a few kilometers. This will be possible since $\dot{M}_{ sec }$ is related to $T_p$, which is itself related to the semi-major axis.

In a flower constellation all the satellites have the same semi-major axis: to implement this correction scheme we need to redefine the concept of flower constellation. The satellites of these new constellations have the same values of $e, i$, and $\omega$, the values of $\varOmega$ and $M$ will be determined by the lattice theory, but the semi-major axis will be slightly corrected for each satellite. We devote the rest of this section to derive a formula for the correction of the semi-major axis that guarantees the same value of $\dot{M}_{ sec }$. That way we will control the secular perturbations.

From Kepler’s third law it is easy to derive the following linear expression,

$$\begin{aligned} \ln {\dot{M}_{ sec }} = -\frac{3}{2} \ln {a} + \beta , \end{aligned}$$

(14)

for some constant $\beta$.

Using Eq. (14), it is possible to obtain for each value of $\dot{M}_{ sec }^{ij}$ a value for $\beta$ (named $\beta ^{ij}$), where $ij$ represents the index of satellite in the flower constellation as in Eq. (3). With the same equation, but changing the value of $\dot{M}_{ sec }^{ij}$ by the reference value $\dot{M}_{ sec }^{00}$ and $\beta$ by the value previously computed ($\beta ^{ij}$), we obtain the corrected semi-major axes:

$$\begin{aligned} \ln {a_{ij}}&= -\frac{2}{3} \left( \ln {\dot{M}_{ sec }^{00}} - \beta ^{ij}\right) \\&= -\frac{2}{3} \left( \ln {\dot{M}_{ sec }^{00}} - \left( \frac{3}{2} \ln {a} + \ln {\dot{M}_{ sec }^{ij}}\right) \right) \\&= -\frac{2}{3} \ln {\dot{M}_{ sec }^{00}} + \ln {a} + \frac{2}{3} \ln {\dot{M}_{ sec }^{ij}} \\&= \ln {a} + \frac{2}{3} \left( \ln {\dot{M}_{ sec }^{ij}} - \ln {\dot{M}_{ sec }^{00}}\right) \\&= \ln {a} + \frac{2}{3} \ln {\frac{\dot{M}_{ sec }^{ij}}{\dot{M}_{ sec }^{00}}}. \end{aligned}$$

Applying the exponential function, we obtain a new value for the semi-major axis,

$$\begin{aligned} a_{ij}&= \exp \left( \ln {a} + \frac{2}{3} \ln {\frac{\dot{M}_{ sec }^{ij}}{\dot{M}_{ sec }^{00}}} \right) \nonumber \\&= a {\cdot } \exp \left( \ln \left( \frac{\dot{M}_{ sec }^{ij}}{\dot{M}_{ sec }^{00}} \right) ^{\frac{2}{3}}\right) \nonumber \\&= a \left( \frac{\dot{M}_{ sec }^{ij}}{\dot{M}_{ sec }^{00}}\right) ^{\frac{2}{3}}. \end{aligned}$$

(15)

The following procedure summarizes the method that we developed to correct the semi-major axis of all the satellites of a flower constellation:

• Given the data of a flower constellation: $N_o, N_{ so }, N_c, a, e, i, \omega , \varOmega$ and $M$, it is possible to compute the values for $\varOmega _{ij}$ and $M_{ij}$ for each satellite using the lattice theory, where $i$ is the orbit number and $j$ is the number of the satellite in its corresponding orbit. The reference satellite is the one with $i=j=0$, which has $\varOmega _{00} = \varOmega$ and $M_{00} = M$.

• Compute the value $\dot{M}_{ sec }^{ij}$ which is different for each satellite. $\dot{M}_{ sec }^{00}$ is considered as the reference value for the slope of $M(t)$, or in other words, the value that all the satellites should have.

• Compute the new values for $a_{ij}$ using Eq. (15).

We conclude that, by slightly modifying the semi-major axis of all the satellites, we obtain a flower constellation whose satellites have the same rate of change of its orbital elements. That is, the secular perturbations affects all the satellites in the same way and, consequently, the secular motion of the satellites will be identical under the $J_2$ effect for all the satellites.

5.2 Non-secular perturbation in a flower constellation

We now tackle the non-secular perturbation. Our aim is to minimize the non-secular motion of the satellites of the constellation to an acceptable value by selecting the suitable initial conditions. In the case of a flower constellation, given the reference satellite whose semi-major axis, argument of perigee, $\varOmega _{00}$, and $M_{00}$ are known, hence, we can determine the values for the eccentricity and the inclination in such a way that the non-secular motion of the satellite is as small as possible.

Once we have a value for the inclination and the eccentricity that provide a low deviation of the reference satellite. Since the remaining satellites only differ from the reference one in the right ascension of the ascending node and the mean anomaly, and we have shown that the deviation changes by a few meters in this case, then the same inclination and eccentricity should be valid for all the satellites. We may conclude that, if we find good parameters for the reference satellite, they are good for the remaining satellites of the constellation.

We have analyzed the dependency of the deviation with respect to the semi-major axis, and we have proved that if we change a few kilometers the semi-major axis in the correction algorithm, it slightly modifies the non-secular motion of the satellite. Consequently, the values for the eccentricity and inclination selected for the reference satellite are valid for all the satellites of the constellation.

6 Example of design

A flower constellation of $N_{ sat }$ satellites, in which the secular motion is controlled by correcting the semi-major axis of the satellites, and the non-secular motion is reduced by a suitable selection of the eccentricity and the inclination, Eq. (2) is satisfied and we have a lattice-preserving flower constellation. Given the phasing parameters $(N_o, N_{ so }, N_c)$ the semi-major axis ($a$), the argument of perigee ($\omega$), the right ascension of the ascending node and mean anomaly of the reference satellite, $\varOmega _{00}$ and $M_{00}$, respectively, it is possible to design a lattice-preserving flower constellation as follows:

• First, we compute the values for the inclination and the eccentricity that reduce the non-secular component of the reference satellite to an acceptable value.

• Then, we correct the semi-major axis of each satellite to control the secular motion of the satellites.

We now illustrate the method with an example. We consider a flower constellation with parameters $N_o = 3, N_{ so } = 9, N_c = 2, a = 29600.137$ km, $\omega = 0^{\circ }, \varOmega _{00} = 0^{\circ }$, and $M_{00} = 0^{\circ }$, which correspond with the parameters of Galileo constellation (Davis et al. 2010).

Given the semi-major axis, the argument of perigee, the right ascension of the ascending node and the mean anomaly of the reference satellite, it is possible to compute the non-secular component in terms of the eccentricity and the inclination as we show in Fig. 3d. Then, to minimize the non-secular component we select $e = 0.01$ and $i = 56.0009^{\circ }$, obtaining a deviation of 551.301 m.

Finally, we correct the semi-major axis to have all the satellites in the same relative orbits and to have also the same slopes for the secular component of the osculating elements to control the secular motion. The obtained values of the corrected semi-major axis and the slopes of the secular component of the osculating elements of each satellite are presented in Table 3.

Table 3 Semi-major axis of Lattice-preserving Galileo Flower Constellation

Notice that, as we mention in Sect. 4.2, if a deviation of $5$ km is accepted then, all flower constellations can be corrected into lattice-preserving flower constellations by slightly modifying the semi-major axis of the satellites.

7 Conclusions

We provide a new procedure to design 2D-LFCs with stable structure even under the $J_2$ effect. These constellations, named Lattice-preserving Flower Constellations, preserve the FC symmetric configurations under the $J_2$ perturbation. This property is achieved through the proper selection of the orbital elements of the satellites in the FC. To achieve that, all the satellites must suffer exactly the same changes in their orbit evolution induced by $J_2$. This has been pursued by modifying the orbital elements. Hence, the lattice of the flower constellation is preserved by using two techniques. The first one consists of the change of the semi-major axes by a few kilometers in such a way that all the satellites have the same slope of the secular part of their osculating elements. The second consists of the search of the values for the eccentricity and the inclination that reduce the deviation as much as possible. Hence, the relative position of the satellites (in the osculating elements space) will be maintained over time, and the initial lattice will remain constant within a certain tolerance.

Lattice-preserving Flower Constellations have direct applications. It implies that the theory of the 3D Lattice Flower Constellation (Davis et al. 2013) (3D-LFC) and the theory of $J_2$ propelled orbits (Mortari et al. 2014) are valid when the full expression of the potential function with the $J_2$ term is included, in cases where the semi-major axes are corrected and the value of the deviation is minimized.

Future research may consist of applying this theory to find GDOP-optimal satellite constellations (Casanova et al. 2013, 2012) for solving global positioning problems.