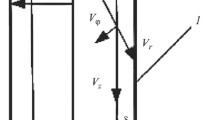
The hydrocyclone is a cylinder-conical apparatus in which, by means of the pressure drop effect, a liquid medium begins circulation as a result of the transformation of the translational motion of the given medium in the tangential input channel into rotational motion in the working volume of the apparatus. The liquid medium, together with the particles suspended in it, enters the cylindrical part of the hydrocyclone through the inlet nozzle, moves downward along the outer spiral, then rises along the inner spiral and exits through the upper channel (nozzle). The part of the suspension deposited under the action of the centrifugal force and other forces on the walls of the apparatus slips downward and exits through the lower nozzle (Fig. 1a). The other part of the suspension moves upward and, together with the stream, exits through the outlet nozzle.

Fig. 1.
figure 1

Diagram for the calculation of the geometric parameters of the cylinder working volume, simulating the working volume of the hydrocyclone.

Full size image

When a liquid + liquid type emulsion, such as water + oil, is separated in the hydrocyclone, water (as the higher-density fraction of the suspension) is thrown to the wall of the apparatus and then diverted through the lower nozzle, and the oil fraction rises and, together with the remaining water in the suspension, is discharged through the outlet nozzle.

Due to the simplicity of construction, the absence of moving parts, and numerous applications, hydrocyclones are widely used in the chemical, mining, food and other industries. Hydrocyclones are also used to solve environmental problems. This type of apparatus can be effectively used in the purification of water from oil pollution.

Quantitative analysis of separation of suspensions in a hydrocyclone is difficult because the process develops in the working volume of equipment of complex cylindroconic shape, with relatively high values of the tangential velocity of the fluid system, and moreover, the mixtures processed in the hydrocyclone can be very condensed and inhomogeneous in terms of particle size.

In publications on the kinetics of the process of suspension separation in a hydrocyclone, in order to overcome calculations difficulties, a number of assumptions have been adopted by the authors to simplify the formulation and solution of the problem.

Quantitative analysis of the process of separation of gaseous and liquid media in cyclone-type apparatuses is discussed, in particular, in [1,2,3,4,5]: the problems of kinematics and kinetics of flows circulating in the working volume of the apparatus were investigated; separation of suspended powder substances, accumulation of the solid phase on the wall of the apparatus, and withdrawal of it from the working volume were studied; methods of practical calculation of the apparatus were proposed. The efficiency of the process of separation of a liquid medium under operating conditions of hydrocyclones combined into a multistage system has been studied experimentally. However, in these studies there is not sufficient theoretical justification of the problems associated with the process of hydrocyclone formation of the processed phases of the suspension and their removal from the working volume of equipment, the dependence of the separating ability of the apparatus on the dispersity of the separated phase, the condensation of the suspension, and others.

Since a correct calculation device is required for the design and laboratory modeling of hydrocyclone equipment, the urgent need for further research is evident.

In this paper, a more substantiated and more general quantitative analysis of the processes of separation of a suspension in a hydrocyclone is proposed, in comparison with known analogs.

Formulation of the problem. When studying the sedimentation process in a heterogeneous liquid + solid system in a hydrocyclone, it is considered that from the point of view of hydrodynamics, the separation of a suspension in this apparatus is a kinetic process in the force field of two interacting and interpenetrating fluid media in a channel bounded by the mating walls of a cylinder and a cone. Since the formalization and quantitative modeling of the process of separation of a suspension in a hydrocyclone is generally difficult, in formulating and solving this problem it is usually simplified taking into account the specific features of the investigated problem.

Bearing in mind that the value of the taper angle of the conical part of the hydrocyclone is generally small, a rationale for the geometric parameters of the cylinder modeling the walls of the working volume of the hydrocyclone is first determined. To do this, regarding the cavity inside the cylinder as a cylindrical coordinate system rφz (see Fig. 1b), the flow of the liquid system in the hydrocyclone is approximately assumed to be an axisymmetric flow of mean thickness h moving along the inner surface of a cylinder of equal volume with a reduced radius R and the same height H as that of the hydrocyclone.

Then, if h1 and R1 are, respectively, the height and radius of the cylindrical part of the hydrocyclone, R2 and h2 are the height and radius of the lower base of the conical part of the hydrocyclone. Then, the radius R of the cylinder simulating this part of the rotor, can be approximated by

$$ R=\sqrt{W/\left(\uppi H\right)}, $$
(1)

where

$$ W=\uppi {R}_1^2{h}_1+\frac{\uppi {h}_2}{3}\left({R}_1^2+{R}_2^2+{R}_1{R}_2\right) $$

is the volume of the working part of the hydrocyclone; and H = h1 + h2 is the height of the hydrocyclone (see Fig. 1a).

If Q is the flow rate of the suspension (device productivity), h = (R – r0) is the thickness of the liquid layer in the cylinder with the reduced radius R, then the flow rate is

$$ {w}_0=\frac{Q}{\uppi \left({R}^2-{r}_0^2\right)}, $$
(2)

where r0 is the radius of the free surface of the liquid layer (see Fig. 1b).

Further, taking into account that the actual separation of the mixture in the hydrocyclone is realized mainly in the descending liquid flow, we shall confine ourselves to studying the process of separation of the suspension inside the cylinder modeling the hydrocyclone.

In order to evaluate the flow regime in a cylinder and justify the use of hydrodynamics of slow motion in the axial z and radial r directions, the formulas for the Reynolds numbers Re z and Re r in these directions can be used:

$$ {\operatorname{Re}}_z={w}_0h\uprho /\upmu, $$
(3)

where w0 is calculated by Eq. (2); ρ and μ are, respectively, the density and dynamic viscosity of the suspension;

$$ {\operatorname{Re}}_r={\upomega}^2R{\uprho \Delta \updelta}^3/\left(18{\upmu}^2\right), $$
(4)

where ω is the angular velocity of the stream; Δ = ρ1 – ρ; ρ1 is the density of solid; and δ is the particle diameter [6].

Assuming that these conditions are met in the framework of the adopted formulation of the problem, a quantitative simulation of the process of separation of the suspension in a hydrocyclone can be conducted.

Justification and physicomathematical modeling of the problem. Analytical investigation of the separating capacity of a hydrocyclone sedimentation tank is based on the scientific postulate about the critical diameter of a particle in a fluid system – the size of a hypothetical particle moving along the least favorable, usually the farthest, trajectory from the point of view of particle precipitation in a sedimentation tank (for example, along the trajectory AB, see Fig. 1b). The particles larger than the critical diameter in this case sink or float.

Let us assume that the fluid flow regime is layered and the Reynolds number Re r (4) is small, then the radial component of the particle velocity can be calculated by the formula [6]

$$ {v}_r=k{\updelta}^2r, $$
(5)

where r is the radial particle coordinate;

$$ k={\upomega}^2\Delta /\left(18\upmu \right),\kern0.5em \Delta <0,k<0. $$
(6)

The axial component v z of the flow velocity is calculated as in the case of a piston flow regime, i.e., from dependence (2).

Following the proposed formalized model of the problem, the kinetics of a hypothetical particle of a given size in a stream swirling inside the cylinder can be analyzed, including “heavy” (water) and “light” (oil) liquid phases, which simulates the flow of this suspension down the working volume of the hydrocyclone.

Based on the differential equation of the particle trajectory in the projection onto the meridional plane rz

$$ dr/{v}_r= dz/{v}_z, $$

taking into account expressions (2) and (6), the following differential equation is obtained:

$$ dr/ kU{\updelta}^2r= dz/{w}_0, $$
(7)

where k is calculated from (6), and U is the correction factor for the suspension thickening [7]:

$$ U={\left(1-c\right)}^3. $$
(8)

By integrating expression (7) in the range from A(r, H) to B(r0, 0) (see Fig. 1b), the relationship between the fluid flow parameters and the separation size (the current critical diameter δ) for a hypothetical particle traveling along the trajectory AB can be obtained:

$$ \updelta (r)=\sqrt{\frac{-{w}_0}{kUH}\ln \left(\frac{r_0}{r}\right)} $$

or, using dependences (2) and (6), in explicit form

$$ \updelta (r)=\sqrt{\frac{18\upmu Q\ln \left({r}_0/r\right)}{{\uppi \upomega}^2\Delta \left({R}^2-{r}_0^2\right) UH}}, $$
(9)

where U is determined from (8).

From assuming in expression (9) that r = R, one arrives at the so-called global δc critical diameter for a particle moving along the trajectory CB,

$$ {\updelta}_{\mathrm{c}}=\sqrt{\frac{18\upmu Q\ln \left({r}_0/R\right)}{{\uppi \upomega}^2\Delta \left({R}^2-{r}_0^2\right) UH}}. $$
(10)

If the liquid water + oil mixture is preliminarily uniformly mixed and its mass distribution function Ф is given, a quantitative analysis of the kinetics of sediment accumulation is carried out on the basis of the parameter characterizing the separation intensity – the clarification factor η (%), as the value reduced in terms of m0 the mass of the floating phase (oil) taking into account the given parameters of the problem and the dispersity of this phase [6]:

$$ \upeta =\frac{m_1}{m_0}=\frac{200}{R^2-{r}_0^2}\underset{r_0}{\overset{R}{\int }}\Phi \left[\updelta (r)\right] rdr, $$
(11)

where m1 is the mass of floating particles; δ(r) is the current critical diameter of the oil particle (9); Φ(δ) is the mass characteristic function of the particle size distribution δ of oil, such that

$$ \Phi \left(\updelta \right)=m\left(\updelta >{\updelta}^{\prime}\right)/{m}_0, $$
(12)

where m0 is the mass of oil in the initial suspension; and m(δ > δ′) is the mass of oil particles of size δ > δ′ in the same liquid system.

In such a case, according to the calculation and the technological procedure, the mass of the oil particles floating up in unit time from the working volume of the apparatus through the upper nozzle is

$$ {m}_1={m}_0\upeta /100, $$
(13)

where η is determined by formula (11).

Equations (9)–(13) are the basis for a quantitative analysis of the process of separation of an oil substance suspended in an aqueous medium in a hydrocyclone. In actual conditions, as a parameter for controlling the separation process, it is expedient to choose the productivity Q of the hydrocyclone.

To improve the efficiency of the separation process, in general, recirculation of the suspension in recirculation mode (including the creation of so-called battery-type devices from hydrocyclones) is generally applied.

Consider the case where it is required to obtain a fugate with the smallest ζ relative oil content by the successive treatment of the clarified suspension (fugate) in the recirculation mode n times. It can be assumed for simplicity that in the fugate at each stage of the clarification process the entrainment coefficient ε = 1 – η has a constant value, then the number n of the recirculation stages must satisfy the inequality

$$ {\upvarepsilon}^n\le \upzeta, $$

or in explicit form

$$ n\le \log \upzeta /\log \upvarepsilon . $$
(14)

The numerical experiment. Physicomechanical parameters of the water + oil suspension were the following: water density ρ = 1000 kg/m3; oil density (average) ρ1 = 850 kg/m3; volume concentration of oil in suspension (conditionally) c = 0.05, 0.1, ..., 0.6 (5, 10, ..., 60%); kinematic viscosity of the suspension (approximate) ν = 10–6, 2·10–6 m2/sec; particle size (from medium-dispersed to coarse-grained) 20·10–6 < δ < 300·10–6 m; flow rate (production capacity) of the hydrocyclone Q = 2, 3, ..., 5 m3/h; inlet pressure p = 100, 200 kPa (H1 = 10, 20 m of water column); the cone angle of the conical part of the hydrocyclone was α = 20°.

Justification of the geometric and regime parameters of the hydrocyclone. Diameter of the inlet nozzle [2] can be described by

$$ {d}_0=\frac{0.017\sqrt{Q}}{\sqrt[4]{100{H}_1}}, $$
(15)

where d0 is the diameter of the nozzle, m; Q is the volumetric productivity of the hydrocyclone, m3/h; H1 is the pressure at the inlet of the hydrocyclone, kPa.

The diameter of the cylindrical part of a hydrocyclone is

$$ {D}_1=5{d}_0, $$

then the radius of the cylindrical part (see Fig. 1b) [2] is

$$ {R}_1=2.5{d}_0, $$
(16)

where d0 is calculated using (15).

Diameter of the upper nozzle (hydrocyclone outlet) is

$$ {D}_3=\frac{Q}{850{D}_1\sqrt{100{H}_1}}, $$

then the radius of the upper nozzle is

$$ {R}_3=\frac{Q}{3400{R}_1\sqrt{100{H}_1}}. $$
(17)

The radius of the lower nozzle is determined by [2]

$$ {R}_2={R}_3/1.4, $$
(18)

where R3 is calculated using (17).

As a result, taking the height of the cylindrical part of the hydrocyclone to be

$$ {h}_1={D}_1/2={R}_1 $$
(19)

and the height of the cylindrical part to be

$$ {h}_2=\left({R}_1-{R}_2\right)\tan \left(\upalpha /2\right), $$
(20)

the following expression is obtained for calculating the hydrocyclone:

$$ W=\uppi {R}_1^2{h}_1+\frac{h_2}{3}\left({R}_1^2+{R}_2^2+{R}_1{R}_2\right), $$
(21)

where R1, R2 are calculated according to Eqs. (16), (18), and h1, h2 – using Eqs. (19), (20).

The height of the hydrocyclone modeling cylinder is

$$ H={h}_1+{h}_2, $$
(22)

the radius of this cylinder, taking into account (22), is determined from Eq. (1).

The flow rate in the inlet nozzle (tangential velocity in the cylindrical part of the hydrocyclone) is

$$ {V}_0=\frac{Q}{900\uppi {d}_0^2}, $$
(23)

where d0 is calculated from formula (15); Q is the flow rate of the suspension at the inlet, m3/h.

It is proposed to determine the distribution of the tangential flow velocity from the dependence [1]

$$ v(r)=\upomega r, $$

where ω is the effective angular velocity of flow, conditionally

$$ \upomega =\frac{V_0h}{1.2{R}_1\left({R}_1-{R}_3\right)}; $$
(24)

V 0 is calculated by formula (23); R1 is the radius of the cylindrical part of the hydrocyclone, determined according to formula (16); R3 is calculated from expression (17).

The radius r0 of the free surface of the flow in a cylinder of radius R is calculated from the formula

$$ {r}_0=\sqrt{R^2-\frac{Q}{3600\uppi {V}_0}}, $$
(25)

where V0 is found from Eq. (23).

As a result, in accordance with formulas (1), (16)–(18), (22)–(25) at (24), (25) and at the selected flow rates of the suspension Q = 3 m3/h, and the inlet pressure in hydrocyclone H1 = 100 kPa, the following values of the task parameters were obtained: R1 = 41 mm; R2 = 4.8 mm; R3 = 6.7 mm; R = 40 mm; r0 = 39 mm; ω = 33 rad/sec; w0 = 3.87 m/sec.

Assuming that ν = 1.6·10–6 m2/sec, the following expression was obtained for the (3) Reynolds number in the axial direction:

$$ {\operatorname{Re}}_z=\frac{w_0\left(R-{r}_0\right)}{\upnu}=\frac{3.87\cdot \left(0.04-0.039\right)}{1.6\cdot {10}^{-6}}=2120. $$

Assuming that Δ = 150 kg/m3, δ = 10–4 m are the process parameters, according to the (4) Reynolds number in the radial direction, under the conditions of applicability of the Stokes law, it was determined that

$$ {\operatorname{Re}}_r=\frac{\upomega^2R{\Delta \updelta}^3}{18{\uprho \upnu}^2}=\frac{77.9^2\cdot 0.04\cdot 150\cdot {\left({10}^{-4}\right)}^3}{18\cdot {10}^3\cdot {\left(1.6\cdot {10}^{-6}\right)}^2}=0.14. $$

Thus, according to the calculated values of the Reynolds numbers in the axial and radial directions, the quantitative analysis carried out in this paper is correct.

Assuming that the oil phase of the suspension is polydisperse, the mass characteristic distribution function of this phase in terms of size is

$$ {\displaystyle \begin{array}{lll}\Phi \left(\updelta \right)=\left\{\begin{array}{l}\begin{array}{lll}1& \mathrm{for}& 0\le \updelta \le {\updelta}_1;\end{array}\\ {}\left({\updelta}_2-\updelta \right)/\left({\updelta}_2-{\updelta}_1\right)\\ {}\begin{array}{lll}1& \mathrm{for}& \updelta \ge {\updelta}_2\end{array},\end{array}\right.& \mathrm{for}& {\updelta}_1<\updelta <{\updelta}_2\end{array}}; $$
(26)

where δ1 = 20·10–6 m, δ2 = 300·10–6 m, respectively, are the minimum and maximum particle diameters of the oil phase, which corresponds to the permissible range of sizes of medium- and coarsely dispersed particles.

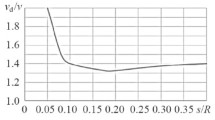
The results of calculations based on the above parameters, Eq. (11), and distribution (26) of the oil phase in the liquid according to the clarification coefficient are presented in the form of graphs in Fig. 2. Analysis of the curves revealed a dependence of the clarification coefficient on the process parameters of the separation process consistent with the physical meaning of the problem (for fixed values of the remaining parameters).

Fig. 2.
figure 2

Clarification coefficient η as a function of the flow rate Q of a medium-weight suspension for various values of dynamic viscosity μ and concentration c of the oil phase: a) H1 = 100 kPa; b) H1 = 200 kPa; μ = 0.001 Pa·sec: 1, 5) с = 5%; 2, 6) c = 10%; μ = 0.002 Pa·sec: 3, 7) с = 5%; 4, 8) c = 10%.

Full size image

Medium-weight suspension. The decay factor η decreases with increasing concentration c, i.e., the efficiency of the slurry separation process is shown to decrease with a thickened slurry (curves 5, 6 and 7, 8, respectively; see Fig. 2b), as well as a greater dynamic viscosity μ (curves 5, 7 and 6, 8, see Fig. 2b).

At the same time, as it should be, the coefficient η also decreases (that is, the severity of separation of the suspension deteriorates) with an increase in the flow rate of the suspension (all the curves in Figs. 2 and 3).

Fig. 3.
figure 3

Clarification coefficient η as a function of flow rate Q of a dense suspension for different values of dynamic viscosity μ and concentration c of the oil phase: a) H1 = 100 kPa; b) H1 = 200 kPa; μ = 0.001 Pa·sec: 1, 5) с = 50%; 2, 6) c = 60%; μ = 0.002 Pa·sec: 3, 7) с = 50%; 4, 8) c = 60%.

Full size image

Very dense suspension. For all the graphs in Figs. 2, 3, an increase in separation intensity is noted together with an increase in the fluid pressure at the hydrocyclone inlet. At the same time, for dense suspensions (on the order of 50 and 60%), the efficiency of the separation process is low and practically barely exceeds 4% (see Fig. 3a, b).

In conditions of an average concentration of the suspension (on the order of 5 and 10%), an increase in the efficiency of the separation process can be ensured by re-treating the suspension in the recirculation mode over a finite number of stages in the separation process calculated by formula (14).

Thus, for example, if the initial suspension with a volume concentration c = 5% of oil is treated at a pressure of H1 = 100 kPa at a flow rate Q = 3 m3/h, a fugate should be produced containing no more than ζ = 0.1 (10%) of the initial oil content in the suspension. Then, for the example under consideration, when ε1 = 1 – η1/100 = 0.859 (see Fig. 2a), according to (14) the number n of processing steps is no more than

$$ n\le \log \upzeta /\log {\upvarepsilon}_1=\log {10}^{-1}/\log 0.859=15.1. $$

Assuming that n = 15, is can be concluded that in order to process the slurry it is necessary (taking into account also the first stage) to carry out only 16 steps of the process of separation of the water + oil suspension. If it is required to reduce the initial oil content by a factor of 100 (down to 1%), then the number n of processing steps is 31. At a pressure of H1 = 200 kPa, flow rate of Q = 3 m3/h, and concentration c = 5% for the degree of cleaning of the suspension from the oil impurities to 10 and 1%, according to Fig. 2 and the calculation, the number of stages of processing is no more than 10 and 18 cycles, respectively.

Conclusions. In accordance with the quantitative analysis of the task, it can be concluded that in the calculated range of hydrocyclone performance values of 2–5 m3/h and for medium and coarse dispersion of the particles of the oil phase in the suspension (particle size variation (20–300)·10–6 m):

  1. 1)

    at a pressure of 100 kPa at the inlet of the apparatus for a medium-weight suspension (the volume concentration of the petroleum phase c is 5, 10%), the value of the clarification coefficient varies from 4.7 to 17.2%, and from 7.8 to 28.8 % at a pressure of 200 kPa;

  2. 2)

    at a pressure of 100 kPa at the input of the apparatus for a highly concentrated suspension (the volume concentration of the oil phase c is 50, 60%), the value of the clarification coefficient varies from 0.4 to 2.5%, and from 0.67 to 4.25% at a pressure of 200 kPa;

  3. 3)

    since for the considered example the calculated values of the global critical diameter are higher than the values of the diameters related to fine particles, it follows (according to the calculation) that the use of the hydrocyclone for separating particles of less than 20 μm from the suspension is ineffective;

  4. 4)

    with the selected technological parameters of the equipment, for effective separation of oily wastewater in hydrocyclones, it is necessary to carry out the process in the recirculation mode.