Scale Properties of Anisotropic and Isotropic Turbulence in the Urban Surface Layer

Abstract

The scale properties of anisotropic and isotropic turbulence in the urban surface layer are investigated. A dimensionless anisotropic tensor is introduced and the turbulent tensor anisotropic coefficient, defined as C, where $C = 3d_{3}\,+\,1 (d_{3}$ is the minimum eigenvalue of the tensor) is used to characterize the turbulence anisotropy or isotropy. Turbulence is isotropic when $C \approx 1$, and anisotropic when $C \ll 1$. Three-dimensional velocity data collected using a sonic anemometer are analyzed to obtain the anisotropic characteristics of atmospheric turbulence in the urban surface layer, and the tensor anisotropic coefficient of turbulent eddies at different spatial scales calculated. The analysis shows that C is strongly dependent on atmospheric stability $\xi = (z-z_{\mathrm{d}})/L_{{\textit{MO}}}$, where z is the measurement height, $z_{\mathrm{d}}$ is the displacement height, and $L_{{\textit{MO}}}$ is the Obukhov length. The turbulence at a specific scale in unstable conditions (i.e., $\xi < 0$) is closer to isotropic than that at the same scale under stable conditions. The maximum isotropic scale of turbulence is determined based on the characteristics of the power spectrum in three directions. Turbulence does not behave isotropically when the eddy scale is greater than the maximum isotropic scale, whereas it is horizontally isotropic at relatively large scales. The maximum isotropic scale of turbulence is compared to the outer scale of temperature, which is obtained by fitting the temperature fluctuation spectrum using the von Karman turbulent model. The results show that the outer scale of temperature is greater than the maximum isotropic scale of turbulence.

1 Introduction

The local homogeneous isotropic turbulence theory, which is widely used at present, claims that the power spectrum of homogeneous isotropic turbulence follows a $-5/3$ power law in the inertial subrange while the structure function is consistent with a 2/3 power law (Frisch 1995). However, many studies suggest that actual turbulence, especially large-scale turbulence, is generally anisotropic, so that the anisotropic turbulence spectral density deviates from the $-5/3$ power law, and the structure function deviates from the 2/3 power law (Lumley and Newman 1977; Arad et al. 1999; Biferale and Vergassola 2001; Choi and Lumley 2001). Many concepts and characteristic parameters have been proposed to describe anisotropic turbulence. For example, Hocking and Hocking (2007) defined the degree of upper atmospheric turbulent anisotropy using the variation of the backscatter power of very high frequency wind-profiler radar using different viewing angles. Darbieu et al. (2015) described anisotropy using the ratio of the horizontal to vertical velocity variance, and Newsom et al. (2008) calculated the anisotropic parameter using the ratio of the integral length of the longitudinal to that of the transverse velocity component. Gurvich (1997) defined turbulent anisotropy according to the ratio of the horizontal fluctuation characteristic scale to the vertical fluctuation characteristic scale based on light-beam scintillation through the turbulence field. Additionally, an anisotropic tensor was introduced to study the transition from anisotropic turbulence to isotropic turbulence (Lumley and Newman 1977). Biferale and Procaccia (2005) described anisotropic features using an odd-order structure function and decompressed turbulence into an isotropic component and anisotropic component using the series expansion method. Wind shear was found to have a relationship with the characteristics of anisotropy in wind-tunnel (Saddoughi 1997), water-channel (Poggi et al. 2003) and numerical simulation studies (Toschi et al. 2000; Ishihara et al. 2002). Yuan et al. (2014) defined the anisotropic parameter as the ratio of the peak wavelength of the light intensity fluctuation spectrum in the horizontal direction to that in the vertical direction, considering the effect of anisotropic turbulence on light propagation.

Many methods have been applied to the analysis of anisotropic features of turbulence; however, isotropic theory is widely used due to its simplicity. The current issue regarding the application of isotropic turbulence theory concerns determining the scale at which the actual turbulence is close to or satisfies the isotropic assumption; thus, isotropic theory can be applied within this range. Turbulence is generally considered to include a number of turbulence eddies with different scales, and the scale of atmospheric turbulence can increase by several orders of magnitude (Panchev 1971), and the outer scale of turbulence is generally considered the maximum isotropic scale (Panchev 1971). The turbulence behaves anisotropically when the scale of turbulence is greater than the outer scale. There are many definitions of the turbulent outer scale, such as the saturated scale of the phase structure function of light waves (Ziad et al. 2000) and the scale of maximum turbulent kinetic energy (TKE) (Klipp 2014). Different measurement methods have been used to examine the turbulent outer scale, which generally ranges from 1 m to 2 km (Consortini et al. 2002; Ziad et al. 2004; Lukin 2005). However, the relationship between the turbulent outer scale and the isotropic scale requires further investigation.

The present study focuses on the anisotropic and isotropic features of turbulence in the urban surface layer. The underlying surface of an urban region is heterogeneous due to complex terrain and the arrangement of buildings, which influence the wind field, temperature field, water vapour and mass distributions. The turbulent features in the urban boundary layer, especially in the surface layer, are affected by the complexity of the urban surface layer. The turbulent features in the urban surface layer are important for the exchange of material, momentum and energy between the urban surface layer and atmosphere, as well as for urban pollution diffusion. In the urban surface layer, the maximum isotropic scale and the degree to which turbulent eddies are isotropic, over a scale greater than the maximum isotropic scale, must be determined. The nature of turbulence varies for boundary-layer flow over different cities, or over different sites in the same city due to the complexity of the urban surface layer. Thus, more experiments must be conducted to study isotropic and anisotropic turbulence in the urban surface layer.

Here, we focus on the issues noted above and seek to elucidate the isotropic and anisotropic features in the urban surface layer. The results are then compared to existing theory. Section 2 presents the experimental and data processing methods, and the experimental results are presented in Sect. 3. The discussion and conclusions are presented in Sect. 4.

2 Experiment and Methods

2.1 Theory and Method

A flow field $U_{i}$ can generally be divided into the mean speed $\bar{{U}}$ and fluctuating components $u_{i}\,(U_i=\bar{{U}}\delta _{1i} +u_i$, where $i= 1,\,2\,,3$, and $\delta _{{\textit{ij}}}$ is the Kronecker symbol; $u_{i}$ is generally denoted using u, v and w, where u is the streamwise velocity fluctuation, v is the transverse velocity fluctuation, and w is the vertical velocity fluctuation.). The interaction between these components depends on the relationship between the turbulent stress and the mean vertical velocity gradient (Stull 1988). The turbulent stress tensor can be expressed dimensionlessly as follows (Lumley and Newman 1977; Choi and Lumley 2001),

$$\begin{aligned} a_{ij} =\frac{\overline{u_i u_j}}{q}-\frac{\delta _{ij} }{3} \qquad \qquad i,j=\left\{ {1,2,3} \right\} . \end{aligned}$$

(1)

where ${q}/{2}={\overline{u_i u_i }}/{2}=\frac{1}{2}\left( \overline{u_1^{2}} +\overline{u_2^{2}} +\overline{u_3^{2}}\right)$ is the TKE. In fact, every symmetric tensor such as $\overline{u_i u_j}/q$ can be decomposed into the sum of an isotropic part $\delta _{{\textit{ij}}}$ and an anisotropic part $a_{{\textit{ij}}}$. After the tensor $a_{{\textit{ij}}}$ is diagonalized by similarity transformation (i.e., the coordinate system is set aligned with the principal axes of the tensor), all elements of $a_{{\textit{ij}}}$ become zero when turbulence behaves isotropically, and non-zero diagonal terms exist in $a_{{\textit{ij}}}$ when turbulence behaves anisotropically (because $a_{{\textit{ij}}}$ is symmetric, the off-diagonal terms are zero based on diagonal transformation). Thus, $a_{{\textit{ij}}}$ is also known as an anisotropic tensor (Lumley and Newman 1977; Choi and Lumley 2001).

Turbulence in the lower atmosphere behaves anisotropically almost all the time; thus, the diagonal terms in $a_{{\textit{ij}}}$ based on diagonal transformation are non-zero, and the deviation of the values of the elements of $a_{{\textit{ij}}}$ from zero reflects the extent of anisotropy. Due to the complexity of the turbulence stress in mathematical methods, it is difficult to denote the anisotropic properties of turbulence. The three eigenvalues of a stress matrix are independent of the coordinate system; hence, the three eigenvalues of the non-dimensional anisotropic tensor $a_{{\textit{ij}}}$ can be used to denote the anisotropic properties of turbulence and sorted by size to yield $d_{1}, d_{2}$ and $d_{3}$, (where $d_{1}+d_{2}+d_{3}= 0$), and a tensor anisotropic coefficient C can be defined as follows (Banerjee et al. 2007)

$$\begin{aligned} C = 1 + 3 d_{3}. \end{aligned}$$

(2)

Turbulence behaves isotropically when $C=$ 1 and one-dimensionally or two-dimensionally when C is zero. It is generally accepted that small-scale turbulence is close to isotropic, whereas large-scale turbulence deviates from the isotropic assumption. Thus, we must decompose the turbulent stress at different scales, and expand the turbulent stress tensor using Fourier transform and focus on the anisotropic tensor in spectral space. Thus, we can obtain the anisotropic spectral tensor $S_{{\textit{ij}}}\,(\kappa )$ whose wavenumber is $\kappa$,

$$\begin{aligned} s_{{\textit{ij}}} (\kappa ) =\frac{E_{{\textit{ij}}} (\kappa )}{p(\kappa )}-\frac{\delta _{{\textit{ij}}}}{3} \quad i,j=\left\{ {1,2,3} \right\} . \end{aligned}$$

(3)

Here $E_{{\textit{ij}}} \left( \kappa \right)$ is the spectral distribution of $\overline{u_i u_j}$ based on Fourier transform, where $p\left( \kappa \right) =E_{ii} \left( \kappa \right) =E_{11} \left( \kappa \right) +E_{22} \left( \kappa \right) +E_{33} \left( \kappa \right)$. $E_{11}\,(\kappa ),\,E_{22}\,(\kappa )$ and $E_{33}(\kappa )$ denote the spectral density at wavenumber $\kappa$, and $E_{12}(\kappa ),E_{13}(\kappa )$ and $E_{23}(\kappa )$ denote the cospectral density at wavenumber $\kappa$. The tensor anisotropic coefficient $C(\kappa )$ for each wavenumber can be calculated similar to Eq. 2. The degree to which the turbulence is close to isotropic can be determined for different scales according to the tensor anisotropic coefficient C.

The turbulent data were detrended by removing the best-fit line, and then a rectanglar window applied for spectral (cospectral) calculations. To decrease spectral (cospectral) density calculations, 1-h velocity data at 10 Hz were divided into several segments. Using a fast Fourier transformation, the turbulent data in each segment can be transformed to the frequency domain, and then to the wavenumber domain to obtain the spatial spectra and cospectra using Taylor’s frozen turbulence hypothesis (Lumley 1965; Wyngaard and Clifford 1977). Then, the components of the tensor matrix $s_{{\textit{ij}}}(\kappa )$ can be obtained by averaging the spectra and cospectra of several segments (details in Appendix).

To compare the isotropic range and the outer scale, the von Karman spectrum model (von Kármán 1948) for one-dimensional data is used to fit the actual spectra,

$$\begin{aligned} \Phi (\kappa )\propto \left( \kappa ^{2}+\frac{1}{L_0^{2}}\right) ^{-5/6}. \end{aligned}$$

(4)

where $L_{0}$ is the turbulent outer scale. Equation 4 is widely used, although many spectral models have been used to describe the turbulence power spectrum. The results of different models are similar (Maire et al. 2008). Equation 4 is used to fit the actual spectrum to deduce turbulence parameters such as $L_{0}$ and the average TKE dissipation rate.

Fig. 1

Power spectra of u (a), and temperature T (b) at 0100 LT on October 4 2013, based on fast Fourier transform. The averaged actual spectra are shown using the filled-circle solid line. The spectrum fitted using Eq. 4 is shown using the solid line, and 95% confidence limits are given by the dotted lines. In (a), the abscissa of the intersection between the $-5/3$ line and the 95% confidence limit is indicated by the vertical dashed line

Figure 1 is an example of fitting the actual u spectral data and temperature (T) data at 0100 local time (LT) on October 4 2013 using Eq. 4. The fitted spectra display good agreement with the actual spectra. For u data (Fig. 1a), three data points in the low-frequency range of the actual spectrum fall outside of the 95% confidence limit, and the high-frequency range of the fitted spectrum approaches the function $\Phi (\kappa )=\alpha _1 \varepsilon ^{2/3}\kappa ^{-5/3}$(Kaimal et al. 1972), where $\alpha _{1}$ is a universal constant approximately equal to 0.5, and $\varepsilon$ is the average TKE dissipation rate per unit mass. Additionally, the lowest wavenumber limit of the $-5/3$ power can be determined as shown in Fig. 1a, which is $\kappa = 0.0072\,\hbox {m}^{-1}$. For temperature data (Fig. 1b), the parameter $L_{0}$ in Eq. 4 can be obtained as 68 m.

Surface-layer structure and turbulent features are strongly dependent on atmospheric stability (Stull 1988), represented by the dimensionless parameter $\xi = (z -z_{\mathrm{d}})/L_{{\textit{MO}}}$, where z is the measurement height, $z_{\mathrm{d}}$ is the displacement height, and $L_{{\textit{MO}}}$ is the Obukhov length $L_{{\textit{MO}}} =-\frac{1}{k_a }\frac{\bar{{T}}}{g}\frac{u_{*}^3 }{\overline{tw}}$, where g is the acceleration due to gravity, T is the air temperature $(T=\bar{{T}}+t), k_{a}$ is the von Karman constant, $k_{a} = 0.4, u_*$ is the friction $\hbox {velocity }\left( u_*^{2}=\left( \overline{uw}^{2}+\overline{vw}^{2}\right) ^{1/2}\right)$, and u, v and w are the three fluctuation velocity components.

2.2 Experiment and Data

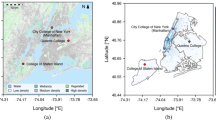
The experiments were performed on the campus of the University of Science and Technology of China (USTC), as shown in Fig. 2. Figure 2a is a map of south Hefei City in China, and Fig. 2b displays the measurement site on the USTC campus corresponding to the shadowed portion of Fig. 2a. As shown in Fig. 2a, the measurement site is a typical urban surface in the area, where roads near the campus often experience heavy traffic. One road to the west of the campus is a bypass road, and one road to the north has eight lanes; these two roads are arterial highways in Hefei City. There are trees and four-storey buildings in most areas of the campus, except the southernmost and northernmost tall buildings (points A and B in Fig. 2b). The tops of the trees are almost as high as the roofs of the four-storey buildings; therefore, the canopy layer of the campus is at one level, which can be used as a canopy plane (Yuan et al. 2016). A meteorological tower was installed on the roof of a building close to the centre of the campus, the top of which is 13 m above the canopy plane. A CSAT3 sonic anemometer was mounted near the top of the tower, with sampling frequency of 10 Hz. The three-dimensional velocity data from the sonic anemometer were used to analyze the anisotropic features of turbulence. Three RM Young 03002 anemometers and three HMP155A temperature and humidity sensors were mounted at three levels on the tower (13, 8 and 5 m above the canopy plane), from which vertical gradients of wind speed, wind direction, temperature and humidity could be calculated.

Fig. 2

Photographs of the measurement site: a Map of Hefei City, b expanded view of the measurement site on the USTC campus, which is denoted by the shaded rectangle in a. Points A and B indicate two high buildings, and Point C in c indicates the site of the meteorological tower

The measurement period was from June 2013 to December 2015, for a total of 781 days. Because of the large variations in meteorological parameters in the atmospheric boundary layer, only data from sunny days were analyzed. Based on the theoretical value of the downwards solar radiative flux (CMA 1996), the days with observed solar flux greater than 70% of the theoretical value were selected as sunny days. The error flag of the sonic anemometer was also used to identify false data. Other quality assurance and quality control for the data were performed according to the suggestions in Foken et al. (2004); thus, approximately 4400 hours of data were statistically analyzed.

3 Experimental Results

3.1 Terrain Feature Analysis

The urban underlying surface is very complex in general, and the complexity consists of thermal and dynamic heterogeneities. Field experiments show that assumptions for ideal conditions, such as horizontally homogeneous surfaces free of obstacles and steady-state conditions, cannot be successfully applied to the boundary layer over heterogeneous surfaces (Roth 1993). The urban surface is difficult to approximate as a plane due to the obvious fluctuations in urban building heights. Therefore, the urban boundary layer can be divided into the urban canopy layer, the roughness layer, the inertial sublayer and the mixed layer (Fernando 2010). However, this is not always the case. At our campus experimental site, trees and four-storey buildings are located in most areas, and excluding some pavements, the mean height of trees and buildings is approximately 12 m; therefore, the canopy layer can be regarded as a plane, namely, the canopy plane. The meteorological tower is close to the centre of the campus and is 200 m from the nearest 16-storey building to the south. The top of the tower is 13 m above the canopy plane, and the top of the tallest building is 36 m above the canopy plane; thus, the influence of the building on the tower is insignificant according to the tilt angle of the wind vectors illustrated in Fig. 3. In Fig. 3, the abscissa represents the azimuth from the north to the wind direction rotating clockwise. The ordinate is the tilt angle of the wind vectors, which is calculated from the ratio of the vertical velocity to the horizontal velocity component obtained from the sonic anemometer. The velocity was sampled at 10 Hz and averaged every 1 h to obtain the mean wind speed. Only data with a wind speed ${>}1\,\hbox {m s}^{-1}$ are shown in Fig. 3. Additionally, Fig. 3 shows that more than 90% of the tilt angles of the wind vectors are less than $4{^{\circ }}$.

Fig. 3

The distribution of the wind vector tilt angle with wind direction. The grey curve is based on Eq. 5

When the flow is in a mean streamline plane, the relationship between the tilt angle $\alpha$ (Eq. 5) of the wind vector and the azimuthal angle of the horizontal wind direction can be expressed as follows (Wilczak et al. 2001)

$$\begin{aligned} \tan \alpha =\frac{\bar{{w}}}{\bar{{U}}}=\tan \varphi \sin \theta , \end{aligned}$$

(5)

where $\alpha$ is the tilt angle of the velocity vector, $\varphi$ is the angle between the mean streamline plane and the horizontal plane, and $\theta$ is the azimuth angle. We obtain the white line in Fig. 3 by fitting Eq. 5. As shown in Fig. 3, the tilt angle of the mean streamline plane is within $2{^{\circ }}$, and the mean streamline plane can be considered a slope from east to west. This slope is mainly affected by the distribution of the buildings on the campus, because the anemometers was levelled to within less than 0.1 degree and the effects of instrument tilt was very small and omitted (Wilczak et al. 2001). The mean vertical velocity, which is normalized by the horizontal wind speed, can be represented as a simple sinusoidal function of the wind azimuth, hence, the experimental site can be considered a homogeneous plane.

3.2 Statistical Features of the Anisotropic Tensor Coefficient

As a case study, the data collected on October 4 2013, which was a sunny day, were analyzed. Figure 4 illustrates the variations in the temperature, wind velocity, wind direction and stability $\xi$ through the day. The temperature shows typical diurnal variations in Fig. 4a, while Fig. 4b shows variations of the horizontal wind speed at the measurement heights of 13 m and 8 m during the day, with mean values of 1.89 and $1.45\hbox { m s}^{-1}$, respectively, which are close to the mean values of 1.9 and $1.6\hbox { m s}^{-1}$ calculated throughout the whole year. Figure 4c presents the variations in wind direction (mainly east-south-easterly), and Fig. 4d illustrates the stability parameter $\xi$, with $\xi =(z-z_{\mathrm{d}})/L_{{\textit{MO}}}$, where $z_{\mathrm{d}}$ is approximately 0.85 times the canopy height (Zou et al. 2015). Notably, the atmospheric stratification is unstable during the day and stable at night, features that correspond to typical boundary-layer characteristics (Stull 1988).

The spectral and cospectral densities were calculated at different frequencies in three directions at 0100 and 1200 LT on October 4 2013. According to Taylor’s frozen turbulence hypothesis, the frequency spectrum and cospectrum can be transformed to the spatial spectrum and cospectrum, and corrections were performed using the method proposed by Wyngaard and Clifford (1977). Then, anisotropic tensors and the turbulent tensor anisotropic coefficient C were calculated using Eq. 3, as shown in Fig. 5. The abscissa represents the scale, and the ordinate represents the turbulent tensor anisotropic coefficient C. The two curves of the coefficient C at 0100 and 1200 LT are shown in Fig. 5, with stability values of 1.01 and $-0.421$, respectively. As can be observed from Fig. 5, the anisotropic coefficient reaches a maximum value when the scale is small, and the anisotropic coefficient decreases gradually as the scale increases. The tensor anisotropic coefficient of a specific scale under stable conditions is less than that under unstable conditions at the same scale.

Fig. 4

Diurnal variations in temperature T (a), wind speed $\bar{U}$, b (at a height of 13 m (solid line) and height of 8 m (dotted line)), wind direction (WD), c and stability $\xi$, d on October 4, 2013

Fig. 5

The tensor anisotropic coefficient at 0100 LT (the dashed line is for stable stratification with $\xi = 1.01$) and 1200 LT (the solid line is for unstable stratification with $\xi = -0.42$) on October 4 2013

Fig. 6

Variation in the turbulent tensor anisotropic coefficient C at different scales $\lambda$ on October 4 2013

Fig. 7

The distribution of the anisotropic coefficient C with $\xi$. The colour bar on the right side denotes the tensor anisotropic coefficient. An explanation of the black bold line can be found in the text

Figure 6 presents the distribution of the turbulent anisotropic coefficient at different scales throughout the day. The turbulent anisotropic coefficient decreases as the scale increases, which is consistent with the results illustrated in Fig. 5. Additionally, the anisotropic coefficient exhibits diurnal variations, and the anisotropic coefficient during the day is significantly greater than that at night at a specific scale. Thus, the turbulence at a specific scale is closer to isotropic during the day and closer to anisotropic at night.

Figure 7 presents the variations in the turbulent tensor anisotropic coefficient with stability in the surface layer, where an obvious relationship exists between the scale of a specific coefficient and the stability. The scale of a specific tensor anisotropic coefficient under unstable conditions is greater than that under stable conditions; under stable stratification, the scale decreases as the stability $\xi$ increases gradually. The turbulence produced by wind shear is mitigated by the stratification. The stronger the stability of the stratification, the less turbulence develops in the vertical direction. As can be observed in Fig. 7, the scale varies little under unstable stratification, which may be related to the measurement height.

The data in Fig. 7 are grouped as four different wind directions, (namely easterly, southerly, westerly and northerly directions respectively), and analyzed as above. Same trends of the distribution of the anisotropic coefficient versus atmospheric stability at different wind direction as Fig. 7 can be found (not shown here), implying that buildings far from the meteorological tower have little influence on the measurements.

3.3 Spectrum of Turbulent Fluctuations and the Maximum Isotropic Scale

Although the isotropic turbulence theory is commonly used, previous analyses showed that the tensor anisotropic coefficient of turbulence in the actual surface layer $\ne 1$, even at a very small scale. Thus, we consider the degree to which the real turbulence agrees with the isotropic assumption, and the scale at which the real turbulence agrees with the isotropic assumption to determine the scale range in which the isotropic theory can be applied. The criteria are set so that the power spectra in the u, v, and w directions obey the $-5/3$ law, and the spectral ratios $({E}_{11}(\kappa )/{E}_{22}(\kappa )$ and ${E}_{11}(\kappa )/{E}_{33}(\kappa ))$ equal 3/4 within the isotropic range (Tennekes and Lumley 1972; Kaimal and Finnigan 1992).

Fig. 8

The maximum anisotropic scale and velocity spectrum fits in three directions (a–c) under the condition of unstable stratification at 1200 LT on October 4 2013; the wind speed is $2.41\,\hbox {m s}^{-1}$

Figures 8 and 9 show the three-dimensional velocity spectrum and the methods used to determine the maximum isotropic scale of turbulence at 0100 and 1200 LT, October 4 2013, with $\xi = 1.01$ and $-0.421$, respectively. The abscissa is the wavenumber $(\kappa = f/\bar{{U}}$, where f is the frequency, $\bar{{U}}$ is the mean wind speed in a 1-h measurement period), and the ordinate is the spectral density. Figure 8a–c show the power spectral density corresponding to u, v and w, respectively. The solid line is the best-fit velocity spectrum, the dotted line is the velocity spectrum of the 95% confidence limit, and the black straight line is the $-5/3$ power law. The part of the $-5/3$ line in the 95% confidence range of the velocity spectrum is considered to obey the $-5/3$ law; as a result, we can determine the minimum wavenumber that obeys the $-5/3$ law. Figure 8 shows that the minimum wavenumbers are $0.0042\hbox { m}^{-1}, 0.0041\hbox { m}^{-1}$ and $0.034\hbox { m}^{-1}$ for the u, v, and w spectra, respectively. In the horizontal direction, the wavenumber range in which the u and v spectra follow the $-5/3$ law is far greater than that in the vertical spectrum. Thus, as shown in Fig. 8d, the minimum wavenumber that satisfies the turbulence isotropy theory is $0.034\hbox { m}^{-1}$ during the measurement period. The corresponding spatial scale is approximately 29 m according to Taylor’s frozen turbulence hypothesis. We define this scale to be the maximum scale of isotropy $\lambda _{{\textit{iso}}}$. Additionally, Fig. 8d shows that in the isotropic range, the ratio of the spectral density of u to w or v to w is close to 3/4. Similar results can be obtained from Fig. 9 under stable conditions, i.e., in the horizontal velocity spectrum, the range that satisfies the isotropic condition is larger than that in the vertical velocity spectrum, and in the measurement period, the maximum turbulent isotropic scale is approximately 18.5 m. Turbulence behaves anisotropically with scale larger than the maximum isotropic scale. Figures 8 and 9 illustrate that under unstable stratification conditions, the maximum isotropic scale is larger than that under stable stratification. Figure 10 presents the variations in the maximum scale over time on October 4 2013; additionally, Fig. 10 illustrates the results based on the Corrsin criterion method (Corrsin 1958; Saddoughi and Veeravalli 1994). In this method, the larger scale limit of locally isotropic behaviour $\lambda _{1}$ given by $\lambda _1 =6\pi (\varepsilon S^{3})^{-1/2}$ where S is the mean shear and $\varepsilon$ is the average TKE dissipation rate per unit mass. The two curves have the same trends, namely, the value of the maximum isotropic scale is larger at noon and smaller in the morning and evening. The difference between the two curves in Fig. 10 may be attributed to not considering convection and thermal stratification in Corrsin’s criterion, which assumes that anisotropy was mainly due to the mean wind shear (Corrsin 1958; Saddoughi and Veeravalli 1994). As we know, the emergence of anisotropy is due to wind shear (Toschi et al. 2000; Poggi et al. 2003), and convection and thermal stratification influence the wind shear at large and small scales. Figure 11 shows the temporal variation in the tensor anisotropic coefficient corresponding to the maximum isotropic scale. The average value of the coefficient is approximately 0.5, and no significant diurnal variation can be observed. Thus, a tensor anisotropic coefficient of 0.5 may be set as the cut-off point between isotropic and anisotropic turbulence, which may be referred to as the critical tensor anisotropic coefficient. Additionally, an obvious relationship exists between the maximum turbulent isotropic scale and the degree of stability (i.e., the heavy black line) shown in Fig. 7.

Fig. 9

The maximum anisotropic scale and velocity spectrum fits in three directions (a–c) under the condition of stable stratification at 0100 LT on October 4 2013; the wind speed is $1.41\,\hbox {m s}^{-1}$

Fig. 10

Temporal variation in the maximum isotropic scale on October 4 2013, based on the method presented herein (solid line) and Corrsin’s criterion (dashed line)

Fig. 11

Temporal variation in the tensor anisotropic coefficient corresponding to the maximum anisotropic scale on October 4 2013

Statistics indicate that the horizontal velocity components u and v are in accordance with the isotropic assumption at a large scale and are coincident with each other. In Fig. 12a, the abscissa is the maximum scale $\lambda _{u}$ of the u spectrum and the ordinate is the maximum scale $\lambda _{v}$ of the v spectrum, both obeying the $-5/3$ law in the inertial subrange. Under unstable stratification, the scale is larger than when the stratification is stable. Figure 12b shows that the horizontal and vertical velocitly components are consistent at a small scale, therefore, $\lambda _{u}$ is larger than the maximum scale $\lambda _{w}$ of the w spectrum obeying the $-5/3$ law at the ordinate. Thus, at a small scale, the u, v and w spectra obey the $-5/3$ law, whereas at a larger scale, only the u and v spectra obey the $-5/3$ law, implying that eddies of a comparatively small scale (namely, the maximum isotropic scale) are nearly consistent with isotropic laws, and those of a larger scale only approach isotropy in the horizontal directions.

3.4 Comparison of the Maximum Isotropic Scale and the Outer Scale of Temperature Turbulence

The $-5/3$ law, which is based on the assumption of local homogeneous isotropy, is widely used in the optical turbulence field, where the fluctuations in the refractive index or temperature are expressed by the von Karman model (Andrews and Phillips 2005). In this model, the characteristic scale of turbulence (von Kármán 1948) is considered the outer scale of turbulence (Andrews and Phillips 2005). According to the Kolmogorov local homogeneous isotropic theory, turbulence at a specific scale less than the outer scale behaves isotropically (Tatarskii 1961); hence, it is necessary to compare the maximum isotropic scale $\lambda _{{\textit{iso}}}$ to the outer scale of the temperature fluctuation. Many methods based on light propagation theory, such as the relationship between the turbulence outer scale of turbulence and fluctuations in the arrival angle, have been used to deduce the outer scale of turbulence (Borgnino 1990; Ziad et al. 2004). Currently, the outer scale of turbulence is determined by fitting temperature fluctuation data with the von Karman spectrum model. Figure 13 presents a scatterplot of the outer scale of temperature fluctuation vs. the maximum isotropic scale obtained from velocity values under stable and unstable stratifications, and shows that the former is larger than the latter. On average, the outer scale of turbulence (or the maximum isotropic scale) under unstable stratification is larger than that under stable conditions.

Fig. 12

Scatterplot of the maximum scales that fit the $-5/3$ law in the u spectrum versus the v spectrum in the horizontal plane (a) and scatterplot of the maximum scale that fit the $-5/3$ law in the u spectrum versus the w spectrum (b)

Fig. 13

Scatterplot of the maximum anisotropic scale versus outer scale of the temperature fluctuation

4 Discussion and Conclusions

We analyzed the characteristics of the turbulent scale in the surface layer of the USTC campus in Hefei City. According to local wind-speed measurements, the underlying surface acts homogeneously. Additionally, tensor anisotropic coefficients were obtained from the correlation spectrum of velocity fluctuations at different turbulent scales. The results show that tensor anisotropic coefficients decrease with scale. Small-scale turbulence with a large tensor anisotropic coefficient behaves closer to isotropic than does large-scale turbulence with a small tensor anisotropic coefficient.

When turbulence meets the local homogeneous and isotropic assumptions, the fluctuation spectrum of the turbulence is in accordance with the $-5/3$ law. Thus, the wavenumber range in which the three velocity components meet the $-5/3$ law can be assumed isotropic, and the maximum scale of the isotropic range can be obtained. The tensor anisotropy coefficient corresponding to the maximum scale of the isotropic range is denoted as the critical anisotropic coefficient. If the tensor anisotropic coefficient of an eddy is larger than the critical value, the eddy can be considered to behave isotropically. Although the diurnal variations in the maximum scale of the isotropic range are obvious, the change in the critical anisotropy coefficient is very small, which demonstrates that this method of obtaining the critical anisotropy coefficient is reasonable. Based on the actual fluctuation spectrum of turbulence, the specific critical anisotropy coefficient can be set to 0.5, and the maximum scale of the isotropic range exhibits an obvious diurnal variation. During the daytime, the maximum isotropic scale is approximately 30 m, larger than the maximum isotropic scale at night. Statistical analysis shows that the maximum isotropic scale strongly depends on the atmospheric stability under stable conditions. The maximum isotropic scale decreases when the degree of stability increases (i.e., $\xi$ increases), and compared to that under stable stratification, the maximum isotropic scale is larger when stratification is unstable, and does not change with the degree of stability. Under unstable conditions, large convective cells extend to the boundary-layer top (Courault et al. 2007), and the current measurement height thus may limit the observation of such structures in the convective boundary layer. Then, if the measurement is obtained at a greater height, the maximum isotropic scale may then be related to the degree of stability when stratification is unstable.

Although other methods have been used to determine the maximum isotropic scale based on laboratory data (Corrsin 1958; Saddoughi and Veeravalli 1994), only the effect of mean shear has been included, and the effects of buoyancy ignored. Convection due to buoyancy can also cause shear at small scales, which can lead to anisotropy. The specific critical anisotropy coefficient in the current study include the effects of shear and buoyancy at large and small scales. Current research shows that turbulence eddies with scales less than the maximum isotropic scale approach isotropy.

Although small-scale eddies can be considered isotropic, they do not reach a complete isotropic state and still behave anisotropically because the tensor anisotropic coefficients at the small scale of approximately $0.5\,\hbox {m}$ <1, as shown in Fig. 5. Based on the definition of the tensor anisotropic coefficients $s_{{\textit{ij}}}$ in Eq. 3, although the dimensionless diagonal elements of $s_{{\textit{ij}}}$ depend on the spectral density that decays as $\kappa ^{-5/3}$, and the other off-diagonal elements depend on the cospectral density that decays as $\kappa ^{-7/3}$, at small scales all elements of $s_{{\textit{ij}}}$ will have the same order. Therefore the definition of the tensor anisotropic coefficient characterizes the anisotropic characteristics at a small scale (Ishihara et al. 2002).

The spectra of the horizontal velocity components u and v are the same at a larger scale; however, the spectra of u (or v) and w are the same only at a small scale. Thus, when the scale is larger than the maximum isotropic scale, the eddy is not isotropic in three-dimensional space but is still isotropic in the horizontal plane.

The turbulent outer scale of refractive index fluctuation or temperature fluctuation has an important influence on the fluctuation characteristics of the amplitude and phase of a propagating light wave. If the scale is larger than the outer scale, the turbulence is anisotropic. Fitting with the von Karman spectrum is often used to quantitatively estimate the outer scale; the turbulent outer scale exhibits a similar dependence as the maximum isotropic scale on atmospheric stability.

We used measurement data recorded at one point to obtain a time series, and one-dimensional data in the horizontal direction based on Taylor’s frozen turbulence hypothesis to analyze the isotropic and anisotropic characteristics of turbulence. The outer scale derived from the turbulent spectrum calculation is also related to the one-dimensional data. Influenced by actual atmospheric stratification and wind shear, the horizontal characteristics cannot effectively represent those in the vertical direction. Therefore, to better understand anisotropic turbulence, fine two-dimensional or even three-dimensional observations are required.

Appendix: Method of Spectrum (Cospectrum) Calculation

The 1-h turbulence data (36,000 observations) were detrended by removing the best-fit line, and divided into several segments. Using fast Fourier transformation, the data in each segment were transformed to the spectral densities, and spectra of several segments were then averaged. First, short segments were established to obtain high-frequency spectra, then longer segments were established to obtain low-frequency spectra.

The details of the procedure are as follows:

• 1. By setting the segment length to 64 $(2^{6} = 64)$, the 1-h turbulence data are divided into 563 segments $(36{,}000 = 562\times 64 + 32)$. For segment lengths ${<}64$, zeros are appended to obtain a segment with a length of 64.

• 2. We use fast Fourier transform to establish the spectral density of each segment.

• 3. All 563 spectra are averaged to obtain a mean spectrum with a minimum frequency of 0.1563 Hz $(10/64 = 0.1563)$.

• 4. The length of a segment is set to $128\,(2^{7} = 128)$, and steps 1–3 repeated to obtain a mean spectrum with a minimum frequency of 0.0781 Hz. A spectral density fragment with a frequency range of 0.0781–0.1563 Hz is inserted at the front of the mean spectrum obtained in step 3, and the mean spectrum obtained in step 3 is updated.

• 5. The segment length is increased and the mean spectrum obtained in the last step updated until the segment length (65,536) is larger than the length of the 1-h turbulence data (36,000) by repeating the steps 1–3. Finally, the frequency spectrum of the 1-h turbulence data is obtained.

• 6. According to Taylor’s frozen turbulence hypothesis, the frequency spectrum can be transformed to the wavenumber spectrum. Corrections were performed for the inertial subrange according to Wyngaard and Clifford (1977).

The cospectra of uv, uw and vw can be calculated following the above method. According to Pan and Chamecki (2016), Taylor’s frozen turbulence hypothesis is not suitable for turbulent flow in the lower region of shear layers, but valid for turbulent flow within the upper region of shear layers. Because the sonic anemometer in our study was installed at $z/h\approx 2\,(z$ is the measurement height, h is the canopy height), Taylor’s hypothesis of frozen turbulence is valid (Pan and Chamecki 2016).