1 Introduction

Low-level jets (LLJs) are a common feature of the nocturnal stable boundary layer (SBL) (Song et al. 2005; Karipot et al. 2009), and have been observed at numerous locations over all continents (e.g., May 1995; Banta et al. 2002; Vera et al. 2006; Todd et al. 2008; Karipot et al. 2009; Foken et al. 2012; Wang et al. 2013a). During nighttime over land, the formation of LLJs is typically associated with inertial oscillations (Blackadar 1957), while baroclinicity, katabatic flows, and frontal systems are some of the other possible causes of LLJ formation (Stull 1988).

LLJs have been associated with the long-range transport of scalars (e.g., Corsmeier et al. 1997; Sogachev and Leclerc 2011; Hong et al. 2012). They are often a significant source of turbulence in the nocturnal SBL given the enhanced shear created in the sub-jet layer (e.g., Mahrt et al. 1979; Mahrt 1999; Mahrt and Vickers 2002; Banta et al. 2002, 2003, 2006; Karipot et al. 2006, 2008; Duarte et al. 2012). Their potential to transport scalars (e.g., \(\hbox {CO}_{2}\), \(\hbox {H}_{2}\hbox {O}\), \(\hbox {O}_{3}\), and pollutants) over hundreds of kilometres during a single night and to modulate near-surface turbulence and fluxes, coupled with their ubiquitous nature, underscores the relevance of LLJs to both the air pollution and eddy-flux communities (Corsmeier et al. 1997; Karipot et al. 2006, 2008; Sogachev and Leclerc 2011).

The turbulence kinetic energy (TKE) budget equation for a coordinate system aligned with the mean wind, assuming zero subsidence, is given by (Stull 1988),

$$\begin{aligned} \underbrace{\frac{\partial \bar{{e}}}{\partial t}}_{S_\mathrm{tg}}=\underbrace{-\bar{{u}}\frac{\partial \bar{{e}}}{\partial x}}_A \underbrace{+\frac{g}{\overline{{\theta }_\mathrm{v}}}\overline{{w}'{\theta }'_\mathrm{v}}}_B \underbrace{ -\overline{{u}'{w}'} \frac{\partial \bar{{u}}}{\partial z}}_{S_\mathrm{hr}} \underbrace{-\frac{\partial \overline{{w}'e}}{\partial z}}_{T_\mathrm{t}} \underbrace{-\frac{1}{\bar{{\rho }}}\frac{\partial \overline{{w}'{p}'}}{\partial z}}_{T_\mathrm{p}} \underbrace{-\varepsilon }_D \end{aligned}$$
(1)

where \(S_\mathrm{tg}\) is the storage term, \(A\) is the advection term, \(B\) is the buoyant production/consumption term, \(S_\mathrm{hr}\) is the shear production term, \(T_\mathrm{t} \) is the turbulent transport term, \(T_\mathrm{p}\) is the pressure transport term, \(D\) is the dissipation term, \(e\) is the instantaneous TKE, \(g\) is the acceleration due to gravity, \(\theta _{v}\) is the virtual potential temperature, \(w\) is the vertical velocity component, \(u\) is the streamwise velocity component, \(\rho \) is the air density, \(p\) is the atmospheric pressure, and \(\varepsilon \) is the dissipation rate of TKE. The partial derivatives \(\partial /\partial t\), \(\partial /\partial x\), and \(\partial /\partial z\) are with respect to time, streamwise direction, and vertical direction, respectively. Overbars indicate averaging and primes indicate fluctuations from the mean. The instantaneous TKE is given by \(e=0.5\left( {{u}'^{2}+{v}'^{2}+{w}'^{2}} \right) \), where \(v\) is the lateral velocity component.

A dimensionless version of Eq. 1 can be obtained by multiplying each term by \(\kappa (z-d)/u_*^{3}\), where \(\kappa \) is the von Kármán constant, \(z\) is the height above the surface, \(d\) is the displacement height, and \(u_*\) is the friction velocity,

$$\begin{aligned} S_\mathrm{tg}^+ =A^{+}+B^{+}+S_\mathrm{hr}^+ +T_\mathrm{t}^+ +T_\mathrm{p}^+ +D^{+}. \end{aligned}$$
(2)

Note that \(B^{+}\equiv \kappa (z-d) B/u_*^3 =-\zeta \), where \(\zeta \) is the Monin–Obukhov stability parameter.

The TKE budget in the surface layer has been studied within the framework of Monin–Obukhov similarity theory (MOST) for many years (Wyngaard and Coté 1971; Högström 1990; Oncley et al. 1996; Frenzen and Vogel 2001; Li et al. 2008). However, as Li et al. (2008) pointed out, many uncertainties still remain, especially on the role played by the transport terms. The classical assumption is that the TKE budget is locally balanced, i.e. the transport terms are either negligible or they cancel each other (McBean and Elliot 1975; Wyngaard 2010). However, experimental results have challenged this assumption, showing evidence of local imbalance and underscoring the importance of the transport terms (e.g., Högström 1990, 1992; Frenzen and Vogel 2001; Li et al. 2008). These studies have reported cases of either excess or insufficient local dissipation, being associated with either TKE gain or loss via the transport terms respectively. The reason for these differences is still an open question (Li et al. 2008). This is especially true in the SBL, where turbulence is affected by LLJs, gravity waves, density currents, and Kelvin-Helmholtz shear instability (Cheng et al. 2005).

The TKE budget in the atmospheric boundary layer under the effect of LLJs was investigated in a few observational studies (Table 1). These studies were conducted for different sites, jet types, and stability conditions, and show that pressure transport plays an important role in the budget near the surface, but at present, there does not appear to be a consensus on whether the pressure transport term acts as a sink or source term.

Table 1 Observational studies reporting results on the pressure and turbulent transport terms (\(T_\mathrm{p}\) and \(T_\mathrm{t}\) respectively) of the TKE budget during (no-)LLJ conditions
Full size table

Smedman et al. (1993, (1994) used aircraft slant profile data collected over the Baltic Sea (near the south-eastern Swedish coast) in their analysis. LLJs were present at heights from 500 to 1500 m, formed by frictional decoupling of the flow due to low sea surface temperatures (a process analogous to the formation of a nocturnal LLJ over land), and stability was near-neutral. In Smedman et al. (1993), the pressure transport term was found to be an important source term in the layer from the base to the top of the LLJ, with larger values at the base of the LLJ, where shear production was a maximum. In the particular case analyzed by Smedman et al. (1994), maximum shear production was also observed at the base of the LLJ, but in the same layer the pressure transport term was a sink. At lower layers down to the surface, the latter was a large source term. They suggested that the pressure transport term was responsible for transporting TKE from the layer of maximum shear production (at the jet base) down to the surface, and also suggested that the turbulence transported towards the surface was ‘inactive’ turbulence (large-scale fluctuations—see Högström 1990), helping to promote mixing in the sub-jet layer but not producing shear stress directly.

At a different site over the Baltic Sea (Stockholm archipelago), Smedman et al. (1995) analyzed the TKE budget for cases characterized by weak to moderate stability and lower-level LLJs (cores at 30 to 150 m above sea level). Tower data collected at 8 and 31 m above the surface were used, and maximum shear production was found closer to the surface (8-m level), and at the same level the pressure transport term was a sink. At the 31-m level the latter was a source term. They concluded that TKE was transported upwards by the pressure transport term, away from the layer of maximum shear production (in agreement with Smedman et al. 1994).

Bergström and Smedman (1995) used data from the same site (Smedman et al. 1995) and analyzed the TKE budget for cases with similar stability but without the presence of a LLJ. They found the pressure transport term to be a source at the 8-m level, and suggested that this was the result of the transport of ‘inactive’ turbulence from upper regions in the boundary layer towards the surface. Contrary to the pressure transport term, the turbulent transport term was found to be small in the studies discussed so far (Smedman et al. 1993, 1994, 1995; Bergström and Smedman 1995).

Over land (south-eastern Kansas, USA), Cuxart et al. (2002) also found significant values for the pressure transport term in the near-surface TKE budget for a night characterized by strong stratification and LLJ activity (jet height from 100 to 200 m above ground level, a.g.l.). They observed that, in a layer from 1.5 to 30 m a.g.l., the pressure transport was a relevant sink, coinciding with maximum shear production. In a layer from 30 to 50 m a.g.l., the pressure transport was a relevant source term. As in Smedman et al. (1995), the results of Cuxart et al. (2002) indicate that TKE was exported away from a layer of maximum shear production near the surface by the pressure transport term. Cuxart et al. (2002) observed significant values for the turbulent transport term as well, but its behaviour was not well-defined (i.e., regarding the orientation of the transport, away from or towards the surface).

The TKE budget under LLJ conditions has also been studied based on numerical simulation data (e.g., Skyllingstad 2003; Muñoz and Garreaud 2005; Conangla and Cuxart 2006; Cuxart and Jiménez 2007; Axelsen and Dop 2009). Modelling approaches included the MM5 mesoscale model, single-column models, and large-eddy simulation. The two transport terms in these studies were practically negligible at layers below and above the jet, i.e., the TKE budget was practically locally balanced. Skyllingstad (2003) and Axelsen and Dop (2009) modelled katabatic flow (jet peak a few metres away from the surface), and found more substantial values for the pressure transport term. It is important to emphasize that the modelling of highly stratified flows is complex, and differences in the result for the transport terms may be simply related to the different modelling approaches and associated parametrizations and simplifications used.

As mentioned previously, the classical assumption is that the near-surface TKE budget is locally balanced, and therefore eventual gains or losses of TKE via the transport terms are expected to result in deviations from MOST. As discussed above, this is a concern especially in the SBL, where near-surface turbulence can be affected by many non-local processes. The applicability of MOST in the presence of LLJs has been discussed in a few studies. Smedman et al. (1995) observed a significant departure from MOST for their dimensionless wind-speed and temperature gradients measured near the surface (8 m) during conditions of weak to moderate stability in the presence of LLJs propagating at low heights (30–150 m) over the Baltic Sea. At the same site and under similar stability, but in the absence of LLJs, Bergström and Smedman (1995) found those dimensionless gradients to adhere to MOST. In Smedman et al. (1995), pointed out that the flow was significantly governed by the proximity of the jet to the surface, being similar to a laboratory wall jet. It is interesting to note that their results show a locally imbalanced TKE budget at the 8-m level, with a large loss of TKE via pressure transport.

In contrast with Smedman et al. (1995), Cheng et al. (2005) found dimensionless gradients of wind speed and temperature near the surface (\(\approx \)3 m) to follow MOST very well during the well-developed stage of a more typical type of LLJ over land (data from a particular night from CASES-99—Great Plains of the United States). The jet was observed at approximately 150 m a.g.l. and near-surface conditions were weakly stable. More recently, Banta et al. (2006) and Banta (2008) analyzed data from the CASES-99 and LAMAR-2003 experiments (strong-wind-speed nights characterized by weak to moderate stability) and found results in apparent conflict with local similarity concepts, as jet speed was found to be a more appropriate velocity scale than surface-layer friction velocity.

The studies referred to above indicate that the behaviour of the transport terms (especially the pressure transport term) and the applicability of MOST are still an open question in the SBL in the presence of LLJs. The results reported so far are practically based on case studies. Further studies using larger datasets encompassing a larger variety of jet and stability conditions are needed for a better understanding of the impact of LLJs on near-surface turbulence.

Addressing the question above, the goal of our study is to investigate the role of LLJs on the modulation of near-surface turbulence in the SBL over land, focusing on the behaviour of the transport terms of the TKE budget, and the applicability of MOST. Flux-tower and acoustic remote sensing data collected over a three-month period in South Carolina, USA are used in the analysis.

Section 2 presents information on the experimental site, instrumentation, data selection, and the processing of turbulence and acoustic remote sensing data. Results and discussion are presented in Sect. 3, starting with a characterization of the LLJ events analyzed (Sect. 3.1), followed by the analysis of the TKE budget and the applicability of MOST (Sect. 3.2). Conclusions are presented in Sect. 4.

2 Measurements and Data Processing

2.1 Experimental Site and Instrumentation

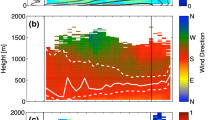
Turbulence data were collected on a tall tower near Beech Island, South Carolina (\(33^{\circ }\)24\(^{\prime }\)20.18\(^{\prime \prime }\)N, \(81^{\circ }\)50\(^{\prime }\)01.96\(^{\prime \prime }\)W, alt. 117 m) in 2009 and 2010. The region is characterized by a mosaic of broken forests (mixed pine) and agricultural lands, with urban, suburban, and industrial areas within 20 km (Fig. 1). Eddy-covariance measurements (three-dimensional wind velocity components, sonic temperature, and concentrations of \(\hbox {CO}_{2}\) and water vapour) were made at 34, 68, and 329 m a.g.l. on the tall tower (Fig. 2) with three-dimensional sonic anemometers (Applied Technologies Inc., model Sx at 34 m, model A at 68 and 329 m; Longmont, Colorado, USA) and \(\hbox {CO}_{2}/\hbox {H}_{2}\hbox {O}\) gas analyzers (Li-Cor Inc., model Li-7500, Lincoln, Nebraska, USA) at a frequency of 10 Hz.

Vertical profiles of mean wind speed and direction, vertical velocity component, echo strength, and standard deviations of wind direction and velocity components were measured using a phased-array boundary-layer Doppler sodar (Remtech Inc., model PA2, Paris, France) operating with a central frequency of 2 kHz. The sodar was operated with a maximum vertical range of 1200 m, a vertical resolution of 20 m, and was programmed to retrieve 15-min averaged profiles. The sodar was deployed at the Savannah River Site (\(33^{\circ }\)20\(^{\prime }\)22.83\(^{\prime \prime }\)N, \(81^{\circ }\)33\(^{\prime }\)51.40\(^{\prime \prime }\)W, alt. 87 m), near Aiken, South Carolina, approximately 26 km from the tall tower (Fig. 1). The sodar site is surrounded by mixed forest spanning several kilometres in all directions.

Fig. 1
figure 1

a Site location in the USA, b local topography map, and c local satellite view (source Google Earth; imagery date: October 5 2010) showing land use. The location of the tall tower (T) and the Remtech sodar (R) are indicated

Full size image
Fig. 2
figure 2

The Savannah River National Laboratory (SRNL) instrumented tall tower used in the study. The two lowest eddy-covariance systems (34- and 68-m levels) can be observed

Full size image

2.2 Data Selection

We selected the months of May, June, and July 2009 for the present study, and considered only nighttime data (2000 to 0500 Eastern Standard Time, EST). Several nights during these months presented LLJ activity lasting for multiple hours, with a high incidence of south-westerly winds. Continuous LLJ activity, formed by (or facilitated by) the stabilization of the atmospheric boundary layer on the regional scale, was a desired feature given the fact that the sodar and tall tower were separated by 26 km. South-westerly flow was also a desired feature, given the orientation of the sonic anemometers on the tall tower (\(210^{\circ }\) azimuth). Winter months were avoided due to the predominance of north-easterly winds (direction in which turbulence is most disturbed by the tower structure).

2.3 Turbulence Data Processing

We processed the turbulence data in 30-min blocks, and used the despiking method described by Vickers and Mahrt (1997) and applied the planar-fit coordinate rotation described by Wilczak et al. (2001) to the wind velocity components. The data were then linearly detrended (Rannik and Vesala 1999). Resulting fluctuations were used to calculate variances and covariances, and only runs with average wind direction between \(070^{\circ }\) and \(350^{\circ }\) were considered to avoid flow distortion due to the tower structure (sonic anemometers were pointed to \(210^{\circ }\)).

We calculated the dissipation rate of TKE (\(\varepsilon \)) by using the inertial dissipation method, based on Kolmogorov’s hypothesis,

$$\begin{aligned} \varepsilon =\frac{2\pi }{\bar{{u}}}\left[ {\frac{f^{5/3}S_{uu} (f)}{\alpha _u}} \right] ^{3/2}, \end{aligned}$$
(3)

where \(\bar{{u}}\) is the average streamwise velocity component, \(S_{uu} (f)\) is the spectral density of \(u\) as a function of natural frequency \(f\), and \(\alpha _u \) is the associated Kolmogorov constant, here taken as 0.5 (Batchelor 1953). In the inertial subrange, \(f^{5/3}S_{uu} (f)\) is assumed to be constant, where \(S_{uu} \propto f^{-5/3}\) (Kolmogorov’s \(-5/3\) power law). This method was also used in the Baltic Sea LLJ studies discussed in Sect. 1 (Smedman et al. 1993, 1994, 1995; Bergström and Smedman 1995).

The power spectrum of \(u\) was calculated for each 30-min run, and bin averaging was employed to smooth the spectra (64 non-overlapping \(f\) classes of logarithmically increasing width were used). We then used the frequency band \(f\)[0.5 : 2.0] Hz to calculate the average of \(f^{5/3}S_{uu} (f)\) and consequently \(\varepsilon \) via Eq. 3 (this frequency band was also used by Piper and Lundquist (2004) to calculate \(\varepsilon \) from similar sonic anemometer data).

Turbulence runs without a well-formed inertial subrange (i.e., presenting non-Kolmogorov turbulence) were removed from the analysis of the TKE budget terms and applicability of MOST. To be considered in the analysis, a given run was required to have an inertial subrange slope within the interval \(-1.69\pm 0.14\) (note that \(-5/3\) = \(-1.67\)), defined based on the average slope \(\pm 2\) standard deviations considering data from the 34- and 68-m levels during LLJs. This criterion led to the removal of 39/589 (\(\approx \)7 %) and 82/258 (\(\approx \)32 %) of the runs corresponding to the LLJ and no-LLJ events analyzed in this study (cf. Sect. 2.4), respectively. Turbulence in these removed runs was characterized by different degrees of non-stationarity.

2.4 Sodar Data Processing and LLJ Selection Criterion

The sodar data were averaged to 30-min profiles in order to allow the comparison with the tall-tower data. These 30-min profiles were used for selecting LLJ events. We used the same criterion used by Banta et al. (2002) for the identification of LLJs, where the first wind-speed maximum above ground level with speed at least \(1.5\hbox { m s}^{-1}\) larger than the adjacent minima above and below is classified as a LLJ. For each sodar profile, an automated routine was used to determine points of maximum and minimum wind speeds and to select a tentative LLJ height based on the \(1.5\hbox { m s}^{-1}\) criterion. Depending on the shape of the wind-speed profile, the determination of the points of maximum and minimum wind speeds—for the purpose of LLJ height selection—is sometimes not trivial. We performed a visual inspection to verify, and if necessary correct, the selections from the automated routine. With this method, we extracted the relevant LLJ information—height \((Z_{j})\), speed \((U_{j})\), and direction (\(\phi _j \))—for the period of interest. Intermittent jets were not considered in this study (see discussion in Sect. 2.2). Only LLJs with duration \(\ge \)2 h (i.e., for a minimum of four consecutive 30-min profiles) were included in the ‘LLJ group’. Similarly, continuous periods (\(\ge \)2 h) without LLJ activity were also determined, providing a contrasting ‘no-LLJ group’ for comparison.

3 Results and Discussion

3.1 LLJ Statistics

Table 2 presents the statistics for the observed LLJs. The period of interest in this study spans from April 30 2009 (2000 EST) to August 1 2009 (0500 EST), only considering the 30-min blocks between 2000 and 0500 EST. The total number of 30-min blocks associated with this period is 1767, and the number of 30-min sodar profiles used in the analysis is 1489 (i.e., \(\approx \)84 % coverage). Sodar data were unavailable or of poor quality during the remaining periods.

Table 2 Statistics of the LLJ events (30-min profiles) observed from May to July 2009, 2000 to 0500 EST
Full size table

Results show a high occurrence rate of LLJs at the experimental site during the months of May–July, where continuous jet activity was observed in 47 % of the profiles analyzed. Interestingly, Karipot et al. (2009) also reported in their climatological study a 47 % jet occurrence rate for their site also in south-eastern USA (northern Florida) for the months of June–August. It is important to note, however, that both continuous jets and intermittent jets were included in their statistics, while in the present study only continuous jets were considered. The results therefore suggest a higher occurrence rate of jets at the South Carolina site.

Fig. 3
figure 3

Histograms of LLJ a height, b speed, and c direction for the 700 jet events (30-min profiles) observed from May to July 2009, 2000 to 0500 EST. These events are associated with continuous jet activity (minimum duration of 2 h)

Full size image

Figure 3 shows histograms of jet height, speed, and direction. For jet height, we can see higher frequencies in the 300–400-m range, especially at 380 m, while jet speed presents a frequency peak in the 10–13-m s\(^{-1}\) range. Regarding jet direction, we can see a higher occurrence in the south-west quadrant, especially between south-west and west. These results are in general agreement with the climatological results reported by Karipot et al. (2009) for their northern Florida site during summer months.

In order to illustrate the general shape of the LLJs analyzed in this study, Fig. 4 presents a composite wind-speed profile for all selected cases (see Table 2). Note the well-defined linear behaviour in the sub-jet layer, with less scatter, and the relatively narrow LLJ core. This linear behaviour was also observed for the Great Plains LLJ (Banta et al. 2003, 2006). Interestingly, the results in Fig. 4 for \(\bar{{u}}/U_j \) in the sub-jet layer are very similar to the results in Banta et al. (2006, Fig. 7c), even down to the intercept at the top of the surface layer \((\bar{{u}}/U_j \approx 0.35)\). Such similarity, even with differences in terrain and climatology between the two experimental sites, suggests a generality of profile properties during LLJs, a fact of relevance to numerical simulation efforts.

Given the location of our experimental site in the upper coastal plains of South Carolina, and considering the proximity of the Appalachian Mountains and the Atlantic Ocean, terrain-induced baroclinicity along with inertial accelerations likely play an important role in the development of the south-westerly jets observed in this study. Pibal observations of the Carolina LLJ by Sjostedt et al. (1990) show a predominance of LLJs with direction parallel to the coastline, with a higher frequency of north-easterly jets during autumn and south-westerly/westerly jets during spring and summer (the case of the present study). Doyle and Warner (1993) investigated the structure and dynamics of the north-easterly Carolina LLJ using a mesoscale numerical model, and found that the jet is formed due to strong baroclinicity in the region between the Appalachian Mountains and the Atlantic Ocean, and that its strength is modulated by strong inertial accelerations. Observations from a site in Maryland (a mid-Atlantic state) during the warm season (Zhang et al. 2006) also indicate the predominance of south-westerly/westerly LLJs. Zhang et al. (2006) investigated the dynamics of the south-westerly LLJ using a mesoscale numerical model, and as with Doyle and Warner (1993), found that baroclinicity (due to the Appalachians Mountains and the Atlantic Ocean) and inertial accelerations play an important role in the development of the LLJ.

Fig. 4
figure 4

Composite wind-speed profile for all LLJ events considered in this study. LLJ speed and height are used as scaling parameters. Error bars indicate \(\pm \)1 standard deviation

Full size image

3.2 TKE Budget

Except for the pressure transport and advection terms, we calculated all the budget terms directly (Eq. 1) for a layer between 34 and 68 m a.g.l. For the calculation of \(S_\mathrm{tg}\), \(B\), and \(S_\mathrm{hr}\), we averaged the values of \(\bar{{e}}\), \(\overline{\theta _\mathrm{v}} \), \(\overline{{w}'{\theta }'_\mathrm{v}} \), and \(\overline{{u}'{w}'} \) observed at 34 and 68 m. The dissipation rate of TKE was calculated using Eq. 3, and the average \(\varepsilon \) between 34 and 68 m was used to calculate \(D\) in Eq. 1. A residual term was calculated as

$$\begin{aligned} R=S_\mathrm{tg} -B-S_\mathrm{hr} -T_\mathrm{t} -D. \end{aligned}$$
(4)

Note that \(R\) includes the sum of the pressure transport and advection terms, in addition to accumulated errors that may eventually occur in the calculation of the right-hand side of Eq. 4. In order to calculate the advection term directly, spatial measurements of TKE in the streamwise direction would be necessary, not easily accomplished with tower-based measurement platforms. Most studies usually neglect the term under the assumption of horizontal homogeneity. With regards to the pressure transport term, its direct calculation depends on accurate measurements of small fluctuations of static atmospheric pressure, which are extremely difficult to obtain with the available sensor technology. Given this issue, the residual approach, despite its limitations, has been widely used to investigate \(T_\mathrm{p}\) (e.g., Högström 1990; Smedman et al. 1993, 1994, 1995; Bergström and Smedman 1995; Li et al. 2008).

Fig. 5
figure 5

Normalized TKE budget terms as a function of stability for the LLJ (left column, red circles) and no-LLJ (right column, blue circles) groups: a, e shear production, b, f dissipation, c, g residual, and d, h turbulent transport. Black bullets are bin averages, and error bars correspond to \(\pm \)1 standard deviation. Curves on the left column correspond to least-square fitting for data points up to \(\zeta =1\)

Full size image

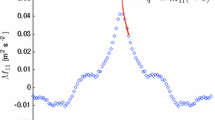
Each term in Eq. 4 was non-dimensionalized according to Eq. 2, using \(\kappa =0.4\), \(d=13.2\hbox { m}, z=51\hbox { m}\) (34–68-m layer midpoint), and the average \(u_*\) between 34 and 68 m. According to MOST, those terms are expected to be a function of \(\zeta \). Figure 5a–d presents the normalized TKE budget terms as a function of \(\zeta \) (i.e., the negative of the normalized buoyant production/consumption term, \(-B^{+}\), calculated for the 34–68-m layer) for the selected LLJ events. The bin averages for each term are plotted together in Fig. 6. It can be seen that shear production and dissipation are the dominant terms of the budget, as expected in the SBL (Wyngaard 2010). The turbulent transport is found to be virtually zero (cf. Fig. 6), and the storage term is found to be negligible (data not shown). The results do not support, however, the concept of a locally-balanced TKE budget. Dissipation is found to have approximately the same magnitude as shear production, and the total local losses, i.e., \(D+B\), therefore exceed the local production, indicating a gain of non-local TKE in the layer. This gain is represented by the residual term, which includes advection and pressure transport.

Fig. 6
figure 6

Normalized TKE budget terms for the LLJ group. Points correspond to the bin averages shown in Fig. 5a–d. Error bars correspond to \(\pm \)1 standard deviation

Full size image

Despite the presence of several large positive values, we see from the bin-averaged values that, on average, \(R^{+}\) is approximately in balance with buoyant consumption. Högström (1990) obtained similar results for a nearly-ideal site over land, flat and with a long uniform upwind fetch, in which the advection of TKE is expected to be negligible (or much reduced) and the residual term is expected to basically represent the pressure transport term (plus eventual accumulated errors). Even though our site characteristics are more complex, the fact that we observed similar results for \(R^{+}\) may suggest that \(R^{+}\approx T_\mathrm{p}^+ \) in our study as well. If the advection term is generally dominant, we expect \(R^{+}\) to present a less systematic behaviour (energy gain/loss) in comparison to the results obtained. Also, the general result of \(S_\mathrm{hr}^+ \approx -D^{+}\), \(T_\mathrm{t}^+ \approx 0\), and \(R^{+}\approx -B^{+}\), assuming \(R^{+}\approx T_\mathrm{p}^+ \), is in agreement with Kaimal and Finnigan (1994) regarding the TKE budget in the SBL.

It is important to note, however, that the advection term is expected to be larger and have a greater influence on \(R^{+}\) during more stable conditions \((\zeta \gtrsim 1)\), and the presence of a LLJ may help to accentuate the contribution of advection. Also, as mentioned previously, any accumulated error that may eventually result from the calculation of the budget terms on the right-hand side of Eq. 4 is reflected in the residual term. Similarly to the advection term, these errors are also expected to be larger and have a greater influence on \(R^{+}\) during more stable conditions, where turbulence is weaker and more intermittent. It is also important to point out that different calculation methods (e.g., choice of \(\Delta z\) in the calculation of \(S_\mathrm{hr}^+ \), turbulence data processing used to calculate fluxes) could potentially lead to different levels of error, with a direct impact on the residual term. In respect to the choice of the averaging period for calculating turbulent fluctuations, in this study we adopted the AmeriFlux standard (30 min), which could be argued to be too long for the study of turbulence in stable conditions. However, we investigated the impact of different averaging periods (30 vs. 5 min, data not shown) on the calculation of the major contributor to the TKE budget, i.e., shear production, and the general result was similar for both approaches.

The results show that \(S_\mathrm{hr}^+ \) and \(D^{+}\) terms follow MOST (local scaling formulation) remarkably well up to \(\zeta \approx 1\) (Fig. 5a, b), corroborating earlier findings by Cheng et al. (2005). This result is in agreement with the concept of \(z\)-less stratification (i.e., turbulence statistics assumed to be independent of \(z\)). The \(z\)-less theory predicts a linear behaviour of those terms with \(\zeta \) (Hong 2010; Grachev et al. 2013). The observed near-zero turbulent transport term (Fig. 5d) is consistent with the concept of a locally-balanced TKE budget (cf. Sect. 1) and \(z\)-less stratification. Note that \(T_\mathrm{t}^+ \) and \(T_\mathrm{p}^+ \) represent the vertical divergence \((\partial /\partial z)\) of the terms \(-\overline{{w}'e} \) and \(-\overline{{w}'{p}'} /\bar{{\rho }}\) respectively (cf. Eq. 1), which is expected to be null in \(z\)-less conditions. The non-zero residual term (Figs. 5c, 6), however, does not support the concept of local equilibrium (\(R^{+}\approx -B^{+})\). The concept of \(z\)-less stratification is also not supported, assuming that \(R^{+}\approx T_\mathrm{p}^+ \) at least for weakly to moderately stable conditions (as discussed previously). Further discussion on \(R^{+}\), \(T_\mathrm{p}^+ \) terms and the observed \(z\)-less breakdown is presented in Sect. 3.2.1.

The normalized TKE budget terms for the no-LLJ group are presented in Figs. 5e–h and 7. We see that the normalized TKE budget terms in both LLJ and no-LLJ groups follow practically the same behaviour, with greater scatter present for the no-LLJ points. In this group, even with the filtering method based on the inertial subrange slope values (cf. Sect. 2.3), some scatter still persists. This scatter is amplified for the residual term, whose behaviour is not as well-defined as for the LLJ group. Turbulence and flow properties for the LLJ and no-LLJ groups are compared below, helping to understand the differences observed in Figs. 5, 6 and 7 for the two groups.

Fig. 7
figure 7

Normalized TKE budget terms for the no-LLJ group. Points correspond to the bin averages shown in Fig. 5e–h. Error bars correspond to \(\pm \)1 standard deviation

Full size image

The near-surface turbulence statistics in Table 3 show that for the LLJ group, average TKE and friction velocity are 30 and 39 % greater than for the no-LLJ group, respectively, and the average Monin–Obukhov stability parameter is 49 % smaller. Average streamwise velocity component and wind shear are 20 and 30 % greater for the LLJ group (also indicated by the histograms in Figs. 8 and 9), respectively. The differences of the median values between both groups are even more pronounced. Table 3 also shows larger standard deviations in the turbulence statistics observed for the no-LLJ group. Note that the \(S_{uu}\) inertial subrange slopes \((\beta )\) for the LLJ group are close to the expected \(-5/3\) value, while more scatter is observed for the no-LLJ group (57 % higher standard deviation), with a reasonably larger amount of runs being rejected by the filter described in Sect. 2.3. These results indicate that the no-LLJ cases are more susceptible to non-stationarity issues associated with lower wind speeds and weaker turbulence, while the LLJ cases tend to present stronger and more well-developed turbulence associated with greater wind speeds. We should also note that the no-LLJ periods are typically characterized by a larger cloud-cover fraction in comparison with the LLJ periods. Clouds may explain the non-formation of jets in some cases, given their impact on the surface energy budget. Using ceilometer data collected at the Savannah River Site, we found a maximum cloud-cover fraction of [2.4 \(\pm \) 2.7, 0.8] oktas for the LLJ events and [4.0 \(\pm \) 2.8, 6.0] oktas for the no-LLJ events (avg \(\pm \) SD, median).

Table 3 Near-surface turbulence statistics (34-m data) for the LLJ and no-LLJ groups, for \(\zeta \) [0:10]
Full size table
Fig. 8
figure 8

Histograms of mean streamwise velocity component at 34 m for the a LLJ and b no-LLJ groups. Statistics are presented in Table 3

Full size image
Fig. 9
figure 9

Histograms of wind shear (calculated between 34 and 68 m) for the a LLJ and b no-LLJ groups. Statistics are presented in Table 3

Full size image

Focusing on the results for the LLJ group, we fitted the following curves to the data in Fig. 5a, b, d,

$$\begin{aligned}&S_\mathrm{hr}^+ =1+c_1 \zeta , \end{aligned}$$
(5)
$$\begin{aligned}&D^{+}=c_2 +c_3 \zeta , \end{aligned}$$
(6)
$$\begin{aligned}&T_\mathrm{t}^+ =c_4, \end{aligned}$$
(7)

where \(c_{1}, c_{2}, c_{3}\), and \(c_{4}\) are constants. Equation 5 is the classical Businger-Dyer relation (Businger et al. 1971; Dyer 1974) for the dimensionless shear production term in stable conditions, and Eq. 6 corresponds to the typical form used for the dimensionless dissipation under the same conditions (Li et al. 2008). We only used data up to \(\zeta =1\) for the curve fitting, given the higher uncertainties at higher stabilities, finding

$$\begin{aligned}&S_\mathrm{hr}^+ =1+4.11\zeta , \end{aligned}$$
(8)
$$\begin{aligned}&D^{+}=-1.24-4.18\zeta , \end{aligned}$$
(9)

and

$$\begin{aligned} T_\mathrm{t}^+ =-0.07. \end{aligned}$$
(10)

With the results above, \(R^{+}(0)\) must equal 0.31 in order to close the budget. We therefore fitted the following curve to the data in Fig. 5c,

$$\begin{aligned} R^{+}=0.31+c_5 \zeta , \end{aligned}$$
(11)

and obtained

$$\begin{aligned} R^{+}=0.31+0.96\zeta . \end{aligned}$$
(12)

The dimensionless shear production term in our study is reasonably close to the prediction [\(c_{1} = 4.11\) vs. 4.7 in Businger et al. 1971; we actually observed an even closer result when limiting the curve fitting to the data up to \(\zeta =0.5\) (results not shown)]. Our results also show an excess of dissipation, being associated with the input of non-local TKE via the pressure transport and advection terms (included in the residual term).

Similar results based on observations over land were reported by Högström (1990), who for weakly stable conditions found

$$\begin{aligned}&S_\mathrm{hr}^+ =1+4.8\zeta , \end{aligned}$$
(13a)
$$\begin{aligned}&D^{+}=-1.24-4.7\zeta , \end{aligned}$$
(13b)
$$\begin{aligned}&T_\mathrm{t}^+ =-0.25, \end{aligned}$$
(13c)

and

$$\begin{aligned} T_\mathrm{p}^+ =0.49+0.9\zeta , \end{aligned}$$
(13d)

with greater reliability for \(\zeta \) up to 0.2, given the available data. The \(T_\mathrm{p}^+ \) term was calculated as a residual, and advection was assumed negligible for the near-ideal site. As discussed previously, the similarity between Eqs. 12 and 13d may indicate that our residual term represents mostly the pressure transport term, at least for conditions of weak to moderate stability. In a later study, Högström (1992) found for neutral conditions \(D^{+}(0)=-1.24\), \(T_\mathrm{t}^+ (0)=0\), and \(T_\mathrm{p}^+ (0)=0.24\). These values are even closer to those found in the present study; the value we found for \(D^{+}(0)\) is exactly the same as the one reported by Högström (1990, (1992).

Högström (1990) suggested that the observed near-surface energy gain via \(T_\mathrm{p}^+ \) was related to ‘inactive’ turbulence (large-scale fluctuations that do not promote the transport of momentum) being injected to the surface layer from the upper regions of the boundary layer. Smedman et al. (1994) found the same result at a different site and observed that TKE was transported away from a layer of strong shear production underneath a LLJ to the surface via pressure transport.

As alluded to earlier, other studies have also reported results indicating that \(T_\mathrm{p} \) is a significant term in the near-surface TKE budget during LLJ conditions (cf. Table 1). These studies were associated with different sites, LLJ types, and stability levels, while the role of the pressure transport term as a sink or a source term varied in each study. Before comparing the results, it is important to emphasize once more the uncertainties associated with the calculation of \(T_\mathrm{p} \). The differences observed across studies could be at least in part related to different approaches used in its calculation, as discussed below.

In all studies cited in Table 1, except Cuxart et al. (2002), the pressure transport term was calculated as a residual. Again, note that this term may include advection (assumed negligible, but may vary from site to site) and accumulated errors from the calculation of other budget terms. Different choices of \(\Delta z\) for the calculation of the gradients, measurement types (tower vs. aircraft), turbulence data processing, and screening methods to remove unsuitable periods for the calculation of the dissipation term are factors that may lead to different levels of error and therefore to differences in \(T_\mathrm{p} \). On the other hand, Cuxart et al. (2002) calculated \(T_\mathrm{p} \) directly, i.e., they used data from sonic anemometers and collocated microbarographs to obtain \(\overline{{w}'{p}'} \). This approach, however, is known to be problematic due to the limitation of the available technology to measure small static pressure fluctuations of interest (Li et al. 2008).

The general result seen in Table 1 is that TKE is exported away from a layer of maximum shear production by the pressure transport term. This layer of maximum shear production can be near the surface (Smedman et al. 1995; Cuxart et al. 2002) or aloft near the base of the LLJ (Smedman et al. 1994), depending on the jet characteristics and stratification in the boundary regions. The former scenario corresponds to a traditional boundary layer, while the latter corresponds to an upside-down boundary layer (Mahrt and Vickers 2002). It is important to note, however, that the results obtained by Smedman et al. (1993) and Bergström and Smedman (1995) do not align with the general result discussed here. Smedman et al. (1993) found \(T_\mathrm{p} \) to be consistently positive at the top and base of LLJs, while Bergström and Smedman (1995) found \(T_\mathrm{p} \) to be positive near the surface in the absence of LLJs. These results indicate that the energy gain via \(T_\mathrm{p} \) may be associated with a different process.

Assuming that our residual term represents mostly the pressure transport term, at least for conditions of weak to moderate stability, three possible explanations for the positive (gain) values we found for the 34–68-m layer during LLJ events are: (i) maximum shear production occurs near the surface, and TKE is transported upwards by \(T_\mathrm{p} \) into the layer; (ii) maximum shear production occurs close to the LLJ, and TKE is transported downwards by \(T_\mathrm{p} \); and (iii) energy from the upper regions in the boundary layer is transported towards the surface layer, regardless of whether the maximum shear production occurs near the surface or aloft near the LLJ, in a process not necessarily associated with LLJs. Our results indicate typically higher turbulence intensities near the surface and decreasing magnitudes with height (not shown), suggesting the presence of a traditional boundary layer and supporting (i) instead of (ii). Explanation (iii) also seems to have value. The fact that we obtained approximately similar results for the no-LLJ group reinforces (i) and (iii). Note that gravity waves are expected to affect \(T_\mathrm{p} \), given the associated oscillations in static atmospheric pressure (Stull 1988). Bergström and Smedman (1995), for instance, found \(T_\mathrm{p} >0\) near the surface for stable, no-LLJ conditions that coincided with evidence of gravity-wave activity for most of the events analyzed.

Even though our results show an approximately similar behaviour of \(R\) for both no-LLJ and LLJ groups, typically presenting positive values, the results indicate that \(R\) is better delineated in the presence of LLJs, where this term is in a closer balance with buoyant consumption. While the results in both groups could be possibly linked with gravity waves—which are a common phenomenon in the SBL—we hypothesize that gravity-wave activity is more consistent during the LLJ events, leading to a more consistent behaviour of \(T_\mathrm{p} \). LLJs are known to promote the generation of gravity waves by shear-flow instability (e.g., Mastrantonio et al. 1976; Shuqing 1985; Wang et al. 2013b), given the fact that LLJs are associated with a stratified, stable flow and given the strong vertical wind shear they impose. It is important to note, however, that the less-consistent behaviour of \(R\) for the no-LLJ group is at least in part related to higher uncertainties in the calculation of the TKE budget terms due to the impact of non-stationarity. Further studies exploring this possible relationship between LLJs, gravity waves, and \(T_\mathrm{p} \) are suggested.

3.2.1 \(Z\)-less Breakdown and \(T_\mathrm{p}\)

As discussed in Sect. 3.2, the shear production term is found to adhere to MOST remarkably well up to \(\zeta \approx 1\) (Fig. 5a), in agreement with the linear \(z\)-less prediction. Above \(\zeta \approx 1\), \(S_\mathrm{hr}^+ \) is found to be typically smaller than the linear prediction, suggesting a breakdown of the \(z\)-less concept. This behaviour has also been reported in other studies (see review by Hong 2010; Grachev et al. 2013), and there is a persisting debate on the validity of the \(z\)-less stratification assumption (Yagüe et al. 2001; Grachev et al. 2005, 2013; Mahrt 2007; Hong 2010).

Using extensive observations over the Arctic pack ice, Grachev et al. (2013) reported that deviations from \(z\)-less theory were associated with non-Kolmogorov turbulence (i.e., turbulence without a well-defined inertial subrange), not expected to adhere to MOST in the first place. They suggested \(Ri_\mathrm{f}\) (the flux Richardson number) \(= 0.20{-}0.25\) as a primary threshold for the applicability of MOST, as they found inertial subrange slopes of velocity spectra to depart from \(-5/3\) for \(Ri_\mathrm{f} > 0.20{-}0.25\). After filtering out the periods with \(Ri_\mathrm{f} \) above the threshold, their results showed adherence to the \(z\)-less limit of MOST, and they concluded that this approach fully explains the controversy on the subject. In other words, the use of data periods characterized by non-Kolmogorov turbulence may explain why previous studies have found a MOST \(z\)-less breakdown, but those periods are not supposed to follow MOST in the first place (note that different screening/selection of periods may lead to different conclusions).

We used the \(Ri_\mathrm{f} \)-based screening method in a first attempt (\(Ri_\mathrm{f} <0.2\) specifically), and our results for \(S_\mathrm{hr}^+ \) and \(D^{+}\) indicated a close agreement with the linear MOST \(z\)-less prediction (even for \(\zeta >1\); results not shown), in agreement with the results of Grachev et al. (2013). However, note that this filtering method is justified only if the inertial subrange slope values depart from \(-5/3\) for \(Ri_\mathrm{f} >0.2\). The inertial subrange slope values we obtained for \(S_{uu} \), different from the results in Grachev et al. (2013), did not display a clear relationship with \(Ri_\mathrm{f} \) (data not shown). Many periods with Kolmogorov turbulence were observed for \(Ri_\mathrm{f} >0.2\), and their removal was not justified. A different screening method was then adopted, based directly on the departure of the inertial subrange slope values from \(-5/3\) (cf. Sect. 2.3). After using this more robust approach for our dataset, our results for \(S_\mathrm{hr}^+ \) (Fig. 5a) indicate \(z\)-less breakdown for \(\zeta \gtrsim 1\). Our results indicate that the presence of Kolmogorov turbulence is not a sufficient criterion to guarantee the applicability of the MOST \(z\)-less concept, as suggested by Grachev et al. (2013).

Based on the results we obtained for the residual term, we hypothesize that an injection of non-local TKE to the 34–68-m layer via pressure transport is responsible for the \(z\)-less breakdown observed for \(S_\mathrm{hr}^+ \) at high stabilities. Obviously, \(T_\mathrm{p}^+ \ne 0\), per se, would already be a sign of \(z\)-less breakdown. It is possible that such turbulence has an ‘inactive’ nature (Högström 1990), i.e., consisted of large-scale fluctuations contributing to the increasing of mixing (standard deviations) but not to the transport of momentum (\(u_*\)).

Both \(S_\mathrm{hr}^+ \) and \(R^{+}\) increase linearly with \(\zeta \) up to \(\zeta \approx 1\), and above that \(R^{+}\) increases faster with \(\zeta \), while \(S_\mathrm{hr}^+ \) increases at a slower rate. As discussed earlier, the effect of advection and accumulated errors on \(R^{+}\) is expected to be larger at higher stabilities, but if we assume that \(R^{+}\) represents mostly \(T_\mathrm{p}^+ \), the increase of mixing due to the injection of ‘inactive’ turbulence via \(T_\mathrm{p}^+ \) could lead to a decrease in the wind-speed gradient and therefore to the decrease of \(S_\mathrm{hr}^+ \) in relation to the linear \(z\)-less prediction, observed for \(\zeta \gtrsim 1\). It is interesting to observe that the dissipation term (Fig. 5b), calculated based on spectral densities in the inertial subrange (small eddy scales), seems to approximately follow the linear \(z\)-less prediction for \(\zeta >1\). This implies that the total energy gain in the considered layer (i.e., via \(S_\mathrm{hr}^+ \) and \(R^{+})\) should be linear with \(\zeta \).

4 Conclusions

The behaviour of near-surface turbulence during nocturnal LLJ events was investigated using a combination of sodar and flux-tower data collected in the upper coastal plains of South Carolina, USA over a three-month period. The analysis focused on the TKE budget near the surface, with special attention to the pressure transport term, and also on the applicability of MOST. Cases with well-developed turbulence were selected for the analysis.

The near-surface TKE budget was found to be locally imbalanced, opposing the classic view of the TKE budget in the SBL. The total local energy losses (buoyant consumption and dissipation) were found to typically exceed local shear production, implying an input of non-local TKE. As the turbulent transport term was found to be practically negligible, the observed additional TKE was attributed to pressure transport and advection, calculated together as a residual term of the budget. The residual was found to be in approximate balance with buoyant consumption. Based on a comparison with previous results in the literature, it was hypothesized that this residual term represented mostly pressure transport.

Previous findings on the near-surface TKE budget in the presence of LLJs also indicate that the turbulent transport is very small, but results for the pressure transport vary (cf. Table 1). It is important to note first that the differences observed across studies could be at least in part related to different approaches used in the calculation of \(T_\mathrm{p} \). The great majority of studies on TKE budget in the atmospheric boundary layer, the current study included, use the residual approach to calculate \(T_\mathrm{p} \). An obvious limitation of this method is that the residual term may include advection (typically assumed negligible, but may vary from site to site) and accumulated errors, which may vary depending on the available measurements and the method used to process the turbulence data.

The general view in previous studies is that TKE is transported away from layers of maximum shear production (at the surface or close to the LLJ core) by pressure transport, but results from studies including Högström (1990), Smedman et al. (1993), and Bergström and Smedman (1995) indicate that TKE may be transported from upper regions in the boundary layer, in a process not necessarily associated with LLJs. In the present study, the behaviour of \(T_\mathrm{p} \) (assumed to be approximately represented by the residual term) was generally similar for periods with and without LLJs, suggesting an upward transport of TKE from a layer of maximum shear production near the surface (as in Smedman et al. 1995 and Cuxart et al. 2002), or more likely, a downward transport from upper regions in the boundary layer. Under LLJ conditions, however, the behaviour of \(T_\mathrm{p} \) was found to be better delineated, with a closer balance between \(T_\mathrm{p} \) and buoyant consumption.

The shear production and dissipation terms during LLJs were found to conform well to the MOST local \(z\)-less predictions in general, corroborating earlier findings by Cheng et al. (2005), with the support of a more extensive dataset. Under very stable conditions, however, shear production was found to depart from the linear prediction. This result indicates that the presence of Kolmogorov turbulence (i.e., well-developed turbulence with inertial subrange slope close to \(-5/3\)) is not a sufficient condition to guarantee the applicability of the MOST \(z\)-less concept, as suggested by Grachev et al. (2013).

It is hypothesized that a gain of non-local TKE via pressure transport (per se an indication of conflict with the \(z\)-less concept) is the cause of the observed behaviour for \(S_\mathrm{hr}^+ \) under very stable conditions (values smaller than the \(z\)-less prediction). Such energy, likely of an ‘inactive’ nature, would affect mixing (by increasing the variance of the velocity components) but not directly \(u_*\), as discussed in Högström (1990). The enhanced mixing would reduce the wind-speed gradient, and therefore \(S_\mathrm{hr}^+ \).

Of relevance to numerical modelling studies of the SBL, the results presented in this study suggest that pressure transport cannot be neglected in the TKE budget. The processes controlling this term remain uncertain. Until a new sensor technology emerges allowing a direct and accurate calculation of the pressure transport term, further studies investigating \(T_\mathrm{p} \) in the SBL via the residual approach using long data records (i.e., not restricted to a case study) would help advance the understanding of this term. Despite the limitations of the residual approach, the emergence of a pattern across different studies would be enlightening.

The present study also found that turbulence during LLJ periods was typically stronger and more well-developed, with an improved and well-defined inertial subrange in comparison with periods without a LLJ. This result has an important implication to flux-tower measurements of local net ecosystem exchange during nighttime stable conditions. It suggests that the use of a \(u_*\) threshold criterion (a common approach in the eddy-flux community—see Aubinet et al. 2012) most likely would result in a selection of periods under the influence of LLJs (average \(u_*\) was found to be 39 % larger for the LLJ group). LLJs may provide the turbulent conditions necessary for calculating fluxes via the eddy-covariance technique, but that does not guarantee that the advective terms contributing to the net ecosystem exchange are negligible (see also Hong et al. 2012). In fact, the LLJs may actually accentuate the advection terms. Neglecting those terms in that case could result in significant errors in the measurements of net ecosystem exchange. This approximation is made in most studies, given the extreme difficulties of measuring advection in the field.