Introduction

The precise modeling of mortality curves in very old age is becoming an important task in aging research and public health (Manto and Vaupel 1995; Vaupel 1997; Vaupel et al. 1998; Horiuchi and Wilmoth 1998; Wilmoth et al. 2000; Weitz and Fraser 2001; Janssen and Kunst 2005; Meslé and Vallin 2006; Oeppen and Vaupel 2006; Vaupel 2010; Stevens et al. 2013; Rolden et al. 2014). The better modeling of mortality curves in very old age would enable the better estimation of maximum human lifespan. Many mathematical models have been proposed for the generation of human survival or mortality curves, including the Gompertz, Weibull, Heligman-Pollard, Kannisto, quadratic, and logistic models (Wachter and Finch 1997; Thatcher et al. 1998; Pletcher 1999; Pletcher et al. 2000; Yadav et al. 2012; Avraam et al. 2013; Gavrilova and Gavrilov 2014; Wrycza and Baudisch 2014). However, the available models still provide poor fit to the empirical mortality curves at very old age (Vaupel et al. 1998; Wachter and Finch 1997; Thatcher et al. 1998). We note that a good fit for advanced ages up to 106 years was obtained by using the Gompertz model without noticeable deceleration (Gavrilov and Gavrilova 2011). The exponential growth in mortality rates for the ages of 40–80 years, which is consistent with the Gompertz law (Gompertz 1825), is not clearly observed for ages above 80 years. Such deviation from the Gompertz law remains a great puzzle to demographers, epidemiologists, biologists, and gerontologists. In fact, a mixture model (Elandt-Johnson and Johnson 1999; Streler 1959) could be adopted to explain the deceleration in mortality in very old age, as the remaining members of the population belong to the long-lived subgroup regarding demographic selection. A mixture model makes far more sense than a simple parametric model because the later treats all humans as though they are clones, while the former recognizes the uniqueness of every individual. In the previous work, we put forward a mathematical model for the simple, efficient, and flexible calculation of survival curves, by utilizing a modified stretched exponential (equivalently an extended Weibull) function (Weon and Je 2009, 2011, 2012). In the present work, we address that this methodology enables the better estimation of the maximum human lifespan for the recent demographic data by providing a more accurate description of the mortality curves in very old age.

In statistics, the mortality rate (or the hazard function/the force of mortality), μ(x) = −dln(s(x))/dx, is mathematically linked to the survival rate, s(x), which monotonically declines from 1 to 0 as age, x, increases. To describe complicated survival curves, a modified stretched exponential survival function, described as s(x) = exp(−(x/α)β(x)), was adopted (Weon and Je 2009, 2011, 2012). Here, the stretched exponent is given by β(x) = ln[−ln(s(x))]/ln(x/α) for age (x), and the characteristic life is accurately measured by detecting the interception point between s(x) and s(α) = exp(−1) (standard deviation in graphical measurements ≈ 3 × 10−5). The α value can serve as a good alternative to the life expectancy at birth (ε) (Wrycza and Baudisch 2014; Weon and Je 2012). The age dependence of the stretched exponent is the critical difference between the modified stretched exponential (Weon and Je 2009, 2011, 2012) and the classical stretched exponential (known as the Kohlrausch–Williams–Watts (Kohlrausch 1854; Williams and Watts 1970) or Weibull (1951)) functions. The scale effect (associated with ‘living longer’), characterized by α, can be ruled out by rescaling age as u = x/α, and the shape effect (associated with ‘growing older’), characterized by β(x), can be used to evaluate the rectangularity of a survival curve (Weon and Je 2012). When a healthy population achieves a rectangular-like survival curve, the β(u) tends to shift towards an ideal curve of β(u) = 7|ln(u)|−1, corresponding to the ideal rectangular survival curve of s(u < 1) ≈ 0.999089 and s(u > 1) ≈ 0 (Weon and Je 2011) (which is not possible in the real world because of population heterogeneity). The assessment of α and the determination of β(x) for a survival curve enables the determination of an exact formula for the mortality curve through μ(x) = (x/α)β(x)[β(x)/x + ln(x/α) dβ(x)/dx] (Weon and Je 2009). Empirically, the quadratic formula of β(x) = −β0 + β1x − β2x2 (β0, β1, β2 > 0) describes the β(x) patterns at very old ages quite well (Weon and Je 2009). Particularly, the quadratic patterns in β(x) lead to the existence of the maximum human lifespan (ω), which can be defined as the specific age of β(x) = −xln(x/α) dβ(x)/dx which is taken by the mathematical constraint of ds(x)/dx → 0 (Weon and Je 2009). This methodology has been well accepted in the recent literature (Amorim et al. 2014; Holmes and Lewis 2014; Lakshminarayanan and Selvadeepa 2014).

Here, we demonstrate that the modified stretched exponential function is useful for providing a better estimation of the maximum human lifespan by describing the human mortality curves in very old age. A representative dataset containing the death rates and the period life tables of Swedish females over the three recent decades (after 1981) was examined. From the Swedish female datasets examined, the important result of gradual decrease in the maximum human lifespan was observed, while the characteristic life gradually increased for the past three decades. This tendency clearly indicates that the human survival curves are becoming increasingly concentrated at very old age, which is consistent with the definition of population aging (Anderson and Hussey 2000; Robine and Michel 2004), while the rectangularization of the survival curves (Weon and Je 2011) is relevant to the compression of morbidity (Fries 1980).

Analysis

Swedish female datasets were selected as being representative of human aging (Weon and Je 2009; 2012). The death rates (period, 1 × 1; Fig. 1a, b) and survival rates from the life tables (period, 1 × 1; Fig. 1c) were separately taken from the Human Mortality Database (http://www.mortality.org) [accessed on 11 August 2014]. The survival curves for Swedish females over three decades (1981–2011) were obtained by taking s(x) = 10−5 lx (in life tables, lx indicates the number of survivors at age (x) normalized by 100,000 people).

Fig. 1
figure 1

Comparison of mortality and survival curves in very old age. a The mortality curves (marked as the death rates) taken for Swedish females during three recent decades (1981–2011) show a gradual downward shift in the curves of the middle-aged (20–80 years). b The up-close mortality curves for very old ages (over 90 years) show divergence in the mortality patterns. This divergence is the main cause of difficulty in the modeling of mortality curves in very old age. c The survival curves taken for Swedish females (from the period life tables) over three decades (1981–2011) show gently decreasing patterns. d The age-dependent stretched exponent, β(x), (marked as the shape effect) shows smooth changes with age after 95 years. By fitting β(x) with quadratic formulas, reliable traces in the mortality curves could be obtained at very old ages

Full size image

The characteristic life (α), indicating the scale effect of the survival curves, was measured for each survival curve through the graphical analysis at s(α) = exp(−1) ≈ 0.367879 (standard deviation in measurements ≈ 3 × 10−5) (Supplementary Table 1). The age-dependent stretched exponent, indicating the shape effect of the survival curves, was obtained by computing β(x) = ln[−ln(s(x))]/ln(x/α) (Fig. 1d). The model mortality curves (Fig. 2) were taken as μ(x) = (x/α)β(x)[β(x)/x + ln(x/α) dβ(x)/dx], based on the quadratic formula β(x) = −β0 + β1x − β2x2 (β0, β1, β2 > 0) for fitting the β(x) patterns (Weon and Je 2009, 2011) (Fig. 1d). The maximum human lifespans (ω) for each calendar year in Fig. 3 were graphically taken at the specific age of β(x) = γ(x) [= −xln(x/α) dβ(x)/dx] for each survival curve (Supplementary Fig. S3).

Fig. 2
figure 2

Reliable fitting of mortality curves in very old age. Despite divergence in the data mortality curves (marked by the black lines, identical to Fig. 1b) over the age of 95 years, the model mortality curves (marked by the red lines) traced the mortality patterns of the data well. (Color figure online)

Full size image
Fig. 3
figure 3

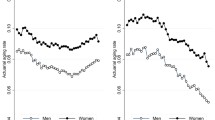
Tracking maximum human lifespan. The maximum human lifespan was estimated with the mathematical constraint of ds(x)/dx → 0 (graphically at the points β(x) = γ(x) in Supplementary Fig. S3). The maximum human lifespans (marked by stars) for each survival curve are illustrated and compared with the characteristic life (marked by the circles) (based on Supplementary Table 1). For Swedish females over three decades (1981–2011), the maximum human lifespan decreased at a constant rate of ~1.6 years per decade, while the characteristic life increased at a rate of ~1.2 years per decade

Full size image

Results and discussion

The data illustrated in Fig. 1 were acquired from the Human Mortality Database (http://www.mortality.org) for Swedish females over three decades (1981–2011), including the death rates for all ages (Fig. 1a) and for very old ages of 90–110 years (Fig. 1b), as well as the survival rates for very old ages of 90–110 years (Fig. 1c). As illustrated in Fig. 1b, the mortality curves appeared to diverge at very old ages (similar to recent observations (Vaupel et al. 1998)), which is the main cause of difficulty in mathematically modeling of the mortality curves in very old age. In contrast, the survival curves showed gently decreasing patterns (Fig. 1c). As described in Analysis, the modified stretched exponential function was adopted to describe the survival curves and to consequently achieve the age-dependent stretched exponents, β(x), (marked by the shape effect) in Fig. 1d. Most importantly, the β(x) curves smoothly changed with age after 95 years. By fitting β(x) to a quadratic formula (Weon and Je 2009), we are able to obtain reliable traces in the old-age mortality curves via the mathematical association between mortality and survival functions.

In Fig. 2, the data mortality curves (taken from the Human Mortality Database; marked by the black lines) were compared with the model mortality curves obtained by fitting β(x) to a quadratic formula (marked by the red lines) (Supplementary Table 1). Despite divergence in the mortality curves over the age of 95 years, the model mortality curves tracked the data mortality patterns quite well. Individual fitting results for each year clearly demonstrated the reliability of the fitting (Supplementary Fig. S1). Differentiation of the model mortality curves demonstrated decline of the mortality rates at very old ages, particularly after 103 years (Supplementary Fig. S2). The deceleration in the mortality of Swedish females in the data from the period of 1981–2011 suggests that the slowing of mortality is relevant for the demographic selection (Perls et al. 2002). Presumably owing to the analysis for different datasets, these results would be quite different from the lack of deceleration in mortality up to 106 years for the 1891 birth cohort of the northern states in the United States (Gavrilov and Gavrilova 2011).

One big advantage of the methodology employed herein is its capability to estimate the maximum human lifespan, which can be determined by the mathematical constraint of ds(x)/dx → 0 (Weon and Je 2009). This methodology was recently adopted in the literature (Amorim et al. 2014; Holmes and Lewis 2014; Lakshminarayanan and Selvadeepa 2014). The precise estimation of the maximum human lifespan has significant biomedical implications. The fitting of β(x) with a quadratic formula allows estimation of the maximum human lifespan at the specific age of β(x) = −xln(x/α) dβ(x)/dx (graphically at the points β(x) = γ(x) in Supplementary Fig. S3). The estimate of the maximum human lifespan is summarized and compared with the characteristic life taken from each survival curve (based on Supplementary Table 1) in Fig. 3. Here, it is shown that for the Swedish female datasets over three decades (1981–2011), the maximum human lifespan gradually decreases at a constant rate of ~1.6 years per decade, while the characteristic life gradually increases at a rate of ~1.2 years per decade. The maximum human lifespans and characteristic lives eventually become closer together over time. This result indicates that the human survival curves became increasingly concentrated at very old age, which is consistent with the definition of population aging (Anderson and Hussey 2000; Robine and Michel 2004).

Death rate data at the highest ages are so sparse that the trajectory of mortality is too erratic to plot (Vaupel et al. 1998). We believe that the modified stretched exponential function is appropriate for the description of the human mortality curves at very old age, as illustrated in Fig. 2, because this methodology is based on the better modeling of the robustly gentle patterns in the survival curves (Fig. 1c), rather than on the divergent patterns in the mortality curves at very old age (Fig. 1b). The fitting results of the mortality curves at very old age (Fig. 2) showed that the dμ(x)/dx patterns ‘almost linearly’ increased with age up to 103 years, where after decrease was observed (Supplementary Fig. S2). The almost linear increase in the dμ(x)/dx curves before 103 years is quite consistent with the quadratic model for the old-age mortality curves (Vaupel et al. 1998). As the characteristic life becomes closer to the maximum human lifespan (Fig. 3), the human survival curves become increasingly concentrated at very old ages. This tendency is relevant to the compression of morbidity suggested by James Fries in 1980, which corresponds to the rectangularization of survival curves (Fries 1980). The compression of morbidity becomes more important in very old age and would be responsible for the concentration of the very old populations. Recently, healthy aging has become more and more important in public health.

Finally, we discuss the demographic implications of the trend in the estimated maximum human lifespan. As seen in Fig. 3, the maximum lifespan for humans gradually decreased at a constant rate during the past few decades. Reaching the maximum lifespan is an extremely rare event for most people, for instance, with 1 in 7 billion (referring to the world population; in the case of Madame Jeanne Calment). The estimated maximum lifespan of around ~125 years does not immediately indicate the biological limit of human lifespan, and is different from the concept of the ‘biological warranty period’ (Carnes and Witten 2014). The continuous decrease of the estimated maximum lifespan (Fig. 3) suggests that the estimated maximum lifespan will become closer to the actual biological limit as people live longer. This finding would be relevant to increasing the probability of surviving beyond 100 years (Carnes et al. 2013), and the continued challenge to raise life expectancy (Carnes et al. 2014). The biological reality is that the vast majority of every cohort born will not come even close to achieving the maximum lifespan. The real concern is what happens if we do successfully push more people into older ages. The plausible answer is an inevitable increase in morbidity that creates a profound challenge to “quality of life”, where “health span” is far more relevant than “life span”.

Human populations are becoming more heterogeneous in terms of health, as technology enables us to save the lives of those who would have died in the past (Carnes and Olshansky 2001). The mortality curve model presented herein would contribute to the description of heterogeneity in demographic research: the stretched exponent, β(x), indicates the degree of heterogeneity in statistical physics or biophysics (β = 1 indicates that the exponential decay is homogeneous) (Benny Lee et al. 2001). Mathematically, the stretched exponential function is a superposition of exponential functions (Richert and Richert 1998). The heterogeneity from exponential mortality patterns of each subpopulation could be described by analyzing the stretched exponents. Importantly analyzing the stretched exponents would help in evaluating the heterogeneity trends in human populations.

The death rates for those 40–80 years of age tend to exponentially increase with age, suggesting the validity of the Gompertz law for Swedish females in the period from 1980 to 2010 (Weon and Je 2012). However, the mechanism for the death rate patterns observed for those 90–110 years of age is not yet clear. Further studies should be carried out on the additional valuable topics of (i) the determinants (Rolden et al. 2014) or causes (Jemal et al. 2005; Yang et al. 2010; Hacking et al. 2011) of the mortality curves observed in very old age, (ii) the mechanisms of the decline in the mortality that would be relevant to the aging mechanisms (Vaupel et al. 1998; Vaupel 2010), and (iii) further validation of the estimated maximum human lifespan from big demographic data. Historic comparisons would be useful, for instance, between a 1891 population and a 2015 population with a biodemographic approach of competing risks simplified to two types: extrinsic (deaths imposed on people by outside forces) and intrinsic deaths (deaths arising from our imperfect biology). Using intrinsic deaths to factor out extrinsic mortality would enable us to reveal the similarities between population mortality patterns (Carnes et al. 2006).

In conclusion, mathematically describing the mortality patterns in humans older than 90 years is becoming important in modern research on aging and public health. How survival or mortality curves evolve with age, particularly in very old age, is a critical question in aging biology, ecology, gerontology, epidemiology, and demography. Utilization of the modified stretched exponential function would be an appropriate approach for the reliable modeling of survival or mortality curves in very old age. The validity and usefulness of the present methodology were demonstrated herein through the analysis of reliable demographic data on Swedish females over the past three decades (1981–2011). Our methodology will contribute to the better tracking and forecasting of aging statistics, which are of great importance for the study of probabilistic limits on human longevity and for the public health policies needed to address the increasing challenges associated with population aging.