The evaluation of target displacement in structural systems using damage-based N₂ (DN₂) method under far-field ground motions for performance-based design theory

Abstract

The aim of this paper is based on the simple nonlinear procedure founded on the Park-Ang damage index model at different constant damage levels to evaluate the target displacement and performance point (P.P.). The mentioned procedure represents the intersection of the pushover capacity curve with the seismic hazard demand curve according to the equivalent period of vibration and damping in ADRS format. Hence, the damage-based response acceleration ratio is determined at different damage levels and periods for developing inelastic spectra from elastic ones. Then, the relation between the strength reduction factor (R-factor) and damage was extended at different damage levels and periods of vibration to predict the target displacement at the desired damage level, known as the performance point. It is worth mentioning that the cited procedure is represented for four hysteresis models, including Elastic-Perfectly-Plastic (EPP), Modified Clough (MC), moderate stiffness-strength deterioration (MSD), and severe stiffness-strength deterioration (SSD) models, to consider the theory for well-design and not well-designed systems in both steel and concrete structures. The mentioned procedure is the N₂ theory development based on the damage model called the DN₂ method in this investigation. Two experimental reinforced concrete bridge piers and three steel moment resisting frame structures with different periods, from low to high duration, are considered to verify the suggested procedure. Statistical results show that the target displacement and P.P. are evaluated appropriately regarding presented equations and proposed methodology compared to previous studies.

1 Introduction

Predicting target displacement at the desired performance level is one of the main issues in performance-based earthquake engineering (PBEE). The estimation of target displacement is used in pushover analysis to push the structure up to the desired performance level for evaluation of structural status in permeance-based design theory. Hence, different estimation methodologies have been proposed by many researchers to estimate the nonlinear target displacement in structural systems. One of the simple methods, which includes the estimation of maximum nonlinear displacement from the maximum linear displacement of the single-degree-of-freedom (SDOF) system with constant damping and period of vibration, has been presented by Veletsos and Newmark (1960) and Veletsos et al. (1965). The mentioned method was comprehensively developed by Miranda and his colleagues (1991, 1994; Miranda 1993, 2000, 2001; Baez and Miranda 2000; Ruiz‐García and Miranda 2003, 2004, 2006, 2007) as an inelastic displacement ratio (IDR). The inelastic displacement ratio is available as the coefficient method in seismic codes, such as FEMA-273 (1997), FEMA-356 (2000), FEMA-440 (2005), and ASCE/SEI 41–17 (2017). The capacity spectrum method, known as CSM, has been adopted by the ATC-40 (1996) code for retrofitting and evaluating reinforced concrete structures using the effective damping ratio and period of vibration (Fajfar 1999; Lin and Chang 2003). The energy balance was introduced by Leelataviwat et al. from 1999 to 2009 (Leelataviwat et al. 1999, 2002, 2007, 2009) based on the intersection of energy demand and capacity to estimate probable nonlinear displacement for use in plastic-based performance design (PBPD) (Goel et al. 2010; Liao and Goel 2014). The N₂ method was first introduced by Fajfar and Fischinger (1988) for regular RC frame systems to estimate nonlinear target displacement based on the intersection of capacity and demand curves. The N₂ method was developed by Fajfar and Gaspersc (1996) to evaluate the structural performance point using the first vibration mode. The proposed procedure, founded by Fajfar, was formulated comprehensively, and the influence of higher vibration modes was considered in this methodology (Fajfar 2000). It is worth mentioning that the N₂ method is applicable to complex structures (Kreslin and Fajfar 2010) and could be used for seismic evaluation of existing and new buildings (Kilar and Fajfar 1997). Additionally, one of the main features of this method is its ability to be used for all kinds of structural systems, such as asymmetric buildings (Dolšek and Fajfar 2007), infill reinforced concrete frames, structural systems with torsional effects (Bhatt and Bento 2011), and others. The mentioned procedure was extended considering higher modes (Kreslin and Fajfar 2010, 2011, 2012) and the N₂ multi-mode procedure (NMP) by Zarrin et al. (2021).

It is worth mentioning that the N₂ method has been represented according to the R-µ-T relationship to evaluate the target displacement. However, the cited method can be extended for damage-based evaluation and design of structures at the desired damage level (Amirchoupani et al. 2023a, b; Farahani et al. 2023). For example, Zhai et al. (2013a, b) developed the IDR for SDOF systems based on the Park-Ang damage index model (Park and Ang 1985) under far-field and mainshock-aftershock ground motions at different constant damage levels and periods of vibration. Moreover, Wen et al. (2014) extended the damage-based IDR for near-field pulse-like records as dangerous earthquakes for ordinary buildings. Recently, Amirchoupani et al. (2023a, b) proposed the damage-based IDR based on hysteresis to input energy intensity to predict target displacement in coefficient method theory, although it could only be applicable to the performance-based design. Although different damage models have been suggested before by many researchers (Powell and Allahabadi 1988; Kraetzig et al. 1989; Kunnath et al. 1997; Ghobarah et al. 1999; Diaz et al. 2017; Su et al. 2017; Mahboubi and Shiravand 2019a, b; Amirchoupani et al. 2021), the Park-Ang damage model is one of the popular indices for assessing damage in structural elements.

The N₂ method is developed in this investigation regarding the well-known damage-based Park-Ang model called the DN₂ procedure under far-field earthquake ground motions. Unlike the N₂ method, which is only based on ductility, the presented theory can consider the influence of hysteresis energy as a principal cause of failure in structural systems, frequency content, and the ultimate displacement of the structural system to estimate the structural status and target displacement. The damage-based N₂ procedure (DN₂) can be used in the energy-based design approach and gives a particular insight into structural behavior. Hence, the damage-based response acceleration ratio for developing inelastic spectra from elastic values and the relation between the strength reduction factor (R-factor) and damage is determined at different damage levels, periods of vibration, and hysteresis models (EPP, MC, MSD, SSD) to estimate target displacement and performance point. Moreover, mathematical equations are suggested for computing the damage-based response acceleration ratio and the R-DI-T relation using least-square nonlinear regression analysis. Two empirical reinforced concrete bridge piers with analytical verification and three designed steel resisting moment structures were adopted to verify the proposed methodology from low- to high-period duration. Statistical results show that the suggested procedure can estimate the performance point and target displacement appropriately, especially in short-period regions, compared to the coefficient method proposed by other researchers.

2 Earthquake ground motions

In this paper, 105 earthquake ground motion pairs, including 210 records from worldwide, were selected for performing nonlinear time history analysis. The earthquake ground motions from far-field sources were chosen in three categories, including 35 pairs recorded on sites with the shear velocity of 750 m/s to 1500 m/s, 365 m/s to 750 m/s, and 185 m/s to 365 m/s, respectively. Based on ASCE/SEI 7 (ASCE/SEI 7–10 2010; ASCE/SEI 7–16 2016), the mentioned categories are known as soil classes B, C, and D, respectively. It is necessary to explain that the recorded ground motions in soft soil sites (E and F soil classes) and pulsive ones are not in the scope of this investigation. The earthquake ground motions were selected from the Pacific Earthquake Engineering Research Center (PEER) from Shallow Crustal Earthquakes in Active Tectonic Regimes in the NGA/WEST 2 project. Tables 1, 2, 3 illustrates the selected ground motion characteristics, including RSN number, event year, earthquake name, station name, moment magnitude (M_w), fault mechanism, Joyner-Boore distance, rapture distance, shear wave velocity, and peak ground acceleration in two horizontal components. The following criterion was considered in ground motion selection:

Table 1 Soil class A, B earthquake ground motions

Table 2 Soil class C earthquake ground motions

Table 3 Soil class D earthquake ground motions

The earthquake ground motions were chosen from (1) recorded data with higher than M_w = 5.5 moment magnitude. The mentioned criteria were selected because the nonlinear behavior of structures in lower values is not probable, and lower values cannot expose the structures to higher risks. (2) recorded data with Joyner-Boore distance (Boore et al. 1997) lower than 80 km. (3) recorded data on free-field, where the influence of soil-structure interaction is not prominent. (4) data with available records in two horizontal directions. (5) recorded data with peak ground acceleration higher than 40 cm/s².

2.1 Methodology

As mentioned before, the DN₂ methodology, known as the damage-based N₂ procedure, was extended for performance-based design and evaluation of structures. As cited in the literature, the extent of the damage model in the N₂ theory can predict structural performance more intuitively. As explained before, the Park-Ang damage model was used in this investigation for developing the N₂ procedure, reference to Eq. (1), given as:

$$DI=\frac{{x}_{m}-{x}_{y}}{{x}_{u}-{x}_{y}}+\beta \frac{{E}_{h}}{{x}_{u}{F}_{y}}=\frac{{\mu }_{m}-1}{{\mu }_{u}-1}+\beta \frac{{E}_{h}}{{\mu }_{u}{F}_{y}{x}_{y}}$$

(1)

where ${x}_{m}$ is the maximum displacement of the system, ${x}_{y}$ is the yield displacement, ${x}_{u}$ is the ultimate displacement of the system, ${E}_{h}$ is the hysteresis energy, ${F}_{y}$ is the yield force of the system, ${\mu }_{m}$ is the ductility of the system, ${\mu }_{u}$ is the ultimate ductility of the system, and $\beta$ is constant parameter defined by experiment and guesswork.

Park-Ang proposed a formula to determine the β coefficient, but the scatter among data was too large. The experimental works illustrate that the value of β coefficient is between − 0.3 to about 1.2 with a median of 0.15 in investigations. Moreover, Zhai et al. (2013b) confirmed that the influence of β coefficient is below 20 percent in short-period regions and lower in long periods. The cited result was confirmed by other researchers, such as Decanini et al. (2004), Panyakapo (2004), Wen et al. (2014), and Amirchoupani et al. (2023a, b). Hence, the β = 0.15 was considered for hysteresis energy calibration in this research paper.

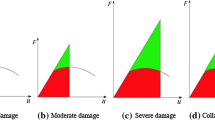
Park-Ang (1985) categorized their damage model into five bounds, including no damage with no cracking, minor damage with light cracks, moderate damage with severe cracking and spalling of concrete cover, severe damage with crushing concrete core and exposure of rebars in the elements, and total collapse of the system, as presented in Table 4. Seven steps in DN₂ methodology are needed for predicting the performance point and damage level in structural models, which are explained in detail, given as:

Table 4 Park-Ang damage model category (Park and Ang 1985)

Step 1: In the first step, structural data and linear acceleration spectrum must be defined due to the desired seismic hazard level, as illustrated in Fig. 1. The vertical axis in the elastic acceleration spectrum curve is acceleration responses, and the horizontal axis is the natural period. The T_c and T_D in the figure represent the end of the acceleration- and velocity-sensitive regions, respectively.

Fig. 1

Structural data and elastic acceleration spectrum

Step 2: In the second step, the acceleration spectrum must be converted to acceleration-displacement (AD) format for elastic SDOF systems, according to given equation:

$${S}_{de}=\frac{{T}^{2}}{4{\pi }^{2}}{S}_{ae}$$

(2)

where T is the fundamental period of vibration, and S_ae is the elastic response acceleration.

Step 3: The damage-based inelastic acceleration spectrum curve must be determined in the third step. Hence, the damage-based inelastic response accelerations regarding the Park-Ang damage model were computed at 30 periods of vibration from 0.1 to 3s, with a 0.1 time-step and four damage levels, including 0.1, 0.25, 0.4, and 0.8, respectively. The considered damage levels are according to the Park-Ang limit states presented in Table 4. It is worth mentioning that damage higher than 0.8 was not considered in this study because higher values expose the structure to probable collapse conditions, and this is not an appropriate status in performance-based design theory. Therefore, the inelastic acceleration spectrum ratio was extended as the proportion of maximum inelastic acceleration to maximum elastic one at four damage levels to obtain the inelastic response acceleration from elastic one at the desired damage level. As illustrated in Fig. 2, the input ground motion, hysteresis model, period of vibration, damping ratio, structural stiffness, mass, ultimate ductility of the system, β coefficient, and target damage level were defined to perform linear and nonlinear time history analysis for achieving elastic (S_ae) and inelastic (S_a) response accelerations. The yield strength of the SDOF system is equal to Fy = m.S_ae, where m is the mass of the SDOF system. Then, the system strength was decreased gradually, and the damage was calculated at each strength level by try and error procedure with less than 1% error. When the computed damage index reached the target value (with a lower than 1% error), the nonlinear response acceleration was utilized as the desired data. Therefore, the response acceleration ratio was calculated as nonlinear to linear response acceleration proportion to predict the inelastic values from elastic ones. The cited procedure was repeated for 30 periods of vibration, four damage levels, four hysteresis models, three ultimate ductility from 4 to 8, and 210 far-field ground motions by performing 302,400 nonlinear time history analysis. The OpenSEES version 3.0.3 and MATLAB 2017 software were used for carrying out linear and nonlinear dynamic analysis and post-processing data, respectively.

Fig. 2

The procedure of damage-based response spectrum calculation

As noted previously, four hysteresis models were used to compute damage-based response acceleration ratios, including Elastic-Perfectly-Plastic (EPP), Modified Clough (MC), moderate stiffness deterioration and strength degradation (MSD), and severe stiffness deterioration and strength degradation (SSD). The mentioned hysteresis models are conventional structural behaviors adapted in the FEMA series (FEMA 273 1997, 2005; FEMA 356 2000), ASCE/SEI 41–17 (2017), and other research studies. The EPP is a popular hysteresis model for simulating the steel structure behavior, and the MC, MSD, and SSD are used to model the concrete structure behaviors. The high stiffness deterioration and strength degradation in concrete structures are generally related to not well-designed systems with high bar slippage, bond-slip behavior, cracking, and spalling of concrete during seismic excitation. Figure 3 shows the EPP, MC, MSD, and SSD hysteresis models used in this investigation under SAC standard loading protocols.

Fig. 3

The hysteresis models, including a EPP b MC c MSD d SSD

Figure 4a illustrates the S_a/S_ae-T spectrum (response acceleration ratio) at different periods of vibration and damage levels. The S_a/S_ae values are decreased by increasing the damage level. However, S_a/S_ae values become constant at middle period ranges, where the nonlinear response acceleration is approximately equal to linear ones. Moreover, the coefficient of variation (COV) among data at different damage levels is not affected by the period of vibration, especially in the short-period region, reference to Fig. 4b. The COV at each damage level is not high, and it helps to have a robust equation to estimate the S_a in different strength levels, especially in higher damage levels where the dispersion among data increases. It is necessary to explain that Fig. 4 is only presented for ${\mu }_{u}=6$ due to the space limitation of the paper. However, the illustrated trend was observed in other ultimate ductility factors.

Fig. 4

The mean and coefficient of variation in response acceleration ratio for ${\mu }_{u}=6$

The influence of the ultimate ductility of the system on the damage-based response acceleration ratio is illustrated in Fig. 5. Figure 5 shows that the differences between response acceleration ratios at each damage level increased by increasing the ultimate ductility of the system. The mentioned trend is amplified in higher damage levels (about 30%), where damage is 0.4 and 0.8. Therefore, the influence of the ultimate ductility on response acceleration ratios is prominent, and this parameter should be considered in the proposed formula.

Fig. 5

The influence of ultimate ductility on damage-based response acceleration ratio

A simplified equation based on the S_a/S_ae-DI-T relation was proposed according to the achieved results for estimating the response acceleration ratio at the desired damage level, with reference to Eq. (3). Table 5 presents the constant parameters in Eq. (3) obtained from the mean of the inelastic response acceleration ratio by conducting the nonlinear least-square regression analysis using the Levenberg–Marquardt method (Bates and Watts 1988) in Excel software. The presented constant parameters relate to damage level, ultimate ductility of the system, and the hysteresis model.

$$\frac{{S}_{a}}{{S}_{ae}}=a+b{\left[\frac{DI}{T}\right]}^{2}$$

(3)

where T is the fundamental period of SDOF system, DI is the damage index, and a, b are constant parameters based on Table 5.

Table 5 Constant parameters based on nonlinear regression analysis for estimating damage-based response acceleration ratio

The bias and standard deviation of the proposed equation was obtained based on following equations, given as:

$${E}_{T, DI}={\left[\frac{{C}_{Sa-i (app)}}{{C}_{Sa-i (ex)}}\right]}_{DI}$$

(4)

$${\sigma }_{T, DI}=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}{\left[\left({E}_{T, DI}\right)-({\overline{E} }_{T,DI})\right]}^{2}}$$

(5)

$${\overline{E} }_{T,DI}=\frac{1}{n}\sum_{i=1}^{n}{({E}_{T, DI})}_{i}$$

(6)

where ${C}_{Sa-i (app)}$ is the estimated response acceleration ratio, ${C}_{Sa-i (ex)}$ is the exact response acceleration ratio from the direct time history analysis, $n$ is the number of data, ${E}_{T, DI}$ is the bias, and ${\overline{E} }_{T,DI}$ is the mean error.

It is worth mentioning that the bias and standard deviation of the proposed equation are presented to indicate the accuracy of the formula for estimating the damage-based acceleration response ratio. Values of ${E}_{T, DI}$ higher than one show an overestimation of the proposed equation, and lower than one illustrates an underestimation. Moreover, values of ${\sigma }_{T, DI}$ as lower than possible indicate a more robust estimation. Figures 6 and 7 demonstrate that the bias and standard deviation at different periods of vibration, damage level, and ultimate ductility of the system are not high and unacceptable. Figure 6 indicates that the bias increases by increasing the damage level and ultimate ductility of the system, which is predictable because the variation among data is amplified in higher values. The mentioned trend is correct in standard deviation among data, according to Fig. 7. Hence, the suggested equation can predict the response acceleration ratio with lower error.

Fig. 6

The bias at a ${\upmu }_{{\text{u}}}=4$, b ${\upmu }_{{\text{u}}}=6$, c ${\upmu }_{{\text{u}}}=8$

Fig. 7

The standard deviation at a ${\upmu }_{{\text{u}}}=4$, b ${\upmu }_{{\text{u}}}=6$, c ${\upmu }_{{\text{u}}}=8$

Step 4: In the fourth step, the damage-based strength reduction factor must be determined according to ${R}_{DI}=\frac{m{S}_{a}}{{F}_{y}}=\frac{{F}_{e}}{{F}_{y}}$, where $m$ is the mass, ${F}_{e}$ is the elastic strength of the SDOF system, and ${F}_{y}$ is the yield strength of the system at desired damage level. Therefore, the strength reduction factor of the SODF system was utilized at 0.1 to 3 s period of vibration, four damage levels, and three ultimate ductility factors. Figure 8 shows the $DI-T-{R}_{DI}$ relation at different damage levels, periods, and ultimate ductility factors, where the ${R}_{DI}$ increases by increasing damage levels. Based on the figure, the ${R}_{DI}$ is sensitive in the short-period region, and mentioned sensitivity increases with the growth of the damage level. Also, the ${R}_{DI}$ becomes constant at medium period ranges, from 0.5 to about 1s, which is related to the level of damage and ultimate ductility. It is necessary to explain that the ${R}_{DI}$ values are affected by the ultimate ductility of the system proportionally, where the ${R}_{DI}$ illustrates higher values in higher ductility levels. The COV in the $DI-T-{R}_{DI}$ relation is below 0.35 and not too high, which is not presented due to space limitations in the paper.

Fig. 8

The R-DI-T relationship at a ${\mu }_{u}=4$, b ${\mu }_{u}=6$, c ${\mu }_{u}=8$

According to observed data, a simplified equation based on the $DI-T-{R}_{DI}$ relation is suggested to evaluate ${R}_{DI}$ in each period of vibration, damage level, and ultimate ductility using the nonlinear regression analysis (similar to Eq. 3), given as:

$${R}_{DI}=a+\left[b\times DI\right]*{exp}^{\left(cT\right)}$$

(7)

where $DI$ is the damage index, $T$ is the period of vibration in SDOF system, and $a,b,c$ are constant parameters achieved from nonlinear regression analysis, presented in Table 6.

Table 6 Constant parameters based on nonlinear regression analysis for estimating R_DI

Step 5: In the fifth step, the nonlinear pushover analysis must be performed by subjecting the structure to a monotonic lateral load pattern. The mentioned analysis would help to find internal forces when the structural system is subjected to earthquake ground shaking. The structural elements yield subsequently, and the stiffness loss occurred due to the increment of the lateral load pattern in the system. Then, the force–displacement relation would be determined by pushover analysis of the MDOF system (multi-degree-of-freedom). The total base shear and top roof displacement at the control node should be considered in the F − ∆ relation, respectively. The appropriate lateral load pattern is a significant issue in pushing the structure to target displacement. In this investigation, the lateral load pattern was defined based on ASCE/SEI 41-17 recommendation, where the vector of lateral loads is specified as follows:

$$P=p\psi =pM\varphi $$

(8)

where $M$ is the mass matrix, and $\varphi$ is the displacement shape. The magnitude and distribution of lateral load are controlled by $p$ and $\psi$. The lateral force in the i-th floor level is equivalent to ${\varphi }_{i}$ of the assumed displacement shape $\varphi$, weighted by the story mass ${M}_{i}$, given as:

$${P}_{i}=p{M}_{i}{\varphi }_{i}$$

(9)

Step 6: In the sixth step, the equivalent SDOF model and capacity diagram must be developed to construct the idealized force–displacement curve. The equation of motion for MDOF systems only consists of the lateral translational degree of freedom, given as:

$$M\ddot{U}+C\dot{U}+R=M1{\ddot{u}}_{g}$$

(10)

where M is the mass matrix, C is the damping matrix, 1 is the unit vector, $\ddot{{u}_{g}}$ is the ground motion acceleration, and $U$ and $R$ are displacements and internal force vectors, respectively. The displacement vector of the structural frame at a generic time is:

$$U=\Phi {x}_{t}$$

(11)

where $\left\{\Phi \right\}$ is displacement shape and ${x}_{t}$ expresses the time-dependent top displacement of structure.

Based on static, $P=R$, where internal forces $R$ are equal to external loads $P$. Therefore, Eq. (11) can be expressed as:

$${\Phi }^{T}M\Phi {\ddot{x}}_{t}+{\Phi }^{T}C\Phi {\dot{x}}_{t}+{\Phi }^{T}M\Phi p=-{\Phi }^{T}M1{\ddot{u}}_{g}$$

(12)

The equation of motion for the equivalent SDOF system is determined by dividing the left hand in Eq. (12) to $-{\Phi }^{T}M1$, given as:

$${m}^{*}\ddot{x}+{F}^{*}=-{m}^{*}{\ddot{u}}_{g}$$

(13)

where the ${m}^{*}$, ${F}^{*}$, and ${D}^{*}$, known as equivalent mass, force, and displacement of the equivalent SDOF system, is given by:

$${m}^{*}={\Phi }^{T}M1=\sum {m}_{i}{\Phi }_{i}$$

(14)

$${D}^{*}=\frac{{x}_{t}}{\Gamma }$$

(15)

$${F}^{*}=\frac{V}{\Gamma }$$

(16)

where $V$ is base shear in MDOF system, expressed as:

$$V=\sum {P}_{i}={\Phi }^{T}M1p=p\sum {m}_{i}{\Phi }_{i}=p{m}^{*}$$

(17)

The $\Gamma$ parameter controls the transformation from MDOF to the SDOF model, which is called as modal participation factor. The $\Gamma$ is:

$$\Gamma =\frac{{\Phi }^{T}M 1}{{\Phi }^{T}M\Phi }=\frac{\sum {m}_{i}{\Phi }_{i}}{{\sum {m}_{i}{\Phi }_{i}}^{2}}=\frac{{m}^{*}}{{\sum {m}_{i}{\Phi }_{i}}^{2}}$$

(18)

It is worth mentioning that the $\Gamma$ is equal to ${PF}_{1}$ in the capacity spectrum method and ${C}_{1}$ in the coefficient method based on ATC-40 (1996) and ASCE/SEI 41-17 codes (ASCE/SEI 41-17 2017), respectively. Hence, the bilinear Force–Displacement curve for the equivalent SDOF can be determined using the equal energy method where the area under pushover and the idealized bilinear curve are the same. The elastic period of vibration in the idealized bilinear curve is specified as follows:

$${T}^{*}=2\pi \sqrt{\frac{{m}^{*}{D}_{y}^{*}}{{F}_{y}^{*}}}$$

(19)

where ${D}_{y}^{*}$ and ${F}_{y}^{*}$ are yield displacement and strength of the system, respectively.

In the end, the idealized bilinear Force–Displacement diagram must be converted to the S_a-Displacement diagram, known as ADRS format, according to the following equation:

$${S}_{a}=\frac{{F}^{*}}{{m}^{*}}$$

(20)

Step 7: In the seventh step, the seismic demand for the SDOF model must be determined regarding Eqs. (21) to (22) proposed by Fajfar (1999, 2000). It should be noted that the R in Eq. (21) is damage-based, which leads to the estimation of S_d in the desired damage level.

$${R}_{DI}=\frac{{S}_{ae}}{{S}_{ay}}$$

(21)

$$ \left\{ {\begin{array}{*{20}c} {S_{d} = \frac{{S_{de} }}{{R_{DI} }}\left( {1 + \left( {R_{DI} - 1} \right)\frac{{T_{C} }}{{T^{*} }}} \right) if T^{*} < T_{c} } \\ {S_{d} = S_{de} if T^{*} \ge T_{c} } \\ \end{array} } \right\} $$

(22)

where ${S}_{ae}$ is the elastic response acceleration, ${S}_{ay}$ is the yield response acceleration, ${S}_{de}$ is the elastic spectral displacement, ${T}_{C}$ is the characteristic period of vibration related to the demand curve, ${T}^{*}$ is the elastic period, ${R}_{DI}$ is the strength reduction factor related to damage, and ${S}_{d}$ is the target displacement.

The seismic demand and capacity in ADRS format are plotted in Fig. 9 to represent structures with ${T}^{*}<{T}_{c}$ and ${T}^{*}\ge {T}_{c}$ conditions, respectively. Based on the figure, the intersection of the dotted line corresponds to the elastic period in the idealized capacity curve with elastic demand in ADRS format is S_ae, known as elastic response acceleration and elastic displacement. In both conditions of ${T}^{*}<{T}_{c}$ and ${T}^{*}\ge {T}_{c}$, the intersection of capacity and inelastic demand correspond to the desired damage level.

Fig. 9

Estimation of target displacement for structures with a ${T}^{*}<{T}_{c}$ and b ${T}^{*}\ge {T}_{c}$ conditions

3 Experimental models for verification

In this paper, two experimental reinforced concrete (RC) bridge pier systems were numerically modeled to verify the proposed method with the fiber element models (FEM) for better understanding. Schoettler et al. (2015) presented a comprehensive report about the RC bridge pier under uniaxial shake table analysis under sequential earthquake ground motions with required time gaps between them. The mentioned time gap was used between earthquake records to cease the system after excitation (Abdollahzadeh et al. 2023). The ground motions were selected from low to high intensity to bring the system near collapse condition, reference to Table 7. It is worth mentioning that the RC bridge pier was designed according to Caltrans provision (Caltrans 2010) and tested at the University of California (Berkeley), as shown in Fig. 10. The model characteristics are presented in Table 8, including material properties and section dimensions.

Table 7 Ground motion characteristics used in verification (Schoettler et al. 2015)

Fig. 10

Full-scale RC bridge pier specimen and cross-section (Schoettler et al. 2015)

Table 8 Material properties and pier dimensions (Schoettler et al. 2015; Amirchoupani et al. 2021)

The RC bridge pier with hollow section configuration was selected in this investigation as a second empirical model, tested by Petrini et al. (2008) in Pavia (Italy) under dynamic analysis. As indicated in Fig. 11, the RC bridge pier was constructed in two sections, including eighteen longitudinal bars confined with 30-millimeter transversal spiral pitches from a 50-centimeter distance from the foundation and 60-millimeter spiral pitches in the upper parts. Table 9 presents the pier dimensions and material properties used in the empirical model. It should be noted that the simulation of ground shaking was performed under the Morgan Hill event in 1984 with M_w = 6.2 and PGA = 0.15 g using shake table analysis.

Fig. 11

Configuration of hollow section bridge pier specimen (Petrini et al. 2008)

Table 9 Dimensions and material properties in Petrini et al. (2008) model (Amirchoupani et al. 2021)

The fiber-based modeling was adapted using the 3D nonlinear beam-column element with five integration points along height by Open System for Earthquake Engineering Simulation (OpenSEES) software (Mazzoni et al. 2006) for numerically modeling the empirical cited models. The Concrete02 material based on Kent and Park’s (1971) hysteresis model was used to model the unconfined (cover) and confined (core) part of the section, and reinforcing material based on the Coffin-Manson equation was defined to consider the mechanical effect of compressive buckling, the transition from elastic behavior to inelastic, strain softening, and low-cycle fatigue, regarding OpenSEES library (the α = 0.506, C_f = 0.361, C_d = 0.6 was used in Coffin-Manson model).

The pier section in different integration points was divided into 150 mesh elements to attain accurate results (Fig. 12a). Moreover, the bond-slip behavior was considered to model the member end rotation regarding the strain penetration between the foundation and RC pier. Hence, the mentioned procedure was employed by defining a zero-length section to compute moment–curvature responses according to bond-slip behavior, as illustrated in Fig. 12b to c. The pointed method (bond-slip modeling with zero-length section) was employed by Zhao and Sritharan (2007), utilizing six parameters to capture bond-slip influence in the connection between elements, as indicated in Fig. 12c.

Fig. 12

a Fiber section model b Distribution of plastic hinge with bond-slip behavior c Uniaxial bond-slip material (Zhao and Sritharan 2007)

The S_y and S_u were computed by Eqs. (23) and (24), given as:

$${S}_{y}=2.54{\left[\frac{{d}_{b}}{8437}\frac{{F}_{y}}{\sqrt{{f}_{c}}}(2\alpha +1)\right]}^{1/\alpha }+0.34$$

(23)

$${S}_{u}=30\sim 40{S}_{y}$$

(24)

where ${d}_{b}$ is rebar diameter in mm units, ${F}_{y}$ is yield strength (MPa), ${f}_{c}$ is the compressive strength of concrete material, $\alpha$ is the constant parameter taken as 0.4 based on CEB-FIP model code 90, and $b$ is initial hardening ratio in the monotonic slip versus bar responses (the S_y = 0.548, S_u = 19.18, b = 0.4, R = 0.75 parameters were used in Schoettler et al. (2015) model and S_y = 0.35, S_u = 12.21, b = 0.4, R = 0.75 for Petrini et al. (2008) model).

The appropriate verification between the empirical and numerical model of Schoettler et al. (2015) under six sequentially ground motions, based on Table 7, is illustrated in Fig. 13. Moreover, the accuracy of Petrini et al. (2008) model under dynamic analysis is presented in Fig. 14. It is worth mentioning that some inaccurate responses between empirical and numerical models arise from solver algorithms and uncertainties in the construction of the empirical model.

Fig. 13

Verification between empirical shake table analysis and numerical fiber-based model

Fig. 14

Verification between empirical Petrini et al. (2008) model and numerical fiber-based model

4 Designed models for verification

In this investigation, three 1-, 7-, and 10-story steel moment resistance structural systems were designed based on ASCE/SEI 7-16 (ASCE/SEI 7-16 2016) loading requirements and AISC 360-16 (AISC 360-16 2016) design requirements to validate the proposed method in different period ranges. The ordinary moment resisting system (OMF) was considered for 1-story, and the intermediate frame (IMF) for 7- and 10-story structures. The response modification factor (R), deflection amplification factor (Cd), and system overstrength (Ω) for the 1-story structure was defined as 3.5, 3, 3, and 8, 5.5, 3 for 7- and 10-story. The 3000 kg/cm² dead load and 1000 kg/cm² live load were considered with seismic load under design seismic hazard level (DE), where the spectral acceleration in short- and long-periods was 0.842 g and 0.379 g, respectively. Moreover, the 5m span length and 3.5 m height are constant in all models, where the total height of 1-, 7-, and 10-story structures are 3.5 m, 24.5 m, and 35 m, respectively. The drift value under seismic load (linear design) is lower than 2.5% for 1-story and 2% for 7- and 10-story. Figure 15 shows the configuration of designed models and their section properties (W-shape) designed using steel material with 2400 kg/cm² yield stress and 3700 kg/cm² ultimate stress.

Fig. 15

The configuration of designed 1-story, 7-story, and 10-story models

5 Discussion

In the first step, the eigenvalue analysis was performed to determine the period of vibration with a higher than 90% mass participating ratio, which it used in the scaling of ground motions from 0.2T to 1.5T for dynamic time history analysis and determination of R_DI in Eq. (7) and S_d in Eq. (22). Table 10 shows the three first periods of structural systems, including two empirical bridge piers and three steel moment structures. In the second step, the pushover analysis on two empirical and three designed models was performed up to the collapse condition. Then, the idealized pushover curve was determined by transforming the MDOF system to an equivalent SDOF system in the base-shear vs top-displacement plot. Figure 16 illustrates the pushover curves of selected models under nonlinear static analysis and the idealized curve up to the collapse condition. The structural properties, including effective stiffness, structural mass, yield strength, yield displacement, and ultimate ductility, are presented in Table 11.

Table 10 Fundamental period of vibration in empirical and designed models

Fig. 16

The pushover analysis of selected models, including a Schoettler et al. (2015) bridge pier b Petrini et al. (2008) bridge pier c 1-story d 7-story e 10-story

Table 11 Structural characteristics under pushover analysis

As explained before, four hysteresis models were considered in this investigation to obtain the target displacement and performance point regarding the probable future earthquakes. Therefore, the cyclic displacement analysis, known as quasi-static analysis, was performed under the SAC loading protocol to obtain the hysteresis behavior of the considered models. Figure 17 illustrates the hysteresis behavior of the two verified empirical bridge piers and two 1- and 7-story steel moment structures, respectively. As indicated in Fig. 17, the hysteresis behavior of RC bridge piers and steel moment structures is similar to MD and EPP hysteresis models, respectively. It is worth mentioning that the cyclic displacement analysis of the 10-story model has not represented due to the identical behavior of this model to 1- and 7-story models. Therefore, the MD and EPP hysteresis behaviors were considered to calculate the constant parameters in obtained equations for estimating the target displacement of RC bridge piers and steel moment structures as the third step.

Fig. 17

The cyclic displacement analysis of selected models, including a Schoettler et al. (2015) bridge pier b Petrini et al. (2008) bridge pier c 1-story d 7-story

In the fourth step, sixteen earthquake records from Table 2 with appropriate spectral matching with seismic hazard level were selected to verify the applicability of the proposed method. Table 12 presents the ground motion characteristics from the PEER NGA West-2 project. It is necessary to explain that the chosen ground motions are based on S_DS = 0.842g and S_D1 = 0.3795g hazard level. In the fifth step, the nonlinear displacement of the top story and structural damage index were determined under S_DS = 1.684g and S_D1 = 0.759g seismic level. The cited seismic hazard level was considered to evaluate selected structures for putting them in higher nonlinearity conditions because higher nonlinearity is generally accompanied by the growth of dispersion and a decrease in the estimation accuracy. In the sixth step, the selected ground motions were scaled to the desired seismic hazard level. Although different ground motion scaling methodologies exist (Kurama and Farrow 2003; Naeim et al. 2004; ASCE/SEI 7-10 2010; Weng et al. 2010; Kalkan and Chopra 2011; O’Donnell et al. 2013; ASCE/SEI 7-16 2016), the normalizing-scaling theory proposed by Amirchoupani et al. (2020) was used to reduce the dispersion among acceleration responses, displacements, and damage index values. In this method, the spectral response acceleration of each record in the acceleration- (if 0.05s < T < 0.5s), velocity- (if 0.5s < T < 2.7s), and displacement-sensitive regions (if 2.7s < T < 4s) were normalized to their acceleration spectrum intensity, Housner intensity, and peak ground displacement, as a first level. The pointed parameters reach one by normalizing response accelerations to the normalizing index. Then, the scaling procedure based on ASCE/SEI 7 code would be performed as a next step.

Table 12 The ground motion characteristics used in verification

In the seventh step, the mean top displacement and general damage index were obtained under dynamic time history analysis, according to ground motions in Table 12. Ghosh et al. (2011) concluded that the Park-Ang damage model could determine based on two global and local approaches to evaluate structural performance. Based on the global approach, the Park-Ang damage index is equal to Eq. (1), but the Park-Ang damage index is $DI=({x}_{mi}-{x}_{yi})/ ({x}_{ui}-{x}_{yi}){|}_{max} +\beta /{V}_{y}{x}_{u}\int d{E}_{h}$, based on the local approach where ${x}_{mi}$ is the maximum drift in the i-th story level, ${x}_{yi}$ is the yield value corresponding to the i-th inter-story ratio, and ${x}_{ui}$ is the ductility capacity equals µ ${x}_{ui}$. The damage index values in Table 13 were determined using the global Park-Ang damage approach.

Table 13 Top displacement and global damage index obtained from time history analysis

The transformation factor (Γ) cited in this study and N₂ theory is equal to PF₁ in ATC-40 (1996) and C₀ in the FEMA series (FEMA 356 2000). The transformation from SDOF to MDOF in Schoettlet et al. (2015), Petrini et al. (2008), and 1-story steel moment resisting frame structures are equal to 1, and in two 7- and 10-story steel structures are 1.44 and 1.5, respectively. Table 14 shows the compression of target displacement based on the approximated method in this study, known as DN₂, and Zhai et al. (2013b) approximate procedure regarding the coefficient method, corresponding to calculated damage values. As represented in Table 14, the target displacement with precise accuracy in structures with short-period duration is estimated compared to the coefficient method proposed by Zhai et al. (2013a, b). Unlike the short-period region, there is no significant difference between the two methods in the high-period structures. Therefore, the target displacement in the long-period region is appropriately predicted in both methods. Hence, the target displacement can be obtained with acceptable accuracy due to the DN₂ method for structural systems in short- and long-period regions.

Table 14 Comparison between direct nonlinear displacement from time history analysis, and approximate DN₂, and Zhai et al. (2013b) method

6 Conclusion

In this investigation, the N₂ theory based on the Park-Ang damage index model, called the damage-based N₂ method (DN₂), was developed to evaluate the target displacement and performance point in structural systems under far-field earthquake ground motions. Hence, the following procedure was recommended:

• 1. The damage-based response acceleration ratio for four hysteresis models, including EPP, MC, MSD, and SSD, were determined at four damage levels, four ultimate ductility factors, and 30 periods of vibration to predict the inelastic values from elastic ones. Then, a simplified equation was proposed to construct inelastic response accelerations regarding nonlinear regression analysis.

• 2. The damage-based strength reduction factor by the relation between the R_DI-T-DI was developed at four damage levels, four ultimate ductility factors, and 30 periods of vibration to estimate the structural damage at the desired hazard level. Then, a simplified equation was suggested to predict this value according to nonlinear regression analysis.

• 3. The inelastic displacement equations for structures with ${T}^{*}<{T}_{c}$ and ${T}^{*}\ge {T}_{c}$ conditions, recommended by Fajfar (2000), were used to estimate performance points and structural status.

The accuracy and applicability of the proposed method were investigated using two verified experimental reinforced concrete bridge piers and three steel moment-resisting frame structures. The mentioned models were subjected to sixteen earthquake ground motion records scaled to arbitrary seismic hazard levels higher than the design level to bring the models into highly nonlinear conditions. Then, the obtained nonlinear top displacements and damage index from direct time history analyses were compared with the DN₂ and damage-based coefficient methodologies suggested before. Statistical results show that:

• 1. The target displacement in short-period structures was appropriately evaluated by the DN₂ method compared to the coefficient method.

• 2. The target displacement in long-period structures with a duration higher than 1s was appropriately assessed by both the DN₂ and coefficient methods.

• 3. The error between obtained top displacements under direct history analysis and DN₂ approximate procedure was below 10% (except in full-scale bridge pier), while the coefficient method shows higher error values.