Quantifying seismic risk in structures via simplified demand–intensity models

Abstract

Performance-based earthquake engineering (PBEE) has traditionally implied the verification of limit states at different earthquake intensities, where recent developments advocate a more risk-consistent approach. This has been primarily investigated for assessing existing structures and typically involves extensive analyses using detailed numerical models and ground motions. For new design, structures must be sized and detailed before more advanced numerical verifications are performed and the final design solution is established. In assessment, simplified procedures have been developed to incorporate further aspects of PBEE and typically comprise extensions to traditional structural analysis methods. Displacement-based assessment is one such method and while it has been extended for PBEE in the past, its use in a risk-oriented context still requires some validation. This article presents such a study, where recent developments in simplified analysis to estimate the exceedance rates of both storey drift and floor acceleration in reinforced concrete frames are described. This gives a method that is simple in its application, since it doesn’t require extensive and detailed numerical modelling or analysis, but also sufficiently accurate in its quantification of performance. While not intended as a substitute to extensive verification analysis, such a method for quantifying structural demand exceedance rates can be used to check results and provide better understanding to risk analysts. The work described herein can also be used in simplified verification analysis of new designs, whereby trial solutions may be verified in a relatively easy manner before more extensive verifications are carried out via non-linear dynamic analysis. It represents a further extension to existing simplified methods that strive toward more advanced performance quantification in line with the needs and goals of PBEE.

1 Introduction

The need for a next-generation approach to quantify building performance saw the introduction of limit states via Vision 2000 (SEAOC 1995) during the 1990s in the US. While this document was well-intended, it has been critiqued in recent years (e.g. Vamvatsikos 2017) for being an intensity-based assessment approach that skirted some issues relating to risk-consistency. The Cornell-Krawinkler performance-based earthquake engineering (PBEE) framework (Cornell and Krawinkler 2000; Cornell et al. 2002) somewhat alleviated these issues in the early 2000s. It allows for a comprehensive description of performance by convoluting probabilistic descriptions of seismic hazard and structural response to compute the mean annual frequency of exceedance (MAFE) of a given limit state. Therefore, the exceedance rate of a certain performance limit state in the structure is focused on rather than the exceedance rate of some level of ground shaking.

Numerous simplified methods have been developed over the years; for example, Fajfar and Dolšek (2012) introduced a pushover-based method by extending aspects of the well-established N2 method. One slight difficulty is that although the method represents a simplification, it requires a detailed numerical model in which dissipative zones are fully sized and knowledge of the placed reinforcement and expected member capacities are required. A pushover analysis is then conducted, which for new design may become a strenuous task as designs are being revised and iterated. Other approaches have been proposed, with Welch et al. (2014) extending the displacement-based assessment (DBA) approach (Priestley 1997; Priestley et al. 2007) by incorporating the initial risk developments of the Cornell et al. (2002) PBEE framework.

Since damage, and subsequently monetary loss, is related to demand parameters like storey drift and floor acceleration, it is arguably more desirable to compute the MAFE of certain levels of storey drift or floor acceleration. Analysis methods like DBA have been extended to risk-related quantities such as MAFE in the past without many studies to specifically examine the degree to which they are actually capable of doing so. Furthermore, most of the work stemming from Cornell et al. (2002) has focused on the estimation of storey drift and relatively little attention has been paid to floor accelerations, despite their importance in overall building performance.

This article extends simplified methods of analysis for reinforced concrete (RC) frames in a more risk-oriented manner. It relates structural demand to an intensity of ground shaking in what is herein referred to as a demand–intensity model. With these demand–intensity models, the closed-form solution introduced originally by Cornell et al. (2002) is extended to give a clear procedure with which to assess and verify structures for both storey drift and floor acceleration demand. This will be applied to two case study buildings and results are compared with extensive numerical analyses and direct integration of the structural response with seismic hazard to compute the MAFE and demonstrate its suitability.

2 Simplified quantification of MAFE

2.1 Establishing a demand–intensity relationship for storey drift

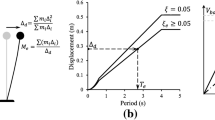
Maximum peak storey drift (MPSD) along the height of a building is a well-known indicator of both structural and non-structural damage. Therefore, the ability to accurately quantify a building’s MPSD with increasing intensity is of paramount interest. Priestley (1997) outlined how by knowing the critical mechanism of a structure, the subsequent response can be established in a relatively simple manner (Fig. 1). Depending on the structural typology and likely mechanism, a number of empirical expressions were provided by Priestley et al. (2007) to estimate this. Essentially, for a given MPSD in a structure, θ_max, the mechanism for a ductile RC frame is expected to be a first mode-based beam-sway mechanism (Fig. 1a). Other methods, such as the generalised interstorey drift spectrum (Miranda and Akkar 2006) looked to characterise the response of structures using a combination of flexural and shear beam response while also accounting for higher mode response contributions. However, it is assumed herein that investigated structures can be sufficiently characterised via their first mode response. Once the mechanism and force–displacement behaviour of the structure have been identified, the performance can be quantified with respect to some definition of seismic hazard. This relies on the use of an equivalent SDOF conversion (Fig. 1b, c) and requires the displaced shape and mass at each floor level j, denoted as Δ_j and m_j, respectively. The effective mass, m_e, effective height, H_e, and displacement capacity, Δ_cap, can be computed (Fig. 1b). The base shear, V_b, effective period, T_e, and system ductility, μ, can then be computed and used to estimate the spectral displacement modification factor, η, to account for system non-linearity, denoted as f(μ) in Fig. 1c. At this point, the effective period and elastic spectral demand at the effective period, Sd(T_e), are known. With some definition of seismic hazard, the return period of the seismic action, T_R, can be established as illustrated in Fig. 1d via the blue arrows. Repeating this for numerous values of θ_max returns its relationship with increasing intensity (i.e. demand–intensity model).

Fig. 1

Fundamental steps of DBA as described by Priestley et al. (2007), where an equivalent SDOF and identify the intensity required to result in the defined level of drift

As described above, the intensity required to exceed a given value of θ_max can be identified at a secant period, T_e. However, since T_e will differ for each value of θ_max in DBA, the resulting intensity measure (IM) (i.e. Sd(T_e)) will also indirectly differ at increasing levels of deformation since the effective periods are no longer the same. In situations where a smoothed code-defined spectrum is used (Fig. 1d), the spectral displacement at the first-mode period, Sd(T₁), can simply be determined as shown in Fig. 1d via the red arrows once the spectrum is known. A first-mode spectral acceleration, Sa(T₁) can then be determined, where the interchangeability between Sd(T) and Sa(T) is implicit. Now the IM is now consistent for all values of θ_max and the demand–intensity relationship (i.e. θ_max vs. Sa(T₁)) can be established. This approach works in situations where the seismic demand is represented by a smoothed design spectrum typically found in codes, but more recent advances advocate the use of probabilistic seismic hazard analysis (PSHA) results in the form of a uniform hazard spectra (UHS) that does not have a fixed spectral shape. By taking advantage of the fact that a site hazard curve determined via PSHA can be represented using a closed-form polynomial expression, “Appendix” derives a relationship to convert Sa(T_e) to Sa(T₁) and address this issue. This demand–intensity relationship can be represented as linear in logspace for MPSD as:

$$\theta_{max} \approx m_{\theta } Sa\left( {T_{1} } \right)^{{b_{\theta } }}$$

(1)

where m_θ and b_θ are coefficients fitted to structural analysis results.

2.2 Establishing a demand–intensity relationship for floor acceleration

Establishing a relationship between the peak floor acceleration (PFA) and ground motion intensity has received some attention in recent years, with studies (Calvi and Sullivan 2014) looking to estimate floor response spectra, whereas others (FEMA 2012) have proposed simplified means of estimating just PFA. Research by Welch (2016) accounted for aspects such as the influence of structural non-linearity and higher modes for the estimation of floor response spectra (Fig. 2). Knowing the spectral demand at mode i for a given definition of seismic input, Sa(T_i), the associated PFA profile, a_j, shown in Fig. 2c is combined using (2) by considering the inelastic contribution of the first two modes vibration and the elastic contribution of the higher modes.

$$a_{\text{j}} = \sqrt {\mathop \sum \limits_{i = 1}^{2} a_{\text{j,i}}^{2} + \mathop \sum \limits_{i = 3}^{n} \left( {a_{\text{j,i}} R_{\text{i}} } \right)^{2} }$$

(2)

where R_i are the individual modal reduction factors and a_j,i is the PFA in mode i of n modes considered at the jth floor given by:

$$a_{\text{j,i}} = \frac{{\phi_{\text{j,i}} \varGamma_{\text{i}} Sa\left( {T_{\text{i}} } \right)}}{{R_{\text{i}} }}$$

(3)

where ϕ_j,i is the ith mode shape value at floor j and Γ_i is the modal participation factor. The modal reduction factors are given as ${\text{R}}_{\text{i}} =\upmu^{{\upalpha_{\text{i}} }}$, where μ is the ductility of structure and α_i are the modal reduction exponents described in Welch (2016) for moment frames as:

$$\alpha_{1} = 1.0$$

(4)

$$\alpha_{2} = \left\{ {\begin{array}{*{20}l} {0.4,} \hfill & {\lambda_{2} \le 0.5} \hfill \\ {\left( {0.17 + 0.46\lambda_{2} } \right) \le 1.0,} \hfill & {\lambda_{2} > 0.5} \hfill \\ \end{array} } \right.$$

(5)

$$\alpha_{3} = \left\{ {\begin{array}{*{20}l} {0.2,} \hfill & {\lambda_{3} \le 0.5} \hfill \\ {0.45\lambda_{3} \le 0.75,} \hfill & {\lambda_{3} > 0.5} \hfill \\ \end{array} } \right.$$

(6)

with higher modes being taken as zero. λ_i is given by:

$$\lambda_{i} = \left| {\frac{{\phi_{n,i} \varGamma_{i} Sa\left( {T_{i} } \right)}}{{\phi_{n,1} \varGamma_{1} Sa\left( {T_{1} } \right)}}} \right|$$

(7)

Fig. 2

Overview of the simplified method proposed by Welch (2016) to estimate PFA

Knowing the PFA profile, a_j, the maximum peak floor acceleration (MPFA) along the height, a_max, for a known seismic input Sa(T₁) is determined as:

$$a_{max} = \mathop {\hbox{max} }\limits_{j} a_{j}$$

(8)

This approach requires some parameters to be identified, most notably the individual elastic periods of vibration, T_i, mode shapes, φ_j,i and the modal reduction factors, R_i. Modal properties are typically obtained using an eigenvalue analysis, meaning that some kind of a numerical model would be needed. A relatively simple elastic model may be constructed to conduct an eigenvalue analysis of the structure and obtain the modal properties, without any explicit need for member force–deformation relationships that would be required at a later stage for extensive verification. As the purpose of these simplified methods of estimating MAFE is not to substitute extensive analysis via numerical modelling but rather serve as a support tool to verify and better understand results, this need of a numerical model is not envisioned to be a limiting factor.

In the end, the demand–intensity relationship for MPFA (i.e. a_max vs. Sa(T₁)) is established. However, this is slightly different to the handling of MPSD since MPFA tends to saturate with increasing intensity as a result of structural yielding. This typically means that a single linear fit in logspace is no longer sufficient over the entire range of response. To this end, O’Reilly and Monteiro (2019) have proposed the following bilinear demand–intensity model:

$$a_{max} \approx \left\{ {\begin{array}{*{20}l} {m_{a,lower} Sa\left( {T_{1} } \right)^{{b_{a,lower} }} ,} \hfill & {Sa\left( {T_{1} } \right) < Sa_{y} \left( {T_{1} } \right)} \hfill \\ {m_{a,upper} Sa\left( {T_{1} } \right)^{{b_{a,upper} }} ,} \hfill & {Sa\left( {T_{1} } \right) \ge Sa_{y} \left( {T_{1} } \right)} \hfill \\ \end{array} } \right.$$

(9)

where m_a,lower, m_a,upper, b_a,lower and b_a,upper are coefficients quantified from response analysis results. The yield spectral acceleration of the structure, Sa_y(T₁), is used to define this interface between the two zones of response. Assuming that the structure is dominated by the first-mode response, this can be estimated as follows:

$$Sa_{y} \left( {T_{1} } \right) = \frac{{V_{y} }}{{m_{\text{e}} }}$$

(10)

where V_y identified from the assessment results of Sect. 2.1 and m_e is as defined in Fig. 1c.

2.3 Estimating the MAFE

The previous sections discussed the quantification of demand–intensity relationships for both MPSD and MPFA. Cornell et al. (2002) described a simplified closed-form solution (Fig. 3) to compute the MAFE with 50% confidence level, λ, using linear demand–intensity models as:

$$\lambda = H\left( {\left( {\frac{{\hat{C}}}{m}} \right)^{{\frac{1}{b}}} } \right)\exp \left[ {\frac{{k^{2} }}{{2b^{2} }}\beta_{TOT}^{2} } \right]$$

(11)

where H is the site hazard model, ${\hat{\text{C}}}$ is the median capacity of a limit state, m and b are generalised demand–intensity model terms, k is a site hazard term and the term β_TOT represents the total uncertainty from both demand and capacity.

Fig. 3

Illustration of the computation of the MAFE of a given limit state capacity in a closed-form solution via the demand–intensity model and site hazard curve

The demand–intensity relationships outlined in previous sections can now be used to compute the MAFE of a given value of θ_max or a_max. Assuming a demand–intensity relationship with coefficients m_θ and b_θ in (1) for MPSD, Vamvatsikos (2013) further developed the initial proposal by Cornell et al. (2002) in (11) and derived more accurate expressions with a more refined site hazard curve fit via the parameters k₀, k₁ and k₂ described in “Appendix” to give:

$$\lambda_{\theta } = \sqrt {\phi_{\theta }^{'} } k_{0}^{{1 - \phi_{\theta }^{'} }} H\left( {\left( {\frac{{\theta_{max} }}{{m_{\theta } }}} \right)^{{\frac{1}{{b_{\theta } }}}} } \right)^{{\phi_{\theta }^{'} }} \exp \left[ {\frac{{k_{1}^{2} \phi_{\theta }^{'} }}{{2b_{\theta }^{2} }}\beta_{TOT,\theta }^{2} } \right]$$

(12)

where φ′_θ is given by:

$$\phi_{\theta }^{'} = \frac{1}{{1 + \frac{{2k_{2} \beta_{TOT,\theta }^{2} }}{{b_{\theta }^{2} }}}}$$

(13)

and the term $\beta_{{{\text{TOT}},\theta }}^{2}$ is the total MPSD dispersion.

For MPFA-based limit states, a bilinear demand–intensity model is adopted and characterised by the best-fit parameters m_a,lower, m_a,upper, b_a,lower and b_a,upper in (9) and the MAFE is given in O’Reilly and Monteiro (2019) as:

$$\lambda_{a} = F_{lower} \left( {Sa_{y} \left( {T_{1} } \right)} \right)G_{lower} + \left[ {1 - F_{upper} \left( {Sa_{y} \left( {T_{1} } \right)} \right)} \right]G_{upper}$$

(14)

where F_lower(Sa_y(T₁)) and F_upper(Sa_y(T₁))) are the lognormal cumulative density function values with corresponding mean values of μ_lower and μ_upper and standard deviations of σ_lower and σ_upper, respectively, which when using the respective coefficients in (9) are described by (15)–(18). Again, the term $\beta_{\text{TOT,a}}^{2}$ is the total dispersion related to the MPFA.

$$\mu = \phi_{a}^{'} \left( {\frac{{\left( {\ln a_{max} - \ln m_{a} } \right)}}{{b_{a} }} - \frac{{k_{1} \beta_{TOT,a}^{2} }}{{b_{a}^{2} }}} \right)$$

(15)

$$\sigma = \frac{{\beta_{TOT,a}^{2} \sqrt {\phi_{a}^{'} } }}{{b_{a} }}$$

(16)

$$\phi_{a}^{'} = \frac{1}{{1 + \frac{{2k_{2} \beta_{TOT,a}^{2} }}{{b_{a}^{2} }}}}$$

(17)

$$G = \sqrt {\phi_{a}^{'} } k_{0}^{{1 - \phi_{a}^{'} }} H\left( {\left( {\frac{{a_{max} }}{{m_{a} }}} \right)^{{\frac{1}{{b_{a} }}}} } \right)^{{\phi_{a}^{'} }} \exp \left[ {\frac{{k_{1}^{2} \phi_{a}^{'} }}{{2b_{a}^{2} }}\beta_{TOT,a}^{2} } \right].$$

(18)

3 Case study application

The previous section outlined a closed-form methodology to computed the MAFE of both storey drift-based and floor acceleration-based limit state definitions. To demonstrate that these simplified methods are in fact capable of estimating the MAFE with reasonable accuracy, two case study buildings are examined here.

Two case study buildings from Haselton et al. (2007) were utilised and comprise a 4 and 8 storey RC moment frame building, denoted by the building design IDs 1003 and 1011, respectively. Further details regarding the structural design details can be found in Haselton et al. (2007). Numerical models were developed in OpenSees (McKenna et al. 2010) using the approach outlined in Haselton et al. (2008). Eigenvalue analyses of the structural models returned a first-mode period of vibration of 1.16 s and 1.70 s for the 4 and 8 storey frames, respectively, which are consistent with the values found by Haselton et al. (2007).

To demonstrate the applicability of the simplified seismic assessment framework previously outlined, a location is required to obtain a site hazard model, H(Sa(T)), with representative values. A site with stiff soil (i.e. V_s,30 = 500 m/s) situated at a latitude and longitude of [42.35°, 13.40°] in the Italian city of L’Aquila was selected and the OpenQuake engine (Monelli et al. 2012) was used to perform PSHA using the SHARE area and fault source model (Woessner et al. 2015). Vibration periods, T, ranging from 0 to 4 s were considered. This resulted in the creation of a site hazard surface illustrated in Fig. 4. The assessment procedure outlined in Sect. 2.1 using the IM conversion of “Appendix” requires that the Vamvatsikos (2013) second-order hazard model fit to be computed for each T considered, which were also quantified.

Fig. 4

Site hazard surface (left) for a site located in the city of L’Aquila, Italy, where the typical seismic hazard curve representation for specific values of T are also shown on the right

To characterise the response of the aforementioned structures, IDA (Vamvatsikos and Allin Cornell 2002) was conducted. A single set of 40 ground motion were selected from the NGA-West2 database (Ancheta et al. 2013) whose source and site characteristics matched those assumed for the chosen site. This was identified by examining the hazard disaggregation at the 475-year return period for T = 1.5 s based on the first mode periods of two buildings. While this use of a single set of ground motion records is not without its criticism, its drawbacks are not expected to greatly influence the conclusions drawn herein.

4 Results

4.1 Extensive approach

Using numerical models for each structure, IDA was conducted to characterise the distribution of both the MPSD and MPFA with respect to intensity. The 16%, 50% and 84% fractiles were computed and are shown in Fig. 5. Notably, the MPSD traces follow the gradual path towards the right-hand side, with a gradual vertical spread of the 16% and 84% fractiles away from the median response, reflecting higher record-to-record variability in the non-linear range of structural response. This is quite typical of IDA results expressed in this format (i.e. MPSD vs. Sa(T₁)) for RC frames with a stable and ductile failure mechanism. On the other hand, one of the distinct characteristics that can be noted from the MPFA results is the tendency of the MPFA values to saturate with increasing intensity, as discussed in Sect. 2.2.

Fig. 5

IDA results of the case study buildings in terms of both MPSD and MPFA

Using the median response illustrated in Fig. 6, the demand–intensity models discussed in Sect. 2 were fitted with (12) and (14) for MPSD and MPFA, respectively. These are illustrated in Fig. 6 for both buildings and demand parameters, where it can be seen how the median response is well-represented in each case by the models. For the case of the MPFA plots in Fig. 6c, d, the values of Sa_y(T₁) illustrated via the dashed horizontal lines were estimated using (10).

Fig. 6

IDA results expressed in terms of the 16%, 50% and 84% fractiles, where the fitted coefficients for the respective demand–intensity models are shown and the horizontal dashed lines in c and d represent the Sa_y(T) for each building

4.2 Simplified approach

For the MPSD demand–intensity model, Sect. 2.1 was followed. An initial value of θ_max to assess the structural response was chosen. Knowing basic building geometry and material properties, the displaced shape was estimated, as per Fig. 1a. With the expected displaced shape of the structure known, the equivalent SDOF’s properties were computed (Fig. 1b) and the displacement reduction factor, η, was estimated using the expression provided by Priestley et al. (2007) for RC frames. The internal member forces generated at this displaced state were computed to give the base shear, V_b, and subsequently the effective period, T_e, as shown in Fig. 1c. The elastic spectral displacement at the effective period, Sd(T_e), was then computed as a function of η as shown in Fig. 1d to result in both Sd(T_e) and T_e being known values. The initial period of the structure, T₁, was estimated as a function of T_e and μ so that the corresponding elastic spectral acceleration, Sa(T₁), could be computed using the approach outlined in “Appendix”. With both θ_max and Sa(T₁) known, this meant that a single point of the MPSD demand–intensity model was identified. Repeating the above steps for different input values of θ_max further populated this demand–intensity model described in (1). Table 1 presents an overview of the pertinent values obtained from the assessment at a number of MPSD values. It can be seen how the points examined cover the full range of response of the structure, with μ varying from 0.66 to 2.90. Taking these values of MPSD demand and intensity, the parameters in (1) were found by performing a least squares regression, illustrated in Fig. 7. Comparing these to those identified in Fig. 6 using the IDA results, a good match is noted. The fact that the two demand–intensity models are almost the same is noted not to be a general trend but rather a coincidence and the coefficients would be expected to vary for other typologies. Furthermore, the linear nature is also expected to hold in situations where the structure does not have a short first mode period of vibration (i.e. where the “equal displacements” approximation is valid and b_θ is approximately 1.0) or suffer from significant strength or stiffness degradation. An example of where this is not the case is for RC frames with masonry infill, where O’Reilly and Monteiro (2019) have shown how their demand intensity model is quite non-linear. A recent study by Nafeh et al. (2019) has also shown that their seismic behaviour ought to be treated with care compared to other structural systems such as the ones examined here.

Table 1 Overview of the simplified assessment results for MPSD for both case study buildings

Fig. 7

Results of the simplified assessment for MPSD with the coefficients fitted with least squares regression for user-defined values of θ_max

For the case of estimating the MPFA demand–intensity model, Sect. 2.2 was implemented. The modal participation factor and modal masses were computed and Table 2 outlines these for the first four modes of both buildings. To estimate the yield spectral acceleration of the structure, Sa_y(T₁), the base shear at yield was computed as per (10) to be 0.22 g and 0.17 g for the 4 and 8 storey buildings, respectively. To estimate the relative spectral demands in each mode, the mean values of the ground motions scaled to the same value of Sa(T₁) for both structures was used and are illustrated in Fig. 8 for both case study structures. By doing this, the relative spectral demands in different modes of vibration were computed with respect to a chosen value of Sa(T₁). To estimate the modal reduction factors, R_i, the modal reduction exponents α_i were computed as a function of the relative modal accelerations, λ_i, and are listed in Table 2.

Table 2 Estimation of modal properties, relative spectral demands and modal reduction exponents as per the explicit method proposed by Welch (2016)

Fig. 8

Relative spectral demands on each case study building as determined from the mean value of the 40 record ground motion set used in IDA

The value of MPFA, a_max, for an input value of Sa(T₁) was estimated by finding the SRSS combination using (2) and taking the maximum value using (8). By repeating this process for a number of Sa(T₁) values, the MPFA demand–intensity intensity models were established. Care was taken to ensure that sufficient points were chosen in both zones of response, corresponding to above and below the yield spectral acceleration, so that the bilinear model could be adequately captured and the salient results are listed in Table 3. These values were then used to computed the bilinear demand–intensity model’s coefficients. The fitted coefficients were constrained to result in a continuous demand–intensity model across the transition point. Figure 9 plots the results listed in Table 3 and shows the coefficients found in each case. Comparing these to the IDA results in Fig. 6, a satisfactory match may also be noted.

Table 3 Overview of the simplified assessment results for MPFA for both case study buildings

Fig. 9

Results of the simplified assessment for MPFA with the coefficients fitted for values of Sa(T₁)

5 Validation of simplified estimation of MAFE

For each approach, the MAFE was computed for increasing demand and the results are plotted in Fig. 10. In order to make a meaningful comparison between the direct integration of the IDA results and the closed-form solutions, compatible assumptions of the various dispersion terms needed to be established. Since the IDA results encompass just record-to-record variability, just the β_DR,θ and β_DR,a terms are non-zero, and their values are identified directly from the IDA results shown in Fig. 6. By implementing these closed-form solutions via both extensive and simplified approaches to quantify the demand–intensity models, Fig. 10 shows them to give relatively accurate predictions of the MAFE in all cases with respect to each other and also the direct integration of the IDA results. This demonstrates that the use of the simplified approaches outlined previously does indeed provide satisfactory predictions of performance when extended to PBEE both in terms of MPSD and also MPFA. As noted previously, such a validation has been lacking in the literature to date. It has been used in the past by Welch et al. (2014) but such a direct comparison of the MAFE of storey drift was not explicitly considered. In addition, a linear hazard curve fit was used when studies (Bradley and Dhakal 2008; Vamvatsikos 2013) have advocated moving away from and adopting more accurate expressions to represent the hazard, such as that adopted here. Furthermore, the approach of converting the IM outlined in “Appendix” is not present in previous work on this specific topic.

Fig. 10

MAFE versus MPSD and MPFA for the case study buildings using different analysis approaches

To further demonstrate the comparison between the values computed by the extensive and simplified approaches, a further example was assessed with non-zero dispersion terms to account for the other sources of uncertainty that would typically be required to be considered in practice. For the drift-based limit state, this capacity threshold was set as 1.0% and for the floor acceleration-based limit state, this was set as 0.25 g as an illustrative example. For both approaches, the hazard model parameters described previously were utilised and are listed in Table 4 along with the demand–intensity model parameters for both assessment approaches. Since deterministic limit state definitions are being used, this implies that the terms β_CR and β_CU are zero. The β_DR and β_DU terms, on the other hand, describe the natural randomness (i.e. aleatory uncertainty mainly related to record-to-record variability) and inherent uncertainty (i.e. epistemic uncertainty typically related to the modelling uncertainty) of the demand, respectively. The β_DR terms were quantified using the fractiles plotted in Fig. 6, whereas reasonable values were chosen for the modelling uncertainty, β_DU,θ and β_DU,a based on empirical quantification studies relating to the response parameter and limit state of interest. For both demand parameters, Table 4 shows how the MAFE calculated using either the extensive or simplified approach outlined here give similar results for both structures and demand parameters.

Table 4 Computation of the MAFE of MPSD and MPFA following an extensive and more simplified approach

6 Role in verification of new designs

The topic discussed here nominally describes a simplified method of estimating MAFE but is noted to have a potentially important role in the refinement and verification of new designs. The idea is not to replace extensive verification analysis, but provide a simple way in which candidate designs can be checked against the performance objectives they aim to deliver. This was noted by Gokkaya et al. (2016), where the safety of structures designed using recommended drift limits the revised US code ASCE 7 (ASCE 2017) were shown to be unconservative. This was shown via extensive dynamic analysis whilst also ensuring various sources of uncertainty were accounted for. A simplified method like the one described here could also have demonstrated the suitability of the design in a similar manner.

Recently, a conceptual design framework (O’Reilly and Calvi 2019) was proposed (Fig. 11a–d), whereby designers begin by focusing solely on the performance objectives and follow some simplifying assumptions to arrive at a number of feasible design solutions. An attractive aspect of this framework is that it brings both storey drift and floor acceleration into the design procedure, then tells the designer which kinds of geometry and material would be required to respect the initial performance objectives for different structural systems (Fig. 11d). It is at this point that designers must choose one of these candidate solutions, detail and then verify them with respect to the initial performance objectives (Fig. 11e–h). However, given that a number of assumptions need to be made to arrive at the feasible design solutions (Fig. 11a–c), some simplified verification and refinement of the chosen structural system at a design spreadsheet level would be desirable. This is contrary to the case where an extensive verification analysis is carried out using detailed numerical models and analysis methods, only to arrive at the conclusion that a slight design modification is required and the whole process needs to be then repeated (i.e. arriving at the red line as opposed to the green line in Fig. 11g). Often, simplified methods can demonstrate to designers that for a specific building typology, their final design solution is within a reasonable range of what an extensive analysis would give (i.e. the blue line in Fig. 11g). In cases where a candidate design may be identified to possess some performance issues during simplified verification, the design may be adjusted in a spreadsheet environment with relative ease. The subsequent extensive verification analysis can then be carried out just once with an increased degree of a priori confidence.

Fig. 11

Illustration of the basic steps of the conceptual design framework proposed by O’Reilly and Calvi (2019) and subsequent performance verification

7 Conclusions

Recent developments in performance-based earthquake engineering (PBEE) are gradually becoming more risk-oriented. While great strides have been made in the research community to develop more advanced aspects beneath the overarching umbrella of PBEE, there is still a need for simple procedures and methods that do not necessarily require time-consuming numerical analyses. This article has discussed such a simplified procedure, where previous analysis methods have been extended and tested to allow the estimation of the mean annual frequency of exceeding (MAFE) of both storey drifts and floor accelerations.

For storey drifts, a displacement-based approach was described and further developed to account for aspects regarding intensity measure consistency. These relate to the fact that when simplified models based on effective stiffness are used in risk assessment, additional attention to detail is required by the analyst to ensure that the correct limit state exceedance rate is computed. This aspect is currently absent from approaches utilising a code-defined response spectrum. For more advanced approaches utilising seismic hazard analysis results directly, a solution to incorporate them has been proposed here.

For floor accelerations, a simplified procedure has been adopted to allow the MAFE of a given peak floor acceleration in a structure to be estimated. This builds upon a recently developed demand–intensity model where the notably bilinear nature of the peak floor acceleration in a typical structure to increasing intensity means that past approaches required an extra degree of care to implement. The developments described in this work not only alleviate some difficulties on the risk computation side but also utilise a novel method to compute floor accelerations via simplified methods.

This overall simplified risk assessment procedure has been outlined collectively and compared to the result of more extensive analysis using detailed numerical models and numerous ground motion simulations. The results have shown that the simplified procedure proposed here is, in fact, capable of providing reliable estimates of MAFE for both demand parameters typically examined in PBEE, a study that has been thus far lacking in the literature.

Appendix: Intensity measure conversion

For a smoothed code spectrum of uniform hazard, the shape is generally fixed and the corresponding value of Sd(T₁) can be simply read by scaling it to match the identified point for the equivalent system and reading the value at T₁, as shown in Fig. 12a. When using PSHA data, where seismic hazard data is typically provided for a specified number of vibration periods, the conversion becomes slightly more complicated. Consider Fig. 12b, where the site hazard curves for two different vibration periods are known. What is essentially happening is that knowing Sa(T_e) for a given return period or mean annual frequency of exceedance (MAFE), Sa(T₁) can be computed via the relation between the hazard curves at the two vibration periods. Since PSHA data is typically provided as raw data in the form of a site hazard curve, H(Sa), it would be desirable if a closed-form means of IM conversion could be established. Here, a relatively simple means of converting from one intensity measure to another was sought. It relies simplifying the site hazard curve, but it is noted that other more detailed and thorough ways of converting from one intnesity measure to another are available (e.g. Suzuki and Iervolino 2019).

Fig. 12

Identification of the seismic demand at the first mode period using a smoothed code spectra, or b site hazard curves

For the site hazard curves shown in Fig. 12b, some past researchers have attempted to provide means with which to fit expressions. Cornell et al. (2002) described how the H(Sa) relationship could be approximated by a straight line in logspace. This linear representation was later expanded to become a second-order polynomial, which also better represents the hazard curve over a wider IM range and is described by:

$$H\left( {Sa} \right) = H = k_{0} \exp \left( { - k_{1} \ln Sa - k_{2} \ln^{2} Sa} \right)$$

(19)

where k₀, k₁ and k₂ are best-fit parameters to be established for each individual hazard curve. As shown in Fig. 12b, these will be two separate hazard curves at T_e and T₁ and are denoted H^e and H¹, respectively. What is of interest here is the value of Sa(T₁) when Sa(T_e) is known when H^e and H¹ are equal. Assuming that the best-fit parameters for both hazard curves are known, it follows that:

$$H^{\text{e}} = k_{0}^{\text{e}} \exp \left( { - k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) - k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)} \right)$$

(20)

$$H^{1} = k_{0}^{1} \exp \left( { - k_{1}^{1} \ln Sa\left( {T_{1} } \right) - k_{2}^{1} \ln^{2} Sa\left( {T_{1} } \right)} \right)$$

(21)

Setting H^e equal to H¹ gives:

$$k_{0}^{\text{e}} \exp \left( { - k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) - k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)} \right) = k_{0}^{1} \exp \left( { - k_{1}^{1} \ln Sa\left( {T_{1} } \right) - k_{2}^{1} \ln^{2} Sa\left( {T_{1} } \right)} \right)$$

(22)

Rearranging to give:

$$\frac{{k_{0}^{\text{e}} }}{{k_{0}^{1} }} = \frac{{\exp \left( { - k_{1}^{1} \ln Sa\left( {T_{1} } \right) - k_{2}^{1} \ln^{2} Sa\left( {T_{1} } \right)} \right)}}{{\exp \left( { - k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) - k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)} \right)}}$$

(23)

and taking the natural logarithm of both sides then gives:

$$\ln \frac{{k_{0}^{\text{e}} }}{{k_{0}^{1} }} = - k_{1}^{1} \ln Sa\left( {T_{1} } \right) - k_{2}^{1} \ln^{2} Sa\left( {T_{1} } \right) + k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) + k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)$$

(24)

Letting ln Sa(T₁) equal X and rearranging gives:

$$\left( {k_{2}^{1} } \right)X^{2} + \left( {k_{1}^{1} } \right){\text{X}} + \left( {\ln \frac{{k_{0}^{\text{e}} }}{{k_{0}^{1} }} - k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) - k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)} \right) = 0$$

(25)

which results in a quadratic polynomial that can be solved as:

$$X = \frac{{ - k_{1}^{1} \pm \sqrt {\left( {k_{1}^{1} } \right)^{2} - 4\left( {k_{2}^{1} } \right)\left( {\ln \frac{{k_{0}^{\text{e}} }}{{k_{0}^{1} }} - k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) - k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)} \right)} }}{{2k_{2}^{1} }}$$

(26)

Substituting back in for X gives:

$$Sa\left( {T_{1} } \right) = \exp \left( {\frac{{ - k_{1}^{1} \pm \sqrt {\left( {k_{1}^{1} } \right)^{2} - 4\left( {k_{2}^{1} } \right)\left( {\ln \frac{{k_{0}^{\text{e}} }}{{k_{0}^{1} }} - k_{1}^{\text{e}} \ln Sa\left( {T_{\text{e}} } \right) - k_{2}^{\text{e}} \ln^{2} Sa\left( {T_{\text{e}} } \right)} \right)} }}{{2k_{2}^{1} }}} \right)$$

(27)

which will return two solutions, one of which will be unrealistic. This expression provides a means with which a common intensity measure can be found for any effective period of vibration, T_e, to give a consistent demand–intensity relationship in Sa(T₁).