Inelastic floor spectra for designing anchored acceleration-sensitive nonstructural components

Abstract

In this study, inelastic floor spectra are developed for designing acceleration-sensitive nonstructural components (NSCs). The parameters response modification (reduction) factor, $R_{\text{cc}}$, and inelastic displacement ratio, $C_{\text{cc}}$, are evaluated to quantify the effects of NSCs inelasticity on their seismic-induced force and displacement demands, respectively. The results of the conducted response history analyses illustrate that the inelastic behavior of NSCs can significantly de-emphasize the effects of their tuning period ratio and viscous damping ratio, and of the characteristics of the primary structure and ground excitation. Due to the quasi-harmonic characteristic of building floor motions, NSC inelasticity is more effective for NSCs attached to buildings than for those attached to the ground. NSC inelasticity is most effective for a low-damping roof-mounted NSC tuned to the first modal period of an elastic building (i.e., the most critical NSC from the design point of view). Adopting even a mild level of inelasticity for tuned NSCs not only decreases their seismic force demands significantly but also reduces their displacement demands. For non-tuning conditions, particularly for rigid NSCs, achieving even a relatively small $R_{\text{cc}}$ (i.e., a small reduction in force demand) leads to a significant increase in NSC displacement and ductility demands suggesting that these NSCs should be designed to remain elastic. Results illustrate that the amplitude of $R_{\text{cc}}$ and $C_{\text{cc}}$ depends on the tuning ratio, viscous damping, and level of inelasticity of NSCs, and to a lesser extent, on the characteristics of the primary structure and ground motion. Simplified yet reliable equations are proposed for the estimation of the parameter $R_{\text{cc}}$ for non-rigid NSCs with different levels of inelasticity and viscous damping.

1 Introduction

Nonstructural components (NSCs) are those elements and subsystems that are not part of the gravity or lateral-force bearing systems but support the functionality of building structures. In other words, the term NSC describes any component in a building that is not part of the structural skeleton, where the structural skeleton usually includes beams, columns, bracings, shear walls, and floor slabs. NSCs range from office supplies to fire safety systems. Because the NSCs category contains such a wide variety of items, they constitute a major part of the cost of typical building structures. Surveying reports following the past earthquakes in the United States and other seismic-prone countries have revealed that damage to NSCs constitutes a sizable portion of cost imposed on building structures that in many cases can far exceed the cost of damage to structural components (McKevitt et al. 1995; Filiatrault et al. 2001, 2002; Myrtle et al. 2005; Gupta and McDonald 2008). Furthermore, failure of NSCs may disrupt the functionality of critical public services such as hospitals, fire stations, power stations, and water treatment plants. Despite their great importance, seismic provisions for designing NSCs in building codes and load standards (e.g., ASCE/SEI 7-16 2016) are rather simple, arguably more prescriptive and with a weaker research-basis than those presented for designing the structural elements. Evidence from previous earthquake events, supported by numerical investigations, consistently suggests that current design provisions and construction methods might fail to protect NSCs against even relatively low-intensity ground motions (Anajafi 2018).

NSCs are usually classified into two broad categories of primarily deformation-sensitive (e.g., glass blocks, prefabricated panels, partitions, and glazing systems) and primarily acceleration-sensitive components (e.g., chimneys, parapets, storage vessels, and fire suppression piping systems). This study focuses on the horizontal seismic responses of anchored, acceleration-sensitive NSCs. In the context of this study, the term NSC implies a secondary system consisting of a component, its support(s), and attachment(s) to the primary structure. The seismic response of an NSC that is housed in a building structure is greatly influenced by two filters that are connected in series: the primary structure and the NSC itself. The ground excitation is first filtered by the primary structure. Due to this filtering effect, the characteristics of floor acceleration motions (i.e., the induced motions at the base of NSCs) are markedly different from those of typical ground acceleration motions. As a second filter, an NSC can further alter the characteristics of the induced floor acceleration motions. As a result of these filtering effects, the acceleration responses of NSCs are usually semi-harmonic (narrow-band) and substantially different from the broad-band characteristic observed in typical ground acceleration motions. The most important components of the two aforementioned filters are summarized in the flowchart presented in Fig. 1. As seen, the primary building filtering effect is characterized by many complex parameters, although some of them are not explicitly (and in some cases adequately) taken into account for designing NSCs in building codes and load standards such as ASCE/SEI 7-16 (Anajafi 2018). The effects of these parameters have been extensively evaluated in the past. For example, it has been shown that the inelastic behavior of the primary structure, except for some special cases (e.g., low-damping non-tuned NSCs attached to structures with localized plasticity), can substantially reduce seismic-induced force demands on NSCs (Lin and Mahin 1985; Toro et al. 1989; Chaudhuri and Villaverde 2008; Sankaranarayanan and Medina 2008; Anajafi 2018).

Fig. 1

The most important components of the two filters that influence the seismic responses of NSCs

The second filter (i.e., an NSC) can be characterized by a tuning ratio (i.e., the ratio of the initial period of an NSC to the fundamental period of the primary structure), the level of nonlinearity (material inelasticity or any other forms of nonlinearity such as rocking), and viscous damping. The effect of the NSCs tuning ratio on their elastic seismic-induced demands has been comprehensively addressed in the literature. Nowadays, it is well understood that the elastic seismic responses of tuned NSCs can be significantly greater than those of non-tuned NSCs. However, very few studies have addressed the influence of NSCs viscous damping and/or nonlinear behavior on their seismic-induced demands. Previous studies have mostly focused on the responses of elastic NSCs and assumed that NSCs exhibit a viscous damping ratio of 5% (e.g., see Naeim et al. 1998; Rodriguez et al. 2002; Adam and Furtmüller 2008; Fathali and Lizundia 2011; Wieser et al. 2013; Wang et al. 2014; Anajafi and Medina 2018a).

The assumption of 5% viscous damping for NSCs is based on engineering judgment rather than experimental investigations. This assumption most likely mimics the rule-of-thump approximation of 5% viscous damping for typical buildings. However, the number of viscous damping mechanisms in buildings (e.g., foundation damping, friction and slippage in steel connections, opening and closing of micro-cracks in concrete members, etc.) is not comparable to those in typical NSCs. The results of a few experimental investigations that have been conducted to estimate the NSCs dynamic characteristics (e.g., Watkins et al. 2009; Watkins 2011; Archila et al. 2012; Astroza et al. 2015) also suggest that the viscous damping ratio of typical NSCs might fall well below the nominal 5% value. This is particularly important given that based on the results of some recent studies, due to the semi-harmonic characteristic of building floor motions, the elastic seismic-induced force demand on NSCs is highly dependent on the value of NSC viscous damping. For example, the elastic force demand on an NSC with 2% damping can be, on average, 1.6 times that on an NSC with 5% damping (NIST GCR 18-917-43 2018; Anajafi and Medina 2019a). Many additional parameters, such as diaphragm flexibility, torsional responses, and also uncertainties in the inelastic behavior of the primary structure, which are usually neglected when quantifying seismic demands on NSCs, can further amplify the NSCs elastic demands. For example, a study on instrumented buildings in California, USA, revealed that the torsional responses of the supporting structure and/or the in-plane flexibility of floor diaphragms can increase seismic-induced force demands on elastic NSCs by factors as great as 1.5 (Anajafi and Medina 2019b). Applying these additional amplification factors can lead to relatively large elastic force demands on NSCs. The abovementioned observations indicate the presence of significant uncertainties in the estimation of seismic-induced demands on NSCs, which are inherent in the characteristics of input ground excitation, primary structure and NSCs themselves. Due to these uncertainties, adopting an elastic design approach for NSCs might complicate the design process and significantly increase construction costs. As an alternative approach, NSC seismic force demand can be limited to a predefined level through incorporating an inelastic mechanism (seismic fuse) into the NSC system (Miranda et al. 2018). As the present study illustrates, this approach can significantly decrease the dependency of NSCs seismic-induced displacement and force demands on the characteristics of the primary structure and NSCs.

A few studies have investigated inelastic floor spectra using the acceleration responses of numerical building models and instrumented buildings (e.g., see Viti et al. 1981; Igusa 1990; Adam and Fotiu 2000; Villaverde 2006; Chaudhuri and Villaverde 2008; Vukobratović and Fajfar 2017; Kazantzi et al. 2018; Obando and Lopez-Garcia 2018). A detailed description of the findings of these studies was provided in Anajafi (2018). For example, Chaudhuri and Villaverde (2008) evaluated the seismic responses of inelastic NSCs attached to the second floor and roof of eight moment resisting frame buildings. In this study, the initial period of NSCs was assumed equal to one of the first four natural periods of the primary structure (in other words, only tuned NSCs were considered); the NSC viscous damping ratio was assumed to be either 0.5% or 2%; and a fixed NSC response modification factor (R_cc) of 6.0 was used. Chaudhuri and Villaverde illustrated that assuming a constant R_cc, displacement ductility demand on tuned NSCs depends on the height and period of the primary structure and is different for the roof and second floor. They also illustrated that, displacement ductility demand on NSCs in tune with the first-mode of the structure is larger for the case of inelastic supporting structure compared with the elastic one. Vukobratović and Fajfar (2017) developed inelastic floor acceleration spectra for a single-degree-of-freedom (SDOF) primary structure with a period of 0.3 s and target displacement ductility values of 1.0 and 2.0. In their study, the NSC viscous damping ratio varied from 1% to 7%, and the NSC target ductility was either 1.0 or 1.5. Vukobratović and Fajfar showed that NSC inelasticity can lead to a substantial decrease of mean floor acceleration spectra (with the exception of rigid NSCs) for both elastic and inelastic primary structure cases. They also showed that, for inelastic NSCs, the effect of NSCs viscous damping ratio on their seismic demand is relatively small. Obando and Lopez-Garcia (2018) developed inelastic constant-R_cc floor spectra for eight elastic buildings exposed to a Gaussian zero-mean random process, which was representative of far-field ground motions. The inelastic spectra were generated for R_cc factors ranging from 2.0 to 8.0 and NSC damping ratios of 2% and 5%. Obando and Lopez-Garcia showed that NSC inelasticity can significantly decrease displacement demands on tuned NSCs (especially those tuned to the first structural mode). They also concluded that for NSC periods greater than the first-mode period of the primary structure, the inelastic spectral displacements tend to the elastic ones implying that the equal-displacement principle applies. Kazantzi et al. (2018) developed constant-ductility floor spectra for recorded acceleration motions of instrumented buildings in California and showed that the inelastic behavior of NSCs can reduce their force and displacement demands.

The abovementioned studies have provided valuable insight into understanding the effect of the inelastic behavior of NSCs. Most importantly, they have consistently shown that NSC inelastic actions can significantly reduce seismic-induced force demands on tuned NSCs. However, many of these studies have used SDOF primary structures or elastic multistory structures. A few studies that incorporated inelastic multistory building models (e.g., Chaudhuri and Villaverde 2008) only focused on tuned NSCs and/or used a single or two levels of inelasticity for NSCs. Furthermore, the results of the studies that have been based on the responses of instrumented buildings might not be always directly applicable to the code-based designed buildings because (i) most of these structures responded in their elastic behavior range; (ii) many of them were constructed before the advent of modern/current seismic design provisions and their responses were affected by significant torsional behavior, in-plane diaphragm flexibility, etc. (for more details, see Anajafi and Medina 2018a, 2019b). The present study uses the acceleration responses of several code-based designed (archetype) building models subject to ground motions with different intensities, which simulate different levels of the primary structure inelasticity. Nonlinear building floor spectra are generated for wider ranges of the NSC viscous damping and level of inelasticity than those used in previous studies. The parameters response modification factor, $R_{\text{cc}}$, and inelastic displacement ratio, $C_{\text{cc}}$, are evaluated to quantify the effects of NSCs inelasticity on their seismic demands. The influence of many parameters related to the characteristics of NSCs, buildings and ground motion excitations on the $R_{\text{cc}}$ and $C_{\text{cc}}$ parameters is addressed. Practical expressions are proposed for the $R_{\text{cc}}$ parameter to be incorporated into the NSCs design equations.

2 Background

Most current seismic provisions for designing NSCs rely on a force-based design philosophy. The amplitude of the lateral seismic force demand prescribed by these provisions is usually a function of the peak horizontal floor acceleration ($PFA$), a component amplification factor, $a_{\text{p}}$, and a component response modification (reduction) factor, $R_{\text{p}}$. For instance, the basic form of the equations provided by ASCE/SEI 7-16 load standard for the estimation of the horizontal peak component acceleration (PCA) demand can be represented by Eq. (1):

$$ PCA = PFA \left( {a_{\text{p}} /R_{\text{p}} } \right) $$

(1)

The PFA parameter in Eq. (1) essentially incorporates the effects of the characteristics of the input ground motion and primary structure. The parameter $a_{\text{p}}$ intends to take into account the NSC tuning effect assuming an elastic NSC behavior. The intention of using the $R_{\text{p}}$ factor is to account for all characteristics of an NSC other than the tuning ratio that include viscous damping, nonlinear behavior, and an inherent overstrength produced in the design process, although in the commentaries of ASCE/SEI 7-16 discussions are not provided as to how these effects are combined. For example, the baseline equations have been proposed for a 5% NSC viscous damping. However, it was recognized during the development of the ASCE/SEI 7 Chapter 13 (Seismic Design Requirements for Nonstructural components) that viscous damping ratios are expected to vary for different types of NSCs. Therefore, lower $R_{\text{p}}$ values were proposed for potentially low-damping NSCs to approximately account for this issue. As another example, in the prescribed equations, NSCs are implicitly treated as SDOF systems with lumped masses. However, it was known that distribution systems (e.g., ductwork, electrical conduit, and cable trays) might exhibit a dynamic behavior significantly different from that of a lumped mass system: such systems exhibit many vibration modes, and the mass mobilized in their possible dominant mode could be much smaller than the total mass of the system. As a result, seismic-induced force demands on a distribution system might be smaller than those on an SDOF system with the same mass and damping. To take into account this behavior, greater $R_{\text{p}}$ values were proposed for distribution systems (Anajafi 2018). Despite the abovementioned descriptions, the values of the $R_{\text{p}}$ factor prescribed in ASCE/SEI 7-16 for different NSCs have been established based on engineering judgment rather than numerical or experimental investigates.

The ASCE/SEI 7-16 approaches for determining the PFA and $a_{\text{p}}$ parameters have been evaluated in many previous studies available in the literature. These studies have shown that the PFA and $a_{\text{p}}$ parameters warrant modifications based on the vertical location of the NSC, the type of the lateral-force resisting system and the height (period) of the primary structure (see Anajafi 2018 for more details). However, research has not been conducted to understand the effects of using the prescribed $R_{\text{p}}$ factors on the seismic responses of NSCs. Using an $R_{\text{p}}$ (i.e., a strength reduction factor) greater than unity implies that NSCs are designed to undergo nonlinear actions. However, the imposed displacement and ductility demands on NSCs designed via adopting these $R_{\text{p}}$ factors have not been systematically and accurately evaluated. The present study intends to extend the body of knowledge on how the inelastic behavior of NSCs can affect their force, displacement and ductility demands.

Recently, the National Institute of Standards and Technology (NIST) sponsored the ATC-120 Project (Seismic Analysis, Design, and Installation of Nonstructural Components and Systems). The first two authors of this paper were members of the project team. As part of this project, improved equivalent-static equations were proposed for designing acceleration-sensitive NSCs. The effects of the nonlinear behavior of NSCs on their seismic-induced force demands were quantified and incorporated into the proposed design equations. One of the objectives of the NIST is to consider these new equations for their eventual adoption into seismic design practice via documents such as the NEHRP recommended seismic provisions and ASCE/SEI 7. The present study, whose parts were presented at the ATC-120 meetings and some were included in the final ATC-120 project report (NIST GCR 18-917-43 2018), develops linear and nonlinear floor spectra for acceleration motions of numerical code-compliant building models that are subjected to ground motion excitations with different characteristics. Four different scenarios are examined for the primary-secondary systems in which NSCs (secondary systems) and primary structures can respond linearly/nonlinearly. Floor acceleration and displacement spectra are generated for a wide range of NSC viscous damping and level of nonlinearity.

In an NSC system, nonlinearity can occur in the component, its connections, supports, attachments, or anchors, and in the form of material inelasticity, geometric nonlinearity, friction, sliding, rocking, or a combination of these items/behaviors (NIST GCR 18-917-43 2018). For NSCs that are attached to buildings through well-behaved ductile bracing or support systems, relying on seismic energy dissipation through NSCs nonlinear behavior can be a reasonable design philosophy. For example, the inelastic deformations of angles used to restrain a generator to a floor or bracing elements used to suspend an equipment from a ceiling can play the role of a seismic fuse and provide the required energy dissipation. For types of NSCs that might be attached to buildings through other details (e.g., wall-anchored equipment, and distribution systems), designs that can result in desirable nonlinear mechanisms might be challenging to implement in practice. Research studies involving experiments are required to identify and quantify different mechanisms of NSC nonlinearity. In this study, consistent with the ATC-120 Project, all potential sources of NSC nonlinearity are lumped together, and SDOF oscillators that exhibit a bilinear hysteretic response (material inelasticity) are used to model nonlinear NSCs. Therefore, in the rest of this paper, the term “inelastic” is used for NSCs in lieu of the general term “nonlinear”.

3 Analysis methodology

The analysis method implemented in this paper consists of conducting nonlinear response history analyses on numerical building and NSC models. Two different suites of ground motions are used as the input excitations for the primary structures, and the mean responses are evaluated to identify behavioral trends.

3.1 Nonstructural components

This study deals with NSCs that can be reasonably modeled as SDOF systems. The floor spectrum method, based on the uncoupled analysis of NSC and primary structure, is used to determine seismic-induced demands on NSCs. This approach is sufficiently accurate for NSCs whose masses are smaller than the primary structure mass by a factor of 1000 or larger (i.e., most typical NSCs) as they do not offer significant dynamic feedback to the primary structure (Adam et al. 2013). For heavier NSCs, this approach might be conservative. Constant-ductility floor spectra are generated for NSC target displacement ductility values varying from 1.0 to 5.0. For constant-$R_{\text{cc}}$ spectra, the component response modification factor, $R_{\text{cc}}$, is varied from 1.0 to 4.0. The assumed NSC viscous damping ratio is between 2% and 8%. A Clough-Johnston bilinear hysteresis model with stiffness degradation (Clough and Johnston 1996) and 3% post-elastic stiffness ratio represents the inelastic behavior of NSCs.

3.2 Structural models

In this study, the primary structures used for generating floor acceleration motions are code-based designed (archetype) special steel moment resisting frame (SMRF) and reinforced concrete cantilever shear wall (RCSW) buildings, which represent flexible and stiff lateral-force resisting systems, respectively. These structures comply with those used in the ATC-63 Project for the evaluation of building seismic performance factors (FEMA P-695 2009). The heights of the buildings under consideration vary from two to 12 stories. Therefore, the focus of this study is on short to midrise buildings that constitute most of building stock in the United States. Figure 2 illustrates the plan configurations of the archetype buildings. The SMRF structures are modeled based on the concentrated plastic hinge concept. The RCSWs are modeled using nonlinear multi-layer shell elements that explicitly model vertical rebars and concrete nonlinearity. Detailed descriptions of the buildings characteristics and their finite element models were provided in Anajafi (2018); NIST GCR 18-917-43 (2018). The primary structures are subjected to ground motions with different intensities including the Design Earthquake (DE) level. Numerical analyses illustrate that the primary structure global ductility demand at the DE level ($\mu_{\text{b}}$ defined in Sect. 3.4) varies from 2.2 for the taller SMRF buildings to 5.3 for the shorter RCSW buildings (NIST GCR 18-917-43 2018). Table 1 illustrates the geometric characteristics and the periods of the first three vibration modes of the archetype structures used in this study. For the RCSWs, the peaks present in the elastic roof acceleration spectra at the DE level are used to estimate the modal periods.

Fig. 2

Plan configurations of the archetype buildings (gravity columns are omitted for clarity)

Table 1 Geometric characteristics and modal periods of the archetype structures

3.3 Ground motions

Two suites of ground motions are utilized for the nonlinear response history analyses. The primary computations are performed using a suite of simulated spectrum-compatible (SC) ground motions. A set of far-field (FF) recorded ground motions is implemented for the evaluation of the sensitivity of the floor spectra results to the choice of the input ground excitation set used for the response history analysis of the primary structure.

The use of SC ground motions can mitigate the record-to-record variability present in the structural responses with respect to when recorded ground motions are utilized. However, as illustrated by Anajafi and Medina (2018b), this record-to-record variability is still sufficiently large to require using a significant number of SC ground motions and conducting statistical analysis on the responses obtained from the individual SC ground motions. To address this issue, a set of 20 SC ground motions are utilized in this study. To generate the SC ground motions, 20 FF records are manipulated using the wavelet adjustment technique proposed by Al Atik and Abrahamson (2010), in a way that the 5%-damped elastic response spectra of the simulated records match the given design (target) spectrum. The target spectrum, which is shown in Fig. 3a, is a risked-based 5%-damped design spectrum for a site of high seismicity in California. This spectrum is compatible with the one used for designing the primary buildings (for more information, see Anajafi and Medina 2018b). Figure 3a depicts the 5%-damped acceleration response spectra for the SC ground motions. As seen, the simulated ground motions are tightly matched to the target spectrum.

Fig. 3

a 5%-damped acceleration response spectra for the 20 SC ground motions; b 5%-damped acceleration response spectra for the 44 unscaled FF ground motions and their amplitude-scaled mean spectrum for the eight-story RCSW structure

The second suite used in this paper, is the FEMA P-695 FF record set including 44 individual recorded ground motions that are (uniformly) amplitude-scaled according to the ASCE/SEI 7-16 seismic provisions. For a given building model, the scale factor is determined such that the average values of the acceleration response spectra from all the records do not fall below 90% of the design response spectrum for any period within $[T_{{{\text{b}}2}} - 2T_{{{\text{b}}1}} ]$. Figure 3b illustrates the individual 5%-damped acceleration spectra for the unscaled (original) FF ground motions, their mean spectrum, and also the amplitude-scaled mean spectrum for a representative building.

Unless mentioned otherwise, the response history analyses are conducted at the DE level using the set of SC ground motions. More specifically, all analysis results are presented for the SC ground motions at the DE level, except for (i) in Sect. 4, harmonic base excitations are utilized; (ii) in Sect. 8.2, the FF suite is also used; (iii) in Sect. 8.3, intensity levels other than the DE are also considered.

3.4 Parameters and nomenclatures used

The most salient parameters and nomenclatures used in this study are presented next:

• NSC = a secondary system consisting of a component, its support(s), attachment(s), and anchor(s). In all equations and definitions presented below, the term component implies the NSC system.

• T_bi = the period of the i-th mode of vibration of the primary building.

• T_c = the elastic (initial) period of a component.

• Tuned NSC = an NSC system with an elastic (initial) period equal to of one of the elastic modal periods of the primary building.

• ${\text{HM region}} =$ the higher-mode region of a floor acceleration spectrum, which includes components with initial periods in the range $0.05T_{{{\text{b}}1}} < T_{\text{c}} \le 0.5T_{{{\text{b}}1}}$.

• FM region = the fundamental-mode region of a floor acceleration spectrum, which includes components with initial periods in the range $0.5T_{{{\text{b}}1}} < T_{\text{c}} \le 1.5T_{{{\text{b}}1}}$.

• PGA = peak ground acceleration.

• PFA = peak floor acceleration.

• PCA = peak component acceleration.

• $\xi_{\text{c}} =$ the viscous damping ratio of a component.

• $S_{\text{dc}} =$ the maximum drift response of an elastic/inelastic component; where drift implies relative displacement with respect to the component attachment point. $S_{\text{dc}}$ is denoted as the component spectral displacement response.

• S_ac = the maximum force demand on an elastic/inelastic component normalized to its operating weight. $S_{\text{ac}}$ is denoted as the component spectral acceleration response.

• $DMF_{cc}=S_{\text{ac}, \xi}/{S_{\text{ac}, 5\%}}$ is the component damping modification factor, which quantifies the dependency of a component force demand on the value of the component viscous damping ratio.

• $\mu_{\text{c}} = S_{\text{dc}} /\Delta_{\text{c}}^{\text{yield}}$ is the target displacement ductility demand on a component; where $\Delta_{\text{c}}^{\text{yield}}$ is the component yield displacement.

• $\mu_{\text{b}} = \Delta_{\text{roof}}^{\text{mean}} /\Delta_{\text{roof}}^{\text{yield}}$ is the global displacement ductility demand on a building; where $\Delta_{\text{roof}}^{\text{mean}}$ is the mean value of the maximum displacement response of the roof from response history analysis under the DE-level SC ground motions; and $\Delta_{\text{roof}}^{\text{yield}}$ is an estimate of the roof yield displacement based on a pushover analysis.

• $R_{\text{cb}} = [S_{\text{ac}} ]_{\text{elastic bldg}} /[S_{\text{ac}} ]_{\text{inelastic bldg}}$ illustrates the reduction or amplification of a component force demand due to the primary building inelastic behavior. The subscript “cb” refers to the component response modification factor due to the building inelastic behavior.

• $R_{\text{cc}} = [S_{\text{ac}} ]_{\text{elastic comp}} /[S_{\text{ac}} ]_{\text{inelastic comp}}$ illustrates the reduction or amplification of a component force demand due to the component inelastic behavior. The subscript “cc” stands for the component response modification factor due to the component inelastic behavior. $R_{\text{cc}}$ is equivalent to the ductility-dependent portion of $R_{\text{p}}$ used in the ASCE/SEI 7-16 provisions.

• $C_{\text{cc}} = [S_{\text{dc}} ]_{\text{inelastic comp}} /[S_{\text{dc}} ]_{\text{elastic comp}}$ is the inelastic displacement ratio of a component.

4 Inelastic response of SDOF systems to harmonic base excitations

Building floor motions (i.e., excitations at the base of NSCs) are inherently narrow-band (pseudo harmonic). Therefore, an evaluation of inelastic spectra for a simple harmonic excitation can provide significant insight into understanding the effect of NSCs inelastic behavior on their seismic-induced demands. Assume that an inelastic SDOF oscillator (i.e., an NSC) with a natural period $T_{\text{c}}$, viscous damping ratio $\xi_{\text{c}}$, displacement ductility demand $\mu_{\text{c}}$, and zero initial conditions, is subjected to a sinusoidal floor (base) excitation with N cycles of loading and an amplitude of PFA. The floor excitation is given by the equation $\ddot{u}_{\text{f}} \left( t \right) = PFA {\text{sin (}}2\pi t/T_{\text{f}} )$, where $T_{\text{f}}$ is the excitation period and $t \le NT_{\text{f}}$ (i.e., the excitation duration is $NT_{\text{f}}$). The oscillator inelastic behavior is modeled according to Sect. 3.1. Constant-ductility spectra are generated and discussed for the harmonic floor excitations with different durations.

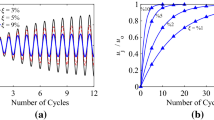
For instance, Fig. 4a presents the normalized 2%-damped constant-ductility acceleration spectra for the SDOF oscillator subjected to the sinusoidal floor excitation with N = 10, assuming different levels of the oscillator inelastic behavior. Figure 4b shows similar results for the 5%-damped spectra. An evaluation of Fig. 4 illustrates that (i) for a given $\mu_{\text{c}}$, the highest reduction of the spectral acceleration response with respect to the elastic oscillator response (i.e., the maximum value of the $R_{\text{cc}}$ spectrum) occurs at the tuning period; (ii) for the non-tuning periods, the inelastic $S_{\text{ac}}$ values approach the elastic ones, regardless of the value of $\mu_{\text{c}}$, implying that $R_{\text{cc}}$ approaches unity; (iii) the effectiveness of the oscillator inelastic behavior, in terms of the spectral acceleration response reduction, is more pronounced for a low-damping oscillator. For instance, consider the reduction in the normalized $S_{\text{ac}}$ values due to adopting a $\mu_{\text{c}}$ of 2.0. As seen, the peak value of $S_{\text{ac}} /PFA$ for the case with $\xi_{\text{c}} = 2\%$ is reduced from 17.8 to 1.7 (i.e., $R_{\text{cc}} = 10.5$), whereas for $\xi_{\text{c}} = 5\%$, this reduction is from 9.6 to 1.5 (i.e., $R_{\text{cc}} = 6.4$). These observations, to some extent, comply with the results of the early studies of Newmark on the inelastic spectra of typical earthquake ground motions (i.e., broad-band excitations).

Fig. 4

Normalized constant-ductility acceleration spectra for an oscillator subjected to the sinusoidal floor excitation with 10 cycles of loading: a$\xi_{\text{c}} = 2\%$; b$\xi_{\text{c}} = 5\%$

The values of the response modification factor and inelastic displacement ratio for the tuning condition are denoted as $R_{\text{cc}}^{\text{tuning}}$ and $C_{\text{cc}}^{\text{tuning}}$, respectively. Figure 5a presents the value of the parameter $R_{\text{cc}}^{\text{tuning}}$ for an oscillator with a $\xi_{\text{c}}$ of 2% exposed to the sinusoidal base excitation with different numbers of loading cycles. Figure 5b illustrates similar graphs for the parameter $C_{\text{cc}}^{\text{tuning}}$. Results show that, for a given $\mu_{\text{c}}$ value, as the number of loading cycles increases, the parameter $R_{\text{cc}}^{\text{tuning}}$ increases and the parameter $C_{\text{cc}}^{\text{tuning}}$ decreases. Therefore, the inelastic behavior of the oscillator is more efficient for an excitation with more cycles (note that, given the definitions, an $R_{\text{cc}}$ value greater than unity and a $C_{\text{cc}}$ value smaller than unity illustrate the positive effect of the oscillator inelasticity). A building floor motion time series is composed primarily of a few harmonics of finite duration (cycles). This implies that building floor motions are somewhere in between ground motions (broad-band excitations) and harmonics with an infinite number of cycles. Therefore, it is expected that the oscillator (i.e., an NSC) inelasticity is more beneficial for reducing the building floor spectral responses than for typical ground spectral responses, especially when the period of the oscillator is close to the predominant period of the floor motion under consideration. This is verified in Sect. 8.1 through the numerical analysis of the archetype buildings.

Fig. 5

a Response modification factor; b inelastic displacement ratio; for an oscillator with $\xi_{\text{c}} = 2\%$ and different $\mu_{\text{c}}$ values exposed to a sinusoidal floor excitation with a resonant period ($T_{\text{f}} = T_{\text{c}}$) and different numbers of loading cycles

5 Constant-ductility floor spectra for the archetype structures

Constant-ductility spectra with different values of component target displacement ductility, $\mu_{\text{c}}$, and viscous damping ratio, $\xi_{\text{c}}$, are generated for acceleration time histories obtained from different floor levels of the archetype buildings subject to the SC ground motions at the DE level. As an example, Fig. 6a and b presents, respectively, the mean normalized 5%-damped acceleration spectra and their corresponding mean response modification factor spectra for the roof level of the two-story SMRF structure assuming different $\mu_{\text{c}}$ values. Figure 6c and d presents, respectively, the mean displacement floor spectra and the corresponding mean inelastic displacement spectra for this example. Figures 7, 8, and 9 illustrate similar graphs for three other representative archetype structures. An evaluation of the peaks present in the elastic roof acceleration spectra suggests that, for the buildings used in this paper, the first two modes (or at most three modes in the case of the 12-story SMRF) might be significantly excited by the SC ground motions. For example, as seen in Fig. 6a, two spikes are present in the elastic roof acceleration spectra of the two-story SMRF that correspond to the first two vibration modes of this structure. For these buildings, the behavior of an elastic floor acceleration spectrum can be studied in three different normalized period regions as discussed next. (i) $T_{\text{c}} \le 0.05T_{\text{b1}}$: short, normalized period region in which NSCs behave essentially as rigid meaning that $S_{\text{ac}} \approx PFA$; (ii) $0.05T_{{{\text{b}}1}} < T_{\text{c}} \le 1.5T_{{{\text{b}}1}}$: modal period region in which the maximum values of $S_{\text{ac}} /PFA$ occur; this period region includes tuning periods (i.e., the first few modes of the primary structure) and a transition region (i.e., non-tuning periods in between the primary structure modal periods); (iii) $1.5T_{\text{b1}} < T_{\text{c}} \le 10.0$ s: long, normalized period region in which the $S_{\text{ac}}$ values are mostly smaller than the $PFA$ response implying a reduction with respect to the $PFA$ demand.

Fig. 6

a Mean normalized spectral acceleration; b mean response modification factor; c mean spectral displacement; d mean inelastic displacement ratio; for the 5%-damped roof spectra of the two-story SMRF building

Fig. 7

a Mean response modification factor; b mean inelastic displacement ratio; for the 5%-damped roof spectra of the eight-story SMRF building

Fig. 8

a Mean response modification factor; b mean inelastic displacement ratio; for the 5%-damped roof spectra of the two-story RCSW building

Fig. 9

a Mean response modification factor; b mean inelastic displacement ratio; for the 5%-damped roof spectra of the eight-story RCSW building

The most salient conclusions of Figs. 6, 7, 8 and 9 are summarized next:

• For the relatively short normalized periods ($T_{\text{c}} /T_{\text{b1}} \le 0.05$), the amplitude of mean $R_{\text{cc}}$ tends to unity regardless of the value of $\mu_{\text{c}}$, whereas mean $C_{\text{cc}}$ values are relatively large even assuming a mild level of NSC inelasticity.

• For NSCs with initial periods close to the primary structure second modal period (i.e., tuned to the second mode), as an NSC experiences inelastic behavior, the floor spectral acceleration responses decrease, whereas the floor spectral displacement responses slightly increase.

• The inelastic behavior of NSCs that are tuned to the primary structure first-mode substantially decreases both floor spectral acceleration and displacement demands. As an example, consider the behavior of the roof spectra of the two-story SMRF structure at $T_{\text{c}} /T_{\text{b1}} =$ 1.0. In this example, assuming an NSC ductility of 3.0 reduces the mean normalized spectral acceleration response from 5.5 to 0.87 (i.e., 84% reduction) and the mean spectral displacement response from 0.80 m to 0.36 m (i.e., 55% reduction).

• In the transition region, NSC inelastic behavior would lead to a significant increase in the floor spectral displacement demands, whereas the spectral acceleration values only slightly reduce. For instance, consider a non-tuning NSC period ratio of 0.50 at the roof spectra of the two-story SMRF structure. In this case, with adopting an NSC ductility of 3.0, the mean normalized floor spectral acceleration demand decreases from 1.9 to 1.3 (i.e., 32% reduction), whereas floor spectral displacement demand increases from 0.07 m to 0.13 m (i.e., 86% increase).

• For NSCs with relatively long normalized periods ($T_{\text{c}} /T_{\text{b1}} = 1.5$), it is observed that $R_{\text{cc}} \approx \mu_{\text{c}}$. In other words, for this period range, the inelastic behavior of NSCs can reduce the roof spectral acceleration demands by a factor that is nearly equal to the value of the NSC target displacement ductility. For these NSCs, the inelastic displacement responses tend to the elastic ones. These observations comply with the predictions of the well-known equal-displacement principle for typical, average inelastic ground spectra.

• The mean $R_{\text{cc}}$ values obtained for NSCs with initial periods close to the first-mode period of the primary structure are more influenced by the inelastic behavior of NSCs (i.e., the value of $\mu_{\text{c}}$). For these NSCs, the values of mean $R_{\text{cc}}$ are substantially greater than those for NSCs with any other periods. A primary reason for this latter observation relates to the number of harmonic cycles with different dominant periods in floor motions. An additional reason lies in the equation used for determining $R_{\text{cc}}$. By definition, the $R_{\text{cc}}$ parameter is the ratio of the elastic $S_{\text{ac}}$ to the inelastic $S_{\text{ac}}$ for a given NSC period. An evaluation of Fig. 6a illustrates that the peak value of an inelastic floor spectrum occurs no longer in the vicinity of the first-mode period of the primary structure but shifts to the smaller periods. This behavior results in more pronounced $R_{\text{cc}}$ values for NSCs with initial periods close to the first-mode period of the structure. These large $R_{\text{cc}}$ values could be viewed as fictitious response modification factors as they fail to illustrate the actual reduction of the peak NSCs force demand across the floor spectrum periods. This issue is further elaborated in Sect. 6.

• NSC inelasticity can significantly reduce the effect of NSCs tuning ratio on their seismic force demands. For $\mu_{\text{c}} >$ 3.0, significant amplifications in the floor spectral acceleration responses with respect to the peak floor acceleration ($PFA$) responses are not present (i.e., Max($S_{\text{ac}} ) \approx PFA$). This observation illustrates that if the design can accommodate $\mu_{\text{c}}$ values greater than 3.0, NSCs can be designed for $PFA$ responses regardless of their periods and viscous damping ratios. Such an approach would significantly simplify the design of NSCs.

• The amplitude of mean $C_{\text{cc}}$ in the vicinity of the primary structure higher modes is very sensitive to the value of $\mu_{\text{c}}$, whereas this sensitivity is not present in the vicinity of the first mode.

• A comparison of the results for different buildings illustrates that, for a given lateral-force resisting system, as the number of stories increases (i.e., the fundamental period of the primary structure increases), the value of mean $R_{\text{cc}}$ in the vicinity of the higher modes increases. For example, assuming $\mu_{c} = 4.0$, the value of mean $R_{\text{cc}}$ for NSCs with initial periods close to the second-mode period of the two-story SMRF is equal to 3.1, whereas this quantity for the case of the eight-story SMRF is greater than 5.7. This observation is relevant because as the number of stories increases, the contribution of the higher modes increases. The results also suggest that NSC inelasticity is more effective for NSCs attached to the SMRF buildings than for those attached to the RCSW buildings. As seen, $R_{\text{cc}}$ values for the SMRF buildings are greater (this is especially highlighted in the vicinity of the first-mode period).

• Drift demands on NSCs that are tuned to the relatively long modal periods of the primary structures can be significantly (and in most cases, unrealistically) large. For instance, according to the results shown in Fig. 6c, the drift demand on an elastic NSC with an initial period close to the first-mode period of the two-story SMRF structure is as large as 0.80 m. Inelastic behavior of NSCs can reduce these values (e.g., to 0.34 m for $\mu_{\text{c}} = 4.0$); however, the reduced values are still sufficiently large to be of concern. Designs that can accommodate these large drift demands are very challenging and even impractical. Furthermore, such drift demands may lead to the pounding of an NSC to the adjacent structural/nonstructural components and undesirable interactions between different parts of an NSC. Hence, designing relatively flexible NSCs to be housed in long-period structures may prove to be very challenging.

It should be noted that some of the abovementioned conclusions were identified in previous studies available in the literature. Most of these studies evaluated the responses of inelastic NSCs attached to either generic frames, elastic multistory numerical building models or instrumented buildings (see the Introduction section). The present paper corroborates and extends the validity of such conclusions to the case of code-based designed (inelastic) supporting buildings.

6 Seismic design implication of the parameter R_cc

The use of design floor spectra can emphasize the importance of the periods of NSCs and primary structures (i.e., tuning ratio) on NSCs seismic demands. However, arguably, in practical purposes, the estimation of the accurate periods of many NSCs and primary structures is very challenging. Designing all NSCs for the demands associated with the most critical NSC period might be a rational (and likely conservative) alternative. One of the main objectives of this paper is to propose representative $R_{\text{cc}}$ values to be incorporated into elastic (basic) NSC design equations. However, as discussed in Sect. 5, the parameter $R_{\text{cc}}$ as computed using the equation provided in Sect. 3.4, might fail to accurately estimate the reduction in the peak value of an inelastic floor spectrum with respect to the peak value of the corresponding elastic spectrum. In this section representative (design) $R_{\text{cc}}$ values are defined as the ratio of the peak elastic $S_{\text{ac}}$ response over an NSC period range to the peak inelastic $S_{\text{ac}}$ response over the same NSC period range. The NSC period ranges considered herein for introducing design $R_{\text{cc}}$ parameters are the higher-mode (HM) and fundamental-mode (FM) regions defined as $0.05T_{{{\text{b}}1}} < T_{\text{c}} \le 0.5T_{{{\text{b}}1}}$ and $0.5T_{{{\text{b}}1}} < T_{\text{c}} \le 1.5T_{{{\text{b}}1}}$, respectively. Given a $\xi_{\text{c}}$ and $\mu_{\text{c}}$, Eq. (2) is used to determine the design $R_{\text{cc}}$ value for the FM region of a floor spectrum:

$$ \left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}} = \frac{{\hbox{max} \left( {S_{\text{ac}} } \right)_{\text{elastic NSC}}\,{\text{over the FM region}}}}{{ {\text{max}}\left( {S_{\text{ac}} } \right)_{\text{inelastic NSC}}\,{\text{over the FM region}}}} $$

(2)

The design $R_{\text{cc}}$ parameter for the HM region of floor spectra is determined using a similar equation. Figure 10a–d depicts the variation of mean $\left( {R_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$ and mean $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ with $\mu_{\text{c}}$ for the roof spectra of four representative archetype buildings. Results in these figures are presented for different $\xi_{\text{c}}$ values. The $R_{\text{cc}} {-}\mu_{\text{c}}$ graph for the equal-displacement rule is also shown for comparison purposes.

Fig. 10

Mean values of the computed design $R_{\text{cc}}$ for the HM and FM regions of the roof spectra of the: a two-story SMRF; b eight-story SMRF; c two-story RCSW; d eight-story RCSW

An evaluation of Fig. 10 shows that

• The mean design $R_{\text{cc}}$ values are significantly smaller than the maximum value of the mean $R_{\text{cc}}$ spectra obtained in Sect. 5. For example, assuming $\xi_{\text{c}} = 5\%$ and $\mu_{\text{c}} = 4.0$, the peak value of the mean $R_{\text{cc}}$ spectrum for the roof level of the two-story SMRF structure in Fig. 6b was 9.6, whereas the corresponding mean $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ value shown in Fig. 10a is only 5.2.

• For a given $\mu_{\text{c}}$ and $\xi_{\text{c}}$, the mean value of $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ is substantially greater than the mean value of $\left( {R_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$.

• For a given $\xi_{\text{c}}$, in most cases, as the value of $\mu_{\text{c}}$ increases, the mean value of the design $R_{\text{cc}}$ parameters, especially $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$, tends to increase monotonically (i.e., without saturation within the $\mu_{\text{c}}$ range of interest).

• A building-to-building variability is observed in the value of the design $R_{\text{cc}}$ parameters, especially the parameter $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$. As seen, the mean values of $\left( {R_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$ for the taller structures are greater than those for the shorter ones. An opposite statement is valid for the $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ parameter. These observations are consistent with the contributions of different modal periods in short- and long-period structures.

• The effect of the inelastic behavior of NSCs on their seismic-induced force demands is more significant for low-damping NSCs. For instance, consider the $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ values shown in Fig. 10a for $\mu_{\text{c}} =$ 3.0. In this case, the mean value of $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ for $\xi_{\text{c}} =$ 5% is 4.5, whereas this quantity for $\xi_{\text{c}} =$ 2% is 7.0 (i.e., 56% greater). This discussion is elaborated in Sect. 7.

• In some cases, especially cases with $\mu_{\text{c}} >$ 3.0 and $\xi_{\text{c}} =$ 5%, the computed design $R_{\text{cc}}$ values are smaller than the prediction of the equal-displacement principle.

7 Effect of the viscous damping ratio of NSCs on their inelastic seismic responses

In a previous study, Anajafi and Medina (2019a) proposed a parameter termed component damping modification factor, $DMF_{\text{cc}}$, to quantify the effect of the variation of NSCs viscous damping from the default 5% on their elastic force demands (see Sect. 3.4 for a more detailed definition of $DMF_{\text{cc}}$). For an elastic tuned NSC, Eq. (3) was proposed to determine the parameter $DMF_{\text{cc}}$. In this equation, $\xi_{\text{c}}$ is the value of NSC viscous damping (e.g., 0.05). Note that the magnitude of $DMF_{\text{cc}}$ for $\xi_{\text{c}} =$ 5% is unity.

$$ DMF_{\text{cc}} = \left[ {\frac{{5.6 - { \ln }\left( {100\xi_{\text{c}} } \right)}}{4.0}} \right]^{2.3} $$

(3)

The present section investigates the effect of NSCs viscous damping ratio on their inelastic seismic force demands. Figure 11a and b illustrates representative elastic and inelastic mean normalized floor acceleration spectra for an archetype building subjected to the DE-level SC ground motions. The results in these figures are presented for three different $\xi_{\text{c}}$ values. Figure 12a and b depicts the corresponding mean $DMF_{\text{cc}}$ spectra. An evaluation of Fig. 12a and b illustrates that, for a given $\xi_{\text{c}}$, the values of the $DMF_{\text{cc}}$ of the elastic spectra are more critical than those of the inelastic spectra. This statement is more highlighted for NSCs with initial periods close to the primary structure modal periods. For instance, the maximum value of mean $DMF_{\text{cc}}$ for the 2%-damped elastic spectrum in Fig. 12a, which occurs at $T_{\text{c}} = T_{{{\text{b}}1}}$, is 1.62, whereas this quantity for the 2%-damped inelastic spectrum shown in Fig. 12b is limited to 1.25. This observation illustrates that seismic-induced demands on elastic NSCs are more influenced by the value of NSC viscous damping than seismic-induced demands on inelastic NSCs.

Fig. 11

Mean normalized roof acceleration spectra for the four-story SMRF building: a$\mu_{\text{c}} = 1.0$; b$\mu_{\text{c}} = 1.5$

Fig. 12

Mean DMF_cc for the roof acceleration spectra of the four-story SMRF building: a$\mu_{\text{c}} = 1.0$; b$\mu_{\text{c}} = 1.5$

Adopting a similar approach as the one used for the design $R_{\text{cc}}$ in Sect. 6, representative design $DMF_{\text{cc}}$ parameters are defined for the HM and FM regions of a floor spectrum. Equation (4) provides the design $DMF_{\text{cc}}$ parameter for the FM region. A similar equation is used to determine $\left( {DMF_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$.

$$ \left( {DMF_{\text{cc}}^{\text{FM}}} \right)_{\text{design}} = \frac{{\hbox{max} \left[ {S_{\text{ac},\xi } } \right] {\text{over the FM region}}}}{{\hbox{max} \left[ {S_{\text{ac},5\% } } \right] {\text{over the FM region}}}} $$

(4)

Figure 13a illustrates the variation of the mean design $DMF_{\text{cc}}$ parameters with $\mu_{\text{c}}$ for the roof acceleration spectra of the four-story SMRF building subjected to the DE-level SC ground motions. Figure 13b presents similar graphs for the roof spectra of the 12-story SMRF building. As seen, for a given $\mu_{\text{c}}$ and $\xi_{\text{c}}$, the mean values of $\left( {DMF_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$ and $\left( {DMF_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ are fairly close to one another. For both $\xi_{\text{c}}$ values of 2% and 8%, the design $DMF_{\text{cc}}$ parameters exhibit an asymptotic behavior (this statement is especially true for the $\left( {DMF_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ parameter). For a given $\xi_{\text{c}}$, this asymptotic value is approximately equal to the square root of the mean design $(DMF_{\text{cc}} )_{\text{design}}$ at $\mu_{\text{c}} =$ 1.0. It should be noted that the values of the design $DMF_{\text{cc}}$ shown in Fig. 13a for the four-story SMRF building are slightly different than the extremum values of the $DMF_{\text{cc}}$ spectra illustrated in Fig. 12 for this structure. This discrepancy is due to the fact that different equations have been used for the computation of $DMF_{\text{cc}}$ shown in these two figures.

Fig. 13

Variation of the mean design DMF_cc parameters with the NSC target ductility for the roof spectra of the a four-story; b 12-story; SMRF building

The results consistently show that NSC inelasticity would significantly de-emphasize the effect of the viscous damping ratio of NSCs on their seismic demands. For example, an evaluation of the $DMF_{\text{cc}}$ values in Fig. 13a illustrates that variation of NSC viscous damping ratio from 5% to 2% increases the force demand on an elastic tuned NSC by 71%, whereas the same variation increases the force demand on an inelastic tuned NSC with a target ductility of 3.0 by 14% only.

8 Additional factors that are influential to the parameters R_cc and C_cc

Sections 5, 6 and 7 addressed the effect of the tuning ratio, viscous damping ratio, and target displacement ductility of NSCs as well as the fundamental period (height) and lateral-force resisting system of the primary structures on the magnitude of the parameters $R_{\text{cc}}$ and $C_{\text{cc}}$. This section investigates additional parameters related to the characteristics of supporting building and input ground motion that can influence the value of the $R_{\text{cc}}$ and $C_{\text{cc}}$ parameters.

8.1 Floor relative height

The contribution of a given structural mode of vibration varies along the height of a building, and hence, the frequency content of seismic-induced acceleration motions varies from floor-to-floor. The harmonics with frequencies close to the building first-mode frequency are more highlighted in the acceleration motions at the building roof than at any other floors, whereas the higher-mode frequencies are more dominant in the lower-floor acceleration responses. Because of these variations in the frequency content of acceleration motions of different floors, the amplitude of the $R_{\text{cc}}$ (and also $C_{\text{cc}}$) spectra for a given NSC frequency could potentially vary from floor-to-floor. This subsection investigates the sensitivity of the amplitude of the parameters $R_{\text{cc}}$ and also $C_{\text{cc}}$ to the relative height (RH) of the point of attachment of an NSC to the primary structure. For the evaluations conducted in this subsection, the assumed $\mu_{\text{c}}$ and $\xi_{\text{c}}$ are 2.0 and 5%, respectively, and the primary structures are subjected to the DE-level SC ground motions.

Figure 14a and b presents, respectively, the mean $R_{\text{cc}}$ and $C_{\text{cc}}$ spectra for different floor levels of a representative SMRF building. In this figure, $RH = 0$ corresponds to the ground level. Figure 15a and b shows similar plots for a representative RCSW building. As consistently seen, for a given NSC normalized period, a floor-to-floor variability exists in the values of $R_{\text{cc}}$ and also $C_{\text{cc}}$. An evaluation of the $R_{\text{cc}}$ and $C_{\text{cc}}$ spectra illustrates that for NSCs tuned to the primary structure first-mode, the largest reduction in both force and displacement demands occurs at the roof level. For NSCs tuned to the higher modes, the largest reductions are observed at the lower floors (e.g., $RH = 0.33$ in Fig. 14a). These behaviors result primarily from the predominant contributions of the first- and higher-modes at the roof and lower-floor levels, respectively. The results also show that reductions of the peak spectral displacement and acceleration demands due to NSC inelasticity are more pronounced in building floor spectra than in ground spectra. This observation, which results from the semi-harmonic characteristic of floor motions (see Sect. 4), implies that the beneficial effects of NSC inelasticity are more pronounced for tuned NSCs attached to a building floor than for tuned NSCs attached to the ground. For example, in Fig. 14a, the maximum value of the mean $R_{\text{cc}}$ spectrum for the roof level is 4.6, whereas this quantity for the ground level is 2.3; the associated mean $C_{\text{cc}}$ values for the roof and ground level shown in Fig. 14b are 0.47 and 0.91, respectively. On the contrary, for NSCs with initial periods in between the primary structure modal periods, the mean $R_{\text{cc}}$ values at the building floors are smaller than those at the ground floor. For these NSCs, the mean $C_{\text{cc}}$ values at the building floors are greater than unity implying an adverse effect of NSC inelasticity. In the case of very short and long normalized periods, the mean values of the $R_{\text{cc}}$ parameter are not sensitive to the floor relative height and tend to those of the ground level. This observation is consistent with the insignificant filtering effect of the primary structures at this NSC period range.

Fig. 14

a Mean response modification factor; b mean inelastic displacement ratio; for different relative heights (RHs) of the six-story SMRF ($\xi_{\text{c}} = 5\%$ and $\mu_{\text{c}} = 2.0$)

Fig. 15

a Mean response modification factor; b mean inelastic displacement ratio; for different relative heights (RHs) of the eight-story RCSW ($\xi_{\text{c}} = 5\%$ and $\mu_{\text{c}} = 2.0$)

8.2 Ground motion excitation type

This section evaluates the dependency of the parameters $R_{\text{cc}}$ and $C_{\text{cc}}$ on the type of the ground motion suite implemented as the input excitation for the primary structure. This evaluation is conducted through a comparison between the results for the SC and FF ground motions at the DE level.

Figures 16 and 17 depict representative mean $R_{\text{cc}}$ and $C_{\text{cc}}$ spectra for the roof level of two representative archetype buildings subjected to the DE-level SC and FF ground motion suites. An evaluation of the results consistently illustrates that the mean values of the $R_{\text{cc}}$ and (and also $C_{\text{cc}}$) spectra are not significantly dependent on the type of the ground motion suite. In fact, the filtering effect of the primary structure outweighs and partially eliminates the importance of the ground motion excitation type. Note that these conclusions are applicable to the ground motion types used in this paper. Further investigation is required for special cases such as ground motions recorded in near-fault regions or soft-soil profiles.

Fig. 16

a Mean response modification factor; b mean inelastic displacement ratio; for the roof spectra of the six-story SMRF building exposed to the DE-level SC and FF ground motions ($\xi_{\text{c}} = 5\%$ and $\mu_{\text{c}} = 2.0$)

Fig. 17

a Mean response modification factor; b mean inelastic displacement ratio; for the roof spectra of the eight-story RCSW building exposed to the DE-level SC and FF ground motions ($\xi_{\text{c}} = 5\%$ and $\mu_{\text{c}} = 2.0$)

8.3 Level of inelastic behavior of the primary structure (or ground motion intensity)

For the response history analyses conducted in Sects. 5–8.2, DE-level ground motions were used under which the primary structures undergo inelastic actions (as discussed in Sect. 3.2, the global ductility demand on the primary structures varies from 2.2 to 5.3). This section investigates the dependency of the parameters $R_{\text{cc}}$ and $C_{\text{cc}}$ on the level of the inelastic behavior of the primary structure (or the ground motion intensity). First, it is informative to evaluate the effect of the primary structure inelasticity on NSCs seismic demands. Numerous studies in the past, referenced in Sect. 1, have addressed this effect. However, these studies mostly used linear-elastic NSCs with $\xi_{\text{c}} = 5\%$. This section uses elastic and inelastic NSCs with two different $\xi_{\text{c}}$ values of 2% and 5%. It is assumed that the responses of the archetype building models at the 0.25 DE level represent the elastic building behavior.

As an example, Fig. 18a shows the parameter $R_{\text{cb}}$ (i.e., the component modification factor due to building inelasticity defined in Sect. 3.4) for the 5%-damped roof spectrum of the six-story SMRF building assuming different component-building inelasticity levels. Figure 18b depicts similar results assuming $\xi_{\text{c}} =$ 2%. An evaluation of Fig. 18 reveals that the reduction in NSC force demand due to building inelasticity is more highlighted for a low-damping tuned elastic NSC. For example, for either the DE or 1.5 DE level, the maximum value of $R_{\text{cb}}$ is observed for an elastic NSC with $\xi_{\text{c}} = 2\%$ that is in tune with the building first-mode. The results presented in Fig. 18 also illustrate that NSC inelasticity can de-emphasize the effect of the primary structure inelastic behavior on NSCs seismic force demands. For example, consider the results shown in Fig. 18b for the 1.5DE level. As seen, in this case, the maximum value of $R_{\text{cb}}$ for the elastic NSC is 3.2, whereas this quantity for the inelastic NSC is 2.6.

Fig. 18

Mean response modification factor due to building inelasticity, for the roof spectra of the six-story SMRF building exposed to the SC ground motions with different intensities: a$\xi_{\text{c}} = 5\%$; b$\xi_{\text{c}} = 2\%$

The rest of this section investigates whether a similar sensitivity to the building inelasticity is observed in the behavior of the parameters $R_{\text{cc}}$ and $C_{\text{cc}}$. Figure 19a and b depicts representative mean $R_{\text{cc}}$ and $C_{\text{cc}}$ spectra for the roof level of the six-story SMRF structure assuming different ground motion intensities. Figure 20a and b illustrates similar results for the eight-story RCSW structure. An evaluation of the results illustrates that as the ground motion intensity increases (i.e., the primary structure transitions from elastic to inelastic range), the critical values of the mean $R_{\text{cc}}$ and $C_{\text{cc}}$ parameters (i.e., the values in the vicinity of the first modal period of the primary structures) would reduce and increase, respectively. These observations illustrate that the building inelasticity would de-emphasize the beneficial effects of NSCs inelastic behavior on their seismic demands. The transition of the primary structure from elastic to inelastic would partially mitigate the semi-harmonic components of the floor motions with periods close to the building first modal period, and as a result, the NSC inelastic behavior becomes less beneficial (Sect. 4 showed that the less dominant the harmonic characteristic of a floor acceleration, the smaller the effect of NSCs inelasticity on their seismic demands). These results also imply that to achieve a target $R_{\text{cc}}$ for an NSC with an initial period tuned to the building first-mode period, the NSC should experience a greater ductility demand if the building can become inelastic than when the building responds elastically. Results of Figs. 19 and 20 illustrate that the value of $R_{\text{cc}}$ for NSCs with initial periods close to the period of the second (and higher) mode is not significantly influenced by the inelasticity of the primary structure. This observation is relevant because the structure inelasticity is associated with the first-mode softening, whereas the higher modes of vibration remain nearly elastic.

Fig. 19

a Mean response modification factor; b mean inelastic displacement ratio; for the 5%-damped roof spectra of the six-story SMRF exposed to the SC ground motions with different intensities ($\mu_{\text{c}} = 2.0$)

Fig. 20

a Mean response modification factor; b mean inelastic displacement ratio; for the 5%-damped roof spectra of the eight-story RCSW exposed to the SC ground motions with different intensities ($\mu_{\text{c}} = 2.0$)

Figure 21a–d illustrates the variation of the mean $\left( {R_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$ and $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ parameters with $\mu_{\text{c}}$ for the 5%-damped roof acceleration spectra of the six-story SMRF and eight-story RCSW buildings subjected to the SC ground motions with different intensities. The results shown in these figures further verify the observations made from Figs. 19a and 20a. As consistently seen, when the ground motion intensity increases, the mean value of $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ decreases, whereas the mean value of $\left( {R_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$ is not very sensitive to the variation of ground motion intensity.

Fig. 21

Variation of the mean design $R_{\text{cc}}$ parameters with the NSC target ductility for the 5%-damped roof spectra of the a and b six-story SMRF; c and d eight-story RCSW; exposed to the SC ground motions with different intensities

9 Simplified equations for the estimation of the design $R_{\text{cc}}$ parameter

The results of Sects. 5–8 illustrated that the value of the parameter $R_{\text{cc}}$ is, to different extents, dependent on the characteristics of the ground motion (GM), supporting building and NSC. In general, $R_{\text{cc}}$ can be expressed as a function of many parameters as given by Eq. (5).

$$R_{\text{cc}} = f\left( {\mu_{\text{c}} , \xi_{\text{c}} , T_{\text{c}} /T_{\text{b1}} ,T_{\text{b1}} , T_{\text{b2}} /T_{\text{b1}} , RH,\mu_{\text{b}} ,GM} \right) $$

(5)

Note that, in this context, the lateral-force resisting system of the supporting building is implicitly accounted for by the $T_{\text{b2}} /T_{\text{b1}}$ ratio. This section intends to simplify Eq. (5) and present practical equations for the estimation of the design $R_{\text{cc}}$ values. Based on the analysis results in the previous sections, the effect of the parameter $T_{\text{b1}}$ is not as significant as the effect of the other parameters. The ultimate objective is to propose design equations for code-based designed buildings with reasonable overstrength values subject to the DE level ground motions. Therefore, the $R_{\text{cc}}$ values for the DE-level SC ground motions are used for the development of the simplified $R_{\text{cc}}$ equations. As a result, the parameters $\mu_{\text{b}}$ and $GM$ are also removed from Eq. (5). Given the complexity of the estimation of NSC force demands for different building floor levels, it might be reasonable (and conservative in many cases) to design all NSCs based on the roof spectra, which tend to exhibit approximately the largest floor spectral acceleration values for all NSCs period ratios. This latter statement can be readily observed from Fig. 22a and b for two representative archetype structures. With the abovementioned descriptions, the remaining parameters from Eq. (5) that will be used for developing design $R_{\text{cc}}$ equations include the supporting building lateral-force resisting system, and the NSC tuning condition, viscous damping ratio and target displacement ductility.

Fig. 22

Mean normalized roof acceleration spectra for different relative heights (RHs) of the a six-story SMRF; b eight-story RCSW; ($\xi_{\text{c}} = 5\%$ and $\mu_{\text{c}} = 2.0$)

Empirical expressions, given by Eq. (6), are proposed to estimate the $\left( {R_{\text{cc}}^{\text{FM}} } \right)_{\text{design}}$ and $\left( {R_{\text{cc}}^{\text{HM}} } \right)_{\text{design}}$. These expressions are primarily applicable to the roof spectra of code-based designed buildings that are subject to the DE-level ground motions.

$$ (R_{\text{cc}} )_{\text{design}} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\alpha \left( {1 - \mu_{\text{c}}^{ - 0.30} } \right)DMF_{\text{cc}} + 1.0, } \quad{\text{NSC tuned to HM}}\\ {\beta \left( {1 - \mu_{\text{c}}^{ - 0.15} } \right)DMF_{\text{cc}} + 1.0 , }\quad{\text{NSC tuned to FM}} \\ \end{array} \quad 1.0 \le \mu_{\text{c}} \le 5.0 } \\ \end{array} } \right. $$

(6)

The coefficients $\alpha$ and $\beta$, for SMRF buildings are equal to 8.0 and 20.0, respectively; and for RCSW buildings are equal to 7.0 and 16.0, respectively. The parameter $DMF_{\text{cc}}$ was given by Eq. (3). Figure 23 illustrates an evaluation of the proposed design $R_{\text{cc}}$ expressions using the computed design $R_{\text{cc}}$ values for the roof level of the studied two- to 12-story SMRF buildings. Figure 24 presents a similar evaluation for the RCSW buildings. Figures 23 and 24 illustrate that the proposed expressions can reasonably capture the mean computed design $R_{\text{cc}}$ values for the studied buildings.

Fig. 23

Evaluation of the proposed $R_{\text{cc}}$ expressions for SMRF structures based on the computed $R_{\text{cc}}$ values for the roof spectra of the studied SMRF archetype buildings

Fig. 24

Evaluation of the proposed $R_{\text{cc}}$ expressions for RCSW structures based on the computed $R_{\text{cc}}$ values for the roof spectra of the studied RCSW archetype buildings

10 Constant-R_cc floor spectra and an evaluation of the R_p factor provided in ASCE/SEI 7-16

Displacement- and force-based approaches are two well-adopted seismic design philosophies for building structures. The use of constant-ductility spectra for designing NSCs (discussions of Sects. 4–9) implies basically adopting a displacement-based design approach. The current ASCE/SEI 7-16 provisions for designing NSCs rely on a force-based method in which a response modification (reduction) factor, $R_{\text{p}}$, is used to account (primarily) for the energy dissipation provided by nonlinear mechanisms in NSCs. However, at present, there is no clear understanding of the inelastic behavior (e.g., displacement responses) of NSCs that are designed based on these $R_{\text{p}}$ factors. In this section, constant-$R_{\text{cc}}$ spectra are developed for two representative archetype buildings to evaluate ductility and displacement demands imposed on NSCs when using an $R_{\text{cc}}$ factor. It should be noted that, as mentioned in Sect. 3.4, the parameter $R_{\text{cc}}$ used in this paper is equivalent to the ductility-dependent portion of $R_{\text{p}}$. The results of this section are also used to further verify the results obtained from previous sections using the constant-ductility floor spectra.

Figure 25a depicts the mean 5%-damped constant-$R_{\text{cc}}$ inelastic spectra for the roof level of a representative SMRF structure subject to the DE-level SC ground motions. In this figure, results are presented for $R_{\text{cc}}$ values ranging from 1.0 (elastic spectrum) to 4.0. Figure 25b–d illustrates the corresponding component displacement ductility demands, $\mu_{\text{c}}$, floor spectral displacement demands, $S_{\text{dc}}$, and inelastic displacement ratios, $C_{\text{cc}}$, respectively. Figure 26a and b presents similar $\mu_{\text{c}}$ and $S_{\text{dc}}$ graphs for a representative RCSW structure.

Fig. 25

a Mean normalized spectral acceleration; b mean displacement ductility demand; c mean spectral displacement; d mean inelastic displacement ratio; for the 5%-damped constant-R_cc roof spectra of the two-story SMRF building

Fig. 26

a Mean displacement ductility demand; b mean inelastic displacement ratio; for the 5%-damped constant-R_cc roof spectra of the two-story RCSW building

An evaluation of the mean $\mu_{\text{c}}$ and $C_{\text{cc}}$ spectra shown in Figs. 25 and 26 reveals that

• Consistent with the results observed from the evaluation of the constant-ductility floor spectra, for the relatively long NSC period ratios (i.e., $T_{\text{c}} /T_{\text{b1}} > 1.5$), the so-called equal-displacement principle applies.

• For NSCs with initial periods close to the first modal period of the primary structure (i.e., tuned to the first mode), as the value of $R_{\text{cc}}$ increases, the mean floor spectral displacement responses significantly decrease. In the meantime, the mean value of $\mu_{\text{c}}$ remains within a reasonable range. As seen in Fig. 25b and d, for this tuning condition, using an $R_{\text{cc}}$ of 4.0 reduces the mean spectral displacement response as much as 52% (i.e., Mean $\left( {C_{\text{cc}} } \right) =$ 0.48), whereas the mean value of $\mu_{\text{c}}$ remains below 2.0.

• For a given $R_{\text{cc}}$, especially for larger $R_{\text{cc}}$ values, the magnitudes of the imposed $\mu_{\text{c}}$ and $C_{\text{cc}}$ on NSCs with initial periods close to the higher modal periods of the primary structures are significantly greater than those on NSCs with initial periods close to the first modal period. For instance, in Fig. 25b, assuming an $R_{\text{cc}}$ value of 4.0, the mean value of $\mu_{\text{c}}$ in the vicinity of the second mode is as great as 12.5, whereas this quantity in the vicinity of the first mode is limited to 1.9. This observation corroborates the results of the previous sections where it was shown that NSC inelasticity is more effective for NSCs tuned to the first mode of the supporting structure.

• For NSCs with initial periods lying in between the primary structure modal periods, the inelastic behavior of NSCs leads to relatively large ductility demands and also inelastic displacement responses greater than the elastic ones. Figure 25a shows that the normalized yield strength (i.e., the normalized elastic floor spectral acceleration value) for these NSCs is already relatively small. Applying an $R_{\text{cc}}$ factor greater than unity leads to even a smaller yield strength and consequently relatively large $\mu_{\text{c}}$ and $C_{\text{cc}}$ values.

• For NSCs that are rigid with respect to the primary structure (e.g., NSCs with initial periods smaller than the second-modal period of the two-story SMRF structure), the inelastic behavior of NSCs results in significantly large (and unrealistic) displacement ductility demands. As seen in Figs. 25 and 26, designing these NSCs for an $R_{\text{cc}}$ value as small as 1.5 results in mean $\mu_{\text{c}}$ demands as great as 20.0. This observation, which complies with the results pertaining to the equal-energy principle for very short period structures subject to typical ground motions, suggests that NSCs with relatively short periods (denoted as rigid herein) should be designed to remain in the elastic region. As observed, the imposed ductility demands on these NSCs could be excessively large. It would be very challenging or even impractical to accommodate these large ductility demands and avoid significant NSC damages and, in many cases, maintain functionality. This conclusion highlights the need to further evaluate the ASCE/SEI 7-16 provisions for NSCs as they allow for designing rigid NSCs with strength-reduction-factors as large as 2.5.

11 Conclusions

Numerous studies have been conducted on the quantification of the seismic responses of acceleration-sensitive nonstructural components (NSCs). These studies, while providing valuable insight into understanding the seismic behavior of NSCs, have mostly assumed a linear-elastic behavior for NSCs and/or their supporting structures. A few studies that have considered the primary structure inelasticity, have mostly used simplified single-degree-of-freedom (SDOF) or multistory generic frame structural models. These studies have generally assumed that NSCs would remain elastic and exhibit a viscous (inherent) damping ratio of 5%. The simplified structural models used in these studies in many cases might not adequately represent code-based designed buildings. Furthermore, recent experimental investigations strongly suggest that typical NSCs might exhibit viscous damping ratios well below the nominal 5% value.

Recently, the National Institute of Standards and Technology (NIST) sponsored the ATC-120 Project on Seismic Analysis, Design, and Installation of Nonstructural Components and Systems. The first two authors of this paper were members of the project team. As part of this project, improved equivalent-static equations were proposed for designing acceleration-sensitive NSCs. The effects of the nonlinear behavior of NSCs and primary structures on NSCs seismic-induced force demands were quantified and incorporated into the proposed design equations. One of the objectives of the NIST is to consider these new equations for their eventual adoption into seismic design practice via documents such as the NEHRP recommended seismic provisions and ASCE/SEI 7. The present study, whose components are part of the final ATC-120 project report (NIST GCR 18-917-43 2018), presents an evaluation of the seismic responses of acceleration-sensitive NSCs assuming that either NSCs, primary structure or both can respond inelastically. The primary structures utilized to generate floor acceleration motions are code-based designed (archetype) special moment resisting frame (SMRF) and reinforced concrete shear wall (RCSW) buildings with different heights varying from two to 12 stories. A suite of 20 spectrum-compatible and a suite of 44 far-field recorded ground motions are used as input excitations at the base of the primary structures. Constant-ductility and constant-R floor spectra are generated for linear and nonlinear primary structures assuming different levels of NSC inelastic behavior and viscous damping. The parameters response modification factor, $R_{\text{cc}}$, and inelastic displacement ratio, $C_{\text{cc}}$, are introduced to quantify the effect of NSCs inelasticity on their seismic-induced force and displacement demands. Results of the nonlinear response history analyses show that:

• Due to the quasi-harmonic characteristic of building floor motions, the beneficial effects of NSC inelasticity are more pronounced for tuned NSCs attached to a building than for tuned NSCs attached to the ground. In this context, tuning refers to the vicinity of the initial period of an NSC system to the predominant period of the excitation at the NSC point of attachment (in the case of building floor motions, the predominant period is one of the first few modal periods of the building).

• NSC inelasticity can significantly reduce the peak values of elastic building floor spectra (which occur in the vicinity of the building model periods). Adopting even a mild level of inelasticity for tuned NSCs (i.e., strictly from a seismic behavior point of view, the most critical NSCs in a building) not only significantly decreases their seismic force demands but also decreases their displacement demands.

• The inelastic behavior of NSCs can significantly de-emphasize the effects of their tuning period ratio and viscous damping ratio, and the effects of the characteristics of supporting building and ground excitation. For example, in the case of an elastic tuned NSC, the variation of the NSC viscous damping ratio from 5% to 2% increases the NSC force demand up to 71%, whereas the same variation increases the force demand on an inelastic tuned NSC with a target displacement ductility of 3.0 by 14% only.

• Adopting an NSC target ductility greater than 3.0 eliminates, on average, any dynamic amplification in floor spectral acceleration ordinates with respect to the peak floor acceleration response. This approach would significantly mitigate the importance of the NSC tuning ratio and damping ratio and simplify the design of NSCs. This is paramount given the significant uncertainties present in the estimation of the mentioned parameters.

• Unlike the tuned NSCs, the inelastic behavior of NSCs with short period ratios (i.e., rigid NSCs) can lead to significantly large NSC displacement ductility demands implying the necessity of the elastic design of these NSCs. This observation highlights the need to further evaluate the ASCE/SEI 7-16 provisions as they allow for designing rigid NSCs with strength-reduction-factors as large as 2.5.

• For NSCs whose initial periods lie in between the modal periods of the primary structure, the inelastic behavior of NSCs would slightly decrease their seismic-induced force demands but at the expense of a significant increase in their displacement demands. For NSCs with initial periods longer than the fundamental period of the building (i.e., the characteristic period of a floor spectrum), the equal-displacement rule applies. For this NSC period range, the parameters $R_{\text{cc}}$ and $C_{\text{cc}}$ for floor spectra are qualitatively analogous to those for typical, average ground spectra.

• The magnitude of $R_{\text{cc}}$ and $C_{\text{cc}}$ depends, to different extents, on many parameters related to the characteristics of NSCs, primary structure and input ground motion excitation. The most influential factors on the mean values of $R_{\text{cc}}$ and $C_{\text{cc}}$ are the NSC tuning period ratio, viscous damping ratio, target displacement ductility, and vertical location within the primary structure. Parameters that are influential to a lesser extent include the level of inelastic behavior, type of lateral-force resisting system, and fundamental period of the primary structure, and the frequency content and intensity of the input ground motion excitation.

• Given an NSC target displacement ductility, the largest beneficial effect of NSC inelasticity (i.e., the largest reduction in the seismic-induced force and displacement demands) is observed for a low-damping, roof-mounted NSC that is tuned to the first mode of an elastic primary structure.

• The largest reduction in NSCs seismic-induced force demands due to the primary structure inelasticity is observed for an elastic low-damping, roof-mounted NSC tuned to the first mode of the primary structure.

It should be noted that some of the abovementioned conclusions were identified in previous studies. Most of these studies used generic frames, SDOF buildings, elastic multistory numerical building models or instrumented buildings (see the Introduction section). The present paper corroborates and extends the validity of such conclusions to the case of code-based designed (inelastic) supporting buildings.

Simplified equations are proposed for the estimation of the $R_{\text{cc}}$ parameter for NSCs attached to code-based designed buildings that are subjected to demands at the design-earthquake level. These equations are a function of the lateral-force resisting system of the supporting building, and of the NSC target ductility, viscous damping ratio and tuning condition under consideration (i.e., tuning to the first mode or to the higher modes).