1 Introduction

In the event of a strong earthquake, emergency inspection of motorway infrastructure is essential. Preventive closure of the motorway until post-seismic inspection may seem as the safest option. However, such an action reduces significantly the serviceability of the network in terms of traffic flow capacity, and may also lead to additional losses due to the obstruction of rescue operations. On the other hand, maintaining traffic after a strong earthquake without inspection can be unsafe, as a number of structures may have already lost a substantial part of their capacity and be at a critical state. But even in the absence of severe damage, the lack of coordinated action may increase the sense of insecurity of the users, leading to further disruption of network operations, and even additional casualties. The need for timely implementation of crisis management systems is therefore quite evident.

Such emergency response systems have been developed for large cities, with the aim of estimating the damage and the casualties in near-real time (Erdik et al. 2003, 2011). Strong motion networks are typically used to record and characterize a seismic event, and allowing damage estimation on the basis of inventories of the seismic vulnerability of the elements at risk. There are only a few attempts to develop emergency response systems for motorway infrastructure, such as the one for the transportation network of the Friuli–Venezia Giulia region in Italy (Codermatz et al. 2003). Anastasopoulos et al. (2015a) introduces a RApid REspnse (RARE) system for metropolitan motorways, which aims to ensure the safety of motorway users in the event of an earthquake. Its development and application requires: (1) development of a detailed GIS-based inventory of motorway infrastructure; (2) installation of an adequately dense strong motion network; and (3) a real-time damage assessment method.

As discussed in Anastasopoulos et al. (2015a), in the event of an earthquake the RARE system records the seismic motions at selected locations along the motorway, and employs an automated procedure to assess the seismic damage of motorway infrastructure in real time. For each structure, the nearest records are used to assess the seismic damage, employing a simplified method which estimates the damage state on the basis of easily-programmable equations. In contrast to previous studies, which focused on developing efficient intensity measures (IMs) (e.g., Housner 1952; Arias 1970), the proposed method develops nonlinear regression models, which correlate the damage state with a number of statistically significant intensity measures (IMs). For each type of structure, the nonlinear regression equations are estimated making use of finite element (FE) simulations.

However, the large number and complexity of bridges encountered along a motorway network presents a significant challenge. The development of rigorous 3D FE models of the bridge–foundation–abutment–soil system is currently feasible, but the computational effort is quite substantial. As discussed in Anastasopoulos et al. (2015b), a large number of nonlinear dynamic time history analyses (of the order of 350) are required to cover a wide range of strong motion characteristics and to generate a statistically significant dataset. At least with the current computing power, such analysis is practically impossible when considering an entire motorway network, which typically includes a few hundreds of bridges. Therefore, to practically implement such a RARE system, it is necessary to develop computationally efficient, simplified but realistic, models of typical motorway bridges.

Such a simplified analysis method has been outlined in Anastasopoulos et al. (2015b), accounting for the contribution of key structural components (deck, piers, abutment bearings), as well as nonlinear soil–structure interaction (SSI). This method aims to estimate the damage state of motorway bridges in real time with reference to response limit states (Priestley et al. 1996) for maximum drift ratio δ r,max , assuming pier failure as critical for the vulnerability of the entire system. This assumption is considered reasonable for the examined bridge typologies. At this point, it should be noted that modes of failure, such as deck unseating, excessive deformation of bearings, and structural damage of the abutment walls, are not addressed in the present work.

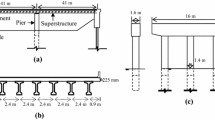
As summarized in Fig. 1a, focusing on the longitudinal direction, the definition of the simplified model requires section analysis of the most vulnerable pier, and computation of spring and dashpot coefficients using simple formulas. A rigorous 3D model of the bridge–foundation–abutment–soil system was developed and used as a benchmark to examine the efficiency of the simplified method. An important assumption for both simplified and rigorous models is that pier damage is based on uniaxial bending, and biaxial bending is not considered. Using a symmetric bridge of the Attiki Odos motorway in Athens (Greece) as an illustrative example, the simplified model was shown to offer an acceptable prediction. One such comparison is reproduced in Fig. 1b, in terms of moment–curvature response of a pier (left) and time histories of deck drift δ (right), indicatively for the Rinaldi_228 record.

Fig. 1
figure 1

a Outline of the simplified model in the longitudinal direction, accounting for key structural components and nonlinear SSI; and b example comparison of the simplified model to the rigorous 3D model in the longitudinal direction, in terms of moment–curvature response of the pier (left) and time histories of deck drift δ (right) for the Rinaldi_228 record

Full size image

Overall, the proposed simplified model has been shown to compare well with the rigorous 3D model when considering the longitudinal direction of seismic loading, even for motions of very strong intensity. The time histories of δ are predicted with adequate accuracy, and the comparison is quite satisfactory in terms of the maximum value. The simplified model slightly over-predicts the response, but the comparison is quite acceptable in terms of M–c loops. Although these models can be claimed to offer an adequately accurate representation of reality (and certainly an improvement compared to overly simplified SDOF models), the effect of the abutments (including retaining walls, embankments, and stoppers) has not been accounted for. Focusing in the longitudinal direction, this paper explores the effects of these components, and extends the simplified method to account for their contribution on the overall response of the bridge.

2 Modelling of abutments

Most motorway bridges are equipped with abutment stoppers, either having a substantial clearance, and therefore being activated after a measurable relative displacement, or being practically in contact with the deck being inactive under service loads, but preventing seismic displacement at the abutments. In the longitudinal direction studied herein, the abutment backwall assisted by the approach slab, the wing-walls and the backfill soil “passive” resistance restrain the movement of the deck, acting as stoppers.

Although the effect of such retention devices is recognized, there are only few studies dealing with the contribution of the abutments and of the corresponding embankments (e.g., Wilson and Tan 1990; Zhang and Makris 2002a, b; Kotsoglou and Pantazopoulou 2007; Tegou et al. 2010; Argyroudis et al. 2013). On the other hand, a substantial amount of experimental work has been conducted for different types of abutments and embankment soils, including monotonic (Duncan and Mokwa 2001; Wilson and Elgamal 2009), cyclic (Thurston 1986a, b, 1987; Maroney and Chai 1994; Maroney et al. 1994; Gadre and Dobry 1998; Rollins and Cole 2006; Heiner et al. 2008; Lemnitzer et al. 2009), and seismic loading (Crouse et al. 1987; Gadre and Dobry 1998). CALTRANS (2013) proposes an empirical method, based on large-scale experiments. As discussed by Siddharthan et al. (1997), the method is largely empirical, it does not account for soil properties and abutment dimensions, and it can only be considered applicable to cases similar to the ones tested.

In our previous work (Anastasopoulos et al. 2015b), the presence of stoppers was ignored and the deck was assumed to have no restraint at the abutments, other than the shear resistance of the bearings. Hence, the previously presented results can be considered realistic, provided that the deck drift δ does not exceed the available clearance (δ c ). As schematically illustrated in Fig. 2, after the available clearance is consumed (i.e., the gap is closed), the stoppers are engaged restricting the movement of the deck, thus undertaking a substantial portion of the inertia forces. This way, the stoppers are actively limiting the deck drift δ below a specific level, aiming to diminish the probability of unseating and to ensure structural integrity under seismic motions exceeding the design limits. Moreover, this limitation of δ by the stoppers protects the bearings from excessive seismic deformations.

Fig. 2
figure 2

Schematic illustration of the effect of abutments on the longitudinal bridge response, showing the developing resistance mechanism when the available clearance is consumed

Full size image

A typical overpass bridge (A01-TE20) of the Attiki Odos Motorway is used as an illustrative example, in order to demonstrate the effect of the stoppers on the dynamic response of the bridge. As illustrated in Fig. 3a, the selected structural system is a 3-span bridge with a continuous prestressed concrete box-girder deck, monolithically connected to reinforced concrete (RC) piers of diameter d = 2 m and height h p  = 8.8 m, and supported by 4 elastomeric bearings at each abutment. Each bearing is 0.3 m × 0.5 m (longitudinal × transverse) in plan and has an elastomer height t = 63 mm, and shear modulus G = 1 MPa. The initial (i.e., elastic) natural period is 0.34 and 0.48 s in the longitudinal and the transverse direction, respectively. The piers are founded on capacity-designed (i.e., according to current seismic code provisions) square B p  = 8 m footings, while the abutments consist of 9 m high retaining walls, founded on rectangular 7 m × 10 m footings.

Fig. 3
figure 3

Example illustration of the effect of abutment stoppers: a typical overpass bridge A01-TE20 of the Attiki Odos motorway, used as an illustrative example; b rigorous 3D model of the bridge, including the foundations, the abutments, and the subsoil; and c time histories of deck drift δ with and without stoppers (using the Rinaldi-228 record as seismic excitation)

Full size image

The seismic performance of the bridge is analyzed employing a rigorous 3D FE model of the bridge–foundation–abutment–soil system (Fig. 3b) using ABAQUS (2013). The deck and the piers are modeled with elastic and inelastic beam elements, respectively. Inelastic pier response is simulated with a nonlinear model, calibrated against the results of RC section analysis using the KSC–RC software (2013). The latter has undeniably some limitations. However, it is capable of capturing with adequate accuracy the inelastic behaviour of the pier up to the exhaustion of the ductility capacity, which is of relevance in the context of a RARE system. Linear elastic springs and dashpots are used to model the compression (K c,b ) and shear stiffness (K s,b ) and damping (C c,b , C s,b ) of the bearings:

$$K_{c,b} = \frac{{E_{c} A}}{t n}$$
(1)
$$K_{s,b} = \frac{G A}{t n}$$
(2)
$$C_{c,b} = \frac{{2 K_{c,b} \xi }}{\omega }$$
(3)
$$C_{s,b} = \frac{{2 K_{s,b} \xi }}{\omega }$$
(4)

where E c : the compression modulus of the elastomer; A: the plan area of the bearing; t: the thickness of the individual elastomer layers; n: the number of individual elastomer layers; G: the shear modulus of the elastomer; ξ: the damping coefficient of the bearing; and ω: the angular frequency of reference (assumed to be equal to the dominant mode of the bridge).

The footings and the abutments are modeled with elastic brick elements, assuming the properties of RC (E = 30 GPa). A 20 m deep homogeneous clay layer of undrained shear strength S u  = 150 kPa is considered, also modeled with brick elements. Nonlinear soil behavior is modeled with a thoroughly validated kinematic hardening model, with a Von Mises failure criterion and associated flow rule (Anastasopoulos et al. 2011). The evolution law of the model consists of a nonlinear kinematic hardening component, which describes the translation of the yield surface in the stress space, and an isotropic hardening component, which defines the size of the yield surface as a function of plastic deformation (Gerolymos and Gazetas 2005). Calibration of model parameters requires knowledge of: (a) soil strength S u for clay and φ for sand; (b) the small-strain stiffness (expressed through G o or V s ); and (c) the stiffness degradation (G–γ and ξ–γ curves).

A tensionless interface is introduced between soil and foundation elements in order to model uplifting and sliding, assuming a friction coefficient μ = 0.7. For the interfaces between the retaining wall and the embankment a maximum shear capacity of 0.5*S u is considered for the cohesive embankment (Powrie 2013), while a friction coefficient μ = tan(0.76φ) is considered for the cohesionless one, according to the minimum value proposed by Potyondy (1961) for sand-to-concrete interface. A reinforced soil embankment is considered (which is quite common for such motorway bridges); it is modeled in a simple manner, applying appropriate kinematic constraints in the transverse direction.

Appropriate “free-field” boundaries are used at the lateral boundaries of the model, while dashpots are installed at its base to simulate the half-space underneath the soil that is included in the 3D model. Additionally, the seismic excitation is applied at the base, thus the bridge superstructure, the foundation soil, and the embankment soil experience seismic shaking. More details on the development of the rigorous model can be found in Anastasopoulos et al. (2011, 2015b).

In the analyses conducted so far (Anastasopoulos et al. 2015b), the effect of stoppers was ignored, assuming that the available clearance has not been consumed. In this paper, special “gap” elements are introduced between the deck and the abutments in order to model the effect of the stoppers. The detailed modelling of the response of expansion joints does not fall within the scope of this paper. More information on the subject can be found in Mitoulis (2012). Furthermore, creep and shrinkage effects or fluctuations of the gap due to thermal loads have not been considered in the present work. An initial clearance δ c is assigned, with the gap elements being activated only in compression and only after δ c is consumed. An example comparison of the response of the bridge, with and without stoppers, is presented in Fig. 3c. The notorious Rinaldi-228 record is used as seismic excitation, aiming to induce a large enough drift to exceed the available clearance and the stoppers to be engaged. For such strong seismic shaking, the comparison confirms that the effect of the stoppers can be quite significant, and should not be ignored. This is consistent with previous research on the subject (e.g., Siddharthan et al. 1997; Wood et al. 2007; Wood 2009), confirming the need to account for abutments stoppers when analyzing the seismic response of bridges in the longitudinal direction.

2.1 Problem definition and analysis methodology

Within the framework of the present work, the recently built Attiki Odos motorway (Athens, Greece) is used as a case study. Nevertheless, the overpass bridge examined herein is considered representative of similar modern motorways. Therefore, both the assumptions and the conclusions of the present study can be considered of more general validity. Based on a detail study of 190 bridges of the Attiki Odos motorway, it is concluded that the most commonly encountered abutment typology is that of a cantilever retaining wall, as shown in Fig. 4. The wall of height H and thickness t w is founded on a footing of width B and thickness t f , positioned with an eccentricity with respect to the wall, as defined by the length b. Although the specific dimensions may vary, this typology is considered representative for a large variety of modern motorway bridges.

Fig. 4
figure 4

Problem definition: commonly-encountered abutment typology, along with its key dimensions

Full size image

Using the A01-TE20 bridge as an illustrative generalized example, an abutment height H = 10.5 m is considered. Two idealized soil profiles are considered, representing cohesive and cohesionless embankment material. In the first case, a homogeneous stiff clay layer of undrained shear strength S u  = 150 kPa is considered. In the latter case, a homogeneous medium-dense sand layer is examined, having a friction angle φ = 35°. As for the previously described FE model, the soil is modeled with hexahedral continuum elements. In both cases, nonlinear soil behavior is modeled with the previously described kinematic hardening model. The latter has been thoroughly validated against physical model tests for: (1) bar-mat retaining walls (Anastasopoulos et al. 2010); (2) surface, embedded, and pile foundations (Anastasopoulos et al. 2011, 2012; Giannakos et al. 2012); and (3) circular tunnels (Tsinidis et al. 2014; Bilotta et al. 2014). It should be noted that the latter is a totally independent validation, which formed part of a “round robin” comparison using centrifuge experiments that were conducted at the University of Cambridge (Lanzano et al. 2012).

Before proceeding to the analysis of the abutment of Fig. 4, the kinematic hardening (KH) model is further validated for the problem studied herein. To allow direct comparison with published theoretical solutions (Rankine 1857), a 2D FE model of a simple gravity wall of height (H) and width (B) is developed and subjected to monotonic lateral pushover analysis. For both soil profiles, a practically frictionless bonded interface is considered (negligible friction coefficient for numerical stability), to be as close as possible to the assumptions of the theoretical solutions. For the same reason, the displacement is applied having constrained the rotational degree of freedom. In the case of the cohesionless soil, the results are also compared to those obtained using a Mohr–Coulomb (MC) constitutive model. As depicted in Fig. 5, the numerical prediction matches well the theoretical solution, both for cohesive (Fig. 5a) and for cohesionless soil (Fig. 5b). As revealed by the deformed meshes with superimposed plastic strain contours (top row), the predicted failure mechanisms and the associated failure wedges compare well with the theoretical solutions, especially for clay. In the case of sand, the inclination is a bit steeper than its theoretical values, something which is attributed to the use of a small cohesion c = 2 kPa, which was necessary for numerical stability. The predicted distribution of horizontal stress with depth (bottom row) also matches the theoretical solution, and the one obtained using a Mohr–Coulomb model (for cohesionless soil).

Fig. 5
figure 5

Validation of the kinematic hardening (KH) model for a gravity wall subjected to lateral pushover with the rotational degree of freedom constrained. Deformed mesh with superimposed plastic strain contours (top row), illustrating the developing failure wedges, and distribution with depth of horizontal stresses (bottom row) for: a cohesive; and b cohesionless soil

Full size image

2.2 Abutment resistance to passive loading at the top

In the previous section, in order to validate the kinematic hardening model, a 2D model of a gravity wall was subjected to static pushover analysis under idealized passive conditions, assuming purely lateral translation with rotational degree of freedom fully constrained. As previously discussed, this simplification was necessary to allow comparison with theoretical solutions. Besides its different geometry, the cantilever wall of a bridge abutment is subjected to slightly—but crucially—different loading conditions when the deck collides on the abutment stoppers. Although this is still passive loading, the loading is applied at the top of the abutment wall (where the stopper is located), and there is of course no rotational restraint. To the best of the authors’ knowledge, the passive resistance of abutment retaining walls subjected to this kind of passive loading is still an unresolved issue.

To investigate the abutment resistance to such passive loading at the top (i.e., at the level of the deck), the previously discussed cantilever retaining wall of the A01-TE20 bridge is subjected to static pushover analysis, with the displacement applied at the top and without any rotational restraint. To reveal the differences between this peculiar type of passive loading compared to traditional passive conditions, a second pushover analysis is conducted imposing a rotational restraint. Initially, the analysis is performed in 2D, assuming plane strain conditions. Then, a more detailed 3D model is developed and used to explore the effect of the 3D geometry of the abutment wall and the contribution of side walls.

Figure 6 summarizes the results of the 2D analyses, for both soil profiles and for both passive loading conditions (with and without rotational restraint). As previously, the comparison is performed in terms of soil failure mechanisms, as revealed by the plots of deformed mesh with superimposed plastic strain contours (top row), and horizontal stress distribution with depth for both soil profiles (bottom row). As suspected, the type of loading has a rather pronounced effect on the failure mechanisms and the stress distributions, for both soil profiles. Moreover, the failure mechanism is qualitatively different for the cohesive (Fig. 6a) and the cohesionless soil profile (Fig. 6b), and also different to the traditional passive failure mechanisms of well-established theoretical solutions.

Fig. 6
figure 6

Abutment cantilever wall modelled in 2D, subjected to passive-type loading at the top and to traditional passive conditions (with rotational restraint). Deformed mesh with superimposed plastic strain contours (top row), illustrating the developing failure mechanism, and distribution with depth of horizontal stresses (bottom row) for: a cohesive; and b cohesionless soil

Full size image

Evidently, a detailed parametric study is required to derive deeper understanding. However, conducting such a study using a rigorous 3D model of the abutment requires quite substantial computational effort. Therefore, the 3D model of the abutment is used as a benchmark in order to explore the degree of realism of an equivalent 2D analysis. In the analyses discussed herein, realistic conditions are assumed for the interfaces between the retaining wall and the embankment, assuming a maximum shear stress capacity of 0.5S u for the cohesive embankment (Powrie 2013), and a friction coefficient μ = tan(0.76φ) for the cohesionless one, according to the minimum value proposed by Potyondy (1961). As shown in Fig. 7, while there are some differences between the two models, the distribution of lateral stresses with depth is quite similar, and as a result the ultimate resistance predicted by the 2D model is quite similar to the one obtained with the more rigorous 3D model. It can be concluded that (at least for the case examined herein) the 3D wall geometry and the presence of side walls do not have a significant effect on the passive resistance of the abutment. Therefore, the 2D model is considered adequately realistic and can be used to conduct the parametric study.

Fig. 7
figure 7

Comparison of the rigorous 3D model to the simpler 2D model subjected to passive-type loading at the top. Deformed mesh with superimposed plastic strain contours (top row), illustrating the developing failure mechanism for cohesive soil, and distribution with depth of horizontal stresses (bottom row) for: a cohesive; and b cohesionless soil

Full size image

3 Dimensional analysis and parametric study

Dimensional analysis is a mathematical tool that emerges from the existence of physical similarity and reveals the relationships that govern natural phenomena (Langhaar 1951). Through dimensional analysis, it is feasible to derive results of generalized applicability and gain deeper understanding of key problem parameters (Makris and Black 2004a, b; Makris and Psychogios 2006; Palmeri and Makris 2008; Karavasilis et al. 2010; Makris and Vassiliou 2010; Pitilakis and Makris 2010; Kourkoulis et al. 2012). For this purpose, a dimensional analysis of a typical bridge abutment is performed, aiming to derive deeper insights on the factors affecting its resistance when subjected to passive-type loading at the top of the wall (i.e., at the deck level).

The analyzed abutment is the one previously described (Fig. 4), which is considered representative for modern motorway bridges. The abutment of total height H is founded on a clayey soil deposit of depth z. The dimensional analysis is performed for a cohesive soil deposit of undrained shear strength S u and density ρ. The formulation is not as straight-forward for cohesionless soil, but the main dimensionless quantities are still considered transferable. Besides the dead load of the cantilever wall, the total mass m of the system also includes the dead load of the embankment soil above the footing, and the vertical load of the deck acting on the abutment.

In the case of the cohesive soil, the total horizontal resistance of the abutment system (F ab ) can be expressed as:

$$F_{ab} = f\left( {B, H, b, h, t_{w} , \rho , g, m, S_{u} } \right)$$
(5)

According to the Vaschy–Buckingham Π-theorem, a dimensionally homogeneous equation involving k variables may be transformed to a function of k-n dimensionless Π-products, where n is the minimum number of reference dimensions necessary for the description of the physical variables. Applying the Π-theorem on Eq. (5), which contains k = 10 independent variables involving n = 3 reference dimensions (i.e., length, mass, and time), obviously results in 7 dimensionless Π-products. In this context, Eq. (5) may be rearranged in dimensionless terms as follows:

$$\frac{F_{ab}}{2S_{u}H +0.5\rho gH^{2}} = f\left( {\frac{B}{H} , \frac{b}{h} , \frac{{t_{w} }}{h} , \frac{{H-h}}{B} , \frac{mg}{{S_{u} B}}}, \frac{\rho bh}{{m}} \right)$$
(6)

The parameter mg/S u B is directly proportional to the ratio x = N/N ult of the static vertical load N (due to the total mass of the abutment and the corresponding load of the deck) to the bearing capacity N ult  = (π + 2)S u B of the strip foundation (i.e., the inverse of the factor of safety against vertical loading FS v ); in the sequel, it will be referred to as 1/FS v or x = N/N ult .

3.1 Verification of the dimensional formulation

The efficiency of the previously described dimensional analysis is verified by comparing the static response of two “equivalent” abutment systems of Fig. 8a (Systems A and B) subjected to static pushover analysis, applying passive-type loading at the top of the wall. System A refers to an H = 10.5 m cantilever wall, founded on a B = 7 m footing on idealized homogeneous cohesive soil of S u  = 150 kPa, density ρ = 1.6 Mgr/m3, and depth H 1 = 19.5 m. The embankment consists of the same soil as the one under the foundation. System B refers to an equivalent system of height H′ = 21 m, founded on a B′ = 14 m footing on S u ′ = 300 kPa soil of depth H 1′ = 39 m. In order for the two systems to exhibit a self-similar response, the factor of safety FS v has to be equal in both cases (Kourkoulis et al. 2012). Therefore, the mass of System B is m′ = 4 m = 470.4 Mgr (since N ult is proportional to B and S u ). Overall, Systems A and B share the same seven dimensionless products of Eq. (6).

Fig. 8
figure 8

Verification of the dimensionless formulation for cohesive soil: a example comparison of two equivalent abutment systems, sharing common dimensionless properties, subjected to passive-type loading at the top; b comparison of the two systems in absolute terms: distribution of horizontal stresses with depth; and c same comparison in dimensionless terms

Full size image

Figure 8b compares the distribution of horizontal stresses σ h with depth z for the two examined systems. As expected, the response of the two systems is different in absolute terms. Nevertheless, when plotting the results in dimensionless terms (Fig. 8c), the differences are eliminated, confirming the effectiveness of the presented dimensional formulation. In the dimensionless plot, the horizontal stress σ h is normalized to the corresponding passive resistance σ hp , while the depth z is normalized with respect to H.

3.2 Parametric study: the effect of key parameters

A parametric study is conducted to gain insights on the key factors affecting the response of the abutment, with emphasis on its resistance to lateral loading at the top. Figure 9 depicts the results of an initial sensitivity analysis, focusing on the effect of four factors on the distribution of dimensionless lateral soil pressures (σ h /σ hp ) with dimensionless depth (z/H). As shown in Fig. 9a, the lateral resistance of the abutment is rather insensitive to its slenderness ratio B/H. However, the considered abutment is a cantilever wall, and the b/h ratio (where b is the width of the footing extending underneath the embankment soil, and h the height of the wall, excluding the footing’s thickness) may be of greater relevance.

Fig. 9
figure 9

Distribution of dimensionless lateral soil pressures σ h /σ hp (where σ hp is the corresponding passive resistance) with dimensionless depth (z/H) for different: a slenderness ratios B/H; b b/h; c factors of safety against purely vertical loading FS V ; and d t w /h

Full size image

This is confirmed by the results of Fig. 9b, where the b/h ratio is shown to affect the distribution of σ h /σ hp with depth, and hence the total lateral resistance of the abutment. It is no surprise that the increase of b/h leads to increase of the total resistance of the system. As shown in Fig. 9c, the factor of safety against purely vertical loading FS v also has a pronounced effect on the developing abutment resistance, as it leads to an alteration of the failure mechanism of the system. In contrast, the ratio of wall thickness t w to its height h (t w /h) does not seem to affect the response to any appreciable extent (Fig. 9d), and can therefore be considered negligible.

A more detailed parametric study is conducted focusing on b/h and FS v , which are the most crucial factors according to the results of the sensitivity analysis. The ratio b/h is parametrically varied from 0 to 0.6 to cover a wide range of abutment geometries, in combination with the entire range of allowable FS v values, for the idealized cohesive and cohesionless soil profile. Figures 10 and 11 present a summary of the failure mechanisms for cohesive and cohesionless soil, respectively, by means of contours of plastic deformation. The developing failure mechanisms vary substantially with both b/h and FS v . For example, in the case of cohesive soil (Fig. 10) and for the b/h = 0 abutment geometry, the decrease of FS v to 1.1 leads to the development of a scoop-type mechanism under the wall footing, instead of the almost pure uplifting that is observed for FS v  ≥ 2.

Fig. 10
figure 10

Plastic deformation contours showing the failure mechanisms for different b/h ratios and factors of safety FS v for cohesive soil

Full size image
Fig. 11
figure 11

Plastic deformation contours showing the failure mechanisms for different b/h ratios and factors of safety FS v for cohesionless soil

Full size image

Following the logic of the previous sections, the ultimate resistance of the abutment subjected to lateral loading at the top, F ab , is normalized to its passive resistance, F p , according to theoretical solutions (Rankine 1857). Figure 12 summarizes the results for the studied b/h ratios, plotting the normalized abutment resistance F ab /F p as a function of the inverse of the safety factor 1/FS V  = N/N ult for both cohesive (Fig. 12a) and cohesionless soil (Fig. 12b). The examined values of FS v range from 10 to about 1.1, covering a reasonable range encountered in modern motorway abutments (3.5–7.5, typically 5). For both soil profiles, the increase of N/N ult (i.e., the decrease of FS V ) leads to an increase of the normalized resistance F ab /F p . For relatively large FS v  ≥ 5, the footing cannot fully mobilize its moment capacity as it is subjected to intense uplifting (see Fig. 10), with soil yielding being limited at the top of the embankment. For relatively low factors of safety, FS v  ≤ 2, uplifting is suppressed and the wall footing is adequately loaded to mobilize its moment–shear capacity to a more appreciable extent. As N/N ult  → 1 (FS v  → 1), the normalized abutment resistance F ab /F p starts decreasing, as the footing is becoming too heavily loaded, and as a result its moment capacity is reduced. An abutment of the examined type may be considered as a partially embedded foundation (embedded on one side only). Under this prism, there are several published studies showing that the moment capacity of a foundation increases with the increase of the vertical load (decrease of the safety factor) till about half its vertical bearing capacity. The same trend is observed for shallow (e.g., Meyerhof 1953; Gourvenec 2007), skirted (e.g., Bransby and Randolph 1998), and embedded foundations (e.g., Gerolymos et al. 2015; Zafeirakos and Gerolymos 2016). The normalized ultimate lateral resistance F ab /F p is also affected by wall geometry, as expressed by the b/h ratio. As it should be expected, the increase of b/h leads to an increase of F ab /F p . The increase of b/h leads to a larger part of the wall footing being situated underneath the embankment soil, leading to mobilization of a deeper failure mechanism (see Figs. 10, 11), and hence to an increase of the ultimate lateral resistance. Two specific examples are also given in Fig. 12, aiming to elucidate the observed performance. The first example refers to the cohesive embankment (Fig. 12a). Considering b/h = 0, the normalized resistance F ab /F p varies from 0.33 for N/N ult  = 0.2 (i.e., FS v  = 5) to 0.51 for N/N ult  = 0.6 (i.e., FS v  = 1.67). The second one refers to the cohesionless embankment (Fig. 12b). Considering N/N ult  = 0.6 (i.e., FS v  = 1.67), F ab /F p varies from 0.38 for b/h = 0, to 0.63 for b/h = 0.6.

Fig. 12
figure 12

Ultimate resistance of the abutment subjected to lateral loading at the top normalized to the theoretical passive resistance (F ab /F p ) as a function of the inverse of the safety factor 1/FS V  = N/N ult and the ratio b/h for: a cohesive; and b cohesionless soil

Full size image

As already mentioned, the ultimate goal of this paper is to develop a simplified method to account for the role of abutments in the seismic response of motorway bridges. In this realm, in addition to the ultimate lateral resistance F ab /F p of the abutment, it is important to have an indication of the inward displacement δ at which the ultimate resistance is attained. Under this prism, Fig. 13 shows an example (for b/h = 0.44 and FSv = 4.68) of the evolution of the distribution of lateral soil pressures with depth with the imposed lateral displacement δ, normalized to the abutment height Η. It becomes evident that a normalized displacement δ/H of the order of 1% is enough to mobilize the ultimate resistance for the examined range of FS v , both for cohesive (Fig. 13a) and for cohesionless soil (Fig. 13b).

Fig. 13
figure 13

Evolution of the distribution of lateral soil pressures with depth with the imposed lateral displacement δ, normalized to the overall wall height Η for: a cohesive; and b cohesionless soil (results shown for b/h = 0.44 and FS v  = 4.68)

Full size image

4 Outline of the simplified method

The previously described overpass bridge A01-TE20 (Fig. 3a) of the Attiki Odos Motorway is used as an illustrative example. Besides its simplicity, the selected system is representative for about 30% of the bridges of the specific motorway, and is also considered quite common for metropolitan motorways in general. The previously described rigorous 3D FE model of Fig. 3b is used as a benchmark, in order to verify the efficiency of the simplified models, which are developed herein. The development of the simplified models is independent from the rigorous model and the latter is only used to verify the efficiency of the simplified.

4.1 Simplified model

As described in more detail in Anastasopoulos et al. (2015b), the simplified model considers an equivalent SDOF system of the most vulnerable pier. As depicted in Fig. 14, the SDOF system is composed of a column having the stiffness, height, and moment–curvature (M–c) response of the pier, and concentrated mass m p :

$$m_{p} = m_{d} \frac{{K_{p} }}{{K_{B} }}$$
(7)

where K p  = 12EI p /h 3 is the stiffness of the pier (E, I p , and h: the Young’s modulus, moment of inertia, and height of the pier, respectively), and K B is the lateral stiffness of the entire bridge, accounting for the shear stiffness K s,b of abutment bearings:

$$K_{B} = \sum K_{s,b} + \sum K_{p }$$
(8)
Fig. 14
figure 14

Outline of the extended simplified model, accounting for key structural components, nonlinear SSI, and abutment system (stoppers, retaining wall, and embankment soil)

Full size image

The shear stiffness of abutment bearings is also accounted for, by adding a lateral spring (K s,l ) and dashpot (C s,l ) at the top of the SDOF system:

$$K_{s,l} = \frac{{\sum K_{s,b} }}{2n}$$
(9)
$$C_{s,l} = \frac{{2 K_{s,l } \xi_{s} }}{\omega }$$
(10)

where n is the number of monolithically connected piers, ξ s is the damping coefficient and ω the angular frequency of the bridge.

In order to account for the bending stiffness of the deck, a rotational spring (K r,l ) and dashpot (C r,l ) are added at the top of the pier. The rotational spring represents the flexural stiffness of the deck, and is computed considering a continuous beam of three equal spans (for the symmetric case of A01-TE20 bridge):

$$K_{r,l} = \frac{{9 EI_{d} }}{{L_{s} }}$$
(11)

where E and I d : the Young’s modulus and moment of inertia of the deck, and L s : the length of each span. For a different number of unequal spans, the equivalent rotational spring can be computed through 2D structural analysis software. The rotational dashpot (C r,l ) is computed as follows:

$$C_{r,l} = \frac{{2 K_{r,l } \xi_{s} }}{\omega }$$
(12)

where ξ s is the damping coefficient and ω the angular frequency of the bridge system.

Nonlinear SSI is also accounted for, employing the simplified method of Anastasopoulos and Kontoroupi (2014). As shown in Fig. 14, the soil–foundation system is replaced by horizontal, vertical, and rotational springs and dashpots. The horizontal (K H and C H ) and vertical (K V and C V ) springs and dashpots can be assumed elastic (see Gazetas 1983), as the considered problem is rocking-dominated. As shown by Gajan and Kutter (2009), the response is rocking-dominated when H p /B p  > 1 (here 1.46), where H p : the total pier height from the foundation level till the deck’s center of mass, and B p: the width of the pier footing. In such a case, the cyclic rotation is much larger than the normalized cyclic sliding displacement, irrespective of the factor of safety FS v . Therefore, the nonlinearities related to sliding can be ignored and the related horizontal springs and dashpots can be reasonably approximated as elastic (see also Anastasopoulos and Kontoroupi 2014). For the rotational degree of freedom, a nonlinear rotational spring is employed, accompanied by a linear dashpot. The nonlinear rotational spring is defined on the basis of moment–rotation (M–θ) relations, computed through 3D FE modelling (Anastasopoulos and Kontoroupi 2014). The response is divided in three phases: (a) quasi-elastic response (θ → 0); (b) nonlinear response (transition stage); and (c) plastic response (ultimate state, large θ).

The initial quasi-elastic rotational stiffness has been shown to be a function of the factor of safety against vertical loading FS v :

$$K_{R,0} = K_{R,elastic} \left( {1 - 0.8\frac{1}{{FS_{v} }}} \right)$$
(13)

where K R,elastic is the purely elastic rotational stiffness (Gazetas 1983):

$$K_{R,elastic} = 3.65\frac{{G b^{3} }}{1 - \nu }$$
(14)

in which b = B/2 (i.e. the half width of the footing), G is the small strain shear modulus of soil, and ν the Poisson’s ratio.

The plastic response refers to the ultimate capacity of the footing, and can be defined on the basis of published failure envelopes (e.g., Gazetas et al. 2012):

$$M_{u} = 0.55 N_{u} B \left( {1 - \frac{{N_{u} }}{{N_{uo} }}} \right)$$
(15)

where N uo is the bearing capacity for purely vertical loading (Meyerhof 1953; Gourvenec 2007):

$$N_{uo} \approx \left( {\pi + 3} \right)S_{u} B^{3}$$
(16)

Finally, the nonlinear response corresponds to the transition phase between quasi-elastic and plastic response. As discussed in Anastasopoulos and Kontoroupi (2014), the M–θ relations can be expressed in non-dimensional form as follows:

$$M/S_{u} B^{3} = f\left( {\theta /\theta_{s} } \right)$$
(17)

where θ s is a characteristic rotation:

$$\theta_{s} \approx \frac{{{\rm N} {\rm B}}}{{4 {\rm K}_{R,0} }}$$
(18)

Through such normalization, a single dimensionless M–θ curve can be obtained. While a nonlinear rotational dashpot would be required, most FE codes only accept a single value of C R . Therefore, a simplifying approximation is necessary to maintain simplicity, with C R being assumed to be a function of the effective rotational stiffness K R , the hysteretic damping ratio ξ, and a characteristic frequency ω:

$$C_{R} \approx \frac{{2 K_{R} \xi }}{\omega }$$
(19)

The damping ratio ξ is computed through the M–θ loops of cyclic pushover analyses. As discussed in Anastasopoulos and Kontoroupi (2014), the normalized damping coefficient C R /K R,elastic ω −1 with respect to θ is a “bell shaped” curve, with its maximum at θ ≈ 10−3 rad (for the foundations examined). The latter can be used to compute C R as a function of FS V only, by means of a reasonable approximation. Additionally, other published analytical expressions could also be used with equally satisfactory results, as long as they are capable to capture the key aspects of the problem.

4.2 Extension to account for abutment stoppers

Based on the results of the previously discussed parametric study, the simplified method is further extended to account for the effect of the abutments and the associated stoppers in the longitudinal direction. Each of the abutments is replaced by an assembly of a gap element, and either a nonlinear spring (K ab ), and a linear dashpot (C ab ) for the cohesionless embankment, or a nonlinear truss element for the cohesive one, added at each side of the model at the deck level (i.e., at the top of the pier), as depicted in Fig. 14. The gap element represents the response of abutment stoppers, accounting for the available clearance between the deck and the stoppers at the top of the abutment in the longitudinal direction. The gap has an overclosure δ c (=0.08 m in this particular case), which is equal to the clearance between the deck and the stoppers. When the available clearance is consumed (when the drift δ = δ c ), the overclosure is consumed and the gap element becomes infinitely stiff, simulating the collision of the deck at the top of the abutment.

It is important to note in Fig. 14 that the gap element is connected in parallel to the spring (K s,l ) and the dashpot (C s,l ) or the truss element respectively, which represent the abutment bearings. For δ < δ c , the gap has not yet engaged (as its overclosure is not yet consumed), but the abutment bearings are offering lateral resistance to the deck. When δ = δ c , the gap is engaged and its “infinite” lateral stiffness governs the response. The deck collision on the stopper leads to loading of the abutment retaining wall in the form of a concentrated load at its top. As previously discussed, the resistance mechanism varies depending on the type of the embankment soil, the b/h ratio, and the factor of safety FS v . The spring–dashpot assembly (or the truss element, respectively) represents the response of the abutment to such concentrated loading at the top, and is calibrated on the basis of the previously discussed parametric static pushover analysis. Ideally, nonlinear dynamic analysis would be required to account for the effect of the dynamic earth pressures at the abutment. Nevertheless, considering that the ultimate scope is to develop a simplified methodology and that a series of parametric analysis is required, the calibration of the stiffness-damping parameters on the basis of static pushover analysis is more straight-forward. In addition, the seismic performance of the simplified model is comparatively assessed using the rigorous 3D model as a benchmark, in which the embankment experiences dynamic loading. Therefore, the comparison remains valid, despite the aforementioned limitation.

In the case of a cohesionless embankment, an elastic–perfectly plastic spring is considered, of stiffness K ab which can be calculated as follows:

$$K_{ab} = \frac{{F_{ab} }}{{\delta_{ab} }}$$
(20)

where F ab is the ultimate capacity of the abutment; and δ ab  = 0.01H (according to the previously presented results) is the displacement at which the ultimate capacity is reached (where H is the total height of the abutment). The ultimate capacity of the abutment is estimated according to Fig. 12 as a function of FS v and b/h, and the passive resistance F p according to Rankine (1857):

$$F_{p} = \frac{1}{2}K_{p} \gamma^{\prime}H^{2}$$
(21)
$$K_{p} = \tan^{2} \left( {45 + \frac{\varphi }{2}} \right)$$
(22)

The accompanying linear dashpot is calculated as follows:

$$C_{ab} = \frac{{2K_{ab} \xi_{ab} }}{\omega }$$
(23)

where ξ ab is the damping coefficient of the embankment soil, calculated according to published ξ–γ curves (Vucetic and Dobry 1991; Ishibashi and Zhang 1993; Ishihara 1996) for an estimated γ; and ω is the angular frequency of the bridge system.

In the case of a cohesive embankment, a nonlinear truss element is considered (instead of the nonlinear spring and the linear dashpot), which allows simulation of the hysteretic response of the abutment–soil system. Such modelling is found to be more effective in the case of the cohesive embankment, as it manages to simulate better its residual deformation during unloading due to its cohesion. Its stiffness is calculated in a similar manner, applying Eq. (20). The ultimate capacity F ab is again calculated according to Fig. 12, considering the passive resistance F p according to Rankine (1857):

$$F_{p} = \frac{{4S_{u} + \gamma^{\prime}H}}{{2{\rm }}}H$$
(24)

5 Effectiveness of the proposed simplified method

The performance of the extended simplified model, accounting for key structural components, nonlinear SSI and the abutments (Fig. 14) is assessed, using the rigorous 3D FE model of the A01-TE20 bridge (Fig. 3b) as a benchmark. The effectiveness of the simplified model is assessed on the basis of slow-cyclic pushover and dynamic time history analyses.

5.1 Slow-cyclic pushover analysis

The two models (simplified and rigorous) are subjected to displacement-controlled slow-cyclic pushover loading. Two load cycles are applied, the first imposing a deck displacement δ = ±0.2 m, and the second one pushing the deck further to δ = ±0.4 m. Figure 15 compares the cyclic F–δ response of the simplified model to that of the rigorous 3D model for the cohesive and for the cohesionless embankment.

Fig. 15
figure 15

Comparison of the simplified model to the rigorous 3D model in terms of slow-cyclic pushover (F–δ) response for: a cohesive; and b cohessionless soil

Full size image

In the case of the cohesive embankment (Fig. 15a), the comparison is quite successful both in terms of ultimate capacity and stiffness. During the first cycle of loading (δ = −0.2 m), the response of the simplified model is practically identical to that of the rigorous 3D model. During subsequent loading cycles, the simplified model slightly overestimates the capacity of the system, as it cannot accurately capture the developing detachment at the soil–abutment interface. When loaded for the first time (δ = −0.2 m), the wall moves together with the embankment soil beneath. However, during unloading (δ = +0.2 m) the soil behind the wall retains some plastic deformation, thus not completely following the movement of the wall. Therefore, during the consequent loading cycle (δ = −0.4 m), the deck collides on the wall, which is not in full contact with the already deformed soil behind the abutment. Such “pinching” behaviour has not been incorporated in the simplified model in order to maintain simplicity. Nevertheless, these differences, which are mainly observed during the 2nd cycle of loading, are not major, especially taking into account the complexity of the resistance mechanisms of the abutment system and the simplicity of the proposed assembly.

Similar conclusions can be drawn for the cohesionless embankment (Fig. 15b). The comparison is slightly worse, but still quite satisfactory considering the simplifying assumptions of the simplified model. As for the previous case, the simplified model captures the response nicely during the first cycle of loading (δ = −0.2 m). During the subsequent loading cycles, the simplified model does not overestimate the capacity of the system, but there are non-negligible differences in terms of the hysteresis loops. The simplified model under-estimates the damping, as it cannot capture the detailed interaction between the abutment and the embankment soil. In contrast to the cohesive embankment, during unloading (δ = +0.2 m) the soil behind the wall tends to follow its outward movement. Due to the absence of cohesion, part of the soil tends to “flow” inside the opening gap, leading to reduction of previously mentioned “pinching” behaviour. Nevertheless, these differences are mainly observed during the 2nd cycle of loading, and are still quite acceptable given the simplicity of the proposed model.

5.2 Dynamic time history analysis

The two models (simplified and rigorous) are subjected to seismic shaking. In order to render the two models directly comparable, the acceleration time history at the pier foundation level, resulting from the dynamic analysis of the rigorous 3D model, is used as seismic excitation for the simplified model. The rigorous 3D model requires substantial computational effort, calling for careful selection of the seismic excitations. Hence, from the 29 records that were used in Anastasopoulos et al. (2015b), 7 characteristic records are selected (Fig. 16): (a) Aegion, which is considered representative of moderate intensity shaking; (b) Duze–090 (Duzce 1999), Lefkada 2003, CHV1-NS (Kefalonia 2014), and TCU068-EW (Chi–Chi 1999), which can be considered representative of medium to strong intensity shaking; and (c) the notorious Rinaldi–228 record (Northridge 1994) containing very strong forward rupture directivity pulses, and the Takatori–000 record (Kobe 1995) containing multiple very strong motion cycles, which are representative of very strong seismic shaking.

Fig. 16
figure 16

Seismic excitations: real records covering a wide range of earthquake scenarios

Full size image

A selection of results is presented herein, focusing on strong to very strong seismic excitations, in which case the drift δ exceeds the available clearance δ c  = 0.08 m and the deck collides on the stoppers activating the resistance of the abutments, which is necessary to verify the efficiency of the extended simplified model. The predictions of the simplified model are compared to the rigorous 3D model (which is considered as a benchmark) in terms of time histories of deck drift δ, for cohesive (Fig. 17) and cohesionless soil (Fig. 18).

Fig. 17
figure 17

Dynamic time history analysis-cohesive soil. Comparison of the simplified model to the rigorous 3D model in terms time histories of deck drift δ for three different seismic excitations: a Duzce Bolu-090; b CHV1_NS (Kefalonia 2015); and c Takatori-000 (Kobe 1995)

Full size image
Fig. 18
figure 18

Dynamic time history analysis-cohesionless soil. Comparison of the simplified model to the rigorous 3D model in terms time histories of deck drift δ for three different seismic excitations: a Duzce Bolu-090; b CHV1_NS (Kefalonia 2015); and c Takatori-000 (Kobe 1995)

Full size image

As shown in Fig. 17, the comparison is quite satisfactory in the case of the cohesive embankment. In all seismic excitations, including the notorious Takatori–000 record, the match is quite acceptable in terms of maximum drift δ ,max and vibration characteristics (dominant period, cycles, and damping). When subjected to the Duzce Bolu-090 seismic excitation (Fig. 17a), the first collision of the bridge deck on the abutment takes place at t = 8.1 s, pushing the abutment roughly 0.03 m inwards. The second collision takes place at t = 8.7 s, leading to a similar inward displacement of the opposite abutment. The discrepancies between the simplified and the rigorous model are considered negligible for all practical purposes. The situation is similar for the CHV1-NS record (Fig. 17b), with two collisions taking place at t = 4.9 and 8.6 s. In the case of the Takatori-000 record, there are several collisions and both abutments are pushed inwards by up to 0.15 m. Even under such intensely plastic response, the prediction of the simplified model is quite acceptable.

In the case of the cohesionless embankment (Fig. 18), the comparison is not as successful. In all cases examined, the response is nicely captured during the first collision of the deck on the stoppers, but the subsequent motion is not captured to the same extent, as it should be expected on the basis of the pushover analysis results. In the case of the Düzce Bolu-090 excitation (Fig. 18a), for example, the deck collides on the stoppers at t = 7.8 s. Up to this point, the comparison between the simplified and the rigorous model is excellent. When the movement of the deck is reversed, t > 7.8 s, the simplified model fails to capture the response. The same applies to the CHV1-NS record, in which case the response is nicely captured until the first collision at t = 4.9 s (Fig. 18b). Interestingly, the simplified model performs well up until the second collision in the case of the Takatori-000 record, in which case the first one takes place at t = 7.4 s and the second one at t = 8.1 s.

The success of the simplified methodology becomes more evident, when examining the results in terms of damage states, in the context of a RARE system. A variety of damage indices (DIs) are available in the literature, to express the seismic damage of a bridge. A widely used DI that refers to the seismic damage of a bridge pier is the maximum drift ratio:

$$\delta_{r,max} = \frac{{\delta_{max} }}{{h_{p} }}*100\%$$
(25)

where: δ max is the maximum deck drift δ; and h p the height of the pier. With reference to response limit states (Priestley et al. 1996) damage states can be defined based on typical values of drift ratio δ r for each damage state. In particular, δ r  < 1% indicates that the bridge pier experiences minor damage, 1% < δ r  < 3% medium to extensive damage, and δ r  > 3% probable collapse. In the examined case, deck drifts δ < 0.088 m (δ r  < 1%) indicate minor damage, 0.264 m < δ < 0.088 m (1% < δ r  < 3%) medium to extensive damage, and δ > 0.264 m (δ r  > 3%) probable collapse. Even for the considered strong to very strong seismic excitations, the differences in terms of δ r,max are not exceeding 15% even for the worst-case scenario, while both models predict the same damage state. Therefore, overall the extended simplified model is considered as a reasonable approximation (excellent for cohesive soil) of the seismic performance of typical motorway bridges in the longitudinal direction.

6 Synopsis and conclusions

In the present paper, the effect of abutment stoppers on the seismic response of motorway bridges in the longitudinal direction has been examined. For this purpose, a rigorous 3D FE model of a representative motorway overpass bridge of the Attiki Odos motorway (Athens, Greece), including the entire bridge–foundation–abutment–soil system, accounting for abutment stoppers, was developed and used as a benchmark (Fig. 3). The effect of abutment stoppers has been shown to be significant, and therefore it must be taken into account for a proper simulation of the seismic response of such bridges.

Subsequently, the resistance mechanism of abutments triggered when the bridge deck collides on the stoppers has been examined. To that end, a rigorous 3D FE model of a typical motorway bridge abutment was developed. The latter consists of a cantilever retaining wall of representative dimensions (Fig. 4), considering both cohesive (clayey) and a cohesionless (sandy) soil. The soil constitutive model is validated against theoretical solutions, considering an idealized 2D gravity wall and applying passive loading according to Rankine (1857), assuming purely lateral translation with rotational degree of freedom fully constrained. Besides its different geometry, the cantilever wall of a bridge abutment is subjected to slightly—but crucially—different loading when the deck collides on the abutment stoppers. The loading is applied at the top of the abutment (where the stopper is located) without any rotational restraint.

To gain insights on the key parameters affecting the abutment resistance to such passive loading at the top, a dimensionless analysis and a comprehensive parametric study were conducted employing the rigorous 3D FE model. The efficiency of the dimensional analysis was verified by comparing the static response of two “equivalent” abutment systems subjected to static pushover analysis, applying passive-type loading at the top of the wall (Fig. 8). The factor of safety against vertical loading (FS v ) and the ratio b/h are shown to be the most important parameters affecting the static behavior and the resistance (F ab ) of cantilever-type bridge abutments. The results of the parametric study are summarized in Fig. 12, plotting the normalized abutment resistance F ab /F p as a function of the b/h ratio and of the inverse of the safety factor 1/FS v  = N/N ult .

Based on the results of the parametric study, the simplified model of Anastasopoulos et al. (2015b) was extended to account for the effect of abutment stoppers in the longitudinal direction (Fig. 14). Each of the abutments is replaced by an assembly of a gap element, and either a nonlinear spring (K ab ), and a linear dashpot (C ab ) for cohesionless embankments, or a nonlinear truss element for cohesive ones, added at each side of the model at the deck level (i.e., at the top of the pier). The gap element represents the response of abutment stoppers, accounting for the available clearance δ c . The spring–dashpot assembly (or truss element, respectively) represents the response of the abutment to concentrated loading at the top, and is calibrated using the dimensionless results of the parametric study (Fig. 12).

The efficiency of the extended simplified model (Fig. 14) was assessed on the basis of slow-cyclic pushover and nonlinear dynamic time history analyses, using the full 3D model as a benchmark. While the comparison is shown to be excellent when considering cohesive soil, in the case of cohesionless soil the discrepancies are more evident. The simplified model captures nicely the response during the first collision of the deck on the stoppers, but the subsequent motion is not as well captured. However, in the context of a RARE system, which is the main focus of the present paper, structural damage is assessed on the basis of the maximum drift δ r,max . It is shown that the differences in terms of δ r,max are not exceeding 15%, even for very strong seismic excitations. Therefore, overall the extended simplified model is considered to offer a reasonable approximation (excellent for cohesive soil) of the seismic performance of typical overpass motorway bridges in the longitudinal direction.