Formation control for autonomous fixed-wing air vehicles with strict speed constraints

Abstract

We present a formation-control algorithm for autonomous fixed-wing air vehicles. The desired inter-vehicle positions are time-varying, and we assume that at least one vehicle has access to a measurement its position relative to the leader, which can be a physical or virtual member of the formation. Each vehicle is modeled with extended unicycle dynamics that include orientation kinematics on SO(3), speed dynamics, and strict constraints on speed (i.e., ground speed). The analytic result shows that the vehicles converge exponentially to the desired relative positions with each other and the leader. We also show that each vehicle’s speed satisfies the speed constraints. The formation algorithm is demonstrated in software-in-the-loop (SITL) simulations and experiments with fixed-wing air vehicles. To implement the formation-control algorithm, each vehicle has middle-loop controllers to determine roll, pitch, and throttle commands from the outer-loop formation control. We present SITL simulations with 4 fixed-wing air vehicles that demonstrate formation control with different communication structures. Finally, we present formation-control experiments with up to 3 fixed-wing air vehicles.

1 Introduction

The number of applications for small and relatively inexpensive uncrewed air vehicles (UAVs) has increased dramatically for a variety of reasons, including the miniaturization of electronic components and motors; improvements in lithium battery performance, safety, and cost; and the availability of measurements from global navigation satellite systems (GNSS). Autonomous multi-vehicle systems have the potential to complete objectives that would be impossible for a single UAV and to do so with minimal human oversight. Potential applications include distributed sensing, cooperative surveillance, precision agriculture, and search and rescue. As another example, coordinated UAVs could be used in a forest-fire scenario to reduce the time required to conduct large-area surveys for search and rescue. Multiple vehicles can coordinate for tasks such as cooperative lifting, rescue missions, and transportation (Ota, 2006). Coordinated UAVs can also be used to take meteorological measurements (Mayer et al., 2012; Bonin et al., 2013; Wainwright et al., 2015; Bonin et al., 2015; Bailey et al., 2020) that can be used to identify the rotation in the wind field that occurs during severe storm formation. These applications require decentralized methods for coordinating and controlling groups of autonomous UAVs.

Surveys of multi-agent formation-control methods are presented in Ren et al. (2007), Olfati-Saber et al. (2007), Murray (2007), Cao et al. (2013), Oh et al. (2015). Many cooperative and formation control approaches have been developed for agents with double-integrator dynamics (Olfati-Saber, 2006; Ren, 2008; Cao & Ren, 2012; Lee & Singh, 2012; Punzo et al., 2014; Guo et al., 2014; Wellman & Hoagg, 2017; Yang & Fan, 2019; Lippay & Hoagg, 2022). Although double-integrator models can be a reasonable approximation for multi-rotor UAVs, they are not suitable for fixed-wing UAVs or wheeled robots, which are subject to nonholonomic constraints (Panagou et al., 2016; Qu, 2009; Low, 2011).

Fixed-wing UAVs offer a variety of advantages over rotary-wing (e.g., multi-rotor) designs. For example, multi-rotor air vehicles use thrust to provide lift. In contrast, fixed-wing aircraft use thrust to produce forward velocity, which, in turn, produces lift by inducing airflow over the wings. This typically reduces the power required for a UAV of a given mass to stay airborne, which increases flight time and payload capacity. Lower power consumption combined with the ability to glide without propulsive power for relatively long distances and to travel efficiently at high speeds are major contributing factors to the popularity of fixed-wing aircraft in commercial aviation. The primary trade-off is that a fixed-wing UAV must move through the air continuously at some minimum airspeed—below which the UAV does not produce enough lift to counteract gravity.

A variety of models have been used for controller design of fixed-wing UAVs. For example, control design can be performed using traditional aircraft dynamics models (Park et al., 2015; Gu et al., 2006; Singh et al., 2003; Mullen et al., 2016; Cordeiro et al., 2020). However, simplified models can be useful for control system design—particularly formation control design—because they involve fewer model parameters than a standard aerodynamic aircraft model. This paper presents a formation-control algorithm for fixed-wing UAVs modeled with extended unicycle dynamics that include orientation kinematics on $\textrm{SO}(3)$, first-order speed dynamics, and a strict constraint on speed. Similar models for fixed-wing UAVs have been used in the literature (Stipanović et al., 2004; Zhang & Liu, 2013; Darbari et al., 2017; Beard et al., 2014; Panyakeow & Meshahi, 2014; de Marina et al., 2017; Yan et al., 2022; Chen et al., 2021; Wang et al., 2019; Cai et al., 2020; Hu et al., 2019; Chao et al., 2012; Ali et al., 2021; Qiu & Duan, 2014; Wang & Xin, 2013; Zhao et al., 2019; Liang et al., 2020; Yu & Liu, 2016). However, these related models do not include orientation kinematics on $\textrm{SO}(3)$, and many do not consider constraints on speed.

Formation control algorithms for UAVs have been designed using a variety of methods. For example, Cai et al. (2020), Zhang et al. (2020), Chao et al. (2012), Qiu and Duan (2014) use model-predictive control, which can accommodate input and state constraints, but can be computationally expensive. The algorithms in Kahagh et al. (2022); Liao et al. (2017) use artificial potential fields to achieve formation control and mission objectives, whereas Liang et al. (2020); Chen et al. (2021); Yan et al. (2022); Wang and Xin (2013); Singh et al. (2003); Cordeiro et al. (2020); Lee and Lee (2021) use Lyapunov-based control design. Similarly, a variety of interagent communication structures have been explored, including leader-to-every-follower communication (Hu et al., 2019; Wang et al., 2019; Liang et al., 2020); undirected communication (Cordeiro et al., 2020; Cai et al., 2020; Ali et al., 2021; Wang & Xin, 2013; Yan et al., 2022; Zhao et al., 2019); and acyclic communication (Wang et al., 2021; Singh et al., 2003). This paper allows for any communication structure that has a spanning tree with the leader as the center vertex. Finally, we note that experimental demonstrations of formation-control algorithms for fixed-wing UAVs include Beard et al. (2006), Park et al. (2015), de Marina et al. (2017), Darbari et al. (2017), Wang et al. (2019), Liao et al. (2017).

This paper presents several new contributions. First, we present and analyze a new formation-control algorithm for fixed-wing UAVs modeled with extended unicycle dynamics. Although this new algorithm shares some features with the algorithm in Heintz and Hoagg (2020a), the algorithm in this paper has several significant improvements. Notably, the algorithm in this paper allows for a broad class of nonlinear control functions, whereas the previous work only allowed for one specific control function. Similarly, this paper allows for a broad class of barrier functions (used to enforce the speed constraints), whereas the previous work only allowed for one specific barrier function. These generalization can be useful because the control and barrier functions can be selected (i.e., tuned) for the capabilities of a specific UAV. We also note that the present paper allows for each agent to have different control and barrier functions. This generality can be useful for control of heterogeneous formations. In addition, the class of barrier functions used in this paper yield improved performance. For example, if exogenous forces (e.g., wind shear and turbulence) drive a UAV’s speed outside its allowable range, then the barrier function in this paper drives the speed back to the allowable range; the barrier function in the earlier work does not have this property. Another important advantage is that the angular velocity control in this paper can be implemented with only 2 actuators, whereas the control in the previous work generally requires 3 actuators.

A second new contribution of this paper is a systematic method for implementing the formation-control algorithm on fixed-wing UAVs. To implement the algorithm, we use middle-loop roll, pitch, and throttle controllers that are commanded by the output of the outer-loop formation control. This paper presents software-in-the-loop (SITL) simulations that demonstrate the implementation with a formation of 4 UAVs. Finally, this paper includes flight experiments with up to 3 UAVs. In these experiments, each UAV obtains feedback of its position and velocity from its onboard sensors and transmits this feedback to other UAVs over a secure ad-hoc wireless network. Some preliminary flight experiments appeared in Heintz and Hoagg (2020b), but this paper goes significantly beyond that preliminary conference publication by presenting complete stability and performance analyses as well as SITL results. In addition, the formation algorithm in this paper is substantially improved relative to the preliminary conference publication, and the experimental results in this paper are more comprehensive.

2 Notation

Let $I_3$ be the $3 \times 3$ identity matrix, and for $j\in \{1,2,3\}$, let $e_j \in {\mathbb R}^3$ be the jth column of $I_3$. Let $\Vert \cdot \Vert$ be the 2-norm.

The special orthogonal group $\textrm{SO}(3)$ is the set of orthogonal matrices in ${\mathbb R}^{3 \times 3}$ with determinant one. The set of skew symmetric matrices in ${\mathbb R}^{3 \times 3}$ is denoted so(3). If $x \in {\mathbb R}^3$, then define

$$\begin{aligned}{}[ x ]_\times \triangleq \left[ {\begin{matrix}0 &{}&{} -e_3^\textrm{T}x &{}&{} e_2^\textrm{T}x \\ e_3^\textrm{T}x &{}&{} 0 &{}&{} -e_1^\textrm{T}x \\ -e_2 ^\textrm{T}x &{}&{} e_1^\textrm{T}x &{}&{} 0 \end{matrix}} \right] \in \textrm{so}(3). \end{aligned}$$

The number of agents (i.e., UAVs) is denoted by the positive integer n. Define the agent index set ${\mathcal I}\triangleq \{1,2,\dots ,n\}$. Unless otherwise stated, all statements in this paper that involve the subscript i are for all $i \in {\mathcal I}$.

3 Nonmenclature

3.1 UAV model

${\textrm{E}}$:

Inertial frame

$o_{\textrm{E}}$:

Origin of ${\textrm{E}}$

$o_i$:

Location of ith agent (i.e., UAV)

$\mathbf {q_i}$:

Position of $o_i$ relative to $o_{\textrm{E}}$

$\mathbf {p_i} \triangleq ^{\mathrm{E\cdot }}\,\,{{\mathbf {q_i}} }$:

Velocity of $o_i$ relative to $o_\textrm{E}$

$q_i \triangleq \mathbf {q_i} \vert _{\textrm{E}}$:

ith agent position

${\textrm{F}}_i$:

ith agent velocity frame

$R_i$:

Rotation matrix from ${\textrm{F}}_i$ to ${\textrm{E}}$

$s_i$:

Speed of ith agent

$\underline{s}_i \ge 0$:

Minimum allowable speed

${\bar{s}}_i > \underline{s}_i$:

Maximum allowable speed

${\mathcal S}_i \triangleq (\underline{s}_i, {\bar{s}}_i)$:

Set of allowable speeds

$v_i \in {\mathbb R}^3$:

Unit vector such that $\mathbf {p_i} \vert _{\mathrm{F_i}} = s_i v_i$

$f_i$:

Speed dynamics

$g_i$:

Speed dynamics input function

$u_i$:

Speed dynamics control input

$\omega _i$:

Angular velocity control input

$y_i \triangleq R_i v_i$:

Pointing direction

$o_\textrm{g}$:

Location of leader

$\mathbf {q_{\textrm{g}}}$:

Position of $o_{\textrm{g}}$ relative to $o_{\textrm{E}}$

$\mathbf {p_{\textrm{g}}} \triangleq ^{\mathrm{E\cdot }}\,\,{{\mathbf {q_{\textrm{g}}}} }$:

Velocity of $o_{\textrm{g}}$ relative to $o_{\textrm{E}}$

$q_{\textrm{g}} \triangleq \mathbf {q_{\textrm{g}}} \vert _ \textrm{E}$:

Leader position

$\chi _i$:

Desired time-varying position for $o_i$ relative to $o_{\textrm{g}}$ resolved in ${\textrm{E}}$

$\chi _{ij}$:

Desired time-varying position for $o_i$ relative to $o_j$ resolved in ${\textrm{E}}$

${\textrm{F}}_{\textrm{g}}$:

Leader velocity frame

$R_{\textrm{g}}$:

Rotation matrix from ${\textrm{F}}_{\textrm{g}}$ to ${\textrm{E}}$

$\upsilon _i \in {\mathbb R}^3$:

Desired position of $o_i$ relative to $o_{\textrm{g}}$ resolved in ${\textrm{F}}_{\textrm{g}}$

$\kappa _i > 0$:

Parameter in Assumption 1

3.2 Formation control algorithm

$\mu _i$:

Scalar function for control

$\rho _i(x) \triangleq \mu _i(\Vert x\Vert ^2)x$:

Control function

$\bar{\rho }_i \triangleq \sup _{x \in {\mathbb R}^3} \Vert \rho _i(x) \Vert$:

Least upper bound on $\Vert \rho _i\Vert$

$\rho _i^\prime$:

Gradient of $\rho _i$

$\beta _i \ge 0$:

Gain on the ith agent’s position error with leader

$\beta _{ij} \ge 0$:

Gain on the ith agent’s position error with agent j

$\xi _i$:

Formation-error function

$k_i \in (0,\kappa _i/\bar{\rho }_i)$:

Gain used in desired velocity

$p_{\textrm{d,i}} \triangleq \dot{q}_\textrm{g}+ \dot{\chi }_i +k_i \rho _i(\xi _i)$:

Desired velocity

$s_{\textrm{d,i}} \triangleq \Vert p_{\textrm{d,i}}\Vert$:

Desired speed

$\varepsilon _i \triangleq \kappa _i - k_i \bar{\rho }_i > 0$:

Parameter for ${\mathcal S}_{\textrm{d,i}}$

${\mathcal S}_{\textrm{d,i}} \triangleq (\underline{s}_i + \varepsilon _i, {\bar{s}}_i - \varepsilon _i )$:

Set of allowable desired speeds

$y_{\textrm{d,i}} \triangleq p_{\textrm{d,i}} / s_{\textrm{d,i}}$:

Desired pointing direction

$h_i$:

Speed barrier function

$h_i^\prime$:

Gradient of $h_i$

$a_i,b_i > 0$:

Gains for $u_i$ control law

$c_i > 0$:

Gain for $\omega _i$ control law

3.3 Stability analysis

${\tilde{q}}_i \triangleq q_\textrm{g}- \chi _i$:

Position error

${\tilde{s}}_i \triangleq s_i - s_{\textrm{d,i}}$:

Speed error

${\tilde{y}}_i \triangleq y_i - y_{\textrm{d,i}}$:

Pointing direction error

3.4 Implementation

$\psi _i, \theta _i, \phi _i$:

Yaw, pitch, roll Euler angles

$\psi _\textrm{g}, \theta _\textrm{g}, \phi _\textrm{g}$:

Yaw, pitch, roll Euler angles of the leader

$\theta _{\textrm{d,i}}$:

Pitch angle command

$\phi _{\textrm{d,i}}$:

Roll angle command

$T_{i}$:

Throttle command

$\sigma _i$:

Heading angle

$\gamma _i$:

Flight-path angle

$\sigma _{\textrm{d,i}}$:

Desired heading angle

$\gamma _{\textrm{d,i}}$:

Desired flight-path angle

$k_{\gamma _i,\textrm{p}}, k_{\gamma _i,\textrm{i}}, k_{\gamma _i,\textrm{d}} > 0$:

PID gains for pitch control

$k_{\sigma _i,\textrm{p}}, k_{\sigma _i,\textrm{i}}, k_{\sigma _i,\textrm{d}} > 0$:

PID gains for roll control

$g = 9.81~\textrm{m}/\textrm{s}^2$:

Acceleration due to gravity

$s_{\textrm{a,i}}$:

Airspeed

$\eta _{0}>0$:

Trim-throttle parameter

$\eta _{\phi }>0$:

Trim-roll parameter

$s_{\mathrm{a_0}}>0$:

Trim-airspeed parameter

$\eta _{s}>0$:

Gain for throttle control

$k_{s_i,\textrm{p}}, k_{s_i,\textrm{i}} >0$:

PI gains for throttle control

$\sigma _{\textrm{g}}$:

Leader heading angle

$\gamma _{\textrm{g}}$:

Leader flight-path angle

$\omega _\textrm{g}$:

Angular velocity of $\textrm{F}_\textrm{g}$ relative to $\textrm{E}$ resolved in $\textrm{F}_\textrm{g}$

4 UAV model and formation control objectives

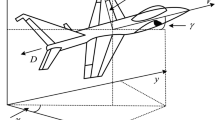
Let $\textrm{E}$ be an inertial frame, that is, a frame in which Newton’s second law is valid. The origin of $\textrm{E}$ is $o_{\textrm{E}}$, which is any convenient point on the Earth’s surface. Let $o_i$ be the location of the ith agent (e.g., the location of the ith vehicle’s center of mass). The position of $o_i$ relative to $o_{\textrm{E}}$ is $\mathbf {q_i}$, and the ith agent’s position $\mathbf {q _i}$ is resolved in $\textrm{E}$ as $q_i \triangleq \mathbf {q_i} \vert _{\textrm{E}}$. The velocity of $o_i$ relative to $o_{\textrm{E}}$ with respect to $\textrm{E}$ is $\mathbf {p_i} \triangleq ^{\textrm{E}\cdot }\,\,{{\mathbf {q_i}} }$.

Let $\textrm{F}_i$ be a frame such that $\mathbf {p_i}$ resolved in $\textrm{F}_i$ is $\mathbf {p_i} \vert _{\mathrm{F_i}} = s_i v_i$, where $v_i \in {\mathbb R}^3$ is a constant unit vector, and for all $t\ge 0$, $s_i(t) \ge 0$ is the speed of the ith agent. For all $t \ge 0$, the speed of the ith agent is subject to the constraint that $s_i(t) \in {\mathcal S}_i \triangleq (\underline{s}_i, {\bar{s}}_i)$, where $0 \le \underline{s}_i < {\bar{s}}_i$.

Let $R_i:[0,\infty ) \rightarrow \text{ SO }(3)$ be the rotation matrix from $\textrm{F}_i$ to $\textrm{E}$. Thus, the ith agent’s velocity $\mathbf {p_i}$ resolved in $\textrm{E}$ is $\mathbf {p_i} \vert _{\textrm{E}} = s_i R_i v_i$, which implies that

$$\begin{aligned} \dot{q}_i (t) = s_i (t) R_i(t) v_i, \end{aligned}$$

(1)

where $q_i(t) \in {\mathbb R}^3$, $s_i(t) \in {\mathcal S}_i$, and $R_i^\textrm{T}(t) \in \textrm{SO}(3)$ are the position, speed, and orientation of the ith agent, and $q_i(0) \in {\mathbb R}^3$ is the initial condition.

The speed of the ith agent satisfies

$$\begin{aligned} \dot{s}_i(t) = f_i(t) +g_i(t)u_i(t), \end{aligned}$$

(2)

where $u_i:[0,\infty )\rightarrow {\mathbb R}$ is the control input, $s_i(0) \in {\mathcal S}_i$ is the initial condition, and $f_i: [0,\infty ) \rightarrow {\mathbb R}$ and $g_i:[0,\infty ) \rightarrow {\mathbb R}\backslash \{0 \}$ are continuous.

The orientation kinematics of the ith agent are

$$\begin{aligned} \dot{R}_i(t) = R_i(t) [\omega _i(t)]_\times , \end{aligned}$$

(3)

where $R_i(0) \in \textrm{SO}(3)$ is the initial condition, and the control input $\omega _i:[0,\infty ) \rightarrow {\mathbb R}^3$ is the angular velocity of $\textrm{F}_i$ relative to $\textrm{E}$ resolved in $\textrm{F}_i$.

The vehicle model (1)–(3) is an extended unicycle model that includes both speed dynamics (2) and orientation kinematics (3) on SO(3). Note that the unit vector in the direction of the velocity $\dot{q}_i$ is given by

$$\begin{aligned} y_i(t) \triangleq R_i(t) v_i. \end{aligned}$$

(4)

Next, let $o_\textrm{g}$ be the location of the leader, which can be a physical agent (e.g., vehicle) or a virtual agent. The position of $o_\textrm{g}$ relative to $o_\textrm{E}$ is $\mathbf {q_\textrm{g}}$, and the velocity of $o_\textrm{g}$ relative to $o_\textrm{E}$ with respect to $\textrm{E}$ is $\mathbf {p_\textrm{g}} \triangleq ^{\mathrm{E\cdot }}\,\,{{\mathbf {q_\textrm{g}}}}$. The leader’s position $\mathbf {q_\textrm{g}}$ is resolved in $\textrm{E}$ as $q_\textrm{g}\triangleq \mathbf {q_\textrm{g}} \vert _\textrm{E}$, which is assumed to be twice continuously differentiable.

Let $\chi _i:[0,\infty )\rightarrow {\mathbb R}^3$ be the time-varying desired position of $o_i$ relative to $o_\textrm{g}$ resolved in $\textrm{E}$. Thus, $\chi _{ij} \triangleq \chi _i - \chi _j$ is the time-varying desired position of $o_i$ relative to $o_j$ resolved in $\textrm{E}$. The objective is to design controls $u_i$ and $\omega _i$ such that:

• (O1) For all $i \in {\mathcal I}$, $\lim _{t \rightarrow \infty } [q_i(t)-q_\textrm{g}(t) - \chi _i(t)] = 0$.

• (O2) For all $i \in {\mathcal I}$, $\lim _{t \rightarrow \infty } [\dot{q}_i(t) - \dot{q}_\textrm{g}(t) - \dot{\chi }_i(t)]=0$.

• (O3) For all $i \in {\mathcal I}$ and for all $t \ge 0$, $s_i(t) \in {\mathcal S}_i$.

Objective (O1) states that each agent approaches its desired relative position with the leader, and (O2) states that each agent approaches its desired relative velocity with the leader. Objective (O3) states that the agents’ speed constraints are satisfied. Although the formation control problem is described in 3 dimensions, the methods in this paper can be specialized to the planar case (i.e., 2 dimensions).

One specialization of the time-varying formation control problem described by (O1)–(O3) is the situation where the desired position of $o_i$ relative to $o_\textrm{g}$ is constant in a leader-fixed frame (e.g., a frame that rotates with the leader). For example, let $\textrm{F}_\textrm{g}$ be a frame that is fixed to $o_\textrm{g}$ and rotates such that one of its orthogonal unit vectors is aligned with the leader’s velocity vector $\mathbf {p_\textrm{g}}$. In this case, we can consider the time-varying desired positions $\chi _i(t) = R_\textrm{g}(t) \upsilon _i$, where $R_\textrm{g}:[0,\infty ) \rightarrow \text{ SO }(3)$ is the rotation matrix from $\textrm{F}_\textrm{g}$ to $\textrm{E}$, and $\upsilon _i \in {\mathbb R}^3$ is the desired position of $o_i$ relative to $o_\textrm{g}$ resolved in $\textrm{F}_\textrm{g}$. Thus, the desired relative positions are constant in the leader-fixed frame $\textrm{F}_\textrm{g}$. In this case, (O1) and (O2) imply that the formation translates with the leader’s position and rotates with the leader’s velocity vector.

Next, we note that it is not possible to satisfy the formation objectives (O1) and (O2) and the speed constraint (O3) for an arbitrary leader trajectory $q_\textrm{g}$ and time-varying desired formation $\chi _i$. Specifically, if (O2) is satisfied, then the ith agent’s velocity $\dot{q}_i$ converges to $\dot{q}_\textrm{g}+ \dot{\chi }_i$. Thus, (O2) implies that we want the ith agent’s speed $s_i(t)$ to equal $\Vert \dot{q}_\textrm{g}(t) + \dot{\chi }_i(t) \Vert$. However, (O3) requires that $s_i(t) \in {\mathcal S}_i$. Thus, if $s_i(t)$ equals $\Vert \dot{q}_\textrm{g}(t) + \dot{\chi }_i(t) \Vert$ and satisfies $s_i(t) \in {\mathcal S}_i$, then the leader trajectory must satisfy $\Vert \dot{q}_\textrm{g}(t) + \dot{\chi }_i(t) \Vert \in {\mathcal S}_i$. Therefore, we make the following assumption.

Assumption 1

There exists $\kappa _i > 0$ such that for all $t \ge 0$, $\Vert \dot{q}_\textrm{g}(t) + \dot{\chi }_i(t) \Vert \in (\underline{s}_i+\kappa _i, {\bar{s}}_i-\kappa _i)$.

Assumption 1 implies that for all $t \ge 0$, $\Vert \dot{q}_\textrm{g}(t) + \dot{\chi }_i(t) \Vert$ is contained in a proper subset of ${\mathcal S}_i$. As $\kappa _i$ approaches zero, Assumption 1 approaches the condition $\Vert \dot{q}_\textrm{g}(t) + \dot{\chi }_i(t) \Vert \in {\mathcal S}_i$, which is necessary to satisfy $\dot{q}_i(t)$ equals $\dot{q}_\textrm{g}(t) + \dot{\chi }_i(t)$ and $\Vert \dot{q}_i(t) \Vert \in {\mathcal S}_i$.

5 Formation control algorithm

Let $\mu _i: [0,\infty ) \rightarrow (0,\infty )$ be continuously differentiable and satisfy the following conditions:

• (C1) $M_i(z) \triangleq \int _0^z \mu _i(w) \, \textrm{d}w$ is radially unbounded.

• (C2) $\sup _{z \ge 0} \sqrt{z} \mu _i(z)$ exists.

Consider the control function $\rho _i: {\mathbb R}^3 \rightarrow {\mathbb R}^3$ defined by

$$\begin{aligned} \rho _i(x) \triangleq \mu _i \left( \Vert x\Vert ^2 \right) x, \end{aligned}$$

(5)

and note that it follows from (5) and (C2) that

$$\begin{aligned} {\bar{\rho }}_i \triangleq \sup _{x \in {\mathbb R}^3} \Vert \rho _i(x) \Vert = \sup _{z \ge 0} \sqrt{z} \mu _i(z) \end{aligned}$$

exists. The control function $\rho _i$ is used to design a desired velocity for each UAV. The formation method in Heintz and Hoagg (2020a) also uses a nonlinear control function to design a desired velocity. However, Heintz and Hoagg (2020a) considers only one specific control function. In contrast, this work allows for a broad class of functions $\rho _i$ based on the choice of $\mu _i$, which need only satisfy (C1) and (C2). It is also worth noting that, unlike Heintz and Hoagg (2020a), this work allows for each agent to have a different control function (i.e., $\rho _i \ne \rho _j$ for $i\ne j$). This generality can be useful for control of heterogeneous formations. The following examples of $\mu _i$ satisfy (C1) and (C2).

Example 1

Let

$$\begin{aligned} \mu _i(z) = (\nu _1 + \nu _2 z )^{-m}, \end{aligned}$$

where $\nu _1,\nu _2 >0$ and $m \in [0.5,1]$. If $\nu _1 \gg \nu _2$, then (5) implies that for all x such that $\Vert x \Vert \ll \nu _1 / \nu _2$, $\rho _i(x) \approx \nu _1^{-m} x$, which implies that $\rho _i$ is approximately linear. In contrast, if $\nu _2 \gg \nu _1$, then (5) implies that for all x such that $\Vert x \Vert \gg \nu _1 / \nu _2$, $\rho _i(x) \approx (\nu _2 \Vert x \Vert ^2)^{-m} x$, which has approximately constant magnitude for $m=0.5$. $\triangle$

Example 2

Let

$$\begin{aligned} \mu _i(z) = {\left\{ \begin{array}{ll} 1, &{} z \in [0,0.5),\\ \begin{array}{l} 1 + \nu _1 (z-0.5)^2 \\ \qquad + \nu _2(z-0.5)^3, \end{array}&{} z \in [0.5,1.5], \\ 1/\sqrt{z}, &{} z \in (1.5,\infty ), \end{array}\right. } \end{aligned}$$

where $\nu _1 = \frac{10\sqrt{6}}{9}-3$ and $\nu _2 = 2-\frac{7\sqrt{6}}{9}$. For all x such that $\Vert x \Vert \in [0,0.5)$, $\rho _i(x) = x$, which is linear. For all x such that $\Vert x \Vert \in [1.5,\infty )$, $\rho _i(x) = x/\Vert x\Vert$, which has constant magnitude. Finally, note that $\mu _i$ is monotonically decreasing on $[0.5,\infty )$. $\triangle$

Example 3

Let

$$\begin{aligned} \mu _i(z) = {\left\{ \begin{array}{ll} 1, &{} z \in [0,0.1),\\ \begin{array}{l} 1 + \nu _1 (z-0.1)^2 \\ \qquad + \nu _2(z-0.1)^3, \end{array} &{} z \in [0.1,0.4], \\ 1/\sqrt{z}, &{} z \in (0.4,\infty ), \end{array}\right. } \end{aligned}$$

where $\nu _1 = \frac{75 \sqrt{10}}{4} - \frac{100}{3}$ and $\nu _2 = \frac{2000}{27}-\frac{2375 \sqrt{10}}{54}$. Similar to Example 2, $\rho _i(x)$ is linear if $\Vert x \Vert$ is small, and $\rho _i(x)$ has constant magnitude if $\Vert x \Vert$ is large. However, $\mu _i$ is monotonically increasing on [0.1, 0.4] and then monotonically deceasing on $[0.4,\infty )$. $\triangle$

Figure 1 shows $\mu _i$ and $\Vert \rho _i \Vert$, where $\mu _i$ is given by Example 1 ($\nu _1 = \nu _2 = 1$, $m = 0.5$), Example 2, and Example 3. For all 3 examples, $\bar{\rho }_i = 1$. Notice that Example 1 and Example 2 are such that for all $z \ge 0$, $\mu _i(z) \le 1$, which implies that $\Vert \rho _i(x) \Vert \le \Vert x\Vert$. In contrast, Example 3 is such that for all $z \in (0.1,1)$, $\mu _i(z) > 1$, which implies that $\Vert \rho _i(x) \Vert > \Vert x\Vert$ over a subset of the domain.

Fig. 1

Examples of $\mu _i$ and the corresponding $\Vert \rho _i \Vert$. Example 1 is shown with with $\nu _1=1$, $\nu _2=1$, and $m=0.5$

Define the formation-error function

$$\begin{aligned} \xi _i \triangleq \beta _i (q_\textrm{g}- q_i + \chi _i) + \sum _{j \in {\mathcal I}\backslash \{ i\}} \beta _{ij} (q_j-q_i+ \chi _{ij}), \end{aligned}$$

(6)

where $\beta _i \ge 0$ is the gain on the ith agent’s position error with the leader, and $\beta _{ij} \ge 0$ is the gain on the ith agent’s position error with agent j. Note that $\xi _i$ is a linear combination of the ith agent’s position error with the leader and the other agents.

To explain the required interagent communication structure, define

$$\begin{aligned} A \triangleq {{\,\textrm{diag}\,}}(\beta _1, \dots , \beta _n) \in {\mathbb R}^{n\times n}, \end{aligned}$$

and let $B \in {\mathbb R}^{n \times n}$ be such that the (i, j)th element is $B_{(i,j)} = -\beta _{ij}$, and the (i, i)th element is $B_{(i,i)} = \sum _{j \in {\mathcal I}\backslash \{i\} } \beta _{ij}$. The matrix B is the weighted Laplacian of the directed graph ${\mathcal G}= ({\mathcal I},{\mathcal E})$, where the edge set is defined as ${\mathcal E}\triangleq \{ (i,j) \in {\mathcal I}\times {\mathcal I}:\beta _{ij} > 0 \}$. The algorithm in this paper requires that the gains $\beta _i \ge 0$ and $\beta _{ij} \ge 0$ are such that $A+B$ is nonsingular. A sufficient condition for nonsingularity of $A+B$ is given by (Zhang & Lewis, 2012, Lemma 1). Specifically, $A+B$ is nonsingular if the directed graph ${\mathcal G}= ({\mathcal I},{\mathcal E})$ has a vertex $l \in {\mathcal I}$ such that $\beta _l >0$ and there is a walk from l to every other vertex. Thus, this paper requires that only one agent has access to a measurement of its position relative to the leader.

Let $k_i \in (0,\kappa _i/{\bar{\rho }}_i)$ be a gain used to determine the ith agent’s desired velocity, which is defined by

$$\begin{aligned} p_{\textrm{d,i}} \triangleq \dot{q}_\textrm{g}+ \dot{\chi }_i +k_i \rho _i(\xi _i). \end{aligned}$$

(7)

In addition, define the ith agent’s desired speed

$$\begin{aligned} s_{\textrm{d,i}} \triangleq \Vert p_{\textrm{d,i}}\Vert . \end{aligned}$$

(8)

Since $\bar{\rho }_i = \sup _{x \in {\mathbb R}^3} \Vert \rho _i(x) \Vert$ exists, it follows that all terms in (7) are bounded. Thus, the desired speed $s_{\textrm{d,i}}$ is bounded. Next, define

$$\begin{aligned} \varepsilon _i \triangleq \kappa _i - k_i \bar{\rho }_i > 0, \qquad {\mathcal S}_{\textrm{d,i}} \triangleq (\underline{s}_i + \varepsilon _i, {\bar{s}}_i - \varepsilon _i ). \end{aligned}$$

The following result shows that the desired speed is not only bounded, but also is such that for all $t \ge 0$, $s_{\textrm{d,i}}(t)$ is in ${\mathcal S}_{\textrm{d,i}}$, which is a proper subset of the set of allowable speeds ${\mathcal S}_i$. This fact is obtained from applying the triangle inequality to (7) and (8) and using Assumption 1.

Fact 1

For all $t \ge 0$, $s_{\textrm{d,i}}(t) \in {\mathcal S}_{\textrm{d,i}} \subset {\mathcal S}_i$.

Next, define the desired pointing direction

$$\begin{aligned} y_{\textrm{d,i}} \triangleq \frac{1}{s_{\textrm{d,i}}} p_{\textrm{d,i}}, \end{aligned}$$

(9)

and note that it follows from Fact 1 that for all $t \ge 0$, $s_{\textrm{d,i}}(t) > 0$, which implies that $y_{\textrm{d,i}}$ is well defined.

To enforce the speed constraint (O3), we consider a speed barrier function $h_i: [0,\infty ) \rightarrow {\mathbb R}$, which is continuously differentiable. The gradient of $h_i$ is $h_i^\prime : [0,\infty ) \rightarrow {\mathbb R}$ defined by

$$\begin{aligned} h_i^\prime (s) \triangleq \frac{\textrm{d}h_i(s)}{\textrm{d}s}. \end{aligned}$$

We assume that $h_i$ satisfies the following conditions:

• (B1) For all $s\in {\mathcal S}_i$, $h_i(s) > 0$.

• (B2) For all $s \in (-\infty ,\underline{s}_i) \cup ({\bar{s}}_i,\infty )$, $h_i(s) < 0$.

• (B3) For all $s \ge {\bar{s}}_i$, $h_i^\prime (s) < 0$.

• (B4) For all $s \le \underline{s}_i$, $h_i^\prime (s) > 0$.

• (B5) For all $(s,s_{\textrm{d}}) \in {\mathcal S}_i \times {\mathcal S}_{\textrm{d,i}}$, $h_i(s)+(s_{\textrm{d}}-s) h_i^\prime (s) > 0$.

Note that (B1) and (B2) imply that $h_i$ is positive inside ${\mathcal S}_i$, equal to zero at the upper limit ${\bar{s}}_i$ and lower limit $\underline{s}_i$, and negative elsewhere. In addition, (B3) and (B4) imply that $h_i$ is strictly decreasing above the upper limit ${\bar{s}}_i$ and strictly increasing below the lower limit $\underline{s}_i$. Finally, (B5) is a technical condition needed to ensure the the formation control is well defined. The next result provides sufficient conditions to ensure that (B3)-(B5) are satisfied.

Fact 2

Assume that (B1) and (B2) are satisfied, and assume that $h_i^\prime$ is continuously differentiable and strictly decreasing. Then, (B3)-(B5) are satisfied.

Proof

Since $h_i^\prime$ is continuous, it follows from (B1) and (B2) that $h_i^\prime ({\bar{s}}_i) <0$. Since, in addition, $h_i^\prime$ is strictly decreasing, it follows that for all $s \ge {\bar{s}}_i$, $h_i^\prime (s) < 0$, which confirms (B3).

Similarly, since $h_i^\prime$ is continuous, it follows from (B1) and (B2) that $h_i^\prime (\underline{s}_i) >0$. Since, in addition, $h_i^\prime$ is strictly decreasing, it follows that for all $s \le \underline{s}_i$, $h_i^\prime (s) > 0$, which confirms (B4).

To prove (B5), let $i\in {\mathcal I}$ and let $s_\textrm{d}\in {\mathcal S}_{\textrm{d,i}}$. Define

$$\begin{aligned} H(s) \triangleq h_i(s) + (s_{\textrm{d}} - s) h_i^\prime (s), \end{aligned}$$

and note that (B3) and (B4) imply that $H({\bar{s}}_i) = (s_{\textrm{d}} - {\bar{s}}_i) h_i^\prime ({\bar{s}}_i) > 0$ and $H(\underline{s}_i) = (s_{\textrm{d}} - \underline{s}_i) h_i^\prime (\underline{s}_i) > 0$. Next, define

$$\begin{aligned} H^\prime (s) \triangleq \frac{\textrm{d}H(s)}{\textrm{d}s} = (s_\textrm{d}- s) \frac{\textrm{d}h_i^\prime (s)}{\textrm{d}s}. \end{aligned}$$

Assume for contradiction that there exists $z_1 \in {\mathcal S}_i$ such that $H(z_1) \le 0$. Since, in addition, $H({\bar{s}}_i) > 0$ and $H(\underline{s}_i) > 0$, it follows that there exists $z_2 \in {\mathcal S}_i$ such that $H^\prime (z_2) = 0$ and $H(z_2) \le 0$. Since $h_i^\prime$ is continuously differentiable and strictly decreasing, it follows that $\left. \frac{\textrm{d}h_i^\prime (s)}{\textrm{d}s} \right| _{s=z_2}<0$. Since, in addition, $H^\prime (z_2) = 0$, it follows the definition of $H^\prime$ that $z_2=s_\textrm{d}$. Thus, $H(z_2) = h_i(s_\textrm{d})$, and since $s_\textrm{d}\in {\mathcal S}_{\textrm{d,i}} \subset {\mathcal S}_i$, it follows from (B1) that $H(z_2)>0$, which is a contradiction. $\square$

The formation method in Heintz and Hoagg (2020a) also uses a barrier function to enforce speed constraints. However, Heintz and Hoagg (2020a) considers only one specific barrier function. In contrast, this work allows for a broad class of barrier functions $h_i$, which need only satisfy (B1)-(B5). The barrier-function method in this paper has several other advantages over the previous work. First, the barrier function in this paper is significantly simpler than that in the previous work; notably, $h_i$ is a function of only speed $s_i$, whereas the method in Heintz and Hoagg (2020a) uses a function of $s_i$ and $s_{\textrm{d,i}}$. Second, the method in Heintz and Hoagg (2020a) can result in comparatively slow response when the speed $s_i$ is near the boundary of ${\mathcal S}_i$. In contrast, the barrier function in this paper can be selected to yield fast response near the boundary of ${\mathcal S}_i$. We also note that this work allows for each agent to have a different barrier function, which can be useful for heterogeneous formations in which the capabilities of each vehicle dictates the allowable aggressiveness each vehicle’s barrier function. Finally, if at some time $\tau \ge 0$, the speed $s_i(\tau )$ is outside ${\mathcal S}_i$, then the barrier function in Heintz and Hoagg (2020a) does not drive the speed $s_i$ into ${\mathcal S}_i$. In contrast, the analysis in the following section demonstrates that the generalized-and-improved barrier function in this paper does drive $s_i$ into ${\mathcal S}_i$. This property is of practical significance because disturbances (e.g., wind) could force the speed outside of ${\mathcal S}_i$. The following 3 examples of $h_i$ satisfy (B1)–(B5).

Example 4

Let $\nu >0$, and let $h_i(s) = \nu ({\bar{s}}_i - s)(s- \underline{s}_i)$. $\triangle$

Example 5

Let $\nu >0$, and let $h_i(s) = \tanh \big (\nu ({\bar{s}}_i - s)(s- \underline{s}_i) \big )$. $\triangle$

Example 6

Let $\nu \in (0,({\bar{s}}_i - \underline{s}_i)/2)$, and let

$$\begin{aligned}h_i(s) = {\left\{ \begin{array}{ll} 1 -\frac{(\underline{s}_i +\nu -s_i)^2}{\nu ^2}, &{} s<\underline{s}_i +\nu , \\ 1, &{} s \in [\underline{s}_i +\nu , {\bar{s}}_i-\nu ], \\ 1 -\frac{(s +\nu - {\bar{s}}_i )^2}{\nu ^2}, &{} s>{\bar{s}}_i -\nu . \end{array}\right. } \end{aligned}$$

Note that for all $s \in [\underline{s}_i +\nu , {\bar{s}}_i-\nu ]$, $h_i(s)=1$. $\triangle$

Figure 2 shows $h_i$ and $h_i^\prime$, where $h_i$ is given by Examples 4–6. Example 4 is similar to the barrier function in Heintz and Hoagg (2020a) (but simpler that than in the previous work because it does not depend on $s_{\textrm{d,i}}$). In Example 4, $h_i$ is quadratic, and $h_i^\prime$ is linear. In this case, if s is near the boundary of ${\mathcal S}_i$, then $\vert h_i(s) \vert< < 1$, and the control $u_i$ (presented below) is small in magnitude and results in slow responses. In contrast, the barrier functions in Examples 5 and 6 have comparatively steep slope near the boundary of ${\mathcal S}_i$. Thus, $\vert h_i(s) \vert$ is small over a comparatively smaller region near the boundary of ${\mathcal S}_i$. This results in faster responses when the speed is near the boundary of ${\mathcal S}_i$.

Fig. 2

Barrier function $h_i$ and its gradient $h_i^\prime$ for Examples 4–6 with $\nu = 1/50$, $\nu = 1/20$, and $\nu =1$, respectively. Note that $\underline{s}_i = 10$ and ${\bar{s}}_i = 30$

Next, the time derivatives of $p_{\textrm{d,i}}$, $s_{\textrm{d,i}}$, $y_{\textrm{d,i}}$ are given by

$$\begin{aligned} \dot{p}_{\textrm{d,i}}&\triangleq \ddot{q}_\textrm{g}+ \ddot{\chi }_i -k_i \rho _i^\prime (\xi _i) \Big ( \beta _i (\dot{q}_i - \dot{q}_\textrm{g}- \dot{\chi }_i) \nonumber \\&\qquad + \sum _{j \in {\mathcal I}\backslash \{ i\}} \beta _{ij} (\dot{q}_i- \dot{q}_j- \dot{\chi }_{ij} ) \Big ), \end{aligned}$$

(10)

$$\begin{aligned} \dot{s}_{\textrm{d,i}}&\triangleq \frac{1}{s_{\textrm{d,i}}} p_{\textrm{d,i}}^\textrm{T}\dot{p}_{\textrm{d,i}}, \end{aligned}$$

(11)

$$\begin{aligned} \dot{y}_{\textrm{d,i}}&\triangleq \frac{\dot{p}_{\textrm{d,i}}-\dot{s}_{\textrm{d,i}} y_{\textrm{d,i}}}{s_{\textrm{d,i}}}, \end{aligned}$$

(12)

where the gradient of $\rho _i$ is $\rho _i^\prime : {\mathbb R}^3 \rightarrow {\mathbb R}^{3 \times 3}$ defined by

$$\begin{aligned} \rho _i^\prime (x)&\triangleq \frac{\partial \rho _i(x)}{\partial x} = \mu _i(\Vert x\Vert ^2) I_3 \nonumber \\&\qquad + 2 \left( \frac{\textrm{d}\mu _i(z)}{\textrm{d}z}\Bigl \vert _{z=\Vert x\Vert ^2} \right) x x^\textrm{T}. \end{aligned}$$

(13)

Finally, consider the formation control laws

$$\begin{aligned} u_i = {\left\{ \begin{array}{ll} \begin{array}{l} \frac{1}{g_i} \Bigg ( \frac{b_i (s_{\textrm{d,i}}-s_i)^3}{h_i(s_i)+(s_{\textrm{d,i}}-s_i) h_i^\prime (s_i)} - f_i \\ \,\, + \frac{ \dot{s}_{\textrm{d,i}} h_i(s_i) + a_i (s_{\textrm{d,i}}-s_i) h_i(s_i)}{h_i(s_i)+(s_{\textrm{d,i}}-s_i) h_i^\prime (s_i)} \Bigg ) \end{array}, &{} \text{ if } s_i \in {\mathcal S}_i, \\ \dfrac{1}{g_i} \Bigg ( \dfrac{b_i (s_{\textrm{d,i}}-s_i)^2}{h_i^\prime (s_i)} - f_i \Bigg ), &{} \text{ if } s_i \not \in {\mathcal S}_i, \end{array}\right. } \end{aligned}$$

(14)

and

$$\begin{aligned} \omega _i&= R_i^\textrm{T}[ y_i ]_\times \Big ( c_i y_{\textrm{d,i}}- y_i^\textrm{T}\dot{y}_{\textrm{d,i}} y_{\textrm{d,i}} + y_i^\textrm{T}y_{\textrm{d,i}}\dot{y}_{\textrm{d,i}} \Big ), \end{aligned}$$

(15)

where $a_i, b_i, c_i > 0$ are control gains.

Note that (14) is continuous, which can be confirmed by evaluating both expressions in (14) at the boundary of ${\mathcal S}_i$. In addition, (B3)-(B5) imply that the denominators in (14) are nonzero.

One important advantage of the formation control presented in this paper relative to that in Heintz and Hoagg (2020a) is that (15) can typically be implemented with one fewer actuator. The approach in Heintz and Hoagg (2020a) generally requires 3 actuators to implement the angular velocity command $\omega _i$. In other words, $\omega _i$ evolves in ${\mathbb R}^3$ rather than a lower dimensional subspace of ${\mathbb R}^3$. In contrast, the angular velocity command (15) evolves in a 2-dimensional subspace, specifically, for all $t \ge 0$, $v_i^\textrm{T}\omega _i(t) = 0$. For example, if $v_i = e_1$, then $\omega _i$ is in the span of $e_2$ and $e_3$, that is, $e_1^\textrm{T}\omega _i = 0$. In particular, $\omega _i$ evolves in the plane that is perpendicular to the direction of flight (i.e., $\mathbf {p_i}$). Thus, $\omega _i$ can be generated by a pair of $\textrm{F}_i$-fixed actuators that generate angular velocities in the plane perpendicular to $\mathbf {p_i}$.

The control (5)–(15) involves $\mu _i$ and $h_i$ as well as the parameters $a_i,b_i,c_i > 0$, $k_i \in (0,\kappa _i / \bar{\rho }_i)$, and $\beta _i,\beta _{ij} \ge 0$.

Increasing the speed gains $a_i$ and $b_i$ tends to cause the speed $s_i$ to converge more quickly to the desired speed $s_{\textrm{d,i}}$. Similarly, increasing the attitude gain $c_i$ tends to cause the pointing direction $y_i$ to converge more quickly to the desired pointing direction $y_{\textrm{d,i}}$. However, increasing $a_i$, $b_i$, and $c_i$ also tends to increase the magnitude of the controls $u_i$ and $\omega _i$. In practice, it may be useful to allow for time-varying speed and attitude gains. We note that the analysis in the next section can be generalized to allow for time-varying gains $a_i,b_i,c_i:[0,\infty ) \rightarrow {\mathcal D}$, where ${\mathcal D}\subset {\mathbb R}$ is bounded. For clarity of the presentation, we focus on the case where $a_i,b_i,c_i > 0$ are constant but emphasize that this is not required.

Next, note that selecting $k_i$ close to the upper limit $\kappa _i / \bar{\rho }_i$ tends to make the desired velocity (7) more responsive to the formation term $\rho (\xi _i)$, which, in turn, tends to make the agents converge more quickly to the desired interagent positions. The upper limit $\kappa _i / \bar{\rho }_i$ on $k_i$ is imposed to guarantee that the desired speed $s_{\textrm{d,i}}$ is in the admissible range ${\mathcal S}_{\textrm{d,i}}$. The upper limit on $k_i$ is determined by the choice of $\mu _i$, the leader’s velocity $\dot{q}_\textrm{g}$, and the rate of change of the formation $\dot{\chi }_i$.

The formation gains $\beta _i$ and $\beta _{ij}$ determine how sensitive $p_{\textrm{d,i}}$ is to errors in the ith agent’s position relative to the leader and the ith agent’s position relative to the jth agent, respectively.

Finally, we note that the control (5)–(15) relies on the leader’s acceleration $\ddot{q}_\textrm{g}$ to calculate the desired acceleration $\dot{p}_{\textrm{d,i}}$. For many practical applications, $\ddot{q}_\textrm{g}$ is relatively small. In this case, simulations and experiments indicate that the control algorithm can be effectively implemented with $\ddot{q}_\textrm{g}=0$. Nevertheless, the experimental flight results reported in this paper compute the control (5)–(15) using an estimate of $\ddot{q}_\textrm{g}$ obtained from a process described in Sect. 10.

6 Stability analysis

In this section, we analyze the closed-loop dynamics (1)–(15). Define the position error, speed error, and pointing direction error

$$\begin{aligned} {\tilde{q}}_i&\triangleq q_i - q_\textrm{g}- \chi _i, \end{aligned}$$

(16)

$$\begin{aligned} {\tilde{s}}_i&\triangleq s_i - s_{\textrm{d,i}}, \end{aligned}$$

(17)

$$\begin{aligned} {\tilde{y}}_i&\triangleq y_i - y_{\textrm{d,i}}, \end{aligned}$$

(18)

and define

$$\begin{aligned} {\mathcal R}_i \triangleq \Big \{ R \in \textrm{SO}(3) :y_{\textrm{d,i}}^\textrm{T}(0) R v_i \ne -1 \Big \}, \end{aligned}$$

which is the set of all orientations except those where the angle from $R v_i$ to $p_{\textrm{d,i}}(0)$ is exactly $\pi$ rad.

The next theorem is the main theoretical result of this paper. The result shows that for almost all initial conditions $( q_i(0),s_i(0), R_i(0) ) \in {\mathbb R}^3 \times {\mathcal S}_i \times \textrm{SO}(3)$, the error state $({\tilde{q}}_i, {\tilde{s}}_i,{\tilde{y}}_i)$ converges to zero exponentially and (O1)–(O3) are satisfied. In fact, the error state converges to zero for all initial conditions except those where the angle from $\dot{q}_i(0)$ to $p_{\textrm{d,i}}(0)$ is exactly $\pi$ rad. The proof of the following theorem is in Appendix A.

Theorem 1

Assume that $A+B$ is positive definite. Then, the following statements hold:

• i) $\big ( {\tilde{q}}_1(t),\ldots , {\tilde{q}}_n(t), {\tilde{s}}_1(t),\ldots ,{\tilde{s}}_n(t),{\tilde{y}}_1(t), \ldots , {\tilde{y}}_n(t) \big ) \equiv 0$ is a Lyapunov stable equilibrium of (1)–(15).

• ii) For all initial conditions $\big (q_i(0), s_i(0), R_i(0) \big ) \in {\mathbb R}^3 \times [0,\infty ) \times {\mathcal R}_i$, ${\tilde{q}}_i$, ${\tilde{s}}_i$, and ${\tilde{y}}_i$ converge to zero exponentially.

• iii) For all initial conditions $\big (q_i(0), s_i(0), R_i(0) \big ) \in {\mathbb R}^3 \times [0,\infty ) \times {\mathcal R}_i$, (O1) and (O2) are satisfied.

• iv) If $s_i(0) \in {\mathcal S}_i$, then (O3) is satisfied.

• v) If $s_i(0) \not \in {\mathcal S}_i$, then there exists $T > 0$ such that for all $t\in [0,T]$, $s_i(t) \not \in {\mathcal S}_i$ and for all $t>T$, $s_i(t) \in {\mathcal S}_i$.

7 Hardware platform

This section describes the experimental fixed-wing UAV platform used in the experiments presented in this paper. The UAVs are Skywalker X8 flying wing foam airframes (see Fig. 3), which consist of 2 wings attached to a fuselage section and reinforced with carbon fiber wing spars. These UAVs are launched with a bungee-based catapult-assist system (see Fig. 4) and skid landed. We note that the formation control implementation presented in the next section can be used with a wide range of fixed-wing aircraft. The UAV is equipped with a Pixhawk flight controller with the ArduPilot firmware, which provides inner-loop control, waypoint navigation, state estimation, and interfaces with a global positioning system (GPS) receiver. An on-board Raspberry Pi obtains state estimates from the Pixhawk, communicates with other UAVs using WiFi, and executes the formation control (5)–(15). A propeller and brushless motor are mounted to the aft end of the fuselage. The motor is controlled by an electronic speed controller (ESC), which is mounted inside the fuselage and receives power from the battery through the Pixhawk power module. The ESC is connected to the Pixhawk using a standard 3-pin servo connector.

Fig. 3

Skywalker X8 airframe

Fig. 4

UAV during catapult-assisted launch

The Pixhawk uses an extended Kalman filter to estimate the UAV’s position, velocity, and attitude using measurements from a 9-DoF inertial measurement unit (IMU), barometer, GPS, and airspeed sensor. These estimates are transmitted to the onboard Raspberry Pi through a universal serial bus connection. These estimates are also used for inner-loop control and waypoint-based navigation. Figure 5 shows the electronics mounted in the fuselage. The UAV is also equipped with a scientific payload for collecting meteorological measurement, which is described in Witte et al. (2017), Bailey et al. (2020) but was not active during the experiments in this article.

Fig. 5

Top view of inside the UAV fuselage showing control electronics

Let $\psi _i$, $\theta _i$, $\phi _i$ denote the yaw, pitch, and roll of the ith UAV using a 3-2-1 Euler sequence. Similarly, let $\psi _\textrm{g}$, $\theta _\textrm{g}$, $\phi _\textrm{g}$ denote the yaw, pitch, and roll of the leader UAV using a 3-2-1 Euler sequence. These attitude measurements are obtained from the onboard IMUs.

To implement the formation control (5)–(15), the Pixhawk on each UAV is set to fly-by-wire-A mode. In this mode, the Pixhawk accepts a commanded pitch angle $\theta _{\textrm{d,i}}$, commanded roll angle $\phi _{\textrm{d,i}}$, and commanded throttle $T_i$. If flown by a human pilot, then the Pixhawk receives these commands from the RC transmitter operated by the pilot. For this autonomous formation-control implementation, the onboard Raspberry Pi provides these commands to the Pixhawk using the MAVLink messaging protocol.

At startup, a secure ad-hoc WiFi network is created, allowing communication between the UAVs. The Raspberry Pi generates MAVLink commands using the DroneKit Python application programming interface and stores the state estimates and associated timestamps in Python class instances, which are broadcast over the ad-hoc WiFi network using the user datagram protocol at approximately 10 Hz.

Fig. 6

Multi-loop implementation of the formation control (5)–(15)

The Python implementation has 4 processes: (1) broadcast UAV state information to the network (i.e., to the other UAVs); (2) receive information from the other UAVs on the network; (3) log information about all agents; and (4) check failsafe conditions, execute the control, and manage the startup and shutdown of the other processes. Communication between processes is achieved using Python thread-safe queues.

8 Formation control implementation

This section presents a multi-loop implementation of the formation-control algorithm (5)–(15) for the fixed-wing UAVs described in Sect. 7. The key aspects of the implementation include: middle-loop controllers, computing the time-varying formation (i.e., $\chi _i$, $\dot{\chi }_i$, $\ddot{\chi }_i$), and accounting for asynchronous feedback. The frame $\hbox {F}_i$ is selected such that $v_i = e_1 = [ 1 \quad 0 \quad 0 ]^\textrm{T}$.

8.1 Middle-loop controllers

The control inputs for the UAV described in Sect. 7 are $\theta _{\textrm{d,i}}$, $\phi _{\textrm{d,i}}$, and $T_i$. In contrast, the formation algorithm (5)–(15) provides controls $u_i$ and $\omega _i$. Thus, we implement middle-loop controllers such that closed-loop UAV dynamics approximate the dynamics (1)–(3). These middle-loop controllers map $u_i$ and $\omega _i$ determined from the formation control (5)–(15) to $\theta _{\textrm{d,i}}$, $\phi _{\textrm{d,i}}$, and $T_i$, which are the control inputs for the UAV. This multi-loop implementation is shown in Fig. 6.

Define the heading angle and flight-path angle

$$\begin{aligned} \sigma _i\triangleq & {} {{\,\textrm{atan2}\,}}(e_2^\textrm{T}\dot{q}_i, e_1 ^\textrm{T}\dot{q}_i) ={{\,\textrm{atan2}\,}}(e_2^\textrm{T}y_i, e_1^\textrm{T}y_i ),\\ \gamma _i\triangleq & {} -\arcsin e_3^\textrm{T}\dot{q}_i / s_i = -\arcsin e_3^\textrm{T}y_i. \end{aligned}$$

Similarly, define the desired heading angle and desired flight-path angle

$$\begin{aligned} \sigma _{\textrm{d,i}}\triangleq & {} {{\,\textrm{atan2}\,}}(e_2^\textrm{T}y_{\textrm{d,i}}, e_1^\textrm{T}y_{\textrm{d,i}} ),\\ \gamma _{\textrm{d,i}}\triangleq & {} \arcsin {-e_3^\textrm{T}y_{\textrm{d,i}}}. \end{aligned}$$

We now present middle-loop controllers that determine $\theta _{\textrm{d,i}}$, $\phi _{\textrm{d,i}}$, and $T_i$. The pitch command $\theta _{\textrm{d,i}}$ is given by

$$\begin{aligned} \theta _{\textrm{d,i}}(t) = \gamma _{\textrm{d,i}}&- k_{\gamma _i,\textrm{p}} \big ( \gamma _{i}(t) - \gamma _{\textrm{d,i}}(t) \big ) \nonumber \\&- k_{\gamma _i,\textrm{i}} \int _0^t \gamma _{i}(\tau ) - \gamma _{\textrm{d,i}}(\tau ) \, \textrm{d}\tau \nonumber \\&- k_{\gamma _i,\textrm{d}} \big (\dot{\gamma }_i(t) -\dot{\gamma }_{\textrm{d,i}}(t) \big ), \end{aligned}$$

(19)

where $k_{\gamma _i,\textrm{p}}, k_{\gamma _i,\textrm{i}}, k_{\gamma _i,\textrm{d}} > 0$ are the proportional, integral, and derivative (PID) gains. The desired-flight-path-angle rate is approximated as $\dot{\gamma }_{\textrm{d,i}} \approx e^\textrm{T}_2 \omega _i$, which follows from the 3-2-1 Euler angle kinematics where the final Euler rotation is small.

The roll command $\phi _{\textrm{d,i}}$ is given by

$$\begin{aligned} \phi _{\textrm{d,i}}(t)&= \arctan \frac{\dot{\sigma }_{\textrm{d,i}}(t) s_i(t) \cos \gamma _i(t) }{g} \nonumber \\&\qquad - k_{\sigma _i,\textrm{p}} \big ( \sigma _i(t) - \sigma _{\textrm{d,i}}(t) \big ) \nonumber \\&\qquad - k_{\sigma _i,\textrm{i}} \int _0^t \sigma _i(\tau ) - \sigma _{\textrm{d,i}}(\tau ) \, \textrm{d}\tau \nonumber \\&\qquad - k_{\sigma _i,\textrm{d}} \big ( \dot{\sigma }_i(t) - \dot{\sigma }_{\textrm{d,i}}(t) \big ), \end{aligned}$$

(20)

where where $k_{\sigma _i,\textrm{p}}, k_{\sigma _i,\textrm{i}}, k_{\sigma _i,\textrm{d}} > 0$ are the PID gains, and $g = 9.81~\textrm{m}/\textrm{s}^2$ is the acceleration due to gravity. The first term in (20) is the roll angle that yields the desired heading rate $\dot{\sigma }_{\textrm{d,i}}$ with speed $s_i$ under the assumption of a coordinated turn (Beard et al., 2014). The desired-heading-angle rate is approximated as $\dot{\sigma }_{\textrm{d,i}} \approx e^\textrm{T}_3 \omega _i/ \cos \gamma _i$, which follows from the 3-2-1 Euler angle kinematics where the final Euler rotation is small.

The throttle command $T_i$ is given by

$$\begin{aligned} T_i&= \eta _{0} +\eta _{\phi } \big ( (\cos \phi _{i}(t) )^{-2} - 1 \big )\nonumber \\&\qquad +\eta _{s} \big ( u_i(t) + s_{\textrm{a,i}}(t) - s_i(t) - s_{\mathrm{a_0}} \big ) \nonumber \\&\qquad - k_{s_i,\textrm{p}} \big ( s_{\textrm{a,i}}(t) - u_i(t) \big ) \nonumber \\&\qquad - k_{s_i,\textrm{i}} \int _0^t s_{\textrm{a,i}}(\tau ) - u_i(\tau ) \, \textrm{d}\tau , \end{aligned}$$

(21)

where $s_{\textrm{a,i}}(t) \in {\mathbb R}$ is the measured airspeed; $\eta _{0}>0$ is the autopilot’s trim-throttle parameter; $\eta _{\phi }>0$ is the autopilot’s trim-roll parameter; $s_{\mathrm{a_0}}>0$ is the autopilot’s trim-airspeed parameter; $\eta _{s}>0$ is a feedback gain; and $k_{s_i,\textrm{p}}, k_{s_i,\textrm{i}} >0$ are PI gains. The second term in (21) is an estimate of the throttle required to counteract increased drag in a turn.

The commands $\theta _{\textrm{d,i}}$, $\phi _{\textrm{d,i}}$, and $T_i$ are computed using (19)–(21). Then, each command is saturated if it lies outside of the autopilot’s acceptable ranges, which, for the Pixhawk, are $[-\pi /9,\pi /9]$ rad for $\theta _{\textrm{d,i}}$, $[-5\pi /18,5\pi /18]$ rad for $\phi _{\textrm{d,i}}$, and [0, 100] for $T_i$. In addition, we implement a standard anti-windup approach to prevent the integral terms in (19)–(21) from increasing in magnitude if the associated command signal is saturated.

8.2 Computing $\chi _i$, $\dot{\chi }_i$, and $\ddot{\chi }_i$

For all simulations and experiments in this paper, we use the leader-frame specialization of this algorithm described in Sect. 4. Specifically, we consider the time-varying desired positions $\chi _i(t) = R_\textrm{g}(t) \upsilon _i$, where $R_\textrm{g}:[0,\infty ) \rightarrow \text{ SO }(3)$ is the rotation matrix from $\textrm{F}_\textrm{g}$ to $\textrm{E}$, and $\upsilon _i \in {\mathbb R}^3$ is the desired position of $o_i$ relative to $o_\textrm{g}$ resolved in $\textrm{F}_\textrm{g}$. Thus, the desired relative positions are constant in the leader-fixed frame $\textrm{F}_\textrm{g}$.

Define the leader’s heading angle and flight-path angle

$$\begin{aligned} \sigma _\textrm{g}= & {} {{\,\textrm{atan2}\,}}(e_2^\textrm{T}\dot{q}_\textrm{g},e_1^\textrm{T}\dot{q}_\textrm{g}), \end{aligned}$$

(22)

$$\begin{aligned} \gamma _\textrm{g}= & {} -\arcsin e_3^\textrm{T}\dot{q}_\textrm{g}/ \Vert \dot{q}_\textrm{g}\Vert , \end{aligned}$$

(23)

and the associated rotation matrix

$$\begin{aligned} R_\textrm{g}\triangleq \left[ \begin{array}{ccc} \cos \gamma _\textrm{g}\cos \sigma _\textrm{g}&{} -\sin {\sigma _\textrm{g}} &{}\sin {\gamma _\textrm{g}} \cos {\sigma _\textrm{g}} \\ \cos {\gamma _\textrm{g}} \sin {\sigma _\textrm{g}} &{} \cos {\sigma _\textrm{g}} &{}\sin {\gamma _\textrm{g}} \sin {\sigma _\textrm{g}} \\ -\sin {\gamma _\textrm{g}} &{} 0 &{} \cos {\gamma _\textrm{g}} \end{array} \right] . \end{aligned}$$

(24)

Next, note that $R_\textrm{g}$ satisfies

$$\begin{aligned} \dot{R}_\textrm{g}= R_\textrm{g}[ \omega _\textrm{g}]_\times , \end{aligned}$$

(25)

where it follows from the 3-2-1 Euler angle kinematics that

$$\begin{aligned} \omega _\textrm{g}= \left[ \begin{array}{c} -\dot{\sigma }_\textrm{g}\sin \gamma _\textrm{g}\\ \dot{\gamma }_\textrm{g}\\ \dot{\sigma }_\textrm{g}\cos \gamma _\textrm{g}\end{array} \right] . \end{aligned}$$

(26)

The time-varying desired positions are given by

$$\begin{aligned} \chi _i(t) = R_\textrm{g}(t) \upsilon _i, \end{aligned}$$

(27)

and it follows from (25) and (27) that

$$\begin{aligned} \dot{\chi }_i(t) = R_\textrm{g}(t) [ \omega _\textrm{g}(t) ]_\times \upsilon _i, \end{aligned}$$

(28)

$$\begin{aligned} \ddot{\chi }_i(t) = \Big ( R_\textrm{g}(t) [ \omega _\textrm{g}(t) ]_\times ^2 + R_\textrm{g}(t) [ \dot{\omega }_\textrm{g}(t) ]_\times \Big ) \upsilon _i. \end{aligned}$$

(29)

Since the leader’s sensor package (i.e., GPS, IMU, and airspeed sensor) provides a measurement of $\dot{q}_\textrm{g}$, we compute $R_\textrm{g}$ directly from (22)–(24). Then, $\chi _i$ is computed from (27). In order to compute $\dot{\chi }_i$ and $\ddot{\chi }_i$ from (28) and (29), we require an estimate of $\omega _\textrm{g}$ and $\dot{\omega }_\textrm{g}$, which are not directly measured. However, the leader’s IMU provides measurements of the yaw rate $\dot{\psi }_\textrm{g}$, pitch rate $\dot{\theta }_\textrm{g}$, and roll rate $\dot{\phi }_\textrm{g}$. Thus, we estimate $\omega _\textrm{g}$ using (26) with $\dot{\sigma }_\textrm{g}= \dot{\psi }_\textrm{g}$ and $\dot{\gamma }_\textrm{g}= \dot{\theta }_\textrm{g}$. Then, we compute $\dot{\chi }_i$ and $\ddot{\chi }_i$ from (28) and (29) using this estimate of $\omega _\textrm{g}$ and the assumption that $\dot{\omega }_\textrm{g}$ is negligible. Note that we performed software-in-the-loop (SITL) simulations and preliminary flight experiments both neglecting $\dot{\omega }_\textrm{g}$ and using a numerical approximation of $\dot{\omega }_\textrm{g}$. The SITL simulations and flight experiments perform better by neglecting $\dot{\omega }_\textrm{g}$.

8.3 State measurement correction

Due to the software architecture imposed by DroneKit and ArduPlane, the state feedback measurements on each UAV are not synchronized with sampling of the control loop. Furthermore, the control loops of the agents are not synchronized with one another. To mitigate this, the timestamp of each measurement is recorded alongside the measurement. Before a measurement is used, it is corrected using first-order Euler integration.

Each agent corrects its own state measurement before broadcasting it, and each receiving agent corrects that measurement again using the time at which the message was received and the time at which its control loop is sampled. Network latency is not accounted for in this method.

9 Software-in-the-loop simulation results

This section presents results of software-in-the-loop (SITL) simulations using the formation control (5)–(15) with the multi-loop implementation described in Sect. 8. For these simulations, one instance of the Python implementation is executed for each UAV, and each instance communicates with a corresponding instance of the Arduplane firmware running in SITL mode. These firmware instances also simulate the dynamics of an aircraft based on a commercial off-the-shelf remote-controlled aircraft (specifically, the Rascal110). Formation control instances communicate with one another over the local network. All software runs on a single Ubuntu machine. In this way, the control algorithms and implementation are tested with a high-fidelity UAV model.

For all simulations, $n=3$ UAVs. The speed dynamics are (2), where $f_i = -0.64 s_i$ and $g_i =0.64$, which implies that the speed dynamics are low pass with unity gain at DC, where the time constant 0.64 is estimated from the closed-loop step response of the UAV with the middle-loop speed control. The speed bounds are $\underline{s}_i= 16$ m/s and ${\bar{s}}_i= 30$ m/s, and the barrier function is given by Example 5 with $\nu = 1/20$. The scalar control function $\mu _i$ is given by Example 1 with $\nu _1 = 50$, $\nu _2 =1$, and $m=0.5$. Let $k_i=3$, $a_i=1$, $b_i=0.1$ and $c_i=0.1$. The desired relative positions are $\upsilon _1 = [-5 \quad 5 \quad 0 ] ^\textrm{T}$ m, $\upsilon _2 = [ -5 \quad -5 \quad -4 ]^\textrm{T}$ m, and $\upsilon _3 = [ -5 \quad -5 \quad 4 ]^\textrm{T}$ m. The formation and middle-loop controls are implemented at 25 Hz.

Fig. 7

Simulation 1: Trajectories of leader and agents in the horizontal plane with time as the vertical axis

Fig. 8

Simulation 1: Agent position relative to the leader $q_i-q_\textrm{g}$ and $\Vert {\tilde{q}}_i\Vert$. The desired relative position $\chi _i$ is shown with a dashed line

In all simulations, a leader UAV flies rectangular trajectories and circular trajectories. First, the leader flies a sequence of 4 waypoints arranged in a rectangle. Next, the leader flies a sequence of 4 waypoints arranged in a rectangle, where the northeast and southwest waypoints are 50 m above the others. Each of these sequences are repeated twice. Finally, the leader executes a circular trajectory with radius 120 m and changes altitude several times. Note that Assumption 1 is satisfied for all agents with $\kappa _i = 3.6$ m/s.

To describe the communication structure used in the SITL simulations, define the neighbor set

$$\begin{aligned} {\mathcal N}_i \triangleq \{ j \in {\mathcal I}:\beta _{ij} > 0 \}. \end{aligned}$$

We examine 3 different communication structures: (1) an undirected line (${\mathcal N}_1 = \{ 2\}$, ${\mathcal N}_2 = \{1,3\}$, ${\mathcal N}_3 = \{2\}$) where only agent 1 has feedback of the leader; (2) a directed line (${\mathcal N}_1 = \emptyset$, ${\mathcal N}_2 = \{1\}$, ${\mathcal N}_3 = \{2\}$) where only agent 1 has feedback of the leader; and (3) a directed line (${\mathcal N}_1 = \emptyset$, ${\mathcal N}_2 = \{1\}$, ${\mathcal N}_3 = \{2\}$) where all agents have feedback of the leader. We now present results from each SITL simulation—one for each communication structure.

Simulation 1

Let ${\mathcal N}_1 = \{ 2\}$, ${\mathcal N}_2 = \{1,3\}$, ${\mathcal N}_3 = \{2\}$, $\beta _1=1$, and $\beta _2 = \beta _3=0$, which implies that only agent 1 has position feedback of the leader. For all $i\in \{1,2,3\}$ and all $j \in {\mathcal N}_i$, let $\beta _{ij}= 1$. Figure 7 shows the UAV trajectories in the horizontal plane, where the vertical axis is time. Figure 8 shows each agent’s position relative to the leader as well as the desired relative position $\chi _i$ in each direction. The figure also shows $\Vert {\tilde{q}}_i\Vert$ versus time. Figure 9 shows the actual and desired speed, flight-path angle, and heading angle of each agent. $\triangle$

Fig. 9

Simulation 1: Actual (solid) and desired (dashed) speed $s_i$, flight-path angle $\gamma _i$, and heading $\sigma _i$. The upper and lower speed bounds are indicated by thin black lines

Fig. 10

Simulation 2: Agent position relative to the leader $q_i-q_\textrm{g}$ and $\Vert {\tilde{q}}_i\Vert$. The desired relative position $\chi _i$ is shown with a dashed line

Fig. 11

Simulation 2: Actual (solid) and desired (dashed) speed $s_i$, flight-path angle $\gamma _i$, and heading $\sigma _i$. The upper and lower speed bounds are indicated by thin black lines

Fig. 12

Simulation 3: Agent position relative to the leader $q_i-q_\textrm{g}$ and $\Vert {\tilde{q}}_i\Vert$. The desired relative position $\chi _i$ is shown with a dashed line

Fig. 13

Simulation 3: Actual (solid) and desired (dashed) speed $s_i$, flight-path angle $\gamma _i$, and heading $\sigma _i$. The upper and lower speed bounds are indicated by thin black lines

Table 1 RMS of $\Vert {\tilde{q}}_i \Vert$ in m, mean RMS of $\Vert {\tilde{q}}_i \Vert$ in m, and mean RMS of the percent error

Simulation 2

This simulation is the same as Simulation 1 except that ${\mathcal N}_1 = \emptyset$, ${\mathcal N}_2 = \{1\}$, ${\mathcal N}_3 = \{2\}$, which implies that the interagent communication is a directed (rather than undirected) line. Simulation Figs. 10 and 11 provide plots similar to those described in Simulation 1. $\triangle$

Simulation 3

This simulation is the same as Simulation 2 except that $\beta _1=\beta _2 = \beta _3=1$, which implies that all agents have position feedback of the leader. Figures 12 and 13 provide plots similar to those described in Simulation 1. $\triangle$

To evaluate performance, we use the root mean square (RMS) of the position error ${\tilde{q}}_i$ for the rectangular and circular portions of the trajectory, which are given by

$$\begin{aligned} {\mathcal P}_{\textrm{r},i}&\triangleq \sqrt{\frac{1}{t_{\mathrm{r,\textrm{f}}}-t_{\textrm{r,0}}} \int _{t_{\textrm{r,0}}}^{t_{\mathrm{r,\textrm{f}}}} \Vert {\tilde{q}}_i(t)\Vert ^2 \, \textrm{d}t }, \end{aligned}$$

(30)

$$\begin{aligned} {\mathcal P}_{\textrm{c},i}&\triangleq \sqrt{\frac{1}{t_{\mathrm{c,\textrm{f}}}-t_{\textrm{c,0}}}\int _{t_{\textrm{c,0}}}^{t_{\mathrm{c,\textrm{f}}}} \Vert {\tilde{q}}_i(t)\Vert ^2 \, \textrm{d}t }, \end{aligned}$$

(31)

where $[t_{\textrm{r,0}},t_{\mathrm{r,\textrm{f}}}]$ and $[t_{\textrm{c,0}},t_{\mathrm{c,\textrm{f}}}]$ correspond to the intervals of the rectangular and circular portions, respectively. For all simulations, $t_{\textrm{r,0}} = 95~\textrm{s}$, $t_{\mathrm{r,\textrm{f}}} = 550~\textrm{s}$, $t_{\textrm{c,0}} = 650~\textrm{s}$, and $t_{\mathrm{c,\textrm{f}}} = 1080~\textrm{s}$. The RMS position errors for each UAV and the RMS position errors averaged over the n UAVs are in Table 1 for each SITL simulation. This table also provides the mean RMS of the percent error, that is, the RMS of $\Vert {\tilde{q}}_i\Vert / \Vert \chi _i \Vert$ averaged over the n UAVs.

In Simulations 1 and 2, UAV 1’s RMS position error is smaller than that of UAV 2, which is smaller than that of UAV 3 as shown in Table 1. UAV 1’s RMS position error is smallest because it has direct feedback of the leader’s position, whereas the other UAVs do not. Furthermore, UAV 2’s RMS position error is smaller than that of UAV 3 because UAV 2 is a walk of length one (in the graph ${\mathcal G}$) from UAV 1, which has access to the leader’s position, whereas UAV 3 is a walk of length 2 from UAV 1. The directed communication (Simulation 2) results in smaller RMS position errors than the undirected communication (Simulation 1). This observation is most likely a result of UAV 1 and UAV 2 using feedback from fewer UAVs for the directed case. Notably, UAV 1 only uses feedback from the leader and UAV 2 only uses feedback from UAV 1. The RMS position error is smallest for Simulation 3 because each UAV has direct feedback of the leader’s position. These simulations suggest that it is desirable for each UAV to be closely connected (i.e., a short walk in the graph ${\mathcal G}$) to a UAV that has a measurement of the leader’s position.

10 Experimental results

This section describes the results of flight experiments using the formation control (5)–(15) with the multi-loop implementation described in Sect. 8. These experiments were conducted at the Lexington Model Airplane Club in Lexington, Kentucky, USA. Each UAV is launched from a bungee launcher and uses the Pixhawk’s built-in automatic takeoff functionality. After all UAVs have been launched, each UAV (except the leader) is switched to fly-by-wire-A mode and formation-control is engaged using a switch on the radio-control transmitter for the corresponding UAV.

The speed dynamics are (2), where $f_i = -0.4 s_i$ and $g_i =0.4$, which implies that the speed dynamics are low pass with unity gain at DC, where the time constant 0.4 is estimated from the closed-loop step response of the UAV with the middle-loop speed control. The barrier function is implemented as $h_i=1$, which implies that the barrier function does not enforce speed bounds. However, the desired speed $s_{\textrm{d,i}}$ is saturated if it lies outside the interval [18, 30] m/s. To avoid stall, the commanded airspeed $u_i + s_{\textrm{a,i}} - s_i$ is saturated if it lies outside the interval [18, 30] m/s. The scalar control function $\mu _i$ is given by Example 1 with $\nu _1 = 2.5\times 10^5$, $\nu _2 = 1$, and $m=0.5$. Let $a_i = 1$, $b_i = 0$, and $c_i(t) = 0.0003 s_{\textrm{d,i}}^2(t)$. In these experiments, the gains $\beta _i$ and $\beta _{ij}$ are implemented as diagonal matrices rather than scalars. This generalization to (6) allows for different gains to be used in each inertial direction. In these experiments, the gain in the vertical direction is less than that in the horizontal plane in order to limit oscillations in $\gamma _i$ while yielding small position errors in the horizontal plane. The values for $\beta _i$ and $\beta _{ij}$ are provided in each experiment. The formation and middle-loop controls are implemented at 10 Hz.

The leader’s acceleration $\ddot{q}_\textrm{g}$ is estimated by assuming that $q_\textrm{g}$ satisfies (1)–(3) with the subscripts i replaced by $\textrm{g}$, and where $v_\textrm{g}= e_1$ and $s_\textrm{g}\triangleq \Vert \dot{q}_\textrm{g}\Vert$. Thus, differentiating (1) yields $\ddot{q}_\textrm{g}= s_\textrm{g}\dot{R}_\textrm{g}e_1 + \dot{s}_\textrm{g}R_\textrm{g}e_1$. We estimate $\dot{s}_\textrm{g}$ using numerical differentiation with a low-pass filter. We compute $\dot{R}_\textrm{g}$ using (25), where $\omega _\textrm{g}$ is computed from (26) using estimates of $\dot{\gamma }_\textrm{g}$ and $\dot{\sigma }_\textrm{g}$. Specifically, $\dot{\gamma }_\textrm{g}$ is estimated using numerical differentiation with a low-pass filter, and $\dot{\sigma }_\textrm{g}$ is estimated as $\dot{\sigma }_\textrm{g}\approx \tfrac{g \tan \phi _\textrm{g}}{ s_\textrm{g}\cos \theta _\textrm{g}}$, which is the relationship for a coordinated turn (Beard et al., 2014).

Experiment 1

During this experiment, the wind was approximately 4 m/s from the northwest, and the ambient temperature was approximately 20$^\textrm{o}$ C. This experiment has a leader UAV and $n=1$ additional UAV. The desired relative position is $\upsilon _1 = [ -10 \quad -10 \quad 20 ]^\textrm{T}$ m, and $\beta _i = {{\,\textrm{diag}\,}}(150,150,45)$. First, the leader UAV flies in a circle with a 120 m radius for approximately 260 s. Next, the leader UAV flies a rectangular flight path based on several waypoints. Figure 14 shows the UAV trajectories in the horizontal plane, where the vertical axis is time. By $t = 20$ s, the UAV has achieved the desired formation relative to the leader and stays in formation for the remainder of the experiment. Figure 15 shows the first circle in the trajectory from an overhead view, and Fig. 16 shows the transition from circles to rectangles from an overhead view. Figure 17 shows the agent’s position relative to the leader as well as the desired relative position $\chi _i$ in each direction. Figure 18 shows the actual and desired speed, flight-path angle, and heading angles of the agent. For this experiment, the RMS errors are ${\mathcal P}_{\textrm{c,1}} = 7.7$ m, and ${\mathcal P}_{\textrm{r,1}} = 8.2$ m, where $t_{\textrm{c,0}} = 40~\textrm{s}$ $t_{\mathrm{c,\textrm{f}}}=250~\textrm{s}$, $t_{\textrm{r,0}}=270~\textrm{s}$, and $t_{\textrm{r,f}} = 960~\textrm{s}$. $\triangle$

Fig. 14

Experiment 1: Trajectories of leader and agent in the horizontal plane with time as the vertical axis. The axes $e_1^\textrm{T}q_i$ and $e_2^\textrm{T}q_i$ are the position of the ith aircraft to the north and east of a fixed GPS reference location, which is the origin of the inertial frame $\textrm{E}$

Fig. 15

Experiment 1: Abbreviated trajectories of the leader and agent in the horizontal plane. The leader follows a circular trajectory and the agent converges to the desired relative position. The axes $e_1^\textrm{T}q_i$ and $e_2^\textrm{T}q_i$ are the position of the ith aircraft to the north and east of a fixed GPS reference location

Fig. 16

Experiment 1: Abbreviated trajectories of the leader and agent in the horizontal plane as the leader transitions from the circular to rectangular trajectory. The agent remains in formation. The axes $e_1^\textrm{T}q_i$ and $e_2^\textrm{T}q_i$ are the position of the ith aircraft to the north and east of a fixed GPS reference location

Fig. 17

Experiment 1: Agent position relative to the leader $q_1-q_\textrm{g}$ and $\Vert {\tilde{q}}_1\Vert$. The desired relative position $\chi _i$ is shown with a dashed line

Fig. 18

Experiment 1: Actual (solid) and desired (dashed) speed $s_i$, flight-path angle $\gamma _i$, and heading $\sigma _i$

Fig. 19

Experiment 2: Trajectories of leader and agents in the horizontal plane with time as the vertical axis. The axes $e_1^\textrm{T}q_i$ and $e_2^\textrm{T}q_i$ are the position of the ith aircraft to the north and east of a fixed GPS reference location

Experiment 2

During this experiment, the wind was approximately 2 m/s from the southwest, and the ambient temperature was approximately 32$^\textrm{o}$ C. This experiment has a leader UAV and $n=2$ additional UAVs. The desired relative positions are $\upsilon _1 = [ -10 \quad 10 \quad 20 ]^\textrm{T}$ m and $\upsilon _2 = [ -10 \quad -10 \quad -20 ]^\textrm{T}$ m, and $\beta _1 = \beta _2 = {{\,\textrm{diag}\,}}(105,105,31.5)$ and $\beta _{12} = \beta _{21} = {{\,\textrm{diag}\,}}(50,50,15)$. The leader UAV flies a rectangular flight path based on several waypoints. Figure 19 shows the UAV trajectories in the horizontal plane, where the vertical axis is time. By $t = 40$ s, the UAVs have achieved the desired formation and stay in formation for the remainder of the experiment. Figure 20 shows the first rectangle in the trajectory from an overhead view. Figure 21 shows each agent’s position relative to the leader as well as the desired relative position $\chi _i$ in each direction. Figure 22 shows the actual and desired speed, flight-path angle, and heading angles of each agent. For this experiment, the RMS errors are ${\mathcal P}_{\textrm{r,1}} = 8.6$ m, and ${\mathcal P}_{\textrm{r,2}} = 8.8$ m, where $t_{\textrm{r,0}}=45~\textrm{s}$ and $t_{\textrm{r,f}} = 680~\textrm{s}$. $\triangle$

Fig. 20

Experiment 2: Abbreviated trajectories of the leader and agents in the horizontal plane. The leader follows a rectangular trajectory and the agents converge to the desired relative positions. The axes $e_1^\textrm{T}q_i$ and $e_2^\textrm{T}q_i$ are the position of the ith aircraft to the north and east of a fixed GPS reference location

Experiment 3

During this experiment, the wind was approximately 2 m/s from the southwest, and the ambient temperature was approximately 32$^\textrm{o}$ C. This experiment has a leader UAV and $n=2$ additional UAVs. This experiment is similar to Experiment 2, but the formation control is only used to control the UAV formation in the horizontal plane (i.e., in 2 dimensions). In this case, the roll command $\phi _{\textrm{d,i}}$ and throttle command $T_i$ are determined from the middle-loop controls (20) and (21). However, the pitch command $\theta _{\textrm{d,i}}$ is determined from a PID control designed to have $e_3^\textrm{T}q_i$ track a constant altitude command. These commands are $-80$ m and $-120$ m for UAV 1 and UAV 2, respectively. Note that the inertial frame is north-east-down, which implies that negative values in the $e_3$ direction correspond to positive altitude. For the formation control in the horizontal plane, the desired relative positions are $\upsilon _1 = [ -10 \quad -10 ]^\textrm{T}$ m and $\upsilon _2 = [ -10 \quad 10 ]^\textrm{T}$ m, and $\beta _1 = \beta _2 = 105$ and $\beta _{12} = \beta _{21} =50$. Note that the desired relative positions and gains in the horizontal plan are the same as those in Experiment 2. The leader UAV flies a rectangular flight path based on several waypoints. Figure 23 shows the UAV trajectories in the horizontal plane, where the vertical axis is time. By $t = 40$ s, the UAVs have achieved the desired formation and stay in formation for the remainder of the experiment. Figure 24 shows each agent’s position relative to the leader and $\chi _i$ in each direction in the horizontal plane. This figure also show the agent’s altitude and the desired altitude. Figure 25 shows the actual and desired speed, flight-path angle, and heading angles of each agent. For this experiment, the RMS errors are ${\mathcal P}_{\textrm{r,1}} = 6.7$ m, and ${\mathcal P}_{\textrm{r,2}} = 8.1$ m, where $t_{\textrm{r,0}}=45~\textrm{s}$ and $t_{\textrm{r,f}} = 570~\textrm{s}$ Note that ${\mathcal P}_{\textrm{r,i}}$ is computed based on the position error in all 3 directions; thus, the results can be compared with those of Experiments 1 and 2. $\triangle$

Fig. 21

Experiment 2: Agent position relative to the leader $q_i-q_\textrm{g}$ and $\Vert {\tilde{q}}_i\Vert$. The desired relative position $\chi _i$ is shown with a dashed line

Fig. 22

Experiment 2: Actual (solid) and desired (dashed) speed $s_i$, flight-path angle $\gamma _i$, and heading $\sigma _i$

The RMS position errors for each UAV and the RMS position errors averaged over the n UAVs are in Table 2 for each experiment. The RMS position errors for Experiments 1 and 2 are similar, which demonstrates that adding the additional UAV does not substantially degrade the performance. The RMS position errors in Experiment 3 is improved relative to Experiment 2, which demonstrates that using formation control only in the horizontal plane (i.e., 2 dimensions) and a separate altitude control can improve performance.

Table 2 also provides the mean RMS of the percent error, that is, the RMS of $\Vert {\tilde{q}}_i\Vert / \Vert \chi _i \Vert$ averaged over the n UAVs. Since Experiment 3 uses formation control only in the horizontal plane and there is no desired relative position $\chi _i$ in the vertical direction, it is not possible to compute a mean RMS of the percent error that is commensurable to those in the other experiments and the SITL simulations. Thus, this metric is not reported in Table 2 for Experiment 3.

The mean RMS of the position errors for the experiments are approximately 6 times larger than those for the rectangular position of the SITL simulation with the comparable communication structure (i.e., Simulation 3). We attribute this to several factors. First, the desired relative positions $\upsilon _i$ in the experiments have larger magnitude than those in the SITL simulations. Large $\Vert \upsilon _i\Vert$ was used in the experiments for safety, specifically, to limit the chance of collisions between UAVs. However, since $\upsilon _i$ is the desired relative position resolved in the leader’s velocity frame $\textrm{F}_\textrm{g}$, it follows that larger $\Vert \upsilon _i\Vert$ results in more aggressive desired trajectories for the UAVs (i.e., $\Vert \chi _i \Vert$ are larger). This difference is reflected by the fact that although the mean RMS position error for the experiments is approximately 6 times larger than those for Simulation 3, the mean RMS of the percent error is only 2 times larger (34% and 35% for Experiments 1 and 2 compared to 18% for Simulation 3). Thus, the more aggressive desired trajectories is a significant driver in the larger RMS position errors for the experiments. Note that these more aggressive desired trajectories result most notably in more aggressive desired speed $s_{\textrm{d,i}}$ as observed by comparing the desired speeds in SITL simulations (see Figs. 9, 11, and 13) to those in the experiments (see Figs. 18, 22 and 25). A second factor contributing to the difference between experiment and SITL simulation is that the UAV model (1)–(3) does not account for attitude dynamics; it only includes attitude kinematics. Furthermore, the unmodeled attitude dynamics may have a larger impact on the experimental results because the experimental UAV has slower attitude dynamics than the SITL UAV. Third, the speed dynamics for the experimental UAV are more uncertain than those of the SITL UAV. For example, the experimental UAV’s throttle response changes as the flight battery is depleted. This effect is not modeled in SITL. Fourth, the SITL simulations do not include time-varying wind, whereas the experiments do. Fifth, the multi-loop control is implemented at 25 Hz for SITL but only 10 Hz for the experiments (because of data-rate limitations in interagent communication and in the interface between the Pixhawk and Raspberry Pi). Sixth, since the experimental UAVs communicate over a wireless mesh network, packet loss occurs frequently in the experiments. This packet loss manifest as time delay in the feedback data. In contrast, packet loss does not occur in SITL.

Fig. 23

Experiment 3: Trajectories of leader and agents in the horizontal plane with time as the vertical axis. The axes $e_1^\textrm{T}q_i$ and $e_2^\textrm{T}q_i$ are the position of the ith aircraft to the north and east of a fixed GPS reference location

Fig. 24

Experiment 3: Agent position relative to the leader $q_i-q_\textrm{g}$ and $\Vert {\tilde{q}}_i\Vert$ in the horizontal plan, and the agent altitude. The desired relative position $\chi _i$ and desired altitude are shown with dashed lines

Appendices

Appendix A

Proof of Theorem 1

Proof

To examine the speed error ${\tilde{s}}_i$, consider the partial Lyapunov-like function $Z_i:{\mathcal S}_i \times {\mathcal S}_{\textrm{d,i}} \rightarrow [0,\infty )$ defined by

$$\begin{aligned} Z_i(s_i,s_{\textrm{d,i}}) \triangleq \frac{1}{2} \left( \frac{s_i-s_{\textrm{d,i}}}{h_i( s_i)}\right) ^2, \end{aligned}$$

(A1)

and it follows that

$$\begin{aligned} \dot{Z}_i(s_i,s_{\textrm{d,i}}){} & {} \triangleq \frac{\partial Z_i(s_i,s_{\textrm{d,i}})}{\partial s_i} \dot{s}_i+\frac{\partial Z_i(s_i,s_{\textrm{d,i}})}{\partial s_{\textrm{d,i}}} \dot{s}_{\textrm{d,i}}\nonumber \\{} & {} =\frac{(s_i-s_{\textrm{d,i}})}{h_i( s_i)^2} \left( \frac{h_i( s_i) - (s_i-s_{\textrm{d,i}})h_i^\prime ( s_i)}{h_i( s_i)} \right) \nonumber \\{} & {} \qquad \times \dot{s}_i - \frac{(s_i-s_{\textrm{d,i}})}{h_i( s_i)^2} \dot{s}_{\textrm{d,i}}. \end{aligned}$$

(A2)

Evaluating (A2) along (2) and (14) and using (17) implies that for all $s_i \in {\mathcal S}_i$,

$$\begin{aligned} \dot{Z}_i(s_i,s_{\textrm{d,i}}) = - \dfrac{a_i {\tilde{s}}_i^2}{h_i( s_i)^2} -\dfrac{b_i {\tilde{s}}_i^4}{h_i( s_i)^3} \le - \frac{a_i}{{\bar{h}}_i^2} {\tilde{s}}_i^2, \end{aligned}$$

(A3)

where

$$\begin{aligned} {\bar{h}}_i \triangleq \max _{s \in {\mathcal S}_i} h_i(s) > 0. \end{aligned}$$

(A4)

Fig. 25

Experiment 3: Actual (solid) and desired (dashed) speed $s_i$, flight-path angle $\gamma _i$, and heading $\sigma _i$

To prove iv), note that $s_{i}(0) \in {\mathcal S}_{i}$. Assume for contradiction that (O3) is not satisfied, which implies that there exists $t_1 > 0$ such that for all $t \in [0,t_1)$, $s_i(t) \in {\mathcal S}_i$ and $h(t_1) = 0$ (i.e., $s_{i}(t_1) = {\bar{s}}_i$ or $s_{i}(t_1) = \underline{s}_i$). Since, in addition, $s_{\textrm{d,i}}(t_1) \in {\mathcal S}_{\textrm{d,i}}$, it follows that ${\tilde{s}}_i(t_1) \ne 0$. Thus, (A1) yields that $\lim _{t \rightarrow t_1} Z_i(s_i(t),s_{\textrm{d,i}}(t)) = + \infty$, which implies that there exists $t_2 \in [0,t_1)$ such that $Z_i(s_i(t_2),s_{\textrm{d,i}}(t_2)) > Z_i(s_i(0),s_{\textrm{d,i}}(0))$. Since for all $t\in [0,t_2]$, $s_i(t) \in {\mathcal S}_i$, it follows from (A3) that

$$\begin{aligned} Z_i(s_i(t_2),s_{\textrm{d,i}}(t_2))&= Z_i(s_i(0),s_{\textrm{d,i}}(0))\\&\qquad + \int _0^{t_2} \dot{Z}_i(s_i(t),s_{\textrm{d,i}}(t)) \, \textrm{d}t\\&\le Z_i(s_i(0),s_{\textrm{d,i}}(0)), \end{aligned}$$

which is a contradiction. Thus, (O3) is satisfied, which confirms iv).

To prove v), assume for contradiction that for all $t\ge 0$, $s_i(t) \not \in {\mathcal S}_i$. Then, it follows from (2) and (14) that for all $t\ge 0$,

$$\begin{aligned} \dot{h}_i(s_i(t)) = h_i^\prime (s_i(t)) \dot{s}_i(t) =b_i {\tilde{s}}_i(t)^2. \end{aligned}$$

(A5)

Since for all $t\ge 0$, $s_i(t) \not \in {\mathcal S}_i$ and $s_{\textrm{d,i}}(t) \in {\mathcal S}_{\textrm{d,i}}$, it follows that ${\tilde{s}}_i(t)^2 > \varepsilon _i^2$, which combined with (A5) implies that for all $t \ge 0$, $\dot{h}_i(s_i(t)) > b_i \varepsilon _i^2$. Let $t_3 = -h_i(s_i(0))/(b_i \varepsilon _i^2)$, and it follows that

$$\begin{aligned} h_i(s_i(t_3))&= h_i(s_i(0)) + \int _0^{t_3} \dot{h}_i(s_i(t)) \textrm{d}t \\&> h_i(s_i(0)) + b_i \varepsilon _i^2 t_3 \\&= 0. \end{aligned}$$

Since $h_i(s_i(t_3)) > 0$, it follows that $s_i(t_3) \in {\mathcal S}_i$, which is a contradiction. Thus, there exists $t_0 > 0$ such that $s_i(t_0) \in {\mathcal S}_i$. Next, note that iv) implies that ${\mathcal S}_i$ is positively invariant. Thus, since $s_i(0) \not \in {\mathcal S}_i$ and $s_i(t_0) \in {\mathcal S}_i$, it follows that there exists $T\in (0,t_0)$ such that for all $t\in [0,T]$, $s_i(t) \not \in {\mathcal S}_i$ and for all $t > T$, $s_i(t) \in {\mathcal S}_i$, which confirms v).

Table 2 RMS of $\Vert {\tilde{q}}_i \Vert$ in m, mean RMS of $\Vert {\tilde{q}}_i \Vert$ in m, and mean RMS of the percent error

Next, define ${\mathcal B}\triangleq \{ {\tilde{y}} \in {\mathbb R}^3 :\Vert {\tilde{y}} \Vert \le 2 \}$, and consider the partial Lyapunov-like function $Y:{\mathcal B}\rightarrow [0,2]$ defined by

$$\begin{aligned} Y({\tilde{y}}_i) \triangleq \tfrac{1}{2} {\tilde{y}}_i^\textrm{T}{\tilde{y}}_i, \end{aligned}$$

(A6)

and it follows that

$$\begin{aligned} \dot{Y}({\tilde{y}}_i) \triangleq \frac{\partial Y({\tilde{y}}_i)}{\partial {\tilde{y}}_i} \dot{{\tilde{y}}}_i = {\tilde{y}}_i^\textrm{T}\dot{{\tilde{y}}}_i. \end{aligned}$$

(A7)

Since $y_i$ and $y_{\textrm{d,i}}$ are unit vectors, it follows that $y_i^\textrm{T}\dot{y}_i = 0$ and $y_{\textrm{d,i}}^\textrm{T}\dot{y}_{\textrm{d,i}} = 0$. Thus, evaluating (A7) along the trajectories of (3) and (15) yields

$$\begin{aligned} \dot{Y}({\tilde{y}}_i)&= - y_{i}^\textrm{T}\dot{y}_{\textrm{d,i}} - y_{\textrm{d,i}}^\textrm{T}\dot{y}_{i}\nonumber \\&= - y_{i}^\textrm{T}\dot{y}_{\textrm{d,i}} - y_{\textrm{d,i}}^\textrm{T}R_{i} [ \omega _i ]_\times v_i\nonumber \\&= - y_{i}^\textrm{T}\dot{y}_{\textrm{d,i}} - c_i y_{\textrm{d,i}}^\textrm{T}R_{i} [ R_i^\textrm{T}[ y_i ]_\times y_{\textrm{d,i}} ]_\times v_i\nonumber \\&\qquad + y_i^\textrm{T}\dot{y}_{\textrm{d,i}} y_{\textrm{d,i}}^\textrm{T}R_{i} [ R_i^\textrm{T}[ y_i ]_\times y_{\textrm{d,i}} ]_\times v_i\nonumber \\&\qquad - y_i^\textrm{T}y_{\textrm{d,i}} y_{\textrm{d,i}}^\textrm{T}R_{i} [ R_i^\textrm{T}[ y_i ]_\times \dot{y}_{\textrm{d,i}} ]_\times v_i. \end{aligned}$$

(A8)

Next, since $[R^\textrm{T}x]_\times = R^\textrm{T}[ x]_\times R$, and $[[x_1]_\times x_2]_\times = -x_1 x_2^\textrm{T}+ x_2 x_1^\textrm{T}$, it follows that

$$\begin{aligned} \dot{Y}({\tilde{y}}_i)&= - y_{i}^\textrm{T}\dot{y}_{\textrm{d,i}} - ( c_i - y_i^\textrm{T}\dot{y}_{\textrm{d,i}}) y_{\textrm{d,i}}^\textrm{T}[ [ y_i ]_\times y_{\textrm{d,i}} ]_\times y_i\nonumber \\&\qquad - y_i^\textrm{T}y_{\textrm{d,i}} y_{\textrm{d,i}}^\textrm{T}[ [ y_i ]_\times \dot{y}_{\textrm{d,i}} ]_\times y_i \nonumber \\&= - y_{i}^\textrm{T}\dot{y}_{\textrm{d,i}} - (c_i - y_i^\textrm{T}\dot{y}_{\textrm{d,i}}) ( 1 - (y_{\textrm{d,i}}^\textrm{T}y_i)^2 )\nonumber \\&\qquad + ( y_i^\textrm{T}y_{\textrm{d,i}} )^2 \dot{y}_{\textrm{d,i}} y_i\nonumber \\&= -c_i ( 1 - (y_{\textrm{d,i}}^\textrm{T}y_i)^2 )\nonumber \\&= -c_i ( 1 - y_{\textrm{d,i}}^\textrm{T}y_i) (1+ y_{\textrm{d,i}}^\textrm{T}y_i). \end{aligned}$$

(A9)

Note that

$$\begin{aligned} Y({\tilde{y}}_i) = 1 - y_{\textrm{d,i}}^\textrm{T}y_i, \end{aligned}$$

(A10)

along the trajectories of (A6) and (A9) yields

$$\begin{aligned} \dot{Y}({\tilde{y}}_i) = -\tfrac{1}{2} c_i {\tilde{y}}_i^\textrm{T}{\tilde{y}}_i \big ( 2 - Y({\tilde{y}}_i) \big ), \end{aligned}$$

(A11)

which is nonpositive because the codomain of Y is [0, 2].

To examine the position error ${\tilde{q}}_i$, differentiating (16), and using (1),(4),(5), and (7) implies that

$$\begin{aligned} \dot{{\tilde{q}}}_i&= s_i y_i -\dot{q}_\textrm{g}- \dot{\chi }_i \\&= k_i \rho _i(\xi _i) + s_i y_i - p_{\textrm{d,i}}. \end{aligned}$$

Since $s_i y_i - p_{\textrm{d,i}} = {\tilde{s}}_i y_i + s_{\textrm{d,i}} {\tilde{y}}_i$, it follows that

$$\begin{aligned} \dot{{\tilde{q}}}_i = k_i \rho _i(\xi _i)+ {\tilde{s}}_i y_i + s_{\textrm{d,i}} {\tilde{y}}_i, \end{aligned}$$

(A12)

where (6) and (16) imply that

$$\begin{aligned} \xi _i = -\beta _i {\tilde{q}}_i - \sum _{j \in {\mathcal I}\backslash \{ i\}} \beta _{ij} ({\tilde{q}}_i - {\tilde{q}}_j). \end{aligned}$$

(A13)

Next, define

$$\begin{aligned} {\tilde{q}} \triangleq \left[ \begin{array}{c} {\tilde{q}}_1 \\ \vdots \\ {\tilde{q}}_n \end{array} \right] , \qquad \xi \triangleq \left[ \begin{array}{c} \xi _1 \\ \vdots \\ \xi _n \end{array} \right] , \end{aligned}$$

and it follows from (A13) that

$$\begin{aligned} \xi = -\big ( (A+B) \otimes I_3 \big ) {\tilde{q}}, \end{aligned}$$

(A14)

where $\otimes$ is the Kronecker product. Since $A+B$ is nonsingular, it follows that (A14) can be viewed as a linear change of variables between $\xi$ and ${\tilde{q}}$. Next, (A12) implies that

$$\begin{aligned} \dot{{\tilde{q}}}&= P(\xi ) + \Delta _1({\tilde{s}}_1 y_1,\ldots ,{\tilde{s}}_n y_n) \nonumber \\&\qquad +\Delta _2(s_{\textrm{d,1}} {\tilde{y}}_1, \ldots , s_{\textrm{d,n}} {\tilde{y}}_n), \end{aligned}$$

(A15)

where

$$\begin{aligned} P(\xi ) \triangleq \left[ \begin{array}{c} k_1 \rho _1(\xi _1) \\ \vdots \\ k_n\rho _n(\xi _n) \end{array} \right] , \end{aligned}$$

(A16)

$$\begin{aligned} \Delta _1({\tilde{s}}_1 y_1,\ldots ,{\tilde{s}}_n y_n) \triangleq \left[ \begin{array}{c} {\tilde{s}}_1 y_1 \\ \vdots \\ {\tilde{s}}_n y_n \end{array} \right] , \end{aligned}$$

(A17)

$$\begin{aligned} \Delta _2(s_{\textrm{d,1}} {\tilde{y}}_1,\ldots , s_{\textrm{d,n}} {\tilde{y}}_n) \triangleq \left[ \begin{array}{c} s_{\textrm{d,1}} {\tilde{y}}_1 \\ \vdots \\ s_{\textrm{d,n}} {\tilde{y}}_n \end{array} \right] , \end{aligned}$$

(A18)

Thus, differentiating (A14) and using (A15) yields

$$\begin{aligned} \dot{\xi }= - \big ( (A+B)\otimes I_3 \big ) \big ( P(\xi ) + \Delta _1+\Delta _2 \big ), \end{aligned}$$

(A19)

where we omit the arguments of $\Delta _1$ and $\Delta _2$ for brevity. Since $A+B$ is nonsingular, it follows from Qu (2009, Theorem 4.25) that there exists a positive-definite diagonal matrix $D \in {\mathbb R}^{n \times n}$ such that $R \triangleq (A+B)^\textrm{T}D + D (A+B)$ is positive definite. Let $d_1,\ldots ,d_n > 0$ denote the diagonal elements of D, that is, $D = {{\,\textrm{diag}\,}}(d_1, \dots , d_n)$. Consider the partial Lyapunov-like function $X: {\mathbb R}^{3n} \rightarrow [0,\infty )$ defined by

$$\begin{aligned} X(\xi ) \triangleq \sum _{i \in {\mathcal I}} d_i k_i M_i(\Vert \xi _i \Vert ^2), \end{aligned}$$

(A20)

where $M_i$ is defined in (C1). Hence, (A20) implies that

$$\begin{aligned} \dot{X}(\xi )&\triangleq \frac{\partial X(\xi )}{\partial \xi } \dot{\xi }\nonumber \\&=\sum _{i \in {\mathcal I}} d_i k_i \frac{\partial M_i(\Vert \xi _i \Vert ^2)}{\partial \xi _i} \dot{\xi }_i\nonumber \\&= \sum _{i \in {\mathcal I}} 2 d_i k_i \mu _i(\Vert \xi _i \Vert ^2) \xi _i^\textrm{T}\dot{\xi }_i\nonumber \\&= \sum _{i \in {\mathcal I}} 2 d_i k_i \rho _i^\textrm{T}(\xi _i) \dot{\xi }_i\nonumber \\&= 2 P^\textrm{T}(\xi ) (D \otimes I_3) \dot{\xi }. \end{aligned}$$

(A21)

Evaluating (A21) along (A19) yields

$$\begin{aligned} \dot{X}(\xi )&= - P^\textrm{T}(\xi ) \Big ( \big ( (A+B)^\textrm{T}D + D(A+B) \big ) \otimes I_3 \Big ) P(\xi ) \nonumber \\&\qquad - 2 P^\textrm{T}(\xi ) \Big ( \big (D (A+B) \big ) \otimes I_3 \Big ) (\Delta _1+\Delta _2) \nonumber \\&= - P^\textrm{T}(\xi ) (R \otimes I_3) P(\xi ) - 2 P^\textrm{T}(\xi ) Q (\Delta _1+\Delta _2)\nonumber \\&\le - 3 \ell _0 P^\textrm{T}(\xi ) P(\xi ) - 2 P^\textrm{T}(\xi ) Q (\Delta _1+\Delta _2), \end{aligned}$$

(A22)

where $Q \triangleq D(A+B) \otimes I_3$, $\ell _0 \triangleq \lambda _{\textrm{min}}(R)/3 > 0$, and $\lambda _{\textrm{min}}$ denotes the minimum eigenvalue. Next, note that

$$\begin{aligned} 0&\le \left( \sqrt{\ell _0}P(\xi ) + \frac{1}{\sqrt{\ell _0}} Q \Delta _1 \right) ^\textrm{T}\nonumber \\&\qquad \times \left( \sqrt{\ell _0}P(\xi ) + \frac{1}{\sqrt{\ell _0}} Q \Delta _1 \right) , \end{aligned}$$

which implies that

$$\begin{aligned} - 2 P^\textrm{T}(\xi ) Q \Delta _1&\le \ell _0 P^\textrm{T}(\xi ) P(\xi ) + \frac{1}{\ell _0} \Delta _1^\textrm{T}Q^\textrm{T}Q \Delta _1\nonumber \\&\le \ell _0 P^\textrm{T}(\xi ) P(\xi ) + \ell _1 \Delta _1^\textrm{T}\Delta _1, \end{aligned}$$

(A23)

where $\ell _1 \triangleq \lambda _{\textrm{max}}(Q^\textrm{T}Q)/\ell _0 > 0$ and $\lambda _{\textrm{max}}$ denotes the maximum eigenvalue. Similarly,

$$\begin{aligned} - 2 P^\textrm{T}(\xi ) Q \Delta _2 \le \ell _0 P^\textrm{T}(\xi ) P(\xi ) + \ell _1 \Delta _2^\textrm{T}\Delta _2. \end{aligned}$$

(A24)

Thus, substituting (A23) and (A24) into (A22), and using (A16)–(A18) yields

$$\begin{aligned} \dot{X}(\xi )&\le - \ell _0 P^\textrm{T}(\xi ) P(\xi ) + \ell _1 \Delta _1^\textrm{T}\Delta _1 + \ell _1 \Delta _2^\textrm{T}\Delta _2 \nonumber \\&= \sum _{i \in {\mathcal I}} - \ell _0 k_i^2 \Vert \rho _i(\xi _i) \Vert ^2 +\ell _1 {\tilde{s}}_i^2+ \ell _1 s_{\textrm{d,i}}^2 \Vert {\tilde{y}}_i \Vert ^2. \end{aligned}$$

(A25)

Finally, let $\underline{r}_i \in (0,2)$ and consider the Lyapunov function $V:{\mathbb R}^{3n} \times {\mathcal B}\times \cdots \times {\mathcal B}\times {\mathcal S}_1 \times \cdots \times {\mathcal S}_n \times {\mathcal S}_{\textrm{d,1}} \times \cdots \times {\mathcal S}_{\textrm{d,n}} \rightarrow [ 0, \infty )$ defined by

$$\begin{aligned} V( \xi ,&{\tilde{y}}_1,\ldots , {\tilde{y}}_n, s_1,\ldots ,s_n, s_{\textrm{d,1}},\ldots , s_{\textrm{d,n}})\nonumber \\&\triangleq \frac{1}{\ell _1} X(\xi )+ \sum _{i \in {\mathcal I}} \bigg ( \frac{4 {\bar{s}}_i^2}{c_i \underline{r}_i} Y({\tilde{y}}_i) + \frac{2 {\bar{h}}_i^2}{a_i} Z_i(s_i,s_{\textrm{d,i}}) \bigg ). \end{aligned}$$

(A26)

Using (A3), (A11) and (A25) to evaluate $\dot{V}$ along the closed-loop trajectories yields that for all $(\xi , {\tilde{y}}_1,\ldots , {\tilde{y}}_n, s_1,\ldots , s_n, s_{\textrm{d,1}},$ $\ldots , s_{\textrm{d,n}}) \in {\mathbb R}^{3n} \times {\mathcal B}\times \cdots \times {\mathcal B}\times {\mathcal S}_1 \times \cdots \times {\mathcal S}_n \times {\mathcal S}_{\textrm{d,1}} \times \cdots \times {\mathcal S}_{\textrm{d,n}}$,

$$\begin{aligned} \dot{V}&\triangleq \frac{1}{\ell _1} \dot{X}(\xi ) + \sum _{i \in {\mathcal I}} \bigg (\frac{4 {\bar{s}}_i^2}{c_i \underline{r}_i} \dot{Y}({\tilde{y}}_i) + \frac{2 {\bar{h}}_i^2}{a_i} \dot{Z}_i(s_i,s_{\textrm{d,i}}) \bigg )\nonumber \\&\le - \sum _{i \in {\mathcal I}} \Bigg ( \frac{\ell _0 k_i^2 }{\ell _1} \Vert \rho _i(\xi _i) \Vert ^2 \nonumber \\&\qquad + \left( \frac{2 \big (2 - Y({\tilde{y}}_i) \big )}{\underline{r}_i} - 1 \right) {\bar{s}}_i^2 \Vert {\tilde{y}}_i \Vert ^2 + {\tilde{s}}_i^2 \Bigg ), \end{aligned}$$

(A27)

where we omit the arguments from $\dot{V}$.

To prove i), define ${\mathcal B}_i \triangleq \{ {\tilde{y}}_i \in {\mathbb R}^3 :\Vert {\tilde{y}}_i \Vert ^2 < 4-\underline{r}_i \}$. Since $2 - Y({\tilde{y}}_i) = 2- \Vert {\tilde{y}}_i \Vert ^2/2$ and $\underline{r}_i \in (0,2)$, it follows from (A27) that for all $(\xi , {\tilde{y}}_1,\ldots , {\tilde{y}}_n, s_1,\ldots , s_n, s_{\textrm{d,1}},$ $\ldots , s_{\textrm{d,n}}) \in {\mathbb R}^{3n} \times {\mathcal B}_1 \times \cdots \times {\mathcal B}_n \times {\mathcal S}_1 \times \cdots \times {\mathcal S}_n \times {\mathcal S}_{\textrm{d,1}} \times \cdots \times {\mathcal S}_{\textrm{d,n}}$,

$$\begin{aligned} \dot{V} \le - \sum _{i \in {\mathcal I}} \left( \frac{\ell _0}{\ell _1} k_i^2 \Vert \rho _i(\xi _i) \Vert ^2 + {\tilde{s}}_i^2 \right) , \end{aligned}$$

which is nonpositive. Thus, the origin is a Lyapunov stable equilibrium, which confirms i).

To prove ii), since $R_i(0) \in {\mathcal R}_i$, it follows from (A10) that $Y({\tilde{y}}_i(0)) = 1 - y_{\textrm{d,i}}^\textrm{T}(0) R_i(0) v_i <2$, which implies that

$$\begin{aligned} r_i \triangleq 2 - Y({\tilde{y}}_i(0)) \in (0,2]. \end{aligned}$$

Furthermore, since (A11) implies that $\dot{Y}({\tilde{y}}_i) \le 0$, it follows that for all $t \ge 0$, $Y({\tilde{y}}_i(t)) \le Y({\tilde{y}}_i(0))$. Thus, for all $t\ge 0$,

$$\begin{aligned} 2 - Y({\tilde{y}}_i(t)) \ge 2 - Y({\tilde{y}}_i(0)) = r_i. \end{aligned}$$

(A28)

Next, consider (A26) with $\underline{r}_i$ replaced by $r_i$, and it follows from (A27) with $\underline{r}_i$ replaced by $r_i$ and (A28) that for all $t \ge t_0$,

$$\begin{aligned} \dot{V} (t)&\le - \sum _{i \in {\mathcal I}} \bigg ( \frac{\ell _0 k_i^2}{\ell _1} \Vert \rho _i(\xi _i(t)) \Vert ^2 \nonumber \\&\qquad + {\bar{s}}_i^2 \Vert {\tilde{y}}_i(t) \Vert ^2 + {\tilde{s}}_i(t)^2 \bigg ), \end{aligned}$$

(A29)

which implies that V is nonincreasing. Thus, V is bounded, which implies that X is bounded. Since, in addition, X is radially unbounded, it follows that $\xi$ is bounded, which implies that there exists $\bar{\xi }_i > 0$ such that for all $t \ge 0$, $\Vert \xi _i(t) \Vert ^2 \le \bar{\xi }_i$. Since, in addition, $\mu _i$ is continuous and its codomain is $(0,\infty )$, it follows that

$$\begin{aligned} \underline{\mu }_i \triangleq \inf _{t \ge 0} \mu _i(\Vert \xi _i(t) \Vert ^2) \ge \min _{z\in [0,\bar{\xi }_i]} \mu _i(z) > 0. \end{aligned}$$

(A30)

Next, it follows from (C2) that

$$\begin{aligned} \bar{\mu }_i \triangleq \max _{z \ge 0} \mu _i(z) > 0, \end{aligned}$$

which implies that

$$\begin{aligned} M_i(\Vert \xi _i \Vert ^2) \le \int _0^{\Vert \xi _i\Vert ^2} \bar{\mu }_i \, \textrm{d}w = {\bar{\mu }}_i \Vert \xi _i\Vert ^2. \end{aligned}$$

(A31)

Thus, using (5), (A30), and (A31) yields that for all $t \ge 0$,

$$\begin{aligned} \Vert \rho _i(\xi _i(t)) \Vert ^2 \ge \underline{\mu }_i^2 \Vert \xi _i(t) \Vert ^2 \ge \frac{ \underline{\mu }_i^2 }{{\bar{\mu }}_i} M_i(\Vert \xi _i(t) \Vert ^2). \end{aligned}$$

(A32)

Next, since for all $t \ge t_0$, $s_i(t) \in {\mathcal S}_i$, it follows from (A1) and (A3) that $\lim _{t \rightarrow \infty } {\tilde{s}}_i(t) = 0$. Since, in addition, for all $t \ge 0$, $s_{\textrm{d,i}}(t) \in {\mathcal S}_{\textrm{d,i}}$, it follows that

$$\begin{aligned} \underline{h}_i \triangleq \inf _{t \ge t_0} h_i(s_i(t)) > 0, \end{aligned}$$

and using (A1) yields that for all $t \ge t_0$,

$$\begin{aligned} {\tilde{s}}_i(t)^2 \ge 2 \underline{h}_i^2 Z_i(s_i(t),s_{\textrm{d,i}}(t)). \end{aligned}$$

(A33)

Substituting (A6), (A32), and (A33) into (A29) implies that for all $t \ge t_0$,

$$\begin{aligned} \dot{V} (t)&\le - \sum _{i \in {\mathcal I}} \bigg ( \frac{\ell _0 k_i^2 \underline{\mu }_i^2}{\ell _1 \bar{\mu }_i} M_i(\Vert \xi _i(t) \Vert ^2) + 2 {\bar{s}}_i^2 Y({\tilde{y}}_i(t)) \nonumber \\&\qquad + 2 \underline{h}_i^2 Z_i(s_i(t),s_{\textrm{d,i}}(t)) \bigg ). \end{aligned}$$

(A34)

Next, define

$$\begin{aligned} \ell _2 \triangleq \min _{i \in {\mathcal I}} \frac{\ell _0 k_i \underline{\mu }_i^2}{\bar{\mu }_i d_i}> 0,\qquad \ell _3 \triangleq \min _{i \in {\mathcal I}} \frac{c_i r_i }{2}> 0,\\ \ell _4 \triangleq \min _{i \in {\mathcal I}} \frac{ \underline{h}_i^2 a_i}{{\bar{h}}_i^2}> 0,\qquad \ell _5 \triangleq \min \, \{ \ell _2,\ell _3,\ell _4\} > 0, \end{aligned}$$

and it follows from (A34) and (A26) that for all $t \ge t_0$,

$$\begin{aligned} \dot{V} (t)&\le - \sum _{i \in {\mathcal I}} \bigg ( \ell _2 \frac{d_i k_i}{\ell _1} M_i(\Vert \xi _i(t) \Vert ^2 ) + \ell _3 \frac{4 {\bar{s}}_i^2}{c_i r_i} Y({\tilde{y}}_i(t)) \\&\qquad + \ell _4 \frac{2 {\bar{h}}_i^2}{a_i} Z_i(s_i(t),s_{\textrm{d,i}}(t)) \bigg )\le -\ell _5 V(t). \end{aligned}$$

Thus, for all $t \ge t_0$, $V(t) \le e^{-\ell _5(t-t_0)} V(t_0)$. Since V converges exponentially to zero, it follows from (A26) that $X(\xi )$, $Y({\tilde{y}}_i)$, and $Z_i(s_i,s_{\textrm{d,i}})$ converge to zero exponentially. Since $Y({\tilde{y}}_i)$ converges to zero exponentially, it follows from (A6) that ${\tilde{y}}_i$ converges to zero exponentially. Next, since for all $t \ge t_0$, $s_i(t) \in {\mathcal S}_i$, it follows from (A1) and (A4) that for all $t \ge t_0$, ${\tilde{s}}_i(t)^2 \le 2 {\bar{h}}_i^2 Z_i(s_i(t),s_{\textrm{d,i}}(t))$. Thus, ${\tilde{s}}_i$ converges to zero exponentially. Finally, note that for all $t \ge t_0$,

$$\begin{aligned} M_i(\Vert \xi _i(t) \Vert ^2) \ge \int _0^{\Vert \xi _i(t)\Vert ^2} \underline{\mu }_i \, \textrm{d}w = \underline{\mu }_i \Vert \xi _i(t)\Vert ^2. \end{aligned}$$

(A35)

Since $X(\xi )$ converges to zero exponentially, it follows from (A20) that $M_i(\xi _i)$ converges to zero exponentially. Thus, (A35) implies that $\xi _i$ converges to zero exponentially, which combined with (A14) implies that ${\tilde{q}}$ converges to zero exponentially, which confirms ii).

To prove iii), since $\lim _{t \rightarrow \infty } {\tilde{q}}_i(t) =0$, it follows from (16) that (O1) is satisfied. Next, note that since $s_{\textrm{d,i}}$ is bounded, $\lim _{t\rightarrow \infty } \xi _i(t) = 0$, $\lim _{t\rightarrow \infty } {\tilde{s}}_i(t) = 0$, and $\lim _{t \rightarrow \infty } {\tilde{y}}_i =0$, it follows from (A12) that $\lim _{t\rightarrow \infty } \dot{{\tilde{q}}}_i(t) =0$, which confirms (O2). $\square$