1 Introduction

The radiative transfer mechanism in astrophysical systems plays a decisive role in the pre-stage star formation process (Juvela 2011). In the interstellar medium (ISM), the thermal processes allow the gas to become denser and hotter, providing the necessary conditions for gravitational collapse. The ISM observations report that the radiative heat-loss mechanism via thermal instability plays an important role in the star formation process in molecular clouds (MCs) (Fukue and Kamaya 2007). Wurster et al. (2018) studied the radiation and non-ideal magnetohydrodynamic (MHD) effects, e.g., ambipolar diffusion, Ohmic resistivity, and the Hall effect, on the collapse of rotating and magnetized molecular cloud cores. Hegmann and Kegel (1996) presented a radiative transfer model in the form of a Fokker-Planck equation, considering the density fluctuations in the system. Patrick and Shu-ichiro (2019) explored the influence of magnetic fields on the formation of pre-stellar dense cores and stellar clusters. Molaro et al. (2016) suggested a new method for probing global properties of the clump and core population in giant molecular clouds (GMCs), based on the study of their overall effect on the reflected X-ray signal. Bethell et al. (2007) calculated the photoionization rates in clumpy MCs. Micic et al. (2013) studied the influence of cooling function on the formation of MCs, using high-resolution three-dimensional simulations of converging flows.

MCs are the main sources of star formation in which the equilibrium temperature is maintained due to the balance of heating and cooling mechanisms (Hollenbach 1988). In the ongoing radiative processes in the star formation mechanism, Jeans instability plays a fundamental role in the gravitational collapse of a gas cloud. Jeans (1902) described the conditions under which a region of gas or plasma can collapse gravitationally and form a new structure, such as a star or a planet. The minimum perturbation wavenumber for which Jeans instability is excited in a system is expressed by the Jeans instability criterion as \(k< k_{j}=(4\pi G \rho _{0})^{1/2}/c_{s}\), where \(G\) is the gravitational constant, \(\rho _{0}\) is the gas density, and \(c_{s}\) is the sound speed. If the wavenumber of perturbations in the system is smaller than the critical Jeans wavenumber, then the system will be unstable and collapse under its own gravity, leading to the formation of structures such as stars and galaxies. In other words, if the size of the perturbation is larger than some critical wavelength of the order \(\lambda _{j}=2\pi /k_{j}\), then the enhanced self-gravity can overpower the excess pressure so that the perturbation grows. Motivated by the works of Jeans (1902), many authors have shown keen interest in exploring the mechanism of star formation and studied Jeans instability in various astrophysical systems, such as gaseous clouds (Chandrasekhar 1961), clumpy MCs (Elmegreen 1989), strongly coupled medium (Janaki et al. 2011; Prajapati and Chhajlani 2013; Dhiman and Sharma 2014; Dasgupta and Karmakar 2019; Dolai and Prajapati 2020), radiative MCs (Prajapati 2022), and self-gravitating optically thick gas-and-dust medium (Kolesnichenko 2023).

A strongly coupled medium refers to a state of matter where the interactions between charged particles, such as ions and electrons, are so strong that they begin to interact with each other through long-range electric and magnetic forces, which can result in the formation of complex structures and patterns. The present work aims to examine the role of heating and cooling effects on the growth rate of the Jeans instability in strongly coupled fluid (for which \(\Pi _{j} \gg 1\), i.e., when average potential energy dominates the kinetic energy of the particles). Previous works include the effects of viscoelastic coefficients (Janaki et al. 2011), electrical resistivity (Prajapati and Chhajlani 2013), rotation (Dhiman and Sharma 2014) and quantum corrections (Sharma and Chhajlani 2014) on the Jeans instability in strongly coupled viscoelastic fluids. Sharma et al. (2015) investigated the Jeans instability of rotating viscoelastic fluids including magnetic fields. Dhiman and Mahajan (2023) studied the gravitational instability in strongly coupled viscoelastic clumpy MCs considering dissipative effects. However, the effects of the magnetic field and rotation were ignored in the considered configuration. Recently, Yang et al. (2023) studied Jeans instability in viscoelastic astrofluids using Eddington-Inspired-Born-Infeld (EiBI) gravity and found that the positive EiBI gravity parameter and effective generalized fluid viscosity act as stabilizing agents whereas the negative EiBI parameter and viscoelastic relaxation time act as destabilizing factors. From the above studies, it is evident that the strong coupling effects in terms of viscoelastic coefficients play a dominant role in investigating the gravitational instability in viscoelastic fluids.

The presence of magnetic fields in MCs is essential for understanding their role in the evolution of dense clouds and star formation process (Braine et al. 2020; Crutcher 2012). Körtgen and Banerjee (2015) showed that dense cores of MCs could build up under all the conditions; however, the star formation process in these cores is either delayed or completely suppressed if the initial field strength is \(B>3\mu \)G. Ibáñez-Mejía et al. (2022) discussed the competition between gravity versus the magnetic fields in the star-forming region of the MCs. Recently, Patidar et al. (2023) investigated the influence of the magnetic field on the Jeans criteria for quantum plasma and found that highly magnetized white dwarfs have a different mass-radius relation than their non-magnetic counterparts, which results in a modified super-Chandrashekhar mass limit. In addition, rotation is a unique characteristic of astrophysical systems such as accretion disks, circumstellar disks, and MCs. The spin angular momenta of the clouds may be due to the orbital rotation of the gas. The observational data show that GMCs have a spin rotation with angular momenta of the order of 100 km s−1 pc per unit mass (Chernin and Efremov 1995). In the gravitational collapse and subsequent star formation processes, the role of the magnetic field and rotation has been studied previously by many authors. However to the best of our knowledge, none of them has studied the combined effects of heating and cooling functions, magnetic field and rotation on the gravitational instability of strongly coupled clumpy MCs.

In this paper, we have analyzed the gravitational instability of strongly coupled MCs and have investigated the effects of rotation, magnetic field, and heat-loss functions on the onset of gravitational collapse. Here, we have considered the modified energy equation for an ideal fluid with heating and cooling functions (Elmegreen 1989) along with standard fluid equations. The paper is organized as follows: Sec. 1 is the introductory in nature and also includes a review of the literature. In Sec. 2, the mathematical model is constructed for the rotating and magnetized clumpy MCs, using the generalized hydrodynamic equations, which include the effect of the Coulomb coupling parameter \(\Pi _{j}\). In Sec. 3, the linearized perturbed equations are obtained, the general dispersion relation is derived using the plane wave solutions, and the results are discussed in parallel wave propagation mode for both the strongly (kinetic) and weakly (hydrodynamic) coupled limits. In Sec. 4, the outcomes of the present work have been summarized.

2 Mathematical model

Consider an infinite homogeneous, self-gravitating clumpy MCs in which the uniform rotation (\({\boldsymbol{\Omega}}(0,0,\Omega _{z})\)) and uniform magnetic field (\(\mathbf{H}(0,0, H_{0})\)) act simultaneously. The considered medium is strongly coupled in nature and hence exhibits both viscous and elastic behaviour in terms of the viscoelastic coefficients. Following Kaw and Sen (1998), the basic equations for the considered system using the generalized hydrodynamic (GH) model are given by (Elmegreen 1989; Janaki et al. 2011; Dhiman and Sharma 2014):

The equation of continuity;

$$ \frac{\partial{\rho}}{\partial{t}} + \nabla \cdot (\rho \textbf{u})=0. $$
(1)

The equation of motion;

$$ \begin{aligned} &\left (1 +\tau _{m} \frac{\partial}{\partial t}\right ) \left [\rho \frac{d \textbf{u}}{dt} + \nabla P -\rho \mathbf{g} -\frac{1}{4 \pi}(( \nabla \times{\textbf{H}})\right . \\ &\left .\times {\textbf{H}})-2 \rho ({\textbf{u}}\times { \boldsymbol{\Omega}}) \right ] = \mu \nabla ^{2} \textbf{u}+\left (\zeta + \frac{\mu}{3}\right )\nabla (\nabla \cdot \textbf{u}). \end{aligned} $$
(2)

The magnetic induction equation;

$$ \frac{\partial \mathbf{H}}{\partial{t}}=\nabla \times \left ( \mathbf{u}\times \mathbf{H}\right ). $$
(3)

The Poisson equation for the gravitational field;

$$ \nabla \cdot \mathbf{g}=-4\pi G\rho. $$
(4)

Here, \(\mathbf{g}=-\nabla \phi \), \(\phi \) is the gravitational potential, \(\textbf{u}, P\) and \(\rho \) represent the fluid velocity, fluid pressure, and fluid density, respectively. \(\tau _{m}\) is the relaxation time or memory parameter, which depends on the viscoelastic coefficients \(\mu \) and \(\zeta \). \({d}/{dt}= ({\partial}/{ \partial t}+\mathbf{u }.\nabla )\) is the convective derivative.

There has been a great deal of concern among researchers about analyzing the role of the radiative heat-loss mechanism in MCs due to its significance in structure formation. Field (1965) studied the effects of temperature and density-dependent radiative heat-loss functions on the thermal stability of a dilute, non-gravitating gas. Later, this problem was extensively studied by many authors, considering the effects of finite Larmor frequency and electrical resistivity (Bora and Talwar 1993), uniform rotation and magnetic field (Aggarwal and Talwar 1969), ion-neutral collisions (Fukue and Kamaya 2007), Hall effect and electron inertia (Prajapati et al. 2010), dust temperature and viscoelastic effects (Sharma et al. 2020) and porosity of the medium (Kaothekar et al. 2022). In these works, the temperature and density-dependent radiative heat-loss functions are considered and it is found that the fundamental thermal instability criterion remains unchanged due to the considered effects. However, when we consider cloud-cloud collisions, the heating and cooling functions are considered to be independent of time (Elmegreen 1989) and these functions are different than those considered by Field (1965) in his work. In the present work, we shall focus on the physical conditions of molecular cloud clumps to analyze the Jeans instability of strongly coupled fluids in the presence of rotation and magnetic fields, considering the heating and cooling effects.

Thus, the energy equation is therefore considered as (Elmegreen 1989);

$$ \frac{1}{\gamma -1} \left ( \frac{d P}{d t} \right )- \frac{\gamma}{\gamma -1}\frac{P}{\rho} \left ( \frac{d \rho}{d t} \right )+\Lambda -\Gamma =0. $$
(5)

where, \(\gamma \) is the ratio of specific heat. The term \(\Lambda \) represents the cooling function, which is attributed to cloud-cloud collisions with an isotropic, Maxwellian distribution of cloud velocities and is defined as;

$$ \small \Lambda =\frac{8C\rho ^{2}c^{3}\pi R_{c}^{2}}{\pi ^{1/2}M_{c}}= \frac{2.3\rho ^{2}c^{3}}{\sigma _{c}}. $$
(6)

Here, \(M_{c},R_{c}\) and \(\sigma _{c}\) respectively denote the average masses, radii, and column densities of the colliding clouds. Further, \(\Gamma =\Gamma _{e} \rho (\frac{\Lambda _{0}}{\rho _{0}})\) describes the heating rate where \(\Gamma _{e}, \Lambda _{0}\) are the values of heating and cooling rate in the equilibrium states.

3 Dispersion relation

The dispersion relation for the considered configuration is obtained using the first-order perturbation method. The basic equations are linearized, considering infinitesimal small perturbations;

$$ \begin{aligned} \mathbf{u}=\mathbf{u_{0}}+\mathbf{u_{1}},\mathbf{H}=\mathbf{H_{0}}+ \mathbf{H_{1}},\rho =\rho _{0}+\rho _{1},& \\ \mathbf{g}=\mathbf{g}_{0}+\mathbf{g}_{1}, P = P_{0} + P_{1}, \end{aligned} $$
(7)

where, \(\rho _{1},g_{1},P_{1}, \mathbf{u}_{1}(v_{x },v_{y}, v_{z})\), and \(\mathbf{H_{1}}(h_{x},h_{y},h_{z})\) denote the perturbations in fluid density, gravitational field, fluid pressure, fluid velocity and magnetic field, respectively. All the above quantities with subscript “0” represent the value of that quantity at equilibrium. In the stability analysis of gravitating fluid, the streaming effects are neglected; hence we put \(\mathbf{u}_{0}=0\). To check the stability of the perturbed system, the arbitrary perturbations can be decomposed into a complete set of normal modes and are analyzed individually. Therefore, assuming the plane wave solutions of each of the perturbed quantity as;

$$ f_{1}(z,t)\propto e^{(i k_{z}z+\omega t)} $$
(8)

where, \(\omega =-i\omega ^{\prime }\) is the perturbation frequency of the harmonic disturbance and \(k_{z}\) is the wavenumber. This allows us to substitute \(\nabla =i k_{z} \mathbf{\hat{z}}\) and \(\partial /\partial t= \omega \) in the perturbed equations obtained after substituting the perturbed quantities (7) into equations (1)-(5), we obtained the following linearized equations;

$$ \begin{aligned} &\left ( 1 +\tau _{m} \omega \right ) \left [ \rho _{0} \omega \mathbf{u_{1}} + i k_{z} \mathbf{\hat{z}} \rho _{0} g_{1} + i k_{z} \mathbf{\hat{z}} P_{1} \right . \\ &\left . -\frac{H_{0}}{4 \pi}\Biggl(ik_{z} h_{x} \mathbf{\hat{x}} \Biggl)-\frac{H_{0}}{4 \pi}\Biggl(ik_{z} h_{y} \mathbf{\hat{y}} \Biggl) -2 \rho _{0} \Biggl(\Omega _{z} v_{y} \mathbf{\hat{x}} \right . \\ &\left .- \Omega _{z} v_{x}\mathbf{\hat{y}}\Biggl) \right ]=-\left ( \zeta + \frac{4\mu}{3}\right ) k^{2} \mathbf{u_{1}}, \end{aligned} $$
(9)
$$ \omega \rho _{1} + i\rho _{0} k_{z} v_{z} =0, $$
(10)
$$ h_{x}=\frac{i k_{z} v_{x} H_{0}}{\omega},~~ h_{y}= \frac{i k_{z} v_{y} H_{0}}{\omega},~~ i k_{z} h_{z}=0, $$
(11)
$$ i k_{z} g_{1}= -4\pi G \rho _{1}, $$
(12)
$$ \omega P_{1}-\omega \gamma c^{2} \rho _{1}+ 4 \omega _{c} P_{1}-2 \omega _{c} \Gamma _{e} c^{2} \rho _{1}=0, $$
(13)

where \(\omega _{c}= (\gamma -1)\Lambda _{0}/(2\rho _{0} c^{2})\) represents the cooling rate (Elmegreen 1989) and is approximated as the inverse of the cloud-cloud collision time. Equation (13) can be simplified as

$$ P_{1}=\gamma c^{2}\left [ \frac{\omega +(2\Gamma _{e}-1)\omega _{c}/\gamma}{\omega +3\omega _{c}} \right ]\rho _{1}. $$
(14)

Using the values of \(\rho _{1}, h_{x}, h_{y}, g_{1}\) and \(P_{1}\) from equations (10)-(12) and (14) in equation (9), we obtain the following dispersion relation after some simplifications and setting \(k_{z}=k\);

$$ \begin{aligned} \Biggl\{ \Biggl[ \left (1+\tau _{m} \omega \right ) \left (\omega ^{2} + V_{A}^{2} k^{2}\right ) \\ +\omega \Biggl[\frac{(\zeta +\frac{4\mu}{3})}{\rho _{0}}\Biggl] k^{2} \Biggl] ^{2} + 4 \omega ^{2} \Omega _{z}^{2}\Biggl\} \times \Biggl\{ \left (1+\tau _{m} \omega \right ) \Biggl[ \omega ^{2} \\ + \gamma c^{2}\left ( \frac{\omega +(2\Gamma _{e}-1)\omega _{c}/\gamma}{\omega +3\omega _{c}} \right ) k^{2}-\omega _{j}^{2}\Biggl] \\ +\omega \left [ \frac{(\zeta +\frac{4\mu}{3})}{\rho _{0}}\right ] k^{2} \Biggl\} =0. \end{aligned} $$
(15)

Equation (15) is the modified form of the dispersion relation for the clumpy cloudy medium in the presence of uniform rotation, magnetic fields, and viscoelastic effects. If the effects of rotation and magnetic field are neglected, we obtain the same dispersion relation as obtained by Dhiman and Mahajan (2023) neglecting dissipative effects in that case. Further, if we neglect the viscoelastic coefficients (\(\zeta =\mu =0\)), roational frequency (\(\Omega _{z}=0\)), magnetic field intensity (\(H_{0}=0\)), the equation (15) reduces to the same dispersion relation obtained by Elmegreen (1989). Also, if the clump stirring processes and cloud-cloud collisions are neglected (i.e. \(\Lambda =\Gamma _{e}=\omega _{c}=0\)), then we obtain the same dispersion relation (17) obtained by Prajapati and Chhajlani (2013) for an infinitely conducting medium without rotation. The dispersion relation (15) is useful to discuss the Jeans instability in a molecular cloud clump undergoing heating and cooling mechanisms. To obtain the instability criterion and effects of the various considered parameters on the growth rate, let us analyze these two factors, separately.

3.1 Kinetic limit

The first factor of the dispersion relation (15) under the kinetic limit (known as the strongly coupled limit) i.e. \(\tau _{m} \omega \gg 1\) reduces to

$$ \begin{aligned} \omega ^{4} + \omega ^{2} \left (2 V_{A}^{2}+2 v_{c}^{2}\right )k^{2} + \left (V_{A}^{4} + v_{c}^{4} +2 v_{c}^{2} V_{A}^{2}\right ) k^{4} \\ + \frac{4 \Omega _{z}^{2}}{\tau _{m}^{2}} =0. \end{aligned} $$
(16)

where \(v_{c}^{2}=(\zeta +\frac{4\mu}{3})/ \rho _{0} \tau _{m}\) is defined as the square of the velocity of the compressional viscoelastic mode. Equation (16) clearly represents non-gravitating, rotating, damped viscoelastic, Alfvén wave mode that is dynamically stable. In the absence of rotation (i.e. \(\Omega _{z}=0\)), equation (16) reduces to

$$ \omega ^{2} + \left (V_{A}^{2} + v_{c}^{2} \right )k^{2}=0. $$
(17)

The above equation represents the magnetosonic mode in the compressional viscoelastic fluid. It is clear that in the absence of rotation, the usual magnetosonic mode is modified due to the presence of viscoelastic coefficients. Thus, due to the presence of uniform rotation, the phase speed of the MHD mode will be significantly affected.

The second factor of the dispersion relation (16) under the kinetic limit reduces to

$$ \omega ^{2} +k^{2} \left [ \gamma c^{2}\left ( \frac{\omega +(2\Gamma _{e}-1)\omega _{c}/\gamma}{\omega +3\omega _{c}} \right ) + v_{c}^{2} \right ]-\omega _{j}^{2} =0. $$
(18)

Equation (18) is the modified form of the dispersion relation obtained by Elmegreen (1989) in the presence of viscoelastic effects. If the parameters; \(\Gamma _{e},\gamma ,\Lambda \), and \(\omega _{c}\) representing the clumpy cloudy medium are neglected, we obtain the same dispersion relation obtained by Janaki et al. (2011). It is very difficult to measure the real values of the viscoelastic coefficients for astrophysical systems. Thus, to study the effects of various parameters on the growth rate of the Jeans instability, we replace \(v_{c}\) in terms of the Coulomb coupling parameter \(\Pi _{j}\), the ion mass and the ion temperature. Following Dolai and Prajapati (2017), the simplified expression of compressional wave velocity \((v_{c})\) in terms of coupling parameter (\(\Pi _{j}\)) is given by

$$ v_{c}^{2}=\frac{0.16T_{i}}{m_{i}}\Pi _{j}. $$
(19)

Here, we have used the following relation between the memory parameter, coupling parameter and compressibility of the medium

$$ \tau _{m}= \frac{\left (\zeta +\frac{4}{3}\mu \right )}{n_{i0}T_{i}[1-\mu _{i}+\frac{4}{15}U(\Pi _{j})]}. $$
(20)

Substituting the value of compressional velocity in terms of the coupling parameter from (19) in (18) and after simplifying the resulting equation, we obtain

$$\begin{aligned} \omega ^{3}+ 3\omega _{c} \omega ^{2}+ \left [k^{2} c^{2} (\gamma + 0.16 \Pi _{j}) -\omega _{j}^{2} \right ] \omega \\ + 3\omega _{c} \left [k^{2} c^{2}\left (\frac{(2\Gamma _{e}-1)}{3} +0.16 \Pi _{j} \right )- \omega _{j}^{2}\right ]=0. \end{aligned}$$
(21)

The dispersion relation (21) shows the influence of the Coulomb coupling parameter and heating and cooling functions on the Jeans instability of clumpy MCs. Using the Guillemin (1949) criterion for the sign of roots, we obtain the following condition for the onset of gravitational instability from the constant term of equation (21) and is given by

$$ k^{2} c^{2}\left (\frac{(2\Gamma _{e}-1)}{3} +0.16 \Pi _{j} \right )- \omega _{j}^{2} < 0. $$
(22)

Condition (22) is termed as Jeans instability criterion. The expression for the critical Jeans wavenumber is given by

$$ k_{j1}= \frac{\omega _{j}}{\sqrt{c^{2}\left ( \frac{(2\Gamma _{e}-1)}{3}+ 0.16 \Pi _{j} \right ) }}. $$
(23)

The above condition of Jeans instability and expression of the Jeans wavenumber show the modified form of the Chandrasekhar (1961) instability criterion \(c_{s}^{2}k^{2}-4\pi G \rho _{0}<0\) (or \(k_{J}<\omega _{j}/c_{s}\)) and is modified due to the presence of the Coulomb coupling parameter (\(\Pi _{j}\)) and heating rate parameter (\(\Gamma _{e}\)). It should be noted that the cooling rate parameter does not affect the Jeans instability criterion or the expression of the Jeans wavenumber. Therefore, it is clear from expression (23) that the Jeans wavenumber decreases with increasing values of \(\Pi _{j}\) and \(\Gamma _{e}\) in the clumpy cloudy medium, which yields that the coupling effects and heating rate postpone the gravitational collapse.

The above theoretical expressions are used to calculate the length scale and Jeans frequency for the considered systems. We now consider the real physical conditions of the MCs for estimating the fundamental plasma parameters. In the region of the molecular cloud clumps, we consider the following parameters; number density of \(H_{2}\) molecules \(n= 10^{3}\) cm−3 (Bergin and Tafalla 2007), mass of \(H_{2}\) molecules \(m_{i} = 3.32\times 10^{-24}g\), ion temperature \(T_{i}=10\)K and Coulomb coupling parameter \(\Pi _{j}=2.0\) (Prajapati 2022). With these values of the parameters, the calculated value of the Jeans frequency is measured to be \(\omega _{j} \simeq 0.52 \times 10^{-13}\) s−1, and the corresponding Jeans wavenumber (using expression (23)) \(k_{j1}\simeq 0.46 \times 10^{-17}\) cm−1. Hence, the Jeans length of the molecular clouds \(\lambda _{j5}\simeq 0.44\) pc which is comparable to the length scale of cores within the cloud clumps (Bergin and Tafalla 2007). It is also observed that the calculated value of the Jeans wavelength is larger than the value calculated by Dhiman and Mahajan (2023) for the clumpy MCs with dissipative effects.

The growth rate of the Jeans instability describes how quickly small perturbations or fluctuations within the cloud grow and amplify over time, leading to the eventual collapse of the cloud. The exact behavior of the growth rate depends on the balance between gravitational forces and pressure forces within the cloud. The growth rate of the Jeans instability depends on several factors, including the density of the gas, heating, and cooling functions, its temperature, and the wavelength of the perturbations. To study the impact of the Coulomb coupling parameter and the heating-cooling rate parameter on the growth rate of instability, let us use the following non-dimensional parameters defined in terms of the Jeans frequency;

$$ \hat{\omega}=\omega /\omega _{j}, \hat{k}=kc/\omega _{j} ~ \text{and} ~ \hat{\omega}_{c}=\omega _{c}/\omega _{j}, $$
(24)

the dispersion relation (21) assumes the following non-dimensional form;

$$\begin{aligned} \hat{\omega}^{3}+ 3 \hat{\omega}_{c} \hat{\omega}^{2}+ \left [\hat{k}^{2} (\gamma + 0.16 \Pi _{j}) -1 \right ] \hat{\omega} \\ + 3\hat{\omega}_{c} \left [\hat{k}^{2}\left ( \frac{(2\Gamma _{e}-1)}{3} +0.16 \Pi _{j} \right )- 1\right ]=0. \end{aligned}$$
(25)

The normalized growth rate of Jeans instability is calculated from (25) for different values of wavenumber and is depicted in the following figures. Figure 1. represents the normalized growth rate of the Jeans instability (\(Re (\hat{\omega})\)) versus the normalized wavenumber (\(\hat{k}\)), for different values of the Coulomb coupling parameter \(\Pi _{j}=0.5\) for weakly coupled plasma (WCP), 1.0 (for viscoelastic fluid), and 2.0 for strongly coupled plasma (SCP). It is clear from the curve corresponding to \(\Pi _{j}=0.5\) that due to the weak coupling between the plasma particles, the growth rate for WCP is observed to be larger than that of SCP (\(\Pi _{j}=2.0\)) and viscoelastic fluid (\(\Pi _{j}=1.0\)). Further, the growth rate of the instability region is decreased due to an increase in the coupling parameter, and the region is further decreased in the case of SCP with \(\Pi _{j}=2.0\). This is because it represents high-frequency oscillations with strong coupling between the plasma particles. The Coulomb coupling parameter thus stabilizes the growth rate of the Jeans instability.

Fig. 1
figure 1

The normalized growth rate of Jeans instability (\(Re ( \hat{\omega})\)) versus normalized wave number \(\hat{k}\) for different values of Coupling parameter \(\Pi _{j}=0.5, 1.0, 2.0\) for fixed values of \(\hat{\omega}_{c}=0.2\) (for dense clumps), \(\Gamma _{e}=1.0\) and \(\gamma =5/3\)

Full size image

Figure 2. depicts the change of the normalized growth rate with normalized wavenumber for the different values of the cooling rate parameter; \(\hat{\omega}_{c} =0.3, 0.6, 1.0\), in the presence (\(\Gamma _{e} =1 \)) of cloud stirring of the molecular cloud. The variation reveals that the growth rate increases with increasing values of the cooling rate \(\hat{\omega}_{c}\), which means that the onset of gravitational instability sets early in the diffused molecular cloud, as compared to dense clouds, which can be validated from the analysis of Elmegreen (1989). Hence, the cooling rate parameter (\(\hat{\omega}_{c}\)) shows destabilizing character against the self-gravitating collapse dynamics by increasing the rate at which structure fomation takes place. It is also clear that the cutoff wavenumber at which the growth rate becomes zero remains the same for each value of the cooling parameter (\(\hat{\omega}_{c}\)).

Fig. 2
figure 2

The normalized growth rate of Jeans instability (\(Re ( \hat{\omega})\)) versus normalized wavenumber \(\hat{k}\) for different values of Cooling parameter \(\ \hat{\omega}_{c}=0.3, 0.6, 1.0\) for fixed values of \(\Pi _{j}=2.0\), \(\Gamma _{e}=1.0\) and \(\gamma =5/3\)

Full size image

In Fig. 3., the growth rate of Jeans instability is depicted for the different values of the heating rate parameter, \(\Gamma _{e} = 0.0, 1.0, 2.0\). From the figure, it is observed that the values of the normalized growth rate of gravitational instability are higher in the absence of heating (\(\Gamma _{e} = 0.0\)) rate parameter as compared to the values in the presence of heating (\(\Gamma _{e} =1.0, 2.0\)) rate parameter. Thus, it is concluded that the heating rate, which arises due to dense cloud stirring, has a stabilizing influence on gravitational instability. In this case, the cutoff wavenumbers at which the growth rate becomes zero are different for the different values of \(\Gamma _{e}\). In the absence of the heating rate parameter (\(\Gamma _{e} = 0.0\)) the cutoff wavenumber is much larger than that in the remaining cases. The suppression of the growth rate with \(\Gamma _{e} \ne 0\) lies in the range of finite perturbation wavenumbers. Thus, we conclude that both coupling and heating rate parameters delay the onset of collapse of MCs and the structure formation.

Fig. 3
figure 3

The normalized growth rate of Jeans instability (\(Re ( \hat{\omega})\)) versus normalized wavenumber \(\hat{k}\) for different values of heating rate \(\Gamma _{e}=0,1.0,2.0\) for fixed values of \(\Pi _{j}=2.0\), \(\hat{\omega}_{c}=0.2\) and \(\gamma =5/3\)

Full size image

3.2 Hydrodynamic limit

Let us now discuss the dispersion properties in the hydrodynamic limit or weakly coupled limit corresponding to \(\tau _{m} \omega \ll 1\). The weakly coupled limit refers to a regime where the interactions between individual particles in the plasma are relatively weak compared to their kinetic energies. In this limit, the first factor of the dispersion relation (15) reduces to

$$\begin{aligned} \omega ^{4} + \omega ^{3} \left (2\tau _{m} v_{c}^{2} k^{2} \right ) + \omega ^{2}\left (4 \Omega _{z}^{2}+ 2 V_{A}^{2} k^{2} + \tau _{m}^{2} v_{c}^{4} k^{4}\right ) \\ + \omega \left ( 2\tau _{m} V_{A}^{2} k^{4} v_{c}^{2} \right ) + V_{A}^{4} k^{4} =0. \end{aligned}$$
(26)

Equation (26) represents a non-gravitating stable mode that includes the effect of rotational frequency, Alfvén wave velocity, and viscoelastic coefficients. It is independent of the heating and cooling parameters of the clumpy MCs. The stability of the system represented by the above equation can be discussed using the Routh-Hurwitz criterion. Accordingly, all the coefficients of the polynomial must be positive, which satisfies the necessary condition of stability. To satisfy the sufficient condition, all the principal diagonal minors must be positive. We calculate the principal diagonal minors, which are given by;

$$ \triangle _{1}= 2 \tau _{m} v_{c}^{2} k^{2} >0, $$
$$ \triangle _{2}= \left ( 4 \Omega _{z}^{2} + V_{A}^{2} k^{2} + v_{c}^{4} k^{4} \right ) \triangle _{1} >0, $$
$$ \triangle _{3}= 4 \tau _{m} ^{2} V_{A}^{2} v_{c}^{4} k^{6} \left ( 4 \Omega _{z}^{2} + \tau _{m} ^{2} v_{c}^{4} k^{4} \right ) >0, $$
$$ \triangle _{4}= V_{A}^{4} k^{4} \triangle _{3} >0. $$

We found that the values all the \(\triangle \) are positive, hence the system represented by equation (26) is a stable system.

The second factor of dispersion relation (15) under the weakly coupled limit reduces to

$$ \begin{aligned} \omega ^{3}+\left [ 3\omega _{c} + \tau _{m} v_{c}^{2} k^{2} \right ] \omega ^{2}+ \left [ \left (c^{2}\gamma + 3\omega _{c} \tau _{m} v_{c}^{2} \right ) k^{2} \right . \\ \left . -\omega _{j}^{2}\right ] \omega + 3\omega _{c} \left [ \frac{k^{2} c^{2} \left (2\Gamma _{e}-1 \right )}{3}- \omega _{j}^{2} \right ]=0. \end{aligned} $$
(27)

Clearly, equation (27) represents the dispersion relation for weakly coupled plasma in a rotating and magnetized clumpy molecular cloud, which is modified due to the presence of viscoelastic coefficients, and heating and cooling functions. The onset of gravitational instability occurs when,

$$ \frac{k^{2} c^{2}\left (2\Gamma _{e}-1 \right )}{3} - \omega _{j}^{2} < 0. $$
(28)

Furthermore, the value of the critical Jeans wavenumber is given by

$$ k_{j2}= \frac{\omega _{j}}{\sqrt{ \frac{c^{2} \left (2\Gamma _{e}-1\right )}{3}}}. $$
(29)

We find that the above Jeans instability criterion is independent of the cooling and Coulomb coupling parameters and is different from the instability criterion obtained in the kinetic limit. In order to observe the Jeans instability and get real values of the critical wavenumber, \(2\Gamma _{e}-1>0\) or \(\Gamma _{e} >0.5\). Elmegreen (1989) suggested the significance of the heating rate parameter in the cloud clump formation. He mentioned that regions without much star formation activity (i.e. \(\Gamma _{e}=0\)) will spontaneously clump into cloud complexes on a variety of scales. This scale ranges from the collisional mean free path up to the scale of the conventional Jeans instability in the interstellar gas disk. The small-scale clumping occurs at approximately the same rate as the large-scale clumping if the component clouds are mildly self-gravitating with \(\frac{\omega _{c}}{\omega _{j}}\sim 1\). Once star formation begins and energy is available to stir the cloud population, thermal equilibrium becomes possible (\(\Gamma _{e}=1\)). Under these circumstances, the Jeans instability is observed, which grows continuously for sufficiently large molecular cloud clumps.

Let us now illustrate the growth rate of the Jeans instability in the hydrodynamic limit. The dimensionless form of dispersion relation (27) is derived using the non-dimensional parameters; (\(\hat{\omega}=\omega /\omega _{j}, \hat{k}=kc/\omega _{j}, \hat{\tau}_{m} = \tau _{m} \omega _{j}\) and \(\hat{\omega}_{c}=\omega _{c}/\omega _{j}\)), as;

$$ \begin{aligned} \hat{\omega}^{3}+ \left [3 \hat{\omega}_{c} + 0.16 \Pi _{j} \hat{\tau}_{m} \hat{k}^{2}\right ] \hat{\omega}^{2}+ \left [\hat{k}^{2} (\gamma + 0.48 \Pi _{j} \hat{\tau}_{m} \hat{\omega}_{c} ) \right . \\ \left . -1 \right ] \hat{\omega} + 3 \hat{\omega}_{c} \left [ \frac{\hat{k}^{2}\left (2\Gamma _{e}-1\right )}{3}- 1\right ]=0. \end{aligned} $$
(30)

Figure 4. shows the variation in normalized growth rate (\(Re ( \hat{\omega})\)) against normalized wave number \(\hat{k}\) for various values of cooling rate parameter; \(\hat{\omega}_{c} =0.3, 0.6, 1.0\), in the presence of heating function \(\Gamma _{e}=1.0\) and relaxation time \(\hat{\tau}_{m}=1.0\). The nature of the curves indicates that the growth rate increases with increasing values of the cooling rate \(\hat{\omega}_{c}\), which is the same as that obtained in Fig. 2. Notably, in the kinetic limit (Fig. 2.), the cutoff wavenumber at which the growth rates become zero is \(\hat{k}_{c1}=1.25\), while in the hydrodynamic limit, it has been increased to \(\hat{k}_{c2}=1.75\). Thus, the cooling function (\(\hat{\omega}_{c}\)) shows destabilizing behaviour on the growth rate of self-gravitational instability and encourages the gravitational collapse of clouds to start the structure formation process.

Fig. 4
figure 4

The normalized growth rate of Jeans instability (\(Re ( \hat{\omega})\)) versus normalized wavenumber \(\hat{k}\) for different values of Cooling parameter \(\hat{\omega}_{c}=0.3, 0.6, 1.0\) for fixed values of \(\Pi _{j}=0.5\), \(\Gamma _{e}=1.0\), \(\tau _{m}=1.0\) and \(\gamma =5/3\)

Full size image

Figure 5. represents the variation in the normalized growth rate (\(Re (\hat{\omega})\)) versus the normalized wavenumber \(\hat{k}\) for different values of heating rate \(\Gamma _{e}=0.0,1.0,2.0\) in the presence of the memory parameter (\(\hat{\tau}_{m}=1.0\)) and cooling rate parameter (\(\hat{\omega}_{c}=0.2\)). The curves show that the growth rate of gravitational instability decreases with the increasing values of heating rate and wavenumber. Hence, it stabilizes the collapse dynamics of the clumpy MCs. Additionally, in the presence and absence of cloud stirring, the cutoff wavenumber is very large in the hydrodynamic regime as compared to the kinetic regime.

Fig. 5
figure 5

The normalized growth rate of Jeans instability (\(Re ( \hat{\omega})\)) versus normalized wavenumber \(\hat{k}\) for different values of heating rate \(\Gamma _{e}=0.0,1.0,2.0\) for fixed values of \(\Pi _{j}= 0.5\), \(\hat{\omega}_{c}=1.0\), \(\tau _{m}=1.0\) and \(\gamma =5/3\)

Full size image

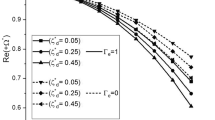
The normalized growth rate of Jeans instability in the hydrodynamic regime is calculated from (30) for different values of wavenumber and depicted in figures. In Fig. 6., the normalized growth rate of the Jeans instability (\(Re (\hat{\omega})\)) is plotted against the normalized wavenumber (\(\hat{k}\)) using (25) and (30) for kinetic and hydrodynamic limits, respectively. From the curves, it is clear that the growth rate is larger for WCP with the Coulomb coupling parameter \(\Pi _{j}= 0.5\) as compared to SCP with the Coulomb coupling parameter \(\Pi _{j}=2.0\) in the presence of cooling and heating functions. This might be because weakly coupled limits exhibit a slower decrease in the growth rate of unstable Jeans modes than strongly coupled limits. The kinetic limit corresponds to the high-frequency limit (\(\omega \tau _{m} \gg 1\)) thus, the growth rate decreases faster than the low-frequency hydrodynamic limit.

Fig. 6
figure 6

Comparison of the normalized growth rate of Jeans instability (\(Re (\hat{\omega})\)) versus normalized wave number \(\hat{k}\) between kinetic limit (with \(\Pi _{j}=2.0\)) and hydrodynamic limit (with \(\Pi _{j}=0.5\)) for fixed values of \(\hat{\omega}_{c}=0.2\), \(\Gamma _{e}=1.0\), \(\hat{\tau}_{m}=1.0\) and \(\gamma =5/3\)

Full size image

4 Conclusions

The radiative heating and cooling mechanisms play a crucial role in the energy transfer and subsequent gravitational collapse in dense clumps of MCs. This paper studies the influence of heating and cooling parameters on the gravitational instability of rotating and magnetized strongly coupled plasma in the clumps of MCs. A dispersion relation for the considered configuration has been derived analytically using the normal mode analysis and discussed in hydrodynamic and kinetic limits. In both cases, the Jeans criteria are modified due to the presence of the Coloumb coupling parameter and heating rate, but uniform rotation and magnetic field do not affect the instability criterion. However, the presence of magnetic field and uniform rotation significantly modify the compressional Alfvén viscoelastic mode. Furthermore, we calculated the growth rate of instability against the wavenumber for both cases and found that the normalized growth rate decreased with increasing wavenumber.

The graphical illustrations show that the Coulomb coupling parameter (\(\Pi _{j}\)) and heating rate parameter (\(\Gamma _{e}\)) stabilizes the growth rate of Jeans instability. The cooling rate parameter (\(\omega _{c}\)) shows a destabilizing character against the self-gravitating collapse dynamics. The dynamical stability of the system has been discussed using the Routh-Hurwitz criterion. The variation of growth rate is also plotted in the hydrodynamic limit to study the effects of heating, and cooling parameter and to compare the growth rates with kinetic limits. We found that the growth rate decreases faster in the kinetic limits than in the hydrodynamic limit. Thus, the collapse rate is slower in the hydrodynamic or weakly coupled limit.

The role of strong coupling effects is ubiquitous in many astrophysical systems, such as white dwarfs, neutron stars and in some regions of MCs, as they exist in strongly coupled states. The numerical parameters are calculated for clumpy MCs and measure the Jeans frequency to be \(\omega _{j} \simeq 0.52 \times 10^{-13}\) s−1, Jeans wavenumber \(k_{j1}\simeq 0.46 \times 10^{-17}\) cm−1. The Jeans length for the MCs is calculated to be \(\lambda _{j5}\simeq 0.44\) pc which is comparable to the length scale of cores within cloud clumps. The present results are helpful to discuss the gravitational collapse in dense clumps of MCs consisting of strongly coupled magnetized plasma with rotation. The inclusion of finite electrical resistivity and the Hall effect is a possible future scope of the present work.