Analysing the region of the rings and small satellites of Neptune

Abstract

The ring system and small satellites of Neptune were discovered during Voyager 2 flyby in 1989 (Smith et al. in Science 246:1422, 1989). In this work we analyse the diffusion maps which can give an overview of the system. As a result we found the width of unstable and stable regions close to each satellite. The innermost Galle ring, which is further from the satellites, is located in a stable region, while Lassel ring ($W= 4000~\text{km}$) has its inner border in a stable region depending on its eccentricity. The same happens to the Le Verrier and Adams rings, they are stable for small values of the eccentricity. They can survive to the close satellites perturbation only for values of $e < 0.012$. When the solar radiation force is taken into account the rings composed by $1~\upmu \text{m}$ sized particles have a lifetime of about $10^{4}$ years while larger particles ($10~\upmu \text{m}$ in radius) can survive up to $10^{5}$ years. The satellites Naiad, Thalassa and Despina can help replenish the lost particles of the Le Verrier, Arago and Lassel rings, while the ejecta produced by Galatea, Larissa and Proteus do not have enough velocity to escape from the satellite gravity.

1 Introduction

Six satellites of Neptune were discovered in 1989 during Voyager 2 flyby: Naiad, Thalassa, Despina, Galatea, Larissa and Proteus (Smith et al. 1989). Proteus is larger compared to the other five satellites, which have radius smaller than 100 km. Triton, the largest satellite, and Nereid completed the Neptune satellite system until the discovery of Hippocamp, the smallest satellite (about 17 km in radius, (Showalter et al. 2019)).

Voyager 2 cameras also imaged a ring system formed by Galle, Le Verrier, Lassel, Arago and Adams rings (Smith et al. 1989). Adams ring is a narrow ring composed by a sample of arcs named Couragé, Liberté, Fraternité, Egalité 1 and 2. These arcs have shown variations in brightness. Le Verrier and Arago rings are also narrow, while Lassel ring is larger and very faint. Galle ring is the innermost ring 2000 km wide. There is also a co-orbital ring with the satellite Galatea (Porco et al. 1995).

Several papers have analysed the origin of the rings of Neptune (Colwell and Esposito 1992, 1993) and the history of the inner small satellites (Banfield and Murray 1992; Zhang and Hamilton 2008). It is also worth to analyse the system nowadays and the connection between the satellites, specially the satellites close to the ring system.

The goal of this work is to analyse the region encompassing the orbits of the small satellites and the ring system of Neptune, as well as the interaction among the satellites and the ring particles. The paper is divided into 4 sections. In Sect. 2 we briefly describe the frequency map analysis (FMA) technique applied for the satellites region and the results regarding the diffusion maps. In Sect. 3 we analyse perturbative forces, solar radiation force and plasma drag, acting in the ring particles and the rôle of each satellite in production ring material. In the last section we discuss our results.

2 Satellites’ region

In this section we analyse the region encompassing the orbits of the small satellites and the rings through the FMA technique. The FMA is useful in identifying chaotic regions in dynamical systems with arbitrary degrees of freedom. FMA has been successfully applied for several dynamical systems (Laskar 1990, 1993; Nesvornỳ and Morbidelli 1998; Robutel and Laskar 2001; Papaphilippou and Laskar 1998).

Following Munõz-Gutiérrez and Giuliatti Winter (2017) we construct diffusion maps by performing a FMA of the quantity $z'(t) = a(t)~\exp (i~\lambda )$ for each test particle in a grid of initial conditions covering the Neptune’s satellites and rings region. We applied the frequency modified Fourier transform (FMFT) algorithm (Šidlichovskỳ and Nesvornỳ 1997) over $z'(t)$ on the adjacent time intervals $[0,T]$ and $[T, 2T]$, where $T$ corresponds to half of the total integration time. We compare the main frequencies $\nu _{1}$ and $\nu _{2}$ from each time interval in order to calculate the diffusion parameter $D$, defined following Robutel and Laskar (2001), Correia et al. (2005) as

$$ D=\frac{{|\nu _{1} - \nu _{2}|}}{{T}}, $$

The $D$ parameter gives a measure of the stability of the orbit of each particle, since the value of $|\nu _{1} - \nu _{2}|$ will be large for those particles in unstable orbits, whereas if this difference is small the particle will be in a stable orbit. The value of $D$ is proportional to the value of $|\nu _{1} - \nu _{2}|$. To construct the diffusion maps, the value of $\log D$ can be plotted in a diagram $a \times e$, in colour scale, for each initial condition of the particle.

We also calculated the diffusion time-scale ($t_{D}$) which is an estimation of the time required for a diffusion of the orbit of the particle in the radial direction. It can be given by $t_{D}= (DP)^{-1}$, where $P$ is the period of the orbit of the particle.

The numerical integration was carried out through the Mercury package (Chambers 1999) using the Burlish Stöer integrator. The dynamical system is formed by Neptune, and its gravity coefficients $J_{2}$ and $J_{4}$, the satellites Naiad, Thalassa, Despina, Galatea, Larissa, Hippocamp, Proteus and Triton and a sample of thousands of massless particles. Table 1 gives the physical parameters of Neptune: mass ($M_{\mathrm{N}}$), radius ($R_{\mathrm{N}}$), and the gravity coefficients $J_{2}$ and $J_{4}$. Table 2 gives the physical parameters of the eight satellites. All the simulations were performed at the Saturn Cluster of the Group of Planetology and Orbital Dynamics at UNESP. The initial positions and velocities of each satellite are given in Table 4. These values were taken from the Horizons website for the Julian Day 2457785.5, which corresponds to the date February 1, 2017.

Table 1 Parameters of Neptune. Extracted from Jacobson (2009)

Table 2 Parameters of the satellites

In order to eliminate the short periodic variations due to the gravity coefficients of Neptune we transform the positions and velocities of the satellites into the geometric elements (Renner and Sicardy 2006). The geometric elements given in Table 5 are the semimajor axis $a~(\times D_{\mathrm{AR}})$, where $D_{\mathrm{AR}}$ is the semimajor axis of the Adams ring ($D_{\mathrm{AR}}=62932.7~\text{km}$ (Table 3)), the eccentricity $e$, the inclination $I$ in degrees, and the angles $\varpi$, $\varOmega$ and $\lambda$ are the longitude of the pericentre, the longitude of the ascending node and the mean longitude, respectively. The parameters of the ring system, semimajor axis in km, width ($W$) in km and optical depth, are described in Table 3. All other orbital elements of the rings, i.e. $e$, $I$, $\varpi$, $\varOmega$ and $\lambda$ were taken as zero.

Table 3 Parameters of Neptune’s rings. Extracted from De Pater and Lissauer (2015), De Pater et al. (2019)

Table 4 Positions ($x$, $y$, $z$) and velocities ($v_{x}$, $v_{y}$, $v_{z}$) of the eight satellites in Neptune inner and Triton reference system (International Celestial Reference Frame—ICRF). The epoch for the state vectors is February 1, 2017 TDB. These values were extracted from the site web HORIZONS^a

In order to produce the diffusion maps we performed numerical integrations of the system for a total time of $10^{4}$ orbital periods of the most external satellite. In the range from $0.6004D_{\mathrm{AR}}$ to $1.29D_{\mathrm{AR}}$ the most external satellite is Larissa, therefore the numerical simulation lasted about 18 years. From $1.3D_{\mathrm{AR}}$ to $2.2009D_{\mathrm{AR}}$ the most external satellite is Proteus, therefore the duration of the numerical integration was about 35 years.

A sample of test particles were distributed in a rectangular diagram, $a \times e$. The initial values were adopted as follows: (i) the semimajor axis $a$ was taken in the range $0.6004D_{\mathrm{AR}}$ to $2.2009D_{\mathrm{AR}}$, with a resolution $\Delta a = {3 \times 10^{-4}}$, (ii) $0 \leq e \leq 0.04$, with $\Delta e = 4 \times 10^{-3}$, (iii) the inclination $I$, longitude of the pericentre $\varpi$, longitude of the ascending node $\varOmega$ and mean longitude $\lambda$ were assumed to be zero.

The diffusion maps were generated for the region encompassing the orbits of the satellites Naiad to Proteus. The position of each satellite is identified by a black dot. In the following figures we describe each region in details.

Figure 1 shows the region where the Galle ring and Naiad are located. A coloured rectangle was plotted in the centre of each initial value of $a$ and $e$. White rectangles indicate that the particle collided or was ejected from the system. The location and ratios of mean motion resonances (MMRs) with Naiad are indicated with black dashed lines and with labels at the top of the figure. The solid black curves correspond to the collision curves. The equations defining such curves are $a_{s}(1+ e_{s}) = a(1-e)$ if $a \geq a_{s}$ and $a_{s}(1 - e_{s}) = a(1 + e)$ when $a \leq a _{s}$, where $a$, $e$, $a_{s}$, $e_{s}$ are the semimajor axis and eccentricity of the particle and the satellite, respectively. The values of the semimajor axis and eccentricity of the satellites were obtained from Table 5. Particles entering this region will cross the orbit of the satellite and will be likely ejected or will collide with the satellite. Most of the particles between these curves will collide with the satellite before the end of the numerical simulation. Since Naiad is a small satellite, it will take longer time for clearing the region between these two curves. Galle ring is located between 0.651$D _{\mathrm{AR}}$ and $0.683D_{\mathrm{AR}}$, in a stable region for almost any value of $e$.

Fig. 1

Diffusion map for Naiad region. Galle ring is located from $0.651D_{\mathrm{AR}}$ to $0.683D_{\mathrm{AR}}$. The width of the ring can is indicated in the figure as a horizontal line. Dashed black lines indicate the location of the MMRs with Naiad. Blue colours correspond to stable regions, while redder colours denote unstable regions

Table 5 Geometric elements of the inner satellites of Neptune system. These values were extracted from Table 4

Thalassa and Despina cleared up the regions between the black curves in a short period of time (Fig. 2). Most of the region between these two satellites is unstable. Despina can hold a coorbital region for values of $e$ smaller than 0.01 (blue rectangles). The MMRs ratios with Naiad (in black colour), Thalassa (in dark blue), Galatea (in orange colour) and Larissa (in red colour) are indicated in the top of the figure. Thalassa and Larissa are close to the 17:18 MMR and Despina and Thalassa are close to the 27:29 MMR. The inner edge of the Lassel ring (0.845$D_{\mathrm{AR}}$) is located in an unstable region overlapping the outer edge (0.846$D_{\mathrm{AR}}$) of the Le Verrier ring. The same overlap occurs between the outer edge of the Lassel ring (0.908$D_{\mathrm{AR}}$) and the inner edge of the Arago ring (0.908$D_{\mathrm{AR}}$).

Fig. 2

Diffusion map for Thalassa and Despina regions. Despina cleared the unstable region. The MMRs with Naiad (in black colour), Thalassa (in dark blue), Galatea (in orange colour) and Larissa (in red colour) are indicated at the top of the figure

Figure 3 shows the diffusion map for the region surrounding the satellite Galatea, its co-orbital ring, Adams ring and its arcs. The Adams ring is located at 1$D_{\mathrm{AR}}$. For small values of $e$ the ring particles are in a stable region. The location of the coorbital ring and Adams ring are shown in black dashed lines. The MMRs are shown at the top of the figure, six MMRs with Galatea (in orange colour) and two MMRs with the satellite Larissa (in red colour). As can be seen the Adams ring is close to the 42:43 MMR with Galatea, as proposed by the confinement mechanism model.

Fig. 3

Diffusion map for Galatea region. Two rings, the co-orbital ring of Galatea and the Adams ring, are located in this region

Larissa region is stable from $1.26D_{\mathrm{AR}}$–$1.4D_{\mathrm{AR}}$ (Fig. 4). The satellite clears the region between the diagonal black curves as expected. MMR’s with Naiad (in black colour), Larissa (in red colour), Hippocamp (in green colour), Galatea (in orange colour) and Despina (1:2d) can be seen in the top of the figure.

Fig. 4

Diffusion map for Larissa region. A stable region is located at $1.26D_{\mathrm{AR}}\mbox{--}1.4D_{\mathrm{AR}}$

Hippocamp is a very small satellite recently discovered by Showalter et al. (2019). The region surrounding this satellite is stable. Several first and second orders MMR with Proteus, Hippocamp and Galatea can be seen in the top of Fig. 5, one of this resonance is between Hippocamp and Proteus, 13:11 MMR. All the MMR’s shown in Fig. 6 is with the satellite Proteus.

Fig. 5

Diffusion map for Hippocamp region. Due to the small effects of the satellite, this region is stable. Hippocamp can be in a 13:11 MMR with the satellite Proteus

Fig. 6

Diffusion map for Proteus region. All the MMRs shown in Fig. 6 are related to the satellite Proteus

Figure 7 shows the diffusion time-scale map for all the region. An unstable region surrounds the satellite Proteus, the largest one. The diffusion time is about $10^{2}$ years. A large stable region can be seen between the orbits of the satellites Larissa and Hippocamp. The rings are also in stable regions (Fig. 8), taking into account only the gravitational effects of the satellites. No dissipative forces were included in the system up to now.

Fig. 7

Diffusion time-scale for the region. The satellites are indicated as black dots

Fig. 8

Diffusion time-scale of the rings: (a) Galle, Le Verrier and Lassel rings and (b) Arago, Galatea co-orbital and Adams rings

Figure 8a shows the diffusion time-scale ($t_{D}$) for the Galle, Le Verrier and Lassel rings for different values of the eccentricity. The average $t_{D}$ is relevant for the rings with large width. In fact it is relevant for the Lassel ring since it is located in different values of $\log D$ (Fig. 2). Galle ring is in a stable orbit with diffusion time of $10^{11}$ years, while the Le Verrier ring has an average diffusion time dependent on the eccentricity. This ring has a very short lifetime for values of $e = 0.012$. The Lassel ring has $t_{D}$ about $10^{9}$ years. Figure 8b shows the diffusion time-scale for the Arago, Galatea co-orbital and Adams rings. Arago ring has a diffusion time from $10^{8}$ to $10^{11}$ years depending on the eccentricity, while the Adams ring particles can survive up to $e \sim 0.012$, after this value of $e$ the ring particle enters the chaotic zone caused by the effects of Galatea. Galatea co-orbital ring can survive up to about $10^{5}$ years.

3 Ring system under perturbative forces

Regarding the dynamics of Neptune’s rings we showed (Sect. 2) that the rings are located in stable positions, some of them are stable only for small values of $e$. However since these rings are composed of very tiny particles, these particles suffer the effects of dissipative forces, such as the solar radiation force. Figure 9 shows the strength of the force due to the oblateness of Neptune ($a_{\mathrm{oblat}}$), the solar radiation force $(a_{\mathrm{SRF}})$ and the gravitational effects of the satellite Triton ($a_{\mathrm{T}}$) on a $1~\upmu \text{m}$ sized particle. These equations are given by (Murray and Dermott 1999; Mignard 1984):

$$\begin{aligned} &a_{\mathrm{oblat}}= \frac{{3GM_{\mathrm{N}} J_{2} R_{\mathrm{N}}^{2}}}{{a^{4}}} \\ &a_{\mathrm{SRF}} = \frac{{3 \varPhi Q_{\mathrm{pr}}}}{{4c \rho r}} \\ &a_{\mathrm{T}} = \frac{{G m_{\mathrm{T}}}}{{(a-a_{\mathrm{T}})}} \end{aligned}$$

where $\varPhi$ is the solar flux, $Q_{\mathrm{pr}}$ is a constant taken as 1 (Mignard 1984), $c$ is the speed of light, $\rho$ is the density of the particle (assumed to be 1 g/cm³), $r$ is the radius of the particle, $m_{\mathrm{T}}$ and $a_{\mathrm{T}}$ are the mass and semimajor axis of Triton, respectively.

Fig. 9

Strength of the forces in Neptune ring system as a function of the distance. The locations of the satellites and the rings are displayed as vertical lines

As can be seen in Fig. 9 the solar radiation force produces less effects on the particles compared to the effects of $J_{2}$ and the gravitational effects of Triton.

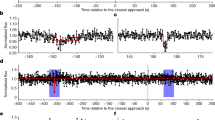
In order to analyse the effects of this dissipative force a sample of numerical simulations of the ring particles under the effects of $J_{2}$ and $J_{4}$ of Neptune and all the eight satellites was carried out. Figure 10 shows the time variation of the eccentricity of a representative particle located in each ring, Galle, Le Verrier, Lassel, Arago and Adams rings.

Fig. 10

Time variation of the eccentricity of a representative particle of each ring. The name of the ring is shown in the top of each figure. Each plot has two curves, without and with the effects of the solar radiation pressure. The effects of this dissipative force is responsible for the small increase in the eccentricity of the 1 μm sized particle

The eccentricity of a representative 1 μm sized particle increases due to the effects of the solar radiation force. However this increase is small (Fig. 10). All the eccentricities remain of order $10^{-3}$. There are two plots related to the Adams ring, the plot labelled Adams-LER 42:43 means that the ring particle is located in the resonance with the satellite Galatea. The confinement due to this resonance reduces the increase in the eccentricity of the ring particle. Adams ring and its arcs are under investigation by Giuliatti Winter et al. (2019).

Due to the increase in the eccentricity, the ring particles can alter their radial excursions, but despite of that they will not cross the orbits of any satellite. The edges of Le Verrier, Lassel and Arago rings will have the overlap increased.

Concerning the co-orbital ring to Galatea our results showed that although all the small particles remained azimuthally confined (no collision with Galatea was detected), the smaller particle (1 μm in radius) performs radial oscillations of about 900 km, while the oscillation of a particle of 10 μm in radius is only ∼ 120 km. These radial excursions do not cross the inner edge of the Adams ring. Larger particles (30 μm, 50 μm and 100 μm in radius), as expected, stay close to the co-orbital region. In $10^{5}$ years the semimajor axis of the smaller particle decreases up to 7000 km, crossing the Arago ring and the outer edge of the Lassel ring (57 200 km).

The timescale for decay of the tiny particles caused by the Poynting-Robertson component gives the time each ring will cross the orbit of the satellite and therefore its lifetime. The Poynting-Robertson component of the solar radiation force provokes a secular decrease in the semimajor axis of the particle and the timescale ($\tau _{\mathrm{pr}}$) can by given by (Mignard 1984)

$$ \tau _{\mathrm{pr}} \sim 10^{6}~r $$

Galle 1 μm sized ring particles will collide with Neptune in $5 \times 10^{5}$ years while larger particles (10 μm in radius) will take $5 \times 10^{6}$ years to reach Neptune. Le Verrier, Lassel, Arago and Adams rings have similar lifetimes, small particles (1 μm in radius) will reach the orbit of a given satellite in $10^{4}$ years and larger particles (10 μm in radius) in $10^{5}$ years. These values are given in Table 6.

Table 6 Lifetime of the rings particles (1 μm and 10 μm in radius) due to Poynting-Robertson effects

Plasma drag can also reduce the lifetime of the ring particles, however, we did not include these force due to few information on the Neptune plasmasphere. The azimuthal force caused by the plasmasphere’s ions in the ring particles is given by (Hedman et at. 2013)

$$ F_{\text{PD}}=\pi a^{2}(n-n_{\mathrm{N}})^{2}r^{2} \rho _{i} $$

where $n_{\mathrm{N}}$ is Neptune’s rotation rate $(n_{\mathrm{N}}\sim 10.9~\text{rad}/\text{day})$ and $\rho _{i}$ is the plasma ion mass density. The plasma drag effect increases the semimajor axis of the particles in the rings region. The estimated time variation of the semimajor axis is

$$ \frac{da}{dt} \sim 10^{-2} \biggl(\frac{\rho _{i}}{1~{\mathrm{amu}}/ {\mathrm{cm}}^{3}} \biggr) \biggl(\frac{1~\upmu \text{m}}{r} \biggr)~\text{km}/\text{year} $$

A very rough estimative was performed by assuming the plasmasphere as composed primarily of $H^{+}$ (1 amu) and number density as $10^{3}/{\text{cm}}^{3}$ (Lyons 1995). We obtained that the semimajor axis of $1~\upmu \text{m}$ sized particles increases of order of 10 km per year. The time to the ring particles cross the orbit of the outer satellite is given in Table 7.

Table 7 Lifetime of the rings particles (1 μm and 10 μm in radius) due to plasma drag effects

We can also analyse the rôle of each satellite in producing ring material. A satellite can produce material due to impacts of interplanetary dust particles (IDPs) onto its surface. The material ejected can feed a tenuous ring. By assuming the impactors mass flux at Neptune’s region as $F_{\mathrm{imp}}^{\infty }=10^{-17}~\mbox{kg}/(\mbox{m}^{2}\,\text{s})$ and the mean velocity of the impactors as $v_{\mathrm{imp}}^{\infty }=3.0~\text{km}/\text{s}$ (Poppe 2016), we determined the mass flux $F_{\mathrm{imp}}$ and velocity $v_{\mathrm{imp}}$ of impactors enhanced by to the gravitational focusing of the planet through the algorithm described in Sfair and Giuliatti Winter 2012 and Madeira et al. (2018). The mass production rate by an icy moon with radius $R$ is (Koschny and Grün 2001; Krivov et al. 2003)

$$ M^{+}=1.2\times 10^{-6} R^{2}F_{\mathrm{imp}} v_{\mathrm{imp}}^{2.46} $$

Figure 11 shows the mass production rate of the neptunian inner satellites Naiad, Thalassa, Despina, Galatea, Larissa and Proteus. The squares refer to the satellites whose escape velocity is higher than the velocity of the dust particles, while the circles are for the satellites whose escape velocity is smaller than the ejecta velocity. Therefore Galatea, Larissa and Proteus can produce dust particles, although most of the grains can not leave the satellites surface. The result regarding the satellite Galatea is derived from Giuliatti Winter et al. (2019).

Fig. 11

Mass production rate of the neptunian inner satellites

A crude estimative can be made by comparing the mass of the ring and the mass production of a satellite immersed on it. The mass of Neptune ring can be calculated using the algorithm presented in Sfair and Giuliatti Winter 2012. Assuming $\tau = 3.3 \times 10^{-3}$ for the Le Verrier and Arago rings their masses are about $5 \times 10^{8}~\text{kg}$ and $4.5 \times 10^{8}~\text{kg}$, respectively. Lassel ring mass is about $6 \times 10^{8}~\text{kg}$. Naiad, Thalassa and Despina can produce dust particles and populate these rings in less than 1000 years. However, these satellites are not immersed in these rings and part of these particles will be lost until they can reach the ring. Nevertheless Naiad, Thalassa and Despina may contribute to the ring population.

4 Discussion

The diffusion maps give an overview of the system populated by small satellites and ring particles of Neptune. The largest unstable region is surrounding Proteus, the large satellite. Between the satellites Larissa and Hippocamp is located the largest stable region. Several MMRs of first and second orders were identified, as examples, Thalassa and Larissa are close to the 17:18 MMR, Despina and Thalassa are close to 27:29 MMR and the recent discovery satellite Hippocamp is in the 13:11 MMR with Proteus.

When only gravitational force is present in the system most of the rings are located in stable regions. The innermost Galle ring is further from the satellites and is located in a stable region, while Lassel ring ($W= 4000~\text{km}$) has its inner border stable depending on its eccentricity. The same occurs to the Le Verrier ring, this ring can survive the perturbations caused by Despina only if its eccentricity is smaller than 0.012. Adams ring is also stable for values of $e < 0.012$.

Solar radiation pressure is important for the ring particles of Jupiter, Saturn, Uranus and even Pluto. In Neptune system this dissipative force causes only very small variations in the eccentricities of the ring particles. The eccentricities of the ring particles are of order $10^{-3}$ due to the gravitational perturbations of the satellites and stay at this same order even when the solar radiation force is taken into account. The particles do not cross the orbits of the satellites when these new values of eccentricity are assumed.

The lifetime of the rings particles is probably dictate by the decreasing in the semimajor axis due to secular effects of the Poynting-Robertson component of the solar radiation force. Although the lifetime caused by the perturbations of the nearby satellites is close to this value (Fig. 8). The lifetime of the rings composed by $1~\upmu \text{m}$ sized particles is about $10^{4}$ years and about $10^{5}$ when the particles are larger ($10~\upmu \text{m}$ in radius). The plasma drag may be an important dissipative force but we need further information to constrain its effects in the ring particles.

The satellites Naiad, Thalassa and Despina can help replenish the lost particles of Le Verrier, Arago and Lassel rings. The velocities of the ejecta particles are larger than the escape velocities and the ejecta particles can reach the rings. However, the satellites Galatea (Giuliatti Winter et al. 2019), Larissa and Proteus also produce ejecta material, but they do not have enough velocity to escape from the satellite gravity.

A paper by Brozović et al. (2019) was published during the revision of this work. Brozović et al. (2019) derived orbital fits for the small inner satellites of Neptune based on data obtained by telescopes, Voyager 2 and the Hubble Space Telescope. They found that the satellites Naiad and Thalassa are in a 73:69 inclination resonance, while Hippocamp and Proteus are in a 13:11 near mean motion resonance.

A detailed analysis of these probably resonances between the satellites and the satellites and ring particles are under investigation.