The 2016 glitch in the Vela pulsar

Abstract

We report the detection of a glitch event in the Vela pulsar, which occurred on 12 December 2016, based on the timing data obtained from observations between January 2016 and February 2018 at frequency centered at 2256 MHz using the Kunming 40-m radio telescope. The timing solutions for the pre- and post-glitch are presented. By fitting the glitch model to the timing data, we found that the post-glitch recovery exhibits two terms with exponential decay with the time scales of 1 d and 6 d, respectively. The glitch parameters are determined with $\Delta \nu _{\mathrm{g}}/\nu =1.431(2)\times 10^{-6}$ and $\Delta \dot{\nu }_{\mathrm{g}}/\dot{\nu }=73.354\times 10^{-3}$. The value of the coupling parameter is calculated to be ∼0.08, implying that the core superfluid is probably not involved in this event. For the glitches with two or more terms with exponential decay in the Vela pulsar, we show that the exponential decays usually exhibit longer time scales with higher degree of glitch recovery. The post-glitch behavior in the slow-down rate $|\dot{\nu }|$ is dominated by a linear decrease process. From detection of the variations in the slopes of the spin-down rates after the exponential recoveries of the 2013 and 2016 glitches, we conclude that no persistent shift was involved in the 2016 glitches.

1 Introduction

There are more than 2650 pulsars known in the Galaxy, which spin down regularly¹ (Manchester et al. 2005). Nevertheless, long-term timing observations revealed timing noises and glitches in the spin frequency ($\nu$) of some pulsars. Timing noise is usually characterized by continuous and erratic fluctuations in the rotation period ($P=\nu ^{-1}$), and is believed to arises in the magnetosphere and/or from the internal of the neutron star, whereas glitches are sudden increases in the spin frequency with a fractional change, $\Delta \nu /\nu$, typically between $10^{-10}$ and $10^{-5}$. The classical glitches are different from the micro-glitches, which have very small amplitude of jumps in spin frequency with positive or negative signature in the change of $\nu$.

Glitches are usually believed to originate from the interior of a neutron star. Two main mechanisms have been proposed to explain the phenomenon. The first mechanism suggests that crustal quakes in the neutron star results in an increasing amount of strain to build up in the crust, which leads to a sudden rearrangement of the moment of inertia (e.g., Ruderman 1991; Ruderman et al. 1998). But this hypothesis is weak as regards explaining the large glitches. The second mechanism is based on a sudden transfer of angular momentum from the faster-rotating crustal neutron superfluid to the rest of the neutron star (e.g., Anderson and Itoh 1975; Ruderman 1976). In addition, the vortex creep hypothesis is successful in explaining the post-glitch relaxation in the Vela pulsar and other pulsars (Alpar et al. 1984).

It is well known that glitches and post-glitch processes reflect the dynamics of the interior of the neutron star rather than magnetospheric phenomena. Hence, we can study the neutron star structure and the physics of ultra-dense matter through observing glitches and measuring their subsequent decay processes. In order to fully understand the glitch process, long-term monitoring of frequent glitching pulsars is very important.

The Vela pulsar (PSR B0833-45 /J0835-4510) is a young pulsar with spin period of 89.3 ms, characteristic age of 11.3 kyr, distance $D\approx 280$ pc, and flux density of $S_{1400}=1100$ mJy (Manchester et al. 2005). It is one of the most active neutron stars, with a spin-down energy loss rate of $\dot{E}=6.9\times 10^{36}$ erg s⁻¹ and emits radio, optical, X-ray and gamma-ray radiations (Abdo et al. 2010). The first known pulsar glitch was detected in the Vela pulsar in 1969 (Radhakrishnan and Manchester 1969), and, since then, a total of 21 such events have been observed from the neutron star^2,3 (Palfreyman et al. 2016), with most of them identified as large glitches having amplitudes on the order $\Delta \nu /\nu \sim 10^{-6}$. One micro-glitch and three small glitches, are also reported to occur with $\Delta \nu /\nu \sim (0.4\mbox{--}199)\times 10^{-9}$ (Cordes et al. 1988; Flanagan 1994; Jankowski et al. 2015; Palfreyman et al. 2016). Furthermore, one jump in the spin-down rate is found to come accompanied by a fractional increase of $\Delta \dot{\nu }/\dot{\nu } \sim (3\mbox{--}600)\times 10^{-3}$. After the sudden jump in spin and spin-down rates, a one recovery process often follows, which includes one to four terms with exponential decay with time scales ranging from 0.5 to 350 d. The latest glitch event was reported to occur on 12 December 2016 (Palfreyman 2016) with $\Delta \nu /\nu \sim 1.43 \times 10^{-6}$. Sarkissian et al. (2017) detected the exponential decay with time scale of 1 d for this event, and Palfreyman et al. (2018) detected an abrupt change in the pulse profile and low linear polarization associated with the glitch.

In this paper, we report the timing observations of the Vela pulsar at a relatively higher frequency (2256 MHz) using the Kunming 40-m radio telescope (KM 40 m). In Sect. 2 we introduce the setup of the observations. Data analysis is shown in Sect. 3 with focus on the recovery from glitch. A discussion is presented in Sect. 4.

2 Observations

Timing observations of the Vela pulsar were carried out with the KM40m radio telescope operated by Yunnan Observatories (YNAO). The details of the antenna parameters were described by Hao et al. (2010). The telescope is equipped with a dual-band S/X receiver operating at the room temperature, and a cooled circularly polarized C-band receiver which was installed in 2016. The system temperatures at S band and C band are 70 K and 30 K, respectively. The central frequencies at S band and C band are around 2256 MHz and 4856 MHz, respectively. After down converting, the intermediate frequency (IF) signals have a bandwidth of 300 MHz at S band and 512 MHz/1024 MHz at C band. Although the telescope site is close to a city, which results in radio frequency interference (RFI), there are still clean bands with widths of 60 to 130 MHz in the bandpass.

The pulsar timing system was built with the Pulsar Digital Filter Bank 4 (PDFB 4), which was developed by the Australian National Telescope Facility (ATNF). Pulsar signals were captured at the backend using a 512-channel configuration, with 1 MHz width for each channel, and sampling time of 64 μs. The recorded data had 30-s sub-integration time and were splitted into 512 bins to form the data archive. The Global Positioning System (GPS) time sever is used to align the hydrogen-maser clock with UTC. And the clock also provides pulse per second and 5 MHz signals for pulsar observation equipment.

Our investigation also incorporated the data obtained from The Parkes Test-Bed Facility (PTE),⁴ which comprises a 12-m antenna and the first generation Phased Array Feed (PAF) receiver (Hotan et al. 2014). The observations of the Vela pulsar using PTE were carried out from 9 February 2016 to 26 February 2017, with each observation typically lasting for 20 min. The captured beam was centered at 1199.5 MHz with a bandwidth of 16 MHz. The output files were converted to psrfits format. A total of 502 observations were identified. The details for the PTE data were described by Sarkissian et al. (2017).

The data reduction was performed using the software psrchive (Hotan et al. 2004). After removing RFI, each observation were summed in domain time, frequency and polarizations to form a total intensity pulse profile. In order to acquire the pulse times of arrival (TOAs), every total intensity profile was cross-correlated with the standard pulse profiles, which have high signal-to-noise ratio (S/N), to determine the pulse times of arrival. We noted that all TOAs were initially measured using the topocentric time provided by the hydrogen-maser clock located at the observatory. Long-term stability of hydrogen-maser plays an important role in millisecond pulsar (MSP) timing. The topocentric clock corrections, determined by daily monitoring of the maser offsets from the GPS time, were included to transform the TOAs to Coordinated Universal Time (UTC). Next, tempo2 (Edwards et al. 2006) was employed to transform the TOAs to the solar system barycenter using Jet Propulsion Laboratories DE421 ephemeris (Folkner et al. 2009). After that, timing residuals were formed and fitted with the timing model to obtain a phase-connected timing solution. The basic timing model for the barycentric pulse phase is the Taylor series,

$$ \phi (t)=\phi _{0}+\nu (t-t_{0})+\frac{1}{2}\dot{\nu }(t-t_{0})^{2}+ \frac{1}{6}\ddot{\nu }(t-t_{0})^{3}+\cdots , $$

(1)

where $\phi _{0}$ is the pulse phase at the reference barycentric time $t_{0}$. Here, $\nu$, $\dot{\nu }$ and $\ddot{\nu }$ are the spin frequency, the frequency’s derivative and the frequency’s second derivative, respectively. Glitches are identified by a sudden discontinuity in the timing residuals relative to a pre-glitch solution. These pulse phase jump can usually be described as increases in the $\nu$ and $\dot{\nu }$ as follows (Edwards et al. 2006):

$$ \begin{aligned}[b] \phi _{\mathrm{g}}&=\Delta \phi +\Delta \nu _{\mathrm{p}}(t-t_{ \mathrm{g}})+ \frac{1}{2}\Delta \dot{\nu _{\mathrm{p}}}(t-t_{ \mathrm{g}})^{2} \\ &\quad {}+\sum _{1}^{i}[1-e^{-(t-t_{\mathrm{g}})/ \tau _{\mathrm{di}}}]\Delta \nu _{\mathrm{di}}\tau _{\mathrm{di}} , \end{aligned} $$

(2)

where $\Delta \phi$ is the offset in pulse phase, $t_{\mathrm{g}}$ is the glitch epoch, and $\Delta \nu _{\mathrm{p}}$ and $\Delta \dot{\nu _{\mathrm{p}}}$ are, respectively, permanent changes in $\nu$ and $\dot{\nu }$ relative to the pre-glitch solution, $\Delta \nu _{\mathrm{d}}$ is the transient frequency increment that decays exponentially with a time scale $\tau _{\mathrm{d}}$. The frequency variation includes the permanent increments $\Delta \nu _{\mathrm{p}}$ and decaying increments $\Delta \nu _{\mathrm{d}}$. Therefore, the frequency jump can be described by $\Delta \nu _{ \mathrm{g}}=\Delta \nu _{\mathrm{p}}+\Delta \nu _{\mathrm{d}}$. The factor $Q$ can be described as the degree of glitch recovery, and it is defined by $Q=\Delta \nu _{\mathrm{d}}/\Delta \nu _{\mathrm{g}}$.

3 Results

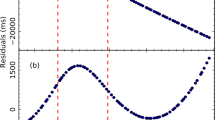
After the glitch event in the Vela pulsar had been reported in Astronomer Telegram (Palfreyman 2016), frequent observations timing of the neutron star were performed using KM 40-m radio telescope. In order to obtain precise and accurate timing solutions (including glitch parameters), it is essential to have well-determined pulsar ephemerides. Based on the large glitch that occurred on 12 December 2016 (MJD 57734.4855), we derived the rotational parameters for the Vela pulsar by fitting the timing model (Eq. (1)) to the pre- and post-glitch data, and the results are presented in Table 1. Uncertainties of 2$\sigma$ in the last quoted digit are given in parentheses. When deriving the parameters in Table 1, we skipped the data for a rapid exponential decay with a time scale of 1 d after the glitch (Sarkissian et al. 2017). For the post-glitch, we obtain the timing solution using the data between MJD 57736 (14 December 2016) and 58151 (2 February 2018). The timing residuals are shown in Fig. 1. It is clearly seen from the figure that the post-glitch spin-down is more noisy. Table 1 displays that the spin-down rate and $\ddot{\nu }$ in the post-glitch are larger than that in the pre-glitch, with the increase in the former by 0.27%. The spin parameters are then extrapolated to the glitch epoch on MJD 57734.4855 using the pre- and post-glitch solutions given in Table 1, but excluding the rapid exponential decay. The glitch parameters are estimated by calculating the fractional jump in $\nu$ and $\dot{\nu }$, giving $\Delta \nu _{\mathrm{g}}/\nu \sim 1.4539(5) \times 10^{-6}$ and $\Delta \dot{\nu }_{\mathrm{g}}/\dot{\nu }\sim 15.7(8)\times 10^{-3}$.

Fig. 1

The timing residual for the Vela pulsar with respect to the timing solutions in Table 1. Top panel: pre-glitch, bottom: post-glitch

Table 1 Timing solutions of the Vela pulsar for pre- and post-glitch

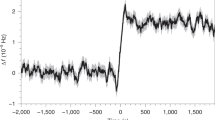
The frequent timing observations of this pulsar make it possible to monitor the recovery process relatively thoroughly. To investigate the spin behavior of the Vela pulsar, the values of $\nu$ and $\dot{\nu }$ were obtained from independent fits to individual sections of the data, each of which is short spanning typically 3–20 d. Figure 2 shows an overview of the spin-down of the Vela pulsar indicating that a large glitch with frequency jump of $\Delta \nu \sim 16.264(6)\times 10^{-6}\mbox{ Hz}$ occurred on MJD 57734.4855. The residual frequencies, shown in Fig. 2(a), were obtained from values at various epochs by subtracting the pre-glitch models. Figure 2(b) is acquired by subtracting the mean frequency values from each side of the glitch epoch. Although most of the frequency jump persists beyond the end of the data span, the expanded plot shown in Fig. 2(b) and the plot of $\dot{\nu }$ presented in Fig. 2(c) indicate that there is at least an initial exponential decay followed by a linear decrease in $|\dot{\nu }|$, with the latter often extending from the end of the initial exponential recovery to the next glitch event. Besides the exponential decay identified by Sarkissian et al. (2017) with a time scale of ∼1 d, we also found that there was obviously one more term for the exponential recovery, whose time constant is >1 d. Due to the large glitch amplitude, the glitch parameters were derived in several steps by fitting Eq. (2) to the timing data between MJD 57720 and 57800. Firstly, we should derive the parameters of the permanent changes in spin at the glitch epoch. We excluded the timing data for the exponential recovery between MJD 57734.5 and 57785 in order to minimize the contamination due to the decay process, and fitted the remaining data with Eq. (2) to estimate $\Delta \nu _{\mathrm{g}}$ and $\Delta \dot{\nu }_{\mathrm{g}}$. Secondly, a single decay with time scale of 1 d was fitted to the TOAs between MJD 57720 and 57800. The post-fit residuals are shown in Fig. 3(a), which suggest the existence of one more decay term. Last, both terms were included with a fixed time scale of 1 d for the first term. Following the method described by Sarkissian et al. (2017), we attempted a series of values for the time scale in the second term and obtained a value of ∼6.0(5) d that gives the smallest rms residual. Residuals for this fit are shown in Fig. 3(b), which demonstrates that the post-glitch behavior is very well modeled by jumps in the spin frequency and spin-down rate together with two exponential decays with time scales of around 1 and 6 d, respectively. The fitting gives the decay parameters listed in Table 2 with $\Delta \nu _{\mathrm{d1}}=7.7(5) \times 10^{-8}\mbox{ Hz}$ and $\Delta \nu _{\mathrm{d2}}=6.05(7)\times 10^{-8}\mbox{ Hz}$. The fractional size of this event was determined with $\Delta \nu _{\mathrm{g}}= 16.01(6)~\upmu \mbox{Hz}$ and $\Delta \nu _{ \mathrm{g}}/\nu =1.431(2)\times 10^{-6}$. The jump of the frequency derivative was resolved using

$$ \Delta \dot{\nu }_{\mathrm{g}}=\Delta \dot{\nu }_{\mathrm{p}}-\frac{ \Delta \nu _{d1}}{\tau _{d1}}-\frac{\Delta \nu _{d2}}{\tau _{d2}}, $$

(3)

which results in $\Delta \dot{\nu }_{\mathrm{g}}/\dot{\nu }=73.354 \times 10^{-3}$. Figure 2 shows that the degree of glitch recovery is very small at $Q=0.85(4)\%$. This result implies that the permanent jump in the frequency dominates the process of glitch recovery, and 99.15% of the initial frequency jump does not decay exponentially. For this glitch event, our results are consistent with the earlier reports that a low $Q$ is commonly detected in large glitches (Yu et al. 2013).

Fig. 2

Glitch in J0835-4510: (a) variations in the rotational frequency $\Delta \nu$ relative to the pre-glitch solution, (b) an expanded plot of $\Delta \nu$, in which the mean post-glitch value has been subtracted from the post-glitch data, and (c) variations of the frequency first derivative $\dot{\nu }$. The red solids are the linear fittings to the pre- and post-glitch linear recovery in $\dot{\nu }$. The vertical dashed line marks the glitch epoch

Fig. 3

The timing residuals. Top panel: the timing residuals with respect to the model with only one decay term of 1 d. Bottom panel: the timing residual with respect to the model with two decay terms of 1.0 d and 6.0 d, respectively

Table 2 Glitch parameters

4 Discussion

We detected a glitch in the Vela pulsar on 12 December 2016 using the KM 40-m radio telescope that is operated by YNAO. This is the 21st glitch event in the Vela pulsar since it was discovered in 1969. The glitch has a fractional size of $\Delta \nu _{\mathrm{g}}/\nu \sim 1.431(2) \times 10^{-6}$, which ranks it the 15th largest in size. Figure 4 shows the amplitudes for all the jumps in the spin frequency, with $\Delta \nu$ spanning $0.0045 \times 10^{-6}\mbox{--}34.7 \times 10^{-6}\mbox{ Hz}$. Except for one micro-glitch and three small glitches, all other events are large with $\Delta \nu /\nu$ between ${\sim} 0.835 \times 10^{-6}$ and $3.1 \times 10^{-6}$, giving an average of ${\sim} 2.1\times 10^{-6}$. In the regime of the vortex model, the lag between the rapidly rotating superfluid and the crust induces a Magnus force leading to crustal stress. When this stress exceeds a critical threshold, the vortices are suddenly unpinned. As a result, angular momentum is transferred to the crust giving rise to a glitch.

Fig. 4

Top panel: the amplitudes of all glitches ($\Delta \nu$) in the Vela pulsar. Bottom panel: the cumulative distribution of amplitude from all glitches observed in the Vela pulsar

Link et al. (1999) analyzed the coupling parameter, $G=A_{g}\nu / \dot{\nu }$, which is the minimum fraction of the moment of inertia that transfers angular momentum to the crust, where $A_{g}$ is the activity parameter. When considering the effect of entrainment, this calculation underestimates $G$ by a factor of about 4 (Andersson et al. 2012). Delsate et al. (2016) calculated the crustal moment of inertia in glitching pulsars and obtained a value of less than 0.2. It is found that the neutron superfluid in the inner crust may not carry enough angular momentum to account for the large glitches observed in the Vela pulsar (Li et al. 2016). For the 2016 glitch, the value of modified $G$ is ∼0.08 implying that core superfluid is probably not involved. For the micro-glitch and three small glitches detected in the Vela pulsar, whose sizes are $\Delta \nu /\nu \sim 0.4\times 10^{-9}$, $12\times 10^{-9}$, $75.6\times 10^{-9}$, and $199\times 10^{-9}$, the values of the modified $G$ are 0.0036%, 0.33%, 1.1% and 20.4%, respectively. Hence, for the three smallest glitches the superfluid in the inner crust is enough to explain the phenomena without involving the core superfluid. But for the glitch in August 1994, which has $\Delta \nu /\nu \sim 199\times 10^{-9}$, the core superfluid was involved in this event, for the reason that this event has a high $A_{g}$ due to a short waiting time of 32 d since the preceding glitch.

Figure 4 also shows the cumulative probability of glitch amplitudes ($\Delta \nu$). It is evident from the figure that the distribution of the glitch size in the Vela pulsar is very different from that of the Crab pulsar, with the latter following a power law relation (Shaw et al. 2018). Figure 5 shows the cumulative probability of the waiting time (the time since their preceding glitches), and the size of each glitch against the corresponding waiting time. The distribution of the waiting time clusters around 1000 d and deviates from the exponential, which imply that glitches in the Vela pulsar occur quasi-periodically, the glitching behavior of Vela pulsar is dominated by a global process, and it is unlikely they would result from scale-invariant or self-organized critical process (Melatos et al. 2008; Shaw et al. 2018). The mean waiting time is around 873 d (∼2.4 y), which is close to the previous statistics of 912 d (Wang et al. 2012).

Fig. 5

Top panel: The cumulative distribution of the waiting times observed in the Vela pulsar. Bottom panel: The waiting time vs. glitch amplitude for 19 glitches in Vela pulsar

Dodson et al. (2002) reported that four exponential terms were detected in the glitch that took place on 16 January 2000 (MJD 51,559) with time scales of 0.53, 3.3, 19 and 125 d. In addition, there were eight glitches between MJD 40280 and 47519, each of them showing two exponential terms with shorter time scales between 3 and 10 d and longer time scales between 14 and 351 d, respectively. The time scales for the rapid exponential recovery of 2016 glitch are about 1 d and 6 d, which values are shorter than the previous values, and the degrees of glitch recovery ($Q$) for the two terms are 0.48(3)% and 0.38(3)%, respectively. Table 3 shows the degrees of glitch recovery and the time scales for the exponential recoveries of the Vela pulsar. The values of $Q$ are small, between 0.000435 and 0.168, and the time scale for these exponential decays ranges from 1 d to 350 d. As shown in Fig. 6, it is apparent that the time scales are usually longer for exponential decays with high $Q$. So far, five pulsars have been detected with two exponential decay terms in one glitch, which are the Vela pulsar, PSRs J1119-6127, J1757-2421, J1803-2137 and J2337+6151 (Yuan et al. 2017). Among these pulsars, the Vela pulsar has the shortest period of 0.089 second, and the most energetic with spin-down energy loss rate of $6.9\times 10^{36}$ erg s⁻¹, which is also the most frequent glitching one with 21 glitches detected since 1969.

Fig. 6

The degree of glitch recovery ($Q$) vs. time scale for the exponential recoveries after glitches in the Vela pulsar

Table 3 Two exponential time scales

It has been reported that the long-term recovery from a large glitch is normally governed by a linear decrease in slow-down rate $|\dot{\nu }|$ (Yuan et al. 2010; Yu et al. 2013). This phenomenon is also seen in the 2016 glitch of the Vela pulsar as shown in Fig. 2. The linear trend generally becomes obvious at the end of the exponential decay and always persists until the next glitch event. It was proposed that the time scale of the linear recovery process depends on constitutive coefficients (e.g. mutual friction and viscosity) whose values remain constant during inter-glitch intervals (Haskell and Melatos 2015). Through fitting the slopes of the linear recovery in $\dot{\nu }$, as shown in Fig. 2(c), we obtain a value for the pre-glitch $\ddot{\nu }$ of ${\sim} 8.17\times 10^{-22}\mbox{ s}^{-3}$ whereas the post-glitch $\ddot{\nu }$ is given by ${\sim} 16.83\times 10^{-22}\mbox{ s}^{-3}$, which is almost double of that in the pre-glitch. Using the timing data between February 2011 and September 2013 obtained from Parkes, the value of $\ddot{\nu }$ is determined to be $10.54\times 10^{-22}\mbox{ s}^{-3}$. These results are consistent with the measurements on $\ddot{\nu }$ by Yu et al. (2013), which ranges from $7.15\times 10^{-22}\mbox{ s}^{-3}$ to $13.26 \times 10^{-22}\mbox{ s}^{-3}$ between September 1994 and December 2009. Akbal et al. (2017) predicted that the 2013 glitch gave rise to a persistent shift, which is a sudden decrease in the spin-down rate, and is expected to last without healing. As for the 2013 and 2016 glitches, the observations of the phenomenon revealed that the post-glitch spin-down rate exhibits slopes that are different from that of the pre-glitch and the shifts vary with time. Hence, no persistent shift was involved. It is possible to infer variations in the torque after the exponential recoveries and we plan to do so in a future paper.