1 Introduction

The stars, gas and dust clouds in galactic disks congregate in spiral patterns and make bountiful structures in the universe. Despite spiral arms beauties and many decades of concerted scientific investigation, much about them remain mysterious. Although the precise theory explaining the origin and evolution of the spiral structures in spiral galaxies is not fully understood, it is widely agreed in the relevant literature that these patterns are gravitationally driven density waves in the stellar disks (Binney and Tremaine 2008; Sellwood 2014). Therefore, the density wave theory is an important tool for studying the dynamics and the evolution of spiral galaxies. In the frame work of this theory and using some approximations and assumptions, Alar Toomre showed that the differentially rotating disks in Newtonian dynamics is stable to all local axisymmetric disturbances if the dimensionless quantity \(Q>1\) (Toomre 1964), where \(Q\) is the Toomre’s \(Q\) parameter (see Eqs. (22) and (23) for the definition of this parameter for fluid and stellar disks respectively). When \(Q<1\), on the other hand, thermal pressure and rotation are unable to stop the collapse of over-dense regions.

In fact, he assumed that the density waves are tightly wound and the stellar orbits of the unperturbed disk are nearly circular. Despite these restrictive assumptions used in deriving this result, it has proved to be remarkably true and widely applicable. However, numerical studies of disk galaxies reveals that this criterion is not enough for complete stability of the stellar self-gravitating disks (Hohl 1971; Miller et al. 1970; Ostriker and Peebles 1973). In other words, these N-body simulations showed that Toomre’s criterion does not provide the global stability of the stellar disks and only guarantees the local stability of them. More specifically, it turned out that simple models of rotationally dominated stellar disks are globally unstable to a pressure dominated bar-like structure.

This kind of gravitational instability can be directly linked to the dark matter problem in spiral galaxies. This link has been known since 1973 when Ostriker and Peebles pointed out that a dark matter halo surrounded the galaxy may be an important stabilizing agent of galactic disks (Ostriker and Peebles 1973) and prevent the rapid bar formation. However, it should be noted that existence of a spherical halo around a rotationally dominated (or cold) disk is not the only way to stabilize the disk. There are other possibilities which can provide the global stability, see Sellwood (2014) for a review of the subject. For example, existence of a massive central bulge would stabilize the disk (Sellwood 1985; Sellwood and Moore 1999; Sellwood and Evans 2001).

The main aim of this paper is to find the generalized Toomre’s local stability criterion in the context of metric \(f(R)\) gravity. As an example of such a study in other modified gravity theories see Milgrom (1989) where the Toomre’s criterion has been derived in the context of modified Newtonian dynamics (MOND). Also, Roshan and Abbassi (2015) have derived the Toomre’s stability criterion in the context of MOG. It is worth to mention that MOG is a Scalar-Tensor-Vector theory of gravity presented to address the dark matter problem (Moffat 2006). Although a considerable amount of work has gone into stability criteria, no study has been performed for investigating these criteria in the context of \(f(R)\) gravity. However, it should be noted that the dynamical stability of spherical systems, and also the stability of spherically symmetric solutions in \(f(R)\) gravity have been widely investigated (see Noureen and Zubair 2015 and Seifert 2007 and references therein for more details). Certainly, the results of this paper could be useful in the numerical simulations of the disk galaxies in \(f(R)\) gravity.

It is worth mentioning that metric \(f(R)\) gravity is one of the simplest modifications to Einstein’s General Relativity (GR). Strictly speaking, the generic action of this theory can be simply obtained just by replacing the Ricci scalar \(R\) with an arbitrary general function of \(R\), namely \(f(R)\), in the Einstein-Hilbert action. Several aspect of this theory have been investigated in the literature. Interests to this theory increased when Carroll et al. proposed that \(f(R)\) gravity can solve the cosmic speedup enigma (Carroll et al. 2004). Although this theory is known as a dark energy model, it has been applied to address the dark matter problem in the galactic scales. For example Capozziello et al. (2007) applied a power-law \(f(R)\) gravity to explain the rotation curves of low surface brightness galaxies. We refer the reader to review papers (Sotiriou and Faraoni 2010; Clifton et al. 2012) for more detail about this theory and its status among the other extended theories of dark energy.

The structure of this paper is as follows. The weak field approximation of metric \(f(R)\) gravity is reviewed briefly in Sect. 2. Also, the coupled Boltzmann and modified Poisson equations are derived. In Sect. 3, by linearizing the field equations, we derive the dispersion relation of tightly wound spiral density waves in both fluid and stellar disks. Furthermore, using the new dispersion relations, we derive the local stability criterion. In fact, we find the generalized version of the Toomre’s stability criterion in the context of metric \(f(R)\) gravity. This new Toomre’s criterion is the main result of this paper. Finally, in Sect. 4, results are discussed.

2 Weak field limit of \(f(R)\) gravity

Here, we briefly review the weak filed limit of \(f(R)\) gravity theory. The weak field limit of this theory has been widely investigated, for a comprehensive review of the subject see Sotiriou and Faraoni (2010), Nojiri and Odintsov (2011), De Felice and Tsujikawa (2010), Capozziello and De Laurentis (2011). The general action for this theory is given by

$$\begin{aligned} S=\frac{1}{16\pi G}\int\sqrt{-g} f(R)d^{4}x+S_{M} \end{aligned}$$
(1)

where \(R, G, g, S_{M}\) are the Ricci scalar, Newton’s gravitational constant, the determinant of the metric tensor and the matter action, respectively. Note that throughout this paper we work in the system of units where the speed of light is \(c=1\). Furthermore, we will assume that \(f(R)\) is analytic about \(R = 0\) so that it can be expanded as a power series

$$\begin{aligned} f(R)=\sum c_{n} R^{n} \end{aligned}$$
(2)

There are some \(f(R)\) models of cosmological interest in the literature that can be expressed in such a form, for example, Starobinsky’s model (Starobinsky 2007)

$$\begin{aligned} f(R)=R+\beta R_{0} \biggl[ \biggl(1+\frac{R^{2}}{R_{0}^{2}} \biggr)^{-m}-1 \biggr] \end{aligned}$$
(3)

can be expressed as

$$\begin{aligned} f(R)=R-\frac{m\beta}{R_{0}}R^{2}+\frac{\beta m (m+1)}{2R_{0}^{3}}R^{4}+\cdots \end{aligned}$$
(4)

Variation of action (1) with respect to metric yield to the metric field equation:

$$ f'R_{\mu\nu}-\frac{f}{2}g_{\mu\nu}- \nabla_{\mu}\nabla_{\nu}f'g_{\mu\nu} \Box f'=8\pi G T_{\mu\nu} $$
(5)

where prime denotes derivative with respect to \(R\), i.e. \(f'(R)=\frac {df}{dR}\), and \(T_{\mu\nu}\) is the energy-momentum tensor. Throughout this paper, we restrict ourselves to the adiabatic approximation in which the evolution of the universe is very slow in comparison with local dynamics. This assumption allows us to use the Minkowski space-time instead of more natural choices such as the Friedmann-Robertson-Walker (FRW) space-time as the background metric (see Clifton et al. 2012 and references cited therein). It should be noted that in the current paper we consider the local gravitational stability of the self-gravitating disks. This means that only the local dynamics of these systems matters for us.

Therefore, in order to write the field equations in the first perturbation order, we decompose metric into the Minkowski metric \(\eta _{\mu\nu}=\operatorname{diag}(+1,-1,-1,-1)\) plus a small perturbation \(h_{\mu\nu }\) (\(|h_{\mu\nu}|\ll1\)) as follows

$$\begin{aligned} ds^{2}=(1+2 \varPhi)dt^{2}-(1-2\varPsi) \bigl(dx^{2}+dy^{2}+dz^{2}\bigr) \end{aligned}$$
(6)

where \(h_{00}=2\varPhi(\mathbf{x},t)\) and \(h_{ij}=2\varPsi(\mathbf{x},t)\delta _{ij}\). We use the transverse gauge, i.e. \(\partial_{i} s^{ij}=0\), where the traceless tensor \(s_{ij}\) is known as the strain and is given by

$$\begin{aligned} s_{ij}=\frac{1}{2} \biggl(h_{ij}-\frac{1}{3} \delta^{kl}h_{kl}\delta _{ij} \biggr) \end{aligned}$$
(7)

Finally, substituting (6) into field equation (5) and keeping only terms linear in perturbations \(\varPhi\) and \(\varPsi\), one can find the following equation for the \((0,0)\) component of the field equation

$$\begin{aligned} f''_{0}\nabla^{4}(2\varPsi- \varPhi)+f'_{0} \nabla^{2}\varPsi=8\pi G \rho \end{aligned}$$
(8)

where \(f^{(n)}_{0}=\frac{d^{n} f}{dR^{n}}|_{R=0}\) and \(\nabla^{4} \psi=\nabla ^{2}(\nabla^{2}\psi)\). Similarly, preserving only the first-order perturbations, the trace of the field equation (5) takes the following form

$$\begin{aligned} 3f''_{0}\nabla^{4}(2\varPsi- \varPhi)+f'_{0} \nabla^{2}(2\varPsi-\varPhi)=8 \pi G \rho \end{aligned}$$
(9)

It must be mentioned that we have assumed the perfect fluid’s energy-momentum tensor for \(T_{\mu\nu}\). Thus \(\rho\) is the rest frame matter density. Equations (8) and (9) all together with the continuity equation and the Euler, make a complete set of equations governing the dynamics of a fluid system in the weak filed limit of \(f(R)\) gravity. In fact, Eqs. (8) and (9) are the analog of the Poisson equation in Newtonian gravity. It is obvious that we have to find the corresponding equations for continuity equation and the Euler equation in the frame work of \(f(R)\) gravity. To do so, it is needed to take into account that metric \(f(R)\) theory is a metric theory of gravity. It is known that in metric theories of gravity the conservation of the energy momentum-tensor holds, i.e. \(\nabla_{\mu}T^{\mu\nu}=0\). Consequently, non-spinning test particles move on the geodesics of the metric tensor \(g_{\mu\nu}\). Therefore, the equation of motion of a test particle in this theory is given by

$$\begin{aligned} \frac{d^{2}x^{i}}{d\tau^{2}}+\varGamma^{i}_{\alpha\beta}\frac{dx^{\alpha}}{d\tau } \frac{dx^{\beta}}{d\tau}=0 \end{aligned}$$
(10)

where \(\tau\) is the proper time along the world line of the test particle. Using the metric component (6), it is straightforward to write Eq. (10) to first order in perturbations

$$\begin{aligned} \frac{d^{2}\mathbf{r}}{dt^{2}}=-\nabla\varPhi \end{aligned}$$
(11)

thus, only the metric potential \(\varPhi\) directly appears in the equation of motion of a test particle. In other words, only \(\varPhi\) appears in the gravitational potential. This is the case also for the continuity and Euler equation. Writing the divergence of the energy-momentum tensor, \(\nabla_{\mu}T^{\mu\nu }=0\), in the Newtonian limit, one can easily verify that the continuity and Euler equations are

$$\begin{aligned}& \frac{\partial\rho}{\partial t}+\nabla\cdot(\rho\mathbf{v})=0 \end{aligned}$$
(12)
$$\begin{aligned}& \frac{\partial\mathbf{v}}{\partial t}+(\mathbf{v}\cdot\nabla)\mathbf {v}=-\frac{1}{\rho}\nabla p-\nabla\varPhi \end{aligned}$$
(13)

Equations (8), (9), (12) and (13) together with the equation of state relating \(p\) and \(\rho\), make a set of equations governing the dynamics of a self-gravitating fluid system.

2.1 The modified Poisson equation in \(f(R)\) gravity

In this section we derive the Poisson equation in the weak field limit of metric \(f(R)\) gravity. For this purpose, it is convenient to combine Eqs. (8) and (9) as a single equation. The result is the analogue the Poisson equation in Newtonian gravity. Using Eqs. (8) and (9), one can show that

$$\begin{aligned} \nabla^{2}\varPsi=-\nabla^{2} \varPhi+\frac{8\pi G}{f'_{0}}\rho \end{aligned}$$
(14)

Now, substituting Eq. (14) into (9), we find

$$\begin{aligned} \bigl(\nabla^{2}-m_{0}^{2}\bigr) \nabla^{2}\varPhi=-4\pi G \alpha \biggl(m_{0}^{2} \rho-\frac{4}{3 }\nabla^{2}\rho \biggr) \end{aligned}$$
(15)

where \(\alpha=1/f'_{0}\) and \(m_{0}\) is defined as

$$\begin{aligned} m_{0}^{2}=-\frac{f'_{0}}{3 f''_{0}} \end{aligned}$$
(16)

in fact, Eq. (15) is the modified version of the Poisson equation. Therefore, loosely speaking, we are dealing with a theory with two free parameters \(\alpha\) and \(\beta\). In the limit \(m_{0}^{2}\rightarrow\infty\) and \(\alpha\rightarrow1\), the standard Poisson equation is recovered, i.e. Eq. (15) takes the form \(\nabla^{2}\varPhi=4\pi G \rho\). Solution of this fourth order Eq. (15) can be written as follows

$$\begin{aligned} \varPhi(\mathbf{r}) =&-4\pi G\alpha\int\int G_{1}\bigl(\mathbf{r}'',\mathbf {r}'\bigr)G_{2}\bigl(\mathbf{r},\mathbf{r}'' \bigr) \\ &{}\times \biggl(m_{0}^{2} \rho\bigl(\mathbf {r}' \bigr)-\frac{4}{3 }\nabla^{2}\rho\bigl(\mathbf{r}' \bigr) \biggr)d^{3}\mathbf {r}'d^{3} \mathbf{r}'' \end{aligned}$$
(17)

where \(G_{1}\) and \(G_{2}\) are the Green functions:

$$\begin{aligned} \begin{aligned} & G_{1}\bigl(\mathbf{r}'', \mathbf{r}'\bigr)=-\frac{1}{4\pi}\frac{e^{-\sqrt {m_{0}^{2}}|\mathbf{r}'-\mathbf{r}''|}}{|\mathbf{r}'-\mathbf{r}''|} \\ & G_{1}\bigl(\mathbf{r},\mathbf{r}''\bigr)=- \frac{1}{4\pi}\frac{1}{|\mathbf{r}-\mathbf{r}''|} \end{aligned} \end{aligned}$$
(18)

it is natural to expect that the free parameters \(\alpha\) and \(m_{0}\) should be fixed by relevant observations. Also, in order to prevent the oscillatory solutions, \(m_{0}^{2}\) should be positive, i.e. \(m_{0}^{2}>0\).

It is worth noting that the gravitational potential of a point source takes the following form

$$\begin{aligned} \varPhi(r)=-\frac{G M \alpha}{r} \biggl[1+\frac{1}{3}e^{-m_{0} r} \biggr] \end{aligned}$$
(19)

This result can be straightforwardly derived from Eq. (17) just by substituting the matter density as \(\rho(\mathbf{r})=M \delta (\mathbf{r})\), where \(M\) is the mass of the point particle.

2.2 The collisionless Boltzmann equation in \(f(R)\) gravity

In this section, we derive the collisionless Boltzamnn equation in the weak field limit of metric \(f(R)\) gravity. This equation is the main equation governing the dynamics of a stellar system. Assume that \(f(x^{\mu}, u^{\mu})\) is the particle’s phase space distribution function. Where \(u^{\mu }=\frac{dx^{\mu}}{d\tau}\) is the four velocity of the particle. In Newtonian dynamics the Boltzmann equation can be expressed as \(\hat {L}[f]=0\), where \(\hat{L}\) is the Liouville operator. It is worth remembering that in metric \(f(R)\) gravity non-spinning test particles move on the geodesics. Therefore with the aid of the geodesic equation, we obtain the covariant, relativistic generalization of the Boltzmann equation

$$\begin{aligned} \hat{L}[f]=u^{\mu}\frac{\partial f}{\partial x^{\mu}} -\varGamma^{\mu }_{\alpha\beta}u^{\alpha}u^{\beta} \frac{\partial f}{\partial u^{\mu}}=0 \end{aligned}$$
(20)

It is straightforward to linearize this equation using the perturbation introduced in Eq. (6). Keeping in mind that in the first order Newtonian limit \(\varGamma^{i}_{00}\simeq\frac{\partial\varPhi}{\partial x^{i}}\) and \(u^{i}\simeq v^{i}=\frac{dx^{i}}{dt}\), we have

$$\begin{aligned} \frac{\partial f}{\partial t}+ \mathbf{v}\cdot\nabla f-\nabla\varPhi\cdot \frac{\partial f}{\partial\mathbf{v}}=0 \end{aligned}$$
(21)

as expected, only metric potential \(\varPhi\) appears in the Boltzmann equation. Mathematically, this equation is the same as the Boltzmann equation in Newtonian dynamics. However, we know that the field equation governing \(\varPhi\) is different from the standard Poisson equation.

3 Local stability of differentially rotating disks in \(f(R)\) gravity

As we mentioned in the introduction, our main purpose in this paper is to find a Toomre-like stability criterion in the context of metric \(f(R)\) gravity. We remind the reader that Toomre’s criterion for a fluid (gaseous) disk is expressed as

$$\begin{aligned} Q_{g}=\frac{v_{s} \kappa}{\pi G\varSigma}>1 \end{aligned}$$
(22)

where \(v_{s}\) is the sound speed in the fluid, \(\kappa\) is the epicycle frequency and \(\varSigma\) is the surface matter density of the disk. Similarly, in the case of a stellar disk this criterion can be written as

$$\begin{aligned} Q_{s}=\frac{\sigma\kappa}{3.36 G\varSigma}>1 \end{aligned}$$
(23)

in this case \(\sigma\) is the radial velocity dispersion. In Newtonian gravity, Toomre’s criterion has been derived for differentially rotating disk where the tight-winding or the WKB approximation is satisfied. In fact, the tight-winding (or WKB) approximation provides some simplifications in the story and, without much loss of generality of the problem, makes analytic description possible and much simpler. In this approximation, the density wave in the disk can locally be regarded as a plane wave. This simplification enables us to find the dispersion relation for this kind of density waves and to describe their propagation in the disk. Therefore, WKB approximation is an indispensable tool for understanding the behavior of density waves in rotating disks in the context of Newtonian gravity. As we shall see in the next sections, in order to do complete stability analysis in \(f(R)\) gravity and find the generalized version of the Toomre’s criterion, we also need to benefit this approximation.

3.1 Self-gravitating fluid disk

In this section, we analyze the behavior of a tightly wound density wave in the framework of metric \(f(R)\) gravity. First, we use the modified Poisson equation (15) in order to calculate the gravitational potential of a tightly wound surface density. Furthermore, we linearize the relevant equations in order to find the dispersion relation for such a density wave.

The continuity equation (12), the Euler equation (13) and the modified Poisson equation (15) are the required equation for studying the gravitational stability of the system. It is important to remember that we also need the equation of state of the fluid to make a complete description. We assume that the background disk is axisymmetric and is placed in \(z = 0\) plane. Using the cylindrical coordinates \((R,\phi, z)\), the continuity equation reads (note that hereafter \(R\) is a coordinate and should not be confused with the Ricci scalar)

$$\begin{aligned} \frac{\partial\varSigma}{\partial t}+\frac{1}{R}\frac{\partial}{\partial R} (\varSigma R v_{R} )+\frac{1}{R}\frac{\partial}{\partial\phi } (\varSigma v_{\phi} )=0 \end{aligned}$$
(24)

where \(\varSigma\) is the surface density and \(v_{R}\) and \(v_{\phi}\) are the velocity components in the radial and azimuthal directions respectively. Since the disk is located in the \(x-y\) plane, there are only two components for the Euler equation. These components can be, respectively, expressed as:

$$\begin{aligned}& \frac{\partial v_{R}}{\partial t}+v_{R} \frac{\partial v_{R}}{\partial R}+\frac{v_{\phi}}{R} \frac{\partial v_{R}}{\partial\phi}-\frac{v_{\phi }^{2}}{R}=- \frac{\partial}{\partial R} (\varPhi+h ) \end{aligned}$$
(25)
$$\begin{aligned}& \frac{\partial v_{\phi}}{\partial t}+v_{R} \frac{\partial v_{\phi }}{\partial R}+\frac{v_{\phi}}{R} \frac{\partial v_{\phi}}{\partial\phi }+\frac{v_{\phi} v_{R}}{R}=- \frac{1}{R}\frac{\partial}{\partial\phi } ( \varPhi+h ) \end{aligned}$$
(26)

where we have chosen a simple barotropic equation of state as \(p=K \varSigma^{\gamma}\), where \(K\) and \(\gamma\) are constant real parameters. Also, \(h\) is the specific enthalpy defined as:

$$\begin{aligned} h= \int\frac{dp}{\varSigma} \end{aligned}$$
(27)

Now, let us perform the following perturbations: \(\varSigma=\varSigma _{0}+\varSigma_{1}\), \(v_{R}=v_{R0}+v_{R1}=v_{R1}\), \(v_{\phi}=v_{\phi 0}+v_{\phi1}\), \(\varPhi=\varPhi_{0}+\varPhi_{1}\) and \(h=h_{0}+h_{1}\). We denote the equilibrium quantities with a “0” subscript and the perturbations with a “1” subscript. After linearization, the fluid equations (24) and (26) can be written as:

$$\begin{aligned}& \frac{\partial\varSigma_{1}}{\partial t}+\frac{1}{R}\frac{\partial }{\partial R} (\varSigma_{0} R v_{R1} )+\varOmega\frac{\partial \varSigma_{1}}{\partial\phi}+\frac{\varSigma_{0}}{R} \frac{\partial v_{\phi 1}}{\partial\phi}=0 \end{aligned}$$
(28)
$$\begin{aligned}& \frac{\partial v_{R1}}{\partial t}+\varOmega\frac{\partial v_{R1}}{\partial\phi}-2\varOmega v_{\phi1}=- \frac{\partial}{\partial R} (\varPhi_{1}+h_{1} ) \end{aligned}$$
(29)
$$\begin{aligned}& \frac{\partial v_{\phi1}}{\partial t}+\varOmega\frac{\partial v_{\phi 1}}{\partial\phi}+\frac{\kappa^{2}}{2\varOmega} v_{R1}=-\frac{1}{R}\frac {\partial}{\partial\phi} (\varPhi_{1}+h_{1} ) \end{aligned}$$
(30)

where \(\varOmega(R)\) is the circular frequency and the epicyclic frequency \(\kappa\) is

$$\begin{aligned} \kappa^{2}(R)=R \frac{d\varOmega^{2}}{dR}+4 \varOmega^{2} \end{aligned}$$
(31)

Also, the modified Poisson equation can be linearized as

$$\begin{aligned} \bigl(\nabla^{2}-m_{0}^{2} \bigr)\nabla^{2}\varPhi_{1} =&-4\pi G \alpha \\ &{} \times \biggl(m_{0}^{2} \varSigma_{1} \delta(z)-\frac{4}{3 }\nabla^{2}\varSigma_{1} \delta(z) \biggr) \end{aligned}$$
(32)

Now, consider an arbitrary spiral surface density perturbation mode as follows

$$\begin{aligned} \varSigma_{1}(R,\phi,t)=H(R)e^{i(F(R)+m \phi-\omega t)} \end{aligned}$$
(33)

where \(\omega\) is the frequency of the mode, \(H\) is a slowly varying function of \(R\) and \(F(R)\) is the shape function. Also, \(m\) is a positive integer, and the perturbation has \(m\)-fold rotational symmetry. The WKB approximation requires that \(\frac{|k R|}{m}\gg1\), where \(k(R)=\frac{dF}{dR}\). In this approximation the pitch angle of the spiral arms is very small at any radius. Therefore, one can conclude that the spiral arms are tightly wound.

Let us find the gravitational potential of the tightly wound spiral perturbation (33) in the neighborhood of a point \((R_{0},\phi_{0})\). Using the properties of WKB approximation, one can expand \(\varSigma_{1}\) as follows (for more detail see Binney and Tremaine 2008)

$$\begin{aligned} \varSigma_{1}(R,\phi,t)\sim\varSigma_{a}(R_{0})e^{i(k(R_{0})R-\omega t)} \end{aligned}$$
(34)

where

$$\begin{aligned} \varSigma_{a}(R_{0})=H(R_{0})e^{i(F(R_{0})+m \phi_{0}-k(R_{0})R_{0})} \end{aligned}$$
(35)

the spiral perturbation (34) is reminiscent of a plane wave with wavenumber \(\mathbf{k} = k\mathbf{e}_{R}\), where \(\mathbf{e}_{R}\) is the unit vector in the radial direction. The potential of a plane wave in a thin disk in the framework of the \(f(R)\) gravity has been derived in Appendix A. Using Eq. (69), the potential can be expressed as

$$\begin{aligned} \varPhi_{1}=-\frac{2\pi G \alpha}{|k|}\frac{m_{0}^{2}}{k^{2}+m_{0}^{2}} \varSigma_{1} \end{aligned}$$
(36)

Regarding the form of \(\varSigma_{1}\) and \(\varPhi_{1}\), any solution of Eqs. (28)–(30) can be expressed as

$$\begin{aligned}& v_{R1}(R,\phi,t)=v_{Ra}(R)e^{i(m \phi-\omega t)} \end{aligned}$$
(37)
$$\begin{aligned}& v_{\phi1}(R,\phi,t)=v_{\phi a}(R)e^{i(m \phi-\omega t)} \end{aligned}$$
(38)
$$\begin{aligned}& h_{1}(R,\phi,t)=h_{a}(R)e^{i(m \phi-\omega t)} \end{aligned}$$
(39)

In Newtonian gravity, using the properties of the WKB approximation, Eqs. (28)–(30) take the following forms respectively (for more detail see Binney and Tremaine 2008)

$$\begin{aligned}& (m \varOmega-\omega)\varSigma_{a}+k\varSigma_{0} v_{Ra}=0 \end{aligned}$$
(40)
$$\begin{aligned}& v_{Ra}=\frac{(m\varOmega-\omega)k(\varPhi_{a}+h_{a})}{\Delta} \end{aligned}$$
(41)
$$\begin{aligned}& v_{\phi a}=-\frac{2i B k(\varPhi_{a}+h_{a})}{\Delta} \end{aligned}$$
(42)

where coefficient functions \(\Delta\) and \(B\) (the Oort constant of rotation) are:

$$\begin{aligned}& \Delta=\kappa^{2}-(m\varOmega-\omega)^{2} \end{aligned}$$
(43)
$$\begin{aligned}& B(R)=- \biggl(\varOmega+\frac {1}{2}R\frac{d\varOmega}{dR} \biggr) \end{aligned}$$
(44)

It is important noting that mathematical form of the Euler equation in the weak field limit of \(f(R)\) gravity is the same as the Newtonian gravity. The only difference between these theories appears in the way by which the disk responds to the perturbation. On the other hand, the Poisson equation determines the response or the behavior of the disk to the perturbation. Since, for obtaining Eq. (41), the Poisson equation has not been used, so we can conclude that they are also true in the weak filed limit of \(f(R)\) gravity. This is the case also for continuity equation (40). Therefore, we skip the details of the calculations for deriving Eqs. (40) and (41), and refer the reader to Chap. 6 of Binney and Tremaine (2008).

Now, we substitute \(v_{Ra}\) from Eq. (41) into Eq. (40) and use Eq. (36). Also, taking into account that \(h_{a}=v_{s}^{2}\frac{\varSigma_{a}}{\varSigma_{0}}\), we find the following dispersion relation

$$\begin{aligned} (m\varOmega-\omega)^{2}=\kappa^{2}-2\pi G |k| \varSigma_{0}\frac{\alpha m_{0}^{2}}{k^{2}+m_{0}^{2}}+k^{2} v_{s}^{2} \end{aligned}$$
(45)

We shall derive the local stability criterion from this dispersion relation. As expected, in the limit \(m_{0}\rightarrow\infty\) and \(\alpha \rightarrow1\), the dispersion relation for WKB modes in Newtonian gravity can easily be recovered. In this paper, we restrict ourselves to the axisymmetric disturbances, i.e. \(m=0\). Since the right-hand-side of (45) is real, then the disk is stable against local axisymmetric disturbances if \(\omega^{2}>0\) and unstable if \(\omega^{2}<0\).

It is worthwhile to mention that Toomre’s criteria (22) and (23) have also been derived for axisymmetric perturbations. However, it cannot be concluded strongly that they are not applicable for local nonaxisymmetric stability. In fact, no general criterion for nonaxisymmetric stability is known in Newtonian gravity.

Now, we consider the general case by adopting non-zero speed of sound. In this case, using the dispersion relation (45), the stability criterion \(\omega^{2}>0\) can be rewritten in the dimensionless form

$$\begin{aligned} X^{4}+\bigl(1+\beta^{2}\bigr)X^{2}- \frac{2\beta\alpha}{Q_{g}}|X|+\beta^{2}>0 \end{aligned}$$
(46)

where

$$\begin{aligned} X=\frac{k}{m_{0}},\qquad\beta=\frac{\kappa}{m_{0} v_{s}} \end{aligned}$$
(47)

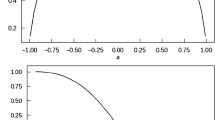
The schematic behavior of the left-hand side (LHS) of Eq. (46) is shown in Fig. 1. It is clear from this figure that, if the minimum value of the LHS is positive, then the condition \(\omega ^{2}>0\) will hold for all wavenumbers and consequently throughout the region that we explore, all solutions that we will find represent stable modes. In other words, the disk is stable against all axisymmetric tightly wound perturbations, if the minimum value of the LHS is positive. It is easy to check that the minimum value of the LHS occurs at \(X_{\mathit{min}}\) given by

$$\begin{aligned} X_{\mathit{min}}=\pm \biggl[-\frac{1+\beta^{2}}{3}A^{1/3}+ \frac{1}{2}A^{-1/3} \biggr] \end{aligned}$$
(48)

where \(A\) is defined as

$$\begin{aligned} A=\frac{Q_{g}}{2\beta\alpha (1+\sqrt{1+\frac{2(1+\beta ^{2})^{3}Q_{g}^{2}}{27\beta^{2}\alpha^{2}}} )} \end{aligned}$$
(49)

The location of this point varies as the parameters \(\alpha\) and \(\beta \) change. Finally the local stability criterion can be expressed as

$$\begin{aligned} Q_{g}>\frac{2\beta\alpha|X_{\mathit{min}}|}{X_{\mathit{min}}^{4}+(1+\beta^{2})X_{\mathit{min}}^{2}+\beta^{2}} \end{aligned}$$
(50)

This is the main result of this section. In fact, Eq. (50) is the generalized version of the Toomre’s local stability criterion for a fluid disk, and should be compared with the standard case given by (22). Since \(X_{\mathit{min}}\) contains \(Q_{g}\), criterion (50) is very complicated than the standard Toomres criterion (i.e. \(Q_{g}>1\)). However, it is straightforward to show that in the limit \(\beta \rightarrow0\) and \(\alpha\rightarrow1\), the right-hand side (RHS) of Eq. (50) equals 1, and the standard Toomre’s criterion is recovered.

Fig. 1
figure 1

Schematic behavior of the LHS of Eq. (46) with respect to \(X\)

Full size image

It is also instructive to plot the neutral stability curves \(\omega=0\) for axisymmetric tightly wound waves in a fluid disk. These curves specify the boundary of the stable and unstable modes/waves. To do so, let us introduce a critical wavelength \(\lambda_{\mathit{crit}}=2\pi/k_{\mathit{crit}}\). Using this definition and the dispersion relation (45), the line separating stable and unstable modes is given by

$$\begin{aligned} Q_{g}(y)=\alpha\sqrt{\frac{4\alpha y}{1+ (\frac{\beta Q_{g}}{2 y\alpha } )^{2}}-4y^{2}} \end{aligned}$$
(51)

where \(y=\lambda/\lambda_{\mathit{crit}}\) and \(\lambda=2\pi/k\). We have plotted the neutral curve for various values of \(\alpha\) and \(\beta\) in Fig. 2. The dashed curves corresponds to Newtonian gravity where \((\alpha,\beta)=(1,0)\).

Fig. 2
figure 2

The boundary of stable and unstable axisymmetric WKB disturbances in a fluid disk for different values of \(\alpha\) and \(\beta \). The dashed curve corresponds to Newtonian gravity where \(\alpha=1\) and \(\beta=0\)

Full size image

Let us first consider the other curves with \(\beta=0\), i.e. curves corresponding to \((\alpha,\beta)=(1.2,0)\) and \((\alpha,\beta)=(0.5,0)\). In this case one can readily show that the Toomre’s criterion (50) is \(Q_{g}>\alpha\). Consequently, if \(\alpha>1\) (as in the case \((\alpha,\beta)=(1.2,0)\)) then a lager \(Q_{g}\) parameter compared with Newtonian gravity is needed to overcome the local gravitational instability. Keeping in mind the physical interpretation of the Jeans instability, this means that the disk needs more gas pressure than it would in Newtonian gravity in order to overcome the gravitational collapse. On the other hand, if \(\alpha<1\) then smaller gas pressure is needed for preventing the collapse.

For the general case \(\beta\neq0\) see the curves \((\alpha,\beta )=(1,0.3)\) and \((\alpha,\beta)=(0.8,0.3)\) in Fig. 2. In this case the neutral curves corresponding to \(\beta\neq0\) lie below the dashed curve. This can not be explained with the above mentioned simple interpretation and one should consider it with more care. In order to describe this result, for the sake of simplicity and with no loss of generality we assume that \(\alpha=1\) and \(\beta\ll1\). We shall see that in reality \(\beta\) is small and our assumption here is a suitable one. Therefor, the RHS of the criterion (50) can be expanded in terms of \(\beta\). Consequently, we have

$$\begin{aligned} Q_{g}>1-\beta^{2}-\frac{3}{2}\beta^{4}+O \bigl(\beta^{5}\bigr) \end{aligned}$$
(52)

Thus in the case \(\alpha=1\), although the gravitational force is supposed to be stronger than the Newtonian case, the required value of \(Q_{g}\) for local stability is always smaller than that of the Newtonian gravity. This situation is reminiscent of the difference between Jeans mass in modified gravity and Newtonian gravity. In fact in modified theories of gravity for which the gravitational force is stronger than that of Newtonian gravity, the Jeans mass is smaller than the standard case, for example see Roshan and Abbassi (2014), Capozziello et al. (2011).

Therefore, comparing the two cases \(\beta=0\), \(\alpha>1\) and \(\alpha=1\), \(\beta>0\) (note that in both cases the gravitational force is stronger than the Newtonian gravitational force), we can conclude that in theories where the gravitational force in the weak field limit is stronger than that of Newtonian gravity, the required value of Toomre’s parameter \(Q_{g}\) for preventing gravitational collapse can be larger or smaller than the corresponding value in Newtonian gravity. In other words, \(Q_{g}\) in these theories is not necessarily larger than that of Newtonian gravity.

In Fig. 3 we show the fluid disk dispersion relation for growing perturbations for various values of \(Q_{g}\) and \(\beta\). The solid curves correspond to \(Q_{g}=0.3\) and \(\beta=0.1\) to 0.5. Furthermore, the dashed curves correspond to \(Q_{g}=0.5\) and \(\beta=0.1\) to 0.5. Also, the dotted curves (\(\beta=0\)) are the corresponding Newtonian dispersion relations for \(Q_{g}=0.3\) and \(Q_{g}=0.5\). As expected, the growth rates tends to increase with decreasing \(Q_{g}\). Also, it is clear form Fig. 3 that the effect of parameter \(\beta\) in Eq. (45) is to stretch the range of instability to small wavenumber while larger \(\beta\) leads to smaller growth rate.

Fig. 3
figure 3

Solutions to the dispersion relation (45) between squared growth rate (\(s^{\prime2}\)) and dimensionless wavenumber (\(k v_{s}/\kappa\)). It has been assumed that \(\alpha=1\). Large \(\beta\) leads to greater instability at small wavenumber

Full size image

3.2 Self-gravitating stellar disk

Similar to the case of the fluid disk, it is straightforward to find the dispersion relation of tightly wound waves in a stellar disk. Since most of the calculations are similar to that of the fluid case, we have briefly derived the dispersion relation in Appendix B. The final result is given by Eq. (74). In the case of axisymmetric perturbations, we may write

$$\begin{aligned} \omega^{2}=\kappa^{2}-2\pi G |k|\varSigma_{0} \frac{\alpha m_{0}^{2}}{k^{2}+m_{0}^{2}}\mathfrak{F}\biggl(\frac{\omega}{\kappa},\frac{k^{2} \sigma _{R}^{2}}{\kappa^{2}}\biggr) \end{aligned}$$
(53)

For a given mode of perturbation, if \(\omega^{2}<0\), then the mode is unstable. Therefore, one may expect that the system is stable against all axisymmetric disturbances if Eq. (53) does not have a solution with \(\omega^{2}<0\). In order to consider this expectation, we write down Eq. (53) as follows

$$\begin{aligned} 1=\frac{2\pi G |k|\varSigma_{0} \alpha m_{0}^{2}}{(k^{2}+m_{0}^{2})(\kappa^{2}-\omega ^{2})}\mathfrak{F}\biggl(\frac{\omega}{\kappa},\frac{k^{2} \sigma_{R}^{2}}{\kappa^{2}} \biggr) \end{aligned}$$
(54)

Now, if \(\omega^{2}<0\), i.e. \(\omega=i \gamma\) where \(\gamma\) is a real number, then the right-hand side (RHS) of Eq. (54) takes the form

$$\begin{aligned} \frac{2\pi G |k| \alpha m_{0}^{2} \varSigma_{0}\kappa^{-2} }{(k^{2}+m_{0}^{2})\sinh\pi s'}\int_{0}^{\pi}e^{-\chi(1+\cos\tau)} \sinh s'\tau \sin\tau d\tau \end{aligned}$$
(55)

where \(s'=i s=\gamma/\kappa\). Also we have used Eq. (76) for the shape function. The schematic behavior of (55) in terms of \(\omega^{2}\) is illustrated in Fig. 4. From this figure we see that the maximum value occurs at \(\omega^{2}=0\). Therefore, if the RHS of Eq. (53) for \(\omega^{2}=0\) is smaller than 1, then there is no tightly wound spiral mode with negative \(\omega^{2}\) which satisfies the dispersion relation (54). Consequently, the self-gravitating disk will be stable to all WKB perturbations. Therefore, the criterion for stability to all wavelengths can be written down as

$$\begin{aligned} \frac{2\pi G |k|\varSigma_{0} \alpha m_{0}^{2}}{(k^{2}+m_{0}^{2})\kappa^{2}}\mathfrak {F}\biggl(0,\frac{k^{2} \sigma_{R}^{2}}{\kappa^{2}}\biggr)< 1 \end{aligned}$$
(56)

this equation can be represented in a more simplified form as

$$\begin{aligned} \frac{\sigma_{R} \kappa}{2\pi G \varSigma_{0}\alpha}>\frac{1}{(1+\beta^{2}\chi )}\frac{ (1-e^{-\chi}I_{0}(\chi) )}{\sqrt{\chi}} \end{aligned}$$
(57)

where \(I_{0}\) is the modified Bessel function of order 0. Also we have used the following identity

$$\begin{aligned} \mathfrak{F}(0,\chi)=\frac{1}{\chi} \bigl(1-e^{-\chi}I_{0}( \chi) \bigr) \end{aligned}$$
(58)

Equation (57) is the main result of this section. In fact, at every location \((R_{0},\phi_{0})\) on the disk, this inequality should be satisfied in order to have local stability to all spiral axisymmetric tightly wound perturbations. As \(\alpha\rightarrow1\) and \(\beta \rightarrow0\), this criterion approaches to the so-called Toomre’s local stability criterion for stellar disk given by (23), again as expected. In Newtonian gravity the RHS of (57) is always larger than that of metric \(f(R)\) gravity. This means that in the context of \(f(R)\) gravity smaller value of Toomre’s parameter is required for local stability of rotating disks. As we discussed in the previous subsection, this result also is the case for a fluid disk.

Fig. 4
figure 4

Equation (55) in terms of \(\omega^{2}\)

Full size image

Although Eq. (57) is our final stability criterion for every perturbation with wavenumber \(k\), if we find the maximum value of the RHS of Eq. (57), then we will find a criterion which guarantees the stability at every location on the disk. Even in Newtonian gravity (where \(\beta=0\)), one has to use numerical analysis to find the maximum value of the RHS (57). Therefore, we need the numeric value of \(\beta\) to find required criterion. However, using an excellent approximation for reduction factor (Elmegreen 2011), we can analytically find the maximum value of RHS of (57). The above mentioned approximation is

$$\begin{aligned} \mathfrak{F}(0,\chi)\simeq\frac{1}{1+\chi} \end{aligned}$$
(59)

In Fig. 5, the solid line is the exact value of \(\mathfrak{F}\) and the dashed line corresponds the approximate value. As it is clear from the figure, the deviation between the two functions is small. Therefore, with the aid of this approximation, we rewrite (57) as follows

$$\begin{aligned} \frac{\sigma_{R} \kappa}{2\pi G \varSigma_{0}\alpha}>\frac{\sqrt{\chi }}{(1+\beta^{2}\chi)(1+\chi)} \end{aligned}$$
(60)

the maximum value of the RHS of this inequality occurs

$$\begin{aligned} \chi=\frac{-1-\beta^{2}+\sqrt{1+14\beta^{2}+\beta^{4}}}{6\beta^{2}} \end{aligned}$$
(61)

stability criterion takes the following form

$$\begin{aligned} Q_{s}>\frac{6\sqrt{6}\alpha\sqrt{g(\beta)-(1+\beta^{2})}}{(g(\beta)+5-\beta ^{2})(g(\beta)+5\beta^{2}-1)} \end{aligned}$$
(62)

where \(g(\beta)=\sqrt{1+14\beta^{2}+\beta^{4}}\). The criterion (62) is the final result of this section. As expected, the free parameters of the theory, i.e. \(\alpha\) and \(m_{0}\), appear in the stability criterion. If we use the same approximation in Newtonian gravity, then we will get the following criterion

$$\begin{aligned} \frac{\sigma_{R} \kappa}{3.14 G \varSigma_{0}}>1 \end{aligned}$$
(63)

this criterion has a little difference with the exact criterion (23). However let us write (63) as \(Q_{s}>1\). As we discussed previously, we expect that \(\beta\) be small in real situations, so the stability criterion can be expanded with respect to \(\beta\) as

$$\begin{aligned} Q_{s}>\alpha-\alpha\beta^{2}+3\alpha\beta^{4}+O \bigl(\beta^{5}\bigr) \end{aligned}$$
(64)

this criterion can be compared with the corresponding criterion for a fluid disk (52). The similarity between the stability criterion of fluid and stellar disk is obvious. Our discussion in the last paragraph of Sect. 3.1 considering the parameter \(Q_{g}\) for a fluid disk, also holds here.

Fig. 5
figure 5

The solid curve is the exact curve for \(\mathfrak{F}(0,\chi)\), and the dashed curve is the approximate one, i.e. Eq. (59)

Full size image

In order to make a comparison between the growth rates in fluid and stellar disks, we have shown the stellar disk dispersion relation (53) in Fig. 6. The solid curves correspond to \(Q_{s}=0.3\) and \(\beta=0.1\) to 0.5. The dashed curves correspond to \(Q_{s}=0.5\) and \(\beta=0.1\) to 0.5. Also, the dotted curves are the corresponding Newtonian dispersion relations for \(Q_{s}=0.3\) and \(Q_{s}=0.5\) where \(\beta =0\). As for a fluid disk, the growth rates increase with decreasing parameter \(Q_{s}\), and the effect of parameter \(\beta\) in Eq. (53) is to stretch the range of instability to small wavenumber. Also larger \(\beta\) leads to smaller growth rate. Comparing Figs. 3 and 6, one can conclude that the growth rate of perturbation in the stellar disk is smaller than that of the fluid disk. In other words, if we consider two patches with the same Toomre’s parameter, one in a fluid disk and one in a stellar disk, the growth rate in the patch on the stellar disk will be smaller than that of the fluid disk.

Fig. 6
figure 6

Solutions to the dispersion relation (53) between squared growth rate (\(s^{\prime2}\)) and dimensionless wavenumber (\(k v_{s}/\kappa\)). It has been assumed that \(\alpha=1\). Large \(\beta\) leads to greater instability at small wavenumber

Full size image

4 Discussion and conclusion

In this paper, the local stability of self-gravitating fluid and stellar disks has been investigated in the framework of metric \(f(R)\) gravity, for which the function \(f(R)\) can be expanded as a power series in terms of Ricci scalar \(R\), see Eq. (2). Thus the results of this paper are applicable only for these models of \(f(R)\). The dispersion relation for the propagation of tightly wound spiral waves has been derived analytically for both fluid and stellar disks. The results are given by Eq. (45) for fluid disk and (53) for the stellar disk.

Also, using the above mentioned dispersion relations, the Toomre’s local stability criterion has been derived in the framework of metric \(f(R)\) gravity. The results are given by Eqs. (50) and (57). An important ingredient of the present study is its possible application of these criteria in N-body simulations of the disk galaxies in the context of \(f(R)\) gravity. It is worth mentioning that the Toomre’s criterion for the fluid disk (50) is complicated than the standard case (22). On the other hand, the generalized Toomre’s criterion for the stellar disk is not so different from its corresponding criterion in Newtonian gravity (23).

As we have discussed, the magnitude of \(m_{0}\) determines the magnitude of deviation between local stability criteria of \(f(R)\) gravity and GR. Therefore, it is necessary to mention that the mass of the effective scalar degree of freedom, \(m_{0}\), may depend upon the density of its environment via the so-called chameleon mechanism (Khoury and Weltman 2004a,b). Obviously, a more careful study is still in order to take into account the chameleon mechanism. Studying this subject is left as a subject of future study.