1 Introduction

The natural satellite capture by a planet has always been a popular topic in celestial mechanics as a way of explaining the origin of various satellites of the system, notably Jupiter’s moon (Nesvorny et al. 2007; Philpotta et al. 2010), and Neptune’s moon (Agnor and Hamilton 2006). Asteroids usually escape or impact the planet when they approach it. In rare cases, the asteroid is captured in a bounded orbit around the planet. This capture is impossible in the framework of the restricted three-body problem with the sun and the planet as primaries. It has been proven that it is impossible to capture an asteroid permanently with a purely gravitational mechanism because almost every particle will pass arbitrarily close to its initial position in phase space (Tanikawa 1983). As a consequence, some non-gravitational scenarios of capture such as gas drag mechanism or a four body such as the planet’s satellite have been proposed to facilitate permanent capture (Pollack et al. 1979; Benner and McKinnon 1995). For the non-gravitational capture mechanism, it is assumed that the asteroid is temporarily captured by gravitational mechanism as the first stage and then the gas drag will make the capture permanently. The capture dynamics and chaotic motion in the restricted three-body problem was thoroughly studied by Belbruno (2005). There are also works about numerical simulations to seek temporarily captured objects (Cline 1979; Paskowitz and Scheeres 2006).

Besides, the old idea of capturing an asteroid to exploit the natural resources becomes popular again as the technology makes it possible (Hasnain et al. 2012; Mazanek et al. 2013). NASA sponsored a study in 2010 to investigate the feasibility of capturing a small near-Earth asteroid (NEA) to the International Space Station (ISS) by 2025 (Brophy et al. 2011). The motivations of capturing an asteroid include gaining convenient access to its resources and contributing to missions aimed at exploring the solar system (McAndrews et al. 2003). In addition, the captured asteroid was proposed against an incoming, threatening body (Massonnet and Meyssignac 2006). Hasnain et al. (2012) studied the acceleration requirement to transport different asteroids to the sphere of influence (SOI) of the earth, along with the impulse or acceleration necessary to capture the asteroid into a bound orbit at the SOI. Cline (1979) studied the utilization of an existing natural satellite of a planet to capture a third body into a closed orbit about the planet. The planet’s satellite was also used to cut down the capture energy in space engineering. The Galileo mission to Jupiter included a flyby of Io near the orbiter’s arrival perijove (D’Amario et al. 1992). Cassini conducted a close flyby of Phoebe before its Saturn Orbit Insertion maneuver (Peralta and Flanagan 1995). Therefore, it is natural to think of utilizing the moon of the earth to lower the velocity of an approaching asteroid to achieve a capture. This is the so-called satellite-aided capture, which was examined by Cline (1979) using a patched two-body analysis that offered very useful asymptotic conditions. Prado studied the escape and capture regions using the restricted three-body model, where the planet and its satellite were regarded as primaries. The escape and capture regions were constructed by scanning the initial values of the massless body in the planar circular and elliptic restricted three-body problem (Prado and Broucke 1995; Prado 1997) and spatial circular restricted three-body problem (Felipe and Prado 1999). In these three references, the restricted three-body model is used to study the trajectory of the spacecraft before and after flyby. The gravitational force of the sun was not considered in this model. Therefore, the problem becomes a two-body problem when the spacecraft leaves the sphere of influence of the secondary primary (either before or after the flyby). It means that the orbit around the larger primary before and after flyby is deterministic (either elliptic or hyperbolic). Actually, the distance from the spacecraft to the larger primary is large either before or after flyby. Take the earth-moon system as an example, the distance is usually about the radius between the earth and moon. At this distance, the perturbation from the sun is large. It means that a stable orbit around the earth after lunar flyby may become unstable (hyperbolic orbit) because of the solar perturbation. In my study, this case happens. When we calculate the energy of the spacecraft with respect to the earth in the two-body problem, the orbit is elliptic. However, when we calculate the Jacobian constant and zero-velocity curve of the spacecraft in the sun-earth restricted three-body problem, the zero-velocity curve is open. This means that the orbit is unstable. It may orbit around the earth for many years before it escapes. It may also escape the earth in less than one loop. It is difficult to predict the motion because of the chaotic characteristics in the restricted three-body problem. The chaotic motion is obvious when the Jacobian constant is close to the critical value (Jacobian constant at L1 libration point). Similarly, a hyperbolic orbit after lunar flyby in the two-body problem may be stable in the sun-earth restricted three-body problem. Therefore, the capture region and escape region will change if the gravity of the sun is considered in the model. Tsui (2000, 2002) used the geometrical parameters to describe the energy exchange between the satellite and the asteroid in the planar four-body problem. Only numerical examples were given to illustrate the possibility of the satellite-aided capture. Besides, utilizing the gravity of the planet’s satellite to escape the planet is also a popular topic in space engineering (Hanson and Deaton 1992; Campagnola et al. 2004).

In this paper, a four-body model, including the sun, the planet, the planet’s satellite, and the fourth body is used to study the capture and escape mechanism. In the presence of the satellite, the energy of the fourth body with respect to the planet can be altered. First, an analytic expression is given to evaluate the analytic energy exchange terms between the satellite and the fourth body. The analytic result is compared to the numerical result and it indicates that the relative error is always less than 10 %. The analytic energy exchange equation is used to give the capture and escape regions. Numerical results are implemented to show the planetary satellite-aided captures and escapes. Besides, some qualitative conclusions can be drawn from this expression. This is intuitive on designing the flyby trajectory. Finally, because of the chaotic motion in the restricted three-body model, a multi-flyby case may occur. The orbit of the spacecraft will be stable after the designed flyby. However, because of the chaotic motion, the spacecraft will approach the moon again after the designed flyby. The unexpected flyby may destabilize the orbit again. Of course, it may also make the orbit more stable. Because the orbit after lunar flyby is not a Keplerian orbit, it is difficult to predict the period of the orbit. It is difficult to predict the multi-flyby condition. This problem is interesting. I intend to study this multi-flyby problem in the future.

2 Planar four-body problem

Consider a four-body system including the sun, the planet, the satellite, and the fourth body. The fourth body can be an asteroid or a spacecraft. Hereafter, we use the asteroid as the fourth body to illustrate the problem. The planet rotates around the sun and the satellite rotates around the planet. The motion of the asteroid is studied when it approaches the planet-moon system. The sun, planet, satellite, and asteroid are denoted as S, P, M, and A, respectively, as shown in Fig. 1. In the inertial reference frame, the dynamical equations of P, M, and A are given by

$$\begin{aligned} &\frac{\mathrm{d}^{2}\boldsymbol{r}_{A}}{\mathrm{d}t^{2}} = - \frac{GM_{S}}{r_{A}^{3}}\boldsymbol{r}_{A} - \frac{GM_{P}}{r_{\mathit{PA}}^{3}}\boldsymbol{r}_{\mathit{PA}} - \frac{GM_{M}}{r_{\mathit{MA}}^{3}} \boldsymbol{r}_{\mathit{MA}}, \end{aligned}$$
(1)
$$\begin{aligned} &\frac{\mathrm{d}^{2}\boldsymbol{r}_{M}}{\mathrm{d}t^{2}} = - \frac{GM_{S}}{r_{M}^{3}}\boldsymbol{r}_{M} - \frac{GM_{P}}{r_{\mathit{PM}}^{3}}\boldsymbol{r}_{\mathit{PM}} + \frac{GM_{A}}{r_{\mathit{MA}}^{3}} \boldsymbol{r}_{\mathit{MA}}, \end{aligned}$$
(2)
$$\begin{aligned} &\frac{\mathrm{d}^{2}\boldsymbol{r}_{P}}{\mathrm{d}t^{2}} = - \frac{GM_{S}}{r_{P}^{3}}\boldsymbol{r}_{P} + \frac{GM_{A}}{r_{\mathit{PA}}^{3}}\boldsymbol{r}_{\mathit{PA}} + \frac{GM_{M}}{r_{\mathit{PM}}^{3}} \boldsymbol{r}_{\mathit{PM}}, \end{aligned}$$
(3)

where G is the gravitational constant; M S , M P , M A , and M M are the masses of the sun, planet, satellite, and the asteroid, respectively.

Fig. 1
figure 1

Geometry of the four-body system

Full size image

Assume that the gravity of the sun dominates the system and the asteroid does not influence the orbit of the planet and satellite. In addition, the satellite does not influence the orbit of the planet. Thus, the planet evolves on a Keplerian orbit around the sun. Therefore, the dynamical equation of the planet can be simplified as

$$ \frac{\mathrm{d}^{2}\boldsymbol{r}_{P}}{\mathrm{d}t^{2}} = - \frac{GM_{S}}{r_{P}^{3}}\boldsymbol{r}_{P} . $$
(4)

The simultaneous equations of Eqs. (1) and (4) give the dynamical equations of motion of the asteroid with respect to the planet.

$$\begin{aligned} \frac{\mathrm{d}^{2}\boldsymbol{r}_{\mathit{PA}}}{\mathrm{d}t^{2}} &= \frac{\mathrm{d}^{2}\boldsymbol{r}_{A}}{\mathrm{d}t^{2}} - \frac{\mathrm{d}^{2}\boldsymbol{r}_{P}}{\mathrm{d}t^{2}} \\ & = - \frac{GM_{S}}{r_{A}^{3}} \boldsymbol{r}_{A} - \frac{GM_{P}}{r_{\mathit{PA}}^{3}}\boldsymbol{r}_{\mathit{PA}} - \frac{GM_{M}}{r_{\mathit{MA}}^{3}}\boldsymbol{r}_{\mathit{MA}} \\ &\quad + \frac{GM_{S}}{r_{P}^{3}} \boldsymbol{r}_{P} . \end{aligned}$$
(5)

When the asteroid enters the planet-satellite system, we assume that the distance between the asteroid and planet is small compared to the distance between the planet and the sun, namely, r PA ≪r P . Then the right-hand side of Eq. (5) can be linearized as

$$\begin{aligned} \frac{\mathrm{d}^{2}\boldsymbol{r}_{\mathit{PA}}}{\mathrm{d}t^{2}} &= - \biggl( \frac{GM_{S}}{r_{P}^{3}}\boldsymbol{I} - 3\frac{GM_{S}\boldsymbol{r}_{P}\boldsymbol{r}_{P}^{T}}{r_{P}^{5}} \biggr) \boldsymbol{r}_{\mathit{PA}} - \frac{GM_{P}}{r_{\mathit{PA}}^{3}}\boldsymbol{r}_{\mathit{PA}} \\ &\quad - \frac{GM_{M}}{r_{\mathit{MA}}^{3}}\boldsymbol{r}_{\mathit{MA}}, \end{aligned}$$
(6)

where I is an identity matrix.

The equation can be transformed to the planet-centered rotating frame. The origin of the frame is the mass center of the planet; the x axis points from the sun to the planet; the z axis is along the direction of the angular momentum of the planet’s orbit; and the y axis forms a right triad with the x and z axes. Assume that the planet rotates around the sun in a circular orbit. Then the dynamical equation can be written as

$$\begin{aligned} &\ddot{\boldsymbol{r}}_{\mathit{PA}} + 2\boldsymbol{\omega}_{P} \times \dot{\boldsymbol{r}}_{\mathit{PA}} + \boldsymbol{\omega}_{P} \times ( \boldsymbol{\omega}_{P} \times \boldsymbol{r}_{\mathit{PA}} ) \\ &\quad = - \omega_{P}^{2} \biggl( I - 3\frac{\boldsymbol{r}_{P}\boldsymbol{r}_{P}^{T}}{r_{P}^{2}} \biggr) \boldsymbol{r}_{\mathit{PA}} \\ &\qquad - \frac{GM_{P}}{r_{\mathit{PA}}^{3}}\boldsymbol{r}_{\mathit{PA}} - \frac{GM_{M}}{r_{\mathit{MA}}^{3}}\boldsymbol{r}_{\mathit{MA}}, \end{aligned}$$
(7)

where ω P is the angular velocity of the planet around the sun.

The equation of motion allows for the nondimensionalization of the model and elimination of all free parameters. More precisely, by taking the orbital radius of planet around the sun r P as the unit length and \(\tau = \frac{1}{\omega_{P}}\)as the unit time, the equations of motion transform into the following parameterless equations:

$$ \begin{cases} \ddot{x} - 2\dot{y} = 3x - \frac{\mu_{P}}{r_{\mathit{PA}}^{3}}x - \frac{\mu_{M}}{r_{\mathit{MA}}^{3}}x_{\mathit{MA}}, \\ \ddot{y} + 2\dot{x} = - \frac{\mu_{P}}{r_{\mathit{PA}}^{3}}y - \frac{\mu_{M}}{r_{\mathit{MA}}^{3}}y_{\mathit{MA}}. \end{cases} $$
(8)

In these dimensionless equations, \(\mu_{P} = \frac{M_{P}}{M_{S}}\) is the dimensionless mass of the planet and \(\mu_{M} = \frac{M_{M}}{M_{S}}\) is the mass of the satellite.

Similarly, the equation of motion of the satellite in the rotating frame is given by

$$ \begin{cases} \ddot{x}_{M} - 2\dot{y}_{M} = 3x_{M} - \frac{\mu_{P}}{r_{\mathit{PM}}^{3}}x_{M} + \frac{\mu_{A}}{r_{\mathit{MA}}^{3}}x_{\mathit{MA}}, \\ \ddot{y}_{M} + 2\dot{x}_{M} = - \frac{\mu_{P}}{r_{\mathit{PM}}^{3}}y_{M} + \frac{\mu_{A}}{r_{\mathit{MA}}^{3}}y_{\mathit{MA}}. \end{cases} $$
(9)

Multiply the first equation in Eq. (8) by \(\dot{x}\) and the second equation by \(\dot{y}\). Then adding them gives

$$ \dot{C} = - \frac{\mu_{M}}{r_{\mathit{MA}}^{3}} ( \dot{x}x_{\mathit{MA}} + \dot{y}y_{\mathit{MA}} ) , $$
(10)

where C is the energy integral in the restricted three-body problem (Szebehely 1967)

$$ C = \frac{1}{2} \bigl( \dot{x}^{2} + \dot{y}^{2} \bigr) - \frac{3}{2}x^{2} - \frac{\mu_{P}}{r_{\mathit{PA}}}. $$
(11)

Similarly, we can obtain the energy integral for the satellite as

$$ \dot{C}_{M} = \frac{\mu_{A}}{r_{\mathit{MA}}^{3}} ( \dot{x}_{M}x_{\mathit{MA}} + \dot{y}_{M}y_{\mathit{MA}} ), $$
(12)

where

$$C_{M} = \frac{1}{2} \bigl( \dot{x}_{M}^{2} + \dot{y}_{M}^{2} \bigr) - \frac{3}{2}x_{M}^{2} - \frac{\mu_{P}}{r_{\mathit{PM}}}.$$

Considering a standard sun–planet–asteroid system by putting μ M =0 in Eq. (8), the system degenerates to a restricted three-body system and the energy integral is constant. In this case, we can obtain the positions of two collinear Lagrange points, x 1,2=±(μ P /3)1/3. Letting the velocity be zero, Eq. (11) defines the zero-velocity curves, which are the bounds of the motion of the asteroid. An increment of C will increase the region in which the asteroid can move. The energy constant at the collinear Lagrange point L 1 is denoted as C 1. The motion will be restricted around the sun or planet depending on its initial states if C<C 1. Therefore, the asteroid will be captured by the planet if the energy integral is smaller than C 1 without the gravitational force of the satellite. This is a necessary condition of the permanent planetary capture in the restricted three-body model. If the asteroid evolves on a heliocentric orbit initially, it has been proven that a permanent capture with a purely sun-planet-asteroid three-body gravitational mechanism is impossible because almost every particle will pass arbitrarily close to its initial position in phase space. As a consequence, some non-gravitational scenarios of capture such as a gas drag mechanism or the fourth body such as the planet’s satellite have to be introduced to facilitate permanent capture.

In the presence of an existing planetary satellite, the energy integral can be altered. Due to the interactions between the satellite and asteroid in Eqs. (8) and (9), the energy integral in Eq. (10) contains μ M and the energy integral in Eq. (12) contains μ A . Although the total energy is conserved, the energy of the asteroid can be altered. Consequently, the asteroid could lose energy to the satellite and could fall into a tight orbit around the planet. It can be seen from Eq. (10) that the energy of the asteroid can only be altered when it approaches the satellite. The energy change is negligible when the asteroid is far from the satellite. When the asteroid is very close to the satellite, the motion of the asteroid is dominated by the gravity of the satellite. To do an order of magnitude estimate of the energy integral change induced by the close approach, we assume that the asteroid flies by the satellite in a hyperbolic orbit, as shown in Fig. 2. A two-body model is used to approximate the motion of the asteroid with respect to the satellite when the asteroid is within the SOI of the satellite. To describe the position of the asteroid with respect to the satellite, a local reference frame is defined, where the x l axis is defined by the periapsis direction of the hyperbolic orbit, the z l axis is along the angular momentum direction, and the y l axis forms a right triad with the x l and z l axes.

Fig. 2
figure 2

Geometrical representation when the asteroid is in the SOI of the satellite

Full size image

In the local reference frame, the position of the asteroid with respect to the satellite can be given by

$$ \begin{cases} \tilde{x}_{\mathit{MA}} = r_{\mathit{MA}}\cos ( f ), \\ \tilde{y}_{\mathit{MA}} = r_{\mathit{MA}}\sin ( f ), \end{cases} $$
(13)

where f is the true anomaly of the hyperbolic orbit.

The position can be expressed in the rotating frame by a coordinate transformation,

$$\begin{aligned} \begin{bmatrix} x_{\mathit{MA}} \\ y_{\mathit{MA}} \end{bmatrix}& = \begin{bmatrix} \cos ( \beta + \theta ) & - \sin ( \beta + \theta ) \\ \sin ( \beta + \theta ) & \cos ( \beta + \theta ) \end{bmatrix} \begin{bmatrix} \tilde{x}_{\mathit{MA}} \\ \tilde{y}_{\mathit{MA}} \end{bmatrix} \\ & = r_{\mathit{MA}} \begin{bmatrix} \cos ( \beta + \theta + f ) \\ \sin ( \beta + \theta + f ) \end{bmatrix}, \end{aligned}$$
(14)

where θ is measured from the PM line to the periapsis direction and β is measured from the SP line to the PM line.

The velocity of the asteroid with respect to the planet can be expressed by the summation of the velocity of the asteroid with respect to the satellite and the velocity of the satellite with respect to the planet. We have

$$ \frac{\mathrm{d}\boldsymbol{r}_{\mathit{PA}}}{\mathrm{d}\tau} = \frac{\mathrm{d}\boldsymbol{r}_{\mathit{PM}}}{\mathrm{d}\tau} + \frac{\mathrm{d}\boldsymbol{r}_{\mathit{MA}}}{\mathrm{d}\tau}. $$
(15)

Because the time of the asteroid staying in the SOI of the satellite is very short, the satellite is assumed to rotate around the planet in a circular orbit during the stage. At some instant, Eq. (15) is projected in an inertial frame whose axes are defined by the axes of the rotating frame. We have

$$\begin{aligned} &\frac{\mathrm{d}\boldsymbol{r}_{\mathit{PM}}}{\mathrm{d}\tau} = \begin{bmatrix} \frac{\mathrm{d}x_{\mathit{PM}}}{\mathrm{d}\tau} \\ \frac{\mathrm{d}y_{\mathit{PM}}}{\mathrm{d}\tau} \end{bmatrix} = r_{\mathit{PM}} \omega_{M} \begin{bmatrix} - \sin \beta \\ \cos \beta \end{bmatrix}, \end{aligned}$$
(16)
$$\begin{aligned} & \begin{aligned}[b] \frac{\mathrm{d}\boldsymbol{r}_{\mathit{MA}}}{\mathrm{d}\tau} &= \begin{bmatrix} \frac{\mathrm{d}x_{\mathit{MA}}}{\mathrm{d}\tau} \\ \frac{\mathrm{d}y_{\mathit{MA}}}{\mathrm{d}\tau} \end{bmatrix} = \begin{bmatrix} \cos ( \beta + \theta ) & - \sin ( \beta + \theta ) \\ \sin ( \beta + \theta ) & \cos ( \beta + \theta ) \end{bmatrix}\\ &\quad \times \begin{bmatrix} - r_{\mathit{MA}}\sin ( f )\frac{\mathrm{d}f}{\mathrm{d}\tau} + \frac{\mathrm{d}r_{\mathit{MA}}}{\mathrm{d}\tau} \cos ( f ) \\ r_{\mathit{MA}}\cos ( f )\frac{\mathrm{d}f}{\mathrm{d}\tau} + \frac{\mathrm{d}r_{\mathit{MA}}}{\mathrm{d}\tau} \sin ( f ) \end{bmatrix}, \end{aligned} \end{aligned}$$
(17)

where ω M is the angular velocity of the satellite around the planet.

The velocity of the asteroid with respect to the planet can be described by the velocity in the rotating frame, which is given by

$$ \frac{\mathrm{d}\boldsymbol{r}_{\mathit{PA}}}{\mathrm{d}\tau} = \begin{bmatrix} \dot{x} - y \\ \dot{y} + x \end{bmatrix}. $$
(18)

From Eqs. (15) and (18) we can solve the velocity in the rotating frame

$$ \left \{ \begin{array}{rl} \dot{x} &= y - r_{\mathit{MA}}\sin ( f + \theta + \beta )\frac{\mathrm{d}f}{\mathrm{d}\tau}\\ &\quad + \frac{\mathrm{d}r_{\mathit{MA}}}{\mathrm{d}\tau} \cos ( f + \theta + \beta ) - r_{\mathit{PM}}\omega_{M}\sin ( \beta ), \\ \dot{y} &= - x + r_{\mathit{MA}}\cos ( f + \theta + \beta )\frac{\mathrm{d}f}{\mathrm{d}\tau} \\ &\quad + \frac{\mathrm{d}r_{\mathit{MA}}}{\mathrm{d}\tau} \sin ( f + \theta + \beta ) + r_{\mathit{PM}}\omega_{M}\cos ( \beta ). \end{array} \right . $$
(19)

Because the asteroid evolves in a hyperbolic orbit, the following relations hold:

$$\begin{aligned} &r_{\mathit{MA}} = \frac{p}{1 + e\cos ( f )}, \end{aligned}$$
(20)
$$\begin{aligned} &\frac{\mathrm{d}r_{\mathit{MA}}}{\mathrm{d}\tau} = \frac{pe\sin ( f )}{ [ 1 + e\cos ( f ) ]^{2}}\frac{\mathrm{d}f}{\mathrm{d}\tau}, \end{aligned}$$
(21)
$$\begin{aligned} &\frac{\mathrm{d}f}{\mathrm{d}\tau} = \frac{\sqrt{p\mu_{M}}}{r_{\mathit{MA}}^{2}} , \end{aligned}$$
(22)

where p is the semi-latus rectum and e is eccentricity of the hyperbola.

Substitution of Eqs. (14), (19)–(22) into Eq. (10) gives

$$\begin{aligned} \dot{C} &= - \frac{\mu_{M}}{r_{\mathit{MA}}^{2}} \biggl[ r_{\mathit{PM}} ( \omega_{M} - 1 )\sin ( f + \theta ) \\ &\quad + \frac{pe\sin ( f )}{ [ 1 + e\cos ( f ) ]^{2}}\frac{\mathrm{d}f}{\mathrm{d}\tau} \biggr]. \end{aligned}$$
(23)

The energy integral change due to the flyby can be obtained by integrating Eq. (23). We have

$$\begin{aligned} \delta C &= - \int_{\tau_{0}}^{\tau_{f}} \frac{\mu_{M}}{r_{\mathit{MA}}^{2}} \biggl[ r_{\mathit{PM}} ( \omega_{M} - 1 )\sin ( f + \theta ) \\ &\quad + \frac{pe\sin ( f )}{ [ 1 + e\cos ( f ) ]^{2}}\frac{\mathrm{d}f}{\mathrm{d}\tau} \biggr] \,\mathrm{d}\tau. \end{aligned}$$
(24)

Using Eq. (22), the independent variable can be changed from time to true anomaly. We have

$$\begin{aligned} \delta C &= - \int_{f_{0}}^{f_{f}} \frac{\mu_{M}}{r_{\mathit{MA}}^{2}} \biggl[ r_{\mathit{PM}} ( \omega_{M} - 1 )\sin ( f + \theta )\frac{r_{\mathit{MA}}^{2}}{\sqrt{p\mu_{M}}} \\ &\quad + \frac{pe\sin ( f )}{ [ 1 + e\cos ( f ) ]^{2}} \biggr] \,\mathrm{d}f \\ &= - \sqrt{\frac{\mu_{B}}{p}} r_{\mathit{PM}} ( \omega_{M} - 1 ) \\ &\quad \times \int_{f_{0}}^{f_{f}} \bigl[ \sin ( f )\cos ( \theta ) + \cos ( f )\sin ( \theta ) \bigr]\, \mathrm{d}f \\ &\quad - \frac{\mu_{M}}{p}e\int_{f_{0}}^{f_{f}} \sin ( f ) \,\mathrm{d}f. \end{aligned}$$
(25)

The two-body approximation is only valid when the asteroid is within the SOI of the satellite. When the asteroid is out of the SOI, the energy integral change due to the gravity of the satellite is negligible. Therefore, the domain of integration can be specified by the true anomalies of the asteroid passing through the SOI. The radius of the SOI of the satellite is given by (Bate et al. 1971)

$$ R_{\mathrm{SOI}} = \biggl( \frac{\mu_{M}}{\mu_{P}} \biggr)^{2/5}r_{\mathit{PM}}. $$
(26)

Then we can obtain the true anomaly of the asteroid when it arrives at the SOI,

$$ f_{c} = \cos^{ - 1} \biggl( \frac{p}{eR_{\mathrm{SOI}}} - \frac{1}{e} \biggr). $$
(27)

Now, the energy integral change due to the satellite’s gravity can be given by

$$\begin{aligned} \delta C &= - \sqrt{\frac{\mu_{M}}{p}} r_{\mathit{PM}} ( \omega_{M} - 1 )\int_{ - f_{c}}^{f_{c}} \bigl[ \sin ( f )\cos ( \theta ) \\ &\quad + \cos ( f )\sin ( \theta ) \bigr] \,\mathrm{d}f - \frac{\mu_{M}}{p}e\int _{ - f_{c}}^{f_{c}} \sin ( f ) \,\mathrm{d}f. \end{aligned}$$
(28)

The integration can be simplified as

$$ \delta C = - \sqrt{\frac{\mu_{M}}{p}} r_{\mathit{PM}} ( \omega_{M} - 1 )\int_{ - f_{c}}^{f_{c}} \cos ( f )\sin ( \theta ) \,\mathrm{d}f. $$
(29)

The integrand depends on the time-varying variable θ. However, it is a slowly changing variable and f is a rapidly changing variable in this system. Therefore, it can be regarded constant in the integration. Then the analytic solution of the integration can be obtained as

$$\begin{aligned} \delta C &= - 2\sqrt{\frac{\mu_{M}}{p}} r_{\mathit{PM}} ( \omega_{M} - 1 )\sin ( \theta )\sin ( f_{c} ) \\ &= - 2\sqrt{\frac{\mu_{M}}{p}} r_{\mathit{PM}} ( \omega_{M} - 1 )\sin ( \theta )\sqrt{1 - \frac{1}{e^{2}} \biggl( \frac{p}{R_{\mathrm{SOI}}} - 1 \biggr)^{2}}. \end{aligned}$$
(30)

It can be seen from Eq. (30) that the energy integral change only depends on the semi-latus rectum, the eccentricity of the hyperbola, and the periapsis direction. The semi-latus rectum and eccentricity determine the shape of the hyperbola and the periapsis direction determines the direction of the hyperbola. This qualitative conclusion is consistent with that of the lunar flyby in a two-body patched conic model (Cline 1979). In the two-body patched conic model, the energy change due to the flyby depends on v inf (the velocity with respect to the satellite at the SOI) and periapsis radius, which determine the shape of the hyperbola, and also the flyby direction, which determines the direction of the hyperbola. Besides, Eq. (30) gives a quantitative estimation of the energy integral change. It provides a more intuitive way to design a lunar flyby capture or escape trajectory or select an asteroid that may be captured through lunar flyby.

From Eq. (30) we know that the periapsis direction of the hyperbola determines the sign of the energy change. It decreases when sinθ>0 and increases when sinθ<0. Therefore, an escape trajectory can be achieved by designing the trajectory to satisfy sinθ<0 and a capture trajectory can be achieved by designing the trajectory to satisfy sinθ>0. To maximize the change of the energy integral, the apse line of the hyperbola should be perpendicular the planet-satellite line. The dependence of the energy integral change on θ is obvious. However, the dependence of the energy integral change on the shape of the hyperbola is not clear. To give a more institutive description, Eq. (30) is rewritten as

$$\begin{aligned} \delta C &= - 2\sqrt{\mu_{M}} r_{\mathit{PM}} ( \omega_{M} - 1 ) \\ &\quad \times \sin ( \theta )\sqrt{\frac{e - 1}{r_{p}e^{2}} - \frac{r_{p} ( 1 + e )}{e^{2}R_{\mathrm{SOI}}^{2}} + \frac{2}{e^{2}R_{\mathrm{SOI}}}}, \end{aligned}$$
(31)

where r p is the periapsis radius of the hyperbola.

It can be seen from Eq. (31) that the energy integral change is a monotonic function of the periapsis radius. To evaluate the validity of the analytic expression, the analytic results are compared to the numerical results, which are obtained by integrating Eqs. (8) and (9) simultaneously. The initial values of the differential equations are determined by the initial states of the satellite with respect to the planet and the parameters of the hyperbola. The relative error between the analytic and numerical results are defined as

$$ C_{\mathrm{err}} = \biggl\vert \frac{\delta C_{a} - \delta C_{n}}{\delta C_{n}} \biggr\vert , $$
(32)

where δC n is the numerical result and δC a is the analytic result.

Figure 3 gives the analytic and numerical results for the case of θ=−0.5π in the sun–earth–moon system. The results in Fig. 3(a) show that the energy integral change increases as the periapsis radius decreases. The relative error between the analytic and numerical results is always less than 10 %, as shown in Fig. 3(b). As the periapsis radius increases, the influence of the gravity of the earth will increase. Therefore, the error increases with the periapsis radius, as shown in Fig. 3(b).

Fig. 3
figure 3

Validation of the analytic energy change in Sun–Earth–Moon System, θ=−0.5π

Full size image

3 Numerical simulations

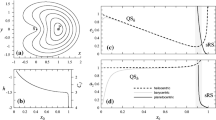
In this section, we focus on the escape and capture conditions. For the capture case, we assume that the asteroid orbits around the sun in an elliptical orbit before it enters the planet-satellite system. If the asteroid orbits around the planet after it leaves the SOI of the satellite, we say that the asteroid belongs to the capture region. Equation (31) is used to identify the orbital parameters of the asteroids that belong to the capture region. Firstly, the capture region can be represented by the parameters of the hyperbola. Given the initial position and velocity of the satellite with respect to the planet and the parameters of the hyperbola, the energy integral before satellite flyby can be obtained by integrating Eqs. (8) and (9) backward in time. Similarly, the energy integral after satellite flyby is obtained by integrating the equations forward in time. Based on the energy integral before and after satellite flyby, the capture region can be achieved. From Eq. (31) we know that the capture region depends on θ, r p , and e. The capture region in the sun–earth–moon system is represented in the e–r p space for different values of θ, as shown in Fig. 4. The capture region expands as expected when θ approaches π/2.

Fig. 4
figure 4

Capture region in the e–r p space for different values of θ

Full size image

In fact, the capture region can be represented by the classical elements of the asteroid’s heliocentric orbit. Given the initial values, we can integrate Eqs. (8) and (9) simultaneously backward in time until the asteroid arrives at the SOI of the planet. Based on the position and velocity of the asteroid in the planet-centered rotating frame at the SOI, the position and velocity of the asteroid with respect to the sun can be obtained as

$$\begin{aligned} &\boldsymbol{r}_{A} = \begin{bmatrix} x + 1 \\ y \end{bmatrix} , \end{aligned}$$
(33)
$$\begin{aligned} &\frac{\mathrm{d}\boldsymbol{r}_{A}}{\mathrm{d}\tau} = \begin{bmatrix} \frac{\mathrm{d}x}{\mathrm{d}\tau} \\ \frac{\mathrm{d}y}{\mathrm{d}\tau} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} \dot{x} - y \\ \dot{y} + x + 1 \end{bmatrix}. \end{aligned}$$
(34)

Having the heliocentric position and velocity, the classical elements of the heliocentric orbit can be constructed. We have

$$\begin{aligned} a_{S} &= \frac{r_{A}}{2 - r_{A} ( \frac{\mathrm{d}r_{A}}{\mathrm{d}\tau} )^{2}} \\ & = \frac{\sqrt{ ( x + 1 )^{2} + y^{2}}}{2 - [ ( \dot{x} - y )^{2} + ( \dot{y} + x + 1 )^{2} ]\sqrt{ ( x + 1 )^{2} + y^{2}}}, \end{aligned}$$
(35)
$$\begin{aligned} \boldsymbol{e}_{S} = \frac{\mathrm{d}\boldsymbol{r}_{A}}{\mathrm{d}\tau} \times \biggl( \boldsymbol{r}_{A} \times \frac{\mathrm{d}\boldsymbol{r}_{A}}{\mathrm{d}\tau} \biggr) - \frac{\boldsymbol{r}_{A}}{r_{A}}, \end{aligned}$$
(36)
$$ \omega_{r} = \tan^{ - 1}\frac{e_{Sy}}{e_{Sx}}, $$
(37)

where a S , e S are the semi-major axis and eccentricity vector of the orbit, respectively. e Sx and e Sx are the components of the eccentricity vector along the x and y axes, respectively. ω r is the angle measured from the sun-planet line to the periapsis direction of the orbit at the SOI.

It can be seen from the analytic energy change equation that the capture region in e–r p space is independent of the angle between the sun-planet line and the planet-satellite line (β). However, the capture in the a S –e S space depends on β. Therefore, if the complete capture region in the a S –e S space is required, we have to integrate the capture regions for all possible values of β. The capture region for θ=0.5π in the a S –e S –ω r space is shown in Fig. 5. The capture regions for other values of θ can be obtained similarly.

Fig. 5
figure 5

Capture region in the a S –e S –ω r space for θ=0.5π

Full size image

Having the capture region, we can simulate the capture process. A point in the capture region of θ=0.5π is selected. The periapsis radius is r p =4×103 km and the eccentricity of the hyperbola is e=2. The angle between the sun-earth line and earth-moon line is β 0=1 radian when the asteroid is at the perilune. The states of the asteroid at the SOI of the earth are obtained by integrating the dynamical equation backward in time. The classical elements of the asteroid’s heliocentric orbit at the SOI are a S =1.0198 AU and e S =0.0503. The trajectory of the asteroid departing from the SOI is shown in Fig. 6(b). The asteroid is captured after lunar flyby. The time history of the energy integral is shown in Fig. 6(a). The energy integral is larger than the critical value before lunar flyby and the lunar flyby reduces it below the critical value. The distances from the asteroid to the earth and moon are shown in Figs. 6(c) and 6(d), respectively. The distance from the earth indicates that the asteroid orbits around the earth in an elliptic orbit and the apogee radius is about 0.005 AU. The distance from the moon indicates that the asteroid only approaches the moon once. The asteroid is far from the moon after lunar flyby and the gravity of the moon is negligible. Therefore, the orbit is stable as long as the energy integral is below the critical value. However, this is not always the case. If the orbit after lunar flyby is resonant with the moon’s orbit, the asteroid will return to the moon after lunar flyby. In this case, the asteroid may escape again.

Fig. 6
figure 6

Capture case for θ=0.5π, r p =4e3 km, and e=2

Full size image

Similarly, another point in the capture region of θ=0.5π is selected. The perilune radius is r p =5e3 km and the eccentricity of the hyperbola is e=2.3. The angle between the sun-earth line and earth-moon line is still β 0=1 radian when the asteroid is at the perilune. The classical elements of the heliocentric orbit at the SOI of the earth are a S =1.0148 AU and e S =0.0474. The trajectory of the asteroid departing from the SOI is shown in Fig. 7(b). We can see that the asteroid approaches the moon three times before it escapes again. The first lunar flyby reduces to energy integral below the critical value and makes it fall into a tight orbit around the earth. The second lunar flyby reduces the energy integral further. The asteroid gets much closer to the moon for the third lunar flyby and escapes from the earth after the third lunar flyby. Therefore, the orbits belonging to the capture region only means that the orbit is bounded just after the first lunar flyby. If the asteroid will not return to the moon, the orbit is stable. However, if the post lunar flyby orbit is resonant with the moon’s orbit, more lunar flybys will occur. The stability of the orbit cannot be guaranteed.

Fig. 7
figure 7

Case of capture for θ=0.5π, r p =5e3 km, and e=2.3

Full size image

The analytic expression for energy integral change can also be used to design planetary escape trajectories. The energy integral change is symmetrical with respect to θ. Therefore, the capture region in the e–r p space becomes the escape region by changing θ to −θ. A point in the escape region of θ=0.5π is selected to simulate the escape case. The perilune radius is r p =5×103 km and the eccentricity of the hyperbola is e=1.68. The angle between the sun-earth line and earth-moon line is β 0=1 radian when the asteroid is at the perilune. Similarly, the classical elements of the asteroid with respect to the planet can be constructed based on the states of the asteroid at the SOI of the satellite.

$$\begin{aligned} &a_{P} = \frac{\mu_{P}\sqrt{x^{2} + y^{2}}}{2\mu_{P} - [ ( \dot{x} - y )^{2} + ( \dot{y} + x )^{2} ]\sqrt{x^{2} + y^{2}}}, \end{aligned}$$
(38)
$$\begin{aligned} &\boldsymbol{e}_{P} = \frac{d\boldsymbol{r}_{\mathit{PA}}}{\mathrm{d}\tau} \times \biggl( \boldsymbol{r}_{\mathit{PA}} \times \frac{d\boldsymbol{r}_{\mathit{PA}}}{\mathrm{d}\tau} \biggr) - \frac{\boldsymbol{r}_{\mathit{PA}}}{r_{A}} . \end{aligned}$$
(39)

The orbital elements of the asteroid with respect to the earth before entering the SOI of the moon are a P =2.01065×105 km and e P =0.96578. The trajectory departing from the perigee is shown in Fig. 8(b). The energy integral is above the critical value after two lunar flybys. The second flyby is the expected one that makes the spacecraft escape. The escape region can be used to design escape trajectories for an interplanetary mission. We only need to transfer the spacecraft to a lunar flyby orbit. It can save much energy compared to a direct transfer from the low earth orbit.

Fig. 8
figure 8

Escape case for θ=−0.5π, r p =5e3 km, and e=1.68

Full size image

4 Conclusion

A planar four-body model is used to study the planetary escape and capture. When the fourth body is in the vicinity of the planet, the equation controlling the energy exchange between the fourth body and the planet’s satellite is derived. Further, the analytic solution to the energy exchange equation is achieved when the satellite orbits around the planet in a circular orbit. The analytic energy exchange equation indicates that the energy of the fourth body will be reduced if the angle measured from the planet-satellite line to the apse line of the fourth body’s hyperbolic orbit with respect to the satellite is less than π. The amount of energy change, depending on the shape parameters of the hyperbola, is also given. Based on the energy exchange equation, the capture and escape regions are represented in different parameter spaces. Several numerical examples are given to illustrate the satellite-aided capture and escape.