1 Introduction

Engineering applications often involve flows at high Reynolds numbers around bluff bodies such as the landing gear of an aircraft. Adverse pressure gradient due to streamline curvature or diverging flow cross-section may affect the boundary layer development over such surfaces and lead to separation resulting in increased drag and aerodynamic noise. The accurate prediction of such flows is of particular interest to improve industrial design. Large Eddy Simulation (LES) is well adapted to predict these unsteady and turbulent flows since the large scale structures influencing the flow are explicitly resolved when only the small dissipative scales are modelled (Sagaut 2006). LES is classically implemented within the Navier–Stokes framework but it can also be used with the Lattice Boltzmann Method (LBM) which is an emerging numerical method becoming popular in particular for subsonic aerodynamic flows and aeroacoustics prediction thanks to its low dissipative character (Marié et al. 2009; Malaspinas and Sagaut 2012; Sengissen et al. 2015; Lucas et al. 2017; Leveque et al. 2018; König et al. 2018). The computational cost for wall-resolved LES (WRLES) on industrial configurations is however high due to the small grid size required near the wall to explicitly resolve the boundary layer dynamics (Piomelli 2008; Bose and Park 2018). Traditional solutions proposed to overcome this limitation can be classified in three categories (Piomelli and Balaras 2002; Larsson et al. 2016): algebraic laws for the tangential velocity near the wall, two-layer zonal models and hybrid Reynolds-Averaged Navier–Stokes (RANS)-LES methods. In the first two methods, termed wall-modelled LES (WMLES), the no-slip boundary condition is replaced by a prescription of the wall shear stress \(\tau _w\) (Larsson et al. 2016) or the determination of the first off-wall node tangential velocity u (see e.g. Bernardini et al. 2016; Wilhelm et al. 2018). WMLES along with Immersed Boundary Conditions in LBM has been presented by Malaspinas and Sagaut (2014).

Two-layer zonal models are based on the resolution of thin boundary layer equations (TBLE) on an embedded grid in the near-wall region. TBLE can be written for flows at equilibrium neglecting the convective, unsteady and pressure gradient terms. This is adapted for attached flows with zero or mild pressure gradient (Tessicini et al. 2002; Piomelli 2008). However for complex flows in industrial applications, non-equilibrium effects may affect the boundary layer dynamics and should be taken into account for better accuracy as shown in Wang and Moin (2002) and Park (2017). To avoid the resolution of TBLE near the wall, the meshless approach of Monfort et al. (2010) and the integral wall model of Yang et al. (2015), recently extended to compressible flows in Catchirayer et al. (2018), are based on analytical models for the tangential velocity profile in the near-wall region taking pressure gradient effects into account. These models are still more complex than algebraic models since in the meshless approach (Monfort et al. 2010) a Gauss quadrature is required to determine the tangential velocity while for the integral wall model (Yang et al. 2015) several coefficients have to be determined from physical constraints and integrated momentum equations at almost each time step.

Algebraic wall models are based on the assumption that, with a proper scaling \(u^*\), the scaled tangential velocity in the boundary layer, \(u^+= u/u^*\), follows a universal algebraic law depending on the scaled distance y to the wall, \(y^+ = y u^* /\nu\), , where \(\nu\) is the kinematic viscosity of the considered fluid. In the viscous sub-layer, the linear law \(u^+ = y^+\) generally used at equilibrium can also be used for non-equilibrium boundary layers (Larsson et al. 2016; Yang et al. 2015). Scalings and algebraic wall laws commonly used in the overlap region of a boundary layer are presented in Table 1. More information can be found in the review papers of Buschmann and Gad-el Hak (2006) and Bose and Park (2018). For equilibrium flows the scaling is generally based on the friction velocity \(u_{\tau }\) and the most popular model is the logarithmic law (“log-law”) for which different values of the von Karman \(\kappa\) and C constants are given in the literature (Zagarola et al. 1997; Marusic et al. 2013). This model is implicit, which means that an iterative method is needed for the determination of the wall shear stress. On the contrary, with explicit models, an explicit expression of the wall shear stress can be derived thus simplifying the near-wall modelling and its numerical implementation. This is the case for the power-law model of Werner and Wengle (1993) as used by Wilhelm et al. (2018).

For a boundary layer involving a pressure gradient, the pressure is supposed constant in the wall normal direction and the pressure gradient acts mainly in the streamwise direction (Schlichting et al. 1955). The following velocity scale is then defined (Mellor 1966):

$$\begin{aligned} u_p = \left( \frac{\nu }{\rho } \frac{dp}{ds}\right) ^{1/3} \end{aligned}$$
(1)

where dp/ds is the streamwise pressure gradient and \(\rho\) is the density of the flow. This velocity scale may be more relevant than the friction velocity \(u_{\tau }\) for flows under pressure gradient in particular for separated boundary layer for which \(u_{\tau }\) becomes zero at a separation or reattachment point. The pressure gradient parameter is defined as in Mellor (1966) and used in Afzal (1996), Skote and Henningson (2002), Breuer et al. (2006) and Gungor et al. (2016):

$$\begin{aligned} p^+ = \frac{\nu }{\rho u_{\tau }^3}\frac{dp}{ds} = \left( \frac{u_p}{u_{\tau }}\right) ^3 \end{aligned}$$
(2)

This parameter is not bounded at a separation or reattachment point since \(u_{\tau }\) vanishes. According to Coleman et al. (2018) and Maciel et al. (2018), none of the near-wall length scales found in the literature are pressure gradient independent and no universal self-similar solution can be expected for boundary layers ranging from quasi-equilibrium to strong adverse pressure gradient turbulent boundary layers. As shown in Skote and Henningson (2002), using the friction velocity \(u_{\tau }\) as the velocity scale, a tangential velocity profile depending on the local pressure gradient and the Reynolds number can be derived for a turbulent boundary layer under adverse pressure gradient. This corresponds to an extended log-law for the overlap region already established by Afzal (1996) and hereafter referred as Afzal’s law:

$$\begin{aligned} u_{Afzal}^+ = \frac{u}{u_{\tau }}=\frac{1}{\kappa }ln(y^+) + C - \frac{2}{\kappa } \ln \left( \frac{\sqrt{1+p^+y^+}+1}{2} \right) + \frac{2}{\kappa }\left( \sqrt{1+p^+y^+}-1\right) \end{aligned}$$
(3)

The wall model defined by Eq.  (3) is not valid at a separation or reattachment point where \(u_{\tau }\) becomes zero. To overcome this singularity, Skote and Henningson (2002) proposed a second version of the model using \(u_p\) as the velocity scale. This second version is however not valid in zero pressure gradient regions where \(u_p = 0\). In a priori validation, Skote and Henningson (2002) showed that the Afzal’s law better follows the velocity profile in a boundary layer under adverse pressure gradient than the classical log-law with a modification of the constant C depending on the pressure gradient. Marsden et al. (2008) found a good agreement between the velocity profiles obtained by wall-resolved LES and the analytical profile given by Eq. (3) in the turbulent region of the boundary layer over a NACA0012 airfoil. The Afzal’s law has been recently successfully used for the prediction of a rod-airfoil tandem (Zhang et al. 2018). The Afzal’s law has been compared to the dynamic wall model of Wang and Moin (2002) by Hou et al. (2016) giving very similar results, better than those obtained using the equilibrium model of Spalding (1961), for the flow over a single cylinder and tandem cylinders which involve separation regions. An extended log-law taking adverse pressure gradient into account based on an Afzal-like law has been successfully applied to complex turbulent flows in Sengissen et al. (2015), Lucas et al. (2017) and Leveque et al. (2018). As shown in Table 1, an equivalent explicit algebraic model extensively validated for pressure gradient boundary layers and separated flows is missing. Breuer et al. (2007) proposed an extended version of the power-law model of Werner and Wengle (1993) taking pressure gradient into account: the Extended Werner and Wengle Improved (EWWI). Its explicit version, the Extended Simplified Werner and Wengle Improved (ESWWI), is however only valid for small first cell heights. Manhart et al. (2008) proposed to combine both velocity scales \(u_{\tau }\) and \(u_p\) in a single one \(u_{\tau p} = \sqrt{u_{\tau }^2+ u_p^2}\) which does not vanish at separation and reattachment points or for vanishing pressure gradient. They derived an explicit extended wall model valid in the viscous sub-layer for boundary layer under pressure gradient. Duprat et al. (2011) extended this wall model outside the viscous sub-layer by taking the Reynolds stresses effects into account besides the pressure gradient effects. The resulting model is however implicit.

An open issue is to know if wall models are valid or not inside separated flow regions. Temmerman et al. (2003) showed that velocity profiles do not comply with the log-law not only in the separated region but also in the reattached zone of a periodic hill flow. The back-flow scaling, based on the maximum averaged back-flow velocity \(U_N\) and its distance \(y_N\) to the wall, is however appropriate for a majority of the separated region. In both studies of Wang and Moin (2002) and Yang et al. (2015), it is suggested that the boundary layer is resolved in separated regions by LES even on a coarse grid since the local Reynolds number is low. In their WMLES of the flow over the 30P-30N airfoil at Reynolds number \(Re = 9 \times 10^6\), Bodart et al. (2013) decided to not use the wall model, but the usual no-slip boundary condition, in the flap storage bay where separated flow is expected. Note that the decision of using or not the wall model is made in pre-processing based on the foreknowledge about the flow. The wall model is consequently used in other regions of separated flow during the calculation.

Table 1 Overview (non-exhaustive) of the most common scalings and algebraic wall models for the overlap region of a turbulent boundary layer; variables and acronyms are defined in the text
Full size table

Complex industrial flows often involve pressure gradient boundary layers leading sometimes to separation. The necessity of taking pressure gradient effects into account in wall models when considering such flows has been established by several studies as reminded in the present introduction. The explicit power-law wall model has been applied for LBM simulations of attached flows in Wilhelm et al. (2018) thus greatly simplifying the near-wall treatment for LBM on Cartesian grids. The objective of the present study is to extend this power-law model for industrial applications involving large adverse pressure gradient and flow separation while preserving the explicit character of the model. The paper is organized as follows. The new explicit wall model is presented in Sect. 2. The numerical method is discussed in Sect. 3 as well as the application of the new wall model in LBM. Validation of this wall model is evaluated in Sect. 4 for three test cases of engineering interest. Conclusions are given in Sect. 5.

2 An Explicit Algebraic Wall Model for Flows Under Adverse Pressure Gradient

2.1 The Power-Law Wall Model

Since the pioneering work of Prandtl (Schlichting et al. 1955) who proposed a one-seventh power-law for boundary layer flows at small Reynolds numbers, the power-law model has long been considered as an alternative to the log-law to describe the flow in turbulent boundary layers and fully developed flows in pipes or channels (Marusic et al. 2010; Cheng and Samtaney 2014). Several authors proposed a power-law with constant parameters (Zagarola et al. 1997) or depending on the Reynolds number (Barenblatt et al. 1997; Castro-Orgaz and Dey 2011) to describe the velocity profile in pipe flows and turbulent boundary layers. According to Afzal (2001), the power-law is an equivalent solution to the log-law for the matching between the inner and outer regions of the boundary layer. A review of the power-law models developed for pipe and channel flows and turbulent boundary layers can be found in Buschmann and Gad-el Hak (2006). The power-law has been used in LES by Murakami et al. (1987) with an exponent adapted to the considered flow (see Table 1) and by Werner and Wengle (1993) with exponent 1/7 for LES of flow over a cube. The later was used more recently in LES by several authors (Temmerman et al. 2003; Chang et al. 2014; Lehmkuhl et al. 2016; Wilhelm et al. 2018).

In this work, the equilibrium power-law model is considered as defined in Wilhelm et al. (2018):

$$\begin{aligned} u^{+}= {\left\{ \begin{array}{ll} y^{+} &{} \quad \text { if } y^{+} \le {} y_c^{+}\\ A (y^{+})^{B} &{}\quad \text { if } y^{+} \ge {} y_c^{+} \end{array}\right. } \end{aligned}$$
(4)

where \(B=1/7\) and \(y_c^{+} = 11.81\) is the scaled height of the viscous sub-layer. By continuity of the velocity profile at \(y_c^{+}\), \(A=(y_c^{+})^{1-B} \approx 8.3\). The scaling is based on the friction velocity \(u_{\tau }\) such as:

$$\begin{aligned} u^{+}= \frac{u}{u_{\tau }}\quad \text { and }\quad y^{+}= \frac{y u_{\tau }}{\nu } \end{aligned}$$
(5)

with the following explicit expression for \(u_{\tau }\):

$$\begin{aligned} u_{\tau }= {\left\{ \begin{array}{ll} \sqrt{\frac{\nu u}{y}} &{} \text { if } y^{+} \le {} y_c^{+}\\ u^{\frac{1}{1+B}} A^{\frac{-1}{1+B}} y^{\frac{-B}{1+B}} \nu ^{\frac{B}{1+B}} &{} \text { if } y^{+} \ge {} y_c^{+} \end{array}\right. } \end{aligned}$$
(6)

In the following, this equilibrium power-law is extended for boundary layers under adverse pressure gradient while remaining explicit. This new law will be termed “APGPL” for Adverse Pressure Gradient Power-Law.

2.2 Development of the Adverse Pressure Gradient Power-Law (APGPL)

According to Larsson et al. (2016), the viscous region of the boundary layer is at equilibrium. As in Yang et al. (2015), a linear velocity profile is used in the viscous sub-layer and only a model for the overlap region of boundary layers under adverse pressure gradient is developed.

As explained in the introduction, no self-similar law of the wall exists for turbulent boundary layer under adverse pressure gradient. The Afzal’s law (extended log-law) presented in Eq. (3) has been validated by several authors. The wall model successfully used in Sengissen et al. (2015), Lucas et al. (2017) and Leveque et al. (2018) to take adverse pressure gradient effect into account is based on the Afzal’s law. It will be called Adverse Pressure Gradient Log-Law (APGLL) in this paper. In particular, a constant \(C_0\) is added to \(y^+\) in the first logarithm of Eq. (3) to correct the model for low \(y^+\) values. This model is however implicit. The APGPL is developed in order to mimic the APGLL but in an explicit way. It has been established according to the following procedure:

  1. 1.

    General form of the APGPL: The APGPL model is developped using the friction velocity \(u_\tau\) as velocity scale and is therefore not valid at a separation or reattachment point where \(u_\tau\) vanishes. Similarly to Eq. (3), a function depending on \(y^{+}\) and \(p^{+}\) is added to the equilibrium power-law:

    $$\begin{aligned} u_{APGPL}^{+} = A(y^{+})^B + f(y^{+},p^{+}) \end{aligned}$$
    (7)

    The constants A and B are maintained equal to the values of the equilibrium power-law. The function f involves free parameters that have to be calibrated.

  2. 2.

    Definition of the function f : An explicit form of the wall law is defined by combining the expressions of \(y^{+}\) and \(p^{+}\) in the function \(f(y^{+},p^{+})\). For example, the product \((y^{+})^3 p^{+}\) is independent of the friction velocity \(u_{\tau }\). Similar mathematical functions as in Eq. (3) are used, namely square root and logarithm, in order to mimic this expression.

  3. 3.

    Calibration of the model: Free parameters of the model involved in the function f are determined by minimizing the error between the APGPL and the APGLL over specified ranges of \(y^{+}\) and \(p^{+}\) values relevant for real engineering applications at high Reynolds numbers. Only adverse pressure gradient effects, that is, positive values of \(p^{+}\), are considered in this work. The ranges \(0< p^{+} < 1\) and \(100< y^{+} < 1000\) are selected. In particular, when used with immersed boundaries or Cartesian grids, the wall model is first applied to a fictitious Ref point located at a larger distance from the wall than the boundary node (Kalitzin and Iaccarino 2002; Tessicini et al. 2002; Roman et al. 2009; Capizzano 2011; Berger and Aftosmis 2012). As shown in Wilhelm et al. (2018), for \(y^+\) values of a few hundred at the boundary node, \(y^+\) can reach values around 1000 at the Ref point.

Several expressions for the function f have been considered, calibrated and tested. The following expression giving the best results in LES (see Sect. 4) is retained for the APGPL:

$$\begin{aligned} \text {for } p^{+}> 0 \text { and } y^{+} > 0,\ u_{APGPL}^{+} = A(y^{+})^B + \alpha \sqrt{y^{+}p^{+}} + \beta (p^{+})^{1/3} \ln {(\gamma (y^{+})^3 p^{+})} \end{aligned}$$
(8)

with \(B = 1/7\), \(A \approx 8.3\), \(\alpha = 7.5789\), \(\beta = -1.4489\), \(\gamma = 191.1799\). The corresponding expression of the tangential velocity in the boundary layer is as follows for \(y > 0\) and \(dp/ds > 0\):

$$\begin{aligned} u = A (u_{\tau })^{B+1} \left( \frac{y}{\nu }\right) ^{B} + \alpha \sqrt{\frac{y}{\rho }\frac{dp}{ds}} + \beta \left( \frac{\nu }{\rho } \frac{dp}{ds}\right) ^{1/3} \ln \left( \gamma \frac{y^3}{\rho \nu ^2} \frac{dp}{ds}\right) \end{aligned}$$
(9)

Note that this expression does not require \(u_\tau \ne 0\) as for Eq. (8).

The term D is defined as:

$$\begin{aligned} D = u - \alpha \sqrt{\frac{y}{\rho }\frac{dp}{ds}} - \beta \left( \frac{\nu }{\rho } \frac{dp}{ds}\right) ^{1/3} \ln \left( \gamma \frac{y^3}{\rho \nu ^2} \frac{dp}{ds}\right) = A (u_{\tau })^{B+1} \left( \frac{y}{\nu }\right) ^{B} \end{aligned}$$
(10)

The following explicit expression of the friction velocity is obtained from the APGPL for \(D \ge 0\):

$$\begin{aligned} u_{\tau } = A^{\frac{-1}{B+1}} \left( \frac{\nu }{y}\right) ^{\frac{B}{B+1}} \left( u - \alpha \sqrt{\frac{y}{\rho }\frac{dp}{ds}} - \beta \left( \frac{\nu }{\rho } \frac{dp}{ds}\right) ^{1/3} \ln \left( \gamma \frac{y^3}{\rho \nu ^2} \frac{dp}{ds}\right) \right) ^\frac{1}{B+1} \end{aligned}$$
(11)

In real flow applications, different flow regions can be encountered, namely with positive or negative values of \(p^{+}\) and D. A specific implementation of the APGPL wall model is thus necessary and will be discussed in Sect. 2.3.

The APGLL and the APGPL are compared in Fig. 1 for \(0.1< p^+ < 1\) and \(30< y^+ < 1000\). The range of \(y^+\) values is extended to lower values than used for the APGPL development to verify its validity until the buffer layer. Note that the equilibrium log and power laws comply for \(50< y^+ < 1000\) as shown in Wilhelm et al. (2018). For low values of \(p^+\), the larger discrepancy between the two wall models is observed at large values of \(y^+\). As \(p^+\) increases, this discrepancy is moved towards small values of \(y^+\). The mean differential \(\overline{\varDelta u^{+}}\) over the range \(30< y^+ < 1000\) presented in Fig. 1b is always lower than \(7\%\). The lower errors are obtained for \(p^+\) values in the middle of the range. This comparison is extended to higher values of \(p^+\) in Fig. 2 to show how the law calibrated for the range \(0< p^+ < 1\) behave for larger values that can be encountered in simulations. The mean error \(\overline{\varDelta u^{+}}\) increases with increasing \(p^+\). However, this error remains lower than \(7.5\%\) and reaches a plateau for high values of \(p^+\).

Fig. 1
figure 1

Comparison of the APGLL and the APGPL (Eq. (8)) (in log-log scale) for the range \(0.1< p^+ < 1\) and \(30< y^+ < 1000\) (a) and mean differential \(\varDelta u^+ = 100*|u_{APGPL}^+ - u_{APGLL}^+|/u_{APGLL}^+\) over the range of \(30< y^+ < 1000\) (b)

Full size image
Fig. 2
figure 2

Mean differential \(\varDelta u^+ = 100*|u_{APGPL}^+ - u_{APGLL}^+|/u_{APGLL}^+\) over the range of \(30< y^+ < 1000\) for \(1< p^+ < 10\) (a) and \(10< p^+ < 100\) (b)

Full size image

2.3 Practical Use of the APGPL

The local streamwise pressure gradient dp/ds is considered, where \(\mathbf {s}\) points in direction of the local wall-parallel flow. Firstly, the APGPL is developed for adverse pressure gradient flows, this means for \(dp /ds > 0\). For favourable or zero pressure gradient, \(dp /ds \le 0\), the equilibrium power-law model should be recovered. Secondly, at a separation or reattachment point, the friction velocity \(u_{\tau }\) becomes zero and the pressure parameter \(p^+\) is not defined. The APGPL written in dimensional scale in Eq. (9), though, is still defined. According to Eq. (11), \(u_{\tau }\) vanishes when the term D vanishes. If D becomes negative, Eq. (11) is no more defined and the APGPL is not valid. D can become negative if the pressure gradient dp/ds is very high or if the tangential velocity u in the boundary layer is low, which is the case in separated flow regions. It will be shown in the results presented in Sect. 4 that D becomes negative near separation zones. As explained in the introduction, it is controversial if a wall model should be used in a separated region of the flow. Consequently, it has been decided not to use a wall model in regions where D is negative. Note that, contrary to Bodart et al. (2013), this decision is made according to the sign of D during the calculation and not in a pre-processing stage.

In the end, the implementation of the APGPL wall model involves three modes defined below. An indicator function \(\gamma (\mathbf{{x}},t)\) is defined specifying which mode of the APGPL wall model is locally active at position \(\mathbf {x}\) at time t:

  1. 1.

    if \(dp /ds (\mathbf{{x}},t) \le 0\), \(\gamma (\mathbf{{x}},t)\) = 1: the equilibrium power-law defined by Eq. (4) is used

  2. 2.

    if \(dp /ds(\mathbf{{x}},t) > 0\) but \(D(\mathbf{{x}},t) < 0\), \(\gamma (\mathbf{{x}},t)\) = 2: no wall model is used, the boundary layer is resolved with a no-slip boundary condition. In this case, the wall shear stress \(\tau _w = \rho u_{\tau }^2\) is calculated according to the linear velocity profile assumption near the wall and the friction velocity is:

    $$\begin{aligned} u_{\tau }= \sqrt{\frac{\nu \left\Vert u \right\Vert }{y}} \end{aligned}$$
    (12)

    where \(\left\Vert u \right\Vert\) is the norm of the tangential velocity obtained by the no-slip boundary condition. Note that the same expression was obtained by Yang et al. (2015) in the limit of wall-resolving case.

  3. 3.

    if \(dp /ds(\mathbf{{x}},t) > 0\) and \(D(\mathbf{{x}},t) \ge 0\), \(\gamma (\mathbf{{x}},t)\) = 3: the APGPL is used with the linear law in the viscous sub-layer:

    $$\begin{aligned} u^{+}= {\left\{ \begin{array}{ll} y^{+} &{} \text { if } y^{+} \le {} y_c^{+}\\ A(y^{+})^B + \alpha \sqrt{y^{+}p^{+}} + \beta (p^{+})^{1/3} \ln {(\gamma (y^{+})^3 p^{+})} &{} \text { if } y^{+} > {} y_c^{+} \end{array}\right. } \end{aligned}$$
    (13)

    with the constants \(A, B, \alpha , \beta , \gamma\) defined in Sect. 2.2.

3 Numerical Method

3.1 Lattice Boltzmann Method and Turbulence Modelling

In this work, the Lattice Boltzmann Method (LBM) is used to solve the weakly compressible Navier–Stokes equations for the velocity \(\mathbf {u}\) and density \(\rho\) in a fluid flow. This emerging method is attractive thanks to the absence of a non-linear term and of a Poisson equation for the pressure and due to its local nature enabling massively parallel simulations (Chen and Doolen 1998; Krüger et al. 2017). In this method, the fluid dynamics is described at the mesoscopic level by the collision and propagation of particles over a discrete lattice. This mechanism is represented by the Boltzmann equation for the particle distribution function \(f(\mathbf {x}, \varvec{\upxi }, t)\) which is the probability density function of particles with velocity \(\varvec{\upxi }\) at time t and position \(\mathbf {x}\).

This work was carried out using the ProLB solver. The Boltzmann equation is discretised in velocity space \(\varvec{\upxi }\) over a D3Q19 (3 dimensions and 19 velocities) lattice. The Dynamic Hybrid Recursive Regularized Bhatnagar-Gross-Krook (DHRR-BGK) LBM model proposed by Jacob et al. (2018) is used to ensure numerical stability and accuracy of the results. Macroscopic quantities of the flow can then be recovered from the moments of the distribution functions:

$$\begin{aligned} \rho (\mathbf{{x}}, t)= & {} \sum \limits _{i=0}^{18} f_i(\mathbf{{x}}, t) \end{aligned}$$
(14)
$$\begin{aligned} \rho (\mathbf{{x}}, t) \mathbf{{u}}(\mathbf {x}, t)= & {} \sum \limits _{i=0}^{18} f_i(\mathbf{{x}}, t) \varvec{\upxi }_i \end{aligned}$$
(15)

where \(0 \le i \le 18\) is the velocity index and \(f_i(\mathbf{{x}}, t)\) is the distribution function discretised in velocity space. Finally, the static pressure p is obtained from the isothermal equation of state:

$$\begin{aligned} p = \rho c_s^2 \end{aligned}$$
(16)

where \(c_s\) is the speed of sound.

Using the DHRR-BGK LBM model, the LES is implicit with the Vreman sub-grid scale model (Vreman 2004) used to estimate the dissipation of the LBM scheme as explained in Jacob et al. (2018).

3.2 Near-Wall Treatment

The near-wall treatment used along with the Lattice Boltzmann method in this work has been extensively detailed in Wilhelm et al. (2018) and only elements necessary for the understanding of the present work are reminded. LBM is applied on a Cartesian cut-cell grid which is not body-fitted, as illustrated in Fig. 3. The LBM scheme can not be completed at the first off-wall nodes termed “Boundary Nodes” (BN). Distribution functions at these nodes are reconstructed from otherwise determined velocity and density. For high Reynolds number flows, it is generally difficult to sufficiently refine the Cartesian grid near a solid boundary to be able to resolve the boundary layer. In this case, a wall model is used to calculate the tangential velocity at boundary nodes.

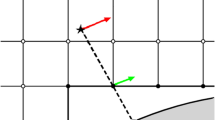
Figure 3 presents the near-wall treatment in two dimensions for the sake of simplicity, but it applies in three dimensions. In particular, the near-wall treatement when using a wall model is presented in Fig. 3a. \(\mathbf {n}\) defines the normal direction to the wall at the considered boundary node \(\bigstar\). In all cases, the normal velocity at the boundary node is zero for a stationary wall. As explained in (Wilhelm et al. 2018) and shown in Fig. 3a, a fictitious point Ref is defined at a distance \(y_{Ref}=2.5 \varDelta x\) from the wall in \(\mathbf {n}\) direction. The Cartesian velocity at the Ref point at time \(t+1\) is calculated from Inverse Distance Weighting (IDW) interpolation of Cartesian velocities at time \(t+1\) at neighbouring nodes \(\blacksquare\) and \(\blacktriangle\). The corresponding tangential velocity \(u_{Ref}^{t+1}\) is then evaluated knowing the local wall normal direction \(\mathbf {n}\). The tangential direction \(\mathbf {s}\) in Fig. 3a is defined by the local and instantaneous tangential to the wall flow direction at the Ref point. In three dimensions, this corresponds to the tangential direction to the wall in the streamwise direction of the local velocity field. The local coordinate system \((\mathbf {n}, \mathbf {s})\) is thus defined at each boundary node \(\bigstar\). The local streamwise pressure gradient dp/ds acting on the boundary layer, and involved in Eq. (8), is evaluated at the boundary node. For this purpose, two fictitious points are first defined at distance \(\varDelta x\) from the boundary node in the upstream and downstream tangential flow directions, where \(\varDelta x\) is the local grid size (see Fig. 3a). The closest grid nodes A and B from these fictitious points are then identified. These nodes can be fluid nodes at which \(\rho\) and \(\mathbf {u}\) are known at time \(t+1\) from the LBM scheme, such as node B, or another boundary node, such as node A, for which values of \(\rho\) and \(\mathbf {u}\) are considered at the previous time step t. The pressure is supposed constant in the wall normal direction and the streamwise pressure gradient is calculated at time \(t+1\) according to :

$$\begin{aligned} \frac{dp}{ds}^{t+1} = \frac{p_B^{t+1} - p_A^{t}}{d_{AB}} = c_s^2\frac{\rho _B^{t+1} - \rho _A^{t}}{d_{AB}} \end{aligned}$$
(17)

where \(d_{AB}\) is the distance between points A and B along the streamwise direction \(\mathbf {s}\), \(p_{A}\) (\(p_{B}\)) is the pressure calculated at the point A (B) using the equation of state \(p= \rho c_s^2\).

Fig. 3
figure 3

Scheme of the near-wall treatment in LBM when a wall model is used (a) or when the boundary layer is resolved (b); the black region is the solid, \(\varDelta x\) is the local grid size, \(\bigstar\): boundary node of interest, \(\blacksquare\) and \(\blacktriangle\): neighbouring fluid nodes of \(\bigstar\), \(\square\) and \(\triangle\): neighbouring boundary nodes of \(\bigstar\), \(\bullet\): reference points

Full size image

The implementation of the APGPL model is described in Table 2. The term D of the APGPL is evaluated at the Ref point according to Eq. (10) using \(u_{Ref}^{t+1}\) and the pressure gradient calculated with Eq. (17) since it is supposed constant in the wall normal direction. With dp/ds and D known at the Ref point, the APGPL mode \(\gamma (\mathbf{{x}}_{Ref},t+1)\) is locally determined.

For \(\gamma (\mathbf{{x}}_{Ref},t+1) = 1\) or 3, the local Reynolds number \(Re_l(y_{Ref}) =y_{Ref} u_{Ref}^{t+1} /\nu\) at the Ref point is compared with the critical local Reynolds number at the upper limit of the viscous sub-layer \(Re_c = (y_c^+)^2\). If \(Re_l(y_{Ref}) \le Re_c\), then both the Ref point and the boundary node are located in the viscous sub-layer and the linear law is used. Otherwise, the friction velocity \(u_{\tau }^{t+1}\) is evaluated using the wall law in the overlap region. The wall-distance y at the boundary node is then compared to the height of the viscous sub-layer \(y_c\) to determine which wall law is to be applied to the boundary node. The tangential velocity \(u(y)^{t+1}\) at the boundary node is obtained from the application of the wall model. A transformation to the Cartesian coordinate system is then performed as needed for the LBM written in a Cartesian system.

In case \(\gamma (\mathbf{{x}}_{Ref},t+1) = 2\), no wall model is used and the near-wall treatment is illustrated in Fig. 3b. The Cartesian velocity vector at the boundary node is reconstructed according to the no-slip boundary condition using an interpolation method as it is generally done for non-body fitted Cartesian grids (Berger and Aftosmis 2012; Iaccarino and Verzicco 2003). The velocity vector is reconstructed by polynomial interpolation of Cartesian velocities at the Ref1, Ref2 and Refw points presented in Fig. 3b. Ref1 and Ref2 are defined in the wall normal direction at distances \(\varDelta x\) and \(2 \varDelta x\) respectively from the boundary node. Similarly to the Ref point, the velocities at Ref1 and Ref2 at time \(t+1\) are obtained by IDW of known velocities at time \(t+1\) at neighbouring nodes \(\blacksquare\) and \(\blacktriangle\). Refw is the projection of the boundary node on the wall in the \(\mathbf{{n}}\) direction. Its velocity corresponds to the boundary condition applied to the wall, which is \(\mathbf{{u}} = \mathbf {0}\) for a no-slip wall. The tangential velocity \(u(y)^{t+1}\) at the boundary node is then calculated by coordinate system transformation and its norm is used to calculate the friction velocity according to Eq.  (12).

Table 2 Implementation of the APGPL model for Cartesian grids in LBM
Full size table

Finally, the density at the boundary node is equated to the density at the Ref point \(\rho (y)^{t+1} = \rho _{Ref}^{t+1}\) according to the assumption of constant pressure in the wall normal direction and where \(\rho _{Ref}^{t+1}\) is obtained by IDW of densities at neighbouring nodes \(\blacksquare\) and \(\blacktriangle\).

4 Validation

In this section, the new APGPL and the well-validated APGLL will be applied to relevant test cases and results will be compared in order to evaluate the accuracy of the new APGPL model.

The APGLL is based on the Afzal’s law defined in Eq. (3) as explained in Sect. 2.2. This law is valid in the overlap region only. In order to extend it to the buffer layer and viscous sub-layer, Eq. (3) is multiplied by a Van-Driest damping function of the form \(1- \exp (-y^+/E)\), where E is a constant:

$$\begin{aligned} u^+= & {} \left( \frac{1}{\kappa }ln(y^+ + C_0) + C - \frac{2}{\kappa } \ln \left( \frac{\sqrt{1+p^+y^+}+1}{2} \right) + \frac{2}{\kappa }\left( \sqrt{1+p^+y^+}-1\right) \right) \nonumber \\&* \left( 1- \exp \left( -\frac{y^+}{E}\right) \right) \end{aligned}$$
(18)

The APGLL is actually used only for adverse pressure gradient flow regions. When the pressure gradient vanishes (\(p^+ =0\)), the equilibrium log-law with Van-Driest damping is recovered from Eq. (18). For favorable pressure gradient flow regions, this equilibrium log-law is also used. The APGLL switches between the equilibrium log-law and the Afzal’s law depending on the sign of the pressure gradient. The resulting model referred as “APGLL model” has a continuous formulation in the whole boundary layer.

The Van-Driest damping function can not be used with the power-law because it would render the model implicit. The term “APGPL model” refers to the model implemented as described in Table 2. In cases where a wall law is used (modes \(\gamma = 1\) or 3), the linear law is implemented in the viscous sub-layer and the power-law with or without pressure gradient effect is used in the overlap region of the boundary layer.

The same adverse pressure gradient, calculated as defined in Sect. 3.2, is used in both models. As a consequence, the APGLL et APGPL models may differ in the viscous sub-layer and buffer layer but should be equivalent in the overlap region. They are compared on three test cases of industrial interest and of increasing complexity involving adverse pressure gradient and boundary layer separation. The flow around a streamlined body, namely the NACA23012 airfoil, with gradual adverse pressure gradient is first considered. The same NACA23012 profile is then considered with ice accretion on the leading edge involving boundary layer separation and reattachment. Finally, the flow around a landing gear is computed. Results are compared with reference data in order to evaluate the validity of the APGPL model. In particular, results obtained with the APGPL model should be as accurate as those obtained with the APGLL model.

4.1 NACA23012 Clean-Airfoil

The capacity of the APGPL model to predict the attached flow around an airfoil at low angles of attack is first evaluated. The flow around the NACA23012 airfoil without ice accretion (“clean airfoil”) experimentally studied by Broeren et al. (2014) at Reynolds number \(Re = 1.88 \times 10^6\) based on the airfoil chord c and Mach number \(Ma = 0.18\) is considered. This test case has been already used by Wilhelm et al. (2018) to validate the equilibrium power-law in LBM with the RANS Spalart-Allmaras turbulence model for low angles of attack at which the flow should remain attached. It has also been numerically studied by König et al. (2015) in LBM using the commercial software PowerFLOW. A Very Large Eddy Simulation (VLES) approach was used in König et al. (2015) along with a wall model based on an extension of the log-law taking among others pressure gradient effects into account.

4.1.1 Numerical Setup

The computational domain is illustrated in Fig. 4. It is the same as used for RANS calculations in Wilhelm et al. (2018) except for the spanwise extension s which corresponds to one third of the experimental model’s span as in König et al. (2015). According to Broeren et al. (2014), the stalling angle of attack is \(14.4^\circ\) for this clean airfoil. Three angles of attack \(\alpha\) are considered before stall with increasing adverse pressure gradient: \(\alpha = 3.08^\circ ; 6.2^\circ\) and \(9.3^\circ\). Uniform free-stream velocity \(U_\infty\) inclined with an angle \(\alpha\) is imposed as a boundary condition and in sponge layers at the inlet and lower surfaces. Uniform free-stream density \(\rho _\infty\) is imposed as a boundary condition and in sponge layers at the outlet and upper surfaces. Frictionless wall condition is imposed on a few cells at the intersection between the inlet and the upper surface and between the lower surface and the outlet. Periodicity is assumed in the spanwise \(\mathbf {z}\) direction. Wall modelling is used for the airfoil surface.

Fig. 4
figure 4

Computational domain and grid for the NACA23012 clean-airfoil test case; c is the airfoil chord

Full size image

4.1.2 Grid Influence at \(\alpha =6.2^\circ\)

As shown in Fig. 4, the computational grid is composed of uniform embedded Cartesian grids where the grid size is halved at each refinement level. The smallest embedded grids are defined by offseted surfaces from the airfoil surface as illustrated in the red box in Fig. 4. Grid convergence study is conducted for \(\alpha =6.2^\circ\). Grids 1, 2 and 3 defined in Table 3 only differs by the number of offsets around the airfoil, the grids being identical in the rest of the domain. Grids 2, respectively 3, is defined by adding one offset to grid 1, respectively 2, thus halving \(y^+\) values at boundary nodes. Grid 3 is represented in Fig. 4. Corresponding averaged \(y^+\) values obtained with the APGPL model are presented in Fig. 5 (values for the APGLL model are very close). The grid being Cartesian, it has a staircase-like form around the solid body explaining the large fluctuations of the \(y^+\) values at boundary nodes. Maximum \(y^+\) values around 250 are obtained for grid 1 but one has to keep in mind that the wall model is first applied to the Ref point with larger \(y^+\) values (see Sect. 3.2).

Table 3 Characteristics of the grids for the NACA23012 clean-airfoil grid convergence study
Full size table
Fig. 5
figure 5

Temporal- and span- averaged \(y^+\) over the NACA23012 clean-airfoil for the APGPL model

Full size image

At this pre-stall angle of attack, statistical steady state should be obtained for the flow around the clean airfoil. Figure 6 presents the convergence history of the lift coefficients obtained with the APGLL and APGPL models. Neither the APGLL nor the APGPL predict a statistically steady flow on Grid 1 even when calculation is run twice as long as for grids 2 and 3. At this grid refinement level, the blunt trailing edge of the NACA profile is not sufficiently discretised and an unsteady separation bubble is predicted at the trailing edge. This bubble is fluttering with the APGLL model leading to the \(C_L\) oscillations observed in Fig. 6a while this unsteadiness is less regular with the APGPL model. In this region, the mode \(\gamma = 2\) of the APGPL is principally used which means that the wall model is not applied. This may explain the different behaviors of the APGLL and APGPL models on grid 1. By refining the grid, the prediction of the flow around the trailing edge is improved and a small but statistically steady recirculation zone is predicted at the trailing edge. A statistically steady state is obtained with grids 2 and 3 after \(15t^*\), where \(t^* = c / U_\infty\).

Fig. 6
figure 6

Convergence history of the lift coefficient for the NACA23012 clean-airfoil using the APGLL (a) or the APGPL (b)

Full size image

For grids 2 and 3, simulations are run for \(15.54t^*\) and temporal statistics are then sampled over \(5.65t^*\). As explained in Wilhelm et al. (2018), far-field integration is more accurate than surface integration to evaluate the lift and drag coefficients with the numerical method used in this work. In particular, the surfaces of the 3D volume in the spanwise direction for far-field integration are defined at \(10\%\) of the airfoil chord from the periodic boundaries. The calculated span is \(60.8\%c\) as shown in Fig. 4 so that the integration is done on \(40.8\%c\). All other post-processed results have been obtained by considering the same restricted span for homogeneity in the results. Time-averaged aerodynamic coefficients obtained with grids 2 and 3 are compared in Table 4 with numerical and experimental references. Results obtained with the Xfoil program (Drela and Youngren 2001) were presented in Wilhelm et al. (2018). Xfoil is based on equations from the integral boundary layer formulation and has been run in a way to bypass the transition mechanism according to the fully turbulent boundary layer assumption done in the present numerical method. elsA results were provided by Airbus using the elsA code (http://elsa.onera.fr/. Accessed 02 Oct 2019) based on the Navier–Stokes equations. Results presented in this paper were obtained by a 2D body-fitted RANS calculation using the Spalart-Allmaras turbulence model with resolved boundary layer. Two sets of experimental measurements are available: the experimental data of Broeren et al. (2014) were corrected for wall-boundary effects of the wind tunnel but the non-corrected values are available in König et al. (2015). Experimentally, the lift was obtained by integration of surface pressure when the drag was obtained by momentum-deficit methods. In LBM-VLES results of König et al. (2015), lift and drag coefficients were calculated by surface integration over the complete model for the lift but over only \(5\%\) of the span for the drag to avoid corner effects. For the RANS body-fitted elsA results, coefficients obtained by far-field integration are presented but very close results were obtained with surface integration. LBM-RANS results presented in Wilhelm et al. (2018) were obtained by far-field integration. The use of different methods to determine these coefficients makes precise comparison difficult. However, the same post-processing is applied for the two grids considered enabling a correct grid convergence study. Grid convergence is similar with both wall models. Lift coefficients obtained with both grids are very similar and slightly higher than references. The drag coefficients predicted with grid 3 are higher than with grid 2 and closer to numerical references. Note that all numerical references give \(C_D\) values higher than experimental data. As explained in König et al. (2015), this may be explained by the turbulent boundary layer assumption used in numerical simulations when the flow may be laminar at some point in the experiments. The present drag coefficients should be compared with the numerical references since the same turbulent boundary layer assumption is involved. In this case, results obtained with grid 3 are in better agreement with numerical reference data. The drag coefficient is however very low in the attached flow region so that the gap between numerical and experimental data is only around 40 drag counts.

Table 4 Time-averaged lift \(C_L\) and drag \(C_D\) coefficients obtained with grids 2 and 3 for the NACA23012 clean-airfoil and compared with numerical and experimental references at \(\alpha =6.2^\circ\), except for data from König et al. (2015) at \(\alpha \approx 6^\circ\); Broeren et al. (2014) data are read from figure 9 in Broeren et al. (2014); experimental and LBM values of König et al. (2015) are read from figure 9 in König et al. (2015)
Full size table

This grid convergence study is completed with the pressure coefficient \(C_p\) profiles, averaged in time and over the span of the airfoil, obtained with grids 2 and 3 in Fig. 7. Oscillations of the pressure profiles obtained with both grids are observed, which increase with grid refinement. This is due to pressure oscillations observed close to the solid surface when using Cartesian grids as explained in Wilhelm et al. (2018). This problem is linked to the use of non-body-fitted grids not only in LBM but also in the Navier–Stokes framework when immersed boundary methods (Capizzano 2011; Tamaki et al. 2017) or cut-cell methods (Berger and Aftosmis 2012) are used. Farfield density and velocity are used for the non-dimensionalization in the \(C_p\) calculation. According to König et al. (2015), quantities measured upstream in the wind tunnel are used for non-dimensionalization in the experiments. This leads to a deviation \(0 \le \varDelta C_p < 0.1\). This may explain some of the discrepancies between experimental and numerical \(C_p\) profiles. The present numerical results should nonetheless be in agreement with elsA results which uses the same nominal quantities for the non-dimensionalization. \(C_p\) profiles obtained with both grids are very close and close to the Xfoil and elsA references independently of the wall model used. A modification of the wall model application has been proposed by Capizzano (2011) and taken up by Tamaki et al. (2017) which smooth out pressure wiggles. However, as shown in Wilhelm et al. (2018), this introduces artificial roughness to the NACA profile and deteriorates the drag coefficient prediction. This method was not used in the present paper for this reason. These pressure oscillations are in fact not detrimental to the results since the predicted pressure coefficients \(C_p\) are oscillating around a mean value which is close to Xfoil and elsA references.

In conclusion, refining the mesh size close to the airfoil surface from grid 2 to grid 3 enables to better predict the drag coefficient, other variables being less influenced by this refinement. Grid 3 is thus used for validation of the APGPL model in the rest of this section.

Fig. 7
figure 7

Time- and span-averaged pressure coefficient \(C_p\) over the NACA23012 clean-airfoil at \(\alpha =6.2^\circ\) obtained with grids 2 and 3 using the APGLL (a) or the APGPL (b) model compared with references; Broeren et al. (2014) experimental data are read from figure 20 in Broeren et al. (2014)

Full size image

4.1.3 Evaluation of the APGPL Model

The behaviour of the APGPL model is illustrated in Fig. 8 with the repartition of the indicator function \(\gamma\), defined in Sect. 2.3, at the last time step of the simulations for the three considered angles of attack. The equilibrium power-law (\(\gamma = 1\)) is used close to the leading edge and in the second part of the airfoil chord. The mode \(\gamma = 3\) is used in regions of high adverse pressure gradient on the upper and lower surfaces of the airfoil. As the angle of attack is increased, the region resolved with \(\gamma = 3\) extends towards the leading edge and a larger part of the upper surface is resolved by taking the adverse pressure gradient into account. The mode \(\gamma = 2\) is active only on the airfoil truncated trailing edge where small flow recirculation occurs. One may observe oscillations of the model between modes 1 and 3. This is due to pressure oscillations observed close to the solid surface when using Cartesian grids, as already mentioned in the previous section. This leads to oscillations of the pressure gradient sign which is one condition for variation between modes 1 and 3 of the APGPL model. However, no numerical instabilities have been observed due to these oscillations of \(\gamma\). Moreover, this is not detrimental for the flow prediction as observed in the previous section and will be observed below.

Fig. 8
figure 8

Indicator function \(\gamma\) at boundary nodes over 20\(\%\) of the calculated NACA23012 clean-airfoil span for the last simulation time step at the three angles of attack considered

Full size image

Lift and drag coefficients obtained with the APGLL and APGPL models for the three angles of attack are compared with references in Fig. 9. \(C_L\) and \(C_D\) coefficients obtained with the APGLL and APGPL models are very close. \(C_L\) is slightly over-estimated compared to the references except for the results of König et al. (2015) from which present results are very close. \(C_D\) values obtained in present WMLES are close to numerical references and slightly higher than experimental data as already discussed in the previous section. For further validation, pressure coefficients obtained at two angles of attack with the APGLL and APGPL models are illustrated in Fig. 10. \(C_p\) profiles obtained with both models are almost identical and close to all the references. All numerical results overestimate \(C_p\) on the lower surface of the airfoil compared to experimental measurements. The results obtained with the APGPL model are of the same accuracy as existing methods.

Fig. 9
figure 9

Time-averaged lift (a) and drag (b) coefficients obtained with the APGLL and APGPL models for the NACA23012 clean-airfoil compared with reference data; experimental data (exp.) of Broeren et al. (2014) are read from figure 9 in Broeren et al. (2014) and the corresponding non-corrected data as well as LBM-VLES results are read from figure 9 in König et al. (2015), Wilhelm et al. (2018) corresponds to results on Grid A in Wilhelm et al. (2018)

Full size image
Fig. 10
figure 10

Time and span-averaged pressure coefficient \(C_p\) over the NACA23012 clean-airfoil at \(\alpha = 6.2^\circ\) (a) and \(\alpha = 9.3^\circ\) (b) compared with references; Broeren et al. (2014) experimental data are read from figures 11 and 20 in Broeren et al. (2014)

Full size image

4.2 NACA23012 Iced-Airfoil

The ability of the APGPL model to predict a three-dimensional unsteady flow with boundary layer separation and reattachment is evaluated by considering the flow around an iced airfoil. The horn ice shape ED1978 presented in Broeren et al. (2014) is added to the leading edge of the NACA23012 airfoil studied in the previous section as illustrated in Fig. 11. This ice shape is composed of two main horns with some roughness and its shapes varies along the spanwise direction. The flow field around this shape involves separation and reattachment in particular downstream of the upper-surface horn. This test case has been studied experimentally in Broeren et al. (2014) and numerically in König et al. (2015). The flow conditions are the same as in the previous section (\(Re = 1.88 \times 10^6\), Ma = 0.18).

Fig. 11
figure 11

Illustration of the NACA23012 airfoil with the horn ice ED1978 on the leading edge (in red) along with an example of the grid used for the calculation (it corresponds to grid A in Fig. 12)

Full size image

4.2.1 Numerical Setup

As illustrated in Fig. 12, almost the same domain size as for the clean airfoil is used for the iced airfoil with a small difference in spanwise length. In the experiment of Broeren et al. (2014), the same ice shape (illustrated in Fig. 11) is reproduced three times over the span of the airfoil. One ice shape is considered in the present numerical simulations considering one third of the measured span which corresponds to \(61.8\%\) of the airfoil chord. The angle of attack \(\alpha = 6.2^\circ\) is considered for which references of lift, drag and pressure coefficients are available. The same boundary conditions as for the clean airfoil are used except for the condition in the spanwise direction. Periodicity can not be used because of the ice shape, frictionless walls are used instead.

Fig. 12
figure 12

Computational domain and grid for the NACA23012 airfoil with horn ice ED1978 test case; c is the airfoil chord

Full size image

4.2.2 Grid Influence

As shown in Fig. 12, boxes defined for grid refinement around the airfoil are extended compared to the clean airfoil case in order to capture the three dimensional structures generated by the iced airfoil. Three grids are defined in the red box of Fig. 12 which differ in particular around the ice shape. In grid A, offsets around the NACA profile are extended by boxes when approaching the leading edge. The discretisation of the ice shape is improved in grid B by an additional offset when the overall region around the ice shape is refined in grid C by an additional box of refinement. The grid size around the rest of the airfoil corresponds to \(c/d_{xmin} = 622\) and \(s/d_{xmin} =384\) for all grids. This leads to mean \(y^+\) values of around 30 on the upper surface and 70 on the lower surface, with maximum values that can reach twice these mean values. Grids characteristics are defined in Table 5. \(\varDelta y_{horn+}\) and \(\varDelta y_{horn-}\) correspond to the maximum heights in y direction of the upper and lower horns.

Table 5 Characteristics of the grids for the horn ice shape ED1978-NACA23012 airfoil case grid convergence study
Full size table

The grid influence study is conducted with the APGPL model. For all calculations, a statistically steady flow solution is obtained after \(17.6t^*\) and temporal statistics are then sampled over \(25t^*\), where \(t^* = c / U_\infty\) is the same as for the clean airfoil in the previous section. All results presented in this section are averaged in time unless otherwise specified. A restricted span is considered for post-processing by removing \(10\%c\) on each side in the spanwise direction as it was done for the clean airfoil thus maintaining a homogeniety in the post-processing. The considered span is then \(41.8\%c\). In this case, this allows to avoid border effects due to the frictionless wall boundary conditions used in the spanwise direction.

Aerodynamic coefficients obtained with the three grids are compared in Table 6 with experimental and numerical references. The result obtained with the APGLL model on grid C is also presented and will be discussed in the next section. As for the clean airfoil, corrected experimental data are taken from Broeren et al. (2014), while non-corrected data are obtained from König et al. (2015). However, unlike for the clean airfoil, experimental lift is obtained by force balance for the iced airfoil while drag is still obtained by momentum-deficit methods. Two sets of data are available in Broeren et al. (2014) which correspond to two types of ice shapes: the ”casting“ and Rapid-Prototype Manufacturing ”RPM“ cases. Some differences exist between the two shapes so that the comparison of both data sets highlights the variation in the results due to variations or uncertainties of the ice shape. Lift coefficients predicted by the three grids are very close and close to references though slightly lower. The drag coefficient is underestimated, in particular with grid A, compared to references, except for the casting which has a lower drag coefficient than the RPM. The differences between the three grids are of the same order of magnitude than the differences between references.

Table 6 Time-averaged lift \(C_L\) and drag \(C_D\) coefficients obtained with grids A, B and C for the ED1978-NACA23012 airfoil case and compared with numerical and experimental references at \(\alpha =6.2^\circ\), except for data from König et al. (2015) at \(\alpha \approx 6^\circ\); Broeren et al. (2014) data are read from figure 19 in Broeren et al. (2014); experimental and LBM values of König et al. (2015) are read from figure 9 in König et al. (2015)
Full size table

Pressure coefficients \(C_p\) are compared in Fig. 13. According to Broeren et al. (2014), experimental profiles are measured around mid-span so that \(C_p\) profile is first presented at mid-span in Fig. 13a. For \(x/c < 0\), several \(C_p\) values may exist for one x/c position due to the presence of the horns so that data are represented with non-connected symbols. \(C_p = 1\) is correctly predicted at the zero velocity point by all grids. \(C_p\) can locally reach low values on the upper-surface horn tip (\(-C_p\) close to 2.5). Results for all grids for \(x/c < 0\) are similar except for the beginning of the plateau on the upper surface. This plateau of \(C_p\) until \(x/c \approx 0.1\) corresponds to the separation region downstream of the upper-surface horn. This separated region is shorter with the ”casting“ ice shape associated with a higher \(-C_p\) plateau level and a faster pressure recovery than with the RPM ice-shape. The same tendency is observed for grid A and B with a \(C_p\) plateau close to the RPM data but with a too rapid pressure recovery. The plateau level is under-estimated with grid C but the pressure recovery is slower indicating a longer separated region closer to references as will be shown below in Table 7. The pressure is then slightly overestimated on the upper and lower surfaces with all three grids. The small \(C_p\) plateau and pressure recovery downstream of the lower-surface horn is correctly reproduced by all grids. The span-averaged \(C_p\) is presented in Fig. 13b with error bars representing the minimum and maximum values of \(C_p\). It shows the same tendency as in the mid-span but highlights that variations of \(C_p\) over the span are principally observed downstream of the upper- and lower-surfaces horns and close to the trailing edge.

Fig. 13
figure 13

Time-averaged pressure coefficient \(C_p\) profiles obtained with the APGPL model on grids A, B and C at mid-span (a) and span-averaged \(C_p\) with error bars representing the minimum and maximum \(C_p\) values (b) and compared with references for the ED1978-NACA23012 airfoil case; Broeren et al. (2014) experimental data are read from figure 20 in Broeren et al. (2014)

Full size image

The positions \((x_R/c)\) of the reattachment point on the upper surface obtained with the APGPL model on grids A, B and C are compared with reference data in Table 7. Results obtained with the APGLL model are discussed in the next section. In numerical results, this position is obtained by the position where the axial velocity becomes zero in the volumetric grid close to the solid surface. This position varies over the airfoil span due to the three-dimensionality of the ice-shape so that minimum, maximum and standard deviation of this position is given to better appreciate this variation. As mentioned before, a smaller recirculation region is obtained with the casting ice shape compared to the RPM ice shape. Results obtained with grids A and B are close and lead to too short recirculation region in agreement with the too rapid pressure recovery observed in Fig. 13. The recirculation region is slightly longer with grid C associated with a standard deviation more than twice the standard deviation obtained with grids A and B. These results are in agreement with previous observations made on the \(C_p\) profiles.

Table 7 Position of reattachment point \(x_R/c\) on the upper surface of the ED1978-NACA23012 airfoil with grids A, B and C and compared with references; \(\overline{x_R/c}\) and \(\sigma _{x_R/c}\) correspond to the mean position of the reattachment point and its standard deviation over the considered span; \((x_R/c)_{min}\) and \((x_R/c)_{max}\) are the minimum and maximum values of \(x_R/c\); experimental minimal and maximal values are taken from figure 21 in Broeren et al. (2014)
Full size table

As a conclusion, improvement of the ice shape discretisation from grid A to grid B does not improve the flow prediction in terms of aerodynamic and pressure coefficients as well as length of the separated region behind the upper-surface horn. In contrast, these results are slightly improved by refining the grid in the separated flow region in grid C. Grid C is used for following evaluation of the APGPL model.

4.2.3 Evaluation of the APGPL Model

An overview of the flow field obtained in WMLES with the APGPL model is given in Figs. 14 and 15. A three-dimensional unsteady flow is generated behind the horns. The large separation region behind the upper-surface horn is identified by streamlines in Fig. 15a in agreement with experimental observations (Broeren et al. 2014) and numerical results of König et al. (2015). The behaviour of the APGPL model is presented in Fig. 15b with the indicator function \(\gamma\). The equilibrium power-law (\(\gamma = 1\)) is used on the horns around the point with zero velocity but also near the reattachment zone on the upper surface. The mode \(\gamma = 2\) without wall model is used at the point with zero velocity on the leading edge and in the onset of the separation region, two regions where the validity of a wall model is indeed not clearly demonstrated. The APGPL with \(\gamma = 3\), taking adverse pressure gradient effects into account, is activated on the horns tips, near the onset of the separation and also after reattachment where the flow is submitted to adverse pressure gradient, similarly to the clean airfoil.

Fig. 14
figure 14

Instantaneous vortices (identified by iso-surface of Q-criterion) coloured by the non-dimensional streamwise \(U_x\) velocity obtained in WMLES with the APGPL model for the ED1978-NACA23012 case

Full size image
Fig. 15
figure 15

Time-averaged axial velocity contours with streamlines (a) and instantaneous axial velocity contours at mid-span with \(\gamma\) distribution at boundary nodes at \(t=30.1 t^*\) (b) for the ED1978-NACA23012 case

Full size image

Aerodynamic coefficients obtained with the APGPL and APGLL models on grid C are given in Table 6. Results obtained with the APGPL model are slightly better but the gap between both present WMLES is of the same order of magnitude than the gap between references. The same conclusion is drawn from the span-averaged pressure coefficients profiles in Fig. 16. Both present WMLES overestimate \(C_p\) on the airfoil. The lower \(-C_p\) plateau and slower pressure recovery obtained with the APGPL model indicates a longer recirculation region confirmed by results presented in Table 7. The length of the separation region varies more in the spanwise direction with the APGPL model than with the APGLL model.

Fig. 16
figure 16

Time and span-averaged pressure coefficient \(C_p\) obtained for the ED1978-NACA23012 case with the APGLL and the APGPL models on grid C and compared with references; Broeren et al. (2014) experimental data are read from figure 20 in Broeren et al. (2014)

Full size image

Results obtained with the APGPL model for the prediction of the iced-airfoil are very similar to the one obtained using the APGLL model. The gap between both present WMLES is of the same order as the gap between the different references.

4.3 LAGOON Landing Gear Model

For further validation of the APGPL model, the flow around a landing gear is considered. The landing gear is one of the most important source of noise of an aircraft (Manoha et al. 2008) and a good prediction of the flow dynamics and the aeroacoustics is of primary importance for noise reduction. The configuration 1 of the LAGOON (LAnding-Gear nOise database for CAA validatiON) project supported by Airbus (Manoha et al. 2008, 2009) and numerically studied in LBM by Sengissen et al. (2015) is considered. Sengissen et al. (2015) in particular used the Afzal’s wall model with an additional term taking curvature effects (Patel and Sotiropoulos 1997) into account and the Approximate Deconvolution Model (ADM) for turbulence modelling (Malaspinas and Sagaut 2011). In this case, the separation is not fixed by sharp edges but instead by smooth curvature giving high importance to the effect of the induced adverse pressure gradient and the near-wall flow prediction.

4.3.1 Numerical Setup

The test case presented in Sengissen et al. (2015) with Reynolds number \(Re = 1.59 \times 10^6\), based on the wheel diameter D, and Mach number Ma = 0.23 is used in this work. The computational domain is presented in Fig. 17. The origin of the domain corresponds to the intersection between the wheel axis and the main leg. Uniform free-stream velocity \(U_\infty\) in streamwise \(-\mathbf {x}\) direction and uniform free-stream pressure \(p_\infty\) are respectively imposed at the inlet and outlet surfaces. Wall modelling is used on the landing-gear surface. All other surfaces are defined as outlets with fixed free-stream pressure. The MEDIUM mesh with 40 million grid points defined in Sengissen et al. (2015) is used. The domain is composed on 10 embedded grids leading to \(y^+\) values varying from 0 to 200 for the landing gear. The calculation is performed up to time \(22 t^*=0.084\) s to obtain a statistically steady flow solution, temporal statistics are then calculated by sampling the flow over \(66t^*=0.25\) s, where \(t^* = D / U_\infty\).

Fig. 17
figure 17

Computational domain and grid for the LAGOON test case; D is the wheel diameter

Full size image

4.3.2 Results and Discussion

The instantaneous vortices and the \(\gamma\) distribution obtained with the APGPL model are presented in Fig. 18 for the last time step of the simulation. Turbulent structures are generated on the wheels and in the wake of the landing gear with massive flow separation downstream of the landing gear. In Fig. 18b, in the upstream part of the main leg, the flow is attached so that the equilibrium power-law is used (\(\gamma = 1\)). Going downstream, the flow is submitted to an adverse pressure gradient and the mode \(\gamma = 3\) is activated until flow separation occurs leading to the mode \(\gamma = 2\). In the downstream part of the main leg in Fig. 18c, this mode is followed by the mode \(\gamma = 3\) where the flow reattaches and the mode \(\gamma = 1\) is recovered in the rear part of the main leg. Concerning the wheels, the equilibrium power-law (\(\gamma = 1\)) is also used in the upstream part when the APGPL (\(\gamma = 3\)) is mostly active in the downstream part and on the wheels sides with some regions without wall model (\(\gamma = 2\)), in particular in the interior part of the wheels where flow separation occurs.

Fig. 18
figure 18

Instantaneous vortices (identified by iso-surface of Q-criterion coloured by the streamwise velocity) (a) and upstream (b) and downstream (c) view of \(\gamma\) distribution at boundary nodes around the landing gear at the last time step obtained in WMLES with the APGPL model

Full size image

A comparison of the mean streamwise velocity U (in \(-\mathbf {x}\) direction) contours predicted by the APGLL and APGPL models on the plane at \(z=0\) in the wake of the landing gear wheels is presented in Fig. 19. The width of the wake downstream of the wheels (\(x \approx -0.5\) m) shrinks more with the APGLL than with the APGPL model. The streamwise velocity obtained with the APGPL model is also lower in the centreline. Figure 20 gives a more precise comparison of the streamwise velocity prediction close the wheels on the middle plane, at \(z = 0\) m, and below, at \(z=-0.104\) m, which corresponds to almost \(70\%\) of the wheel radius. Results are compared with experimental LDV data and results obtained by Sengissen et al. (2015) on the same mesh. Velocity profiles obtained with the APGLL and APGPL models differ somewhat near the wheels in the centreline (\(y = 0\)) and near \(y = 0.1\) m as can also be observed in Fig. 19. However, both models are able to predict the rapid velocity reduction near \(y = \pm 0.15\) m and the region of low velocity behind the wheels and their axis on the plane at \(z=0\) (Fig. 20a–c). At \(z = -0.104\) m (Fig. 20d), the velocity reduction is also well predicted in the wheels wakes at \(y= \pm 0.08\) m.

Fig. 19
figure 19

Mean streamwise velocity U contours predicted by the APGLL (a) and APGPL (b) models on the plane at \(z=0\) for the LAGOON case

Full size image
Fig. 20
figure 20

Mean streamwise velocity profiles in different sections downstream of the wheels of the LAGOON

Full size image

Mean streamwise velocity fluctuations predicted by WMLES are compared with LDV data and Sengissen et al. (2015) results in Fig. 21. Fluctuation levels are slightly higher with present WMLES compared to the results of Sengissen et al. (2015) close to the wheels (Fig. 21a, b). Only resolved fluctuations in LES are considered in Fig. 21 which may explain the fact that all WMLES underestimate the fluctuation levels compared to LDV data on the plane at \(z=0\) as explained in Sengissen et al. (2015). Results obtained with the APGPL model are however in fair agreement with results of Sengissen et al. (2015).

Fig. 21
figure 21

Mean streamwise velocity fluctuations \(U\prime _{RMS} = \sqrt{\overline{u'u'}}\) profiles in different sections downstream of the wheels of the LAGOON

Full size image

The validation of the APGPL model is completed by the comparison of the pressure coefficient on one landing gear wheel in Fig. 22. WMLES results with the APGLL and APGPL models are in good agreement with previous results (Sengissen et al. 2015) and with experimental data obtained with pressure taps on the wheel centreline for \(-120 ^\circ< \theta < 120 ^\circ\). For \(|\theta | > 120 ^\circ\), the APGPL model results are still in fairly good agreement with the APGLL model results. Both models give oscillations of \(C_p\) near \(|\theta | \approx 90 ^\circ\) and \(|\theta | \approx 130 ^\circ\) which are linked with the staircase-like form of the grid around solid surfaces as already discussed in the previous sections.

Fig. 22
figure 22

Mean pressure coefficient \(C_p\) along one LAGOON wheel centreline as a function of the angular position \(\theta\) on the wheel. Positive (respectively negative) \(\theta\) values correspond to positive (respectively negative) z values. See Figs. 20 and 21 for the caption

Full size image

An interesting validation step for the LAGOON case concerns the near-field acoustics prediction based on Power Spectral Density (PSD) of wall pressure fluctuations. Experimental data using unsteady pressure transducers (kulite) are available at locations shown in Fig. 23a. Pressure signals at the corresponding points obtained by WMLES are sampled at a frequency of 60kHz over the last 0.25 s of the calculation. The PSD are calculated using the Welch’s procedure with five blocks and \(50\%\) of overlapping and considering Hann windowing as in Sengissen et al. (2015) for result’s consistency. Results are compared in Fig. 23. All WMLES give similar results in fair agreement with experimental data except for \(f > 6 kHz\) which is the cut-off due to the grid resolution as explained in Sengissen et al. (2015). Local peaks at 1000 Hz and 1500 Hz for kulites 1, 4 and 13 are well reproduced by WMLES.

Fig. 23
figure 23

Power spectral density of the pressure signal on kulite sensors on the LAGOON wheel

Full size image

For all validation parameters, results obtained with the APGPL model are very similar to the one obtained using the APGLL model, which is the primary objective of the present work. Moreover, the accuracy of present WMLES is similar to the one of Sengissen et al. (2015) and results in good agreement with experimental data are obtained on this complex geometry of engineering interest.

5 Conclusion

A new explicit wall model based on the power-law for boundary layer under adverse pressure gradient has been developed based on an existing adverse pressure gradient log-law. The main objective was to preserve the explicit character of the equilibrium power-law model by extending it to boundary layers subjected to adverse pressure gradient frequently encountered in engineering applications. The new model, termed Adverse Pressure Gradient Power Law (APGPL) model, is composed of three modes that can be active simultaneously in different regions of a flow. In regions of favourable or no pressure gradient, the equilibrium power-law is used. In regions exposed to adverse pressure gradient, the APGPL is used. The APGPL is however not valid in regions of separation where no wall model is then used assuming a low local Reynolds number and a direct resolution of the boundary layer.

The APGPL model is validated based on the Lattice Boltzmann Method applied on Cartesian grids for which the use of a wall model is required when considering turbulent flows. Results are compared with an adverse pressure gradient log law (APGLL) based on the Afzal’s law. A streamlined body is first studied considering a NACA profile subjected to smooth adverse pressure gradient. The attached flow is well reproduced in terms of lift and draft coefficients and pressure profile. The same NACA profile is then considered with ice accretion on the leading edge inducing boundary layer separation and reattachment. Finally, the flow around a landing-gear, for which massive separation occurs, is simulated. It is verified that, with the APGPL model, the no-wall model mode is active in regions of separation. The obtained results are very similar to results given by the APGLL model and in good agreement with experimental and numerical references. The APGPL model has been proven to give good results for both bluff body and streamline body flows while being explicit. No iterative method is required for the calculation of the flow quantities at the boundary node thus simplifying the near-wall treatment. This is of great interest for further developments of efficient boundary treatment for Immersed Boundary Models.