Sensible-Enthalpy-Based Conditional Moment Closure Model for Homogeneous Charge Compression Ignition with Temperature Inhomogeneity

Abstract

This paper presents a sensible-enthalpy-based conditional moment closure (CMC) model for homogeneous charge compression ignition (HCCI) with temperature inhomogeneity. The focus of study is placed on the effects of a conditioning variable on the prediction of heat release rates and developing the mixing models for sensible enthalpy, a reacting scalar. The sensible-enthalpy-based CMC model is validated a priori with 2-D direct numerical simulation (DNS) data for HCCI, and compared with the total-enthalpy-based formulation. Sensible enthalpy is shown to be strongly correlated with temperature, which makes sensible enthalpy well suited for a conditioning variable in CMC for HCCI. Results show that sensible-enthalpy-based CMC performs well for the prediction of heat release rates for all temperature stratification levels investigated in this study, while total-enthalpy-based CMC leads to the overprediction of heat release rates when the temperature stratification level is high. While conditional fluctuations of species mass fractions are substantial, sensible-enthalpy-based CMC is found to accurately estimate heat release rates during ignition, as well as reaction rates of key species, due to substantially suppressed conditional temperature fluctuations. The mapping closure models for the probability density function (PDF) and conditional dissipation rates of sensible enthalpy are proposed. The proposed models are found to capture the characteristics of reactive scalar mixing.

1 Introduction

The homogeneous charge compression ignition (HCCI) engine is regarded as an effective alternative to the traditional internal combustion engines due to its great potential in increasing the thermal efficiency and reducing NOx and soot emissions [1,2,3]. Over the past decades, significant progress in the understanding of the HCCI process has been made [3]. However, the development of effective HCCI engines is still constrained by some key challenges, such as limiting peak heat release rates and controlling ignition timing [1,2,3,4,5]. The focus of this paper is on the modeling of HCCI with temperature inhomogeneity, which has a potential to limit peak heat release rates in high load conditions, prevent knocking, and control ignition timing [6,7,8,9].

In simulating HCCI with temperature inhomogeneity, several combustion models, including the multi-zone model [9, 10], the flamelet model [11,12,13], and the conditional moment closure (CMC) model [14,15,16], have been developed. The multi-zone approach is constructed based on the view that ignition processes under HCCI conditions are governed only by chemical kinetics, neglecting turbulence-chemistry interactions at small scales. Cook et al. [12] developed a total-enthalpy-based flamelet model that can describe the effects of thermal stratification on ignition and reactive scalar evolution [12]. Salehi et al. [15] developed a first order CMC model for HCCI, where total enthalpy is chosen as a conditioning variable. The total-enthalpy-based flamelet and CMC models are shown to perform well for small temperature stratification levels [12, 15]. However, when large temperature stratification is imposed, conditional fluctuations of reacting scalars become large and the first order closure of chemical reaction rates overpredicts heat release rates [15]. To deal with the large conditional fluctuations, Salehi et al. [16] used the scalar dissipation rate as an additional conditioning variable. The double-conditioning CMC model led to a significantly improved result over the single-conditioning CMC model.

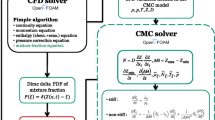
In this paper, a sensible-enthalpy-based CMC model for HCCI with temperature inhomogeneity is proposed and compared with the total-enthalpy-based formulation. The effects of a conditioning variable on the reaction rate closure are investigated using direct numerical simulation (DNS) data for the ignition of lean n-heptane/air mixtures under HCCI conditions. For sensible-enthalpy-based CMC, of importance are the mixing models for sensible enthalpy, which have not been extensively investigated in ignition problems. Here, the mapping method is proposed to model the probability density function (PDF) and conditional dissipation rates of sensible enthalpy, a reacting scalar. The proposed model for the reactive scalar mixing is validated with the DNS data.

2 Conditional Moment Closure for HCCI

2.1 Conditionally averaged equations

In CMC, the density weighted conditionally averaged reacting scalars are defined as,

$$ Q_{\phi}(\eta;\vec{x},t) = \frac{\langle{\rho \phi|\xi(\vec{x},t)=\eta}\rangle}{\langle{\rho |\xi(\vec{x},t)=\eta}\rangle}, $$

(1)

where η is the sample space variable for a conditioning variable, ξ. $\vec {x}$ and t are the space and time coordinates. ϕ is a reacting scalar and ρ is the density. The angular brackets denote ensemble averaging subject to the condition defined on the right of the vertical bar. In the conditional averaging procedure, averaging is taken for samples that have a particular value of a conditioning variable.

The equations for the conditional average reacting scalars can be obtained using standard CMC derivation procedure [14]. Denoting $()|\eta \equiv ()|\xi (\vec {x},t)=\eta$, the equations for the conditional mean mass fractions in homogeneous conditions can be written as,

$$ \frac {\partial Q_{i}} {\partial t} = -v_{\eta} \frac {\partial Q_{i}} {\partial \eta} + \left\langle{N_{\xi}| \eta}\right\rangle \frac {\partial^{2} Q_{i}} {\partial \eta^{2}} + \frac {\langle \rho \dot {\omega_{i}}|\eta \rangle} {\rho_{\eta}}, $$

(2)

where Q_i is the conditional mean mass fraction of species i. v_η is the convective velocity in η space, which results from a source term in the equation for a conditioning variable. For total enthalpy, it is given as $v_{\eta } = \left \langle { \frac {1} {\rho } \frac {Dp} {Dt} | \eta } \right \rangle$, where p is pressure. For sensible enthalpy, the heat release rate term is also included. N_ξ is the scalar dissipation rate defined as N_ξ = D∇ξ ⋅∇ξ, where D is the molecular diffusivity. The unity Lewis number assumption is used. $\dot \omega _{i}$ is the chemical reaction rate of species i, and ρ_η = 〈ρ|η〉. In Eq. 2, the primary CMC closure hypothesis is used. The spatial derivatives of the conditionally averaged quantities are neglected, which is valid for the cases studied here [15].

The density-weighted averages of heat release rates, species mass fractions, and temperature can be obtained by integration of the conditional averages weighted by the PDF in conditioning variable space:

$$ \widetilde{\phi} = {\int}_{\eta_{min}}^{\eta_{max}} Q_{\phi} \widetilde{P}(\eta) d\eta, $$

(3)

where η_min and η_max are the minimum and maximum values of η, respectively. $\widetilde {P}(\eta )$ is the density-weighted PDF of either total enthalpy or sensible enthalpy. For total enthalpy, the presumed beta PDF can be used [17,18,19]. The modeling of the PDF and conditional dissipation rates of sensible enthalpy is presented in Section 2.3.2.

2.2 Conditioning variable

The key underlying assumption of CMC is the existence of a scalar that shows strong correlations with other reacting scalars. The strong correlation allows for accurate estimation of chemical reaction rates using the conditionally averaged reacting scalars.

The performance of CMC depends on the degree of correlations between the conditioning variable, ξ, and the reacting scalar, ϕ. For HCCI with temperature inhomogeneity, total enthalpy, h_t, has been proposed as a conditioning variable [15]. Here, sensible enthalpy is proposed as a conditioning variable for HCCI. Sensible enthalpy is related to total enthalpy of the mixture as,

$$ h_{t} = \sum\limits_{i} Y_{i} h_{i,t} = \sum\limits_{i} Y_{i} (h_{i,s} + {\Delta} h^{\circ}_{f,i}) = h_{s} + \sum\limits_{i} Y_{i} {\Delta} h^{\circ}_{f,i}, $$

(4)

where h_t,i, h_s,i, and ${\Delta } h^{\circ }_{f,i}$ are total enthalpy, sensible enthalpy, and the enthalpy of formation for the species i, respectively. The key advantage of using sensible enthalpy as the conditioning variable is that sensible enthalpy is strongly correlated with temperature [20]. For ignition and combustion of hydrocarbon fuels, chemical reaction rates show strong nonlinear dependence on temperature, leading to the sensitivity of the reaction rates to temperature. For the samples having a particular value of sensible enthalpy, temperature fluctuations are expected to be small throughout an ignition process. As a result, the estimation of the reaction rates can be made accurate. As a conditioning variable, sensible enthalpy is preferable to temperature because the equation for the conditional mean temperature is more complex than that of sensible enthalpy [20]. Sensible enthalpy was suggested as a conditioning variable for premixed combustion firstly by Bilger [21]. Kronenburg [20] adopted sensible enthalpy as a second conditioning variable in the double-conditioning CMC for non-premixed combustion to capture local extinction.

For CMC with total enthalpy being a conditioning variable, the PDF of the conditioning variable, $\widetilde {P}(\eta )$, and the conditional scalar dissipation rate, 〈N_ξ|η〉, can be approximated using the models developed for conserved scalar mixing, e.g., [17,18,19, 22,23,24]. In low Mach number flows, when differential diffusion effects are neglected, the equation for total enthalpy resembles that for a conserved scalar, except for the additional pressure-time-derivative term in the total enthalpy equation. The spatial variations of the in-cylinder pressure in HCCI engines are negligible as compared with the pressure itself, except for knocking conditions. Therefore, the mixing statistics of total enthalpy can be modeled by extending extensive studies on conserved scalar mixing and non-premixed combustion [17,18,19, 22,23,24]. However, since sensible enthalpy is a reacting scalar, the modeling of the PDF and the conditional dissipation rate of sensible enthalpy is considered as a challenge. Chemical reactions tend to steepen scalar gradients, influencing the PDF and the scalar dissipation rates. The effects of chemical reactions on scalar mixing statistics in ignition problems have not yet been studied extensively. A mapping approach to resolve this problem will be presented later in Section 2.3.2.

2.3 Closure models

2.3.1 First-order closure for chemical reaction rates

With the assumption that reactive scalars are strongly correlated with a conditioning variable, the reaction rates averaged with the condition that the samples have a particular value of the conditioning variable can be approximated as,

$$ \langle \rho \dot {\omega_{i}}|\eta \rangle = \dot {\omega_{i}}(\rho_{\eta},{Q_{i}},{Q_{T}}). $$

(5)

2.3.2 Mapping method for the probability density function and conditional scalar dissipation rates

The difficulty of modeling the mixing of sensible enthalpy stems from the existence of chemical reactions that tend to steepen scalar gradients. Due to the reaction-induced steepening, the PDF and the dissipation statistics of sensible enthalpy are qualitatively different from those of a conserved scalar. Here, a mapping method is presented to model such mixing terms.

The key idea of the proposed method is to use the mapping from a total enthalpy field to a sensible enthalpy field. Here, the mixing statistics of total enthalpy, including the PDF and conditional scalar dissipation rates, are assumed to be modeled accurately, for instance, by extending the mixing models developed for a conserved scalar. The conditional mean species mass fractions and temperature solved in sensible-enthalpy-based CMC are then utilized to obtain mapping between the total enthalpy field and the sensible enthalpy field. Here, the following mapping between the total enthalpy coordinate and the sensible enthalpy coordinate is proposed:

$$ \eta_{t} = \eta_{s} + \sum\limits_{i} Q_{i} {\Delta} h^{\circ}_{f,i}(T_{0}), $$

(6)

where η_t and η_s are the sample space variable of total enthalpy and of sensible enthalpy, respectively. T₀ is the reference temperature. Since the development of mixing models used for sensible-enthalpy-based CMC is of our primary interest, the conditional mean mass fractions, Q_i, are defined and solved in sensible enthalpy space. All information necessary to obtain the mapping, the terms on the r.h.s. of Eq. 6, are available in sensible-enthalpy-based CMC.

Using the mapping relationship in Eq. 6, the PDF of sensible enthalpy, P(η_s), and the conditional scalar dissipation rate, $\langle N_{h_{s}} | \eta _{s} \rangle$, can be modeled if the PDF of total enthalpy, P(η_t), and the conditional dissipation rate of total enthalpy, $\langle N_{h_{t}} | \eta _{t} \rangle$, are provided. However, at certain stages of ignition, the mapping between sensible enthalpy and total enthalpy can be non-monotonic, which can make the mapping mixing models inaccurate. To deal with the non-monotonic mapping, a simple averaging approach is used. When non-monotonicity is encountered, conditional mean species mass fractions Q_i in the sensible enthalpy coordinate are averaged as,

$$ {Q_{i}}^{\prime} = \frac{{{\sum}_{j}^{N}} {Q_{i,j}}}{N} \text{\hspace{0.2cm} when \hspace{0.2cm}} {\eta_{t}}^{\prime} = \eta_{t}, $$

(7)

where the summation is taken over all the intersection points of the mapping curve as shown in Fig. 1. Q_i,j is the conditional mean mass fraction at the j-th intersection point. N is the number of those intersection points. η_t^′ is the sample space variable for total enthalpy. Using the interpolated species mass fractions, a smoothed mapping curve is obtained as,

$$ {\eta_{s}}^{\prime} = {\eta_{t}}^{\prime} - \sum\limits_{i} {Q_{i}}^{\prime} {\Delta} h^{\circ}_{f,i}(T_{0}). $$

(8)

It has been found that after the modification, the mapping curves become monotonic in the cases considered here.

Fig. 1

Schematic of the modification to the mapping curve

Using Eq. 8, the PDF of sensible enthalpy can be modeled as,

$$ P\left( {\eta_{s}}^{\prime}\right) = P\left( {\eta_{t}}^{\prime}\right) \frac{d{\eta_{t}}^{\prime}}{d{\eta_{s}}^{\prime}}, $$

(9)

where the PDF of total enthalpy is obtained from the presumed PDF method, e.g., the beta PDF in terms of the mean and variance of total enthalpy [17,18,19]. A similar idea can be applied to modeling the conditional dissipation rate of sensible enthalpy. The dissipation rate of sensible enthalpy can be written as

$$ N_{h_{s}} = D \nabla h_{s} \cdot \nabla h_{s} = D \left( \frac{d{h_{s}}}{d{n_{s}}}\right)^{2}, $$

(10)

where n_s is the coordinate along the normal direction, ∇h_s/|∇h_s|. The dissipation rate of total enthalpy can be written in a similar way. Assuming that the gradient of sensible enthalpy is well aligned with that of total enthalpy, we obtain

$$ N_{h_{s}} \approx \left( \frac{d{h_{s}}}{d{h_{t}}}\right)^{2} N_{h_{t}}. $$

(11)

The conditional dissipation rate of sensible enthalpy can then be approximated as

$$ \left\langle N_{h_{s}} | {\eta_{s}}^{\prime} \right\rangle \approx \left\langle \left( \frac{d{h_{s}}}{d{h_{t}}}\right)^{2} N_{h_{t}} | {\eta_{t}}^{\prime} \right\rangle \approx \left\langle N_{h_{t}} | {\eta_{t}}^{\prime} \right\rangle \left( \frac{d{\eta_{s}}^{\prime}}{d{\eta_{t}}^{\prime}} \right)^{2}. $$

(12)

It is assumed in Eq. 12 that $\left (\frac {d{h_{s}}}{d{h_{t}}}\right )^{2}$ and $N_{h_{t}}$ are statistically independent, and that $\left \langle \left (\frac {dh_{s}}{dh_{t}}\right )^{2} | {\eta _{s}}^{\prime } \right \rangle \approx \left (\frac {d{\eta _{s}}^{\prime }}{d{\eta _{t}}^{\prime }}\right )^{2}$. The approximation works better when conditional fluctuations in the mapping relation are smaller.

The PDF modeling in Eq. 9 requires the non-monotonic mapping. This requirement can be relaxed as follows. In the non-monotonic region, we have

$$ P({\eta_{t}}) \delta{\eta_{t}} = \sum\limits_{i = 1}^{N_{k}} P({\eta_{s,i}})\delta{\eta_{s,i}}, $$

(13)

where δη_s,i denotes a region in the sensible enthalpy space that maps onto δη_t in the total enthalpy space. When the mapping is not monotonic, there can be multiple regions in sensible enthalpy space, which correspond to a given region, δη_t, in total enthalpy space, as shown in Fig. 2. N_k is the number of such regions. With the assumption that the PDF of η_t is equally distributed in the corresponding η_s space within the non-monotonic regions, the sensible enthalpy PDF can be approximated as

$$ P({\eta_{s,i}}) = P({\eta_{t}}) \frac{\delta{\eta_{t}}}{{\sum}_{i = 1}^{N_{k}}\delta{\eta_{s,i}}}. $$

(14)

When the mapping is monotonic, Eq. 14 becomes equivalent to Eq. 9.

Fig. 2

Schematic of the sensible enthalpy PDF modeling with non-monotonic mapping

When sensible enthalpy is used as a conditioning variable, the conditional mean species mass fractions are solved in sensible enthalpy space. The PDF and conditional dissipation rates of total enthalpy are obtained from the mean mixing fields of total enthalpy. Using the mapping between total enthalpy space and sensible enthalpy space, the PDF and the conditional scalar dissipation rates used for the sensible-enthalpy-based CMC model are then obtained.

3 Direct Numerical Simulation

The low Mach number, variable density formulation is used for DNS of HCCI. The mass, momentum, species, and energy conservation equations are solved. For energy conservation, the equation for total enthalpy is solved. For multi-component species transport, the Hirschfelder and Curtiss model with the mixture-averaged diffusion coefficients [25, 26] is used, and the correction velocity is added to ensure the overall mass conservation. The equations are solved using a second-order, conservative finite-difference method for DNS and LES [27]. For the velocity, the second-order centered finite difference scheme is used for spatial derivatives. The fifth-order weighted essentially non-oscillatory (WENO) scheme [28] is used for the convection terms in the scalar equations. A second-order semi-implicit Crank-Nicholson method is used for time integration. An operator splitting method is used for the integration of stiff chemical reactions.

To evaluate the performance of the proposed CMC model, 2-D constant volume DNSs of lean n-heptane/air ignition under HCCI conditions are conducted. The simulation conditions for the DNS cases are similar to those in Yoo et al. [29], and are summarized in Table 1. The main difference from the previous DNS in Yoo et al. [29] is that in this study, a larger computational domain is used. The initial pressure is p₀ = 40 atm. The initial mixture composition is a homogeneous n-heptane/air mixture with an equivalence ratio, ϕ₀, of 0.3. The velocity fields are prescribed using the Passot-Pouquet spectrum with zero mean velocity, the root mean square (r.m.s.) velocity fluctuations, u^′, of 0.5 m/s, and the most energetic length scale, l_e, of 1.2 mm. The Kolmogorov scales for the initial fields are around 25 μm. The temperature field is initialized using a Passot-Pouquet spectrum modified for a scalar. The mean temperature, $\bar T_{0}$, is set to be 934 K. The integral length scale of temperature, l_Te, is 1.2 mm, while the levels of temperature fluctuations in the spectrum are varied. The r.m.s. temperature fluctuations considered here are 15 K, 30 K, 60 K, and 100 K for Cases 1, 2, 3, and 4, respectively.

Table 1 Initial and simulation conditions for the DNS cases

The periodic computational domain with the size of 6.4 mm × 6.4 mm is discretized using 1024 × 1024 grid points for all cases. A chemical mechanism of Liu et al. [30] is used, which consists of 185 reactions involving 43 species. DVODE [31] is used for the time integration of the chemical reaction part in the operator splitting method. Thermodynamic and transport properties are evaluated using CHEMKIN and TRANSPORT packages [25]. For the present DNS, the temperature layer is resolved with about 16 grid points, and each radical layer about 6 grid points. The grid sensitivity and time step sensitivity study has been performed on a 3.2 mm × 3.2 mm domain using three grid resolutions, 256 × 256, 512 × 512 and 1024 × 1024, and the time step size in a range of 0.3 μs–1.2 μs. The relative error for the ignition delay is within 0.15% for the grid size of 6.25 μm and the timestep of 1.0 μs as compared with the reference simulation with the grid size of 3.125 μm and the timestep of 0.6 μs. The time step of 1 μs and the grid size of 6.25 μm is chosen from the sensitivity study.

The temperature r.m.s. fluctuation levels in Table 1 are taken from previous DNS studies of HCCI [15, 29] and cover a broad range of HCCI conditions. Dronniou and Dec [32] reported temperature r.m.s. fluctuations in their HCCI engine to be around 20K at the top dead center (TDC) and to continue to rise during the expansion stroke. Higher levels of the temperature inhomogeneity than those reported in [32] are used in the present study. However, it is to be noted that due to turbulence dissipation, the initially imposed temperature r.m.s. fluctuations decay before the ignition occurs in the present DNS cases.

4 Results and Discussion

The sensible-enthalpy-based CMC model, CMChs, is validated with 2-D DNS data and compared with the total-enthalpy-based formulation, CMCht. The emphasis is placed on the effects of the choice of a conditioning variable on conditional fluctuations of reacting scalars and the reaction rate closure. The performance of the proposed models for PDF and conditional dissipation rates of sensible enthalpy is also investigated. When presenting the results, a normalized sample space variable, ζ, is also used. The sample space variable η is normalized by using the minimum and maximum of the corresponding enthalpy at a given time, η_min and η_max, as,

$$ \zeta = \frac{\eta-\eta_{min}}{\eta_{max}-\eta_{min}}. $$

(15)

The time is normalized using the ignition delay time, defined as the time of the maximum heat release rate.

4.1 Temperature fields

Figure 3 shows the temperature fields at various ignition stages, along with iso-scalar surfaces of total enthalpy and of sensible enthalpy. For the iso-scalar surfaces, the value of sensible enthalpy is chosen to demarcate ignition spots. The value used in iso-scalar surfaces of total enthalpy is obtained from the mapping relation in Eq. 6. In Fig. 3, for Case 3 at t^∗ = 0.2, where t^∗ is the normalized time, the iso-h_s and iso-h_t surfaces overlap with each other, indicating that during an early stage of fuel oxidation total enthalpy is well correlated with sensible enthalpy. At t^∗ = 0.6, ignition begins to occur in localized spots with higher temperature. At t^∗ = 0.99, the iso-h_t surface deviates from the iso-h_s surface in some regions. For Case 4, a similar trend is observed.

Fig. 3

Temperature fields and iso-scalar surfaces of sensible enthalpy and of total enthalpy at various stages of ignition. at^∗ = 0.2 for Case 3 $({{T_{0}}^{\prime }}= 60K)$, bt^∗ = 0.6 for Case 3 $({{T_{0}}^{\prime }}= 60K)$, ct^∗ = 0.99 for Case 3 $({{T_{0}}^{\prime }}= 60K)$, dt^∗ = 0.2 for Case 4 $({{T_{0}}^{\prime }}= 100K)$, et^∗ = 0.6 for Case 4 $({{T_{0}}^{\prime }}= 100K)$, and ft^∗ = 0.99 for Case 4 $({{T_{0}}^{\prime }}= 100K)$. The magenta contour lines represent iso-h_t surfaces, while the black ones represent iso-h_s surfaces

4.2 Conditional fluctuations of reacting scalars

Figure 4 shows the conditional r.m.s. fluctuations of the temperature and the fuel mass fraction for Case 4, which are represented as error bars on top of the corresponding conditional mean values. The conditional fluctuation is defined as ϕ^′ = ϕ −〈ϕ|η〉, representing the deviation from the conditional average 〈ϕ|η〉. The level of conditional fluctuations shows how the reactive scalars are correlated with the conditioning variable. The smaller fluctuations lead to the better estimation of conditional mean reaction rates. The conditional fluctuations of temperature are substantially reduced when sensible enthalpy is taken as the conditioning variable. This implies the strong correlation of temperature with sensible enthalpy. The conditional fluctuations of the fuel mass fraction are also reduced for the sensible enthalpy conditioning, while the reduction is not as substantial as that for the temperature.

Fig. 4

Conditional mean and r.m.s. fluctuations of a temperature and b fuel mass fraction for Case 4 $({{T_{0}}^{\prime }}= 100\mathrm {K})$ at t^∗ = 0.99 (red solid lines: conditional mean based on sensible-enthalpy conditioning, blue dashed-dotted lines: conditional mean based on total-enthalpy conditioning, error bars: conditional r.m.s. fluctuations)

4.3 Heat release rate prediction and reaction rate closure

To illustrate the effects of a conditioning variable on the reaction rate closure, heat release rates for Case 4 at t^∗ = 0.955 are shown in Fig. 5. Together with the conditionally averaged values, the scatter plot for heat release rates is also shown. With conditioning, fluctuations of heat release rates for a given value of sensible enthalpy are smaller than those based on total enthalpy conditioning. Such fluctuations are induced by the fluctuations in the species mass fractions, as indicated by the results in Fig. 4. For total enthalpy conditioning, both temperature and species mass fractions fluctuate substantially for this case, which leads to more fluctuations around the conditional mean reaction rates. As a result, CMCht leads to the substantial overprediction of heat release rates. On the other hand, the sensible-enthalpy-based closure, CMChs, leads to an excellent prediction of the conditional mean heat release rates, even with fluctuations in heat release rates around the conditional mean values. This is because temperature fluctuations are substantially suppressed, when sensible enthalpy is used as the conditioning variable. The errors in the first-order reaction rate closure come from non-linearity in reaction rates. The errors due to strong non-linear dependence of the reaction rates on temperature are suppressed in the sensible-enthalpy-based closure.

Fig. 5

Scatter plot and conditional means for heat release rates for Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.955 (black dashed-dotted line: CMCht, black circles: DNS data with total-enthalpy conditioning, red solid line: CMChs, red diamonds: DNS data with sensible-enthalpy conditioning; small blue and green circles represent the scatter data for heat release rates plotted in the normalized total enthalpy coordinate and in the normalized sensible enthalpy coordinate, respectively)

Figure 6 shows the conditionally averaged heat release rates at different time instants for Cases 3 and 4. For Case 3 with $T^{\prime }_{0}= 60$ K, CMCht tends to overpredict the heat release rates as the ignition progresses. For Case 4 with $T^{\prime }_{0}= 100$ K, the CMCht results show substantial deviations from the DNS results at all stages of the ignition process. Results for CMChs are in excellent agreement with the DNS data for all the cases. For Case 1 with $T^{\prime }_{0}= 15$ K, both CMChs and CMCht results are in excellent agreement with the DNS data at all time instants.

Fig. 6

Normalized conditional mean heat release rates for Case 1 $({{T_{0}}^{\prime }}= 15K)$ at at^∗ = 0.2, bt^∗ = 0.6, and ct^∗ = 0.99; Case 3 $({{T_{0}}^{\prime }}= 60K)$ at dt^∗ = 0.2, et^∗ = 0.6, and ft^∗ = 0.99; and Case 4 $({{T_{0}}^{\prime }}= 100K)$ at gt^∗ = 0.2, ht^∗ = 0.6, and it^∗ = 0.99 (blue circles: DNS data with total-enthalpy conditioning, blue dashed- dotted lines: CMCht, red diamonds: DNS data with sensible-enthalpy conditioning, red solid lines: CMChs)

In Figs. 7 and 8, the conditionally averaged reaction rates of H₂O₂ and OH at different time instants for Cases 1, 3 and 4 are shown. OH and H₂O₂ are key species in the ignition of a hydrocarbon-air mixture under HCCI conditions. H₂O₂ forms first and remains relatively inert. H₂O₂ then decomposes rapidly into OH radicals, leading to rapid ignition [33].

Fig. 7

Conditional mean reaction rates of H₂O₂ for Case 1 $({{T_{0}}^{\prime }}= 15K)$ at at^∗ = 0.2, bt^∗ = 0.6, and ct^∗ = 0.99; Case 3 $({{T_{0}}^{\prime }}= 60K)$ at dt^∗ = 0.2, et^∗ = 0.6, and ft^∗ = 0.99; and Case 4 $({{T_{0}}^{\prime }}= 100K)$ at gt^∗ = 0.2, ht^∗ = 0.6, and it^∗ = 0.99 (blue circles: DNS data with total-enthalpy conditioning, blue dashed- dotted lines: CMCht, red diamonds: DNS data with sensible-enthalpy conditioning, red solid lines: CMChs)

Fig. 8

Conditional mean reaction rates of OH for Case 1 $({{T_{0}}^{\prime }}= 15K)$ at at^∗ = 0.2, bt^∗ = 0.6, and ct^∗ = 0.99; Case 3 $({{T_{0}}^{\prime }}= 60K)$ at dt^∗ = 0.2, et^∗ = 0.6, and ft^∗ = 0.99; and Case 4 $({{T_{0}}^{\prime }}= 100K)$ at gt^∗ = 0.2, ht^∗ = 0.6, and it^∗ = 0.99 (blue circles: DNS data with total-enthalpy conditioning, blue dashed-dotted lines: CMCht, red diamonds: DNS data with sensible-enthalpy conditioning, red solid lines: CMChs)

In Fig. 7, for Case 1 with $T^{\prime }_{0}= 15$ K, the reaction rates of H₂O₂ predicted by CMCht are in good agreement with the DNS data before the thermal runaway. At the time of the maximum heat release rate, the results predicted by CMCht deviate slightly from the DNS data in most reaction layers. Results from CMChs are in excellent agreement with the DNS data. For Case 3 with $T^{\prime }_{0}= 60$ K, CMCht leads to large errors at t^∗ = 0.6, when the temperature in some hot regions reaches around 1000K and H₂O₂ begins to decompose rapidly. CMChs well captures this change in the H₂O₂ reaction. At t^∗ = 0.99, large errors remain in the CMCht results, while CMChs performs well. For Case 4 with $T^{\prime }_{0}= 100$ K, CMCht results deviate substantially from the DNS results at all the time instants. CMChs well captures the rates of H₂O₂ reactions.

Figure 8 shows the assessment of CMChs and CMCht in estimating conditionally averaged reaction rates for the OH mass fraction. A trend is similar to that for H₂O₂. CMCht results in large errors for the OH reaction rates after the H₂O₂ decomposition occurs, and CMChs well captures the rates of the OH reactions. While the results from CMChs deviates from the DNS data for Case 1 at t^∗ = 0.6 and Case 3 at t^∗ = 0.2 in Fig. 8, it is noted that the radical concentrations and reaction rates are very small at these time instants.

4.4 Mapping relationship

Figure 9 shows the mapping relationship between sensible enthalpy and total enthalpy for Cases 1, 3, and 4. In this a priori study, the conditional mean species mass fractions, Q_i, are obtained by conditionally averaging the DNS data. The original mapping is then obtained using Eq. 6. When the mapping is non-monotonic, the reconstructed monotonic mapping is obtained using Eqs. 7 and 8. For Case 1, the mapping curves are almost linear and monotonic from t^∗ = 0.2 to t^∗ = 0.99, indicating that total enthalpy and sensible enthalpy are closely correlated. The closure of the PDF and the conditional scalar dissipation rate are expected to perform well with this kind of mapping. For Case 3, the mapping at an early stage, t^∗ = 0.2, is linear and monotonic. As the ignition occurs and the ignition fronts propagate, the mapping becomes non-linear and non-monotonic. In the flat region of the mapping curve, there are large conditional temperature fluctuations when total enthalpy is chosen as the conditioning variable. For Case 4, the mapping curves are non-linear at all ignition stages. The mapping curve becomes non-monotonic after t^∗ = 0.2. The modified mapping curves are monotonic. The levels of conditional fluctuations in the mapping relation for Cases 1 and 4 are shown in Fig. 10.

Fig. 9

Mapping curve for PDF and conditional scalar dissipation rate modeling. a Case 1 $({{T_{0}}^{\prime }}= 15K)$ at t^∗ = 0.2, bt^∗ = 0.6, and ct^∗ = 0.99. d Case 3 $({{T_{0}}^{\prime }}= 60K)$ at t^∗ = 0.2, et^∗ = 0.6, and ft^∗ = 0.99. g Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.2, ht^∗ = 0.6, and it^∗ = 0.99 (red solid lines: original mapping curve η_t–η_s, green squares: modified mapping curve ${\eta _{t}}^{\prime }$–${\eta _{s}}^{\prime }$)

Fig. 10

Mapping curve and conditional fluctuations. a Case 1 $({{T_{0}}^{\prime }}= 15K)$ at t^∗ = 0.6, and bt^∗ = 0.99. c Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.6, and dt^∗ = 0.99

The non-monotonic part of the mapping curve corresponds to ignition fronts where sensible enthalpy changes rapidly. The non-monotonicity may originate from the negative temperature coefficient (NTC), turbulent fluctuations, or the differential diffusion effects. The effects of the differential diffusion are investigated by performing DNS cases with the unity Lewis number assumption. As shown in Fig. 11, the differential diffusion effects in the present cases are minor and the mapping is still non-monotonic in the unity Lewis number cases. The chemical mechanism of Liu et al. [30] reproduces the NTC effects in the present cases. The NTC effects can lead to non-monotonicity in the mapping, because of the non-monotonic dependence of ignition delay on temperature, which can distort the initially monotonic mapping. The non-monotonic dependence of ignition delay on temperature also tends to increase conditional fluctuations of species mass fractions, especially those of radicals. Fluctuations in heat release rates in Fig. 5 are related to such fluctuations in species mass fractions. However, it is found that first-order closure works well even with such conditional fluctuations when sensible enthalpy is taken as a conditioning variable. Overall, the non-monotonicity in the present cases is not substantial. The simple averaging approach in Eqs. 7 and 8 is found to be sufficient in removing the non-monotonicity in the present cases.

Fig. 11

Effects of differential diffustion on the mapping curve. a Case 3 $({{T_{0}}^{\prime }}= 60K)$ at t^∗ = 0.6, b Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.2, and c Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.6 (red solid lines: mapping curve η_t–η_s, blue dashed lines: mapping curve η_t–η_s from the corresponding DNS cases with the unity Lewis number assumption – Cases 5 and 6)

Non-monotonic mapping can also result from the stratification of mixture composition. With a single conditioning variable based on enthalpy, the dependence of ignition delay on the mixture composition can lead to conditional fluctuations of species mass fractions in ignition fronts. Depending on the correlation between mixture stratification and thermal stratification, non-monotonic mapping can result. Our assumption is that for lean mixtures that are of interest in HCCI, this non-monotonicity can be dealt with an ad hoc modification, such as that proposed in Section 2.3.2. The degree of mixture inhomogeneity that is acceptable within the proposed approach warrants further investigation but is beyond the scope of this paper and will be investigated in future work. When the level of mixture inhomogeneity is beyond the acceptable level, double-conditioning CMC adopting another conditioning variable related to the mixture inhomogeneity needs to be used.

4.5 PDF and conditional dissipation rates of sensible enthalpy

To obtain the mean heat release rates and the averages of reacting scalars, including the species mass fractions, density and temperature, the conditional averages weighted by the PDF of the conditioning variable are integrated in the conditioning variable space as in Eq. 3. In addition to the conditional averages, the PDF of a conditioning variable is thus of critical importance to accurate prediction. Here, the mapping approach for the PDF of sensible enthalpy is validated.

Figure 12 shows the PDFs of sensible enthalpy and of total enthalpy for Cases 1, 3, and 4. The modified monotonic mapping is used to evaluate the sensible enthalpy PDF using Eq. 9. The total enthalpy PDF has one peak, and is not far from the Gaussian distribution. The width of PDF tends to decrease with time, as mixing occurs. The PDF of total enthalpy is well described by the presumed beta PDF in the present cases. The PDF of sensible enthalpy shows qualitatively different behaviors. Initially, when ignition is not much progressed, the shape of the sensible enthalpy PDF is similar to that of the total enthalpy PDF. As ignition progresses, ignited hot spots are generated, which makes another peak at higher values of sensible enthalpy. For Case 1, where the initial temperature inhomogeneity is weak, the ignition delay for different mixtures is not significantly different and ignition progresses almost simultaneously. As a result, the entire PDF is moving towards higher values of sensible enthalpy as ignition progresses. As the initial temperature inhomogeneity increases, the PDF of sensible enthalpy shows two peaks, one on the lower sensible enthalpy side for unigited spots and the other on the higher sensible enthalpy side for ignited spots. The proposed model captures all such trends in the evolution of the sensible enthalpy PDF.

Fig. 12

PDF of sensible enthalpy and total enthalpy for Case 1 $({{T_{0}}^{\prime }}= 15K)$ at at^∗ = 0.2, bt^∗ = 0.6, and ct^∗ = 0.99; Case 3 $({{T_{0}}^{\prime }}= 60K)$ at dt^∗ = 0.2, et^∗ = 0.6, and ft^∗ = 0.99; and Case 4 $({{T_{0}}^{\prime }}= 100K)$ at gt^∗ = 0.2, ht^∗ = 0.6, and it^∗ = 0.99 (blue circles: total-enthalpy PDF from DNS, blue dashed-dotted lines: beta PDF for total enthalpy, red diamonds: sensible-enthalpy PDF from DNS, red solid lines: modeled sensible-enthalpy PDF using total-enthalpy PDF from DNS, green dashed lines: modeled sensible-enthalpy PDF using beta PDF for total-enthalpy)

Figure 13 shows the comparison of the sensible enthalpy PDFs obtained using the two proposed PDF modeling approaches. When non-monotonicity exists in the mapping, the PDF of sensible enthalpy can be modeled using the two approaches proposed in Section 2.3.2. The first approach, Eq. 9, employs the monotonic mapping reconstruction, while the second one, Eq. 14, does not require monotonicity in the mapping. Even for Case 4, where the degree of the non-monotonicity is the most significant, the modeled PDFs using the two approaches are very similar to each other.

Fig. 13

Comparison of the PDFs of sensible enthalpy predicted by the two different approaches, Eqs. 9 and 14, for Case 4 $({{T_{0}}^{\prime }}= 100K)$ at at^∗ = 0.6 and bt^∗ = 0.99 (red diamonds: sensible-enthalpy PDF from DNS; green dashed lines: modeled PDF using modified mapping, Eq. 9, and DNS PDF for total-enthalpy; blue solid lines: modeled PDF using equal-distribution assumption, Eq. 14, and DNS PDF for total-enthalpy)

The modeled conditional dissipation rates for sensible enthalpy are shown in Fig. 14. Conditional dissipation rates of sensible enthalpy represent small-scale molecular mixing rates and are responsible for describing turbulence-chemistry interactions at small scales in CMC. The proposed mapping method well reproduces the trends, but leads to the overprediction as the ignition process progresses in Cases 3 and 4. For Case 1, where $T^{\prime }_{0}= 15$ K, the mapping is almost linear and conditional fluctuations in the mapping relation are small as shown in Fig. 10. The assumptions made in the modeling are thus well satisfied, and the proposed model works well for this case. As the level of temperature inhomogeneity increases, conditional fluctuations in the mapping relation also increase. Fluctuations in the alignment of the sensible enthalpy gradient and the total enthalpy gradient, and those in the ratio of the magnitudes of the scalar gradients also become larger. This leads to the overprediction of the conditional dissipation rate across the ignition fronts for Cases 3 and 4. However, for the unburnt regions, where conditional fluctuations in the mapping relation are small, the proposed model works well. The conditional scalar dissipation is thus expected to be well predicted until the onset of ignition. The conditional dissipation rates of total enthalpy are from the DNS data, and a model for the conditional dissipation rates of total enthalpy is to be used in actual engine simulation. The improvement of the conditional scalar dissipation model warrants further investigation.

Fig. 14

Conditional dissipation rates of sensible enthalpy for a Case 1 $({{T_{0}}^{\prime }}= 15K)$ at t^∗ = 0.6, b Case 3 $({{T_{0}}^{\prime }}= 60K)$ at t^∗ = 0.6, c Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.6, d Case 1 $({{T_{0}}^{\prime }}= 15K)$ at t^∗ = 0.99, e Case 3 $({{T_{0}}^{\prime }}= 60K)$ at t^∗ = 0.99, and f Case 4 $({{T_{0}}^{\prime }}= 100K)$ at t^∗ = 0.99 (red diamonds: DNS, red solid lines: mapping method)

4.6 Heat release rate

Figure 15 shows the time evolution of mean heat release rates for Cases 1, 3, and 4. CMChs produces excellent results when the PDF of sensible enthalpy is taken from DNS. When the PDF of sensible enthalpy is modeled using the mapping method with the presumed beta PDF of total enthalpy, CMChs performs well for Cases 1, 2, and 3 where the initial temperature r.m.s. fluctuations are below 60 K. The monotonic mapping reconstruction, Eqs. 7 and 8, is used. For Case 4 with the initial temperature r.m.s. fluctuation of 100 K, CMChs overpredicts the mean heat release rates during intermediate stages of ignition, and underpredicts the results near the time when the mean heat release rates reach their maximum. When the PDF of sensible enthalpy is modeled using the mapping method with the total enthalpy PDF taken from DNS, CMChs slightly overpredicts the mean heat release rates during the intermediate stages of ignition. The overprediction is due to the slight overprediction of the PDF across the ignition fronts, as denoted by the black dashed line in Fig. 12h. Even though the overprediction in PDF is small, the heat release rates across the ignition fronts are high, resulting in the slight overprediction in the overall heat release rates in Fig. 15c. Overall, CMChs leads to much improved prediction over CMCht. CMCht performs well when the initial temperature inhomogeneity is small. As the level of temperature inhomogeneity increases, CMCht overpredicts the mean heat release rates.

Fig. 15

Time evolution of total heat release rates for a Case 1 $({{T_{0}}^{\prime }}= 15K)$, b Case 3 $({{T_{0}}^{\prime }}= 60K)$, and c Case 4 $({{T_{0}}^{\prime }}= 100K)$ (red diamonds: DNS, magenta dotted lines: CMCht integrated using the beta PDF for total enthalpy, blue dashed-dotted lines: CMCht integrated using the total enthalpy PDF from DNS data, red solid lines: CMChs integrated using the sensible enthalpy PDF obtained using the mapping method and the beta PDF for total enthalpy, red short-dashed lines: CMChs integrated using the sensible enthalpy PDF obtained using the mapping method and the total enthalpy PDF from DNS data, green long-dashed lines: CMChs integrated using the sensible enthalpy PDF from DNS data)

5 Conclusions

The sensible-enthalpy-based CMC model for HCCI with temperature inhomogeneity is proposed. The proposed model is validated a priori with 2D DNS data for ignition of a lean n-heptane/air mixture in homogeneous isotropic turbulence, and compared with the total-enthalpy-based CMC model. Results show that sensible-enthalpy-based CMC substantially improves the prediction of heat release rates over total-enthalpy-based CMC. The improvement in the reaction rate closure results from the strong correlation of sensible enthalpy with temperature on which chemical reaction rates exponentially depend on. While conditional fluctuations of species mass fractions are substantial, sensible-enthalpy-based CMC is found to accurately estimate heat release rates during ignition, as well as reaction rates of key species, due to substantially suppressed conditional temperature fluctuations. While total-enthalpy-based CMC performs well when the initial temperature r.m.s. fluctuation is less than 30 K for the present cases, it tends to overpredict heat release rates as temperature stratification becomes stronger. The mapping method is proposed to model the PDF and conditional dissipation rates of sensible enthalpy. The mapping method based on the conditional averaging is found to capture the qualitatively different trends of reacting scalar mixing than those of passive scalar mixing.