Non-Adiabatic Surface Effects on Step-Induced Boundary-Layer Transition

Abstract

The effect on step-induced boundary-layer transition of surface temperatures different from the adiabatic-wall temperature was investigated for a (quasi-) two-dimensional flow at large Reynolds numbers and at both low and high subsonic Mach numbers. Sharp forward-facing steps were mounted on a flat plate and transition was studied non-intrusively by means of the temperature-sensitive paint technique. The experiments were conducted in the Cryogenic Ludwieg-Tube Göttingen with various streamwise pressure gradients and temperature differences between flow and model surface. A reduction of the ratio between surface and adiabatic-wall temperatures had a favorable influence on step-induced transition up to moderate values of the step Reynolds number and of the step height relative to the boundary-layer displacement thickness, leading to larger transition Reynolds numbers. However, at larger values of the non-dimensional step parameters, the increase in transition Reynolds number for a given reduction in the wall temperature ratio became smaller. Transition was found to be insensitive to changes in the wall temperature ratio for step Reynolds numbers above a certain value. Up to this limiting value, the relation between the relative change in transition location (with respect to its value for a smooth surface) and the non-dimensional step parameter was essentially unaffected by variations in the wall temperature ratio. The present choice of non-dimensional parameters allows the effect of the steps on transition to be isolated from the influence of variations in the other factors, provided that both transition locations on the step and smooth configurations are measured at the same conditions.

1 Introduction

Skin-friction drag is the major source of drag for typical business jet and commercial transport aircraft in cruising flight, contributing about half of the total aircraft drag [1]. The boundary layer on current transport aircraft is mostly turbulent [2]. Substantial skin-friction drag reduction can be obtained by maintaining laminar flow over large portions of the aircraft surfaces: in fact, at the high Reynolds numbers typical for transport aircraft, the skin-friction coefficient of laminar flow is about one order of magnitude lower than that for turbulent flow [3, 4]. Aircraft surfaces can be designed to achieve extended regions of favorable pressure gradient, thus allowing large areas of laminar flow to be attained without the need for active flow control systems (Natural Laminar Flow, NLF) [5,6,7,8,9]. Past research has demonstrated the effectiveness of NLF technology for aircraft surfaces with zero to moderate sweep angles (approx. $\varphi$ < 15–20^∘), where transition is generally induced by amplification of streamwise instabilities [5,6,7,8,9,10]. Nowadays, NLF technology is a practical reality for sailplanes, general aviation aeroplanes and business jets [5, 10, 11], and has been also verified to be a powerful tool for drag reduction on smooth surfaces of transport aeroplanes at cruise conditions [6, 9, 12]. However, when fuel is stored inside NLF wings and the aircraft is operated after extensive exposure to sunlight, the effect of a non-adiabatic surface on boundary-layer transition has to be accounted for. With these start conditions, the wing surfaces would be warmer than the surrounding air during take-off and climb, and this temperature difference may also persist well into the early cruise phase. This can lead to a marked reduction of the extent of the laminar region in these flight phases, as compared to design [13]. Another major concern about the practicability of NLF technology is related to the achievability of surface smoothness compatible with NLF requirements [12]. Surface imperfections can induce the amplification of existing (or potentially existing) disturbances within the laminar boundary layer and/or the generation of additional instabilities, thus leading to premature transition to turbulence [8, 14, 15]. Imperfections such as bumps and waviness can be present on aircraft surfaces, but their size and shape on surfaces manufactured using modern techniques for metallic and composite materials appear to be suitable for laminar flow [3, 10]. This was demonstrated in flight experiments on aerodynamic surfaces that did not receive any special contour or surface waviness modification [5, 10]. Further imperfections that can affect NLF surfaces are steps and gaps: they would exist at surface discontinuities, such as a joint between leading-edge part and wing box [12], and would also arise from the installation of leading-edge panels, high-lift devices, inspection and access panels, etc. [14, 15]. Manufacturing tolerances must be specified for the shape and dimension of the imperfections so that laminar flow can still be achieved, without, however, being overly stringent [12, 16]. Allowable tolerances can be provided only after the effects of the surface imperfections on boundary-layer transition have been understood and quantified [3, 12, 14,15,16,17]. This work focuses on the influence of forward-facing steps on boundary-layer transition. Past experimental and numerical research examined the effect on transition of forward-facing steps only for specific surface geometries and flow conditions [14, 16,17,18,19,20,21,22,23,24]. More recently, the influence of forward-facing steps on boundary-layer transition was systematically investigated for various streamwise pressure gradients and chord Reynolds numbers in experiments at low and high subsonic Mach numbers [25, 26]. Past work, however, did not examine the effect of forward-facing steps on transition in combination with the influence a non-adiabatic surface, except for only one single case studied in [22] with regard to boundary-layer stability. Extensive knowledge is available on the influence of a non-adiabatic wall on boundary-layer stability and transition on smooth surfaces. Boundary-layer linear stability theory predicts a stabilizing (destabilizing) effect of wall cooling (heating) for a subsonic two-dimensional flow over a smooth surface when the examined fluid is a gas such as air or nitrogen [8, 27,28,29]. This effect is due to the strong sensitivity of the streamwise instability mechanism to changes in the curvature of the mean-velocity profile at the wall [8, 29, 30], which can be determined by a variation in surface heat flux. As can be shown by a consideration of the two-dimensional, steady, boundary-layer momentum equation in the near-vicinity of a wall (subscript $w)$ for a flat plate without pressure gradient [30]:

$$ \mu_{w} \left( {\frac{\partial^{2}U}{\partial z^{2}}} \right)_{w} =-\frac{\mathrm{d}\mu} {\mathrm{d}T}\left( {\frac{\partial T}{\partial z}} \right)_{w} \left( {\frac{\partial U}{\partial z}} \right)_{w} $$

(1)

wall cooling in air and gaseous nitrogen ((∂T/∂z) _w > 0 and dμ /dT > 0, where μ is the fluid dynamic viscosity, T the temperature and z the wall-normal coordinate) tends to make the curvature of the mean-velocity profile at the wall (∂²U/∂z²) _w more negative and thus the mean-velocity profile more convex than for the adiabatic-wall case. This is effective in delaying transition in scenarios with predominant streamwise instability mechanism, i.e., on surfaces with zero to moderate sweep angles [8]. In contrast, wall heating in air and gaseous nitrogen (dμ /dT > 0 and (∂T/∂z) _w < 0) tends to make the curvature of the mean-velocity profile at the wall less negative, or even positive. If (∂²U/∂z²) _w > 0, the mean-velocity profile has an inflection point within the boundary layer; the related inviscid instability is strong and generally leads to earlier transition than for the boundary layer on an adiabatic wall [8, 29, 30]. Experimental [31,32,33,34] and numerical results [28, 35, 36] for smooth surfaces confirmed the predictions for the influence of a non-adiabatic wall on boundary-layer stability and transition.

The effect on step-induced transition of surface temperatures T _w different from the adiabatic-wall temperature T _aw has been investigated for the first time in this work. Experiments were conducted in a (quasi-) two-dimensional flow at freestream Mach numbers M = 0.35 and 0.77 and chord Reynolds numbers up to Re = 13 ⋅ 10⁶ with various streamwise pressure gradients and wall temperature ratios T _w /T _{a w} . The test conditions are relevant for NLF surfaces with zero to moderate sweep angles, on which the predominant mechanism leading to transition is the amplification of streamwise instabilities [5,6,7,8,9,10]. Sharp, nominally two-dimensional forward-facing steps were mounted on a two-dimensional flat plate [25, 26, 34, 37] and studied in the Cryogenic Ludwieg-Tube Göttingen (DNW-KRG) [38, 39]. Transition was detected non-intrusively by means of the Temperature-Sensitive Paint (TSP) technique [40, 41]. Analogous to other thermographic methods, such as infrared thermography, boundary-layer transition is detected by measuring the temperature change from the laminar to the turbulent regime [33, 34, 37, 41]. TSP is a coating with incorporated temperature-sensitive, luminescent molecules, which is applied onto the surface of interest. When excited by light in a specific wavelength range, the luminophores emit light in a different wavelength range, the intensity of which decreases at larger temperatures [40]. The distribution of light emitted by the TSP is detected by means of a camera, thus enabling the global measurement of the temperature variation between the laminar and turbulent flow domains and therefore of boundary-layer transition [40, 41].

2 Experimental Setup

2.1 Cryogenic Ludwieg-tube Göttingen (DNW-KRG)

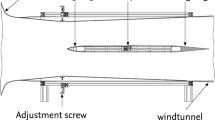
The tests were conducted in the Cryogenic Ludwieg-Tube Göttingen [38]. It is a low-turbulence [39] Ludwieg-tube facility [42] that uses nitrogen as test gas. A sketch of DNW-KRG is shown in Fig. 1: the dark and light blue areas pertain to the facility components where the gas can be charged to the desired pressure p _c and temperature $T_{c}$, and to where they are (generally) kept at atmospheric conditions, respectively. After charging all components upstream of the fast-acting valve to the desired test conditions, this valve is opened in less than one-tenth of a second, whereby the gas accelerates into the test section and, simultaneously, an expansion fan moves with the speed of sound into the storage tube. By increasing the pressure and decreasing the temperature of gaseous nitrogen, the facility is capable of achieving Reynolds and Mach numbers characteristic of transport aircraft cruising at high subsonic or transonic speeds [38].

Fig. 1

Principle sketch of the DNW-KRG wind tunnel [39]

The test section is 0.4 m wide, 0.35 m high and 2 m long and has adaptive upper and lower walls that allow interference-free contours to be set [33, 34, 38, 43]. Two-dimensional (i.e., spanwise-invariant) models with chord length c $\le$ 0.2 m are clamped into turntables mounted at the side walls of the test section. Details on the wind tunnel instrumentation and on its accuracy are given in [33, 34, 38, 39], whereas the optical setup used for the TSP measurements discussed in this work is presented in Section 2.3.

By virtue of the working principle of the DNW-KRG facility, the gaseous nitrogen charged at high pressure in the storage tube quickly expands after the fast-acting valve is opened, whereby this expansion provides a fast temperature drop in the flow; subsequently, this lower temperature remains nearly constant during the actual run, while the model temperature drifts just slightly from its pre-run values. When the pre-run model temperature and the charge temperature of the gas are essentially the same, this leads to a temperature difference between flow and model surface during a run [33, 34, 38, 44]. In this standard case, the ratio between model surface temperature and adiabatic-wall temperature T _w /T _{a w} is significantly larger than 1. It will be named “standard T _w /T _{a w} ” throughout this work. As discussed in Section 1, T _w /T _{a w} > 1 enhances boundary-layer instability on a smooth surface and can cause transition to occur earlier than in the adiabatic-wall case. On the other hand, the temperature difference between flow and model surface enables very accurate transition detection using the TSP measurement technique [40, 41] at DNW-KRG [25, 26, 33, 34, 44]. The value of the standard wall temperature ratio at DNW-KRG depends mainly on the magnitude of the total temperature drop in the incoming gas (i.e., on the freestream Mach number and on the charge temperature) and on the thermal properties of the model. For a model made from austenitic stainless steel and coated with a 0.12 mm thick layer of temperature-sensitive paint, such as that investigated in the present work (see Section 2.2), the wall temperature ratio at T _c ∼ 288 K is in the range T _w /T _{a w} = 1.040-1.065 for M = 0.77. It decreases to T _w /T _{a w} = 1.020-1.040 for M = 0.35. The influence of the wall temperature ratio on the experimental data can be examined by means of an unconventional test procedure [33, 34, 38], which uses an additional component of the DNW-KRG facility: its gate valve (see Fig. 1). Test section and storage tube are separated when the gate valve is closed, so that the gas in the test section, where the model is installed, can be conditioned independently of the gas in the storage tube. At the same time, the temperature of the gas within the storage tube is kept at the appropriate value that allows the desired test conditions during the run to be attained [33, 34]. This “pre-conditioning procedure” provided an opportunity of implementing a wall temperature ratio during the actual testing time lower than the standard T _w /T _{a w} , which will be referred to as “reduced T _w /T _{a w} ” throughout this work.

2.2 Wind tunnel model and instrumentation

The PaLASTra two-dimensional wind tunnel model [25, 26, 34] was examined in the present study. The shape adopted for the model cross-section is shown in Fig. 2a. A flat surface was designed for the largest part of the model upper side: in this manner the pressure gradient was essentially uniform on a large portion of this model side (approx. 20% $< x$/c < 70%). This was the region of main interest in this work.

Fig. 2

a PaLASTra model cross-section [34] with sketch of the model construction [25, 26]; b typical step contour (step-1 configuration, step height h= 29 μm), as measured by means of a contact profilometer [37]

The wind tunnel model is made from austenitic stainless steel. Two-dimensional steps (uniform in spanwise direction) of a desired height can be mounted at the chordwise location x _h /c = 35% by installing shims of appropriate thickness at the interface between the two parts comprising the model (see Fig. 2). With this design, the shape of the imperfection (abrupt step, perpendicular to the surface, with sharp corners - see Fig. 2b) was assured to be the same for all configurations examined configuration in this work. The spanwise non-uniformity of the step was within ± 1μm, measured using a contact profilometer with a vertical resolution of ±0.8 nm [37]. The model instrumentation is shown in Fig. 3. The PaLASTra model was coated with a temperature-sensitive paint [40, 41] for non-intrusive transition detection. TSP formulation [46], surface quality, acquisition and elaboration of the TSP images were the same as those discussed in [34]. The optical setup for the TSP measurement at DNW-KRG is presented in Section 2.3.

Fig. 3

Overview of the PaLASTra model instrumentation [25, 26, 34]. Top view of the model with the leading edge at the top of the image

The model was also equipped with pressure taps for measuring the pressure distribution and thermocouples for monitoring the model temperature evolution during a test run [25, 26, 34]. The circular shape of the orifices, the tap diameter (0.25 mm) and the sharpness of the orifice edges were ensured for all pressure taps, including those embedded in the TSP coating. This was accomplished via additional treatment of the orifices after TSP application [34, 45]. The TSP was applied in pockets machined into the model surface, so that the final model contour did not present variations from the designed one. As it can be seen in Fig. 3, a strip of width Δ(x/c) = 5% around the step location was left uncoated: the sharpness of the step was thus ensured by creating it between two metallic surfaces.

2.3 Optical setup for TSP measurement at DNW-KRG

The optical setup for transition detection at DNW-KRG by means of the TSP technique was the same as that described in [34]. The setup is displayed in Fig. 4. The TSP hardware had to be installed behind the side walls of the wind tunnel test section, because perpendicular access to the model was not possible due to the adaptive upper and lower walls. Cameras and light sources were installed on both test section side walls and were mounted directly inside the turntables, where the model was also fixed. A big advantage of this setup was that the image of the model surface observed by the cameras did not change even if the model was rotated to a different angle-of-attack, because the whole turntable (camera and light sources included) also rotated when changing this angle. The cameras used for image acquisition were two miniaturized charge-coupled device (CCD) cameras with 12-bit dynamic range and a 1392 × 1024 pixels sensor. Each camera was equipped with a pinhole lens with a focal length of 4 mm. High-pass spectral filters with a cutoff wavelength of λ = 590 nm were mounted between camera lens and CCD chip. The optical filters allowed the light emitted by the temperature-sensitive paint to be captured while at the same time blocking light at shorter wavelengths. As can be seen in Fig. 4a, each camera was mounted in one turntable, from where the model upper surface could be observed. The excitation light for the temperature-sensitive paint was supplied by four high-power light emitting diodes (LEDs) installed in the turntables behind suitable windows. This is shown by the illumination windows in Fig. 4. A picture taken inside the test section with the LEDs turned on is shown in Fig. 4b, where the red fluorescence of the TSP can also be seen. The specified excitation center wavelength of the LEDs was λ = 405 nm; band-pass filters for the wavelength range 375-445 nm were placed in front of the LEDs in order to block light from lower and higher wavelengths.

Fig. 4

Sketch of the optical setup for TSP measurement at DNW-KRG (a) and model mounted in the DNW-KRG test section, as seen from a downstream position (b) [34]

3 Test Parameters and Experimental Conditions

The described experimental setup allowed Mach number, Reynolds number, streamwise pressure gradient, wall temperature ratio and step height to be changed independently of each other, which was essential for the present study. The Mach number M used in this work is the ratio of velocity and speed of sound of the freestream. The experiments were conducted at two Mach numbers: M = 0.35 and 0.77. These covered flow conditions relevant for different flight phases of transport aircraft employing NLF surfaces with zero to moderate sweep angle [5, 6, 8, 9]: initial climb phase, final descent phase and cruise conditions. The Reynolds number Re is based on the model chord length c = 0.2 m, on the freestream velocity U_∞ and on the freestream kinematic viscosity ν_∞. The present investigations were conducted at chord Reynolds numbers up to Re = 13 ⋅ 10⁶. Such Reynolds numbers are relevant for the control surfaces and for the wing region at approx. 50% to 80% wing span of the aforementioned NLF transport aircraft. The examined test conditions also covered typical flight conditions for aircraft with piston and turboprop engines, and also for business jets [5]. The Hartree parameter β_H of the self-similar solution of the boundary-layer equations (Falkner-Skan equation) [47, 48] was selected as the characteristic parameter for the pressure distribution. Of main interest were measurements at both considered Mach numbers with favorable streamwise pressure gradients (β_H > 0), which are the most relevant for an NLF surface. Nevertheless, also zero (β_H = 0) and adverse pressure gradients (β_H > 0) were examined. The range of investigated streamwise pressure gradients was -0.017 ≤ β_H ≤ 0.112. Forward-facing steps of height h = 29, 60 and 89 μm were installed on the model upper side at x_h/c = 35%. The corresponding model configurations will be referred as “step-1”, “step-2” and “step-3” configurations throughout this work, whereas the step-less configuration will be named “smooth configuration”. The charge temperature of the gas in the DNW-KRG storage tube was set to T _c ∼ 288 K for all test conditions, but the model surface temperature was varied using the pre-conditioning procedure described in Section 2.1. This enabled investigation of the influence of a non-adiabatic model surface on boundary-layer transition. The wall temperature ratio T _w /T _{a w} was chosen as the characteristic parameter for the thermal boundary condition at the model surface. Both standard and reduced T _w /T _{a w} were implemented. Details on the data acquisition and post-processing, on the repeatability and reproducibility of the results, on the evaluation of the aforementioned parameters and on their uncertainty are given in [33, 34, 37]. The Reynolds number, the Mach number and the Hartree parameter were strictly controlled parameters: appreciable deviations in these quantities were not tolerated, so that the remaining deviations were not larger than ΔRe = ± 0.15 ⋅ 10⁶, ΔM = ± 0.001 and ${\Delta } \beta _{\mathrm {H}} = \pm$ 0.002, respectively. These three parameters were well repeatable and reproducible [34, 37]. The wall temperature ratio, however, could not be set at a particular value with an accuracy comparable to that of the other parameters [34]. Small differences between the temperature of the model surface and that of the gas in the storage tube lead to appreciable variations of the wall temperature ratio between test runs (Δ(T _w /T _aw ) ∼ 0.004 for a difference of 1 K between model and gas temperature at M = 0.77 and T _c = 288 K). The actual value of the wall temperature ratio will be accounted for in the analysis of the results (see Section 5). It should be also noted that only a few tests at reduced wall temperature ratio could be completed with the step-3 configuration. This was due to the large number of particle impacts onto the model leading edge which damaged the TSP after operation of the gate valve, which was necessary for the pre-conditioning procedure [37].

4 Results

The experiments focused on the influence of a non-adiabatic model surface on boundary-layer transition in the presence of forward-facing steps. For the same wind tunnel model, the effect of a non-adiabatic surface on transition with the smooth configuration has been discussed in [34] for M = 0.77, whereas the influence of forward-facing steps at standard T _w /T _{a w} for M = 0.35 and 0.77 has been presented in [26] and [25], respectively. These results will not be discussed in detail here; nevertheless, the results from [25, 26, 34] will be shown for comparison. The results showing the effect of a non-adiabatic surface on transition with the smooth configuration at M = 0.35 are reported in Appendix A.1. The influence of the wall temperature ratio on step-induced boundary-layer transition is presented in this section for two of the cases examined at M = 0.77 with the step-2 configuration, whereas surface temperature effects observed for one of the cases examined at M = 0.35 with the step-3 configuration are reported in Appendix A.2. These results and the following discussion (see Section 5) are taken from [37].

The first case is at M = 0.77, $\beta _{\mathrm {H}} =$ 0.076 and Re = 6 ⋅ 10⁶. The wall temperature ratio was reduced from T _w /T _{a w} = 1.047 to 1.008. The surface pressure distributions are presented in Fig. 5. The results obtained with the smooth configuration at the same test conditions and standard wall temperature ratio (T _w /T _{a w} = 1.045) are also shown for comparison. The surface pressure distributions obtained at different wall temperature ratios were essentially coincident. The pressure distributions obtained with smooth and step-2 configurations were in excellent agreement for most of the chord length, except for the region around the step location. A zoomed-in plot of this region is shown in Fig. 5b. The presence of the step caused these small differences in the pressure coefficient, which are however characterized by large local gradients. Immediately upstream and immediately downstream of the step edge, the boundary layer was no longer accelerated as on the smooth configuration, but rather strongly decelerated. These very pronounced, adverse pressure gradients can be seen in results from Direct Numerical Simulations (DNS) [17, 23], but in this work they could not be measured very close to the step because of the limited spatial resolution of the surface pressure measurements. This aspect has to be kept in mind when the region in vicinity of the step 34% <x/c < 36% is examined; otherwise, the line connecting the pressure coefficients measured by the pressure taps at x/c = 34% and 36% might be misinterpreted. Note also that the pressure coefficient measured at a certain location is that obtained from the average pressure over the orifice cross-section.

Fig. 5

Surface pressure distributions for different wall temperature ratios and model configurations at M = 0.77, Re = 6 ⋅ 10⁶ and β_H = 0.076. a over the whole chord length; b zoomed-in around the step. The gray bar indicates the step location. Note that the black and red lines are essentially coincident, although the wall temperature ratio for the two cases was different. The small deviations of the pressure distribution for the smooth configuration (blue line) from an “ideally smooth” one were due to small model contour variations remaining after treatment of the TSP surface [34, 37]

The TSP results are shown in Fig. 6. In these TSP results and in those presented later in this work, bright and dark areas correspond to the laminar and turbulent boundary layers, respectively, and the flow is from the left. The detected (natural) transition location and the step location are indicated by yellow dashed and solid red lines, respectively. As already discussed in [34], the detected value of the transition location $x_{\mathrm {T}}$ is the average of the transition locations evaluated at ten spanwise sections. The evaluation sections were in regions sufficiently distant from the side walls and from the turbulent wedges which arose from the pressure taps in the nose region (see Fig. 6). Of the ten spanwise sections, five were at 0.33 $\le$ y/b $\le$ 0.44, and the remaining five at 0.56 $\le$ y/b $\le$ 0.7. (y is the spanwise coordinate, b the model span, see Fig. 3.) The chordwise TSP intensity distributions measured at the evaluation sections were analyzed by means of an algorithm capable of detecting the maximal value of the gradient of the intensity ratio in the transitional region [33, 34, 37]. (The distribution of the TSP intensity ratio is a function of the surface temperature distribution and therefore of the wall shear-stress distribution [40, 41].) The transitional region is defined as the region between the point at which the TSP intensity ratio starts to increase from laminar values $x_{\mathrm {T,start}}$ and that at which it reaches turbulent values $x_{\mathrm {T,end}}$. The location in the transitional region corresponding to the maximal slope of the intensity ratio was used to define the transition location $x_{\mathrm {T}}$ in the present work.

Fig. 6

TSP results for different wall temperature ratios and model configurations at M = 0.77, Re = 6 ⋅ 10⁶ and β_H = 0.076. a smooth configuration, T _w /T _{a w} = 1.045, no transition; b step-2 configuration (h/δ_1,h = 0.66), T _w /T _{a w} = 1.047, x_T/c = 65 ± 1.2%; c: step-2 configuration (h/δ_1,h = 0.68), T _w /T _{a w} = 1.008, x_T/c = 72 ± 2.7%

The effect of the forward-facing step on boundary-layer transition at standard T _w /T _{a w} was to induce transition at $x_{\mathrm {T}}$/c = 65%. (With the smooth configuration, the boundary layer remained laminar over the whole model upper surface – see Fig. 6a and b). The influence of the reduction of T _w /T _{a w} in the presence of the step was to delay transition (see Fig. 6b and c). Since the surface pressure distributions were essentially unchanged, the movement of the transition location was only due to the stabilizing effect of the reduced wall temperature ratio. Note that the effect on boundary-layer transition of the reduction of T _w /T _{a w} was favorable, even though the relative step height h/δ_1,h had slightly increased. (h/δ_1,h is the boundary-layer displacement thickness at the step location in the undisturbed boundary layer.) The variation in h/δ_1,h was however small: ${\Delta } (h$/δ_1,h) = 0.02 (i.e., 3%). In Fig. 6, it can be seen that the contrast between laminar and turbulent regions decreases at lower T _w /T _{a w} , since the temperature difference between the laminar and the turbulent domain is thereby also reduced [33, 34]. Note also that the number of turbulent wedges is larger with the lower wall temperature ratio. The two turbulent wedges in the mid-span area arose from pressure taps in the leading-edge region and are common to all TSP results in this work. Pressure taps have been shown to cause the formation of turbulent wedges not only in experiments at high unit Reynolds numbers [33, 34, 45], but also on wind tunnel models with larger chord examined at lower chord Reynolds numbers [49]. The additional turbulent wedges observed in this work were due to the impact of particles onto the model leading edge and onto the step surface when the pre-conditioning procedure was used in the presence of a large temperature difference between the two sides of the DNW-KRG gate valve (see Section 2.1). In spite of this, natural transition could still be measured in the regions where enough space was available in the spanwise direction between turbulent wedges.

The effect of a non-adiabatic surface for the step-2 configuration is now examined for a case at M = 0.77, Re = 10 ⋅ 10⁶ and $\beta _{\mathrm {H}} =$ 0.096. The larger Reynolds number led to a smaller boundary-layer displacement thickness and thus to a larger relative step height h/δ_1,h, as compared to that of the case presented above. As can be seen in Fig. 7, the surface pressure distributions obtained at different wall temperature ratios were in agreement also in this case. The pressure distributions obtained with different model configurations were also in agreement, except for the region around the step location, as discussed above with regard to Fig. 5.

Fig. 7

Surface pressure distributions for different wall temperature ratios and model configurations at M = 0.77, Re = 10 ⋅ 10⁶ and β_H = 0.096. a over the whole chord length; b zoomed-in around the step location. The gray bar indicates the step location

The TSP results are shown in Fig. 8. At standard T _w /T _{a w} , the presence of the forward-facing step led transition to occur at $x_{\mathrm {T}}$/c = 44%, more than ${\Delta } (x_{\mathrm {T}}$/c) = 20% further upstream than the corresponding location for the smooth configuration (see Fig. 8a and b). As can be seen in Fig. 8b and c, transition was measured with the step-2 configuration at approximately the same location for both standard and reduced T _w /T _{a w} . In this case, a variation in the wall temperature ratio had a negligible influence on boundary-layer transition in the presence of forward-facing steps (at least for the considered change of T _w /T _{a w} ).

Fig. 8

TSP results for different wall temperature ratios and model configurations at M = 0.77, Re = 10 ⋅ 10⁶ and β_H = 0.096. a smooth configuration, T _w /T _{a w} = 1.060, x_T/c = 66 ± 1.2%; b step-2 configuration (h/δ_1,h = 0.88), T _w /T _{a w} = 1.056, x_T/c = 44 ± 0.5%; c: step-2 configuration (h/δ_1,h = 0.92), T _w /T _{a w} = 1.023, x_T/c = 44 ± 0.9%

5 Analysis of the Results

This section will focus on the analysis of the results obtained at M = 0.77. Since the trends observed at M = 0.35 are similar to those found at M = 0.77, the results obtained at the lower Mach number are not analyzed here. The analysis of the results at M = 0.35 is presented in Appendix A.3.

The results obtained at M = 0.77 with all configurations at reduced T _w /T _{a w} are collected in Fig. 9, where the transition Reynolds number Re_xT = $U_{\mathrm {\infty } }x_{\mathrm {T}}$/$\nu _{\mathrm {\infty } }$ is plotted as a function of the Hartree parameter. The results obtained at standard T _w /T _{a w} are shown for comparison by solid lines; these are 2^nd order polynomial functions fitted to the experimental data [25]. The data point enclosed by a black circle represents a lower limit for Re_xT at these conditions, since the boundary layer had remained laminar over the whole model upper surface. In this case, the transition Reynolds number was evaluated by taking a value of $x_{\mathrm {T}}$/c = 94%, but this could be even larger if the model chord length would have been larger.

Fig. 9

Transition Reynolds number as a function of the Hartree parameter at M = 0.77. Symbols: data obtained at reduced T _w /T _{a w} ; lines: data obtained at standard T _w /T _{a w} (fitted functions – see text)

5.1 Step-1 configuration (h/δ _1,h < 0.5)

The favorable effect of a lower wall temperature ratio on boundary-layer transition can clearly be seen in Fig. 9 for the step-1 configuration (green symbols, compared to the green lines). Note that the reduction of T _w /T _{a w} had a favorable effect on boundary-layer transition in the presence of forward-facing steps, even though the height of the step relative to the boundary-layer thickness became larger. The change in h/δ_1,h for the step-1 configuration was, however, not very marked: even at the largest Reynolds number considered here, h/δ_1,h was reduced by ${\Delta } (h$/$\delta _{1,h}) \sim$ 0.02 as the wall temperature ratio was decreased from T _w /T _{a w} = 1.063 to 1.006. As the model surface temperature T _w was reduced to values close to or below the adiabatic-wall temperature T _{a w} , the transition Reynolds number for the step-1 configuration was increased to values almost coincident with those obtained with the smooth configuration at standard T _w /T _{a w} . At small and moderate pressure gradients (approx. $\beta _{\mathrm {H}}<$ 0.07), the values of Re_xT for the step-1 configuration at reduced T _w /T _{a w} were even larger than those obtained with the smooth configuration at standard T _w /T _{a w} . In these cases, the sensitivity of the transition location to the influence of the step was weaker than with larger Hartree parameters [25], so that the corresponding variation of the transition location was small. The reduction of T _w /T _{a w} thus led to a marked shift of the transition location.

The results are collected as plots of Re_xT/Re_xT,aw vs. T _w /T _{a w} in Fig. 10, where the adiabatic-wall transition Reynolds number Re_xT,aw has been evaluated in the same manner as in [33, 34]. Colored symbols correspond to the results obtained with the step-1 configuration, whereas the open black squares correspond to the data points from the smooth configuration [34]. They are fitted by the power function shown by a dashed line, i.e., Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 4 [34]. Error bars are shown only for part of the results.

Fig. 10

Relative variation of transition Reynolds number as a function of the wall temperature ratio with the step-1 configuration at M = 0.77. Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 4 [34] and (T _w /T _{a w} )^− 3.5 are the functions fitted to the results obtained with the smooth and step-1 configurations, respectively

The results obtained with the step-1 configuration are in agreement (within the data scatter) with those from the smooth configuration, showing a comparable sensitivity of the transition Reynolds number to changes in wall temperature ratio. However, the data obtained with the step-1 configuration lie in the upper range of the bounds of data from the smooth configuration: these data presented a less pronounced variation of Re_xT/Re_xT,aw as a function of T _w /T _{a w} . The function Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 3.5 is used to fit the data from the step-1 configuration. This function is shown by a solid line in Fig. 10.

5.2 Step-2 and step-3 configurations (0.5 ≤ h/δ _1,h ≤ 1.5)

Up to a certain Hartree parameter, a reduction in wall temperature ratio generally led to an increase in transition Reynolds number also for the step-2 configuration: this can be seen in Fig. 9 (red symbols, compared to red lines). At these conditions, the wall temperature ratio had a favorable influence on boundary-layer transition, although the relative step height increased as the wall temperature ratio was reduced. (The change in h/δ_1,h was, however, less than Δ(h/$\delta _{1,h})\sim$ 0.05 even for a variation in wall temperature ratio of ${\Delta } (T_{w}$/T _aw ) ∼ 0.05.) At β_H < 0.08, the transition Reynolds number obtained with the step-1 configuration at standard T _w /T _{a w} (green line) was almost reproduced on the step-2 configuration by reducing T _w /T _{a w} . At larger Hartree parameters, the increase in transition Reynolds number due to lower T _w /T _{a w} progressively decreased, until it vanished at the largest Hartree parameters. With the step-3 configuration (cyan symbols and lines in Fig. 9), the small increase in transition Reynolds number observed at $\beta _{\mathrm {H}}$ = 0.066 and 0.084 with a reduced wall temperature ratio was within the measurement uncertainty.

The results obtained with the step-2 and step-3 configurations are collected in Fig. 11 as a plot of Re_xT/Re_xT,aw vs. T _w /T _{a w} . This plot is prepared in a manner analogous to that described in Section 5.1 for the step-1 configuration. The function fitted to the experimental results with the step-1 configuration (see Fig. 10) is shown by a solid line.

Fig. 11

Relative variation of transition Reynolds number as a function of the wall temperature ratio with the step-2 and step-3 configurations at M = 0.77. Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 3.5 is the function fitted to the results obtained with the step-1 configuration, whereas groups of data obtained with the step-2 and step-3 configurations with different sensitivity of transition to changes in wall temperature ratio are fitted by the functions Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 2 and (T _w /T _{a w} )^− 1

In general, the sensitivity of boundary-layer transition to changes in wall temperature ratio was further reduced with the step-2 and step-3 configurations, as compared to that of the step-1 configuration (and, clearly, also to that of the smooth configuration). Three groups of data can be identified in Fig. 11. A first group of data shows a variation of Re_xT/Re_xT,aw with changing wall temperature ratio which can be fitted by the function Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 2 (dotted line in Fig. 11). A second group of data presents a sensitivity to changes in T _w /T _{a w} that is lower than that of the first group; the data are better fitted by the function Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 1 (dashed line in Fig. 11). The remaining data show that the transition Reynolds number is nearly independent of the wall temperature ratio.

5.3 Discussion

The different sensitivity of the transition Reynolds number to changes in T _w /T _{a w} may be related to the value of the non-dimensional step parameter at which transition is examined. In order to analyze this effect, the change in transition location $s =$ (x_T-x _h )/(x_T,0-x _h ) is plotted as a function of the step Reynolds number Re$_{h} = U_{\infty }h$/$\nu _{\infty }$ and of the relative step height h/δ_1,h in Fig. 12a and b, respectively. (x_T and $x_{\mathrm {T,0}}$ are the transition locations measured with the step and smooth configurations, respectively, and $x_{h}$ the step location.) This representation of the results has been already used in [25, 26]. In Fig. 12b, the results obtained at reduced wall temperature ratio are also plotted against the relative step height h/δ_1,h obtained at standard T _w /T _{a w} for the same test conditions. This is not strictly correct, because h/δ_1,h increases slightly as T _w /T _{a w} is reduced, but this choice facilitates the comparison of the results obtained with different thermal conditions on the model surface. (In contrast, the step Reynolds number Re _h is independent of T _w /T _{a w} .) The results obtained at standard wall temperature ratio are shown by red symbols, with the corresponding fitted functions being shown by red lines [25]. The results obtained at reduced wall temperature ratio are shown by blue symbols. Note here that the value of $x_{\mathrm {T,0}}$ used to determine s for these data points is also that obtained at standard T _w /T _{a w} . The data points at reduced wall temperature ratio are quite well fitted by 3^rd and 2^nd order polynomial functions in Fig. 12a and b, respectively; these functions are shown by blue lines. At approx. Re _h < 1500 and h/δ_1,h < 0.5 (i.e., with the step-1 configuration), a reduction of T _w /T _{a w} led to a displacement of transition location to an even more downstream position than $x_{\mathrm {T,0}}$. Thereby, values of s even larger than 1 were obtained. The very large values of s pertain to cases with $x_{\mathrm {T,0}}$ quite close to the step location $x_{h}$, i.e., with small values of the denominator in s. As an example, at $\beta _{\mathrm {H}}$ = 0.036 and Re$_{h}\sim$ 870 (h/$\delta _{1, h}\sim$ 0.3), the measured transition locations $x_{\mathrm {T,0}}$/c = 44% and $x_{\mathrm {T}}$/c = 51% led to an increase in s to about 180%. With increasing step Reynolds number and relative step height, the difference between the values of s obtained at standard and reduced T _w /T _{a w} decreases progressively.

Fig. 12

Relative change in transition location at M = 0.77 as a function of the step Reynolds number (a) and of the relative step height (b)

At Re$_{h}\sim$ 2700 and h/$\delta _{1,h}\sim$ 0.8 there seems to be a change in sensitivity of the transition location to variations in T _w /T _{a w} . At values of Re _h and h/δ_1,h lower than these critical values, boundary-layer transition was influenced by the surface heat flux. This influence became weaker with increasing step Reynolds number and relative step height. The values of s obtained at standard and reduced T _w /T _{a w} are essentially coincident for Re _h > 2700 and h/δ_1,h > 0.8: at these conditions, a change in the wall temperature ratio (in the examined range) had a negligible effect on boundary-layer transition in the presence of forward-facing steps. It should be emphasized that, although the transition location was insensitive to variations in T _w /T _{a w} , it was not so close to the step location: it occurred already for approx. 20% $<s<$ 40%. This different behavior of boundary-layer transition with respect to changes in T _w /T _{a w} can be explained as the result of the following effects, which counteract the favorable influence of the wall temperature ratio:

• A first effect that leads to weakening of the influence of the wall temperature ratio on boundary-layer transition is the step-induced amplification of streamwise instabilities in the vicinity of the step location. To a first approximation, the disturbance amplification due to the presence of the step can be taken as independent of the wall temperature ratio: this has been observed in results from DNS at M = 0.8 [22], where an increase in wall temperature ratio from T _w /$T_{aw}\sim$ 0.9 to 1 did not lead to major changes in the step-induced increment of the amplification factors ${\Delta } N$. (N is the natural logarithm of the amplification ratio of boundary-layer disturbances and is often simply called “N-factor” [8, 50].) With increasing non-dimensional step parameters (Re _h and h/δ_1,h), this contribution to the overall amplification of the disturbances increases, and the step-independent contribution accordingly decreases. The growth rates of streamwise instabilities in the regions far away from the step location are still decreased by a reduction in wall temperature ratio, but this effect leads to smaller displacements of the transition location, as compared to those observed with the smooth configuration. This is consistent with the general reduction of the variation of Re_xT/Re_xT,aw as a function of T _w /T _{a w} in the presence of larger steps, which has been seen in Sections 5.1 and 5.2.

• Another finding that has to be considered is the different sensitivity of boundary-layer transition to variations in T _w /T _{a w} , which has been observed for the step-2 and step-3 configurations (see Fig. 11). This is illustrated for three cases with the step-2 configuration at M = 0.77 and $\beta _{\mathrm {H}}=$ 0.096 but at different chord Reynolds numbers. The corresponding data points in Fig. 11 (orange triangles) have different values of Re_xT/Re_xT,aw in the range 1.05 $\le T_{w}$/T _{a w} ≤ 1.06, even though T _w /T _{a w} varies little. (Note that the case at Re = 10 ⋅ 10⁶ was the case with negligible influence on boundary-layer transition of a variation in wall temperature ratio discussed in Section 4 – see Figs. 7 and 8). The surface pressure distributions in the region around the step location are presented in Fig. 13a. As shown in this figure, the surface pressure distributions at different chord Reynolds numbers were essentially coincident. However, transition occurred in regions where the local pressure gradients were different. The chordwise intensity distributions from the TSP results, obtained at the spanwise location y/b = 0.36, are shown in Fig. 13b. The location where transition started was $x_{\mathrm {T,start}}\sim$ 40% and 50% at Re = 10 and 8 ⋅ 10⁶, respectively. The local pressure gradient was still adverse in the first case, whereas in the second case the favorable global pressure gradient had been recovered already.

  As discussed in [33], boundary-layer transition is less sensitive to changes in the wall temperature ratio when it occurs in a region of adverse pressure gradient, where the curves of N-factors of streamwise instabilities (Tollmien-Schlichting waves) present a large gradient. The evolution of N-factors of Tollmien-Schlichting waves with different frequencies and propagation direction fixed to zero degrees (see [25, 26, 33, 34]) was studied using compressible, linear, local stability theory, under the assumption of quasi-parallel flow [8, 28]. The stability computations were performed by means of the stability-analysis tool LILO [51]. Inputs for the stability computations were the measured inflow parameters as well as wall-normal velocity and temperature profiles, which were obtained from boundary-layer computations performed using the laminar boundary-layer solver COCO [52] and assuming an isothermal wall [25, 26, 33, 34]. COCO is a program to compute the wall-normal velocity and temperature profiles of steady, compressible, laminar boundary layers along swept, conical wings. In practice, the equations for two-dimensional flow appear as the limiting case of the equations for an infinite swept wing, which are a specific case of the equations for a conical wing. The system of equations resulting after discretization is solved by a Newton-Raphson method [52]. As shown semi-quantitatively in Fig. 14 for the aforementioned case at Re = 10 ⋅ 10⁶, an adverse pressure gradient results in a large gradient of the N-factor envelope curve (which is the curve connecting the maxima of N for all amplified waves at each streamwise location). The envelope curves obtained for the smooth and step-2 configurations are shown by a black dashed line and a red solid line, respectively. It should be emphasized here that the N-factors computed for the step-2 configuration are not correct, since the amplification of streamwise instabilities near the step location cannot be captured with the used numerical tools [52]. The N-factor envelope curve for the step-2 configuration is presented in Fig. 14 for illustrative purposes, since it follows only the changes in the streamwise pressure distribution (shown by a thin black line). Nevertheless, N-factor envelope curves computed by means of linear stability theory and DNS for a flat plate with zero pressure gradient, shown in [23], present a comparable development downstream of the step.

  The slope of the N-factor envelope curve in the region 37% $<x$/c < 44% is larger than that of the smooth-configuration curve. At Re = 10 ⋅ 10⁶, transition started approximately in the middle of the region where $\partial N$/∂(x/c) is large; this location is shown by a gray bar. The sensitivity of boundary-layer transition to changes in T _w /T _{a w} is expected to be low in this case [33]. In contrast, at Re = 8 ⋅ 10⁶, transition started in the region of (recovered) favorable pressure gradient downstream of the step location, where $\partial N$/∂(x/c) is small. This location is indicated by a red bar in Fig. 14. (The N-factor envelope curve for Re = 8 ⋅ 10⁶ is not shown here; it has a similar shape to that for Re = 10 ⋅ 10⁶, but with lower values of the N-factors.) Boundary-layer transition is thus expected to be more sensitive to changes in T _w /T _{a w} at Re = 8 ⋅ 10⁶ than at Re = 10 ⋅ 10⁶: this is confirmed by the experimental observations. The results at Re = 9 ⋅ 10⁶ are similar to those obtained at Re = 10 ⋅ 10⁶: very likely, this was due to the influence of the local adverse pressure gradient on boundary-layer transition ($x_{\mathrm {T,start}}\sim$ 43%).

• Although a reduction of T _w /T _{a w} has a favorable influence in the attached flow regions, it also leads to an increase of the amplification factors in the separated flow regions. This effect has been discussed in numerical studies of a smooth backward-facing step placed on a flat plate at zero pressure gradient [53]. For the same test case of [53], a similar influence was observed for wall suction [54], which was found to have locally a destabilizing influence in the separation bubble occurring downstream of the step. (The overall effect of continuous suction was, however, found to be stabilizing.) In the experiments on sharp backward-facing steps presented in [55], the effect of localized suction was shown to depend strongly on the location of the suction region. Suction slots located slightly upstream of the re-attachment location were the most effective in preventing transition, because they markedly reduced the streamwise extent of the separated flow region. In contrast, the favorable effect of localized suction in the region downstream of re-attachment was weak, and became even detrimental when the suction slots were placed in the separated flow region immediately downstream of the step. Both the stabilizing and destabilizing effects of wall cooling and wall suction are basically due to the increase in wall curvature of the mean-velocity profile. This can be seen in Eq. 1 for the case of wall cooling: when the flow is attached, the velocity gradient at the wall is positive (i.e., (∂U/∂z) _w > 0), and the effect of wall cooling is to make more negative the curvature of the mean-velocity profile at the wall. However, when the flow is separated, the velocity gradient at the wall is negative (i.e., (∂U/∂z) _w < 0), and wall cooling leads to a more positive curvature of the mean-velocity profile at the wall (although the mean-velocity profiles “are still fuller away from the wall” [53]). The reversed mean-velocity profile is more pronounced at lower wall temperature ratios (see also [56]), leading to larger growth rates in the separated flow region [53]. Thus, a reduction in wall temperature ratio has three effects: first, it reduces the growth rates in the attached flow region; secondly, it reduces the size of the separated flow regions; and thirdly, it enhances amplification in the separated flow regions [53]. For a flat plate at zero pressure gradient, numerical investigations performed up to M = 0.8 showed that there exists a critical value of T _w /T _{a w} below which the overall effect of surface cooling in the presence of smooth backward-facing steps and bumps is destabilizing [53]. This counteracting effect in the separated flow regions, as opposed to a favorable effect in the attached flow regions, is an additional contribution to the reduction of sensitivity of boundary-layer transition to changes in T _w /T _{a w} in the presence of forward-facing steps. The amplification of streamwise instabilities in the separated flow regions becomes more pronounced at larger values of Re _h and h/δ_1,h, and this is further enhanced by a reduced wall temperature ratio; therefore, the aforementioned counteracting effect is also expected to become more pronounced at larger values of Re _h and h/δ_1,h.

• Finally, the boundary layer becomes thinner with decreasing wall temperature ratio, which leads to larger values of the relative step height. (The step Reynolds number Re _h remains unchanged.) This variation seems negligible for the range of h/δ_1,h examined with the step-1 configuration (Δ(h/δ_1,h) $\le$ 0.02), but it could have a (small) influence on boundary-layer transition for the step-2 and step-3 configurations, where ${\Delta } (h$/δ_1,h) ≤ 0.05. This variation in h/δ_1,h due to a change in T _w /T _{a w} was, however, smaller than or comparable to the uncertainty in h/δ_1,h.

Fig. 13

Results obtained for different chord Reynolds numbers at M = 0.77, β_H = 0.096 and standard T _w /T _{a w} . Step-2 configuration. a surface pressure distributions near the step location. b normalized TSP intensity distributions extracted at y/b= 0.36 from the TSP results. The gray bars indicate the step location

Fig. 14

Distributions of amplification factors of streamwise instabilities (envelopes only). Re = 10 ⋅ 10⁶, M = 0.77, β_H = 0.096 and standard T _w /T _{a w} , computed using linear stability theory. (The amplification factors close to the step have not been captured correctly – see text.) The red dashed line indicates the step location

Considering also the analysis of the results obtained at M = 0.35 (see Appendix A.3), one can conclude that, up to h/$\delta _{1,h} \sim$ 0.8-0.9, a reduction in the wall temperature ratio allowed larger laminar runs to be achieved for both examined Mach numbers, independent of the value of the transition location at standard T _w /T _{a w} . At h/δ_1,h > 0.8-0.9, transition was still influenced by the thermal condition at the model surface when it occurred at approx. x_T/c > 48-52% (measured at standard T _w /T _{a w} ), whereas the change in transition location for $x_{\mathrm {T}}$/c < 48-52% was found to be negligible. (x/$c \sim$ 48-52% is the end of the recovery zone downstream of the step.) In any case, Re$_{h} \sim$ 2700 appears as a limiting value for wall temperature effects on boundary-layer transition at both examined Mach numbers, at least for the variation of T _w /T _{a w} attainable in these tests.

5.4 Effect of forward-facing steps on boundary-layer transition at the same, reduced wall temperature ratio

It is now interesting to examine the relative change in transition location due to the effect of forward-facing steps with respect to its value measured at the same, reduced wall temperature ratio: this enables one to demonstrate whether the functional relation obtained at standard T _w /T _{a w} (red line in Fig. 12 [25]) holds also for different thermal conditions at the model surface. In this case, the value of $x_{\mathrm {T,0}}$ used to evaluate the relative change in transition location s = (x_T-x _h )/(x_T,0-x _h ) is that measured with the smooth configuration but at reduced T _w /T _{a w} . The results are plotted as s vs. Re _h in Fig. 15a. The function fitted to the experimental data at standard T _w /T _{a w} (see Fig. 12a [25]) is shown by a solid line in the figure. Note that the number of experimental data present in this plot is markedly reduced as compared to that in Fig. 12a [25], since the number of completed runs at reduced T _w /T _{a w} had been strongly limited by surface contamination (see Section 4). The results in Fig. 15a show a trend similar to that observed for the cases at standard T _w /T _{a w} . The larger deviations of the experimental data from the fitted function are mainly due to different values of T _w /T _{a w} for x_T and $x_{\mathrm {T,0}}$: for example, in the case of the data point at $\beta _{\mathrm {H}} =$ 0.076 and Re _h = 2400, $x_{\mathrm {T}}$ and $x_{\mathrm {T,0}}$ were measured at T _w /T _{a w} = 1.005 and 1.031, respectively. A means to compensate for these differences is, however, available when transition is measured for both configurations (with and without steps) and at both wall temperature ratios (standard and reduced T _w /T _{a w} ). If these four measurements are available, the adiabatic-wall transition locations $x_{\mathrm {T,} {aw}}$ and $x_{\mathrm {T0},{aw}}$ for step configuration and smooth configuration, respectively, can be evaluated. The relative change in transition location is defined in this case as $s_{aw} =$ (x_T,aw – $x_{h})$ / (x_T0,aw – $x_{h})$. The adiabatic-wall transition locations x_T0,aw and $x_{\mathrm {T},{aw}}$ are obtained from the adiabatic-wall transition Reynolds numbers Re_xT0,aw and Re_xT,aw, respectively (see Section 5.1 and [33, 34]), as $x_{\mathrm {T0},{aw}}$ = Re_xT0,aw/Re and $x_{\mathrm {T},{aw}}$ = Re_xT,aw/Re. (Re_xT0,aw is the adiabatic-wall transition Reynolds number for the smooth configuration.) The relative change in transition location s _{a w} is plotted as a function of Re _h in Fig. 15b. The step Reynolds number Re _h is that obtained at reduced T _w /T _{a w} . (This choice has a negligible influence on the representation of the results, since Re _h is independent of T _w /T _{a w} .) After the data have been “corrected” for adiabatic-wall conditions, the plot provides an even better correlation of the experimental results, as compared to that presented in Fig. 15a. The experimental data in Fig. 15b are well approximated by the function determined at standard T _w /T _{a w} , which is shown by a solid line.

Fig. 15

a relative change in transition location as a function of the step Reynolds number at T _w /T _{a w} = 0.994-1.016. The transition location x_T,0, obtained on the smooth configuration, was also measured at reduced T _w /T _{a w} . b relative change of the adiabatic-wall transition location as a function of the step Reynolds number. M = 0.77. Error bars shown only for part of the results

The plots of s vs. h/δ_1,h (with $x_{\mathrm {T0}}$ measured with the smooth configuration but at reduced T _w /T _{a w} ) and of $s_{aw}$ vs. h/δ_1,h are now shown here, since the trends are similar to those presented in Fig. 15.

6 Conclusion

The effect of a non-adiabatic surface on step-induced transition was investigated in the Cryogenic Ludwieg-Tube Göttingen by means of the temperature-sensitive paint measurement technique. The experiments were conducted in a (quasi-) two-dimensional flow at low and high subsonic Mach numbers M = 0.35 and 0.77 and large Reynolds numbers with various streamwise pressure gradients. The influence on step-induced transition of surface temperatures different from the adiabatic-wall temperature was studied using a two-dimensional flat plate with sharp forward-facing steps mounted on the test surface. The results showed a notable influence of surface heat flux on boundary-layer transition even in the presence of forward-facing steps up to a step Reynolds number of Re$_{h} \sim$ 2700 and a relative step height of h/$\delta _{1,h} \sim$ 0.8-0.9: a certain reduction of the ratio between surface and adiabatic-wall temperatures T _w /T _{a w} led to an increase in the transition Reynolds number. This influence became, in general, less pronounced as the non-dimensional step parameters increased. At Re _h > 2700, transition was found to be insensitive to changes in wall temperature ratio in the examined range. This was observed also at h/δ_1,h > 0.8-0.9, unless the boundary layer lasted over the recovery zone downstream of the step without undergoing transition: in this case, surface heat flux maintained its influence on boundary-layer transition. This change in transition sensitivity to a reduction in the wall temperature ratio at larger step Reynolds numbers can be explained as the result of the following effects: the increased contribution of the step-induced amplification to the overall disturbance amplification, the influence of the local flow deceleration due to the step, the adverse effect of wall cooling in the separated flow regions and the thinning of the boundary layer.

The present results show that the influence of a non-adiabatic surface on boundary-layer transition has to be accounted for in criteria for allowable size of forward-facing steps on natural laminar flow surfaces, especially in the case of natural laminar flow wings when fuel is stored inside them and the aircraft is operated after extensive exposure to sunlight. This consideration concerns, however, the effect of the wall temperature ratio on the transition Reynolds number in absolute terms. If the change in transition location is analyzed with respect to its value at the same test conditions (wall temperature ratio included) but with the smooth configuration, and expressed relative to the step location, the effect of forward-facing steps on boundary-layer transition is independent of the thermal condition at the model surface (at least up to Re$_{h} \sim$ 2700 and h/$\delta _{1,h} \sim$ 0.8-0.9). In this range of parameters, the relative change in transition location $s =$ (x_T-x _h )/(x_T,0-x _h ) appears to be a universal function of the non-dimensional step parameters. In fact, this representation of the results allows the effect of the step on transition to be “isolated” from that of the surface heat flux, insofar as the sensitivity of boundary-layer transition to changes in the wall temperature ratio remains approximately unchanged. At approx. Re _h > 2700 and h/δ_1,h > 0.8-0.9, the change in transition sensitivity to variations in T _w /T _{a w} has to be accounted for by the relations between $s =$ (x_T-x _h )/(x_T,0-x _h ) and the aforementioned non-dimensional step parameters. At these conditions, however, transition occurs at a location close to that of the step, so that this change in the functional relations between $s =$ (x_T-x _h )/(x_T,0-x _h ) and the non-dimensional step parameters is mainly interesting for boundary-layer tripping, but not for the design of an aerodynamic surface with natural laminar flow technology.

Finally, it should be remarked that the above considerations hold for the examined variations of wall temperature ratio. It is likely that strong wall cooling (to values of T _w /T _{a w} significantly lower than those implemented in this work) would lead to a shift in the transition location even at Re _h > 2700. Nevertheless, if present, this effect would be expected to weaken as the non-dimensional step parameters are increased.

Appendix

1.1 A.1 Non-Adiabatic Surface Effects on Boundary-Layer Transition for the Smooth Configuration at M = 0.35

The transition Reynolds number measured on the smooth configuration Re_xT,0 is plotted as a function of the Hartree parameter $\beta _{\mathrm {H}}$ in Fig. 16 for the lower examined Mach number M = 0.35. The results obtained at standard and reduced T _w /T _{a w} are shown by blue and red symbols, respectively. The data points enclosed by black circles indicate lower limits for Re_xT,0 achievable at these conditions, since the boundary layer remained laminar over the whole model upper surface. In these cases, even larger values of Re_xT,0 may have been possible if the model chord length would have been larger. Only a few representative error bars for the results are actually plotted in the figure.

Fig. 16

Transition Reynolds number as a function of the Hartree parameter with the smooth configuration at M = 0.35

The favorable influence of flow acceleration (β_H > 0) on boundary-layer transition can clearly be seen by a look at the results obtained for a certain range of wall temperature ratios (either blue or red symbols): a larger value of the Hartree parameter led to a larger value of Re_xT,0. Moreover, at fixed streamwise pressure gradient, a lower value of wall temperature ratio also led to an increase in transition Reynolds number. These trends are in line with expectations [30] and with the experimental results obtained with the same configuration at = 0.77 [34]. Note that the actual value of the wall temperature ratio at reduced T _w /T _{a w} conditions obviously influenced the value of Re_xT,0. For example, the reduced wall temperature ratio was T _w /T _{a w} = 0.981 and 1.007 at $\beta _{\mathrm {H}} =$ 0.060 and 0.071, respectively: the corresponding increase in transition Reynolds number obtained at $\beta _{\mathrm {H}} =$ 0.071 was ${\Delta }$Re$_{x \mathrm {T,0}} \sim$ 0.8 ⋅ 10⁶, whereas at least ${\Delta }$Re$_{x \mathrm {T,0}} \sim$ 1.5 ⋅ 10⁶ was obtained at $\beta _{\mathrm {H}} =$ 0.060 (see Fig. 16). Moreover, the transition Reynolds number was found in [34] to be nearly independent of the chord Reynolds number: this is confirmed also here for the lower Mach number M = 0.35.

The results are now presented in Fig. 17 in the form Re_xT,0/Re_xT0,aw vs. T _w /T _{a w} , i.e., in the same manner as in Figs. 10 and 11. The results obtained at different pressure gradients are shown by symbols with different colors. The approximation function Re_xT,0/Re_xT0,aw = (T _w /T _{a w} )⁻⁷ from [32] is shown by a dashed line. The open symbols show the data points for which the boundary layer remained laminar over the whole model upper surface as the wall temperature ratio was reduced (see above). The experimental data are well fitted by the function Re_xT,0/Re_xT0,aw = (T _w /T _{a w} )⁻⁷ [32]. Different streamwise pressure gradients do not have a marked influence on the plot of Re_xT,0/Re_xT0,aw vs. T _w /T _{a w} .

Fig. 17

Relative variation of transition Reynolds number as a function of the wall temperature ratio with the smooth configuration at M = 0.35

1.2 A.2 TSP Results at M = 0.35

A reduction of the wall temperature ratio can lead to a marked shift of boundary-layer transition into a more downstream location even in the presence of forward-facing steps. This is shown by the TSP results in Fig. 18, which were obtained at $\beta _{\mathrm {H}}$ = 0.033, M = 0.35 and Re = 4.75 ⋅ 10⁶, i.e., at Mach and Reynolds numbers lower than those examined in Section 4. At the standard wall temperature ratio (T _w /T _{a w} = 1.023-1.032), the boundary layer remained laminar over the whole model upper surface with the smooth configuration, whereas transition was induced at $x_{\mathrm {T}}$/c = 59% by the influence of the largest forward-facing step considered in this work (see Fig. 18a and b). For the same step configuration (step-3), the boundary layer remained laminar over the whole upper surface of the model as the wall temperature ratio was reduced to T _w /T _{a w} = 0.966 (Fig. 18c). The pressure distributions obtained for this case will be presented in Appendix A.3.3, where the behavior of step-induced transition under the influence of the wall temperature ratio will be discussed for the results at M = 0.35.

Fig. 18

TSP results for different wall temperature ratios and model configurations at M = 0.35, Re = 4.75 ⋅ 10⁶ and β_H = 0.033. a smooth configuration, T _w /T _{a w} = 1.023, no transition; b step-3 configuration (h/δ_1,h = 0.92), T _w /T _{a w} = 1.032, x_T/c = 59 ± 1.1%; c: step-3 configuration (h/δ_1,h = 0.96), T _w /T _{a w} = 0.966, no transition

1.3 A.3 Analysis of the Results at M = 0.35

The results obtained at M = 0.35 with all configurations at reduced T _w /T _{a w} are collected in Fig. 19, where the transition Reynolds number Re_xT = $U_{\infty }x_{\mathrm {T}}$/$\nu _{\infty }$ is plotted as a function of the Hartree parameter. The results obtained at standard T _w /T _{a w} are shown for comparison by solid lines; these are 2^nd order polynomial functions fitted to the experimental data [26]. The data points enclosed by black circles represent lower limits for Re_xT at these conditions, since the boundary layer had remained laminar over the whole model upper surface. For the dashed circle in Fig. 19, the boundary layer remained laminar over the whole model upper surface only with the step-3 configuration at reduced T _w /T _{a w} . In the cases with laminar boundary layer over the whole model upper surface, the transition Reynolds number was evaluated by taking a value of $x_{\mathrm {T}}$/c = 94%, but this could be even larger if the model chord length would have been larger. Note in Fig. 19 that the values of Re_xT for the step-1 configuration at reduced T _w /T _{a w} were even larger than those obtained with the smooth configuration at standard T _w /T _{a w} . Up to a certain Hartree parameter, a reduction in wall temperature ratio generally led to an increase in transition Reynolds number also for the step-2 configuration (red symbols, compared to red lines, in Fig. 19). At $\beta _{\mathrm {H}} <$ 0.04, the value of Re_xT obtained at reduced T _w /T _{a w} was close to or even larger than that obtained for the smooth configuration at T _w /T _{a w} = 1.022-1.036 (blue line). At larger Hartree parameters, the increase in transition Reynolds number due to lower T _w /T _{a w} progressively decreased, until it vanished at the largest Hartree parameters. Marked changes in the transition location due to a favorable influence of the wall temperature ratio were observed also with the step-3 configuration (cyan symbols and lines in Fig. 19), so that the transition Reynolds number of the smooth configuration (but at larger T _w /T _{a w} – blue line) was completely recovered with the step-3 configuration at lower wall temperature ratio. It should be emphasized here that, as shown in Fig. 18c, at $\beta _{\mathrm {H}} =$ 0.033 and T _w /T _{a w} = 0.966 the boundary layer remained laminar over the whole upper surface of the wind tunnel model with the step-3 configuration.

Fig. 19

Transition Reynolds number as a function of the Hartree parameter at M = 0.35. Symbols: data obtained at reduced T _w /T _{a w} ; lines: data obtained at standard T _w /T _{a w} (fitted functions – see text)

1.3.1 A.3.1 Step-1 configuration (h/δ _1,h < 0.5) at M = 0.35

The results obtained with the step-1 configuration at M = 0.35 are collected as a plot of Re_xT/Re_xT,aw vs. T _w /T _{a w} in Fig. 20, in the same manner as for M = 0.77 in Fig. 10 and Fig. 11. Colored symbols correspond to the results obtained with the step-1 configuration, whereas the open black squares correspond to the data points from the smooth configuration (see Fig. 17). They are fitted by the power function shown by the dashed line, i.e., Re_xT/Re_xT,aw = (T _w /T _{a w} )⁻⁷ [32]. The power function fitted to the experimental data obtained with the step-1 configuration is shown by a solid line. At some test conditions with the step-1 configuration, the boundary layer at reduced T _w /T _{a w} remained laminar over the whole model upper surface; the corresponding data points are indicated by open colored symbols. Error bars are shown only for part of the results.

Fig. 20

Relative variation of transition Reynolds number as a function of the wall temperature ratio with the step-1 configuration at M = 0.35. Re_xT/Re_xT,aw = (T _w /T _{a w} )⁻⁷ [32] and (T _w /T _{a w} )⁻⁵ are the functions fitted to the results obtained with the smooth and step-1 configurations, respectively

The sensitivity of boundary-layer transition to variations in the wall temperature ratio was, in general, reduced, as compared to that observed for the smooth configuration. Nevertheless, some results obtained with the step-1 configuration are still in agreement with those from the smooth configuration. The function Re_xT/Re_xT,aw = (T _w /T _{a w} )⁻⁵ provides a better overall fit than Re_xT/Re_xT,aw = (T _w /T _{a w} )⁻⁷[32], which had been used for the smooth configuration at the same Mach number (see Appendix A.1).

1.3.2 A.3.2 Step-2 and step-3 configurations (0.5 $\le h / \delta _{1,h} \le$ 1.5) at M = 0.35

The results obtained with the step-2 and step-3 configurations are collected in Fig. 21 as a plot of Re_xT/Re_xT,aw vs. T _w /T _{a w} . This plot is prepared in a manner analogous to those described in Sections 5.1 and 5.2 and in Appendix A.3.1. The function fitted to the experimental results with the step-1 configuration (see Fig. 20) is shown by a solid line.

Fig. 21

Relative variation of transition Reynolds number as a function of the wall temperature ratio with the step-2 and step-3 configurations at M = 0.35. Re_xT/Re_xT,aw = (T _w /T _{a w} )⁻⁷ [32] and (T _w /T _{a w} )⁻⁵ are the functions fitted to the results obtained with the smooth and step-1 configurations, respectively; they also fit well groups of data obtained with the step-2 and step-3 configurations. Re_xT/Re_xT,aw = (T _w /T _{a w} )^− 2.5 is the function fitted to the data points with reduced sensitivity obtained with the step-2 configuration at β_H = 0.06

At least two groups of data can be identified in this plot: the data points at $\beta _{\mathrm {H}}$ $\ge$ 0.06 show a reduced or even negligible variation of Re_xT/Re_xT,aw, whereas all other results present a sensitivity of the transition Reynolds number to changes in T _w /T _{a w} that is comparable to that observed with the step-1 configuration. In some cases, the data points are well fitted by the function Re_xT/Re_xT,aw = (T _w /T _{a w} )⁻⁷ [32], which was used to fit the results obtained with the smooth configuration (see Appendix A.1); this is shown in Fig. 21 by a dashed line. The dotted line shows the function Re_xT/Re_xT,aw = (T _w /T _{a w} )^−2.5, which was fitted to the data points with reduced sensitivity obtained with the step-2 configuration at $\beta _{\mathrm {H}} =$ 0.06.

1.3.3 A.3.3 Discussion of the results at M = 0.35

The results obtained at M = 0.35 are analyzed here in the light of the considerations of Section 5.3. The change in transition location $s =$ (x_T-x _h )/(x_T,0-x _h ) is plotted as a function of Re _h and h/δ_1,h in Fig. 22, in the same manner as for M = 0.77 in Fig. 12. The data points at reduced wall temperature ratio (blue symbols) are approximately fitted by 2^nd order polynomial functions, shown in Fig. 22 as blue lines. The results obtained at standard wall temperature ratio (red symbols) with the corresponding fitted functions (red lines) are from [26]. A glance at Fig. 22 shows that the experimental data at lower T _w /T _{a w} are more scattered than in the corresponding plots at M = 0.77 (Fig. 12); this is especially noticeable when plotted as s vs. h/δ_1,h (Fig. 22b). Nevertheless, a clear increase in laminar run length with reduced wall temperature ratio can be seen at step Reynolds numbers up to Re$_{h} \sim$ 2700 and for most of the examined values of h/δ_1,h. In many cases, the transition location in the presence of forward-facing steps but at smaller T _w /T _{a w} was even at a more downstream position than that obtained with the smooth configuration at standard T _w /T _{a w} , leading to $s >$ 1. In general, the difference between the values of s obtained at M = 0.35 at standard and reduced wall temperature ratios decreases at larger Re _h and h/δ_1,h, but the trends are less obvious than those observed at M = 0.77. In the case of s vs. Re _h (Fig. 21a), no appreciable shift of the transition location due to changes in T _w /T _{a w} was observed at Re _h > 2700, whereas a clear limiting value of this type for the relation s vs. h/δ_1,h could not be found.

Fig. 22

Relative change in transition location at M = 0.35 as a function of the step Reynolds number (a) and of the relative step height (b)

The scatter of the data at reduced T _w /T _{a w} is partially due to the different values of T _w /T _{a w} that were implemented: the scatter in the values of T _w /T _{a w} was generally more pronounced than that at larger Mach numbers. For example, the values of wall temperature ratio for the cases at h/δ_1,h = 0.41 (β_H = 0.060), 0.47 (β_H = 0.071) and 0.51 (β_H = -0.017) are: T _w /T _{a w} = 0.989, 1 and 0.973, respectively; the corresponding values of s are: s = 108%, 103% and 130%. Moreover, the boundary layer remained laminar over the whole upper surface of the model in some of the cases at reduced wall temperature ratio. The corresponding data points in Fig. 22 are enclosed by black circles. In these cases, the value assigned to the transition location was $x_{\mathrm {T}}$/c = 94%, but even larger values may have been possible if the model chord length would have been larger. Nevertheless, the different results obtained at h/$\delta _{1, h} \sim$ 0.91-0.92 are due to the different sensitivity of boundary-layer transition to changes in T _w /T _{a w} ; this can be seen also in Fig. 21 (step-2 configuration at $\beta _{\mathrm {H}} =$ 0.066 and step-3 configuration at $\beta _{\mathrm {H}} =$ 0.033). At $\beta _{\mathrm {H}} =$ 0.033, Re = 4.75 ⋅ 10⁶ and T _w /T _{a w} = 1.032, transition was found at $x_{\mathrm {T}}$/c = 59%, but the boundary layer remained laminar over the whole upper surface of the model as the wall temperature ratio was reduced to T _w /T _{a w} = 0.966 (see Fig. 18b and c). For the case at $\beta _{\mathrm {H}} =$ 0.066, which was examined at Re = 9 ⋅ 10⁶, transition was measured at $x_{\mathrm {T}}$/c = 47% at T _w /T _{a w} = 1.032; a reduction of the wall temperature ratio to T _w /T _{a w} = 0.988 led only to a negligible change in the transition location. (The TSP images for this latter case are not shown here, but the TSP intensity distribution for the result at T _w /T _{a w} = 1.032 is presented below in Fig. 23b.) The surface pressure distributions for both considered cases are shown in Fig. 23a. The corresponding chordwise intensity distributions for the step configurations at standard T _w /T _{a w} , obtained from the TSP results at the spanwise location y/b = 0.64, are presented in Fig. 23b. In the first of the two cases (β_H = 0.066), transition was initiated at T _w /T _{a w} = 1.032 in the recovery region downstream of the step location, where the pressure gradient was adverse (and the slope of the N-factor envelope curve pronounced); for the reasons discussed in Section 5.3 with regard to the cases at M = 0.77, the sensitivity of boundary-layer transition to changes in T _w /T _{a w} is low under these conditions. In contrast, transition was measured in the second case (β_H = 0.033) at $x_{\mathrm {T}}$/c = 59%, in a region where the streamwise pressure gradient of the smooth configuration had been already recovered: the transition sensitivity to variations in the wall temperature ratio is large under these conditions, in line with the considerations of Section 5.3.

Fig. 23

Results obtained for test conditions at M = 0.35 that showed different sensitivity of boundary-layer transition to changes in T _w /T _{a w} . The shown results were obtained at standard T _w /T _{a w} . a surface pressure distributions (zoomed-in around the step location). b normalized TSP intensity distributions obtained at y/b= 0.64 from the TSP results in the presence of the steps. The gray bars indicate the step location

1.3.4 A.3.4 Effect of forward-facing steps on boundary-layer transition at the same, reduced wall temperature ratio for M = 0.35

The results obtained at M = 0.35 are plotted as s vs. h/δ_1,h in Fig. 24a, where the values of $x_{\mathrm {T,0}}$ and h/δ_1,h are those obtained at reduced T _w /T _{a w} . The number of experimental data present in this plot is markedly reduced as compared to that at standard T _w /T _{a w} (see Fig. 22 and [26]), since the number of completed runs at reduced T _w /T _{a w} had been strongly limited by surface contamination (see Section 4). Moreover, in some cases at reduced T _w /T _{a w} the boundary layer remained laminar on the whole upper surface of the model (see Appendices A.1 and A.3.1-A.3.3), so that these data were not used in this analysis. The function fitted to the experimental data at standard T _w /T _{a w} (see Fig. 22b and [26]) is shown by a solid line in the figures. Some of the (few) experimental results show a behavior different from that observed at standard T _w /T _{a w} . Another parameter, however, has to be accounted for in these plots: the value of the wall temperature ratio at which the transition locations $x_{\mathrm {T}}$ and $x_{\mathrm {T,0}}$ were measured. The larger deviations of the experimental data from the fitted functions are mainly due to different values of T _w /T _{a w} for $x_{\mathrm {T}}$ and $x_{\mathrm {T,0}}$. As discussed in Section 5.4, a means to compensate for these differences is the use of $s_{aw}$ = (x_T,aw- $x_{h})$/(x_T0,aw-x _h ) as characteristic parameter for the change in transition location, where $x_{\mathrm {T},{aw}}$ and $x_{\mathrm {T0},{aw}}$ are the adiabatic-wall transition locations for step and smooth configurations, respectively. The relative change in transition location $s_{aw}$ is plotted as a function of h/δ_1,h in Fig. 24b. The value of δ_1,h used in this figure is obtained from laminar boundary-layer computations, performed using COCO [52] with the smooth configuration and adiabatic wall. The agreement of the data points with the approximation function for standard T _w /T _{a w} is better than that obtained in Fig. 24a. This confirms the influence of the wall temperature ratio on the data scatter observed in Fig. 22, where the relative change in transition location s = (x_T-x _h )/(x_T,0-x _h ) was used to represent the results. Up to h/$\delta _{1,h} \sim$ 0.8, the relation between the relative change in transition location and the relative step height remains essentially unaffected by the thermal condition at the model surface, provided that both $x_{\mathrm {T}}$ and x_T,0 were measured at the same wall temperature ratio. At h/δ_1,h > 0.8-0.9, however, the change in sensitivity of boundary-layer transition to variations in T _w /T _{a w} has to be taken into account (see Section 5.3 and Appendix A.3.3). When a reduction in T _w /T _{a w} leads to larger values of $x_{\mathrm {T,0}}$ but to a negligible change in $x_{\mathrm {T}}$, lower values of $s_{aw}$ are obtained, as compared to the corresponding values of s at standard T _w /T _{a w} . This can be seen for the data point at h/$\delta _{1,h} \sim$ 1 in Fig. 24b.

Fig. 24

a relative change in transition location as a function of the relative step height at T _w /T _{a w} = 0.983-1.007. The transition location x_T,0, obtained on the smooth configuration, was also measured at reduced T _w /T _{a w} . b relative change of the adiabatic-wall transition location as a function of the step Reynolds number. M = 0.35

The plots of s vs. Re _h (with $x_{\mathrm {T0}}$ measured with the smooth configuration but at reduced T _w /T _{a w} ) and of $s_{aw}$ vs. Re _h are not presented here, since the trends are in line with those shown in Fig. 24.