On the Evolution of the Flow Field in a Spark Ignition Engine

Abstract

The development of the turbulent flow field inside a spark ignition engine is examined by large-eddy simulation (LES), from the intake flow to the tumble break-down. Ten consecutive cold flow engine cycles on a coarse and twenty cycles on a fine grid are simulated and compared to experiments of the same engine. The turbulent subgrid scales are modeled by the standard Smagorinsky and by the recently developed Sigma model. A comparison of the intake flow is made against Particle Image Velocimetry (PIV) measurements along horizontal and vertical lines and to an LES simulation performed by the Darmstadt group. Furthermore, we show the first LES comparison to Magnetic Resonance Velocimetry (MRV conducted by Freudenhammer et al.) measurements, which provided the 3D flow field inside a full scale dummy of the entire upper cylinder head including the valve seat region, at a time which mimics inflow conditions of the corresponding engine. Our LES is in good qualitative and quantitative agreement with the simulation and the experiments, with the notable exception of the measured in-cylinder pressure, which is discussed in detail and compared to 0D simulations and simulations from other groups. A criterion is proposed for estimating the number of cycles needed in a simulation, if experimental data is available. We put emphasis on the flow in the valve seat region, where turbulence is generated, and discuss the formation of the large scale tumble motion, including a comparison of the radial velocity fields on rolled-up planes around the valve seat. Here, spots of high velocities were found in the under flow region, which cannot been seen by the ensemble averaged MRV measurement. Within the compression stroke, a 2D vortex center identification algorithm is applied on slices inside the combustion chamber, yielding a 3D visualization of the tumble vortex, which is found to have a “croissant-like” shape. The tumble vortex trajectory is plotted on the symmetry plane and compared to measurements. Finally, we consider a modified definition of the (turbulent) integral length scale that provided further insight to the tumble break-down process.

1 Introduction

The turbulent flow field at the time of spark ignition is known to be of key importance for the efficiency of combustion in gasoline engines. The flow field has to mix the fuel with the oxidizer homogeneously in order to provide a combustible mixture at the spark plug and moreover to wrinkle the flame front to enhance the consumption rate. Therefore, turbulence is crucial for the working principal of the spark ignition engine, but only if it is available at the right amount and at the right place inside the combustion chamber, meaning that too strong eddies could lead to missfire or unstable working conditions. Even after many years of experimental and numerical investigations, the development of the in-cylinder flow field is still not fully understood. A deeper understanding of the formation of the turbulent environment will be a relevant step towards the reduction of cycle-to-cycle variations (CCV), which lower the efficiency of the spark ignition engine. The negative side effects of turbulence, like CCV, are known for many years but due to the poor optical accessibility, the focus had to be put first on the development of appropriate tools to study in-cylinder processes. Experiments inside the combustion chamber of optical accessible single cylinder research engines are nowadays available and 3D computational fluid dynamics (CFD) simulations are able to resolve the full unsteady turbulent flow field. Both approaches depend on each other and the boundary conditions, assumptions and limitations have to be known from both sides (experiment and simulation). From the simulation perspective, only LES simulations can cope at the moment with the unsteady turbulent flow inside the combustion engine with acceptable cost-to-time performance. During the last 20 years, LES simulations were applied to study the in-cylinder aerodynamics and combustion processes in reciprocating engines [3, 12, 16, 30, 32, 49], where one of the first LES engine simulations was performed in 1992 by Naitho et al. [31]. A motivation of the application of LES to engine flows is given by Haworth et al. [18] and a review about numerical simulations of engines and experimental measurement techniques as such by Drake et al. [10].

The challenge in better understanding in-cylinder phenomena does not only lie in the application of the measurement techniques and numerical models to the engine, it is also about how to post-process, visualize and analyze the produced data. In-cylinder flow dynamics are judged and studied by integral quantities like the swirl, tumble number, turbulence intensity or discharge coefficients, which are very useful for the engineers in the preliminary design of an engine, but they do not give any insight about local flow structures. More advanced analyses include the measurement of integral length scales of the turbulent flow field. For a direct measurement of the length scales, the velocity has to be simultaneously measured at different locations. By applying the temporal or spatial auto-correlation function to these velocities, the integral time and length scales can be obtained. Corcione and Valentino [7] applied the two-point laser Doppler velocimetry (LDV) to calculate the integral length scales inside a diesel engine. Hong and Chen [20] applied these techniques to a single cylinder research engine with a pent-roof combustion chamber and measured a lateral length scale of about 3.9 mm at 30 ^∘ before top dead centre (bTDC). They have analyzed the cross- and longitudinal-correlations, with a variable distance between the two probe volumes of a maximum of 7.5 mm and concluded that the integral length scale is influenced by the in- and outflow jets and by the piston motion. In the work of Auriemma et al. [1] and later by Reitz et al. [40], experimentally obtained lateral length scales were compared to a 3D RANS (Reynolds averaged Navier Stokes) simulation, where the turbulent length scales were directly obtained from the k- 𝜖 turbulence model - so that only the length scale of the assumed fully developed turbulence could be computed. Unsurprisingly, a good agreement was only achieved by adjusting the turbulent kinetic energy, implying a limited ability of the RANS approach to properly model the length scales inside the engine. In other areas of turbulent combustion, integral lengths scales are commonly considered [5, 6, 24]. Di Mare et al. [27] examined different quality criteria for LES of in-cylinder aerodynamics, where one of the criteria was based on the integral length scale.

For further insight of the flow structures in the combustion chamber, Particle Image Velocimetry (PIV) was applied in many experimental studies. This technique requires modifications to the engine and provides velocity information inside a predefined part of the combustion chamber. Accompanying the optical research engines, the aerodynamics can also be studied in stationary flow benches. Here, the cylinder head with a fixed open valve is mounted on a cylinder with the bore and diameter of the corresponding engine. The flow bench is then fed with compressed air under engine relevant conditions. Unfortunately, this approach only gives global flow quantities like the discharge coefficient of the valves or the tumble and swirl number. Although only a small time interval of the intake stroke can be covered by this approach, the complexity of the measurement compared to a reciprocating engine is dramatically reduced, which offers the possibility to use different experimental equipment and a wider interrogation window. Recently, the Magnetic Resonance Velocimetry (MRV) has been applied to a 1:1 full scale dummy of an optical research engine by Freudenhammer et al. [14]. The MRV measurements provide full 3D velocity data inside the upper part of the combustion chamber and the intake ports. Freudenhammer et al. compared their MRV measurements to PIV [2] data obtained from the corresponding engine and showed a good quantitative agreement among the experiments. Hence, MRV measurements should be well suited for the validation of the 3D flow fields predicted by CFD.

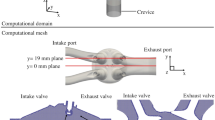
In this work, multi-cycle LES simulations are presented for motored operating conditions. The numerical approach delivers complete 3D velocity fields throughout the entire combustion chamber, valve seat regions and intake and exhaust ports without modifications to the real engine geometry. The focus of this work is on the development of the (turbulent) flow inside the combustion chamber. In Fig. 1, the different zones and phases, which are important for the development of the flow, are drawn schematically [19]. The flow upstream of the intake valves (zone 1) and around the valve seat (zone 2) will be discussed and compared to MRV measurements. Especially the valve seat region is of paramount interest, since turbulence is generated there, convected to the combustion chamber, and causes the big coherent structures (zone 3). Afterwards, the tumble motion will be investigated by tracking its rotational centre throughout the complete combustion chamber (zone 4) and the tumble-break down will be monitored by two-point velocity correlations in the compression stroke.

Fig. 1

Sketch of the evolution of the (turbulent) flow field: flow upstream of the intake valves (1), flow around the valve seat (2), tumble flow inside the combustion chamber during the intake stroke (3), tumble compression (4) and (after) tumble break-down (5)

2 Engine and Experiment

The optical research engine, which is part of the “Darmstadt engine workshop” (www.rsm.tu-darmstadt.de), operated by Dreizler and coworkers [2] has been chosen for this investigation, due to the extensive available data base for the flow field validation. This spark ignition engine features a pent-roof cylinder head with two inclined intake and exhaust valves. Optical access is provided through the piston and liner. The key-parameters of this optical engine are shown in Table 1. Instantaneous velocity fields on the tumble symmetry plane inside the combustion chamber were measured by two-dimensional two-component particle image velocimetry (PIV) [2] at 800 rpm.

Table 1 Specifications of the optical research engine operated by the Dreizler-group and operating conditions for the PIV measurement [2]. TDC is denoted within the power-stroke, where a stands for after and b for before TDC

For the flow bench measurement, a 1:1 scaled Polyamide model of the same engine was investigated by Freudenhammer et al. [14] using Magnetic Resonance Velocimetry (MRV). This measurement technique is able to resolve the ensemble averaged velocity field in a confined geometry. It is usually applied for medical research, for instance to study the flow in blood vessels. Since MRV does not require an optical access, it is well suited for very complex geometries. For the MRV measurements, water was used as a working medium. The flow rate of the MRV measurement was adjusted to mimic the inflow conditions at 270 ^∘bTDC (800 rpm) of the corresponding optical research engine. Two flow rates of 2 m ³/h and 4 m ³/h for the MRV measurement were chosen, yielding Reynolds-numbers of 22500 and 45000, respectively. The two MRV measurements can be scaled to match the velocity fields of the corresponding PIV measurement, with velocity scaling factors of 41.70 and 20.64 [14]. The Mach-number inside the valve gap for the PIV measurement was estimated to be 0.066 for a valve lift of 9.21 mm, so that compressibility effects can be neglected. Since the MRV technique is only able to measure mean velocities, the intake valves were kept at a fixed position and the piston replaced by an outlet. At 270 ^∘bTDC, one can assume that the flow is not accelerated, as the piston is not accelerated then.

A comparison of the PIV and MRV measurements is shown in Fig. 2, illustrating a good agreement of both measurements in the upper half of the cylinder and strong deviations in the lower half. The differences arise from the missing piston in the MRV measurement, so that the flow is not redirected by the piston towards the cylinder head. (The different velocity scales arise from the different working fluids for the PIV and MRV measurement, ensuring Reynolds-similarity).

Fig. 2

Contour plot of the (phase) averaged velocity magnitude at 270 ^∘bTDC within the tumble symmetry plane from PIV (left) [2] and the MRV (right) [14]. A good agreement in the upper half of the cylinder is achieved, which makes MRV well suited to provide additional information in the valve seat region. (The deviating region of the flow field is faded out)

3 Numerical Modelling

For the simulation of the in-cylinder aerodynamics, the open source tool box Openfoam is used, to solve the Favre-filtered equations for mass (1), momentum (2), and energy (3) on a moving grid:

$$\begin{array}{@{}rcl@{}} \frac{\partial (\overline{\rho})}{\partial t} + \frac{\partial (\overline{\rho} \widetilde{u}_{j})}{\partial x_{j}} = 0 \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} \frac{\partial \left( \overline{\rho} \widetilde{{u}}_{i}\right)}{\partial t} + \frac{\partial (\overline{\rho} \widetilde{u}_{i} \widetilde{u}_{j})}{\partial x_{j}} = \frac{\partial\overline{\tau_{ij}}}{\partial x_{j}}+\frac{\partial \tau^{\text{sgs}}_{ij}}{\partial{x_{j}}}-\frac{\partial \overline{p}}{\partial x_{i}} \end{array} $$

(2)

$$ \frac{\partial (\overline{\rho} \widetilde{e})}{\partial t} + \frac{\partial (\overline{\rho} \widetilde{u}_{j} \widetilde{e} ) }{\partial x_{j}} + \frac{\partial (\overline{\rho}\widetilde{K})}{\partial t}+ \frac{\partial (\overline{\rho} \widetilde{K} \widetilde{u}_{j})}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} \left( \alpha_{\text{eff}} \frac{\partial{\widetilde{e}}}{\partial x_{j}} \right) - \frac{\partial}{\partial x_{j}} (\overline{p} \widetilde{u}_{j}) $$

(3)

Within the governing equations, the overline <−> denotes LES filtered and the tilde $<\widetilde {}>$ Favre filtered quantities, with $\overline {\rho }$ as the density, $\widetilde {u_{j}}$ as the velocity vector, $\overline {p}$ as the pressure and $\overline {\tau }_{ij}$ as the viscous shear stress tensor. In order to account for the mesh motion, all convective fluxes were calculated relative to the moving grid [9]. For the unresolved subgrid stresses τ _sgs, the standard Smagorinsky model [45] with a model constant of 0.062 was chosen and the Sigma model [34] with a model constant of 1.35, which was previously tested for engines by Misdariis et al. [28] and by Nguyen et al. [33]. The molecular viscosity is calculated by the Sutherland law [47]. The total internal energy consists of the internal energy $\widetilde {e}$ and the kinetic energy $\widetilde {K}$= 1/2 $\widetilde {v}_{i}^{2}$. The sum of laminar and turbulent thermal diffusivity is denoted as α _eff. The pressure is calculated by a pressure-velocity-density coupling for flows at arbitrary Mach-number proposed by Demirdžić [8, 13]. This approach does not limit the time step size according to the speed of the sound, hence allows to progress in time with bigger steps, using an implicit second-order scheme. The convective scalar-fluxes are discretized with a total variation diminishing scheme (TVD-scheme), using the Sweby limiter [48]. For the momentum equation, a switch between a central differencing scheme (CDS) and TVD-scheme is applied: a CDS is normally used, which is replaced by a TVD-scheme in regions with Mach-numbers greater than 0.3 to avoid numerical problems [32] on the one hand, and to avoid the unacceptable numerical dissipation that would come with a pure TVD-scheme on the other hand.

3.1 Numerical setup

Simulations of internal combustion engine require special attention to the grid quality and structure, since the cells inside the combustion chamber have to adjust to the piston and valve motion. A high grid quality in terms of high orthogonality, low skewness and small expansion rates is a stringent requirement for LES, in particular to avoid numerical instabilities and dissipation that would lead to insufficient turbulent levels. A mesh motion strategy is applied without topological changes on multiply grids, on which the mesh quality stays high. The results are then mapped to the new grid. Target grids for every 5 ^∘CA are created prior to the simulation, where 5 ^∘CA corresponds to a piston motion of less than 4 mm. For the mesh motion, a Laplace equation is solved that yields a smooth mesh deformation velocity field u _{c e l l,k} :

$$ \frac{\partial}{\partial x_{k}} \left( \gamma \frac{\partial{u_{cell,k}}} {\partial x_{k}} \right)=0 $$

(4)

Each mesh point is then just shifted by the deformation velocity multiplied with the width of the time step. The boundary conditions for Eq. 4 are effectively no-slip conditions, with the exceptions of expanding boundaries (valve stem and cylinder liner), where the condition $\frac {\partial u_{cell,k}}{\partial x_{k}} =0$ is applied. An artificial stiffness for the mesh motion is introduced by the diffusion coefficient γ, to control the mesh motion [23].

The complete meshing work-flow is automated and performed exclusively by open source tools [21, 22, 32]. The valves are closed by ”curtains”, which are internal walls around the valve seat. The grids are based on hexahedral cells with a local mesh refinement at the spark plug and valve seat region. The effort of building a ”flow-oriented” grid for a combustion engine is considerable and even more difficult to embed into an automated meshing work-flow. Furthermore, it will be more difficult to apply higher order schemes on it, which is crucial for an LES. Therefore, we have kept the cells inside the complete combustion chamber equidistant, refined and adapted to the walls only at the boundaries. However, we would like to note that this can lead to slightly larger errors in the calculation of the shear stress of the intake jet. For the coarse grid, inside the combustion chamber, the average cell size is 1 mm, inside the valve seat region it is 0.125 to 1 mm, and at the spark plug 0.25 mm. Inside the inlet and outlet manifolds, away from the valves, the mesh resolution was reduced to 2 mm. A second, refined grid uses a cell size of 0.5 mm inside the combustion chamber. In total, 144 grids are used for the full cycle with 0.9 to 1.2 millions of grid cells for the coarse mesh and 2.0 to 5.7 millions of cells for the fine mesh at TDC and BDC, respectively. The refinement of two inside the combustion chamber (from 1 mm to 0.5 mm) means that the number of cells has been increased by 8, the time-step width reduced by 2, and the computational effort increased by 16. The piston top-land crevice volume was blocked and the geometric compression ratio adapted, accordingly. Figure 3 shows the coarse mesh on a cut through the valves with an open intake valve, the cylinder head of the fine grid, and the complete computational domain.

Fig. 3

From left: Engine grid on a cut through the valves with opened intake valve (coarse mesh), top view of the cylinder head (fine mesh) and full computational domain

Since the grid size determines the local filter size and the spacing of our mesh is changing during compression, expansion and valve motion, it will have a direct impact on the results. Fortunately, the cells inside the combustion chamber experience a piston displacement of no more than 4 mm, where we assume that the error in the local filter size is small. We would like to stress, that the mapping strategy with this small displacement intervals is the reason for the relative high amount of mapping intervals (144). As comparison, Enaux et al. [12] uses 41 grids to cover a complete cycle of a similar engine, with an average grid spacing of 0.8 mm. It has to be guaranteed that the moving grids are overlapping precisely on the target grids to not lose mass or momentum. Here, the mesh motion can be based on either imposing the displacement of the moving boundaries or using its velocity. In our approach, as mentioned above, the velocity of the moving boundaries is used together with the time step width to calculate the displacement. Hence, the displacement of the moving boundary is only first-order in time accurate, so that a small time step is needed to ensure a good overlapping between the grids.

3.2 Simulation setup

The simulation is started at 360 ^∘bTDC, when the intake and exhaust valves are open and the fluid assumed to be at rest in the entire domain. A time-varying absolute pressure is imposed at positions of 530 mm upstream of the intake valves and 360 mm downstream of the exhaust valves, where the pressure is known from measurements. The inlet temperature is set to 295 K. A no-slip boundary condition is applied to all walls, for which the temperature was fixed to 333 K. No additional wall modelling was added for the heat transfer. Ten consecutive cold flow engine cycles were calculated on the coarse and twenty on the fine grid.

The time step was calculated from a maximum CFL number of 2 based on the convective velocity. The most time consuming part of the simulation is the opening and closing of the valves, when the mesh inside the valve gap has a resolution of 0.125 mm and velocities around 300 m/s occur, leading to time steps smaller than one micro second. However, once the valves are closed, the time step size increases to almost 50 micro seconds. Table 2 shows how much computational time is required for the different phases of the cycle on the fine and coarse mesh, performed on 16 CPUs (AMD Opteron - Type 6234) with a total of 192 cores.

Table 2 Computational time for one engine cycle performed with 196 CPUs on the fine and coarse mesh presented for the different time intervals: valve overlap, intake valve closing, exhaust valve closing

4 Results

The in-cylinder pressure evolution is discussed first. The numerical model has a compression ratio of 8.5:1, which conforms to the engine specification. Figure 4 shows the simulated in-cylinder pressure of the motored test case for the fine and coarse mesh configuration. Both curves have a very similar in-cylinder pressure distribution compared to the measurement for the intake and exhaust stroke, but overpredict the peak-pressure by 17 %. At the closure of the inlet valves the simulated pressure is in very good agreement with the measurement, however, this does not imply that the in-cylinder mass is correct. Since only the in-cylinder trapped mass (mass coming into the engine) can be estimated from the flow meter of the test bench, the total in-cylinder mass (trapped mass + residual gas) remains unknown. A temperature measurement inside the combustion chamber would help for a better estimate of the in-cylinder mass at intake valve closure, which unfortunately does not exist. The work of Baumann et al. [3] confirms our simulation, as they first calculated a very similar, too high peak-pressure. They then lowered the in-cylinder mass by adjusting the intake pressure to make the peak-pressure fit. We do not follow this approach, because the in-cylinder pressure at inlet valve closure in our simulation agrees well with the experiment. The in-cylinder mass in our simulations at IVC was ∼542 mg for the simulations on the fine and coarse mesh using the Smagorinsky model and ∼536 mg on the coarse mesh using the Sigma model.

Fig. 4

In-cylinder pressure [bar] evolution for the complete cycle given by a LES on a fine grid (blue) with the Smagorinsky model and on coarse grid with the Smagorinsky (red) and Sigma model (orange). Simulation results are compared against experiment (black) and another engine cold-flow simulation of the same engine under the same operating conditions performed by Baumann et al. [3]

To ensure that our simulations and the work by Baumann do not share a (unknown) common mistake leading to the overprediction of pressure, we have calculated the in-cylinder pressure resulting from an isentropic compression under different assumptions. For this purpose, a 0D model for the compression and expansion of the optical engine was made, which includes an empirical model for the convective heat transfer proposed by Woschni [51] and a simplified blow-by model [35]. The 0D simulations are initialized with the measured in-cylinder pressure at intake valve closure of 1.055 bar and air of 300 K. In Fig. 5 the results of the 0D simulations are presented and compared to the experiment. It is observed that for isentropic compression and expansion, the peak in-cylinder pressure is overpredicted by 28 % to the measurement, whereas our non-adiabatic 3D-CFD simulation lead to an overprediction of 17 %. In fact, around 20 % of the total in-cylinder mass should be removed by blow-by gasses to justify the lower measured in-cylinder pressure. Recent studies underline our observations of the missmatch of the peak-pressure inside optical research engines, where Rakopoulos et al. [39] used a blow-by model within a CFD simulation of an optical engine, to match the experimental data. For the case investigated here, we find that the geometrical compression ratio for isentropic compression and expansion should be lowered from 8.5:1 to 7.5:1 to fit the measurement.

Fig. 5

Estimation of the in-cylinder pressure during the compression and expansion stroke (IVC → EVO) given by a 0D simulation for an adiabatic case (blue), with heat transfer (red), with blow-by (gold), and with reduced compression ratio (brown) compared to a measured in-cylinder pressure (black) under motored operating conditions

Blow-by, as another likely explanation for a deviating peak pressure, is hard to quantify. The alternative explanation of a strong effect of heat transfer is also not trivial to assess in an LES, where accurate boundary layer modeling for momentum and heat transfer is still not fully solved [42–44]. (It should however be pointed out that the wall heat transfer is somewhat less critical in motored operation). Decreasing the compression ratio should also not be a desired solution, since it will require (a) modifications to the engine geometry, that may influence the in-cylinder flow field and (b) will change the temperature evolution during compression, hence the viscosity and consequently the turbulence [41]. It is, however, perceivable that large amounts of gas are trapped between the piston-rings and in the piston top-land crevice (piston top-ring is 74.5 mm positioned underneath the piston head), lowering the in-cylinder mass temporally during the compression stroke, while releasing it partially to the cylinder back during the expansion phase. Given the great uncertainty in this explanation, we have chosen to simulate the case as it is and to accept the resulting deviation in the peak-pressure. (We would like to stress that not capturing the peak-cylinder may not be critical under motored conditions, but certainly under fired operation).

4.1 Engine LES quality assessment

The mesh adequacy was assessed by investigating the turbulent to laminar viscosity ratio. Figure 6 shows the contour plots of the instantaneous turbulent to laminar viscosity ratio (ν _t /ν _l ) in the valve plane at 270 ^∘bTDC and within the tumble symmetry plane at 90 ^∘bTDC for the Smagorinsky model on the coarse and fine grid and for the Sigma model on the coarse grid. The ratio stays lower than 20 in all simulations, with the exception of certain points when the Sigma model is used. Like similar criteria, this criterion should not be seen as a sufficient criterion for an “accurate or good LES” and can only be seen as an indicator [15, 25, 26, 36]. Alternatives for the assessment of the quality of an LES are the length scale resolution parameter [37], which was recently used by Montorfano et al. [29] to estimate the quality of a LES in a valve/piston assembly or the resolution index [38], which was used by Baumann et al. [3]. The length scale resolution parameter requires the size of the Kolmogorov scales, which is not known for the engine in this investigation and therefore rejected as quality criterion. Also the resolution index requires the local kinetic energy inside the combustion chamber, which is difficult to calculate based on cycle averaged data, because the motion of the large scale motion (tumble vortex) has to be taken into account, too, which is not trivial, since the centre of the tumble is changing from cycle to cycle. We therefore omitted this criterion, too.

Fig. 6

Contour plots of the turbulent to laminar viscosity ratio of single cycles within the valve plane at 270 ^∘bTDC (upper row) and symmetry tumble plane at 90 ^∘bTDC for the fine simulation and coarse simulation using the Smagorinsky model and for the coarse simulation with the Sigma model

Figure 7 shows the velocity fluctuations at 90 ^∘bTDC on the tumble symmetry plane for the fine and coarse simulation performed with the Smagorinsky model and on the coarse mesh with the Sigma model. The results converge nicely with grid refinement for the simulations with the Smagorinsky model. It is clear that the number of necessary samples is strongly dependent on the quantity that needs to be studied. Where a mean flow field in stable engine operation will be well sampled after very few cycles, higher moments of velocity or scalars will require more, the statistical analysis of cyclical variations might even require thousands of cycles. At stable engine operation, assuming statistical independence of Gaussian distributed samples u i′, the standard error σ ^∗ of the mean $\overline {u}$ due to the finite number n of samples is given as:

$$\begin{array}{@{}rcl@{}} \sigma^{*}=\frac{\sigma}{\sqrt{n}} \: \: \: \: with \:\: \sigma=\sqrt{\frac{1}{n}{\sum}_{j=1}^{n}{(u_{j}-\overline{u})^{2}}} \end{array} $$

(5)

This means that the statistical error only drops with the square root of the number of samples - a larger number of samples has a small effect. The engine experiments by Baum et al. [2] show that the error indeed drops like $1/\sqrt {n}$, providing indirect evidence that the samples in the investigated engine are statistically independent.

Fig. 7

Velocity fluctuations taken from the fine (20 cycles) and coarse grid (10 cycles) using the Smagorinsky model and from simulations using the Sigma model (10 cycles), compared to the PIV measurements and from the fine grid simulations (0.8 mm, 50 cycles) of Baumann et al. [3]. (The fluctuations have been sampled within the tumble symmetry plane on horizontal lines underneath the fire deck)

Based on this information, we would like to propose a criterion for the necessary number of cycles required in a simulation, if the experimental data is known. We suggest that in a simulation, it is not efficient to drive the statistical sampling error σ _s,ϕ = σ ^∗ of a mean quantity ϕ to a significantly smaller value than the combined modeling and numerical error. This combined modeling and numerical error σ _m,n,ϕ can be estimated by the difference of a mean ϕ _s from the simulation and the mean from the experiment ϕ _e (assuming a large number of samples in the experiments). In other words, a sufficient number of samples has been achieved once e _s,ϕ ≈|ϕ _s −ϕ _e | is reached, with $e_{s,\phi } \approx \sigma /\sqrt {n}$, where σ would be estimated from the available samples.

In practice, this criterion could be tested by drawing error bars at a distance from the mean results of a simulation. The simulation would then have to be continued as long as most experimental data points lie within the narrowing error bars ($1/\sqrt {n}$), but can be stopped when the error bars have become so narrow that most experimental data points lie outside the error bars. In other words, the simulation would be run until it becomes clear that a really good agreement with the experiments is no longer likely.

Figure 8 shows the u- and v-velocity components, phase averaged over 5 and 20 cycles at 270 ^∘bTDC at 10 and 30 mm underneath the fire deck together with the error bars derived. It can be seen that the error from 5 to 20 cycles decreases and that there are already points for which the statistical error is small compared to the deviation from the experiment - so that based on the proposed criterion, 20 cycles would be sufficient to assess how well the simulation agrees with the experiment.

Fig. 8

Phase averaged velocity components taken from 5 (orange) and 20 (blue) cycles, simulated on the fine mesh with the Smagorinsky model at 270 ^∘bTDC within the tumble symmetry plane at -10 and -30 mm underneath the fire deck compared to the PIV measurement

4.2 Valve seat region

An important area inside the combustion engine is the valve seat region, from where the flow enters the combustion chamber, thus governing the development of the (turbulent) flow field (see Fig. 1). Therefore, the flow field on curtain planes around the valves is evaluated first and compared to the MRV measurement. A cylindrical coordinate system is introduced with its origin in the centre of the intake valve and along the valve stem. The radial velocity component was calculated for both intake valves, accordingly. The curtain surface has a radius r of 16.5 mm and a height h of 10 mm. This surface covers the complete entrance area around the valve from the top of the valve to the cylinder head. Figure 9 shows the annular valve seat plane, where the range of -90 ^∘<𝜃<90^∘ will be denoted as overflow region and the rest of the curtain as underflow.

Fig. 9

Valve curtain in cylindrical coordinate system for valve 1 and the cylinder head with the position of valves 1 and 2

Figure 10 shows the ensemble averaged radial velocity field within the unwound valve curtain of valve 1 of the MRV measurement and the phase averaged radial velocities obtained from 10 LES cycles (coarse grid, Smagorinsky model) of valve 1 and the instantaneous radial velocity fields of both intake valves. It is clear that the flow is gradually increasing from 𝜃=−180^∘ to 𝜃=−90^∘, where regions with negative radial velocities (backflow) are observed at the upper part of the valve curtain next to the cylinder head, indicating flow separation. (A detailed description of flow separation in the valve seat region can be found in the work of Weclas et al. [50]). The instantaneous velocity fields in Fig. 10 show large amounts of turbulent fluctuations, in particular in the underflow region. In the average fields, the highest velocities appear in the overflow region.

Fig. 10

Rolled-upped ensemble averaged radial velocity on the valve curtain of valve 1 given by the MRV measurement (Re=45000) and averaged and instantaneous radial velocity contour plots from the intake valve curtains given by the LES obtained from 10 cold flow LES (Smagorinsky model) cycles on the coarse grid

Figure 11 shows the percentage of the mass flow passing the valve curtain of valve 1 for the LES and MRV for bins of 10 ^∘. In the window of -50 ^∘<𝜃<50^∘, around 72 % of the total mass is inducted according to the MRV and LES. In the range of -180 ^∘<𝜃<−90^∘, the mass flow profile for the MRV and LES is smoother than on the positive 𝜃 side, where the two intake streams merge, which may cause instabilities in the flow.

Fig. 11

Percentage of the total mass flow over the inlet valve 1 of a mean from 10 LES cycles (coarse) at 270 ^∘bTDC and the MRV measurement, determined for bins of 10 ^∘

4.3 Valve plane

The flow passes the valve curtain and enters the combustion chamber (zone 3 in Fig. 1) and starts forming a large tumble vortex. Figure 12 shows the contour plot of the velocity magnitude as obtained by the MRV measurement (Re=45000) and LES (Re=32200) in a cut through the valves. The Reynolds-number in the LES was calculated for the inlet pipe, 100 mm upstream of the bifurcation, consistent with the position in the MRV measurement. The flow passing the upper tip of the valve is denoted as overflow and the lower stream as underflow, according to Freudenhammer et al. [14] and illustrated in Fig. 12. The fluid enters the combustion chamber as a “planar jet-like” flow, where the highest flow velocities are obtained in the valve seat area. In the upper part of the cylinder head, the velocity fields from the MRV and LES are qualitatively comparable to each other, but in the MRV measurement a bigger penetration length of the upper jet is observed in the overflow region. The flow detaches at the upper tip of the intake valve and forms a recirculation zone underneath it.

Fig. 12

Contour plot of the ensemble average velocity magnitude [m/s] for the MRV experiment (left) and for the LES (right) phase average at 270 ^∘CA over ten cold flow engine cycles (coarse mesh, Smagorinsky model), on a cut through valves (top) and on the cross-tumble plane (bottom)

In the underflow region, the flow changes significantly across the valve seat. It is not accelerated over the full cross-sectional area, only in a small layer along the lower tip of the valve. The smaller velocities and backflow at the lower valve seat area are caused by recirculation zones created by the sharp edge of the intake port in the underflow region. Those recirculation zones induce losses (less in-cylinder filling), but they also force the flow to pass the upper part of the valve seat to enter the combustion chamber, which enhances the tumble motion. In the cross-tumble plane (Fig. 12), the flow is accelerated after the valve stem and branches towards the liner wall and center line. The branch towards the liner, impinges at the wall and spreads towards the exit (or towards the piston in the LES). In the middle of the cross-tumble plane, the flow in-between the two intake valves merges together, locally forming a single planar jet. The coalescence of the two jets in-between the intake valves leads to oscillations of the merged single jet in the LES, which will reduce the reproducibility of the flow field inside the engine. Furthermore, in the LES results, the flow impinges on the liner wall at a lower position, and a thicker layer with higher velocities is predicted. This needs further investigations, since the wall modeling for LES is a challenging problem and not touched in the scope of this work.

4.4 Tumble plane

Figure 13 shows the horizontal and vertical sampling positions within the tumble plane on which in Fig. 14, the phase averaged flow fields, calculated from ten LES cycles on the coarse mesh (Smagorinsky model), the phase averaged flow fields given by the PIV measurement at 270 ^∘bTDC and the MRV data (Re=45000) are shown. A good agreement between the PIV and LES is achieved. As in this flow bench measurement, the piston was replaced by a steady outlet manifold, only the upper part of the combustion chamber to the position y=-20 mm should be taken for a comparison to the PIV measurement and LES. However, above the y=-20 mm position, a good agreement is achieved for the MRV measurement compared to the LES and PIV measurement. In the LES simulation, the spark plug was not removed, which caused a recirculation zone downstream of it.

Fig. 13

Sample positions on the tumble symmetry plane for the comparison of velocity profiles along (a) vertical lines at positions in x-direction at ±30 mm, ±10 mm and 0 mm and (b) along horizontal lines in y-direction at 0 mm, -10 mm, -30 mm and -40 mm. The coordinate y* is normalized by the current height of the combustion chamber, ranging from 0 on the piston head to 1 at the fire deck. In the centre of the tumble plane, a big vortex is shown and velocity vectors u and v for the illustration of the definition of the auto-correlation functions

Fig. 14

Velocity magnitude plot given by the PIV measurement taken from an average of 2700 motored cycles (left), by the MRV (middle) and the velocity magnitude contour plot obtained from an average of ten cycles from the LES (coarse grid, Smagorinsky model, right) within the tumble symmetry plane. Note that the MRV velocity data deviates due to the use of a different fluid

In Fig. 15, the velocity components in the x- and y-directions are plotted for all measurements and LES results at 270 ^∘bTDC and in Fig. 16, for the LES and PIV at 90 ^∘bTDC, along the lines indicated in Fig. 13. A good agreement among the measurements and simulations is achieved, where at 270 ^∘bTDC the vertical velocity profiles from LES and PIV deviate to the MRV data below 20 mm of the fire deck, due to the missing piston in the MRV measurement. Interestingly, the velocity profiles calculated with the Sigma model are deviating at 90 ^∘bTDC to the experiment, where the simulations performed with the Smagorinsky model still match the experiment well. The velocity profiles from the cycles with the Sigma model rather follow the trend of the simulation by Baumann et al. [3], who used the Smagorinsky model, but with a higher model constant (C _s =0.165). Apparently, the velocity fields seem to be more sensitive to the turbulence model and model constant in the compression phase, as in the intake phase. The comparison of the present LES data to that of Baumann et al. [3] and to the PIV and MRV measurements shows that the flow field is captured sufficiently well to justify the further analysis presented in the following sections.

Fig. 15

Mean velocity profiles on vertical lines under the fire deck, phase averaged over ten LES engine cycles with the Smagorinsky model on the coarse mesh (red), twenty LES cycles with the Smagorinsky model on the fine mesh (blue), ten LES cycles with the Sigma model (orange), from the LES by Baumann [3] (grey), from PIV and from MRV at Re=22500 and 45000 at 270 ^∘bTDC

Fig. 16

Phase averaged velocity components in x- and y-directions obtained from ten LES cycles on the coarse grid (red) and twenty LES cycles on the fine mesh (blue) using the Smagorinky model, from ten cycles with the Sigma model on the coarse grid (orange), from the fine grid LES simulation by Baumann et al. [3] (grey) and the corresponding PIV-measurement (black) within the tumble symmetry plane at 90 ^∘bTDC

4.5 Tumble vortex identification

For the identification of the large scale vortex motion, a 2D tracking algorithm proposed by Graftieaux et al. [17] is used. It was already applied in the past to instantaneous velocity fields of an optical research engine, for example by Druault et al. [11], who studied the cycle-to-cycle variability of the in-cylinder flow and more recently by Stiehl et al. [46] for the interaction of the engine flow to the fuel spray inside a stratified direct injection engine. The vortex identification function Γ in the integral form is defined as:

$$\begin{array}{@{}rcl@{}} {\Gamma}(x)= \frac{1}{V} {\int}_{V} \left( \frac{x^{*}}{\vert x^{*} \vert} \times \frac{u^{*}}{\vert u^{*} \vert}\right) \cdot n\: dV \end{array} $$

(6)

In Eq. 6, V denotes the 2D integration domain, x the position at which the function Γ is evaluated, x ^∗ the location of any point within the integration domain, u ^∗ the velocity at x ^∗ and n the normal vector to the 2D integration domain. The 2D vortex tracking algorithm is applied on 2D planes separated by 1 mm in z-direction, throughout the entire combustion chamber for multiple cycles (coarse LES) within the compression stroke. For each 2D plane a contour field of the centre of the tumble vortex is obtained, which is bounded between -1 <Γ<1. The negative Γ-values indicate the location of a clock-wise turning vortex (towards the exhaust side) and positive Γ-values a counter clock-wise vortex. For Γ=±1, the centre of a ”perfect circular 2D vortex” would be obtained, which is hardly achievable, since the flow field is very complex. In Fig. 17, two instantaneous iso-contour plots of the volumetric Γ-field are shown (fine mesh). The tumble flow has a ”croissant-like” shape and branches towards the positive and negative z-direction. Bücker et al. [4] also applied the Γ-criterion for the flow field of an optical research engine and found a ”c-shaped” tumble vortex during the compression stroke, which looks very similar to our ”croissant-liked” shape. However, they have applied it to a pseudo volumetric velocity field obtained by multiple stereoscopic PIV measurements at different planes, which cannot be used to study cyclic variability of the tumble vortex.

Fig. 17

A 3D representation of the Γ-field obtained by the 2D vortex detection algorithm at 90 ^∘bTDC for the fine mesh simulation. The light yellow color represents an iso-value of the Γ-field of -0.65 and the dark brownish color an iso-value of -0.8

In Fig. 18, a top view of the ”tumble-croissant” at 90 ^∘bTDC is shown for 6 different LES cycles (coarse mesh, Smagorinsky model). In each cycle, the shape is different, which illustrates the complexity and variability of the flow field. In order to trail the tumble trajectory, the maximum Γ-value within the tumble symmetry plane was tracked from 180 ^∘bTDC to 20 ^∘bTDC. The tumble centre is plotted for 4 different cycles in Fig. 19, where the dots represent the position of the tumble centers and its color defining the corresponding ^∘CA within the compression stroke. For all 4 cycles, the tumble centre starts at different positions and follows a different path, but moves consistently for all cycles towards the exhaust side. The movement towards the exhaust side of the tumble vortex is governed by the rotational direction of the tumble and by the piston which pushes the tumble upwards. At around 90 ^∘bTDC the tumble centre changes its direction and moves towards the spark plug (intake-side). The trend of the trajectory is well captured by the LES. For a better representation in the high scatter of the tumble trajectories, the tumble trajectories of 7 cycles are shown together in Fig. 20 and compared to the PIV measurements. The trajectories are very similar for all cycles, except for cycle 7, which follows a very different path. This shows that sudden flow field irregularities from one cycle to the next cycle appear - as an example of cyclic variations.

Fig. 18

The Γ iso-contour (-0.65 and -0.8) plots obtained by the LES (coarse) at 90 ^∘bTDC for different cycles

Fig. 19

Tumble trajectory from 180 ^∘bTDC to 20 ^∘bTDC within the tumble symmetry plane for four LES cycles compared to the averaged trajectory from the PIV measurement

Fig. 20

Tumble trajectory from 180 ^∘bTDC to 20 ^∘bTDC within the tumble symmetry plane for different cycles and compared to the averaged tumble trajectory from the PIV measurement

The tumble vortex is compressed by the upward motion of the piston, reducing its size. In Fig. 21, the volume of the ”tumble-croissant” for an iso value of Γ=-0.65 is plotted for the compression stroke. At 90 ^∘bTDC the tumble volume starts to collapse to the same value for each cycle. From here, the tumble center starts to change its direction towards the spark plug and branches towards the negative and positive z-axis as seen in Fig. 17.

Fig. 21

Volume of the tumble vortex for an iso-value of -0.65 of the Γ-field for different cycles within the compression stroke

4.6 Two-point velocity correlation

The two-point correlation functions of the velocity fluctuations along horizontal lines inside the combustion chamber are computed for the fine grid. They relate two velocity vector components to each other as a function of their distance r [38]. In total, 5 different locations were chosen within the tumble symmetry plane, for the sampling of the velocity at the (normalized) y*-coordinates shown in Fig. 13. The normalized two-point correlation function reads:

$$ R_{\alpha}(r)=\frac{\langle u_{\alpha}^{\prime}(x)u_{\alpha}^{\prime}(x+r) \rangle} {\langle u_{\alpha}^{\prime}(x)^{2} \rangle} $$

(7)

In Eq. 7, the velocity fluctuations $u^{\prime }$ are defined as the deviation of the instantaneous velocities $\widetilde {u}$ of a cycle k from the LES phase average $\langle \widetilde {u}\rangle$ over N cycles, where α denotes a velocity component in the direction α (Einstein summation is not implied).

$$ u^{\prime}=\widetilde{u} - \langle \widetilde{u}\rangle,\: \text{with} \: \:\: \langle{\widetilde{u}}\rangle = \frac{1}{N}\sum\limits_{k=1}^{N} \widetilde{u}_{k} $$

(8)

The classical two-point correlation should be applied on homogeneous, isotropic turbulence with enough statistics for a fully converged result (thousands of consecutive cycles, according to Baum et al. [2]). These requirements are almost impossible to meet in an engine or an LES. However, the correlation function can provide useful insight into the tumble break-down process, if we alter the definition such that it will include the tumble vortex and subsequent coherent structures. Therefore, we propose a modified version of the classical two-point correlation function, which also considers coherent structures and not just the turbulent fluctuations:

$$ R_{\alpha}^{\delta}(r)=\frac{ \langle u_{\alpha}^{\delta}(x)u_{\alpha}^{\delta}(x+r) \rangle } {\langle u_{\alpha}^{\delta}(x)^{2} \rangle} $$

(9)

Equation 9 shows the adjusted correlation function, which only differs in the use of a different velocity fluctuation u ^δ. This u ^δ denotes the deviation of the instantaneous resolved velocities $\widetilde {u}$ from the spatial mean $\overline {\widetilde {u} }$ along the reference line in x-direction with the length l, which is bounded by the liner walls. For the tumble plane the integration bounds are equal to the size of the bore (l=86m m). This means that the velocity fluctuations u ^δ are defined relative to a line moving with the mean velocity, resulting from compression only.

$$ u^{\delta}= \widetilde{u} - \overline{\widetilde{u} },\: \text{with} \: \:\: \overline{\widetilde{u} } = \frac{1}{l} {\int}_{-l/2}^{\: l/2} \widetilde{u} \: dx $$

(10)

A perfect correlation of 1 appears, when the velocities at a specific distance are always identical, which is obviously true for r =0. In order to illustrate the two-point correlation, a vortex is sketched in Fig. 13, where the orange velocity vectors at y* =0.5 exhibit a negative (cross) correlation (pointing in opposed directions). Thus, a change in the sign of the correlation functions, can be interpreted as the “radius” of a vortex. The cross-correlation relates the velocity components in y-direction at two points separated in x-direction to each other (red arrows at y* =0.84 in Fig. 13).

In Fig. 22, the normalized two-point correlation coefficients along the 5 horizontal lines underneath the cylinder head are plotted from 125 ^∘bTDC (IVC) to 0 ^∘bTDC for every 25 ^∘CA with the classical (R _α ) and modified version of the correlation function $(R^{\delta }_{\alpha })$. The piston position for the corresponding ^∘CA is marked with arrows underneath the cross-correlation plot and shall demonstrate the ”biggest possible vortex size” that would fit inside the combustion chamber. Figure 22 shows a very noisy pattern for the cross-correlation coefficients obtained by the classical auto-correlation function (R _α ), which is to be expected due to the combination of few samples and small turbulent length scales. The cross-correlation coefficients $R^{\delta }_{\alpha }$, however, show a smooth pattern and imply that the integral length scale is decreasing with compression. Interestingly, the classical and modified correlation functions are very similar at TDC, giving evidence that the tumble motion is completely transferred to turbulence.

Fig. 22

Two-point auto-correlation coefficients of the (turbulent) velocity fluctuations $u^{\prime }$ (classical formulation, left column) and for the velocity fluctuations u ^δ (right column), for an average of twenty cycles obtained by the LES simulation on the fine grid, along the horizontal reference lines within the tumble symmetry plane. The distance of the piston head to its location at top dead center is illustrated by arrows, representing the biggest possible vortex that could fit inside the combustion chamber

The further discussion will be based on the results of the modified correlation function $R^{\delta }_{\alpha }$. From 125 ^∘bTDC (IVC) to 100 ^∘bTDC the cross-correlation changes only one time its sign and stays negative for all 5 sampling locations, which implies the appearance of only one big vortex. If we assume that the tumble centre will be in the middle of the plane (y* =0.5), it will have a diameter of around 60 mm at 125 ^∘bTDC. At 75 ^∘bTDC the cross-correlation curves start changing its sign, which indicates the appearance of new vortices. In fact, 3 vortices can be suspected at y* =0.5 at 75 ^∘bTDC with a vortex diameter of around 20 mm each. By approaching the end of the compression stroke, the diameter of the vortices are in the order of the piston-to-cylinder head distance and the cross-correlation curves get a ”wiggling” pattern. At 50 ^∘bTDC the first minima of the cross-correlation curve is roughly at the same position as the corresponding piston-to-cylinder head distance (orange arrow). From here, the tumble occupies the entire combustion chamber, and will have contact to liner walls, piston-top and cylinder head. In Fig. 17, it is clearly seen that the tumble is already at 90 ^∘bTDC constricted by the geometry. Now, the piston will effectively compress the tumble and the large scale motion will break-down into a highly irregular flow field with multiple vortices - the break-down of the tumble into smaller scales. The highly turbulent flow field with many small vortices is shown for the cross-correlation curves for 0 ^∘bTDC.

From the normalized two-point correlation coefficients $R^{\delta }_{\alpha }$, the integral length scale L _δ was calculated for the 5 horizontal sampling positions during compression, according to Eq. 11, with q as the distance where the autocorrelation function firstly intersects with the zero line.

$$\begin{array}{@{}rcl@{}} L_{\delta} = {{\int}_{0}^{q}} R^{\delta}_{\alpha}(r) \: dr \end{array} $$

(11)

Figure 23 shows the lateral integral length scales obtained from the cross-correlation function $R^{\delta }_{\alpha }$ for 7 instantaneous cycles. It has to be mentioned, that this length scales should not be confused with the integral length scales of the turbulent fluctuations, rather be seen as a characteristic length scale of big coherent structures. The length scales are scattering for the different cycles, showing the biggest deviations to each other at 50 ^∘bTDC (tumble vortex touches the walls) and the lowest scatter at TDC. The lower scatter of the length scales at TDC can be explained by the length scales itself, where smaller vortices tend to behave more equally than big vortices. Overall, however, the lateral length scales are continuously decreasing, reaching values of 15 mm at intake valve closure to 0.8 mm at TDC.

Fig. 23

Lateral length scales calculated from the auto-correlation coefficient curves $R^{\delta }_{\alpha }$, provided by the LES on the fine grid along horizontal lines within the tumble symmetry plane for 7 instantaneous cycles and the average of twenty cycles

5 Conclusions

Large-eddy simulations of an optical research engine were performed for motored operation with two different grid spacings of 1 mm (coarse) and 0.5 mm (fine) inside the combustion chamber. The in-cylinder pressure distribution for the full cycle was examined, showing a good agreement for the LES on both grids during the gas exchange, in particular at the opening and closing events, compared to the experiment. However, an overprediction of the peak in-cylinder pressure was obtained by 17 %. A theoretical study of the compression and a comparison to an independent LES simulation of the same engine provided considerable evidence for the correctness of our simulation.

A criterion for an estimate of the needed number of cycles has been proposed and tested on our simulation data sets of 20 cycles.

The predicted velocity agreed qualitatively and quantitatively well with the PIV data and in the upper part of the cylinder volume also with the MRV data, even though MRV was conducted under stationary conditions and with water as a fluid. To the best of the authors’ knowledge, this is the first comparison of PIV and LES velocity fields to MRV data in the valve seat region. The mass flow around the valve curtain area was in good agreement. Recirculation zones within the valve seat region reduce the in-cylinder filling. Around 72 % of the total mass flow comes via the overflow region into the cylinder. However, looking on instantaneous contour plots around the valve seats, the highest velocities are observed in small spots in the underflow area. The standard Smagorinsky (C _s =0.062) model worked well, considering the complexity of the engine flow. The direct comparison with the Sigma model and the simulation by Baumann et al. [3] revealed sensitivities of the turbulence models and model constants during the compression phase, which were not seen during the intake stroke. A good match between the MRV, PIV measurements and the LES simulation was achieved.

The tumble shape and its motion was calculated by a 2D vortex identification algorithm on 2D slices throughout the entire combustion chamber. During the compression it takes a ”croissant-like” shape that branches towards the positive and negative z-axis until it collapses and disappears. Its shape and trajectory is different form cycle to cycle during the compression. The tumble is moving towards the exhaust side and changes its direction at around 90 ^∘bTDC. From the shift in direction, the tumble volume drops as the vortex cannot move freely and is guided by the upwards moving piston.

With the help of the modified definition of the velocity fluctuations for the two-point auto-correlation, it was possible to better observe the tumble break-down. The cross-correlations of the velocity fluctuations along horizontal lines within the tumble symmetry plane showed the reduction of the tumble size, while approaching the end of the compression phase. The tumble has the biggest diameter at the start of the compression (125 ^∘bTDC) of around 60 mm with a piston-to-cylinder head distance of 75 mm. The cross-correlation curves show that once the tumble has been ”squeezed” sufficiently, the big vortex is split into several smaller vortices, which can be already seen as the onset of tumble break-down - when one big tumble vortex breaks down into several smaller vortices. In this picture of tumble break-down, the tumble would have a natural tendency to stay ”circular” rather than ”ellipsoid”, leading to a break-down of the one major vortex into several sub-vortices. A big advantage of this method is that first quantifications of the tumble break-down process can be already obtained with a low number of samples (cycles).