1 Introduction

Electric load forecasting, a time series forecasting task, plays an essential role in social, economic, and various other aspects of the energy sector [1]. In particular, electric load forecasting can be categorized into three types according to the forecasting horizon, namely, short-term, medium-term, and long-term load forecasting [2,3,4,5]. Short-term load prediction (STLF) is one of the most important aspects of deregulated grid planning and operation. Accurate load forecasting can be helpful for efficient energy management [6]. However, the prediction accuracy of STLF is influenced by many factors [7, 8], such as insufficient historical data, economic environment, development status, unstable meteorological environment, seasonal changes, and the development of the power grid. Therefore, the electrical charge has large fluctuation and uncertainty characteristics, which means accurate prediction is still a challenge.

In the past few years, many models have been developed for STLF, which can be divided into mathematical-statistical models and machine learning models [9]. Mathematical- statistical models include autoregressive integrated moving average models [10, 11], regression methods [12], and linear regression models [13]. These methods can provide high predictive accuracy for linear systems. However, the predictive accuracy of nonlinear forecasting tasks is limited [14]. Therefore, these methods are not suitable for highly complex and nonlinear electricity load prediction.

The other approach is machine learning models such as artificial neural networks (ANNs) [15], support vector regression (SVR) [16], deep neural networks (DBNs) [17], broad learning systems (BLSs) [18], and long short-term memory (LSTM) [19]. They have been applied to various fields such as economic [20] and construction [21]. The machine learning model can directly learn the relationship between input and output. Therefore, such models have better learning ability for complex and nonlinear electric data compared with mathematical-statistical models. For example, SVR is proposed based on the structural risk minimization criterion, which can provide promising prediction accuracy without much computational cost. DBN is a deep learning network structure composed of multiple restricted Boltzmann machines so that it provides powerful nonlinear data processing capabilities. As a new single-layer incremental neural network, BLS is proposed by using enhancement nodes and feature nodes, which greatly reduce the cost of prediction and confer strong competitiveness [22]. LSTM is established by introducing a forgetting mechanism with different units to extract useful features in time series data, supplying more reliable and accurate prediction performance in STLF. Therefore, the LSTM method can also obtain outstanding performance [23, 24].

Although these machine learning models have been used in load forecasting and achieve satisfactory prediction accuracy, they also have certain shortcomings, such as excessive training time and overfitting [25, 26]. Furthermore, smart power grid development involving many influencing factors and new energies, leading to increasing uncertainty and volatility of the electrical charge. Therefore, a traditional single model cannot achieve promising prediction results.

To improve the prediction accuracy of a single model, ensemble hybrid models are proposed by combining several neural networks to optimize single models. In [27], deep neural network (DNN) and LSTM were rationally combined to perform the forecasting operation. In [28], researchers presented a network based on deep residual networks with a convolution structure to carry out STLF. He [29] et al. proposed a model based on least absolute shrinkage and a selection operator-quantile regression neural network for probability density forecasting. In [30], researchers proposed a wind power probability density forecasting method based on cubic spline interpolation and support vector quantile regression. In [31], researchers proposed a new forecasting method based on multi-order fuzzy time series, technical analysis, and a genetic algorithm.

On the other hand, the “divide and conquer” method has been combined in some hybrid models for predictive tasks. These hybrid models often introduce decomposition-based methods to decompose the predictive series into multiple components and then feed the components into the neural network to obtain the prediction results. The decomposition methods mainly include wavelet transform (WT) [32], Fourier transform (FT) [32, 33], empirical mode decomposition (EMD) [34], singular spectrum analysis (SSA) [35,36,37], variational mode decomposition (VMD) [36,37,38,39], and empirical wavelet transform (EWT) [40]. For example, in [41], researchers rationally combined ANN and WT technology to improve the forecasting ability. Based on EMD and DBN, the EMD-DBN hybrid network for STLF was proposed in [42]. In [43], researchers proposed a hybrid incremental learning approach composed of discrete wavelet transform (DWT), EMD, and RVFL, which obtains promising results in STLF. By combining EWT, LSTM, and regularized extreme learning machine, Li [44] proposed a hybrid model for wind speed forecasting. In [45], the author proposed a novel ensemble method based on ensemble empirical mode decomposition, least absolute shrinkage, and a selection operator–quantile regression neural network for forecasting wind power. In [46], researchers proposed a novel decomposition-ensemble learning approach based on the complete ensemble empirical mode decomposition and stacking-ensemble learning based on machine learning algorithms to forecast wind energy. In [47], researchers combine bi-directional LSTM with WT, EMD, ensemble EMD, and EWT respectively to predict wind speed.

Although this type of hybrid model can achieve better prediction results, it also has the following shortcomings:

  1. 1)

    FT method is suitable for the exactly or approximately periodic time-dependent phenomena but performs poorly when series are non-stationary [48]. On the other hand, VMD is suitable for narrowband signals but performs poorly for wide-band non-stationary signals [37]. However, power load data series have non-stationary signal or wide-band signal characteristics. Therefore, FT and VMD have limited application in STLF tasks. SSA is a non-parametric technique based on the principles of multivariate, and few parameters are required to model the series under analysis. However, there are no general rules for the selection of parameters in SSA [48]. The decomposition accuracy of WT is linked with the parameters of the filter base function; however, improper parameter selection may degenerate the decomposition accuracy of WT [48]. Furthermore, EMD easily produces mode aliasing, resulting in the attenuation of accuracy [48]. Although the EWT method can provide high decomposition accuracy, it easily produces redundant components, resulting in a large computational cost.

  2. 2)

    For the regression task, the existing hybrid machine learning methods [27, 28] rarely consider the compromise between prediction accuracy and computation cost. Actually, it is a very challenging problem to design a hybrid machine learning method that can not only provide high prediction accuracy but also has a reasonable computational cost.

  3. 3)

    Most existing models rarely consider how to use the prediction residual to establish a residual neural network model [42,43,44,45,46,47,48]. In fact, the prediction residual includes the effective prediction information. By mining the prediction residual information, the prediction accuracy of the model can be effectively improved.

To solve the abovementioned problems, a novel decomposition-based ensemble model is proposed for the STLF task in this paper. The decomposition method can decompose the raw power load data into multiple components, effectively smoothing nonlinear and non-stationary power load sequence signals to obtain competitive predictive performance. Therefore, an optimized empirical wavelet transform (OEWT) method is developed by rationally combining the approximate entropy (APEN) method [49] with the EWT method to improve the decomposition accuracy and eliminate redundant components. The EWT is first introduced to smooth the original power load data, which can solve the problem of parameter selection in the WT method and mode aliasing in the EMD. Then, APEN is used to determine similar components obtained by EWT and perform merging, which can reduce redundant decomposition information. LSTM can extract more useful features in time series data and supply more reliable and accurate prediction performance. Furthermore, the BLS is a new method that uses less computational cost to obtain better prediction performance. Therefore, a new hybrid machine learning method [named master learner (ML)] is proposed by rationally combining the LSTM with BLS in series, which can not only provide high prediction accuracy but also has a reasonable computational cost. In the master learner, a residual learning model [named residual learner (RL)] is developed to extract the effective predictive information from residual results. To further enhance the robustness of the proposed model, another BLS [named auxiliary learner (AL)] is adopted to connect the input and output of the proposed hybrid model. Specifically, the prediction result of ML will be fed into the input layer of AL, which means that the ML will expand the training data. Therefore, by rationally combining ML and AL, the proposed hybrid model can obtain outstanding prediction results.

In summary, the main contributions of our work are as follows:

  1. 1)

    The OEWT method is proposed by rationally combining the EWT with APEN to improve the decomposition accuracy and eliminate redundant components.

  2. 2)

    A new hybrid machine learning method (named master learner) is proposed by rationally combining the LSTM with BLS in series, which can effectively provide the prediction without significantly increasing the computational cost.

  3. 3)

    The residual learning model (named residual learner) is developed to extract the effective predictive information from residual results, which can further improve predictive accuracy.

  4. 4)

    An auxiliary learner is established based on the master learner, which can rationally connect the input layer and output layer of our prediction block to enhance the robustness and prediction accuracy of the model.

  5. 5)

    A novel decomposition-based ensemble model was first proposed for the STLF task by rationally combining the OEWT method, master learner, residual learner, and auxiliary learner, which can provide high predictive accuracy and satisfactory robustness in STLF.

The rest of the paper is described according to the following structure. In Section 2, the framework and related theories of the proposed model are introduced. Section 3 is data analysis and parameter settings. Section 4 is the case study with discussions. Finally, a conclusion is given in Section 5.

2 The forecasting framework

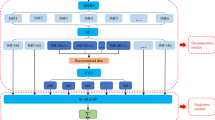
The framework of the proposed model is divided into two parts: the decomposition block and the forecast block. Figure 1 shows the framework of the proposed model. First, the power load data are decomposed into multiple subseries data points by OEWT. Second, each subseries data point is trained and predicted by the forecast block. Specifically, the forecast block is divided into ML and AL. In the ML, the preliminary prediction results are obtained by using the LSTM. Then, the prediction residuals caused by the LSTM are sent to the RL for learning. Here, the RL is the BLS. The preliminary prediction results of the LSTM and the residual learning results of the RL are superimposed as the prediction result of the ML. In the AL, the prediction results of the ML are recombined with the subseries data as the input of the AL to obtain the final predicted result of each subseries data. Finally, by combining the prediction results of each subseries data set, the final prediction result of the original data can be obtained.

Fig. 1
figure 1

The proposed short-term load forecasting framework consists of the decomposition block and forecast block

Full size image

2.1 Decomposition Block

Due to the high uncertainty and volatility of the power load data, the EWT divides the power load data into multiple components to smooth the power load data. The most significant advantage of this method is that it can decompose signals adaptively, and its fundamental idea is to obtain the intrinsic mode of the signal by devising a proper wavelet filter bank. However, although the EWT method can provide high decomposition accuracy, it easily produces redundant components, resulting in a large computational cost. To guarantee decomposition accuracy and eliminate redundant components to reduce the computational cost, OEWT is proposed by rationally combining the APEN and the EWT method. Here, APEN is a nonlinear dynamic parameter that is used to quantify the regularity and volatility of time series fluctuations, which can effectively reduce the redundant components of EWT. Specifically, the decomposition steps of the OEWT are as follows:

  • Step 1: Adaptive spectrum division. First, the Fourier spectrum of the time series \(g\left(t\right)\) is normalized to \(\left[0,\pi \right]\). Second, the sequence \({\left\{{M}_{i}\right\}}_{k=1}^{M}\), which is composed of the maximum value \(M\) of the Fourier spectrum and regularized to \(\left[{0,1}\right]\), is recorded and rearranged according to the magnitude \({M}_{1}\geq {M}_{2}\geq \cdots \geq {M}_{M}\). Then, to decide the number of components \(N\), the threshold value \({M}_{M}+\kappa \left({M}_{1}-{M}_{M}\right)\) is set, where\(\kappa \in \left({0,1}\right)\) is the relative amplitude ratio. \(N\) is set to the number of maxima greater than the threshold in \({\left\{{M}_{i}\right\}}_{k=1}^{M}\). Finally,\({\omega }_{n}\) is set to be the midpoint of the corresponding frequencies of the two adjacent maximum values above the threshold, where \(n={1,2},\cdots ,N-1\), \({\omega }_{0}=0\), and \({\omega }_{N}=\pi\). With each \({\omega }_{n}\) as the centre, a transition phase \(2\tau_n\) is defined, where \(\tau_n=\chi\omega_n, 0<\chi<1\).

    $${\hat{T}}_{n}\left(\omega \right)=\left\{\begin{array}{c}1 , if\left|\omega \right|\leq (1-\nu ){\omega }_{n}\\ {cos}\left[\frac{\pi }{2}\beta \left(\frac{1}{2\nu {\omega }_{n}}\left(\left|\omega \right|-\left(1-\nu \right){\omega }_{n}\right)\right)\right],\\ if\left(1-\nu \right){\omega }_{n}\leq \left|\omega \right|\leq \left(1+\nu \right){\omega }_{n}\\ 0 , otherwise\end{array}\right.$$
    (1)
    $${\hat{P}}_{n}\left(\omega \right)=\left\{\begin{array}{c}1 , if\left(1+\nu \right){\omega }_{n}\leq \left|\omega \right|\leq \left(1-\nu \right){\omega }_{n+1}\\ {cos}\left[\frac{\pi }{2}\beta \left(\frac{1}{2\nu {\omega }_{n+1}}\left(\left|\omega \right|-\left(1-\nu \right){\omega }_{n+1}\right)\right)\right],\\ if\left(1-\nu \right){\omega }_{n+1}\leq \left|\omega \right|\leq \left(1+\nu \right){\omega }_{n+1}\\ {sin}\left[\frac{\pi }{2}\beta \left(\frac{1}{2\nu {\omega }_{n}}\left(\left|\omega \right|-\left(1-\nu \right){\omega }_{n}\right)\right)\right],\\ if\left(1-\nu \right){\omega }_{n}\leq \left|\omega \right|\leq \left(1+\nu \right){\omega }_{n}\\ 0 , otherwise\end{array}\right.$$
    (2)
    $$\beta \left(x\right)=\left\{\begin{array}{c}0 , ifx<0\\ and \beta \left(x\right)+\beta \left(1-x\right)=1\forall x\in \left[{0,1}\right]\\ 1 , ifx\geq 1\end{array}\right.$$
    (3)
    $$\beta \left(x\right)={x}^{4}\left(35-84x+70{x}^{2}-20{x}^{3}\right)$$
    (4)

  • Step 2: Construct the wavelet function and scaling function. By using the construction methods of the Littlewood-Paley and Meyer wavelets, the scaling function \({\hat{T}}_{n}\left(\omega \right)\) and the wavelet function \({\hat{P}}_{n}\left(\omega \right)\) are constructed, which are denoted as formula (1) and formula (2), respectively. In these formulas, \(\nu <{min}_{n}\left\{\left({\omega }_{n+1}-{\omega }_{n}\right)/\left({\omega }_{n+1}+{\omega }_{n}\right)\right\}\), the function \(\beta \left.(x\right)\) is an arbitrary function that satisfies \({C}^{k}\left(\left[{0,1}\right]\right)\), as shown in formula (3). Many functions satisfy this property, and the most commonly used function is (4) [50].

  • Step 3: Empirical wavelet transform. The detailed coefficient \({K}_{g}^{\epsilon }\left(n,t\right)\) and the approximate coefficient \({K}_{g}^{\epsilon }\left(0,t\right)\) can be obtained by the inner product of \(g\left(t\right)\) with \({\hat{T}}_{n}\left(\omega \right)\) and, \({\hat{P}}_{n}\left(\omega \right)\), respectively. The calculation process is shown in formulas (5) and (6), respectively.

    $$\begin{aligned}{K}_{g}^{\epsilon }\left(n,t\right)={\langle}g,{{\mathrm{P}}}_{n}{\rangle}=\int g\left(\tau \right)\bar{{{\mathrm{P}}}_{n}\left(\tau -t\right)}d\tau \\={F}^{-1}\left(G\left(\omega \right)\bar{{\hat{P}}_{n}\left(\omega \right)}\right)\end{aligned}$$
    (5)
    $$\begin{aligned}K_g^\epsilon\left(0,t\right)=\langle g,T_1\rangle=\int g\left(\tau\right)\bar{T_1\left(\tau-t\right)}d\tau\\=F^{-1}\left(G\left(\omega\right)\left(\omega\right)\bar{{\hat T}_1\left(\omega\right)}\right)\end{aligned}$$
    (6)

where \({\bar{P}}_{n}\) and \({\bar{T}}_{1}\) represent the complex conjugates of \({P}_{n}\) and \({T}_{1}\), respectively. \(G\left(\omega \right)\) represents the Fourier transform of \(g\left(t\right)\). \({F}^{-1}(\bullet )\)represents the inverse Fourier transform. By convolution operations of \({K}_{g}^{\epsilon }\left(0,t\right)\) and \({{\mathrm{T}}}_{1}\left(t\right)\), \({K}_{g}^{\epsilon }\left(n,t\right)\) and \({{\mathrm{P}}}_{n}\left(t\right)\), respectively, the components \({e}_{0}\left(t\right)\) and \({e}_{n}\left(t\right)\) can be obtained. As shown in formulas (7) and (8).

$${e}_{0}\left(t\right)={K}_{g}^{\epsilon }\left(0,t\right)*{{\mathrm{T}}}_{1}\left(t\right)$$
(7)
$${e}_{n}\left(t\right)={K}_{g}^{\epsilon }\left(n,t\right)*{{\mathrm{P}}}_{n}\left(t\right)$$
(8)

  • Step 4: Eliminate redundant components by APEN. First, the algorithm-related parameters \(m\) and \(r\) are defined, where\(m\) is an integer and represents the length of the comparison vector, and \(r\) is a real number, which represents a measure of similarity. Usually, choose the parameter \(m=2\) or \(m=3\), \(r=0.2\times std\) (\(std\) is the standard deviation of the time series). Then, reconstruct the m-dimensional vector \({E}_{n}\left(1\right),{E}_{n}\left(2\right),\cdots ,{E}_{n}\left(T-m+1\right)\) as shown in formula (9).

    $${E}_{n}\left(M\right)=\left[{e}_{n}\left(M\right),{e}_{n}\left(M+1\right),\cdots ,{e}_{n}\left(M+m+1\right)\right],$$
    $$M={1,2},\cdots ,T-m+1$$
    (9)

For \(1\leq M\leq T-m+1\), count the number of vectors that meet the conditions \({C}_{M}^{m}\left(r\right)=(number of {E}_{n}\left(j\right) such that d\left[{E}_{n}\left(M\right),{E}_{n}\left(j\right)\right]\leq r)/(T-m+1)\), where \(d\left[{E}_{n},{E}_{n}^{*}\right]\) is defined as \(d\left[{E}_{n},{E}_{n}^{*}\right]=\underset{M}{max}\left|{e}_{n}\left(a\right)-{e}_{n}^{*}\left(a\right)\right|\). \({e}_{n}\left(a\right)\) is the element of the vector \({E}_{n}\left(M\right)\). \(d\) represents the distance between vectors \({E}_{n}\left(M\right)\) and \({E}_{n}\left(j\right)\), which is determined by the maximum difference of the corresponding elements. The value range of \(j\) is \(\left[1,T-m+1\right]\), including \(M=j\). By defining \({\psi }^{m}\left(r\right)\) as formula (10), APEN is expressed as \(APEN={\psi }^{m}\left(r\right)-{\psi }^{m+1}\left(r\right)\). Finally, APEN values of all components are calculated. Based on the APEN of each component, an interval ρ is defined to reorganize the components that are in the same interval into a new subseries as the output of the OEWT.

$${\psi }^{m}\left(r\right)={\left(T-m+1\right)}^{-1}{\sum }_{M=1}^{T-m+1}{log}\left({C}_{M}^{m}\left(r\right)\right)$$
(10)

2.2 Forecast block

The forecast block consists of two parts: the ML and the AL. The ML can provide a compromise between prediction accuracy and computation cost. The AL can improve the prediction accuracy and robustness of the model. The specific description of the ML and AL is given as follows:

  1. 1)

    Master Learner

The existing hybrid machine learning methods rarely consider the balance between prediction accuracy and computation cost. In addition, the prediction residual includes the effective prediction information. To balance the prediction accuracy and computational cost, and mine the prediction residual information, the ML is designed by mixing the LSTM and BLS, and the mixed model is named BLSTM. In this model, LSTM is used for a preliminary prediction. Then, the prediction residuals caused by the LSTM are sent to the RL for learning. Here, the RL is the BLS. Finally, the preliminary prediction results of the LSTM and the residual learning results of the RL are superimposed as the prediction result of the ML. Specifically, the design process is given as follows:

First, LSTM is used to make a preliminary prediction. Let \(\{{x}_{1},{x}_{2},\cdots,{x}_{T}\}\) denote a typical input sequence for an LSTM, where \({x}_{t}\in {R}^{k}\) represents a k-dimensional vector of real values at the \(t\) time step. To establish temporal connections, the LSTM defines and maintains an internal memory cell state throughout the whole life cycle, which is the most important element of the LSTM structure. The memory cell state \({s}_{t-1}\) interacts with the intermediate output \({h}_{t-1}\) and the subsequent input \({x}_{t}\) to determine which elements of the internal state vector should be updated, maintained, or erased based on the outputs of the previous time step and the inputs of the present time step. In addition to the internal state, the LSTM structure also defines input node \({g}_{t}\), input gate \({i}_{t}\), forget gate \({f}_{t}\), and output gate \({o}_{t}\). The formulations of all nodes in an LSTM structure are given by formulas (11) to (16).

$${f}_{t}=\sigma ({W}_{fx}{x}_{t}+{W}_{fh}{h}_{t-1}+{b}_{f})$$
(11)
$${i}_{t}=\sigma ({W}_{ix}{x}_{t}+{W}_{ih}{h}_{t-1}+{b}_{i})$$
(12)
$${g}_{t}=\phi \left({W}_{gx}{x}_{t}+{W}_{gh}{h}_{t-1}+{b}_{g}\right)$$
(13)
$${o}_{t}=\sigma ({W}_{ox}{x}_{t}+{W}_{oh}{h}_{t-1}+{b}_{o})$$
(14)
$${s}_{t}={g}_{t} {i}_{t}+{s}_{t-1}{f}_{t}$$
(15)
$${h}_{t}=\phi \left({s}_{t}\right){o}_{t}$$
(16)

where \({W}_{gx}\), \({W}_{gh}\), \({W}_{ix}\),\({W}_{ih}\), \({W}_{fx}\), \({W}_{fh}\), \({W}_{ox}\), and \({W}_{oh}\)are weight matrices for the corresponding inputs of the network activation functions; \(\sigma\) represents the sigmoid activation function, while φ represents the tanh function.

Then, the prediction residuals caused by LSTM are learned by the RL. Here, BLS can use less computational cost to obtain better prediction performance. Therefore, BLS was selected as the RL. More details about BLS will be given in the AL.

Finally, by superimposing the prediction result of LSTM and the prediction result of RL, the final prediction result of ML can be obtained.

  1. 2)

    Auxiliary Learner

By using the prediction results of ML to expand the training data, the prediction accuracy and robustness of the model can be improved. To achieve this goal, the AL is introduced.

In the AL, the output of the ML and the original subseries data is reorganized as the input of the AL, which can be considered feedback. Therefore, through the proposed feedback, the connection between the ML and the AL is realized. Another BLS is chosen as the machine learning model in the AL. The structure of BLS is shown in Fig. 2. Specifically, the theory of BLS can be concluded as follows:

Fig. 2
figure 2

The framework of the broad learning system

Full size image

Let the input data \(X\) form \(n\) feature nodes \({J}_{i}\) through feature mapping, as shown in formula (17). All feature nodes are combined and defined as \({J}^{n}=\left[{J}_{1},{J}_{2},\cdots {J}_{n}\right]\). Then, \(m\) enhancement nodes \({E}_{k}\) are acquired by enhancing and transforming with \({J}^{n}\), as shown in formula (18). In formulas (17) and (18), \(\eta (\bullet )\) is a linear transformation by default, and \(\xi (\bullet )\) is a nonlinear activation function. Generally, the hyperbolic tangent function in formula (19) can be selected as the activation function. \({W}_{{e}_{i}}\), \({W}_{{h}_{k}}\), \({\delta }_{{e}_{i}}\), and \({\delta }_{{h}_{k}}\) are randomly generated weight matrices and bias matrices, which are fine-tuned by a sparse encoder [18]. All enhancement nodes are combined and defined as \({E}^{m}=\left[{E}_{1}, {E}_{2},\cdots, {E}_{m}\right]\). The symbol \(B\) is introduced for the convenience of representation, expressed as \(B=\left[{J}^{n}|{E}^{m}\right]\).

$${J}_{i}=\eta \left(\mathrm{X}{\mathrm{W}}_{{e}_{i}}+{\delta }_{{e}_{i}}\right),i={1,2},\cdots ,n$$
(17)
$${E}_{k}=\xi \left({J}^{n}{W}_{{h}_{k}}+{\delta }_{{h}_{k}}\right),k={1,2},\cdots ,m$$
(18)
$$\xi \left(x\right)={tan}hx$$
(19)

From Fig. 2, the final prediction value of BLS \(\hat{Y}\) can be expressed as \(\hat{Y}=BW\). Here, \(W\) represents the weight matrix between the feature nodes, enhancement nodes, and output Y. Since \({W}_{{e}_{i}}\), \({\delta }_{{e}_{i}}\), \({W}_{{h}_{k}}\), and \({\delta }_{{h}_{k}}\) are randomly generated and fine-tuned by the sparse encoder, they remain unchanged. Moreover, the actual value \(Y\) is known when training. So

$$W={B}^{+}Y$$
(20)

, where \({B}^{+}\) is the pseudo-inverse of \(B\). Ridge regression is used to find a suitable \(W\) to transform the above problem into

$${arg\;}\underset{W}{min}\;\left({\parallel\hat Y-Y\parallel}_2^2+\lambda{\parallel W\parallel}_2^2\right).$$
(21)

Here, \(\lambda\) is the regularization parameter; when \(\lambda \to 0\), the solution is

$$W=\left(\lambda I+BB^T\right)^{-1}B^TY.$$
(22)

Where \(I\) is the identity matrix. Specifically, we have that

$$B^+=\underset{\lambda\rightarrow 0}{lim}\left(\left(\lambda I+BB^T\right)^{-1}B^T\right).$$
(23)

Since the subseries data are decomposed from the original power load data through the decomposition block, the final prediction result of the model can be obtained by superimposing the prediction results of all subseries data.

3 Data analysis and parameter settings

3.1 Data sets

The data set, which is used as the experimental sample in this paper, is the historical load data of New South Wales (NSW), Australia, in 2009. The sampling interval of the data set is 30 min, so 48 load data samples are contained in one day. Figure 3 shows the data of 1,000 sampling points. From the figure, we can find that the load data fluctuate greatly at the peak. Table 1 shows the statistical data of this data set, including the maximum, minimum, average, and standard deviation. To avoid the negative impact of singular sample data on the prediction accuracy, the load data are normalized and restricted to the range of [0,1] before the experiment. The normalization formula is shown in (24).

$${\tilde{y}}_{i}=\frac{{y}_{max}-{y}_{i}}{{y}_{max}-{y}_{min}}$$
(24)

Here, \({\tilde{y}}_{i}\)is the normalized result, \({y}_{i}\) is the load data at a certain moment, and \({y}_{max}\) and \({y}_{min}\) are the maximum and minimum values in the load data, respectively.

Table 1 The statistical data of the historical load data of NSW
Full size table
Fig. 3
figure 3

Load data of New South Wales, Australia in 2009

Full size image

3.2 Performance estimation

The accuracy of the prediction result needs to be evaluated by the evaluation function. This paper uses common evaluation methods in load forecasting to assess the prediction performance, including the root mean square error (RMSE) and the mean absolute error (MAE). They are defined in formulas (25) and (26).

$$RMSE=\sqrt{\frac{1}{n}{{\sum }_{i=1}^{n}\left({\hat{y}}_{i}-{y}_{i}\right)}^{2}}$$
(25)
$$MAE=\frac{1}{n}\sum _{i=1}^{n}\left|{\hat{y}}_{i}-{y}_{i}\right|$$
(26)

where \({\hat{y}}_{i}\) is the predicted data, \({y}_{i}\) is the real data, and \(n\) is the total number of test samples. For both evaluation indicators, the smaller the value is, the higher the accuracy of the prediction.

3.3 Parameter settings

The parameter settings are significant for the prediction accuracy of the model. Before the formal experiment, some pre-experiments are conducted to filter out the best parameters. In the forecast block, the number of hidden nodes and the learning rate of LSTM have a more significant impact on the prediction performance. Furthermore, the number of feature nodes and enhancement nodes of BLS are essential parameters that affect its prediction accuracy. To find the optimal parameters in LSTM and BLS, the controlled variable method is adopted. According to experience, we conducted pre-experiments on different hidden nodes (\([100, 300]\) with an interval of 10) and learning rate \(\left(\right[0.001, 0.01]\) with a gap of 0.001) of LSTM. Moreover, pre-experiments with different feature nodes and enhancement nodes (both in \([1, 30]\) with one as the interval) of BLS are conducted. Meanwhile, RMSE is selected as the evaluation index. The pre-experimental results are shown in Fig. 4.

Fig. 4
figure 4

RMSE performance of the LSTM and BLS pre-experiment

Full size image

From Fig. 4(a), the results show that when the learning rate of LSTM varies from 0.006 to 0.01, its prediction performance is unstable. In this interval, the hidden nodes dominate in prediction performance. However, when the learning rate varies from 0.005 to 0.001, the prediction performance remains relatively stable, and the hidden nodes also have little effect on prediction performance. Meanwhile, from Fig. 4(b), the results show that the number of enhancement nodes in BLS will not significantly impact its prediction performance. For the feature nodes, when the number of feature nodes is within 10, the RMSE of the prediction results shows a rising trend and then falls. However, when the number of feature nodes increases to 10, the performance of the model does not change much while the number of feature nodes increasing.

There is a specific connection between the load value at a certain moment and the load value before that moment. How long this correlation performance lasts is a question worthy of discussion. Therefore, we conducted a pre-experiment on the parameter of input data dimension in [1, 48] (0.5 to 24 h), and the experimental results are shown in Fig. 5. The pre-experiment result shows that when the input data dimension increases from 1 to 15 (0.5 to 7.5 h), the prediction performance of the model gradually improves. However, when the input data dimension is greater than 15 (after 7.5 h), the prediction performance of the model does not significantly improve with the increase of the input data dimension. Therefore, we can conclude that the load value at a certain moment has a strong correlation with the load value within 7.5 h before that moment.

Fig. 5
figure 5

RMSE performance of the input data dimensions pre-experiment

Full size image

Based on the pre-experiment results, we set the number of hidden nodes and learning rate of LSTM to 200 and 0.005, respectively, and the number of feature nodes and enhancement nodes of BLS to 24 and 15, respectively. The dimension of the input data of the forecast block is set to 48 (24 h). In the OEWT, the parameter of comparison vector length m is set to 2, the similarity measure \(r\) is set to \(0.2\times std\), and the interval ρ is set to 0.1.

To confirm the performance of the proposed model, other methods were compared with our model. Moreover, a series of experiments were also performed to determine the optimal parameters of these methods. Each model in different parameter values was run 20 times, and the average RMSE was used as the evaluation index. Due to space limitations, more specific experimental results have been provided in the Supplementary File. As a result, the optimal parameters of each model are selected and shown in Table 2.

Table 2 The parameter settings of the comparison method
Full size table

3.4 Method for model assessment

To verify the stability of our method and avoid overfitting, K-fold cross-validation is used to test the model. The data set is divided into the training set, validation set, and test set. The training set is used to train forecasting models, the validation set is used to select the best performing models, and the testing set for result evaluation.

Furthermore, to compare the differences between our model and other models, statistical analysis is introduced. A multicomparison statistical procedure is first applied to test the null hypothesis that all learning algorithms obtained the same results on average. Specifically, we used the Friedman test [51, 52]. If the Friedman test rejected the null hypothesis, post hoc tests were applied. Here, the post hoc test is the Nemenyi test. If the corresponding average rank of two models differs by at least a critical distance CD, then we speculate that there are obvious differences between the two methods. The calculation of CD is shown in formula (27), where \({n}_{l}\) is the number of learning algorithms, \({n}_{ds}\) is the number of data sets, and \({q}_{\alpha }\) is the critical value based on the Studentized Range statistic [53].

$$CD={q}_{\alpha }\sqrt{\frac{{n}_{l}({n}_{l}+1)}{6{n}_{ds}}}$$
(27)

4 Case study

According to the parameters set in Section 3, we divide the 2009 data set into four parts according to the seasons, namely, spring, summer, autumn, and winter. Therefore, the influence of seasons can be eliminated. Note that each seasonal data set includes 3 months. The data of the previous two months are used as the training set and validation set. Specifically, K-fold cross-validation is used to divide the training set and the validation set. The data of the following month are used as the test set for formal experiments. In addition, because power plants often need to allocate power loads in advance, a multi-step forecasting experiment 6 h ahead is performed to test the performance of the model in multistep prediction. Figure 6 shows the difference between single-step prediction and multi-step prediction. Specifically, the data from 1 to 48 is used to predict the data of 49 in single-step prediction; the data from 1 to 48 is used to predict the data from 49 to 60 in multi-step prediction.

Fig. 6
figure 6

The difference between single-step prediction and multi-step prediction

Full size image

To verify the effectiveness of our model, it is compared with the state-of-the-art machine learning methods and hybrid models, including the ANN, RBFNN, DBN, RVFL, EMD-DBN, SWT-LSTM, DWT-EMD-RVFL, and EMD-BLS. Each compared method was trained and tested on a personal computer 64-bit operating system, 8.00 GB, RAM, Intel(R) Core (TM) i5-7300HQ, CPU@2.50. The forecasting results of each model are shown in Table 3, where the first and second-best predictive results from the compared methods are emphasized in bold text and italic, respectively.

Table 3 Forecast errors of each model in single-step and multi-step prediction
Full size table

4.1 Single-step prediction

In the single-step prediction experiment, the prediction duration is 0.5 h. Interestingly, via the two evaluation criteria, we can observe that our proposed model is predominant over the others in each season, as shown in Table 3. Furthermore, EMD-BLS obtains the second-best predictive accuracy in each season, but the prediction performance of EMD-BLS is still much worse than that of our model.

4.2 Multi-step prediction

To explore the performance of our model on multi-step prediction, we conducted experiments 6 h ahead of the forecast. It can be seen from Table 3 that as the forecast length increases, the RMSE and MAE values of all models increase, which indicates that the accuracy of the prediction will gradually decrease with the increase of the forecast length, as well as our model. However, interestingly, it can be seen from Table 3 that our model still has the best predictive performance compared with the eight others models. Furthermore, RVFL obtains the second-best predictive accuracy in spring and autumn. EMD-DBN and RBFNN obtain the second-best predictive accuracy in summer and winter, respectively.

4.3 Model assessment

The experimental results of K-fold cross-validation are shown in Table 4. In the experiment, the fold number K was set to 8, and each fold was repeated 5 times. From Table 4, it can be seen that the difference between the validation-RMSE and the test-RMSE is small, which indicates the reliable convergence and stability of our model.

Table 4 The experimental results of K-fold cross-validation
Full size table

To compare the differences between the algorithms in Table 3, statistical analysis is conducted. Since 8-fold cross-validation is performed in each season, and each fold is repeated 5 times, the number of data sets \({n}_{ds}\) is 160. Furthermore, the number of learning algorithms \({n}_{l}\) is 9. By calculation, the Friedman test rejected the null hypothesis that all nine learning algorithms performed the same on average. Therefore, we applied the post hoc Nemenyi test at \(\alpha =0.1\) to test the difference between the algorithms. In this condition, the value of CD is 0.87. The Friedman diagram is shown in Fig. 7. In the Friedman diagram, if the two models have no overlapping area, it proves that there are obvious differences between the two models. Figure 7 shows that our model has obvious differences from other models, except EMD-BLS.

Fig. 7
figure 7

The results of the Friedman test (If the two models have no overlapping area, it proves that there are obvious differences between the two models)

Full size image

4.4 Effect of OEWT, master learner (ML), Residual Learner (RL), and Auxiliary Learner (AL)

To evaluate the effect of OEWT, ML, RL, and AL, we compared our model (OEWT-BLSTM-BLS) with EWT-BLSTM-BLS, BLSTM-BLS, OEWT-LSTM-BLS, and OEWT-BLSTM. All models are used to forecast the load data of the four seasons in single steps and multi-steps. The forecasting results and running time are shown in Table 5.

Table 5 Forecast errors of each model in single-step and multi-step prediction
Full size table
  1. 1)

    Effect of OEWT

To verify the effectiveness of OEWT, we first compared OEWT-BLSTM-BLS with BLSTM-BLS. The difference between OEWT-BLSTM-BLS and BLSTM-BLS is that the former contains OEWT, and the latter does not contain OEWT. From Table 5, the experimental results show that OEWT-BLSTM-BLS has better prediction performance than BLSTM-BLS. This indicates that the OEWT can effectively smooth nonlinear and non-stationary power load sequence signals to obtain competitive predictive performance.

To verify the performance of OEWT and EWT, we compared EWT-BLSTM-BLS with OEWT-BLSTM-BLS. The difference between EWT-BLSTM-BLS and OEWT-BLSTM-BLS is that the former only uses a single EWT, and the latter contains EWT and APEN. From Table 5, the experimental results show that OEWT-BLSTM-BLS has better prediction performance than EWT-BLSTM-BLS in most cases. Furthermore, OEWT-BLSTM-BLS has a significantly lower computation time than EWT-BLSTM-BLS. This indicates that OEWT not only guarantees the compromise in prediction accuracy but also significantly reduces the computational cost.

  1. 2)

    Effect of Master Learner and Residual Learner

To verify the performance of the master learner (BLSTM) and the residual learner (RL), we compare OEWT-BLSTM-BLS with OEWT-LSTM-BLS. The difference between OEWT-BLSTM-BLS and OEWT-LSTM-BLS is that the former has an additional residual learner BLS in BLSTM, and the latter does not contain this learner. From Table 5, the experimental results show that OEWT-BLSTM-BLS has better prediction performance than OEWT-LSTM-BLS. This indicates that by introducing the RL into LSTM, the master learner (BLSTM) has better performance than LSTM; the also indicates the RL can further improve the prediction accuracy by extracting the effective predictive information from residual results.

  1. 3)

    Effect of Auxiliary Learner

To verify the performance of the AL, we compared OEWT-BLSTM-BLS with OEWT-BLSTM. Here, the AL is BLS. The difference between OEWT-BLSTM-BLS and OEWT-BLSTM is that the former contains an AL, and the latter does not. From Table 5, the experimental results show that OEWT-BLSTM-BLS has better prediction performance than OEWT-BLSTM. This indicates that the AL can also further improve the prediction accuracy.

4.5 Discussion

The above experimental results indicate our model can not only effectively obtain better performance but also provide promising robustness on the STLF task. The reason behind this fact is that the proposed decomposition-based ensemble model rationally combines the OEWT, master learner, residual learner, and auxiliary learner. Specifically, (1) OEWT is developed to decompose the power load data into multiple sub-time series, which can effectively smooth nonlinear and non-stationary electric loads and eliminate redundant decomposition components that lead to an increase in computational cost. (2) the master learner integrates the advantages of LSTM and BLS, which can effectively compromise the computation cost and the prediction accuracy. (3) the residual learner is developed to learn the prediction residuals of LSTM, which can mine the effective prediction information hidden in the prediction residual to improve the prediction accuracy. (4) the auxiliary learner is established to rationally connect the input layer and output layer of our prediction block, further improving prediction accuracy and robustness.

5 Conclusions

The problem of parameter selection in WT or mode aliasing in EMD may result in the attenuation of decomposition accuracy. Although the EWT method can provide high decomposition accuracy, it easily produces redundant components, resulting in a large computational cost. Furthermore, the prediction residuals include effective prediction information. However, most existing models rarely consider how to use the prediction residual to establish a residual learning model. In addition, most existing hybrid machine learning methods rarely consider the compromise between prediction accuracy and computational cost. To overcome the above issues, this paper proposes a novel decomposition-based ensemble model including OEWT, master learner, residual learner, and auxiliary learner for STLF tasks. Experimental results show that the proposed model not only has high predictive accuracy and robustness but also low computational cost.

In the future, the proposed decomposition-based ensemble model plans to be applied to other predictive tasks such as wind speed, photovoltaics, 5G base station flow, and traffic flow.